Task and Configuration Space Compliance of
Continuum Robots via Lie Group and Modal Shape Formulations

Referring to Fig. 1, we define the arc length distance along the central backbone as $s\in[0,L]$, where $L$ is the total length of the central backbone. We also assume the central backbone has a high slenderness ratio consistent with the assumption of negligible shear strains, i.e. a Kirchhoff rod. The central backbone can therefore be described by the curvature distribution along the backbone in three directions, $\mathbf{u}(s)=[u_{x},u_{y},u_{z}]^{\mathrm{T}}\in\hbox{I \kern-5.0ptR}^{3}$. At a given arc length $s$, we assign a local body frame $\mathbf{T}(s)\in SE(3)$ with its z-axis tangent to the central backbone curve:

where ${}^{0}\mathbf{R}_{t}(s)$ and ${}^{0}\mathbf{p}(s)$ are the orientation¹¹1We use the notation ${}^{b}\mathbf{R}_{a}$ to denote the orientation of frame {A} with respect to frame {B}. Also, frame {A} has its origin denoted by $\mathbf{a}$. of the local body frame in the base frame {0} and the position of the origin of frame {T} in frame {0}. As the body frame traverses the central backbone curve, it undergoes a twist $\boldsymbol{\eta}(s)=[\mathbf{u}(s)^{\mathrm{T}},\mathbf{e}_{3}^{\mathrm{T}}]^{\mathrm{T}}\in\hbox{I \kern-5.0ptR}^{6}$, where $\mathbf{e}_{3}=[0,0,1]^{\mathrm{T}}$ denotes the local tangent unit vector. Furthermore, it satisfies the following differential equation [28]:

where $\left(\cdot\right)^{\prime}$ denotes the derivative with respect to $s$ and the hat operator $\left(\;\widehat{\cdot}\;\right)$ forms the standard matrix representations of $so(3)$ and $se(3)$ from the vector forms $\mathbf{u}$ and $\boldsymbol{\eta}$, respectively.

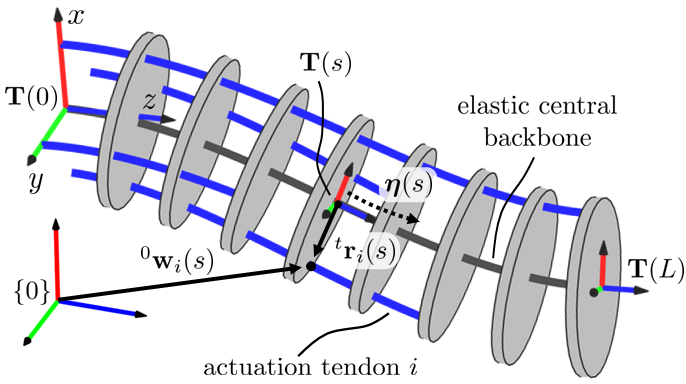
We now make a choice to express the curvature distribution $\mathbf{u}(s)$ as a weighted sum of polynomial functions. We denote the polynomial functions as $\boldsymbol{\phi}_{x}(s)$, $\boldsymbol{\phi}_{y}(s)$, and $\boldsymbol{\phi}_{z}(s)$ and the weights as $\mathbf{c}_{x}$, $\mathbf{c}_{y}$, and $\mathbf{c}_{z}$, for the $x$, $y$, and $z$ directions, respectively. The curvature $\mathbf{u}(s)$ is therefore:

where the columns of $\boldsymbol{\Phi}(s)\in\hbox{I \kern-5.0ptR}^{3\times{}m}$ form a modal shape basis, and $\mathbf{c}\in\hbox{I \kern-5.0ptR}^{m}$ is a vector of constant modal coefficients.

We choose the Chebyshev polynomials of the first kind for the modal functions since their roots are also the Chebyshev nodes, resulting in optimal approximation. They can be computed recursively:

where we shift the domain $x\in[-1,1]$ to $s\in[0,L]$ via the transformation $x(s)=(2s-L)/L$. The benefit of this modal shape approach to modeling the kinematics of continuum robots is that variable curvature shapes with any desired choice of fidelity can be modeled by a suitable choice of the modal shape basis order. We will show below how this approach bridges the gap between prior constant-curvature configuration-space compliance and Kirchhoff rod task-space compliance models.

For a given configuration $\mathbf{c}$, the body frame $\mathbf{T}(s)$ is found by integrating (2). As reviewed in [29], a variety of Lie group integration methods could be used for this, including an approach based on the Magnus expansion that we use here, following our result in [30]. After integrating (2), the spatial curve is given via a product of matrix exponentials:

where the particular form of $\mathbf{\Psi}_{i}$ depends on the choice of integration method [29, 30].

To model the kinematics of the tendon paths, we follow the approach used in [31]. Assuming $p$ tendons, the tendon path is expressed in the moving frame $\mathbf{T}(s)$ and is given by:

The position of a point along the tendon path is given in the world frame by:

Noting that vector norms are invariant under rotations, the length of the $i^{th}$ tendon is therefore given by:

where $s_{a_{i}}$ is the central backbone arc length at which the tendon is anchored to the spacer disk/end disk, and ${}^{t}\mathbf{w}^{\prime}_{i}(s)={{}^{0}\mathbf{R}}_{t}^{\mathrm{T}}{}^{0}\mathbf{w}^{\prime}_{i}(s)$ is found by taking the derivative of (7) with respect to $s$ and substituting (3), ${}^{0}\mathbf{p}^{\prime}(s)={{}^{0}\mathbf{R}}_{t}(s)\mathbf{e}_{3}$, and ${}^{0}\mathbf{R}^{\prime}_{t}(s)={{}^{0}\mathbf{R}}_{t}(s)\widehat{\mathbf{u}}(s)$:

Using the equations above, we also define two instantaneous kinematics Jacobians that will be used to formulate the configuration space and task space compliance matrices. Noting that the vector of modal coefficients $\mathbf{c}$ uniquely defines the configuration of the robot, we define the configuration space Jacobian as the Jacobian relating small changes in the tendon lengths to small changes in the modal coefficients:

For a given external wrench $\mathbf{w}_{h}$ on the tip of the segment and a perturbation $\delta\mathbf{x}_{h}$ in the end pose, we have a corresponding change in the forces applied to the actuation tendons $\boldsymbol{\tau}$ and a corresponding change in the bending energy stored in the segment, where the bending energy is given by (14). Following the principle of virtual work, we have:

where $\delta\boldsymbol{\ell}$ is a change in the tendon length. Referring to (11) and (10), we substitute (16) and $\delta E=\frac{\partial{}E}{\partial\mathbf{c}}^{\mathrm{T}}\delta\mathbf{c}$ to arrive at the statics of the segment about a given configuration:

We then take small perturbations of this statics expression:

where $\mathbf{C}_{\tau}$ and $\mathbf{C}_{w_{h}}$ are defined as:

The matrix $\mathbf{C}_{\tau}$ is the contribution to the compliance matrix of the forces on the tendons at the current configuration, and $\mathbf{C}_{w_{h}}$ is the contribution due to the external wrench. $\mathbf{C}_{\tau}$ can be readily affected by using actuation redundancy (internal preload) and $\mathbf{C}_{w_{h}}$ depends only on the external load. In a robot without actuation redundancy, $\boldsymbol{\tau}$ is determined by $\mathbf{w}_{h}$ through the statics equation. Therefore $\mathbf{C}_{\tau}$ and $\mathbf{C}_{w_{h}}$ are not completely independent. In a robot with actuation redundancy, these two matrices are independent.

By defining the joint-level stiffness $\mathbf{K}_{\ell}$ as a diagonal stiffness matrix containing the stiffness of individual actuation lines, i.e., $\mathbf{K}_{\ell}(i,i)=\frac{\delta\tau_{i}}{\delta\ell_{i}}$, we can use $\delta\boldsymbol{\tau}=\mathbf{K}_{\ell}\delta\boldsymbol{\ell}$ and $\delta\boldsymbol{\ell}=\mathbf{J}_{\ell c}\delta\mathbf{c}$ in (25), combine like terms, and solve for $\delta\mathbf{c}$:

We then substitute this expression into $\delta\mathbf{x}_{h}=\widetilde{\mathbf{J}}_{\xi c}\delta\mathbf{c}$ to arrive at the compliance matrix:

As a result of our analytic kinematic expressions, (29) bears resemblance to the results of prior works on stiffness modulation of rigid-link parallel robots, where one defines an active stiffness term dependent on the joint-level forces and the derivative of the Jacobian. and a passive stiffness term dependent on joint-level stiffness [35, 36, 37]. Compared to a rigid-link parallel robot stiffness matrix model, additional terms for tendon-actuated continuum robots include the Hessian of the bending energy and a term with the joint forces multiplied by the derivatives of the configuration-space Jacobian.

We now present the configuration space compliance matrix for a tendon-actuated continuum segment with variable curvature deflections. Our formulation can be seen as an extension of the compliance matrix in [6] to the case of variable curvature continuum robots. The resulting expression does not require computation of the task space Jacobian and its derivatives, and is therefore less computationally expensive. Furthermore, it does not require knowledge of the external wrench as required by the task-space compliance, so we believe it can be used for compliant motion control as done in [6], but for cases where large external loads produce variable curvature deflections.

Referring to (24), we first define the external wrench projected into the configuration space, denoted as $\mathbf{w}_{c}$:

Taking small perturbations of (30) results in

where $\mathbf{C}_{\tau}$ was given in (25). We now substitute $\delta\boldsymbol{\tau}=\mathbf{K}_{\ell}\mathbf{J}_{\ell c}\delta\mathbf{c}$, combine like terms, and solve for $\delta\mathbf{c}$:

Computing the change in the configuration for a small change in the projected wrench, i.e. $\delta\mathbf{c}=\mathbf{C}_{c}\delta\mathbf{w}_{c}$, results in the following configuration-space compliance matrix:

Note that (33) does not require that the task-space Jacobian and its derivatives be computed. It also does not require knowledge of the external wrench. It does, however, in the general case require knowledge of the actuation tendon forces. These forces can come either directly from force sensors placed in series with the actuation tendons [6, 12] or from estimates obtained via the commanded motor current. In special cases where $\mathbf{J}_{\ell c}$ constant, e.g. segments with constant pitch tendon routing and negligible torsional deflections as in Section V, $\mathbf{C}_{\tau}$ is zero and the actuation tendon forces do not need to be measured.

Both the configuration-space and task-space compliance matrices require the modal coefficients $\mathbf{c}$ to define the segment’s configuration. There are two ways to obtain $\mathbf{c}$. The first is using the shape sensing approach presented in [18]. This approach requires integration of shape-sensing hardware, but the benefit is that it does not require a potentially computationally expensive mechanics model.

The second way to obtain $\mathbf{c}$ is with a mechanics model like the ones presented in [30, 9]. After solving the mechanics model, $\mathbf{c}$ can be obtained by converting the collocation values into modal coefficients, as shown in [38]. Using a mechanics model to obtain $\mathbf{c}$ does not require shape-sensing, but does require an estimate of the external wrench applied to the segment, which may be known a-priori in some cases or can be measured using a load cell attached to the end effector.

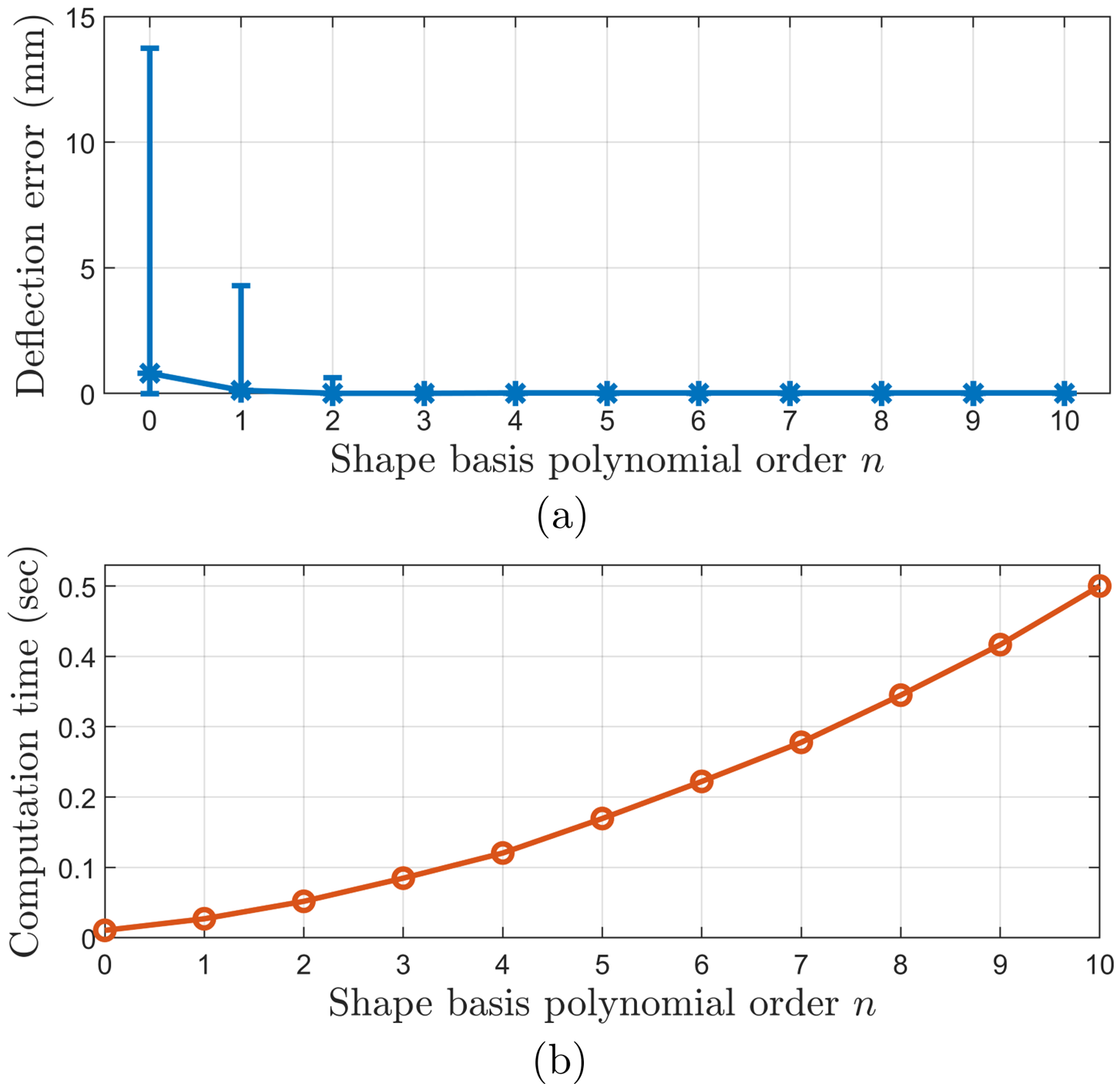
We first compare the deflections predicted by our compliance matrix in (21) to the deflections predicted by a Kirchhoff rod model, solved following the method in [38] which combined orthogonal collocation and Lie group integration. We considered a 2 mm diameter Nitinol rod with a length of 200 mm and combinations of $\pm$1 N tip forces and $\pm$0.5 Nm tip wrenches, generating a set of 2187 rod shapes. For each shape, we applied small steps of 0.1 N and 0.05 Nm to increment the applied force/moment (6 deflections for each shape) and recomputed the Kirchhoff rod model. We then used (21) to predict the deflection for each wrench increment. For (21), we used the same Chebyshev series for the $x$, $y$, and $z$ directions, but varied the order of the Chebyshev series from $n=0$ to $n=10$, i.e. when $n=0$, $\mathbf{\Phi}$ had three columns, and when $n=10$, $\mathbf{\Phi}$ had 33 columns. We used 10 integration steps when computing $\mathbf{T}(L)$ regardless of $n$. We then computed the tip translational deflection error:

where $\Delta\mathbf{p}_{gt}\in\hbox{I \kern-5.0ptR}^{3}$ is the deflection predicted by the Kirchhoff rod model and $\Delta\mathbf{p}_{m}\in\hbox{I \kern-5.0ptR}^{3}$ is the deflection from (21). The solvers were run using MATLAB 2021a on an Intel i7-11700 CPU.

The mean/max absolute deflection error results are shown in Table I and Fig. 2. We see that as $n$ is increased, the analytic expression rapidly converges to the simulated Kirchhoff rod deflection. We also observe that computation time increases with $n$, showing a tradeoff between the compliance matrix accuracy and computation cost.

The primary source of computational cost is in computing the derivatives of $\mathbf{J}_{\xi c}$. For $n=10$, estimating these derivatives accounts for approximately 95% of the computation time. We are currently using finite differences to estimate these derivatives, but we believe it is possible to derive these derivatives analytically and reduce computation cost. Methods from [29] to reduce the number of Lie brackets needed to calculate $\mathbf{J}_{\xi c}$ could also reduce computation cost.

A benefit of our formulation, in contrast to other approaches to computing the compliance matrix, is that it allows a trade-off between computation cost and accuracy to be made depending on the application need. A high-order model (large $n$) to be used when computing the statics model to accurately predict the spatial shape of the continuum robot, but use a lower-order model (small $n$) to compute the compliance matrix for online compliant motion control or predicting local deflections.

To reduce computation cost, one may ask whether it is possible to neglect the term that includes the derivatives of the task-space Jacobian and external wrench. While this term is typically negligible for stiff rigid-link robots [39], it was shown in [40] that this term is not negligible for robots with compliant actuators. Here we show a similar result for continuum robots, by computing (21) while neglecting this term using the same set of 2187 rod shapes and increments in wrench described above, and comparing again to the local deflections predicted by the Kirchhoff rod model. The mean absolute position and orientation errors are given in Table. II. We observe that while the speed of computing (21) increases significantly, the maximum position and orientation errors are high when neglecting this term. We also observe that increasing the number of modal coefficients does not significantly improve the modeling error when neglecting the task space Jacobian derivatives.

In this section, we describe the experimental validation of our method on a tendon-actuated continuum segment, shown in Fig. 3. The continuum segment central backbone is 300.6 mm in length and the kinematic radius of the actuation tendons is 65.2 mm. Two actuators are integrated into the base, which drive the actuation tendons that bend the segment. In the end-disk are four string encoders that measure the deflections of the segment to estimate $\mathbf{c}$. In [18], it was shown that this shape sensing approach, which is purely kinematic and does not require a mechanics model, can estimate the end disk position to within 5% of total arc length, or 14.4 mm of position error.

Metal bellows in the segment’s flexible backbone structure make it approximately 1950 times stiffer in torsion that in bending, so we neglect the torsional deflections and use the following modal shape basis:

where $\boldsymbol{\phi}_{x}^{\mathrm{T}}(s)=\boldsymbol{\phi}_{y}^{\mathrm{T}}=\begin{bmatrix}T_{0}&T_{1}&T_{2}\end{bmatrix}^{\mathrm{T}}$. With this choice of $\mathbf{\Phi}$ and since the strings and actuaton tendons are routed in constant-pitch radius paths, $\mathbf{J}_{\ell c}$ is constant, and $\mathbf{C}_{\tau}=\mathbf{0}$.

The experimental setup used to validate the compliance matrix model is shown in Fig. 3. In order to experimentally validate our approach, we attached a force/torque sensor (Bota Systems Rokubi™) to the end effector of the segment. The segment was actuated to five different joint space configurations in the segment’s workspace. The angles of the first and second actuators, denoted as $\theta_{1}$ and $\theta_{2}$, respectively, are given in Table III. At each configuration, the unloaded configuration of the segment was measured using the string encoders. A mass was then attached to the force/torque sensor via a wire-rope hung over a pulley. The segment’s new deflected configuration and the applied wrench was then measured. This was repeated for each configuration using 10 different combinations of wire rope direction and masses ranging from 2 lbs to 10 lbs, resulting in a total of 50 measured deflections.

Across the 50 deflections, the mean and maximum deflection was 14.3 mm and 66.7 mm, respectively. The first 10 deflections used for the first joint-space configuration were used to calibrate the model parameters $EI_{x}=EI_{y}$ and $k_{1}=k_{2}$. We did this by solving for the values of these parameters that minimized the least-squared error between the model predicted deflection and the experimentally measured deflection, solved with lsqnonlin() in MATLAB. The resulting calibrated values were $EI_{x}=EI_{y}=3.20$ Nm² and $k_{1}=k_{2}=1.23\text{e}5$ N/m.

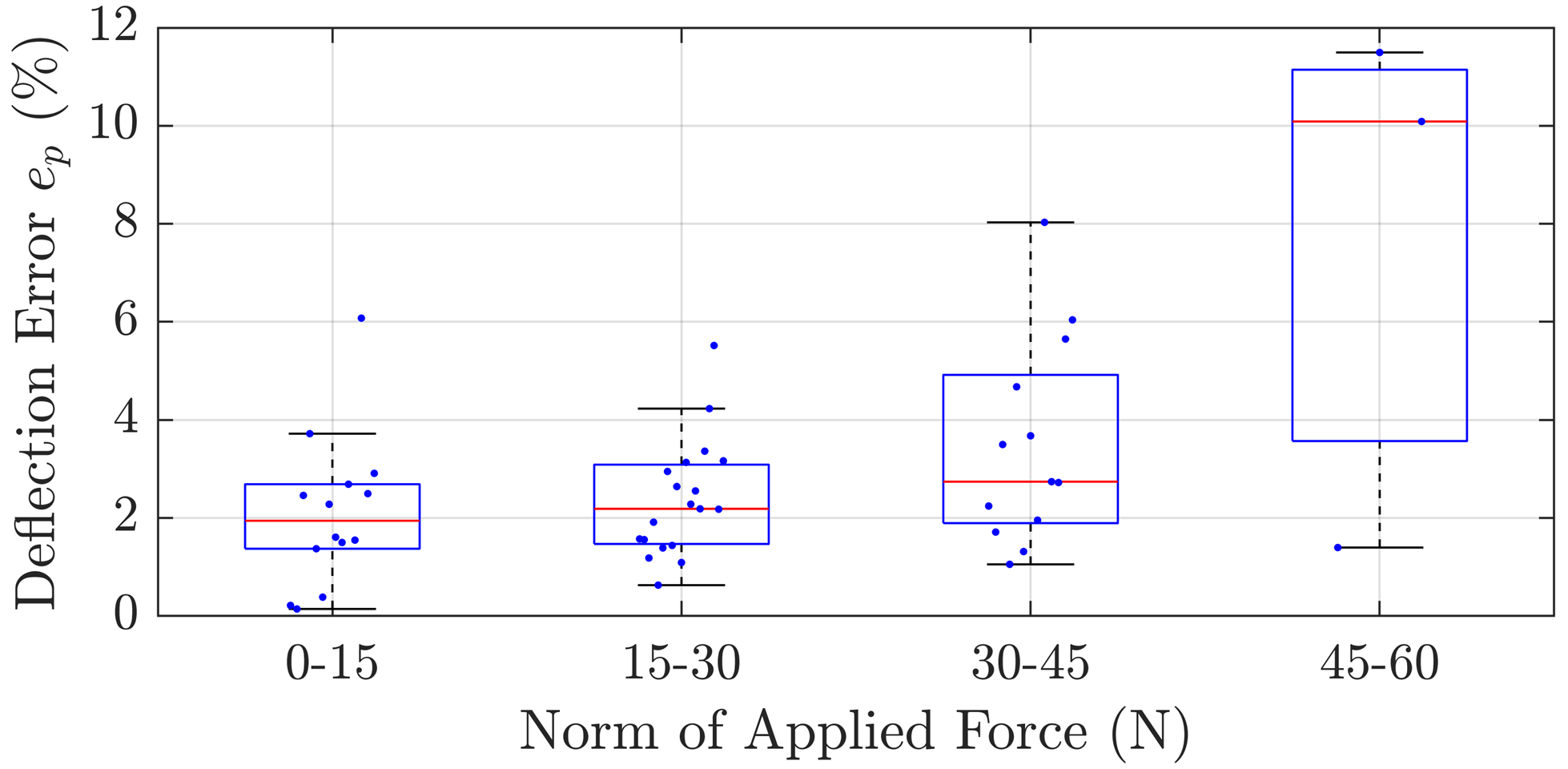
The remaining 40 deflections were used to validate the model. Comparing the measured and model-predicted deflections, the mean and max absolute error $e_{p}$ from 34 was 9.1 mm and 34.6 mm, respectively, or 3.0% and 11.5% of the backbone length. Since the compliance matrix is only a local estimate of the deflection behavior, it is expected that larger deflections result in larger error in the predicted deflection. Figure 4 shows predicted deflection error for different norms of applied force. We observe that, as expected, predicted deflection error tends to increase as the applied force increases.