Technical Report # KU-EC-08-5:
QR-Adjustment for Clustering Tests Based on Nearest Neighbor Contingency Tables
Abstract
The spatial interaction between two or more classes of points may cause spatial clustering patterns such as segregation or association, which can be tested using a nearest neighbor contingency table (NNCT). A NNCT is constructed using the frequencies of class types of points in nearest neighbor (NN) pairs. For tests based on NNCTs (i.e., NNCT-tests), the null pattern is either complete spatial randomness (CSR) of the points from two or more classes (called CSR independence) or random labeling (RL). The RL pattern implies that the locations of the points in the study region are fixed, while the CSR independence pattern implies that they are random. The distributions of the NNCT-test statistics depend on the number of reflexive NNs (denoted by ) and the number of shared NNs (denoted by ), both of which depend on the allocation of the points. Hence and are fixed quantities under RL, but random variables under CSR independence. However given the difficulty in calculating the expected values of and under CSR independence, one can use their observed values in NNCT analysis, which makes the distributions of the NNCT-test statistics conditional on and under CSR independence. In this article, I use the empirically estimated expected values of and under CSR independence pattern to remove the conditioning of NNCT-tests (such a correction is called the QR-adjustment, henceforth). I present a Monte Carlo simulation study to compare the conditional NNCT-tests (i.e., tests with the observed values of and are used) and unconditional NNCT-tests (i.e., empirically QR-adjusted tests) under CSR independence and segregation and association alternatives. I demonstrate that QR-adjustment does not significantly improve the empirical size estimates under CSR independence and power estimates under segregation or association alternatives. For illustrative purposes, I apply the conditional and empirically corrected tests on two example data sets.
Keywords: Association; complete spatial randomness; conditional test; nearest neighbor contingency table; random labeling; spatial clustering; spatial pattern; segregation
∗corresponding author.
e-mail: elceyhan@ku.edu.tr (E. Ceyhan)
1 Introduction
Spatial patterns have been studied extensively and have important implications in many fields such as epidemiology, population biology, and ecology. It is of practical interest to study the univariate spatial patterns (i.e., patterns of only one class) as well as multivariate patterns (i.e., patterns of multiple classes) (Pielou, (1961), Whipple, (1980), and Dixon, (1994, 2002)). For convenience and generality, I call the different types of points as “classes”, but a class label can stand for any characteristic of a measurement at a particular location. For example, the spatial segregation pattern has been investigated for species (Diggle, (2003)), age classes of plants (Hamill and Wright, (1986)), fish species (Herler and Patzner, (2005)), and sexes of dioecious plants (Nanami et al., (1999)). Many of the epidemiological applications are for a two-class system of case and control labels (Waller and Gotway, (2004)).
In this article, for simplicity, I describe the spatial point patterns for two classes only; the extension to multi-class case is straightforward. The null pattern is usually one of the two (random) pattern types: complete spatial randomness (CSR) of two or more classes or random labeling (RL) of a set of fixed points with two classes. That is, when the points from each class are assumed to be uniformly distributed over the region of interest, the the null hypothesis is the CSR of points from two classes. This type of CSR pattern is also referred to as “population independence” in literature (Goreaud and Pélissier, (2003)). In the univariate spatial analysis, CSR refers to the pattern in which locations of points from a single class are random over the study area. To distinguish the CSR of points from two-classes and CSR of points from one class, I call the former as “CSR independence” and the latter as “CSR”, henceforth. Note that CSR independence is equivalent to the case that RL procedure is applied to a given set of points from a CSR pattern in the sense that after points are generated uniformly in the region, the class labels are assigned randomly. When only the labeling of a set of fixed points (the allocation of the points could be regular, aggregated, or clustered, or of lattice type) is random, the null hypothesis is the RL pattern.
Many tests of spatial segregation have been developed in literature (Orton, (1982)). These include comparison of Ripley’s or functions (Ripley, (2004)), comparison of nearest neighbor (NN) distances (Diggle, (2003), Cuzick and Edwards, (1990)), and analysis of nearest neighbor contingency tables (Pielou, (1961), Meagher and Burdick, (1980)). Nearest neighbor contingency tables (NNCTs) are constructed using the frequencies of classes of points in NN pairs. Kulldorff, (2006) provides an extensive review of tests of spatial randomness that adjust for an inhomogeneity of the densities of the underlying populations. Pielou, (1961) proposed various tests and (Dixon, (1994)) introduced an overall test of segregation, cell-, and class-specific tests based on NNCTs for the two-class case and extended his tests to multi-class case (Dixon, (2002)). These tests based on NNCTs (i.e., NNCT-tests) were designed for testing the RL of points. Pielou, (1961) used the usual Pearson’s -test of independence for detecting the segregation of the two classes. Due to the ease in computation and interpretation, Pielou’s test of segregation is frequently used for both CSR independence and RL patterns. However it has been shown that Pielou’s test is not appropriate for testing RL (Meagher and Burdick, (1980), Dixon, (1994)). Dixon, (1994) derived the appropriate (asymptotic) sampling distribution of cell counts using Moran join count statistics (Moran, (1948)) and hence the appropriate test which also has a -distribution (Dixon, (1994)). For the two-class case, Ceyhan, (2006) compared these tests, extended the tests for testing CSR independence, and demonstrated that Pielou’s tests are only appropriate for a random sample of (base, NN) pairs. Furthermore, Ceyhan, (2007) proposed three new overall segregation tests. Since Pielou’s test is not appropriate, NNCT-tests only refer to Dixon’s overall test and the three new segregation tests proposed by Ceyhan, (2007). However the distributions of the NNCT-test statistics depend on the number of reflexive NNs (denoted by ) and the number of shared NNs (denoted by ), both of which depend on the allocation of the points. Hence and are fixed under RL, but random under CSR independence. But expectations of and seem to be not available analytically under the CSR independence, so their observed values were used by Ceyhan, (2007). In this article, I replace the expectations of and by their empirical estimates under CSR independence. Such a correction for removing the conditional nature of NNCT-tests is called “QR-adjustment”, henceforth.
The NNCT-tests are designed for testing a more general null hypothesis, namely, randomness in the NN structure, which usually results from CSR independence or RL. The distinction between CSR independence and RL is very important when defining the appropriate null model for each empirical case, i.e., the null model depends on the particular context. Goreaud and Pélissier, (2003) discuss the differences between these two null hypotheses and demonstrate that the misinterpretation is very common. They assert that under CSR independence the (locations of the points from) two classes are a priori the result of different processes (e.g., individuals of different species or age cohorts), whereas under RL some processes affect a posteriori the individuals of a single population (e.g., diseased versus non-diseased individuals of a single species). Notice that although CSR independence and RL are not same, they lead to the same null model (i.e., randomness in NN structure) for NNCT-tests, since a NNCT does not require spatially-explicit information.
I consider two major types of (bivariate) spatial clustering patterns, namely, association and segregation as alternative patterns. Association occurs if the NN of an individual is more likely to be from another class. Segregation occurs if the NN of an individual is more likely to be of the same class as the individual; i.e., the members of the same class tend to be clumped or clustered (see, e.g., Pielou, (1961)). For more detail on these alternative patterns, see (Ceyhan, (2007)). I assess the effects of QR-adjustment on the size of the NNCT-tests under CSR independence and on the power of the tests under the segregation or association alternatives by an extensive Monte Carlo study.
Throughout the article I adopt the convention that random quantities are denoted by capital letters, while fixed quantities are denoted by lower case letters. I describe the construction of NNCTs in Section 2.1, provide Dixon’s tests in Sections 2.2 and 2.4, empirical significance levels of the tests in Section 3, two illustrative examples in Section 5, and discussion and conclusions in Section 6.
2 Nearest Neighbor Contingency Tables and Related Tests
2.1 Construction of the Nearest Neighbor Contingency Tables
NNCTs are constructed using the NN frequencies of classes. I describe the construction of NNCTs for two classes; extension to multi-class case is straightforward. Consider two classes with labels . Let be the number of points from class for and be the total sample size, so . If I record the class of each point and the class of its NN, the NN relationships fall into four distinct categories: where in cell , class is the base class, while class is the class of its NN. That is, the points constitute (base, NN) pairs. Then each pair can be categorized with respect to the base label (row categories) and NN label (column categories). Denoting as the frequency of cell for , I obtain the NNCT in Table 1 where is the sum of column ; i.e., number of times class points serve as NNs for . Furthermore, is the cell count for cell that is the sum of all (base, NN) pairs each of which has label . Note also that ; ; and . By construction, if is larger (smaller) than expected, then class serves as NN more (less) to class than expected, which implies (lack of) segregation if and (lack of) association of class with class if . Hence, column sums, cell counts are random, while row sums and the overall sum are fixed quantities in a NNCT.
| NN class | ||||
|---|---|---|---|---|
| class 1 | class 2 | sum | ||
| class 1 | ||||
| base class | class 2 | |||
| sum | ||||
Observe that, under segregation, the diagonal entries, for , tend to be larger than expected; under association, the off-diagonals tend to be larger than expected. The general alternative is that some cell counts are different than expected under CSR independence or RL.
In the two-class case, Pielou, (1961) used Pearson’s -test of independence to detect any deviation from CSR independence or RL. But, under CSR independence or RL, this test is liberal, i.e., has larger size than the nominal level (Ceyhan, (2006)), hence not considered in this article. Dixon, (1994) proposed a series of tests for segregation based on NNCTs. He first devised four cell-specific tests in the two-class case, and then combined them to form an overall test. For his tests, the probability of an individual from class serving as a NN of an individual from class depends only on the class sizes (i.e., row sums), but not the total number of times class serves as NNs (i.e., column sums).
2.2 Dixon’s Cell-Specific Tests
The level of segregation is estimated by comparing the observed cell counts to the expected cell counts under RL of points that are fixed. Dixon demonstrates that under RL, one can write down the cell frequencies as Moran join count statistics (Moran, (1948)). He then derives the means, variances, and covariances of the cell counts (frequencies) in a NNCT (Dixon, (1994, 2002)).
The null hypothesis under RL is given by
| (1) |
Observe that the expected cell counts depend only on the size of each class (i.e., row sums), but not on column sums.
The cell-specific test statistics suggested by Dixon are given by
| (2) |
where
| (3) |
with , , and are the probabilities that a randomly picked pair, triplet, or quartet of points, respectively, are the indicated classes and are given by
| (4) | ||||||
Furthermore, is the number of points with shared NNs, which occur when two or more points share a NN and is twice the number of reflexive pairs. Then where is the number of points that serve as a NN to other points times. One-sided and two-sided tests are possible for each cell using the asymptotic normal approximation of given in Equation (2) (Dixon, (1994)). The test in Equation (2) is the same as Dixon’s when ; same as when (Dixon, (1994)). Note also that in Equation (2) four different tests are defined as there are four cells and each is testing the deviation from the null case in the respective cell. These four tests are combined and used in defining an overall test of segregation in Section 2.4.
Under CSR independence, the null hypothesis, the test statistics, and the variances are as in the RL case for the cell-specific tests, except for the fact that the variances are conditional on and .
2.3 The Status of and under CSR Independence and RL
Note the difference in status of the variables and under CSR independence and RL models. Under RL, and are fixed quantities; while under CSR independence, they are random. The quantities given in Equations (1), (3), and all the quantities depending on these expectations also depend on and . Hence these expressions are appropriate under the RL pattern. Under CSR independence pattern they are conditional variances and covariances obtained by using the observed values of and . The unconditional variances and covariances can be obtained by replacing and with their expectations.
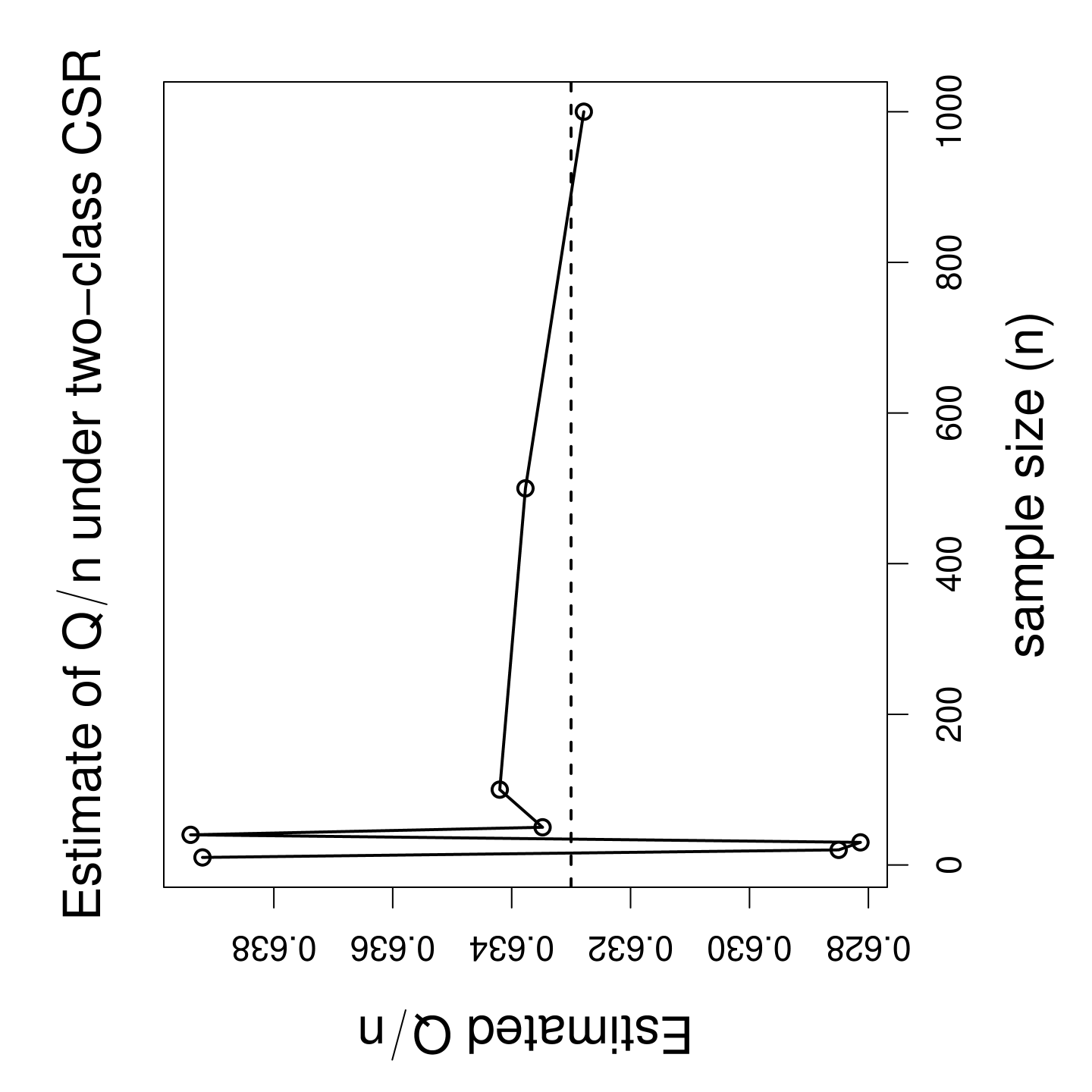
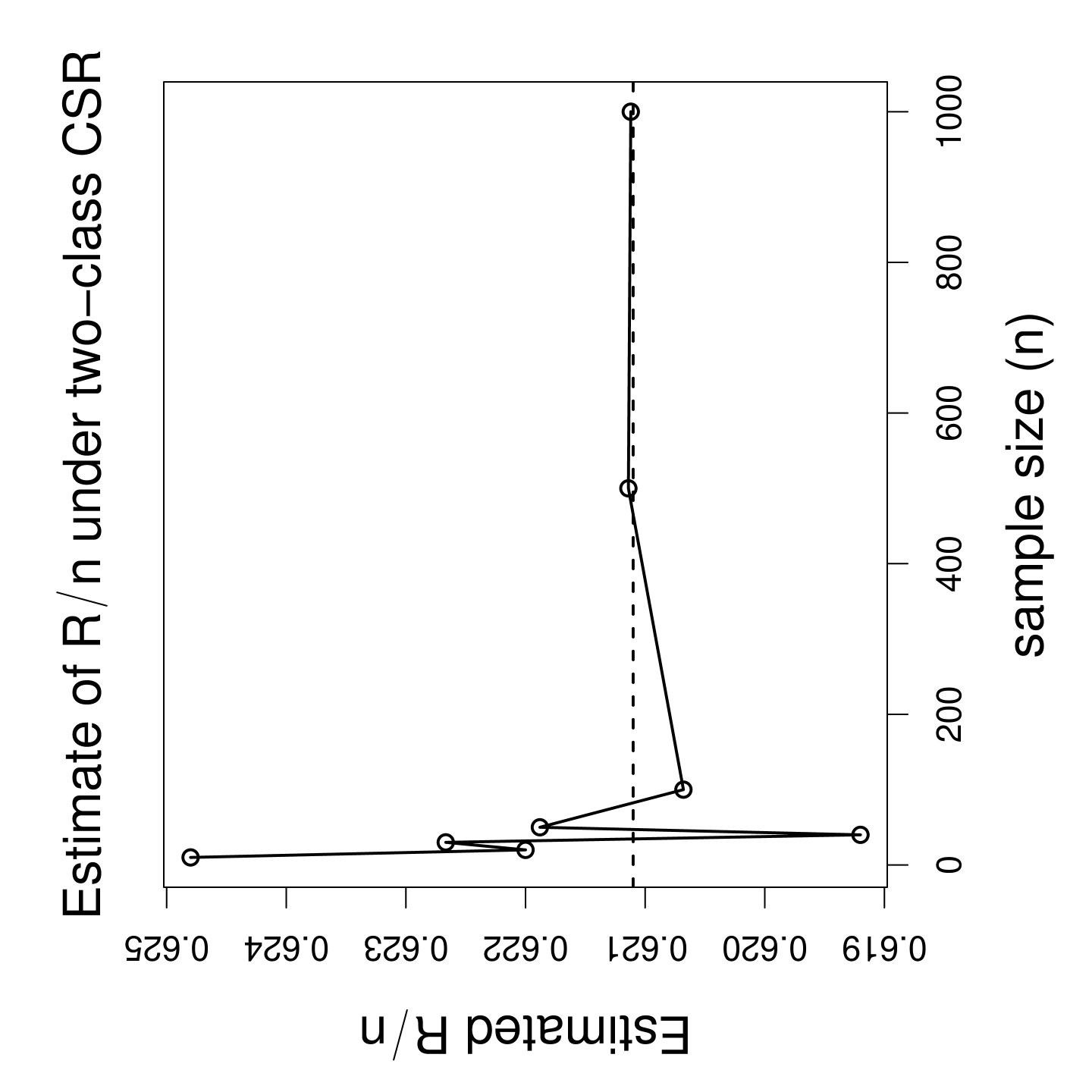
Unfortunately, given the difficulty of calculating the expectations of and under CSR independence, Ceyhan, (2007) employed the conditional variances and covariances (i.e., the variances and covariances for which observed and values are used) even when assessing their behavior under CSR independence pattern. Alternatively, I can estimate the values of and empirically as follows. I generate points that are iid (independently and identically distributed) from , the uniform distribution on the unit square. I repeat this procedure times. At each Monte Carlo replication, I calculate and values, and record the ratios and . I plot these ratios in Figure 1 as a function of sample size . Observe that the ratios seem to converge as increases. For homogeneous planar Poisson pattern, I have and . Hence, I replace and by and , respectively, to obtain the QR-adjusted variances and covariances.
2.4 Dixon’s Overall Segregation Test
Dixon’s overall test of segregation tests the hypothesis that expected cell counts in the NNCT are as in Equation (1). In the two-class case, he calculates for both and combines these test statistics into a statistic that is asymptotically distributed as under RL (Dixon, (1994)). The suggested test statistic is given by
| (5) |
where are as in Equation (1), are as in Equation (3), and
| (6) |
Dixon’s statistic given in Equation (5) can also be written as
where (Dixon, (1994)).
Under CSR independence, the expected values, variances and covariances are as in the RL case. However, the variance and covariance terms include and which are random under CSR independence and fixed under RL. Hence Dixon’s test statistic asymptotically has a -distribution under CSR independence conditional on and . Replacing and by their empirical estimates given in Section 2.3, I obtain the QR-adjusted version of Dixon’s test which is denoted by .
2.5 Version I of the New Segregation Tests
Ceyhan, (2007) proposed tests based on the correct sampling distribution of the cell counts in a NNCT under CSR independence or RL. In defining the new segregation or clustering tests, I follow a track similar to that of Dixon’s (Dixon, (1994)) where he defines a cell-specific test statistic for each cell and then combines these four tests into an overall test.
For cell , let
| (7) |
Furthermore, let be the vector of values concatenated row-wise and let be the variance-covariance matrix of based on the correct sampling distribution of the cell counts. That is, where
with is as in Equation (3) if and as in Equation (6) if and . Since is not invertible, I use its generalized inverse which is denoted by (Searle, (2006)). Then the first version of segregation tests suggested by Ceyhan, (2007) is
| (8) |
which asymptotically has a distribution.
Under CSR independence, the expected values, variances, and covariances related to are as in the RL case, except they are not only conditional on column sums (i.e., on ), but also conditional on and . Hence has asymptotically distribution conditional on column sums, and under CSR independence. Replacing and by their empirical estimates given in Section 2.3, I obtain the QR-adjusted version of this test which is denoted by , which is still conditional on column sums.
2.6 Version II of the New Segregation Tests
For cell , let
| (9) |
Furthermore, let be the vector of concatenated row-wise and let be the variance-covariance matrix of based on the correct sampling distribution of the cell counts. That is, where
Since is not invertible, I use its generalized inverse . Then second version of the tests proposed by Ceyhan, (2007) is
| (10) |
which asymptotically has a distribution under RL. Note that can be obtained from used in Equation (5) by multiplying entry-wise with the matrix . This version of the segregation test is asymptotically equivalent to Dixon’s segregation test.
Under CSR independence, the expectations, variances, and covariances related to are as in the RL case, but the variances and covariances are conditional on and . Hence, the asymptotic distribution of is also conditional on and . Replacing and with their empirical estimates, I obtain the QR-adjusted version of this test which is denoted by and is not conditional any more.
2.7 Version III of the New Segregation Tests
Notice that version I is a conditional test (conditional on column sums), while version II is asymptotically equivalent to Dixon’s test, Furthermore, both Dixon’s test and version II incorporate only row sums (i.e., class sizes) in the NNCTs.
Ceyhan, (2007) suggests another test statistic which uses both the column sums (i.e., number of times a class serves as NN) and row sums and is not conditional on the column sums. Let
| (11) |
Let be the vector of values concatenated row-wise and let be the variance-covariance matrix of based on the correct sampling distribution of the cell counts. That is, where the explicit forms of are provided in (Ceyhan, (2007)). Since is not invertible, I use its generalized inverse . Then the proposed test statistic by (Ceyhan, (2007)) for overall segregation is the quadratic form which asymptotically has a distribution.
Under CSR independence, the discussion related to and derivation of are as in the RL case; however, the variance and covariance terms (hence the asymptotic distribution) are conditional on and . Replacing and with their empirical estimates, I obtain the QR-adjusted version of this test which is denoted by .
Remark 2.1.
Extension to Multi-Class Case: So far, I have described the segregation tests for the two class case in which the corresponding NNCT is of dimension . The cell counts for the diagonal cells have asymptotic normality. For the off-diagonal cells, although the asymptotic normality is supported by Monte Carlo simulation results (Dixon, (2002)), it is not rigorously proven yet. Nevertheless, if the asymptotic normality held for all cell counts in the NNCT, under RL, Dixon’s test and version II would have distribution, versions I and III would have distribution asymptotically. Under CSR independence, these tests will have the corresponding asymptotic distributions conditional on and . The QR-adjusted versions can be obtained by replacing and with their empirical estimates.
3 Empirical Significance Levels of NNCT-Tests under the CSR Independence
For the null case, CSR independence, I simulate the CSR case only with classes 1 and 2 (i.e., and ) of sizes and , respectively. At each of replicates, I generate data for some sample size combinations of points iid from . These sample size combinations are chosen so that one can examine the influence of small and large samples, and the relative abundance of the classes on the tests. The corresponding test statistics are recorded at each Monte Carlo replication for each sample size combination. Then I record how many times the -value is at or below for each test to estimate the empirical size. I present the empirical sizes for NNCT-tests in Table 2, where is the empirical significance level for Dixon’s test, and are for versions I, II, and III, respectively, and , and are for the corresponding QR-adjusted versions. The empirical sizes significantly smaller (larger) than .05 are marked with c (ℓ), which indicate that the corresponding test is conservative (liberal). The asymptotic normal approximation to proportions is used in determining the significance of the deviations of the empirical size estimates from the nominal level of .05. For these proportion tests, I also use to test against empirical size being equal to .05. With , empirical sizes less (greater) than .0464 (.0536) are deemed conservative (liberal) at level.
Observe that the (unadjusted) NNCT-tests are about the desired level (or size) when and are both , and mostly conservative otherwise. The same trend holds for the QR-adjusted versions. Furthermore, comparing the empirical sizes of QR-adjusted versions with those of unadjusted ones, I see that for almost all cases they are not significantly different (at based on tests on equality of the proportions).
| Empirical significance levels of the NNCT-tests | ||||||||
| conditional (i.e., unadjusted) | unconditional (i.e., QR-adjusted) | |||||||
| (10,10) | .0432c | .0593ℓ | .0461c | .0439c | .0470 | .0595ℓ | .0486 | .0365c,< |
| (10,30) | .0440c | .0451c | .0421c | .0410c | .0411c | .0465 | .0381c | .0461c,> |
| (10,50) | .0482 | .0335c | .0423c | .0397c | .0497 | .0345c | .0411c | .0431c |
| (30,10) | .0390c | .0411c | .0383c | .0391c | .0402c | .0423c | .0379c | .0436c |
| (30,30) | .0464 | .0544ℓ | .0476 | .0427c | .0492 | .0552ℓ | .0478 | .0409c |
| (30,50) | .0454c | .0507 | .0481 | .0504 | .0411c | .0517 | .0464 | .0515 |
| (50,10) | .0529 | .0326c | .0468 | .0379c | .0510 | .0334c | .0428c | .0402c |
| (50,30) | .0429c | .0494 | .0468 | .0469 | .0405c | .0518 | .0466 | .0492 |
| (50,50) | .0508 | .0494 | .0497 | .0499 | .0528 | .0494 | .0524 | .0488 |
| (50,100) | .0560ℓ | .0501 | .0564ℓ | .0516 | .0556ℓ | .0493 | .0573 | .0494 |
| (100,50) | .0483 | .0463c | .0492 | .0479 | .0495 | .0457 | .0501 | .0460 |
| (100,100) | .0504 | .0524 | .0519 | .0489 | .0513 | .0524 | .0523 | .0463c |
4 Empirical Power Analysis
To evaluate the power performance of the QR-adjusted and unadjusted NNCT-tests, I only consider alternatives against the CSR pattern. That is, the points are generated in such a way that they are from an inhomogeneous Poisson process in a region of interest (unit square in the simulations) for at least one class. Furthermore, the tests considered in this article seem to have the desired nominal level for large samples under CSR, and QR-adjustment is not necessary under the RL pattern. Hence I avoid the alternatives against the RL pattern; i.e., I do not consider non-random labeling of a fixed set of points that would result in segregation or association.
4.1 Empirical Power Analysis under Segregation Alternatives
For the segregation alternatives (against the CSR pattern), three cases are considered. I generate for and for . In the pattern generated, appropriate choices of will imply and to be more segregated than expected under CSR. That is, it will be more likely to have NN pairs than mixed NN pairs (i.e., or pairs). The three values of I consider constitute the three segregation alternatives:
| (12) |
Observe that, from to (i.e., as increases), the segregation gets stronger in the sense that and points tend to form one-class clumps or clusters. By construction, the points are uniformly generated, hence exhibit homogeneity with respect to their supports for each class, but with respect to the unit square these alternative patterns are examples of departures from first-order homogeneity which implies segregation of the classes and . The simulated segregation patterns are symmetric in the sense that, and classes are equally segregated (or clustered) from each other.



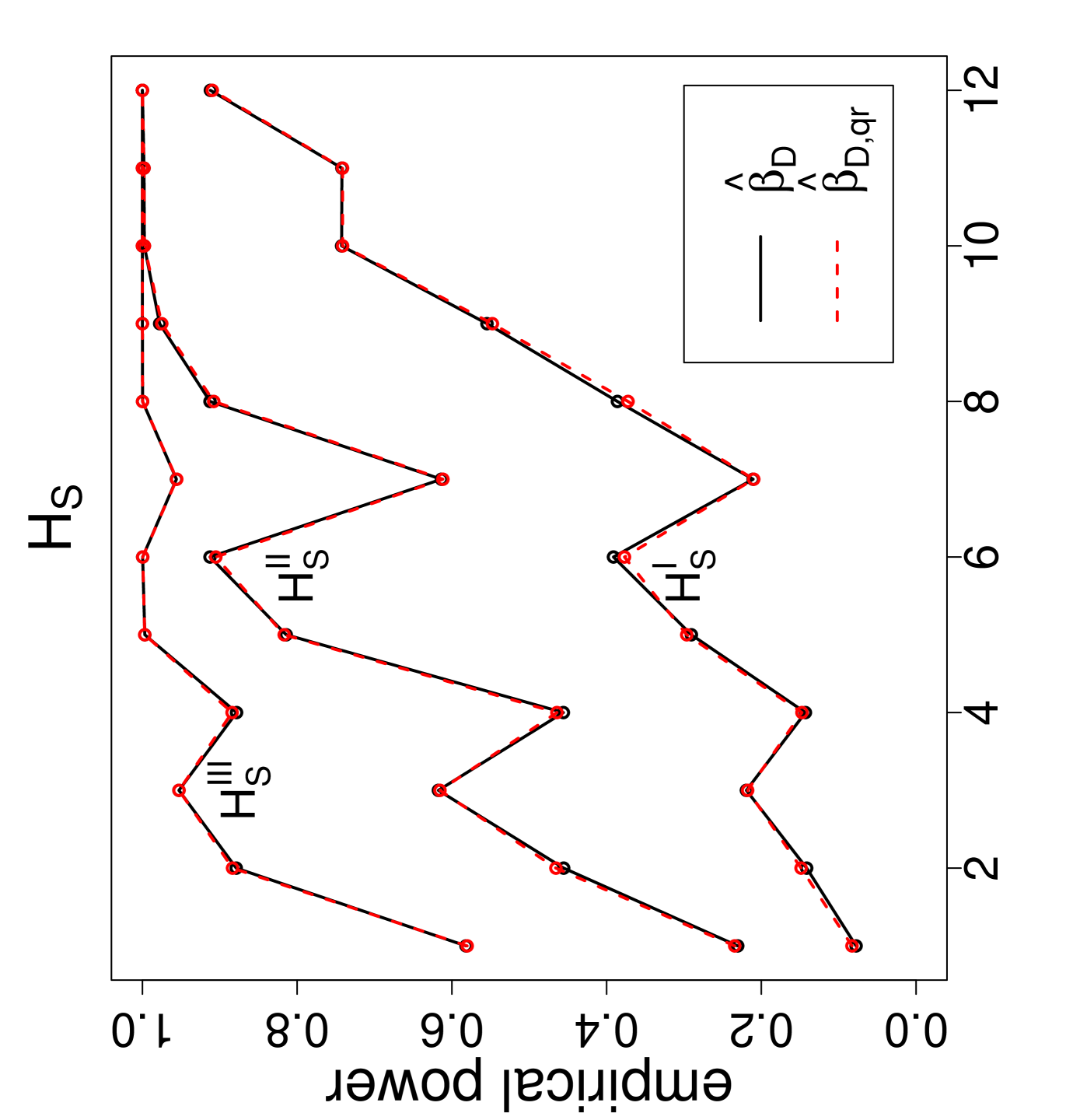
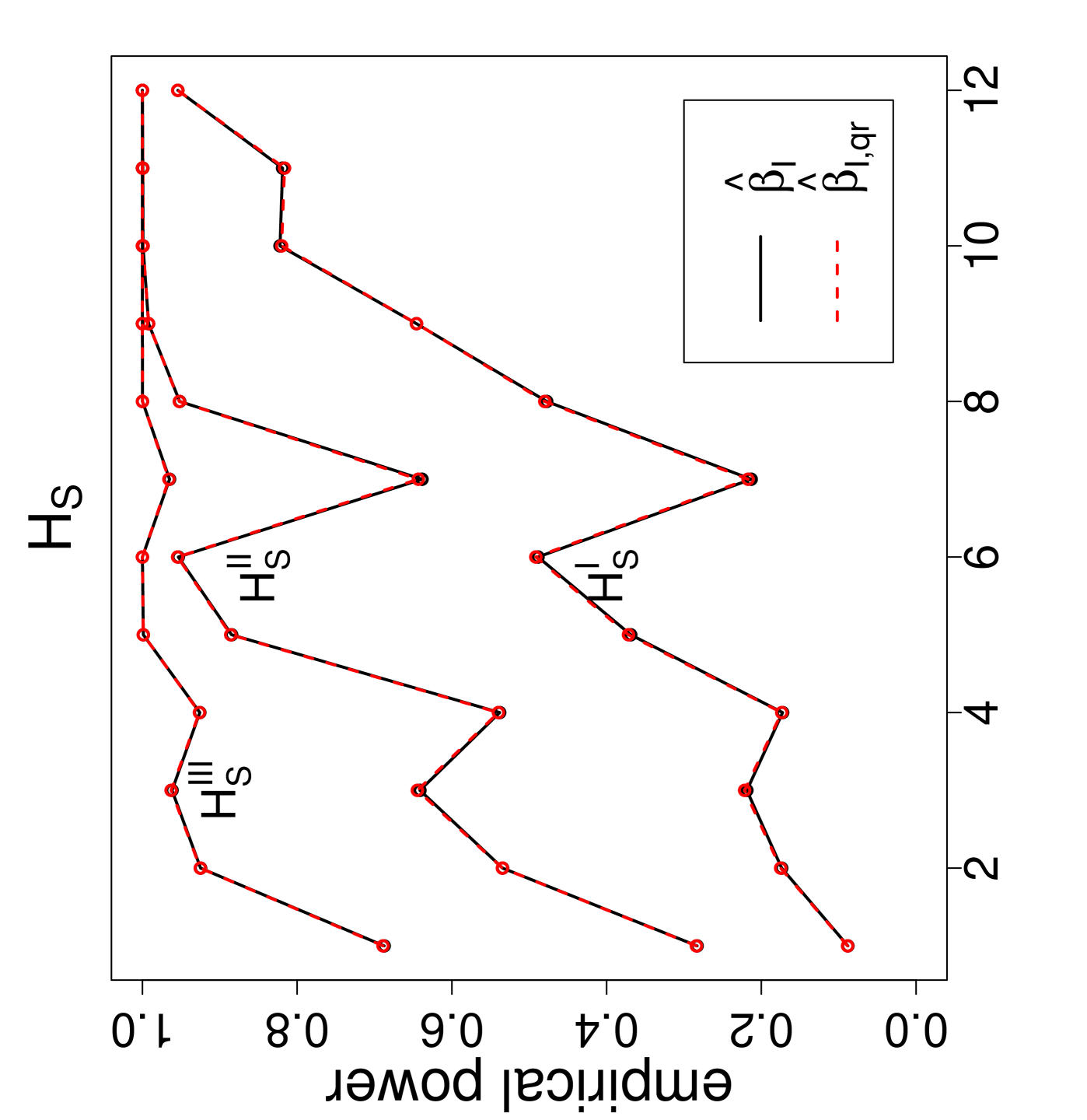
The power estimates against the sample size combinations are presented in Figure 3, where is for Dixon’s test, , , and are for versions I, II , and III, respectively, and the QR-adjusted versions are indicated by in their subscripts. Observe that, as gets larger, the power estimates get larger. For the same values, the power estimate is larger for classes with similar sample sizes. Furthermore, as the segregation gets stronger, the power estimates get larger. The NNCT-tests have about the same power performance under these segregation alternatives. Notice also that for small samples the power estimates of the QR-adjusted versions are slightly larger but for other sample size combinations the power estimates for the QR-adjusted versions and the unadjusted versions are virtually indistinguishable.
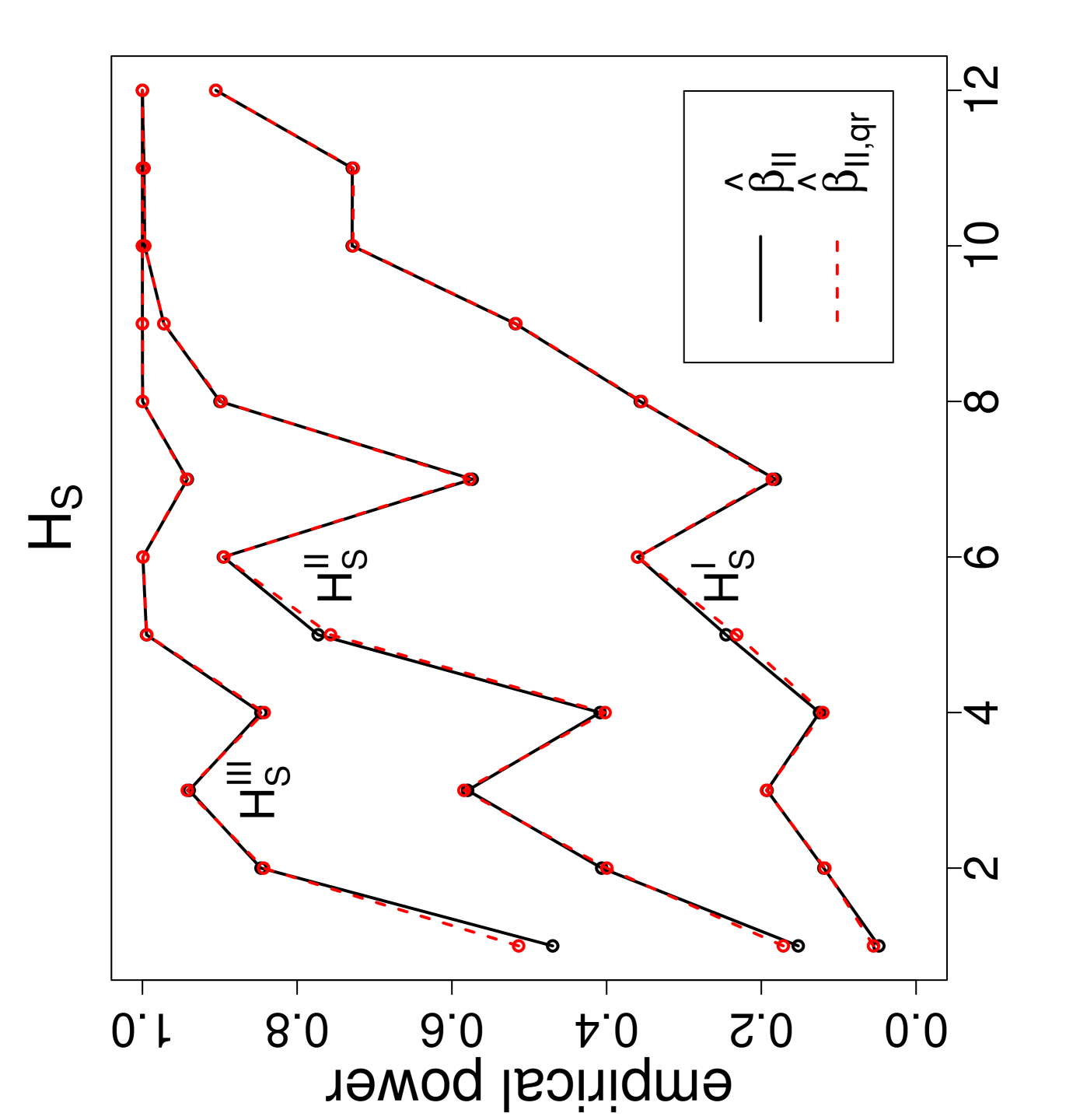
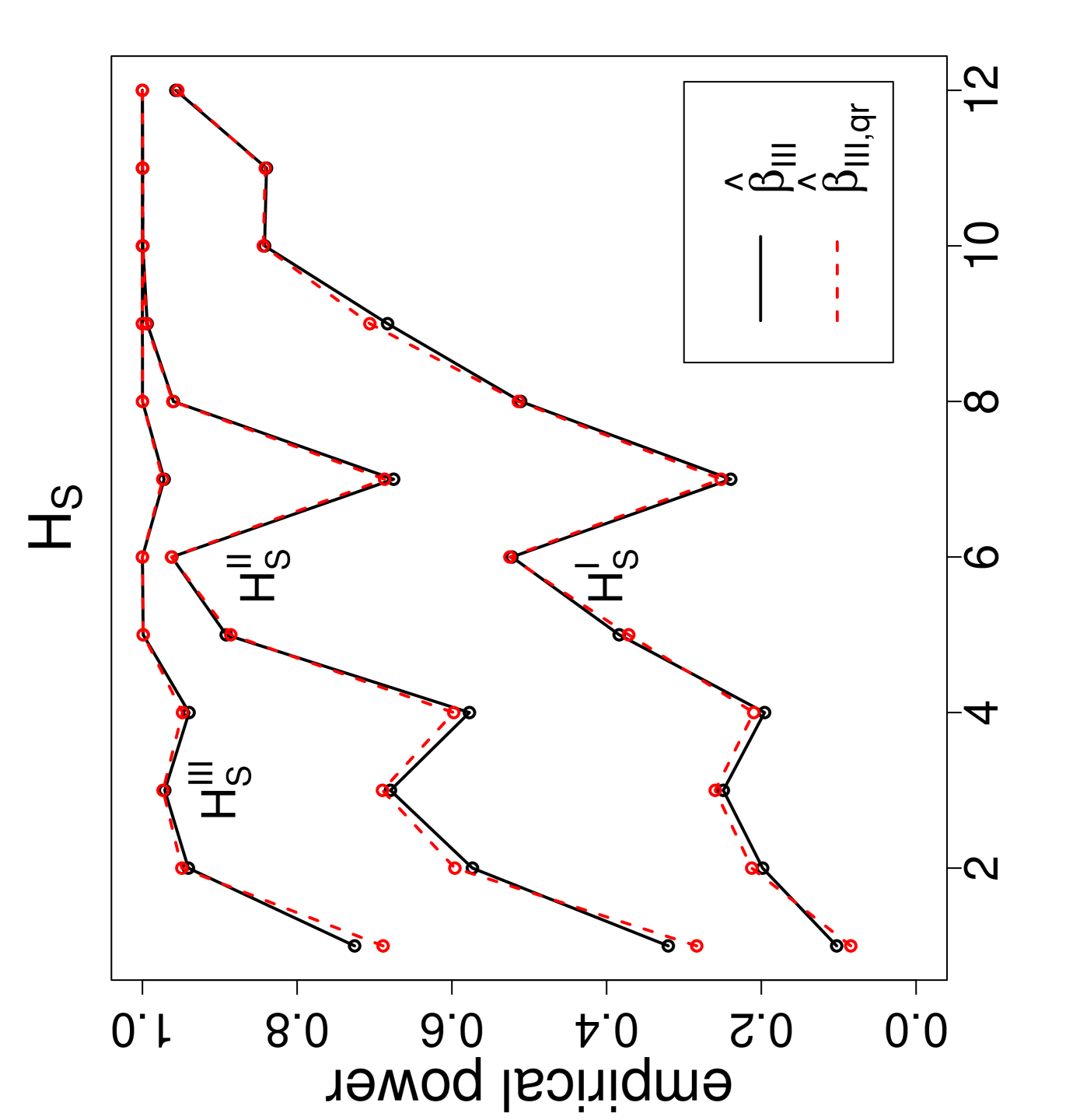
4.2 Empirical Power Analysis under Association Alternatives
For the association alternatives (against the CSR pattern), I also consider three cases. First, I generate for . Then I generate for as follows. For each , I pick an randomly, then generate as where with and . In the pattern generated, appropriate choices of will imply and are more associated than expected. That is, it will be more likely to have NN pairs than self NN pairs (i.e., or ). The three values of I consider constitute the three association alternatives:
| (13) |
Observe that, from to (i.e., as decreases), the association gets stronger in the sense that and points tend to occur together more and more frequently. By construction, points are from a homogeneous Poisson process with respect to the unit square, while points exhibit inhomogeneity in the same region. Furthermore, these alternative patterns are examples of departures from second-order homogeneity which implies association of the class with class .


The power estimates under the association alternatives are presented in Figure 5, where labeling is as in Figure 3. Observe that, for similar sample sizes as gets larger, the power estimates get larger at each association alternative. Furthermore, as the association gets stronger, the power estimates get larger at each sample size combination. The NNCT-tests have about the same power estimates under these association alternatives. Furthermore the QR-adjusted versions of the tests virtually have the same power estimates as the unadjusted versions; for the smaller samples QR-adjusted version has slightly lower power estimates.
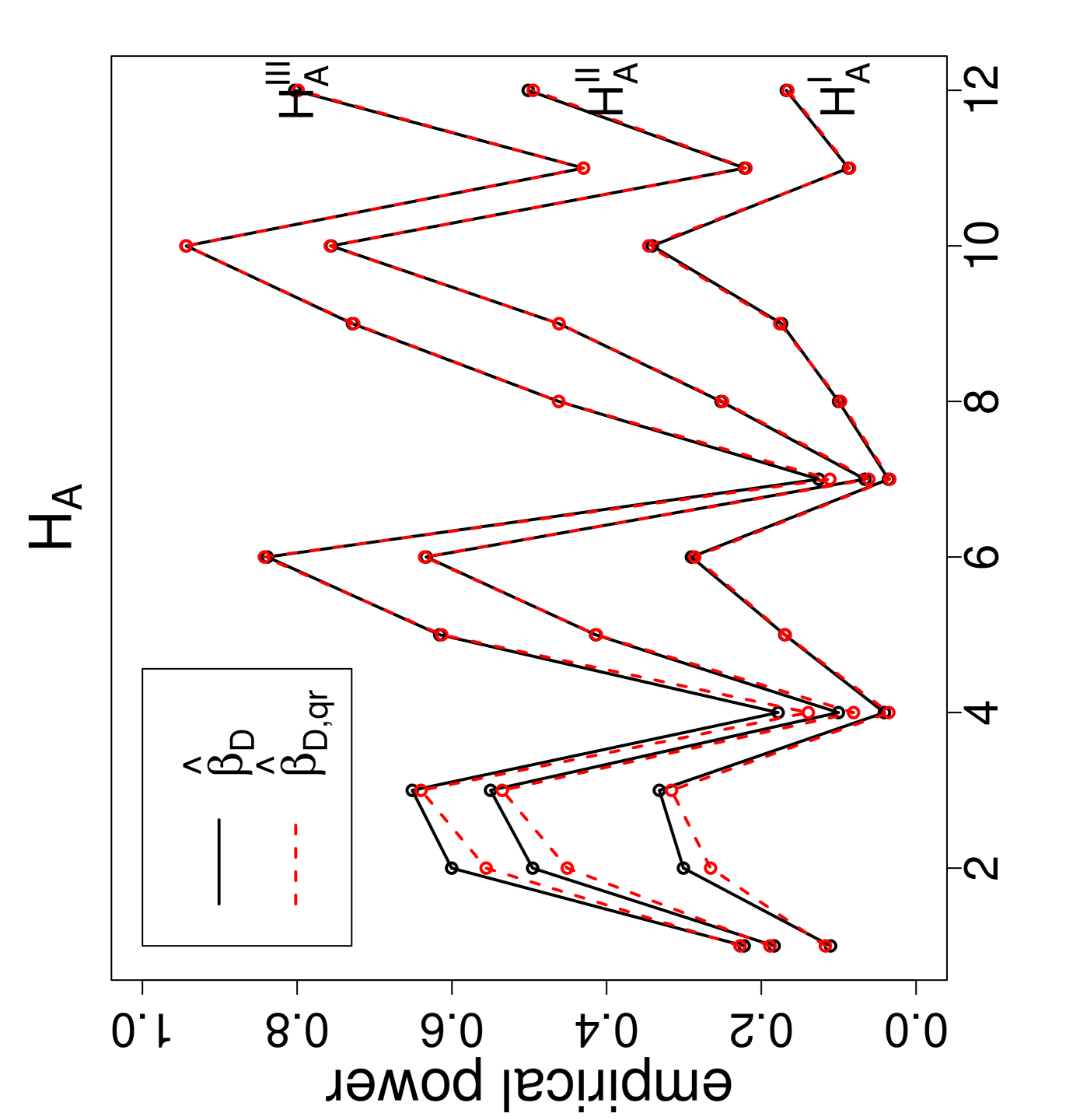
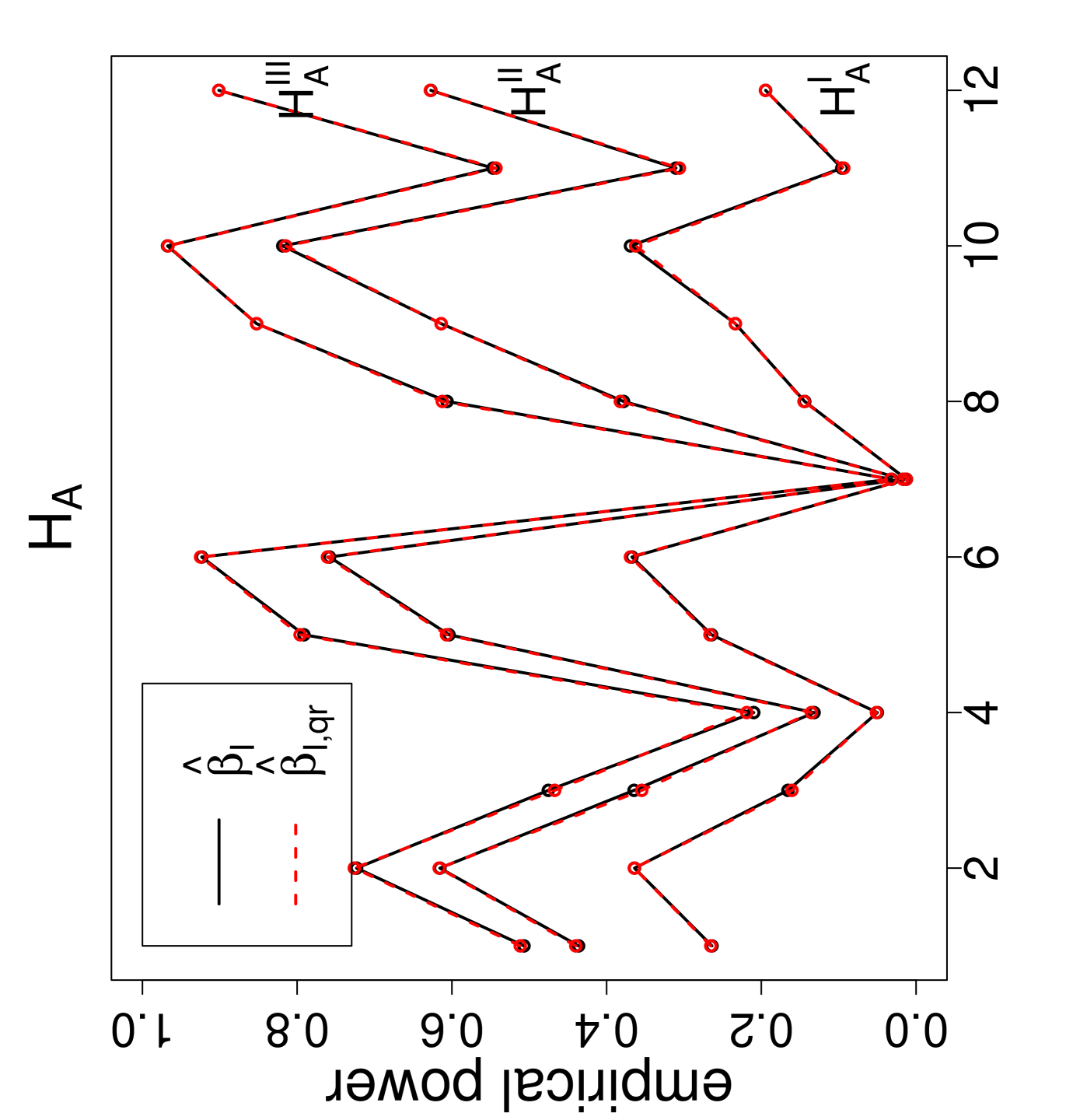
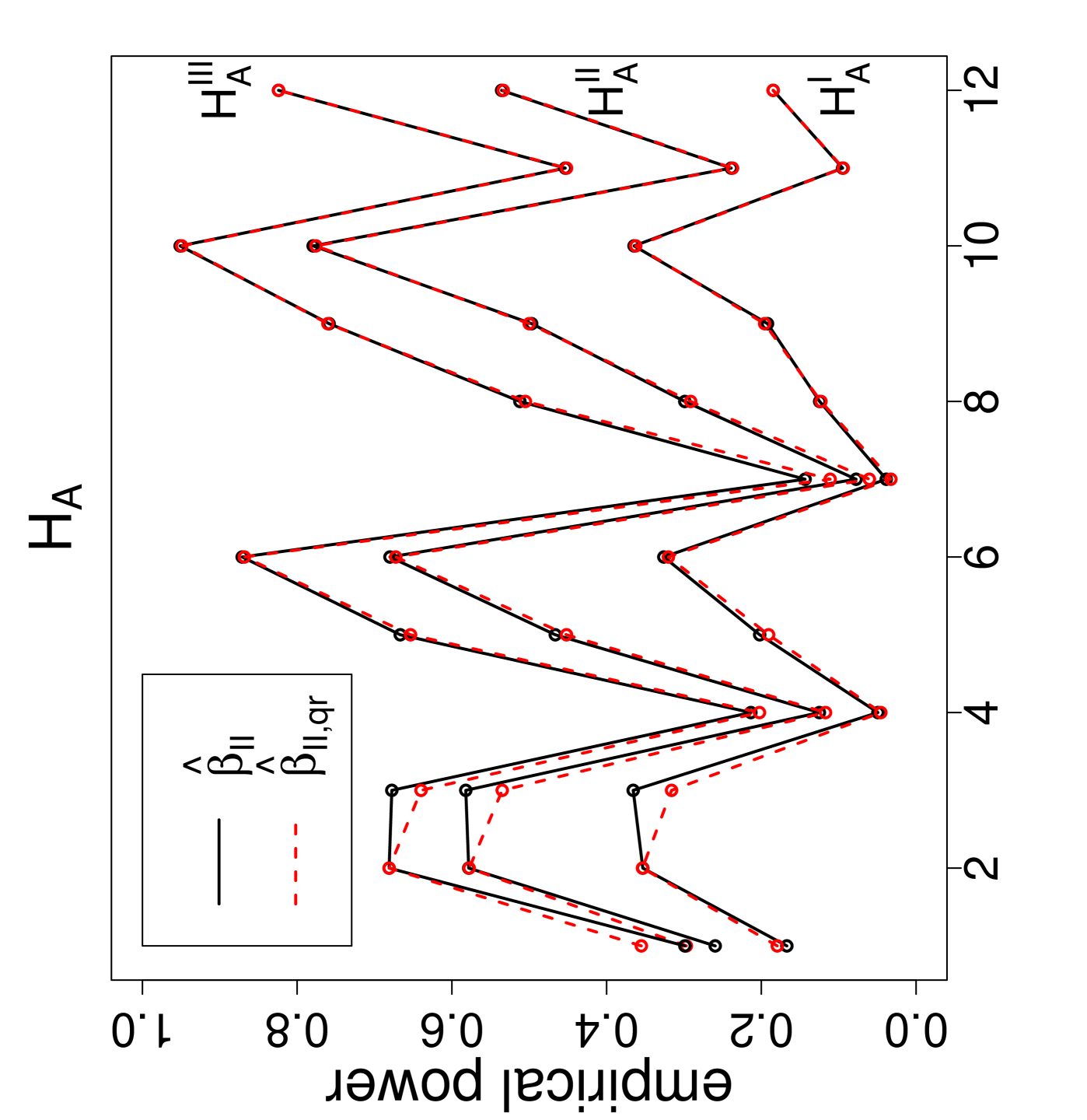
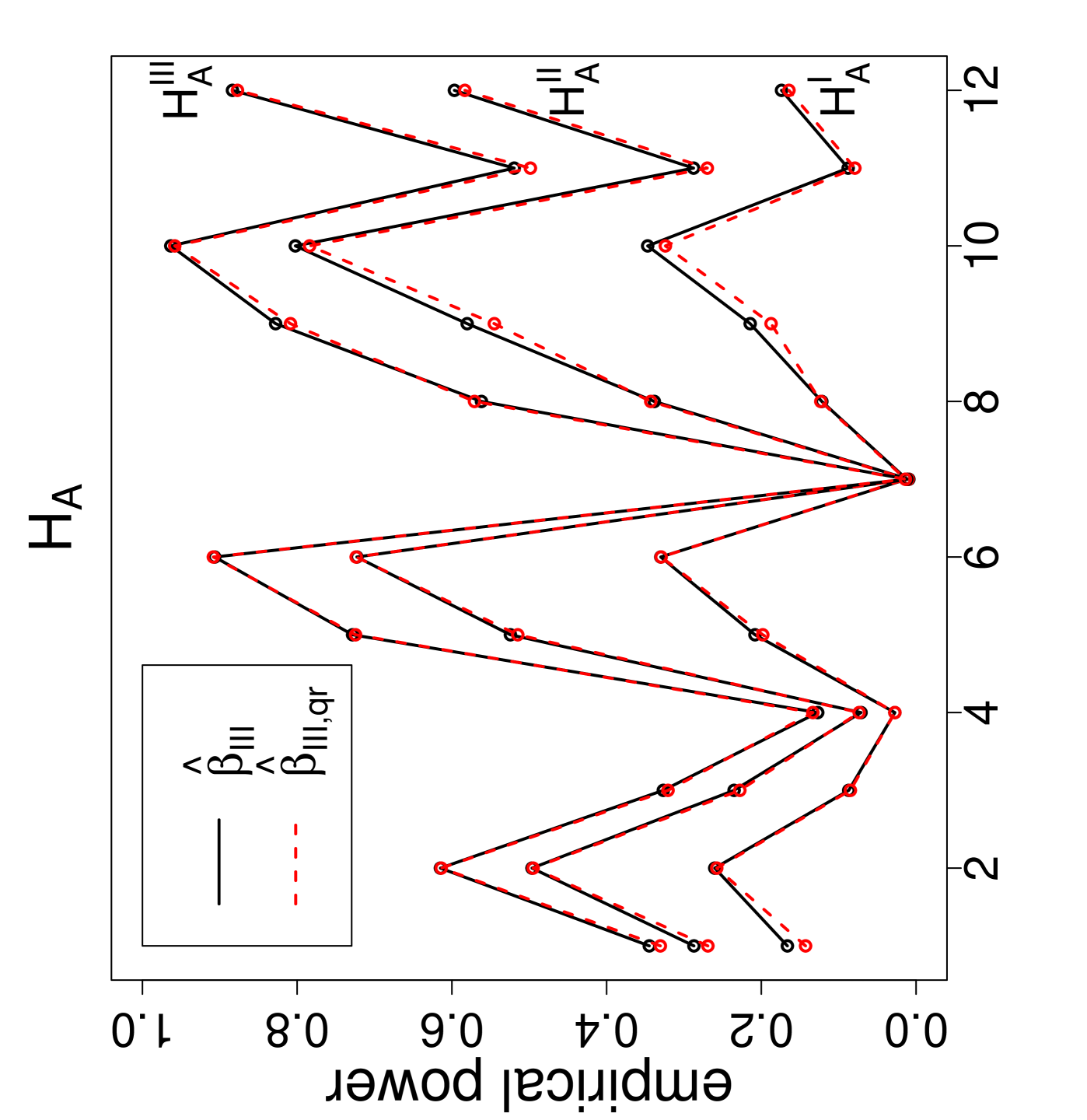
Remark 4.1.
Main Result of Monte Carlo Simulation Analysis: Based on the simulation results under CSR independence of the points, I observe that none of the NNCT-tests I consider has the desired level when at least one sample size is small so that the cell count(s) in the corresponding NNCT have a high probability of being . This usually corresponds to the case that at least one sample size is or the sample sizes are very different in the simulation study. When sample sizes are small (hence the corresponding cell counts are ), the asymptotic approximation of the NNCT-tests is not appropriate. So Dixon, (1994) recommends Monte Carlo randomization for his test when some cell count(s) are in a NNCT. I extend this recommendation for all the NNCT-tests discussed in this article. Furthermore, among the NNCT-tests, Dixon’s and version III tests seem to be affected by the QR-adjustment more than the other tests in terms of empirical size. But QR-adjustment does not necessarily improve the results of the NNCT-analysis under CSR independence, as the empirical sizes of the adjusted and unadjusted versions are not significantly different. Furthermore, the QR-adjustment does not significantly improve the power performance under segregation and association alternatives. In fact the power estimates of QR-adjusted and unadjusted tests were about the same under these alternatives.
5 Examples
I illustrate the tests on two examples: an ecological data set, namely swamp tree data (Good and Whipple, (1982)), and an artificial data set.
5.1 Swamp Tree Data
Good and Whipple, (1982) considered the spatial patterns of tree species along the Savannah River, South Carolina, U.S.A. From this data, Dixon, (2002) used a single 50m 200m rectangular plot to illustrate his tests. All live or dead trees with 4.5 cm or more dbh (diameter at breast height) were recorded together with their species. Hence it is an example of a realization of a marked multi-variate point pattern. The plot contains 13 different tree species, four of which comprise over 90 % of the 734 tree stems. The remaining tree stems were categorized as “other trees”. The plot consists of 215 water tupelo (Nyssa aquatica), 205 black gum (Nyssa sylvatica), 156 Carolina ash (Fraxinus caroliniana), 98 bald cypress (Taxodium distichum), and 60 stems of 8 additional species (i.e., other species). I will only consider live trees from the two most frequent tree species in this data set (i.e., water tupelos and black gums). So a NNCT-analysis is conducted for this data set. If segregation among the less frequent species were important, a more detailed or a NNCT-analysis should be performed. The locations of these trees in the study region are plotted in Figure 6 and the corresponding NNCT together with percentages based on row and grand sums are provided in Table 3. For example, for water tupelo as the base species and black gum as the NN species, the cell count is 54 which is 26 % of the 211 black gums (which is 54 % of all 394 trees). Observe that the percentages and Figure 6 are suggestive of segregation for all three tree species since the observed percentages of species with themselves as the NN are much larger than the row percentages.
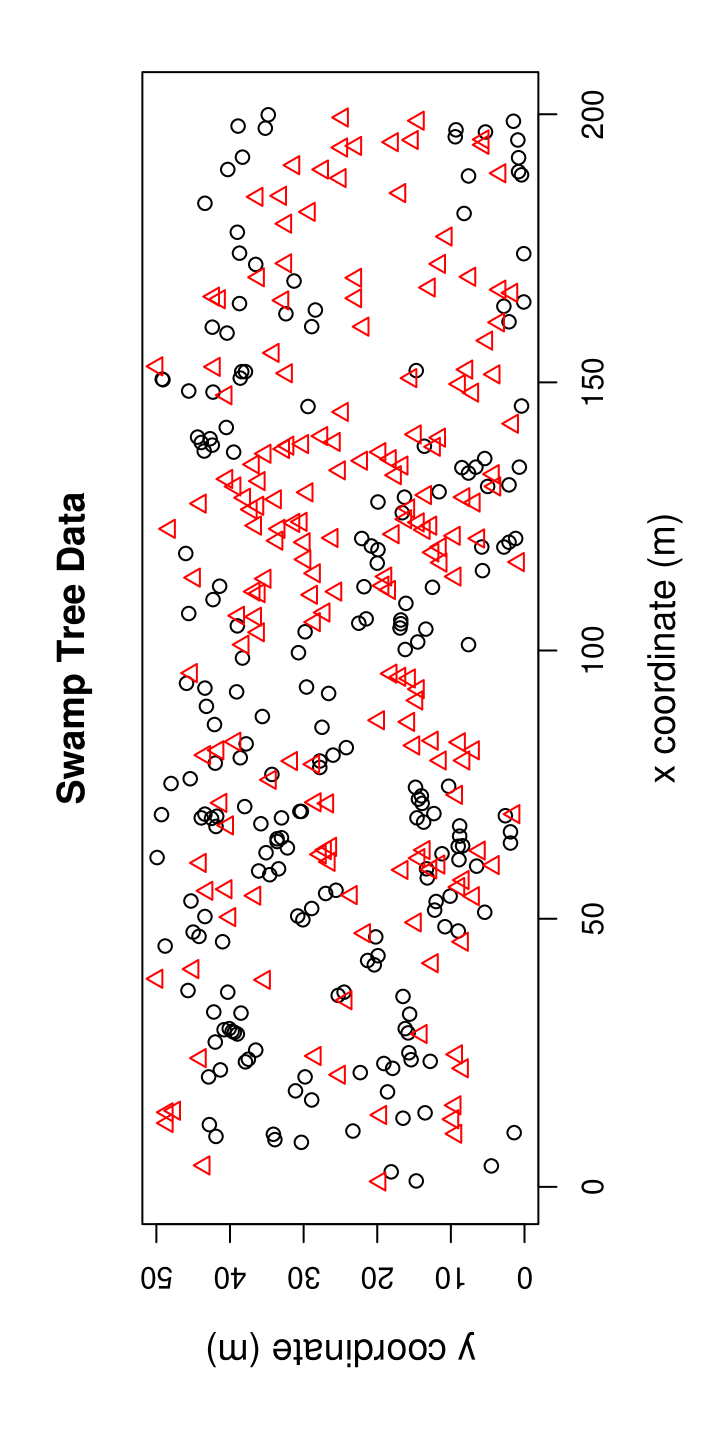
| NN species | ||||
|---|---|---|---|---|
| W.T. | B.G. | sum | ||
| W.T. | 157 (74 %) | 54 (26 %) | 211 (54 %) | |
| base species | B.G. | 52 (28 %) | 131 (72 %) | 183 (46 %) |
| sum | 209 (53 %) | 185 (47 %) | 394 (100 %) | |
The locations of the tree species can be viewed a priori resulting from different processes so the more appropriate null hypothesis is the CSR independence pattern. Hence our inference will be a conditional one (see Section 2.3) if I use the observed values of and . I observe and for this data set, and the empirical estimates for these sample sizes are and . I present the tests statistics and the associated -values for NNCT-tests in Table 4. Observe that the test statistics all decrease with the QR-adjustment, however this decrease is not substantial to alter the conclusions. Based on the NNCT-tests, I find that the segregation between both species is significant, since all the tests considered yield significant -values, and the diagonal cells (i.e., cells and ) are larger than expected.
| NNCT-test statistics and the associated -values | |||
| for swamp tree data | |||
| 52.72 | 52.08 | 52.14 | 52.66 |
| () | () | () | () |
| 51.98 | 51.35 | 51.41 | 51.92 |
| () | () | () | () |
5.2 Artificial Data Set
In the swamp tree example, although the test statistics for unadjusted and QR-adjusted versions are different for Pielou’s and Dixon’s tests and -values for QR-adjusted versions are larger than unadjusted ones, I have the same conclusion: there is strong evidence for segregation of tree species. Below, I present an artificial example, a random sample of size 100 (with -points and -points uniformly generated on the unit square). The question of interest is the spatial interaction between and classes. I plot the locations of the points in Figure 7 and the corresponding NNCT together with percentages are provided in Table 6. Observe that the percentages are suggestive of mild segregation, with equal degree for both classes.

| NN class | ||||
|---|---|---|---|---|
| sum | ||||
| 30 (60 %) | 20 (40 %) | 50 (50 %) | ||
| base class | 19 (38 %) | 31 (62 %) | 50 (50 %) | |
| sum | 49 (49 %) | 51 (51 %) | 100 (100 %) | |
The data is generated to resemble the CSR independence pattern, so I assume the null pattern is CSR independence, which implies that our inference will be a conditional one if I use the observed values of and . I observe and for this data set, and the empirical estimates for these sample sizes are and . I present the tests statistics and the associated -values for NNCT-tests in Table 6. Observe that the test statistics all decrease with the QR-adjustment, however this decrease is not substantial to alter the conclusions. Based on the NNCT-tests, I find that the spatial interaction between and is not significantly different from CSR independence.
In both examples although QR-adjustment did not change the conclusions, it might make a difference if the pattern is a close call between CSR independence and segregation/association. That is, if a segregation test has a -value about .05, after the QR-adjustment, it might get to be significant or insignificant, depending on the case.
| NNCT-test statistics and the associated | |||
| -values for the artificial data | |||
| 3.36 | 3.02 | 3.07 | 3.30 |
| (.1868) | (.0825) | (.2152) | (.0693) |
| 3.32 | 2.97 | 3.04 | 3.25 |
| (.1906) | (.0846) | (.2192) | (.0713) |
6 Discussion and Conclusions
In this article, I discuss the effect of QR-adjustment on segregation or clustering tests based on nearest neighbor contingency tables (NNCTs). These tests include Dixon’s overall test (Dixon, (1994)), and the three new overall segregation tests introduced by (Ceyhan, (2007)). QR-adjustment is performed on these tests based on NNCTs (i.e., NNCT-tests) when the null case is the CSR of two classes of points (i.e., CSR independence), since under CSR independence, the NNCT-tests depend on number of reflexive NNs (denoted by ) and the number of shared NNs (denoted by ), both of which depend on the allocation of the points. When the observed values of and are used, the NNCT-tests are conditional tests, which might bias the results of the analysis. Given the difficulty in calculating the expected values of and under CSR independence, I estimate them empirically based on extensive Monte Carlo simulations, and substitute these estimates for expected values of and (which is called the QR-adjustment in this article).
I compare the empirical sizes and power estimates of the NNCT-tests with extensive Monte Carlo simulations. Based on the Monte Carlo analysis, I find that QR-adjustment does not affect the empirical sizes of the tests. Moreover, QR-adjustment does not have a substantial influence on these NNCT-tests under the segregation or association alternatives. Thus, one can use the QR-adjusted or the unadjusted versions of the NNCT-tests.
References
- Ceyhan, (2006) Ceyhan, E. (2006). On the use of nearest neighbor contingency tables for testing spatial segregation. Accepted for publication in Environmental and Ecological Statistics.
- Ceyhan, (2007) Ceyhan, E. (2007). New tests for spatial segregation based on nearest neighbor contingency tables. Under review.
- Cuzick and Edwards, (1990) Cuzick, J. and Edwards, R. (1990). Spatial clustering for inhomogeneous populations (with discussion). Journal of the Royal Statistical Society, Series B, 52:73–104.
- Diggle, (2003) Diggle, P. J. (2003). Statistical Analysis of Spatial Point Patterns. Hodder Arnold Publishers, London.
- Dixon, (1994) Dixon, P. M. (1994). Testing spatial segregation using a nearest-neighbor contingency table. Ecology, 75(7):1940–1948.
- Dixon, (2002) Dixon, P. M. (2002). Nearest-neighbor contingency table analysis of spatial segregation for several species. Ecoscience, 9(2):142–151.
- Good and Whipple, (1982) Good, B. J. and Whipple, S. A. (1982). Tree spatial patterns: South Carolina bottomland and swamp forests. Bulletin of the Torrey Botanical Club, 109:529–536.
- Goreaud and Pélissier, (2003) Goreaud, F. and Pélissier, R. (2003). Avoiding misinterpretation of biotic interactions with the intertype -function: population independence vs. random labelling hypotheses. Journal of Vegetation Science, 14(5):681 –692.
- Hamill and Wright, (1986) Hamill, D. M. and Wright, S. J. (1986). Testing the dispersion of juveniles relative to adults: A new analytical method. Ecology, 67(2):952–957.
- Herler and Patzner, (2005) Herler, J. and Patzner, R. A. (2005). Spatial segregation of two common Gobius species (Teleostei: Gobiidae) in the Northern Adriatic Sea. Marine Ecology, 26(2):121–129.
- Kulldorff, (2006) Kulldorff, M. (2006). Tests for spatial randomness adjusted for an inhomogeneity: A general framework. Journal of the American Statistical Association, 101(475):1289–1305.
- Meagher and Burdick, (1980) Meagher, T. R. and Burdick, D. S. (1980). The use of nearest neighbor frequency analysis in studies of association. Ecology, 61(5):1253–1255.
- Moran, (1948) Moran, P. A. P. (1948). The interpretation of statistical maps. Journal of the Royal Statistical Society, Series B, 10:243–251.
- Nanami et al., (1999) Nanami, S. H., Kawaguchi, H., and Yamakura, T. (1999). Dioecy-induced spatial patterns of two codominant tree species, Podocarpus nagi and Neolitsea aciculata. Journal of Ecology, 87(4):678–687.
- Orton, (1982) Orton, C. R. (1982). Stochastic process and archeological mechanism in spatial analysis. Journal of Archeological Science, 9:1–23.
- Pielou, (1961) Pielou, E. C. (1961). Segregation and symmetry in two-species populations as studied by nearest-neighbor relationships. Journal of Ecology, 49(2):255–269.
- Ripley, (2004) Ripley, B. D. (2004). Spatial Statistics. Wiley-Interscience, New York.
- Searle, (2006) Searle, S. R. (2006). Matrix Algebra Useful for Statistics. Wiley-Intersciences.
- Waller and Gotway, (2004) Waller, L. A. and Gotway, C. A. (2004). Applied Spatial Statistics for Public Health Data. Wiley-Interscience, NJ.
- Whipple, (1980) Whipple, S. A. (1980). Population dispersion patterns of trees in a Southern Louisiana hardwood forest. Bulletin of the Torrey Botanical Club, 107:71–76.