Terminating cases of flooding
Abstract
Basic synchronous flooding proceeds in rounds. Given a finite undirected (network) graph , a set of sources initiate flooding in the first round by every node in sending the same message to all of its neighbours. In each subsequent round, nodes send the message to all of their neighbours from which they did not receive the message in the previous round. Flooding terminates when no node in sends a message in a round. The question of termination has not been settled - rather, non-termination is implicitly assumed to be possible.
We show that flooding terminates on every finite graph. In the case of a single source , flooding terminates in rounds if is bipartite and rounds with otherwise, where and are the eccentricity of and diameter of respectively. For communication/broadcast to all nodes, this is asymptotically time optimal and obviates the need for construction and maintenance of spanning structures. We extend to dynamic flooding initiated in multiple rounds with possibly multiple messages. The cases where a node only sends a message to neighbours from which it did not receive any message in the previous round, and where a node sends some highest ranked message to all neighbours from which it did not receive that message in the previous round, both terminate. All these cases also hold if the network graph loses edges over time. Non-terminating cases include asynchronous flooding, flooding where messages have fixed delays at edges, cases of multiple-message flooding and cases where the network graph acquires edges over time.
1 Introduction
Flooding is one of the most fundamental of all graph/network algorithms - for example, to achieve broadcast in networks [2, 31]. The algorithm that is usually implemented is: (i) initiator nodes send a message to all their neighbours, (ii) on first receipt, receiving nodes send the message to every neighbour from which they did not receive and (iii) on subsequent receipts, the receiving node does not send the message to any neighbour. This algorithm checks if the message has been received before, to ensure termination. It requires each node records a previous event in its state, making it a stateful protocol. We consider the pure version of flooding, i.e. algorithms that are ‘amnesiac’ in the sense that they hold no record or memory of any event beyond the immediate round. Thus, implemented algorithms that are stateless are amnesiac. The basic pure flooding algorithm is as follows.
Definition 1.1.
Synchronous amnesiac flooding algorithm. Let be an undirected graph, with vertices and edges (representing a network where the vertices represent the nodes of the network and edges represent the connections between the nodes). Computation proceeds in synchronous ‘rounds’ where each round consists of nodes receiving messages being sent from neighbours. A receiving node sends messages to some neighbours in the next round. No messages are lost in transit. The algorithm is defined by the following conditions.
-
(i)
All nodes from a subset of sources or ‘initial nodes’ send a message to all of their neighbours in round 1.
-
(ii)
In subsequent rounds, every node that received from a neighbour in the previous round, sends to all, and only those, nodes from which it did not receive . Flooding terminates when is no longer sent to any node in the network.
Hitherto, it was not known whether a stateless flooding algorithm exists that terminates on every graph. In this paper, we show that basic amnesiac flooding is itself such an algorithm. The termination times for a single source are rounds if is bipartite and rounds with otherwise, where and are the eccentricity of and diameter of respectively. These times are asymptotically time optimal. The difference in times between bipartite and non-bipartite graphs means that a stateless algorithm can approximate the topology or diameter/eccentricities of a network in certain cases.
Gopal, Gopal and Kutten [14] highlighted the memory requirement inherent in stateful flooding and its overhead on fast networks. For example, when multiple messages are being flooded, nodes need to keep a record of the messages they have seen and search through their data structure whenever a message arrives before deciding if it can be further flooded. This is also a limitation for low memory devices, e.g. sensor networks. We show that not only amnesiac flooding of the same message in a single round, but also amnesiac flooding of multiple messages initiated in multiple rounds, where at most one message is sent along any given edge each round, terminates.
One advantage of the stateful variant of flooding is that it can be used to construct spanning structures, such as spanning trees, which can be subsequently re-used for efficient communication [25, 2, 31, 38]. It is not easy to maintain these structures in dynamic conditions, i.e. when edges/nodes are being added or removed. We show that even when edges are being arbitrarily or adversarially removed from the graph, amnesiac flooding with the correct forwarding rules will still terminate. Under some other forwarding rules, termination is not guaranteed. Termination is also not guaranteed in asynchronous models where the delivery time of messages on edges can vary - we show this with a non-terminating delivery schedule over the edges and even with a single edge with delayed delivery in some pathological cases. Note that amnesiac flooding uses rules that avoid forwarding to the most recently chosen nodes - similar ideas have been used before in distributed computing, e.g. in social networks [10] and broadcasting [12].
There are numerous applications of flooding as a distributed algorithm. It is often used to set up spanning trees[25, 2, 31, 38] and solving leader election. For example, the time-optimal leader election of Peleg [30] utilises continuous flooding of node s to determine the node with the highest while using a condition on the node s to achieve and detect termination. Kutten et al [23], on the other hand, use controlled stateful flooding and resulting spanning tree for efficient time and message leader election. Processes such as random walks [35, 36, 13, 23, 24] and its deterministic variant Rotor-Router (or Propp) machine [22, 8] can also be seen as restricted variants of flooding. Finally, in some models such as population protocols, the low memory makes termination very difficult to achieve leading to research that tries to provide termination e.g. [26].
Flooding-based algorithms (or flooding protocols) appear in areas ranging from GPUs, high performance, shared memory and parallel computing, to mobile ad-hoc networks (MANETs), Mesh Networks, Complex Networks etc [37]. Rahman et al [32] show that flooding can even be adopted as a reliable and efficient routing scheme, comparable to sophisticated point-to-point forwarding schemes, in some ad-hoc wireless mobile network applications. Adamek et al [1] and Karp and Kung [21] further offer stateless (flooding and other) solutions for routing.
This paper is structured as follows. In section 2, we prove that, for the simple case of a single message being flooded from a set of initial nodes in round , all nodes receive the message at most twice and hence amnesiac flooding terminates (Theorem 2.2). This result is used to derive sharp bounds for the number of rounds it takes for flooding to terminate, in section 3 (Theorem 3.9). Amnesiac flooding is extended in section 4 to dynamic cases where multiple messages are flooded in any round. The flooding algorithms are categorized by whether a node sends a chosen received message to neighbours from which it did not receive any message in the previous round, or whether the node sends to all neighbours from which it did not receive . We show that, in the first case, and also the second case if messages are ranked, no flooded message is received more than twice and therefore flooding terminates if the number of messages is finite (Theorems 4.4 and 4.8). In section 5 we present non-terminating cases of amnesiac flooding for both single-message and multiple-message flooding. Conclusions are drawn in section 6.
Sections 2 and 3 of this paper have essentially appeared earlier as conference publications at STACS 2020 [20] and PODC 2019 [18], and on Arxiv [19]. The proof of time to termination was presented for the case of a single source, but the same proof also provides the time calculation for the multi-source case simply by replacing distances of a node from the initial node by distances of from the set of initial nodes . Since those publications, Turau [40, 41] has worked on finding optimal sets of sources of a given size that minimize termination time for multi-source flooding. The parts of this paper from section 4 onwards on dynamic flooding, which require the use of a more powerful proof method, have not been published previously.
2 Termination
Throughout this paper, when we refer to ‘flooding’ we will mean either the amnesiac flooding of Definition 1.1 or another amnesiac version of flooding defined in context in the relevant section. In this section we prove that (amnesiac) flooding initiated from any set of initial nodes, all at once, terminates.
Definition 2.1.
Let be the graph and a set of initial nodes. The round-sets are defined as:
Clearly, if for some , then for all .
Theorem 2.2.
Any node is contained in at most two distinct round-sets.
Proof Define to be the set of finite sequences of consecutive round-sets of the form:
| (1) |
In (1), is the start-point and is the duration of . Note that, a node belonging to and may also belong to other in (1). If a node occurs in three different round-sets , and , then the duration between and , and , or and will be even. Consider the subset of of sequences of the form (1) where is even. To prove that no node is in three round-sets, it suffices to prove that is empty.
We assume that is non-empty and derive a contradiction. Let be the subset of comprising sequences of minimum (even) duration , i.e.
| (2) |
Clearly, if is non-empty then so is . Let be the sequence with earliest start-point , i.e.
| (3) |
where
| (4) |
By (1), there exists . Choose node which sends a message to in round . As is a neighbour of , either sends a message to in round or sends a message to in round . We show that each of these cases leads to a contradiction.
Case (i) sends a message to in round
In this case, there must be a round which is either round 0 and is an initial node in , or received a message in round . Thus, the sequence
| (5) |
has which is even and so . As , by (4)
| (6) |
But, from (5), and, from (4), . Thus, by (6),
which is a contradiction.
Case (ii) sends a message to in round
By the definition of , the smallest possible value of is 2. However, it is not possible to have in this case as then
and sends a message to in round . As we chose to be such that sends a message to in round this cannot happen because cannot send a message to and to in consecutive rounds by the definition of rounds. So,
where . Consider the sequence
| (7) |
As receives a message from in round and sends a message to in round , it is clear that . Thus, . As is even, so is and therefore . Now, and so, as , we have, by (2),
| (8) |
As from (7) and from (3), we have, by (8),
This contradiction completes the proof.
Definition 2.3.
(For section 3 only - superscripts have a different use in section 4.) Given , we use a superscript 1 to indicate that belongs to a round-set for the first time, and a superscript 2 to indicate that it belongs to a round-set for the second time, i.e.
means that
and
means that
Theorem 2.2 implies that for , where is the number of vertices of , and therefore flooding always terminates. In the next section we give sharp bounds for the number of rounds to termination, in terms of the eccentricity of initial nodes and the diameter of .
3 Time to termination
The question of termination of network flooding is non-trivial when cycles are present in . The simple cases when is an even cycle and when is an odd cycle, as in figure 1 (where an arrow indicates a message received by a node in the given round), display quite different termination behaviours.
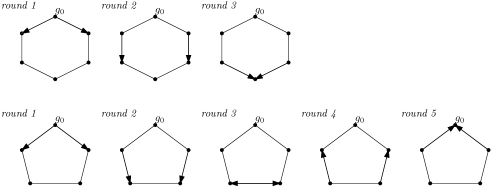
The even cycle terminates remotely from the initial node , after round where is the eccentricity of in . On the other hand, flooding on the odd cycle returns a message to the initial node and terminates after round resulting in a longer flooding process than the even cycle despite having fewer nodes and a smaller value of . In this section, we show that these observations can be largely generalized to arbitrary graphs. Observe that in the even cycle every node receives the message only once, whereas in the odd cycle every node receives the message twice. We show that, in general graphs, this difference is due to the absence or presence of neighbouring nodes that are equidistant from the set of initial nodes , called ‘ec nodes’ below.
Definition 3.1.
Let be a graph with vertex set and edge set and let be a set of initial nodes. We will use the following definitions.
-
(i)
For each , the distance set will denote the set of points which are a distance from . i.e.
where, for any ,
and is the usual distance function in graph .
-
(ii)
A node is an equidistantly-connected node, abbreviated ec node, iff it has a neighbour equidistant from , i.e. iff there there exists such that and
-
(iii)
The eccentricity of , denoted , is defined as
-
(iv)
The graph is ec-bipartite iff has no ec nodes.
Note that neighbouring initial nodes are ec nodes as they are both a distance 0 from . We have the following basic properties of distance sets and nodes.
Lemma 3.2.
Let be a graph and be a set of initial nodes.
-
(i)
For all and , and .
-
(ii)
For all , and such that and are neighbours, sends a message to in round , i.e. all nodes at a distance from send to all their neighbours which are a distance in round .
-
(iii)
If and is an node, then .
Proof For (i), clearly every node at a distance from receives a message in round and so . Furthermore, every message received in round will have travelled at most edges away from and so could not have reached a node which is at a distance from . Thus, .
For (ii), we note that the only circumstance in which a node in ( by (i)) does not send to a neighbour in in round is if sent a message to in round . This would need to be in the round-set , i.e. which contradicts (i) which has as .
For (iii), if and is an node, then by Definition 3.1(ii) there is an point equidistant from , i.e. such that and are neighbours. If then and send a message to each other in round 1 and so . This means that , as is an initial node and . If then, by (i) of this lemma, and so both and receive messages in round . Also, by (i), neither sends a message in round as . Thus, and send messages to each other in round . As this will be the second time they receive a message we have that
All nodes in a graph without nodes, belong to at most one round-set.
Lemma 3.3.
Let be a graph and be a set of initial nodes. Then has an ec node if and only if has a node that is in two round-sets.
Proof Suppose that has no nodes. Assume, on the contrary, that has nodes that appear in two round-sets. Let be the earliest round which contains a node such that and be a neighbour of which sends to in round , so that . Then, for some and by Lemma 3.2(i). Thus, and so . As is a neighbour of , , , or . If then and are nodes contrary to our supposition that has no nodes. If then by Lemma 3.2(i), which is contrary to the assertion that . If then , by Lemma 3.2(i), and so as . By Lemma 3.2(ii), sends to in round . This is contrary to sending to in round . Thus, our assumption that has nodes that appear in two round-sets is false.
Conversely, suppose that has an node , ( by Lemma 3.2(i)) say where . Then by Lemma 3.2(iii).
In the case of a single initial node, bipartite graphs do not have any nodes.
Lemma 3.4.
Let be a graph and suppose that contains a single initial node . Then, is bipartite iff it has no nodes.
Proof It is easy to see that nodes equidistant from the initial node must belong to the same partite set. A graph is bipartite iff no edge connects two such nodes, and this is the case iff has no nodes by Definition 3.1(ii).
From Lemma 3.3 we see that nodes in graphs without ec nodes only receive a message once. For these graphs the time to termination is the number of rounds taken for the message to reach the most distant points from the set of initial nodes . This is just the eccentricity of , .
Theorem 3.5.
Let be a graph and be a set of initial nodes with eccentricity . Then, flooding will have terminated after round if and only if is ec-bipartite
Proof
Corollary 3.6.
Let be a graph and suppose that contains a single initial node of eccentricity . Then, flooding will have terminated after round if and only if is bipartite
Proof Follows from Lemma 3.4, Theorem 3.5 and the fact that .
To find the time to termination in general graphs we need to find a bound on when nodes can belong to a round-set for the second time. As nodes can only belong to at most two round-sets, by Theorem 2.2, this will give a bound for termination of flooding in general graphs. The following lemma relates the round-sets of second occurrences of neighbouring nodes.
Lemma 3.7.
Let be a graph and a set of initial nodes. If and for some , and if is a neighbour of , then
Proof Let be the distance of from , i.e. . Then, as , by Lemma 3.2(i). As is a neighbour of , or or .
Case .
As are neighbours they are both nodes. Thus, by Lemma 3.2(iii), and . Therefore, and .
Case .
If () then, as by Lemma 3.2(i), it must be the case that . If and () then, as by Lemma 3.2(i), it must be the case that . If and then, as , sends to in round and so (). As , it must be the case that .
Case , g does not send to h in round j.
In this case, as , sends to in round . Thus, () and therefore, as by Lemma 3.2(i), it must be the case that .
Case , g sends to h in round j.
In this case . We show that . Assume, on the contrary, that . Then, by Lemma 3.2(i), and thus . Hence, by Lemma 3.2(i), . Also, as . To summarize:
So, sends to in round and sends to in round by the case assumption. This is a contradiction. Thus, the assumption that is false and, as , it follows that . This completes the proof.
Corollary 3.8.
Let be a graph and be a set of initial nodes. Then has an ec node if and only if all nodes are in exactly two round-sets.
Proof Follows from Lemmas 3.3 and 3.7.
We can now give bounds for time to termination of flooding for graphs that have ec nodes.
Theorem 3.9.
Let be a graph that is not ec-bipartite with diameter . Then, flooding terminates after round where is in the range
Proof If is not ec-bipartite it has an node , by Definition 3.1(iv). By Lemma 3.2(iii), where . Let be an arbitrary node in other than . Then, there is a path
where . By repeated use of Lemma 3.7,
Thus,
| (9) |
Put . From (9), as and as ,
and, as is any ec node,
As is not ec-bipartite, by Theorem 3.5 and the proof is complete.
Corollary 3.10.
Let be a graph and be a set of initial nodes which contain an ec node. Then, flooding terminates after round where is in the range
Proof Follows from Theorem 3.9 as for any ec node in .
Corollary 3.11.
Let be a non-bipartite graph with diameter and a single initial node of eccentricity . Then, flooding terminates after round where is in the range .
Proof Put so that . Then, by Theorem 3.9, flooding terminates after rounds where is in the range
Figure 2 shows that the bounds are sharp. Sharpness of the upper bound is shown by the graph on the left in which flooding terminates after rounds. The slightly complicated graph on the right terminates after rounds, demonstrating sharpness of the lower bound and also showing that flooding can terminate in a non-bipartite graph before round where is the diameter. In both graphs is the initial node.

The clear separation in the termination times of bipartite and non-bipartite graphs, in the case of a single initial node, does not carry over neatly to the general case of multiple initial nodes. For the general case, it is the presence or otherwise of ec nodes that is the distinguishing property and we have defined ec-bipartite graphs for this purpose. Unlike the single node case, having ec nodes or not in the multiple initial node case cuts across the bipartite/non-bipartite boundary, i.e. bipartite graphs may have ec points and non-bipartite graphs may not. The recent work by Turau [40] looks at termination times in terms of the ‘k-flooding problem’ which aims to find a set S of size k such that amnesiac flooding when started concurrently by all nodes of S terminates in the least number of rounds.
4 Dynamic flooding
So far, we have considered flooding of a single message which initiates at a single point in time in round 0, albeit possibly from several nodes. In this section we show that amnesiac flooding will still terminate in dynamic settings where multiple floodings are initiated from multiple nodes in multiple rounds with multiple messages, even when floodings from previous initiations have not completed. We consider floodings in which nodes receiving messages in a given round only send a single message per edge in the next round. The case of ‘parallel flooding’, where multiple floodings operate independently of each other resulting in nodes possibly sending multiple messages along an edge in a round, terminates trivially given the results in sections 2 and 3.
There are two general cases in which messages are being flooded by nodes with initial rounds respectively, such that at most one message per edge per round is sent. In the first case, a node that receives messages in a round sends one of the received messages to all neighbours from which it did not receive any message. In the second case, the node sends to all neighbours from which it did not receive . We call these two cases ‘partial-send’ and ‘full-send’ respectively. We subdivide the second case into the subcase ‘ranked full-send’ where the messages are ranked and the highest ranked received message is sent on, and the subcase ‘unranked full-send’ where a random message is sent on.
Definition 4.1.
Amnesiac flooding algorithms for dynamic flooding. Let be a graph, be possibly different initiating nodes flooding possibly different messages with possibly different initial rounds respectively, where the subscript distinguishes the floodings (i.e ). We assume a node does not initiate flooding (initiation means sends a message to all of its neighbours in the next round) of a message in a round in which it receives a message. Consider the properties below for an algorithm for flooding multiple messages, where denotes the set of all neighbours of a node and the subset of neighbours of from which receives message in round .
-
(i)
For all , sends message to all of its neighbours in round .
-
(ii)
Suppose a node receives messages from neighbours in round . Let be such that . Then, in round , sends to all neighbours in and sends no other message.
-
(iii)
Suppose a node receives messages from neighbours in round and that the of each message is the subscript . Let be the largest such that . Then, in round , sends to all neighbours in and sends no other message.
-
(iv)
Suppose a node receives messages from neighbours in round . Let be such that . Then, in round , sends to all neighbours in and sends no other message.
The flooding algorithm defined by (i) and (ii) is called partial-send, that defined by (i) and (iii) is called ranked full-send and that defined by (i) and (iv) is called unranked full-send.
In 4.1 and 4.2 below we show that, in the cases of partial-send and ranked full-send flooding of multiple messages, no node receives a given message more than twice, and so flooding terminates when the number of messages is finite. As a further extension to the basic flooding model of sections 2 and 3, both of these results hold in a dynamic setting where the graph may lose edges or nodes over time. In section 5.3, the general case of unranked full-send flooding of multiple messages is shown not to terminate even if the number of messages is finite.
4.1 Multiple messages - partial-send flooding
It may seem that flooding initiated by a node in round can be simulated as a round 0 flooding by adding an extra path of length to so that the message arrives at in round - in this way reducing the problem to the simple case of only round 0 floodings of sections 2 and 3. However, flooding initiations in later rounds can easily produce the same node in evenly spaced round-sets which cannot be simulated by any graph floodings from round 0 only, by the proof of Theorem 2.2. So, the suggested simulation by a larger graph is not possible in general and an alternative proof is needed.
In the remainder of the paper, for nodes and , will mean ‘ sends some message to ’, i.e. receives some message from , and will mean ‘ sends message to ’, i.e. receives message from . We shall also use to mean ‘does not send’ in a similar way.
Definition 4.2.
Let be a graph with nodes and edges . An even flooding cycle , abbreviated ef cycle, is a mapping for some where , such that for all . Arithmetic on elements of is modulo . Whilst is a cycle, its image is a closed walk but not necessarily a cycle in - see the example in figure 3. A message , where , in round is a clockwise message along and a message , where , is an anticlockwise message.

In any given round, there will be a number of messages sent clockwise along and a number of messages anticlockwise. Our interest is in the number of messages sent in each direction from evenly spaced points of . (We will refer to and , loosely, as ‘points’ of .)
Lemma 4.3.
Let be a graph, flooding be partial-send as in Definition 4.1 and let be an ef cycle. For all let
Then, for all ,
| (10) |
Proof By induction on . In round , every initial node is yet to send a message and thus there are neither clockwise nor anticlockwise messages and so (10) holds trivially. Assume that (10) holds for some . It is convenient to define the corresponding sets of points of receiving messages for all :
Clearly,
| (11) |
We show that . A clockwise message , where is even, is sent in round in the following cases:
-
(a)
and in round ,
-
(b)
and in round , but was an initial node about to send to all neighbours or received a message from an external neighbour, i.e. other than or , in round .
The set of messages sent clockwise from , for even , in round as per case (a) is . We denote the set of even such that sends a clockwise, equivalently anticlockwise, message in round as per case (b), by . Thus,
Similarly,
Thus,
A similar inductive argument shows that .
Theorem 4.4.
Let be a graph and flooding be partial-send. Suppose that initial node floods message in round . Then, if
| (12) |
is a succession of sent messages, no node can occur more than twice in (12). Thus, no flooded message is received more than twice by a node in partial-send flooding which therefore terminates if the number of floodings of messages is finite.
Proof Assume, on the contrary, that there is a sequence of sends (12) in which some node occurs at least three times. Such a sequence of sends does not occur when the flooding of in round is the only flooding in as then, by Theorem 2.2, a message cannot be received more than twice by a node. If only is flooded, there is with such that
| (13) |
i.e. the succession of sends in (12) cannot proceed beyond rounds, and therefore a sequence of sends via some nodes
| (14) |
preventing sending to in (13). Define an ef cycle by:
| (15) |
We now consider the messages sent clockwise and anticlockwise along edges of after round as per the partial-send flooding of all messages in the statement of this theorem. The following notation for subsets of will be used where :
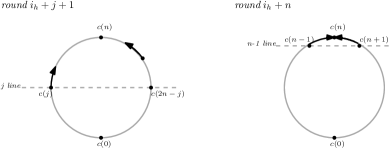
We shall prove that for all with , the number of messages sent clockwise in round along above the line in the left-hand illustration in figure 4, from points of of equal parity to , is less than or equal to the number of messages sent anticlockwise above the line, from points of equal parity to . Precisely, if
then
| (16) |
The proof is by induction. For , by Lemma 4.3,
Assume that (16) holds for some with . We show that (16) continues to hold for . For , define the set of points of above the line that are either initial nodes in round or receive messages from neighbours external to :
A clockwise message is sent in round with points , i.e. , with of equal parity to , in the following cases:
-
(a)
and in round . This corresponds to being in the set .
-
(b)
is an initial node or received a message externally in round . This means . Note that, from (12) and (15), as , in round . Thus, in round and so . Hence, .
From (a) and (b),
| (17) |
An anticlockwise message is sent in round with points , i.e. , with of equal parity to , in the following cases:
-
(a’)
and in round . This corresponds to being in the set . Note that, from (12) and (15), as , in round . Thus, in round and so . Hence, .
-
(b’)
is an initial node or received a message externally in round . This means .
From (a’) and (b’),
| (18) |
Now, and as points in send messages in both clockwise and anticlockwise directions along in round and therefore cannot have received messages from either direction in round and so cannot belong to either or . Therefore, from (17) and (18), to prove the inductive step , it suffices to prove that
| (19) |
By definition, are points of of opposite parity to . Thus, , and , and so (19) follows as by induction. Thus, (16) holds for all with .
Put in (16). Then, , in round by (15) and (12), and so . As , . Thus, , i.e. (by (15)) in round . (See the right-hand illustration in figure 4.) This contradicts (12) in which in round . Thus, the assumption that (12) contains some node more than twice is incorrect.
An example of multiple messages being flooded by a partial-send algorithm is the flooding of the details and price of an item that a node purchases. For example, a node receiving the details and prices of purchases of the item from its neighbour nodes might select the cheapest and pass on the information of the cheapest available item to neighbours from which it did not receive messages about the item in the previous round. There would be no reason to send a message to a neighbour from which details of a more expensive item had been received in the previous round as that neighbour would already have made the purchase - hence a partial-send flooding algorithm would be used.
The special case of Theorem 4.4, where the same message is flooded by all initial nodes, generalizes multi-source flooding of sections 2 and 3 to the case where sources may initiate floodings in different rounds.
Corollary 4.5.
Flooding of a single message from multiple sources initiating in possibly different rounds always terminates.
Corollary 4.5 alongside the duality with ‘reverse’ flooding can be used to show termination of algorithms such as leader election [30] which may have deviations from the strict flooding algorithm. For example, a ‘sink’ node, which receives messages from all neighbours in a certain round , reverse floods a message to all neighbours in round as part of the algorithm. This might occur when (forward) flooding has not completed in other parts of the graph. It is not clear that this abnormal behaviour at such a sink node is not out of step and cannot combine with other uncompleted flooding to cause non-termination. (Note that the node cannot be considered an initial node in round as it received messages in round .)
Corollary 4.6.
Let be a graph which is flooded with a single message from round 1 as in Definition 1.1. Suppose that node is a sink node in round , i.e. for all neighbours of . Further, suppose that flooding proceeds according to the algorithm in Definition 1.1 except that in round sends to all of its neighbours. Then, the resulting flooding process terminates.
Proof The state of flooding in any round which determines the subsequent states of flooding is defined by a relation making into a bidirected graph [11] where edges may be undirected, directed one way or directed both ways as in our illustrations of rounds in figures:
Let the normal flooding process, where adheres strictly to the flooding algorithm in round , terminate after round and let the sequence of states from round 1 be:
| (20) |
We need to show that flooding terminates from the state given by:
| (21) |
Consider the reverse flooding of (20), in which received messages become sent messages and sink nodes become initial nodes, i.e. given by the sequence of states:
| (22) |
where, for any state , is the inverse relation . The node is an initial node in as is a sink node in state in forward flooding. Let
| (23) |
The following
are successive states of flooding as in (22) except that is not an initial node in . By Corollary 4.5, this flooding terminates say after additional succeeding states :
By duality, the sequence
| (24) |
terminates at . Now, by (23), and so does not receive any messages in state . Thus, by Corollary 4.5, the flooding sequence of states obtained from (24), where is an initial node in state as in (21),
will terminate from the state (after some additional succeeding states).
4.2 Multiple messages - ranked full-send flooding
Here, messages are flooded as per Definition 4.1 conditions (i) and (iii). The rank of message is the integer . Messages are ranked according to the round they were flooded, and messages flooded in the same round by different nodes also have different ranks, i.e.
| (25) |
Note that, unlike in partial-send flooding, a node may send a message to a node from which it has just received a message. However, the message sent will be different (of higher rank) to the one received (see figure 5).

We will prove that a message cannot be received by a node more than twice in ranked full-send flooding by defining round-sets with respect to the different messages.
Definition 4.7.
Let be a graph flooded by ranked full-send flooding with initiating nodes and corresponding rounds denoted as in Definition 4.1. For each of these messages , the round-sets of are defined as:
So, round-sets are defined for each message after it is flooded. They comprise nodes that receive the message or a higher ranked message.
Theorem 4.8.
Given any flooded message where , any node receives at most twice. Thus, ranked full-send flooding terminates if the number of messages flooded is finite.
Proof Assume that a node receives a message more than twice. If receives three or more times, then there are evenly spaced rounds and , where is even, in which receives . By Definition 4.7, is in the corresponding round-sets of for those rounds. So, if is the set of finite sequences of consecutive round-sets satisfying:
| (26) |
and
| (27) |
then is non-empty. (For the purposes of the proof, we only require that in round and do not require that receives in that round.) Define the subset of of sequences of minimum (even) duration and in with earliest start point . By (27), there exists which receives message in round . Choose node which sends message to in round . Observe that, as sends in round and and so was initially flooded earlier than round ,
| (28) |
Now, either does not send a message to in round or does send a message to in round . We show that each of these cases leads to a contradiction.
Case (i) does not send a message to in round
As is a neighbour of , sends a message to in round . Now, does not send a lower ranked message than to in round - otherwise which does receive a higher ranked message than in round from some neighbour would, by the flooding algorithm in Definition 4.1(iii), send a higher ranked message to in round contradicting the case assumption that does not send any message to in round . Thus, sends a message , where , to in round and so is an initial node flooding or it receives in round . Hence, by (25) as . Therefore, by Definition 4.7, . Consider the sequence
| (29) |
By (28), we have that receives in round and so . Also, . Thus, at (29) satisfies (26) and (27) and so . Its duration is the same as that of but its start point is earlier, contrary to our choice of as having the earliest start point.
Case (ii) sends a message to in round
Here, as , it follows that and so . If , then and
As , receives or a newer message , by Definition 4.1(iii), in round . Also, sends in round . Thus, cannot receive in round as that would contradict basic flooding. Neither can receive a newer in round as that would mean that would not be sent in round by Definition 4.1(iii). It follows that cannot be 2. So, we have the sequence
As and, by (28), receives in round , (26) and (27) are satisfied by and so . The duration of , , is smaller than the duration of which was chosen to have the smallest even duration. This is the required contradiction and completes the proof of the theorem.
Ranked full-send flooding may be used where time-sensitive information is being rapidly disseminated from various sources. For example, the prices of stocks and shares. A received node may act on such timely information continuously in an unspecified way and will send the newest information from the most reliable sources to all neighbours who did not forward that information. Note that the unrefined ranked full-send algorithm may result in a node receiving older information from a more distant mode later on. This may or may not present a problem depending on the way a node acts on received information.
Uses of the flooding algorithm for broadcasting will need to ensure that every message is received by any given node in some round. It is easy to see that (time-)ranked full-send flooding achieves this if the same single node floods the sequence of messages to broadcast a stream of messages. If a newly flooded message is received by a node in some round for the first time, this will be before any newer message is received by , and therefore will send , in round , to all neighbours of which did not send to in round . From this, it is clear that all neighbours of will have received by round .
Corollary 4.9.
If (in ranked full-send flooding) a single node floods messages with initial rounds respectively, then every node receives every message and no node receives a given message more than twice.
If different nodes flood different messages, it cannot be guaranteed that every node receives every message in either partial-send or full-send flooding. One solution is for different messages received by a node, to be sent to neighbours in different successive rounds. This would be needed if message size is restricted as in a CONGEST model [31] of message passing. The flooding process from the point of view of an observer of the progress of a given flooding of a message , would appear as delays of more than one round between when is received and sent by a node. Such delays could lead to non-termination of the flooding of , as is discussed in subsections 5.1 and 5.2 below. Another solution, if message size is unrestricted as in the LOCAL model [31] of message passing, is basic flooding of all messages as in sections 2 and 3, independently and in parallel. This can result in growing message sizes as more and more messages of infinitely many would be flooded. A better solution is a parallel flooding version of ranked full-send flooding where a node which receives both older and some newer messages initially flooded by the same node, only sends the newer message. This reduces message size and all older and newer messages broadcast by any node are still received by every node. This follows by Corollary 4.9 applied to the observer of the sequence of floodings broadcast by a given node, which would effectively be ranked full-send flooding emanating from that node. It also means that, for the infinite sequences of messages flooded over time by a set of broadcasting nodes, at most messages are sent along any link in any round, thus requiring only a fixed finite size of message for transmission. Moreover, no record of previous rounds is kept.
4.3 Loss of edges or nodes during flooding
In the termination results Theorems 2.2, 4.4 and 4.8, we assume that the graph is fixed for the duration of the flooding process. Flooding proceeds in rounds acting on a fixed graph in all rounds, where is a fixed set of nodes and a fixed set of edges. The proofs in Theorems 2.2, 4.4 and 4.8 are unaffected if we allow the possibility of edge loss as flooding progresses, i.e. flooding proceeds in rounds on respective graphs:
| (30) |
Allowing loss of nodes follows easily. Given a graph and a node , let be the edges in not incident with . Then, is the subgraph of induced by the subset of nodes and is the subgraph of in which is isolated, i.e. with the same nodes as but with edges incident with removed. Clearly, given the sequence of graphs (30), flooding terminates on the sequence of graphs with monotonically decreasing sets of edges:
if and only if it terminates on the sequence of graphs where becomes isolated:
It follows, inductively, that flooding terminates on any sequence of graphs of the form:
5 Non-terminating cases
In this section, cases of amnesiac floodings that do not terminate generally are given.
5.1 Asynchronous flooding
We consider firstly an asynchronous message passing model in which an adaptive adversary can cause flooding to be non-terminating. In the model, the computation still proceeds in global synchronous rounds but the adversary can decide the delay of message delivery on any link. A message cannot be lost and will eventually be delivered, but the adversary can decide in which round to deliver the message. The adaptive adversary can decide on individual link delays for a round, based on the state of the network for the present and previous rounds (i.e. node states, messages in transit and message history). Otherwise, the flooding algorithm is the same as for the synchronous case. We show that the adversary can force asynchronous flooding to be non-terminating by adaptively choosing link delays. Consider the triangle graph in figure 6. In round 0, has a message as the source node which is then flooded. Figure 6 illustrates rounds 1-5. Both and send to each other in round 2. In round 3, sends to but the adversary makes hold the message for one round, indicated by a circled node. After that, in round 4, and send to each other. In any given round, the corresponding bidirected graph determines in which ways flooding can proceed. As the bidirected graphs in rounds 2 and 4 are equivalent (by a relation- and adversary-preserving isomorphism), flooding can proceed from round 4 in similar ways as from round 2 with the edges and interchanged and the adversary acting on node as before. The repeated adversarial intervention can prevent flooding from terminating.

5.2 Fixed delays at edges
In the asynchronous example in figure 6 above, the delay was caused by an adversary at node . The duration of message transmission along the edges and depended on whether the adversary was receiving or sending the message. If the delay along any edge is fixed and the same in both directions on the triangle graph, then flooding terminates. This raises the question of whether flooding terminates on any graph if delays along edges are the same in both directions. Consider the example in figure 7 below. We have a weighted graph with edges labelled by positive integers representing the message transit time in either direction.
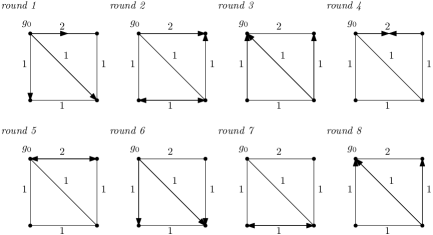
Flooding proceeds with respect to a global clock, the non-negative integer ticks of which define rounds. Flooding is initiated in round 1 when node sends to all neighbours. Message transit time is given in terms of the number of ticks of the clock taken. Arrowheads at nodes indicate a message being received at a node. Arrowheads not at nodes (as in round 4 of figure 7) indicate messages in transit. The arrowheaded graph in a round determines how flooding proceeds. As the arrowheaded graphs in rounds 3 and 8 are identical, flooding does not terminate.
5.3 Multiple messages - unranked full-send flooding
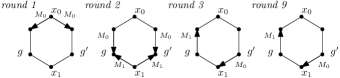
If a flooding algorithm for multiple messages chooses to send a received message to all neighbours from which it did not receive that message, and another node receiving the same messages chooses a different message then that can lead to non-termination. In figure 8, is flooded by in round 1 and by in round 2. Nodes and differ in the message they choose to forward in round 3. As a result the very same messages will be sent in round 9 and non-termination will ensue.
5.4 Addition of edges or nodes during flooding
In the simple example in figure 9 below, node initiates flooding in round 1. Edge is added in round 2. The message is sent to from to along that edge in round 3 and circulates in the graph forever. In the case of graphs that are odd cycles, if ranked full-send flooding is continuous, a later higher-ranked flooded message will eventually eliminate such lower-ranked rogue messages. However, if the graph has even cycles, it is possible for such a lower-ranked message to pass higher-ranked messages and evade elimination infinitely often.

6 Conclusion
In this paper we have shown that synchronous flooding terminates on any finite graph and that no node receives the message more than twice. From this we derived sharp bounds for termination times. We have extended to dynamic settings of potential use for applications such as broadcast and leader election algorithms, with multiple initiation times and messages. Our proofs showed that sequences of flooded messages originating from a given source could not survive longer in the presence of other dynamically flooded messages than if flooded alone from that source, and so termination and time to termination results carry over from the basic non-dynamic case. For ranked full-send flooding, we assumed that message ranking respected the order of time of initiation. This has a simpler proof. It is possible that some applications may rank messages otherwise. In fact, Theorem 4.8 can be proved without this assumption in a similar way to Theorem 4.4 using ef cycles.
Multiple-message flooding could be extended to the case where a given node floods different messages to different neighbours simultaneously when initiating a flooding. This would compound the problem of delivering every message to every node, if broadcast is the objective. This problem can be solved in network topologies which have multiple edge-disjoint Hamilton cycles - common examples include complete graphs, n-cubes [27], tori [3], star networks [33], [9] and transposition graphs [17] - or in graphs that may not be hamiltonian but may have edge-disjoint circuits [7] which visit every node in which nodes but not edges may be repeated. Multiple messages are sent in a given direction along different edge-disjoint circuits. Messages are forwarded by a node along the circuit on which they arrived. This guarantees that all messages sent by all nodes are received. However, the broadcast of a message takes at least as many rounds as there are vertices in the graph, unlike flooding which takes no more than about twice the diameter number of rounds. To improve the time taken to broadcast messages, when there are fewer such messages circulating in the network, a receiving node could forward a message received by a circuit edge further along that circuit, but also send the message to other unused edges in a ‘flooding’ fashion to hasten the broadcast. Such a flooding algorithm would be amnesiac, as the sending of messages would be determined only by the received messages in the previous round. Variations of such algorithms on different topologies can be simulated on a small scale and properties compared using temporal logic model checkers [4].
Another possible area of investigation is the design of ‘functional’ self-healing algorithms [5, 6] such that an ongoing flooding will still terminate despite nodes being adversarially deleted or inserted with judicious insertion of edges and maintaining of other invariants such as connectivity and expansion[28, 29, 16, 39, 15, 34].
References
- [1] Jordan Adamek, Mikhail Nesterenko, James Scott Robinson, and Sébastien Tixeuil. Stateless reliable geocasting. In 36th IEEE Symposium on Reliable Distributed Systems, SRDS 2017, Hong Kong, Hong Kong, September 26-29, 2017, pages 44–53. IEEE Computer Society, 2017.
- [2] H.Attiya and J.Welch.. Distributed Computing: Fundamentals, Simulations and Advanced Topics. John Wiley and Sons, 2004.
- [3] M.M.Bae and B.Bose. Edge disjoint Hamiltonian cycles in k-ary n-cubes and hypercubes. IEEE Transactions on Computers 52(10) (2003) 1271-1284, 2003. DOI: https://doi.org/10.1109/TC.2003.1234525.
- [4] R. Bani-Abdelrahman. Specification and verification of network algorithms using temporal logic. PhD thesis. Loughborough University, UK, 2019.
- [5] Armando Castañeda, Danny Dolev, and Amitabh Trehan. Compact routing messages in self-healing trees. Theoretical Computer Science, 709:2 – 19, 2018. Special Issue of ICDCN 2016 (Distributed Computing Track). DOI: https://doi.org/10.1016/j.tcs.2016.11.022
- [6] Armando Castañeda, Jonas Lefévre, and Amitabh Trehan. Fully compact routing in low memory self-healing trees. In Proceedings of the 21st International Conference on Distributed Computing and Networking, ICDCN 2020, New York, NY, USA, 2020. Association for Computing Machinery. DOI: doi:10.1145/3369740.3369786
- [7] P.A.Catlin. Supereulerian graphs: a survey. J. Graph Theory 16(2) (1992) 177-196, 1992.
- [8] Joshua N. Cooper and Jeol Spencer. Simulating a random walk with constant error. Combinatorics, Probability and Computing, 15(6):815–822, 2006.
- [9] P.Derakhshan and W.Hussak. Optimal bounds for disjoint Hamilton cycles in star graphs. Int. J. Found. Comp. Sci 29(3) (2018) 377-389, 2018. DOI: https://doi.org/10.1142/S0129054118500090.
- [10] B.Doerr, M.Fouz and T.Friedrich. Social networks spread rumors in sublogarithmic time. Electronic Notes in Discrete Mathematics. 38 (2011) 303-308, 2011.
- [11] J.Edmonds and E.L.Johnson. Matching: A Well-Solved Class of Integer Linear Programs. In: M.Jünger, G.Reinelt and G.Rinaldi (eds.), Combinatorial Optimization - Eureka, You Shrink!. Lecture Notes in Computer Science 2570 (2003) 27-30, Springer, 2003. DOI: https://doi.org/10.1007/3-540-36478-1_3.
- [12] Robert Elsässer and Thomas Sauerwald. The power of memory in randomized broadcasting. In Proceedings of the Nineteenth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA ’08, pages 218–227, Philadelphia, PA, USA, 2008. Society for Industrial and Applied Mathematics.
- [13] C. Gkantsidis, M. Mihail, and A. Saberi. Random walks in peer-to-peer networks: Algorithms and evaluation. Performance Evaluation, 63(3):241–263, 2006.
- [14] Ajei S. Gopal, Inder S. Gopal, and Shay Kutten. Fast broadcast in high-speed networks. IEEE/ACM Trans. Netw., 7(2):262–275, 1999.
- [15] Tom Hayes, Navin Rustagi, Jared Saia, and Amitabh Trehan. The forgiving tree: a self-healing distributed data structure. In PODC ’08: Proceedings of the twenty-seventh ACM symposium on Principles of distributed computing, pages 203–212, New York, NY, USA, 2008. ACM.
- [16] Thomas P. Hayes, Jared Saia, and Amitabh Trehan. The forgiving graph: a distributed data structure for low stretch under adversarial attack. Distributed Computing, pages 1–18, 2012. DOI: http://dx.doi.org/10.1007/s00446-012-0160-1.
- [17] W.Hussak. Disjoint Hamilton cycles in transposition graphs. Disc.App.Math. 206 (2016) 56-64, 2016. DOI: https://doi.org/10.1016/j.dam.2016.02.007.
- [18] Walter Hussak and Amitabh Trehan. On termination of a flooding process. In Peter Robinson and Faith Ellen, editors, Proceedings of the 2019 ACM Symposium on Principles of Distributed Computing, PODC 2019, Toronto, ON, Canada, July 29 - August 2, 2019., pages 153–155. ACM, 2019.
- [19] Walter Hussak and Amitabh Trehan. On the termination of a flooding process. CoRR, abs/1907.07078,2019.
- [20] Walter Hussak and Amitabh Trehan. On the Termination of Flooding. In Christophe Paul and Markus Bläser, editors, 37th International Symposium on Theoretical Aspects of Computer Science (STACS 2020), volume 154 of Leibniz International Proceedings in Informatics (LIPIcs), pages 17:1–17:13, Dagstuhl, Germany, 2020. Schloss Dagstuhl–Leibniz-Zentrum für Informatik.
- [21] Brad Karp and H. T. Kung. Gpsr: Greedy perimeter stateless routing for wireless networks. In Proceedings of the 6th Annual International Conference on Mobile Computing and Networking, MobiCom ’00, page 243?254, New York, NY, USA, 2000. Association for Computing Machinery.
- [22] Adrian Kosowski and Dominik Pajak. Does adding more agents make a difference? A case study of cover time for the rotor-router. J. Comput. Syst. Sci., 106:80–93, 2019.
- [23] Shay Kutten, Gopal Pandurangan, David Peleg, Peter Robinson, and Amitabh Trehan. On the complexity of universal leader election. J. ACM, 62(1):7:1–7:27, 2015.
- [24] Shay Kutten, Gopal Pandurangan, David Peleg, Peter Robinson, and Amitabh Trehan. Sublinear bounds for randomized leader election. Theoretical Computer Science, 561:134 – 143, 2015. Special Issue on Distributed Computing and Networking.
- [25] N.Lynch. Distributed Algorithms. Morgan Kaufmann Publishers, San Mateo, CA,1996.
- [26] Othon Michail and Paul G. Spirakis. Terminating population protocols via some minimal global knowledge assumptions. Journal of Parallel and Distributed Computing, 81-82:1 – 10, 2015.
- [27] K. Okuda and S. W. Song Revisiting Hamiltonian decomposition of the hypercube. Proceedings 13th Symposium on Integrated Circuits and Systems Design 2000, IEEE Computer Society, pp. 55-60, 2000. DOI: https//doi.org/10.1109/SBCCI.2000.876008.
- [28] Gopal Pandurangan, Peter Robinson, and Amitabh Trehan. DEX: self-healing expanders. Distributed Comput., 29(3):163–185, 2016. DOI: https://doi.org/10.1007/s00446-015-0258-3
- [29] Gopal Pandurangan and Amitabh Trehan. Xheal: a localized self-healing algorithm using expanders. Distributed Computing, 27(1):39–54, 2014. DOI: http://dx.doi.org/10.1007/s00446-013-0192-1.
- [30] David Peleg. Time-optimal leader election in general networks. J. Parallel Distributed Comput., 8(1):96–99, 1990.
- [31] David Peleg. Distributed Computing: A Locality Sensitive Approach. SIAM, 2000.
- [32] A.Rahman, W.Olesinski and P.Gburzynski. Controlled flooding in wireless ad-hoc networks, In: Proc. IWWAN’04, pp.73-78, 2004.
- [33] M.Rosenfeld, Z.Ryjacek, R.Cada and T.Kaiser. Disjoint Hamilton cycles in the star graph. Inf. Proc. Lett. 110 (2009) 30-35, 2009. DOI: https://doi.org/10.1016/j.ipl.2009.10.001.
- [34] Jared Saia and Amitabh Trehan. Picking up the pieces: Self-healing in reconfigurable networks. In IPDPS. 22nd IEEE International Symposium on Parallel and Distributed Processing., pages 1–12. IEEE, April 2008.
- [35] Atish Das Sarma, Danupon Nanongkai, and Gopal Pandurangan. Fast distributed random walks. In PODC, pages 161–170, 2009.
- [36] Atish Das Sarma, Danupon Nanongkai, Gopal Pandurangan, and Prasad Tetali. Efficient distributed random walks with applications. In PODC, 2010.
- [37] A.Tanenbaum. Computer Networks, Pearson Prentice Hall, 2011.
- [38] G.Tel. Introduction to Distributed Algorithms. Cambridge University Press, New York, NY, 1994.
- [39] Amitabh Trehan. Algorithms for self-healing networks. Dissertation, University of New Mexico, 2010. URL: http://proquest.umi.com/pqdlink?did=2085415901
- [40] V.Turau. Analysis of amnesiac flooding. arXiv:2002.10752., 2020. https://arxiv.org/abs/2002.10752
- [41] Volker Turau. Stateless Information Dissemination Algorithms. In Structural Information and Communication Complexity - 27th International Colloquium, SIROCCO, pages 183–199, Springer, June 2020.