Arias_Paola
Testing a new WISP Model with Laboratory Experiments
Abstract
We explore the phenomenological consequences of a model with axion-like particles and hidden photons mixing with photons. In this model, the hidden photon is directly coupled to the photon, while the axion coupling is induced by an external electromagnetic field. We consider vacuum effects on a polarised photon beam, like changes in the ellipticity and rotation angles.
1 Introduction
In this work we would like to go beyond the straightforward extension of the Standard Model, namely the one-missing-particle paradigm. On the one hand, seems timely, due to the extraordinary refinement in sensitivity of latest years of experiments looking for WISPs (Weakly Interactive Slim Particles). On the other hand, there are some proposals of more complex models with rich phenomenology, such as [1], where they consider a model with a hidden photon (HP) coupled to an axion-like field (ALP), and the kinetic mixing term. Also in [2] a model with axion-like particle + hidden photon was invoked to explain the 3.55 keV line in the spectra of galaxy clusters. More recently a similar model was considered [3], where the pseudo-scalar boson is the QCD axion, which is coupled to the hidden photon. We have chosen to follow the construct in [2], therefore the hidden photon is the mediator between visible and hidden sector. In this work we are interested in observables effects of this model, focusing on vacuum effects, like dichroism and birefringence.
2 The model and equations of motion
We consider the following effective Lagrangian:
Here is the photon field, the HP field and is the ALP. The HP is directly coupled to photons via the kinetic mixing term, parametrised by . As it is well known, defining and , removes the kinetic mixing, but at the price to inherit a coupling in the mass sector between photons and HPs, and also a term of the form , meaning an explicit coupling between photons and ALPs.
We start assuming a photon beam source of frequency , propagating in direction, and the plane wave approximation, i.e, , and . We also include an homogeneous magnetic field , oriented in the direction. Additionally, we assume no external hidden fields are present. Secondly, we linearise the equations of motion assuming the external electromagnetic field is much stronger than the photon source , and terms of the form , , can be neglected. Finally, considering a relativistic approximation, i.e, , we find the following equations111We work in the gauge and .:
| (1) |
| (2) |
Where and are the parallel and perpendicular components of the photon field to the external magnetic field, respectively. Equations (1) and (2) are of the Schroedinger-type, , where Eq. (1) is the usual one for a model of HP-photon oscillation. To solve Eq. (2) we introduce a rotation matrix that diagonalises the Hamiltonian, i.e, , where the eigenvalues are given by: , and , with:
| (3) |
The rotation matrix can be conveniently written in terms of two angles, and :
The states and are sterile to matter currents. Note that the limit can be obtained by taking when and when .
The evolution of the interaction states can be obtained from the evolution of mass eigenstates, related by , prime fields being mass eigenstates. Solving for both amplitudes of the photon after transversing a region of length we find:
| (4) | |||||
| (5) |
3 Ellipticity and rotation effects
After transversing the magnetic region , the beam has changed its amplitude and phase as we see in Eqs. (4)-(5), meaning that the beam develops a small ellipticity component and a rotation of the polarisation plane. Thus, the amplitudes evolve according to , the constant of proportionality being the initial polarisation angle, , with respect to the direction of the magnetic field . The change in the ellipticity and rotation angles it is given, respectively, by and . After some manipulation of we find:
| (6) | |||||
| (7) |
A similar analysis for gives and .
Let us point out that the dimensionless parameter , defined in Eq. (3), can be used to define two different regimes: , which translates into and , which translates into , if , or , if . In Fig. (1) we present exclusion plots to the ALP parameters using both ellipticity and rotation measurements.
Ellipticity effects: Let us first focus on the small mass region, where and thus, : this parameter space can remain uncovered if: i) there is a cancellation between the parallel and perpendicular contributions , which happens if both and . ii) and and , where we take as benchmark measured value of the ellipticity angle, as suggested by [4]. For instance, for , the opposite holds, meaning , and therefore the small mass region can be constrained up to eV-1, see Fig. (1). Going below those values of it is not possible due to the cancellation explained in i). On the other hand, for the opposite aforementioned condition also holds, but we see some stripes or gaps in sensitivity in the low mass region. They appear because when the condition , where is fulfilled, the ellipticity angle drops below . These gaps in sensitivity can be covered either by changing slightly any of the parameters: . Finally, for masses eV, the condition is no longer fulfilled and the angle starts slowly to approach to as grows over . When , the expression for the ellipticity angle is well approximated by
| (8) |
This is almost the same expression of the ellipticity angle for the photon-ALP model (see e.g. [5]), but with the replacement of by the ALP to photon coupling . If , then the above equation changes, replacing and an overall minus sign. Eq. (8) explains the already familiar V shape in the mass region eV.
Rotation effects: In the low mass region eV, the conditions and hold, thus we can approximate and . Therefore, in the low mass region the rotation angle is mass independent. This gives us the smallest to be constrained as
| (9) |
As the mass grows, we move to the weak mixing regime , where the ALP starts to decouple from the photon and HP. The change in the polarisation plane can be well approximated as (for )
| (10) |
When the difference goes to and the right hand side of the above equation cancels. This is the limit where the ALP decouples, and therefore the rotation effect is only due to the HP.
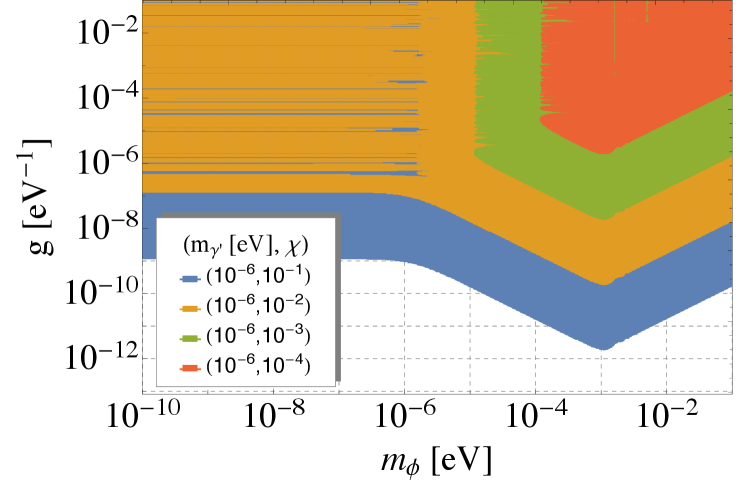
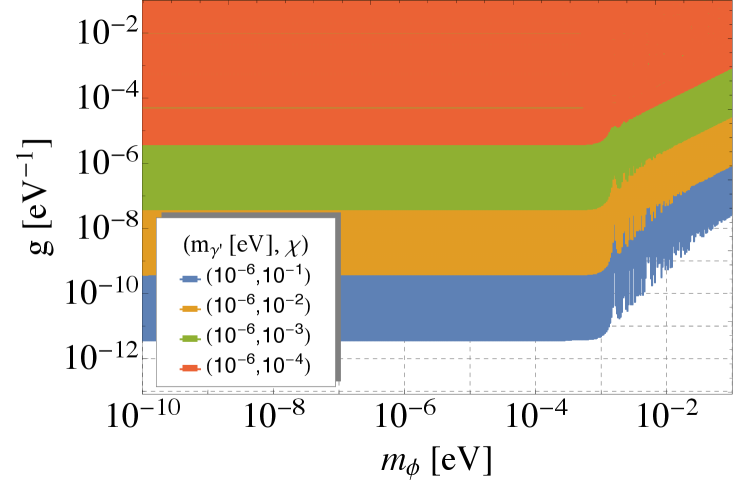
4 Conclusions
In this work we have considered a model that mixes photons, ALPs and HPs, we have shown interesting features on observable effects, in this case rotation of the polarisation plane and ellipticity of the beam. The parameters of the model can still be reasonably constrained using existing results from laboratory experiments. The next step is to consider more stringent scenarios, such as stellar production and early universe.
Acknowledgments: This work has been supported by FONDECYT project 1161150.
References
- [1] E. Masso and J. Redondo, JCAP 0509 (2005) 015
- [2] J. Jaeckel, J. Redondo and A. Ringwald, Phys. Rev. D 89 (2014) 103511 doi:10.1103/PhysRevD.89.103511
- [3] K. Kaneta, H. S. Lee and S. Yun, Phys. Rev. Lett. 118 (2017) no.10, 101802 doi:10.1103/PhysRevLett.118.101802
- [4] F. Della Valle, A. Ejlli, U. Gastaldi, G. Messineo, E. Milotti, R. Pengo, G. Ruoso and G. Zavattini, Eur. Phys. J. C 76 (2016) no.1, 24.
- [5] G. Raffelt and L. Stodolsky, Phys. Rev. D 37 (1988) 1237.