\wocname

EPJ Web of Conferences \woctitleLattice2017 ¹¹institutetext: Johann Wolfgang Goethe-Universität Frankfurt am Main, Institut für Theoretische Physik, Max-von-Laue-Strasse 1 D-60438 Frankfurt am Main, Germany ²²institutetext: Dipartimento di Fisica, UniversitÃ di Roma “Tor Vergata" and INFN, Sezione di Roma 2, Via della Ricerca Scientifica - 00133 Rome, Italy ³³institutetext: Centro Fermi - Museo Storico della Fisica e Centro Studi e Ricerche Enrico Fermi, Compendio del Viminale, Piazza del Viminiale 1, I-00184, Rome, Italy ⁴⁴institutetext: Higgs Centre for Theoretical Physics, School of Physics and Astronomy, The University of Edinburgh, Edinburgh EH9 3JZ, Scotland, UK ⁵⁵institutetext: Helmholtz Institut für Strahlen-und Kernphysik (Theorie), Nussallee 14-16 Bethe Center for Theoretical Physics, Nussallee 12 UniversitÃt Bonn, D-53115 Bonn, Germany

Testing a non-perturbative mechanism for elementary fermion mass generation: numerical results

\firstnameStefano \lastnameCapitani 11 \firstnameGiulia Maria \lastnamede Divitiis 22 \firstnamePetros \lastnameDimopoulos\fnsep Speaker, 2233 dimopoulos@roma2.infn.it \firstnameRoberto \lastnameFrezzotti 22 \firstnameMarco \lastnameGarofalo 44 \firstnameBastian \lastnameKnippschild 55 \firstnameBartosz \lastnameKostrzewa 55 \firstnameFerenc \lastnamePittler 55 \firstnameGiancarlo \lastnameRossi 2233 \firstnameCarsten \lastnameUrbach 55

Abstract

Based on a recent proposal according to which elementary particle masses could be generated by a non-perturbative dynamical phenomenon, alternative to the Higgs mechanism, we carry out lattice simulations of a model where a non-abelian strongly interacting fermion doublet is also coupled to a doublet of complex scalar fields via a Yukawa and an “irrelevant" Wilson-like term. In this pioneering study we use naive fermions and work in the quenched approximation. We present preliminary numerical results both in the Wigner and in the Nambu-Goldstone phase, focusing on the observables relevant to check the occurrence of the conjectured dynamical fermion mass generation effect in the continuum limit of the critical theory in its spontaneously broken phase.

1 Introduction

In Refs. Frezzotti:2014wja ; Frezzotti:2013raa a novel approach to the mass generation of elementary particles and the mass hierarchy problem has been proposed. It is based on a Non-Perturbative (NP) mechanism whose existence can be tested by studying, with the help of Lattice QCD (LQCD) simulations, the properties of a non-Abelian (SU(3) gauge) toy-model where an isospin doublet of strongly interacting fermions is coupled to a complex scalar field via Yukawa and Wilson-like terms. The Lagrangian of the toy-model reads:

	$\displaystyle{\cal L}_{\rm{toy}}(\Psi,A,\Phi)={\cal L}_{kin}(\Psi,A,\Phi)+{\cal V}(\Phi)+{\cal L}_{Wil}(\Psi,A,\Phi)+{\cal L}_{Yuk}(\Psi,\Phi)\,,$		(1)
	$\displaystyle\quad{\cal L}_{kin}(\Psi,A,\Phi)=\frac{1}{4}(F\cdot F)+\bar{\Psi}_{L}{\mbox{$\not\!\!\cal D$}}\Psi_{L}+\bar{\Psi}_{R}{\mbox{$\not\!\!\cal D$}}\,\Psi_{R}+\frac{1}{2}{\,\hbox{tr}\,}\big{[}\partial_{\mu}\Phi^{\dagger}\partial_{\mu}\Phi\big{]}$		(2)
	$\displaystyle\quad{\cal V}(\Phi)=\frac{\mu_{0}^{2}}{2}{\,\hbox{tr}\,}\big{[}\Phi^{\dagger}\Phi\big{]}+\frac{\lambda_{0}}{4}\big{(}{\,\hbox{tr}\,}\big{[}\Phi^{\dagger}\Phi\big{]}\big{)}^{2}$		(3)
	$\displaystyle\quad{\cal L}_{Yuk}(\Psi,\Phi)=\ \eta\,\big{(}\bar{\Psi}_{L}\Phi\Psi_{R}+\bar{\Psi}_{R}\Phi^{\dagger}\Psi_{L}\big{)}\,,$		(4)
	$\displaystyle\quad{\cal L}_{Wil}(\Psi,A,\Phi)=\frac{b^{2}}{2}\rho\,\big{(}\bar{\Psi}_{L}{\overleftarrow{\cal D}}_{\mu}\Phi{\cal D}_{\mu}\Psi_{R}+\bar{\Psi}_{R}\overleftarrow{\cal D}_{\mu}\Phi^{\dagger}{\cal D}_{\mu}\Psi_{L}\big{)}\,,$		(5)

where $b^{-1}=\Lambda_{UV}$ is the UV-cutoff. We denote with $\Psi_{L}=(u_{L}\,\,d_{L})^{T}$ and $\Psi_{R}=(u_{R}\,\,d_{R})^{T}$ the fermion iso-doublets. The Yukawa and Wilson-like terms are given by Eqs. (4) and (5), respectively. The latter is a six-dimensional operator multiplied by $b^{2}$ for dimensional reasons. The Yukawa coupling and the Wilson-like parameter are denoted by $\eta$ and $\rho$ , respectively. The scalar field $\Phi=(\phi,-i\tau^{2}\phi^{*})$ is a $2\times 2$ matrix with $\phi$ an iso-doublet of complex scalar fields. It obeys a quartic scalar potential denoted by the term ${\cal V}(\Phi)$ of eq. (3) where $\mu_{0}^{2}$ and $\lambda_{0}$ are, respectively, the (bare) values for the squared mass and the self-interaction coupling constant of the scalar field. Moreover $F_{\mu\nu}^{a}$ is the field strength for the gluon field ( $A_{\mu}^{a}$ with $a=1,2,\dots,N_{c}^{2}-1$ ). Finally, the covariant derivatives are given by:

{\cal D}_{\mu}=\partial_{\mu}-ig_{s}\lambda^{a}A_{\mu}^{a}\,,\qquad\overleftarrow{\cal D}_{\mu}=\overleftarrow{\partial}_{\mu}+ig_{s}\lambda^{a}A_{\mu}^{a}\,,

(6)

A study of the unification of electroweak and strong interactions based on the above proposal has been presented in Ref. Frezzotti:2016bes . On-going work on the toy-model has been reported in Ref. Capitani:2016ycp .

2 Symmetries and properties of the model

The toy-model respects Lorentz, gauge, and $C$ , $P$ , $T$ and $CPF_{2}$ symmetries (see Ref. Frezzotti:2014wja ). Moreover it enjoys an exact symmetry under the global transformations $\chi_{L}$ and $\chi_{R}$ defined as:

\begin{array}[]{lcl}\chi_{L}:\tilde{\chi}_{L}\otimes(\Phi\rightarrow\Omega_{L}\Phi),&&\chi_{R}:\tilde{\chi}_{R}\otimes(\Phi\rightarrow\Omega_{R}\Phi),\\ \hskip-28.45274pt\text{with\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ }\tilde{\chi}_{L}:\Psi_{L}\rightarrow\Omega_{L}\Psi_{L},&&\tilde{\chi}_{R}:\Psi_{R}\rightarrow\Omega_{R}\Psi_{R},\\ \hskip 17.07182pt\bar{\Psi}_{L}\rightarrow\bar{\Psi}_{L}\Omega_{L}^{\dagger},&&\hskip 18.49411pt\bar{\Psi}_{R}\rightarrow\bar{\Psi}_{R}\Omega_{R}^{\dagger},\\ \hskip-31.2982pt\text{where\leavevmode\nobreak\ \leavevmode\nobreak\ }\hskip 17.07182pt\Omega_{L}\in SU(2)_{L},&&\hskip 18.49411pt\Omega_{R}\in SU(2)_{R}.\\ &&\\ &&\\ \end{array}\vskip-25.6073pt

(7)

The toy-model (1), similarly to the LQCD case, is power-counting renormalizable with counter-terms constrained by the exact symmetries of the Lagrangian. In particular, thanks to the exact $\chi\equiv\chi_{L}\otimes\chi_{R}$ symmetry, owing to the inclusion of the scalar field in the Wilson term, there is no power divergent fermion mass terms, unlike to the Wilson-LQCD case. However the pure fermionic chiral transformations, $\tilde{\chi}\equiv\tilde{\chi}_{L}\otimes\tilde{\chi}_{R}$ , do not constitute a symmetry of ${\cal L}_{\rm{toy}}$ due to the presence of the Yukawa and Wilson terms (for non-zero values of $\eta$ and $\rho$ ).

The physical implications of the toy-model depend crucially on the phase, Wigner or Nambu-Goldstone (NG), of the scalar potential ${\cal V}(\Phi)$ . Following the line of argument of Ref. Frezzotti:2014wja it can be shown that $\tilde{\chi}$ -symmetry enhancement takes place in the Wigner phase at a critical value of the Yukawa coupling. In fact by working in a way analogous to Ref. Bochicchio:1985xa one can get the renormalised Schwinger-Dyson equation (SDE) under $\tilde{\chi}_{L}$ transformations¹¹1Thanks to parity symmetry a similar equation holds for the $\tilde{\chi}_{R}$ transformations.:

\partial_{\mu}\langle Z_{\partial\tilde{J}}\tilde{J}^{L,i}_{\mu}(x)\,\hat{\cal O}(0)\rangle\!=\!\langle\tilde{\Delta}_{L}^{i}\hat{\cal O}(0)\rangle\delta(x)-({\eta-\overline{\eta}})\,\langle{O_{Yuk}^{L,i}}(x)\,\hat{\cal O}(0)\rangle+{\ldots}+{\mbox{O}(b^{2})}\,,

(8)

in which the operator mixing under renormalisation of the $d$ =6 operators with the two $d$ =4 ones has been taken into account and the current (the four-divergence of which is renormalised by $Z_{\partial\tilde{J}}\equiv Z_{\partial\tilde{J}}(\eta;g^{2}_{s},\rho,\lambda_{0})$ ) is defined by:

\tilde{J}_{\mu}^{L\,,i}=\bar{\Psi}_{L}\gamma_{\mu}\frac{\tau^{i}}{2}\Psi_{L}-\frac{b^{2}}{2}\rho\Big{(}\bar{\Psi}_{L}\frac{\tau^{i}}{2}\Phi{\cal D}_{\mu}\Psi_{R}-\bar{\Psi}_{R}\overleftarrow{\cal D}_{\mu}\Phi^{\dagger}\frac{\tau^{i}}{2}\Psi_{L}\Big{)}\,.

(9)

Notice that thanks to the $\chi$ -symmetry discretisation effects in Eq. (8) are of $\mbox{O}(b^{2})$ while the ellipses stand for possible contributions owing to possible NP operator mixing. The SDE of Eq. (8) becomes a WTI at a critical value of the Yukawa coupling, $\eta=\eta_{cr}(g^{2}_{s},\rho,\lambda_{0})$ , obtained by $\eta_{cr}(g^{2}_{s},\rho,\lambda_{0})-\bar{\eta}(\eta_{cr};g^{2}_{s},\rho,\lambda_{0})=0$ . In this case $\tilde{\chi}$ -symmetry restoration occurs, up to discretisation effects of $\mbox{O}(b^{2})$ , scalars get decoupled from quark and gluons, fermion mass is expected to vanish, and Eq. (8) becomes:

\partial_{\mu}\langle Z_{\partial\tilde{J}}\tilde{J}^{L,i}_{\mu}(x)\,\hat{\cal O}(0)\rangle\!=\!\langle\tilde{\Delta}_{L}^{i}\hat{\cal O}(0)\rangle\delta(x)+{\mbox{O}(b^{2})}\,,

(10)

In the Wigner phase no spontaneous symmetry breaking (SSB) effect takes place, so the operator mixing is expected to follow perturbation theory arguments; as a consequence there are no ellipses in Eq. (10). In the NG phase instead, a $\tilde{\chi}$ SSB effect is expected to occur triggered by residual cutoff effects of $\mbox{O}(b^{2})$ , yielding new operator mixing terms of NP nature. In that case it is conjectured that Eq. (8) takes the form:

\partial_{\mu}\langle Z_{\partial\tilde{J}}\tilde{J}^{L,i}_{\mu}(x)\,\hat{\cal O}(0)\rangle_{\eta_{cr}}=\langle\tilde{\Delta}_{L}^{i}\hat{\cal O}(0)\rangle_{\eta_{cr}}\delta(x)+C_{1}\Lambda_{s}\langle{[\overline{\Psi}_{L}\frac{\tau^{i}}{2}{\cal U}\Psi_{R}+\mbox{h.c.}]}\hat{\cal O}(0)\rangle+{\mbox{O}}(b^{2})

(11)

where ${\cal U}$ is a dimensionless non-analytic function of $\Phi$ given by

{\cal U}=\frac{\Phi}{\sqrt{\Phi^{\dagger}\Phi}}=\frac{v+\sigma+i\,\overrightarrow{\tau}\,\overrightarrow{\pi}}{\sqrt{(v+\sigma)^{2}+\overrightarrow{\pi}\,\overrightarrow{\pi}}}\,.

(12)

The RGI term $C_{1}\Lambda_{s}\bar{\Psi}_{L}\frac{\tau^{i}}{2}{\cal U}\Psi_{R}$ is $\chi_{L}\otimes\chi_{R}$ invariant²²2Note that a mass term of the form $[\bar{\Psi}_{L}\Psi_{R}+\bar{\Psi}_{R}\Psi_{L}]$ is not invariant under $\chi_{L}\otimes\chi_{R}$ transformations. and is well defined only in the NG phase in which $\langle\Phi\rangle=v\neq 0$ . $\Lambda_{s}$ stands for the scale of strong interactions that in our simulation setup (see next section) is identified with $\Lambda_{QCD}$ .

3 Lattice simulations and results

In this preliminary numerical study of the toy-model we have performed lattice simulations in the quenched approximation, where gauge and scalar fields can be generated independently. The verification or falsification process of the NP mechanism for fermionic mass generation is totally unaffected by the present choice to carry out simulations within the (computationally cheap) quenched fermion approximation. We have employed naive Dirac fermions for which the $\chi_{L}\otimes\chi_{R}$ symmetry is exact. We have used the symmetric covariant derivative, $\tilde{\nabla}_{\mu}$ , throughout because with this choice the Wilson-like action term has symmetry properties (see BSMLAT17_1 , sect. 2) such that, even in the presence of fermion doublers, the value of $\eta_{cr}$ is unique. In order to avoid exceptional configurations due to the possible presence of fermionic zero modes the twisted mass term, $i\mu_{Q}\bar{\Psi}\gamma_{5}\tau^{3}\Psi$ , has been added in the lattice action (see Ref. Frezzotti:2000nk ). The soft $\chi_{L}\otimes\chi_{R}$ symmetry breaking owing to the presence of the twisted mass term is eliminated in the limit $\mu_{Q}\rightarrow 0$ . For full discussion of the lattice setup we refer the reader to the companion contribution at this conference BSMLAT17_1 .

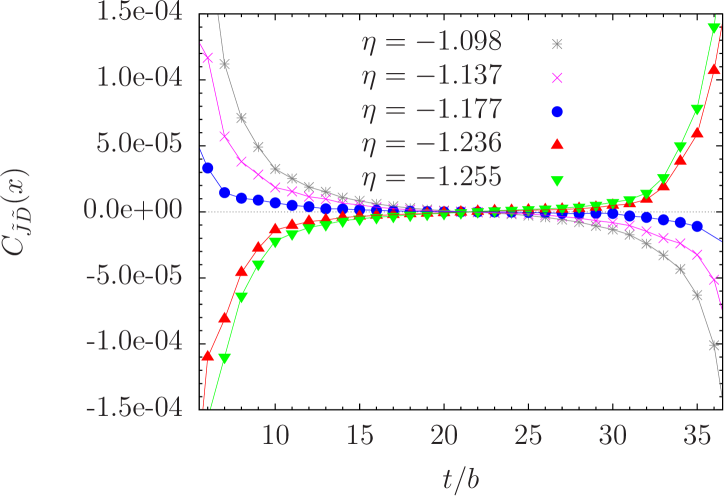
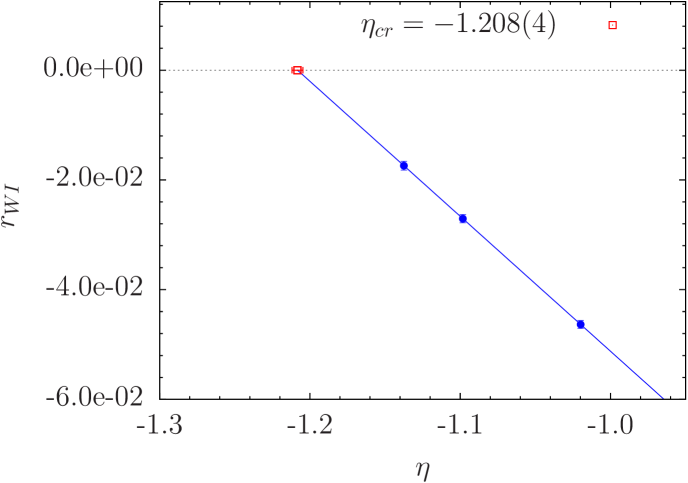
Refer to caption — (a) An example of the behaviour of the correlation function $C_{\tilde{J}\tilde{D}}(x)\equiv\langle\tilde{J}_{0}^{V,\,3}(x)\tilde{D}^{S,\,3}(0)\rangle$ against the Euclidean time for several values of $\eta$ at a certain value of $b\mu_{Q}=0.0224$ .

In these proceedings we present a preliminary status of the simulations and analysis of the results. We have performed simulations on a lattice volume $16^{3}\times 40$ at one value of the gauge coupling ( $\beta=5.85$ ) which corresponds to a lattice spacing of about $a=0.123$ fm. Our lattice scale is given by $r_{0}=0.5$ fm determined in quenched LQCD in Refs Guagnelli:1998ud and Necco:2001xg . For simulations in the Wigner and NG phases we keep fixed the value of the Wilson parameter ( $\rho=1.961$ ), the renormalised values of the $\sigma$ -mass and the renormalised scalar coupling, i.e. $r_{0}^{2}m^{2}_{\sigma}=1.276(6)$ and $\lambda_{R}=\frac{m_{\sigma}^{2}}{2v_{R}^{2}}=0.4377(31)$ . The statistics are 240 gauge $\times$ scalar configurations for several values of the Yukawa coupling, $\eta$ , and at least three values of the twisted mass parameter, $\mu_{Q}$ for each value of $\eta$ . For noise reduction we have used locally smeared scalar fields in the lattice action.

3.1 Determination of the critical Yukawa coupling in the Wigner phase

In order to avoid unnecessary contributions in the SDEs due to the presence of the twisted mass regulator in our lattice action, we employ the vector combination of $L$ -handed and $R$ -handed isotriplet currents, which obeys the following renormalized SDE (for $x\neq 0)$ :

\partial_{\mu}\langle Z_{\tilde{J}}\tilde{J}^{V,3}_{\mu}(x)\,\tilde{D}^{S,3}(0)\rangle\!=({\eta-\eta_{cr})\,\langle\tilde{D}^{S,3}}(x)\,\tilde{D}^{S,3}(0)\rangle+{\mbox{O}(b^{2})}

(13)

where we have defined:

	$\displaystyle\hskip 0.0pt\tilde{J}_{0}^{V,\,3}(x)$	$\displaystyle=$	$\displaystyle\tilde{J}_{0}^{L,\,3}(x)+\tilde{J}_{0}^{R,\,3}(x),$
	$\displaystyle\hskip 0.0pt\tilde{D}^{S,\,3}(x)$	$\displaystyle=$	$\displaystyle\bar{\Psi}_{L}(x)\left[\Phi,\frac{\tau^{3}}{2}\right]\Psi_{R}(x)-\bar{\Psi}_{R}(x)\left[\frac{\tau^{3}}{2},\Phi^{\dagger}\right]\Psi_{L}(x)$		(14)

and

\hskip 0.0pt\tilde{J}_{0}^{L/R,\,3}(x)=\frac{1}{2}\left[\bar{\Psi}_{L/R}(x-\hat{0})\gamma_{0}\frac{\tau_{3}}{2}U_{0}(x-\hat{0})\Psi_{L/R}(x)+\bar{\Psi}_{L/R}(x)\gamma_{0}\frac{\tau_{3}}{2}U_{0}^{\dagger}(x-\hat{0})\Psi_{L/R}(x-\hat{0})\right].

(15)

In the Wigner phase at $\eta=\eta_{cr}$ the correlation function $C_{\tilde{J}\tilde{D}}(x_{0})\equiv\sum_{\vec{x}}\langle\tilde{J}_{0}^{V,3}(x)\tilde{D}^{S,3}(0)\rangle$ is expected to vanish thanks to the restoration of the $\tilde{\chi}$ –symmetry. This behaviour can be noticed, as a tendency, by looking at the data in Fig. 1(a), where the correlator $C_{\tilde{J}\tilde{D}}(x_{0})$ is shown for several values of $\eta$ at a certain value of $b\mu_{Q}=0.0224$ (in lattice units). The vanishing of $\lim_{\mu_{Q}\to 0}C_{\tilde{J}\tilde{D}}(x_{0})$ at $\eta=\eta_{cr}$ implies, in the absence of massless particles (which we explicitly check in our simulations), that all the on-shell matrix elements of $\tilde{J}_{0}^{V,3}$ must vanish in the same limit.

These remarks in turn suggest to determine $\eta_{cr}$ by looking at the renormalized SDE of vector- $\tau^{3}$ $\tilde{\chi}$ transformations, namely

\partial_{\lambda}\tilde{J}_{\lambda}^{V,3}(x)=k_{\tilde{J}}(\eta-\eta_{cr})\tilde{D}^{S,3}(x)+{\rm O}(b^{2})\;,\quad k_{\tilde{J}}=Z_{\partial\tilde{J}}^{-1}\frac{\eta-\bar{\eta}}{\eta-\eta_{cr}}

(16)

with $k_{\tilde{J}}$ analytic in $\eta$ at $\eta=\eta_{cr}$ and O(1) (see [7] about $Z_{\partial\tilde{J}}$ ). This being an operator equation (with the form of a Ward Identity at $\eta=\eta_{cr}$ ) that holds on-shell for arbitrary intermediate states, it looks convenient to study the ratio

r_{WI}(x_{0})=\frac{\partial_{0}\sum_{\vec{x}}\,\langle\tilde{J}_{0}^{V,3}(x)D^{S,3}(0)\rangle}{\sum_{\vec{x}}\,\langle D^{S,3}(x)D^{S,3}(0)\rangle}=k_{\tilde{J}}(\eta-\eta_{cr})+{\rm O}(b^{2})\;.

(17)

Indeed taking the average of $r_{WI}(x_{0})$ over a $x_{0}$ –window where only few low-lying states contribute to the correlators in the ratio one gets a quantity,

r_{WI}^{[\tau_{1},\tau_{2}]}(\eta,\mu_{Q})\equiv\frac{1}{\tau_{2}-\tau_{1}}\sum_{x_{0}=\tau_{1}}^{\tau_{2}}r_{WI}(x_{0};[\tau_{1},\tau_{2}])\;,

(18)

with reduced statistical noise and small O( $b^{2}\Lambda_{s}^{2}$ ) deviations from $k_{\tilde{J}}(\eta-\eta_{cr})$ . In particular, if $\eta_{cr}$ is determined by imposing the condition

r_{WI}^{[\tau_{1},\tau_{2}]}(\eta=\eta_{cr};\mu_{Q}=0)=0

(19)

for an appropriate time window $[\tau_{1},\tau_{2}]$ kept fixed in physical units at different lattice spacings, the O( $b^{2}\Lambda_{s}^{2}$ ) cutoff effect in eq. (17), and the resulting one on the estimate of $\eta_{cr}$ at each $\beta$ , by construction will scale nicely towards zero as $b^{2}\to 0$ , thereby having no impact on the properties of the critical model that are established in the continuum limit.

The extrapolation of $r_{WI}^{[\tau_{1},\tau_{2}]}(\eta,\mu_{Q})$ to $\mu_{Q}=0$ is easy in the Wigner phase, where absence of spontaneous symmetry breaking of $\chi$ -symmetry ³³3The study of the present toy model in the Wigner phase is possibly the first example in the literature of a local field theory where confinement due to strong interactions takes place in the absence of spontaneous chiral symmetry breaking. and parity invariance entail an analytic dependence of $r_{WI}$ on $\mu_{Q}^{2}$ , which happens to be numerically small and comparable to the statistical errors in the explored $\mu_{Q}$ -range ( $b\mu_{Q}=0.0224,0.0316,0.0387$ ).

The resulting values of $r_{WI}^{[\tau_{1},\tau_{2}]}(\eta;\mu_{Q}=0)$ , for $[\tau_{1},\tau_{2}]=[1.72,2.21]$ fm are shown in Fig. 1(b). Our preliminary result for the critical value of the Yukawa coupling determined in this way at $\beta=5.85$ is $\eta_{cr}=-1.208(4)$ .

3.2 Dynamically generated fermion mass in the NG phase

In the NG phase the $\chi_{L}\otimes\chi_{R}$ symmetry is broken to the $\chi_{V}$ -symmetry. Moreover, at $\eta_{cr}$ the $\tilde{\chi}_{L}\otimes\tilde{\chi}_{R}$ symmetry, according to our conjecture, is expected to be spontaneously broken due to O $(b^{2})$ effects. In Ref. Frezzotti:2014wja it has been argued that in the NG phase the local effective action density of the model⁴⁴4The scalar potential here, $V_{\mu^{2}_{\Phi}<0}(\Phi)$ , is written in terms of the renormalised parameters $\mu^{2}_{\Phi}$ and $\hat{\lambda}$ . In the expression (20) one could add one or more kinds of kinetic term of ${\cal U}$ that are proportional to $\Lambda_{s}$ . However, for $v\gg\Lambda_{s}$ which is the typical regime for our mechanism these terms will be negligible. reads:

\Gamma^{NG}=\frac{1}{4}(F\cdot F)+\bar{Q}\mbox{$\not\!\!D$}Q+\frac{1}{2}\rm{Tr}\left[\partial_{\mu}\Phi^{\dagger}\partial_{\mu}\Phi\right]+V_{\mu^{2}_{\Phi}<0}(\Phi)+(\eta-\eta_{cr})(\bar{\Psi}_{L}\langle\Phi\rangle\Psi_{R}+{\mbox{h.c.}})+c_{1}\Lambda_{s}(\bar{\Psi}_{L}{\cal U}\Psi_{R}+{\mbox{h.c.}}).

(20)

We also note that in the NG phase the Wilson-like term gets effectively a form analogous to the one of the Wilson term in Lattice QCD. Indeed by setting $r=bv\rho$ (with $v$ the scalar field vev) and neglecting quantum field fluctuations the Wilson-like term in the toy model lattice action can be rewritten in the form

{\cal L}_{Wil}^{QCD}(\Psi,A)=-\frac{br}{2}\left(\bar{\Psi}_{L}D^{2}\Psi_{R}+\text{h.c.}\right).

Simulations in the NG phase are performed by employing the same values for the set of the parameters ( $\beta$ , $\lambda_{R}$ , $\rho$ ) and the lattice volume as in the Wigner phase.

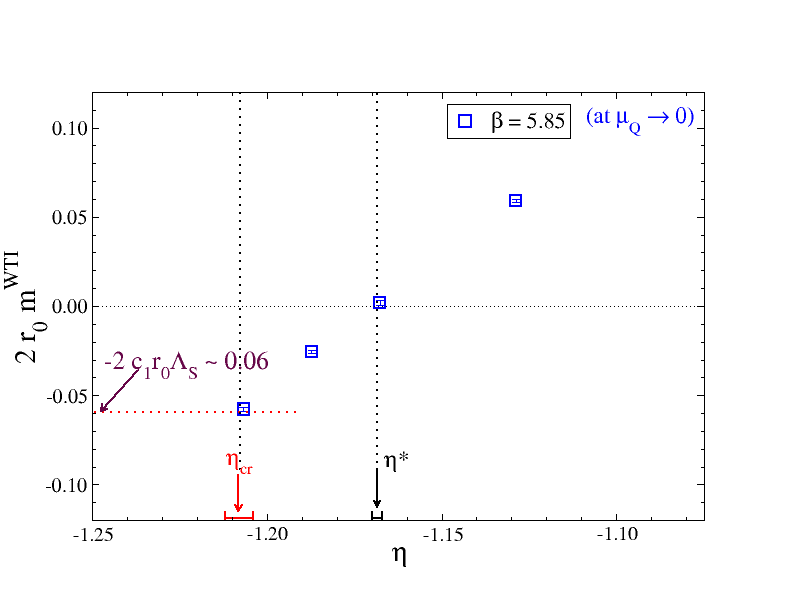
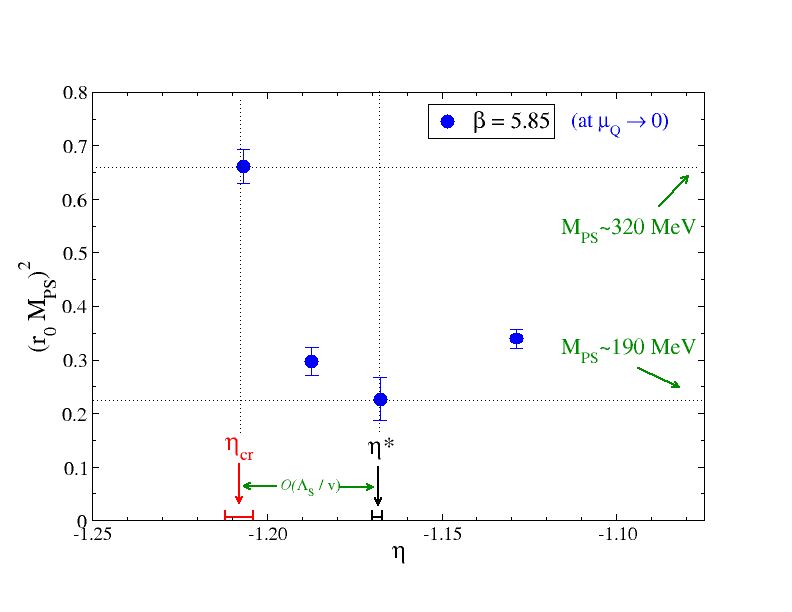
The effective quark mass (in the $\mu_{Q}=0$ limit) can be read off from the axial $\tilde{\chi}$ WTI, e.g.

2m^{WTI}=\dfrac{b^{-1}\partial_{0}\langle 0|\widetilde{J}^{A\pm}_{0}|M_{PS^{\pm}}\rangle}{\langle 0|P^{\pm}|M_{PS^{\pm}}\rangle}

(21)

where

\widetilde{J}^{A\pm}_{0}(x)=\bar{\Psi}(x-\hat{0})\gamma_{0}\gamma_{5}\dfrac{\tau_{1}\pm i\tau_{2}}{2}U_{0}(x-\hat{0})\Psi(x)+\bar{\Psi}(x)\gamma_{0}\gamma_{5}\dfrac{\tau_{1}\pm i\tau_{2}}{2}U_{0}^{\dagger}(x-\hat{0})\Psi(x-\hat{0})

is the one-point-split current associated to the fermionic ( $\tilde{\chi}$ ) axial transformations and $P^{\pm}(x)=\bar{\Psi}(x)\gamma_{5}\dfrac{\tau_{1}\pm i\tau_{2}}{2}\Psi(x)$ is the pseudoscalar density.

In Fig. 2(a) we show results for the bare quark mass (multiplied by a factor of two) in units of $r_{0}$ against the Yukawa coupling. The results have been obtained using Eq. (21) at several values of $(\eta,\mu_{Q})$ . For each value of $\eta$ a linear extrapolation to $\mu_{Q}=0$ has been performed. Small deviations from linearity are possible and their impact is presently under study by extra simulations at further $\mu_{Q}$ values and more elaborate fits. At $\eta=\eta_{cr}$ , where the Yukawa quark mass term gets cancelled, the $m^{WTI}$ is expected to be equal to the conjectured quark mass of NP origin, $c_{1}\Lambda_{s}$ . As it can be seen from that figure, based on our preliminary data, a rough estimate of the bare quark mass⁵⁵5The work for the quark mass renormalisation is on-going. The method is described in the companion contribution BSMLAT17_1 . in $r_{0}$ units is $-2r_{0}c_{1}\Lambda_{s}\simeq 0.06$ . Passing now to Fig. 2(b) where $(r_{0}M_{\text{PS}})^{2}$ is shown against the Yukawa coupling we notice that at $\eta=\eta_{cr}$ the corresponding value for the pseudoscalar mass is rather large (of about 320 MeV or larger). We would also like to draw the attention to an interesting feature which occurs at the value of the Yukawa coupling, namely $\eta^{*}$ , at which $m^{WTI}$ vanishes. With the help of the effective action density of Eq. (20) one can deduce that, defining $m^{WTI}\equiv(\eta^{*}-\eta_{cr})v+c_{1}\Lambda_{s}=0$ entails $\eta^{*}=\eta_{cr}-c_{1}\Lambda_{s}/v$ . Our data gives evidence that $\eta^{*}-\eta_{cr}\neq 0$ which further supports the conclusion that the dynamically generated quark mass is non-zero⁶⁶6Subsequent work following our presentation at Lattice 2017 has provided further numerical results at two lattice spacings, which strenghtens the evidence in favour of the dynamical fermion mass generation mechanism that is discussed here, see bsm_forthcoming ..

4 Summary and further developments

We have discussed a toy-model that exemplifies a novel NP mechanism proposed in Ref. Frezzotti:2014wja for dynamical fermion mass generation. The fundamental property of the mechanism consists in the enhancement of the QCD symmetries in such a way that fermion masses emerge in a natural way tHooft:1979rat , being independent from the Yukawa interaction and the scalar field. Thanks to the NP character of the mechanism the physical implications and predictions of the associated toy-model can be tested with the help of simulations on the lattice. We have presented preliminary results based on simulations in the quenched approximation at one value of the lattice spacing. Our results for the dynamically generated effective fermion mass and the associated pseudoscalar meson mass in the NG phase, barring cutoff effects, are of O $(\Lambda_{s})$ . Since the presentation at the conference we have performed more simulations at the present lattice spacing and improved our methods of analysis. We have also carried out simulations at a second value of the lattice spacing in order to be able to check the scaling behaviour both of the fermion mass and the pseudoscalar meson mass. All these results that show rather smooth scaling properties will be presented soon in bsm_forthcoming .

Acknowledgements
We acknowledge support from INFN, via the convention INFN-Cineca which made available to us the CPUtime for carrying out numerical simulations on Galileo, Marconi A1 and Marconi A2 clusters. Support from the Sino-German CRC110 research network is also gratefully acknowledged.

References

(1) R. Frezzotti, G.C. Rossi, Phys. Rev. D92, 054505 (2015), 1402.0389
(2) R. Frezzotti, G.C. Rossi, PoS LATTICE2013, 354 (2014), 1312.1069
(3) R. Frezzotti, M. Garofalo, G.C. Rossi, Phys. Rev. D93, 105030 (2016), 1602.03684
(4) S. Capitani et al., PoS LATTICE2016, 212 (2016), 1611.03997
(5) M. Bochicchio, L. Maiani, G. Martinelli, G.C. Rossi, M. Testa, Nucl. Phys. B262, 331 (1985)
(6) R. Frezzotti, P.A. Grassi, S. Sint, P. Weisz (Alpha), JHEP 08, 058 (2001), hep-lat/0101001
(7) S. Capitani et al., Testing a non-perturbative mechanism for elementary fermion mass generation: lattice setup, in Proceedings, 35th International Symposium on Lattice Field Theory (Lattice2017): Granada, Spain, to appear in EPJ Web Conf.
(8) M. Guagnelli, R. Sommer, H. Wittig (ALPHA), Nucl. Phys. B535, 389 (1998), hep-lat/9806005
(9) S. Necco, R. Sommer, Nucl. Phys. B622, 328 (2002), hep-lat/0108008
(10) in preparation.
(11) G. ’t Hooft, Naturalness, chiral symmetry, and spontaneous chiral symmetry breaking in Recent Developments in Gauge Theories. Proceedings, Nato Advanced Study Institute, Cargese, France, August 26 - September 8, 1979, NATO Sci. Ser. B 59, 135 (1980)