Testing planet formation from the ultraviolet to the millimeter
Abstract
Gaps imaged in protoplanetary discs are suspected to be opened by planets. We compute the present-day mass accretion rates of seven hypothesized gap-embedded planets, plus the two confirmed planets in the PDS 70 disc. The accretion rates are based on disc gas surface densities from C18O observations, and planet masses from simulations fitted to observed gaps. Assuming accretion is Bondi-like, we find in eight out of nine cases that is consistent with the time-averaged value given by the current planet mass and system age, . As system ages are comparable to circumstellar disc lifetimes, these gap-opening planets may be undergoing their last mass doublings, reaching final masses of for the non-PDS 70 planets, and for the PDS 70 planets. For another fifteen gaps without C18O data, we predict by assuming their planets are accreting at their time-averaged . Bondi accretion rates for PDS 70b and c are orders of magnitude higher than accretion rates implied by measured U-band and H fluxes, suggesting most of the accretion shock luminosity emerges in as yet unobserved wavebands, or that the planets are surrounded by dusty, highly extincting, quasi-spherical circumplanetary envelopes. Thermal emission from such envelopes or from circumplanetary discs, on Hill sphere scales, peaks at wavelengths in the mid-to-far-infrared and can reproduce observed mm-wave excesses.
keywords:
planets and satellites: formation – planets and satellites: general – planets and satellites: fundamental parameters – protoplanetary discs – planet–disc interactions1 Introduction
The Atacama Large Millimeter Array (ALMA) has revealed gaseous protoplanetary discs to be ringed and gapped, with HL Tau (ALMA Partnership et al. 2015) and discs from the DSHARP (Andrews et al., 2018) and MAPS (Oberg et al., 2021) surveys providing stunning examples (see also Cieza et al. 2019; Andrews 2020). The annular structures observed at orbital distances of au are commonly interpreted as being carved by protoplanets within the gaps, by analogy with shepherd satellites opening gaps in planetary rings (e.g. Goldreich & Tremaine 1979). A few dozen candidate planets have been so hypothesized with masses of several Earth masses to a few Jupiter masses (Zhang et al. 2018; figure 1 of Lodato et al. 2019; and Table 1 of this paper).
So far disc-embedded protoplanets have been directly imaged in one system: PDS 70b and c are confirmed in the near-infrared to orbit at au within the central clearing of the system’s transitional disc (Keppler et al. 2018; Haffert et al. 2019; Wang et al. 2020, 2021, and references therein). These protoplanets, each estimated to be of order a Jupiter mass, have been imaged at multiple wavelengths, from the ultraviolet at 336 nm (Zhou et al., 2021) to H (Haffert et al., 2019) to the sub-millimeter continuum (Isella et al., 2019; Benisty et al., 2021). Aside from PDS 70b and c, all other planets proposed to explain disc sub-structures remain undetected. There are unconfirmed near-infrared point sources in HD 163296 (Guidi et al. 2018) and Elias 24 (Jorquera et al. 2021), and kinematical evidence for planetary perturbations to the rotation curve in HD 163296 (Teague et al. 2018; Teague et al. 2021).
Are the disc gaps and rings imaged by ALMA and in the infrared (e.g. Asensio-Torres et al. 2021) really caused by planets? What can we hope to learn from DSHARP discs and similar systems about how planets form? At the top of the list of measurables should be the planetary mass accretion rate and how it depends on and ambient disc properties like density and temperature. The planet masses inferred from modeling disc sub-structures are frequently dozens of Earth masses (e.g. Dong & Fung 2017; Zhang et al. 2018; our Table 1),111The gaps simulated by Zhang et al. (2018) and similar works are opened because of the repulsive Lindblad torques exerted by planets. These planet-disk simulations neglect accretion onto the planet (cf. Rosenthal et al. 2020 and references therein). large enough that an order-unity fraction of their mass should be in the form of accreted hydrogen. For such planets with self-gravitating gas envelopes, accretion may be hydrodynamic, i.e. regulated by how much mass the surrounding nebula can deliver to the planet through transonic/supersonic flows (e.g. D’Angelo et al. 2003; Machida et al. 2010; Tanigawa & Tanaka 2016; Ginzburg & Chiang 2019a). This phase is distinct from an earlier thermodynamic phase of gas accretion limited by the rate at which the nascent envelope can cool and contract quasi-hydrostatically (e.g. Lee & Chiang 2015; Ginzburg et al. 2016; Chachan et al. 2021). Are the inferences of planets still immersed in their parent discs consistent with our ideas of hydrodynamic accretion? To what final masses should we expect the hypothesized planets to grow?
This paper takes stock of the developing landscape of disc sub-structures and directly imaged protoplanets to address these and other questions. Our goal is to assess what we have learned (if anything) about planet formation from the multi-wavelength observations, and how theory fares against data. In these early days, the analysis is necessarily at the order-of-magnitude level. We begin in Section 2 by documenting our sources (mostly DSHARP) for disc and putative planet properties. These quantities are used in Section 3 to estimate the present-day according to theory and to evaluate whether the corresponding planet growth timescales make sense in comparison to the system ages. The mass accretion rates are also used to evaluate accretion luminosities, and we discuss how accretion may be playing out in the circumplanetary environments of PDS 70b and c. In Section 4, we summarize and offer an outlook.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| Name | [] | [Myr] | [au] | [] | [g cm-2] | [g cm-2] | ||
| Sz 114 | 0.17 | 1 | 39 | N/A | 0.1 | |||
| GW Lup | 0.46 | 2 | 74 | N/A | 0.08 | |||
| Elias 20 | 0.48 | 0.8 | 25 | N/A | 0.08 | |||
| Elias 27 | 0.49 | 0.8 | 69 | N/A | 0.09 | |||
| RU Lup | 0.63 | 0.5 | 29 | N/A | 0.07 | |||
| SR 4 | 0.68 | 0.8 | 11 | N/A | 0.05 | |||
| Elias 24 | 0.78 | 0.2 | 57 | N/A | 0.09 | |||
| TW Hya-G1 | 0.80 | 8 | 21 | 0.08∗ | ||||
| TW Hya-G2 | 0.80 | 8 | 85 | 0.09∗ | ||||
| Sz 129 | 0.83 | 4 | 41 | N/A | 0.06 | |||
| DoAr 25-G1 | 0.95 | 2 | 98 | N/A | 0.07 | |||
| DoAr 25-G2 | 0.95 | 2 | 125 | N/A | 0.07 | |||
| IM Lup | 1.1 | 0.5 | 117 | 0.1∗ | ||||
| AS 209-G1 | 1.2 | 1 | 9 | N/A | 0.04 | |||
| AS 209-G2 | 1.2 | 1 | 99 | 0.06∗ | ||||
| HD 142666 | 1.58 | 10 | 16 | N/A | 0.05 | |||
| HD 169142 | 1.65 | 10 | 51 | 0.07∗ | ||||
| HD 143006-G1 | 1.78 | 4 | 22 | N/A | 0.04 | |||
| HD 143006-G2 | 1.78 | 4 | 51 | N/A | 0.05 | |||
| HD 163296-G1 | 2.0 | 10 | 10 | N/A | 0.07∗ | |||
| HD 163296-G2 | 2.0 | 10 | 48 | 0.08∗ | ||||
| HD 163296-G3 | 2.0 | 10 | 86 | 0.08∗ | ||||
| PDS 70b | 0.88 | 5 | 22 | 0.07∗ | ||||
| PDS 70c | 0.88 | 5 | 34 | 0.08∗ |
2 Observational Data
Table 1 compiles disc and candidate planet properties taken directly from the literature or derived therefrom. Quantities of interest include the host stellar mass and planet mass , the gas and dust surface densities and at planet orbital distance , and the local disc aspect ratio . To the nineteen DSHARP protoplanets modeled by Zhang et al. (2018) we add the one candidate protoplanet in HD 169142 (Dong & Fung, 2017), the two candidates in TW Hya (Dong & Fung, 2017), and the two confirmed planets in PDS 70 (Keppler et al., 2018; Haffert et al., 2019).
2.1 Gas surface densities
We focus on systems for which emission from optically thin C18O has been spatially resolved. More abundant isotopologues of CO are usually optically thick (including 13CO; van der Marel et al. 2015; Favre et al. 2019) and as such yield only lower limits on . Hydrogen surface densities derived from C18O emission are nonetheless uncertain. The gas-phase CO:H2 abundance ratio is hard to determine; it may be lower in protoplanetary discs than in the interstellar medium (ISM) because of condensation of CO onto dust grains or chemistry driven by cosmic rays (e.g. Schwarz et al. 2018). We will try to account for the possibility of gas-phase CO depletion in what follows. Surface densities at the centers of gaps where planets supposedly reside may also be overestimated if gaps are spatially underresolved, with emission from gap edges contaminating the emission at gap center. Such contamination might not be too serious for the gaps considered in this subsection, whose radial widths are larger (marginally) than the corresponding ALMA beams. Also, simulations predict gas density variations less than a factor of 10 across gaps for (e.g. Dong et al. 2017, top left panel of their figure 8).
Of the twenty-four planets in our sample we have measurements of based on C18O emission (in conjunction with other emission lines) for nine planets in six systems.
2.1.1 Gas surface density: AS 209
The protoplanetary disc around AS 209 has five annular gaps in dust continuum emission at orbital radii and au (Guzmán et al., 2018; Huang et al., 2018). Zhang et al. (2018) demonstrated that the four gaps from au can be produced by a single planet situated within the outermost gap at 99 au (see their figure 19). Favre et al. (2019) and Zhang et al. (2021) observed a broad gap in C18O (2-1) emission extending from 60 to 100 au. Favre et al. (2019) modeled the emission using the DALI thermo-chemical code (Bruderer, 2013) and took the gas density profile to include two gaps coincident with the dust gaps at 61 and 99 au. They showed these two gas gaps could be smeared by the ALMA beam into a single wide gap like that observed in molecular emission. At the bottom of the 99 au gap where the planet is believed to reside, they fitted (see the blue and green curves in their figure 6).
Zhang et al. (2021) modeled the C18O emission using the thermo-chemical code RAC2D (Du & Bergin, 2014), including only a single gap. They initialized their models with an ISM-like which decreased from CO freeze-out and chemistry over the simulation duration of 1 Myr. They found at 99 au (their figure 16), similar to Favre et al. (2019). Zhang et al. (2021) also considered the possibility that there is no gap in H2 and that the observed gap in C18O is due to being somehow locally depleted beyond the predictions of RAC2D. Assuming a total gas-to-dust ratio of by mass (their table 2), they estimated in this super-depleted scenario at 99 au (their figure 5; see also Alarcón et al. 2021 who advocated on separate grounds for a depleted CO:H2 ratio in AS 209).
2.1.2 Gas surface density: HD 163296
Dust continuum observations of HD 163296 reveal gaps centred at 10, 48, and 86 au (Isella et al., 2016; Huang et al., 2018), each opened by a separate planet according to Zhang et al. (2018). Isella et al. (2016) fitted the emission at au from three CO isotopologues assuming an ISM-like value of and found at 48 au and at 86 au (their figure 2, blue curve; note the gap radii in their figure are about 20% larger than the values we use because they used a pre-GAIA source distance). The thermo-chemical models of Zhang et al. (2021) predict roughly consistent values of and respectively (see their figure 16). If instead the CO:H2 abundance is much lower than predicted by their models and the gas-to-dust ratio is (their table 2), then and (their figure 5).
The above estimates of are combined to yield the full ranges quoted in Table 1, for HD 163296-G2 at 48 au, and for HD 163296-G3 at 86 au.
2.1.3 Gas surface density: IM Lup
IM Lup presents a shallow gap at au in millimeter continuum images (Huang et al., 2018) which Zhang et al. (2018) attributed to a 10-30 planet. Zhang et al. (2021) found in their RAC2D modeling which includes CO freeze-out and chemistry (their figure 16). Alternatively, for a super-depleted CO:H2 scenario and gas-to-dust ratio of 100 (their table 2), (their figure 5). We allow for both possibilities and take .
2.1.4 Gas surface density: HD 169142
HD 169142 features an annular gap at 50 au in near-infrared scattered light (Quanz et al., 2013) and mm-wave continuum emission (Fedele et al., 2017). In C18O emission, Fedele et al. (2017) found evidence for a cavity inside au and used DALI to infer near the cavity outer edge (their figure 5, top left panel, blue curve). Midplane gas temperatures according to the same thermo-chemical model (figure 5, bottom center panel) are K, higher than the CO freeze-out temperature of 20 K. CO may still be depleted for other reasons (Schwarz et al. 2018) but without a model we cannot quantify the uncertainty.
2.1.5 Gas surface density: TW Hya
Near-infrared scattered light images reveal annular gaps at au (TW Hya-G1) and 85 au (TW Hya-G2) (van Boekel et al., 2017). The inner gap may also have been detected in the mm continuum by Andrews et al. (2016), albeit slightly outside the gap in scattered light (their figure 2). Nomura et al. (2021) studied TW Hya in the transition of C18O. Near the inner gap they measured a wavelength-integrated line flux of 5 mJy beam-1 km s-1 (their figure 2, middle panel, orange curve). We extrapolate their radial intensity profile, which cuts off at 80 au, to the outer gap at 85 au and estimate there a flux of 1 mJy beam-1 km s-1. Using temperatures of 60 K and 20 K for the inner and outer gaps respectively (section 2.3.3), we convert these fluxes to C18O column densities (e.g. Mangum & Shirley, 2015, their equation B2). Then assuming and a 18OO gas-phase abundance ratio of (e.g. Qi et al., 2011), we calculate and for the two gaps. These surface densities could be underestimated by factors of 70 and 30 (assuming a gas-to-dust ratio of 100), respectively, if CO is somehow super-depleted (Zhang et al. 2019, their figure 8, second panel, blue curve). Thus we have for TW Hya-G1 and for TW Hya-G2.
2.1.6 Gas surface density: PDS 70
Facchini et al. (2021) studied PDS 70 in the transition of , but the beam size at this wavelength was too large to resolve the cavity within which the two planets reside. We therefore resort to using the C18O emission just outside the cavity to place an upper limit on the gas surface density near the planets. Following the same procedure as for TW Hya, we convert the observed C18O flux outside the cavity into an H2 surface density. We use 30 K as the gas excitation temperature at 80 au, close to the H2CO excitation temperature measured by Facchini et al. (2021, their figure 7). The gas surface density so derived is . We pair this upper limit with a lower limit derived from optically thick 12CO in the transition. The smaller beam associated with the higher frequency of this transition allowed the cavity to be resolved by Facchini et al. (2021). Near the positions of the planets at au, the observed 12CO line flux is 37 K km s-1, which for an assumed temperature of K (scaled from 30 K at 80 au using for a passively irradiated disk; Chiang & Goldreich 1997) yields a lower bound on of . The temperatures quoted above are high enough to avoid CO freeze-out, though we cannot rule out that gas-phase CO is depleted from other effects (Schwarz et al., 2018).
2.2 Dust surface densities
The dust surface density and the dust optical depth (typically evaluated at mm wavelengths) are related by
| (1) |
The opacity depends on the grain size distribution. We allow to range from 0.4 to 3 cm2 per gram of dust,222The ALMA continuum data used in our study were taken at wavelengths ranging from 0.85 mm to 1.27 mm. Our adopted factor-of-seven uncertainty in is larger than the expected variation of across this wavelength range (at fixed grain size), so for simplicity we ignore the wavelength dependence on when computing from the ALMA observations. following model size distributions by Birnstiel et al. (2018) which include grains up to 1 cm in size. For a given temperature , we infer from the specific intensity :
| (2) |
where is the Planck function.
Surface densities may be overestimated inside gaps that are spatially underresolved. This may be a much more serious problem for than for (cf. section 2.1) because simulations predict dust surface densities to vary by orders of magnitude across gaps carved by planets, with dust gradients steepened by aerodynamic drag (e.g. figure 1 of Paardekooper & Mellema 2004; figure 8 of Dong et al. 2017; figure 4 of Binkert et al. 2021). We caution that the values of we derive may therefore be grossly overestimated. See also Jennings et al. (2021), whose work we describe below.
2.2.1 Dust surface density: DSHARP systems
For all nineteen of the DSHARP planets, we estimate at gap center using equation (1) and the optical depth profiles in figure 6 of Huang et al. (2018).
Three of the DSHARP gaps, AS 209-G2 ( au), Elias 24 ( au), and HD 143006-G1 ( au), have bottoms that fall below the 2 noise floor at , although apparently only marginally so. For Elias 24 and HD 143006-G1, we set . For AS 209-G2, while portions of the gap lie below the noise floor, at gap center there is actually a local maximum (ring) of emission that rises above the noise. We use the peak optical depth of this ring, , to evaluate . The “W"-shaped gap profile for AS 209-G2 resembles transient structures found in two-fluid simulations of low-mass planets embedded in low-viscosity discs (Dong et al., 2017; Zhang et al., 2018).
In their re-analysis at higher spatial resolution of the DSHARP data, Jennings et al. (2021, their figure 12) found evidence for deeper dust gaps than originally measured by Huang et al. (2018) for GW Lup, HD 163296-G2, SR 4, AS 209-G1, and HD 143006-G1. The re-analyzed gaps in the mm continuum are deeper by at least a factor of 10 and in most cases much more. We make a note of these sources in Table 1, but continue to use the Huang et al. (2018) results to compute for consistency with the rest of our analysis.
2.2.2 Dust surface density: TW Hya
For TW Hya-G1 at 21 au we calculate using equations (1)-(2) with mJy beam-1 (figure 2, middle panel, purple curve of Nomura et al. 2021) and K (section 2.3.3). For TW Hya-G2 at 85 au we estimate using mJy beam-1 (this is an extrapolation of the intensity profile measured by Nomura et al. 2021 which does not extend beyond 70 au) and K. Our estimates of are consistent with those plotted in figure 3 of Nomura et al. (2021).
2.2.3 Dust surface density: HD 169142 and PDS 70
For the gap in HD 169142 and central clearing in PDS 70, the continuum emission falls below the 3 noise floor of the observations (0.21 mJy beam-1 and 0.0264 mJy beam-1, respectively; Fedele et al. 2017; Benisty et al. 2021). For assumed temperatures of K in HD 169142 and K in PDS 70, the corresponding upper limits on the dust column are and , respectively.
2.3 Disc scale height
2.3.1 Disc scale height: DSHARP systems
For most of the DSHARP sample, we adopt the estimates listed in table 3 of Zhang et al. (2018), computed assuming a passive disc irradiated by its host star. For AS 209-G2, all three gaps in HD 163296, and IM Lup, we use more sophisticated estimates of from table 2 of Zhang et al. (2021). In AS 209, Zhang et al. (2021) used the observed 13CO emission surface to fit for (since their CO isotopologue data do not extend down to AS 209-G1 at 9 au, we only apply this scale height relation to AS 209-G2 at 99 au). Note that Zhang et al. (2018) found a similar value, at 99 au, reproduced the multi-gap structure of AS 209. For HD 163296 and IM Lup, Zhang et al. (2021) obtained excellent fits to the spectral energy distributions (their figure 4) using and , respectively.333 The values of obtained by Zhang et al. (2021), if interpreted as a standard isothermal hydrostatic disc gas scale height, imply gas temperatures that differ from the gas temperatures obtained from thermo-chemical and radiative transfer modeling by these same authors (their figure 7). This is because the latter temperatures are solved assuming a fixed density field (specified by ), and no provision is made to iterate the density field to ensure simultaneous hydrostatic and radiative equilibrium. There is no rigorous justification for using either set of temperatures to compute the gas scale height; we use as tabulated by Zhang et al. (2021) for convenience (their parameters and in table 2, inserted into their equation 3 with ).
2.3.2 Disc scale height: HD 169142
Fedele et al. (2017) simultaneously fitted the surface density and temperature profiles in HD 169142. We use their aspect ratio of at the gap position; this is similar to the value of found by Dong & Fung (2017) in fitting the gap width to their planet-disk simulations. The aspect ratio relates to the disc midplane temperature following where is the sound speed, is the mean molecular weight, is Boltzmann’s constant, is the proton mass, is the Keplerian orbital frequency, and is the gravitational constant. The implied temperature at the gap position is 40 K.
2.3.3 Disc scale height: TW Hya
Calahan et al. (2021) obtained a good fit to the spectral energy of TW Hya using (their figure 5). From this scaling we calculate and at the inner ( au) and outer ( au) gap positions, respectively. These aspect ratios correspond to temperatures of 58 K and 20 K.
2.3.4 Disc scale height: PDS 70
Absent direct estimates of the temperature in the PDS 70 cavity, we estimate the disc scale height using arguments similar to those in section 2.1.6. Facchini et al. (2021) derived an H2CO excitation temperature near the disc midplane of 33 K at 80 au (see their figure 7). Setting this equal to the gas kinetic temperature there, we calculate at 80 au, and then scale to the location of the planets assuming (Chiang & Goldreich, 1997). We find and 0.08 at the locations of PDS 70b and c. Keppler et al. (2018) found a similar temperature profile in their radiative transfer models of the PDS 70 disc.
2.4 Planet and stellar masses
2.4.1 Planet masses and stellar masses : DSHARP systems
Zhang et al. (2018) used their grid of planet-disk hydrodynamical simulations to estimate the planet masses that can reproduce the radial widths and in some cases the radial positions of DSHARP gaps. Their table 3 gives for different dust grain size distributions and the Shakura & Sunyaev (1973) viscosity parameter . Here we consider . Values of appear incompatible with various mm-wave observations (Pinte et al., 2016; Teague et al., 2016; Flaherty et al., 2017) including the multi-gap structure of some discs (Dong et al., 2017; Zhang et al., 2018). Planet masses inferred by Zhang et al. (2018) increase with viscosity as ; more massive planets are required to counteract faster diffusion of gas to open the same width gap. Thus to obtain an upper limit on we use the entries corresponding to in table 3 of Zhang et al. (2018), and for a lower limit we take their values for and divide by two in a crude extrapolation down to . This procedure gives a range on that typically spans a factor of 8, and that encompasses the variation in due to different dust size distributions.
For HD 163296-G3, we increase the upper bound on to based on the fit to non-Keplerian kinematical data from Teague et al. (2018) and Teague et al. (2021). Note that their mass estimate is based on planet-disc simulations assuming , and that lowering lowers the planet mass required to reproduce the same non-Keplerian velocity signature ( according to equation 16 of Zhang et al. 2018). For Elias 24, the range in Table 1 overlaps with mass estimates inferred from infrared photometry of an unconfirmed point source at au (Jorquera et al. 2021). The candidate point source in HD 163296 is located at au (Guidi et al. 2018) and as such cannot be identified with the planets inferred at and 86 au (Zhang et al. 2018) of interest here.
For most of the DSHARP systems we use stellar masses derived from stellar evolution tracks and listed in table 1 of Andrews et al. (2018). For IM Lup, AS 209, and HD 163296 we use instead and respectively, calculated from gas disc rotation curves by Teague et al. (2021) as part of the MAPS survey (Oberg et al., 2021).
2.4.2 Planet and stellar masses: HD 169142 and TW Hya
By comparing the observed gaps in HD 169142 and TW Hya with their grid of planet-disk simulations, Dong & Fung (2017) estimated planet masses of in HD 169142, in TW Hya-G1, and in TW Hya-G2. These values were derived for viscosities . For consistency with our adopted range of (see section 2.4.1), we apply the same scaling from Zhang et al. (2018) and shift all limits from Dong & Fung (2017) down by a factor of two.
2.4.3 Planet and stellar masses: PDS 70
Masses of PDS 70b and c derived from near-infrared spectral energy distributions and cooling models vary widely (Müller et al., 2018; Keppler et al., 2018; Christiaens et al., 2019; Mesa et al., 2019; Wang et al., 2020; Stolker et al., 2020). For simplicity we take for both planets, which brackets most literature estimates relying on cooling models.444In later sections, and in particular the discussion surrounding Figures 5 and 6, we will consider the possibility that the observed near-infrared emission does not arise from a planet passively cooling into empty space (as assumed by the cooling models) but one which sits below a hot accretion shock boundary layer. In this scenario our adoption of planetary masses for PDS 70b and c drawn from the passive cooling models will lead to an inconsistency. Our hope is that our estimated mass range of is not seriously impacted; it should not be as long as the posited accretion luminosities are not much larger than the observed near-infrared luminosities (; Wang et al. 2020). It may also help to have the accretion columns be localized to “hot spots” on the planet, like they are for magnetized T Tauri stars (e.g. Gregory et al. 2006), leaving the rest of the planet passively cooling. This range is consistent with masses for PDS 70b derived by Wang et al. (2021) based on dynamical stability constraints. They calculated a 95% upper limit of 10 , with roughly equal probability per log mass from 1-10 (see their figure 5).
The mass of the star is (Keppler et al., 2019).
3 Planetary Accretion Rates and
Gap Properties
Most of the gap-opening planets in our sample have inferred masses large enough that the self-gravity of their gas envelopes should be significant. In this regime, further accretion of gas from the disc may no longer be limited by Kelvin-Helmholtz cooling of the envelope but may instead be regulated by the hydrodynamics of the surrounding nebula. Hydrodynamical forces include, in principle, pressure, planetary gravity, stellar tides, and rotation, all in 3D. The simplest form of hydrodynamical accretion is Bondi accretion, which describes spherically symmetric (zero angular momentum) flow onto a point mass (e.g. Frank et al., 2002). For a point mass embedded in a disc, the Bondi rate is given by:
| (3) |
(e.g. Ginzburg & Chiang 2019a). While it ignores many effects, Bondi accretion appears to fit the results of 3D isothermal hydrodynamic simulations of accreting planets by D’Angelo et al. (2003), both in magnitude and in the scaling (see figure 1 of Tanigawa & Tanaka 2016 which re-prints their data). We have inserted in equation (3) a factor of 0.25 to match the normalization of the relation measured by D’Angelo et al. (2003) at . These authors found that at higher masses, flattens away from an scaling; this flattening is due to the conflating effect of gap opening, i.e. in equation (3) decreases with for masses as deeper gaps are opened. Note that the accretion rates measured by D’Angelo et al. (2003) may be sensitive to their mass removal prescription, which reduces the mass density inside the innermost 10% of the planet’s Hill sphere by some fraction every simulation timestep. This prescription effectively renders the planet a sink cell and maximizes .
The corresponding planet mass doubling time is
| (4) |
We test the theory of planet accretion (Bondi accretion) by comparing the doubling time to the age of the system . We expect . Steady and ongoing growth over the planet’s age corresponds to (equivalently ). Alternatively, we may be observing the planet after it has largely finalized its mass, in which case . We would not expect to find as a planet is unlikely to be caught in a short-lived episode of significant growth.
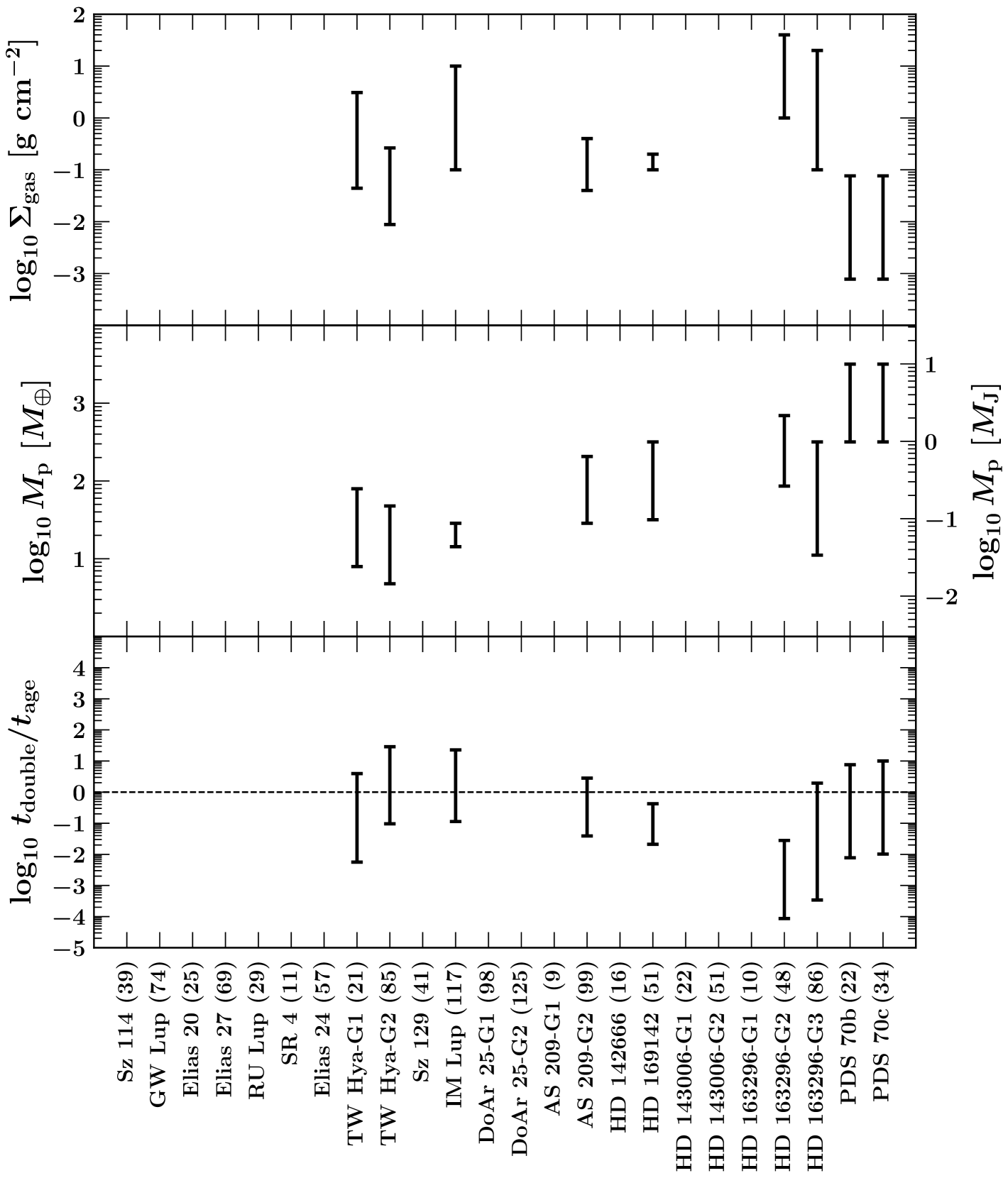
3.1 Bondi accretion rates from C18O, and vs.
Figure 1 plots the ratio for each of the nine protoplanets with measured from C18O observations (section 2.1). We find that appears in the majority of cases to be consistent with unity, although the error bars, which reflect the combined uncertainty in and , are large. The result is physically plausible and indicates that the planets are currently accreting at rates close to the values time-averaged over their system ages, . For TW Hya-G1, AS 209-G2, HD 169142, and HD 163296-G3, if and , near the lower ends of their ranges in Table 1. Lower planet masses imply lower disc viscosities () insofar as (Zhang et al. 2018 and section 2.4.1). Lower gas surface densities argue against speculative super-depleted CO scenarios and support thermo-chemical models (DALI, Bruderer 2013; RAC2D, Du & Bergin 2014) that account for the usual ways that CO can be depleted, freeze-out and chemistry.
The gap HD 163296-G2 at au does not meet our expectation that . For this case the computed value of is driven by the large Jupiter-scale mass that Zhang et al. (2018) inferred from the observed deep and wide dust gap (Isella et al. 2016; Huang et al. 2018). Such a massive planet seems inconsistent with there being hardly any depression in the gas at this location (Zhang et al. 2021, their figure 16 and section 4.3.2). Rodenkirch et al. (2021) modeled the HD 163296 disc and found that a Jovian-mass planet at 48 au would deplete the gas density by a factor of 10 for (their figure 5). We speculate that a planet much less massive than Jupiter might reproduce the dust and gas observations and bring into closer agreement with , if such a lower-mass planet caused only modest gas pressure variations that led to stronger dust variations via aerodynamic drift (Paardekooper & Mellema, 2004; Dong et al., 2017; Drążkowska et al., 2019; Binkert et al., 2021). Another possibility is that there is no planet at all inside the HD 163296-G2 gap, as a planet can create gaps not centered on its orbit; figure 8 of Dong et al. (2018) explicitly models this scenario for HD 163296.
3.2 and
Fifteen of the twenty-four gaps in our sample lack published C18O data, precluding us from estimating and by extension . An alternate approach is to reverse the logic by first assuming that (i.e. assuming ), inserting this accretion rate into equation (3), and solving for :
| (5) |
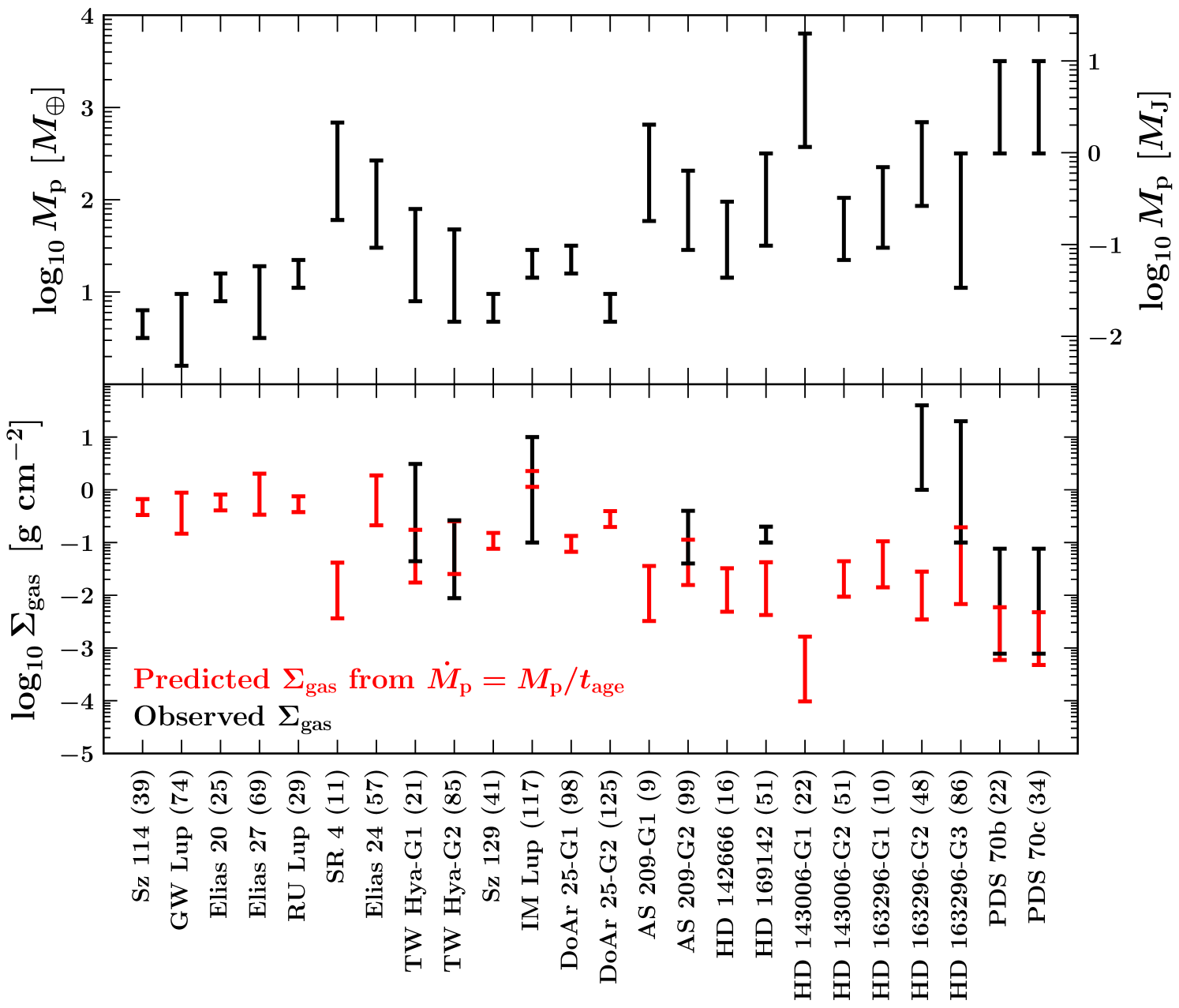
In other words, we assume the planets without C18O data are like the eight we identified in Figure 1 with C18O data showing evidence for — we posit that all are actively accreting from their surrounding discs, and that none are being observed in a short-lived growth phase. We view the values of so computed as predictions for future observations.
Figure 2 shows in red the gas surface densities predicted by equation (5). The values range from to , with a factor of 2-10 uncertainty in any given system stemming from the adopted range of planet masses . Note that if , the red points shift down. Plotted in black for comparison are the values inferred from the measured C18O fluxes (same data plotted in the top panel of Figure 1). In some systems the predictions (red) overlap only with the lower end of values bracketed by the data (black) because favors lower , as mentioned at the beginning of section 3.1.
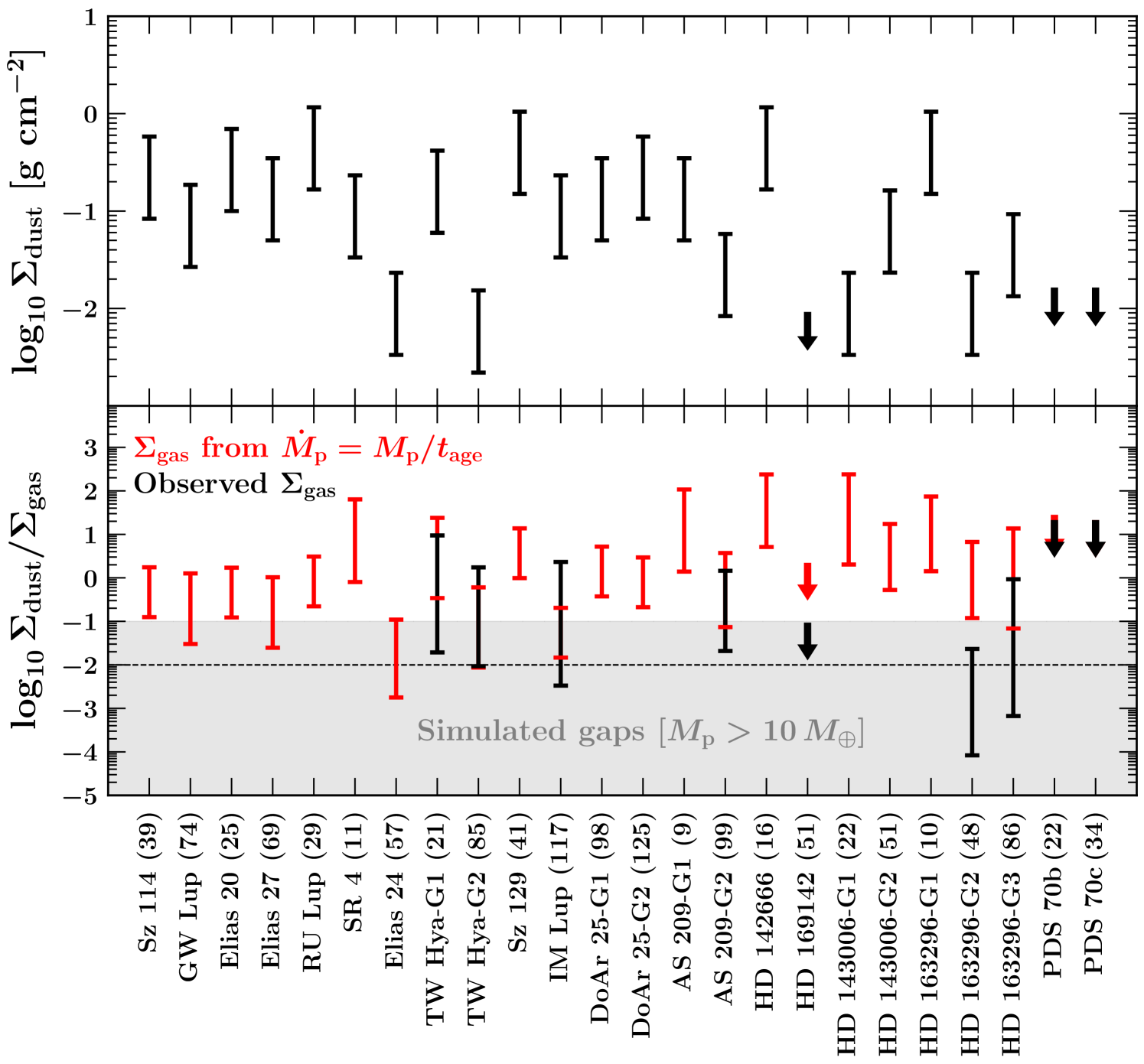
The top panel of Figure 3 displays inferred from the mm continuum observations (section 2.2). The error bars account for a factor of 7 uncertainty in the grain opacity but not the potential overestimation of from gaps being inadequately resolved (more discussion on this below). In the bottom panel, we combine these values of with inferred from C18O data to plot, in black, the empirical dust-to-gas ratios . The red points are semi-theoretical as they take from Figure 2 as predicted by equation (5).
The shaded bar in Figure 3 marks the range of dust-to-gas ratios found in simulated gaps (Dong et al. 2017). The simulations are initialized with spatially uniform dust-to-gas ratios near the solar value of 10-2. The ratios then evolve as aerodynamic drag causes dust to drift relative to gas. Across most of the gap, dust-to-gas ratios decrease as dust is diverted into local gas pressure maxima near gap edges. One gas pressure maximum coincides with the planet’s orbit at gap center. Dust that collects in this co-orbital gas ring raises to 0.1 (about ten times the solar value) for (Dong et al. 2017). Elsewhere within the gap, . Such subsolar metallicities appear inconsistent with most of the data plotted in Figure 3.
The apparent disagreement between theory and observation could arise from some systematic error in or ( according to equation 5). It could also point to an error in the simulations’ assumed initial condition of solar dust abundance. We think the most likely explanation is that the empirical values of are overestimated because the dust gaps are underresolved. Figure 3 suggests the measurement error in is at least a factor of 10-100. Errors of this magnitude are not necessarily surprising given how steep dust gradients can be in the simulations, especially for (Dong et al. 2017, third row of their figure 8). Indeed Jennings et al. (2021, their figure 12) re-analyzed the DSHARP data and found deeper bottoms to the dust gaps in GW Lup, SR 4, AS 209-G1, HD 143006-G1, and HD 163296-G2, in many instances by orders of magnitude relative to Huang et al. (2018).
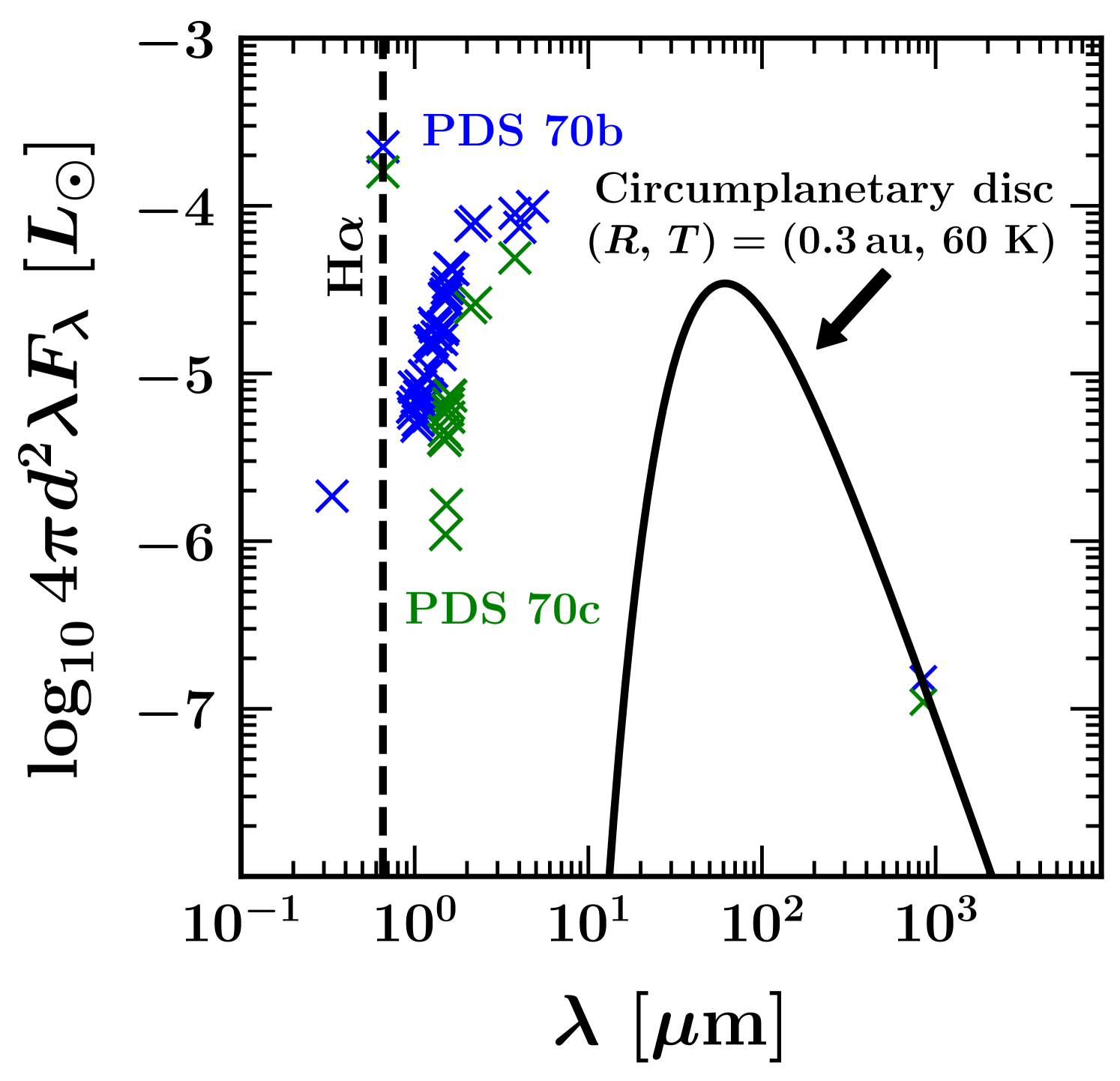
3.3 Accretion luminosities, and the spectral energy distributions of the PDS 70 planets
From the average accretion rate we can predict the bolometric accretion luminosities of planets in our sample (e.g. Frank et al., 2002):
| (6) |
For the non-PDS 70 planets, we take radii to be for and for . These scalings apply to planets that have finished cooling and contracting (e.g. Ginzburg & Chiang, 2019b) and therefore probably underestimate . We fix for the PDS 70 planets, following fits by Wang et al. (2020) to the observed near-infrared photometry.555Wang et al. (2020) derived these radii by fitting blackbodies to the near-infrared spectral energy distributions of PDS 70b and c assuming no extinction. The radii may change by order-unity factors if there is circumplanetary extinction, as proposed later in this section.
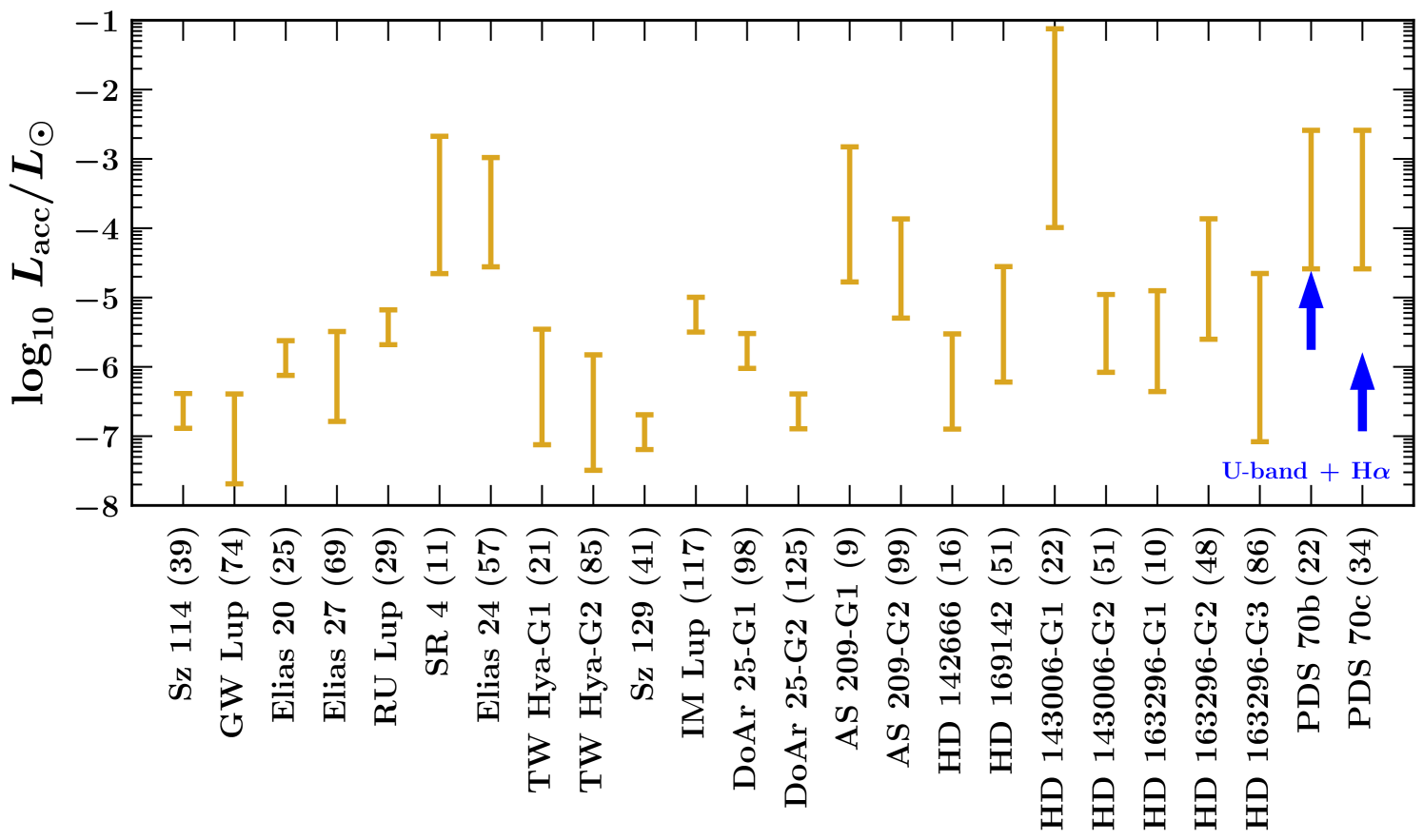
Figure 4 also marks in blue the observed luminosities of PDS 70b and c at the short wavelengths thought to characterize the hot accretion shock. For PDS 70b, Zhou et al. (2021) estimated from the measured U-band (336 nm) and H luminosities. This value includes a bolometric correction for the hydrogen continua, calculated using a slab model (Valenti et al., 1993) having parameters similar to those estimated for the accretion shock (Aoyama & Ikoma, 2019). PDS 70c has so far only been detected in H emission (Hashimoto et al., 2020), so we conservatively set . Figure 4 shows that these luminosities (in blue) sit a factor of 100 below our estimates based on the time-averaged (in yellow).
There are at least two ways to reconcile our theorized high accretion luminosities for PDS 70b and c with the low short-wavelength luminosities observed to date. One possibility is that the bulk of the accretion luminosity emerges in as yet unobserved wavebands. In the accretion shock model of Aoyama et al. (2021), most of the power comes out in the hydrogen Lyman- emission line. Their model for PDS 70b predicts a total accretion luminosity (see their figure 1). Alternatively, the observed U-band and H fluxes may be highly attenuated by dust and therefore underestimate when not corrected for extinction (Hashimoto et al., 2020). These two explanations are not mutually exclusive; reality could be some combination of high dust extinction and high Lyman- luminosity. In either scenario the true could be , compatible with our Bondi accretion rate estimates.
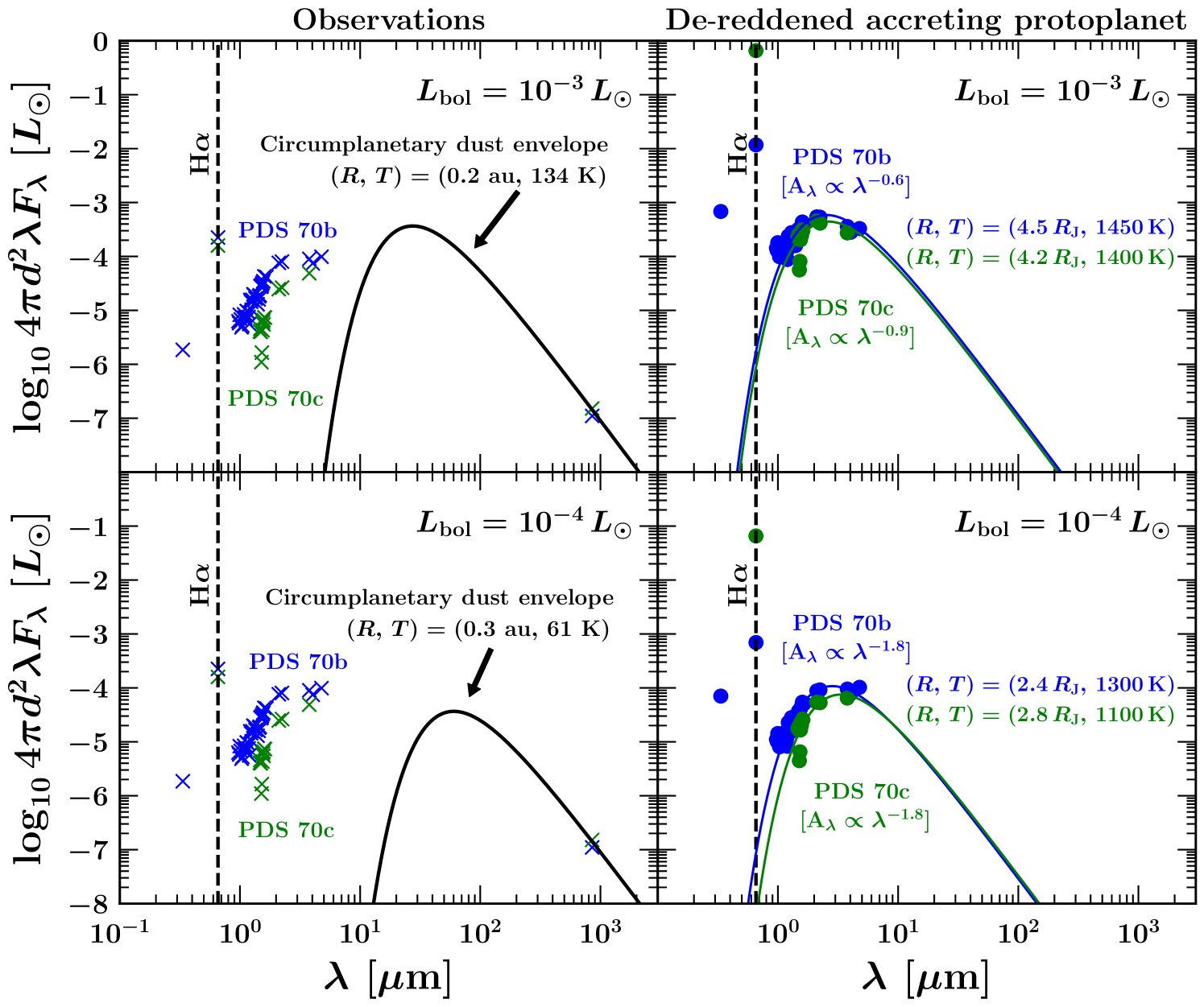
We illustrate in Figures 5 and 6 how these two possibilities impact our interpretation of the spectral energy distributions (SEDs) of PDS 70b and c. Figure 5 describes the no-extinction case. Here the short-wavelength luminosity generated from the accretion shock is , released mostly in some unobserved waveband, possibly H Ly (Aoyama et al. 2021). That the observed luminosity in the near-infrared (see tables 3 and 4 of Wang et al. 2020) is comparable to our predicted may not be a coincidence. Most of the near-infrared power may derive from the half of the radiation generated in the shock that is emitted toward and re-processed by cooler layers below the shock (see Aoyama et al. 2020 for a model that details how the accretion power is re-processed).
In this extinction-free scenario the observed fluxes from the ultraviolet to the near-infrared are not significantly extincted by dust. At the same time we know the circumplanetary environment should contain dust to explain the mm-wave continuum emission imaged by Isella et al. (2019) and Benisty et al. (2021). For this mm-bright dust to not obscure our line of sight to the planet, it should be distributed in a circumplanetary disc (CPD), viewed face on or approximately so. Figure 5 shows blackbody emission from a single-temperature CPD, heated primarily by radiation from the star to an assumed K, with a radius fitted to the mm-wave observations. The fitted CPD radius is 0.3 au, roughly 20% of the Hill sphere radius .
Figure 6 shows a high-extinction scenario. Wang et al. (2020) ruled out interstellar extinction because the host star appears unextincted, and circumstellar extinction seems negligible because the planets reside within a transitional disc cavity. Thus we are left with circumplanetary extinction, from dust brought to the planet by the nebular accretion flow, pervading the planet’s Hill sphere. To obscure our line of sight to the accretion shock, this dust should be distributed more-or-less spherically around the planet, in a geometry similar to the thick torii found in 3D hydro-simulations by Fung et al. (2019, see their figure 2). The left panels of Figure 6 demonstrate how Hill-sphere-sized dusty spheres/torii can reproduce the measured sub-mm fluxes.
The right panels of Figure 6 show what the extinction-corrected intrinsic SED of the accreting planet might look like. We adopt power laws for how the extinction varies with wavelength , with the slope and normalization chosen such that the extinction-corrected luminosity in the U-band + H is comparable to the extinction-corrected luminosity in the near-infrared, with both summing to an assumed bolometric luminosity ( for the bottom panels, for the top; see the figure annotations and caption for details). Our V-band extinction for PDS 70b is for , and for . The de-reddened near-infrared SEDs still conform approximately to blackbodies, about as well as they do without any extinction correction applied (cf. Wang et al. 2020). Our extinction-corrected effective temperatures are higher than non-corrected values, 1100–1450 K vs. 1000–1200 K. Our corrected planet radii are also larger, 2.4–4.5 vs. 2–2.7 . In this interpretation the extinction-corrected near-infrared radius corresponds to the depth at which radiation emitted by the accretion shock boundary layer thermalizes, at the base of a dusty accretion flow. The analogy would be with actively accreting Class 0 protostars (e.g. Dunham et al. 2014) or “first” or “second” protostellar cores (Larson 1969; Bate et al. 2014) at the centres of infalling dusty envelopes.
4 Summary and Outlook
Planets are suspected to open the gaps and cavities imaged in protoplanetary discs at millimeter and infrared wavelengths. From the literature we have compiled the modeled masses and orbital radii of the putative gap-opening planets, together with local disc properties including the dust and gas surface densities and , and the gas disc thickness . Our sample contains 22 hypothesized planets and 2 confirmed orbital companions (PDS 70b and c). From these data we have evaluated:
-
1.
Present-day planetary gas accretion rates for the subset of 9 planets (including PDS 70b and c) for which the ambient gas density can be usefully constrained from molecular line observations including optically thin C18O. We assumed, consistent with some theories of planet formation, that accretion from the surrounding disc onto the planet is Bondi-like. For 8 of the 9 planets, accretion rates are such that mass doubling times are comparable to stellar ages of Myr — this assumes the non-PDS 70 planets have masses , the PDS 70 planets have , and the gas-phase CO:H2 abundance ratios are close to those found in thermo-chemical models. Since circumstellar gas discs have typical lifetimes of several Myr, our finding that for these 8 planets suggests we are observing them during their last doublings. The one planet that does not fit this pattern is the one supposedly inside HD 163296-G2 ( au), for which we find if as estimated by Zhang et al. (2018). We suggest the true planet mass in this gap is smaller, and could actually be zero if the gap is created by a planet located elsewhere, following Dong et al. (2018).
-
2.
Gas surface densities at the bottoms of 24 gaps where planets are supposed to reside. For 9 systems we compiled literature estimates of based on observed C18O intensity maps. For the remaining 15 systems we inferred assuming the gaps host planets undergoing Bondi accretion at the average rate . The predicted gas surface densities range from to .
-
3.
Dust surface densities and dust-to-gas ratios inside gaps. In many cases based on observations are supersolar, by contrast to the typically subsolar ratios found at the bottoms of dust-filtered gaps in planet-disc simulations (Dong et al. 2017). We suggest may be overestimated by the current ALMA observations as they may not be resolving steep dust gradients inside gaps (see also Jennings et al. 2021). Under-resolution is less of a problem for insofar as simulations predict gas gradients to be shallower than dust gradients.
-
4.
Accretion luminosities of protoplanets. For the PDS 70 planets we predict , a factor of 10-100 larger than observed in the U-band and H. Most of the short-wavelength accretion power might be emitted in wavebands as yet unobserved, e.g. H Lyman- as predicted by recent accretion shock models (Aoyama et al., 2021). Alternatively, a dusty, quasi-spherical, circumplanetary envelope might be absorbing much of the outgoing ultraviolet/optical radiation. We sketched different spectral energy distributions (SEDs) based on these scenarios. A large fraction of the power is expected to emerge at wavelengths ranging from the mid to far-infrared.
The hypothesis that the disc substructures imaged by ALMA are caused by embedded planets is now supported on several grounds. A planet can reproduce the observed positions of multiple gaps in a given system (e.g. in AS 209; Dong et al. 2017, 2018; Zhang et al. 2018). A planet can also reproduce observed non-Keplerian velocity signatures in the disc rotation curve (e.g. in HD 163296; Teague et al. 2018; Teague et al. 2021; Pinte et al. 2020). To this evidence favoring planets we can now add consistency with planet accretion theory. The data are pointing to Neptune-mass planets accreting at Bondi-like rates inside gaps filled with low-viscosity () gas.
From here there are any number of avenues for future investigation. To list just a few:
-
1.
Advancing beyond our Bondi-inspired formula (3) for . Bondi accretion neglects many effects, among them stellar tides that become important when the planet’s Bondi radius exceeds its Hill radius (e.g. Rosenthal et al. 2020), anisotropic 3D flow fields (e.g. Cimerman et al. 2017), and thermodynamics (e.g. Ginzburg & Chiang 2019a who distinguished between hydrodynamic and thermodynamic runaway). The sensitivity of simulated accretion rates to sink-cell (e.g. D’Angelo et al. 2003) and other planetary boundary conditions should be studied.
-
2.
Accounting for how the gap density evolves with time because of disc photoevaporation, repulsive planetary torques, etc., while the planet accretes. For example, in the gap clearing theories of Ginzburg & Chiang (2019a), the planet mass doubling timescale is longer than the instantaneously measured by a factor that ranges up to 15, increasing as the disc viscosity decreases and the gap depletes more rapidly with time. This correction factor based on disk evolution should be incorporated into comparisons between and .
-
3.
More molecular line data to test our predictions for , and higher spatial resolution to map steep profiles. New data are now available for the GM Aur disc, including spatially resolved dust continuum and CO observations (Huang et al. 2020, 2021; Schwarz et al. 2021), anchored by a total disc gas mass estimate from HD emission (McClure et al., 2016). Spatially resolved disc surveys have so far targeted brighter discs (Andrews et al., 2018; Oberg et al., 2021) and are consequently biased toward higher . Assuming planets will always be found with , higher corresponds to lower planet masses (equation 5). By this logic, targeting less luminous, less massive discs while keeping all other factors fixed may uncover higher mass planets. In any case expanding survey samples are necessary for understanding planet occurrence rates and demographic trends (Cieza et al., 2019).
-
4.
Planetary accretion shock models (Aoyama et al., 2020, 2021) need to be tested observationally across the ultraviolet-optical spectrum, with current arguments based on a single emission line (H) replaced by joint constraints from multiple lines and the continuum. The accretion shock theory also needs to connect more smoothly to models of the cooler, infrared-emitting layers of the planet (e.g. BT-Settl; Baraffe et al. 2015); at the moment how radiation from shocked layers heats cooler layers is not accounted for (but see section A1 of Aoyama et al. 2020 for a first step). Detection of molecular absorption lines in the infrared (Cugno et al., 2021; Wang et al., 2021) may constrain the degree of accretional heating, and how much dust is brought in.
Acknowledgements
We thank Yuhiko Aoyama, Steve Beckwith, Jenny Calahan, Yayaati Chachan, Ruobing (Robin) Dong, Jeffrey Fung, Sivan Ginzburg, Jane Huang, Masahiro Ikoma, Gabriel-Dominique Marleau, Jason Wang, Ke (Coco) Zhang, Shangjia Zhang, Yifan Zhou, and Zhaohuan Zhu, for discussions and feedback on our study. We also thank Takayuki Muto for a helpful referee report. This work was supported by an NSF Graduate Research Fellowship (DGE 2146752) and used the matplotlib (Hunter, 2007) and scipy (Virtanen et al., 2020) packages.
Data availability
The data compiled in this work are available upon request to the authors.
References
- ALMA Partnership et al. (2015) ALMA Partnership et al., 2015, ApJ, 808, L3
- Alarcón et al. (2021) Alarcón F., et al., 2021, arXiv e-prints, arXiv:2109.06263
- Andrews (2020) Andrews S. M., 2020, ARA&A, 58, 483
- Andrews et al. (2016) Andrews S. M., et al., 2016, ApJ, 820, L40
- Andrews et al. (2018) Andrews S. M., et al., 2018, ApJ, 869, L41
- Aoyama & Ikoma (2019) Aoyama Y., Ikoma M., 2019, ApJ, 885, L29
- Aoyama et al. (2020) Aoyama Y., Marleau G.-D., Mordasini C., Ikoma M., 2020, arXiv e-prints, arXiv:2011.06608
- Aoyama et al. (2021) Aoyama Y., Marleau G.-D., Ikoma M., Mordasini C., 2021, ApJ, 917, L30
- Asensio-Torres et al. (2021) Asensio-Torres R., et al., 2021, A&A, 652, A101
- Baraffe et al. (2015) Baraffe I., Homeier D., Allard F., Chabrier G., 2015, A&A, 577, A42
- Bate et al. (2014) Bate M. R., Tricco T. S., Price D. J., 2014, MNRAS, 437, 77
- Benisty et al. (2021) Benisty M., et al., 2021, ApJ, 916, L2
- Binkert et al. (2021) Binkert F., Szulágyi J., Birnstiel T., 2021, MNRAS, 506, 5969
- Birnstiel et al. (2018) Birnstiel T., et al., 2018, ApJ, 869, L45
- Blondel & Djie (2006) Blondel P. F. C., Djie H. R. E. T. A., 2006, A&A, 456, 1045
- Bruderer (2013) Bruderer S., 2013, A&A, 559, A46
- Calahan et al. (2021) Calahan J. K., et al., 2021, ApJ, 908, 8
- Chachan et al. (2021) Chachan Y., Lee E. J., Knutson H. A., 2021, arXiv e-prints, arXiv:2101.10333
- Chiang & Goldreich (1997) Chiang E. I., Goldreich P., 1997, ApJ, 490, 368
- Christiaens et al. (2019) Christiaens V., Cantalloube F., Casassus S., Price D. J., Absil O., Pinte C., Girard J., Montesinos M., 2019, ApJ, 877, L33
- Cieza et al. (2019) Cieza L. A., et al., 2019, MNRAS, 482, 698
- Cimerman et al. (2017) Cimerman N. P., Kuiper R., Ormel C. W., 2017, MNRAS, 471, 4662
- Cugno et al. (2021) Cugno G., et al., 2021, A&A, 653, A12
- D’Angelo et al. (2003) D’Angelo G., Kley W., Henning T., 2003, ApJ, 586, 540
- Dong & Fung (2017) Dong R., Fung J., 2017, ApJ, 835, 146
- Dong et al. (2017) Dong R., Li S., Chiang E., Li H., 2017, ApJ, 843, 127
- Dong et al. (2018) Dong R., Li S., Chiang E., Li H., 2018, ApJ, 866, 110
- Drążkowska et al. (2019) Drążkowska J., Li S., Birnstiel T., Stammler S. M., Li H., 2019, ApJ, 885, 91
- Du & Bergin (2014) Du F., Bergin E. A., 2014, ApJ, 792, 2
- Ducourant et al. (2014) Ducourant C., Teixeira R., Galli P. A. B., Le Campion J. F., Krone-Martins A., Zuckerman B., Chauvin G., Song I., 2014, A&A, 563, A121
- Dunham et al. (2014) Dunham M. M., et al., 2014, in Beuther H., Klessen R. S., Dullemond C. P., Henning T., eds, Protostars and Planets VI. p. 195 (arXiv:1401.1809), doi:10.2458/azu_uapress_9780816531240-ch009
- Facchini et al. (2021) Facchini S., Teague R., Bae J., Benisty M., Keppler M., Isella A., 2021, AJ, 162, 99
- Favre et al. (2019) Favre C., et al., 2019, ApJ, 871, 107
- Fedele et al. (2017) Fedele D., et al., 2017, A&A, 600, A72
- Flaherty et al. (2017) Flaherty K. M., et al., 2017, ApJ, 843, 150
- Frank et al. (2002) Frank J., King A., Raine D. J., 2002, Accretion Power in Astrophysics: Third Edition. Cambridge University Press
- Fung et al. (2019) Fung J., Zhu Z., Chiang E., 2019, ApJ, 887, 152
- Ginzburg & Chiang (2019a) Ginzburg S., Chiang E., 2019a, MNRAS, 487, 681
- Ginzburg & Chiang (2019b) Ginzburg S., Chiang E., 2019b, MNRAS, 490, 4334
- Ginzburg et al. (2016) Ginzburg S., Schlichting H. E., Sari R., 2016, ApJ, 825, 29
- Goldreich & Tremaine (1979) Goldreich P., Tremaine S., 1979, Nature, 277, 97
- Gregory et al. (2006) Gregory S. G., Jardine M., Simpson I., Donati J. F., 2006, MNRAS, 371, 999
- Guidi et al. (2018) Guidi G., et al., 2018, MNRAS, 479, 1505
- Guzmán et al. (2018) Guzmán V. V., et al., 2018, ApJ, 869, L48
- Haffert et al. (2019) Haffert S. Y., Bohn A. J., de Boer J., Snellen I. A. G., Brinchmann J., Girard J. H., Keller C. U., Bacon R., 2019, Nature Astronomy, 3, 749
- Hashimoto et al. (2020) Hashimoto J., Aoyama Y., Konishi M., Uyama T., Takasao S., Ikoma M., Tanigawa T., 2020, AJ, 159, 222
- Huang et al. (2018) Huang J., et al., 2018, ApJ, 869, L42
- Huang et al. (2020) Huang J., et al., 2020, ApJ, 891, 48
- Huang et al. (2021) Huang J., et al., 2021, arXiv e-prints, arXiv:2109.06224
- Hunter (2007) Hunter J. D., 2007, Computing In Science & Engineering, 9, 90
- Isella et al. (2016) Isella A., et al., 2016, Phys. Rev. Lett., 117, 251101
- Isella et al. (2019) Isella A., Benisty M., Teague R., Bae J., Keppler M., Facchini S., Pérez L., 2019, ApJ, 879, L25
- Jennings et al. (2021) Jennings J., Booth R. A., Tazzari M., Clarke C. J., Rosotti G. P., 2021, arXiv e-prints, arXiv:2103.02392
- Jorquera et al. (2021) Jorquera S., et al., 2021, AJ, 161, 146
- Keppler et al. (2018) Keppler M., et al., 2018, A&A, 617, A44
- Keppler et al. (2019) Keppler M., et al., 2019, A&A, 625, A118
- Larson (1969) Larson R. B., 1969, MNRAS, 145, 271
- Lee & Chiang (2015) Lee E. J., Chiang E., 2015, ApJ, 811, 41
- Lodato et al. (2019) Lodato G., et al., 2019, MNRAS, 486, 453
- Machida et al. (2010) Machida M. N., Kokubo E., Inutsuka S.-I., Matsumoto T., 2010, MNRAS, 405, 1227
- Mangum & Shirley (2015) Mangum J. G., Shirley Y. L., 2015, PASP, 127, 266
- McClure et al. (2016) McClure M. K., et al., 2016, ApJ, 831, 167
- Mesa et al. (2019) Mesa D., et al., 2019, A&A, 632, A25
- Müller et al. (2018) Müller A., et al., 2018, A&A, 617, L2
- Nomura et al. (2021) Nomura H., et al., 2021, ApJ, 914, 113
- Oberg et al. (2021) Oberg K. I., et al., 2021, arXiv e-prints, arXiv:2109.06268
- Paardekooper & Mellema (2004) Paardekooper S. J., Mellema G., 2004, A&A, 425, L9
- Pinte et al. (2016) Pinte C., Dent W. R. F., Ménard F., Hales A., Hill T., Cortes P., de Gregorio-Monsalvo I., 2016, ApJ, 816, 25
- Pinte et al. (2020) Pinte C., et al., 2020, ApJ, 890, L9
- Pohl et al. (2017) Pohl A., et al., 2017, ApJ, 850, 52
- Qi et al. (2011) Qi C., D’Alessio P., Öberg K. I., Wilner D. J., Hughes A. M., Andrews S. M., Ayala S., 2011, ApJ, 740, 84
- Quanz et al. (2013) Quanz S. P., Avenhaus H., Buenzli E., Garufi A., Schmid H. M., Wolf S., 2013, ApJ, 766, L2
- Rodenkirch et al. (2021) Rodenkirch P. J., Rometsch T., Dullemond C. P., Weber P., Kley W., 2021, A&A, 647, A174
- Rosenthal et al. (2020) Rosenthal M. M., Chiang E. I., Ginzburg S., Murray-Clay R. A., 2020, MNRAS, 498, 2054
- Schwarz et al. (2018) Schwarz K. R., Bergin E. A., Cleeves L. I., Zhang K., Öberg K. I., Blake G. A., Anderson D., 2018, ApJ, 856, 85
- Schwarz et al. (2021) Schwarz K. R., et al., 2021, arXiv e-prints, arXiv:2109.06228
- Shakura & Sunyaev (1973) Shakura N. I., Sunyaev R. A., 1973, A&A, 500, 33
- Stolker et al. (2020) Stolker T., Marleau G. D., Cugno G., Mollière P., Quanz S. P., Todorov K. O., Kühn J., 2020, A&A, 644, A13
- Tanigawa & Tanaka (2016) Tanigawa T., Tanaka H., 2016, ApJ, 823, 48
- Teague et al. (2016) Teague R., et al., 2016, A&A, 592, A49
- Teague et al. (2018) Teague R., Bae J., Bergin E. A., Birnstiel T., Foreman-Mackey D., 2018, ApJ, 860, L12
- Teague et al. (2021) Teague R., et al., 2021, arXiv e-prints, arXiv:2109.06218
- Valenti et al. (1993) Valenti J. A., Basri G., Johns C. M., 1993, AJ, 106, 2024
- Virtanen et al. (2020) Virtanen P., et al., 2020, Nature Methods, 17, 261
- Wang et al. (2020) Wang J. J., et al., 2020, AJ, 159, 263
- Wang et al. (2021) Wang J. J., et al., 2021, AJ, 161, 148
- Zhang et al. (2018) Zhang S., et al., 2018, ApJ, 869, L47
- Zhang et al. (2019) Zhang K., Bergin E. A., Schwarz K., Krijt S., Ciesla F., 2019, ApJ, 883, 98
- Zhang et al. (2021) Zhang K., et al., 2021, arXiv e-prints, arXiv:2109.06233
- Zhou et al. (2021) Zhou Y., et al., 2021, AJ, 161, 244
- van Boekel et al. (2017) van Boekel R., et al., 2017, ApJ, 837, 132
- van der Marel et al. (2015) van der Marel N., van Dishoeck E. F., Bruderer S., Pérez L., Isella A., 2015, A&A, 579, A106