Testing the criterion for correct convergence in the complex Langevin method

In the CLM, the original real variables $x_{k}$ are complexified as $x_{k}\to z_{k}=x_{k}+iy_{k}\in\mathbb{C}$ and one considers a fictitious time evolution of the complexified variables $z_{k}$ using the complex Langevin equation given, in its discretized form, by

where $t$ is the fictitious time with a stepsize $\epsilon$. The second term $v_{k}(z)$ on the right-hand side is called the drift term, which is defined by holomorphic extension of the one

for the real variables $x_{k}$. The variables $\eta_{k}(t)$ appearing on the right-hand side of eq. (2) are a real Gaussian noise with the probability distribution $\propto e^{-\frac{1}{4}\sum_{t}\eta_{k}(t)^{2}}$, which makes the time-evolved variables $z^{(\eta)}_{k}(t)$ stochastic. The expectation values with respect to the noise $\eta_{k}(t)$ are denoted as $\langle\cdots\rangle_{\eta}$ in what follows.

Let us consider the expectation value of an observable $\mathcal{O}(x)$. In the CLM, one computes the expectation value of the holomorphically extended observable $\mathcal{O}(x+iy)$ as

where $P(x,y;t)$ is the probability distribution of $x^{(\eta)}(t)$ and $y^{(\eta)}(t)$ defined by

Then, the correct convergence of the CLM implies the equality

where the right-hand side is the expectation value of $\mathcal{O}(x)$ in the original theory (1). A proof of eq. (6) was given in refs. Aarts:2009uq ; Aarts:2011ax , where the notion of the time-evolved observable $\mathcal{O}(z;t)$ plays a crucial role. In particular, it was pointed out that the integration by parts used in the argument cannot be justified when the probability distribution (5) falls off slowly in the imaginary direction. In ref. Nishimura:2015pba , it was noticed that the wrong convergence associated with the zeroes of the fermion determinant Mollgaard:2013qra is actually due to the slow fall-off of the probability distribution (5) toward the singularities of the drift term.

While this argument provided theoretical understanding of the cases in which the CLM gives wrong results, the precise condition on the probability distribution was not specified. Furthermore, there is actually a subtlety in defining the time-evolved observable $\mathcal{O}(z;t)$ as we discuss in the next subsection.

Here we review the refined argument for justification of the CLM, which leads to the condition for correct convergence Nagata:2016vkn .

The basic idea in proving the equality (6) is to consider the time evolution of the expectation value $\Phi(t)$, which is given by

where we have defined the time-evolved observable

Note that if $\mathcal{O}(z)$ and $v(z)$ are holomorphic, so is $\mathcal{O}_{\epsilon}(z)$. Expanding the right-hand side of (8) with respect to $\epsilon$ and integrating $\eta$ out, one can rewrite (7) as

where we have defined a differential operator

acting on a holomorphic function of $z_{k}$, and the symbol $\mbox{\bf:}\cdots\mbox{\bf:}$ implies that the derivatives are moved to the right, i.e., $\mbox{\bf:}(f(x)+\partial)^{2}\mbox{\bf:}=f(x)^{2}+2f(x)\partial+\partial^{2}$.

Taking the $\epsilon\to 0$ limit in (9), one naively obtains

and a finite time evolution of $\Phi(t)$ as

Assuming that (12) is valid for finite $\tau$ at arbitrary $t$, one can derive the time evolution of an equivalent system of real variables by induction with respect to $t$, from which eq. (6) follows.

The expressions such as (9) and (12) need some care, though. In order for the $\epsilon$-expansion (9) to be valid, the integral on the right-hand side should be convergent for all $n$. In order for the expression (12) to be valid for finite $\tau$, the integral on the right-hand side should be convergent for all $n$, and on top of that, the infinite sum over $n$ should have a finite convergence radius, which may depend on $t$.

The issues raised above are nontrivial since the drift term $v_{k}(z)$ in the differential operator (10) can become large for some $z=x+iy$, which appears with the probability distribution $P(x,y;t)$. Defining the magnitude of the drift term $u(z)$ in a suitable manner, the most dominant contribution from $\tilde{L}^{n}$ in (9) and (12) can be estimated as $\tilde{L}^{n}\sim u(z)^{n}$. Therefore, the integral appearing in the infinite series can be estimated as

where we have defined the probability distribution of $u(z)$ by

In order for (11) to be valid, (13) should be finite for arbitrary $n$, which requires that $p(u;t)$ should fall off faster than any power law. In order for the infinite series (12) to have a finite convergence radius, $p(u;t)$ should fall off exponentially or faster. Since the latter condition is slightly stronger than the former, it can be regarded as a necessary and sufficient condition for correct convergence in the CLM.

In the previous argument Aarts:2009uq ; Aarts:2011ax , eq. (11) was derived in a continuous time formulation, where the time evolution of the probability distribution $P(x,y;t)$ was converted to the time evolution of the observable using integration by parts. If the integration by parts can be justified and eq. (11) indeed holds, the right-hand side of (11) should vanish in the long time limit. This was proposed as a necessary condition for correct convergence in the CLM. On the other hand, it was implicitly assumed that the infinite series in (12) has an infinite convergence radius. This assumption is actually too strong, though, as we have discussed above. Our refined argument based on induction only requires that the infinite series in (12) should have a finite convergence radius at arbitrary $t$. This leads to a condition, which is slightly stronger than the condition required for justifying the integration by parts as one can see from our derivation of (11) based on the $\epsilon$-expansion.

As we mentioned in the previous subsection, the situation in which the CLM fails can be classified into two cases. One is the case in which the complexified variables make long excursions in the imaginary directions (the excursion problem) Aarts:2009uq ; Aarts:2011ax , and the other is the case in which the drift term has singularities and the complexified variables come close to these points frequently (the singular-drift problem) Nishimura:2015pba . In both these cases, the magnitude of the drift term tends to become large, and the probability distribution of the drift term can have a power-law behavior at large magnitude. Thus, our criterion can detect these two problems in a unified manner, and more importantly, it enables us to determine precisely the parameter region in which these problems occur. The usefulness of our criterion was demonstrated in ref. Nagata:2016vkn for two simple one-variable models, which suffer from the excursion problem and the singular drift problem, respectively, in some parameter region. Whether it is useful also for systems with many degrees of freedom is the issue we address in what follows.

In the present work, we use the so-called gauge cooling to reduce the excursion problem or the singular-drift problem as much as possible. Here we briefly review the basic idea of this technique using the system (1) as a simple example.

Suppose the original system (1) has a symmetry under $x_{k}^{\prime}=g_{kl}x_{l}$, where $g_{kl}$ is an element of a Lie group. Upon complexification $x_{k}\to z_{k}$, the symmetry of the action and the observables is enhanced to $z_{k}^{\prime}=g_{kl}\,z_{l}$, where $g_{kl}$ is an element of a Lie group obtained by complexifying the original Lie group. Using this fact, one can improve the Langevin process (2) as

where the first line represents the gauge cooling. At each Langevin step, one chooses an appropriate transformation function $g$ depending on the previous configuration in such a way that possible problems of the CLM are avoided.

This gauge cooling was originally proposed as a technique to solve the excursion problem Seiler:2012wz , but later it was shown to be useful also in solving the singular-drift problem Nagata:2015ijn ; Nagata:2016alq . Theoretical justification of this technique was given explicitly in refs. Nagata:2015uga ; Nagata:2016vkn .

Let us consider 2dYM with an SU($N_{\rm c}$) gauge group, which is defined by

where $n$ represents a site on a $N_{\rm t}\times N_{\rm s}$ lattice with periodic boundary conditions and $U_{12}(n)$ represents the plaquette defined in terms of the link variables $U_{n\mu}\in\text{SU}(N_{\rm c})$ by $U_{12}(n)=U_{n,1}\,U_{n+\hat{1},2}\,U_{n+\hat{2},1}^{\dagger}\,U_{n,2}^{\dagger}$ with $\hat{\mu}$ being the unit vector in the $\mu$ direction $(\mu=1,2)$. This system can be solved analytically using the character expansion Balian:1974ts ; Migdal:1975zg ; Rothe:1992nt , and the partition function is given by

where $I_{n}(x)$ is the modified Bessel function of the first kind and $V=N_{\rm t}N_{\rm s}$ is the number of sites on the lattice.

The parameter $\beta$ in (18) is related to the gauge coupling constant $g$ by $\beta=1/g^{2}$, and it is usually taken to be real positive, in which case the action is real and the sign problem does not occur. Note, however, that the model itself is well defined also for complex $\beta$, in which case the action is complex and the sign problem occurs. Since the analytic solution (19) remains valid for complex $\beta$, this simple gauge theory serves as a useful testing ground for methods which aim at solving the sign problem.

In order to apply the CLM to the 2dYM with complex $\beta$, we complexify the link variables as $U_{n\mu}\mapsto{\cal U}_{n\mu}\in{\rm SL}(N_{\rm c},{\mathbb{C}})$ and extend the action and the observables to holomorphic functions of the complexified variables. For instance, the plaquette is extended to

and the action is extended to

Note that the Hermitian conjugate of $U_{n\mu}$ is replaced with the inverse of ${\cal U}_{n\mu}$ so that the action becomes a holomorphic function of the complexified link variables ${\cal U}_{n\mu}$.

A fictitious time evolution of the complexified link variables is defined by the complex Langevin equation with gauge cooling as

where $t$ is the discretized Langevin time with a stepsize $\epsilon$. The SU($N_{\rm c}$) generators $t_{a}\ (a=1,\cdots,N_{\rm c}^{2}-1)$ are normalized as ${\rm tr\,}(t_{a}t_{b})=\delta_{ab}$ and the real Gaussian noise $\eta_{an\mu}(t)$ is normalized as $\langle\eta_{a^{\prime}n^{\prime}\mu^{\prime}}(t^{\prime})\eta_{an\mu}(t)\rangle_{\eta}=2\delta_{a^{\prime}a}\delta_{n^{\prime}n}\delta_{\mu^{\prime}\mu}\delta_{t^{\prime}t}$. The drift term $v_{an\mu}$ is defined by

The gauge transformation in (22) represents the gauge cooling, where $g_{n}$ takes values in ${\rm SL}(N_{\rm c},{\mathbb{C}})$. In this model, the complexified link variables can have large components in the non-compact direction of SL(${N_{\rm c}},\mathbb{C}$) Makino:2015ooa , which represents the excursion problem. We try to avoid this problem as much as possible by using the gauge cooling. For that purpose, we define the unitarity norm,

which measures the deviation of the link variables from SU($N_{\rm c}$), and choose the gauge transformation in (22) in such a way that the norm ${\cal N}$ is minimized Seiler:2012wz .

Let us define the magnitude $u_{n}(\mathcal{U})$ of the drift term at site $n$ by

with $v_{an\mu}(\mathcal{U})$ being the drift term (24). Then, the probability distribution of the drift term can be defined as

where $P(\mathcal{U})$ represents the probability distribution of $\mathcal{U}_{n\mu}(t)$ in the $t\rightarrow\infty$ limit. This definition of $p(u)$ respects the ${\rm SU}(N_{\rm c})$ gauge symmetry of the original theory.

Here we present our results obtained by the CLM. Following Makino:2015ooa , we choose $N_{\rm c}=2$, the lattice size $N_{\rm s}=N_{\rm t}=4$ and $\beta=1.5\,e^{i\theta}$ with various $\theta$. The simulation was performed for the total Langevin time $t\sim 500$ with a fixed stepsize $\epsilon=10^{-5}$.

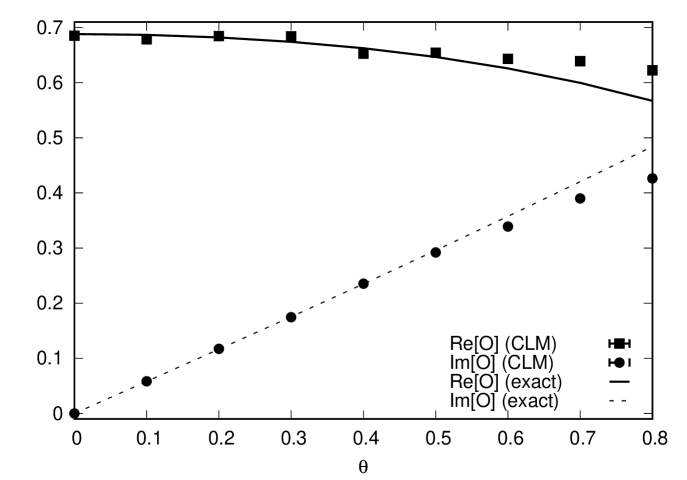
In Fig. 1 (Left), we show the expectation value of the average plaquette defined by

as a function of $\theta$, which agrees with the result obtained in ref. Makino:2015ooa . In particular, the CLM fails to reproduce the exact results for $\theta\gtrsim 0.6$. As was reported in ref. Makino:2015ooa , the unitarity norm (25) is under control for all the parameters investigated and, in particular, it does not blow up even for the cases in which the CLM gives wrong results. In ref. Makino:2015ooa , the scatter plot of the average plaquette was also studied, but the results for $\theta\gtrsim 0.6$ were not able to detect the existence of the excursion problem.

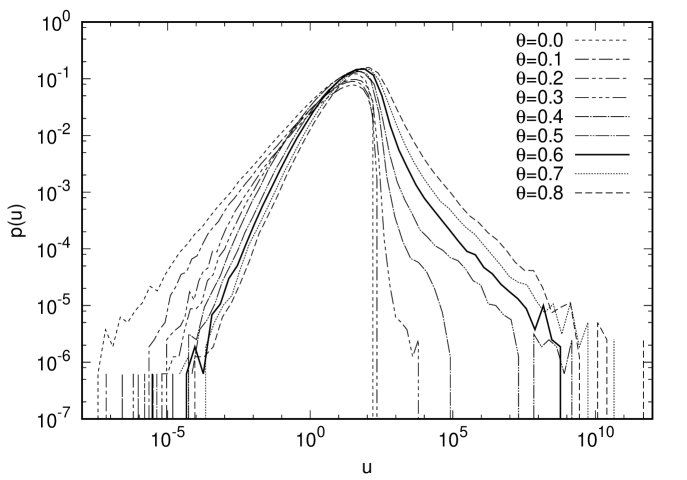
In Fig. 1 (Right), we show the probability distribution (27) of the drift term for various $\theta$. We find that the distribution falls off exponentially or faster for $\theta\lesssim 0.4$, while it falls off only by a power law for $\theta\gtrsim 0.6$. This implies that our criterion based on the probability distribution of the drift term can indeed tell the parameter region in which the CLM gives correct results.

The partition function of the model is given by Bloch:2012bh

where $N_{\rm f}$ is the number of flavors and $m>0$ represents the degenerate quark mass. The dynamical variables consist of two general $N\times(N+\nu)$ complex matrices $\Phi_{k}\ (k=1,2)$, where the integer $\nu$ represents the topological index. The action $S_{\rm b}$ in (29) is given by

where $\Psi_{k}\ (k=1,2)$ are $(N+\nu)\times N$ matrices defined by

The reason for introducing new matrices representing the Hermitian conjugate of $\Phi_{k}$ will be clear shortly. The Dirac operator $D$ in (29) is given by

where $\mu$ is the chemical potential. The effective action of this model reads

When one tries to apply Monte Carlo methods to this model, the sign problem occurs for $\mu\neq 0$ due to the complex fermion determinant $\det(D+m)$. To see that, let us note first that the Dirac operator $D$ satisfies the relation

for any $\mu$. This implies that all the nonzero eigenvalues of $D$ are paired with the ones with the sign flipped. When $\mu=0$, $D$ is anti-Hermitian and its eigenvalues are purely imaginary, which implies that the determinant $\mathrm{det}(D+m)$ is real semi-positive. On the other hand, when $\mu\neq 0$, $D$ is no longer anti-Hermitian and its eigenvalues can take complex values. In this case, the determinant $\mathrm{det}(D+m)$ is complex in general, which causes the sign problem. Since the model is actually analytically solvable, it serves as a useful toy model for investigating the sign problem that occurs in finite density QCD.

Let us apply the CLM to the cRMT with $\mu\neq 0$. First we consider real variables corresponding to the real part and the imaginary part of $(\Phi_{k})_{ij}$ and complexify these variables. The action and the observables are extended to holomorphic functions of these complexified variables by analytic continuation. It is easy to convince oneself that this simply amounts to disregarding the constraint (31) and extending the action and the observables to holomorphic functions of $\Phi_{k}$ and $\Psi_{k}$ ($k=1,2$).

A fictitious time evolution of the complex matrices $\Phi_{k}$ and $\Psi_{k}$ ($k=1,2$) is given by the complex Langevin equation with gauge cooling as

where $W=m^{2}-XY$ is an $N\times N$ matrix. The $N\times(N+\nu)$ matrices $\eta_{k}(t)$ have components taken from complex Gaussian variables normalized by $\langle\eta_{k,ij}(t)\eta_{k^{\prime},i^{\prime}j^{\prime}}^{*}(t^{\prime})\rangle_{\eta}=2\delta_{kk^{\prime}}\delta_{ii^{\prime}}\delta_{jj^{\prime}}\delta_{tt^{\prime}}$. Eq. (37) represents the gauge cooling with $g\in\mathrm{GL}(N,\mathbb{C})$ and $h\in\mathrm{GL}(N+\nu,\mathbb{C})$, which are obtained by complexifying the $\mathrm{U}(N)\times\mathrm{U}(N+\nu)$ symmetry of the original model (29).

In ref. Mollgaard:2013qra , the same model was studied by the CLM without gauge cooling, and it was found that one obtains wrong results for small quark mass or large chemical potential. The reason for this failure is the singular-drift problem Nishimura:2015pba , which occurs due to eigenvalues of $(D+m)$ close to zero. In ref. Nagata:2016alq , we proposed to use the gauge cooling to avoid the singular drift problem as much as possible.³³3While the gauge cooling is found to be useful in avoiding the singular drift problem in the present model, it is found to be ineffective in a similar model Stephanov:1996ki according to a recent study Bloch:2017sex . There, three different types of “norm” were considered so that the gauge transformations $g$ and $h$ in (37) can be determined by minimizing them. A counterpart of the unitarity norm (25) in gauge theory, which is called the Hermiticity norm, can be defined as

which measures the violation of the relation (31). It turned out, however, that the gauge cooling with this norm does not reduce the singular drift problem. This led us to consider a norm that is related directly to the eigenvalue distribution of the Dirac operator. A simple choice is given by

which measures the deviation of the Dirac operator (34) from an anti-Hermitian matrix. The gauge cooling with this norm has an effect of making the eigenvalue distribution of $D+m$ narrower in the real direction. Another choice is given by

where $\xi$ is a real parameter and $\alpha_{a}$ are the real semi-positive eigenvalues of $M^{\dagger}M$ with $M=D+m$. In eq. (41), we take a sum over the $n_{\rm ev}$ smallest eigenvalues of $M^{\dagger}M$. The gauge cooling with this norm has an effect of achieving $\alpha_{a}\gtrsim 1/\xi$ and suppressing the appearance of small $\alpha_{a}$. Since $\alpha_{a}\gtrsim 1/\xi$ implies $|\lambda_{a}|^{2}\gtrsim 1/\xi$, where $\lambda_{a}$ are the eigenvalues of $M$, it is also expected to suppress the appearance of $\lambda_{a}$ close to zero. In some cases, the use of the norm (40) or (41) causes the excursion problem. In order to avoid this, we consider a combined norm

where $s$ $(0\leq s\leq 1)$ is a tunable parameter.

Let us discuss how we define the probability distribution of the drift term. Here we set the topological index $\nu=0$ for simplicity so that the dynamical variables $\Phi_{k}$ and $\Psi_{k}$ are $N\times N$ square matrices. We denote the drift terms of $\Phi_{k}$ and $\Psi_{k}$ by $F_{k}$ and $G_{k}$ ($k=1,2$), and represent the eigenvalues of $(F_{k}^{\dagger}F_{k})^{1/2}$ and $(G_{k}^{\dagger}G_{k})^{1/2}$ by $v_{k}^{(a)}$ and $w_{k}^{(a)}$ ($a=1,\cdots,N$), respectively. Then we define the probability distribution of the drift term as

where $P(\Phi,\Psi)$ is the probability distribution of $\Phi_{k}(t)$ and $\Psi_{k}(t)$ in the $t\rightarrow\infty$ limit. This definition of $p(u)$ respects the $U(N)\times U(N)$ symmetry of the original theory.

Here we present our results obtained by the CLM. Following previous works Mollgaard:2014mga ; Nagata:2016alq , we choose $\nu=0$, $N_{\rm f}=2$, $N=30$, $\tilde{\mu}\equiv\mu\sqrt{N}=2$ with various $\tilde{m}\equiv mN$. The simulation was performed for the total Langevin time $t=10$ with a fixed stepsize $\epsilon=5\times 10^{-5}$. For gauge cooling, we use the combined norm $\hat{\mathcal{N}}_{i}(s)$ defined in (42) with $s=0.01$.

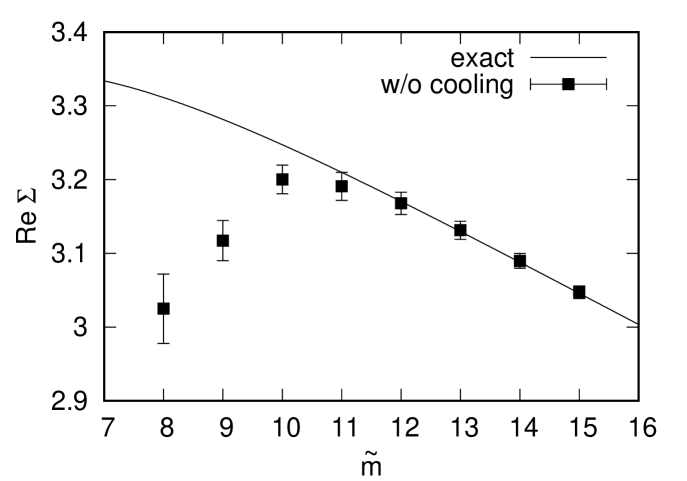
In Fig. 2 (Left), we show the real part of the chiral condensate

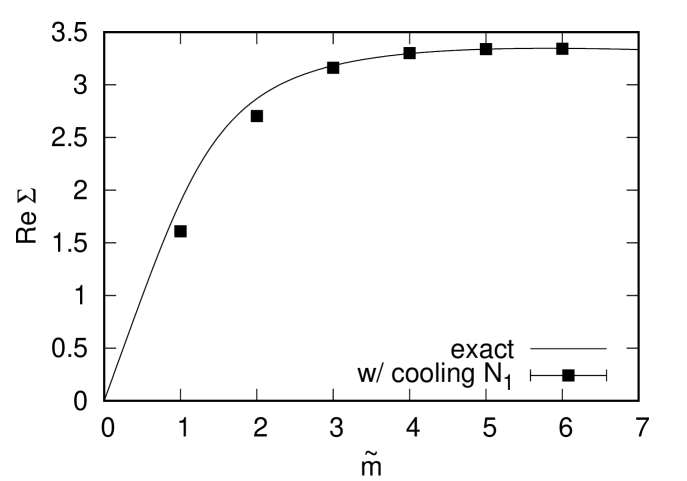
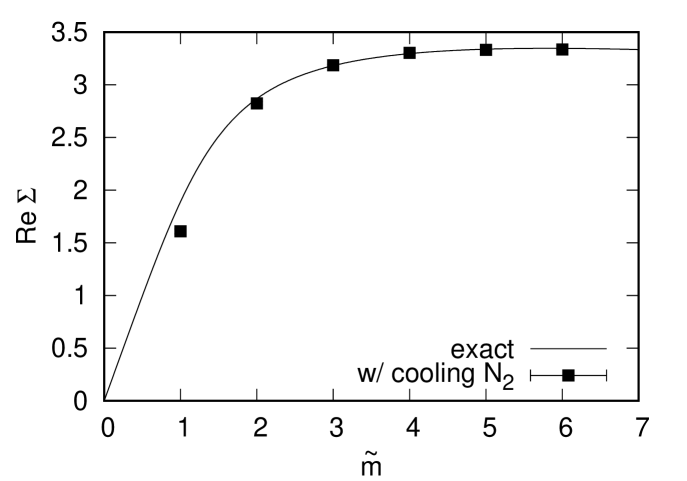
obtained by the CLM with or without gauge cooling and compare it with the exact result given in ref. Osborn:2004rf . In the case without gauge cooling (Top), we find that the result of the CLM deviates from the exact result for $\tilde{m}\lesssim 11$. On the other hand, in the case with gauge cooling using the norm $\hat{\mathcal{N}}_{1}$ (Middle), we find that the result of the CLM deviates from the exact result for $\tilde{m}\lesssim 2$. When we use the norm $\hat{\mathcal{N}}_{2}$ (Bottom) instead, the deviation occurs for $\tilde{m}\lesssim 1$.

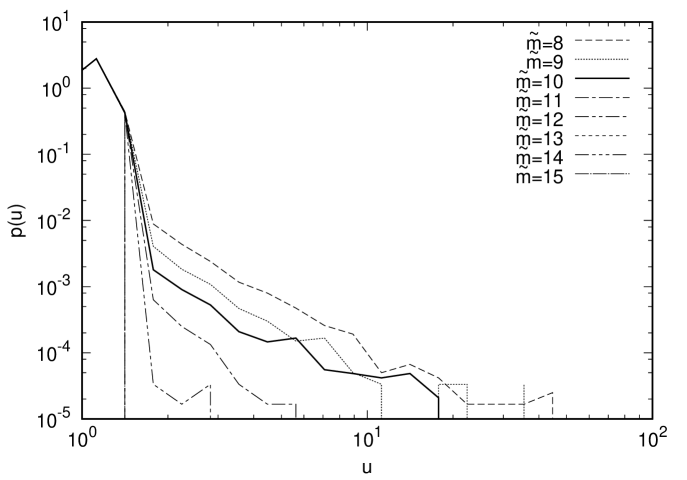
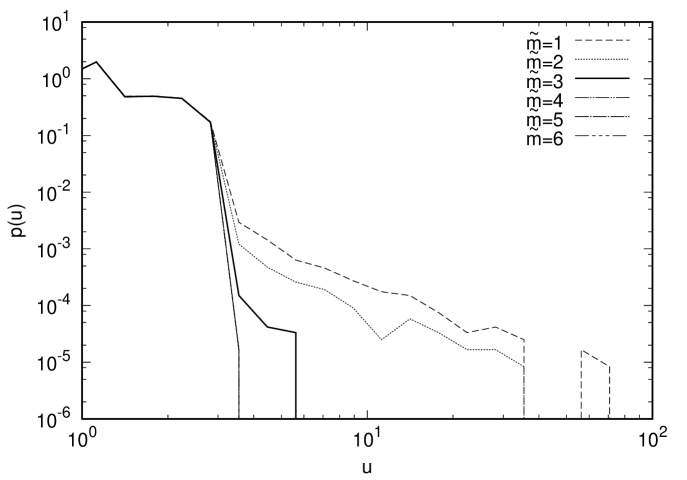
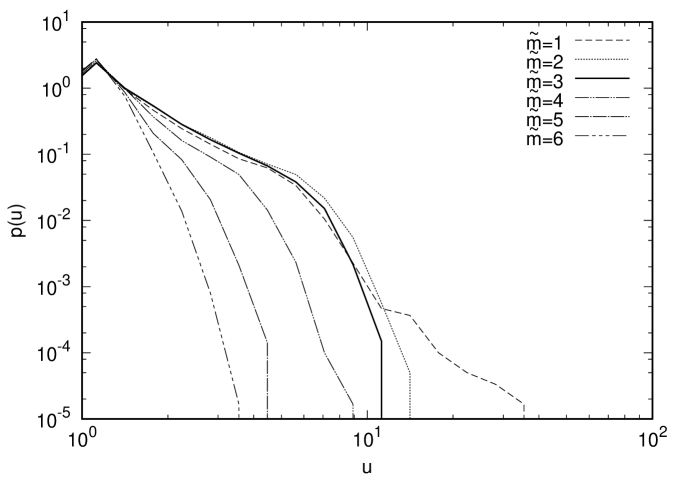
In Fig. 2 (Right), we show the probability distribution $p(u)$ of the drift term obtained by the CLM with or without gauge cooling focusing on the parameter region in which the result starts to deviate from the exact result. In the case without gauge cooling (Top), we find that the probability distribution falls off exponentially or faster for $\tilde{m}\gtrsim 12$, while it develops a power-law tail for $\tilde{m}\lesssim 11$. In the case with gauge cooling using the norm $\hat{\mathcal{N}}_{1}$ (Middle), we find that the probability distribution falls off exponentially or faster for $\tilde{m}\gtrsim 3$, while it develops a power-law tail for $\tilde{m}\lesssim 2$. When we use the norm $\hat{\mathcal{N}}_{2}$ (Bottom) instead, the probability distribution falls off exponentially or faster for $\tilde{m}\gtrsim 2$, while it develops a power-law tail for $\tilde{m}\lesssim 1$. This implies that the probability distribution of the drift term can indeed tell the parameter region in which the CLM gives correct results.