Testing the strength of the $\textnormal{U}_{A}(1)$ anomaly at the chiral phase transition in two-flavour QCD

One of the peculiar features of Quantum Chromodynamics (QCD) is the spontaneous and explicit breaking of chiral symmetry. In the case with two massless quark flavours the theory is invariant under global transformations with elements of

$$\textnormal{SU}_{L}(2)\times\textnormal{SU}_{R}(2)\times\textnormal{U}_{A}(1)\times\textnormal{U}_{V}(1)\,.$$

(1)

The $\textnormal{U}_{A}(1)$ symmetry, however, is anomalously broken on the quantum level due to the Adler-Bell-Jackiw, or chiral, anomaly. In particular, the conservation equation for the axial vector current reads

$$\partial_{\mu}A^{j}_{\mu}(x)=-\delta_{j0}\frac{N_{f}\,g_{0}^{2}}{32\pi^{2}}\varepsilon^{\alpha\beta\mu\nu}\textnormal{Tr}\big{[}F_{\alpha\beta}(x)F_{\mu\nu}(x)\big{]}=-\delta_{j0}N_{f}Q(x)\,,$$

(2)

where $Q(x)$ denotes the operator associated with the topological charge density and

$$A^{j}_{\mu}(x)=\bar{\psi}(x)\gamma_{\mu}\gamma_{5}(\tau^{j}/2)\psi(x)\,,$$

(3)

is the axial current, including the Pauli matrices $\tau^{j}$ for $j=1,2,3$ and $\tau^{0}=\mathbf{1}$. Due to this anomalous breaking, the spontaneous breaking of chiral symmetry leads to three Goldstone bosons only, neutral and charged pions, while the $\eta^{\prime}$ meson retains a finite mass, even for vanishing light quark masses [1, 2].

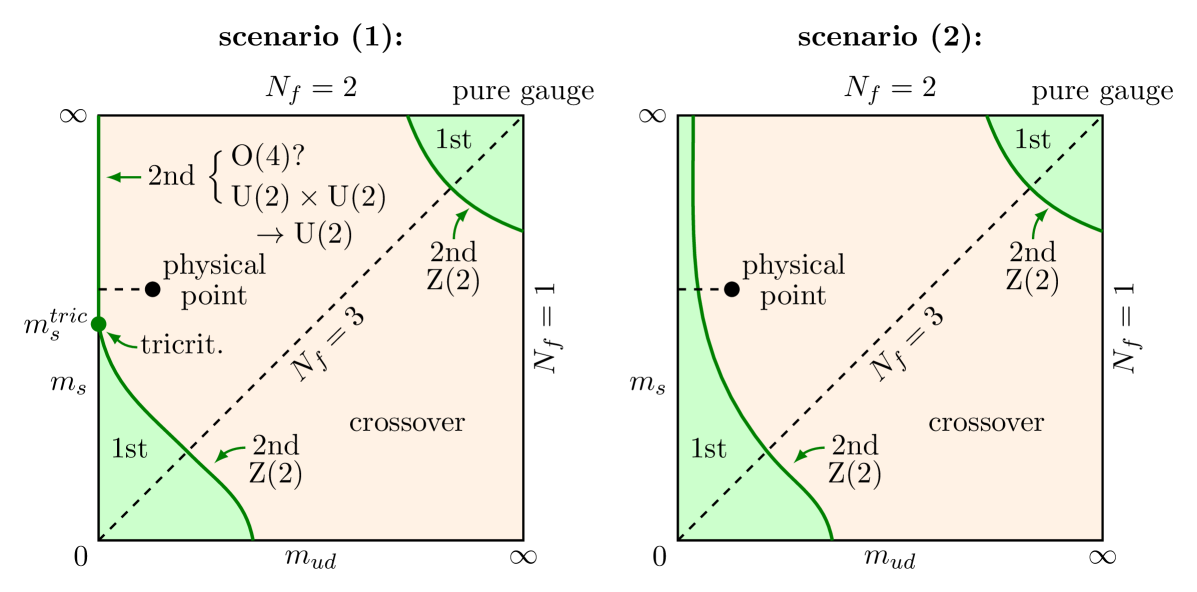
The fate of the anomalous breaking of the $\textnormal{U}_{A}(1)$ symmetry at finite temperature plays a key role for the properties of the QCD phase diagram. In particular, the phase transition in the chiral limit of the light ($u$ and $d$) quarks is sensitive to the possible restoration of the $\textnormal{U}_{A}(1)$ symmetry at the critical temperature, which could change the order and/or the universality class of the transition (see Refs. [3, 4, 5]). The two possible scenarios for the QCD phase diagram in dependence of the masses of the three lightest quarks are shown in Fig. 1. In scenario (1), the 2nd order chiral critical line reaches the $m_{ud}=0$ axis in a tricritical point at $m_{s}^{tric}$, rendering the chiral transition 2nd order from this point on. The universality class in this scenario depends on the strength of the breaking of $\textnormal{U}_{A}(1)$ at the chiral transition. If the effect of the breaking is negligible, i.e. the symmetry effectively restored, the transition will be in the $\textnormal{U}(2)\times\textnormal{U}(2)\to\textnormal{U}(2)$ [4, 5] universality class (alternatively a $\textnormal{SU}(2)\times\textnormal{SU}(2)\times Z_{4}\to\textnormal{SU}(2)$ universality class has also been proposed [6]) rather than in the standard $\textnormal{O}(4)$ universality class [3] for a substantial breaking of $\textnormal{U}_{A}(1)$. It is also possible that the restoration of the $\textnormal{U}_{A}(1)$ symmetry is sufficient to keep the transition first order for all values of the strange quark mass [3]. This is scenario (2) in Fig. 1. The question which of the two scenarios is realised is the only remaining completely open qualitative question of the phase diagram at vanishing chemical potential. Among the main problems to answer this questions are the inability to simulate directly in the chiral limit and the similarity of the different types of scaling behaviour. Investigating the fate of the $\textnormal{U}_{A}(1)$ symmetry at the chiral phase transition offers a viable alternative to the above methods (see our earlier paper [7] for a more detailed discussion and references).

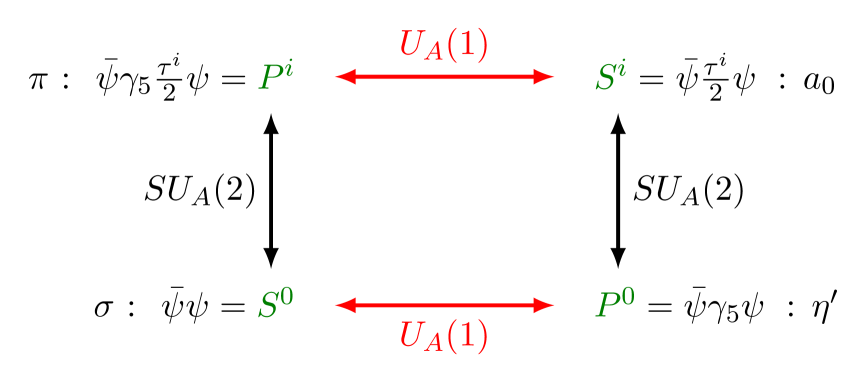
The pattern of chiral symmetry restoration can be investigated using correlation functions of operators connected by the individual symmetries (see also [8]). One particular example are iso-vector correlation functions in vector $V^{j}_{\mu}(x)=\bar{\psi}(x)\gamma_{\mu}\gamma_{5}(\tau^{j}/2)\psi(x)$ and axial vector $A^{j}_{\mu}(x)$ channels, which are related by the $\textnormal{SU}_{A}(2)$ rotation. Consequently, the restoration of chiral symmetry implies the degeneracy of the associated correlation functions. Of particular relevance for the $\textnormal{U}_{A}(1)$ symmetry are correlation functions in scalar and pseudoscalar channels. Including the iso-singlet operators (opening up new channels for the investigation of the effective symmetry restoration, see Ref. [9], for instance), they are related by $\textnormal{SU}_{A}(2)$ and $\textnormal{U}_{A}(1)$ transformations as shown in Fig. 2. The iso-vector operators $P^{i}$ and $S^{i}$ are comparably easy to compute on the lattice, due to the absence of disconnected diagrams, so that they have become the standard channels to look at to test for $\textnormal{U}_{A}(1)$ symmetry restoration. Since we are considering an effective restoration of the symmetry, we expect the renormalised correlation functions to become degenerate.

A number of studies have looked at the effective restoration of the $\textnormal{U}_{A}(1)$ symmetry in lattice QCD, mostly focussing on the low mode spectrum of the Dirac operator or chiral susceptibilities [10, 11, 12, 13, 14]. In contrast, we pursue a complementary approach, using the correlation functions, in particular, the screening masses. Screening masses probe the long distance properties of the correlation functions and are free of contact terms, which contaminate chiral susceptibilities, for instance. Apart from screening masses, the correlation functions include additional information in terms of matrix elements. The details of our strategy are explained in [7], where the iso-vector screening masses obtained from $16\times 32^{3}$ lattices have been published. Here we extend this study to larger volumes, the matrix elements of the correlation functions and present first results for iso-singlet screening masses, which provide additional information about the symmetry restoration pattern. Earlier accounts of our study have been reported in [15, 16, 17, 18].

We perform simulations with two flavours of $O(a)$ improved Wilson fermions [19], with the non-perturbatively estimated clover coefficient from Ref. [20], and Wilson’s gauge action. The simulations employ deflation accelerated versions of the Schwarz [21, 22] and (twisted) mass [23, 24, 25] preconditioned algorithms. We vary the temperature by changing the lattice spacing via the lattice coupling $\beta$, keeping the temporal extent fixed at $N_{t}=16$. For more details concerning the simulation algorithms, lines of constant physics and scale setting see [7]. In the approach to the chiral limit we use several quark masses and volumes to control finite size effects. A list of temperature scans with the results for the critical temperatures is given in Tab. 1

Our main observables are correlation functions in spatial direction, so called screening correlators [26]. For a particular mesonic operator $O$ the screening correlation function is given by

$$C_{O}(x_{\mu})=\int d^{3}x_{\perp}\left<O(x_{\mu},\vec{x}_{\perp})O^{\dagger}(0)\right>\,.$$

(4)

Here $x_{\mu}$ (we take $x_{\mu}=z$) is the coordinate of the direction in which the correlation function is evaluated and $\vec{x}_{\perp}$ is the coordinate vector in the orthogonal directions. The equality of the renormalised correlation functions of channels related by a particular symmetry signals its effective restoration. Previously we have focussed on correlation functions with iso-vector operators, i.e. operators including a Pauli matrix $\tau^{i}$, for which only quark connected correlation functions contribute. Here we will also present first results for quark disconnected correlation functions, enabling us to compute correlation functions in iso-singlet channels. The details will be discussed in Sec. 4.

On a periodic lattice of extent $L_{z}$, the leading order of the spectral representation, including only the groundstate contribution, of a correlation function $C_{O}(z)$ is given by

$$C_{O}(z)=\frac{\big{|}Z_{O}\big{|}^{2}}{M_{O}}\Big{(}e^{-M_{O}z}+e^{-M_{O}(L_{z}-z)}\Big{)}\,.$$

(5)

The exponential decay of $C_{O}(x_{\mu})$ with $x_{\mu}$ defines the ‘screening mass’ $M_{O}$ in this channel and the proportionality constant contains the matrix element $Z_{O}$. Consequently, the equality of the correlation functions not only implies the equivalence of the screening masses, but also of the renormalised matrix elements $\mathcal{Z}_{O}Z_{O}$, where $\mathcal{Z}_{O}$ are the multiplicative renormalisation factors.

We start with the discussion of the results for correlation functions in the iso-vector channels. In particular, we look at the correlation functions from Eq. (4) in pseudoscalar $P^{i}$, scalar $S^{i}$, vector $V^{i}$ and axial vector $A^{i}$ channels. In this section we conveniently drop the superscript $i$ for brevity. Iso-vector correlation functions include a connected part only, which we evaluate using point sources. We typically use 48 point sources per configuration with random starting positions. We first focus on the screening mass differences,

$$\Delta M_{O_{1}O_{2}}=M_{O_{1}}-M_{O_{2}}\,,$$

(6)

which are direct measures for the effective restoration of the symmetries. These differences are extracted from plateaus in the effective masses of the ratios of the correlation functions in the individual channels, taking into account the leading order contributions from excited states.

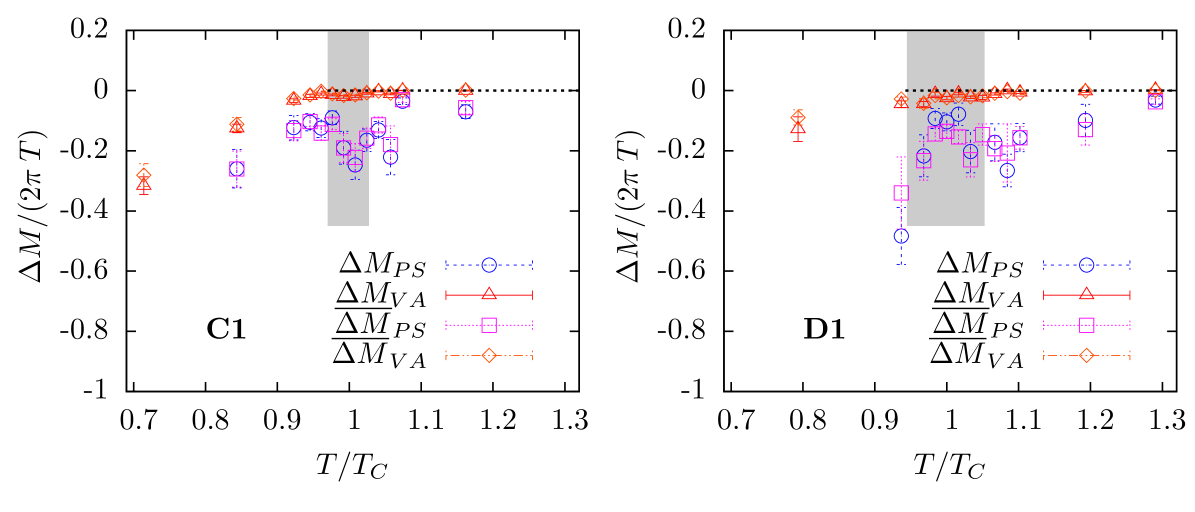
The results for the screening mass differences on the $32^{3}$ volumes, scans C1 and D1, as obtained in [7], are shown in Fig. 3. We observe an approximate degeneracy of $M_{V}$ and $M_{A}$, indicating the effective restoration of $\textnormal{SU}_{A}(2)$ at $T_{c}$. The difference $\Delta M_{PS}$ is non-vanishing at $T_{c}$, meaning $\textnormal{U}_{A}(1)$ is still broken for these quark masses. This finding is in qualitative and quantitative agreement with findings from staggered [27], domain wall [10, 28, 29] and overlap [11, 30] fermion formulations. In the approach to the chiral limit the difference decreases. To obtain an estimate in the chiral limit we perform a linear chiral extrapolation of $\Delta M_{PS}$ (averaging over the transition region and using the spread of results as a systematic uncertainty; see Ref. [7]). The results from the averaging procedure for scans B1_κ, C1 and D1 versus the quark mass are shown as the grey points in Fig. 5 together with their chiral extrapolation, the grey point at $m_{ud}=0$. To enable an assessment whether the breaking is weak or strong in the chiral limit, Fig. 5 also includes a phenomenologically estimate for the mass difference in the chiral limit and at the physical point in full QCD at $T=0$ [7]. A comparison between the chiral extrapolation and the phenomenological estimate shows that the $\textnormal{U}_{A}(1)$ breaking screening-mass difference is comparably small at $T_{c}$, indicating a weak breaking or even a restoration of the $\textnormal{U}_{A}(1)$ symmetry at $m_{ud}=0$.

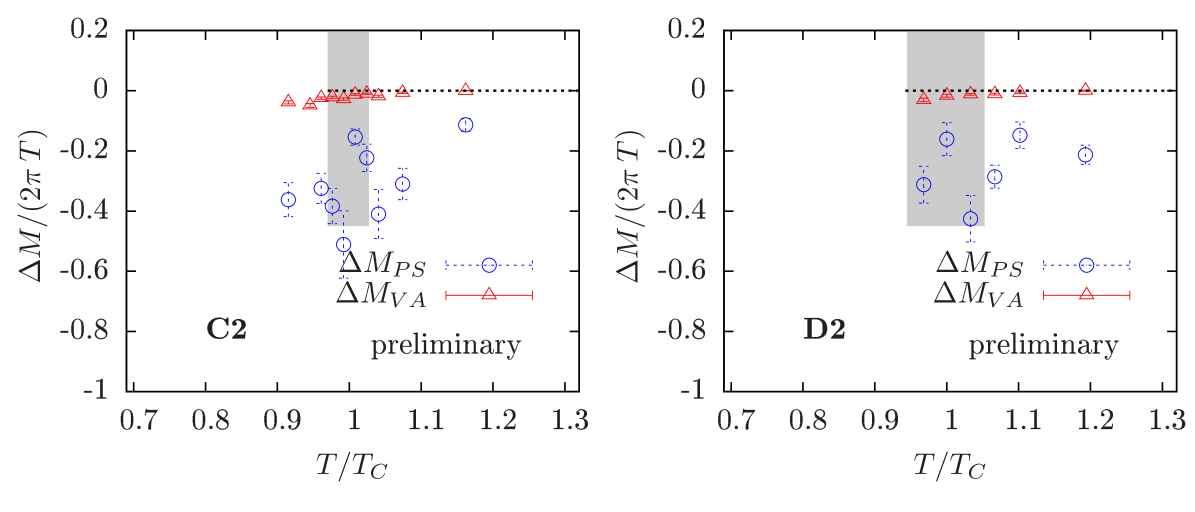
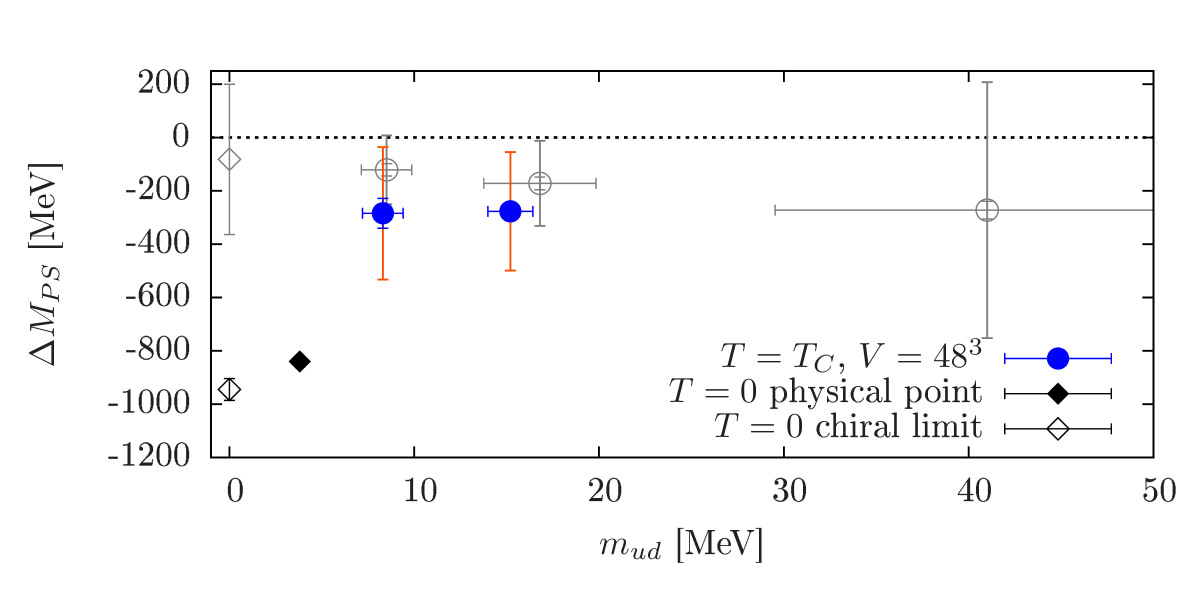
For the $(L/a)^{3}=32^{3}$ volumes and smaller quark masses, the value for $m_{\pi}L$, with $m_{\pi}$ the $T=0$ pion mass, becomes smaller than 3. To be able to extend the study to smaller quark masses and to test for finite size effects, we have thus repeated the computations on $48^{3}$ lattices. The results for the screening mass differences on these new scans C2 and D2 are shown in Fig. 4. While the results for $\Delta M_{VA}$ look very similar to the ones from the $32^{3}$ volumes, $\Delta M_{PS}$ tends to become larger with increasing volume. The result for $\Delta M_{PS}$ at $T_{c}$, once more averaged over the transition region, are shown in Fig. 5. One can see the tendency towards larger screening mass differences with increasing volume. This tendency seems to remain for the chiral limit. To perform a reliable chiral extrapolation, however, we need to extend the simulations to smaller quark masses and increase the statistics for scan D2.

To extend our study to smaller quark masses we have started a temperature scan at the physical pion mass, labelled E2 in Tab. 1. So far only results at $T>T_{c}$ ($T_{c}$ estimated using $\textnormal{O}(4)$ scaling [7]) are available, for which we have performed measurements with 16 point sources per configuration. The results are shown in Fig. 6. While the results for $T/T_{c}>1.1$ indicate a smaller

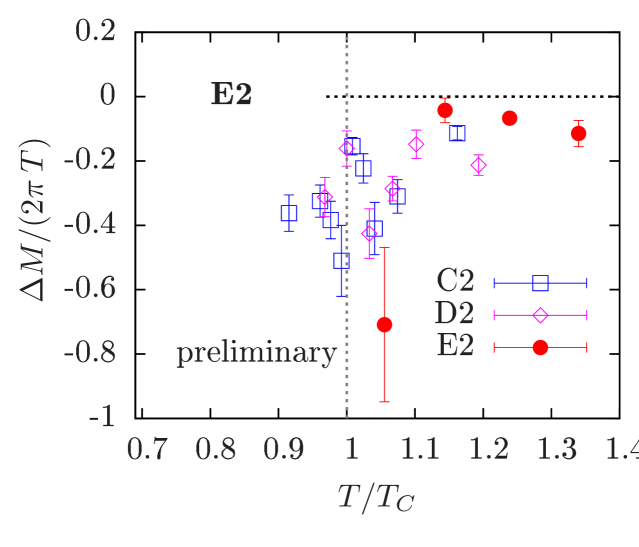
value for $\Delta M_{PS}$ the one at $T/T_{c}\approx 1.05$ is further away from zero as for scans C2 and D2 at similar values for $T/T_{c}$. The latter, however, lacks statistics and thus can still change considerably. We are currently increasing precision and are extending the runs to $T_{c}$ and below.

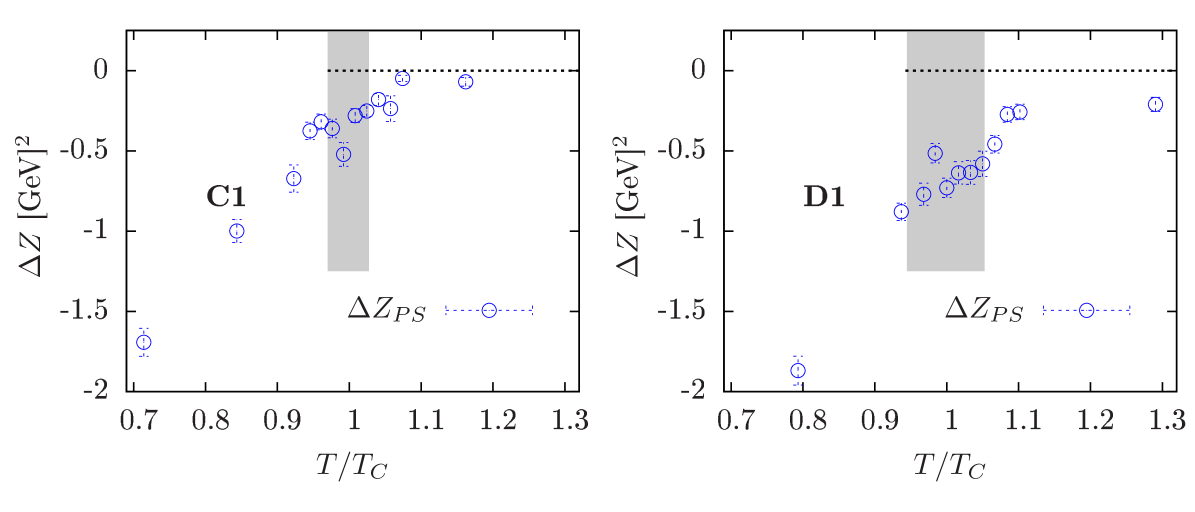
An alternative observable extracted from correlation functions are the matrix elements $Z_{O}$ from Eq. (5). In contrast to the screening masses, however, these observables demand multiplicative renormalisation. The analogue to $\Delta M_{PS}$ for the matrix elements is the renormalised difference

$$\Delta Z_{PS}=\mathcal{Z}_{P}|Z_{P}|-\mathcal{Z}_{S}|Z_{S}|\,.$$

(7)

For the determination of $\mathcal{Z}_{P}$, we have interpolated the results from [31] as discussed in [7]. The determination of $\mathcal{Z}_{S}$ is a bit more involved and we refer to the renormalisation of the chiral condensate in [7] for the details. The renormalised difference is plotted for scans C1 and D1 in Fig. 7. As the screening mass difference, $\Delta Z_{PS}$ remains non-zero at $T_{c}$. In contrast to $\Delta M_{PS}$, however, $\Delta Z_{PS}$ shows a tendency to increase when the quark mass is lowered.

Iso-singlet correlation functions open up new channels to investigate the chiral symmetry restoration pattern. In two-flavour QCD with degenerate quark masses, the difference between iso-vector and iso-singlet correlation function is the presence of quark disconnected diagrams for the latter. In this section we will distinguish explicitly between iso-vector $O^{i}$ and iso-singlet $O^{0}$ operators/correlation functions. Introducing quark connected $C^{\rm conn}_{\mathcal{O}}(z)$ and quark disconnected $C^{\rm disc}_{\mathcal{O}}(z)$ correlation functions, defined by traces over quark propagators as depicted in Fig. 8, iso-vector and iso-singlet correlation functions of an operator $O$ are given by,

$$C_{O^{i}}(z)=-\frac{1}{2}C^{\rm conn}_{\mathcal{O}}(z)\quad\textnormal{and}\quad C_{O^{0}}(z)=-\frac{1}{2}C^{\rm conn}_{\mathcal{O}}(z)+C^{\rm disc}_{\mathcal{O}}(z)\,.$$

(8)

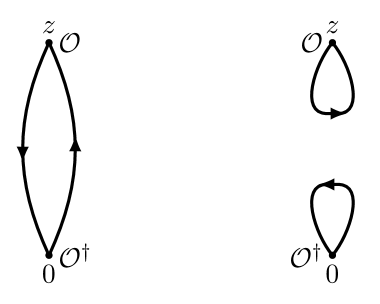
Here $\mathcal{O}$ refers to the operator in Dirac and colour space only, excluding the flavour matrices from the operator $O$, and the correlation functions include only a single fermion propagator (since $u$ and $d$ propagators are indistinguishable in QCD when quark masses are degenerate). Note, that the iso-singlet correlation function might include a constant contribution, which is a finite size effect resulting from imperfect sampling of topological sectors [32]. The constant piece is absent in the shifted correlator $\tilde{C}(z)=C(z)-C(z+1)$ [33], which we use to fit the correlation function in the $P^{0}$ channel.

We will focus on correlation functions in $P$ and $S$ channels at $T_{c}$. The transformation relations between iso-vector and iso-singlet channels are shown in Fig. 2. We see that the inclusion of the disconnected diagrams enables to test the effective restoration of both symmetries using $P$ and $S$ correlation functions. In particular, in the case that $\textnormal{SU}_{A}(2)$ is restored, for which we have seen indications above, we expect a degeneracy of $P^{0}$ and $S^{i}$, as well as $P^{i}$ and $S^{0}$ correlation functions. If, the $\textnormal{U}_{A}(1)$ symmetry remains broken, correlation functions in $P^{i}$ and $S^{i}$ channels and $P^{0}$ and $S^{0}$ channels remain non-degenerate.

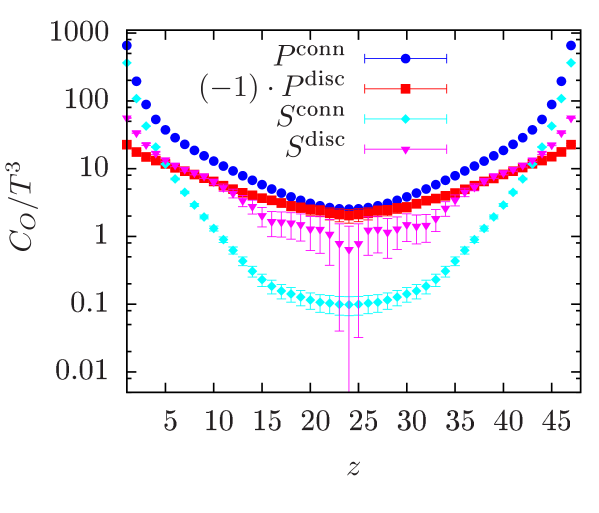
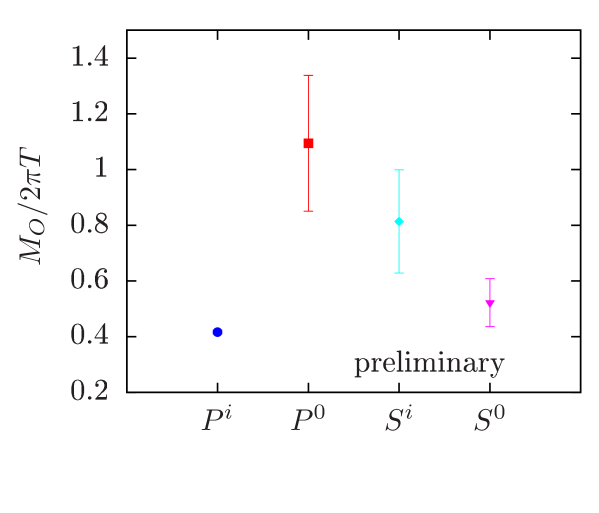
We will first compare the connected and disconnected parts of the correlation functions, shown in the left panel of Fig. 9. The disconnected correlation functions have been computed with 32 Hadamard probing vectors for hierarchical probing [34]. While the magnitude of connected and disconnected correlation functions in the $P$ channel is similar, the disconnected correlator is negative, leading to a large cancellation. At $T=0$ this cancellation results in the exponential decay of the iso-singlet correlator with the $\eta^{\prime}$ mass. In the $S$ channel, both correlation functions are positive, but the disconnected correlation function has a slower exponential decay and thus governs the iso-singlet correlator. To investigate the pattern of chiral symmetry restoration, we have extracted the iso-singlet screening masses from the correlators, which we compare to the iso-vector screening masses in the right panel of Fig. 9. Both, the screening masses in $P^{i}$ and $S^{0}$ channels, as well as in $P^{0}$ and $S^{i}$ channels agree within (their large) uncertainties, confirming the effective restoration of $\textnormal{SU}_{A}(2)$. At the same time, also the screening masses in $P^{0}$ and $S^{0}$ channels are non-degenerate, indicating a residual breaking of $\textnormal{U}_{A}(1)$, as seen in the previous section.

Note, that the results are preliminary in the sense that currently the statistics is not sufficient to extract the iso-singlet screening masses reliably. In particular, the screening masses in Fig. 9 (except for $M_{P^{i}}$) have been extracted without taking excited states into account. This is problematic since the signals become lost in noise already at comparably small values of $z$. The obvious next task is to increase statistics and to confirm the results presented in this section.

In this proceedings article we have updated our initial study [7] to larger volumes, showed first results for a scan at physical light quark masses, extended our set of observables and presented first results for the extension to iso-singlet correlation functions. Larger volumes show the tendency to strengthen the effect of the anomalous breaking of the $\textnormal{U}_{A}(1)$ symmetry. However, a chiral extrapolation of the screening mass difference at $T_{c}$ is currently not possible for the larger volumes, lacking a third quark mass. We are currently extending our simulations to the physical quark mass, for which we have shown first results. Additional observables are renormalised matrix elements of the screening correlators. Evaluated on the $32^{3}$ volumes, they tend to show an increase in the strength of the breaking of $\textnormal{U}_{A}(1)$ for smaller quark masses. A first look at screening masses in iso-singlet channels at $T_{c}$ for scan C2 shows that the breaking of $\textnormal{U}_{A}(1)$ is also present in $P^{0}$ and $S^{0}$ channels, while invariance under $\textnormal{SU}_{A}(2)$ transformations appears to be restored. To be able to reliably extract information from the iso-singlet correlators, however, a substantial increase in precision is mandatory.