The AHA-Tree: An Adaptive Index for HTAP Workloads

Lu Xing Purdue University, West Lafayette, IN47907-2107 xingl@purdue.edu and Walid G. Aref Purdue University, West Lafayette, IN47907-2107 aref@purdue.edu

Abstract.

In this demo, we realize data indexes that can morph from being write-optimized at times to being read-optimized at other times nonstop with zero-down time during the workload transitioning. These data indexes are useful for HTAP systems (Hybrid Transactional and Analytical Processing Systems), where transactional workloads are write-heavy while analytical workloads are read-heavy. Traditional indexes, e.g., B⁺-tree and LSM-Tree, although optimized for one kind of workload, cannot perform equally well under all workloads. To migrate from the write-optimized LSM-Tree to a read-optimized B⁺-tree is costly and mandates some system down time to reorganize data. We design adaptive indexes that can dynamically morph from a pure LSM-tree to a pure buffered B-tree back and forth, and has interesting states in-between. There are two challenges: allowing concurrent operations and avoiding system down time. This demo benchmarks the proposed AHA-Tree index under dynamic workloads and shows how the index evolves from one state to another without blocking.

1. Introduction

Refer to caption — (a) A diagram of an ideal index evolution under the oscillating read-heavy and write-heavy workloads

New data-intensive applications impose new requirements on data systems. The term Hybrid Transactional and Analytical Processing (HTAP, for short) is coined to represent the ever-increasing need to address hybrid requirements, mainly to offer online analytics over online transactional data. Typical HTAP workloads include heavy transactional workloads at times as well as heavy analytical queries at other times. HTAP systems need to support workload changes over time. For example, this is observed as a diurnal pattern in one of the RocksDB use cases at Meta (Cao et al., 2020), and is also observed in (Daghistani et al., 2021) where the number of tweets fluctuate across the day.

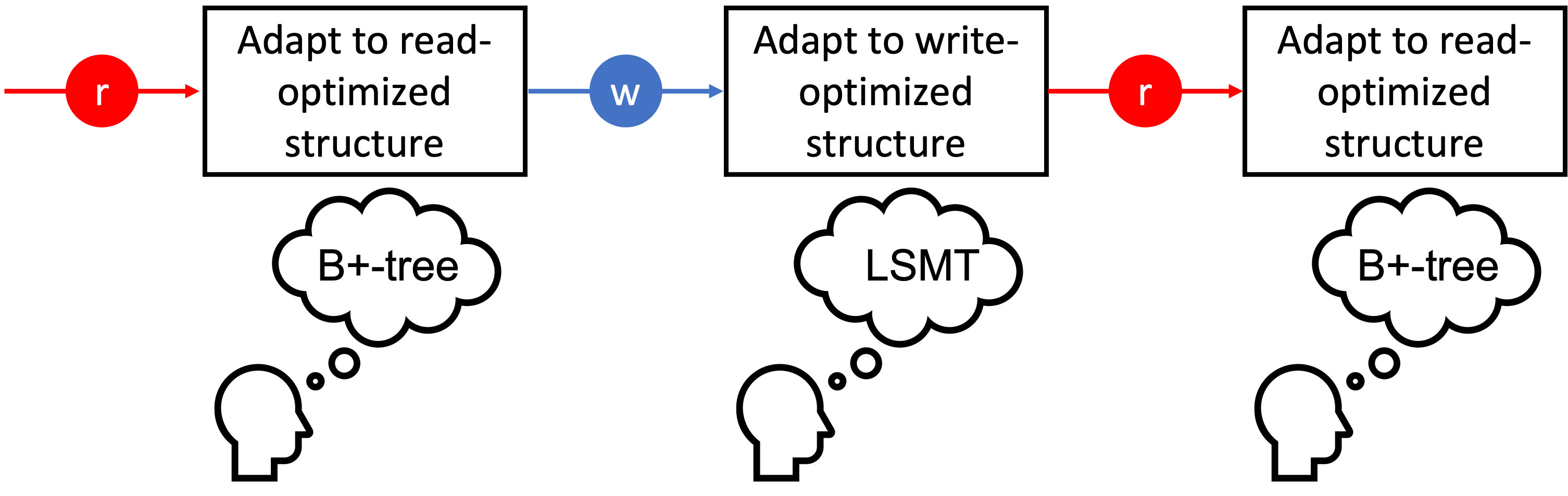
In this demo, we demonstrate a data index termed the Adaptive Hotspot-Aware tree index, (the AHA-tree, for short) that is suitable for HTAP workloads. The AHA-tree can adapt and morph from being write-optimized at times, e.g., behave like an LSM-tree, to being read-optimized at other times, e.g., behave like a B⁺-tree. We stress-test the AHA-tree over one of the most observed changing workloads; one that oscillates between being write-heavy at times to being read-heavy at other times. This pattern is practical in some applications, e.g., in a social media app, where users post comments actively during the day, and browse content at night. This corresponds to the oscillating write-heavy posting comments, and read-heavy browsing workloads, which is repeated daily. Another observation over real datasets is that operations are focused on hotspots. Thus, theAHA-tree only adapts the structure where hotspot data is stored, which is more time efficient.

Among the analytical workloads, we focus on simple range search queries as we can control the amount of selected data by the query. Traditional static indexes, e.g., the B⁺-tree (Bayer and McCreight, 1970; Comer, 1979) and Log-Structured Merge Tree (LSM-Tree) (O’Neil et al., 1996) that are optimized for only one operation are either optimized for range search query or optimized for write operations, respectively. They cannot achieve the same throughput performance in the case of an oscillating write-heavy and read-heavy workloads.

The ideal index for the oscillating workload is to make the index behave as an LSM-Tree in the write-heavy phase, and behave as a B⁺-tree in the read-heavy workload as in Figure 1(a). In this demonstration, we present AHA-tree which is an adaptive index being hotspot-aware. We showcase baseline indexes and the AHA-tree under oscillating workloads. The AHA-tree can adapt itself and catch with the optimal static index within that workload. We also display the intermediate structure of the AHA-tree during adapting. However, as this demo illustrates, under certain workloads, the overall throughput of the AHA-tree is competitive compared to the read-optimized index (i.e., the B⁺-tree) and the write-optimized index (i.e., the LSM-Tree). A trade-off between current performance and future performance is demonstrated for the AHA-tree. Meanwhile, being an adaptive index, the AHA-tree takes time to adapt. The throughput during the adaptation phase can be low, and this is the tradeoff, but this does not compare to having significant down time to migrate data to suit the new workload or to maintain dual structures, one for each workload type.

2. Background

The structure of the AHA-tree is inspired by the buffer tree (Arge, 2003), where the AHA-tree can be viewed as a tree part (a B⁺-tree) plus a buffer part (an LSM-Tree), and lies perfectly in the middle between a B⁺-tree and an LSM-Tree. However, a buffer tree may not solve the problem of oscillating workloads as it is still a static structure.

The core of adaptation is how to place the buffered data. During a read-heavy workload, buffered data is migrated gradually to the leaf nodes so that range searches access the index as if it is a B⁺-tree. During the write-heavy workload, data is buffered in batches as if it is an LSM-tree to avoid I/Os caused by individual insertions.

Making the buffer tree adaptive introduces several challenges including:

(1)

How to query the buffer tree?
(2)

How to maximize the write throughput?
(3)

How to minimize the number of file compactions?

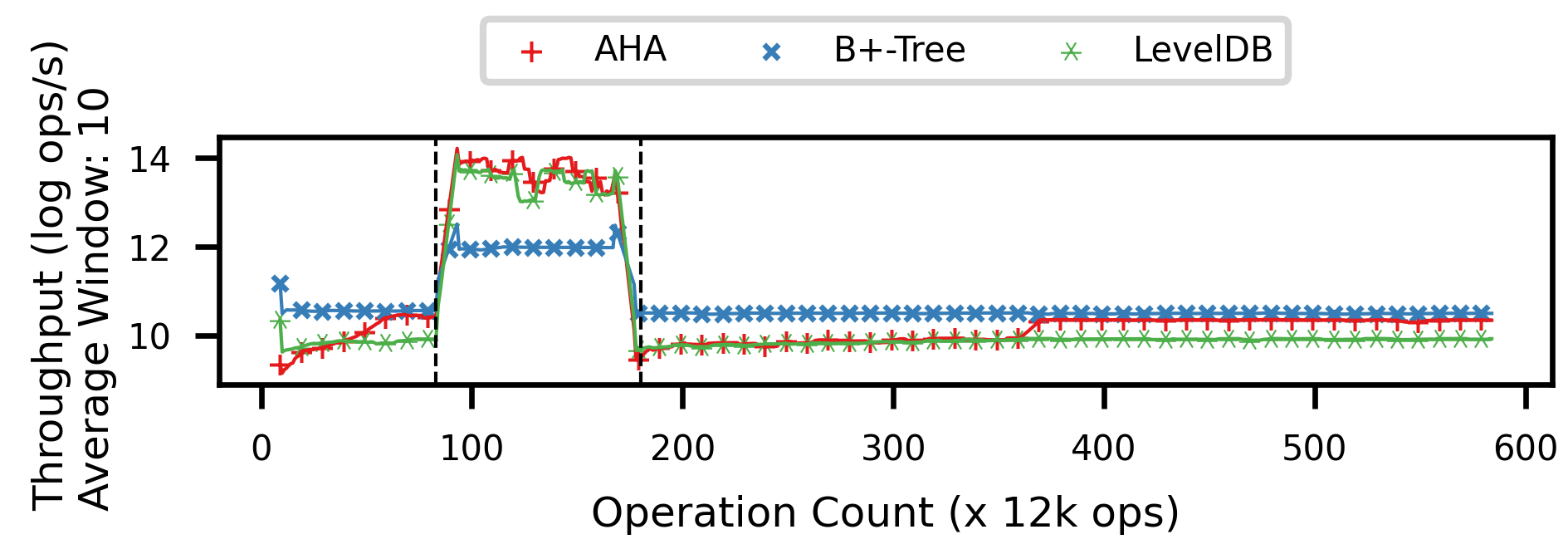
We propose techniques to address the above challenges given the observation that real datasets are skewed with hotspots. We apply these techniques in the proposed Adaptive Hotspot-Aware Tree, or AHA-tree, for short. We compare the three indexes as in Figure 1(b). All indexes are pre-constructed before the first operation. The workload starts from range search queries only, and transitions to update-only when 1 million operations have finished. After another 1 million updates, the workload is transitioned to range search queries only. The AHA-tree is able to adapt itself as its throughput climbs during the first workload phase. In the update phase, the AHA-tree is competitive with LevelDB. In the third phase (the read-heavy range search queries phase), the AHA-tree can still adapt itself although finish after more operations than the first phase.

3. Overview of the AHA-tree

In this section, we summarize the basic components of the AHA-tree as well as how insertions and range search queries are performed in the AHA-tree. Then, we briefly explain the adaptation process.

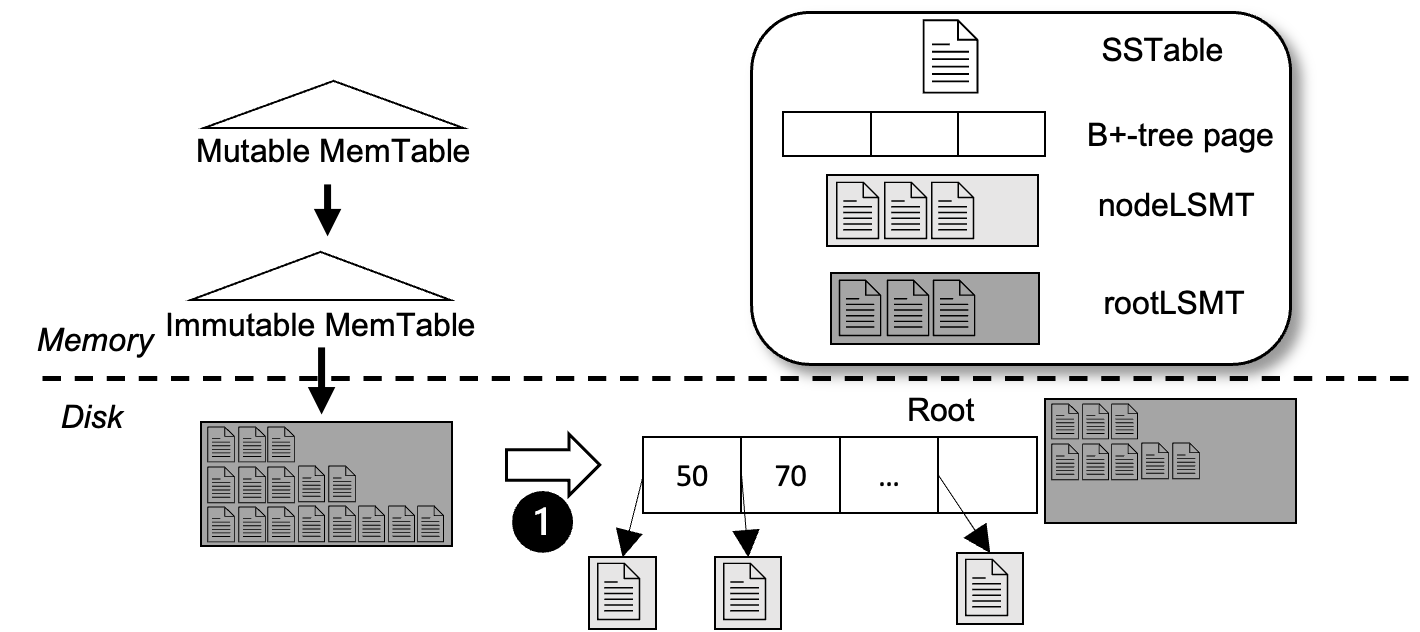
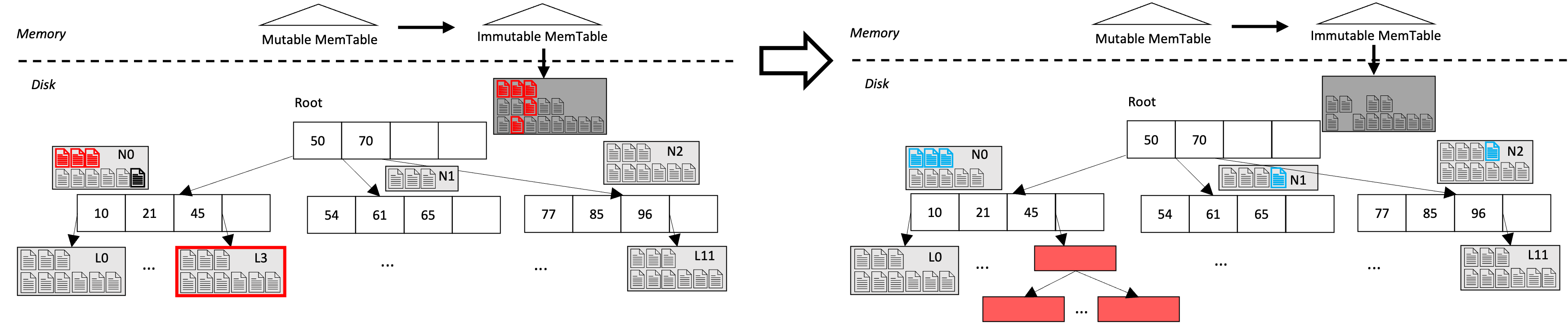
The Index Structure. The AHA-tree combines the LSM-Tree, the B⁺-tree, and the buffer tree. Under a write-heavy workload, all write operations are performed as if the AHA-tree is an LSM-Tree. Under a read-heavy workload within a hotspot, all range search queries are as if the AHA-tree is a B⁺-tree (Figure 1(a)). A key challenge is how to maintain a valid index structure. We use a buffer tree (Arge, 2003)-like structure as the intermediate structure. The buffer of the root node (rootLSMT) is an LSM-Tree that accepts all the incoming writes. When a buffer overflows, data items are dispatched to the buffers of the children. The buffer of the leaf node (nodeLSMT) is also an LSM-Tree. The AHA-tree keeps the invariant that data in rootLSMT are fresher than data in nodeLSMT; the closer nodeLSMT to the root, the fresher the data. This invariant is enforced at all times.

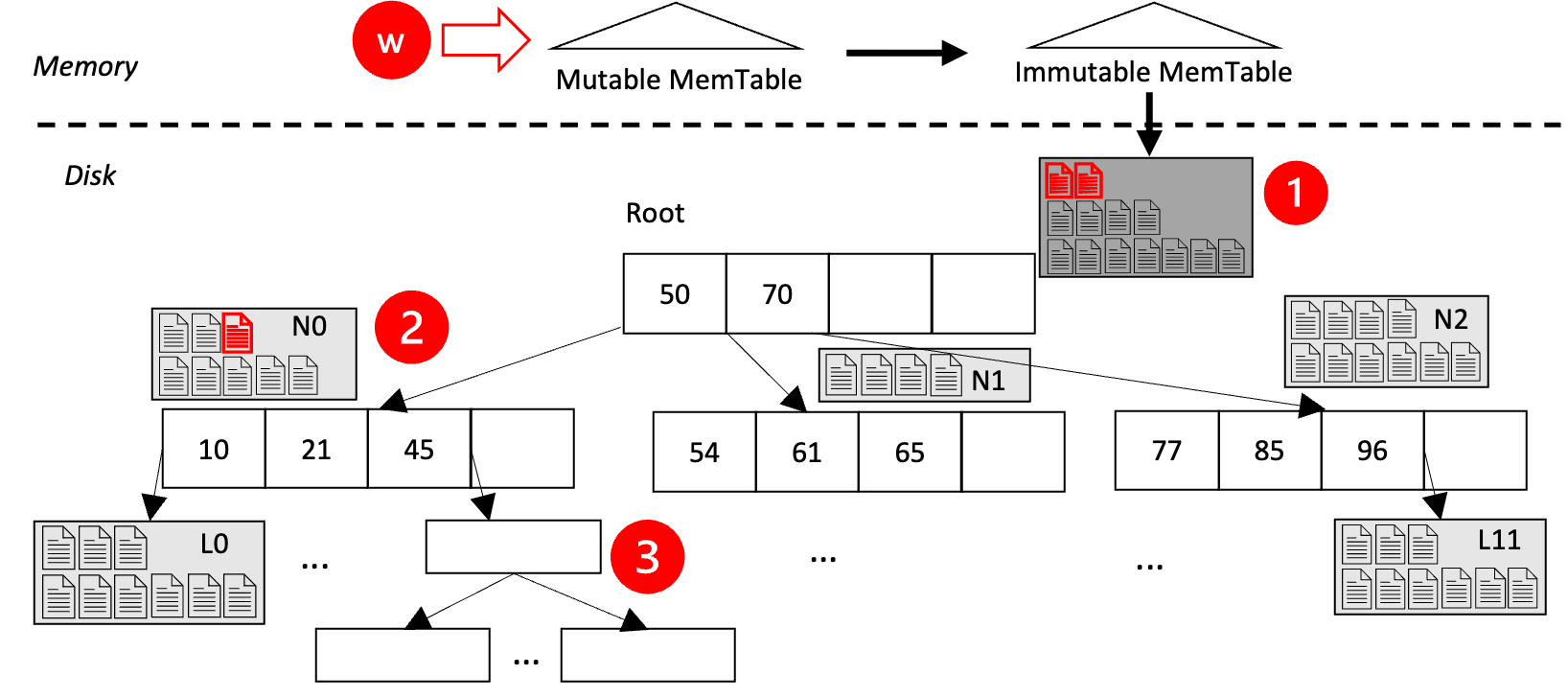
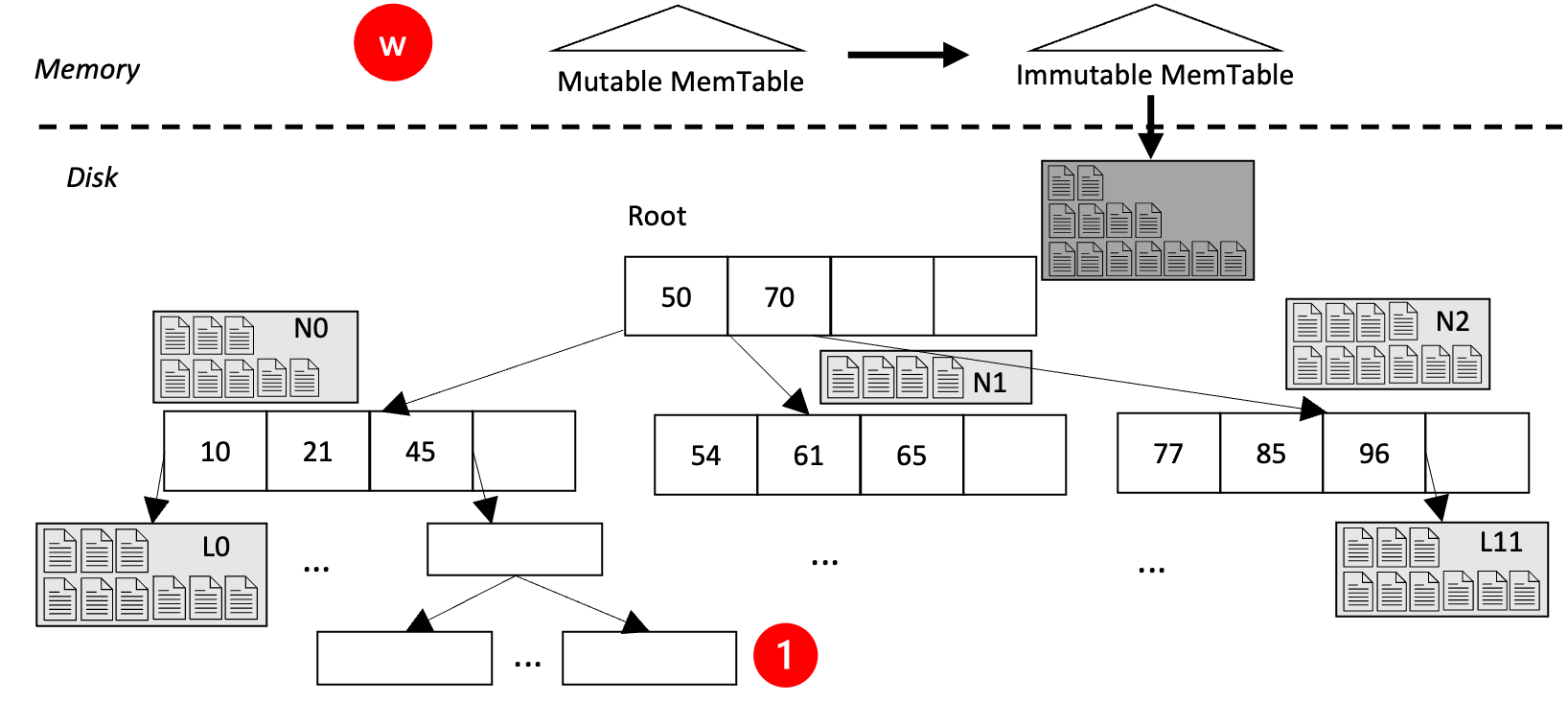
Insert. Updates are first buffered in the root node’s rootLSMT MemTable. Once this buffer becomes full, data items are written to disk in a persistent file, termed an SSTable (MemTables and SSTables are as used in LevelDB (lev, [n.d.]) and RocksDB (roc, [n.d.])). An SSTable is added to level-0 of rootLSMT. In Figure 2(a), Step 1 shows the transformation from an LSM-Tree to the construction of the initial tree structure. Both the rootLSMT and nodeLSMT have a size limit that when reached for a rootLSMT or nodeLSMT of a non-leaf node, a level-emptying process is triggered. If nodeLSMT of a leaf node reaches the size limit, it is split to multiple leaf nodes each with one nodeLSMT. New routing keys are added to the parent of this leaf node, and this may be propagated up til the root.

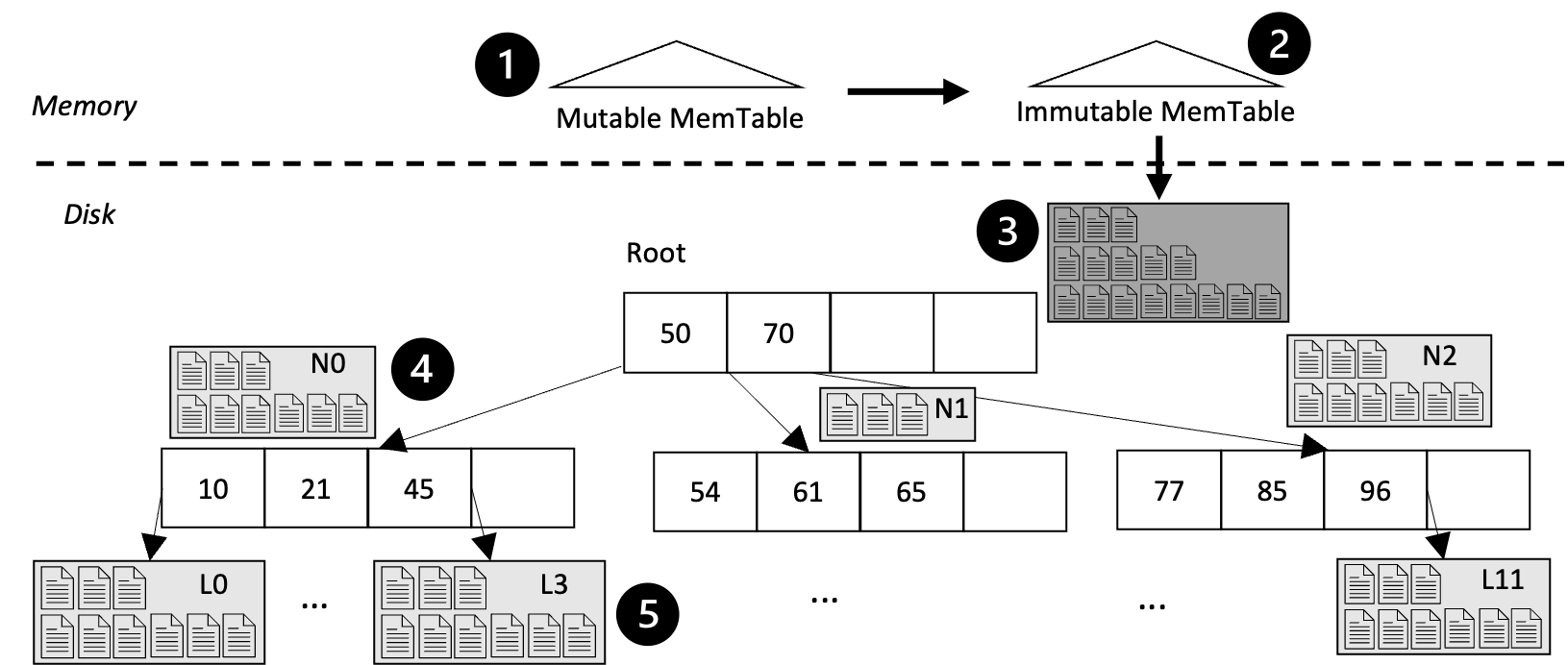
Range Search. Unlike the buffer tree (Arge, 2003), range search queries in the AHA-tree are not batched because we want to minimize the latency of individual queries. Since the requested date items may reside in all nodeLSMT and leaf pages that have a range that overlaps the query, we rely on a merged iterator to produce sorted results. In Figure 2(b), Range Query [45, 49] starts from the MemTable and to rootLSMT that has the freshest data on disk. Then, the query follows the link in the tree page, and finds the appropriate data in nodeLSMT of N0 as well as Leaf Node L3.

Adapting. AHA-tree starts to adapt when there is a range search query based on a forming hotspot. The range query records the touched nodes, and sends them to the background thread. To adapt, data of nodeLSMTs that are inside the hotspot are flushed down to the leaf level, and the leaf nodes are transformed into leaf pages.

4. Demonstration Scenario

Figure 3 gives the workflow of our demo that constitutes data generation, index construction, initial adaptation upon the first range search phase, updates on adapted AHA-tree during the update phase, as well as the following range search phase. We will demonstrate, via visualization, the evolution of the AHA-tree for alternating write- and read-heavy workloads. We will show how the AHA-tree adapts in the hotspot region while the other parts of the structure remain unchanged. We provide several knobs s.t. users can visualize the evolution and performance (online throughput and latency) of the AHA-tree under various workload conditions.

We will contrast the performance of the AHA-tree against the B⁺-tree and the LSM-tree under the same conditions. We will provide the users with a simulation knob to identify the location of the hotspot. Users will visualize the simulation of how the index evolves along with its performance. By switching to a read-only workload, we will show how the AHA-tree performs during the adaptation process and how other two indexes stay static, as well as how the AHA-tree eventually performs after the adaptation process is complete as in Figure 1(b). Upon switching to a write-only workload again, we will show the AHA-tree’s throughput and demonstrate the trade-offs between different adaptation techniques.

Knob 1: Data distribution and analytics data size. The demonstration starts by generating artificial datasets in uniform or Zipfian distributions. Data is loaded into the indexes, including the AHA-tree, the B⁺-tree and the LSM-Tree. Users will visualize that how different data distributions may have an effect on the adaptation outcome, and the result after changing the skewness of the Zipfian distribution. In the demonstration, the data size involved in the analytics process is determined by changing the size of the range search. We change the size of the range search as well as make the size dynamically, and show a comparison of the throughputs and latencies among the three index alternatives.

Knob 2: Enabling/Disabling Adaptation. By toggling between enabling and disabling adaptation, users can observe the throughput difference between the two scenarios and the comparison with the baseline indexes, e.g., the B⁺-tree and the LSM-Tree.

Knob 3: Enabling/Disabling Seek Compaction. LevelDB’s LSM-tree offers seek compaction to enhance read latency. Seek compaction is triggered after multiple seeks on one file. We present how this technique performs compared to the adapting AHA-tree.

Knob 4: Lazy vs. Eager Adaptation. Adaptation can be triggered by each individual range query lazily or by one range query that encloses the entire hotspot region. Typically, the hotspot location can be predicted beforehand. Figure 4 shows the result after adapting for Hotspot Region [46, 50]. To answer a range query, the AHA-tree is traversed top down in all nodeLSMTs, starting at rootLSMT and moving to the child node that overlaps [46, 50], finally reaching the leaf node. Hotspot data is marked in red in the left panel. All the nodeLSMTs are recorded, and are sent to the background thread.

The resulting tree has a hybrid structure as in Figure 4 right panel, with the hotspot in a B⁺-tree-like structure, and the other nodeLSMTs almost unchanged. Since during hotspot data compaction and flush down, cold spot data that coexists in the original files gets flushed down as well, and is marked in blue in Figure 4 right panel.

In Eager Adaptation, hotspot range [46, 50] is issued as a range query beforehand. In contrast, lazy adaptation relies on the range queries in the workload. Users will be able to visualize the index structure after full adaptation. Users will also observe the throughput over time of lazy and eager adaptation.

Knob 5: Balanced vs. Unbalanced Leaf Transformation. To adapt a leaf node with a nodeLSMT into multiple leaf pages, the straightforward way is to re-compact all the files in nodeLSMT and write data items into new pages. However, this incurs re-compaction overhead. We will demonstrate another way to transform leaf nodes that results in an unbalanced leaf structure as in Figure 4. This relies on the fact that the Level- $i$ ( $i>0$ ) of the LSM-Tree has sorted files. The transformation takes two steps. First, each file of Level- $i$ ( $i>0$ ) of the nodeLSMT is assigned to a new leaf node. Next, the new node with only one file is split into multiple leaf pages as in Figure 4.

Knob 6: Batched vs. Single Inserts. After AHA-tree has been fully adapted, future inserts may insert hotspot data directly into the leaf pages as in Figure 5(b). Inserts in the cold spot region are still batched into the LSM-tree’s memory components before being flushed to the the nodeLSMTs. On the other hand, batched inserts are still batched in memory as in Figure 5(a). This raises a trade-off between current and future performance. Batched inserts are more write-optimized and behave as an LSM-Tree except that Step 3 (See Figure 5(a)), requires merging files with leaf pages. The overhead takes place while adapting during the next read-heavy phase. While for single insertion, price is paid during write operations and no more adaptation is needed at later range search phase. Users will observe the throughput differences between the two choices.

Knob 7: Even vs. Sound-remedy Assignment. When the leaf node with nodeLSMTs are written into leaf pages, the straightforward way is to evenly assign data items across multiple pages. However, this results in waves of misery (Glombiewski et al., 2019; Xing et al., 2021) and later range queries may suffer depending on the number of update operations. Without mitigating this issue, the AHA-tree may experience throughput degradation when adapting back to a read-heavy workload. To handle this issue, we pack the leaf pages in the initial adaptation phase according to the sound remedy policy introduced in (Glombiewski et al., 2019; Xing et al., 2021). Later in the update phase, hot data are inserted one-by-one using single inserts that prevents waves of misery from happening. We will demonstrate the differences in page utilization distribution between these two assignments. We will also show the throughput with and without the Sound Remedy policy.

5. Related Work

Numerous studies have been conducted in improving the write performance of tree-like structures (Arge, 2003; Graefe, 2004; Bender et al., 2015; Zeighami, 2019). Research has been conducted to improve the LSM-Tree’s read performance, including using Bloom filters (Bloom, 1970) to improve LSM-Tree point reads, using a hierarchically-stacked Bloom filters to improve range search (Luo et al., 2020) and using a sorted view across multiple files to improve range search (Zhong et al., 2021). There are numerous research studies for adaptive indexes, e.g., database cracking (Idreos et al., 2007), adaptive hybrid indexes (Anneser et al., 2022), VIP-hashing (Kakaraparthy et al., 2022), SA-LSM (Zhang et al., 2022), LASER (Saxena et al., 2023), B^link-hash (Cha et al., 2023) among others.

Acknowledgements.

Walid G. Aref acknowledges the support of the National Science Foundation under Grant Number IIS-1910216.

References

(1)
lev ([n.d.]) [n.d.]. LevelDB. https://github.com/google/leveldb
roc ([n.d.]) [n.d.]. RocksDB. https://github.com/facebook/rocksdb
Anneser et al. (2022) Christoph Anneser, Andreas Kipf, Huanchen Zhang, Thomas Neumann, and Alfons Kemper. 2022. Adaptive hybrid indexes. In Proceedings of the 2022 International Conference on Management of Data. 1626–1639.
Arge (2003) Lars Arge. 2003. The buffer tree: A technique for designing batched external data structures. Algorithmica 37 (2003), 1–24.
Bayer and McCreight (1970) Rudolf Bayer and Edward McCreight. 1970. Organization and maintenance of large ordered indices. In Proceedings of the 1970 ACM SIGFIDET (Now SIGMOD) Workshop on Data Description, Access and Control. 107–141.
Bender et al. (2015) Michael A Bender, Martin Farach-Colton, William Jannen, Rob Johnson, Bradley C Kuszmaul, Donald E Porter, Jun Yuan, and Yang Zhan. 2015. An introduction to B-trees and write-optimization. login; magazine 40, 5 (2015).
Bloom (1970) Burton H Bloom. 1970. Space/time trade-offs in hash coding with allowable errors. Commun. ACM 13, 7 (1970), 422–426.
Cao et al. (2020) Zhichao Cao, Siying Dong, Sagar Vemuri, and David HC Du. 2020. Characterizing, modeling, and benchmarking $\{$ RocksDB $\}$ $\{$ Key-Value $\}$ workloads at facebook. In 18th USENIX Conference on File and Storage Technologies (FAST 20). 209–223.
Cha et al. (2023) Hokeun Cha, Xiangpeng Hao, Tianzheng Wang, Huanchen Zhang, Aditya Akella, and Xiangyao Yu. 2023. Blink-hash: An adaptive hybrid index for in-memory time-series databases. Proceedings of the VLDB Endowment 16, 6 (2023), 1235–1248.
Comer (1979) Douglas Comer. 1979. Ubiquitous B-tree. ACM Computing Surveys (CSUR) 11, 2 (1979), 121–137.
Daghistani et al. (2021) Anas Daghistani, Walid G Aref, Arif Ghafoor, and Ahmed R Mahmood. 2021. Swarm: Adaptive load balancing in distributed streaming systems for big spatial data. ACM Transactions on Spatial Algorithms and Systems 7, 3 (2021), 1–43.
Glombiewski et al. (2019) Nikolaus Glombiewski, Bernhard Seeger, and Goetz Graefe. 2019. Waves of misery after index creation. (2019).
Graefe (2004) Goetz Graefe. 2004. Write-optimized B-trees. In Proceedings of the Thirtieth international conference on Very large data bases-Volume 30. 672–683.
Idreos et al. (2007) Stratos Idreos, Martin L Kersten, Stefan Manegold, et al. 2007. Database Cracking.. In CIDR, Vol. 7. 68–78.
Kakaraparthy et al. (2022) Aarati Kakaraparthy, Jignesh M Patel, Brian P Kroth, and Kwanghyun Park. 2022. VIP hashing: adapting to skew in popularity of data on the fly. Proceedings of the VLDB Endowment 15, 10 (2022), 1978–1990.
Luo et al. (2020) Siqiang Luo, Subarna Chatterjee, Rafael Ketsetsidis, Niv Dayan, Wilson Qin, and Stratos Idreos. 2020. Rosetta: A robust space-time optimized range filter for key-value stores. In Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data. 2071–2086.
O’Neil et al. (1996) Patrick O’Neil, Edward Cheng, Dieter Gawlick, and Elizabeth O’Neil. 1996. The log-structured merge-tree (LSM-tree). Acta Informatica 33 (1996), 351–385.
Saxena et al. (2023) Hemant Saxena, Lukasz Golab, Stratos Idreos, and Ihab F Ilyas. 2023. Real-time LSM-trees for HTAP workloads. In 2023 IEEE 39th International Conference on Data Engineering (ICDE). IEEE, 1208–1220.
Xing et al. (2021) Lu Xing, Eric Lee, Tong An, Bo-Cheng Chu, Ahmed Mahmood, Ahmed M Aly, Jianguo Wang, and Walid G Aref. 2021. An experimental evaluation and investigation of waves of misery in r-trees. arXiv preprint arXiv:2112.13174 (2021).
Zeighami (2019) Sepanta Zeighami. 2019. Nested b-tree: efficient indexing method for fast insertions with asymptotically optimal query time. Ph.D. Dissertation.
Zhang et al. (2022) Teng Zhang, Jian Tan, Xin Cai, Jianying Wang, Feifei Li, and Jianling Sun. 2022. SA-LSM: optimize data layout for LSM-tree based storage using survival analysis. Proceedings of the VLDB Endowment 15, 10 (2022), 2161–2174.
Zhong et al. (2021) Wenshao Zhong, Chen Chen, Xingbo Wu, and Song Jiang. 2021. $\{$ REMIX $\}$ : Efficient Range Query for $\{$ LSM-trees $\}$ . In 19th USENIX Conference on File and Storage Technologies (FAST 21). 51–64.