The Ameyalli-Rule: Logical Universality in a 2D Cellular Automaton
Abstract
We present a new spontaneously emergent glider-gun in a 2D Cellular Automaton and build the logical gates NOT, AND and OR required for logical universality. The Ameyalli-rule is not based on survival/birth logic but depends on 102 isotropic neighborhood groups making an iso-rule, which can drive an interactive input-frequency histogram for visualising iso-group activity and dependent functions for filtering and mutation. Neutral inputs relative to logical gates are identified which provide an idealized striped-down form of the iso-rule.
keywords: cellular automata, iso-rule, glider-gun, logical gates, universality
1 Introduction
The Ameyalli-rule111Ameyalli means a spring of running water in Nahuatl, a language spoken in central Mexico. is a new result that continues our search for 2D Cellular Automata (CA) with glider-guns and eaters capable of logical universality. Since the publication of Conway’s Game-of-Life[5] with its survival/birth s23/b3 logic, many other “Life-Like” survival/birth combinations have been examined[3] but none seem to have come close[11] to achieving the complexity of behaviour of the Game-of-Life itself.
To study the basic principles of CA universal computation in a more general context, glider-guns and logical gates have been demonstrated outside survival/birth “Life-Like” constraints, but still within isotropic rule-space where all possible flips/spins of a neghborhood pattern give the same input. Isotropic rules are preferable to enact logical universality because their dynamics have no directional bias and computational machinery operates in any orientation. Examples include the 3-value 7-neighbour hexagonal Spiral-rule[1], and for a binary 2d Moore neigborhood, the Sapin-rule[13], and four rules in our own published results demonstrating logical universality — the first was the anisotropic X-Rule[7], followed by the isotropic Precursor-rule[8], the Sayab-rule[9] and the Variant-rule[10].
These rules were found from a short-list[7, 8]
within an input-entropy scatter-plot[17, 18] sample of
93000+ isotropic rules, which classify rule-space between order,
chaos and complexity. The input-entropy criteria in this sample
follow “Life-Like” constraints to the extent that the rules are
binary, isotropic, with a 33 Moore neighborhood —
![]() — and with the parameter, the
density of 1s in the full 512 rule-table, similar to the
Game-of-Life where . The short-list consists of rules
that feature emergent gliders within the ordered zone of the plot.
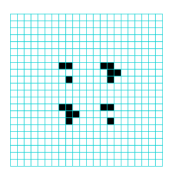
The Ameyalli-rule was found from the same
short-list. Its 2-phase orthogonal emergent glider — one type found to date
— is shown in figure 2.
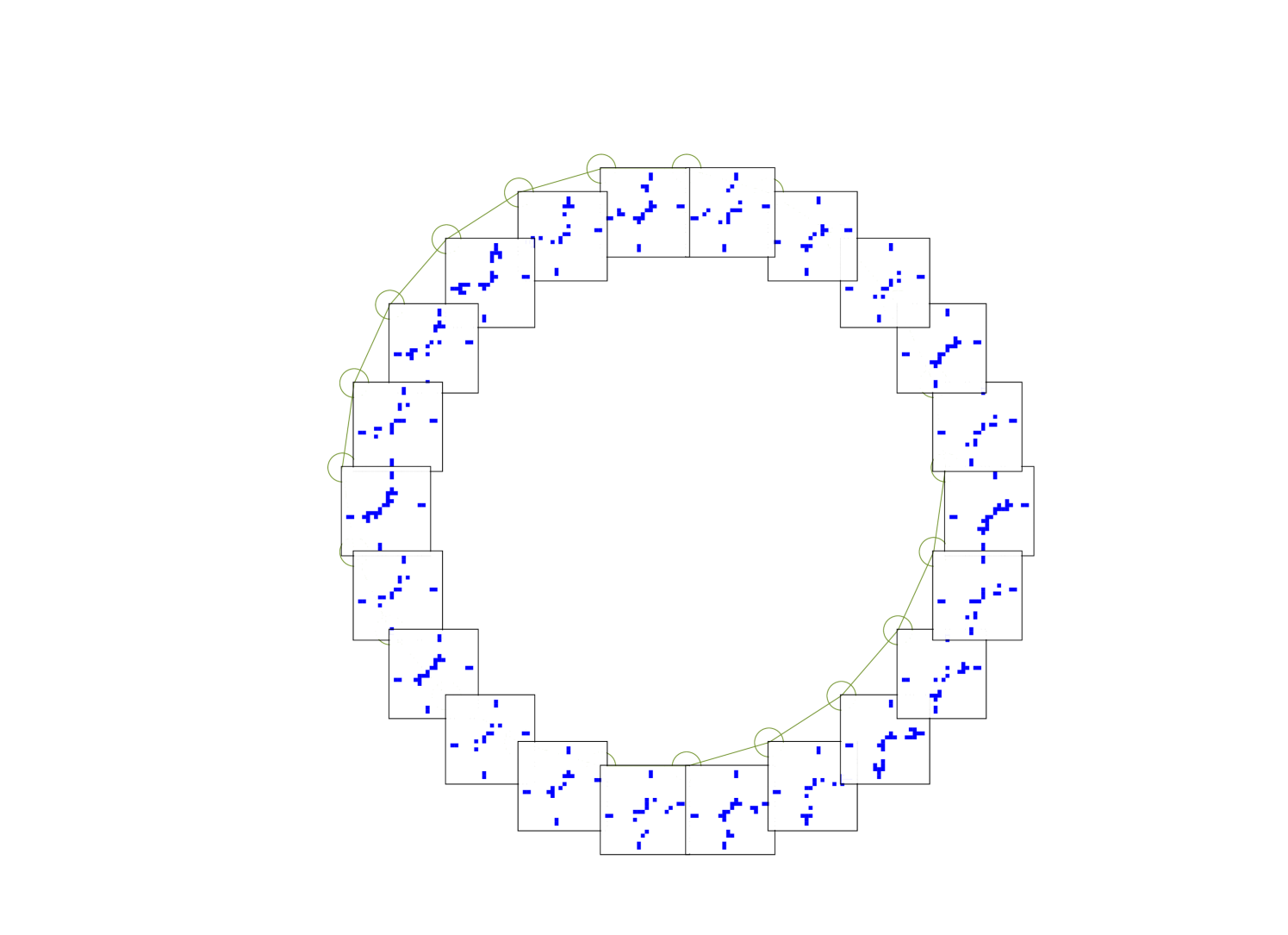
Its glider-gun (figures 3 and 4) also emerges
spontaneously from a random initial state in a similar way to the
Sapin-rule[13], the Sayab-rule[9], and the
Spiral-rule[1], but with a lower
probability, whereas the glider-guns for the other rules listed above,
including the Game-of-Life, require careful construction.
— and with the parameter, the
density of 1s in the full 512 rule-table, similar to the
Game-of-Life where . The short-list consists of rules
that feature emergent gliders within the ordered zone of the plot.
The Ameyalli-rule was found from the same
short-list. Its 2-phase orthogonal emergent glider — one type found to date
— is shown in figure 2.
Its glider-gun (figures 3 and 4) also emerges
spontaneously from a random initial state in a similar way to the
Sapin-rule[13], the Sayab-rule[9], and the
Spiral-rule[1], but with a lower
probability, whereas the glider-guns for the other rules listed above,
including the Game-of-Life, require careful construction.
The Ameyalli-rule is most efficiently defined and mutated as a 102-bit iso-rule[19], where any mutation conserves isotropy. An in-depth definition of isotropic rules, iso-rules based on iso-groups, including alternative notations — the full rule-table, symmetry classes, iso-rule prototypes, and the iso-rule in hexadecimal — are presented in section 5. These notations relate to DDLab[20] and can be redefined for Golly[6]. Figure 1 shows the Ameyalli iso-rule, and the mutations that were made to create the eaters A and B.


eater-Beater-A
It turn out that a large proportion, 60/102, of Ameyalli iso-rule inputs are neutral with respect its glider-gun/eater system (section 6.1) so this system can be equivalently generated by a vast family of mutant iso-rules. The identities of the Ameyalli and other logically universal rules are centered on their glider-gun/eater systems, which is best represented by a stripped-down “idealized” version of the iso-rule with all neutral inputs set to zero.
The paper is organised into the following sections: (2) describes the glider-gun, gliders, eaters, and collisions, (3) outlines logical universality, 4 demonstrates the logical gates, (5) defines the iso-rule, (6) gives methods for iso-rule activity by the input-frequency histogram (IFH), for filtering and mutation, and for idealising the iso-rule, and 7 is a summary and discussion of the issues.
(1)  (2)
(2)  (1)
(1)  (2)
(2) 
4 time-steps are shown across a fixed background with phases labelled (1) and (2).
2 The glider-gun, gliders, eaters, and collisions

The essential ingredients for a recipe to create CA logical universality are gliders, glider-guns, eaters, and appropriate collisions.
A glider is a special kind of oscillator, a mobile pattern that recovers its form but in a displaced position, thus moving at a given velocity. A rule with the ability to support a glider, together with a stable eater, and a diversity of interactions between gliders and eaters, provides the first hint of potential universality.
Although many rules can be found with these properties, the really essential and most elusive ingredient is a glider-gun, a dynamic structure that ejects gliders periodically into space. A glider-gun can also be seen as an oscillator that adds to its form periodically to shed gliders. If can be regarded as a periodic attractor[17], especially if confined by eaters as in figure 3.
In the case of the Ameyalli-rule, as already noted, a glider-gun may emerge spontaneously from a random pattern — only one type has been observed so far. In other cases a glider-gun can sometimes be constructed from smaller components, as for the very first glider-gun created by Gosper for the Game-of-Life. These glider-guns are such elaborate structures that the probability of their spontaneous emergence is negligible.
Another essential requirement is that gliders colliding sideways can self-destruct leaving no residue, and that the resulting gap in the glider-gun-stream is sufficiently wide to allow a following glider to pass through. The Ameyalli-rule satisfies all these requirements as illustrated in figures 4 to 9.


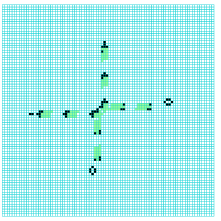


collision between a
stationary eater-B and
a glider noving North
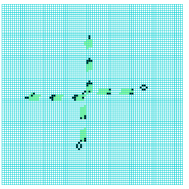
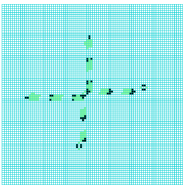
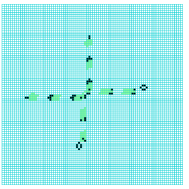
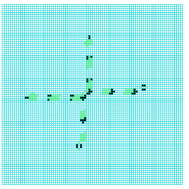
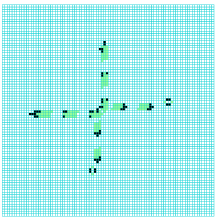
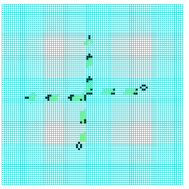 collision between a
collision between a
2-phase eater-A and
a glider moving South

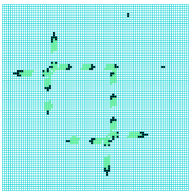
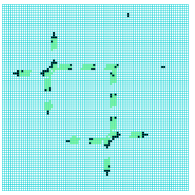
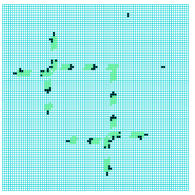
3 Logical Universality
Traditionally the proof for universality in CA is based on the Turing Machine or an equivalent mechanism, but in another approach by Conway[2], a CA is universal in the full sense if it is capable of the following,
-
1.
Data storage or memory.
-
2.
Data transmission requiring wires and an internal clock.
-
3.
Data processing requiring a universal set of logic gates NOT, AND, and OR, to satisfy negation, conjunction and disjunction.
This paper is confined to proving condition 3 only — for universality in the logical sense. To demonstrate universality in the full sense as for the Game-of-Life, it would be necessary to also prove conditions 1 and 2, or to prove universality in terms of the Turing Machine, as was done by Randall[12] for the Game-of-Life.
4 Logical Gates
Logical universality in the Ameyalli-rule, as in the Game-of-Life, is based on Post’s Functional Completeness Theorem (FCT)[4]. This theorem guarantees that it is possible to construct a conjunctive (or disjunctive) normal form formula using only the logical gates NOT, AND and OR.
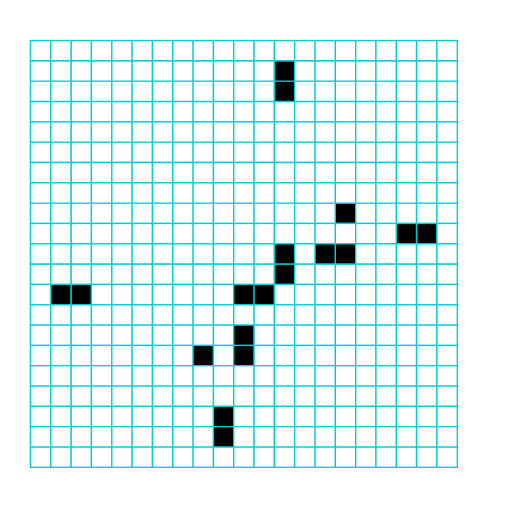
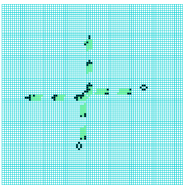
Using a specific right-angle collision, two gliders can self-destruct leaving no residue as shown in figure 6. Applying this property between glider-gun streams and a glider/gap sequence with the correct spacing and phases representing a “string” of information, its possible to build the logical gates NOT, AND and OR, illustrated in figures 7, 8 and 9. Gaps in a string are indicated by grey circles, dynamic trails are included, and B-type eaters are positioned to eventually stop gliders. Note that the leading bit of a moving glider/gap information sequence appears on the left in its string representation.
4.1 NOT gate
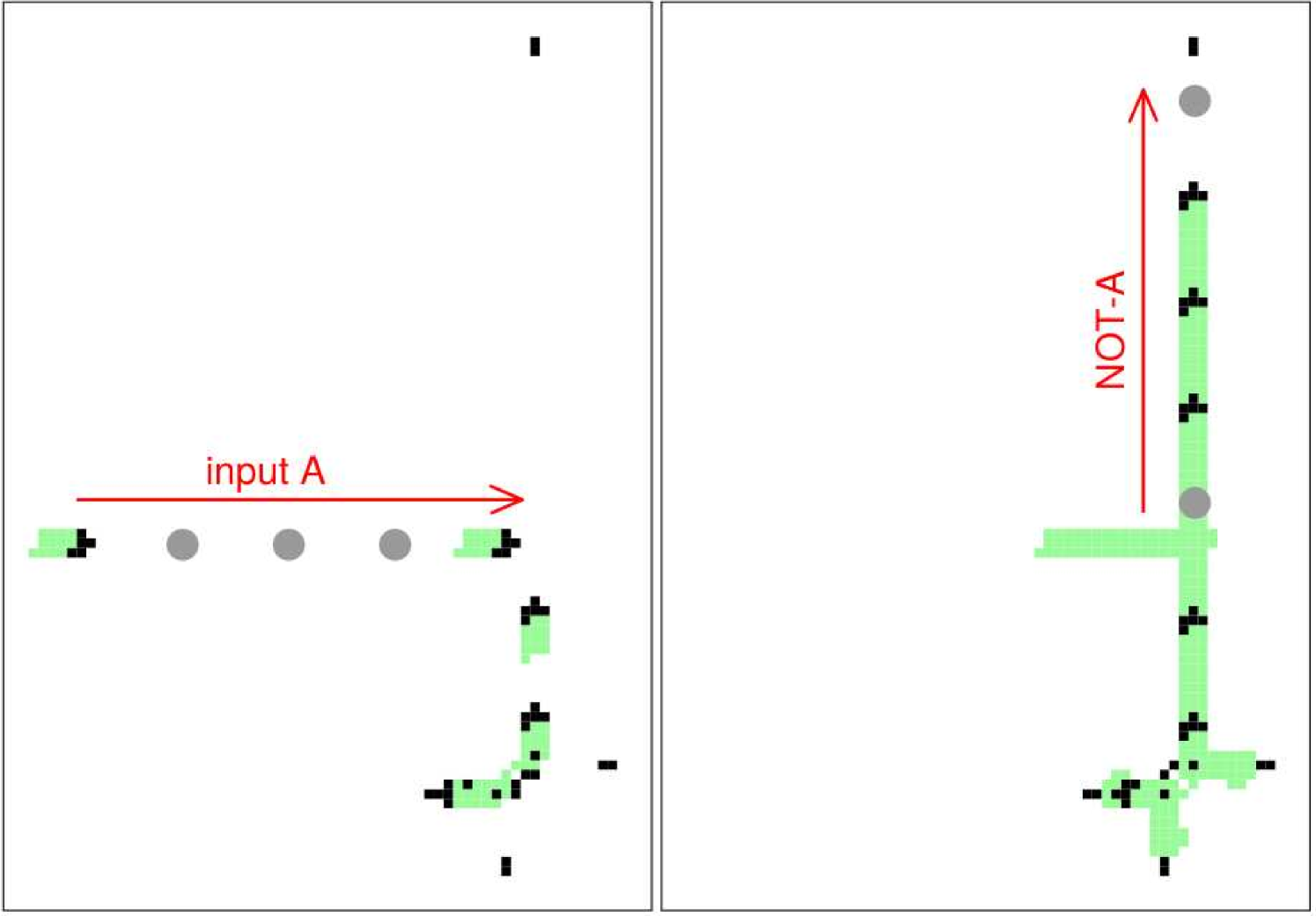
4.2 AND gate
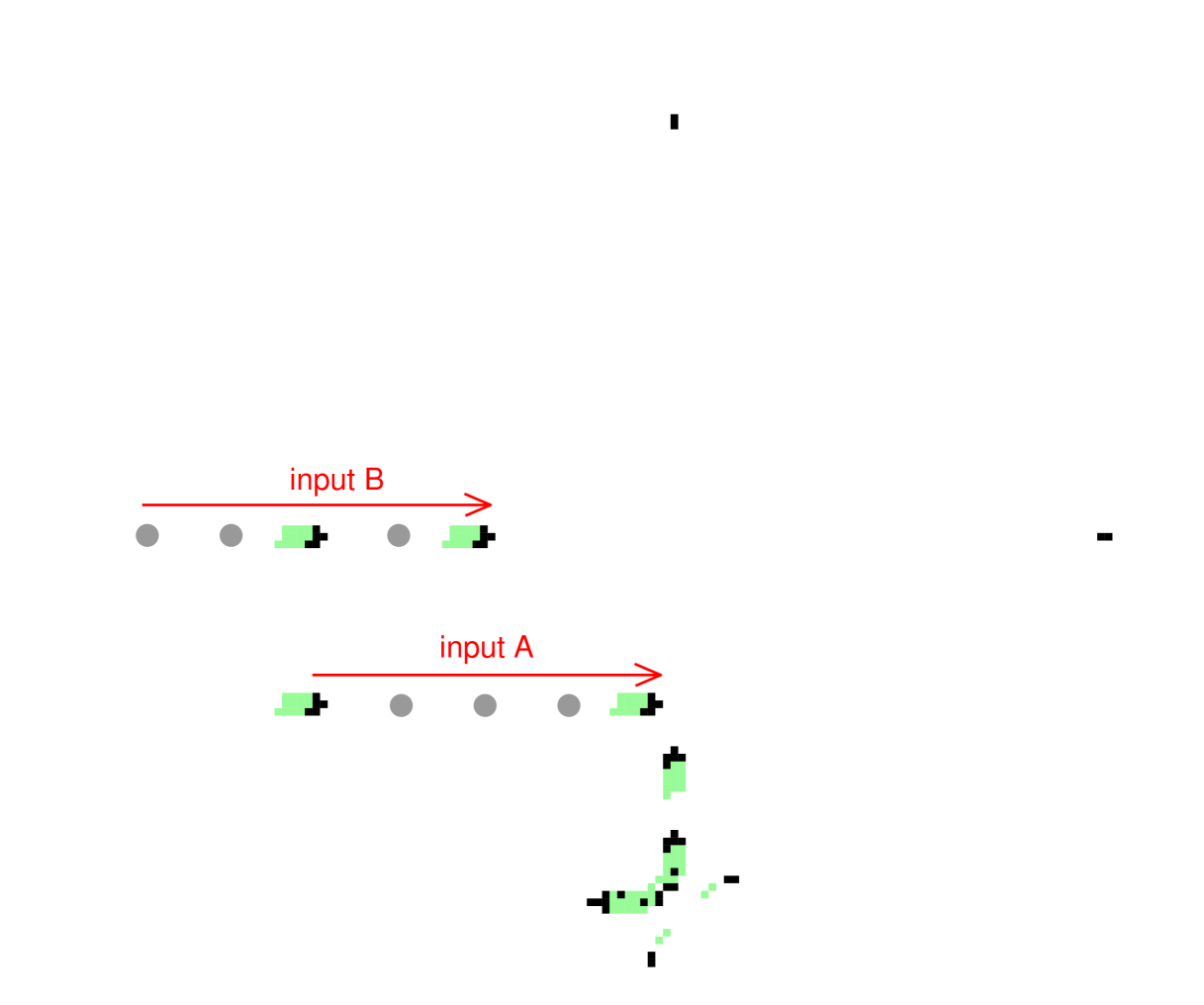
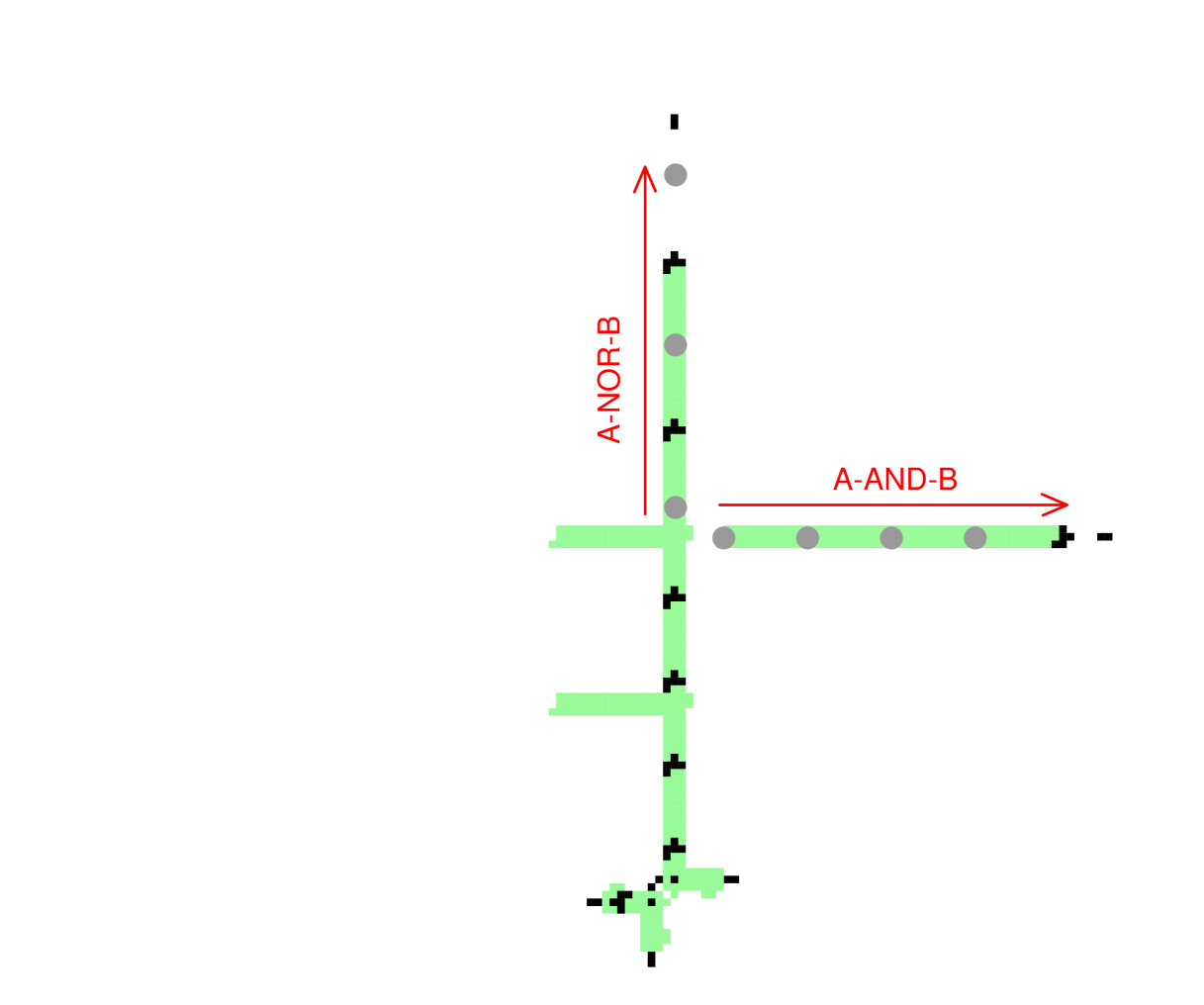
xxx The dynamics making this AND gate first makes an intermediate NOT-A (North 01110 – figure 7) which interacts with input B to simultaneously produce both A-AND-B (East 10000), and the A-NOR-B (North 01010) which will be required to make the OR gate in figure 9.
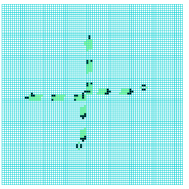
4.3 OR gate
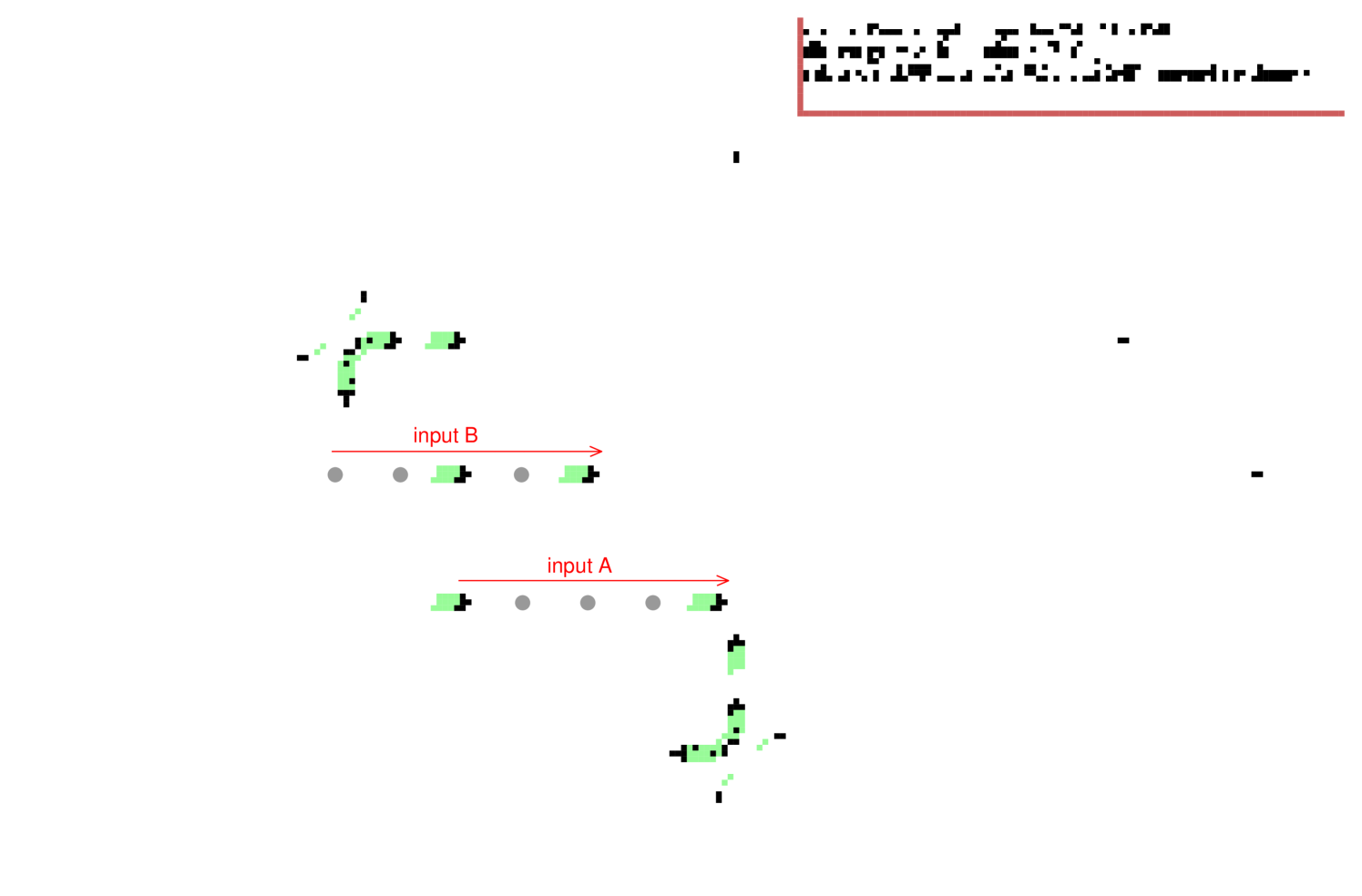
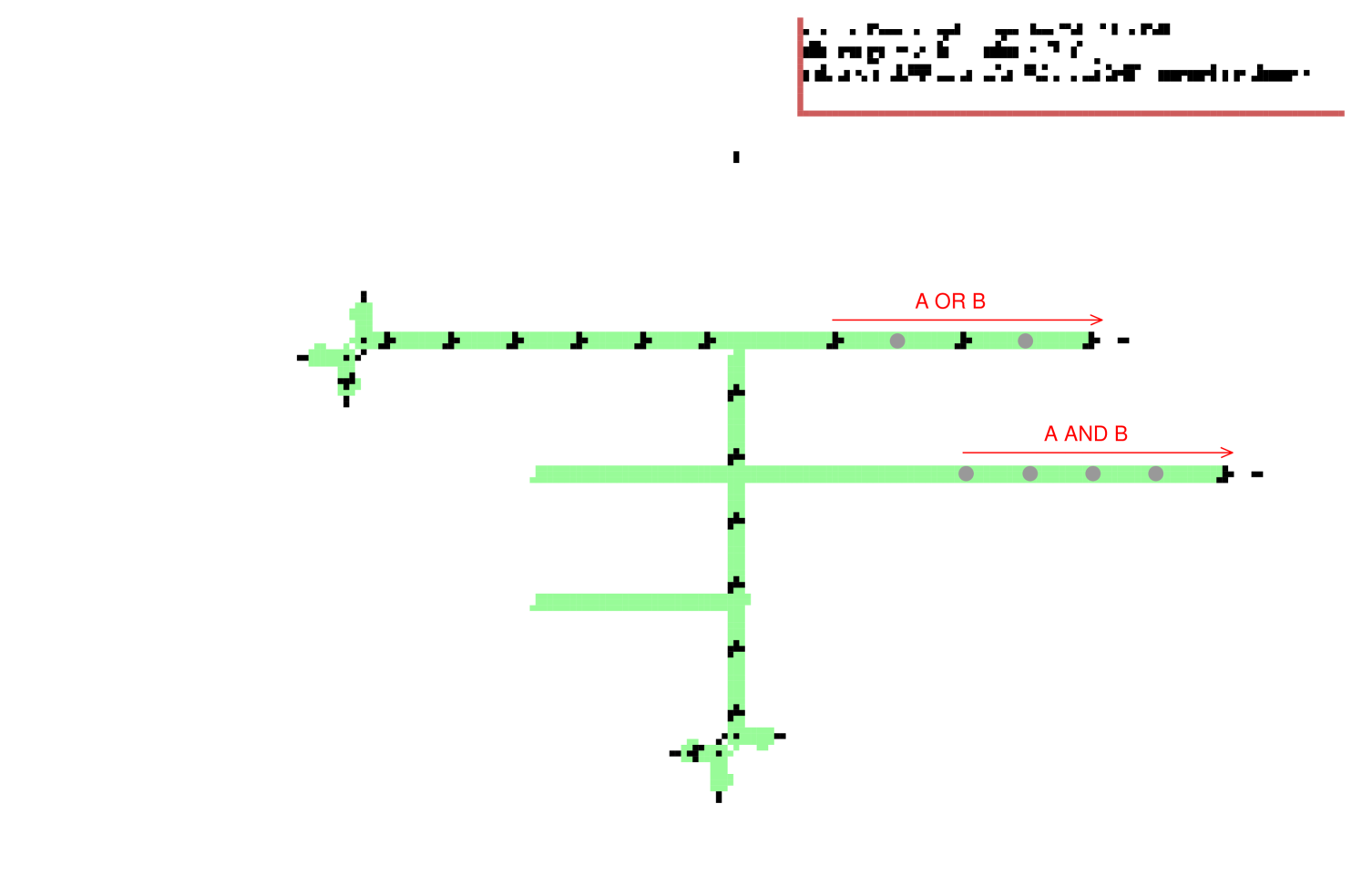
xxx The dynamics making this OR gate first makes an intermediate NOT-A (North 01110 – figure 7) which interacts with input B to make A-NOR-B (North 01010 – figure 8) which interacts with the upper glider-stream shooting East to make A-OR-B (East 10101). A residual bi-product is A-AND-B (East 10000 – figure 8).
5 The Ameyalli-Rule definition
An isotropic CA rule based on a 2d binary 33 Moore neighborhood —
![]() — can be defined by a series of methods that become ever simpler, clearer, and more concise,
illustrated in figures 10, 11, and 12.
In all these methods, a descending order (from left to right) of the neighborhood’s
decimal equivalent is employed, in line with Wolfram’s classic
convention[14, 15] — rule-tables can then be expressed in decimal
or hexadecimal[18].
— can be defined by a series of methods that become ever simpler, clearer, and more concise,
illustrated in figures 10, 11, and 12.
In all these methods, a descending order (from left to right) of the neighborhood’s
decimal equivalent is employed, in line with Wolfram’s classic
convention[14, 15] — rule-tables can then be expressed in decimal
or hexadecimal[18].
The decimal equivalent of a 3
pattern is taken as a string in the order
876
543
210
— for example,
the pattern
![]() is the binary string 001110111 (119 in decimal),
representing the full rule-table index 119 (figure 10),
the symmetry class 119 (figure 11),
and iso-rule index 66 (figure 12).
is the binary string 001110111 (119 in decimal),
representing the full rule-table index 119 (figure 10),
the symmetry class 119 (figure 11),
and iso-rule index 66 (figure 12).
5.1 full lookup-table

(a) Neighborhood patterns in descending decimal equivalent order from
 -
to
-
to
 .
(511 to 0) if each row from the upper matrix is continued in the lower matrix.
Ameyalli-rule neighborhoods that input 1 are colored red.
.
(511 to 0) if each row from the upper matrix is continued in the lower matrix.
Ameyalli-rule neighborhoods that input 1 are colored red.

(b) The Ameyalli-rule showing just inputs follows the upper and lower matrices above, set alongside each other giving a continuous descending decimal equivalent order 511 to 0. This is the full rule-table (rcode). 154 inputs=1 are colored black. =154/512=0.3.
5.2 symmetry class table — iso-groups

101-68 67-34 33-0
5.3 iso-rule
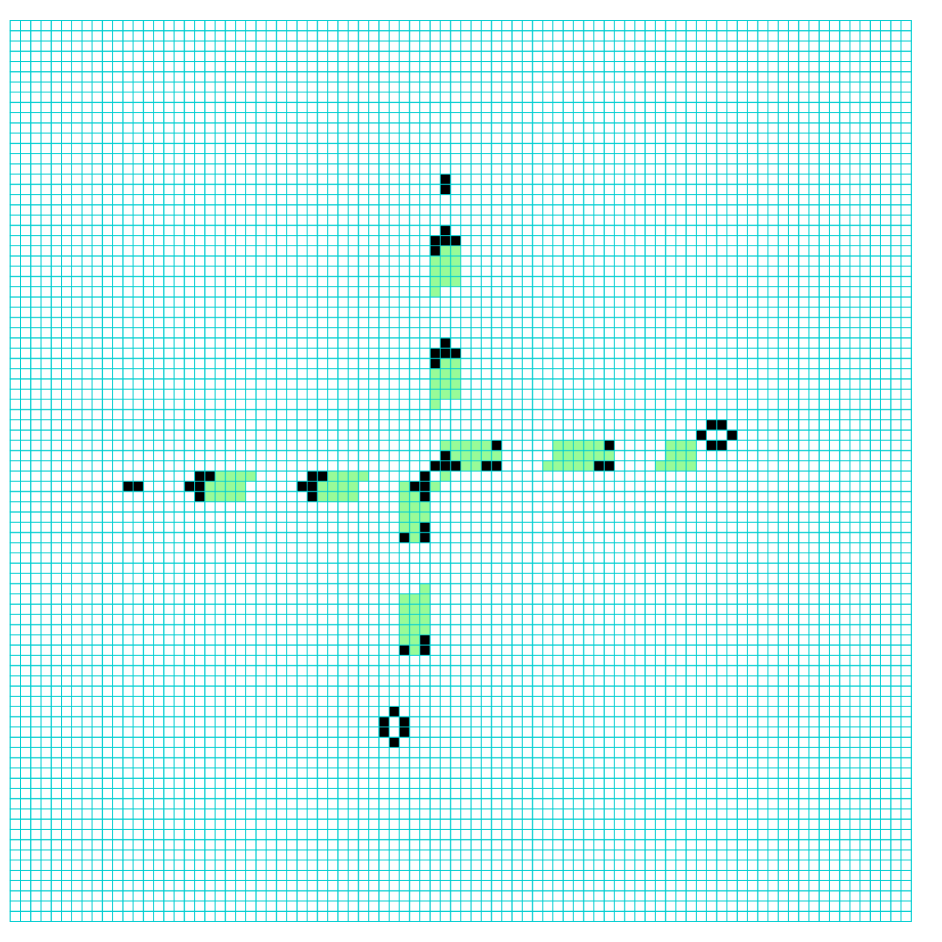
The iso-rule[19, 18] depends on just the 102 prototype neighborhoods in figure 12(a) with a rule-table index 101-0, following the symmetry class table in figure 11 but with the rest of the group taken as read and omitted. The iso-rule shown in figure 12(b) is then just a 102 length bit-string (indexed 101-0) listing prototype inputs, 1 or 0.
Besides simplicity and brevity, an advantage of the iso-rule is that any mutation conserves isotropy. The iso-rule has many other advantages222The iso-rule method applies in general to a variety of CA neighborhood templates, in 1d, hex/square-2d, and 3d, including multi-value as well as binary[19, 18].[19, 18] when studying isotropic CA as compared to a full or symmetry class rule-table. The iso-rule provides a more direct entropy scatter plot for automatically classifying isotropic rule-space, and as shown in section 6, it provides a concise input-frequency histogram (IFH) with its functions of mutation and filtering.

(a) 102 iso-group prototypes

(b) the iso-rule indexed 101-0, left to right.
(b) The Ameyalli iso-rule compacts the information in (b) into a simple bit-string, here shown as a DDLab graphic with 1/0 inputs shown as black/green.
The iso-rule is expressed in hexadecimal (iso-hex)=2642a3a9088a4490000b545090 by breaking the bit-string into 4-bit segments (with a complete segment on the right). For example, the hexadecimals of the 7 segments on the right b545090 are given by 1011=b, 0101=5, 0100=4, 0101=5 ,0000=0, 1001=9, 0000=0.
The Hensel string translated for Golly[6], generated automatically in DDLab[20, 18] is B2ci3ar4krtz5cq6c7ce/S01e2ek3qj4kt5ceayq6cki7c8.
6 iso-rule input-frequency-histogram (IFH)
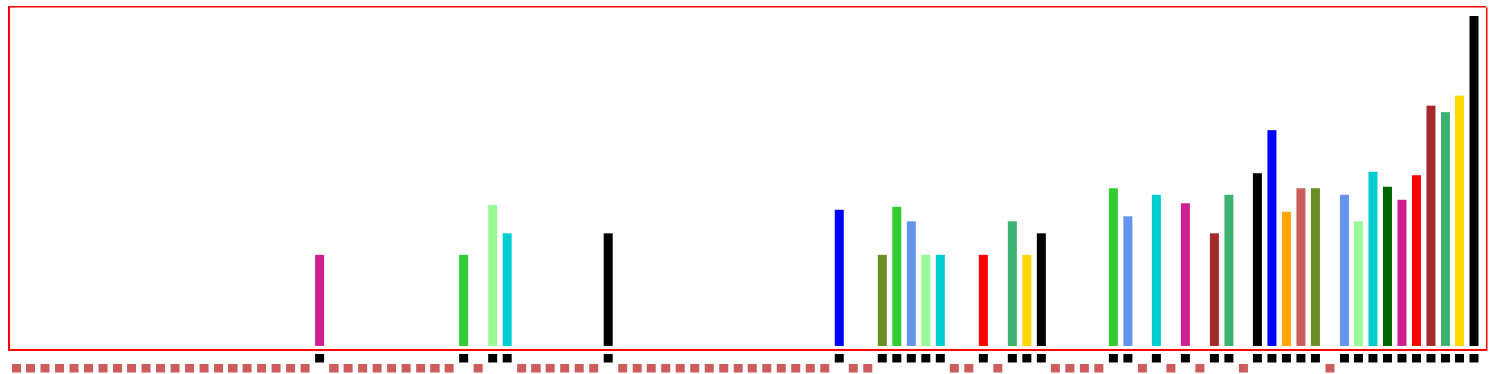
The input frequency histogram (IFH)[17, 19], a method in DDLab[20, 18], allows a dynamic view of the activity of a rule-table in relation to the current iterating space-time pattern, with options to interactively filter and mutate the current rule. Any isolated periodic pattern can be investigated to ascertain which rule-table inputs333The IFH applies to any type of rule-table, full and totalistic as well as iso-rules. are responsible for maintaining the pattern and to what extent.


Four Ameyalli gliders moving East.
far left: colors by value with green dynamic trails.
near left: colors corresponding to IFH colors.

For example, in figure 13 the space-time pattern consists of four non-stop Ameyalli gliders on a lattice with periodic boundaries. The IFH accommodates 102 columns to indicate the level of activity444In figures 13,14,15, the measures are averaged over a moving window of 100 time-steps to stabilise the IFH. The number of trailing hits (lookups at index of the iso-rule-table) at each time-step is recorded, and converted to , the fraction (0 to 1) of all possible hits , where is lattice size, (100) is the size of the moving window of time-steps, and (102) is the iso-rule size. is converted to log2 to amplify infrequent hits, which sets the column height. of each iso-group — the frequency of iso-rule inputs, indexed from 101 to 0 (left to right) as in figure 12. Only 15 bars appear showing which inputs are active and to what extent, noting that the bar height is log2 of the actual frequency to amplify infrequent hits. Mutating the iso-rule at any of these bar indices disrupts the gliders, but mutating at any other index makes no difference to the gliders themselves, but would very probably disrupt any other Ameyalli pattern. We call such inactive inputs “neutral” relative to the particular space-time pattern.
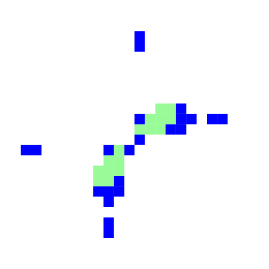
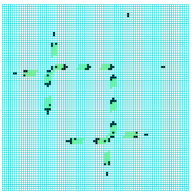
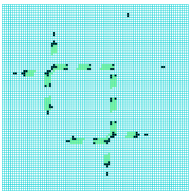
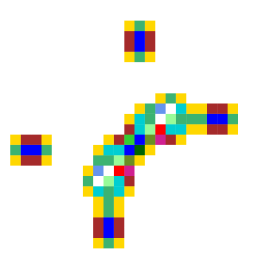 The Ameyalli-rule glider-gun contained by type-B eaters as in figure 3.
The Ameyalli-rule glider-gun contained by type-B eaters as in figure 3.
far left: colors by value with green dynamic trails.
near left: colors corresponding to IFH colors.


 eater-Beater-A
eater-Beater-A
The iso-rules in hexadecimal hex are compared below:
26 42 a3 a9 08 8a 44 90 00 0b 54 50 90 —Ameyalli-rule
19 bd 5d 56 af 65 bb 7c 1a 37 fd 54 90 —after all 70 inactive mutations
In figure 14 the (periodic) space-time pattern is the Ameyalli glider-gun system contained by eaters-B, similar to figure 3, In this case 32 iso-groups are active, the rest are neutral indicated by missing columns. In DDLab, on-the-fly key-hits will progressively filter active columns from high to low, marked by black blocks. Filtering excludes drawing these cells in the space-time pattern, or alternatively just marks the neutral bars. Other key-hits progressively mutate the iso-rule at column positions from low to high, marked by black blocks, so neutral inputs are preferentially mutated, either by flipping the input, or setting zero. In this way its possible to mutate any or all neutral inputs, and as expected, experiment confirms there is no effect on the given glider-gun system.
6.1 The idealized iso-rule
Here we construct the IFH compatible with the logical gates in section 4 in order to derive a stripped down “idealized” form of the logically universal Ameyalli iso-rule. Employing the logical gates themselves is impractical because their dynamics is non-periodic. Instead, in figure 15 we construct an “intensive” periodic space-time pattern that includes all the dynamical structures that make the logical gates, with two interacting glider-guns to make mutually destructive 900 glider collisions, as well as gliders destroyed by collisions with both eaters A and B. This results in 47 active bars, but the majority are absent representing neutral inputs. Any or all mutations to these neutral inputs has no affect on the “intensive” space-time pattern, and when tested, the logical gates in section 4 are preserved. We suggest that if all these neutral inputs are set to zero, the resulting idealized iso-rule will form an appropriate starting point for further Ameyalli studies.

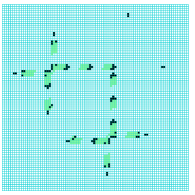
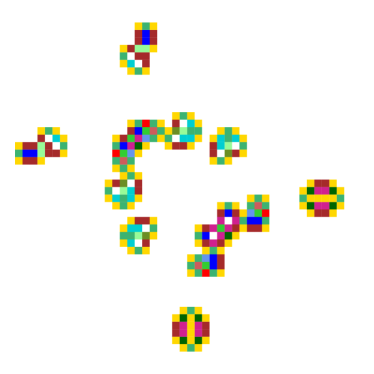 An intensive Ameyalli periodic space-time pattern
An intensive Ameyalli periodic space-time pattern
far left: colors by value with green dynamic trails.
near left: colors corresponding to IFH colors.
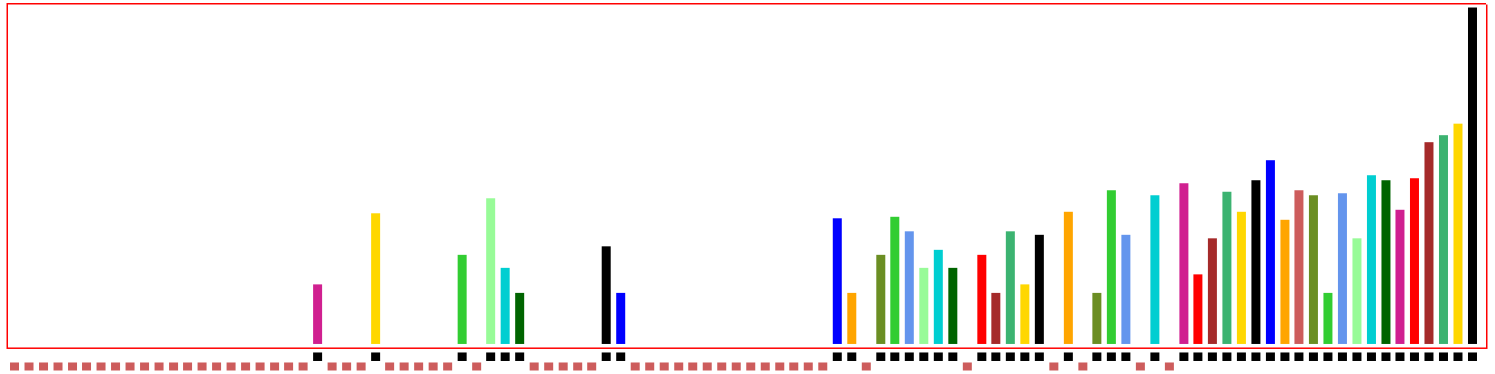


The iso-rules in hexadecimal hex are compared below:
26 42 a3 a9 08 8a 44 90 00 0b 54 50 90 —Ameyalli iso-rule
00 00 01 00 08 00 00 10 00 03 54 50 90 —idealized Ameyalli iso-rule
The idealized Hensel string translated for Golly[6] is B2ci3ar5q/S01e2ek3qj4t5y
7 Summary and Discussion
The Ameyalli iso-rule is another example of the search for glider-guns, then building logical gates. Its spontaneously emergent glider-gun was found from the input-entropy scatter-plot samples that favoured both order and emergent gliders. Minor mutations created two types of eater to stop the glider stream. With these ingredients, and by adjusting collision dynamics according to precise timing and points of impact, we were able to build the logical gates NOT, AND and OR required for logical universality.
Further mutations would possibly uncover other artefacts of interest, but for a better appreciation of the causal links between these significant dynamical patterns and the responsible iso-groups inputs, we applied the input-frequency histogram (IFH) method, which also revealed neutral inputs where mutations have no effect. As we have shown for the Ameyalli, setting neutral inputs to zero relative to an intensive glider-gun/eater system will reduce logically universal iso-rules to their stripped down or “idealized” form where gliders, eaters, glider-guns, and logical gates continue to be supported. The essential identity of Ameyalli, and other logically universal CA, are these dynamical objects together with the significant part of the iso-rule table that drives them. However, the possibility is there to configure neutral inputs to create other unpredicted but relevant structures.
An idealized logically universal iso-rule is the primitive of its huge family of mutants that perform the same basic functions. The dynamics of idealized versions of all the logically universal iso-rules mentioned in this paper, including the game-of-Life, are worth investigating in further work.
8 Acknowledgements
The experiments were realised using DDLab, Mathematica and Golly. Figures were made with DDLab. This collaborative work began in 2017 at a workshop in Ariege, France, and also at the Autonomous University of Zacatecas, Mexico and in London, UK. J. M. Gómez Soto acknowledges his residency at the DDLab Complex Systems Institute and financial support from the Research Council of México (CONACyT).
References
- [1] Adamatzky,A., and A.Wuensche, “Computing in Spiral Rule Reaction-Diffusion Hexagonal Cellular Automaton”, Complex Systems, Vol 16, 277-297, 2006. preprint pdf
- [2] Berlekamp E,R., J.H.Conway, R.K.Guy, “Winning Ways for Your Mathematical Plays”, Vol 2. Chapt 25 “What is Life?”, 817-850, Academic Press, New York, 1982.
- [3] Eppstein,D. “Growth and Decay in Life-Like Cellular Automata”, in “Game of Life Cellular Automata”, edited by Andrew Adamatzky, Springer Verlag, 2010.
- [4] Francis Jeffry Pelletier and Norman M. Martin, “Post’s Functional Completeness Theorem”, Notre Dame Journal of Formal Logic , Vol.31, No.2, 1990.
- [5] Gardner,M., “Mathematical Games – The fantastic combinations of John Conway’s new solitaire game ’life’ ”. Scientific American 223. pp. 120–123, 1970.
- [6] Golly Game of Life Home Page. http://golly.sourceforge.net
- [7] Gómez Soto,J.M., and A.Wuensche, “The X-rule: universal computation in a non-isotropic Life-like Cellular Automaton”, JCA, Vol 10, No.3-4, 261-294, 2015. preprint: http://arxiv.org/abs/1504.01434/
- [8] Gómez Soto, J.M., and A.Wuensche, “X-Rule’s Precursor is also Logically Universal”, Journal of Cellular Automata, Vol.12. No.6, 445-473, 2017. preprint: http://arxiv.org/abs/1504.01434/
- [9] Gómez Soto, J.M., and A.Wuensche, “Logically Universaly from a Minimal 2D Glider-Gun”, Complex Systems), vol 27, Issue 1, 2017.
- [10] Gómez Soto, J.M., and A.Wuensche, “Another Logically Universal Rule: The Variant-Rule”, Journal of Cellular Automata, Vol.15. No.3, 147-173, 2020. preprint: https://arxiv.org/abs/1909.08224/
- [11] Minondo,I, and C.A.Reiter, “Is Life Alone in the Universe of Symmetric Cellular Automata?” Journal of Cellular Automata, Vol.15. No.5-6, 359-357, 2021.
- [12] Randall,P, “Turing Universality of the Game of Life”, Collision-Based Computing, Andrew Adamatzky Ed. Springer Verlag, 2002.
- [13] Sapin,E, O. Bailleux, J.J. Chabrier, and P. Collet. “A new universel automata discovered by evolutionary algorithms”, Gecco2004, Lecture Notes in Computer Science, 3102:175187, 2004.
- [14] Wolfram,S., “Statistical Mechanics of Cellular Automata”, Reviews of Modern Phisics, vol 55, 601-644, 1983.
- [15] Wolfram,S., “A New Kind of Science”, Wolfram Media, Champaign, IL., 2002.
- [16] Wuensche,A., and M.Lesser, “The global Dynamics of Cellular Automata”, Santa Fe Institute Studies in the Sciences of Complexity, Addison-Wesley, Reading, MA, 1992. link
- [17] Wuensche,A., “Classifying Cellular Automata Automatically; Finding gliders, filtering, and relating space-time patterns, attractor basins, and the Z parameter”, COMPLEXITY, Vol.4/no.3, 47-66, 1999. link
- [18] Wuensche,A.,“Exploring Discrete Dynamics – Second Edition, Luniver Press, 2016. http://www.ddlab.org/download/dd_manual_2018
- [19] Wuensche,A, and J.M.Gómez Soto, “Isotropic Cellular Automata: the DDLab iso-rule Paradigm”, Journal of Cellular Automata, Vol.15. No.5-6, 439-470, 2021. preprint: https://arxiv.org/abs/2008.11279
-
[20]
Wuensche,A., Discrete Dynamics Lab (DDLab), 1993-2021.
http://www.ddlab.org - [21]