This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

The average distance problem with an Euler elastica penalization111This paper will appear in Interfaces and Free Boundaries.

Qiang Du Department of Applied Physics and Applied Mathematics and Data Science Institute, Columbia University, New York, NY, 10027, USA. Email: qd2125@columbia.edu. Supported in part by NSF DMS-2012562 and DMS-1937254.    Xinyang Lu Corresponding author. Department of Mathematical Sciences, Lakehead University, Thunder Bay, Ontario, P7B 5E1, Canada AND Department of Mathematics and Statistics, McGill University, 805 Sherbrooke St. W., Montreal, QC H3A 0B9, Canada. Email: xlu8@lakeheadu.ca. Supported in part by NSERC Discovery Grant and internal Lakehead University grants.    Chong Wang Department of Mathematics, Washington and Lee University, Lexington, VA, 24450, USA. Email: cwang@wlu.edu.
Abstract

We consider the minimization of an average distance functional defined on a two-dimensional domain Ω\Omega with an Euler elastica penalization associated with ∂Ω\partial\Omega, the boundary of Ω\Omega. The average distance is given by

∫Ωdistp⁡(x,∂Ω)​d⁡x\int_{\Omega}\operatorname{dist}^{p}(x,\partial\Omega)\,{\operatorname{d}}x

where p≥1p\geq 1 is a given parameter, and dist⁡(x,∂Ω)\operatorname{dist}(x,\partial\Omega) is the Hausdorff distance between {x}\{x\} and ∂Ω\partial\Omega. The penalty term is a multiple of the Euler elastica (i.e., the Helfrich bending energy or the Willmore energy) of the boundary curve ∂Ω{\partial\Omega}, which is proportional to the integrated squared curvature defined on ∂Ω\partial\Omega, as given by

λ​∫∂Ωκ∂Ω2​d⁡ℋ⌞​∂Ω1,\lambda\int_{\partial\Omega}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}_{\llcorner\partial\Omega}^{1},

where κ∂Ω\kappa_{\partial\Omega} denotes the (signed) curvature of ∂Ω\partial\Omega and λ>0\lambda>0 denotes a penalty constant. The domain Ω\Omega is allowed to vary among compact, convex sets of ℝ2\mathbb{R}^{2} with Hausdorff dimension equal to 22. Under no a priori assumptions on the regularity of the boundary ∂Ω\partial\Omega, we prove the existence of minimizers of Ep,λE_{p,\lambda}. Moreover, we establish the C1,1C^{1,1}-regularity of its minimizers. An original construction of a suitable family of competitors plays a decisive role in proving the regularity.

Keywords. average-distance problem, regularity, Euler elastica, Willmore energy

Classification. 49Q20, 49K10, 49Q10

1 Introduction

The curvature of boundaries plays an important role in many physical and biological models. For instance, the elasticity of cell membranes is strongly correlated to its bending, and thus to its curvature. One way to quantify the bending energy per unit area of closed lipid bilayers was proposed by Helfrich in [18], and is now commonly referred to as “Helfrich bending energy”. A related notion, from differential geometry, is the “Willmore energy”, which measures how much a surface differs from the sphere [13]. In 2D, the Willmore energy simplifies to be a multiple of the integrated squared curvature, which is also commonly referred as the Euler elastica.

Easy access to the boundary is also relevant in nature: many processes such as heat dissipation, waste disposal and nutrient absorption, are more efficient when the whole body has “easy access” to its boundary. One way to quantify the “average accessibility” for points of a set Ω⊂ℝ2\Omega\subset\mathbb{R}^{2} to the boundary ∂Ω\partial\Omega is an energy functional of the form

Ω⟼∫Ωdistp⁡(x,∂Ω)​d⁡x,\Omega\longmapsto\int_{\Omega}\operatorname{dist}^{p}(x,\partial\Omega)\,{\operatorname{d}}x{\color[rgb]{0,0,1},} (1.1)

for a given parameter p≥1p\geq 1.

There are other energy functionals sharing similar geometric features with (1.1). For example, (1.1) is formally similar to the average-distance functional associated with a given domain Ω⊂ℝ2\Omega\subset\mathbb{R}^{2},

Σ⟼∫Ωdistp⁡(x,Σ)​d⁡x,\Sigma\longmapsto\int_{\Omega}\operatorname{dist}^{p}(x,\Sigma)\,{\operatorname{d}}x, (1.2)

where the unknown Σ\Sigma varies among compact subsets of Ω¯\bar{\Omega}. In many existing studies, Σ\Sigma is assumed to be a connected set with its Hausdorff dimension equal to 11 and its one dimensional Hausdorff measure is to be bounded from above by a specified constant. Problems of this type are used in many modeling applications, such as urban planning and optimal pricing. For a (non-exhaustive) list of references on the average-distance problem we refer to the works by Buttazzo et al. [2, 3, 8, 9] and [4, Chapter 3.3]. Also related are the papers by Paolini and Stepanov [22], Santambrogio and Tilli [24], Tilli [27], Lemenant and Mainini [20], Slepčev [25], and the review paper by Lemenant [19]. Meanwhile, if Σ\Sigma is assumed to vary among sets Ω\Omega consisting of discrete points with a fixed cardinality, say kk, then the minimization of the functional in (1.2), often named the quantization error in this case, is related to the centroidal Voronoi tessellations [11] and kk-means, which are widely studied in subjects such as vector quantization, signal compression, sensor and resource placement, geometric meshing, and so on [12]. Similar variational problems entailing a competition between classical perimeter and nonlocal repulsive interaction were studied by Muratov and Knüpfer [21], Goldman, Novaga and Ruffini [17], and Goldman, Novaga and Röger [16]. Figalli, Fusco, Maggi, Millot, and Morrini studied a competition between a nonlocal ss-perimeter and a nonlocal repulsive interaction term [14].

In this work, we consider the average distance energy functional as a functional of the domain Ω\Omega with Σ=∂Ω\Sigma=\partial\Omega and penalized by the Euler elastica of ∂Ω\partial\Omega, as given by

Ep,λ​(Ω)=∫Ω distp​(x,∂Ω)​𝑑x+λ​∫∂Ωκ∂Ω2​𝑑ℋ⌞​∂Ω1,\displaystyle E_{p,\lambda}(\Omega)=\int_{\Omega}\text{ dist}^{p}(x,\partial\Omega)\ dx+\lambda\int_{\partial\Omega}\kappa_{\partial\Omega}^{2}d{\cal{H}}_{\llcorner\partial\Omega}^{1},

where p≥1,λ>0p\geq 1,\lambda>0 are given parameters, with λ\lambda proportional to a bending constant, and ℋ⌞​∂Ω1\mathcal{H}_{\llcorner\partial\Omega}^{1} denotes the Hausdorff measure restricted on ∂Ω\partial\Omega. For further properties of the Hausdorff measure, we refer to [1]. We consider a free boundary problem associated with the minimization of Ep,λE_{p,\lambda} among domains Ω\Omega in the following admissible set

𝒜:={Ω:Ω⊂ℝ2​ is compact, convex and Hausdorff two-dimensional}.\displaystyle{\cal{A}}:=\{\Omega:\Omega\subset\mathbb{R}^{2}\text{ is compact, convex and Hausdorff two-dimensional}\}.

For any Ω1,Ω2∈𝒜\Omega_{1},\Omega_{2}\in{\cal{A}}, define the metric in 𝒜\cal{A} as

d​(Ω1,Ω2):=ℋ2​(Ω1​△​Ω2),\displaystyle d(\Omega_{1},\Omega_{2}):={\cal{H}}^{2}(\Omega_{1}\triangle\Omega_{2}), (1.3)

where △\triangle denotes the symmetric difference of the two sets and ℋ2{\cal{H}}^{2} denotes the two-dimensional Hausdorff measure.

The term

∫∂Ωκ∂Ω2​d⁡ℋ⌞​∂Ω1\int_{\partial\Omega}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}_{\llcorner\partial\Omega}^{1}

is the integrated squared curvature [10]. Since we do not make any a priori assumptions on the regularity of the boundary ∂Ω\partial\Omega, we need to make sense of the integrand κ∂Ω\kappa_{\partial\Omega}. For future reference we will define it as follows: let γ\gamma be an arc-length parameterization of ∂Ω\partial\Omega, and define

∫∂Ωκ∂Ω2​d⁡ℋ⌞​∂Ω1:={∫0ℋ1​(∂Ω)|γ′′|2​d⁡sif ​γ∈H2​((0,ℋ1​(∂Ω));ℝ2),+∞otherwise.\int_{\partial\Omega}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}_{\llcorner\partial\Omega}^{1}:=\left\{\begin{array}[]{cl}{\displaystyle{\int_{0}^{\mathcal{H}^{1}(\partial\Omega)}|\gamma^{\prime\prime}|^{2}\,{\operatorname{d}}s}}&\text{if }\gamma\in H^{2}((0,\mathcal{H}^{1}(\partial\Omega));\mathbb{R}^{2}),\\ &\\ +\infty&\text{otherwise}.\end{array}\right. (1.4)

Here, ℋ1​(∂Ω)\mathcal{H}^{1}(\partial\Omega) denotes the total length of ∂Ω\partial\Omega. That is, we are reducing our minimization problem to quite regular sets, i.e. domains Ω\Omega whose boundaries admit an H2H^{2} regular arc-length parameterization. Therefore, we are considering the minimization problem

inf{\displaystyle\inf\bigg{\{} ∫Ω distp​(x,∂Ω)​d⁡x+λ​∫0ℋ1​(∂Ω)|γ′′|2​d⁡s:ℋ1​(∂Ω)>0,\displaystyle\int_{\Omega}\text{ dist}^{p}(x,\partial\Omega)\,{\operatorname{d}}x+\lambda\int_{0}^{\mathcal{H}^{1}(\partial\Omega)}|\gamma^{\prime\prime}|^{2}\,{\operatorname{d}}s:\mathcal{H}^{1}(\partial\Omega)>0,
|γ′|=1,γ([0,ℋ1(∂Ω)]) is the boundary of a compact convex set}.\displaystyle|\gamma^{\prime}|=1,\ \gamma([0,\mathcal{H}^{1}(\partial\Omega)])\text{ is the boundary of a compact convex set}\bigg{\}}.

We note first a simple rescaling analysis where the domain Ω\Omega is stretched by a factor ϵ>0\epsilon>0. Given the two-dimensional nature, if ϵ>1\epsilon>1, then the average distance functional is scaled by no more than ϵ2+p\epsilon^{2+p} but no less than ϵ2\epsilon^{2}. Meanwhile, the Euler elastica gets scaled by 1/ϵ1/\epsilon. This shows that the optimal Ω\Omega, if exists, must have a suitable and finite size for any prescribed λ>0\lambda>0. Indeed, the energy considered might be viewed as a competition between access to the boundary and the elastic stiffness of the boundary.

The main result of this paper is:

Theorem 1.1.

Given p≥1,λ>0p\geq 1,\lambda>0, any minimizer Ω\Omega of Ep,λE_{p,\lambda} is C1,1C^{1,1}-regular with a Lipschitz constant at most

C=C​(p,λ):=λ−1​p​(C1+1)p−1​π​C12+2​C2,\displaystyle C=C(p,\lambda):=\sqrt{\lambda^{-1}p(C_{1}+1)^{p-1}\pi C_{1}^{2}+2C_{2}},

where

C1=C1​(p,λ):=(p+1)​(p+2)​(24λ)p+1​(2​(1+π​λ))p+2,\displaystyle C_{1}=C_{1}(p,\lambda):=(p+1)(p+2)\left(\frac{24}{\lambda}\right)^{p+1}(2(1+\pi\lambda))^{p+2}, (1.5)
C2=C2​(p,λ):=32​(λ−1+π)2+32​2​C1​π​(λ−1+π)5/2,\displaystyle C_{2}=C_{2}(p,\lambda):=32(\lambda^{-1}+\pi)^{2}+32\sqrt{2C_{1}\pi}(\lambda^{-1}+\pi)^{5/2}, (1.6)

are constants independent of Ω\Omega. That is, the boundary ∂Ω\partial\Omega admits a C1,1C^{1,1}-regular, arc-length parameterization γ:[0,ℋ1​(∂Ω)]⟶ℝ2\gamma:[0,\mathcal{H}^{1}(\partial\Omega)]\longrightarrow\mathbb{R}^{2} such that

|γ′​(t1)−γ′​(t2)|≤C​|t1−t2||\gamma^{\prime}(t_{1})-\gamma^{\prime}(t_{2})|\leq C|t_{1}-t_{2}|

for any t1,t2t_{1},t_{2}.

The rest of the paper is organized as follows: Section 2 is dedicated to proving some auxiliary estimates on elements of minimizing sequences. Existence of minimizers is shown in Section 3, while C1,1C^{1,1}-regularity is established in Section 4. Finally, in Section 5, we explore several future directions to further our understanding of the penalized average distance problem. Technical results concerning properties of convex sets used in this paper will be presented in the Appendix.

2 Estimates

This section is dedicated to establishing quantitative bounds on the diameter and the area of any domain associated with the minimizing sequences of Ep,λE_{p,\lambda}. In particular, the main result is Lemma 2.3, which provides a uniform upper bound on the diameter, crucial to the proof of the existence of minimizers.

Remark: It is worth noting that, due to (1.4), any set Ω\Omega whose boundary is not C1C^{1}-regular will have infinite energy, since a corner on ∂Ω\partial\Omega with a discontinuous tangent corresponds to the Dirac measure in the curvature measure κ∂Ω\kappa_{\partial\Omega}. Thus we can restrict ourselves to C1C^{1}-regular sets.

Lemma 2.1.

Given p≥1p\geq 1, λ>0\lambda>0, for any Ω∈𝒜\Omega\in\cal A, it holds that

diam⁡(Ω)≥4​π​λEp,λ​(Ω).\operatorname{{\operatorname{diam}}}(\Omega)\geq\frac{4\pi\lambda}{E_{p,\lambda}(\Omega)}. (2.7)

Then, for any minimizing sequence Ωn⊆𝒜\Omega_{n}\subseteq\cal A (that is, Ep,λ​(Ωn)→inf𝒜Ep,λE_{p,\lambda}(\Omega_{n})\to\inf_{\cal A}E_{p,\lambda}), it holds that

diam⁡(Ωn)≥2​π​λ1+π​λ\operatorname{{\operatorname{diam}}}(\Omega_{n})\geq\frac{2\pi\lambda}{1+\pi\lambda} (2.8)

for all sufficiently large nn.

Proof.

Consider an arbitrary Ω∈𝒜\Omega\in\cal{A}. Choose x,y∈∂Ωx,y\in\partial\Omega such that |x−y|=diam⁡(Ω)|x-y|=\operatorname{{\operatorname{diam}}}(\Omega). Note that Ω⊆B​(x,diam⁡(Ω))\Omega\subseteq B(x,\operatorname{{\operatorname{diam}}}(\Omega)), hence due to the convexity of Ω\Omega (see Lemma A.1), it follows that

ℋ1​(∂Ω)≤π​diam⁡(Ω).\mathcal{H}^{1}(\partial\Omega)\leq\pi\operatorname{{\operatorname{diam}}}(\Omega).

As ∂Ω\partial\Omega is a closed convex curve with winding number equal to 11, and our restriction on the curvature term ensures that the boundary is H2H^{2} regular, it follows that

∫∂Ω|κ∂Ω|​d⁡ℋ⌞​∂Ω1=2​π,\int_{\partial\Omega}|\kappa_{\partial\Omega}|\,{\operatorname{d}}\mathcal{H}_{\llcorner\partial\Omega}^{1}=2\pi,

and by Hölder’s inequality it holds that

Ep,λ​(Ω)≥λ​∫∂Ωκ∂Ω2​d⁡ℋ⌞​∂Ω1≥4​π2​λℋ1​(∂Ω)≥4​π​λdiam⁡(Ω),E_{p,\lambda}(\Omega)\geq\lambda\int_{\partial\Omega}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}_{\llcorner\partial\Omega}^{1}\geq\frac{4\pi^{2}\lambda}{\mathcal{H}^{1}(\partial\Omega)}\geq\frac{4\pi\lambda}{\operatorname{{\operatorname{diam}}}(\Omega)},

hence (2.7).

To prove (2.8), we show first that inf𝒜Ep,λ<+∞\inf_{\cal A}E_{p,\lambda}<+\infty. Consider the unit ball B:=B​((0,0),1)B:=B\big{(}(0,0),1\big{)}, and note that

inf𝒜Ep,λ\displaystyle\inf_{\cal A}E_{p,\lambda} ≤Ep,λ​(B)=∫Bdistp⁡(x,∂B)​d⁡x+λ​∫∂Bκ∂B2​d⁡ℋ⌞​∂B1≤π3+2​π​λ.\displaystyle\leq E_{p,\lambda}(B)=\int_{B}\operatorname{dist}^{p}(x,\partial B)\,{\operatorname{d}}x+\lambda\int_{\partial B}\kappa_{\partial B}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial B}\leq\frac{\pi}{3}+2\pi\lambda. (2.9)

Let Ωn⊆𝒜\Omega_{n}\subseteq\cal A be an arbitrary minimizing sequence. Clearly, since Ep,λ​(Ωn)→inf𝒜Ep,λE_{p,\lambda}(\Omega_{n})\to\inf_{\cal A}E_{p,\lambda}, for all sufficiently large nn, it holds that

Ep,λ​(Ωn)≤inf𝒜¯Ep,λ+2−π3​≤(​2.9​)​2+2​π​λ,\displaystyle E_{p,\lambda}(\Omega_{n})\leq\inf_{\bar{\cal A}}E_{p,\lambda}+2-\frac{\pi}{3}\overset{\eqref{inf E}}{\leq}2+2\pi\lambda, (2.10)

and (2.7) gives diam⁡(Ωn)≥2​π​λ1+π​λ\operatorname{{\operatorname{diam}}}(\Omega_{n})\geq\dfrac{2\pi\lambda}{1+\pi\lambda}, hence (2.8).

∎

In the following, we will use the definition of the total variation of a function uu, which is defined as follows. Let Ω⊂ℝn\Omega\subset\mathbb{R}^{n} be an open set and let u∈L1​(Ω)u\in L^{1}(\Omega), then

‖u‖T​V=sup{∫Ωu​div​ϕ​𝑑x:ϕ∈Cc1​(Ω;ℝn),‖ϕ‖L∞​(Ω)≤1},\displaystyle||u||_{TV}=\sup\left\{\int_{\Omega}u\;\text{div}\phi\;dx:\phi\in C_{c}^{1}(\Omega;\mathbb{R}^{n}),||\phi||_{L^{\infty}(\Omega)}\leq 1\right\},

and

‖u‖B​V=‖u‖L1+‖u‖T​V.\displaystyle||u||_{BV}=||u||_{L^{1}}+||u||_{TV}.
Lemma 2.2.

Given p≥1p\geq 1, λ>0\lambda>0, and Ω∈𝒜\Omega\in{\cal A}, it holds that

ℋ2​(Ω)≥π​λ22​Ep,λ​(Ω)2.\mathcal{H}^{2}(\Omega)\geq\frac{\pi\lambda^{2}}{2E_{p,\lambda}(\Omega)^{2}}. (2.11)

Moreover, given a minimizing sequence Ωn⊆𝒜\Omega_{n}\subseteq{\cal A} (that is, Ep,λ​(Ωn)→inf𝒜Ep,λE_{p,\lambda}(\Omega_{n})\to\inf_{\cal A}E_{p,\lambda}), we have

ℋ2​(Ωn)≥π​λ28​(1+π​λ)2\mathcal{H}^{2}(\Omega_{n})\geq\frac{\pi\lambda^{2}}{8(1+\pi\lambda)^{2}} (2.12)

for all sufficiently large nn.

To simplify notations, for future reference, given a point z∈ℝ2z\in\mathbb{R}^{2}, we let zxz_{x} (resp. zyz_{y}) denote the xx (resp. yy) coordinate of zz. And given points x,y∈ℝ2x,y\in\mathbb{R}^{2}, we denote by

⟦x,y⟧:={(1−s)​x+s​y:s∈[0,1]}\llbracket x,y\rrbracket:=\{(1-s)x+sy:s\in[0,1]\}

the line segment between xx and yy.

Proof.

Consider an arbitrary Ω∈𝒜\Omega\in\cal{A}. Choose arbitrary points x¯,y¯∈∂Ω\bar{x},\bar{y}\in\partial\Omega such that |x¯−y¯|=diam⁡(Ω)|\bar{x}-\bar{y}|=\operatorname{{\operatorname{diam}}}(\Omega). Endow ℝ2\mathbb{R}^{2} with a Cartesian coordinate system, with the origin at the midpoint (x¯+y¯)/2(\bar{x}+\bar{y})/2, such that

x¯=(−diam⁡(Ω)/2,0),y¯=(diam⁡(Ω)/2,0).\bar{x}=(-\operatorname{{\operatorname{diam}}}(\Omega)/2,0),\quad\bar{y}=(\operatorname{{\operatorname{diam}}}(\Omega)/2,0).

Let γ:[0,ℋ1​(∂Ω)]⟶∂Ω\gamma:[0,\mathcal{H}^{1}(\partial\Omega)]\longrightarrow\partial\Omega be an arc-length parameterization, and without loss of generality we impose γ​(0)=x¯\gamma(0)=\bar{x}. We make and prove the following claims.

  • •

    γ′​(0)x=0\gamma^{\prime}(0)_{x}=0.
    Assume the opposite, i.e., γ′​(0)x≠0\gamma^{\prime}(0)_{x}\neq 0. For |ε|≪1|\varepsilon|\ll 1, since γ\gamma is C1C^{1}-regular, it holds that γ​(ε)=x¯+ε​γ′​(0)+vε\gamma(\varepsilon)=\bar{x}+\varepsilon\gamma^{\prime}(0)+v_{\varepsilon}, for some vector vεv_{\varepsilon} with |vε|=o​(ε)|v_{\varepsilon}|=o(\varepsilon) as ε→0\varepsilon\to 0. Since y¯−x¯\bar{y}-\bar{x} is parallel to the xx-axis, it follows that

    dd⁡t​|y¯−γ​(t)||t=0=limε→0|y¯−(x¯+ε​γ′​(0))|−|y¯−x¯|+o​(ε)ε=γ′​(0)x≠0,\frac{\,{\operatorname{d}}}{\,{\operatorname{d}}t}|\bar{y}-\gamma(t)|\bigg{|}_{t=0}=\lim_{\varepsilon\to 0}\frac{|\bar{y}-(\bar{x}+\varepsilon\gamma^{\prime}(0))|-|\bar{y}-\bar{x}|+o(\varepsilon)}{\varepsilon}=\gamma^{\prime}(0)_{x}\neq 0,

    hence t=0t=0 is not a maximum for t↦|y¯−γ​(t)|t\mapsto|\bar{y}-\gamma(t)|. This contradicts

    |y¯−x¯|=diam⁡(Ω)=maxx∈∂Ω⁡|y¯−x|,|\bar{y}-\bar{x}|=\operatorname{{\operatorname{diam}}}(\Omega)=\max_{x\in\partial\Omega}|\bar{y}-x|,

    and the claim is proven.

Refer to caption

x¯\bar{x}y¯\bar{y}γ​(t1)\gamma(t_{1})γ​(t2)\gamma(t_{2})∂Ω\partial\Omegaxx-axis

Figure 1: Schematic representation of the construction.

Without loss of generality, we can further impose γ′​(0)=(0,1)\gamma^{\prime}(0)=(0,1). Consider the region Ω∩{y≥0}\Omega\cap\{y\geq 0\}. Set

t1:=inf{t:γ′​(t)y=1/2},t_{1}:=\inf\{t:\gamma^{\prime}(t)_{y}=1/2\},

where γ​(t)y\gamma(t)_{y} denotes the yy-coordinate of γ​(t)\gamma(t). By Hölder’s inequality, it follows that

14​t1≤‖γy′‖T​V​(0,t1)2t1≤∫∂Ωκ∂Ω2​d⁡ℋ⌞​∂Ω1≤Ep,λ​(Ω)λ⟹t1≥λ4​Ep,λ​(Ω).\displaystyle\frac{1}{4t_{1}}\leq\frac{\|\gamma_{y}^{\prime}\|^{2}_{TV(0,t_{1})}}{t_{1}}\leq\int_{\partial\Omega}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega}\leq\frac{E_{p,\lambda}(\Omega)}{\lambda}\Longrightarrow t_{1}\geq\frac{\lambda}{4E_{p,\lambda}(\Omega)}. (2.13)

Since 1/2≤γy′​(t)≤11/2\leq\gamma_{y}^{\prime}(t)\leq 1 for any t∈[0,t1]t\in[0,t_{1}], it holds that γ​(t1)y≥t1/2\gamma(t_{1})_{y}\geq t_{1}/2. Due to the convexity of Ω∩{y≥0}\Omega\cap\{y\geq 0\}, both line segments ⟦γ​(t1),x¯⟧\llbracket\gamma(t_{1}),\bar{x}\rrbracket and ⟦γ​(t1),y¯⟧\llbracket\gamma(t_{1}),\bar{y}\rrbracket are contained in Ω\Omega, hence △​x¯​γ​(t1)​y¯⊆Ω\triangle\bar{x}\gamma(t_{1})\bar{y}\subseteq\Omega. By construction, the triangle △​x¯​γ​(t1)​y¯\triangle\bar{x}\gamma(t_{1})\bar{y} has base ⟦x¯,y¯⟧\llbracket\bar{x},\bar{y}\rrbracket and height ⟦γ​(t1),(γ​(t1)x,0)⟧\llbracket\gamma(t_{1}),(\gamma(t_{1})_{x},0)\rrbracket, hence

ℋ2​(△​x¯​γ​(t1)​y¯)=12​|x¯−y¯|⋅|γ​(t1)y|≥diam⁡(Ω)​t14.\mathcal{H}^{2}(\triangle\bar{x}\gamma(t_{1})\bar{y})=\frac{1}{2}|\bar{x}-\bar{y}|\cdot|\gamma(t_{1})_{y}|\geq\frac{\operatorname{{\operatorname{diam}}}(\Omega)t_{1}}{4}. (2.14)

By repeating the same construction for Ω∩{y≤0}\Omega\cap\{y\leq 0\}, we get the existence of t2≥λ4​Ep,λ​(Ω)t_{2}\geq\frac{\lambda}{4E_{p,\lambda}(\Omega)} such that the triangle △​x¯​γ​(t2)​y¯\triangle\bar{x}\gamma(t_{2})\bar{y} satisfies

ℋ2​(△​x¯​γ​(t2)​y¯)=12​|x¯−y¯|⋅|γ​(t2)y|≥diam⁡(Ω)​t24.\mathcal{H}^{2}(\triangle\bar{x}\gamma(t_{2})\bar{y})=\frac{1}{2}|\bar{x}-\bar{y}|\cdot|\gamma(t_{2})_{y}|\geq\frac{\operatorname{{\operatorname{diam}}}(\Omega)t_{2}}{4}. (2.15)

Combining (2.14) and (2.15) gives

ℋ2​(Ω)≥diam⁡(Ω)​t14+diam⁡(Ω)​t24​≥(​2.7​),(​2.13​)​π​λ22​Ep,λ​(Ω)2,\mathcal{H}^{2}(\Omega)\geq\frac{\operatorname{{\operatorname{diam}}}(\Omega)t_{1}}{4}+\frac{\operatorname{{\operatorname{diam}}}(\Omega)t_{2}}{4}\overset{\eqref{diam-low},\eqref{inf t0}}{\geq}\frac{\pi\lambda^{2}}{2E_{p,\lambda}(\Omega)^{2}},

hence (2.11).

To prove (2.12), note that the above arguments give

ℋ2​(Ωn)​≥(​2.11​)​π​λ22​Ep,λ​(Ωn)2​≥(​2.10​)​π​λ28​(1+π​λ)2,\mathcal{H}^{2}(\Omega_{n})\overset{\eqref{a-low}}{\geq}\frac{\pi\lambda^{2}}{2E_{p,\lambda}(\Omega_{n})^{2}}\overset{\eqref{inf E2}}{\geq}\frac{\pi\lambda^{2}}{8(1+\pi\lambda)^{2}},

for any sufficiently large nn, and proof of (2.12) is complete.

∎

Lemma 2.3.

Given p≥1p\geq 1, λ>0\lambda>0, for any Ω∈𝒜\Omega\in\cal A it holds that

diam⁡(Ω)≤(p+1)​(p+2)​(24λ)p+1​Ep,λ​(Ω)p+2.\operatorname{{\operatorname{diam}}}(\Omega)\leq(p+1)(p+2)\left(\frac{24}{\lambda}\right)^{p+1}E_{p,\lambda}(\Omega)^{p+2}. (2.16)

Moreover, for any minimizing sequence Ωn⊆𝒜\Omega_{n}\subseteq\cal A (that is, Ep,λ​(Ωn)→inf𝒜Ep,λE_{p,\lambda}(\Omega_{n})\to\inf_{\cal A}E_{p,\lambda}) it holds that

diam⁡(Ωn)≤C1\operatorname{{\operatorname{diam}}}(\Omega_{n})\leq C_{1} (2.17)

for all sufficiently large nn, with C1C_{1} defined in (1.5).

Proof.

Similar to the proof of Lemma 2.2, consider an arbitrary Ω∈𝒜\Omega\in\cal A, and choose arbitrary points x¯,y¯∈∂Ω\bar{x},\bar{y}\in\partial\Omega such that |x¯−y¯|=diam⁡(Ω)|\bar{x}-\bar{y}|=\operatorname{{\operatorname{diam}}}(\Omega). Endow ℝ2\mathbb{R}^{2} again with a Cartesian coordinate system, with the origin at the midpoint (x¯+y¯)/2(\bar{x}+\bar{y})/2, such that

x¯=(−diam⁡(Ω)/2,0),y¯=(diam⁡(Ω)/2,0).\bar{x}=(-\operatorname{{\operatorname{diam}}}(\Omega)/2,0),\quad\bar{y}=(\operatorname{{\operatorname{diam}}}(\Omega)/2,0).

In the proof of Lemma 2.2 we have shown the existence of a point q∈∂Ωq\in\partial\Omega (e.g., the point γ​(t1)\gamma(t_{1})) such that

△​x¯​q​y¯⊆Ω,|qy|≥λ8​Ep,λ​(Ω).\triangle\bar{x}q\bar{y}\subseteq\Omega,\qquad|q_{y}|\geq\frac{\lambda}{8E_{p,\lambda}(\Omega)}. (2.18)
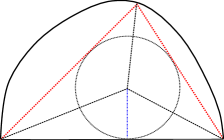
Refer to caption

x¯\bar{x}y¯\bar{y}qqqc⊥q_{c}^{\bot}qcq_{c}∂Ω\partial\Omega

Figure 2: Schematic representation of the construction. Here represented only the region Ω∩{y≥0}\Omega\cap\{y\geq 0\}. Notice that the sides of △​x¯​q​y¯\triangle\bar{x}q\bar{y} are tangents of the incircle.

Let qcq_{c} be the incenter of △​x¯​q​y¯\triangle\bar{x}q\bar{y}, and note that for any z∈△​x¯​qc​y¯z\in\triangle\bar{x}q_{c}\bar{y} it holds that

dist⁡(z,∂(△​x¯​q​y¯))=dist⁡(z,⟦x¯,y¯⟧).\operatorname{dist}(z,\partial(\triangle\bar{x}q\bar{y}))=\operatorname{dist}(z,\llbracket\bar{x},\bar{y}\rrbracket).

Denote by qc⊥∈⟦x¯,y¯⟧q_{c}^{\bot}\in\llbracket\bar{x},\bar{y}\rrbracket the projection of qcq_{c} on ⟦x¯,y¯⟧\llbracket\bar{x},\bar{y}\rrbracket, and set

D1:=|x¯−qc⊥|,D2:=|y¯−qc⊥|,r:=|qc−qc⊥|.D_{1}:=|\bar{x}-q_{c}^{\bot}|,\qquad D_{2}:=|\bar{y}-q_{c}^{\bot}|,\qquad r:=|q_{c}-q_{c}^{\bot}|.

Clearly, D1+D2=diam⁡(Ω)D_{1}+D_{2}=\operatorname{{\operatorname{diam}}}(\Omega), and direct computation gives

∫Ωdistp⁡(z,∂Ω)​d⁡z\displaystyle\int_{\Omega}\operatorname{dist}^{p}(z,\partial\Omega)\,{\operatorname{d}}z ≥∫△​x¯​qc​y¯distp⁡(z,∂Ω)​d⁡z≥∫△​x¯​qc​y¯distp⁡(z,⟦x¯,y¯⟧)​d⁡z\displaystyle\geq\int_{\triangle\bar{x}q_{c}\bar{y}}\operatorname{dist}^{p}(z,\partial\Omega)\,{\operatorname{d}}z\geq\int_{\triangle\bar{x}q_{c}\bar{y}}\operatorname{dist}^{p}(z,\llbracket\bar{x},\bar{y}\rrbracket)\,{\operatorname{d}}z
=∫△​x¯​qc​y¯zyp​d⁡z=∫0D1∫0rD1​xyp​d⁡y​d⁡x+∫0D2∫0rD2​xyp​d⁡y​d⁡x\displaystyle=\int_{\triangle\bar{x}q_{c}\bar{y}}z_{y}^{p}\,{\operatorname{d}}z=\int_{0}^{D_{1}}\int_{0}^{\frac{r}{D_{1}}x}y^{p}\,{\operatorname{d}}y\,{\operatorname{d}}x+\int_{0}^{D_{2}}\int_{0}^{\frac{r}{D_{2}}x}y^{p}\,{\operatorname{d}}y\,{\operatorname{d}}x
=rp+1​(D1+D2)(p+1)​(p+2)=rp+1​diam⁡(Ω)(p+1)​(p+2).\displaystyle=\frac{r^{p+1}(D_{1}+D_{2})}{(p+1)(p+2)}=\frac{r^{p+1}\operatorname{{\operatorname{diam}}}(\Omega)}{(p+1)(p+2)}. (2.19)

To estimate rr, note that the sides ⟦x¯,qc⟧\llbracket\bar{x},q_{c}\rrbracket and ⟦y¯,qc⟧\llbracket\bar{y},q_{c}\rrbracket satisfy

|x¯−y¯|=diam⁡(Ω)≥max⁡{|x¯−qc|,|y¯−qc|}.|\bar{x}-\bar{y}|=\operatorname{{\operatorname{diam}}}(\Omega)\geq\max\{|\bar{x}-q_{c}|,|\bar{y}-q_{c}|\}.

Since qcq_{c} is the incenter of △​x¯​q​y¯\triangle\bar{x}q\bar{y} and the sides of △​x¯​q​y¯\triangle\bar{x}q\bar{y} are tangents of the incircle, we have

ℋ2​(△​x¯​q​y¯)=12​diam⁡(Ω)​|qy|=12​(diam⁡(Ω)+|x¯−qc|+|y¯−qc|)​r.\mathcal{H}^{2}(\triangle\bar{x}q\bar{y})=\frac{1}{2}\operatorname{{\operatorname{diam}}}(\Omega)|q_{y}|=\frac{1}{2}(\operatorname{{\operatorname{diam}}}(\Omega)+|\bar{x}-q_{c}|+|\bar{y}-q_{c}|)r{\color[rgb]{1,0,0}.}

Thus, we infer

r≥|qy|3​≥(​2.18​)​λ24​Ep,λ​(Ω).r\geq\frac{|q_{y}|}{3}\overset{\eqref{inf qy}}{\geq}\frac{\lambda}{24E_{p,\lambda}(\Omega)}.

Plugging into (2.19) gives

(λ24​Ep,λ​(Ω))p+1⋅diam⁡(Ω)(p+1)​(p+2)≤∫Ωdistp⁡(z,∂Ω)​d⁡z≤Ep,λ​(Ω),\left(\frac{\lambda}{24E_{p,\lambda}(\Omega)}\right)^{p+1}\cdot\frac{\operatorname{{\operatorname{diam}}}(\Omega)}{(p+1)(p+2)}\leq\int_{\Omega}\operatorname{dist}^{p}(z,\partial\Omega)\,{\operatorname{d}}z\leq E_{p,\lambda}(\Omega),

hence (2.16).

To prove (2.17), note that for any minimizing sequence it holds that

Ep,λ​(Ωn)​≤(​2.10​)​2​(1+π​λ)⟹diam⁡(Ωn)​≤(​2.16​)​(p+1)​(p+2)​(24λ)p+1​(2​(1+π​λ))p+2=C1E_{p,\lambda}(\Omega_{n})\overset{\eqref{inf E2}}{\leq}2(1+\pi\lambda)\Longrightarrow\operatorname{{\operatorname{diam}}}(\Omega_{n})\overset{\eqref{diam-high}}{\leq}(p+1)(p+2)\left(\frac{24}{\lambda}\right)^{p+1}(2(1+\pi\lambda))^{p+2}=C_{1}

for all sufficiently large nn.

∎

3 Proof of existence

Set

𝒜¯:=completion of ​𝒜​ with respect to the metric ​d,\bar{\cal A}:=\text{completion of }{\cal A}\text{ with respect to}\text{ the metric }d,

where dd is defined in (1.3).

Lemma 3.1.

Given a compact set Σ⊆ℝ2\Sigma\subseteq\mathbb{R}^{2}, and a sequence of curves {γk}:[0,1]⟶Σ\{\gamma_{k}\}:[0,1]\longrightarrow\Sigma satisfying

supk‖γk′‖B​V<+∞,supkℋ1​(γk​([0,1]))<+∞,\sup_{k}\|\gamma_{k}^{\prime}\|_{BV}<+\infty,\qquad\sup_{k}\mathcal{H}^{1}(\gamma_{k}([0,1]))<+\infty,

where ∥⋅∥B​V\|\cdot\|_{BV} denotes the BV norm, then there exists a curve γ:[0,1]⟶Σ\gamma:[0,1]\longrightarrow\Sigma, such that (upon subsequence) it holds that:

  1. 1.

    γk→γ\gamma_{k}\rightarrow\gamma in CαC^{\alpha} for any α∈[0,1)\alpha\in[0,1),

  2. 2.

    γk′→γ′\gamma_{k}^{\prime}\rightarrow\gamma^{\prime} in LpL^{p} for any p∈[1,∞)p\in[1,\infty),

  3. 3.

    γk′′​⇀∗​γ′′\gamma_{k}^{\prime\prime}\;{\overset{*}{\rightharpoonup}}\;\gamma^{\prime\prime} in the space of signed Borel measures.

The is a classical result (see for instance [25], to which we refer for the proof).

Lemma 3.2.

If a minimizing sequence Ωn⊆𝒜\Omega_{n}\subseteq{\cal A} converges to some Ω∈𝒜¯\𝒜\Omega\in\bar{{\cal A}}\backslash{\cal A}, then Ω\Omega must be either be a point or a line segment.

Proof.

The compactness of Ω\Omega can be guaranteed by Lemma 2.3. To see that Ω∈𝒜¯\𝒜\Omega\in\bar{{\cal A}}\backslash{\cal A} is convex, let us consider an arbitrary pair of points P,Q∈ΩP,Q\in\Omega, t∈(0,1)t\in(0,1), we now show that (1−t)​P+t​Q∈Ω(1-t)P+tQ\in\Omega. Consider sequences Pn,Qn∈ΩnP_{n},Q_{n}\in\Omega_{n} such that Pn→PP_{n}\to P, Qn→QQ_{n}\to Q: since each Ωn\Omega_{n} is convex, (1−t)​Pn+t​Qn∈Ωn(1-t)P_{n}+tQ_{n}\in\Omega_{n}. By Lemma 3.1, we know ‖φn−φ‖C0​([0,1];ℝ2)→0\|\varphi_{n}-\varphi\|_{C^{0}([0,1];\mathbb{R}^{2})}\to 0. As a consequence,

dℋ​(∂Ωn,∂Ω)→0d_{\mathcal{H}}(\partial\Omega_{n},\partial\Omega)\to 0

too. This allows us to choose, for each nn, another point zn∈Ωz_{n}\in\Omega such that |zn−((1−t)​Pn+t​Qn)|≤dℋ​(∂Ωn,∂Ω)|z_{n}-((1-t)P_{n}+tQ_{n})|\leq d_{\mathcal{H}}(\partial\Omega_{n},\partial\Omega). By construction, now the sequences (1−t)​Pn+t​Qn(1-t)P_{n}+tQ_{n} and znz_{n} have the same limit. As (1−t)​Pn+t​Qn→(1−t)​P+t​Q(1-t)P_{n}+tQ_{n}\to(1-t)P+tQ, and zn→zz_{n}\to z, hence z=(1−t)​P+t​Qz=(1-t)P+tQ, using the compactness of Ω\Omega finally gives z∈Ωz\in\Omega. Then if Ω\Omega contains non collinear points x,y,zx,y,z, by convexity △​x​y​z⊆Ω\triangle xyz\subseteq\Omega, which would give the contradiction Ω∈𝒜\Omega\in{\cal A}. ∎

Lemma 3.3.

Given a sequence Ωn⊆𝒜\Omega_{n}\subseteq\mathcal{A}, such that Ep,λ​(Ωn)E_{p,\lambda}(\Omega_{n}) is bounded, then there exists Ω∈𝒜\Omega\in\mathcal{A} such that a subsequence of Ωn\Omega_{n} (still denoted by Ωn\Omega_{n}) converges to Ω\Omega with respect to the metric dd defined in (1.3).

Proof.

By (2.7) and (2.16), we have

(p+1)​(p+2)​(24λ)p+1​Ep,λ​(Ωn)p+2≥diam⁡(Ωn)≥4​π​λEp,λ​(Ωn),(p+1)(p+2)\left(\frac{24}{\lambda}\right)^{p+1}E_{p,\lambda}(\Omega_{n})^{p+2}\geq\operatorname{{\operatorname{diam}}}(\Omega_{n})\geq\frac{4\pi\lambda}{E_{p,\lambda}(\Omega_{n})},

hence supndiam⁡(Ωn)<+∞\sup_{n}\operatorname{{\operatorname{diam}}}(\Omega_{n})<+\infty, i.e. Ωn\Omega_{n} has uniform bounded diameters. Note also that supnEp,λ​(Ωn)<+∞\sup_{n}E_{p,\lambda}(\Omega_{n})<+\infty implies

supn∫∂Ωnκ∂Ωn2​d⁡ℋ⌞​∂Ωn1<+∞,\sup_{n}\int_{\partial\Omega_{n}}\kappa_{\partial\Omega_{n}}^{2}\,{\operatorname{d}}\mathcal{H}_{\llcorner\partial\Omega_{n}}^{1}<+\infty,

i.e. the curvatures of Ωn\Omega_{n} are uniformly square integrable. Then, by letting γn:[0,2​π]⟶ℝ2\gamma_{n}:[0,2\pi]\longrightarrow\mathbb{R}^{2} being constant speed parameterizations of ∂Ωn\partial\Omega_{n}, we have that a subsequence γn\gamma_{n} satisfies all the hypotheses of Lemma 3.1, concluding the proof. ∎

Based on Lemma 2.1, Lemma 2.2, Lemma 2.3 and Lemma 3.3, we get the following corollary.

Corollary 3.4.

Any minimizer (if they exist at all) satisfies estimates (2.8), (2.12) and (2.17).

Lemma 3.5.

For any p≥1,λ>0p\geq 1,\lambda>0, the functional Ep,λE_{p,\lambda} admits a minimizer in 𝒜\cal{A}.

Proof.

Consider a minimizing sequence Ωn⊆𝒜\Omega_{n}\subseteq{\cal A}. Since Ep,λE_{p,\lambda} is invariant under rigid movements, we can assume that (0,0)∈Ωn(0,0)\in\Omega_{n} for any nn. In view of (2.10), without loss of generality, we can also impose

supnEp,λ​(Ωn)≤2​(1+π​λ).\sup_{n}E_{p,\lambda}(\Omega_{n})\leq 2(1+\pi\lambda).

Then by Lemma 2.3 we get supndiam⁡(Ωn)≤C1\sup_{n}\operatorname{{\operatorname{diam}}}(\Omega_{n})\leq C_{1}, hence

Ωn⊆B​((0,0),C1)for any ​n.\Omega_{n}\subseteq B((0,0),C_{1})\quad\text{for any }n.

Thus Ωn\Omega_{n} is a sequence of uniformly bounded, compact sets, and there exists (upon subsequence, which we do not relabel) a limit set Ω∈𝒜¯\Omega\in\bar{{\cal A}} such that Ωn→Ω\Omega_{n}\to\Omega in the metric dd (defined in (1.3)).

We claim

∫Ωdistp⁡(z,∂Ω)​d⁡z\displaystyle\int_{\Omega}\operatorname{dist}^{p}(z,\partial\Omega)\,{\operatorname{d}}z =limn→+∞∫Ωndistp⁡(z,∂Ωn)​d⁡z,\displaystyle=\lim_{n\to+\infty}\int_{\Omega_{n}}\operatorname{dist}^{p}(z,\partial\Omega_{n})\,{\operatorname{d}}z, (3.20)
∫∂Ωκ∂Ω2​d⁡ℋ⌞​∂Ω1\displaystyle\int_{\partial\Omega}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega} ≤lim infn→+∞∫∂Ωnκ∂Ωn2​d⁡ℋ⌞​∂Ωn1.\displaystyle\leq\liminf_{n\to+\infty}\int_{\partial\Omega_{n}}\kappa_{\partial\Omega_{n}}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega_{n}}. (3.21)

The latter, i.e. (3.21), follows rather straightforwardly from the lower semicontinuity of the H2H^{2} norm.

We need to prove (3.20). In the following, it is useful to recall Lemma A.1, which states that the diameter is continuous with respect to the convergence in 𝒜\mathcal{A}. We split the sums

∫Ωndistp⁡(z,∂Ωn)​d⁡z\displaystyle\int_{\Omega_{n}}\operatorname{dist}^{p}(z,\partial\Omega_{n})\,{\operatorname{d}}z =∫Ωn\Ωdistp⁡(z,∂Ωn)​d⁡z+∫Ωn∩Ωdistp⁡(z,∂Ωn)​d⁡z,\displaystyle=\int_{\Omega_{n}\backslash\Omega}\operatorname{dist}^{p}(z,\partial\Omega_{n})\,{\operatorname{d}}z+\int_{\Omega_{n}\cap\Omega}\operatorname{dist}^{p}(z,\partial\Omega_{n})\,{\operatorname{d}}z,
∫Ωdistp⁡(z,∂Ω)​d⁡z\displaystyle\int_{\Omega}\operatorname{dist}^{p}(z,\partial\Omega)\,{\operatorname{d}}z =∫Ω\Ωndistp⁡(z,∂Ω)​d⁡z+∫Ωn∩Ωdistp⁡(z,∂Ω)​d⁡z,\displaystyle=\int_{\Omega\backslash\Omega_{n}}\operatorname{dist}^{p}(z,\partial\Omega)\,{\operatorname{d}}z+\int_{\Omega_{n}\cap\Omega}\operatorname{dist}^{p}(z,\partial\Omega)\,{\operatorname{d}}z,

and note that

|∫Ωn\displaystyle\bigg{|}\int_{\Omega_{n}} distp(z,∂Ωn)dz−∫Ωdistp(z,∂Ω)dz|\displaystyle\operatorname{dist}^{p}(z,\partial\Omega_{n})\,{\operatorname{d}}z-\int_{\Omega}\operatorname{dist}^{p}(z,\partial\Omega)\,{\operatorname{d}}z\bigg{|}
≤∫Ωn\Ωdistp⁡(z,∂Ωn)​d⁡z+∫Ω\Ωndistp⁡(z,∂Ω)​d⁡z\displaystyle\leq\int_{\Omega_{n}\backslash\Omega}\operatorname{dist}^{p}(z,\partial\Omega_{n})\,{\operatorname{d}}z+\int_{\Omega\backslash\Omega_{n}}\operatorname{dist}^{p}(z,\partial\Omega)\,{\operatorname{d}}z (3.22)
+∫Ωn∩Ω|distp⁡(z,∂Ωn)−distp⁡(z,∂Ω)|​d⁡z.\displaystyle+\int_{\Omega_{n}\cap\Omega}|\operatorname{dist}^{p}(z,\partial\Omega_{n})-\operatorname{dist}^{p}(z,\partial\Omega)|\,{\operatorname{d}}z. (3.23)

Moreover,

∫Ωn\Ωdistp⁡(z,∂Ωn)​d⁡z\displaystyle\int_{\Omega_{n}\backslash\Omega}\operatorname{dist}^{p}(z,\partial\Omega_{n})\,{\operatorname{d}}z ≤ℋ2(Ωn\Ω)diam(Ωn)p≤ℋ2(Ωn\Ω)C1p→0,\displaystyle\leq\mathcal{H}^{2}(\Omega_{n}\backslash\Omega)\operatorname{{\operatorname{diam}}}(\Omega_{n})^{p}\leq\mathcal{H}^{2}(\Omega_{n}\backslash\Omega)C_{1}^{p}\to 0,
∫Ω\Ωndistp⁡(z,∂Ω)​d⁡z\displaystyle\int_{\Omega\backslash\Omega_{n}}\operatorname{dist}^{p}(z,\partial\Omega)\,{\operatorname{d}}z ≤ℋ2(Ω\Ωn)diam(Ω)p≤ℋ2(Ω\Ωn)C1p→0,\displaystyle\leq\mathcal{H}^{2}(\Omega\backslash\Omega_{n})\operatorname{{\operatorname{diam}}}(\Omega)^{p}\leq\mathcal{H}^{2}(\Omega\backslash\Omega_{n})C_{1}^{p}\to 0,

hence

limn→+∞∫Ωn\Ωdistp⁡(z,∂Ωn)​d⁡z=limn→+∞∫Ω\Ωndistp⁡(z,∂Ω)​d⁡z=0.\lim_{n\to+\infty}\int_{\Omega_{n}\backslash\Omega}\operatorname{dist}^{p}(z,\partial\Omega_{n})\,{\operatorname{d}}z=\lim_{n\to+\infty}\int_{\Omega\backslash\Omega_{n}}\operatorname{dist}^{p}(z,\partial\Omega)\,{\operatorname{d}}z=0.

To prove

limn→+∞∫Ωn∩Ω|distp⁡(z,∂Ωn)−distp⁡(z,∂Ω)|​d⁡z=0,\lim_{n\to+\infty}\int_{\Omega_{n}\cap\Omega}|\operatorname{dist}^{p}(z,\partial\Omega_{n})-\operatorname{dist}^{p}(z,\partial\Omega)|\,{\operatorname{d}}z=0,

denote by dℋd_{\mathcal{H}} the Hausdorff distance, and by the mean value theorem, it holds that

∫Ωn∩Ω\displaystyle\int_{\Omega_{n}\cap\Omega} |distp⁡(z,∂Ωn)−distp⁡(z,∂Ω)|​d⁡z\displaystyle|\operatorname{dist}^{p}(z,\partial\Omega_{n})-\operatorname{dist}^{p}(z,\partial\Omega)|\,{\operatorname{d}}z
≤∫Ωn∩Ω|dist⁡(z,∂Ωn)−dist⁡(z,∂Ω)|⋅p​supz∈Ωn∩Ω(max⁡{dist⁡(z,∂Ωn),dist⁡(z,∂Ω)})p−1​d⁡z\displaystyle\leq\int_{\Omega_{n}\cap\Omega}|\operatorname{dist}(z,\partial\Omega_{n})-\operatorname{dist}(z,\partial\Omega)|\cdot p\sup_{z\in\Omega_{n}\cap\Omega}\Big{(}\max\{\operatorname{dist}(z,\partial\Omega_{n}),\operatorname{dist}(z,\partial\Omega)\}\Big{)}^{p-1}\,{\operatorname{d}}z
≤ℋ2​(Ωn∩Ω)​dℋ​(∂Ωn,∂Ω)⋅p​C1p−1≤π​C12​dℋ​(∂Ωn,∂Ω)⋅p​C1p−1→0.\displaystyle\leq\mathcal{H}^{2}(\Omega_{n}\cap\Omega)d_{\mathcal{H}}(\partial\Omega_{n},\partial\Omega)\cdot pC_{1}^{p-1}\leq\pi C_{1}^{2}d_{\mathcal{H}}(\partial\Omega_{n},\partial\Omega)\cdot pC_{1}^{p-1}\to 0.

Thus both terms (3.22) and (3.23) converge to zero, and (3.20) is proven.

Combining with (3.20) gives

Ep,λ​(Ω)≤lim infn→+∞Ep,λ​(Ωn)=inf𝒜¯Ep,λ,E_{p,\lambda}(\Omega)\leq\liminf_{n\to+\infty}E_{p,\lambda}(\Omega_{n})=\inf_{\bar{\cal A}}E_{p,\lambda},

hence Ω\Omega is effectively a minimizer of Ep,λE_{p,\lambda}. Since Ω\Omega is the limit of Ωn⊆𝒜\Omega_{n}\subseteq\mathcal{A}, based on Lemma 3.2 and Corollary 3.4, we have Ω∈𝒜\Omega\in\mathcal{A}.

∎

4 Proof of regularity

This section completes the proof of Theorem 1.1 by establishing the desired regularity of the minimizers. A few technical estimates used in the proof are left as separate lemmas proved at the end of the section.

Proof of Theorem 1.1.

Let Ω\Omega be a minimizer of Ep,λE_{p,\lambda}, and let γ\gamma be an arc-length parameterization of ∂Ω\partial\Omega. Assume there exist M,εM,\varepsilon, t1<t2t_{1}<t_{2} such that

|γ′​(t2)−γ′​(t1)|=M​ε,t2−t1=ε.\displaystyle|\gamma^{\prime}(t_{2})-\gamma^{\prime}(t_{1})|=M\varepsilon,\qquad t_{2}-t_{1}=\varepsilon. (4.24)

The quantity ε\varepsilon is assumed to be vanishingly small, and estimates involving ε\varepsilon will be in general valid for sufficiently small ε\varepsilon, rather than all ε\varepsilon. The goal is to find an upper bound for MM.

Without loss of generality, upon rigid movements, we can assume t1=0t_{1}=0, t2=εt_{2}=\varepsilon. Endow ℝ2\mathbb{R}^{2} with a Cartesian coordinate system with

γ​(0)∈{x≥0,y=0}γ​(ε)∈{y≥0,x=0},γ′​(0)=(0,1).\gamma(0)\in\{x\geq 0,y=0\}\qquad\gamma(\varepsilon)\in\{y\geq 0,x=0\},\qquad\gamma^{\prime}(0)=(0,1). (4.25)

We first give an estimate on γ​(ε)y\gamma(\varepsilon)_{y}. Using Hölder’s inequality, and recalling the fact that

κ∂Ω≪ℋ⌞​∂Ω1,d⁡κ∂Ωd⁡ℋ⌞​∂Ω1∈L2​(0,ℋ1​(∂Ω);ℝ),\kappa_{\partial\Omega}\ll\mathcal{H}^{1}_{\llcorner\partial\Omega},\qquad\frac{\,{\operatorname{d}}\kappa_{\partial\Omega}}{\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega}}\in L^{2}(0,\mathcal{H}^{1}(\partial\Omega);\mathbb{R}),

for any t∈[0,ε]t\in[0,\varepsilon], it holds that

Ep,λ​(Ω)λ\displaystyle\frac{E_{p,\lambda}(\Omega)}{\lambda} ≥∫γ​([0,t])κ∂Ω2​d⁡ℋ⌞​∂Ω1=∫0t|γ′′|2​d⁡s≥|γ′​(t)−γ′​(0)|2ε≥|γ′​(t)y−1|2ε\displaystyle\geq\int_{\gamma([0,t])}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega}=\int_{0}^{t}|\gamma^{\prime\prime}|^{2}\,{\operatorname{d}}s\geq\frac{|\gamma^{\prime}(t)-\gamma^{\prime}(0)|^{2}}{\varepsilon}\geq\frac{|\gamma^{\prime}(t)_{y}-1|^{2}}{\varepsilon}
⟹|γ′​(t)y−1|=1−γ′​(t)y≤ε​Ep,λ​(Ω)/λ⟹γ′​(t)y≥1−ε​Ep,λ​(Ω)/λ,\displaystyle\Longrightarrow|\gamma^{\prime}(t)_{y}-1|=1-\gamma^{\prime}(t)_{y}\leq\sqrt{\varepsilon E_{p,\lambda}(\Omega)/\lambda}\Longrightarrow\gamma^{\prime}(t)_{y}\geq 1-\sqrt{\varepsilon E_{p,\lambda}(\Omega)/\lambda},

hence

γ​(ε)y\displaystyle\gamma(\varepsilon)_{y} =∫0εγ′​(t)y​d⁡t≥∫0ε[1−ε​Ep,λ​(Ω)/λ]​d⁡t=ε​[1−ε​Ep,λ​(Ω)/λ]\displaystyle=\int_{0}^{\varepsilon}\gamma^{\prime}(t)_{y}\,{\operatorname{d}}t\geq\int_{0}^{\varepsilon}[1-\sqrt{\varepsilon E_{p,\lambda}(\Omega)/\lambda}]\,{\operatorname{d}}t=\varepsilon[1-\sqrt{\varepsilon E_{p,\lambda}(\Omega)/\lambda}]

On the other hand, as we imposed γ​(ε)y≥0\gamma(\varepsilon)_{y}\geq 0, we have

γ​(ε)y=|γ​(ε)y|=|∫0εγ′​(t)y​d⁡t|≤∫0ε|γ′​(t)y|​d⁡t≤ε.\gamma(\varepsilon)_{y}=|\gamma(\varepsilon)_{y}|=\bigg{|}\int_{0}^{\varepsilon}\gamma^{\prime}(t)_{y}\,{\operatorname{d}}t\bigg{|}\leq\int_{0}^{\varepsilon}|\gamma^{\prime}(t)_{y}|\,{\operatorname{d}}t\leq\varepsilon.

In particular,

ε−Ep,λ​(Ω)/λ​ε3/2≤γ​(ε)y≤ε,\varepsilon-\sqrt{E_{p,\lambda}(\Omega)/\lambda}\varepsilon^{3/2}\leq\gamma(\varepsilon)_{y}\leq\varepsilon,

therefore,

γ​(ε)y=ε+O​(ε3/2).\displaystyle\gamma(\varepsilon)_{y}=\varepsilon+O(\varepsilon^{3/2}). (4.26)

Construct the competitor Ωε\Omega_{\varepsilon} in the following way:

  1. 1.

    denote by t±t_{\pm} the two times such that γ′​(t±)=(±1,0)\gamma^{\prime}(t_{\pm})=(\pm 1,0), and by t⊥t_{\bot} the time such that γ′​(t⊥)=(0,−1)\gamma^{\prime}(t_{\bot})=(0,-1). Since we imposed γ′​(0)=(0,1)\gamma^{\prime}(0)=(0,1), without loss of generality we can assume that the tangent direction turns counterclockwise, i.e.,

    ε<t−<t⊥<t+<ℋ1​(∂Ω).\varepsilon<t_{-}<t_{\bot}<t_{+}<\mathcal{H}^{1}(\partial\Omega).

    Note that

    2t⊥−t−\displaystyle\frac{2}{t_{\bot}-t_{-}} =|γ′​(t⊥)−γ′​(t−)|2t⊥−t−≤∫γ​([t−,t⊥])κ∂Ω2​d⁡ℋ⌞​∂Ω1≤Ep,λ​(Ω)λ​≤(​2.9​)​2​λ−1+2​π\displaystyle=\frac{|\gamma^{\prime}(t_{\bot})-\gamma^{\prime}(t_{-})|^{2}}{t_{\bot}-t_{-}}\leq\int_{\gamma([t_{-},t_{\bot}])}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega}\leq\frac{E_{p,\lambda}(\Omega)}{\lambda}\overset{\eqref{inf E}}{\leq}2\lambda^{-1}+2\pi
    ⟹t⊥−t−≥1λ−1+π.\displaystyle\Longrightarrow t_{\bot}-t_{-}\geq\frac{1}{\lambda^{-1}+\pi}.

    Similarly, we get

    min⁡{ℋ1​(∂Ω)−t+,t+−t⊥,t−}≥1λ−1+π.\displaystyle\min\{\mathcal{H}^{1}(\partial\Omega)-t_{+},\ t_{+}-t_{\bot},\ t_{-}\}\geq\frac{1}{\lambda^{-1}+\pi}. (4.27)
  2. 2.

    Define the vector field v:[t−,t+]⟶ℝ2v:[t_{-},t_{+}]\longrightarrow\mathbb{R}^{2} as

    v​(s):={(cos⁡(π2​(1+s−t−t⊥−t−)),sin⁡(π2​(1+s−t−t⊥−t−))),if ​s∈[t−,t⊥],(cos⁡(π2​(1+t+−st+−t⊥)),−(t+−st+−t⊥)2​sin⁡(π2​(1+t+−st+−t⊥))),if ​s∈[t⊥,t+].\displaystyle v(s):=\left\{\begin{array}[]{cl}\left(\cos\Big{(}\frac{\pi}{2}(1+\frac{s-t_{-}}{t_{\bot}-t_{-}})\Big{)},\sin\Big{(}\frac{\pi}{2}(1+\frac{s-t_{-}}{t_{\bot}-t_{-}})\Big{)}\right),&\text{if }s\in[t_{-},t_{\bot}],\\ \left(\cos\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)},-\Big{(}\frac{t_{+}-s}{t_{+}-t_{\bot}}\Big{)}^{2}\sin\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)}\right),&\text{if }s\in[t_{\bot},t_{+}].\end{array}\right. (4.30)

    Note first that vv is continuous (smooth outside t⊥t_{\bot}), and direct computation gives

    v′​(s)={π/2t⊥−t−​(−sin⁡(π2​(1+s−t−t⊥−t−)),cos⁡(π2​(1+s−t−t⊥−t−))),if ​s∈[t−,t⊥),(π/2t+−t⊥sin(π2(1+t+−st+−t⊥)),π/2t+−t⊥(t+−st+−t⊥)2cos(π2(1+t+−st+−t⊥))+2t+−s(t+−t⊥)2sin(π2(1+t+−st+−t⊥)))if ​s∈(t⊥,t+].v^{\prime}(s)=\left\{\begin{array}[]{cl}\frac{\pi/2}{t_{\bot}-t_{-}}\left(-\sin\Big{(}\frac{\pi}{2}(1+\frac{s-t_{-}}{t_{\bot}-t_{-}})\Big{)},\cos\Big{(}\frac{\pi}{2}(1+\frac{s-t_{-}}{t_{\bot}-t_{-}})\Big{)}\right),&\text{if }s\in[t_{-},t_{\bot}),\\ \Big{(}\frac{\pi/2}{t_{+}-t_{\bot}}\sin\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)},\frac{\pi/2}{t_{+}-t_{\bot}}\Big{(}\frac{t_{+}-s}{t_{+}-t_{\bot}}\Big{)}^{2}\cos\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)}&\\ +2\frac{t_{+}-s}{(t_{+}-t_{\bot})^{2}}\sin\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)}\Big{)}&\text{if }s\in(t_{\bot},t_{+}].\end{array}\right.

    In particular,

    limt→t⊥−v′​(t)=π/2t⊥−t−​(0,−1),limt→t⊥+v′​(t)=π/2t+−t⊥​(0,−1),\lim_{t\to t_{\bot}^{-}}v^{\prime}(t)=\frac{\pi/2}{t_{\bot}-t_{-}}(0,-1),\qquad\lim_{t\to t_{\bot}^{+}}v^{\prime}(t)=\frac{\pi/2}{t_{+}-t_{\bot}}(0,-1),

    i.e., the left and right limit differ just by a multiplicative constant. This observation is crucial, since it implies that the tangent derivative of the arc-length reparameterization of vv does not jump at t=t⊥t=t_{\bot} (recall also that γ′\gamma^{\prime} does not jump at t=t⊥t=t_{\bot}, hence the tangent derivative of the arc-length reparameterization of γ+c​v\gamma+cv does not jump at t=t⊥t=t_{\bot}, for any c>0c>0). We claim:

    ‖v′‖L∞\displaystyle\|v^{\prime}\|_{L^{\infty}} ≤max⁡{π/2t⊥−t−,4t+−t⊥}≤4​(λ−1+π)<+∞,\displaystyle\leq\max\Big{\{}\frac{\pi/2}{t_{\bot}-t_{-}},\frac{4}{t_{+}-t_{\bot}}\Big{\}}\leq 4(\lambda^{-1}+\pi)<+\infty, (4.31)
    ‖v′′‖L∞\displaystyle\|v^{\prime\prime}\|_{L^{\infty}} ≤16​(λ−1+π)2<+∞.\displaystyle\leq 16(\lambda^{-1}+\pi)^{2}<+\infty. (4.32)

    The proofs of both claims are presented in Lemma 4.1 below.

  3. 3.

    Let γε\gamma_{\varepsilon} be the curve such that

    γε​(t):={(2​γ​(t)x,2​γ​(t)y)if ​t∈[0,ε],γ​(t)+(0,γ​(ε)y)if ​t∈[ε,t−],γ​(t)+γ​(ε)y​v​(t)if ​t∈[t−,t+],(γ​(t)x​(1+γ​(0)xγ​(0)x−γ​(t+)x)−γ​(t+)x​γ​(0)xγ​(0)x−γ​(t+)x)if ​t∈[t+,ℋ1​(∂Ω)].\gamma_{\varepsilon}(t):=\left\{\begin{array}[]{cl}(2\gamma(t)_{x},2\gamma(t)_{y})&\text{if }t\in[0,\varepsilon],\\ \gamma(t)+(0,\gamma(\varepsilon)_{y})&\text{if }t\in[\varepsilon,t_{-}],\\ \gamma(t)+\gamma(\varepsilon)_{y}v(t)&\text{if }t\in[t_{-},t_{+}],\\ \left(\gamma(t)_{x}\left(1+\frac{\gamma(0)_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}}\right)-\frac{\gamma(t_{+})_{x}\gamma(0)_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}}\right)&\text{if }t\in[t_{+},\mathcal{H}^{1}(\partial\Omega)].\end{array}\right. (4.33)

    Note that γϵ\gamma_{\epsilon} defined in (4.33) is injective. Let ∂Ωε\partial\Omega_{\varepsilon} be the image of γε\gamma_{\varepsilon}, and Ωε\Omega_{\varepsilon} be the bounded region of the plane delimited by ∂Ωε\partial\Omega_{\varepsilon}. This will be our competitor. Observe first that, as γ′​(t+)=(1,0)\gamma^{\prime}(t_{+})=(1,0),

    limt→t+−γε′​(t)=(1+γ​(ε)y​π/2t+−t⊥)​(1,0),limt→t++γε′​(t)=(1+γ​(0)xγ​(0)x−γ​(t+)x)​(1,0),\displaystyle\lim_{t\to t_{+}^{-}}\gamma_{\varepsilon}^{\prime}(t)=\left(1+\gamma(\varepsilon)_{y}\frac{\pi/2}{t_{+}-t_{\bot}}\right)(1,0),\qquad\lim_{t\to t_{+}^{+}}\gamma_{\varepsilon}^{\prime}(t)=\left(1+\frac{\gamma(0)_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}}\right)(1,0),

    i.e., the left and right limit differ just by a multiplicative constant. This observation is again crucial, since it implies that the tangent derivative of the arc-length reparameterization of γ+γ​(ε)y​v\gamma+\gamma(\varepsilon)_{y}v does not jump at t=t+t=t_{+}.

Intuitively, for t∈[0,H1​(∂Ω)]t\in[0,H^{1}(\partial\Omega)] the competitor γε\gamma_{\varepsilon} is constructed from γ\gamma by:

  1. 1.

    a homothety of center (0,0)(0,0) and ratio 2 for t∈[0,ε]t\in[0,\varepsilon],

  2. 2.

    a translation of the vector (0,γ​(ε)y)(0,\gamma(\varepsilon)_{y}) for t∈[ε,t−]t\in[\varepsilon,t_{-}],

  3. 3.

    adding the smooth vector field γ​(ε)y​v​(t)\gamma(\varepsilon)_{y}v(t) for t∈[t−,t+]t\in[t_{-},t_{+}],

  4. 4.

    a scaling of factor 1+γ​(0)xγ​(0)x−γ​(t+)x1+\frac{\gamma(0)_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}} and then translation to the right by γ​(t+)x​γ​(0)xγ​(0)x−γ​(t+)x\frac{\gamma(t_{+})_{x}\gamma(0)_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}} in the xx direction for t∈[t+,ℋ1​(∂Ω)]t\in[t_{+},\mathcal{H}^{1}(\partial\Omega)].

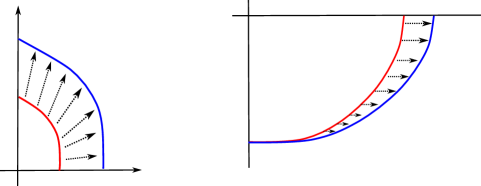
Refer to caption

0xx-axisyy-axis∂Ω\partial\Omega∂Ωε\partial\Omega_{\varepsilon}γ​(0)\gamma(0)γ​(ε)\gamma(\varepsilon)γε​(0)\gamma_{\varepsilon}(0)γε​(ε)\gamma_{\varepsilon}(\varepsilon)xx-axis{x=γ​(t+)x}\{x=\gamma(t_{+})_{x}\}∂Ω\partial\Omega∂Ωε\partial\Omega_{\varepsilon}γ​(ℋ1​(∂Ω))=γ​(0)\begin{subarray}{c}\gamma(\mathcal{H}^{1}(\partial\Omega))\\ =\gamma(0)\end{subarray}γε​(ℋ1​(∂Ω))=γε​(0)\begin{subarray}{c}\gamma_{\varepsilon}(\mathcal{H}^{1}(\partial\Omega))\\ =\gamma_{\varepsilon}(0)\end{subarray}γ​(t+)=γε​(t+)\begin{subarray}{c}\gamma(t_{+})\\ =\gamma_{\varepsilon}(t_{+})\end{subarray}

Figure 3: Representation of the construction of the competitor γε\gamma_{\varepsilon}, for t∈[0,ε]t\in[0,\varepsilon] (left) and t∈[t+,ℋ1​(∂Ω)]t\in[t_{+},\mathcal{H}^{1}(\partial\Omega)] (right).

It is straightforward to check compactness and convexity for Ωε\Omega_{\varepsilon}. Moreover, denoting by γ~ε\tilde{\gamma}_{\varepsilon} the arc-length reparameterization of γε\gamma_{\varepsilon}, the curvature of γ~ε\tilde{\gamma}_{\varepsilon} is still a function (instead of a more generic measure), as the is γε\gamma_{\varepsilon} always constructed from γ\gamma via translation, scaling, or sum with smooth vector fields, and the tangent derivative γ~ε′\tilde{\gamma}_{\varepsilon}^{\prime} never jumps at “junction points” (i.e., for t=ε,t−,t⊥,t+,ℋ1​(∂Ω)t=\varepsilon,t_{-},t_{\bot},t_{+},\mathcal{H}^{1}(\partial\Omega)).

Next, to estimate Ep,λ​(Ωε)−Ep,λ​(Ω)E_{p,\lambda}(\Omega_{\varepsilon})-E_{p,\lambda}(\Omega), we claim

∫Ωεdistp⁡(z,∂Ωε)​d⁡z−∫Ωdistp⁡(z,∂Ω)​d⁡z\displaystyle\int_{\Omega_{\varepsilon}}\operatorname{dist}^{p}(z,\partial\Omega_{\varepsilon})\,{\operatorname{d}}z-\int_{\Omega}\operatorname{dist}^{p}(z,\partial\Omega)\,{\operatorname{d}}z ≤ε⋅p​(C1+1)p−1​π​C12/2+(2​ε)p+1​π​(C1+1).\displaystyle\leq\varepsilon\cdot p(C_{1}+1)^{p-1}\pi C_{1}^{2}/2+(2\varepsilon)^{p+1}\pi(C_{1}+1). (4.34)
∫∂Ωεκ∂Ωε2​d⁡ℋ⌞​∂Ωε1−∫∂Ωκ∂Ω2​d⁡ℋ⌞​∂Ω1\displaystyle\int_{\partial\Omega_{\varepsilon}}\kappa_{\partial\Omega_{\varepsilon}}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega_{\varepsilon}}-\int_{\partial\Omega}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega} ≤ε​(C2−M22)+O​(ε3/2),\displaystyle\leq\varepsilon\Big{(}C_{2}-\frac{M^{2}}{2}\Big{)}+O(\varepsilon^{3/2}), (4.35)

with

C2=32​(λ−1+π)2+32​2​C1​π​(λ−1+π)5/2C_{2}=32(\lambda^{-1}+\pi)^{2}+32\sqrt{2C_{1}\pi}(\lambda^{-1}+\pi)^{5/2}

defined in (1.6).

Step 1. Proof of (4.35). Using the notation from (4.33), we make the following claims:

∫γ​([ε,t−])κ∂Ω2​d⁡ℋ⌞​∂Ω1\displaystyle\int_{\gamma([\varepsilon,t_{-}])}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega} =∫γε​([ε,t−])κ∂Ωε2​d⁡ℋ⌞​∂Ωε1,\displaystyle=\int_{\gamma_{\varepsilon}([\varepsilon,t_{-}])}\kappa_{\partial\Omega_{\varepsilon}}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega_{\varepsilon}}, (4.36)
∫γε​([t+,ℋ1​(∂Ω)])κ∂Ωε2​d⁡ℋ⌞​∂Ωε1−∫γ​([t+,ℋ1​(∂Ω)])κ∂Ω2​d⁡ℋ⌞​∂Ω1\displaystyle\int_{\gamma_{\varepsilon}([t_{+},\mathcal{H}^{1}(\partial\Omega)])}\kappa_{\partial\Omega_{\varepsilon}}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega_{\varepsilon}}-\int_{\gamma([t_{+},\mathcal{H}^{1}(\partial\Omega)])}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega} ≤O​(ε3/2),\displaystyle\leq O(\varepsilon^{3/2}), (4.37)
∫γε​([t−,t+])κ∂Ωε2​d⁡ℋ⌞​∂Ωε1−∫γ​([t−,t+])κ∂Ω2​d⁡ℋ⌞​∂Ω1\displaystyle\int_{\gamma_{\varepsilon}([t_{-},t_{+}])}\kappa_{\partial\Omega_{\varepsilon}}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega_{\varepsilon}}-\int_{\gamma([t_{-},t_{+}])}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega} ≤ε​C2+O​(ε3/2),\displaystyle\leq\varepsilon C_{2}+O(\varepsilon^{3/2}), (4.38)
∫γ​([0,ε])κ∂Ω2​d⁡ℋ⌞​∂Ω1−∫γε​([0,ε])κ∂Ωε2​d⁡ℋ⌞​∂Ωε1\displaystyle\int_{\gamma([0,\varepsilon])}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega}-\int_{\gamma_{\varepsilon}([0,\varepsilon])}\kappa_{\partial\Omega_{\varepsilon}}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega_{\varepsilon}} ≥M2​ε2.\displaystyle\geq\frac{M^{2}\varepsilon}{2}. (4.39)

The proof of all four assertions are quite technical, and for reader’s convenience, will be done in Lemmas 4.2 and 4.3 below. Combining (4.36), (4.37), (4.38), and (4.39) gives

∫Ωεκ∂Ωε2​d⁡ℋ⌞​Ωε1≤∫Ωκ∂Ω2​d⁡ℋ⌞​Ω1+ε​(C2−M22)+O​(ε3/2),\int_{\Omega_{\varepsilon}}\kappa_{\partial\Omega_{\varepsilon}}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\Omega_{\varepsilon}}\leq\int_{\Omega}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\Omega}+\varepsilon\Big{(}C_{2}-\frac{M^{2}}{2}\Big{)}+O(\varepsilon^{3/2}),

hence (4.35).


Step 2. Proof of (4.34). Recall that, the construction of the competitor Ωε\Omega_{\varepsilon} in (4.33) gives also

  1. (1)

    γ​(ε)y>γ​(0)x>0\gamma(\varepsilon)_{y}>\gamma(0)_{x}>0.

  2. (2)

    For t∈[ε,ℋ1​(∂Ω)]t\in[\varepsilon,\mathcal{H}^{1}(\partial\Omega)] the competitor γε​(t)\gamma_{\varepsilon}(t) is obtained by translating γ​(t)\gamma(t) by a vector of length at most 2​ε2\varepsilon. Moreover, it holds

    γ​(t)x−γ​(t+)xγ​(0)x−γ​(t+)x​γ​(0)x≤2​ε,∀t∈[ε,ℋ1​(∂Ω)],\frac{\gamma(t)_{x}-\gamma(t_{+})_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}}\gamma(0)_{x}\leq 2\varepsilon,\qquad\forall t\in[\varepsilon,\mathcal{H}^{1}(\partial\Omega)],

    since by construction we have γ​(0)x≤2​ε\gamma(0)_{x}\leq 2\varepsilon, and γ​(0)\gamma(0) is the point with the most positive xx coordinate, which ensures γ​(t)x−γ​(t+)xγ​(0)x−γ​(t+)x≤1\frac{\gamma(t)_{x}-\gamma(t_{+})_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}}\leq 1.

  3. (3)

    For t∈[0,ε]t\in[0,\varepsilon], the competitor γε​(t)\gamma_{\varepsilon}(t) is obtained by scaling γ​(t)\gamma(t) by a factor of 2.

One readily checks for all tt it holds that |γε​(t)−γ​(t)|≤2​ε|\gamma_{\varepsilon}(t)-\gamma(t)|\leq 2\varepsilon, and

dℋ​(∂Ωε,∂Ω)≤2​ε.d_{\mathcal{H}}(\partial\Omega_{\varepsilon},\partial\Omega)\leq 2\varepsilon.

Thus, by the mean value theorem, for each point x∈Ωε∩Ωx\in\Omega_{\varepsilon}\cap\Omega it holds that

distp⁡(x,∂Ωε)−distp⁡(x,∂Ω)\displaystyle\operatorname{dist}^{p}(x,\partial\Omega_{\varepsilon})-\operatorname{dist}^{p}(x,\partial\Omega) ≤(dist⁡(x,∂Ωε)−dist⁡(x,∂Ω))\displaystyle\leq(\operatorname{dist}(x,\partial\Omega_{\varepsilon})-\operatorname{dist}(x,\partial\Omega))
⋅p​(supz∈Ωε∩Ωmax⁡{dist⁡(x,∂Ωε),dist⁡(x,∂Ω)})p−1\displaystyle\qquad\cdot p(\sup_{z\in\Omega_{\varepsilon}\cap\Omega}\max\{\operatorname{dist}(x,\partial\Omega_{\varepsilon}),\operatorname{dist}(x,\partial\Omega)\})^{p-1}
≤2​ε⋅p​(diam⁡(Ω)+2​ε)p−1​≤(​2.17​)​ε⋅2​p​(C1+1)p−1,\displaystyle\leq 2\varepsilon\cdot p(\operatorname{{\operatorname{diam}}}(\Omega)+2\varepsilon)^{p-1}\overset{\eqref{diam-h}}{\leq}\varepsilon\cdot 2p(C_{1}+1)^{p-1},

with C1C_{1} defined in (1.5). Thus, by convexity of Ω\Omega,

ℋ2​(Ωε∩Ω)≤ℋ2​(Ω)≤π​(diam⁡(Ω)/2)2.\mathcal{H}^{2}(\Omega_{\varepsilon}\cap\Omega)\leq\mathcal{H}^{2}(\Omega)\leq\pi(\operatorname{{\operatorname{diam}}}(\Omega)/2)^{2}{\color[rgb]{1,0,0}.}

It follows that

∫Ωε∩Ωdistp⁡(x,∂Ωε)​d⁡x−∫Ωdistp⁡(x,∂Ω)​d⁡x\displaystyle\int_{\Omega_{\varepsilon}\cap\Omega}\operatorname{dist}^{p}(x,\partial\Omega_{\varepsilon})\,{\operatorname{d}}x-\int_{\Omega}\operatorname{dist}^{p}(x,\partial\Omega)\,{\operatorname{d}}x ≤ε⋅2​p​(C1+1)p−1​ℋ2​(Ωε∩Ω)\displaystyle\leq\varepsilon\cdot 2p(C_{1}+1)^{p-1}\mathcal{H}^{2}(\Omega_{\varepsilon}\cap\Omega)
≤ε⋅p​(C1+1)p−1​π​C12/2.\displaystyle\leq\varepsilon\cdot p(C_{1}+1)^{p-1}\pi C_{1}^{2}/2. (4.40)

Then note that, since by construction we have dℋ​(∂Ωε,∂Ω)≤2​εd_{\mathcal{H}}(\partial\Omega_{\varepsilon},\partial\Omega)\leq 2\varepsilon, it follows that

∫Ωε\Ωdistp⁡(x,∂Ωε)​d⁡x≤(2​ε)p​ℋ2​(Ωε\Ω)\displaystyle\int_{\Omega_{\varepsilon}\backslash\Omega}\operatorname{dist}^{p}(x,\partial\Omega_{\varepsilon})\,{\operatorname{d}}x\leq(2\varepsilon)^{p}\mathcal{H}^{2}(\Omega_{\varepsilon}\backslash\Omega) ≤\displaystyle\leq (2​ε)p⋅2​ε​ℋ1​(∂Ωε)\displaystyle(2\varepsilon)^{p}\cdot 2\varepsilon\mathcal{H}^{1}(\partial\Omega_{\varepsilon}) (4.41)
≤\displaystyle\leq (2​ε)p+1​π​(diam⁡(Ω)+4​ε)≤(2​ε)p+1​π​(C1+1).\displaystyle(2\varepsilon)^{p+1}\pi(\operatorname{{\operatorname{diam}}}(\Omega)+4\varepsilon)\leq(2\varepsilon)^{p+1}\pi(C_{1}+1).

The inequality ℋ2​(Ωε\Ω)≤2​ε​ℋ1​(∂Ωε)\mathcal{H}^{2}(\Omega_{\varepsilon}\backslash\Omega)\leq 2\varepsilon\mathcal{H}^{1}(\partial\Omega_{\varepsilon}) is due to the convexity of Ωε\Omega_{\varepsilon}, the fact that dℋ​(∂Ωε,∂Ω)≤2​εd_{\mathcal{H}}(\partial\Omega_{\varepsilon},\partial\Omega)\leq 2\varepsilon, and Lemma A.3. Combining (4.40) and (4.41) gives

∫Ωεdistp⁡(x,∂Ωε)​d⁡x−∫Ωdistp⁡(x,∂Ω)​d⁡x\displaystyle\int_{\Omega_{\varepsilon}}\operatorname{dist}^{p}(x,\partial\Omega_{\varepsilon})\,{\operatorname{d}}x-\int_{\Omega}\operatorname{dist}^{p}(x,\partial\Omega)\,{\operatorname{d}}x ≤ε⋅p​(C1+1)p−1​π​C12/2+(2​ε)p+1​π​(C1+1).\displaystyle\leq\varepsilon\cdot p(C_{1}+1)^{p-1}\pi C_{1}^{2}/2+(2\varepsilon)^{p+1}\pi(C_{1}+1). (4.42)

Thus (4.34) is proven.


Combining (4.34) and (4.35) we finally infer

Ep,λ​(Ωε)\displaystyle E_{p,\lambda}(\Omega_{\varepsilon}) −Ep,λ​(Ω)\displaystyle-E_{p,\lambda}(\Omega)
=∫Ωεdistp⁡(x,∂Ωε)​d⁡x−∫Ωdistp⁡(x,∂Ω)​d⁡x+λ​(∫∂Ωεκ∂Ωε2​d⁡ℋ⌞​∂Ωε1−∫∂Ωκ∂Ω2​d⁡ℋ⌞​∂Ω1)\displaystyle=\int_{\Omega_{\varepsilon}}\operatorname{dist}^{p}(x,\partial\Omega_{\varepsilon})\,{\operatorname{d}}x-\int_{\Omega}\operatorname{dist}^{p}(x,\partial\Omega)\,{\operatorname{d}}x+\lambda\bigg{(}\int_{\partial\Omega_{\varepsilon}}\kappa_{\partial\Omega_{\varepsilon}}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega_{\varepsilon}}-\int_{\partial\Omega}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega}\bigg{)}
≤ε⋅p​(C1+1)p−1​π​C12/2+(2​ε)p+1​π​(C1+1)+λ​(ε​(C2−M22)+O​(ε3/2)).\displaystyle\leq\varepsilon\cdot p(C_{1}+1)^{p-1}\pi C_{1}^{2}/2+(2\varepsilon)^{p+1}\pi(C_{1}+1)+\lambda\bigg{(}\varepsilon\Big{(}C_{2}-\frac{M^{2}}{2}\Big{)}+O(\varepsilon^{3/2})\bigg{)}.

Note also that the term (2​ε)p+1​π​(C1+1)(2\varepsilon)^{p+1}\pi(C_{1}+1) can be absorbed into O​(ε3/2)O(\varepsilon^{3/2}), due to the condition p≥1p\geq 1, hence

Ep,λ​(Ωε)−Ep,λ​(Ω)≤λ​(ε​(λ−1​p​(C1+1)p−1​π​C12/2+C2−M22)+O​(ε3/2)).E_{p,\lambda}(\Omega_{\varepsilon})-E_{p,\lambda}(\Omega)\leq\lambda\bigg{(}\varepsilon\Big{(}\lambda^{-1}p(C_{1}+1)^{p-1}\pi C_{1}^{2}/2+C_{2}-\frac{M^{2}}{2}\Big{)}+O(\varepsilon^{3/2})\bigg{)}.

The minimality assumption on Ω\Omega, and the arbitrariness of ε>0\varepsilon>0 then imply

λ−1​p​(C1+1)p−1​π​C12/2+C2−M22≥0\displaystyle\lambda^{-1}p(C_{1}+1)^{p-1}\pi C_{1}^{2}/2+C_{2}-\frac{M^{2}}{2}\geq 0
⟹M≤λ−1​p​(C1+1)p−1​π​C12+2​C2=C,\displaystyle\Longrightarrow M\leq\sqrt{\lambda^{-1}p(C_{1}+1)^{p-1}\pi C_{1}^{2}+2C_{2}}=C,

and the proof is complete.

∎

Lemma 4.1.

Under the hypotheses of Theorem 1.1, assertions (4.31) and (4.32) hold.

Proof.

We use the same notations from the proof of Theorem 1.1. Since

v′​(s)={π/2t⊥−t−​(−sin⁡(π2​(1+s−t−t⊥−t−)),cos⁡(π2​(1+s−t−t⊥−t−))),if ​s∈[t−,t⊥),(π/2t+−t⊥sin(π2(1+t+−st+−t⊥)),π/2t+−t⊥(t+−st+−t⊥)2cos(π2(1+t+−st+−t⊥))+2t+−s(t+−t⊥)2sin(π2(1+t+−st+−t⊥)))if ​s∈(t⊥,t+],v^{\prime}(s)=\left\{\begin{array}[]{cl}\frac{\pi/2}{t_{\bot}-t_{-}}\left(-\sin\Big{(}\frac{\pi}{2}(1+\frac{s-t_{-}}{t_{\bot}-t_{-}})\Big{)},\cos\Big{(}\frac{\pi}{2}(1+\frac{s-t_{-}}{t_{\bot}-t_{-}})\Big{)}\right),&\text{if }s\in[t_{-},t_{\bot}),\\ \Big{(}\frac{\pi/2}{t_{+}-t_{\bot}}\sin\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)},\frac{\pi/2}{t_{+}-t_{\bot}}\Big{(}\frac{t_{+}-s}{t_{+}-t_{\bot}}\Big{)}^{2}\cos\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)}&\\ +2\frac{t_{+}-s}{(t_{+}-t_{\bot})^{2}}\sin\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)}\Big{)}&\text{if }s\in(t_{\bot},t_{+}],\end{array}\right.

it follows that

|v′​(s)|≤π/2t⊥−t−for any ​s∈[t−,t⊥),|v^{\prime}(s)|\leq\frac{\pi/2}{t_{\bot}-t_{-}}\qquad\text{for any }s\in[t_{-},t_{\bot}),

and

|v′​(s)|\displaystyle|v^{\prime}(s)| =[(π/2t+−t⊥)2sin2(π2(1+t+−st+−t⊥))+(π/2t+−t⊥)2(t+−st+−t⊥)4cos2(π2(1+t+−st+−t⊥))\displaystyle=\bigg{[}\Big{(}\frac{\pi/2}{t_{+}-t_{\bot}}\Big{)}^{2}\sin^{2}\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)}+\Big{(}\frac{\pi/2}{t_{+}-t_{\bot}}\Big{)}^{2}\Big{(}\frac{t_{+}-s}{t_{+}-t_{\bot}}\Big{)}^{4}\cos^{2}\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)}
+4​(t+−s)2(t+−t⊥)4​sin2⁡(π2​(1+t+−st+−t⊥))\displaystyle\qquad+4\frac{(t_{+}-s)^{2}}{(t_{+}-t_{\bot})^{4}}\sin^{2}\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)}
+4π/2t+−t⊥(t+−s)3(t+−t⊥)4cos(π2(1+t+−st+−t⊥))sin(π2(1+t+−st+−t⊥))]1/2\displaystyle\qquad+4\frac{\pi/2}{t_{+}-t_{\bot}}\frac{(t_{+}-s)^{3}}{(t_{+}-t_{\bot})^{4}}\cos\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)}\sin\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)}\bigg{]}^{1/2}
≤[(π/2t+−t⊥)2+4+π(t+−t⊥)2]1/2≤4t+−t⊥\displaystyle\leq\bigg{[}\Big{(}\frac{\pi/2}{t_{+}-t_{\bot}}\Big{)}^{2}+\frac{4+\pi}{(t_{+}-t_{\bot})^{2}}\bigg{]}^{1/2}\leq\frac{4}{t_{+}-t_{\bot}}

for any s∈(t⊥,t+]s\in(t_{\bot},t_{+}]. Thus (4.31) is proven.

To prove (4.32), note that for s∈[t−,t⊥)s\in[t_{-},t_{\bot}) it holds that

v′′​(s)=−(π/2t⊥−t−)2​(cos⁡(π2​(1+s−t−t⊥−t−)),sin⁡(π2​(1+s−t−t⊥−t−))),v^{\prime\prime}(s)=-\bigg{(}\frac{\pi/2}{t_{\bot}-t_{-}}\bigg{)}^{2}\left(\cos\Big{(}\frac{\pi}{2}(1+\frac{s-t_{-}}{t_{\bot}-t_{-}})\Big{)},\sin\Big{(}\frac{\pi}{2}(1+\frac{s-t_{-}}{t_{\bot}-t_{-}})\Big{)}\right),

hence |v′′​(s)|≤(π/2t⊥−t−)2|v^{\prime\prime}(s)|\leq\bigg{(}\dfrac{\pi/2}{t_{\bot}-t_{-}}\bigg{)}^{2}. Similarly, for s∈(t⊥,t+]s\in(t_{\bot},t_{+}], it holds that

v′′​(s)\displaystyle v^{\prime\prime}(s) =(−(π/2t+−t⊥)2cos(π2(1+t+−st+−t⊥)),\displaystyle=\bigg{(}-\bigg{(}\frac{\pi/2}{t_{+}-t_{\bot}}\bigg{)}^{2}\cos\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)},
π/2t+−t⊥​[−2​(t+−s)(t+−t⊥)2​cos⁡(π2​(1+t+−st+−t⊥))+(t+−st+−t⊥)2​π/2t+−t⊥​sin⁡(π2​(1+t+−st+−t⊥))]\displaystyle\qquad\frac{\pi/2}{t_{+}-t_{\bot}}\bigg{[}\frac{-2(t_{+}-s)}{(t_{+}-t_{\bot})^{2}}\cos\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)}+\Big{(}\frac{t_{+}-s}{t_{+}-t_{\bot}}\Big{)}^{2}\frac{\pi/2}{t_{+}-t_{\bot}}\sin\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)}\bigg{]}
−2t+−s(t+−t⊥)2π/2t+−t⊥cos(π2(1+t+−st+−t⊥))−2(t+−t⊥)2sin(π2(1+t+−st+−t⊥))),\displaystyle\qquad-2\frac{t_{+}-s}{(t_{+}-t_{\bot})^{2}}\frac{\pi/2}{t_{+}-t_{\bot}}\cos\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)}-\frac{2}{(t_{+}-t_{\bot})^{2}}\sin\Big{(}\frac{\pi}{2}(1+\frac{t_{+}-s}{t_{+}-t_{\bot}})\Big{)}\bigg{)},

therefore, using (4.27),

|v′′​(s)|\displaystyle|v^{\prime\prime}(s)| ≤(4t+−t⊥)2≤16​(λ−1+π)2,\displaystyle\leq\bigg{(}\frac{4}{t_{+}-t_{\bot}}\bigg{)}^{2}\leq 16(\lambda^{-1}+\pi)^{2},

hence (4.32) is proven. ∎

The rest of the section contains the proofs of the technical estimates needed in the above proof.

Lemma 4.2.

Under the hypotheses of Theorem 1.1, assertions (4.36), (4.37) and (4.39) hold.

Proof.

We use the same notations from the proof of Theorem 1.1.

Proof of (4.36). By construction, for any t∈[ε,t−]t\in[\varepsilon,t_{-}], γε​(t)\gamma_{\varepsilon}(t) differ from γ​(t)\gamma(t) by a translation, thus the curvature of these two segments are always equal, hence (4.36).

Proof of (4.37). For t∈[t+,ℋ1​(∂Ω)]t\in[t_{+},\mathcal{H}^{1}(\partial\Omega)] we have

γε​(t)\displaystyle\gamma_{\varepsilon}(t) =(γ​(t)x​(1+γ​(0)xγ​(0)x−γ​(t+)x)−γ​(t+)x​γ​(0)xγ​(0)x−γ​(t+)x,γ​(t)y),\displaystyle=\left(\gamma(t)_{x}\left(1+\frac{\gamma(0)_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}}\right)-\frac{\gamma(t_{+})_{x}\gamma(0)_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}},\gamma(t)_{y}\right),
γε′​(t)\displaystyle\gamma_{\varepsilon}^{\prime}(t) =(γ′​(t)x​(1+γ​(0)xγ​(0)x−γ​(t+)x),γ′​(t)y),\displaystyle=\left(\gamma^{\prime}(t)_{x}\left(1+\frac{\gamma(0)_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}}\right),\gamma^{\prime}(t)_{y}\right),
γε′′​(t)\displaystyle\gamma_{\varepsilon}^{\prime\prime}(t) =(γ′′​(t)x​(1+γ​(0)xγ​(0)x−γ​(t+)x),γ′′​(t)y).\displaystyle=\left(\gamma^{\prime\prime}(t)_{x}\left(1+\frac{\gamma(0)_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}}\right),\gamma^{\prime\prime}(t)_{y}\right).

We claim

γ​(0)x≤∫0ε|γ′​(t)x|​d⁡t≤ε3/2​Ep,λ​(Ω)/λ,γ​(0)x−γ​(t+)x≥λ2​Ep,λ​(Ω).\displaystyle\gamma(0)_{x}\leq\int_{0}^{\varepsilon}|\gamma^{\prime}(t)_{x}|\,{\operatorname{d}}t\leq\varepsilon^{3/2}\sqrt{E_{p,\lambda}(\Omega)/\lambda},\qquad\gamma(0)_{x}-\gamma(t_{+})_{x}\geq\frac{\lambda}{2E_{p,\lambda}(\Omega)}. (4.43)

In view of (4.25), and noting that for any t∈[0,ε]t\in[0,\varepsilon] it holds that

Ep,λ​(Ω)λ\displaystyle\frac{E_{p,\lambda}(\Omega)}{\lambda} ≥∫γ​([0,t])κ∂Ω2​d⁡ℋ⌞​∂Ω1=∫0t|γ′′|2​d⁡s≥|γ′​(t)−γ′​(0)|2ε≥|γ′​(t)x|2ε\displaystyle\geq\int_{\gamma([0,t])}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega}=\int_{0}^{t}|\gamma^{\prime\prime}|^{2}\,{\operatorname{d}}s\geq\frac{|\gamma^{\prime}(t)-\gamma^{\prime}(0)|^{2}}{\varepsilon}\geq\frac{|\gamma^{\prime}(t)_{x}|^{2}}{\varepsilon}
⟹|γ′​(t)x|≤ε​Ep,λ​(Ω)/λ,\displaystyle\Longrightarrow|\gamma^{\prime}(t)_{x}|\leq\sqrt{\varepsilon E_{p,\lambda}(\Omega)/\lambda},

it follows that

|γ​(0)x−γ​(ε)x|=|γ​(0)x|≤∫0ε|γ′​(t)x|​d⁡t≤ε3/2​Ep,λ​(Ω)/λ.|\gamma(0)_{x}-\gamma(\varepsilon)_{x}|=|\gamma(0)_{x}|\leq\int_{0}^{\varepsilon}|\gamma^{\prime}(t)_{x}|\,{\operatorname{d}}t\leq\varepsilon^{3/2}\sqrt{E_{p,\lambda}(\Omega)/\lambda}.

Now recall that by construction γ′​(t+)=(1,0)\gamma^{\prime}(t_{+})=(1,0), γ′​(ℋ1​(∂Ω))=γ′​(0)=(0,1)\gamma^{\prime}(\mathcal{H}^{1}(\partial\Omega))=\gamma^{\prime}(0)=(0,1), |γ′|≡1|\gamma^{\prime}|\equiv 1 for a.e. tt, and let τ∈(t+,ℋ1​(∂Ω))\tau\in(t_{+},\mathcal{H}^{1}(\partial\Omega)) be time for which γ′​(τ)=(1/2,3/2)\gamma^{\prime}(\tau)=(1/2,\sqrt{3}/2). Thus

Ep,λ​(Ω)λ\displaystyle\frac{E_{p,\lambda}(\Omega)}{\lambda} ≥∫γ​([t+,τ])κ∂Ω2​d⁡ℋ⌞​∂Ω1=∫t+τ|γ′′|2​d⁡s≥|γ′​(τ)−γ′​(t+)|2τ−t+=1τ−t+\displaystyle\geq\int_{\gamma([t_{+},\tau])}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega}=\int_{t_{+}}^{\tau}|\gamma^{\prime\prime}|^{2}\,{\operatorname{d}}s\geq\frac{|\gamma^{\prime}(\tau)-\gamma^{\prime}(t_{+})|^{2}}{\tau-t_{+}}=\frac{1}{\tau-t_{+}}
⟹τ−t+≥λ/Ep,λ​(Ω),\displaystyle\Longrightarrow\tau-t_{+}\geq\lambda/E_{p,\lambda}(\Omega),

and since γx′≥0\gamma_{x}^{\prime}\geq 0 on [t+,ℋ1​(∂Ω)][t_{+},\mathcal{H}^{1}(\partial\Omega)], and γx′≥1/2\gamma_{x}^{\prime}\geq 1/2 for all t∈[t+,τ]t\in[t_{+},\tau], it follows that γ​(0)x−γ​(t+)x≥γ​(τ)x−γ​(t+)x≥λ2​Ep,λ​(Ω)\gamma(0)_{x}-\gamma(t_{+})_{x}\geq\gamma(\tau)_{x}-\gamma(t_{+})_{x}\geq\frac{\lambda}{2E_{p,\lambda}(\Omega)}, hence (4.43) is proven. Consequently,

|γ​(0)xγ​(0)x−γ​(t+)x|≤2​(ε​Ep,λ​(Ω)/λ)3/2=O​(ε3/2).\bigg{|}\frac{\gamma(0)_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}}\bigg{|}\leq 2(\varepsilon E_{p,\lambda}(\Omega)/\lambda)^{3/2}=O(\varepsilon^{3/2}).

Therefore,

|γε′|−4\displaystyle|\gamma_{\varepsilon}^{\prime}|^{-4} =(|γx′|2​(1+γ​(0)xγ​(0)x−γ​(t+)x)2+|γy′|2)−2\displaystyle=\left(|\gamma_{x}^{\prime}|^{2}\Big{(}1+\frac{\gamma(0)_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}}\Big{)}^{2}+|\gamma_{y}^{\prime}|^{2}\right)^{-2}
=(1+|γx′|2​2​γ​(0)xγ​(0)x−γ​(t+)x+|γx′|2​(γ​(0)xγ​(0)x−γ​(t+)x)2)−2=1+O​(ε3/2).\displaystyle=\left(1+|\gamma_{x}^{\prime}|^{2}\frac{2\gamma(0)_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}}+|\gamma_{x}^{\prime}|^{2}\bigg{(}\frac{\gamma(0)_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}}\bigg{)}^{2}\right)^{-2}=1+O(\varepsilon^{3/2}).

Observe that for t∈[t+,ℋ1​(∂Ω)]t\in[t_{+},\mathcal{H}^{1}(\partial\Omega)] we have

κ∂Ωε=|γε′′|γε′|−γε′​⟨γε′′,γε′⟩|γε′|3||γε′|,\displaystyle\kappa_{\partial\Omega_{\varepsilon}}=\frac{\left|\frac{\gamma_{\varepsilon}^{\prime\prime}}{|\gamma_{\varepsilon}^{\prime}|}-\gamma_{\varepsilon}^{\prime}\frac{\langle\gamma_{\varepsilon}^{\prime\prime},\gamma_{\varepsilon}^{\prime}\rangle}{|\gamma_{\varepsilon}^{\prime}|^{3}}\right|}{|\gamma_{\varepsilon}^{\prime}|},
⟨γε′′,γε′⟩=γx′​γx′′​(1+γ​(0)xγ​(0)x−γ​(t+)x)2+γy′​γy′′=⟨γ′,γ′′⟩+O​(ε3/2)=O​(ε3/2).\displaystyle\langle\gamma_{\varepsilon}^{\prime\prime},\gamma_{\varepsilon}^{\prime}\rangle=\gamma_{x}^{\prime}\gamma_{x}^{\prime\prime}\left(1+\frac{\gamma(0)_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}}\right)^{2}+\gamma_{y}^{\prime}\gamma_{y}^{\prime\prime}=\langle\gamma^{\prime},\gamma^{\prime\prime}\rangle+O(\varepsilon^{3/2})=O(\varepsilon^{3/2}).

Here we use the fact that

⟨γ′′,γ′⟩=12​dd⁡t​|γ′|2=0,\langle\gamma^{\prime\prime},\gamma^{\prime}\rangle=\frac{1}{2}\frac{\,{\operatorname{d}}}{\,{\operatorname{d}}t}|\gamma^{\prime}|^{2}=0, (4.44)

since γ\gamma is parameterized by arc-length. And we have

∫t+ℋ1​(∂Ω)|γε′′|2|γε′|4​d⁡t\displaystyle\int_{t_{+}}^{\mathcal{H}^{1}(\partial\Omega)}\frac{|\gamma_{\varepsilon}^{\prime\prime}|^{2}}{|\gamma_{\varepsilon}^{\prime}|^{4}}\,{\operatorname{d}}t =∫t+ℋ1​(∂Ω)(|γ′′|2+|γx′′|2​2​γ​(0)xγ​(0)x−γ​(t+)x+|γx′′|2​(2​γ​(0)xγ​(0)x−γ​(t+)x)2)​(1+O​(ε3/2))​d⁡t\displaystyle=\int_{t_{+}}^{\mathcal{H}^{1}(\partial\Omega)}\bigg{(}|\gamma^{\prime\prime}|^{2}+|\gamma_{x}^{\prime\prime}|^{2}\frac{2\gamma(0)_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}}+|\gamma_{x}^{\prime\prime}|^{2}\left(\frac{2\gamma(0)_{x}}{\gamma(0)_{x}-\gamma(t_{+})_{x}}\right)^{2}\bigg{)}(1+O(\varepsilon^{3/2}))\,{\operatorname{d}}t
=∫t+ℋ1​(∂Ω)|γ′′|2​d⁡t+O​(ε3/2),\displaystyle=\int_{t_{+}}^{\mathcal{H}^{1}(\partial\Omega)}|\gamma^{\prime\prime}|^{2}\,{\operatorname{d}}t+O(\varepsilon^{3/2}),

hence (4.37).

Proof of (4.39). In the time interval [0,ε][0,\varepsilon], the competitor is obtained by scaling by a factor of 2, and direct computations give that the integrated squared curvature scales by a factor of 1/21/2. Thus based on (4.24) we get

∫0ε|dd⁡t​(γ′|γ′|)|2​𝑑t\displaystyle\int_{0}^{\varepsilon}\bigg{|}\frac{\,{\operatorname{d}}}{\,{\operatorname{d}}t}\bigg{(}\frac{\gamma^{\prime}}{|\gamma^{\prime}|}\bigg{)}\bigg{|}^{2}\ dt −12​∫0ε|dd⁡t​(γε′|γε′|)|2​𝑑t\displaystyle-\frac{1}{2}\int_{0}^{\varepsilon}\bigg{|}\frac{\,{\operatorname{d}}}{\,{\operatorname{d}}t}\bigg{(}\frac{\gamma_{\varepsilon}^{\prime}}{|\gamma_{\varepsilon}^{\prime}|}\bigg{)}\bigg{|}^{2}\ dt
=12​∫0ε|dd⁡t​(γ′|γ′|)|2​𝑑t=12​∫0ε|γ′′|2≥M22​ε,\displaystyle=\frac{1}{2}\int_{0}^{\varepsilon}\bigg{|}\frac{\,{\operatorname{d}}}{\,{\operatorname{d}}t}\bigg{(}\frac{\gamma^{\prime}}{|\gamma^{\prime}|}\bigg{)}\bigg{|}^{2}\ dt=\frac{1}{2}\int_{0}^{\varepsilon}\left|\gamma^{\prime\prime}\right|^{2}\geq\frac{M^{2}}{2}\varepsilon, (4.45)

hence (4.39). ∎

Lemma 4.3.

Under the hypotheses of Theorem 1.1, assertion (4.38) holds.

Proof.

We use the same notations from the proof of Theorem 1.1. In the time interval [t−,t+][t_{-},t_{+}], γε\gamma_{\varepsilon} is given by

γε​(t)=γ​(t)+γ​(ε)y​v​(t),t∈[t−,t+].\gamma_{\varepsilon}(t)=\gamma(t)+\gamma(\varepsilon)_{y}v(t),\qquad t\in[t_{-},t_{+}].

Note first that since Ω\Omega is a minimizer of Ep,λE_{p,\lambda}, it must hold

∫γ​([t−,t+])κ∂Ω2​d⁡ℋ⌞​∂Ω1<+∞,\int_{\gamma([t_{-},t_{+}])}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega}<+\infty,

and recalling our definition of integrated squared curvature in (1.4), it follows that the Radon-Nikodym derivative d⁡κ∂Ωd⁡ℋ⌞​∂Ω1\frac{\,{\operatorname{d}}\kappa_{\partial\Omega}}{\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega}} is square integrable. In terms of the parameterization γε\gamma_{\varepsilon}, this gives

1|γε′|​dd⁡t​(γε′|γε′|)=1|γε′|​(γε′′|γε′|−γε′​⟨γε′′,γε′⟩|γε′|3)∈L2​(0,ℋ1​(∂Ω);ℝ).\frac{1}{|\gamma_{\varepsilon}^{\prime}|}\frac{\,{\operatorname{d}}}{\,{\operatorname{d}}t}\bigg{(}\frac{\gamma_{\varepsilon}^{\prime}}{|\gamma_{\varepsilon}^{\prime}|}\bigg{)}=\frac{1}{|\gamma_{\varepsilon}^{\prime}|}\left(\frac{\gamma_{\varepsilon}^{\prime\prime}}{|\gamma_{\varepsilon}^{\prime}|}-\gamma_{\varepsilon}^{\prime}\frac{\langle\gamma_{\varepsilon}^{\prime\prime},\gamma_{\varepsilon}^{\prime}\rangle}{|\gamma_{\varepsilon}^{\prime}|^{3}}\right)\in L^{2}(0,\mathcal{H}^{1}(\partial\Omega);\mathbb{R}).

Recall (4.26), that is, γ​(ε)y=ε+O​(ε3/2)\gamma(\varepsilon)_{y}=\varepsilon+O(\varepsilon^{3/2}), and as γ\gamma is parameterized by arc-length (i.e., |γ′|=1|\gamma^{\prime}|=1 for a.e. tt), and vv was defined in (4.30) (in particular, |v′||v^{\prime}| was uniformly bounded from above), it follows that

|γε′|=1+2​ε​⟨γ′,v′⟩+O​(ε3/2).|\gamma_{\varepsilon}^{\prime}|=\sqrt{1+2\varepsilon\langle\gamma^{\prime},v^{\prime}\rangle+O(\varepsilon^{3/2})}.

Then, for any α∈ℝ\alpha\in\mathbb{R} and sufficiently small ε\varepsilon, we have

|γε′|α=1+α​ε​⟨γ′,v′⟩+O​(ε3/2).|\gamma_{\varepsilon}^{\prime}|^{\alpha}=1+\alpha\varepsilon\langle\gamma^{\prime},v^{\prime}\rangle+O(\varepsilon^{3/2}). (4.46)

Calculation shows that

1|γε′|​dd⁡t​(γε′|γε′|)\displaystyle\frac{1}{|\gamma_{\varepsilon}^{\prime}|}\frac{\,{\operatorname{d}}}{\,{\operatorname{d}}t}\bigg{(}\frac{\gamma_{\varepsilon}^{\prime}}{|\gamma_{\varepsilon}^{\prime}|}\bigg{)} =γε′′|γε′|2−γε′​⟨γε′′,γε′⟩|γε′|4\displaystyle=\frac{\gamma_{\varepsilon}^{\prime\prime}}{|\gamma_{\varepsilon}^{\prime}|^{2}}-\gamma_{\varepsilon}^{\prime}\frac{\langle\gamma_{\varepsilon}^{\prime\prime},\gamma_{\varepsilon}^{\prime}\rangle}{|\gamma_{\varepsilon}^{\prime}|^{4}}
=γ′′+ε​v′′|γε′|2−γε′|γε′|4​(⟨γ′′,γ′⟩+ε2​⟨v′′,v′⟩+ε​⟨γ′′,v′⟩+ε​⟨γ′,v′′⟩)+ higher order terms.\displaystyle=\frac{\gamma^{\prime\prime}+\varepsilon v^{\prime\prime}}{|\gamma_{\varepsilon}^{\prime}|^{2}}-\frac{\gamma_{\varepsilon}^{\prime}}{|\gamma_{\varepsilon}^{\prime}|^{4}}\big{(}\langle\gamma^{\prime\prime},\gamma^{\prime}\rangle+\varepsilon^{2}\langle v^{\prime\prime},v^{\prime}\rangle+\varepsilon\langle\gamma^{\prime\prime},v^{\prime}\rangle+\varepsilon\langle\gamma^{\prime},v^{\prime\prime}\rangle\big{)}+\text{ higher order terms}.

Based on (4.44), we observe:

  1. 1.

    As both |v′||v^{\prime}| and |v′′||v^{\prime\prime}| are uniformly bounded from above, the term ε2​⟨v′′,v′⟩\varepsilon^{2}\langle v^{\prime\prime},v^{\prime}\rangle is of order O​(ε2)O(\varepsilon^{2}).

  2. 2.

    The norm of ε​γε′​⟨γ′,v′′⟩/|γε′|4\varepsilon\gamma_{\varepsilon}^{\prime}\langle\gamma^{\prime},v^{\prime\prime}\rangle/|\gamma_{\varepsilon}^{\prime}|^{4} is estimated by

    ε​|γε′​⟨γ′,v′′⟩|γε′|4|≤ε​|γ′|⋅|v′′||γε′|3≤ε​‖v′′‖L∞+O​(ε2).\varepsilon\bigg{|}\frac{\gamma_{\varepsilon}^{\prime}\langle\gamma^{\prime},v^{\prime\prime}\rangle}{|\gamma_{\varepsilon}^{\prime}|^{4}}\bigg{|}\leq\varepsilon\frac{|\gamma^{\prime}|\cdot|v^{\prime\prime}|}{|\gamma_{\varepsilon}^{\prime}|^{3}}\leq\varepsilon\|v^{\prime\prime}\|_{L^{\infty}}+O(\varepsilon^{2}). (4.47)
  3. 3.

    The norm of ε​γε′​⟨γ′′,v′⟩/|γε′|4\varepsilon\gamma_{\varepsilon}^{\prime}\langle\gamma^{\prime\prime},v^{\prime}\rangle/|\gamma_{\varepsilon}^{\prime}|^{4} is estimated by

    ε​|γε′​⟨γ′′,v′⟩|γε′|4|≤ε​|γ′′|⋅|v′||γε′|3.\varepsilon\bigg{|}\frac{\gamma_{\varepsilon}^{\prime}\langle\gamma^{\prime\prime},v^{\prime}\rangle}{|\gamma_{\varepsilon}^{\prime}|^{4}}\bigg{|}\leq\varepsilon\frac{|\gamma^{\prime\prime}|\cdot|v^{\prime}|}{|\gamma_{\varepsilon}^{\prime}|^{3}}. (4.48)

Thus combining (4.44), (4.47) and (4.48) gives

∫t−t+|γε′\displaystyle\int_{t_{-}}^{t_{+}}\bigg{|}\gamma_{\varepsilon}^{\prime} ⟨γε′′,γε′⟩|γε′|4|2dt=∫t−t+|γε′|γε′|4(⟨γ′′,γ′⟩+ε2⟨v′′,v′⟩+ε⟨γ′′,v′⟩+ε⟨γ′,v′′⟩)|2dt+ higher order terms\displaystyle\frac{\langle\gamma_{\varepsilon}^{\prime\prime},\gamma_{\varepsilon}^{\prime}\rangle}{|\gamma_{\varepsilon}^{\prime}|^{4}}\bigg{|}^{2}\,{\operatorname{d}}t=\int_{t_{-}}^{t_{+}}\bigg{|}\frac{\gamma_{\varepsilon}^{\prime}}{|\gamma_{\varepsilon}^{\prime}|^{4}}\big{(}\langle\gamma^{\prime\prime},\gamma^{\prime}\rangle+\varepsilon^{2}\langle v^{\prime\prime},v^{\prime}\rangle+\varepsilon\langle\gamma^{\prime\prime},v^{\prime}\rangle+\varepsilon\langle\gamma^{\prime},v^{\prime\prime}\rangle\big{)}\bigg{|}^{2}\,{\operatorname{d}}t+\text{ higher order terms }
≤∫t−t+|γε′|−6​|ε​⟨γ′′,v′⟩+ε​⟨γ′,v′′⟩|2​d⁡t+O​(ε3)\displaystyle\leq\int_{t_{-}}^{t_{+}}|\gamma_{\varepsilon}^{\prime}|^{-6}\big{|}\varepsilon\langle\gamma^{\prime\prime},v^{\prime}\rangle+\varepsilon\langle\gamma^{\prime},v^{\prime\prime}\rangle\big{|}^{2}\,{\operatorname{d}}t+O(\varepsilon^{3})
≤2​∫t−t+|γε′|−6​(|ε​⟨γ′′,v′⟩|2+|ε​⟨γ′,v′′⟩|2)​d⁡t+O​(ε3)\displaystyle\leq 2\int_{t_{-}}^{t_{+}}|\gamma_{\varepsilon}^{\prime}|^{-6}(|\varepsilon\langle\gamma^{\prime\prime},v^{\prime}\rangle|^{2}+|\varepsilon\langle\gamma^{\prime},v^{\prime\prime}\rangle|^{2})\,{\operatorname{d}}t+O(\varepsilon^{3})
=2​ε2​∫t−t+|γε′|−6​(|⟨γ′′,v′⟩|2+|⟨γ′,v′′⟩|2)​d⁡t+O​(ε3)\displaystyle=2\varepsilon^{2}\int_{t_{-}}^{t_{+}}|\gamma_{\varepsilon}^{\prime}|^{-6}\left(|\langle\gamma^{\prime\prime},v^{\prime}\rangle|^{2}+|\langle\gamma^{\prime},v^{\prime\prime}\rangle|^{2}\right)\,{\operatorname{d}}t+O(\varepsilon^{3})
≤2​ε2​‖v′‖L∞2​∫t−t+|γε′|−6​|γ′′|2​d⁡t+O​(ε2).\displaystyle\leq 2\varepsilon^{2}\|v^{\prime}\|_{L^{\infty}}^{2}\int_{t_{-}}^{t_{+}}|\gamma_{\varepsilon}^{\prime}|^{-6}|\gamma^{\prime\prime}|^{2}\,{\operatorname{d}}t+O(\varepsilon^{2}).

In view of (4.46), we get

∫t−t+|γε′|−6​|γ′′|2​d⁡t≤2​∫t−t+|γ′′|2​d⁡t≤2​∫∂Ωκ∂Ω2​d⁡ℋ⌞​∂Ω1<+∞,\int_{t_{-}}^{t_{+}}|\gamma_{\varepsilon}^{\prime}|^{-6}|\gamma^{\prime\prime}|^{2}\,{\operatorname{d}}t\leq 2\int_{t_{-}}^{t_{+}}|\gamma^{\prime\prime}|^{2}\,{\operatorname{d}}t\leq 2\int_{\partial\Omega}\kappa_{\partial\Omega}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega}<+\infty,

hence

2​ε2​‖v′‖L∞2​∫t−t+|γε′|−6​|γ′′|2​d⁡t≤O​(ε2).2\varepsilon^{2}\|v^{\prime}\|_{L^{\infty}}^{2}\int_{t_{-}}^{t_{+}}|\gamma_{\varepsilon}^{\prime}|^{-6}|\gamma^{\prime\prime}|^{2}\,{\operatorname{d}}t\leq O(\varepsilon^{2}).

Thus

∫t−t+|γε′​⟨γε′′,γε′⟩|γε′|4|2​d⁡t≤O​(ε2),\int_{t_{-}}^{t_{+}}\bigg{|}\gamma_{\varepsilon}^{\prime}\frac{\langle\gamma_{\varepsilon}^{\prime\prime},\gamma_{\varepsilon}^{\prime}\rangle}{|\gamma_{\varepsilon}^{\prime}|^{4}}\bigg{|}^{2}\,{\operatorname{d}}t\leq O(\varepsilon^{2}),

and

∫γ​([t−,t+])κ∂Ωε2​d⁡ℋ⌞​∂Ωε1\displaystyle\int_{\gamma([t_{-},t_{+}])}\kappa_{\partial\Omega_{\varepsilon}}^{2}\,{\operatorname{d}}\mathcal{H}^{1}_{\llcorner\partial\Omega_{\varepsilon}} =∫t−t+|1|γε′|​dd⁡t​(γε′|γε′|)|2​d⁡t=∫t−t+|γε′′|γε′|2−γε′​⟨γε′′,γε′⟩|γε′|4|2​d⁡t\displaystyle=\int_{t_{-}}^{t_{+}}\bigg{|}\frac{1}{|\gamma_{\varepsilon}^{\prime}|}\frac{\,{\operatorname{d}}}{\,{\operatorname{d}}t}\bigg{(}\frac{\gamma_{\varepsilon}^{\prime}}{|\gamma_{\varepsilon}^{\prime}|}\bigg{)}\bigg{|}^{2}\,{\operatorname{d}}t=\int_{t_{-}}^{t_{+}}\bigg{|}\frac{\gamma_{\varepsilon}^{\prime\prime}}{|\gamma_{\varepsilon}^{\prime}|^{2}}-\gamma_{\varepsilon}^{\prime}\frac{\langle\gamma_{\varepsilon}^{\prime\prime},\gamma_{\varepsilon}^{\prime}\rangle}{|\gamma_{\varepsilon}^{\prime}|^{4}}\bigg{|}^{2}\,{\operatorname{d}}t
=∫t−t+|γε′′|γε′|2|2​d⁡t+O​(ε2).\displaystyle=\int_{t_{-}}^{t_{+}}\bigg{|}\frac{\gamma_{\varepsilon}^{\prime\prime}}{|\gamma_{\varepsilon}^{\prime}|^{2}}\bigg{|}^{2}\,{\operatorname{d}}t+O(\varepsilon^{2}).

Again, in view of (4.46), it follows that

∫t−t+\displaystyle\int_{t_{-}}^{t_{+}} |γε′′|γε′|2|2​d⁡t=∫t−t+|γ′′+ε​v′′|γε′|2|2​d⁡t\displaystyle\bigg{|}\frac{\gamma_{\varepsilon}^{\prime\prime}}{|\gamma_{\varepsilon}^{\prime}|^{2}}\bigg{|}^{2}\,{\operatorname{d}}t=\int_{t_{-}}^{t_{+}}\bigg{|}\frac{\gamma^{\prime\prime}+\varepsilon v^{\prime\prime}}{|\gamma_{\varepsilon}^{\prime}|^{2}}\bigg{|}^{2}\,{\operatorname{d}}t
=∫t−t+(⟨γ′′+ε​v′′,γ′′+ε​v′′⟩)​(1−4​ε​⟨γ′,v′⟩+O​(ε3/2))​d⁡t+ higher order terms\displaystyle=\int_{t_{-}}^{t_{+}}(\langle\gamma^{\prime\prime}+\varepsilon v^{\prime\prime},\gamma^{\prime\prime}+\varepsilon v^{\prime\prime}\rangle)(1-4\varepsilon\langle\gamma^{\prime},v^{\prime}\rangle+O(\varepsilon^{3/2}))\,{\operatorname{d}}t+\text{ higher order terms }
=∫t−t+(|γ′′|2+2​ε​⟨γ′′,v′′⟩+ε2​|v′′|)​(1−4​ε​⟨γ′,v′⟩+O​(ε3/2))​d⁡t+ higher order terms\displaystyle=\int_{t_{-}}^{t_{+}}(|\gamma^{\prime\prime}|^{2}+2\varepsilon\langle\gamma^{\prime\prime},v^{\prime\prime}\rangle+\varepsilon^{2}|v^{\prime\prime}|)(1-4\varepsilon\langle\gamma^{\prime},v^{\prime}\rangle+O(\varepsilon^{3/2}))\,{\operatorname{d}}t+\text{ higher order terms }
≤(1+4​ε​‖v′‖L∞)​∫t−t+|γ′′|2​d⁡t+2​ε​‖v′′‖L∞​∫t−t+|γ′′|​d⁡t+O​(ε3/2)\displaystyle\leq(1+4\varepsilon\|v^{\prime}\|_{L^{\infty}})\int_{t_{-}}^{t_{+}}|\gamma^{\prime\prime}|^{2}\,{\operatorname{d}}t+2\varepsilon\|v^{\prime\prime}\|_{L^{\infty}}\int_{t_{-}}^{t_{+}}|\gamma^{\prime\prime}|\,{\operatorname{d}}t+O(\varepsilon^{3/2})
≤(1+4​ε​‖v′‖L∞)​∫t−t+|γ′′|2​d⁡t+2​ε​‖v′′‖L∞​(ℋ1​(∂Ω)​∫t−t+|γ′′|2​d⁡t)1/2+O​(ε3/2)\displaystyle\leq(1+4\varepsilon\|v^{\prime}\|_{L^{\infty}})\int_{t_{-}}^{t_{+}}|\gamma^{\prime\prime}|^{2}\,{\operatorname{d}}t+2\varepsilon\|v^{\prime\prime}\|_{L^{\infty}}\bigg{(}\mathcal{H}^{1}(\partial\Omega)\int_{t_{-}}^{t_{+}}|\gamma^{\prime\prime}|^{2}\,{\operatorname{d}}t\bigg{)}^{1/2}+O(\varepsilon^{3/2})
≤∫t−t+|γ′′|2​d⁡t+4​ε​‖v′‖L∞​Ep,λ​(Ω)/λ+2​ε​‖v′′‖L∞​ℋ1​(∂Ω)​Ep,λ​(Ω)/λ+O​(ε3/2).\displaystyle\leq\int_{t_{-}}^{t_{+}}|\gamma^{\prime\prime}|^{2}\,{\operatorname{d}}t+4\varepsilon\|v^{\prime}\|_{L^{\infty}}E_{p,\lambda}(\Omega)/\lambda+2\varepsilon\|v^{\prime\prime}\|_{L^{\infty}}\sqrt{\mathcal{H}^{1}(\partial\Omega)E_{p,\lambda}(\Omega)/\lambda}+O(\varepsilon^{3/2}). (4.49)

Note that

4​‖v′‖L∞​Ep,λ​(Ω)/λ\displaystyle 4\|v^{\prime}\|_{L^{\infty}}E_{p,\lambda}(\Omega)/\lambda +2​‖v′′‖L∞​ℋ1​(∂Ω)​Ep,λ​(Ω)/λ\displaystyle+2\|v^{\prime\prime}\|_{L^{\infty}}\sqrt{\mathcal{H}^{1}(\partial\Omega)E_{p,\lambda}(\Omega)/\lambda}
≤32​(λ−1+π)2+32​2​C1​π​(λ−1+π)5/2=C2\displaystyle\leq 32(\lambda^{-1}+\pi)^{2}+32\sqrt{2C_{1}\pi}(\lambda^{-1}+\pi)^{5/2}=C_{2}

in view of (1.6), (2.17), (4.31), (4.32), and Lemma A.1. Hence (4.38) follows from (4.49). ∎

5 Conclusion

In this paper we investigated the minimization problem for the average distance functional defined for a two-dimensional domain with respect to its boundary, subject to a penalty proportional to the Euler elastica of the boundary. We proved the existence and C1,1C^{1,1}-regularity of minimizers, mainly relying on the method of contradictions by constructing suitable competitors. Echoing the large amount of existing studies that have exclusively focused on either the 1D average distance problem or the 2D Willmore energy question, by considering variational problems associated with combined energy functional, this study enriches and deepens our understanding of penalized average distance problem. Questions on the exact shape of a minimizer are still open and worth investigating in future. Limiting behaviors of the minimizers, property scaled with respect to λ\lambda, as λ→0\lambda\to 0 and λ→∞\lambda\to\infty may also shed light to this class of free boundary problems.


Acknowledgement The authors would like to thanks the referees for their careful reading and for their valuable suggestions to improve the quality of the manuscript.


Appendix A

Here we collect some results about convex sets, convergence in 𝒜\mathcal{A}, and their effect on geometric quantities, such as perimeter, diameter, etc.. One elementary yet crucial observation is that, given a two-dimensional convex set Ω∈𝒜\Omega\in\mathcal{A}, then every point x∈𝒜x\in\mathcal{A} has a set U⊆ΩU\subseteq\Omega of positive area containing xx.

Lemma A.1.

[26, p. 1] Let n≥2n\geq 2 and let A,B⊂ℝnA,B\subset\mathbb{R}^{n} be two convex bodies (i.e., compact convex sets with non-empty interior). If A⊂BA\subset B, then the monotonicity of perimeters holds, i.e.

ℋn−1​(∂A)≤ℋn−1​(∂B).\displaystyle\mathcal{H}^{n-1}(\partial A)\leq\mathcal{H}^{n-1}(\partial B). (A.1)

As a consequence, since any set with diameter dd is contained in a ball of diameter dd, we have

ℋ1​(∂Ω)≤π​diam⁡(Ω),for all ​Ω∈𝒜.\mathcal{H}^{1}(\partial\Omega)\leq\pi\operatorname{{\operatorname{diam}}}(\Omega),\qquad\text{for all }\Omega\in\mathcal{A}.
Lemma A.2.

Consider a sequence Ωn⊆𝒜\Omega_{n}\subseteq\mathcal{A}, converging to Ω∈𝒜\Omega\in\mathcal{A} in the topology of 𝒜\mathcal{A}, such that ⋃nΩn⊆K\bigcup_{n}\Omega_{n}\subseteq K for some compact set KK,. Then diam⁡(Ωn)→diam⁡(Ω)\operatorname{{\operatorname{diam}}}(\Omega_{n})\to\operatorname{{\operatorname{diam}}}(\Omega).

Proof.

Consider a sequence Ωn⊆𝒜\Omega_{n}\subseteq\mathcal{A}, converging to Ω\Omega in the topology of 𝒜\mathcal{A}. As Ωn\Omega_{n} are compact, there exist xn,yn∈Ωnx_{n},y_{n}\in\Omega_{n} such that |xn−yn|=diam⁡(Ωn)|x_{n}-y_{n}|=\operatorname{{\operatorname{diam}}}(\Omega_{n}). By our assumption that Ωn⊆𝒜\Omega_{n}\subseteq\mathcal{A} are all contained in a given compact set KK, we have, up to a subsequence, xn→xx_{n}\to x, yn→yy_{n}\to y for some x,y∈Ωx,y\in\Omega. Thus it is clear that

diam⁡(Ωn)=|xn−yn|→|x−y|≤diam⁡(Ω).\operatorname{{\operatorname{diam}}}(\Omega_{n})=|x_{n}-y_{n}|\to|x-y|\leq\operatorname{{\operatorname{diam}}}(\Omega).

We need to exclude the strict inequality case. This is achieved by a contradiction argument: assume the opposite, i.e. there exist v,w∈Ωv,w\in\Omega such that |v−w|>|x−y||v-w|>|x-y|. Then, we claim that there exist sequences vn,wnv_{n},w_{n} of points in Ωn\Omega_{n} such that, up to a subsequence, vn→vv_{n}\to v, wn→ww_{n}\to w. This, because of the opposite, would leave the existence of some set U⊆ΩU\subseteq\Omega of positive area, containing either vv or ww, such that there are no sequence of points in Ωn\Omega_{n} that enter into UU. This contradicts the fact that Ωn\Omega_{n} is converging to Ω\Omega in the topology of 𝒜\mathcal{A}. The proof is thus complete. ∎

Lemma A.3.

Given convex sets Ωε,Ω\Omega_{\varepsilon},\Omega such that dℋ​(∂Ωε,∂Ω)≤δd_{\mathcal{H}}(\partial\Omega_{\varepsilon},\partial\Omega)\leq\delta, it holds

ℋ2​(Ωε\Ω)≤2​δ​ℋ1​(∂Ωε).\displaystyle\mathcal{H}^{2}(\Omega_{\varepsilon}\backslash\Omega)\leq 2\delta\mathcal{H}^{1}(\partial\Omega_{\varepsilon}). (A.2)
Proof.

Clearly, Ωε\Ω\Omega_{\varepsilon}\backslash\Omega is entirely contained in

{x∈Ωε:dist⁡(x,Ωε)≤δ},\{x\in\Omega_{\varepsilon}:\operatorname{dist}(x,\Omega_{\varepsilon})\leq\delta\},

i.e. the part of the tubular neighborhood of ∂Ωε\partial\Omega_{\varepsilon} with thickness δ\delta that lies inside Ωε\Omega_{\varepsilon}.

We now use an approximation argument: we approximate ∂Ωε\partial\Omega_{\varepsilon} with convex polygons Pn⊆ΩεP_{n}\subseteq\Omega_{\varepsilon}, e.g. by choosing nn point x1,n,⋯,xn,n∈∂Ωεx_{1,n},\cdots,x_{n,n}\in\partial\Omega_{\varepsilon} such that supi|xi+1,n−xi,n|≤2​ℋ1​(∂Ωε)/n\sup_{i}|x_{i+1,n}-x_{i,n}|\leq 2\mathcal{H}^{1}(\partial\Omega_{\varepsilon})/n, and then connecting xi+1,nx_{i+1,n} to xi,nx_{i,n} with line segments.

Note that the area of the difference is continuous with respect to such an approximation, i.e. ℋ2​(Pn\Ω)↗ℋ2​(Ωε\Ω)\mathcal{H}^{2}(P_{n}\backslash\Omega)\nearrow\mathcal{H}^{2}(\Omega_{\varepsilon}\backslash\Omega). It is then a straightforward computation to check that

ℋ2​({x∈Pn:dist⁡(x,Pn)≤δ})≤2​δ​ℋ1​(∂Pn),\mathcal{H}^{2}(\{x\in P_{n}:\operatorname{dist}(x,P_{n})\leq\delta\})\leq 2\delta\mathcal{H}^{1}(\partial P_{n}),

for all sufficiently large nn. ∎

References

  • [1] Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. The Clarendon Press, Oxford University Press, New York, 2000.
  • [2] Buttazzo, G., Mainini, E., Stepanov, E.: Stationary configurations for the average distance functional and related problems, Control Cybernet., 38, 1107-1130, 2009.
  • [3] Buttazzo, G., Oudet, E., Stepanov, E.: Optimal transportation problems with free Dirichlet regions, in: Variational methods for discontinuous structures, in: Progr. Nonlinear Differential Equations Appl., Birkhäuser, Basel, 51, 41-65, 2002.
  • [4] Buttazzo, G., Pratelli, A., Solimini, S., Stepanov, E.: Optimal urban networks via mass transportation, Lecture Notes in Mathematics, Springer-Verlag, Berlin, 2009.
  • [5] Buttazzo, G., Pratelli, A., Stepanov, E.: Optimal pricing policies for public transportation networks, SIAM J. Optim., 16, 826-853, 2006.
  • [6] Buttazzo, G., Santambrogio, F.: A model for the optimal planning of an urban area, SIAM J. Math. Anal., 37, 514-530, 2005.
  • [7] Buttazzo, G., Santambrogio, F.: A mass transportation model for the optimal planning of an urban region, SIAM Rev., 51, 593-610, 2009.
  • [8] Buttazzo, G., Stepanov, E.: Optimal transportation networks as free Dirichlet regions for the Monge-Kantorovich problem, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5), 2(4), 631-678, 2003.
  • [9] Buttazzo, G., Stepanov, E.: Minimization problems for average distance functionals, in: Calculus of variations: topics from the mathematical heritage of E. De Giorgi, vol. 14 of Quad. Mat., Dept. Math., Seconda Univ. Napoli, Caserta, 48-83, 2004.
  • [10] Carmo, M. P. do: Differential Geometry of Curves and Surfaces, Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1976.
  • [11] Du, Q., Faber, V., Gunzburger, M.: Centroidal Voronoi tessellations: Applications and algorithms. SIAM review, 41, 637–676, 1999.
  • [12] Du, Q., Gunzburger, M., Ju, L.: Advances in studies and applications of centroidal Voronoi tessellations. Numerical Mathematics: Theory, Methods and Applications, 3, 119-142, 2010.
  • [13] Du, Q., Liu, C., Ryham, R., Wang, X.: A phase field formulation of the Willmore problem, Nonlinearity, 18, 1249-1267, 2005.
  • [14] Figalli, A., Fusco, N., Maggi, F., Millot, V., Morini, M., Isoperimetry and Stability Properties of Balls with Respect to Nonlocal Energies, Commun. Math. Phys., 336, 441-507, 2015.
  • [15] Giusti, E.: Minimal Surfaces and Functions of Bounded Variation. Monographs in Mathematics, 80, Basel-Boston-Stuttgar, 1984.
  • [16] Goldman, M., Novaga, M., Röger, M., Quantitative estimates for bending energies and applications to non-local variational problems, Proc. R. Soc. Edinb. A, 150-1, pp. 131-169, 2020.
  • [17] Goldman, M., Novaga, M., Ruffini, B., On minimizers of an isoperimetric problem with long-range interactions under a convexity constraint, Anal. PDE, 11-5, pp. 113-1142, 2018.
  • [18] Helfrich, W.: Elastic properties of lipid bilayers: theory and possible experiments, Zeitschrift für Naturforschung. Teil C: Biochemie, Biophysik, Biologie, Virologie, 28, 693-703, 1973.
  • [19] Lemenant, A.: A presentation of the average distance minimizing problem, Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI), 390, 117-146, 2011.
  • [20] Lemenant, A., Mainini, E.: On convex sets that minimize the average distance, ESAIM Control Optim. Calc. Var., 18, 1049-1072, 2012.
  • [21] Muratov, C., Knüpfer, H., On an Isoperimetric Problem with a Competing Nonlocal Term II: The General Case, Commun. Pure Appl. Math., 67-12, pp. 1974-1994, 2014.
  • [22] Paolini, E., Stepanov, E.: Qualitative properties of maximum distance minimizers and average distance minimizers in ℝn{\mathbb{R}}^{n}, J. Math. Sci. (N.Y.), 122 (3), 3290-3309, 2004.
  • [23] Royden, H., Fitzpatrick, P.: Real Analysis, Fourth Edition, Prentice Hall, 2010.
  • [24] Santambrogio, F., Tilli, P.: Blow-up of optimal sets in the irrigation problem, J. Geom. Anal., 15, 343-362, 2005.
  • [25] Slepčev, D.: Counterexample to regularity in average-distance problem, Ann. Inst. H. Poincaré Anal. Non Linéaire, 31,169-184, 2014.
  • [26] Stefani, G.: On the monotonicity of perimeter of convex bodies, J. Convex Anal., 25(1), 093-102, 2018.
  • [27] Tilli, P.: Some explicit examples of minimizers for the irrigation problem, J. Convex Anal., 17, 583-595, 2010.
  • [28] Wijsman, R. A.: Convergence of Sequences of Convex Sets, Cones and Functions. II, Trans. Amer. Math. Soc., 123 (1), 32-45, 1966.