The charge and mass symmetry breaking in the system
Abstract
In the framework of the Faddeev equations in configuration space, we investigate the (1460) meson as a resonant state of the kaonic system. We perform calculations for the particle configurations and within two models: the model, in which all three particles are distinguishable, and the model when two particles are identical. The models differ in their treatment of the kaon mass difference and the attractive Coulomb force between the pair. We found that the Coulomb shift adds over 1 MeV to the three-body binding energy. The expected correction to the binding energy due to mass redistribution from to is found to be negligible, up to a maximum of 6% of the relative mass correction. At the same time, the symmetry of the wave function is distorted depending on the mass ratio value. We found that the repulsive interaction plays essential role in the binding energy of the system and report the mass of 1461.8 or 1464.1 MeV for the neutral (1460) and 1466.5 or 1468.8 MeV for the charged (1460) resonances, respectively, depending on the parameter sets for and interactions.
I Introduction
Few-body physics has received interest for decades. Since 1961, when the Faddeev equations Fad in the momentum representation were formulated and a few years later the Faddeev-Noyes equations in configuration space were suggested Noyes1968 , special attention has been given to three-body systems constituted by nucleons, mesons, two nucleons and a meson, two mesons and a nucleon, quarks, and three-particle cluster systems. At low energies, the general approach for solving the three-body problem is based on the use of methods for studying the dynamics of three particles in discrete and continuum spectra. Among the most powerful approaches are the method of Faddeev equations in momentum Fad ; Fad1 or coordinate Noyes1968 ; Noyes1969 ; Gignoux1974 ; FM spaces. However, the method of hyperspherical harmonics, the variational method in the harmonic-oscillator basis, and the variational method complemented with the use of explicitly correlated Gaussian basis functions has been successfully employed for the solution of a few-body problem in atomic, nuclear, high energy physics, and even in condensed matter physics RKez2019 .
Three-body systems can be composed of three identical particles ( model), two identical and the third one ( model), and three non-identical particles ( model). The , , and baryons are examples of the quantum system with three and two identical quarks, while 3 (cluster model for 12C), (3He), and (3H) nucleon systems are composed of three and two identical particles FSV19 , respectively. One can also have systems with a meson and two baryons or two mesons and a baryon, such as kaonic clusters , , , and , which are considered as systems with two identical or three non-identical particle, depending on the configuration of the particles or theoretical approach for the description of kaonic clusters. When two identical particles are fermions or bosons the wave functions of the three-body kaonic clusters are antisymmetric or symmetric, correspondingly, with respect to the two identical particles exchange.
The kaonic clusters , , and were intensively studied in the framework of the Faddeev equations in momentum and coordinate representation Ikeda2007A ; Shevchenko2007A ; Ikeda2007 ; Shevchenko2007B ; Ikeda2009 ; Ikeda2010 ; Torres2010 ; 5 ; K2015 ; FV ; FVK20 . The Faddeev equations were used to study four-body kaonic clusters (see review RKezNNNK ). It is a very challenging task to solve the Faddeev equations exactly and usually introduce some reasonable approximations of the Faddeev equations, such as the use of separable potentials, energy-independent kernels, on-shell two-body scattering amplitudes, the Faddeev-type Alt-Grassberger-Sandhas equations’ AGS . In the framework of the fixed-center approximation for the Faddeev equations, dynamically generated three-body resonances formed via meson-meson and meson-baryon interactions were studied (see 13 ; 12 ; 922 ; Oset2020 and references herein).
The (1460) pseudoscalar was a subject of interest since the middle of the seventieths. In 1976, the first high statistics study of the process was carried out at SLAC, using a 13 GeV incident beam Brandenburg . The partial-wave analysis of the system in this reaction led to the report of the first evidence for a strangeness-one pseudoscalar meson with a mass of 1400 MeV and a width of 250 MeV. A few years later the ACCORD collaboration DAUM1981 using SLAC beam at 63 GeV investigated the diffractive process and the data sufficient for partial-wave analysis extending up to a mass of 2.1 GeV were collected. The data analysis confirmed the existence of a broad resonance with a mass of 1460 MeV. However, even the 2018 PDG PDG2018 did not list the (1460) as an ”established particle”. In the most recent studies of the resonance structure in decays using collision, data collected at 7 and 8 TeV with the LHCb experiment LHCb , and the precise measurements of the (1260), (1270) and (1460) resonances are made. Within a model-independent partial-wave analysis performed for the (1460) resonance, it is found that the mass is roughly consistent with previous studies Brandenburg ; DAUM1981 . They showed the evidence for the K(1460) in and channels and confirmed the resonant nature of the (1460) with the mass 1482.403.5815.22 MeV and width 335.606.208.65 MeV. Thus, the (1460) is listed in the 2020 PDG PDG2020 and in the most recent PDG PDG2022 .
Several theoretical models Izgur85 ; Longacre90 ; Albaladejo ; Torres2011 ; RKSh.Ts2014 ; KezerasVail2015 ; Parganlija2017 ; SHY19 ; KezerasPRD2020 ; Torrez2021 ; Meisner2022 considered the dynamic generation of the pseudoscalar (1460) resonance as three mesons: . The first time the resonance (1460) was considered as a excitation of the kaon in a unified quark model in Ref. Izgur85 and the mass 1450 MeV for this resonance was obtained. In Ref. Longacre90 within the isobar assumption shown that the final-state interaction leads to the formation of an exotic () threshold enhancement with a mass around 1500 MeV and a width of approximately 200 MeV. Assuming isospin symmetry in the effective kaon-kaon interactions that are attractive for the pair and repulsive for the pair, in Ref. Torres2011 the (1460) pseudoscalar resonance was studied as the system. The authors have performed the investigation of the system using two methods: the single-channel variational approach in the framework of the model KanadaJido ; JidoKanada , and the Faddeev equations in momentum representation. In the latter case, the authors determined the two-body on-shell matrices for and interactions using the Bethe-Salpeter equation in a couple-channel approach and considered the on-shell factorization method. Dynamic generation of the pseudoscalar (1460) resonance was considered in Ref. Albaladejo , by studying interactions between the and scalar resonances and the lightest pseudoscalar mesons. In Torres2011 have included and channels. The same channels have been considered in an effective way in Ref. Albaladejo . In Ref. RKSh.Ts2014 using the single-channel description of the system in the framework of the hyperspherical harmonics method was obtained a reasonable agreement with experimental data for the mass of the (1460) resonance. Authors Parganlija2017 , based on the extended version of the linear sigma model GellMann60 ; Gasiorowicz69 ; Ko94 , discussed to what extent it is possible to interpret the pseudoscalar meson () as excited states. In a framework of the Faddeev equations in configuration space using the model system was investigated in Ref. KezerasPRD2020 . In Ref. SHY19 the system was considered based on the coupled-channel complex-scaling method by introducing three channels , , and . The resonance energy and width were determined using two-body potentials that fit two-body scattering properties. The model potentials having the form of one-range Gaussians were proposed based on the experimental information related to and resonances. In this model, the interaction depends on the pair isospin. In particular, the isospin triplet interaction is essentially weaker than the isospin singlet interaction in the channel . The most recently in Ref. Meisner2022 the three-body system in channel is studied in a formalism that satisfies two-body and three-body unitarity using the isobar approach, where the two-body interaction is parametrised via the and poles.
There are the following physical particle configurations of the system: , , , . In these configurations, there are particles and antiparticles, that have different masses, isospins, and electric charges. The and configurations can be considered in the framework of Faddeev equations as an model with two identical particles. The configurations and present the system with three non-identical particles due to the different masses and isospins of mesons. The latter two configurations must be considered within the Faddeev formalism as the system. Theoretical approaches for these systems utilizing average masses of particles can lead to the loss of important information about the nature of the systems. In particular, the formalization of the kaons as identical particles allows us to discuss an exchange effect as was discussed for the system YA07 .
We focus on the particle configurations and for the bound three-body system. Previously, the kaonic resonance is considered within the model using average kaon masses and disregarding the Coulomb force. Considering the Coulomb potential or difference of the masses of kaons, we propose the model for the description of the and particle configurations rigorously within the Faddeev equation in configuration space. One of the objectives of this paper is to compare the binding energies of the system obtained within the and models using the same interaction potentials. This allows us to draw a conclusion on the model’s validity. We show that the proper averaging procedure within the model leads to the model with a negligible correction of the binding energy - up to a maximum of 6% of the relative mass correction. For the higher relative mass correction, the model is unacceptable, and one must use the model.
In this paper we focus on the single-channel description of the system in the absence of the and inelastic channels. It is worth noticing that despite its simplicity, the single-channel model can reproduce the mass of the resonance. The smallness of the kinetic energy of the kaons in a bound system in comparison with the kaon mass, makes possible the study of the single channel using a non-relativistic potential model. While the single-channel and non-relativistic potential model description clearly do not fully represent reality, it still allows us to address the issues related to the charge and mass symmetry breaking in the system and the validity of the model. In the and models, we are using -wave and two-body potentials Torres2011 and in the model experimental kaon masses, as the inputs.
This paper is organized as follows. In Secs. II and III we present the Faddeev equations in configuration space for and models and their application for the and configurations. Averaged mass and potential approaches which lead to the reduction of the model to the one are given in Secs. IV and V, respectively. Results of numerical calculations for and models are presented in Sec. VI. The concluding remarks follow in Sec. VII.
II Faddeev equations in configuration space
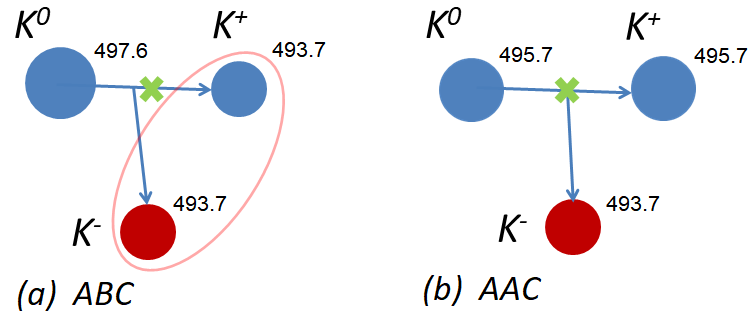
The three-body problem can be solved in the framework of the Schrödinger equation or using the Faddeev approach in the momentum Fad ; Fad1 or configuration Noyes1968 ; FM ; K86 spaces. The Faddeev equations in the configuration space have different forms depending on the type of particles and can be written for: i. three non-identical particles; ii. three particles when two are identical; iii. three identical particles. The identical particles have the same masses and quantum numbers. In the particle configurations and the and , and and have equal masses, respectively. However, these particle configurations cannot be considered in the framework of the model because and are antiparticles of and , respectively, hence, are non-identical particles. Moreover, in the particle configuration the and are a particle and antiparticle, respectively, which have the same masses but different charges. The non-identical particles are un-exchangeable bosons. Thus, the and particle configurations each consist of three non-identical particles and must be treated within the ABC model.
II.1 Faddeev equations for the ABC model
In the Faddeev method in configuration space, alternatively, to the finding the wave function of the three-body system using the Schrödinger equation, the total wave function is decomposed into three components Noyes1968 ; FM ; K86 :
| (1) |
Each Faddeev component corresponds to a separation of particles into configurations , . The Faddeev components are related to their own set of the Jacobi coordinates and , . There are three sets of Jacobi coordinates. The total wave function is presented by the coordinates of one of the sets shown in Eq. (1) for . The mass-scaled Jacobi coordinates and are expressed via particle coordinates and masses in the following form:
| (2) |
In Eq. (1), each component depends on the corresponding coordinate set which is expressed in terms of the chosen set of mass-scaled Jacobi coordinates. The orthogonal transformation between three different sets of the Jacobi coordinates has the form:
| (3) |
where
Here, is the total mass of the system. The components , , and satisfy the Faddeev equations in the coordinate representation written in the form FM :
| (4) |
Here, is the kinetic energy operator with and is the interaction potential between the pair of particles , . In the system of equations (4), the independent variables are and and can be chosen to be and , where is or , or . After that, the remaining coordinates are expressed by the chosen coordinates according to the Jacobi coordinates transformation (3).
II.2 Faddeev equations for the AAC model
The system of Eqs. (4) can be reduced to a simpler form for a case of two identical particles when a particle in the model is replaced by a particle . In this case, for the Bose particles, the total wave function of the system is decomposed into the sum of the Faddeev components and corresponding to the and types of rearrangements:
III The model versus for and particle configurations
We study the system using the available -wave effective phenomenological and potentials Torres2011 and considering the and kaon’s experimental masses and charges based on Ref. PDG2022 . This leads to the consideration of the resonance according to the following neutral or charged particle configurations: , , , . For the description of the system within the and models, we focus, as on the representative, on the following two particle configurations: and . The configuration includes the Coulomb interaction and and have the same masses but are non-identical that make three particles distinguishable. The configuration does not include the Coulomb interaction and two particles and have the same masses but are non-identical. Therefore, the exact treatment of the and particle configurations must be done within the model. We consider -wave pair potentials. Hence, the bound state problem for the system should be formulated using the Faddeev equations in the -wave approach K2015 . In the -wave approach for the particle configuration Eqs. (4) reads:
| (6) |
In Eqs. (6) , and are the -wave and potentials, while , and are the components of the Coulomb potential related to the electrostatic interaction depending on the mass-scaled Jacobi coordinate of the corresponding Faddeev components , , and . A consideration of the Coulomb interaction in the framework of the Faddeev formalism is a challenging problem Mer80 . Following FSV19 , we consider the Coulomb interaction included on the left-hand side of the Faddeev equations (6) as a perturbation.
The Coulomb attraction in the violates the symmetry and makes three kaons distinguishable. If one neglects the Coulomb attraction in the in Eqs. (6), even the equality of and masses does not allow to treat the configuration in the framework of the model. However, if one considers and as identical particles with masses equal to the average of their masses and neglects the Coulomb attraction, can be considered within the model. A schematic for the is presented in Fig. 1 when it is treated as and models. Within the model the Faddeev equations (5) for two identical particles in the three-body system for the -wave interparticle interactions can be written in the following form:
| (7) |
In Eqs. (7) the and are the -wave Faddeev components of the wave function, and the exchange operator acts on the particles’ coordinates only.
The particle configuration also can be considered within the model, if one considers and as identical particles with masses equal to the average of their masses. In this case, Eqs. (7) describe configuration with only difference that interaction should be replaced by the potential.
IV The mass difference of kaons: from the to model
In the previous studies system was considered within the model. Such consideration is valid if we ignore the difference between and masses and the Coulomb interaction between charged kaons. As the first step for a realistic consideration, we are using the experimental kaon masses instead of the average kaon mass used in the model. After that, we consider that the pair is the kaonic pair and antikaon is considered as the particle . Within this model, the masses of and kaons are varied around the average value of the kaon mass . These variations have different signs for the and kaons. In other words, we consider the model with variable masses of the and kaons but keeping the sum of masses of the kaon pair constant. This approach allows us to understand how the binding energy of the is sensitive to the variation of the and masses.
Consider the particles in the model, where is the antiparticle, have masses , , and , and can be numbered manually as
| (8) |
where is small and kaons are particles 1 and 2 and the antikaon is particle 3. Following Friar at al. F90 , we write the kinetic energy operator in terms of the individual momenta of the particles in the center-of-mass as:
| (9) |
This expression follows from the Taylor series for the . In the first order perturbation theory, the correction for the energy can be presented as , where and
| (10) |
Here, the is the coordinate part of the wave function .
Within the model, , due to . In the model, this relation is approximately satisfied
| (11) |
The possible value for the is restricted so that . The linear approximation Eq. (9) is applicable when we consider only the first two terms of the Taylor series for the function near the point . The next quadratic terms of the expansion cannot be compensated similarly to Eq. (11) due to the alternating series of the Tailor expansion: , .
V Coulomb interaction: from the to model
Let us ignore the repulsive potential acting between the and kaons. Such truncation shifts the three-body energy to a fixed value. After that the equation for the Faddeev component in Eqs. (6) is eliminated. Also, we can neglect the Coulomb interaction and consider only the nuclear interaction between kaons and antikaon. The corresponding system of equations reads:
| (12) |
where, for simplicity, we denoted and . Assuming that the difference of the potentials and is small one can introduce the average potential
| (13) |
so that
| (14) |
and rewrite Eqs. (12) in the form
| (15) |
In the first order of the perturbation theory, by averaging Eqs. (15), one obtains
| (16) |
where and are the solutions of Eqs. (15) with the potential , when is omitted, that gives the energy of . Therefore, from (16) we obtain
| (17) |
For equal kaon masses the functions and are the same and, therefore, and . By adding the algebraic equations in (17), we obtain . In other words, in the first order of perturbation theory, the average potential gives .
Now let’s assume that masses of and are equal to their average mass. The Coulomb potential is a perturbation with respect to the strong kaon-kaon interaction. The Coulomb potential can be treated within the given above scheme. One can denote the Coulomb part of the potential as . The is proportional to the and () is proportional to the (). Here, the mass-scaled Jacobi coordinate corresponds to the channel and is expressed by coordinates and of the channel . The is the coordinate in the channel conjugated to the channel and is expressed via coordinates and of the channel (see Eq. (4)).
The average potential is . The defines the difference between the channels’ potentials and . One can repeat the procedure presented by Eqs. (16)-(17) and finally for the with the Coulomb interaction obtains the following equation that corresponds to the model:
| (18) |
where
| (19) |
and the masses of the kaons are equal to their average mass. The is the Coulomb charge parameter.
VI Numerical Results
VI.1 Interaction potentials
In the present work, we use the -wave effective potentials for and interactions from Ref. Torres2011 . The is an attractive interaction that makes the system bound, while the interaction is described by a repulsive potential. The and potentials are written in the form of one range Gaussian:
| (20) |
where and are the strength (depth) and the range of the potential, respectively. In calculations are used two model potentials A and B with the set of parameters listed in Table 1.
| Parameters of potential | ||||
| Set A ( fm) | Set B ( fm) | |||
| Interaction | (), MeV | (), MeV | (), MeV | (), MeV |
| 0 | 104 | 0 | 313 | |
VI.2 From the to model: Effects of kaons mass difference and Coulomb force
Within the theoretical formalism presented in the previous sections, we calculate the binding energies of the and and of the bound pairs. The three-particle energy , due to the kaon-antikaon interactions, but with the omitted interaction between two kaons, is another significant characteristic of the three-particle kaonic system. An analysis of the shows that the repulsive interaction plays essential role in the resonance energy.
The results of calculations of these energies for the and particle configurations in the and models are presented in Table 2.
The analysis of the results leads to the following conclusions:
i. the binding energies and of and calculated in the model, with the average kaon masses MeV, and model are the same. Thus, the difference of the kaon masses does not affect and : the mass distinguishability is not important for and energies when the Coulomb interaction is neglected. The difference of 2.5 MeV for and 2.3 MeV for is related to the parameter sets A and B for and interactions, respectively;
ii. the mass distinguishability has a small effect on the binding energy of pairs;
iii. the consideration of the Coulomb interaction in the framework of the model leads to an increase of the binding energy and the energy of the bound pair in the particle configuration for the parameter sets A and B for and interactions, respectively;
iv. the repulsive interaction plays an essential role in the binding energy of the system. The comparison of the and of and energies shows that contribution of the repulsive interaction decreases the three-particle binding energy by about and for the set of parameters A and B, respectively;
v. finally, the mass of neutral resonance in the () model is 1464.1 Mev and 1461.8 MeV for the parameter sets A and B for and interactions, respectively. The mass of the charged resonance in the () model is 1468.8 MeV and 1466.5 MeV for the parameter sets A and B for and interactions, respectively. Our results for the mass of neutral and charged (1460) resonance obtained within the model are in reasonable agreement with the reported experimental value of the (1460) mass PDG2022 .
Note, in contrast to the mass of the resonance, calculations of the width using the Faddeev equations for the model in momentum representation ( MeV) Torres2011 and configuration space ( MeV) KezerasPRD2020 , variational method ( MeV) Torres2011 , hyperspherical harmonics method ( MeV) RKSh.Ts2014 did not reproduce the quite sizeable experimental width, 335.606.208.65 MeV LHCb ; PDG2022 . In Ref. Longacre90 reported the width of approximately 200 MeV for the resonance and Albaladejo presented the estimation for the width of MeV for resonance. The study of the within the non-perturbative three–body dynamics did not calculate the width for this system.
We calculate the width follow KezerasPRD2020 using A and B sets for the potential parameters listed in Table 1. The comparison of the widths obtained in the and models shows that they are close enough with a negligible difference about 1 - 2 MeV: MeV and MeV for the potential with A and B parameter sets, respectively.
In this work we study the resonance considering only the channel . One could also have channels like and . These channels are included, in an effective way, in Albaladejo , using Faddeev equations in momentum space by Martinez Torres et al. Torres2011 , and employing the complex-scaling method Dote2015 in the semi-relativistic framework in Ref. SHY19 . While the formation of the resonance could be due to the channel mainly, the inclusion of other channels may have a relevant role in its mass and, more importantly, in its width. However, consideration of these channels in Torres2011 gives a significantly smaller width ( MeV) than our single-channel result. Resonance positions in three-channel and two-channel and calculations presented in SHY19 demonstrate that the coupling to the channel is significant to reproduce the large width of the resonance and the coupling to channel makes a large contribution to the mass of the resonance. However, the consideration of the coupled-channel and and variation of the interaction range and strength of the one-range Gaussian potentials did not reproduce the experimental width. In Ref. Parganlija2017 the channels , , and are quoted as “decaying channels”. These channels require two-body dynamics either beyond wave (to form or ) or well above 1 GeV (to form ), and these effects are not included in Albaladejo ; Torres2011 ; SHY19 . It is then natural that the width reported in those and present works is much smaller than the one quoted indicated in Brandenburg ; DAUM1981 ( MeV) or in the recent LHCb analysis LHCb ( MeV).
| model | ||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||
| model | ||||||||||||||||||||||||||||||||||||||||||||||||
| Resonance | System | Mass, MeV | Potentials | |||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||
VI.3 The mass-symmetry breaking in the pair: from the to model
Let us start with the bosonic model with two identical particles with the average mass of two kaons and violate the mass-symmetry of this model by changing the masses of two identical particles but keeping the total mass of the pair constant. Such mass redistribution leads to the transformation of the model with the symmetric wave function with respect to the exchange of particles to the model with a lack of this symmetry. Now, in the pair of ”identical” particles, we have the masses
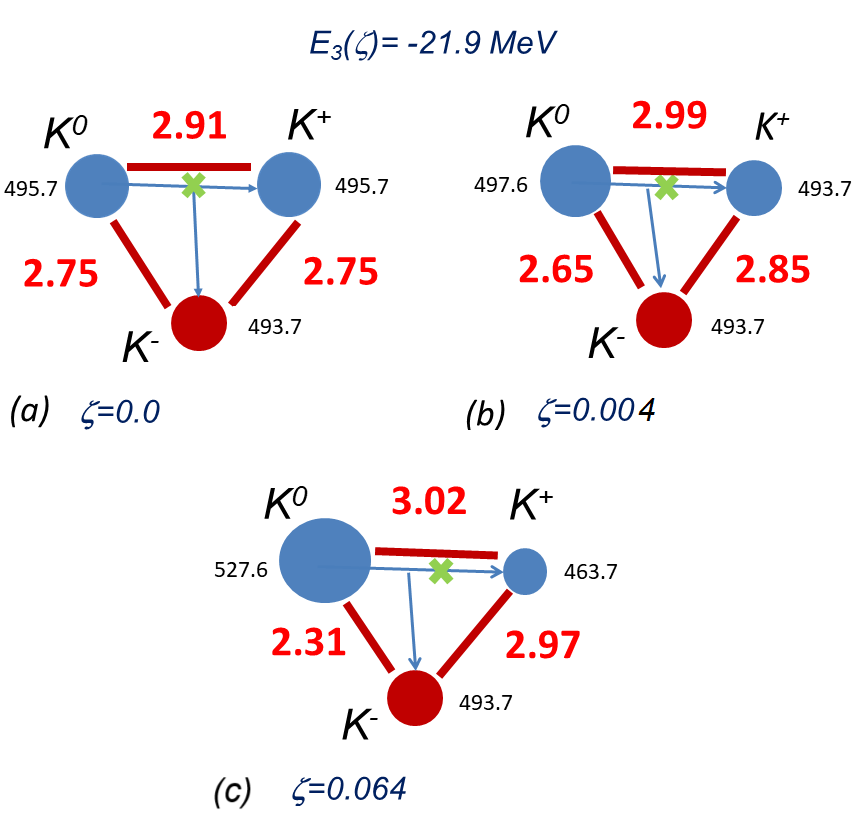
where the average mass of the pair and is a mass scaling parameter that can be varied. The total mass of this pair is constant: . The kaonic system with the mass and variable masses and , must be considered within the model. The cases when and correspond to the model with average masses of and kaons and the model that describes with the experimental masses of kaons, respectively.
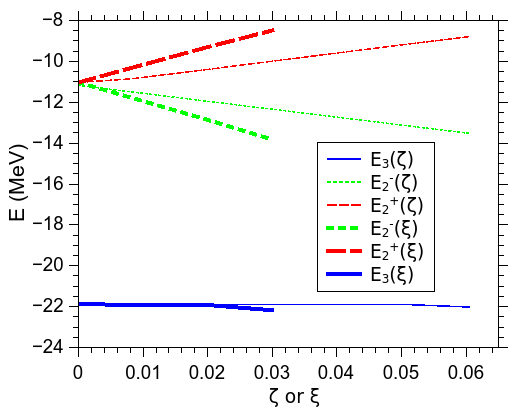
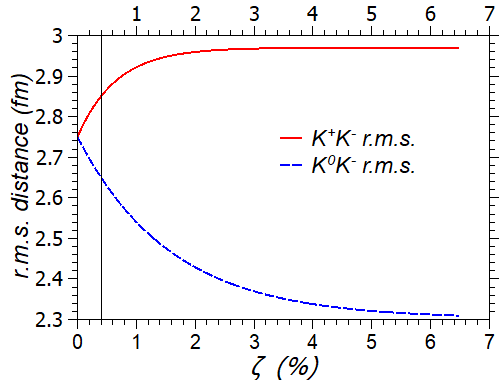
Results of calculations of the binding energy within the model with variable masses of two kaons and the energy of the bound and kaon pairs as functions of the mass scaling parameter are shown in Fig. 2. The total energy does not depend on the mass redistribution between and kaons up to 0.06. The later value shows when the limit of the approximation (11) is reached. However, the bound and kaon pairs energies are sensitive to the variation of the parameter . The and kaon pairs energies and , which correspond to the increase of the mass and the decrease of the mass from the average value to the experimental mass, increases and decreases, respectively, with the increase. Thus, the redistribution of the mass between two kaons violates the exchange symmetry of the wave function in the model and leads to the model that gives the same total energy as the model, but increases and decreases energies of the bound kaon pairs. The violation of the wave function symmetry from the symmetric with respect to the exchange of particles to a wave function without such symmetry should affect the average distance between kaons. To demonstrate that we calculated the root mean squared () distances between kaons. The latter is illustrated in Fig. 3, the left panel, by presenting the distances between kaon pairs for the particle configuration for the different values of . In the model and one gets the isosceles triangle. Consideration of experimental masses in the model leads to the different root mean squared distances between particles. In Fig. 3, the right panel, is shown the dependence of the distances on . One can conclude that the mass flow affects the distances between kaons up to . This effect is non-linear and tends to saturate.
According to Eq. (2) and Eq. (4), the mass-scaled coordinates in the model are and . These coordinates in the model are , , and have a -dependence. Thus, the dependence of pair potentials as a function of the coordinate in Eq. (4) is expressed as a -dependence.
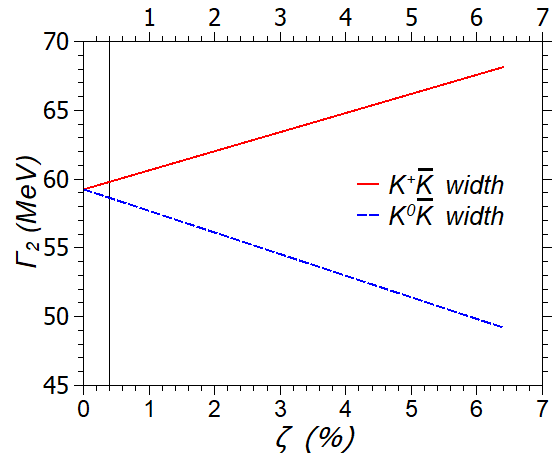
One would assume that three-body kinetic energy operator is affected by the mass scaling parameter . However, in the first order perturbation theory for , as we have shown in Section IV, the kinetic energy matrix element does not depend on . The binding energy is also a constant. This means the matrix element of the total potential energy does not changed with the increasing. Because the width is evaluated from the imaginary part of the complex potentials, the three-body width is also independent on the parameter and is the same in the and models. The two-body and subsystems do not have the compensation mechanism due to the absence of the third particle that has the three-body system as expressed by Eqs. (10)-(11). Two-body widths depend on the mass scaling parameter and repeat the dependence as depicted in Fig. 4. The widths of the and pairs are the same, MeV, in the model (). In the model, , the widths are MeV and MeV for the and , respectively, for the set of the parameters B.
VI.4 From the to model through asymmetry of and potentials
Above we considered the bosonic model and its transformation to the model due to changing the masses of two identical particles. However, the bosonic model can be also transformed to the model in the case when interactions in the and pairs are different. For example, in Ref. SHY19 to interpret the three-body resonance as K(1460) were used two-body potentials with the different strength and range parameters. In our consideration of the particle configuration the kaon-antikaon interaction we use the same strong interaction in the and pairs. However, interactions in the and pairs are different due to the Coulomb attraction between and . The latter means that even if one considers the average mass for and kaons, the configuration should be described within the model. Let us demonstrate this in general via a model where a strong interaction in the and pairs is different by introducing scaled potentials
In the last expressions is the average potential of the and pairs, is the potential scaling parameter and when . Within this model we calculate the binding energies of the and the bound pairs and by keeping the average potential constant. In Fig. 2 are shown dependencies of the binding energy of the and energies () and () of the and pairs, respectively, on the potential scaling factor . Results when correspond to the model, while the increment of leads to the model. The increase of leads to the increase or decrease of the two-body energies of the and pair, respectively. At the same time, the binding energy of the system remains unchanged up to a value of , as is demonstrated in Fig. 2 and can be seen from Eq. (17). A similar situation was demonstrated in the previous subsection when the mass scaling parameter increases up to the value of .
The Coulomb attraction acting in the single kaon-antikaon pair leads also to the model and increases three-body energy by 1.5 MeV and 1.3 MeV for the parameter sets A and B for and interactions, respectively. It can be noted that the averaging procedures presented in sections IV and V allow us to consider the Coulomb interaction in the model.
VII Conclusions
In the framework of the Faddeev equations in configuration space, we investigated the (1460) resonance dynamically generated via the system. We considered the system as the and particle configurations that are analyzed using and models. We demonstrated that the model can be reduced to the one, where the wave function is symmetric with respect to the exchange of identical particles. The reduction is possible by averaging the masses of the pair or averaging and potentials, if they are different.
It is shown that the repulsive interaction plays essential role in the binding energy of the system: contribution of the repulsive interaction decreases the three-particle binding energy by about 38% and 25% for the A and B parameter sets, respectively.
Our three-body non-relativistic single-channel model predicts a quasi-bound state for the system. The mass of neutral resonance calculated in the model for the particle configuration is 1464.1 MeV or 1461.8 MeV, while the mass of the charged resonance for the particle configuration is 1468.8 MeV or 1466.5 MeV. These values are obtained for the parameter sets A and B for and interactions, respectively. The results are in fair agreement with the experimental value of the (1460) mass, 1482.403.5815.22 MeV PDG2022 .
Due to the Coulomb attraction of three-body binding energy increases, and the energy shift is 1.5 and 1.3 MeV for the parameter sets A and B for and interactions, respectively. Let us note that within the model, consideration of the Coulomb attraction is also possible using the averaging procedure for the Coulomb potential. The binding energy of and calculated in the model with the average kaon masses and in the model with the experimental kaon masses are the same. Effectively, the model can reproduce the binding energy obtained in the model if the corresponding relative correction of masses is not larger than 6%. Thus, the small difference of the kaon masses does not affect the binding energy of the kaonic system when the Coulomb interaction is neglected.
An increase in the mass difference of the kaons leads to the mass-symmetry violation of the system with the same binding energy. However, when the relative mass correction exceeds 6% the binding energies calculated using the and models differ. It should be noted that this effect has not been reported before. The three-body kaonic system allows us to demonstrate this effect clearly. One can consider similar nuclear systems, for example, or , instead of the kaonic system but the effect will be small due to a small difference between the proton and neutron masses. We have found that mass correction does not change three-body energy, however, violates the exchange symmetry that affects the model wave function symmetry.
In the model, there is the exchange symmetry, related to the symmetric localization of identical particles. In contrast to the model, consideration of experimental masses in the model leads to the violation of this symmetry. This indicated by different root mean squared distances between kaons. The different distances between kaons are due to different kaon masses and/or potentials in the and models.
We considered the system using the single-channel description with effective -wave potentials. Some refinements can be done, such as using more realistic two-body potentials, including -wave components, and/or considering the coupled-channel approach. It is important to note that the choice of the model and assumptions made in our analysis can always have an impact on the results. Therefore, it is essential to carefully consider the limitations and uncertainties for description system relating to the mass and charge symmetry braking.
Acknowledgments
This work is supported by the National Science Foundation grant HRD-1345219 and DMR-1523617 awards Department of EnergyNational Nuclear Security Administration under Award Number NA0003979 DOD-ARO grant #W911NF-13-0165.
References
- (1) L. D. Faddeev, Scattering theory for a three-particle system. ZhETF 39, 1459 (1961); [Sov. Phys. JETP 12, 1014 (1961)].
- (2) H. P. Noyes and H. Fiedeldey, In: Three-Particle Scattering in Quantum Mechanics (Gillespie, J., Nutall, J., eds.), p. 195. New York, Benjamin, 1968.
- (3) L.D. Faddeev, Mathematical problems of the quantum theory of scattering for a system of three particles. Proc. Math. Inst. Acad. Sciences USSR 69, 1-122 (1963).
- (4) H. P. Noyes In: Three-Body Problem in Nuclear and Particle Physics (Proceedings of the 1st Int. Conf., Birmingham, 1969), (McKee, J. S. C., Rolph, P. M., eds.), p. 2. Amsterdam, North-Holland, 1970.
- (5) C. Gignoux, C., Laverne, and S. P. Merkuriev, Solution of the Three-Body Scattering Problem in Configuration Space, Phys. Rev. Lett. 33, 1350 (1974).
- (6) L.D. Faddeev and S.P. Merkuriev, Quantum Scattering Theory for Several Particle Systems (Kluwer Academic, Dordrecht, 1993) pp. 398.
- (7) R. Ya. Kezerashvili, Few-Body Systems in Condensed Matter Physics Few-Body Syst. 60, 52 (2019).
- (8) I. Filikhin , V. M. Suslov and B. Vlahovic, breakup within isospinless model, J. Phys. G: Nucl. Part. Phys. 46, 105103 (2019).
- (9) Y. Ikeda and T. Sato, Strange dibaryon and coupled channel equation. arXive:nucl-th/0701001 (2007).
- (10) N. V. Shevchenko, A. Gal and J. Mares, Phys. Rev. Lett. 98, 082301 (2007).
- (11) Y. Ikeda and T. Sato, Strange dibaryon and system. Phys. Rev. C 76, 035203 (2007).
- (12) N. V. Shevchenko, A. Gal, J. Mares and J. Revai, Phys. Rev. C 76, 044004 (2007).
- (13) Y. Ikeda and T. Sato, Resonance energy of the system. Phys. Rev. C 79, 035201 (2009).
- (14) Y. Ikeda, H. Kamano, and T. Sato, Energy dependence of interactions and resonance pole of strange dibaryons. Prog. Theor. Phys. 124, 533 (2010).
- (15) A. Martinez Torres and D. Jido, molecule state with and studied with a three-body calculation. Phys. Rev. C 82, 038202 (2010).
- (16) S. Maeda, Y. Akaishi and T. Yamazaki, Strong binding and shrinkage of single and double nuclear systems (K-pp, K-ppn, K-K-p and K-K-pp) predicted by Faddeev-Yakubovsky calculations, Proc. Jpn. Acad. Ser. B 89 (2013) 418; arXiv:1307.3957v3 [nucl-th]
- (17) R. Ya. Kezerashvili, S. M. Tsiklauri, I. Filikhin, V. M. Suslov and B. Vlahovic, Three-body calculations for the system within potential models. J. Phys. G: Nucl. Part. Phys. 43, 065104 (2016).
- (18) I. Filikhin and B. Vlahovic, Lower bound for quasi-bound state energy. Phys. Part. Nucl. 51, 979-987 (2020).
- (19) I. Filikhin and B. Vlahovic, and R. Ya. Kezerashvili, Particle representation for system. SciPost Phys. Proc. 3, 044 (2020).
- (20) R. Ya. Kezerashvili, S. M. Tsiklauri, and N. Zh. Takibayev, Search and research of and antikaonic clusters. Prog. Part. Nucl. Phys. 121, 103909 (2021).
- (21) E. O. Alt, P. Grassberger, and W. Sandhas, Reduction of the three - particle collision problem to multichannel two - particle Lippmann-Schwinger equations. Nucl. Phys. B 2, 167 (1967).
- (22) E. Oset, A. Martinez Torres, K.P. Khemchandani, L. Roca, J. Yamagata, Two, three, many body systems involving mesons. Progress in Part. and Nucl. Phys. 67, 455 (2012).
- (23) A. Martinez Torres, K. P. Khemchandania, D. Jido, Y. Kanada-Eniyo, and E. Oset, Three-body hadron systems with strangeness. Nucl. Phys. A 914, 280-288 (2013).
- (24) J. M. Dias, V. R. Debastiani, L. Roca, S. Sakai, and E. Oset, Binding of the and systems. Phys. Rev. D 96, 094007 (2017).
- (25) A. Martínez Torres, K. P. Khemchandani, L. Roca, E. Oset, Few-body systems consisting of mesons. Few-Body Syst. 61, 35 (2020).
- (26) G. W. Brandenburg, et al., Evidence for a new strangeness-one pseudoscalar meson. Phys. Rev. Lett. 36, 1239 (1976).
- (27) C. Daum, et al., Diffractive production of strange mesons at 63 GeV. Nucl. Phys. B 187, 1 (1981).
- (28) M. Tanabashi et al., Particle Data Group 2018, Reviewe of particle physics. Phys. Rev. D 98, 030001 (2018).
- (29) LHCb collaboration, R. Aaij et al., Studies of the resonance structure in decays. Eur. Phys. J. C 78, 443 (2018).
- (30) P. A. Zyla et al. (Particle Data Group), The review of particle physics, Prog. Theor. Exp. Phys. 2020, 083C01 (2020).
- (31) R.L. Workman et al. (Particle Data Group), Review of particle physics, Prog. Theor. Exp. Phys. 2022, 083C01 (2022).
- (32) S. Godfrey and N. Isgur, Mesons in a relativized quark model with chromodynamics. Phys. Rev. D 32, 189 (1985).
- (33) R. S. Longacre, meson as a molecule. Phys. Rev. D 42, 874 (1990).
- (34) M. Albaladejo, J. A. Oller, and L. Roca, Dynamical generation of pseudoscalar resonances. Phys. Rev. D 82, 094019 (2010).
- (35) A. Martinez Torres, D. Jido, and Y. Kanada-En’yo, Theoretical study of the system and dynamical generation of the resonance. Phys. Rev. C 83, 065205 (2011).
- (36) R. Ya. Kezerashvili and Sh. M. Tsiklauri, Study of the system in hyperspherical formalism. EPJ Web Conf. 81, 02022 (2014).
- (37) R. Ya. Kezerashvili, S. M. Tsiklauri, and N. Zh. Takibayev, Lightest kaonic nuclear clusters. In Proceedings, 12th Conference on the Intersections of Particle and Nuclear Physics (CIPANP 2015): Vail, Colorado, USA, May 19-24, 2015 (2015) [arXiv:1510.00478].
- (38) D. Parganlija and F. Giacosa, Excited scalar and pseudoscalar mesons in the extended linear sigma model. Eur. Phys. J. C 77, 450 (2017).
- (39) S. Shinmura, K. Hara and T. Yamada, Effects of attractive and repulsive interactions in three-body resonance. Proc. 8th Int. Conf. Quarks and Nuclear Physics (QNP2018), JPS Conf. Proc., 023003 (2019).
- (40) I. Filikhin, R. Ya. Kezerashvili, V. M. Suslov, S.M. Tsiklauri, and B. Vlahovic, Three-body model for resonance. Phys. Rev. D 102, 094027 (2020).
- (41) B. B. Malabarba, X-L Ren, K. P. Khemchandani, and A. Martínez Torres, Partial decay widths of (2170) to kaonic resonances. Phys. Rev. D 103, 016018 (2021).
- (42) X. Zhang, C. Hanhart, U-G. Meißner, and J-J. Xie, Remarks on non-perturbative three–body dynamics and its application to the system. Eur. Phys. J A 58,22 (2022).
- (43) M. Gell-Mann and M. Levy, The axial vector current in beta decay. Nuovo Cim. 16, 705 (1960).
- (44) S. Gasiorowicz and D. A. Geffen, Effective Lagrangians and field algebras with chiral symmetry. Rev. Mod. Phys. 41, 531 (1969).
- (45) P. Ko and S. Rudaz, Phenomenology of scalar and vector mesons in the linear sigma model. Phys. Rev. D 50, 6877 (1994).
- (46) Y. Kanada En’yo, D. Jido, molecular state in a three-body calculation. Phys. Rev. C 78, 025212 (2008).
- (47) D. Jido, Y. Kanada-En’yo, molecule state with and studied with a three-body calculation. Phys. Rev C 78, 035203 (2008).
- (48) T. Yamazaki and Y. Akaishi, Basic nuclear cluster, , and its enhanced formation in the reaction, Phys. Rev. C 76, 045201 (2007).
-
(49)
A.A. Kvitsinsky, Yu.A. Kuperin, S.P. Merkuriev, A.K. Motovilov
and S.L. Yakovlev, N-body Quantum Problem in Configuration Space. Fiz. Elem. Chastits At. Yadra 17, 267 (1986) (in Russian);
http://www1.jinr.ru/Archive/Pepan/1986-v17/v-17-2.htm - (50) J. L. Friar, B. F. Gibson and G. L. Payne, n-p mass difference and charge-symmetry breaking in the trinucleons, Phys. Rev. C 42, 1211 (1990).
- (51) S. P. Merkuriev, On the three-body Coulomb scattering problem, Ann. Phys. (N.Y.) 130, 395 (1980).
- (52) A. Dote, T. Inoue, and T. Myo, Prog. Theor. Exp. Phys. 2015, 043D02 (2015).