The azimuthal asymmetry in meson production in ultraperipheral heavy ion collisions
Abstract
We present a detailed study of vector meson photoproduction in ultraperipheral heavy ion collisions (UPCs). Using the dipole model, we develop a framework for the joint impact parameter and transverse momentum dependent cross sections. We compute the unpolarized cross section and azimuthal angular correlation for photoproduction with defined as the angle between the ’s transverse transverse momentum and its decay product pion meson’s transverse momentum. Our result on unpolarized coherent differential cross section gives excellent description to the STAR experimental data. A first comparison between theoretical calculation and experimental measurement on the azimuthal asymmetry, which results from the linearly polarized photons, is performed and reasonable agreement is reached. We find out the characteristic diffractive patterns at both RHIC and LHC energies and predict the impact parameter dependent azimuthal asymmetries for photoproduction by considering UPCs and peripheral collisions. The future experimental measurements at RHIC and LHC relevant to our calculations will provide a tool to rigorously investigate the coherent and incoherent production of vector meson in UPCs, as well as to probe the nuclear structure in heavy ion collisions.
1 Introduction
Ultraperipheral collisions (UPCs) of heavy ions at the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC) offer a great opportunity to explore nuclear structure with beams of quasi-real photons before the Electron Ion Collider (EIC) era. In UPCs the strong hadronic interaction is suppressed, and the photon-nucleus (A) interactions involving photons emitted from one of the colliding nuclei are expected to be dominant. Due to the large flux of quasi-real photons, A interactions are enhanced by a factor as compared to those in proton-nucleus (pA) or electron-nucleus (eA) collisions where is the nuclear charge number. Among many exciting directions of UPC studies, see for example Hagiwara:2017fye ; Hatta:2019ocp , diffractive vector mesons photoproduction on nuclei provide access to the three dimensional gluon tomography of nucleus as well as stringent tests of the color glass condensate (CGC) description of saturation physics. Because of this, such processes have been extensively studied from both theoretical Donnachie:1987pu ; Ryskin:1992ui ; Brodsky:1994kf ; Nemchik:1996cw ; Klein:1999qj ; Munier:2001nr ; Kopeliovich:2001xj ; Kowalski:2003hm ; Kowalski:2006hc ; Rebyakova:2011vf ; Guzey:2013qza ; Lappi:2010dd ; Guzey:2016piu ; Xie:2016ino ; Cai:2020exu and experimental Breitweg:1998nh ; Chekanov:2002xi ; Khachatryan:2016qhq ; Adamczyk:2017vfu ; STAR:2019yox ; Sirunyan:2019nog ; Acharya:2020sbc sides during the past few decades.
Recently, significant and asymmetries for meson production in UPCs have been observed by STAR collaboration Daniel , where is the angle between the produced meson’s transverse momentum and its decay product pion’s transverse momentum. As the angular distribution of final state decayed pions contains the information of the polarization of , the observed angular correlation between and pion can be converted into the correlation between the transverse spin vector and the transverse momentum for , thus the asymmetry can serve as the meson’s spin analyzer. The investigations of such polarization dependent observable in vector meson production certainly open a new window to study the small- structure of heavy nuclei as well as the associated nontrivial QCD dynamics.
Motivated by the recent measurement by STAR collaboration at RHIC Daniel , we carry out a detailed analysis of the azimuthal asymmetry for diffractive meson production in UPCs. The underlying physics of asymmetry is rather different and will be addressed in a future work. Our calculation is formulated in a conventional method: the quasi-real photon is treated as the color dipole of a quark-antiquark pair which recombines to form a vector meson after scattering off the CGC state inside a nucleus. To account for the asymmetry within the dipole model, the key insight is that the incident photon is highly linearly polarized along the direction of its transverse momentum. The correlation between the initial state photon’s polarization and transverse momentum will be transferred to that for the final state vector meson. Notice that the Eikonal approximation employed in the dipole approach plays a crucial role in preserving spin information after the quark-antiquark pair experiences multiple gluon re-scattering.
As a matter of fact, the gauge bosons (photons/gluons) being highly linearly polarized in the small limit have been recognized as a common feature of the gauge theories in a series of publications Metz:2011wb ; Li:2019yzy ; Li:2019sin . It was shown in Refs. Metz:2011wb ; Dominguez:2011br ; Boer:2010zf ; Akcakaya:2012si ; Dumitru:2015gaa ; Kotko:2015ura ; Boer:2017xpy ; Marquet:2017xwy ; Gutierrez-Reyes:2019rug ; Scarpa:2019fol ; Kishore:2018ugo that the linear polarization of photons/gluons can be probed through the azimuthal asymmetries in two particles correlations. For instance, the QED calculations Li:2019yzy ; Li:2019sin predict a sizable azimuthal asymmetry for pure electromagnetic dilepton production in heavy ion collisions. Such modulation has been clearly seen in a recent STAR measurement Adam:2019mby . In particular, the computed impact parameter dependent asymmetry is in excellent agreement with the experimental data for the UPC case, while the QED calculation in peripheral collisions slightly overestimates the asymmetry in the centrality region . With it being experimentally confirmed, the linearly polarized quasi-real photon beam in heavy ion collisions can be used as a powerful tool to explore the novel QCD phenomenology as well. The current work represents the first effort towards this direction.
The paper is organized as follows. In Sec. 2, we derive the joint impact parameter and transverse momentum dependent cross section in UPCs including both the coherent and incoherent vector meson photoproduction contributions. In Sec. 3, we present numerical estimations of polarization averaged and azimuthal asymmetries for diffractive production at RHIC and LHC energies. Reasonable good agreement with the STAR measurements are reached. Finally, the paper is summarized in Sec. 4.
2 Theoretical setup
2.1 The polarization dependent wave functions
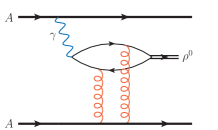
In this paper, we consider vector meson production in UPCs, . In this process, as shown in Fig. 1, one of the nuclei can be considered as the source of quasi-real photons that scatter off the other nucleus. The quasi-real photon-nucleus interaction is treated as the quark-antiquark color dipole scattering off the target nucleus in the dipole picture. After the dipole-nucleus collision, quark-antiquark pair subsequently recombines to form a vector meson. The calculation of the polarization averaged cross sections for both the coherent and incoherent vector meson production in UPCs are well formulated within the dipole model in the literatures Ryskin:1992ui ; Brodsky:1994kf . Extending the analysis to the polarization dependent case is the main purpose of the present work. At high energy, the transverse positions of the quark and antiquark are not altered in the scattering process under the eikonal approximation. Thus the production amplitude can be conventionally expressed as the convolution of the dipole scattering amplitude and the overlap between the vector meson and photon wave functions in position space,
| (1) |
where is the nucleus recoil transverse momentum. and are the magnitudes of transverse polarization vectors for the incident quasi-real photon and final outgoing vector meson, respectively. The polarization dependent wave function ( ) of the quasi-real photon (vector meson) is determined from light cone perturbation theory at leading order in the section below. denotes the fraction of the photon’s light-cone momentum carried by the quark. is the elementary amplitude for the scattering of a dipole of size on a target nucleus at the impact parameter of the collision.
For coherent vector meson production, the dipole interacts with the nucleus as a whole and leaves the nucleus in the ground state after the collision. As a comparison, in the incoherent production process the photon interacts with a nucleon inside the nucleus to produce a vector meson leaving the nucleus in an excited state. The coherent cross section is obtained by averaging the amplitude over the position of the nucleon in the nucleus before squaring it , while the incoherent one is given by the variance . Following Refs. Kopeliovich:2001xj ; Lappi:2010dd , the incoherent production amplitude squared (neglecting nuclear correlation) takes the form,
| (2) |
where is the nuclear atomic number and in the IPsat model Kowalski:2003hm ; Kowalski:2006hc . is the nuclear thickness function. is the dipole-nucleon scattering amplitude. Eq. (2) has a clear physical interpretation: The dipole scatters independently off the nucleons inside a nucleus, whose distribution in the transverse plane is given by , and the dipole can further interact with the rest of the target nucleons. While only elastic interactions are allowed in diffractive process, the inelastic re-scattering would make the process not diffractive and, hence, should be rejected. The probability of not having inelastic scattering is given by the factor .
We now move on to work out the polarization dependent photon’s wave function. For an ultrarelativistic charged heavy ion, the dominant component of the induced electromagnetic gauge potential is the plus component. The wave function of such a longitudinally polarized photon can be perturbatively calculated directly. Alternatively, by invoking the Ward identity argument, one can derive the same wave function with polarization vector instead of for a quasi-real photon that carries momentum Li:2019sin , where is the four-momentum for the beam nucleus. This actually is an essential reason why the small photons/gluons are highly linearly polarized for a given in the TMD description of photon/gluon distributions. The forward polarization dependent wave function at leading order reads
| (3) |
where . And and are the quark and antiquark helicities, and are their color indices. and denote the quark mass and quark’s electric charge number with flavor , is the charge of the nucleus. is a modified Bessel function of the second kind, in its argument is defined as with , where is the proton mass.
In analogy to the photon wave function, the forward transversely polarized vector meson wave function is given by Kowalski:2003hm ; Kowalski:2006hc ,
| (4) |
where the scalar part will be specified shortly.
Combining Eqs. (3) and (4), and summing over the color and helicities of the quark and antiquark, we obtain the overlaps between the photon and the vector meson wave functions,
| (5) |
Note that a phase factor is included to account for the non-forward correction Bartels:2003yj ; Hatta:2017cte (see also the application of this phase factor in a model calculation in proton-proton elastic scatterings Hagiwara:2020mqb ). As we focus on low transverse momentum region where the produced meson transverse momentum is of the order of with the nuclear radius, is sufficiently small compared to the relevant value of . Therefore we will neglect the phase to further simplify the expression. By doing so, the overlap of photon and meson wave functions can be cast into the following form after integrating out the azimuthal angle of ,
| (6) |
where the correlation between and in is ignored Hatta:2016dxp ; Zhou:2016rnt . In Eq. (6), it can be clearly seen that the photon’s polarization vector manifestly couples to meson’s one. As mentioned in the introduction, the coupling of the spin states is the consequence of the Eikonal approximation employed in our calculation.
2.2 The polarization dependent differential cross section
The purpose of the current work is to investigate the angular correlation between the vector meson’s transverse spin vector and its decayed pion’s transverse momentum. At leading order in perturbative QCD, the meson’s transverse momentum is equal to the sum of the incident photons’ transverse momentum and . It is then natural to formulate the transverse momentum dependent cross section in the framework of TMD factorization, which reads
| (7) |
where and are the produced vector meson’s transverse momentum and rapidity, respectively. The photon TMD distribution is denoted as which will be computed below using the equivalent photon approximation, where longitudinal momentum fraction is fixed as at leading order. Correspondingly, the longitudinal momentum fraction transferred to the vector meson via the dipole-nucleus interaction is given by .
We proceed by explicitly separating the coherent and incoherent contributions,
| (8) |
where and is the angle between and . We have replaced with in the above formula. A pre-coefficient is introduced here to account for the real part of the amplitude as well as the skewedness effect. In our numerical estimations, we simply neglect these effects and set to be equal to 1. In Eq. (8), the coherent and incoherent scattering amplitudes are respectively given by
| (9) | ||||
| (10) |
where denotes the overlap of the virtual photon wave function and the vector meson wave function,
| (11) |
It is now worthwhile to point out that the impact parameter of the two colliding nuclei is implicitly integrated out in Eq. (8). Therefore, one can not compute the observables in UPCs using Eq. (8). It is necessary to introduce an impact parameter dependent cross section, from which the UPC observables can be estimated by integrating out from to . Such a formalism actually has been developed long ago in the context of evaluating the electromagnetic dilepton production in UPCs Vidovic:1992ik ; Hencken:1993cf . Previously, the dependent azimuthal asymmetries for dilepton production was studied following the same method Li:2019sin .
The precise determination of the joint transverse momentum and impact parameter dependence crucially relies on the assumption that the lepton pair or vector meson is locally produced in the transverse plane of nucleus. This requirement is satisfied as long as the vector meson’s mass is much larger than the inverse of the nucleus radius. The probability amplitude for coherently producing a meson at the position inside two nuclei is then proportional to,
| (12) |
where is the EM gauge potential induced by nucleus . The dependence of the dipole amplitude is suppressed for brevity. Note that each incident ion can serve as a source of photons and a target. So the production amplitude contains two contributions, shown in Fig. 2, corresponding to the right-moving photon source (denoted as nucleus ) and the left-moving source (denoted as nucleus ). Since these two possibilities are indistinguishable, they should be summed up on the amplitude level rather than on the cross section level.
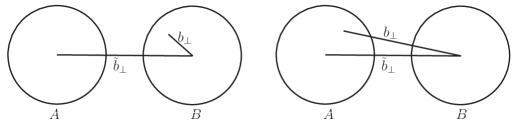
We now Fourier transform the above expression to momentum space,
| (13) |
where a nontrivial phase arises together with a normal delta function which ensures transverse momentum conservation. Due to the different phase factors and , a large destructive interference could occur between two contributions as shown below. Such destructive interference of in UPCs was first proposed by Klein and Nystrand Klein:1999gv , and verified by the STAR measurement Abelev:2008ew . Later, the authors of the paper Zha:2018jin suggested that this phenomenon could also be studied in hadronic heavy ion collisions.
After combining with the conjugate amplitude, it yields phases for the diagonal terms and for the interference term, where is the photon’s transverse momentum in the conjugate amplitude, which is not necessarily identical to that in the amplitude. One eventually ends up with the joint and dependent cross section,
| (14) |
where is related to the coherent photon TMD via the relation , and will be specified shortly. is constrained by the transverse momentum conservation: . The diagonal term and the interference term from the coherent production contribution are presented in the last four lines. The incoherent production contribution is given in the second line, where the interference term is ignored due to its smallness at low transverse momentum. To demonstrate the destructive interference effect, one can carry out integration and obtains the delta function associated with the diagonal term and for the interference term 111It can be readily seen that the integrated cross section is reduced to Eq. (8) provided that the interference term is neglected.. It now becomes evident that two contributions at have an opposite sign resulting from the vector product structure . For the fully symmetrical case , this effect leads to a complete cancelation between the last four lines at . Such cancelation can be intuitively understood as the consequence of the parity conservation. In the general case without integration, the cross section is reduced by this destructive interference effect mainly in the low region.
To facilitate the numerical estimation, we replace the vector product structure in Eq. (14) with Boer:2009nc ,
| (15) |
where the polarization states of the produced have been summed over. We now argue that the asymmetry under investigation is essentially equivalent to the measured angular correlation between and the final state pion’s transverse momentum . Due to the angular momentum conservation, the decay amplitude of the process must be proportional to where is the azimuthal angle of and denotes meson’s helicity state. This immediately implies that there exits a angular correlation of the type provided that the vector meson is linearly polarized. As a consequence, once summing over all polarization states of the vector meson, the correlation appears in the above cross section formula will be converted into the one which is exactly the observable that has been measured by the STAR experiment.
3 Phenomenology
We proceed to perform the numerical estimations of the asymmetry using Eq. (14) in this section. First of all, let us collect all ingredients that are necessary for numerical calculations. We start with introducing the parametrization for the dipole scattering amplitude whose formal operator definition is given by,
| (16) |
The dipole amplitude is usually obtained by solving the BK equation with the initial condition being fitted to the experimental data or derived from the MV model. However, the numerical implementation of the impact parameter dependent BK equation is a highly non-trivial task. For simplicity, we instead use a phenomenological parametrization for the dependence of the dipole amplitude Kowalski:2003hm ; Kowalski:2006hc ,
| (17) |
where, as mentioned before, is the dipole-nucleon scattering amplitude. The nuclear thickness function is determined with the Woods-Saxon distribution in our numerical calculation. Note that is the total dipole-proton cross section for a dipole of size . In literatures there are many parameterizations available for the dipole-proton cross section. Here we adopt a modified IPsat model in which the impact parameter dependence of the dipole-nucleon scattering amplitude has been factorized out Lappi:2010dd
| (18) |
where is proportional to the DGLAP evolved gluon distribution in the Bartels, Golec-Biernat and Kowalski (BGBK) parametrization Bartels:2002cj . In our numerical estimations, we adopt a simpler parametrization for the gluon distribution known as the Golec-Biernat and Wüsthoff (GBW) model Golec-Biernat:1998js ; Golec-Biernat:1999qd ,
| (19) |
where GeV is the saturation scale. We use the parameters and Kowalski:2006hc which were determined by fitting to HERA data.
For the scalar part of the vector meson wave function, we use “Gaus-LC” wave function also taken from Refs. Kowalski:2003hm ; Kowalski:2006hc
| (20) |
where , for meson. An alternative parametrization, the “boosted Gaussian” wave function is also widely used in the study of exclusive production of vector meson. The existing HERA data is reasonably well described by estimations of vector meson photoproduction employing either wave function model.
The photon distribution at low transverse momentum is commonly computed with the equivalent photon approximation, also often referred to as the Weizscker-Williams method, in which the photon flux is calculated by treating the fields of charged relativistic heavy ions as external, i.e., classical electromagnetic field. This method has been widely used to compute UPC observables, see for example Refs. Klein:2018fmp ; Zha:2018tlq . The photon distribution derived in the equivalent photon approximation is given by Bertulani:1987tz ; Vidovic:1992ik
| (21) |
where is the nuclear charge form factor, is the proton mass. Similarly, one has . The nuclear charge form factor is commonly determined with the Woods-Saxon distribution,
| (22) |
where (Au: 6.38 fm, pb: 6.62 fm) is the nuclear radius and (Au: 0.535 fm, Pb: 0.546 fm) is the skin depth, is the normalization factor. Alternatively, one can use the form factor in momentum space from the STARlight MC generator Klein:2016yzr ,
| (23) |
where fm, and fm. This parametrization numerically is very close to the Woods-Saxon distribution, and will be used in our numerical evaluation. Due to the neutron skin effect and the surrounding pion cloud, the effective nuclear strong interaction radius is larger than its EM radius. To fit RHIC data Adamczyk:2017vfu , we compute the thickness function with the radius fm and the depth fm for a gold target. For a lead target, we simply re-scale these numbers by multiplying a factor . We determine by noticing that the meson wave function reads . This would imply a replacement of by . The effective charge for then is .
For the unrestricted UPC case, the asymmetry is averaged over the impact parameter range . However, RHIC-STAR measures photoproduction cross section together with the double electromagnetic excitation in both ions. Neutrons emitted at forward angles from the scattered nuclei are detected by zero-degree calorimeters (ZDCs), and used as a UPC trigger. Requiring that UPCs are accompanied by forward neutron emission alters the impact parameter distribution compared with unrestricted UPC events. In order to incorporate the experimental conditions in the theoretical calculations, one can define a “tagged” UPC cross section
| (24) |
Where the probability of emitting a neutron from the scattered nucleus is often parameterized as Baur:1998ay
| (25) |
which is denoted as the “1n” event, while for emitting any number of neutrons (“Xn” event), the probability is given by
| (26) |
with . As a matter of fact, the mean impact parameter is dramatically reduced in interactions with Coulomb dissociation.
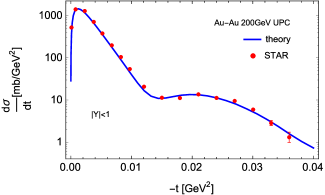
With all these ingredients, we are ready to perform numerical study of the azimuthal asymmetries for meson production in heavy ion collisions. To test the theoretical calculation, we first compute the azimuthal averaged cross section for coherent photoproduction of and compare with experimental data from the STAR collaboration Adamczyk:2017vfu . In particular, we calculate the differential cross section with the Mandelstam variable , and the rapidity is integrated out in the region to match the STAR measurement. Notice that the incoherent component has been subtracted out in STAR measurement. Therefore, we exclude the first term in Eq. (14) and integrate over the azimuthal angle , namely only the first term in Eq. (15) needs to be considered. As shown in Fig. 3, our theoretical result represented by blue curve describes the experimental data perfectly in identifying the minima and peaks, as well as the overall shapes.
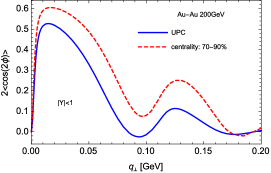
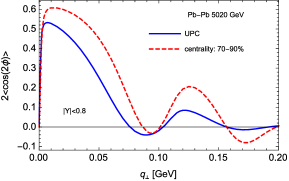
The numerical results for the azimuthal asymmetries for at RHIC and LHC energies are presented in Fig. 4, where the azimuthal asymmetry, i.e., the average value of is defined as,
| (27) |
We use exactly the same setups as that in the unpolarized case but including both the coherent and incoherent components. Since we are considering the average value of , only the second term in Eq. (15) contributes. We can see clearly the diffractive pattern with two minima visible in distribution, such characteristic feature is also identified in the STAR preliminary measurement. The distribution for the average value of can be easily understood as the asymmetry is almost entirely generated in the coherent scattering, while both the coherent and incoherent production contribute to the azimuthal averaged cross section. At the relative large transverse momentum(), most of meson’s transverse momentum originates from the nucleus. Based on this observation, one, after few steps of algebraic manipulations, can show that the asymmetry is proportional to the slope of distribution which gets very large near the first minima of the diffractive pattern. This can be clearly seen from our numerical result, where the second peak of the asymmetry located at the first minima of the unpolarized cross section. Nevertheless, as the first attempt, our result shown in the left plot in Fig. 4(solid line) describes the STAR preliminary data Daniel reasonably well in terms of finding the correct depths of the dips. However, slightly larger for the locations of the dips are found from our theoretical calculation comparing to those in STAR preliminary data, which suggests an increase in effective nuclear size in our calculation when considering polarized case. In order to investigate the impact parameter dependence, we also show in Fig. 4 the comparison between UPC and peripheral collisions at RHIC energy GeV in Au-Au collisions and at LHC energy GeV in Pb-Pb collisions, we take centralities as an example in peripheral collisions 222For peripheral collisions with relative large impact parameter, the coherent photon-nucleus interaction still dominates over hadronic reactions in vector meson production STAR:2019yox . . With the increase of impact parameter, we see slightly shift of the location for the dips. We also predict measurable difference between UPC and peripheral collisions at both RHIC and LHC.
4 Conclusion
In summary, we have studied the azimuthal angular correlation in vector meson production in ultraperipheral heavy ion collisions, where is defined as the angle between vector meson’s transverse spin vector and its transverse momentum. The asymmetry essentially results from the linear polarization of incident coherent photons, which just has been experimentally confirmed by the recent STAR measurement of a modulation in pure electromagnetic lepton pair production Adam:2019mby . The asymmetries evaluated in the dipole model for photoproduction at RHIC and LHC energies are shown to be rather sizable. Admittedly, the perturbative treatment for must be legitimately criticized due to the lack of a hard scale in the problem. However, one might expect that the angular correlation structure is not altered by the non-perturbative effect, for which a more sophisticated phenomenological method is required. Nevertheless, we found that our calculation turns out to be in reasonably good agreement with the measurement by STAR collaboration. As mentioned in the introduction, a significant asymmetry in production was also observed at RHIC. This observable could potentially give the access to the non-trivial gluon GTMD/Wigner distribution and will be addressed in a future publication.
The obtained transverse momentum dependent asymmetries have a distinctive diffractive pattern which undoubtly opens a new window to investigate the coherent and incoherent production of vector meson. As demonstrated by the present study, quasi-real photon beams with linear polarization in heavy ion collisions can be used as a powerful tool to explore novel QCD phenomenology. Meanwhile, as a byproduct of this work, we developed a formalism to compute the joint impact parameter and transverse momentum dependent cross sections that enables us to reliably extract dependence in UPCs. The Fourier transform of distribution would provide crucial information on the transverse spatial distribution of gluons inside a nucleus, which is one of the central scientific goals in the forthcoming EIC era.
Acknowledgements.
J. Zhou thanks Zhang-bu Xu, James Daniel Brandenburg, and Chi Yang for helpful discussions. J. Zhou has been supported by the National Science Foundations of China under Grant No. 11675093. Y. Zhou has been supported by the National Science Foundations of China under Grant No. 11675092. The work of H. X. is supported by the research startup funding at South China Normal University and Science and Technology Program of Guangzhou (No. 2019050001). CZ is supported by the China Postdoctoral Science Foundation under Grant No. 2019M662317.Note added: After the manuscript was posted on arXiv, a related preprint Zha:2020cst appeared soon, where the similar result for the azimuthal asymmetry was obtained.
References
- (1) Y. Hagiwara, Y. Hatta, R. Pasechnik, M. Tasevsky and O. Teryaev, Phys. Rev. D 96, no. 3, 034009 (2017) doi:10.1103/PhysRevD.96.034009 [arXiv:1706.01765 [hep-ph]].
- (2) Y. Hatta, M. Strikman, J. Xu and F. Yuan, Phys. Lett. B 803, 135321 (2020) doi:10.1016/j.physletb.2020.135321 [arXiv:1911.11706 [hep-ph]].
- (3) A. Donnachie and P. V. Landshoff, Phys. Lett. B 185, 403 (1987). doi:10.1016/0370-2693(87)91024-0
- (4) M. G. Ryskin, Z. Phys. C 57, 89 (1993). doi:10.1007/BF01555742
- (5) S. J. Brodsky, L. Frankfurt, J. F. Gunion, A. H. Mueller and M. Strikman, Phys. Rev. D 50, 3134 (1994) doi:10.1103/PhysRevD.50.3134 [hep-ph/9402283].
- (6) J. Nemchik, N. N. Nikolaev, E. Predazzi and B. G. Zakharov, Z. Phys. C 75, 71 (1997) doi:10.1007/s002880050448 [hep-ph/9605231].
- (7) S. Klein and J. Nystrand, Phys. Rev. C 60, 014903 (1999) doi:10.1103/PhysRevC.60.014903 [hep-ph/9902259].
- (8) S. Munier, A. M. Stasto and A. H. Mueller, Nucl. Phys. B 603, 427 (2001) doi:10.1016/S0550-3213(01)00168-7 [hep-ph/0102291].
- (9) B. Z. Kopeliovich, J. Nemchik, A. Schafer and A. V. Tarasov, Phys. Rev. C 65, 035201 (2002) doi:10.1103/PhysRevC.65.035201 [hep-ph/0107227].
- (10) H. Kowalski and D. Teaney, Phys. Rev. D 68, 114005 (2003) doi:10.1103/PhysRevD.68.114005 [hep-ph/0304189].
- (11) H. Kowalski, L. Motyka and G. Watt, Phys. Rev. D 74, 074016 (2006) doi:10.1103/PhysRevD.74.074016 [hep-ph/0606272].
- (12) V. Rebyakova, M. Strikman and M. Zhalov, Phys. Lett. B 710, 647 (2012) doi:10.1016/j.physletb.2012.03.041 [arXiv:1109.0737 [hep-ph]].
- (13) T. Lappi and H. Mantysaari, Phys. Rev. C 83, 065202 (2011) doi:10.1103/PhysRevC.83.065202 [arXiv:1011.1988 [hep-ph]]; Phys. Rev. C 83, 065202 (2011) doi:10.1103/PhysRevC.83.065202 [arXiv:1011.1988 [hep-ph]]; Phys. Rev. C 87, no. 3, 032201 (2013) doi:10.1103/PhysRevC.87.032201 [arXiv:1301.4095 [hep-ph]].
- (14) V. Guzey and M. Zhalov, JHEP 1310, 207 (2013) doi:10.1007/JHEP10(2013)207 [arXiv:1307.4526 [hep-ph]].
- (15) V. Guzey, E. Kryshen and M. Zhalov, Phys. Rev. C 93, no. 5, 055206 (2016) doi:10.1103/PhysRevC.93.055206 [arXiv:1602.01456 [nucl-th]]; arXiv:2002.09683 [hep-ph].
- (16) Y. p. Xie and X. Chen, Eur. Phys. J. C 76, no. 6, 316 (2016) doi:10.1140/epjc/s10052-016-4170-1 [arXiv:1602.00937 [hep-ph]]; Nucl. Phys. A 959, 56 (2017) doi:10.1016/j.nuclphysa.2016.12.010 [arXiv:1805.05901 [hep-ph]]; Int. J. Mod. Phys. A 33, no. 14n15, 1850086 (2018) doi:10.1142/S0217751X18500860 [arXiv:1805.11480 [hep-ph]].
- (17) Y. Cai, W. Xiang, M. Wang and D. Zhou, arXiv:2002.12610 [hep-ph].
- (18) J. Breitweg et al. [ZEUS Collaboration], Eur. Phys. J. C 6, 603 (1999) doi:10.1007/s100529901051 [hep-ex/9808020].
- (19) S. Chekanov et al. [ZEUS Collaboration], Eur. Phys. J. C 24, 345 (2002) doi:10.1007/s10052-002-0953-7 [hep-ex/0201043].
- (20) V. Khachatryan et al. [CMS Collaboration], Phys. Lett. B 772, 489 (2017) doi:10.1016/j.physletb.2017.07.001 [arXiv:1605.06966 [nucl-ex]].
- (21) L. Adamczyk et al. [STAR Collaboration], Phys. Rev. C 96, no. 5, 054904 (2017) doi:10.1103/PhysRevC.96.054904 [arXiv:1702.07705 [nucl-ex]].
- (22) J. Adam et al. [STAR Collaboration], Phys. Rev. Lett. 123, no. 13, 132302 (2019) doi:10.1103/PhysRevLett.123.132302 [arXiv:1904.11658 [hep-ex]].
- (23) A. M. Sirunyan et al. [CMS Collaboration], Eur. Phys. J. C 79, no. 8, 702 (2019) doi:10.1140/epjc/s10052-019-7202-9 [arXiv:1902.01339 [hep-ex]].
- (24) S. Acharya et al. [ALICE Collaboration], arXiv:2002.10897 [nucl-ex].
- (25) J. D. Brandenburg et al. [STAR Collaboration], talk presented in Quark Matter 2019, Wuhan, China.
- (26) A. Metz and J. Zhou, Phys. Rev. D 84, 051503 (2011) [arXiv:1105.1991 [hep-ph]].
- (27) C. Li, J. Zhou and Y. J. Zhou, Phys. Lett. B 795, 576 (2019) doi:10.1016/j.physletb.2019.07.005 [arXiv:1903.10084 [hep-ph]].
- (28) C. Li, J. Zhou and Y. J. Zhou, Phys. Rev. D 101, no. 3, 034015 (2020) doi:10.1103/PhysRevD.101.034015 [arXiv:1911.00237 [hep-ph]].
- (29) F. Dominguez, J. W. Qiu, B. W. Xiao and F. Yuan, Phys. Rev. D 85, 045003 (2012) [arXiv:1109.6293 [hep-ph]].
- (30) D. Boer, S. J. Brodsky, P. J. Mulders and C. Pisano, Phys. Rev. Lett. 106, 132001 (2011) [arXiv:1011.4225 [hep-ph]].
- (31) E. Akcakaya, A. Schäfer and J. Zhou, Phys. Rev. D 87, no. 5, 054010 (2013) [arXiv:1208.4965 [hep-ph]].
- (32) A. Dumitru, T. Lappi and V. Skokov, Phys. Rev. Lett. 115, no. 25, 252301 (2015) [arXiv:1508.04438 [hep-ph]].
- (33) P. Kotko, K. Kutak, C. Marquet, E. Petreska, S. Sapeta and A. van Hameren, JHEP 1509, 106 (2015) [arXiv:1503.03421 [hep-ph]].
- (34) D. Boer, P. J. Mulders, J. Zhou and Y. j. Zhou, JHEP 1710, 196 (2017) doi:10.1007/JHEP10(2017)196 [arXiv:1702.08195 [hep-ph]].
- (35) C. Marquet, C. Roiesnel and P. Taels, Phys. Rev. D 97, no. 1, 014004 (2018) doi:10.1103/PhysRevD.97.014004 [arXiv:1710.05698 [hep-ph]].
- (36) D. Gutierrez-Reyes, S. Leal-Gomez, I. Scimemi and A. Vladimirov, arXiv:1907.03780 [hep-ph].
- (37) F. Scarpa, D. Boer, M. G. Echevarria, J. P. Lansberg, C. Pisano and M. Schlegel, arXiv:1909.05769 [hep-ph].
- (38) R. Kishore and A. Mukherjee, Phys. Rev. D 99, no. 5, 054012 (2019) doi:10.1103/PhysRevD.99.054012 [arXiv:1811.07495 [hep-ph]].
- (39) J. Adam et al. [STAR Collaboration], arXiv:1910.12400 [nucl-ex].
- (40) Y. Hatta, B. W. Xiao and F. Yuan, Phys. Rev. Lett. 116, no. 20, 202301 (2016) doi:10.1103/PhysRevLett.116.202301 [arXiv:1601.01585 [hep-ph]].
- (41) J. Zhou, Phys. Rev. D 94, no. 11, 114017 (2016) doi:10.1103/PhysRevD.94.114017 [arXiv:1611.02397 [hep-ph]].
- (42) M. Vidovic, M. Greiner, C. Best and G. Soff, Phys. Rev. C 47, 2308 (1993). doi:10.1103/PhysRevC.47.2308
- (43) K. Hencken, D. Trautmann and G. Baur, Phys. Rev. A 49, 1584 (1994). doi:10.1103/PhysRevA.49.1584; Phys. Rev. A 51, 1874 (1995) doi:10.1103/PhysRevA.51.1874 [nucl-th/9410014].
- (44) S. R. Klein and J. Nystrand, Phys. Rev. Lett. 84, 2330 (2000) doi:10.1103/PhysRevLett.84.2330 [hep-ph/9909237].
- (45) B. I. Abelev et al. [STAR Collaboration], Phys. Rev. Lett. 102, 112301 (2009) doi:10.1103/PhysRevLett.102.112301 [arXiv:0812.1063 [nucl-ex]].
- (46) W. Zha, L. Ruan, Z. Tang, Z. Xu and S. Yang, Phys. Rev. C 99, no. 6, 061901 (2019) doi:10.1103/PhysRevC.99.061901 [arXiv:1810.10694 [hep-ph]].
- (47) D. Boer, P. J. Mulders and C. Pisano, Phys. Rev. D 80, 094017 (2009) doi:10.1103/PhysRevD.80.094017 [arXiv:0909.4652 [hep-ph]].
- (48) J. Bartels, K. J. Golec-Biernat and K. Peters, Acta Phys. Polon. B 34, 3051 (2003) [hep-ph/0301192].
- (49) Y. Hatta, B. W. Xiao and F. Yuan, Phys. Rev. D 95, no. 11, 114026 (2017) doi:10.1103/PhysRevD.95.114026 [arXiv:1703.02085 [hep-ph]].
- (50) Y. Hagiwara, Y. Hatta, R. Pasechnik and J. Zhou, arXiv:2003.03680 [hep-ph].
- (51) J. Bartels, K. J. Golec-Biernat and H. Kowalski, Phys. Rev. D 66, 014001 (2002) doi:10.1103/PhysRevD.66.014001 [hep-ph/0203258].
- (52) K. Golec-Biernat and M. Wüsthoff, Phys. Rev. D 59 (1999) 014017.
- (53) K. Golec-Biernat and M. Wüsthoff, Phys. Rev. D 60 (1999) 114023.
- (54) S. Klein, A. H. Mueller, B. W. Xiao and F. Yuan, Phys. Rev. Lett. 122, no. 13, 132301 (2019) doi:10.1103/PhysRevLett.122.132301 [arXiv:1811.05519 [hep-ph]]; arXiv:2003.02947 [hep-ph].
- (55) W. Zha, J. D. Brandenburg, Z. Tang and Z. Xu, arXiv:1812.02820 [nucl-th].
- (56) C. A. Bertulani and G. Baur, Phys. Rept. 163, 299 (1988). doi:10.1016/0370-1573(88)90142-1
- (57) S. R. Klein, J. Nystrand, J. Seger, Y. Gorbunov and J. Butterworth, Comput. Phys. Commun. 212, 258 (2017) doi:10.1016/j.cpc.2016.10.016 [arXiv:1607.03838 [hep-ph]].
- (58) G. Baur, K. Hencken and D. Trautmann, J. Phys. G 24, 1657 (1998) doi:10.1088/0954-3899/24/9/003 [hep-ph/9804348].
- (59) W. Zha, J. D. Brandenburg, L. Ruan, Z. Tang and Z. Xu, [arXiv:2006.12099 [hep-ph]].