The diverse lives of massive protoplanets in self-gravitating discs
Abstract
Gas giant planets may form early-on during the evolution of protostellar discs, while these are relatively massive. We study how Jupiter-mass planet-seeds (termed protoplanets) evolve in massive, but gravitationally stable (), discs using radiative hydrodynamic simulations. We find that the protoplanet initially migrates inwards rapidly, until it opens up a gap in the disc. Thereafter, it either continues to migrate inwards on a much longer timescale or starts migrating outwards. Outward migration occurs when the protoplanet resides within a gap with gravitationally unstable edges, as a high fraction of the accreted gas is high angular momentum gas from outside the protoplanet’s orbit. The effect of radiative heating from the protoplanet is critical in determining the direction of the migration and the eccentricity of the protoplanet. Gap opening is facilitated by efficient cooling that may not be captured by the commonly used -cooling approximation. The protoplanet initially accretes at a high rate (), and its accretion luminosity could be a few tenths of the host star’s luminosity, making the protoplanet easily observable (albeit only for a short time). Due to the high gas accretion rate, the protoplanet generally grows above the deuterium-burning mass-limit. Protoplanet radiative feedback reduces its mass growth so that its final mass is near the brown dwarf-planet boundary. The fate of a young planet-seed is diverse and could vary from a gas giant planet on a circular orbit at a few AU from the central star to a brown dwarf on an eccentric, wide orbit.
keywords:
Stars: planetary systems, protoplanetary discs, brown dwarfs – Accretion, accretion disks –Methods: Numerical – Hydrodynamics – Radiative Transfer1 Introduction
Observational advances over the last 20 years have made possible the discovery of a large number of exoplanets (see the “Extrasolar Planets Encyclopaedia"; http://exoplanet.eu). Most of these exoplanets are gas giants, as these are easier to detect with the main current methods (radial velocity, transits) than small, rocky planets like Earth.
Two theoretical models have been proposed for the formation of gas giant planets, (i) core accretion, and (ii) gravitational fragmentation of protostellar discs.
In the core accretion model (Safronov, 1972; Goldreich & Ward, 1973; Mizuno, 1980; Bodenheimer & Pollack, 1986; Pollack et al., 1996) the cores of giant planets form in circumstellar discs by coagulation of dust particles to progressively larger objects, until a core with a few Earth masses has formed. Such a core subsequently accretes an envelop of gas from the disc. One of the main drawbacks of this model is that, in its standard formulation, requires a few million years to form gas giants, a timescale which may be long when compared to the observed lifetimes of circumstellar discs (on the order of a few Myr; Haisch et al., 2001; Hernández et al., 2008; Muzerolle et al., 2010). Moreover, this model seems unlikely to be able to produce massive planets on wide orbits (Kraus et al., 2008, 2014; Marois et al., 2008; Faherty et al., 2009; Ireland et al., 2011; Kuzuhara et al., 2011; Kuzuhara et al., 2013; Aller et al., 2013; Bailey et al., 2014; Rameau et al., 2013; Naud et al., 2014; Galicher et al., 2014), like e.g. the planets around HR8799.
A second way to form gas giants is by gravitational fragmentation of protostellar discs (Kuiper, 1951; Cameron, 1978; Boss, 1997). This model circumvents the timescale problem of the core accretion theory, as planets form on a dynamical timescale, i.e. within a few yr. One of the main issues relating to this model is whether protostellar discs are able to fragment or not. There are two criteria for disc fragmentation, (i) the Toomre criterion (Toomre, 1964) that postulates that the disc must be massive enough in order gravity to dominate over the local thermal and centrifugal support, and (ii) the Gammie criterion (Gammie, 2001; Johnson & Gammie, 2003; Rice et al., 2005) that asserts that the disc must be able to cool fast enough, i.e. on a dynamical timescale (see Takahashi et al., 2016a, for an alternative view). There has been relative consensus that these two criteria can be satisfied at distances AU from the star hosting the disc; therefore discs can fragment at such distances (Rafikov, 2005; Matzner & Levin, 2005; Whitworth & Stamatellos, 2006; Boley et al., 2006; Stamatellos & Whitworth, 2008). This fact, together with the discovery of exoplanets on wide orbits, may suggest two modes of gas giant planet formation: core accretion that forms planets close to the host star, and disc fragmentation that forms planets on wide orbits (Boley, 2009).
Many studies suggesting that planets form by disc fragmentation, refer to the initial mass of the fragments produced. The initial fragment mass (e.g. Stamatellos & Whitworth, 2009a, b) is determined by the opacity limit for fragmentation, i.e. the minimum mass a fragment produced by fragmenting gas may have (e.g. Low & Lynden-Bell, 1976; Rees, 1976; Silk, 1977; Boss, 1988; Masunaga & Inutsuka, 1999; Whitworth & Stamatellos, 2006). However, once a fragment forms in a disc it evolves: it migrates within the disc, accretes gas from the disc opening a gap, and inevitable increases in mass (Zhu et al., 2012; Hall et al., 2017).
Previous studies (Stamatellos & Whitworth, 2009a, b; Kratter et al., 2010; Zhu et al., 2012) suggest that the most likely outcome of disc fragmentation is brown dwarfs. Stamatellos & Whitworth (2009a) performed an ensemble of 12 simulations of self-gravitating, fragmenting discs producing in total objects; 67% of these objects are brown dwarfs, 30% are low-mass hydrogen burning stars and only 3% are planets. Additionally, they point out that the objects that end up as planets () they are ejected from the disc quickly after their formation, thus avoiding any subsequent gas accretion. These ejected planets contribute to the suspected large population of free-floating planets. Stamatellos & Whitworth (2009a) also argue that objects that remain in the disc, although they are planets when they form (i.e. their mass is below ), they grow in mass to become either brown dwarfs or hydrogen-burning stars.
Another problem of the disc fragmentation theory is whether planets forming early on in protoplanetary discs are able to avoid fast inward migration towards their parent star. Previous studies suggest the giant planets that form in relatively massive protoplanetary discs migrate inwards rapidly, on a timescale reminiscent of Type I migration, without opening up a gap in the disc (Vorobyov & Basu, 2005, 2006; Baruteau et al., 2011; Michael et al., 2011; Malik et al., 2015). However, this has been questioned by the studies of Lin & Papaloizou (2012) and Cloutier & Lin (2013) that show that planets may migrate outwards due to gravitational edge mode instabilities. Stamatellos (2015) showed that planets are able to open gaps as they become more massive by accreting gas from the disc; by doing so, their inward migration slows down or even changes to outward migration.
An interesting variant of the gravitational fragmentation theory is the tidal downsizing hypothesis (see review by Nayakshin, 2017a), in which clumps that form by disc fragmentation contract slowly while they migrate inwards. They may eventually get tidally disrupted, losing mass and possibly leaving behind a solid core. Nayakshin (2017b) find that the final fate of a clump forming in the disc depends on how efficiently it cools and identifies two possible outcomes for the clump: it becomes either a brown dwarf on a wide orbit or a planet within 20 AU from the central star. He concludes that even though disc fragmentation may commonly happen, only a small fraction of stars may have giant planets on wide orbits; this is corroborated by observations (Brandt et al., 2014; Galicher et al., 2016; Vigan et al., 2017) which show that only 1-10% of star host gas giant planets on wide orbits.
Recent ALMA observations of the disc of the young star HL Tau (ALMA Partnership et al., 2015) have revealed the presence of multiple gaps at mm wavelengths. These gaps may be carved either by planets (Dipierro et al., 2015) or be due to other processes (Takahashi & Inutsuka, 2014; Gonzalez et al., 2015; Takahashi et al., 2016b). HL Tau is an extremely young object (Greaves et al., 2008) that shows signs of outflows in the form of jets and infall from its parent cloud. Its disc is relatively massive (0.1-0.15 M☉; Testi et al., 2015) and presumably is still being fed with gas by its ambient cloud. Such gaps have been observed in other discs e.g. in TW Hydra (Andrews et al., 2016) and in HD 163296 (Isella et al., 2016). Numerical simulations using resistive MHD have suggested that discs form at an early stage during star formation and that they may be relatively massive in comparison to the mass of their host stars (Machida et al., 2010, 2011a, 2011b, 2014). ALMA observations strongly support that discs exist from the Class 0 phase (Tobin et al., 2016). They appear to be relatively massive and extended, and they appear to have spiral arms indicative of gravitational instabilities (Pérez et al., 2016; Tobin et al., 2016). The possible presence of planets in such young discs raises the exciting possibility that planets may form much faster than it has been previously thought and therefore their early evolution, no matter how they have formed, will occur within a relatively massive disc.
In this paper we study the evolution of a Jupiter-like planet-seed, referred to as the protoplanet, which finds itself within a protostellar disc that is massive enough for its self-gravity to be important for its evolution. The assumed disc is close to being gravitationally unstable, meaning that weak spiral arms may develop, but the disc does not fragment. We use the term protoplanet even though we refer to an object that only starts off as planet in the disc (irrespective of its formation mechanism). This object may accrete mass to eventually stop being a planet and become a brown dwarf (). Our aim is to investigate the whether such an object may actually survive as a planet by performing a set of numerical experiments. We expand on the work of Stamatellos (2015), exploring a wider parameter space. More specifically we investigate the effect of different disc viscosity, dust opacities, the orientation of the protoplanet’s orbit, the protoplanet’s initial orbital radius, and the effect of the radiation from the host star and the protoplanet itself. We therefore examine in detail how robust are the results of Stamatellos (2015). Additionally, we explore the reasons behind the different results with previous studies, comparing with simulations using a parameterized prescription for the disc cooling (-cooling approximation).
We describe the initial condition of the simulations performed in Section 2, and in Section 3 the hydrodynamic method used and its ingredients (radiative transfer method, opacities, radiative feedback). We present the first set of simulations performed and their results in Section 4, commenting in detail on how fast the protoplanet grows in mass, and how its orbital properties (semi-major axis, eccentricity) change during its early evolution. In Section 5, we compare the results of our simulations with those of previous studies that employ the -cooling approximation. In Section 6, we examine in detail the evolution of protoplanets at different radii from the central star. In Section 7, we present possibly the more realistic set of simulations, in which both radiative feedback from the planet and the host star are taken into account. Finally, in Section 8 we discuss the implications of this work for planet formation and evolution studies.
2 Computational setup
We assume a star with initial mass that is attended by a protostellar disc with mass and initial radius AU. The disc is modelled by SPH particles. The discs that we model are chosen so that they are not gravitationally unstable (). Therefore, they are not expected to develop strong spiral arms (unless these are induced from the protoplanet).
The disc initial surface density is
| (1) |
and the disc temperature
| (2) |
where is determined by the disc mass and radius, and the distance from the central star measured on the disc midplane. The above density and temperature profiles are consistent with observations of late-phase (T Tauri) discs but the properties of discs in the early-phase are uncertain (MacFarlane & Stamatellos, 2017). Andrews et al. (2009) observed a sample of circumstellar discs in Ophiuchus and estimated a disc surface density that drops with the distance from the host star as . In Taurus-Auriga and Ophiuchus-Scorpius star formation regions, Andrews & Williams (2007) find a median ; they also find a temperature profile that drops with distance as . Osterloh & Beckwith (1995) find that the disc temperature drops with radius, with an exponent . We note though that the profile defined in Equation 2 is the initial disc temperature profile but as the disc evolves it acquires a temperature profile self-consistently within the radiative hydrodynamic simulation.
The disc is allowed to relax, i.e. to evolve without a protoplanet, for 3 outer orbital periods ( kyr). A protoplanet with a mass of is then embedded in the disc. The protoplanet’s initial orbital velocity is set the same as the orbital velocity of the local gas, i.e. Keplerian (including the contribution from the disc mass within the radius of the protoplanet). We additionally assume an initially circular orbit ().
The choice of the initial disc mass () is intentionally conservative. If the protoplanet has formed by disc fragmentation then numerical studies indicate that a disc needs to have mass at least a few tenths (e.g. the simulations of Stamatellos et al., 2011a, suggest that a disc around a star needs to be more massive than in order to fragment).
The choice of the initial mass of the protoplanet (1 ) is also conservative. The minimum mass of an object forming by gravitational fragmentation is set by the thermodynamics of gas, as in order for a condensation to collapse, the energy delivered by compression needs to be efficiently radiated away. The energy loss of a fragment is determined by its opacity, so this is usually referred to as the opacity limit for fragmentation (e.g. Whitworth & Stamatellos, 2006; Whitworth et al., 2007). Theoretical studies estimate a minimum mass for fragmentation to be (Low & Lynden-Bell, 1976; Rees, 1976; Silk, 1977; Boss, 1988; Masunaga & Inutsuka, 1999; Boyd & Whitworth, 2005; Whitworth & Stamatellos, 2006; Boley et al., 2010; Kratter et al., 2010; Forgan & Rice, 2011; Rogers & Wadsley, 2012). We therefore study a system in which both the disc mass and the initial protoplanet mass are close to the lower limits that they may have, if the protoplanet has formed by disc fragmentation. However, our study is general and applies even for planets that have formed by core accretion.
3 Computational methods
3.1 Gas hydrodynamics and radiative transfer
We use the SPH code seren (Hubber et al., 2011a, b) to treat the disc thermodynamics. The code uses an octal tree to compute gravity and find neighbours, multiple particle timesteps for optimisation, and a 2nd Runge-Kutta integration scheme. We use a time-dependent artificial viscosity (Morris & Monaghan, 1997) with parameters , and , so as to reduce artificial shear viscosity. The chemical and radiative processes that determine the disc temperature are treated with the diffusion approximation of Stamatellos et al. (2007) and Forgan et al. (2009). The net radiative heating rate for an SPH particle is
| (3) |
where is the specific internal energy of the particle, and , , its density and temperature, respectively. The positive term on the right hand side represents heating by the various radiation sources (star, protoplanet, and pseudo-background radiation field; see Section 3.4), and ensures that the gas and dust cannot cool radiatively below the pseudo-background temperature . is the Stefan-Boltzmann constant, is the mass-weighted mean column-density, and and are suitably adjusted Rosseland- and Planck-mean opacities (see Stamatellos et al., 2007, for details). The method takes into account compressional heating, viscous heating, heating by the background radiation field, and radiative cooling/heating. The method has previously applied to disc studies (Stamatellos & Whitworth, 2008, 2009b; Stamatellos et al., 2011a) and has given similar results with grid-based computational methods (Boley et al., 2006; Cai et al., 2008). The method used has been shown that may overestimate the column density through which the disc gas cools (Wilkins & Clarke, 2012; Young et al., 2012; Lombardi et al., 2015) by a factor of a few; however, considering that the dust opacity in discs is not known accurately enough, this limitation of the method is not critical for the results presented in this paper. The detailed treatment of radiative transfer is important when considering how the gas fragments but it is not expected to be crucial (at least qualitatively) for the issues relating to the mass growth and migration of protoplanets already formed in the disc that are discussed in this paper.
3.2 Opacities
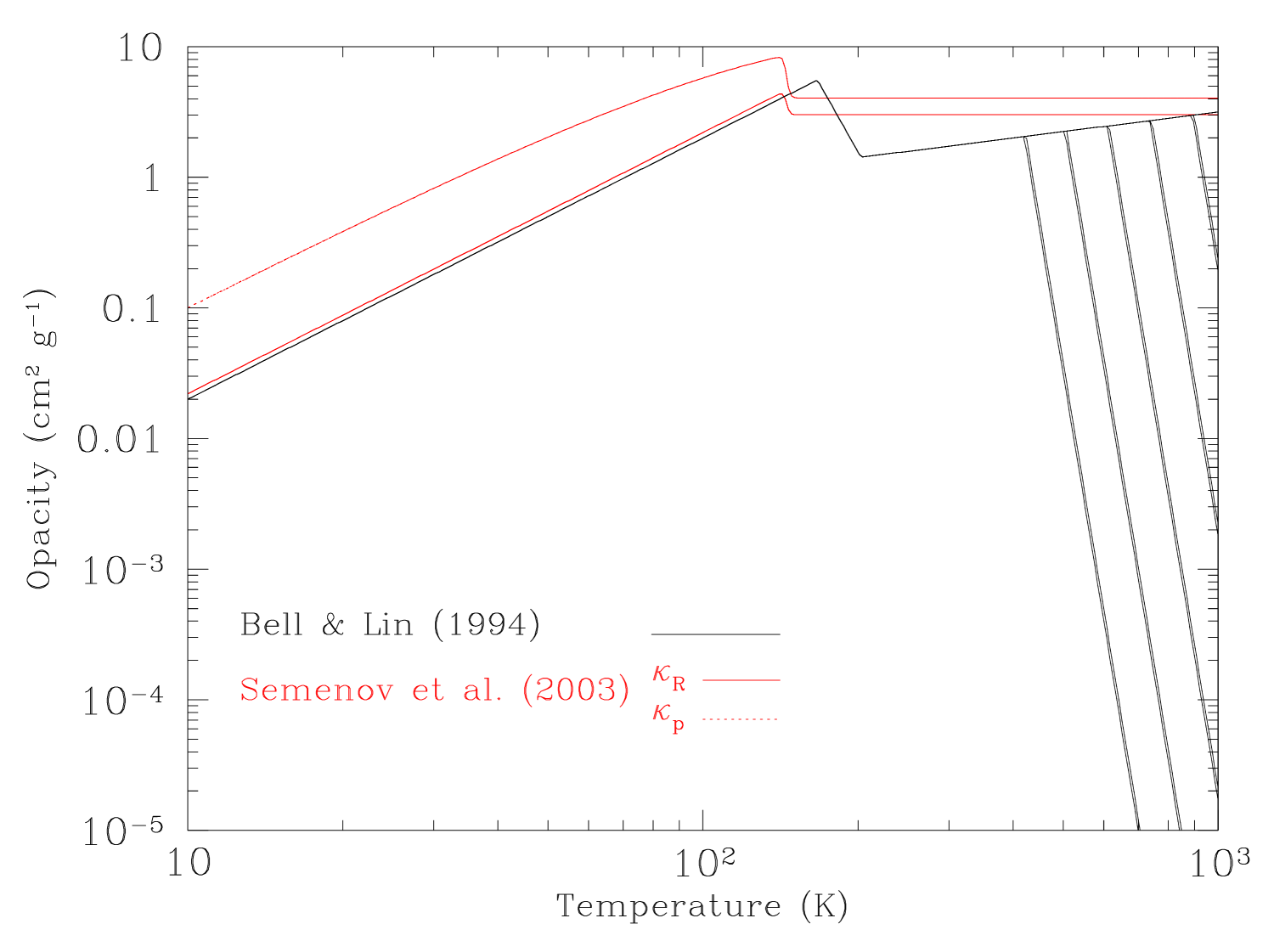
We use two prescriptions for the opacity the disc (see Figure 1):
-
1.
The Bell & Lin (1994) opacity which is parameterized as
(4) where , , are constants that depend on the species and the physical processes that contribute to the opacity at different densities and temperatures (note that Planck mean and Rosseland mean opacities are assumed to be the same). For the temperatures in the discs we simulate here (up to K) the opacity is due to dust grains that at low temperatures are coated with ice, which evaporates at higher temperatures. The dust grains start to evaporate at around 1,000 K.
-
2.
The Semenov et al. (2003) model includes similar physical processes but the dust considered includes spherical and aggregate particles of various sizes that consist of ice, organics, troilite, silicates and iron. This composition is thought to be more appropriate for the conditions found in protoplanetary discs.
The Semenov et al. Rosseland mean opacity is similar to the Bell & Lin one at temperatures up to K but higher at larger temperatures by up to a factor of 2. At such temperatures the optically thick parts of the disc cool less efficiently when using the Semenov et al. opacity. The Semenov et al. Planck mean opacity is larger by a factor of 5 than the Bell & Lin one, which means that the optically thin parts of the disc cool more efficiently.
The above two sets of opacities are widely used in the literature. However, the composition of dust in discs is rather uncertain, especially since significant dust growth may occur, lowering the opacity. It is unclear whether dust growth is significant at the early disc phase that we study here.
3.3 Sinks
Sink particles are used to represent the central star and the protoplanet (Bate et al., 1995). Sink particles interact with the rest of the computational domain only through their gravity (and their luminosity if their radiative feedback in considered, see below). The sink radius of the central star is AU, and the sink radius of the protoplanets is AU. This value is chosen to be smaller than the Hill radius of the protoplanet, i.e. the region around it where the its gravity dominates over the gravity of the star:
| (5) |
For example, when a Jovian planet is at 50 AU away from the central star then its Hill radius is AU. The Hill radius may increase as the protoplanet accretes material from the disc or it may decrease as the protoplanet moves closer to the central star.
Gas particles accrete onto a sink when they are within the sink radius and bound to the sink (Hubber et al., 2011b). The accretion rate onto the sink is computed by calculating the increase of the sink mass over a time interval that is comparable to the dynamical time of each particle at the edge of of the sink.
3.4 Radiative feedback from the protoplanet and the star
The radiation feedback from the protoplanet is taken into account (in a subset of the simulations) using the method described in Stamatellos (2015). We use the method of Stamatellos et al. (2011b) & Stamatellos et al. (2012) that invoke a pseudo-ambient radiation field with temperature due to radiation from the protoplanet (see also Stamatellos et al., 2007; Stamatellos & Whitworth, 2009a). This pseudo-ambient temperature sets the minimum temperature that the gas can attain if it cools radiatively. The contribution from the protoplanet is set to
| (6) |
where is the position on the disc midplane, and and are the luminosity and position of the protoplanet, respectively. The above approximation may overestimate the effect of the feedback in optically thick regions of the disc, that are well-shielded from the protoplanet (see discussion in Mercer & Stamatellos, 2017).
The luminosity of the protoplanet is set to
| (7) |
where is the mass of the protoplanet, is the accretion rate on to it, and the assumed accretion radius. is the fraction of the accretion energy that is radiated away at the photosphere of the protoplanet, rather than being expended driving jets (Machida et al., 2006; Offner et al., 2009), or deposited within the protoplanet (e.g. Baraffe et al., 2017).
The exact amount of the energy radiated away from the protoplanet depends on the detailed properties of the accretion shock around the protoplanet (Zhu, 2015; Marleau et al., 2017; Szulágyi & Mordasini, 2017; Mordasini et al., 2017). If this protoplanet has formed by gravitational instabilities in the disc then the accretion happens onto the second hydrostatic core (e.g. Larson, 1969; Stamatellos & Whitworth, 2009b). The radius of the second core is uncertain: (Masunaga & Inutsuka, 2000; Tomida et al., 2013; Vaytet et al., 2013; Bate, 2014; Tsukamoto et al., 2015). Here we assume , but the results of this work are not sensitive on this assumption. The accretion luminosity of the protoplanet is significant due to the relatively high accretion rate onto it during the initial stages of its evolution and can dominate over the stellar luminosity in the disc region around the protoplanet (Owen, 2014; Stamatellos, 2015; Montesinos et al., 2015), especially for the Jupiter-like planet-seeds in high-mass discs that we study here.
If the protoplanet has formed by disc fragmentation, on top of the significant accretion luminosity, it will also radiate energy due to its contraction. This energy release is on the order of 0.1 L☉ (Inutsuka et al., 2010), which is similar to the one expected from accretion. Therefore, the protoplanet’s luminosity is deemed to play an important role in its evolution (Nayakshin & Cha, 2013; Stamatellos, 2015; Benítez-Llambay et al., 2015). We do not take this radiation explicitly into account in the simulations presented in this paper but we have performed runs with smaller resulting in higher luminosity for the protoplanet. These runs give qualitatively similar results to the ones we discuss in this paper.
The radiation feedback from the star is taken into account (in a subset of the simulations) by invoking an additional pseudo-ambient temperature,
| (8) |
where is the distance from the central star on the disc midplane, and the temperature at AU from the star. The total pseudo-ambient temperature (due to the central star and the protoplanet) is then set to
| (9) |
where is the contribution from the protoplanet. Note that the radiative feedback from the star is fixed in time for simplicity, whereas the radiative feedback from the protoplanet is variable and depends on the accretion rate of gas onto it as it moves within the disc.
4 Simulations of prototoplanets evolving in young discs
We follow the evolution of a protoplanet embedded in the disc for 20 kyr (approximately 20 disc outer orbital periods). The initial mass of the protoplanet is and it is placed at distance 50 AU. In this first set of simulations we ignore any radiative feedback from the central star. The effect of irradiation from the central star will be studied in Sections 7 and in Appendix B. We perform the following 5 numerical experiments (see Table 1):
-
1.
Run 1: No radiative feedback from the central star nor the protoplanet are included (hereafter referred to as the standard run).
-
2.
Run 2: Radiative feedback from the protoplanet is included.
-
3.
Run 3: Same as the standard run but with higher viscosity (viscosity ; in all other runs).
-
4.
Run 4: Same as the standard run but in which the protoplanet has an orbit that has an initial inclination of with respect to the disc midplane.
- 5.
| Run id | Opacity | |||||
|---|---|---|---|---|---|---|
| (AU) | (MJ) | (AU) | ||||
| Run 1 | BL946 | 40 | 24 | 40 | 0.035 | |
| Run 2 | BL946 | 40 | 15 | 17 | 0.0012 | |
| Run 3 | BL946 | 40 | 29 | 37 | 0.13 | |
| Run 4 | BL946 | 40 | 25 | 36 | 0.017 | |
| Run 5 | SEM037 | 40 | 31 | 53 | 0.17 |
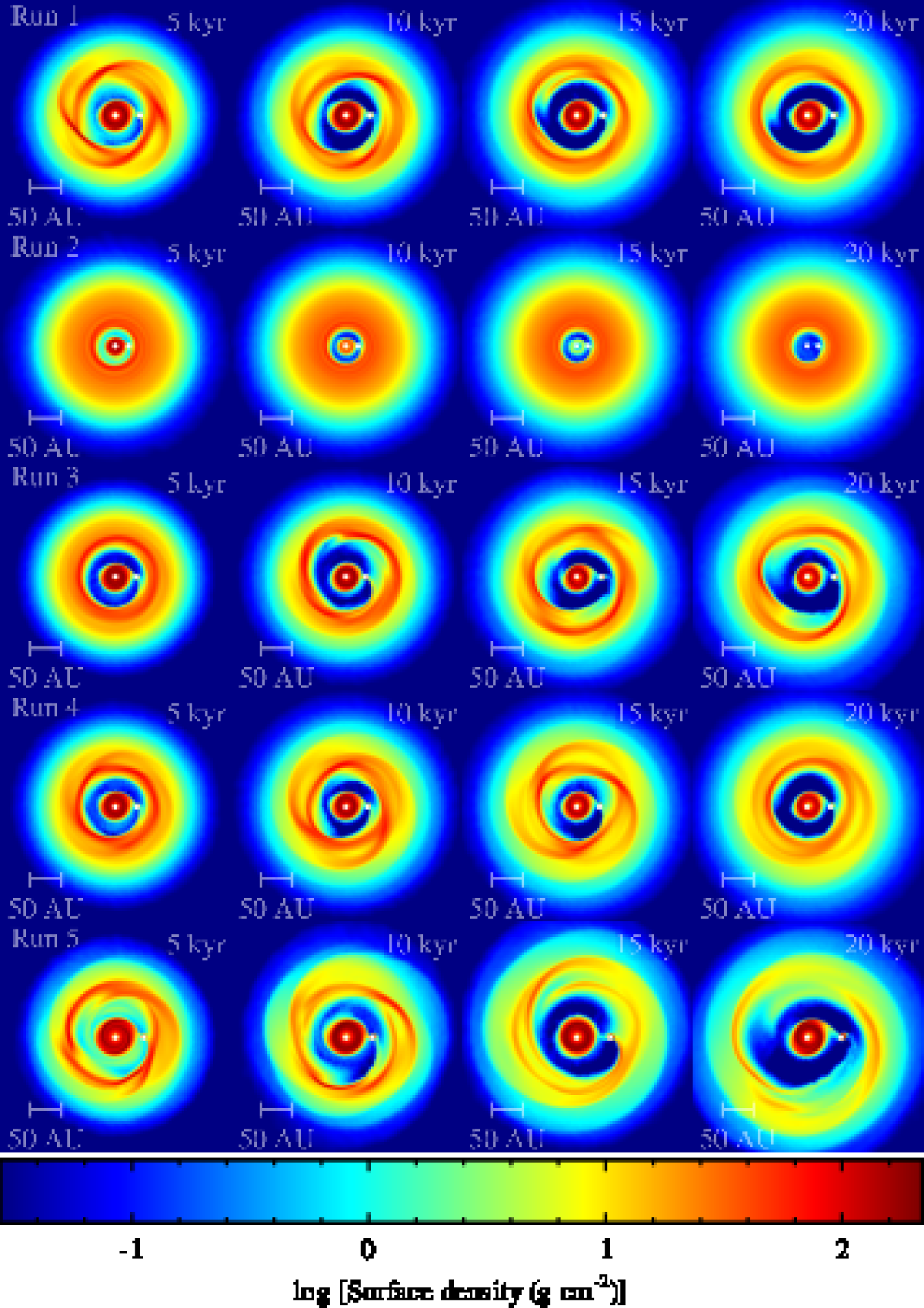
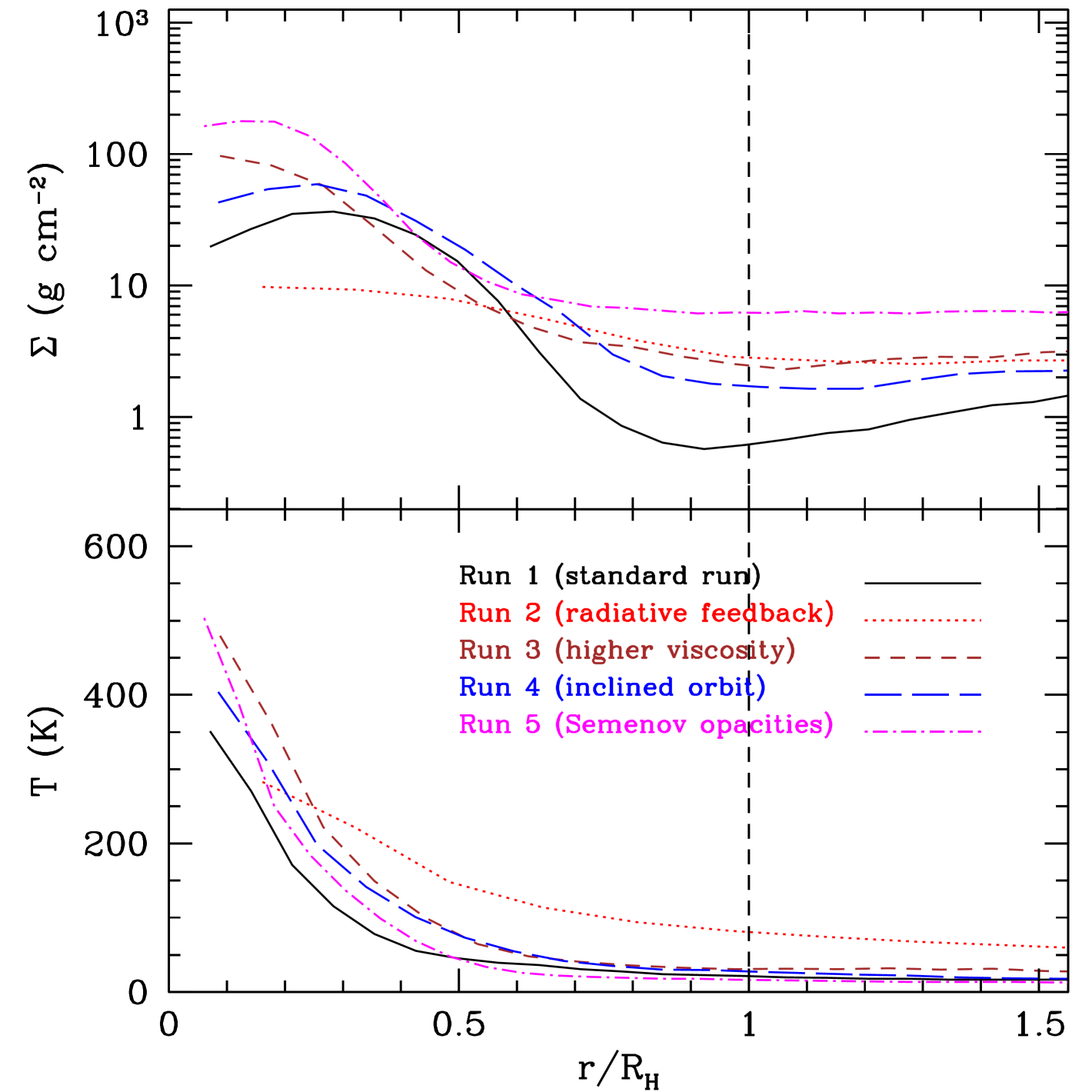
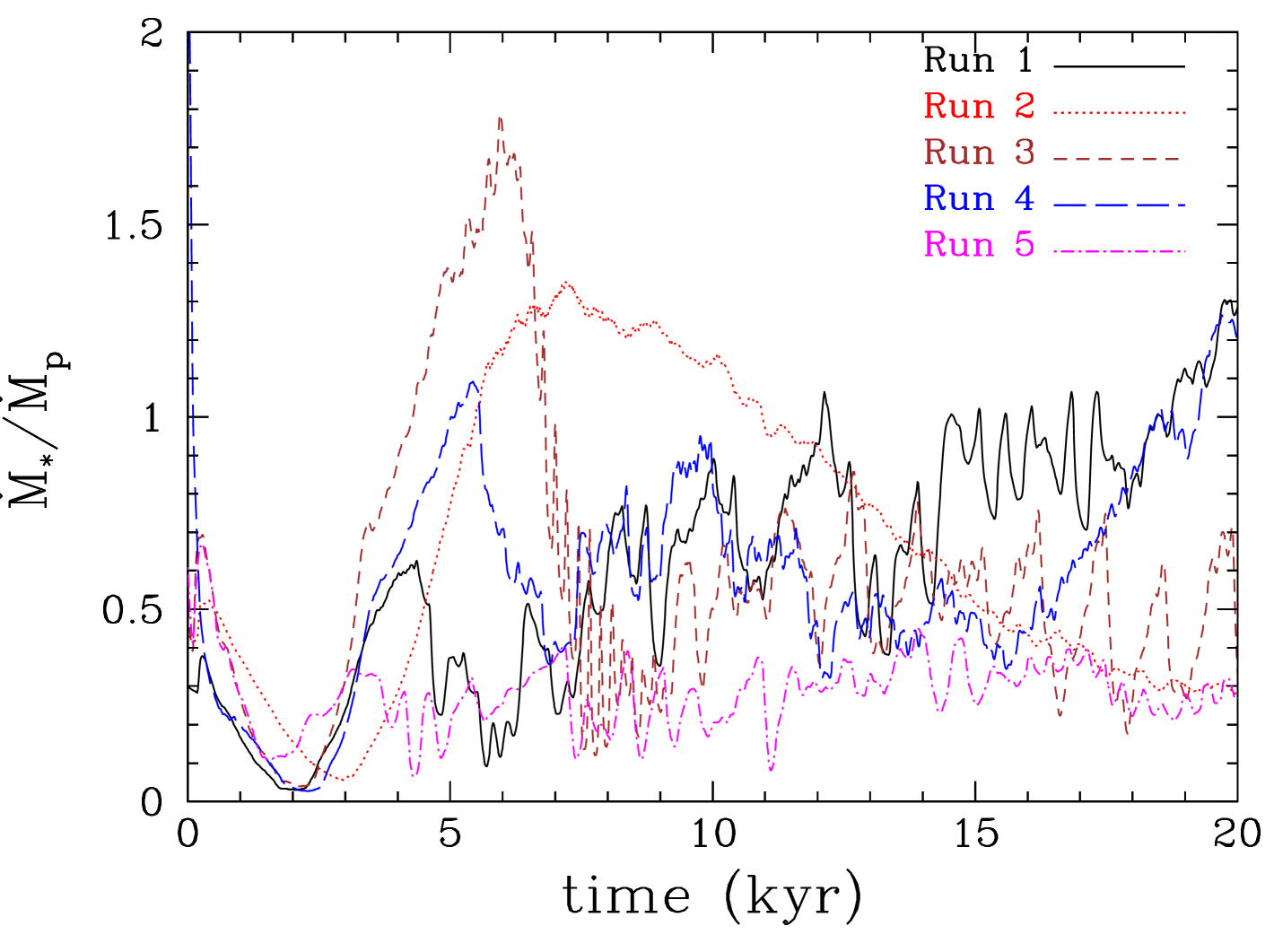
The evolution of the disc surface density for all 5 runs is shown in Figure 2. We calculate the migration timescale as
| (10) |
where is the protoplanet’s semi-major axis. In all runs the protoplanet initially migrates inwards fast (see Tables 7-7), with a migration timescale of yr, as previous studies have found (Vorobyov & Basu, 2006; Baruteau et al., 2011; Michael et al., 2011; Zhu et al., 2012; Malik et al., 2015). However, as the protoplanet migrates inwards it considerably grows in mass by accreting gas from the disc. Eventually the protoplanet is able to open up a gap and the migration slows down (for the case with radiative feedback from the protoplanet; migration timescale yr) or even changes to an outward direction (migration timescale yr) in the rest of the runs (see Stamatellos, 2015). After a gap is opened up, the protoplanet grows in mass slowly, by accreting a significant amount of material from the disc outside its orbit. An important difference of this study from previous ones (e.g. Baruteau et al., 2011; Michael et al., 2011) is that the protoplanet is allowed to grow in mass. This is especially significant for the case of self-gravitating discs as the protoplanet evolves in a relatively massive disc with a significant amount of gas available for accretion. In the following subsections we discuss in detail the evolution of the protoplanet within the disc in the different runs we have performed.
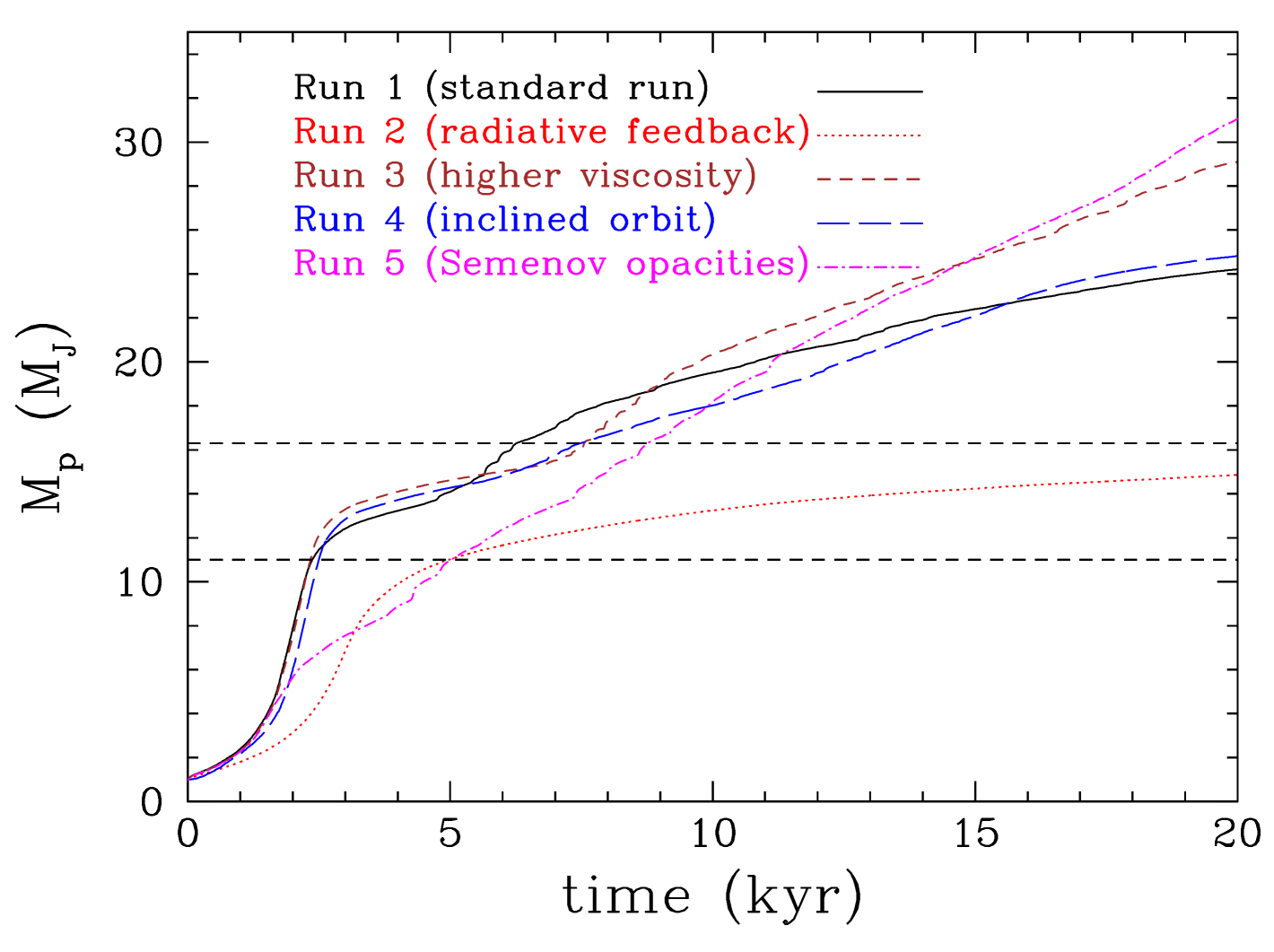
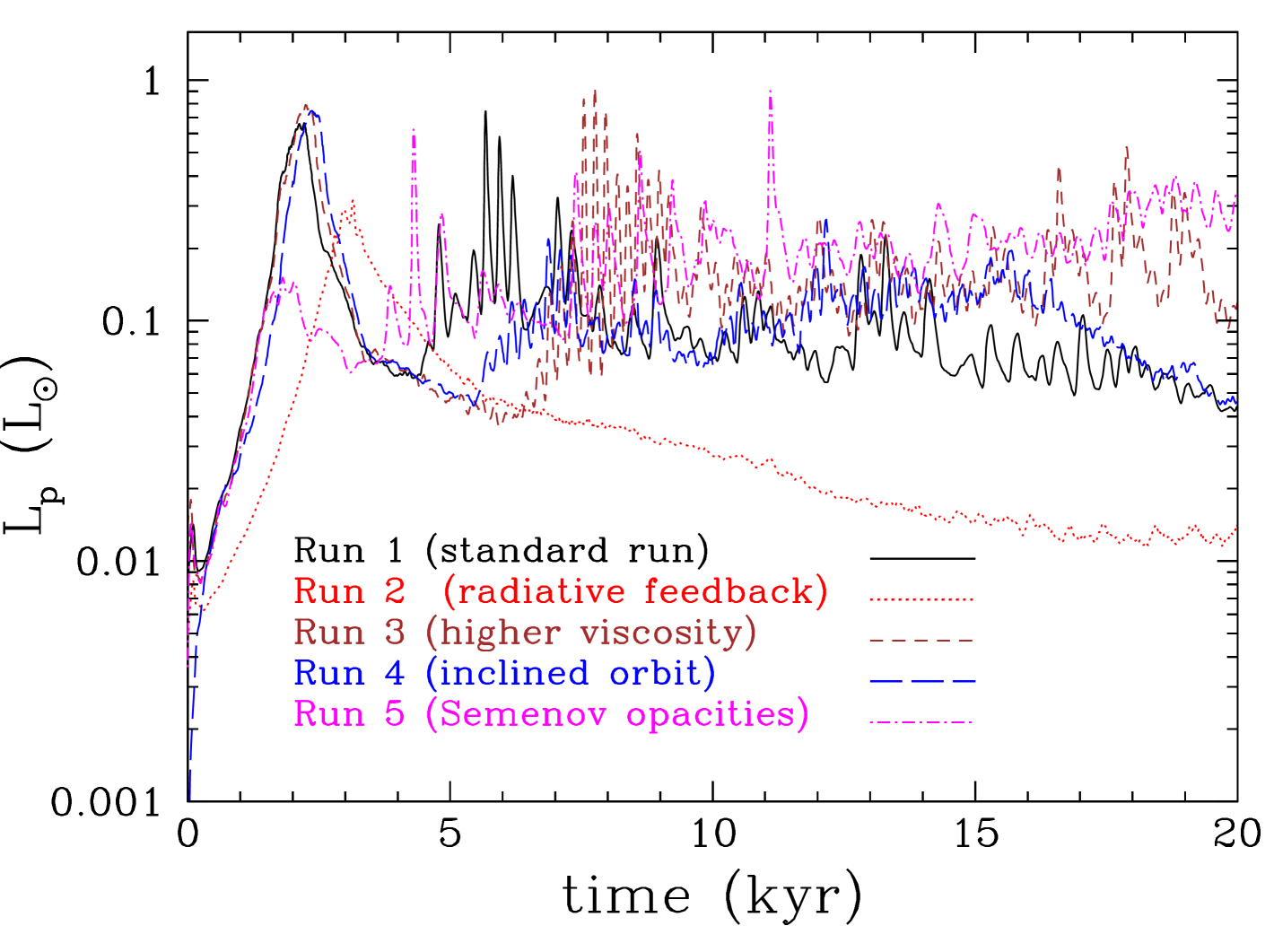
4.1 Protoplanet mass growth
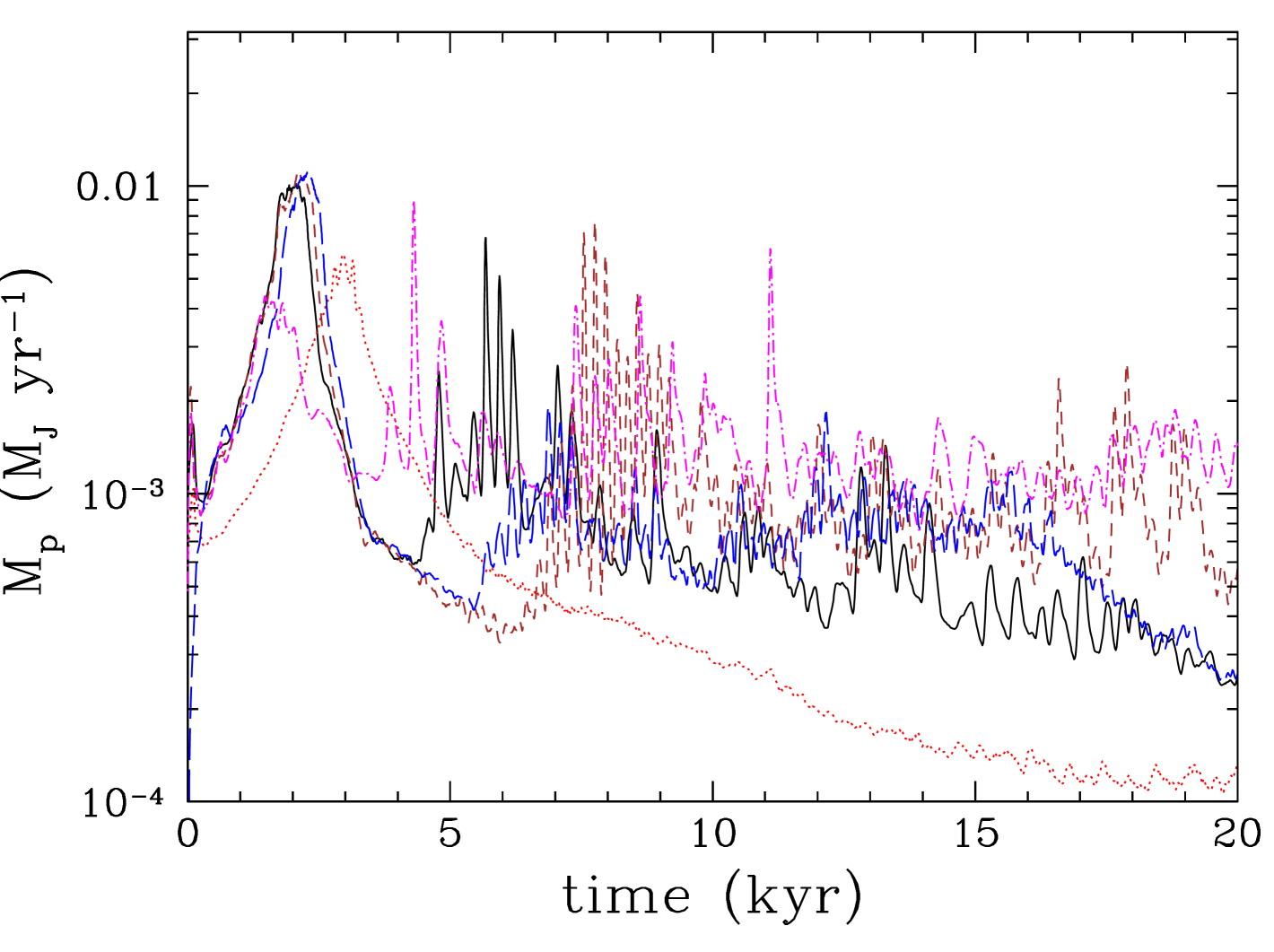
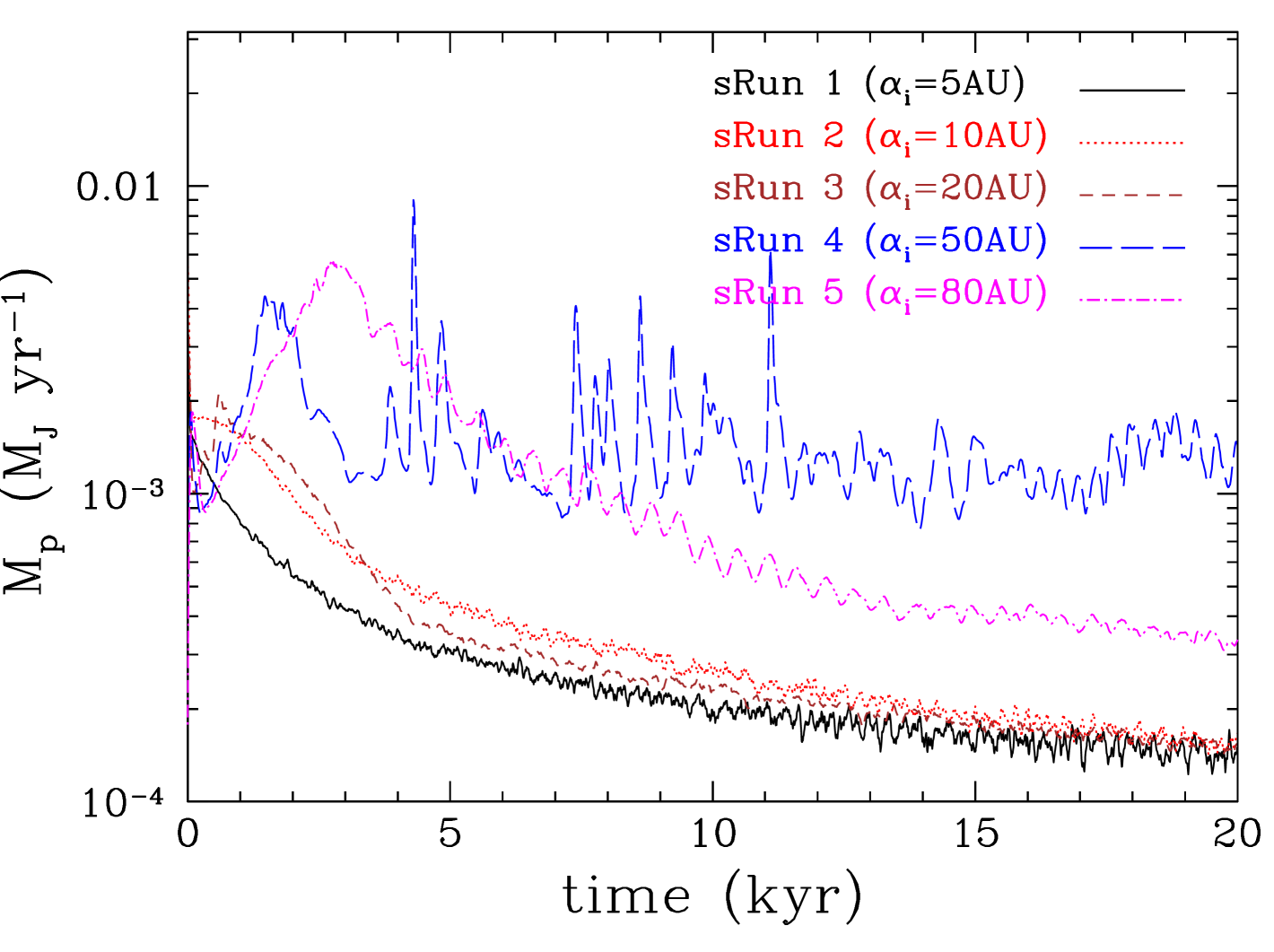
The protoplanet grows in mass initially very fast as it opens up a gap but its mass increase slows down once the gap is opened up (see Figure 4). The accretion rate onto the protoplanet (see Figure 4, top) is relatively high () during the gap opening phase but then it drops down; nevertheless, accretion continues through streams within the gap (Lubow & D’Angelo, 2006). Similarly high accretion rates are also seen in previous studies (D’Angelo & Lubow, 2008; Ayliffe & Bate, 2009; Zhu et al., 2012; Gressel et al., 2013). The resulting luminosity of the protoplanet (see Figure 4, bottom) could rival the luminosity of the young star making its detection easier in terms of the sensitivity required. However, this phase of high accretion lasts only for a relatively short time, making such a detection difficult. These luminosity estimates are only up to a few times higher than the luminosities estimated from hot-start models of planet formation (Marley et al., 2007; Mordasini, 2013; Mordasini et al., 2017). The value of the luminosity depends on the accretion radius, which in our model is set assuming that gas accretion happens onto the second core formed after the temperature at centre of the protoplanet-precursor clump reaches K and molecular hydrogen dissociates (e.g. see Stamatellos & Whitworth, 2009b). The accretion rate onto the protoplanet decreases after the gap is opened up but thereafter it shows many spikes, some with periodicity similar to the orbital period of the planet at each specific time, indicating periodic interactions with spiral structures in the disc that drive gas accretion onto the protoplanet. Such spikes are absent when the radiative feedback of the planet is taken into account (Run 2) as strong spiral features are suppressed. There is a delay of kyr between the gap opening and the gap edges becoming gravitationally unstable, driving accretion onto the protoplanet. The delay is longer for protoplanets that are closer to the central star, i.e. in a warmer region of the disc, as more gas needs to accumulate for the gap edges to become unstable. The accretion rate onto the protoplanet is generally lower when the protoplanet’s radiative feedback is included in the simulation as seen in previous studies (Nayakshin & Cha, 2013; Stamatellos, 2015; Gárate et al., 2017).
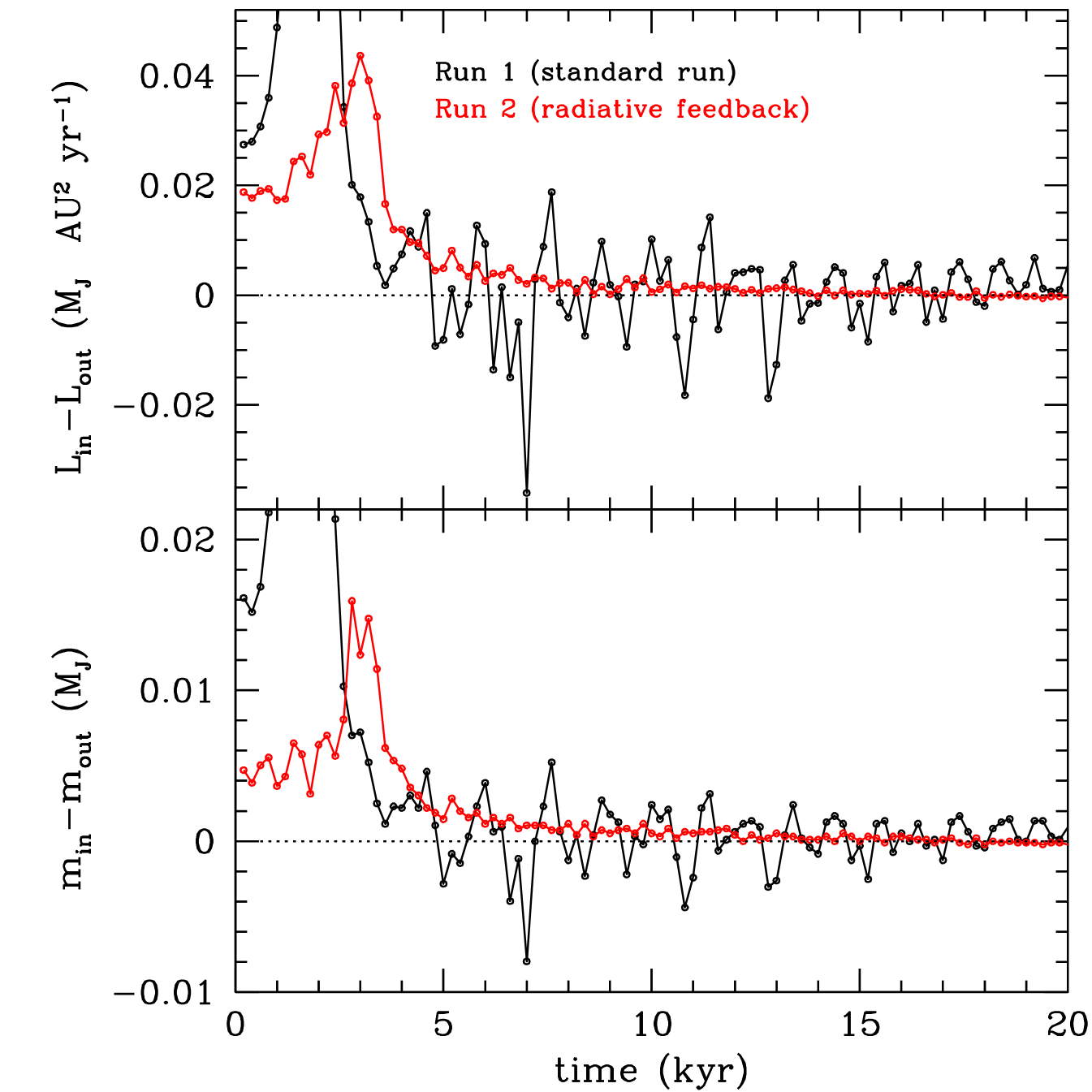
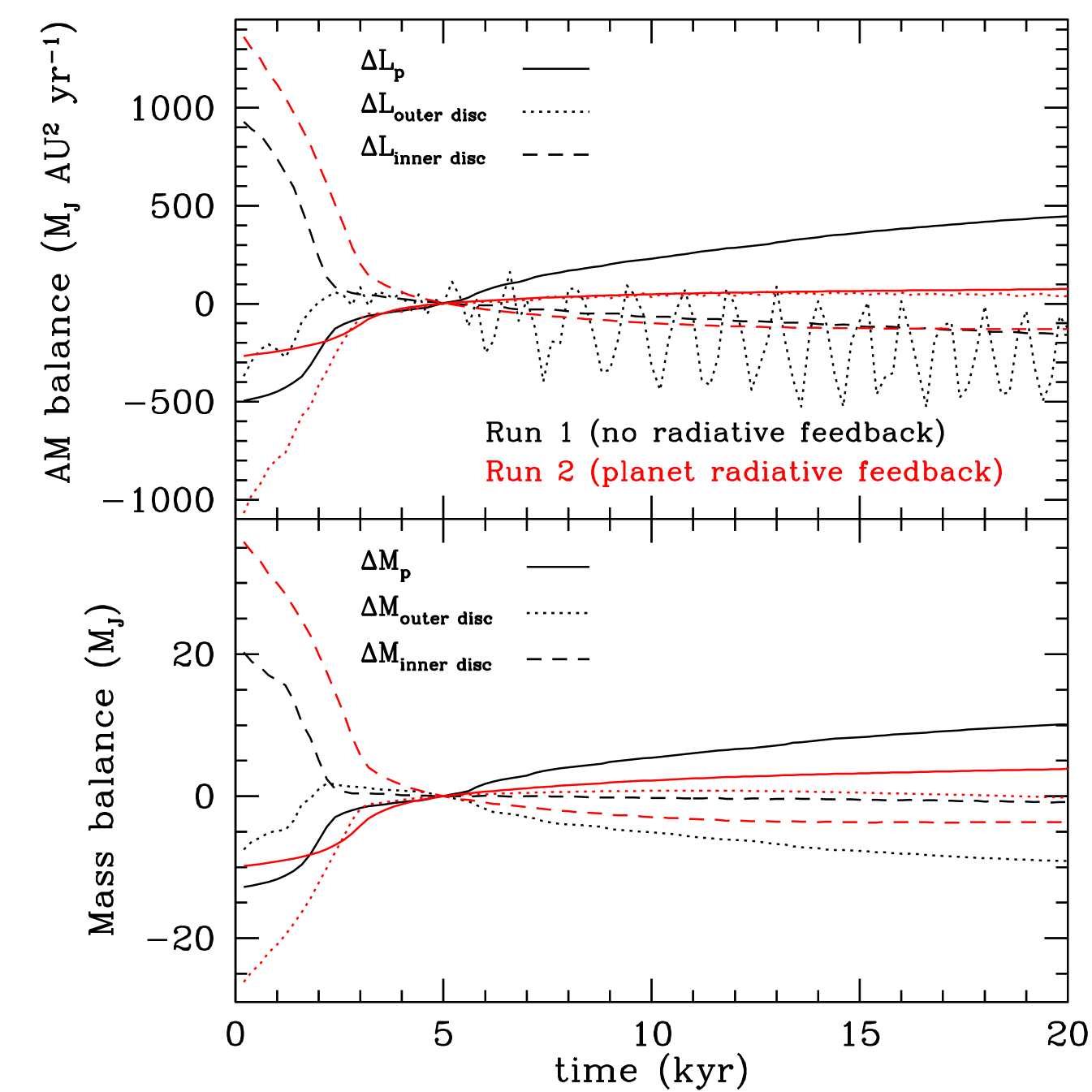
The way that gas is accreted onto the protoplanet depends on the dynamical state of the protostellar disc. In Figure 6 we plot the difference between the angular momentum of the gas entering the protoplanet’s Hill sphere from inside the protoplanet’s orbit (), and the angular momentum of the gas entering the Hill sphere from outside the protoplanet’s orbit (). To calculate these we use the mass of gas within distance 111 The same result is obtained for a different outer limit, e.g. if we consider the gas within distance from the protoplanet. from the protoplanet that moves towards the protoplanet from inside its orbit (), and the gas that moves towards the protoplanet from outside its orbit () (Figure 6, bottom). During the initial gap opening phase, in both cases, gas is accreted onto the protoplanet mostly from the inner disc. After the initial gap opening phase ( kyr), we see that for the run including the protoplanet’s radiative feedback (Run 2, red), in which the disc is gravitationally stable because of the effect of the protoplanet’s feedback, most of of the accreted gas comes from inside the protoplanet’s orbit. The total accreted gas in this case has lower angular momentum than the protoplanet, so that the protoplanet’s angular momentum decreases. On the other hand, in the case without the feedback (Run 1, black), the disc is gravitationally unstable and a high fraction of the accreted gas (up to almost 50%) comes from outside the protoplanet’s orbit. This gas has higher angular momentum than the protoplanet.
This can also be seen in Figure 6 where we plot the change of angular momentum (top) and mass (bottom) of the protoplanet (, ), the inner disc (i.e. the disc inside the protoplanet’s orbit; , ), and the outer disc (, ). In Run 1 the protoplanet increases in mass while the outer disc mass decreases, whereas in Run 2, in which the protoplanet’s feedback is included, the outer disc mass remains almost steady (after 5 kyr) whereas the inner disc mass decreases as the mass of the protoplanet increases.
Apart from the run with the protoplanet’s radiative feedback, there are only relatively subtle differences in the accretion onto the protoplanets in the other runs. As expected, for a higher disc viscosity the gap opens up at a later time (Crida et al., 2006), but thereafter the accretion rate into the protoplanet is higher, resulting in a higher final mass.
The gap opens up faster in the run with the Semenov et al. (2003) opacities, which are generally larger than the Bell & Lin (1994) opacities, and the accretion rate thereafter is larger by a factor of than in the other runs. This is because the Semenov et al. (2003) opacities correspond to more efficient cooling (see Nayakshin, 2017b), and therefore: (i) the disc is cooler, enabling the quick opening of the gap, and (ii) the thermal pressure of the circumplanetary disc is lower and gas accretion is not opposed as much as in the other runs. The dependence of the accretion rate and the final mass of the object on the assumed opacity seems to be different from what is seen in Nayakshin (2017b). However, what matters is not the opacity itself but the cooling of the gas around the protoplanet. Nayakshin (2017b) employs an opacity that regulates gas cooling both in optically thin and optically thick regimes (i.e. the Planck-mean and Rosseland-mean opacities are the same), whereas the Semenov et al. (2003) opacity account of the differences between these regime. The higher Planck-mean opacity of Semenov et al. (2003) results in more efficient cooling in the optically thin regions (see Equation 3; in the optically thin limit the denominator on the right hand side is dominated by the term). Therefore as in Nayakshin (2017b) our results mean that the gas accretion onto the protoplanet with more efficient cooling is higher. Similar results are also found by Ormel et al. (2015a, b) when studying accretion onto massive solid planet cores.
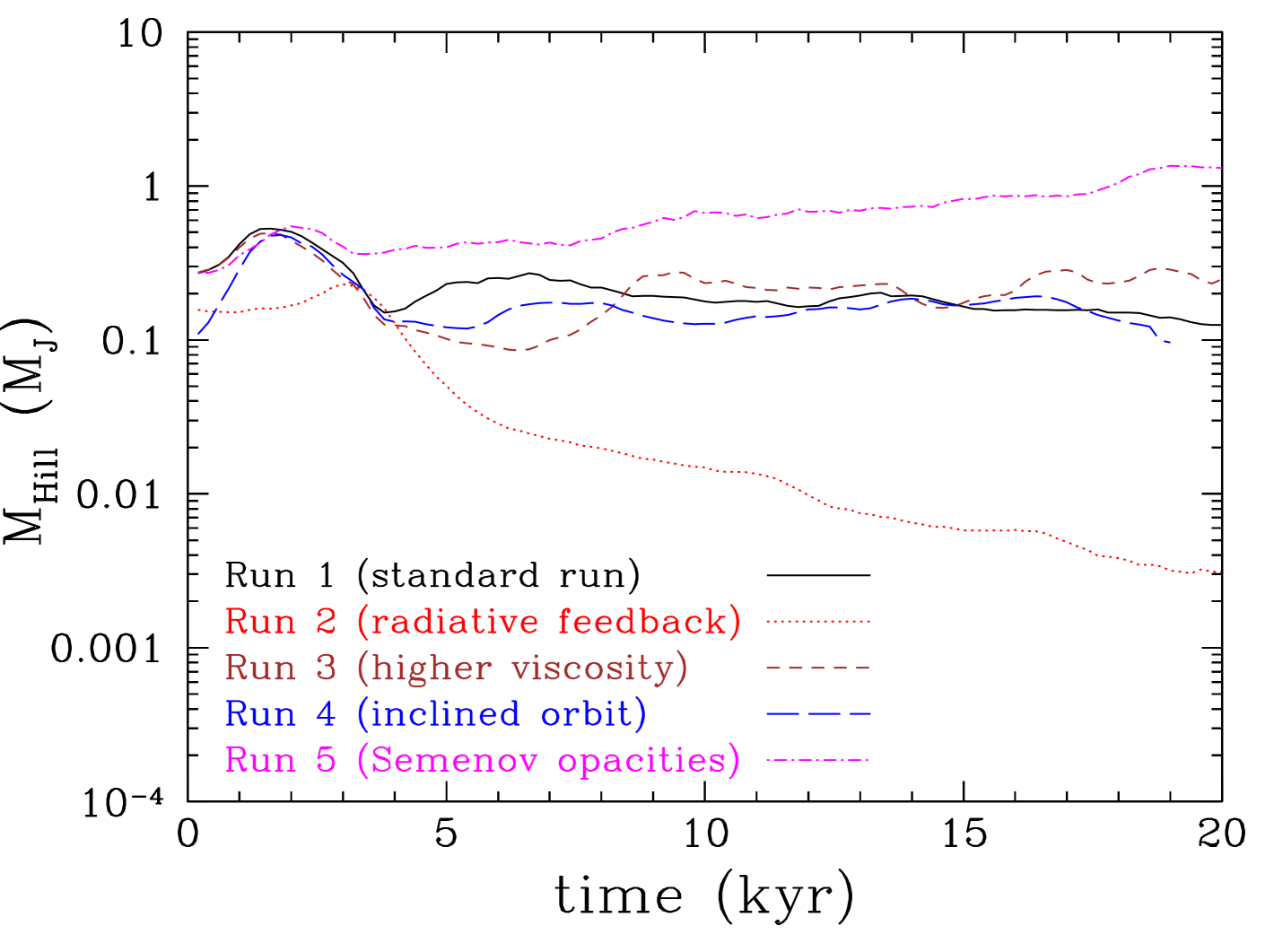
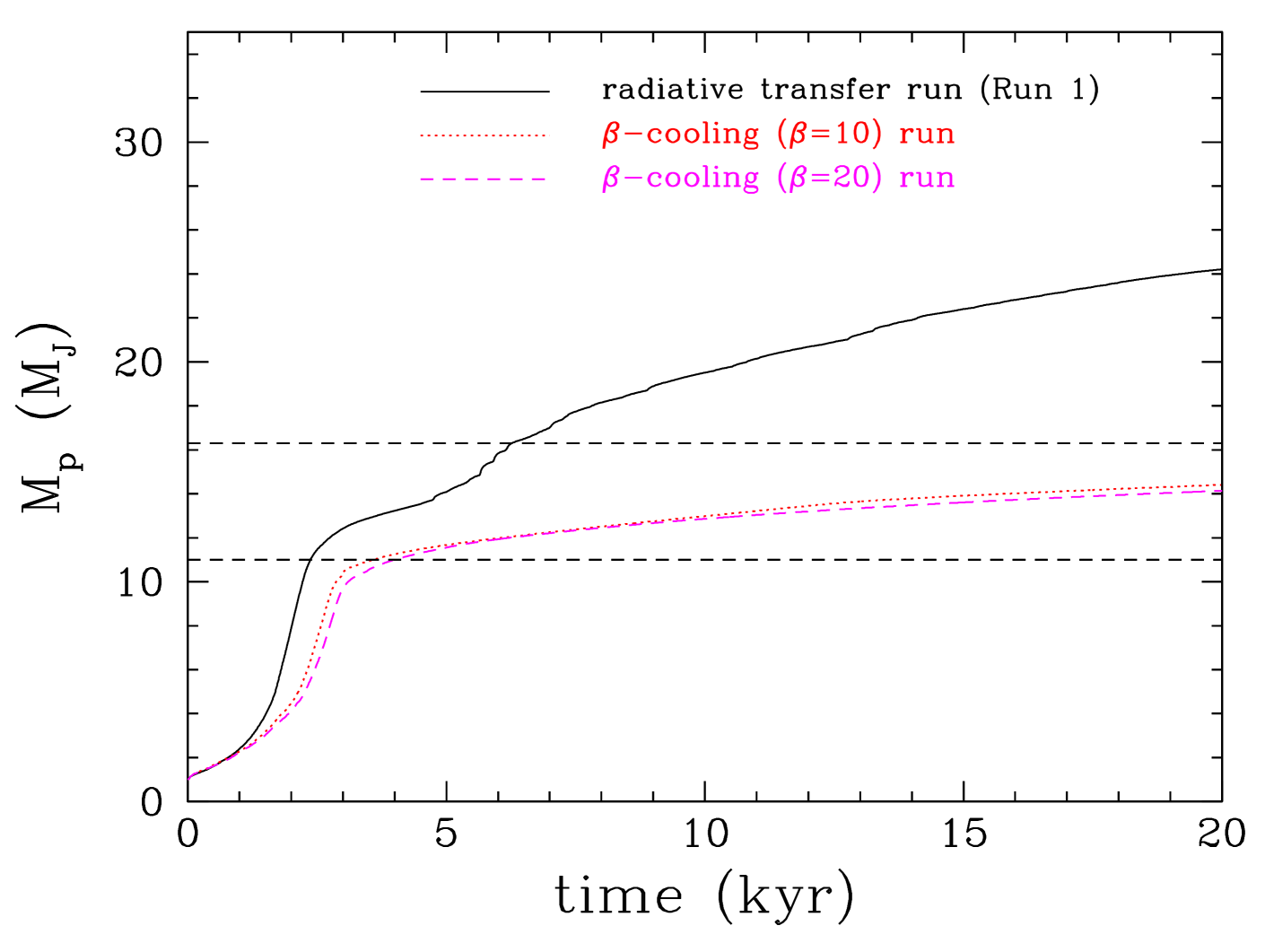
We see that in all cases, apart from the one in which the protoplanet radiative feedback has been included, the protoplanet’s final mass (i.e. the mass at the end of the hydrodynamic simulation; kyr) is in the brown dwarf regime (). The protoplanet’s mass in the case in which its radiative feedback is taken into account is at the borderline between the planetary and brown dwarf regime. However, it is expected that the protoplanet will continue to accrete gas and eventually become a brown dwarf (unless the disc dissipates by other processes, like e.g. photo-evaporation, on a faster timescale). Nevertheless, when the protoplanet’s radiative feedback is taken into account the mass growth of the protoplanet has been suppressed and, at the end of the simulation, its mass is lower by a factor of than in the other runs.
4.2 Protoplanet migration
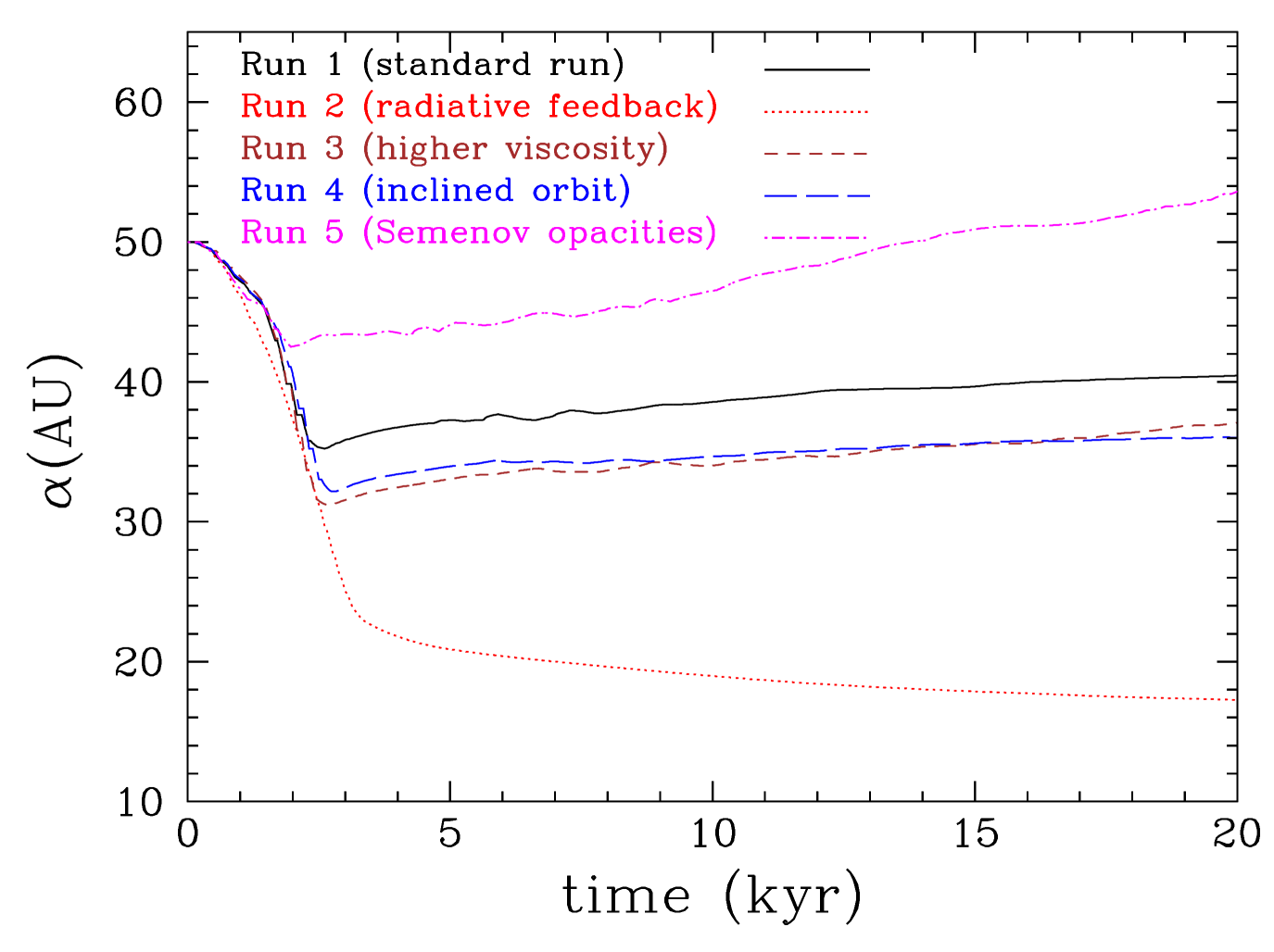
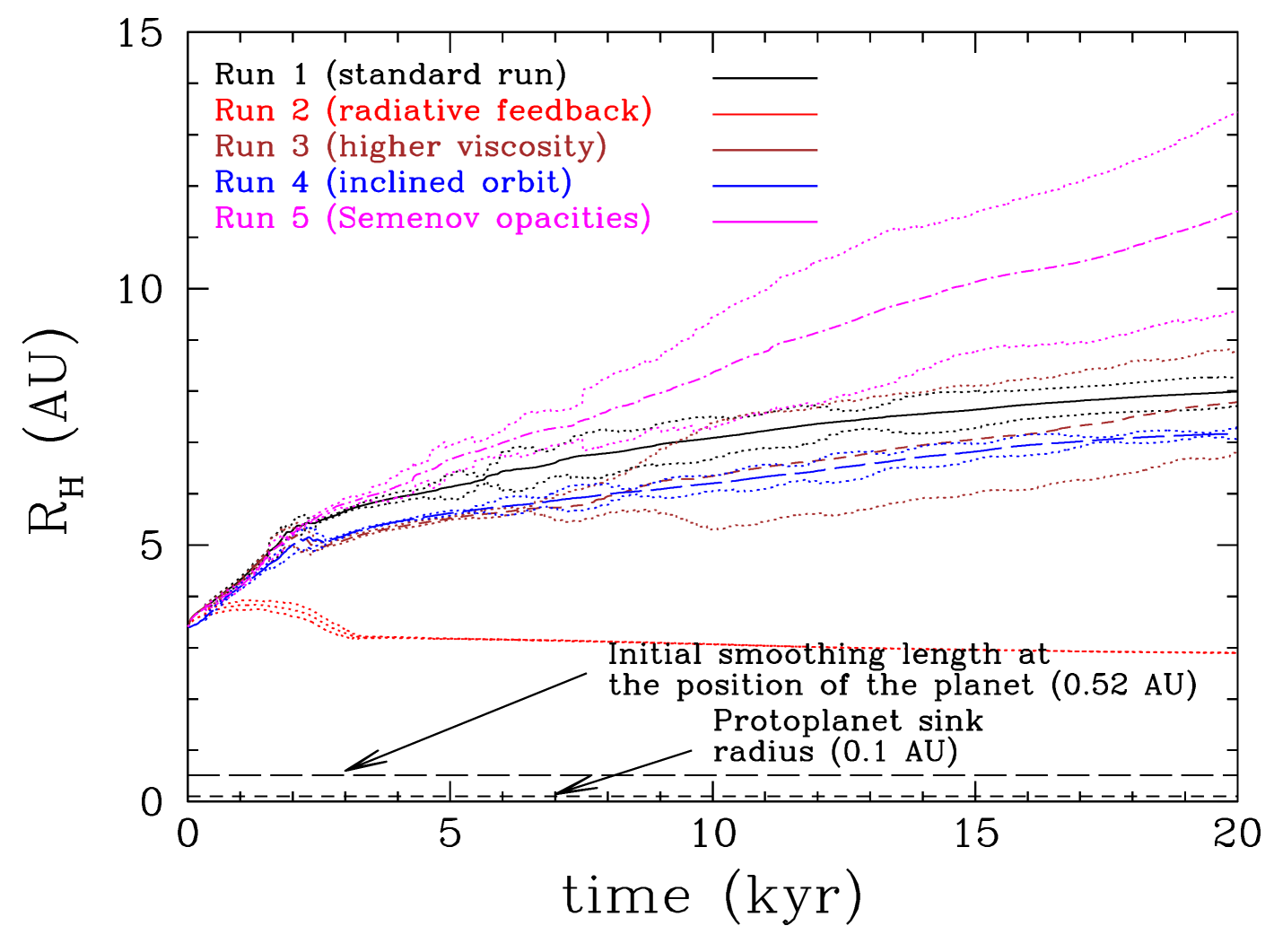
The protoplanet initially interacts strongly with the disc resulting in fast inward migration, similar to the Type I migration for low-mass planets in low-mass discs. The migration timescale is only yr and it is similar for all 5 runs (see Figures 7, 8 and Tables 7, 7). However, once a gap opens up the migration stalls; this happens at different times for each run. When the planet orbit plane is not the same with the disc midplane (Run 3) it is more difficult for the protoplanet to open up a gap. In the same way, the more viscous is the disc (Run 4) the more difficult is to open up a gap (e.g Crida et al., 2006; Malik et al., 2015). In both cases there is delay in opening up a gap and the protoplanet migrates further inwards (but only by AU compared with the other runs). In the four runs without radiative feedback from the protoplanet, the protoplanet switches to a slow outward migration. At the end of the simulations (20 kyr) the protoplanet’s semi-major axis has moved to 40, 38, and 36 au, for Runs 1, 2, and 3, respectively, from an initial semi-major axis of 50 au. In Run 5 with the higher opacity (faster cooling) (Semenov et al., 2003) the gap opens up quicker and the protoplanet starts migrating outwards reaching a semi-major axis of 53 AU at the end of the simulation.
The case that it is distinctly different is the one in which the radiative feedback from the planet is taken into account (Run 2). In this case the opening up of the gap is more difficult as the protoplanet heats its circumplanetary disc but also the host protostellar disc (Marley et al., 2007; Nayakshin & Cha, 2013; Benítez-Llambay et al., 2015; Montesinos et al., 2015; Stamatellos, 2015; Szulágyi & Mordasini, 2017). Therefore the gap opens at a later time ( kyr later) and the protoplanet migrates closer to central star. Its inward migration continues after the gap is opened up but at a much longer timescale ( yr; typical of Type II migration). At the end of the simulations (20 kyr) the protoplanet is at 18 AU from the central star.
Lin & Papaloizou (2012) and Cloutier & Lin (2013) have shown that when a planet resides in a gap that has gravitationally unstable edges, gas is brought into the planet’s co-orbital region by the spiral arms, resulting in a positive torque that pushes the planet outwards. This is indeed what we see here in the runs without the radiative feedback from the protoplanet. In these runs, a significant amount of the gas accreted onto the protoplanet is high angular momentum material coming from outside the protoplanet’s orbit (see Figs. 6-6). On the other hand, when the radiative feedback from the protoplanet is taken into account the temperature at the edges of the gap is raised, they are not gravitationally unstable anymore, and the protoplanet accretes a higher fraction of lower angular momentum gas from the disc inside its orbit.
Contrary to previous studies of (Baruteau et al., 2011; Michael et al., 2011; Malik et al., 2015), we allow the protoplanet to accrete gas and grow in mass. By growing in mass, it is more capable to open up a gap. In previous studies mass is accumulated in the circumplanetary disc and therefore contributed to strongly couple the protoplanet with the gaseous disc in which it is formed. This behaviour is also seen in the simulations of Nayakshin & Cha (2013). However, the crucial difference with previous studies is that we use a more detailed prescription for the radiative transfer in the disc. Our prescription allows the circumstellar and circumplanetary material to moderate the efficiency of its cooling as it becomes more or less dense, whereas the studies of Baruteau et al. (2011) and Malik et al. (2015) use the -cooling approximation, in which the cooling time is proportional to the local orbital period of the gas, i.e. . In Section 5 we discuss this issue in detail.
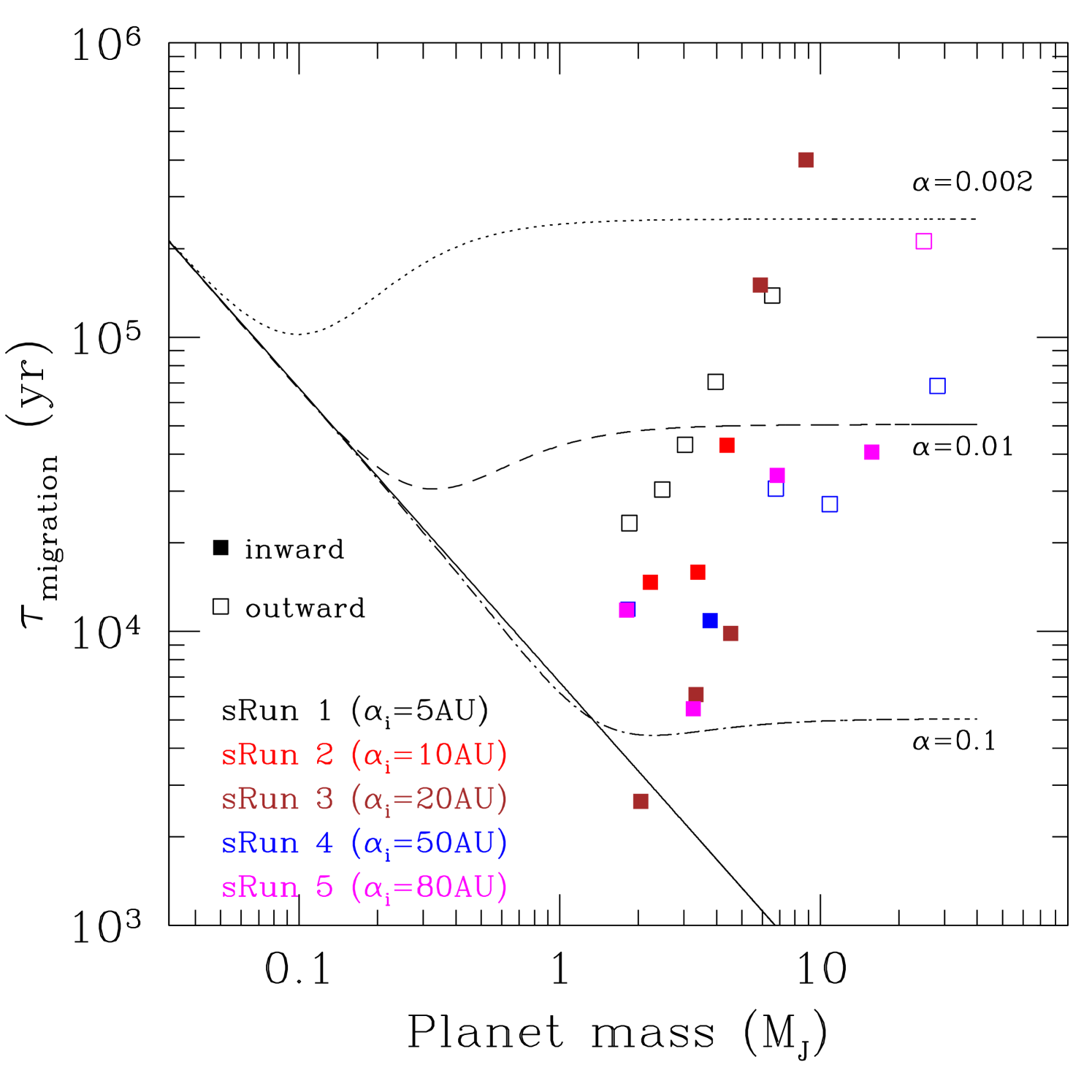
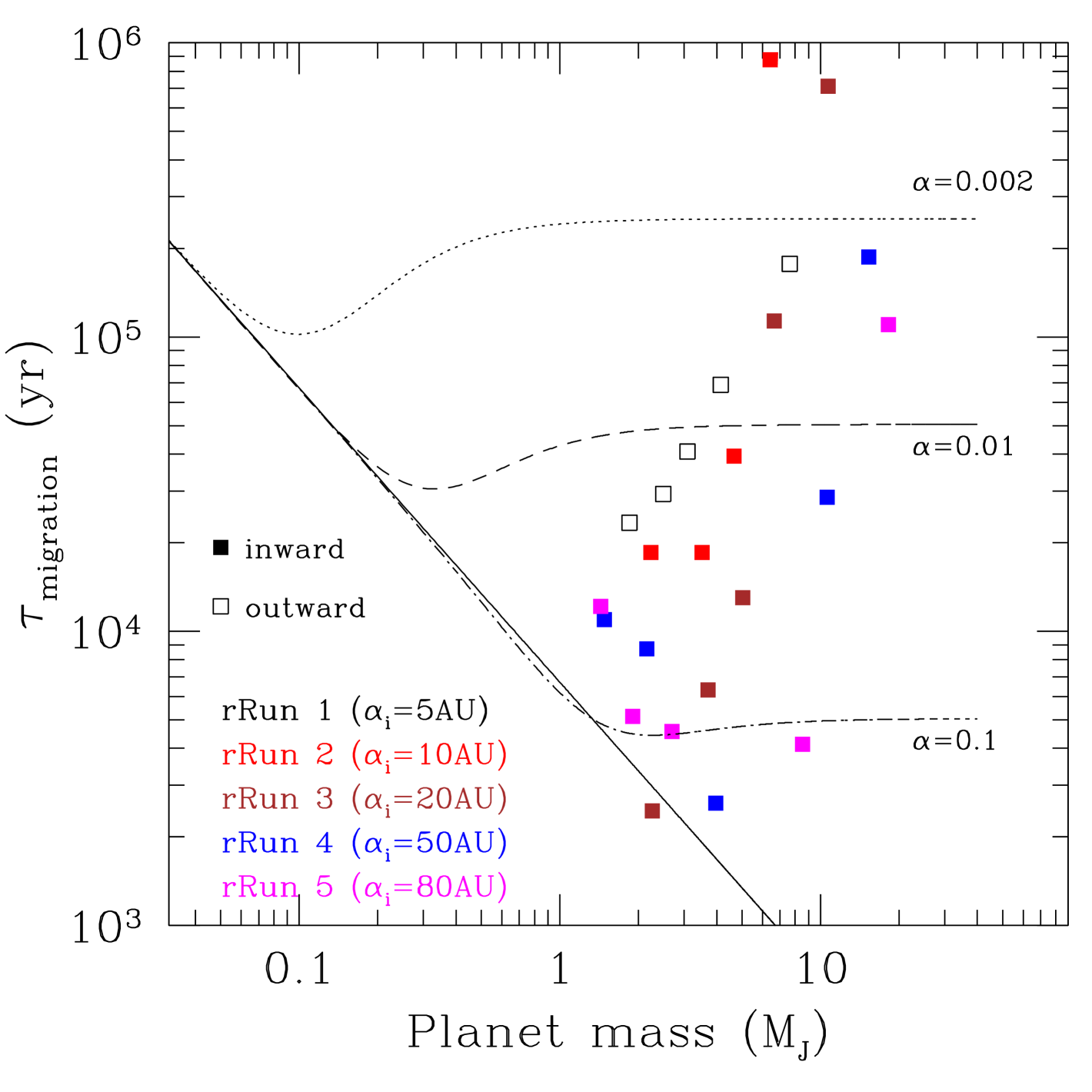
The estimated migration timescales () are shown in Table 7, and the migration rates () inTable 7. These values are calculated at 5 different times during the simulations. The migration timescales for all 5 runs are plotted against the protoplanet mass in Figure 8. On the same graph we plot the estimated migration timescales for Type I and Type II migration as calculated by Ward (1997) and Tanaka et al. (2002) (see also Bate et al., 2003).
The Type I migration rate estimated by Tanaka et al. (2002) is
| (11) |
where is the exponent of the disc surface density profile (), the orbital radius of the planet, the surface density of the disc at the position of the planet, the disc thickness at the position of the planet, and the planet’s angular frequency. The rate of migration of the Type II case is set by the viscous evolution of the disc (e.g. Bate et al., 2003):
| (12) |
where is the disc viscosity parameter. We note though that the actual Type II migration timescale may vary from the above approximation (Crida & Morbidelli, 2007; Duffell et al., 2014; Dürmann & Kley, 2015, 2017). For example, Dürmann & Kley (2015, 2017) find that due to gas crossing through the gap Type II migration may be faster or slower. The total rate of migration, combining the Type I and Type II regimes, is therefore
| (13) |
is the transition mass between Type I and Type II migration (Ward, 1997) and is set to
| (14) |
The migration timescale is therefore
| (15) |
We calculate the migration timescales from the above equations assuming a planet at AU in a disc with , , and . In Figure 8, we plot 3 cases that correspond to different disc viscosity (). We note that these calculations are for planets in low-mass discs at specific regimes: Tanaka et al. (2002) study 3D discs including both Lindbland and corotational resonances assuming an isothermal disc, whereas Ward (1997) study a 2D disc ignoring corotational resonances. These calculations are not applicable for the cases we examine in this paper. Therefore, these analytic solutions are plotted in the graph in Figure 8 merely for reference, so as to put our results in context with the classic picture of Type I and Type II migration.
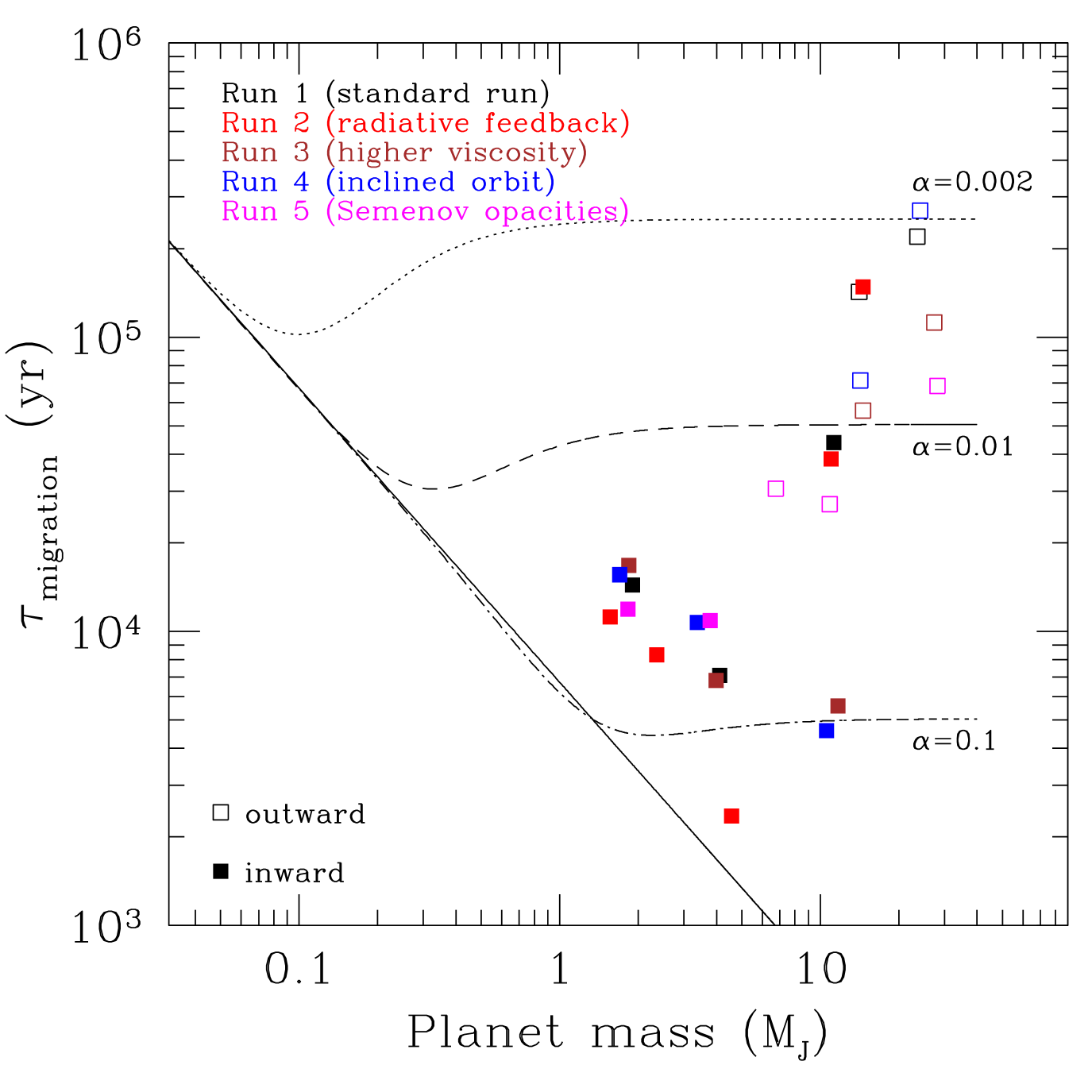
The migration timescales in Figure 8 are plotted for 5 different times in the simulation: 0.7, 1.5, 2.5, 5 and 18 kyr. As the mass of the protoplanet increases with time, the same graph may be used to track the evolution of the migration timescale with time. In all runs the protoplanet initially migrates inwards on timescales similar to the Type I migration timescale of a planet, i.e. yr. As the protoplanet moves towards the host star and grows in mass, the migration timescale becomes shorter (down to yr), but once the gap opens up the migration slows down and eventually the protoplanet starts moving outwards in all runs apart from the case when its radiative feedback is taken into account. In this case, inward migration continues albeit at a much longer timescale, similar to the Type II migration case ( yr).
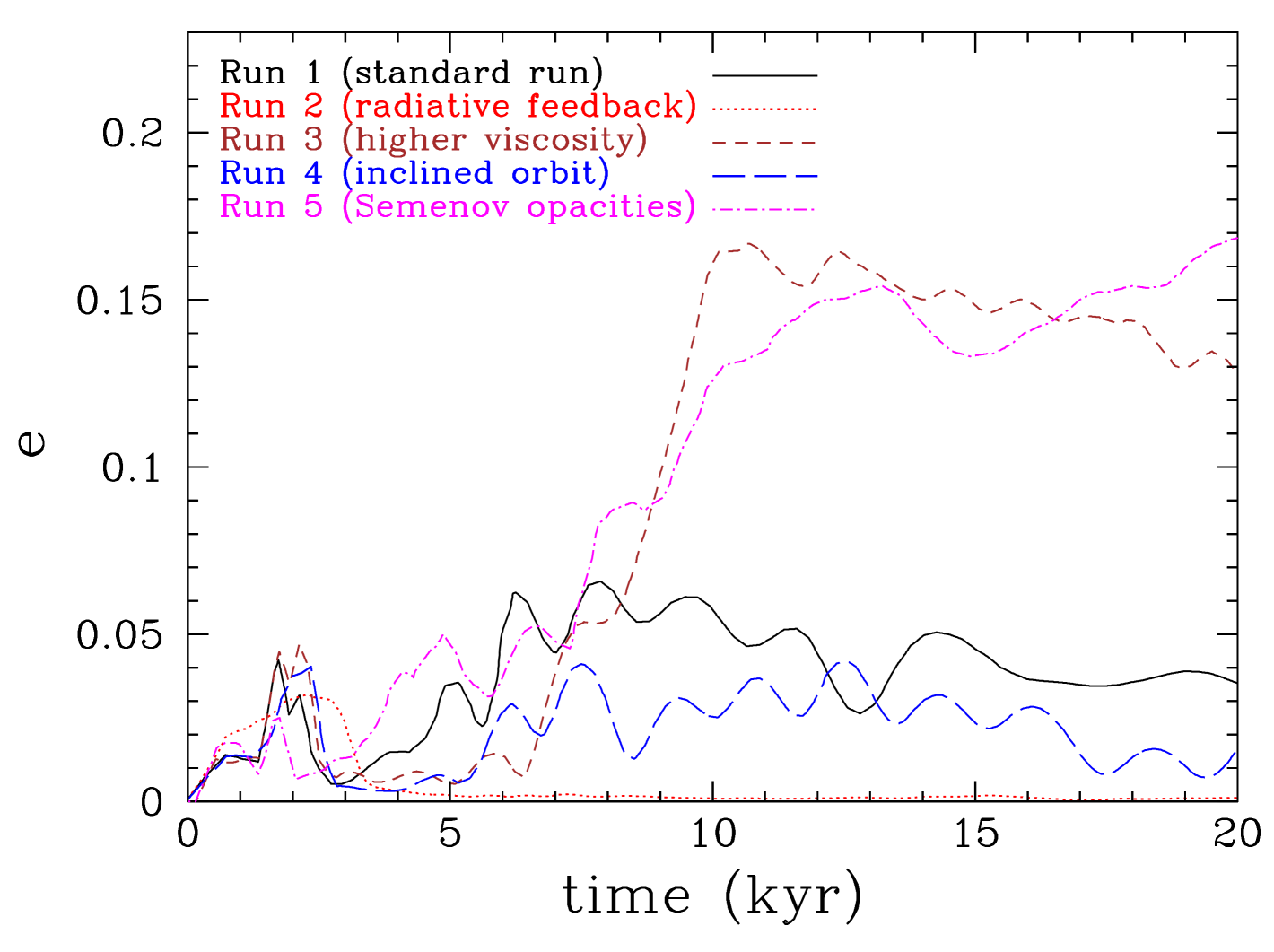
4.3 Eccentricity
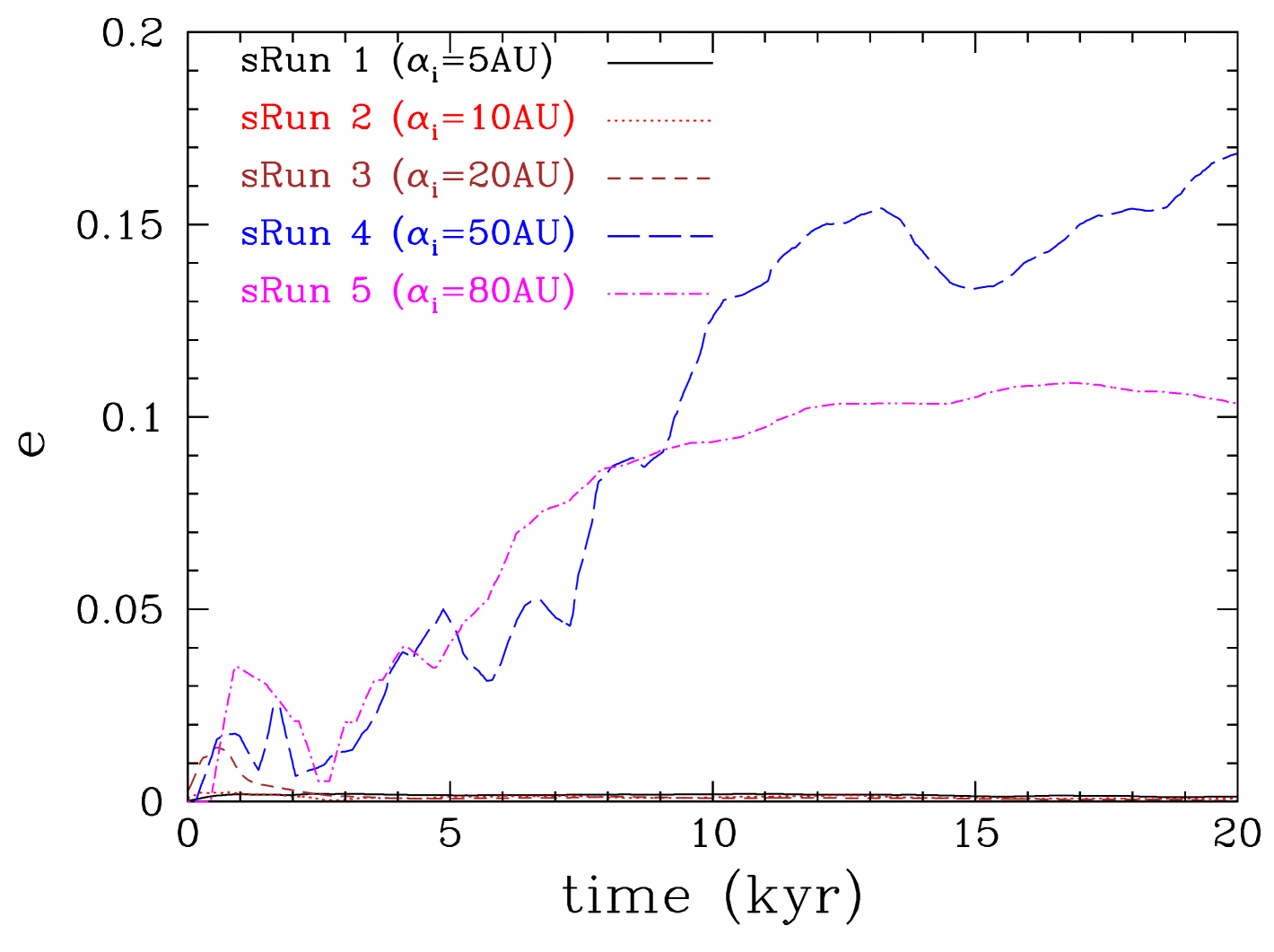
The eccentricity of the protoplanet grows as the protoplanet interacts with the gravitationally unstable disc (see Figure 9). The growth pattern is rather stochastic with the eccentricity growing up to . Even if the eccentricity after this initial growth period dampens with time due to secular interactions with the disc, these initial interactions can provide the seed for subsequent eccentricity growth (Goldreich & Sari, 2003; Duffell & Dong, 2015). Therefore, disc-planet interactions, while the disc is still relatively massive, may help explain the observed high eccentricities of giant planets in systems that are thought to contain only one planet (Wright et al., 2011; Dunhill & Stamatellos, 2018). In the case when the radiative feedback of the protoplanet is taken into account (Run 2), the eccentricity initially grows during the gap opening phase but then it is dampened quickly, as there is no strong stochastic driving, so that the protoplanet ends up in a nearly circular orbit. Therefore, interactions within a gravitationally unstable disc is necessary for eccentricity growth to occur.
4.4 Protoplanet on an inclined orbit
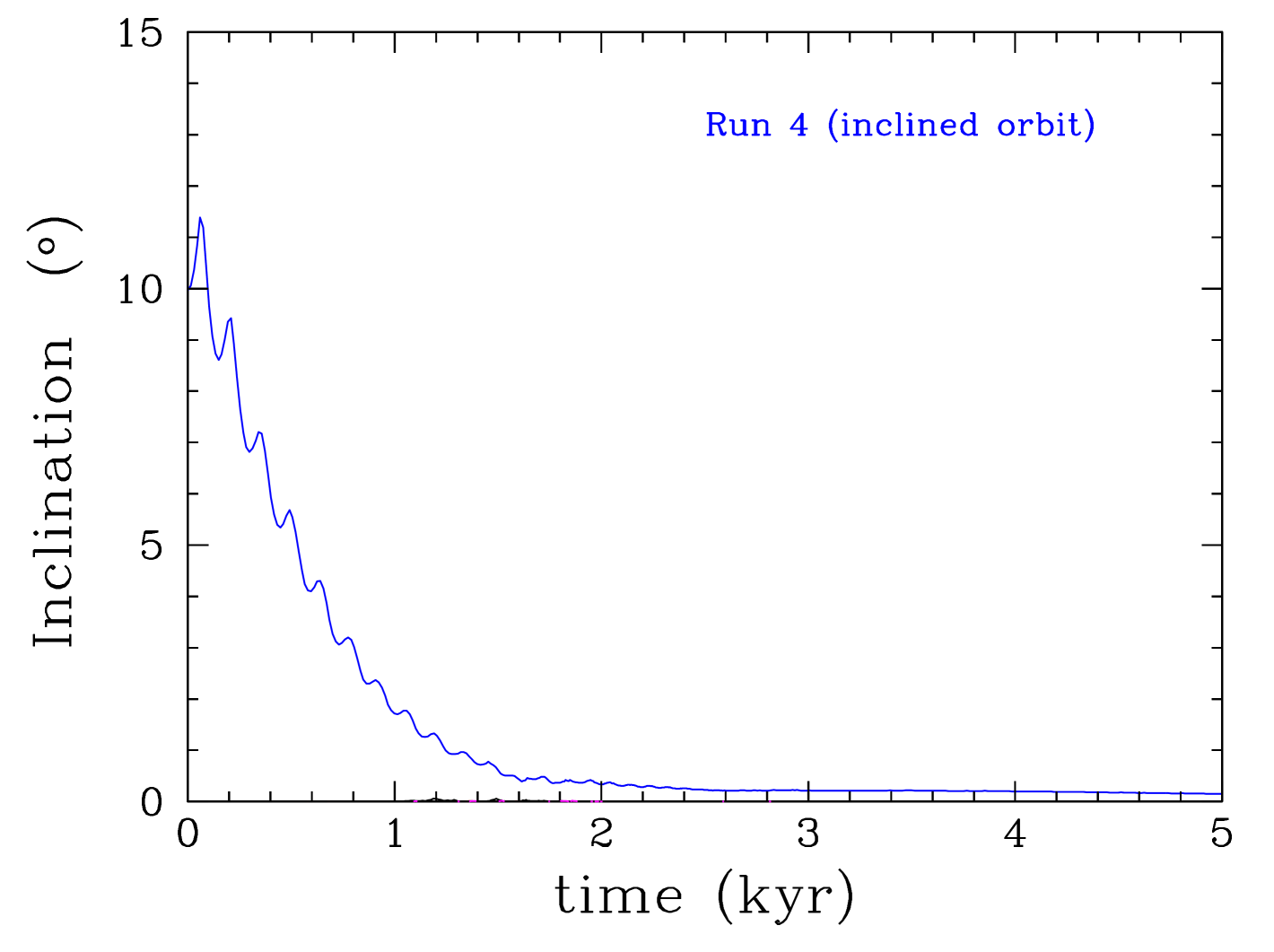
The protoplanet in the run in which its orbit is inclined (Run 4, blue lines) shows a mass growth that resembles closely the standard run (see Figure 4). This is because the protoplanet’s orbit inclination gets smaller quickly as the protoplanet crosses through the disc midplane. Within kyr ( orbits) the protoplanet’s orbit has been aligned with the disc midplane (inclination has become zero, see Figure 10). Therefore, the long-term evolution of a protoplanet is not significantly different if the protoplanet initially forms on an inclined orbit in a relatively massive protostellar disc.
4.5 Gap opening
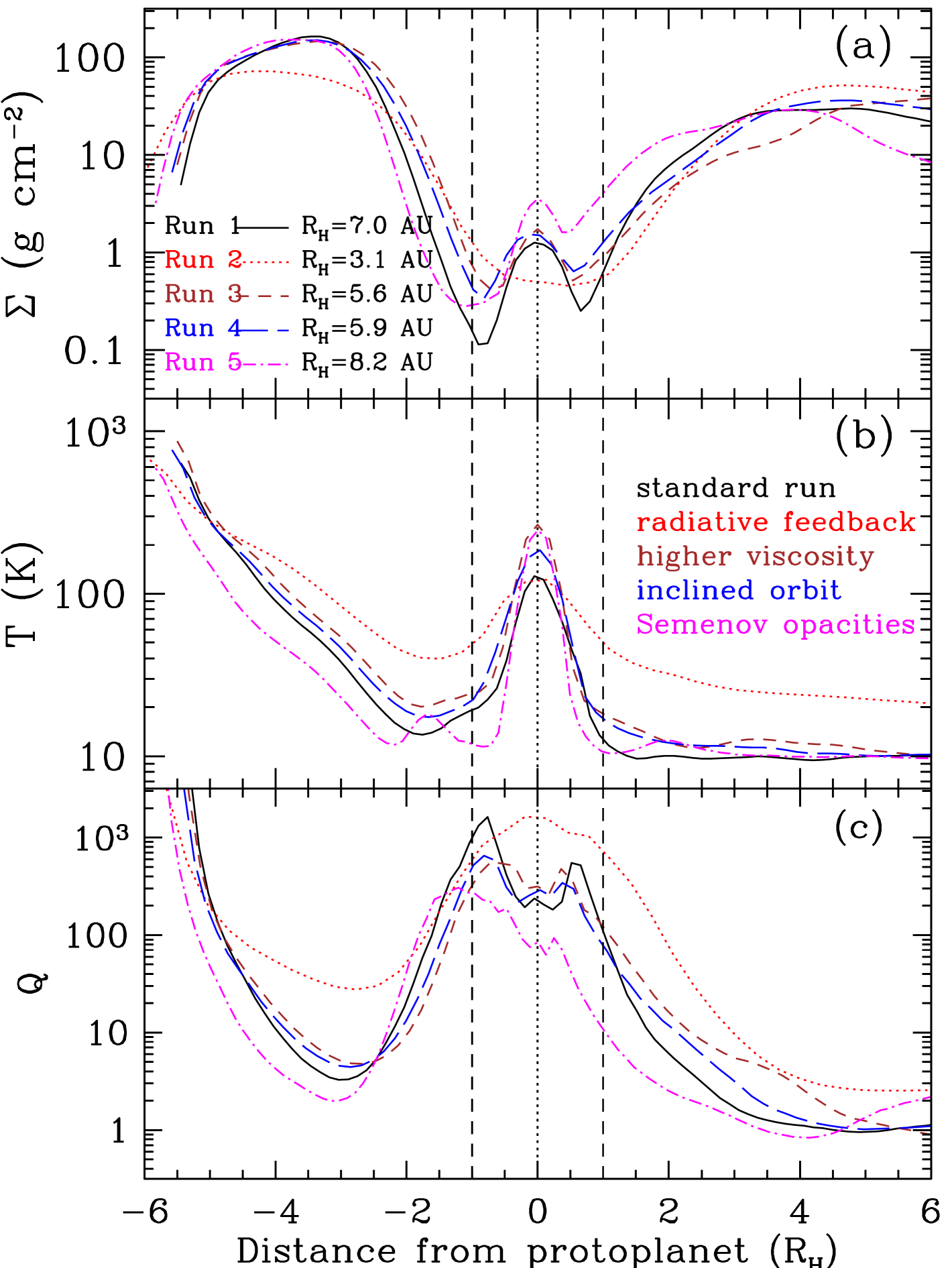
The surface density, the temperature profile and the Toomre parameter Q for the region around the protoplanet for all five runs are shown in Figure 11 (on the protoplanet’s corotational frame). The snapshots correspond to kyr, i.e. after the gap has been opened up in the disc. The gap size is a few Hill radii and rather similar for all runs (note though that the size of the Hill radius is different in each run, as the protoplanet is on different orbits in different runs). The increase of surface density towards the protoplanet within the Hill radius corresponds to the circumplanetary disc (see section below).
The surface density at the boundaries of the Hill radius is asymmetric (Figure 11a). In Run 2 (which includes the protoplanet’s radiative feedback) the surface density at the inner boundary of the protoplanet’s Hill radius (e.g. at ) is higher than the surface density at outer boundary of the Hill radius (e.g. at ) whereas in all other runs the outer boundary surface density is higher. This is consistent with the point made in the previous subsection, i.e. that a large fraction of gas is accreted onto the protoplanet from outside its orbit when the gap edges are gravitationally unstable. The asymmetry is more pronounced for Run 5 (higher opacity run) which also exhibits shorter outward migration timescales (see Table 7 and Figure 8). The disc temperature (Figure 11b) at the run with the protoplanet feedback is higher than in the other runs, which results in stabilizing the disc edges as the Q parameter is larger than (Figure 11c). The temperature of the disc around the protoplanet is lower for the higher opacity run (Run 5) which helps opening up the gap fast and results in higher gas accretion onto the protoplanet.
4.6 Circumplanetary discs
The properties of the circumplanetary discs in all 5 runs are shown in Figure 12 and the time evolution of the Hill radius and the mass within it for the protoplanet in each run are shown in Figures 14 and 14. The typical circumplanetary disc mass is about , which means that the disc is resolved by SPH particles, i.e. approximately 7 smoothing lengths (assuming a nearly 2D disc). The sink radius of the protoplanet is set to 0.1 AU so it is always smaller than the Hill radii of the protoplanets at all times, in all runs (see Figure 14). The circumplanetary discs are therefore just resolved and the presented properties near the planet are probably resolution dependent. We expect that the surface density and the temperature near the planet are underestimated. In Run 2 (with protoplanet feedback) the circumplanetary disc is smaller (with mass of ; see Figure 14) as the protoplanet is closer to the parent star; therefore the circumplanetary disc is just resolved in this case (only by smoothing lengths).
Despite the above drawback, by comparing the derived properties we see that in Run 2, with the protoplanet radiative feedback, the circumplanetary disc is hotter than in the other runs, as expected. Radiative feedback from the protoplanet together with the gas thermodynamics (Gressel et al., 2013) are important in determining the properties of circumplanetary discs. Further studies with higher resolution are needed for more secure results. Additionally, the presence of magnetic field may also play a significant role (Gressel et al., 2013; Fujii et al., 2014) but we do not examine this case here.
We note that we do not find temperatures in the circumplanetary discs higher than a few hundred Kelvin in contrast to the simulations of Szulágyi (2017), in which they find that temperatures close to the protoplanet rise up to a few thousand Kelvin. However, their simulations are able to resolve the region down to , which can indeed become very hot. We note though that the Szulágyi (2017) simulations do not include the effect of molecular hydrogen dissociation at K (nor the ionisation of hydrogen and the first and second ionisation of helium), so they may overestimate the temperatures in the inner region. When we compare the temperatures farther out in the circumplanetary disc (e.g. at ) we see that the temperatures that we find here are lower than the ones in Szulágyi (2017).
4.7 Accretion onto the central star
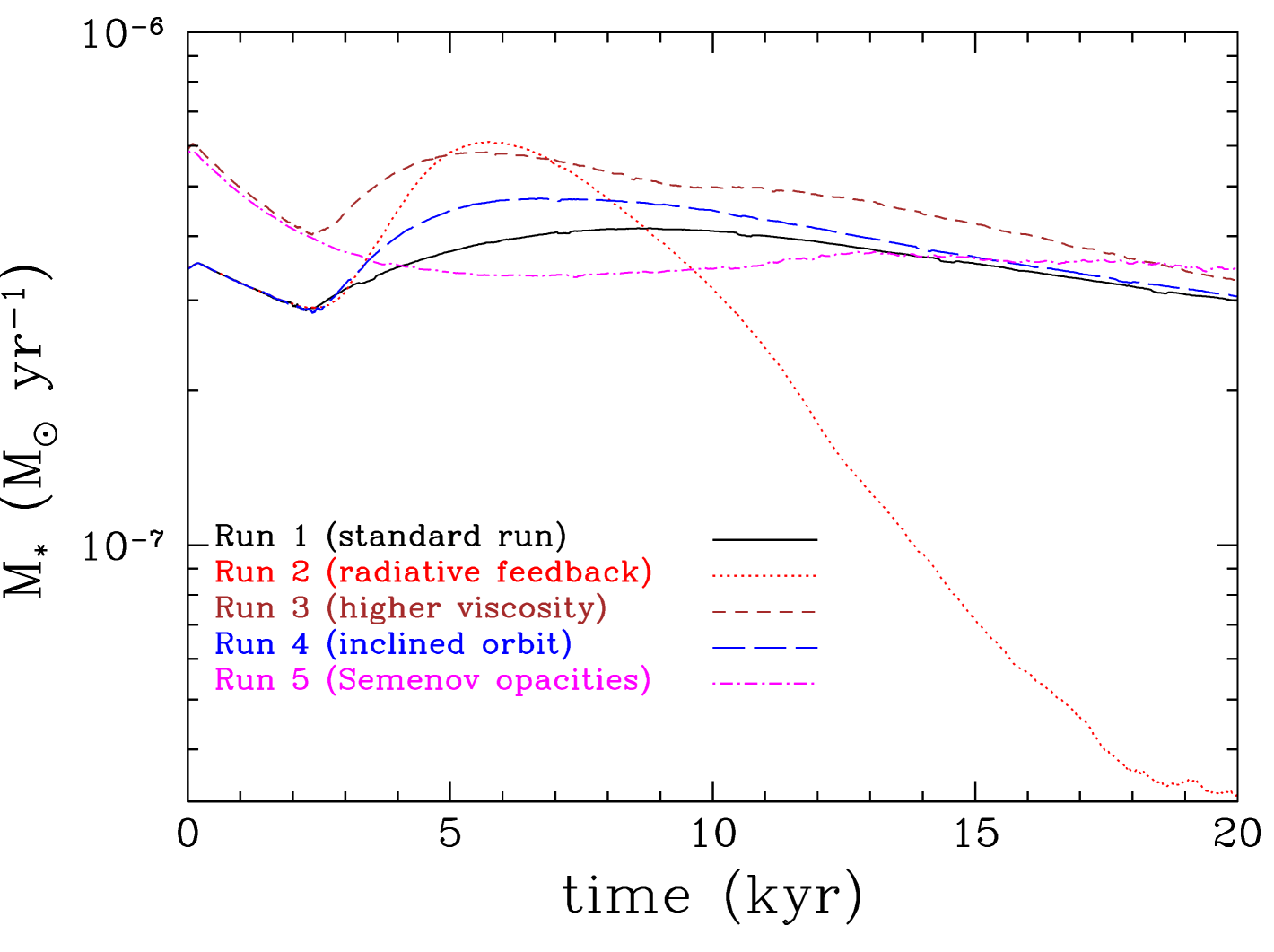
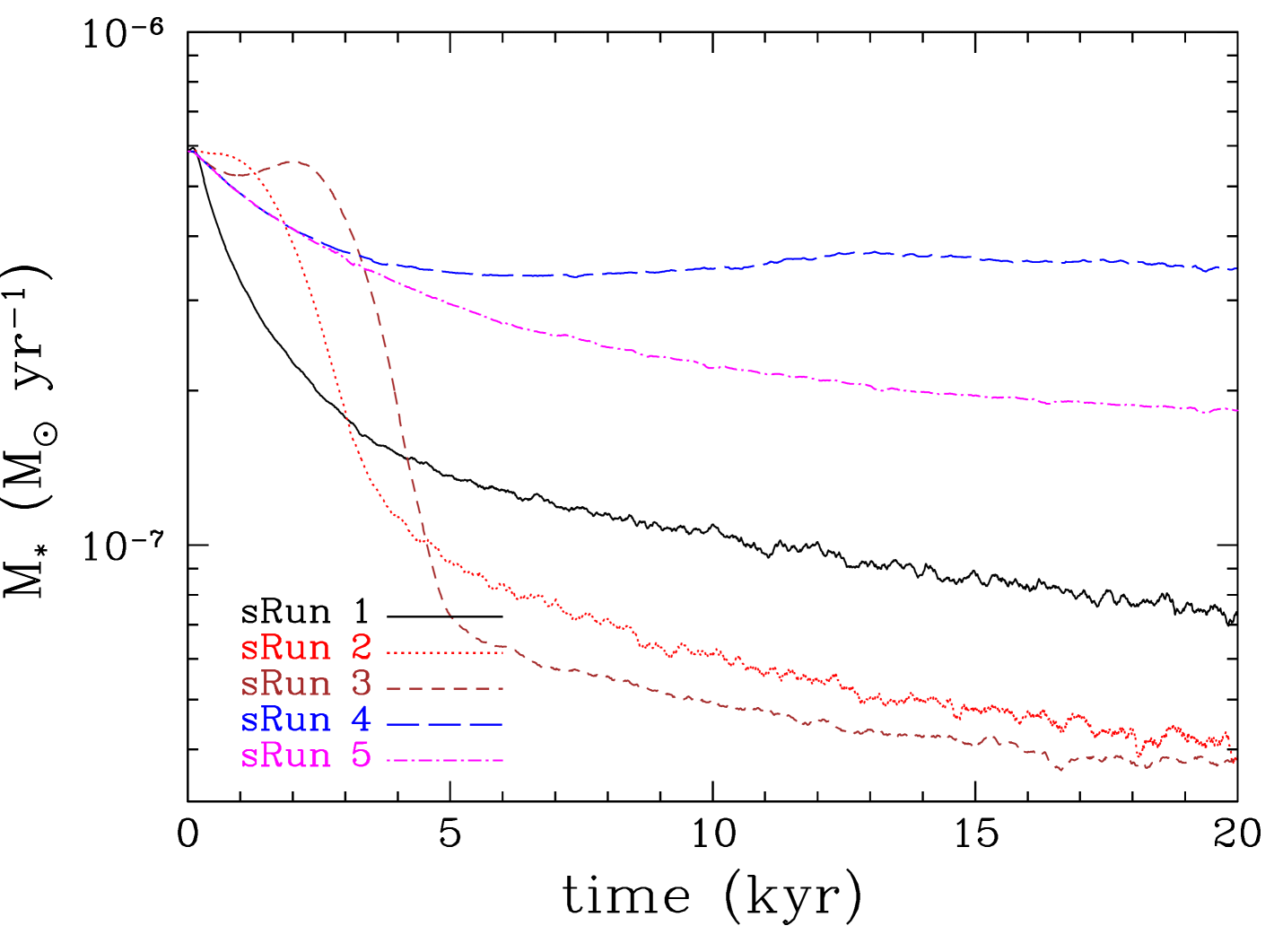
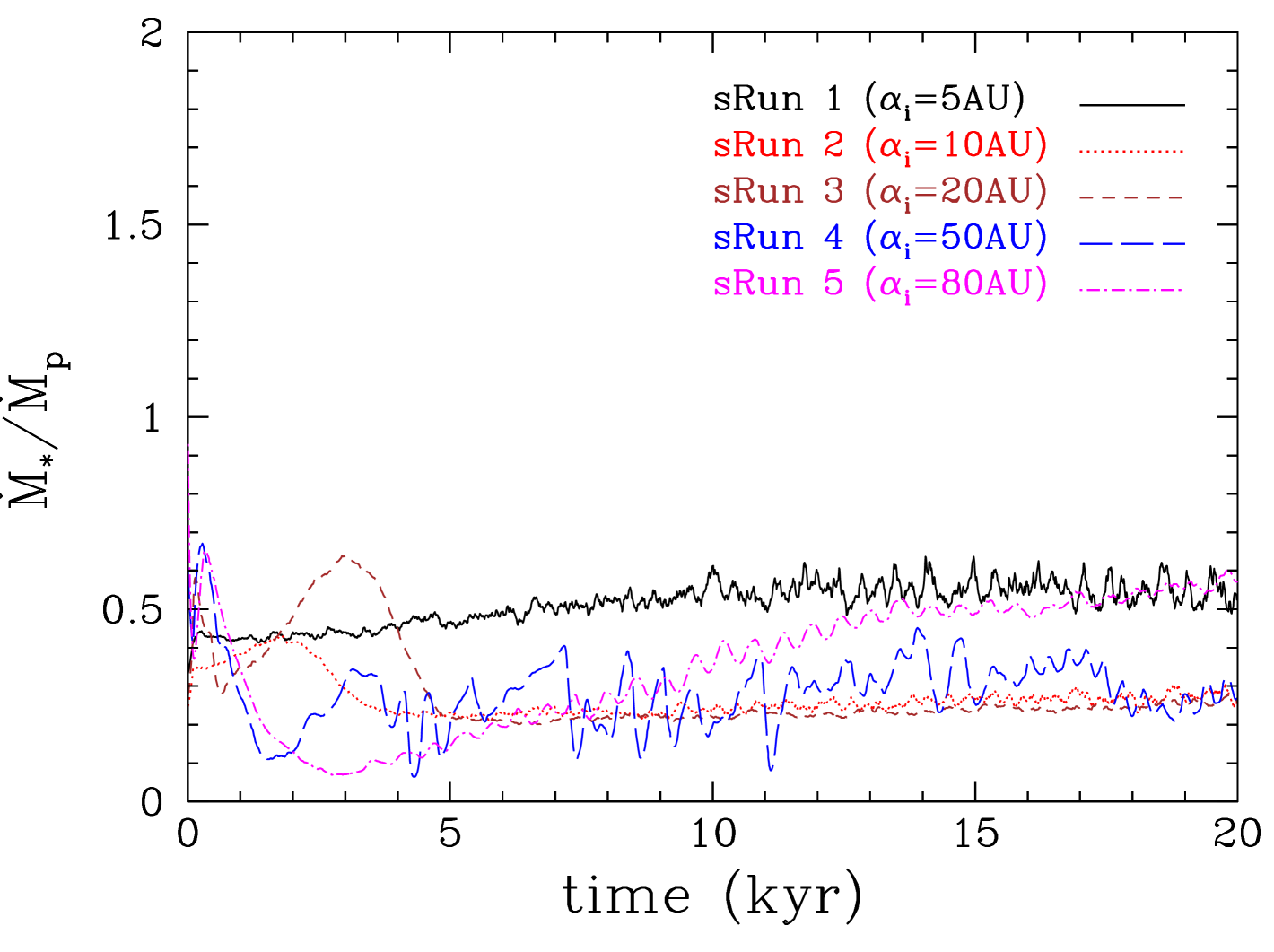
The presence of a protoplanet in the disc regulates the accretion rate onto the star (see Figure 15). Interestingly, the accretion rate onto the protoplanet during the initial stages of its evolution that we model here, is comparable to the accretion rate onto the star itself. During the gap opening phase it can be even ten times higher. This is consistent with previous studies of planets embedded in lower-mass discs (Nelson et al., 2000; Lubow & D’Angelo, 2006; Owen, 2014). During this phase the accretion rate onto the star decreases but as the protoplanet moves closer to the star and once the gap opens up, the accretion rate onto the star increases by a factor of a few, as the protoplanet acts to drive accretion onto the star; the closer the protoplanet orbit to the star and the higher its mass, the higher the accretion rate onto the star becomes. At this stage, and for a few thousand years, the accretion rate onto the star may become higher than the accretion rate onto the protoplanet. In Run 5 (with the Semenov opacities) the protoplanet stays sufficiently away from the star so that the accretion rate onto the star is not affected.
In Run 2 (with protoplanet feedback) the protoplanet migrates closer to the star than in the other runs, and the accretion rate onto the star increases significantly until a cavity forms around the star; thereafter, the accretion rate drops considerably as the presence of the protoplanet starves the star from gas. At the same time the protoplanet experiences similar gas starvation as it resides within the same cavity. This stage can be thought as similar to the transition disc phase (see review by Espaillat et al., 2014). However, the accretion rate onto the protoplanet is still higher than the accretion onto the star by a factor of 2. In this case the star-protoplanet system behaves as a low mass-ratio binary system with a circumbinary disc, in which the secondary component (i.e. the protoplanet) accretes more than the primary component (i.e. the star) (Artymowicz & Lubow, 1994, 1996). In such systems, secondaries increase in mass faster than primaries, resulting in an almost equal-mass binaries (e.g. Satsuka et al., 2017). However, in the case of a planetary-mass companion, its mass cannot become comparable to that of the star; even if an unlikely high accretion rate of is maintained for yr, then the protoplanet’s mass will increase only by .
4.8 The role of the accretion rate onto the protoplanet
The actual accretion rate onto the protoplanet is important as it regulates the strength of its radiative feedback, which it turn determines whether the edges of the gap opened by the protoplanet are gravitationally unstable (so that the protoplanet migrates outwards), or gravitationally stable (so that protoplanet migrates inwards). The luminosity of the protoplanet, , is proportional to the accretion rate, , onto the protoplanet (see Equation 7), therefore the temperature due to the presence the protoplanet (see Equation 6) scales as . The Toomre parameter, that determines whether the gap edges are gravitationally unstable is , where is the epicyclic frequency, and the sound speed (we assume that the distance, , is measured from the protoplanet). Hence, or equivalently
| (16) |
Therefore, there is only a weak dependence of the Toomre parameter on the accretion rate onto the protoplanet. If we assume that the actual accretion rate is 10 times lower than the one we estimate in the simulations we present here, then the Q value is lower only by a factor of (assuming that the other parameters remain the same). Then the Q value in the outer edge of the gap in the run with the protoplanet radiative feedback (see Figure 11, red line) will drop from 3 to 2.3, i.e. the gap edge will still be gravitationally stable (). We conclude the value of the accretion rate onto the protoplanet is not critical, at least qualitatively, regarding the effect of radiative feedback on the migration of the protoplanet.
5 Comparison with -cooling studies
We compare the results of the simulations presented here with previous studies that employ the -cooling approximation, in which the cooling time in the disc is proportional to the local orbital period. In this case the specific internal energy of each SPH particle is set to
| (17) |
where is the mean molecular weight, and the adiabatic exponent. The cooling rate of each particle is set to
| (18) |
where
| (19) |
is the distance on the disc midplane, and
| (20) |
We perform simulations with and , i.e. relatively long cooling times. These are similar to the ones used before in these type of studies: Baruteau et al. (2011) use , whereas Malik et al. (2015) use . Otherwise, the parameters of the simulations were the same as in Run 1. We note that considering these long cooling times the discs are gravitationally stable and they are not expected to show any spiral structure in the absence of the protoplanet. We compare the simulation we performed with the results in Run 1 in which radiative transfer is treated self-consistently with the method of Stamatellos et al. (2007) (see Section 3.1).
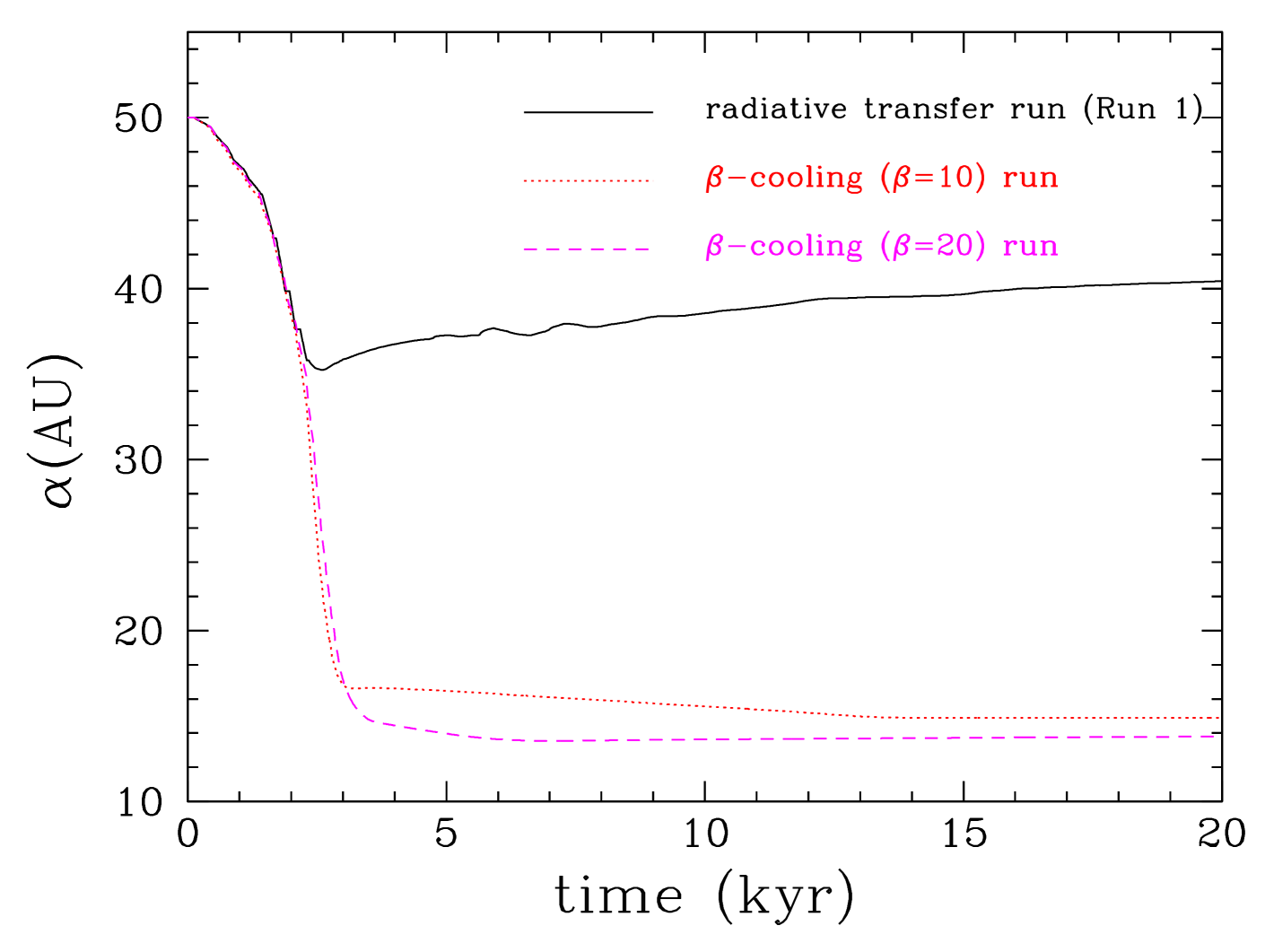
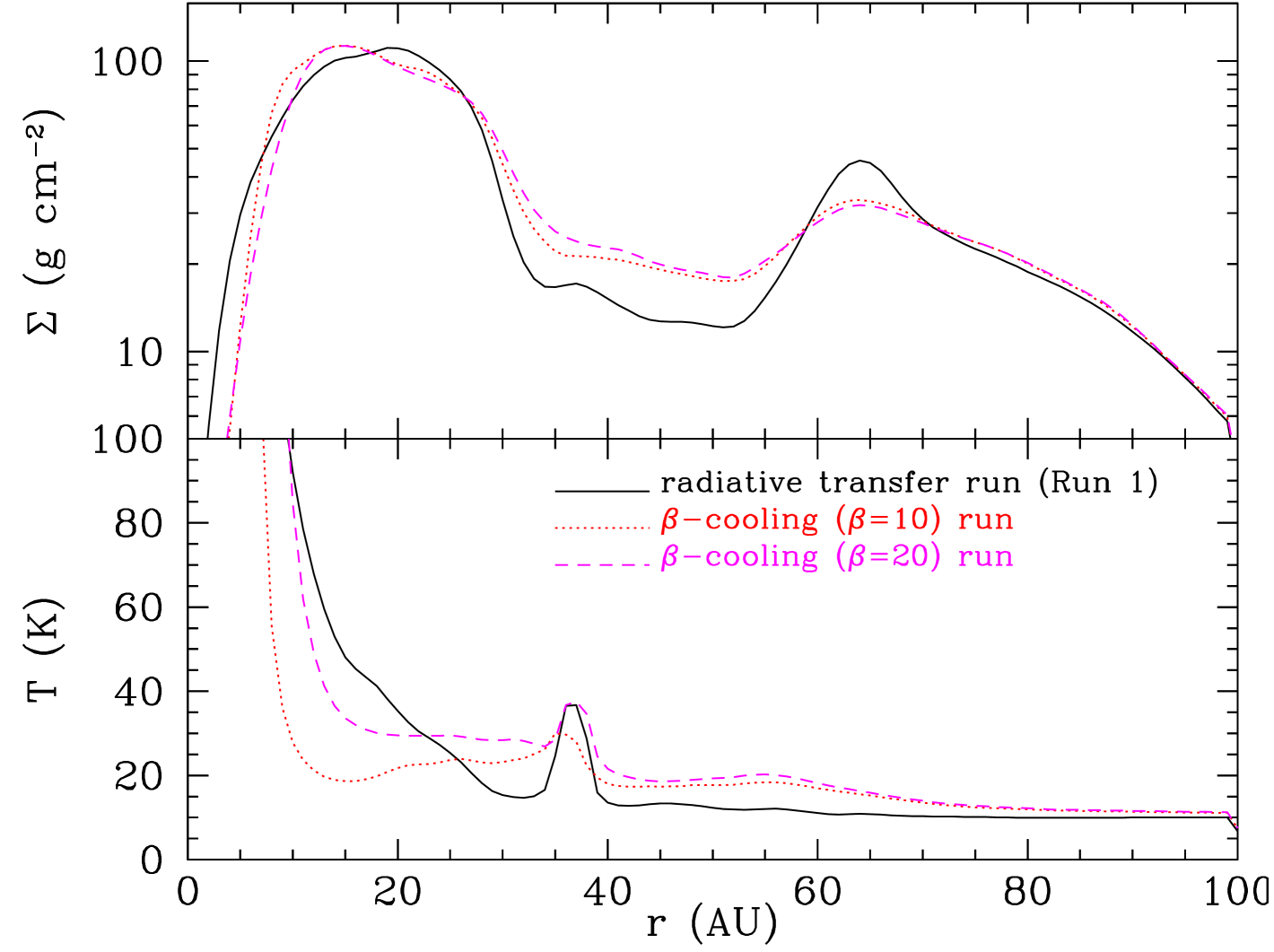
We see (Figure 17) that in the runs that use the -cooling approximation the protoplanet is not able to open up a gap and the migration is fast, as previous studies have found, and stops only once the protoplanet has reached the inner cavity around the star. During migration the accretion onto the protoplanet is much lower than in the runs in which the radiative transfer is treated in more detail. The reason for this is that in the -cooling runs (that as in previous studies use rather large values; 15, 20, 30) the actual cooling is too slow compared with the cooling provided by the more detailed method, so that the protostellar disc is hotter (see Figure 17, bottom) and therefore the opening of a deep gap is not possible (Crida et al., 2006). Additionally, the cooling in the outer circumplanetary disc is inefficient, resulting in slower accretion of gas onto the protoplanet, limiting its mass growth. We discuss in detail the effect of cooling on the mass growth of the protoplanet and on gap opening in Section 4.1.
Therefore, the detailed treatment of radiation transfer in the disc and the vicinity of the protoplanet, i.e. how the circumstellar and circumplanetary discs heat and cool, is important for determining the migration and mass growth of a protoplanet evolving in a young, massive disc.
6 The effect of the protoplanet’s orbital radius (without radiative feedback from protoplanet/star
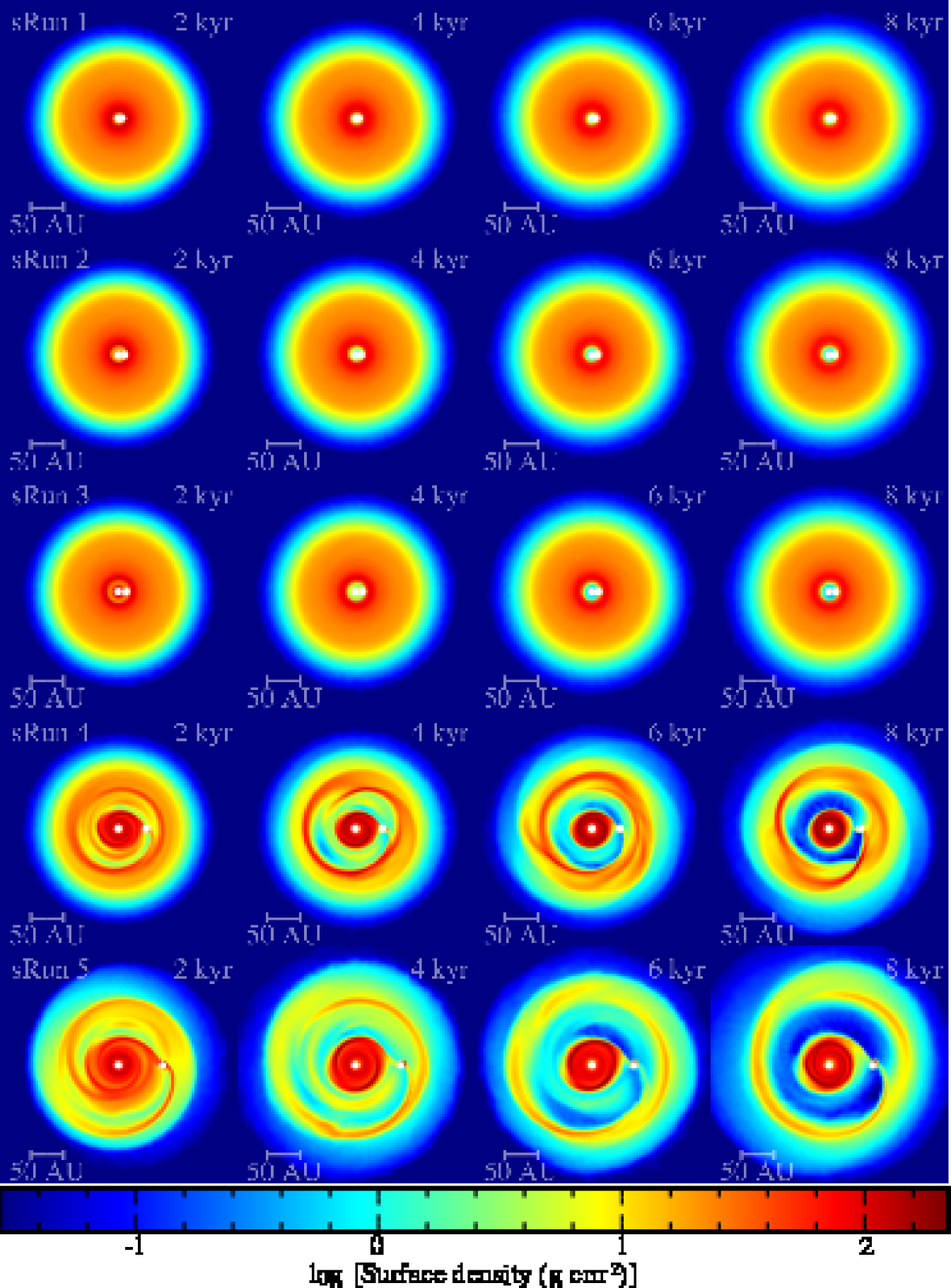
We now examine the evolution of Jupiter-mass protoplanets that are embedded at different orbital radii within protostellar discs (see Figure 18). The details of the 5 runs (hereafter referred to as sRuns) are shown in Table 2. A protoplanet is initially placed at 5, 10, 20, 50 and 80 AU from the central star at a circular orbit. The opacities used for these runs are the ones by Semenov et al. (2003). For these runs we do not include radiative feedback from the star nor the protoplanet. The migration timescales for each run and the associated migration velocities are shown in Tables 7 and 7.

| Run id | |||||
|---|---|---|---|---|---|
| (MJ) | (AU) | (MJ) | (AU) | ||
| sRun1 | 1 | 5 | 6.8 | 6.7 | 0.0013 |
| sRun2 | 1 | 10 | 9.4 | 8.8 | 0.007 |
| sRun3 | 1 | 20 | 9.1 | 9.9 | 0.0002 |
| sRun4 | 1 | 50 | 31 | 53 | 0.17 |
| sRun5 | 1 | 80 | 26 | 72 | 0.10 |
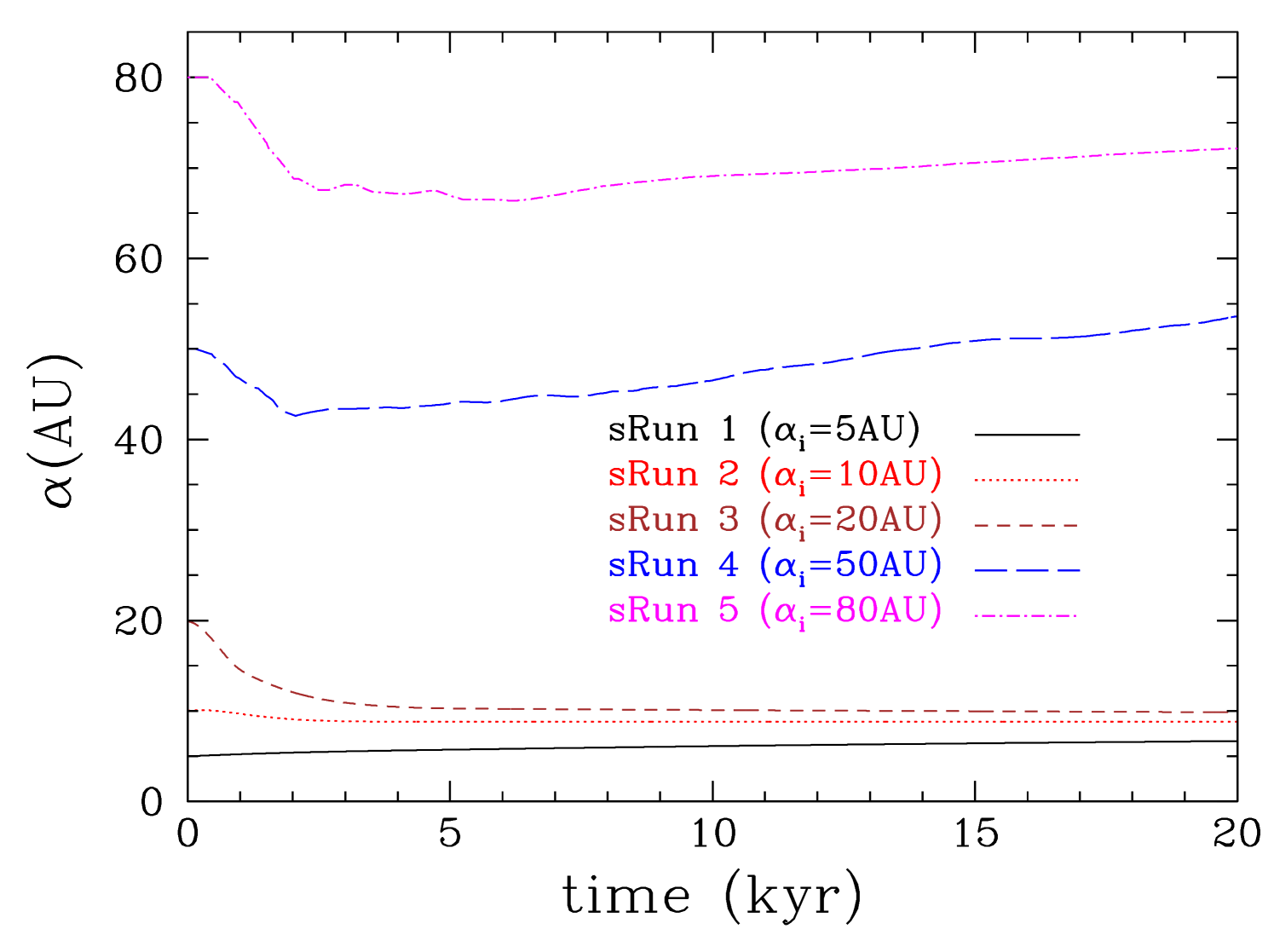
The semi-major axis evolution of the protoplanets is shown in Figure 20. When the protoplanet is initially placed in the outer disc region (which is characterised by a low Toomre-Q parameter) it migrates inwards on a Type I migration timescale ( yr), but once a gap opens up the inward migration stops and it changes into outward migration (see Figure 20). On the other hand, when the protoplanet is placed in the inner disc region ( AU) it migrates inwards initially on a Type I migration timescale ( yr) and once the gap is opened up the migration continues to be inwards; however it slows down and occurs on a timescale typical of Type II migration ( yr; see Figure 20). As pointed out in the previous section, a necessary requirement for outward migration is interactions with a gravitationally unstable outer gap edge. In the inner disc region close to the central star the disc is hotter and therefore stable, so that outward migration does not happen. The only exception is the run in which the protoplanet initially placed at 5 AU; in this run the protoplanet migrates outwards (but only slightly) throughout the simulated time because it resides near the outer edge of a quickly formed inner cavity around the central star. It accretes less gas than in the other runs; mainly it accretes high angular momentum gas from the outer edge of the cavity, as indicated by the lack of strong inner wake.
We conclude that the survival of the protoplanet on a relatively wide orbit (assuming that it has formed on this wide orbit) is secured when the disc is massive and cool enough for gravitationally unstable edges to develop. If the protoplanet forms in the outer disc region then its initial inward migration will turn into an outward migration once it opens up a gap in the disc. If the protoplanet forms in the inner disc region its inward migration will slow down considerably (migration timescale of yr; see Table 7) so it can stay on a wide orbit once the disc has dissipated (assuming that the disc dissipates fast enough).
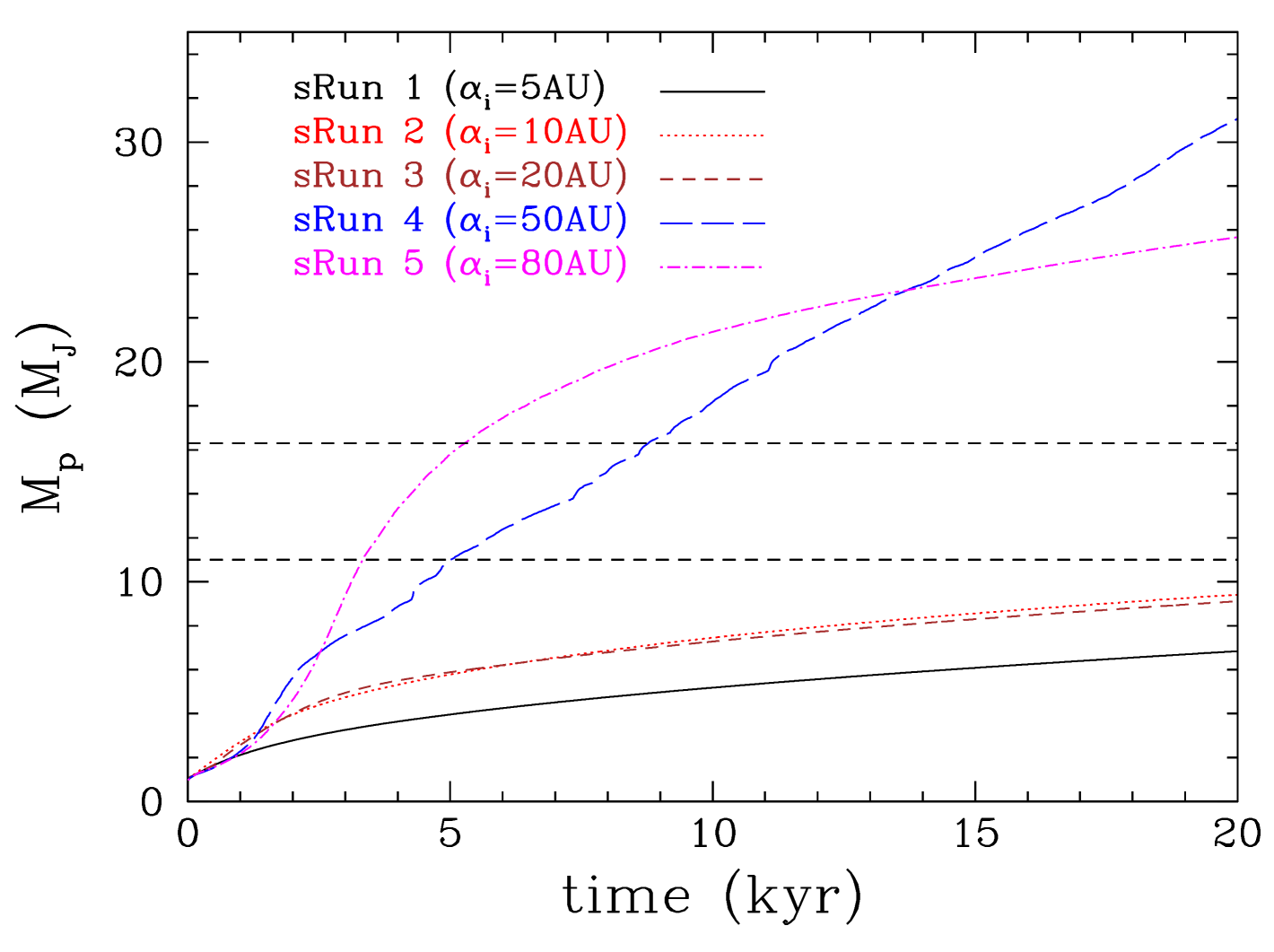
The mass growth of the protoplanet also depends on its location in the disc (see Figure 22). Protoplanets placed in the outer disc region accrete gas while they open up a gap and they continue to accrete gas at a high rate as they migrate outwards in the disc (Figure 22, top). They increase in mass considerably becoming brown dwarfs by the end of the simulated 20 kyr, with a mass of MJ. Their corresponding accretion luminosities are L☉ (see also Inutsuka et al., 2010) (Figure 22) and therefore they may be readily observable if observed while they are still young. On the other hand, protoplanets that form in the inner disc region quickly find themselves within a gas-poor cavity formed around the central star and accretion onto them happens at a much lower rate than on protoplanets in the outer disc region (Figure 22). Their mass growth is slower and their final mass at the end of the simulation is below the deuterium burning limit ( MJ). However, their mass continues to increase so they may also end up as brown dwarfs if the disc dissipates slowly. If the longer term disc dissipation happens on a shorter timescale than the viscous one in other ways, e.g. by photoevaporation (Alexander et al., 2006; Owen et al., 2010) or by disc winds (Suzuki & Inutsuka, 2009; Suzuki et al., 2010; Suzuki & Inutsuka, 2014; Gressel et al., 2015; Bai, 2016) (see review by Alexander et al., 2014), then the mass of the protoplanet will remain below the deuterium burning limit (see discussion by Kratter et al., 2010).
The eccentricity of the protoplanet in the different runs is shown in Figure 23. Protoplanets in the outer disc region interact with the gravitationally unstable gap edges resulting in eccentricity growth (). Protoplanets in the inner disc region interact in a gravitationally stable disc and their orbits remain nearly circular. Therefore, for a protoplanet to to have a significantly eccentric orbit it needs to have formed at a sufficiently large distance from the central star. Protoplanets formed by gravitationally instability naturally form at such large radii when the disc can be both gravitationally unstable and cool fast enough (Stamatellos & Whitworth, 2009a; Boley, 2009). Giant planets are difficult to form by core accretion at such large radii. Therefore, eccentric giant planets on wide orbits in single-planet systems may have formed due to gravitational instabilities.
The accretion rate onto the central star also depends on the orbital radius of the protoplanet (Figure 24). A protoplanet in the inner disc region quickly (within a few kyr) forms a cavity around the central star. During this period the accretion rate onto the star is high, as the protoplanet drives gas accretion onto the star. After the central cavity opens up the protoplanet starves the star from gas, with the accretion rate dropping considerably. Mass flows through the inner cavity through accretion streams as in a circumbinary disc (Artymowicz & Lubow, 1996) but accretion happens preferentially onto the protoplanet, the lower mass object of the system as expected: the protoplanet’s accretion rate is twice that of the star’s (Figure 24).
7 The effect of the protoplanet’s orbital radius (with radiative feedback from the protoplanet/star)
We now examine the evolution of a 1-MJ protoplanet placed at different orbital radii within a protostellar disc, including the radiative feedback from the protoplanet and from the central star as described in Section 3.1 (see also Appendix B) (setting K for the pseudo-background temperature due to the central star). These simulations (see Table 3, Figure 25) probably represent more realistically the evolution of a protoplanet within a young disc. We use the Semenov et al. (2003) opacities for this set of runs.
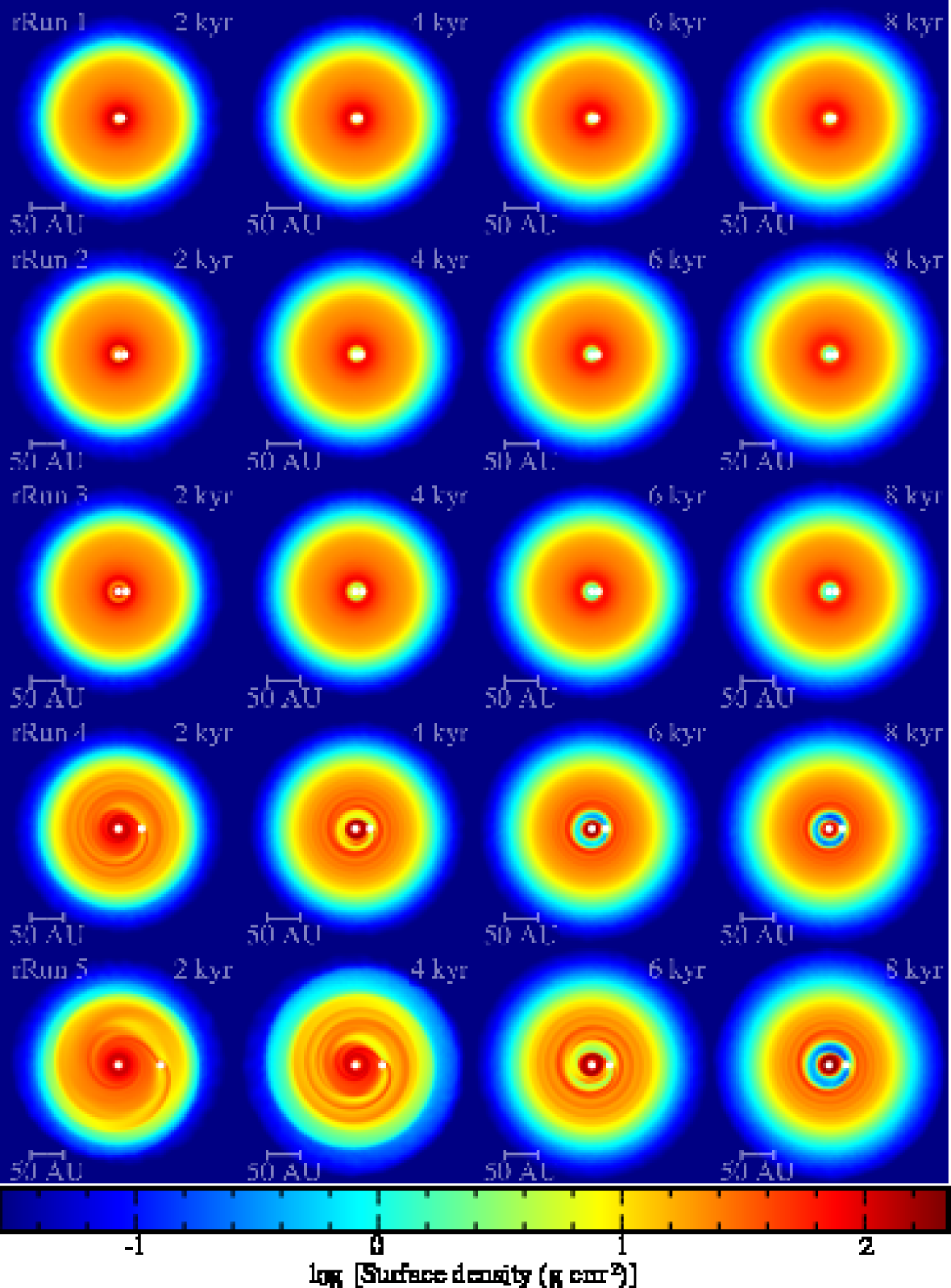
| Run id | |||||
|---|---|---|---|---|---|
| (MJ) | (AU) | (MJ) | (AU) | ||
| rRun1 | 1 | 5 | 8.0 | 6.6 | 0.0020 |
| rRun2 | 1 | 10 | 11.4 | 9 | 0.0026 |
| rRun3 | 1 | 20 | 11.1 | 10 | 0.0008 |
| rRun4 | 1 | 50 | 15.6 | 18 | 0.0005 |
| rRun5 | 1 | 80 | 18.7 | 24 | 0.0015 |
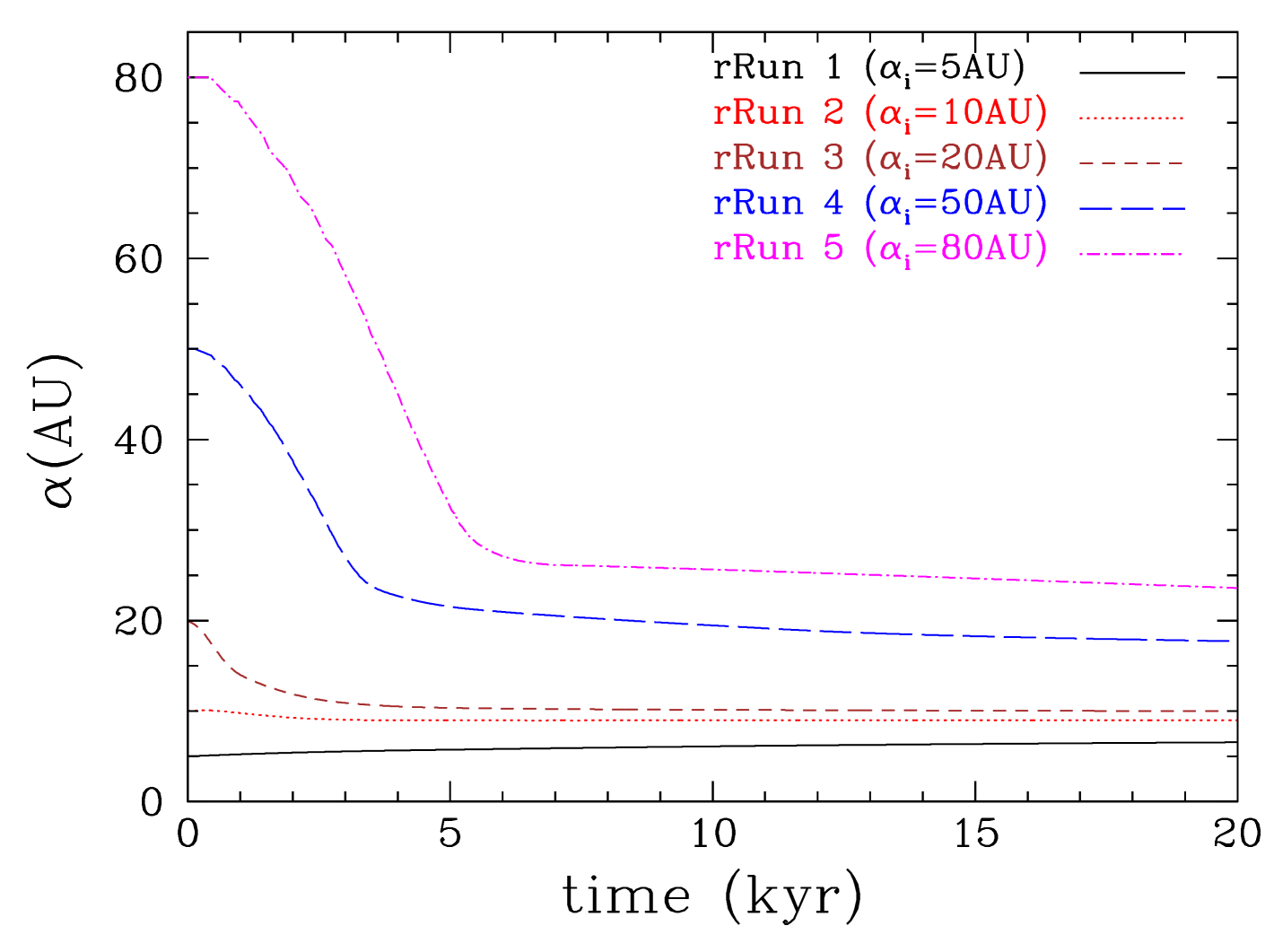
The semi-major axis evolution of the protoplanet is shown in Figure 27. As in the previous runs the protoplanet migrates inwards while opening up a gap (or a cavity, if its initial semi-major axis is small enough, i.e. AU). As in the previous runs without radiative feedback, a protoplanet that orbits close to the central star ( AU) migrates slightly outwards. For protoplanets that are initially in the inner disc region, their radiative feedback does not play an important role, and their evolution is quite similar to the case without any feedback, as presented in Section 6. The edges of the gap opened up by the protoplanet are already hot and gravitationally stable; therefore, the protoplanet continues to migrate inwards but at a slower pace (Figure 27). On the other hand, radiative feedback from the protoplanet plays an important role for planets that are initially in the outer, relatively cold disc region. This radiative feedback heats the gap edges, stabilising them and ensuring that the protoplanets continue to migrate inwards in contrast to the case without radiative feedback, in which, after the gap opens up, the protoplanet migrate outwards.
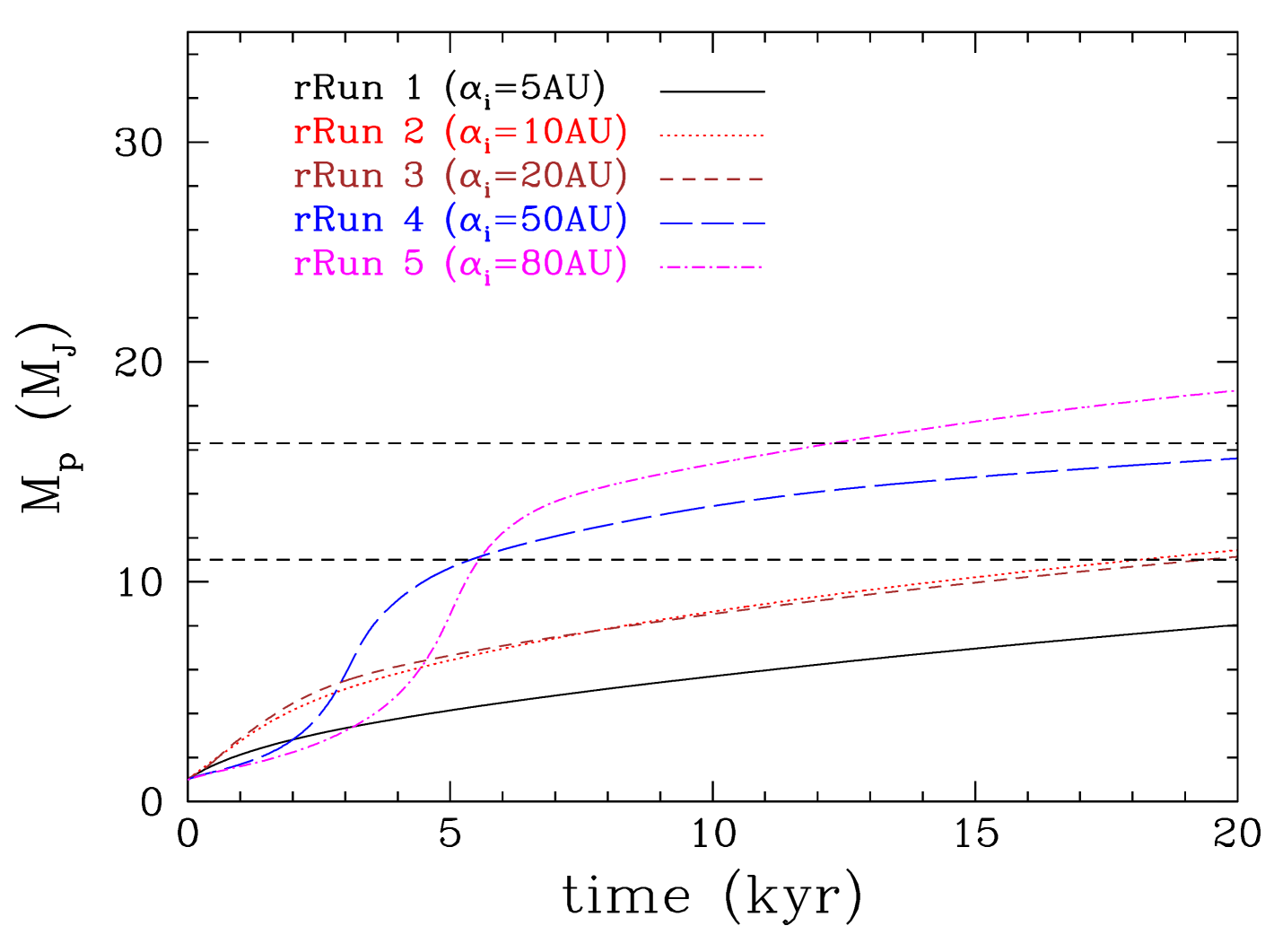
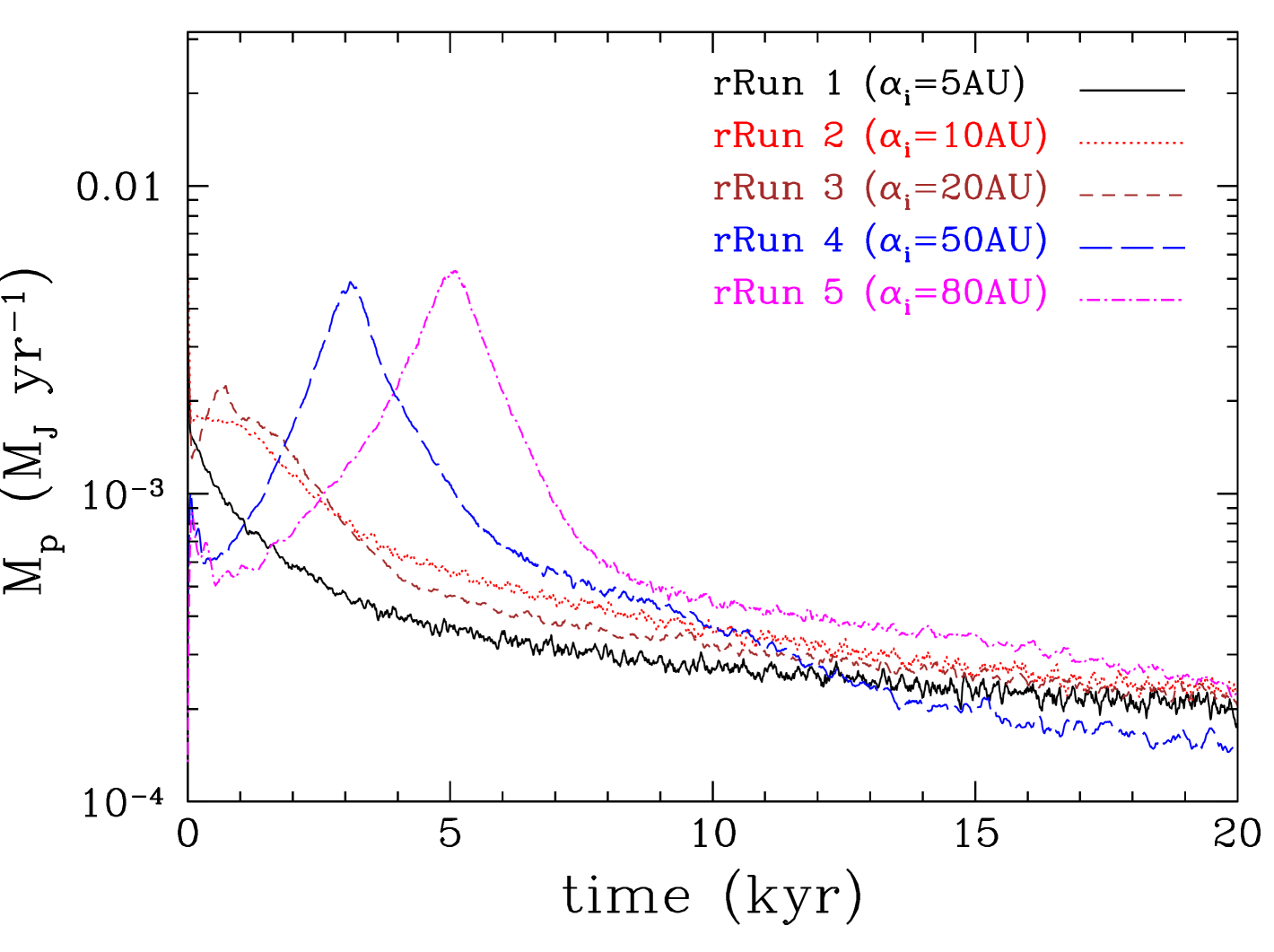
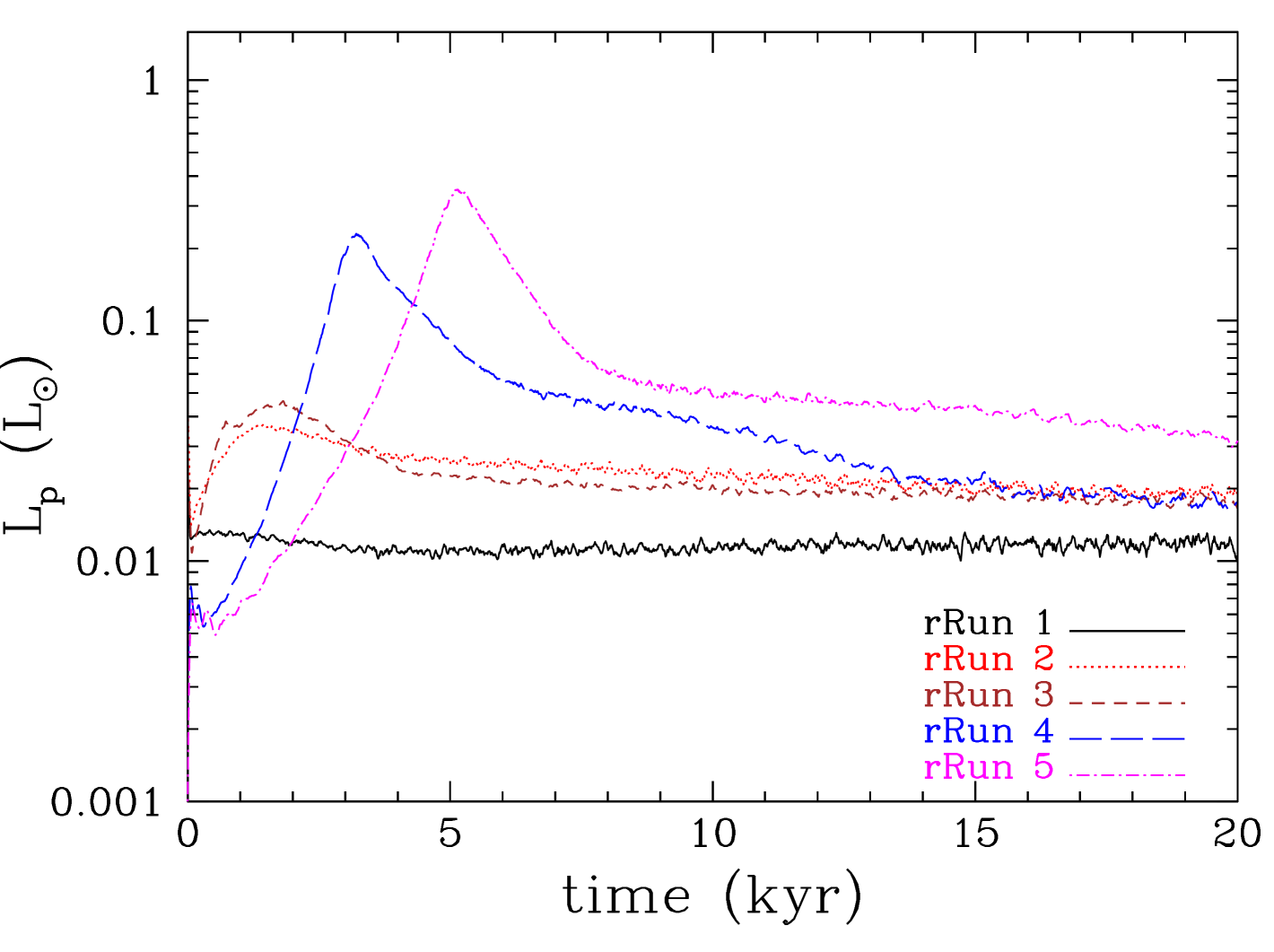
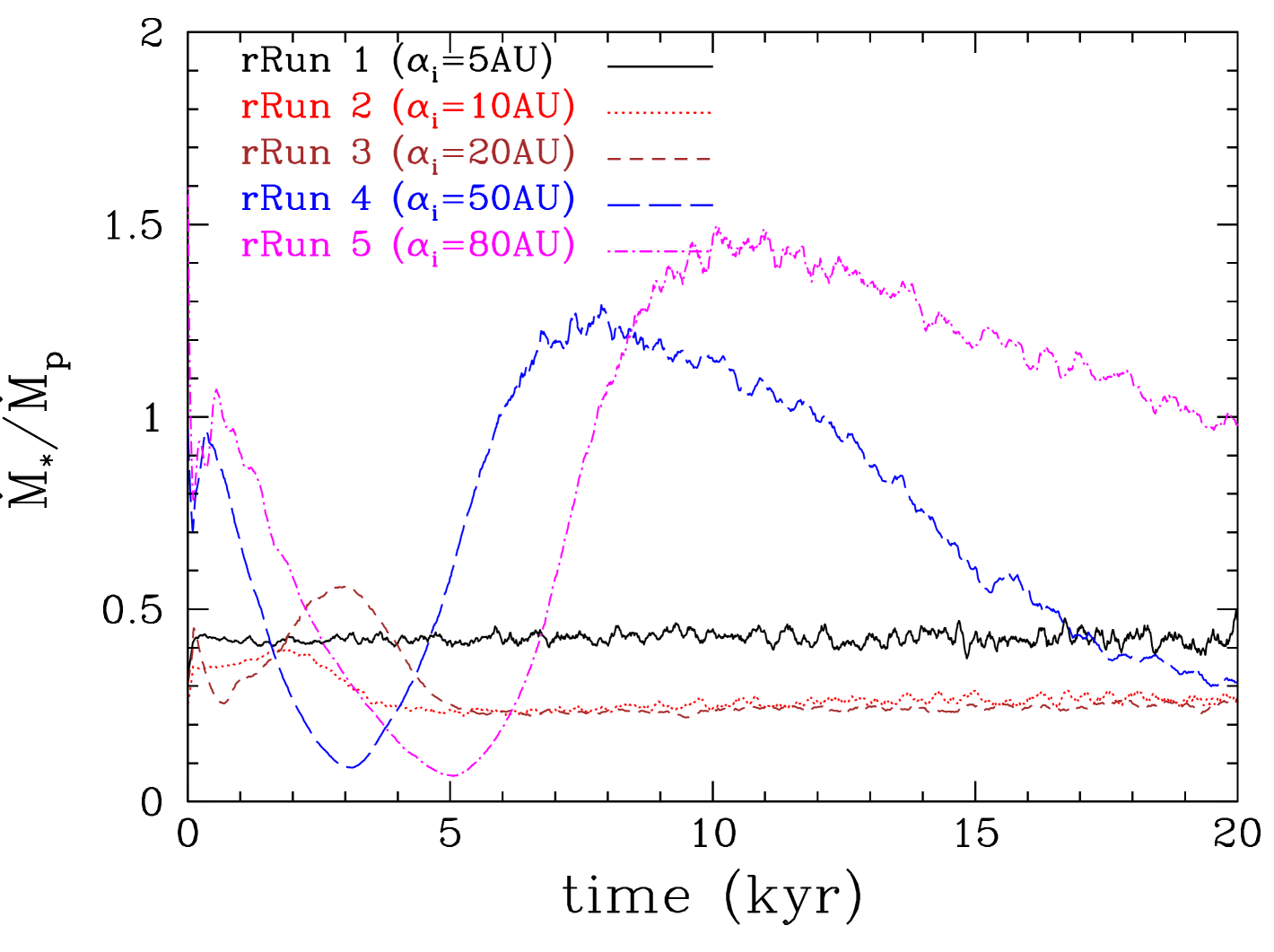
Similarly to the previous case, we find that interaction with the gravitationally stable gap edges suppresses excessive mass growth so that the protoplanet’s mass is near the brown dwarf-planet limit (Figure 29). Protoplanets that form in the inner disc region find themselves in the inner cavity around the star and their masses are just below the deuterium-burning limit. Protoplanets that form further away from the star go through a longer gap-opening phase as they migrate within the gas-rich disc and they accrete more mass, so that their final mass at the end of the simulation is just above the deuterium burning limit. Due to this longer gap-opening phase, protoplanets in the outer disc region show a strong peak in their accretion rates (Figure 29, top) and high corresponding luminosities, which at the earliest phases of the protoplanets’ evolution can reach a few tenths of the solar luminosity (Figure 29, bottom).
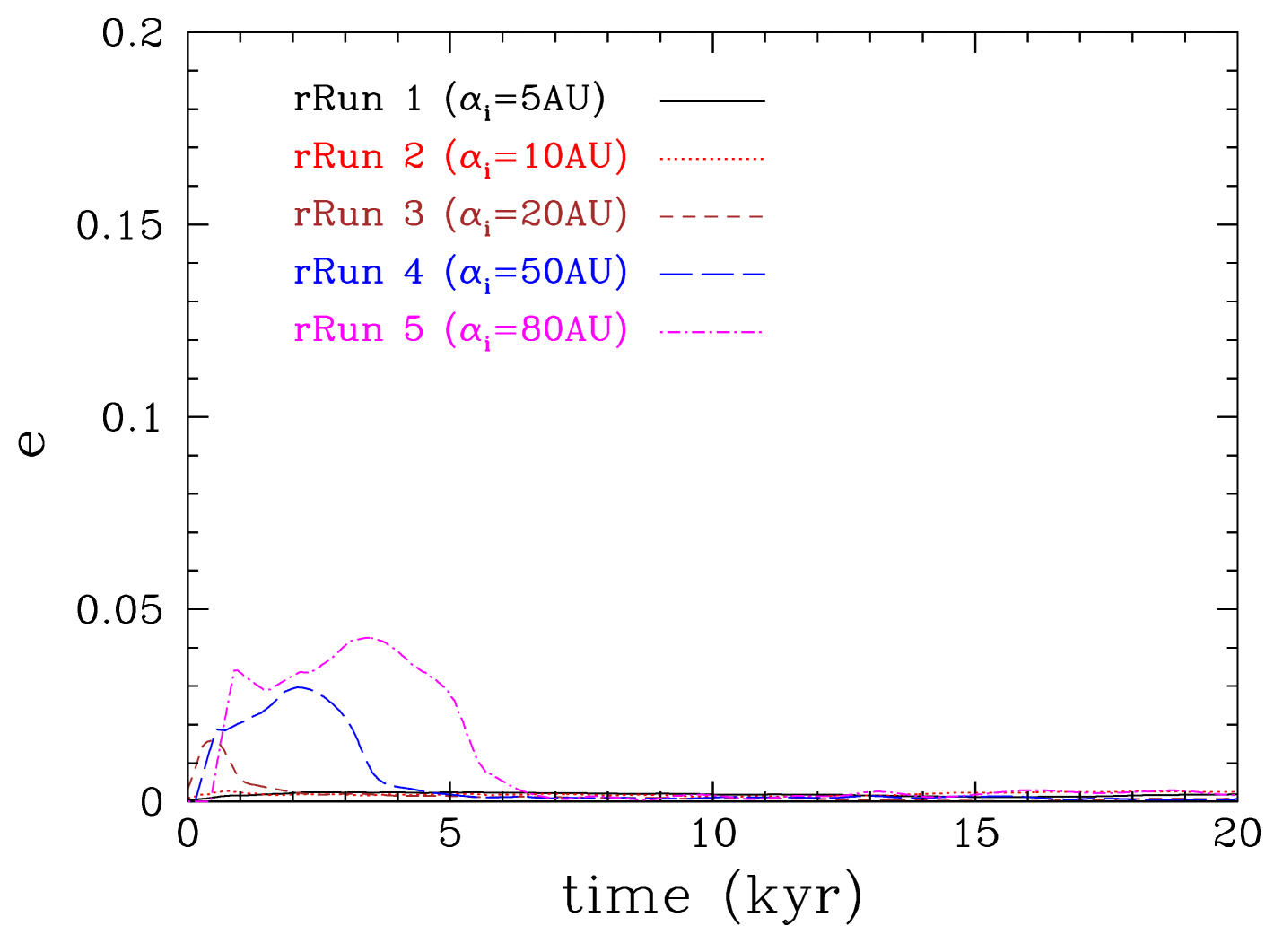
The eccentricity of the protoplanet orbit initially grows during the gap opening phase but thereafter it quickly dampens so that protoplanets at any given radii end up with nearly circular orbits. We find that interactions with a gravitationally stable disc dampen the eccentricity effectively.
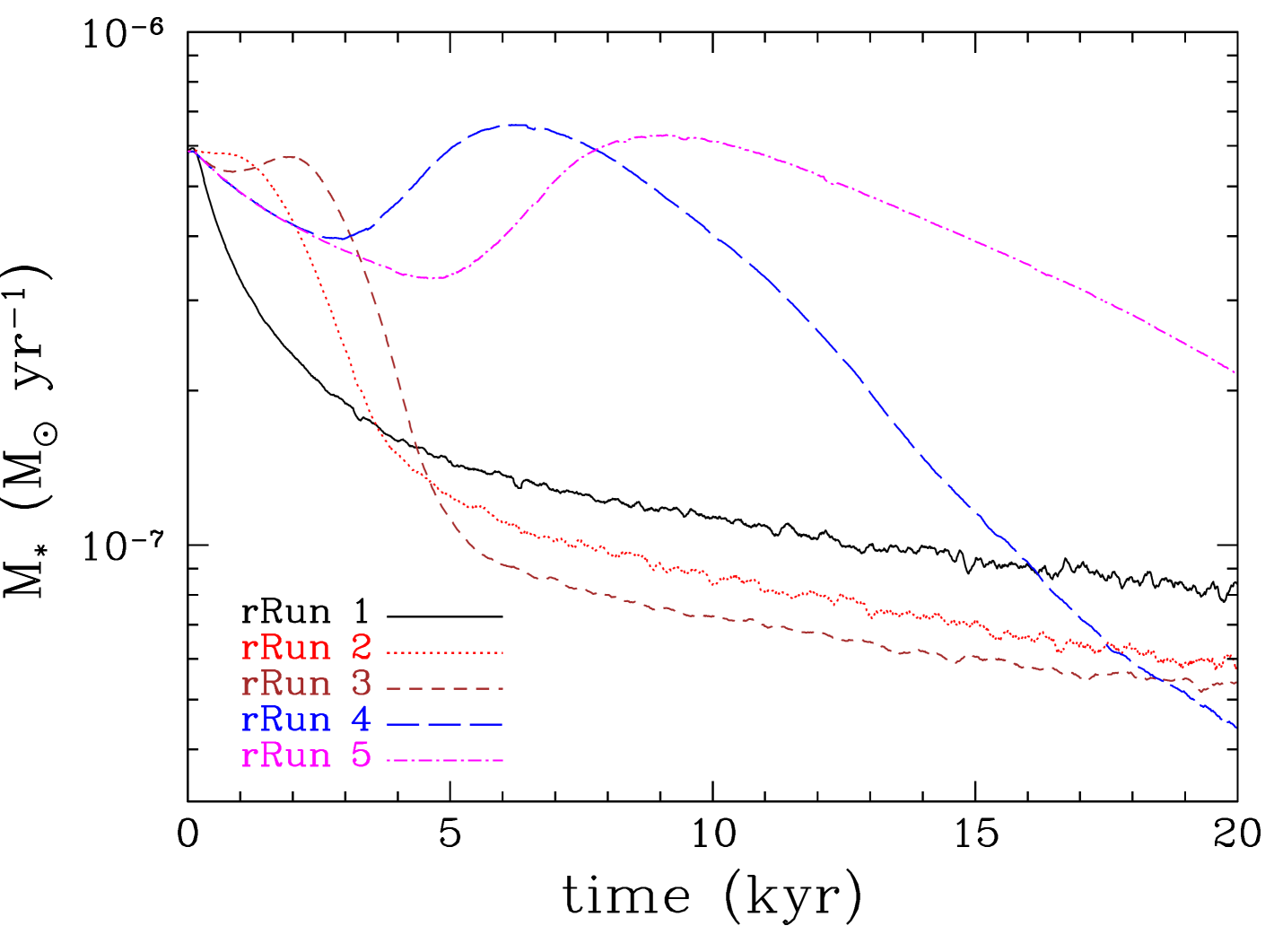
The accretion rate onto the central star is sensitive to the position of the protoplanet in the disc (Figure 31, top). When the protoplanet is in the inner disc region it starves off the young star so that the accretion rate onto it is only half the accretion onto the protoplanet (Figure 31, bottom). When the protoplanet is in the outer disc region, the accretion onto the central star is heavily suppressed during the gap opening phase, whereas it is enhanced significantly immediateley afterwards and for a few thousand years (Figure 31, bottom). However, in all cases the accretion rate onto the protoplanet is higher than the accretion rate onto the star at the end of the simulation.
We conclude that radiative feedback from the protoplanet plays an important role for its orbital evolution and its mass growth only for protoplanets that are formed in outer cold region of a protoplanetary disc. Such protoplanets may have formed by gravitational fragmentation during an early stage of the disc’s formation and evolution, while these discs are still relatively massive (e.g. MacFarlane & Stamatellos, 2017).
8 Summary & Discussion
The final fate of a planet that forms in a protostellar disc is determined by how the two interact with each other. Disc-planet interactions are more critical if the planet forms early-on during its parent disc evolution, while this disc is relatively massive and possibly non-axisymmetric. The effect of the disc is two-fold: (i) it exchanges angular momentum with the planet, to facilitate migration (inward or outward), (ii) it exchanges mass with the planet allowing it to grow (but the opposite may also be possible, see Nayakshin, 2017a).
Here, we presented simulations of the evolution of a Jupiter-like planet-seed in a relatively-massive disc (0.1 M☉) around a Sun-like star (1 M☉), expanding on the work of Stamatellos (2015). The disc is massive enough for its gravity to play an important role in the system’s evolution, but not massive enough to fragment due to the development of gravitational instabilities (). We do not restrict the formation mechanism of the planetary seed, although it is rather unlikely that such a protoplanet may have formed by core accretion early-on during the disc’s lifetime (i.e. within several yr). On the other hand, such large planet-seeds form naturally fast (on a dynamical timescale) by disc fragmentation. Nevertheless, the results of this paper are independent of the assumed planet formation scenario.
The evolution of such a planet-seed (protoplanet) is followed for a relatively short duration corresponding to the disc lifetime (20 kyr; see Appendix C for the long term evolution) but even within such a short timescale disc-planet interactions are important for determining the properties of the protoplanet. It has been suggested that the strong nature of the planet-disc interactions and the inability of the planet to open up a gap in such a massive disc, may lead to rapid inward migration (Michael et al., 2011; Baruteau et al., 2011; Malik et al., 2015) and the demise of the planet as it falls onto its parent star. The findings of our simulations contradict the results of these studies as we find that the protoplanet is able to open up a gap in the disc so that its fast inward migration is halted (as also pointed out in Stamatellos, 2015). However, we encounter an alternative problem: the protoplanet grows in mass by accreting gas from the disc, so that in most cases it becomes a brown dwarf (Stamatellos & Whitworth, 2009a, 2011; Kratter et al., 2010; Zhu et al., 2012). The final state of the planet depends on where it has formed in the disc, but also on the physics that are at play during its evolution. More specifically, this work demonstrates that radiative heating from the young accreting protoplanet plays an critical role; this radiative feedback is currently not well understood nor constrained (Marleau et al., 2017; Szulágyi & Mordasini, 2017). The main results of this work are discussed and placed in a wider context in the following subsections.
8.1 Protoplanet mass growth
Gas accretion is significant during the initial stages of the protoplanet’s evolution, during the gap-opening phase. In most of the simulations presented here, the protoplanet grows to the planet-brown dwarf mass-limit (13 MJ) within a few thousand years. Once the gap is opened up, accretion occurs mainly from inside the protoplanet’s orbit. However, a fraction of it is also accreted from outside the protoplanet’s orbit; when the gap edges are gravitationally unstable (low Toomre-Q, i.e ), then an almost equal amount of gas is accreted from outside the protoplanet’s orbit. The accretion rate onto the protoplanet is higher for higher viscosity, and for more efficient cooling (note that cooling is modulated by the opacity). The role of radiation feedback from the protoplanet is critical as it considerably decreases the accretion rate of gas onto it and therefore its final mass. The effect of radiation feedback from the central star is rather minimal (Appendix B). We also found a dependence of the protoplanet’s final mass on its initial position within the disc: a planet that is relatively closer to the central star ( AU) quickly opens up a cavity around its parent star and resides near the outer edge of this cavity. In this case, the star-protoplanet system behaves as a low mass-ratio binary system attended by a circumbinary disc. In such a system gas flows to the star and the protoplanet only through streams that pass through the Lagrangian points of the system (Artymowicz & Lubow, 1994, 1996), and therefore accretion is slow. These are the only cases (with or without radiative feedback from the protoplanet) that the protoplanet’s mass remains within the planetary regime at the end of the simulations. As the mass loss of the disc due to accretion onto the star and the protoplanet is lower in this case, the disc is expected to live longer, allowing other processes, e.g. photo-evaporation (Alexander et al., 2006; Owen et al., 2010) or disc winds (Suzuki & Inutsuka, 2009; Suzuki et al., 2010; Suzuki & Inutsuka, 2014; Fromang et al., 2013; Lesur et al., 2013; Bai & Stone, 2013; Gressel et al., 2015; Bai, 2016), to disperse the disc fast enough for the protoplanet to survive as a planet, not a brown dwarf. Another way to suppress mass growth is to eject the protoplanet from the disc (in multiple-planet systems) so that it ends up as a free-floating planet (Li et al., 2015, 2016; Mercer & Stamatellos, 2017).
8.2 Protoplanet Migration
Disc-planet interactions result in an initial phase of fast inward migration that lasts for a few thousand years, apart from the runs in which the protoplanet is very close to its parent star ( AU); in these runs the protoplanet’s orbit changes only slightly as it quickly opens up a cavity around the star. The migration timescale for this initial phase is yr, i.e. similar to the Type I migration timescale established for planet migration in low-mass discs. This is consistent with previous studies (Michael et al., 2011; Baruteau et al., 2011; Malik et al., 2015). However, we find that the protoplanet is always able to open up a gap in the disc, and thereafter the migration pattern diverges from that in previous studies.
We find that if the gap edges are gravitationally unstable (low Toomre-Q, i.e ), then the protoplanet starts migrating outwards on a timescale yr, as a high fraction of the gas it accretes (almost about 50%) is higher angular momentum gas from outside its orbit. If the gap edges are gravitationally stable (i.e. in the runs with protoplanet radiative feedback, or when the protoplanet is closer to the star, in a hotter disc region) then the migration continues to be inwards but on a longer, Type II migration timescale, i.e. yr, with the planet accreting mainly lower-angular momentum gas from inside its orbit.
Contrary to previous studies we have allowed the protoplanet to grown in mass, and, critically, we have used a more sophisticated treatment of the radiative transfer rather than the commonly used -cooling approximation (Baruteau et al., 2011; Malik et al., 2015). The method we use allows the gas to modulate its cooling/heating depending on its properties (density, temperature); this enables gap opening and facilitates enhanced mass growth of the circumplanetary disc and of the planet.
In the present calculations this “accretion from outside" that is responsible for initiating outward migration is driven by the gravitational instability in the outer disc. However, it is possible this may be promoted by any mechanism that makes large amplitude fluctuations in the outer disc, such as the magneto-rotational instability (MRI, but see Gressel et al., 2012) or other instabilities.
8.3 Protoplanet Eccentricity
The eccentricity of a protoplanet grows up to 0.05 during the initial gap opening phase. Thereafter, two patterns are seen: protoplanets that reside within a gap with gravitationally unstable gap edges show further eccentricity growth up to , whereas the eccentricity of protoplanets within a gap with stable edges dampens, making their orbits nearly circular. The eccentricity growth is not monotonic but shows a stochastic pattern, characteristic of both periodic and random interactions with condensations present near the gap edges. In the long term runs ( yr) we see further eccentricity growth up to (see Appendix C). Almost in all cases that we examined here we see a minimum eccentricity growth of a few 0.01 which may provide the seed for further eccentricity growth (Goldreich & Sari, 2003; Duffell & Dong, 2015). Therefore, early protoplanet interactions with a massive, but gravitationally stable disc may explain in some cases the high eccentricities of giant planets in single-planet systems (Wright et al., 2011; Dunhill & Stamatellos, 2018). On the other hand, we see that protoplanets ending up in the inner disc region ( AU), tend to have circular orbits.
8.4 Effect on the parent star
We find that in most cases the accretion rate onto the protoplanet is higher or at comparable to the accretion rate onto the star. If the protoplanet is close enough to the central star, it creates a cavity, resides within it (at its outer edge), and seemingly starves off the central star from gas, accreting most of the incoming gas. This stage shows similarities with the transition disc phase (Espaillat et al., 2014).
8.5 Observability of protoplanets
The luminosity of a protoplanet can be quite high during the initial stages of its evolution, as the accretion rate on it is relatively high (typically , but could be up to 10 times higher during the gap opening phase). Assuming a relatively large radius for the protoplanet of (which is expected for a protoplanet that has formed by disc fragmentation), we find a typical accretion luminosity of a few (see also Inutsuka et al., 2010). Combined with the fact that the protoplanet starves off its central star from gas, it may make its detection easier.
The high accretion phase lasts only for a few yr and therefore only a small fraction of transition discs (assuming that they all are due to planetary companions) are expected to be seen in this high-luminosity phase. If transition discs live for 1 Myr, then, from timescale arguments, we suggest that only a small percentage, to , of transition discs may have observable, high-luminosity protoplanets (or brown dwarfs).
8.6 Circumplanetary discs
Protoplanets are attended by circumplanetary discs that are fed with gas from the disc. We find that these discs are hotter than their surroundings and therefore easier to observe. Their temperatures are a few hundred Kelvin and they are hotter when radiative feedback from the protoplanet is taken into account. If the protoplanet migrates outwards its circumplanetary disc becomes more massive () and larger AU.
A protoplanet could be detected indirectly through its circumplanetary disc (Szulágyi et al., 2017). The circumplanetary disc of a young luminous protoplanet is hotter than in the case of non-luminous protoplanet (see Figure 12), therefore it would emit significant long-wavelength radiation even if it is not particularly dense. This long-wavelength radiation would escape mostly unattenuated from the system, whereas short-wavelength radiation that is emitted from the protoplanet may be significantly attenuated, especially if the protoplanet orbits a young embedded protostar (e.g. in a Class 0 object).
8.7 Conclusions
Our study shows that the final fate of a Jupiter-like planet-seed formed early-on during the life of a protostellar disc depends both on the initial properties of the seed (e.g. its initial orbit), and the physical processes that are at play (e.g. the role of the protoplanet’s accretion luminosity). The protoplanet may end up as a massive giant planet on a circular orbit close to its parent star or as a low- or high- mass brown dwarf on an eccentric wide orbit.
The parameter space has not been fully explored. It is expected that the initial disc mass will play an important role as it will determine to a wide extent whether the disc is close to being gravitationally unstable or not. Additionally, the initial mass of the protoplanet is important; lower-mass planet-seeds (i.e. a few tenths of the mass of Jupiter) will grow in mass slower and may have a better chance to survive as planets (Nayakshin, 2017a; Malik et al., 2015).
We have assumed that a protoplanet has fully formed (i.e. it is a bound object) at the beginning of the simulation. However, if the planet has formed by disc fragmentation then the formation timescale of the clump and how this evolves to a bound object should be taken into account (Boley et al., 2010; Zhu et al., 2012). Previous studies have shown that a large fraction of these pre-protoplanet clumps may be disrupted, with only a few of them surviving (Boley et al., 2010; Tsukamoto et al., 2015; Hall et al., 2017).
The protoplanets is our simulations are represented by sink particles that accrete gas as this approaches within AU from them. The use of sinks in hydrodynamic simulations is needed to avoid small timesteps but it could lead to enhanced gas accretion that may depend on how well the circumplanetary disc is resolved. The study of how the accretion rate onto the protoplanet varies with resolution and with respect to the hydrodynamic method used (e.g. SPH vs grid-based) is important but outside the scope of this paper. However, we note that the accretion rates onto the protoplanets that we obtain in this work are similarly high (within a factor of a few) as the accretion rates obtained from previous studies (D’Angelo & Lubow, 2008; Ayliffe & Bate, 2009; Zhu et al., 2012; Gressel et al., 2013), which use different numerical methods and disc-planet initial setups.
The physical processes involved are also important. We have shown that the disc thermodynamics, i.e. how fast the disc heats and cools, affects the accretion rate onto the protoplanet (see also Nayakshin, 2017b), its ability to open up a gap in the disc, and its final mass and orbital radius. The -cooling approximation (e.g. Baruteau et al., 2011), in which the cooling rate is proportional to the local orbital period, does not properly capture the thermodynamics of the circumstellar and circumplanetary disc, and may underestimate the mass flow onto the protoplanet and its ability to open up a gap. We also found that the protoplanet accretion luminosity is significant in shaping the properties of the disc in the vicinity of the planet and may stabilize the edges of the gap in which the planet resides, altering its migration pattern.
Therefore, there are many uncertainties regarding the final fate of a young protoplanet that needs to be taken into account in population synthesis models (e.g. Mordasini et al., 2009; Forgan & Rice, 2013; Nayakshin, 2017a) in order for numerical results on planet formation at an early phase during the protostellar disc evolution to be compared with the observed properties of exoplanets. The observational evidence that only 1-10% of star host gas giant planets on wide orbits (Brandt et al., 2014; Galicher et al., 2016; Vigan et al., 2017), corresponds to the final outcome of the planet formation process which does not necessarily reflect the properties of newly formed planet-seeds in young protostellar discs.
Acknowledgements
We thank the referee for carefully reading the original manuscript and for providing many suggestions that have improved the paper. DS thanks Sergei Nayakshin, Alex Dunhill and Anthony Mercer for useful discussions. Simulations were performed using the UCLAN HPC facility and the COSMOS Shared Memory system at DAMTP, University of Cambridge operated on behalf of the STFC DiRAC HPC Facility. This equipment is funded by BIS National E-infrastructure capital grant ST/J005673/1 and STFC grants ST/H008586/1, ST/K00333X/1. Seren has been developed and maintained by David Hubber, who we thank for his help. Surface density plots were produced using splash (Price, 2007). DS acknowledge support from STFC Grant ST/M000877/1. This work was supported from a Royal Society-Daiwa Foundation International Exchanges award between UCLAN and Nagoya University.
Appendix A Migration timescales and velocities for each set of simulations
In this Section we present the migration timescales and the corresponding migration velocities for the set of runs in Tables 1,2, and 3.
| 0.7 kyr | 1.5 kyr | 2.5 kyr | 5 kyr | 18 kyr | |
|---|---|---|---|---|---|
| (kyr) | |||||
| Run1 | 14 | 0.7 | 44 | -140 | -220 |
| Run2 | 11 | 8 | 2.4 | 38 | 150 |
| Run3 | 17 | 6.8 | 5.6 | -56 | -112 |
| Run4 | 15 | 11 | 0.5 | -71 | -270 |
| Run5 | 12 | 11 | -31 | -27 | -68 |
| 0.7 kyr | 1.5 kyr | 2.5 kyr | 5 kyr | 18 kyr | |
|---|---|---|---|---|---|
| (AU kyr-1) | |||||
| Run1 | 3.4 | 6.4 | 0.8 | -0.26 | -0.18 |
| Run2 | 4.4 | 5.2 | 15 | 0.5 | 0.12 |
| Run3 | 2.9 | 6.7 | 6.0 | -0.59 | -0.3 |
| Run4 | 3.2 | 4.2 | 7.7 | -0.5 | -0.13 |
| Run5 | 4.1 | 4.2 | -1.4 | -1.6 | -0.8 |
| 0.7 kyr | 1.5 kyr | 2.5 kyr | 5 kyr | 18 kyr | |
|---|---|---|---|---|---|
| (kyr) | |||||
| sRun1 | -23 | -30 | -43 | -70 | -140 |
| sRun2 | 15 | 16 | 43 | ||
| sRun3 | 2.6 | 6 | 10 | 150 | 400 |
| sRun4 | 12 | 11 | -30 | -27 | -70 |
| sRun5 | 12 | 5.5 | 34 | 41 | -210 |
| 0.7 kyr | 1.5 kyr | 2.5 kyr | 5 kyr | 18 kyr | |
|---|---|---|---|---|---|
| (AU kyr-1) | |||||
| sRun1 | -0.2 | -0.17 | -0.13 | -0.08 | -0.05 |
| sRun2 | 0.7 | 0.6 | 0.21 | 0.005 | 0.004 |
| sRun3 | 6.7 | 2.2 | 1.2 | 0.07 | 0.025 |
| sRun4 | 4.1 | 4.2 | -1.4 | -1.6 | -0.8 |
| sRun5 | 7.0 | 14 | 2.0 | 1.7 | -0.3 |
| 0.7 kyr | 1.5 kyr | 2.5 kyr | 5 kyr | 18 kyr | |
|---|---|---|---|---|---|
| (kyr) | |||||
| rRun1 | -23 | -29 | -41 | -70 | -180 |
| rRun2 | 19 | 19 | 40 | 880 | |
| rRun3 | 2.4 | 6.3 | 13 | 140 | 710 |
| rRun4 | 11 | 8.7 | 2.6 | 29 | 190 |
| rRun5 | 12 | 5.1 | 4.5 | 4. | 110 |
| 0.7 kyr | 1.5 kyr | 2.5 kyr | 5 kyr | 18 kyr | |
|---|---|---|---|---|---|
| (AU kyr-1) | |||||
| rRun1 | -0.21 | -0.18 | -0.13 | -0.008 | -0.04 |
| rRun2 | 0.5 | 0.5 | 0.2 | 0.01 | |
| rRun3 | 6.9 | 2.1 | 0.9 | 0.09 | 0.014 |
| rRun4 | 4.5 | 5.0 | 13 | 0.8 | 0.1 |
| rRun5 | 6.6 | 15.0 | 15.0 | 8.4 | 0.2 |
Appendix B The effect of radiation from the central star on the direction of migration
The effect of radiative feedback from the protoplanet is important only when the energy that is fed back to the disc alters its dynamical state. In this section we examine how important radiative feedback from the protoplanet is, when the central star is also heating the disc.
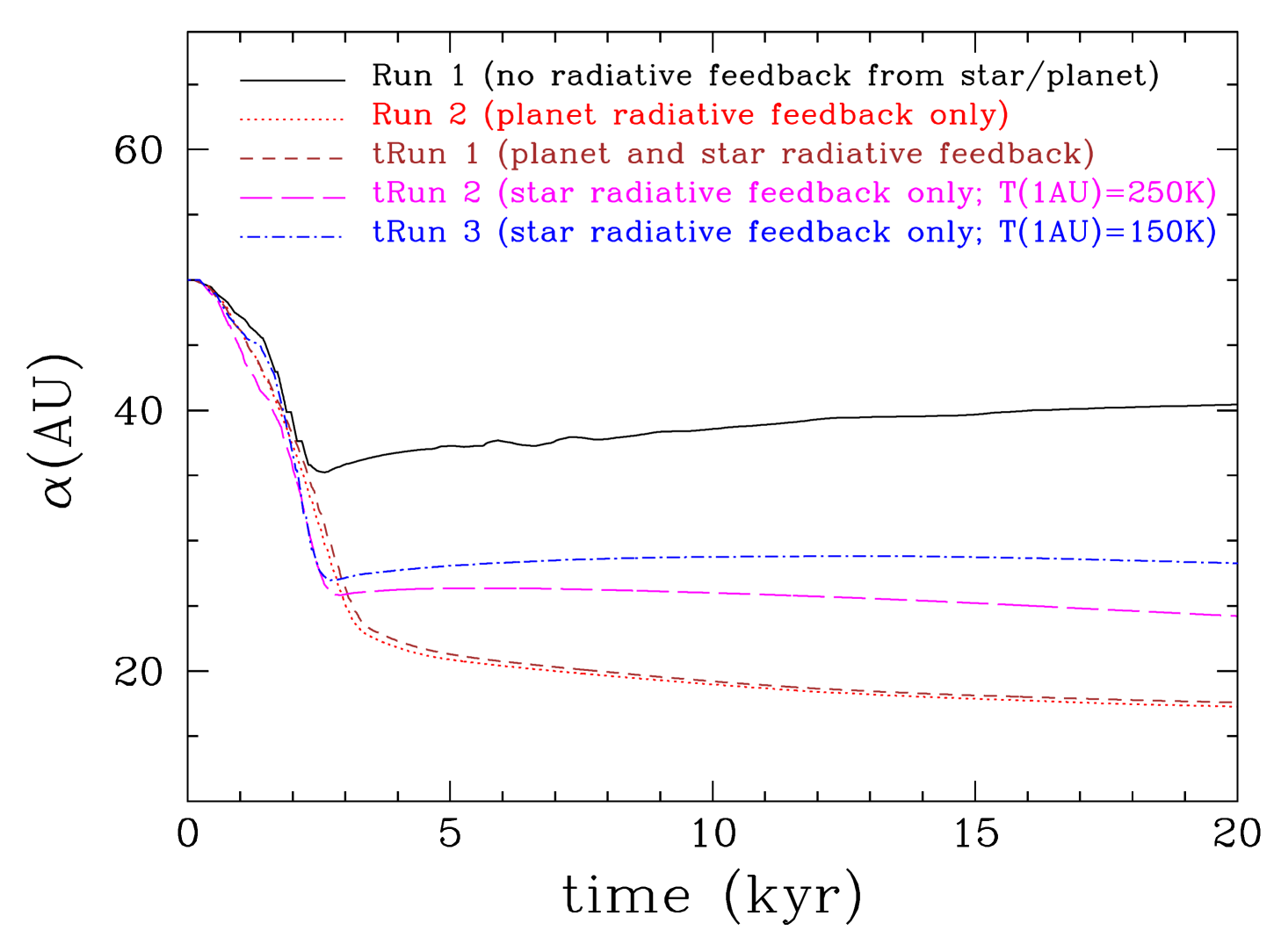
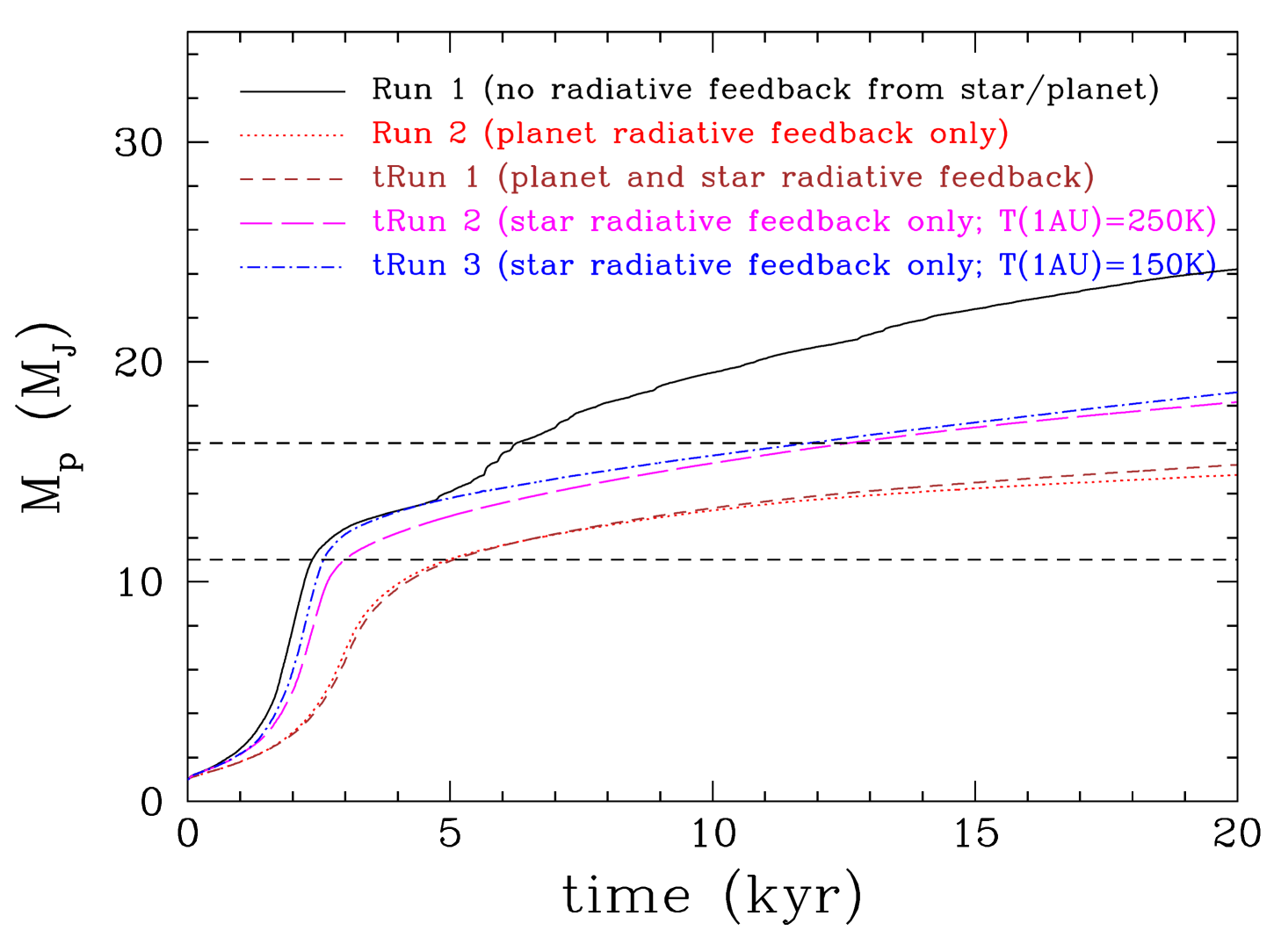
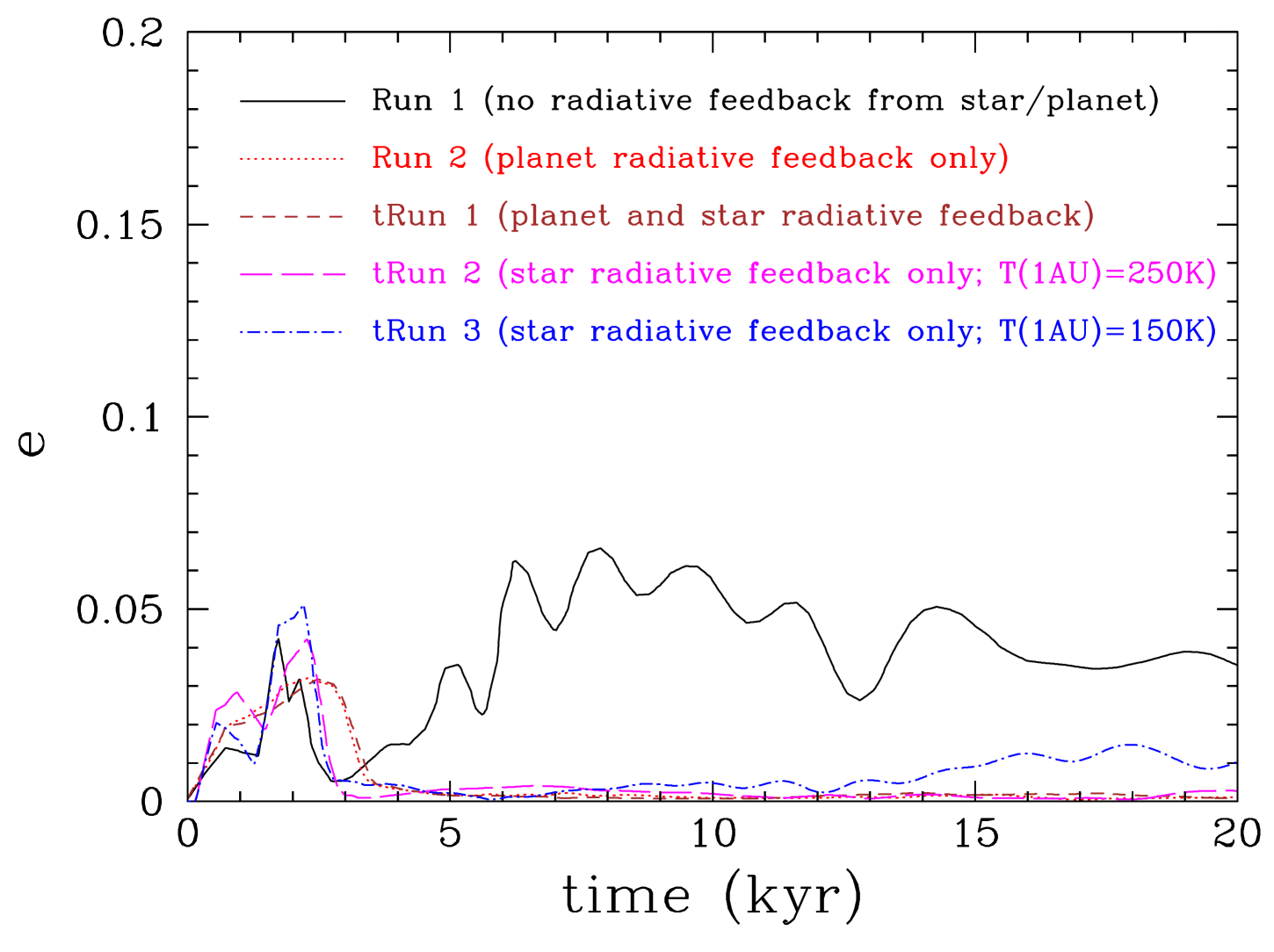
We compare 5 simulations simulations of an initially 1-MJ protoplanet placed at 50 AU from the central star in a 0.1-M⊙ disc: (i) without any radiative feedback (Run1; same as in Section 4), (ii) with protoplanet radiative feedback only (Run2; same as in Section 4), (iiii) with protoplanet and star radiative feedback (tRun1; T(1AU)=250 K), and (iv) only with stellar radiative feedback (tRun2 with T(1AU)=250 K; tRun3 with T(1AU)=150 K). The protoplanet’s orbital radius, mass, eccentricity are shown in Figure 32.
We see by comparing the runs with stellar feedback (tRun 2, tRun3) with the run without any feedback (Run1) that the protoplanet needs more time to open up a gap because the disc is hotter. Therefore the protoplanet migrates further inward in these runs. When the stellar feedback is not high enough (tRun 3) the protoplanet, after opening up the gap, migrates outwards, whereas when the feedback is stronger (tRun 2) the migration continues inwards but at a much longer timescale. In any case the mass growth of the protoplanet is slower when the stellar feedback is included (Figure 32, middle). The eccentricity of the protoplanet is lower (Figure 32, middle), but if the feedback is not strong enough there is a small eccentricity growth (tRun3).
We also see that there is almost no difference in the evolution of the protoplanet when stellar radiative heating is added on top of the protoplanet radiative heating (compare Run2 and tRun1 in Figure 32.) The effect of the protoplanet feedback is to heat and therefore stabilize the gap edges, so that the feedback from the central star has no additional effect. We conclude that radiative heating from the protoplanet plays a more critical role in the protoplanet’s evolution than heating from the central star
Appendix C Long-term protoplanet evolution
The simulations presented so far have followed the evolution of the protoplanet in the disc only for 20 kyr, i.e. for a relatively short duration compared to the estimated disc lifetimes (a few Myr). In this section, we present simulations in which we follow 3 representative simulations for much longer, i.e. 100 kyr (see Figure 33). The details of the simulations are shown in the graphs. These simulations are computationally time-consuming and cannot be performed for all the runs presented in this paper.
In the run with protoplanet radiative feedback (Figure 33; blue lines) the inward migration continues at a very slow rate and the protoplanet eventually ends up at an orbit with a semi-major axis of about 10 AU from the central star. Its mass growth also continues and at the end of the simulation it has become a low-mass brown dwarf (mass ). There is no eccentricity growth in this run and the protoplanets orbit remain circular, as radiative feedback from the protoplanet stabilises the gap edges. The outcome of this simulation is a low-mass brown dwarf at a close-orbit near its star.
In the two runs without radiative feedback from the protoplanet (Figure 33; black and red lines), the protoplanet continues to migrate outwards at a slow pace for the run with the Bell & Lin (1994) opacities (black line) and at a faster pace for the run with the Semenov et al. (2003) opacities (which are generally larger). In the latter case, the protoplanet has reached a semi-major axis of AU at the end of the simulation. However, in both runs the protoplanet has grown considerably in mass to become a mid to high-mass brown dwarf (mass ). The objects in the two runs sustain significant eccentricity growth reaching at the end of the simulation. The outcomes of these two simulations are high-mass brown dwarfs on wide, eccentric orbits around their stars. Therefore, for a protoplanet to end up as a planet it either needs to accrete at a much lower rate or the disc needs to dissipate within a relatively short timescale.
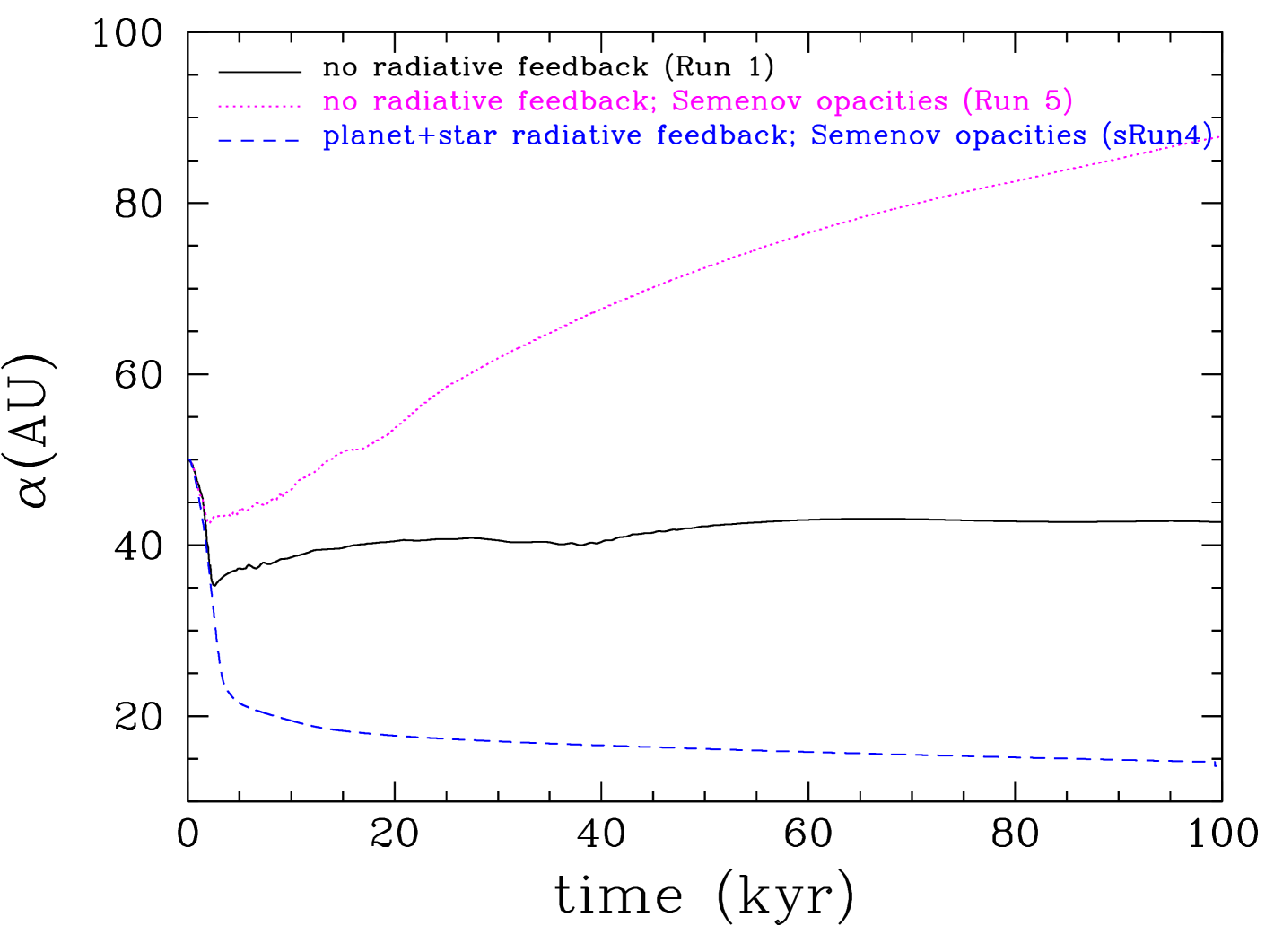
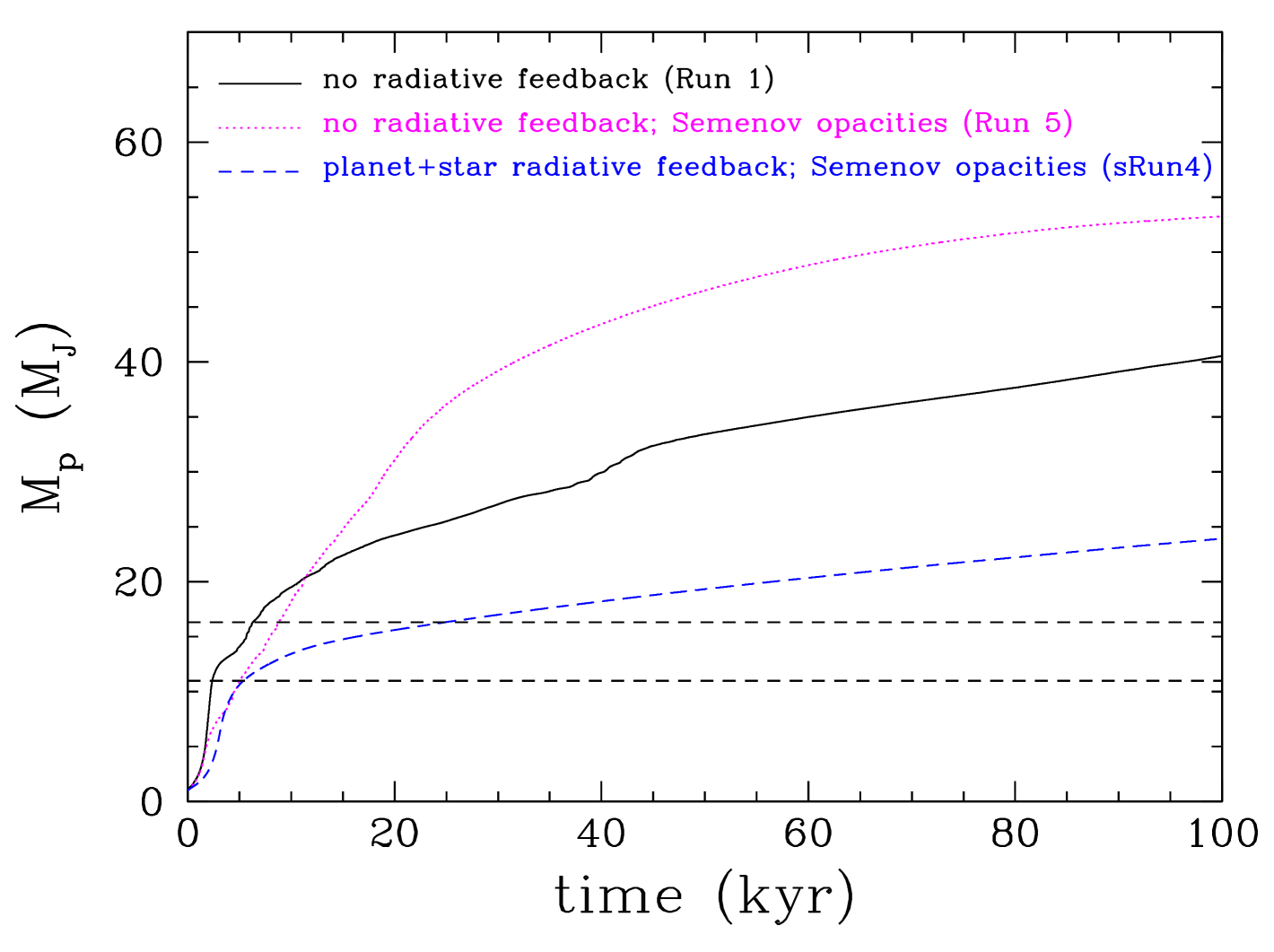
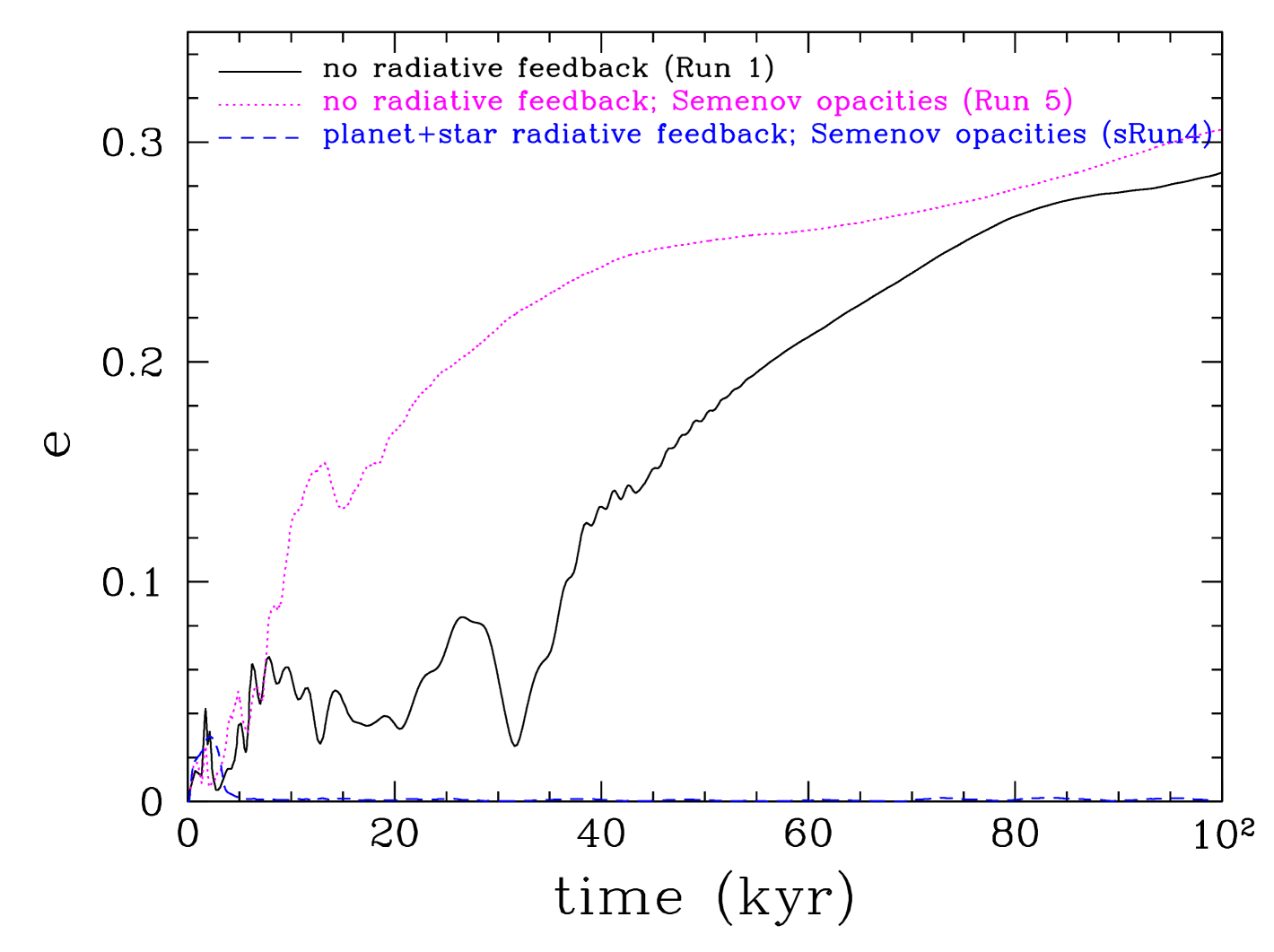
References
- ALMA Partnership et al. (2015) ALMA Partnership et al., 2015, ApJ, 808, L3
- Alexander et al. (2006) Alexander R. D., Clarke C. J., Pringle J. E., 2006, MNRAS, 369, 216
- Alexander et al. (2014) Alexander R., Pascucci I., Andrews S., Armitage P., Cieza L., 2014, Protostars and Planets VI, Eds. H. Beuther, R. Klessen, C. Dullemond, T. Henning, University of Arizona Press,
- Aller et al. (2013) Aller K. M., et al., 2013, ApJ, 773, 63
- Andrews & Williams (2007) Andrews S. M., Williams J. P., 2007, ApJ, 659, 705
- Andrews et al. (2009) Andrews S. M., Wilner D. J., Hughes A. M., Qi C., Dullemond C. P., 2009, ApJ, 700, 1502
- Andrews et al. (2016) Andrews S. M., et al., 2016, ApJ, 820, L40
- Artymowicz & Lubow (1994) Artymowicz P., Lubow S. H., 1994, ApJ, 421, 651
- Artymowicz & Lubow (1996) Artymowicz P., Lubow S. H., 1996, ApJ, 467, L77
- Ayliffe & Bate (2009) Ayliffe B. A., Bate M. R., 2009, MNRAS, 393, 49
- Bai (2016) Bai X.-N., 2016, ApJ, 821, 80
- Bai & Stone (2013) Bai X.-N., Stone J. M., 2013, ApJ, 767, 30
- Bailey et al. (2014) Bailey V., et al., 2014, ApJ, 780, L4
- Baraffe et al. (2017) Baraffe I., Elbakyan V. G., Vorobyov E. I., Chabrier G., 2017, A&A, 597, A19
- Baruteau et al. (2011) Baruteau C., Meru F., Paardekooper S.-J., 2011, MNRAS, 416, 1971
- Bate (2014) Bate M. R., 2014, MNRAS, 442, 285
- Bate et al. (1995) Bate M. R., Bonnell I. A., Price N. M., 1995, MNRAS, 277, 362
- Bate et al. (2003) Bate M. R., Lubow S. H., Ogilvie G. I., Miller K. A., 2003, MNRAS, 341, 213
- Bell & Lin (1994) Bell K. R., Lin D. N. C., 1994, ApJ, 427, 987
- Benítez-Llambay et al. (2015) Benítez-Llambay P., Masset F., Koenigsberger G., Szulágyi J., 2015, Nature, 520, 63
- Bodenheimer & Pollack (1986) Bodenheimer P., Pollack J. B., 1986, Icarus, 67, 391
- Boley (2009) Boley A. C., 2009, ApJ, 695, L53
- Boley et al. (2006) Boley A. C., Mejía A. C., Durisen R. H., Cai K., Pickett M. K., D’Alessio P., 2006, ApJ, 651, 517
- Boley et al. (2010) Boley A. C., Hayfield T., Mayer L., Durisen R. H., 2010, Icarus, 207, 509
- Boss (1988) Boss A. P., 1988, ApJ, 331, 370
- Boss (1997) Boss A. P., 1997, Science, 276, 1836
- Boyd & Whitworth (2005) Boyd D. F. A., Whitworth A. P., 2005, A&A, 430, 1059
- Brandt et al. (2014) Brandt T. D., et al., 2014, ApJ, 794, 159
- Cai et al. (2008) Cai K., Durisen R. H., Boley A. C., Pickett M. K., Mejía A. C., 2008, ApJ, 673, 1138
- Cameron (1978) Cameron A. G. W., 1978, Moon and Planets, 18, 5
- Cloutier & Lin (2013) Cloutier R., Lin M.-K., 2013, MNRAS, 434, 621
- Crida & Morbidelli (2007) Crida A., Morbidelli A., 2007, MNRAS, 377, 1324
- Crida et al. (2006) Crida A., Morbidelli A., Masset F., 2006, Icarus, 181, 587
- D’Angelo & Lubow (2008) D’Angelo G., Lubow S. H., 2008, ApJ, 685, 560
- Dipierro et al. (2015) Dipierro G., Price D., Laibe G., Hirsh K., Cerioli A., Lodato G., 2015, MNRAS, 453, L73
- Duffell & Dong (2015) Duffell P. C., Dong R., 2015, ApJ, 802, 42
- Duffell et al. (2014) Duffell P. C., Haiman Z., MacFadyen A. I., D’Orazio D. J., Farris B. D., 2014, ApJ, 792, L10
- Dunhill & Stamatellos (2018) Dunhill A. C., Stamatellos D., 2018, MNRAS submitted,
- Dürmann & Kley (2015) Dürmann C., Kley W., 2015, A&A, 574, A52
- Dürmann & Kley (2017) Dürmann C., Kley W., 2017, A&A, 598, A80
- Espaillat et al. (2014) Espaillat C., et al., 2014, Protostars and Planets VI, Eds. H. Beuther, R. Klessen, C. Dullemond, T. Henning, University of Arizona Press, pp 497–520
- Faherty et al. (2009) Faherty J. K., Burgasser A. J., Cruz K. L., Shara M. M., Walter F. M., Gelino C. R., 2009, AJ, 137, 1
- Forgan & Rice (2011) Forgan D., Rice K., 2011, MNRAS, 417, 1928
- Forgan & Rice (2013) Forgan D., Rice K., 2013, MNRAS, 432, 3168
- Forgan et al. (2009) Forgan D., Rice K., Stamatellos D., Whitworth A. P., 2009, MNRAS, 394, 882
- Fromang et al. (2013) Fromang S., Latter H., Lesur G., Ogilvie G. I., 2013, A&A, 552, A71
- Fujii et al. (2014) Fujii Y. I., Okuzumi S., Tanigawa T., Inutsuka S.-i., 2014, ApJ, 785, 101
- Galicher et al. (2014) Galicher R., et al., 2014, A&A, 565, L4
- Galicher et al. (2016) Galicher R., et al., 2016, A&A, 594, A63
- Gammie (2001) Gammie C. F., 2001, ApJ, 553, 174
- Gárate et al. (2017) Gárate M., Cuadra J., Montesinos M., 2017, preprint, (arXiv:1711.01372)
- Goldreich & Sari (2003) Goldreich P., Sari R., 2003, ApJ, 585, 1024
- Goldreich & Ward (1973) Goldreich P., Ward W. R., 1973, ApJ, 183, 1051
- Gonzalez et al. (2015) Gonzalez J.-F., Laibe G., Maddison S. T., Pinte C., Ménard F., 2015, MNRAS, 454, L36
- Greaves et al. (2008) Greaves J. S., Richards A. M. S., Rice W. K. M., Muxlow T. W. B., 2008, MNRAS: Letters, 391, L74
- Gressel et al. (2012) Gressel O., Nelson R. P., Turner N. J., 2012, MNRAS, 422, 1140
- Gressel et al. (2013) Gressel O., Nelson R. P., Turner N. J., Ziegler U., 2013, ApJ, 779, 59
- Gressel et al. (2015) Gressel O., Turner N. J., Nelson R. P., McNally C. P., 2015, ApJ, 801, 84
- Haisch et al. (2001) Haisch Jr. K. E., Lada E. A., Lada C. J., 2001, ApJ, 553, L153
- Hall et al. (2017) Hall C., Forgan D., Rice K., 2017, MNRAS, 470, 2517
- Hernández et al. (2008) Hernández J., Hartmann L., Calvet N., Jeffries R. D., Gutermuth R., Muzerolle J., Stauffer J., 2008, ApJ, 686, 1195
- Hubber et al. (2011a) Hubber D., et al., 2011a, Astrophysics Source Code Library, p. 2010
- Hubber et al. (2011b) Hubber D. A., Batty C. P., Mcleod A., Whitworth A. P., 2011b, A&A, 529, A27
- Inutsuka et al. (2010) Inutsuka S., Machida M. N., Matsumoto T., 2010, ApJ, 718, L58
- Ireland et al. (2011) Ireland M. J., Kraus A. L., Martinache F., Law N., Hillenbrand L. A., 2011, ApJ, 726, 113
- Isella et al. (2016) Isella A., et al., 2016, Physical Review Letters, 117, 251101
- Johnson & Gammie (2003) Johnson B. M., Gammie C. F., 2003, ApJ, 597, 131
- Kratter et al. (2010) Kratter K. M., Murray-Clay R. A., Youdin A. N., 2010, ApJ, 710, 1375
- Kraus et al. (2008) Kraus A. L., Ireland M. J., Martinache F., Lloyd J. P., 2008, ApJ, 679, 762
- Kraus et al. (2014) Kraus A. L., Ireland M. J., Cieza L. A., Hinkley S., Dupuy T. J., Bowler B. P., Liu M. C., 2014, ApJ, 781, 20
- Kuiper (1951) Kuiper G. P., 1951, National Academy of Sciences (USA), 37, 1
- Kuzuhara et al. (2011) Kuzuhara M., Tamura M., Ishii M., Kudo T., Nishiyama S., Kandori R., 2011, AJ, 141, 119
- Kuzuhara et al. (2013) Kuzuhara M., et al., 2013, ApJ, 774, 11
- Larson (1969) Larson R. B., 1969, MNRAS, 145, 271
- Lesur et al. (2013) Lesur G., Ferreira J., Ogilvie G. I., 2013, A&A, 550, A61
- Li et al. (2015) Li Y., Kouwenhoven M. B. N., Stamatellos D., Goodwin S. P., 2015, ApJ, 805, 116
- Li et al. (2016) Li Y., Kouwenhoven M. B. N., Stamatellos D., Goodwin S. P., 2016, ApJ, 831, 166
- Lin & Papaloizou (2012) Lin M.-K., Papaloizou J. C. B., 2012, MNRAS, 421, 780
- Lombardi et al. (2015) Lombardi J. C., McInally W. G., Faber J. A., 2015, MNRAS, 447, 25
- Low & Lynden-Bell (1976) Low C., Lynden-Bell D., 1976, MNRAS, 176, 367
- Lubow & D’Angelo (2006) Lubow S. H., D’Angelo G., 2006, ApJ, 641, 526
- MacFarlane & Stamatellos (2017) MacFarlane B. A., Stamatellos D., 2017, MNRAS, 472, 3775
- Machida et al. (2006) Machida M. N., Inutsuka S.-i., Matsumoto T., 2006, ApJ, 649, L129
- Machida et al. (2010) Machida M. N., Inutsuka S., Matsumoto T., 2010, ApJ, 724, 1006
- Machida et al. (2011a) Machida M. N., Inutsuka S., Matsumoto T., 2011a, PASJ, 63, 555
- Machida et al. (2011b) Machida M. N., Inutsuka S., Matsumoto T., 2011b, ApJ, 729, 42
- Machida et al. (2014) Machida M. N., Inutsuka S.-i., Matsumoto T., 2014, MNRAS, 438, 2278
- Malik et al. (2015) Malik M., Meru F., Mayer L., Meyer M., 2015, ApJ, 802, 56
- Marleau et al. (2017) Marleau G.-D., Klahr H., Kuiper R., Mordasini C., 2017, ApJ, 836, 221
- Marley et al. (2007) Marley M. S., Fortney J. J., Hubickyj O., Bodenheimer P., Lissauer J. J., 2007, ApJ, 655, 541
- Marois et al. (2008) Marois C., Macintosh B., Barman T., Zuckerman B., Song I., Patience J., Lafrenière D., Doyon R., 2008, Science, 322, 1348
- Masunaga & Inutsuka (1999) Masunaga H., Inutsuka S., 1999, ApJ, 510, 822
- Masunaga & Inutsuka (2000) Masunaga H., Inutsuka S., 2000, ApJ, 531, 350
- Matzner & Levin (2005) Matzner C. D., Levin Y., 2005, ApJ, 628, 817
- Mercer & Stamatellos (2017) Mercer A., Stamatellos D., 2017, MNRAS, 465, 2
- Michael et al. (2011) Michael S., Durisen R. H., Boley A. C., 2011, ApJ, 737, L42
- Mizuno (1980) Mizuno H., 1980, Progress of Theoretical Physics, 64, 544
- Montesinos et al. (2015) Montesinos M., Cuadra J., Perez S., Baruteau C., Casassus S., 2015, ApJ, 806, 253
- Mordasini (2013) Mordasini C., 2013, A&A, 558, A113
- Mordasini et al. (2009) Mordasini C., Alibert Y., Benz W., 2009, A&A, 501, 1139
- Mordasini et al. (2017) Mordasini C., Marleau G.-D., Mollière P., 2017, A&A, 608, A72
- Morris & Monaghan (1997) Morris J. P., Monaghan J. J., 1997, Journal of Computational Physics, 136, 41
- Muzerolle et al. (2010) Muzerolle J., Allen L. E., Megeath S. T., Hernández J., Gutermuth R. A., 2010, ApJ, 708, 1107
- Naud et al. (2014) Naud M.-E., et al., 2014, ApJ, 787, 5
- Nayakshin (2017a) Nayakshin S., 2017a, PASA, 34, e002
- Nayakshin (2017b) Nayakshin S., 2017b, MNRAS, 470, 2387
- Nayakshin & Cha (2013) Nayakshin S., Cha S.-H., 2013, MNRAS, 435, 2099
- Nelson et al. (2000) Nelson R. P., Papaloizou J. C. B., Masset F., Kley W., 2000, MNRAS, 318, 18
- Offner et al. (2009) Offner S. S. R., Klein R. I., McKee C. F., Krumholz M. R., 2009, ApJ, 703, 131
- Ormel et al. (2015a) Ormel C. W., Kuiper R., Shi J.-M., 2015a, MNRAS, 446, 1026
- Ormel et al. (2015b) Ormel C. W., Shi J.-M., Kuiper R., 2015b, MNRAS, 447, 3512
- Osterloh & Beckwith (1995) Osterloh M., Beckwith S. V. W., 1995, ApJ, 439, 288
- Owen (2014) Owen J. E., 2014, ApJ, 789, 59
- Owen et al. (2010) Owen J. E., Ercolano B., Clarke C. J., Alexander R. D., 2010, MNRAS, 401, 1415
- Pérez et al. (2016) Pérez L. M., et al., 2016, Science, 353, 1519
- Pollack et al. (1996) Pollack J. B., Hubickyj O., Bodenheimer P., Lissauer J. J., Podolak M., Greenzweig Y., 1996, Icarus, 124, 62
- Price (2007) Price D. J., 2007, Publications of the Astronomical Society of Australia, 24, 159
- Rafikov (2005) Rafikov R. R., 2005, ApJ, 621, L69
- Rameau et al. (2013) Rameau J., et al., 2013, ApJ, 772, L15
- Rees (1976) Rees M. J., 1976, MNRAS, 176, 483
- Rice et al. (2005) Rice W. K. M., Lodato G., Armitage P. J., 2005, MNRAS, 364, L56
- Rogers & Wadsley (2012) Rogers P. D., Wadsley J., 2012, MNRAS, 423, 1896
- Safronov (1972) Safronov V. S., 1972, Evolution of the protoplanetary cloud and formation of the earth and planets.. Keter Publishing House
- Satsuka et al. (2017) Satsuka T., Tsuribe T., Tanaka S., Nagamine K., 2017, MNRAS, 465, 986
- Semenov et al. (2003) Semenov D., Henning T., Helling C., Ilgner M., Sedlmayr E., 2003, A&A, 410, 611
- Silk (1977) Silk J., 1977, ApJ, 214, 152
- Spiegel et al. (2011) Spiegel D. S., Burrows A., Milsom J. A., 2011, ApJ, 727, 57
- Stamatellos (2015) Stamatellos D., 2015, ApJ, 810, L11
- Stamatellos & Whitworth (2008) Stamatellos D., Whitworth A. P., 2008, A&A, 480, 879
- Stamatellos & Whitworth (2009a) Stamatellos D., Whitworth A. P., 2009a, MNRAS, 392, 413
- Stamatellos & Whitworth (2009b) Stamatellos D., Whitworth A. P., 2009b, MNRAS, 400, 1563
- Stamatellos & Whitworth (2011) Stamatellos D., Whitworth A., 2011, in European Physical Journal Web of Conferences. European Physical Journal Web of Conferences, p. 05001 (arXiv:0911.3662), doi:10.1051/epjconf/20111605001
- Stamatellos et al. (2007) Stamatellos D., Whitworth A. P., Bisbas T., Goodwin S., 2007, A&A, 475, 37
- Stamatellos et al. (2011a) Stamatellos D., Maury A., Whitworth A., André P., 2011a, MNRAS, 413, 1787
- Stamatellos et al. (2011b) Stamatellos D., Whitworth A. P., Hubber D. A., 2011b, ApJ, 730, 32
- Stamatellos et al. (2012) Stamatellos D., Whitworth A. P., Hubber D. A., 2012, MNRAS, 427, 1182
- Suzuki & Inutsuka (2009) Suzuki T. K., Inutsuka S.-i., 2009, ApJ, 691, L49
- Suzuki & Inutsuka (2014) Suzuki T. K., Inutsuka S.-i., 2014, ApJ, 784, 121
- Suzuki et al. (2010) Suzuki T. K., Muto T., Inutsuka S.-i., 2010, ApJ, 718, 1289
- Szulágyi (2017) Szulágyi J., 2017, ApJ, 842, 103
- Szulágyi & Mordasini (2017) Szulágyi J., Mordasini C., 2017, MNRAS, 465, L64
- Szulágyi et al. (2017) Szulágyi J., van der Plas G., Meyer M. R., Pohl A., Quanz S. P., Mayer L., Daemgen S., Tamburello V., 2017, preprint, (arXiv:1709.04438)
- Takahashi & Inutsuka (2014) Takahashi S. Z., Inutsuka S.-i., 2014, ApJ, 794, 55
- Takahashi et al. (2016a) Takahashi S. Z., Tsukamoto Y., Inutsuka S., 2016a, MNRAS, 458, 3597
- Takahashi et al. (2016b) Takahashi S. Z., Tomida K., Machida M. N., Inutsuka S.-i., 2016b, MNRAS, 463, 1390
- Tanaka et al. (2002) Tanaka H., Takeuchi T., Ward W. R., 2002, ApJ, 565, 1257
- Testi et al. (2015) Testi L., et al., 2015, ApJ, 812, L38
- Tobin et al. (2016) Tobin J. J., et al., 2016, ApJ, 818, 73
- Tomida et al. (2013) Tomida K., Tomisaka K., Matsumoto T., Hori Y., Okuzumi S., Machida M. N., Saigo K., 2013, ApJ, 763, 6
- Toomre (1964) Toomre A., 1964, ApJ, 139, 1217
- Tsukamoto et al. (2015) Tsukamoto Y., Takahashi S. Z., Machida M. N., Inutsuka S., 2015, MNRAS, 446, 1175
- Vaytet et al. (2013) Vaytet N., Chabrier G., Audit E., Commerçon B., Masson J., Ferguson J., Delahaye F., 2013, A&A, 557, A90
- Vigan et al. (2017) Vigan A., et al., 2017, A&A, 603, A3
- Vorobyov & Basu (2005) Vorobyov E. I., Basu S., 2005, ApJ, 633, L137
- Vorobyov & Basu (2006) Vorobyov E. I., Basu S., 2006, ApJ, 650, 956
- Ward (1997) Ward W. R., 1997, Icarus, 126, 261
- Whitworth & Stamatellos (2006) Whitworth A. P., Stamatellos D., 2006, A&A, 458, 817
- Whitworth et al. (2007) Whitworth A. P., Bate M. R., Nordlund A&A., Reipurth B., Zinnecker H., 2007, Protostars and Planets V, p. 459
- Wilkins & Clarke (2012) Wilkins D. R., Clarke C. J., 2012, MNRAS, 419, 3368
- Wright et al. (2011) Wright J. T., et al., 2011, PASP, 123, 412
- Young et al. (2012) Young M. D., Bertram E., Moeckel N., Clarke C. J., 2012, MNRAS, 426, 1061
- Zhu (2015) Zhu Z., 2015, ApJ, 799, 16
- Zhu et al. (2012) Zhu Z., Hartmann L., Nelson R. P., Gammie C. F., 2012, ApJ, 746, 110