The effect of collision-coagulation on the mean relative velocity of particles in turbulent flow: systematic results and validation of model.
Abstract
The mean radial component of relative velocity (MRV) between pairs of inertial particles is studied, where the particles are advected by turbulent flow and undergo collision-and-coagulation. A previously proposed phenomenological model of MRV for low-inertia particles (Saw & Meng, 2022) is corrected (improved) and shown to produce better predictions of the MRV as a function of particle separation distance . Then, using direct numerical simulation (DNS), the relationship between the DNS-produced MRV and particle/turbulent parameters is studied. The results show that for particles with near-zero Stokes numbers (), the MRV is roughly independent of . At larger , the magnitude of MRV increases with and this change is most pronounced when . Assuming that the relative particle velocities are derived from fluid velocity differences associated with a nominal resonant length scale, we find an empirical relation between this resonant scale and Stokes number such that the resonant scale has the form: , where . We show that, coupled with this empirical result, the aforementioned MRV model could be extended to predict MRV for any finite , and we further show that the predictions are accurate against the DNS results. Our results also suggest that the extended model could also accurately account for possible Reynolds number () effect by simply allowing and to be functions of . We also find that when the particle diameter is smaller than the Kolmogorov length scale, the MRV for particles with the same is independent of the particle diameter. By studying the MRV under different Reynolds numbers (), we find that for particles with , the MRV is independent of . For larger , dependence is observed such that the coefficients and decrease with .
1 Introduction
The collision and coagulation of inertial particles in turbulent flow is a common and important physical process in both scientific research and industrial applications. For example, the collision rate between small droplets in atmospheric clouds affects precipitation (Shaw, 2003; Grabowski & Wang, 2013). In astrophysical environments such as protoplanetary disks, the collision of dust grains is a step in the formation of planetesimal (Johansen et al., 2009; Pan et al., 2011). In turbulent spray combustion, the distribution and the size of fuel droplets affect the efficiency of energy conversion (Smith et al., 2002). (Saffman & Turner, 1956) studied the collision rate of no-inertia particles in turbulent flow and obtained the collision rate: , in which and are the mean concentrations of two kinds of particles, respectively, and are their radii. The mean radial relative velocity of zero-inertia particles is . Unlike fluid particles, inertial particles are preferentially concentrated in the high strain and low vorticity region of turbulent flow, resulting in an inhomogeneous distribution, which is also called particle clustering (Squires & Eaton, 1991; Saw et al., 2008). In addition, the relative velocity of inertial particles increases at contact in turbulent flow (Bragg & Collins, 2014). These two effects make the collision rate of inertial particles in turbulent flow is larger than that of fluid particles and difficult to calculate. In (Sundaram & Collins, 1997), the relationship among the collision rate, particle clustering and particle relative radial velocity was presented: , in which is the particle diameter, is the radial distribution function (RDF) when the particle separation distance is equal to , and is the mean radial relative velocity (MRV) of particles. is the spatial volume of the domain. This finding makes it possible to study the particle RDF and MRV independently and to predict the collision rate of inertial particles in different situations. This paper focuses on the MRV of inertial particles, and the following also focuses on the current state of research related to the relative velocity of particles.
The particle Stokes number is a dimensionless quality characterizing the inertia of particles, is equal to the ratio of the particle relaxation time to the Kolmogorov time scale of the flow. The theoretical studies show that for particles with medium Stokes number, they have a path-history effect in turbulent flow. When particles are at the same position, their velocities have low correlation, resulting in high relative velocity. This phenomenon is called sling effect or caustics (Wilkinson & Mehlig, 2005; Wilkinson et al., 2006; Falkovich et al., 2002). The mean radial relative velocity is the relative velocity of particles projected in the radial direction: , which is also the first-order structure function of particle relative velocity. If the collision-coagulation of particles is not considered, since the turbulent velocity is isotropic at small scale, . In most numerical simulation studies, collision and coagulation of particles are not considered, therefore these works often investigated higher order particle relative velocity structure function, the second-order structure function for example, or particles mean negative radial relative velocity , to indirectly obtain the trend of the MRV. The results show that the value of and of the particles increase gradually with the increase of the particle Stokes number, and the growth is significant when , which is consistent with the finding of the sling effect/caustics (Bewley et al., 2013; Ireland et al., 2016). In (Falkovich et al., 2002) and (Wilkinson & Mehlig, 2005), they think that the sling effect or caustics becomes more significant with the increase of the turbulent Reynolds number. However, the numerical results show that for small particles, and are only weakly dependent on turbulent Reynolds number (Ireland et al., 2016). For particles with , they decrease with increasing Reynolds number (Bec et al., 2010; Rosa et al., 2013).
In (Saw & Meng, 2022), they find that when particles collide and coagulate, the magnitude of MRV increases significantly in the range of the separation distance is close to the particle diameter . They also propose a MRV phenomenological model to illustrate the relationship between MRV and the separation distance . Based on their results, we first make an improvement for the MRV phenomenological model. Then, the collision-coagulation is considered in our numerical simulation, the relationship between the MRV with particles and turbulent parameters is studied directly. The contents of this paper are organized as follows. In Section 2, we describe the numerical method that are used to simulate homogeneous isotropic turbulence and particle motion with the consideration of particle collision-coagulation. The improvement of the MRV phenomenological model is shown in section 3. The results from DNS are discussed in Section 4. A summary and main conclusion are given in Section 5.
2 Simulation method
Direct numerical simulation (DNS), which fully solves the Navier-Stokes equation in both spatial and temporal space, is used to study the particle laden flow in this paper. The incompressible Navier-Stokes equations are solved in a cube which has periodic boundary condition in three directions and the length of which is :
| (1) |
| (2) |
Where , , and are velocity, pressure, density and the kinetic viscosity of turbulent flow. is the forcing scheme, added in the large scale region of turbulence to maintain the statistics stationary (Eswaran & Pope, 1988). The N-S equations are transformed from physical space to wavenumber space, which is called the pseudo-spectral method. The 2/3-method is used to deal with aliasing error raised by the convection term in 1 (Rogallo, 1981).
The influence of the turbulent Reynolds number on the particle MRV is studied in this paper, the range of Reynolds number we choose is , where is the Taylor microscale Reynolds number. In different cases, , 1.21, 1.38, where is the maximum wavenumber, and Courant number , 0.0401, and 0.0865 respectively. The detailed parameters are shown in table 1. The simulation method and the DNS parameters are the same with (Meng & Saw, 2023). In (Meng & Saw, 2023), a higher resolution simulation is conducted to study the possible effects of the sub-Kolmogorov intermittency on the RDF of particle, using at . The result indicates that the effect of unresolved sub-Kolmogorov intermittency may modify slightly the inertial clustering exponent but would not cause any significant changes to the qualitative trends of particle RDF. Therefore, it can be considered that the sub-Kolmogorov intermittency will not have effect on the main results in this paper.
| flow 1 | 256 | 0.001 | 0.0326 | 0.3519 | 0.2386 | 0.0132 | 0.1750 | 0.5073 | 1.4416 | 84 |
| flow 2 | 256 | 0.001 | 0.1013 | 0.5684 | 0.2187 | 0.0100 | 0.0993 | 0.6151 | 1.0822 | 124 |
| flow 3 | 512 | 0.001 | 0.9472 | 1.226 | 0.1544 | 0.0057 | 0.0325 | 0.7398 | 0.6034 | 189 |
Particles in this paper are small and heavy, the particle diameter is much smaller than the Kolmogorov length scale and the particle density is much larger than the density of flow . The basic physical process of particle collision-coagulation is considered in this paper, therefore the gravitational effect and the inter-particle hydrodynamic interaction are not included in simulation system. Particles and turbulent flow are only one-way coupling. Under these hypotheses, particles are only conducted by the Stokes drag force, the motion equation of particles is shown below (Maxey & Riley, 1983):
| (3) |
where is particle velocity, is the flow velocity at particle position, and is particle relaxation time.
Particles will collide and create a new particle with the conservation of momentum and mass when the particle separation distance is equal to or less than the sum of the particle radii. To avoid successive collisions with larger particles created by collision-coagulation, larger particles are removed from the system as soon as they are created. In this situation, in order to maintain the equilibrium of the particles in the system, a fixed number of particles are added to the system at certain time steps, and these new particles have the same parameters as the initial particles. After 10 turbulent characteristic integration times, the particles in the system reach stability. It is important to note that, only monodisperse particles are considered in the calculation of the MRV, which means the relative velocity between particles with different is not taken into account. The influences of particle Stokes number and the particle size on MRV are studied in this paper, the range of we choose is and the particle diameters are , , and , where . It should be noted that the diameter size of the particles is only used to determine whether collisions occur between the particles, the inter-particle hydrodynamic is not considered.
3 Correction (improvement) of the MRV phenomenological model
Here, we present a correction (improvement) of the MRV phenomenological model proposed by Saw & Meng (2022) and show that this substantially improve the model’s accuracy. We begin with a brief introduction of the model. The model describes the relationship between MRV and the particle separation distance in the limit, such that:
| (4) |
where () is the probability for a sample of to turn out positive (negative) and the constants , depends on the flow energy dissipation rate (Saw & Meng, 2022). As a first-order account, the skewness in the distribution of particle relative velocities were neglected which leads to , and . is a conditional probability density function (PDF) of defined as . is the angle between the relative velocity and the relative displacement of a particle-pair. Saw & Meng (2022) argue that PDF of may be constructed using the (statistical) central-limit theorem, such that:
| (5) |
where is the circular normal distribution, and , a variance parameter, may be inferred by matching the model produced transverse-to-longitudinal ratio of structure functions (TLR) of the particle relative velocities to the one measured directly in experiment or DNS (Saw & Meng, 2022). In (Saw & Meng, 2022), the model predicts MRV that agrees best with DNS outcome when is calibrated using the fourth-order structure functions instead of the second-order which one would normally expect since MRV is a low order statistics. This suggests that the model may be incomplete(Saw & Meng, 2022).
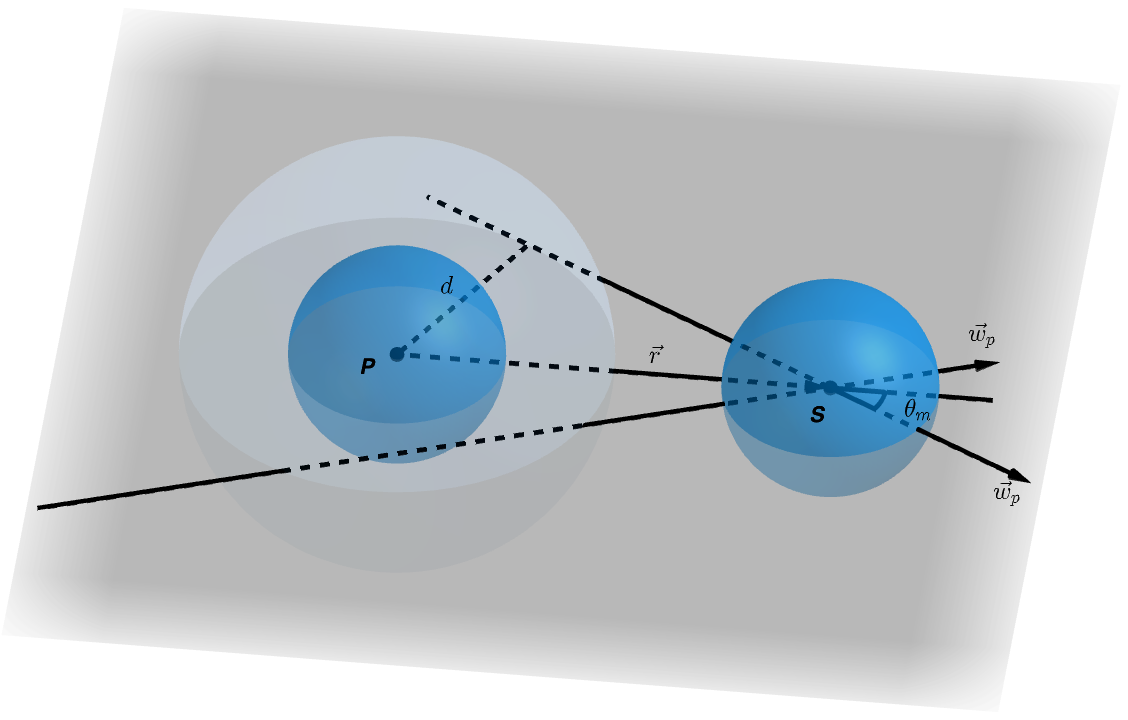
According to the idealized picture of particle collision-coagulation process described in (Saw & Meng, 2022), as shown in Figure 1, the small scale trajectory of particle can be regarded as rectilinear at separation close to the particle diameter . Since particles collide and coagulate when , according to the geometrical analysis, the angle between and cannot be smaller than , which is a value related to the ratio of to : . This lower bound of affects the symmetry of the PDF of particle relative velocity, therefore (also ) should not be fixed at 0.5 but should equals a value that varies with (which in turns varies with ). Thus, we change the probability of a realization of being positive and negative to:
| (6) |
which also satisfy .
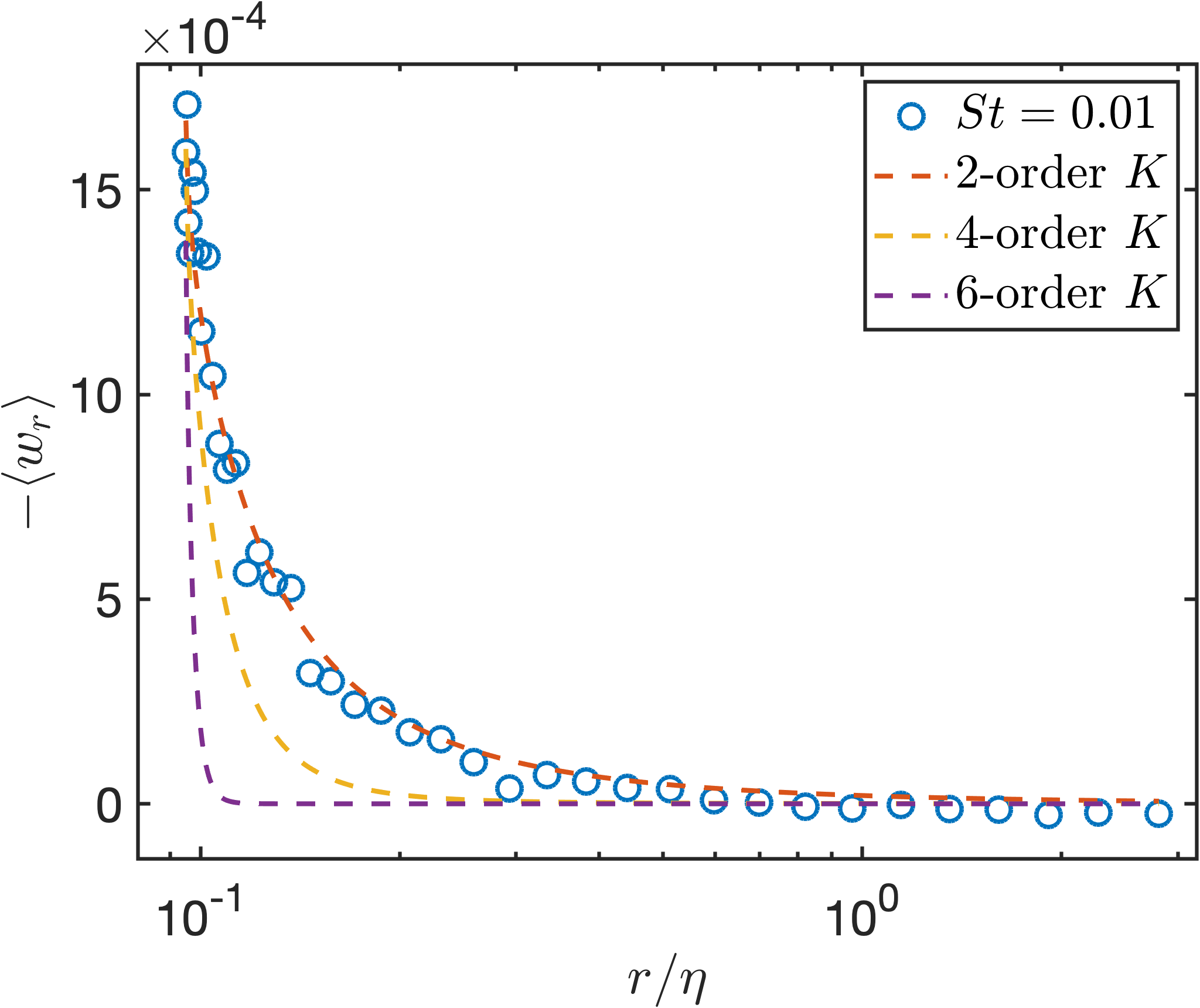
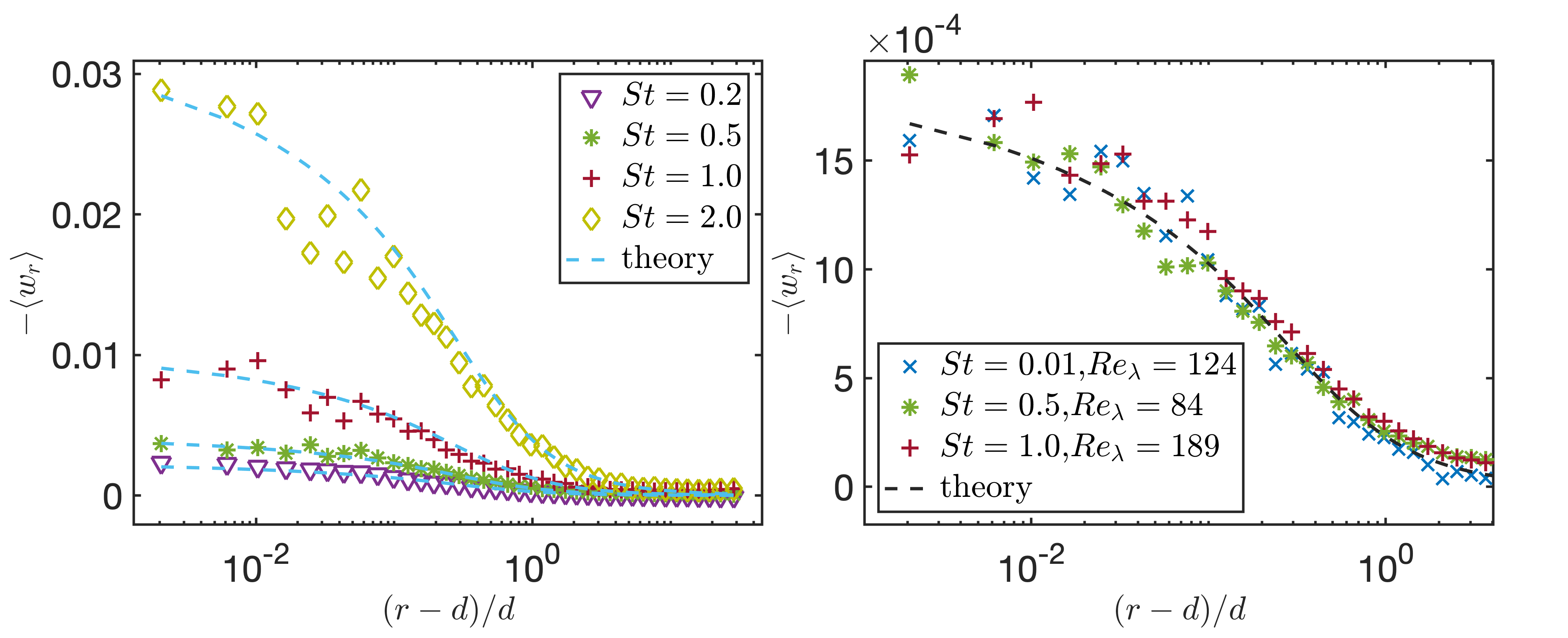
Bringing the revised into Eq.4 and using Eq.5 where is calibrated by the measured (via DNS) second-, fourth-, and sixth-order structure functions of particle relative velocity respectively, the new MRV model predictions is compared with the DNS results, as shown in Figure 1. We see that the second-order calibration produces result with the best agreement with DNS, and which is significantly better than that in (Saw & Meng, 2022). This provide strong support for the validity of the MRV model since second-order statistics are the most appropriate (orthodox) reference for the determination of , which is itself a variance parameter analogous to in the Gaussian distribution.
4 Results and Discussion
4.1 Stokes number dependence
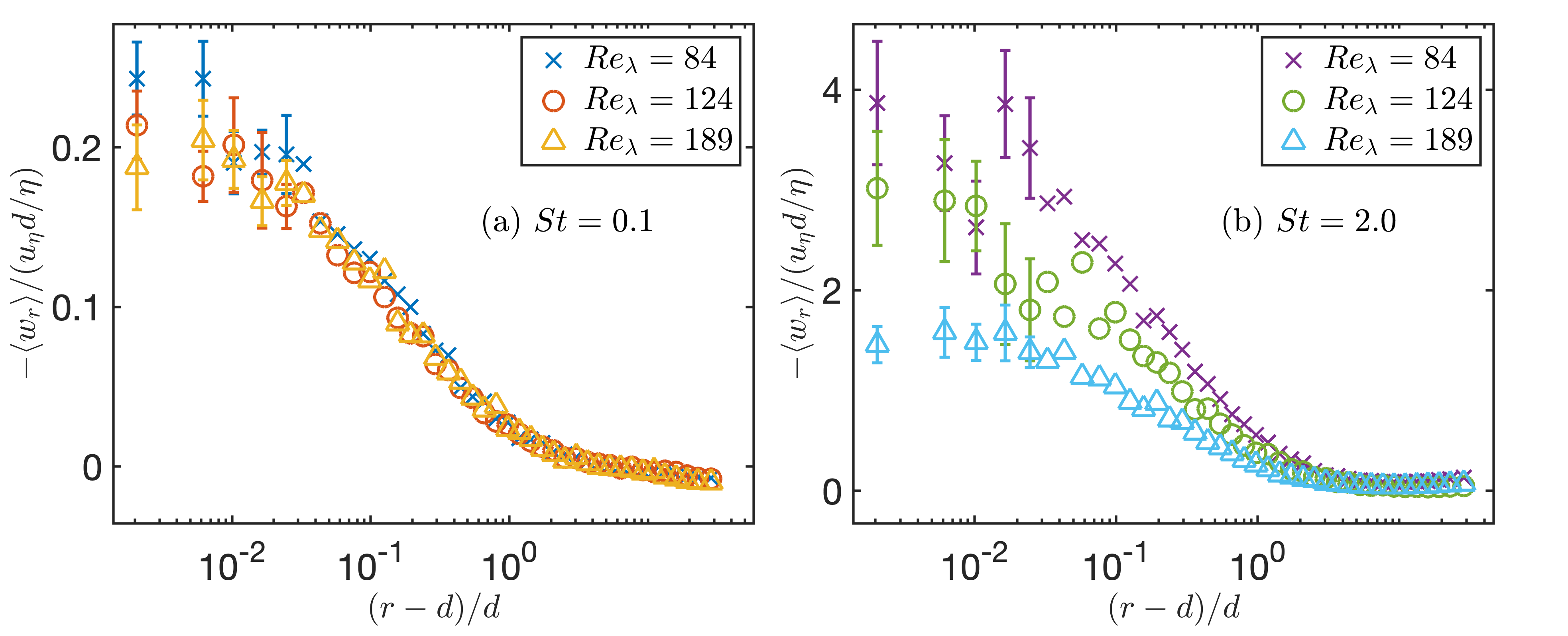
In order to study the variation of the MRV with the particle Stokes number, particles with different are introduced into the system respectively, the range of is from 0.01 to 2.0. In each case, the turbulent Reynolds number and particle size are the same. The MRV for particles with different is shown in Figure 2.
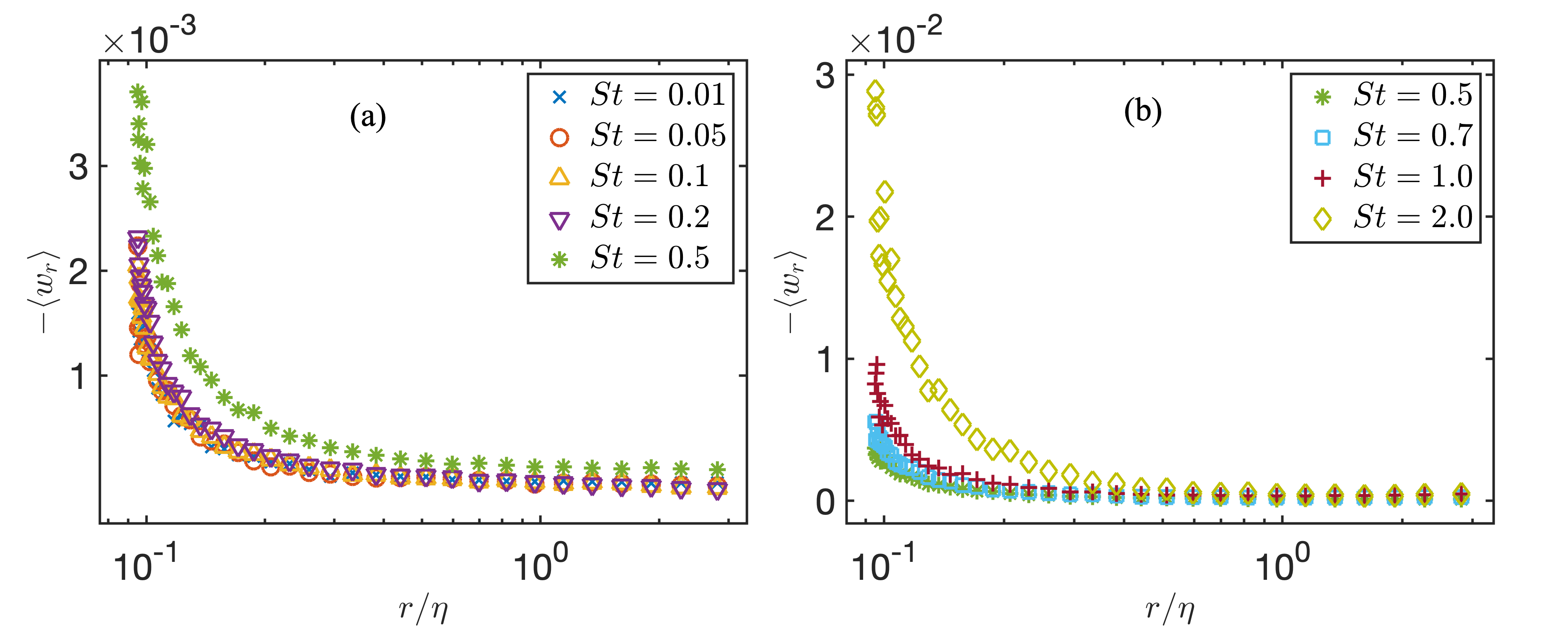
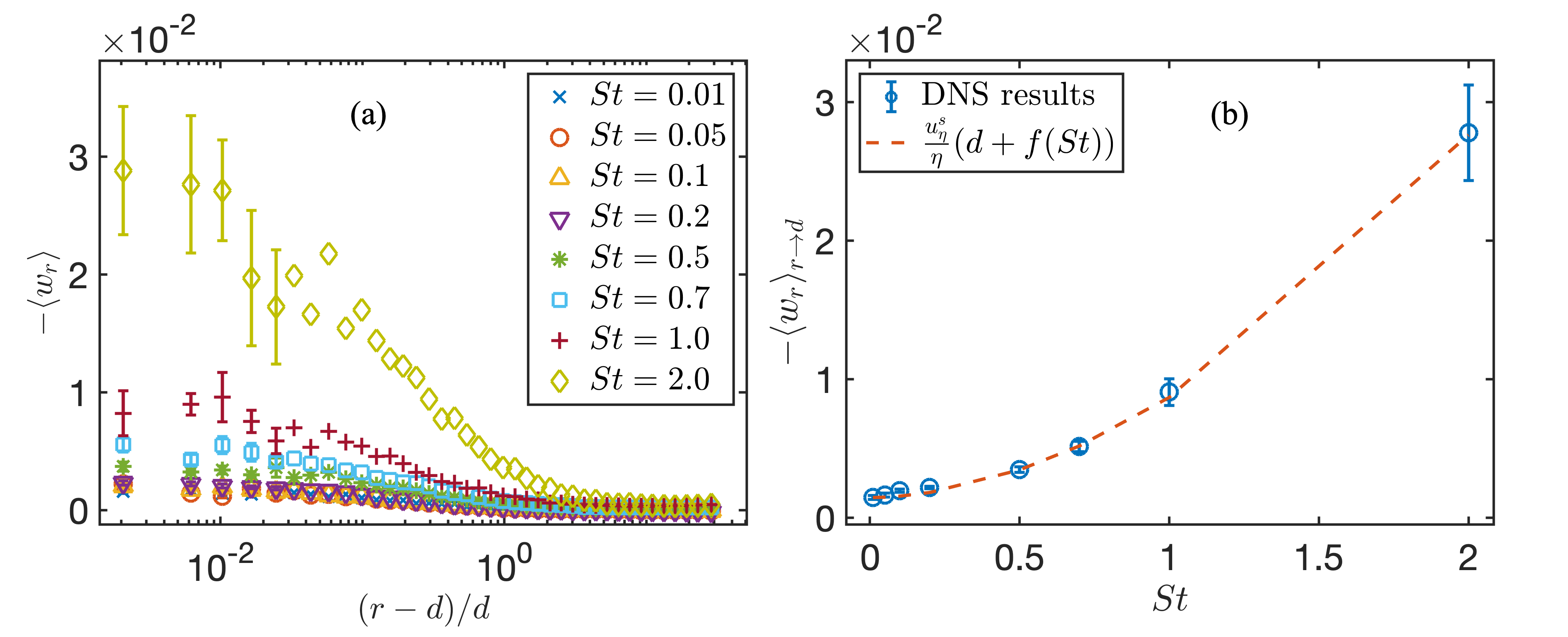
First we can see from these figures that the magnitude of MRV increases gradually as the separation distance decreases, which is consistent with the results in (Saw & Meng, 2022). Furthermore, it also shows that for particles with , the MRV barely changes with increasing Stokes number. However, when , the magnitude of MRV increases significantly as increases. In order to illustrate the trend of the MRV when is close to , the MRV against for particles with different Stokes number is shown in Figure 3 (a). We can see that with the decrease of the particle separation distance , the magnitude of MRV increases sharply at the first time. Then, it becomes flatten when is close to the particle diameter . According to this phenomenon, we assume that the value of MRV at can be regarded as the value of that at , which we call . The relationship between and the particle Stokes number is shown in Figure 3 (b), where the value of MRV is normalized by the Kolmogorov velocity . We can see that follows a convex function with .
When the Stokes number is much less than unity, the trajectory of inertial particles is close to that of fluid particles and thus are strongly influenced by the local flow velocity. In small scale range, the relative velocity of particles can be obtained by sampling the gradient of turbulent velocity(Ireland et al., 2016; Biferale et al., 2014). Thus, in the limit of small Stokes number, MRV is nearly -independent. While for particles with larger , they have larger kinetic relaxation time, and the motion of particles at current time will be affected by the flow velocities encountered on their historical trajectories, which is called path-history effect. In this situation, the correlation between velocities of nearby particles is low and a large relative velocity is obtained at contact. This phenomenon is called sling effect or caustic (Falkovich et al., 2002; Wilkinson & Mehlig, 2005). Earlier studies show that when , the sling effect is getting pronounced (Falkovich & Pumir, 2007; Ireland et al., 2016), which is consistent with results in this paper.
Based on the above theoretical understanding, we expect the trend of MRV versus Stokes number to be related to a ”nominal” or ”resonant” length scale which could be imagined as the nominal spatial scale (in the turbulence’s energy spectrum) at which the inertial particles derive their momentum (or energy) from the advecting flow. This resonant scale is simply the particle separation when Stokes number is near zero due to passive advection, but it should increase with for heavier particles. We assume that for the Stokes numbers selected in this paper, this resonant scale does not exceed the Kolmogorov length scale , so that the statistics of the flow velocity can be regarded as a linear function of spatial scale. Then, we explore a relationship between the value of MRV at with the particle Stokes number of the form:
| (7) |
where , which comes from the second-order structure function of turbulent velocity at the small scale limit. We found from the DNS (it represents the difference between the average value and the root mean square). In Eq.7, represents the difference between the resonant scale at which particles couple most efficiently to the flow and , and has the form . By performing curve fitting on the DNS results (Fig. 3b), we get , . Fig .3(b) shows the plot of Eq.7 using the above obtained values of () and the corresponding DNS result. Bringing into the function yields , which satisfies the assumption made above.
4.2 Reynolds number dependence
First, we study the MRV for particles with (e.g., ) in different cases, which is shown in Figure 4 (a). According to the results in Section 4.1, particles with are mainly affected by the local turbulent velocity. Defining the characteristic local velocity of turbulent flow at as , the MRV in Figure 4 (a) is normalized by this value. It can be seen that the MRV in different cases collapse, which indicates that the MRV is independent to turbulent Reynolds number for . While for larger (e.g. ), which is shown in Figure 4 (b), the magnitude of MRV, which is also normalized by , decreases with increasing . Based on the theory in Eq.7, this result indicates that the spatial scale where particles are affected by the non-local flow in their historical trajectories decreases with increasing.
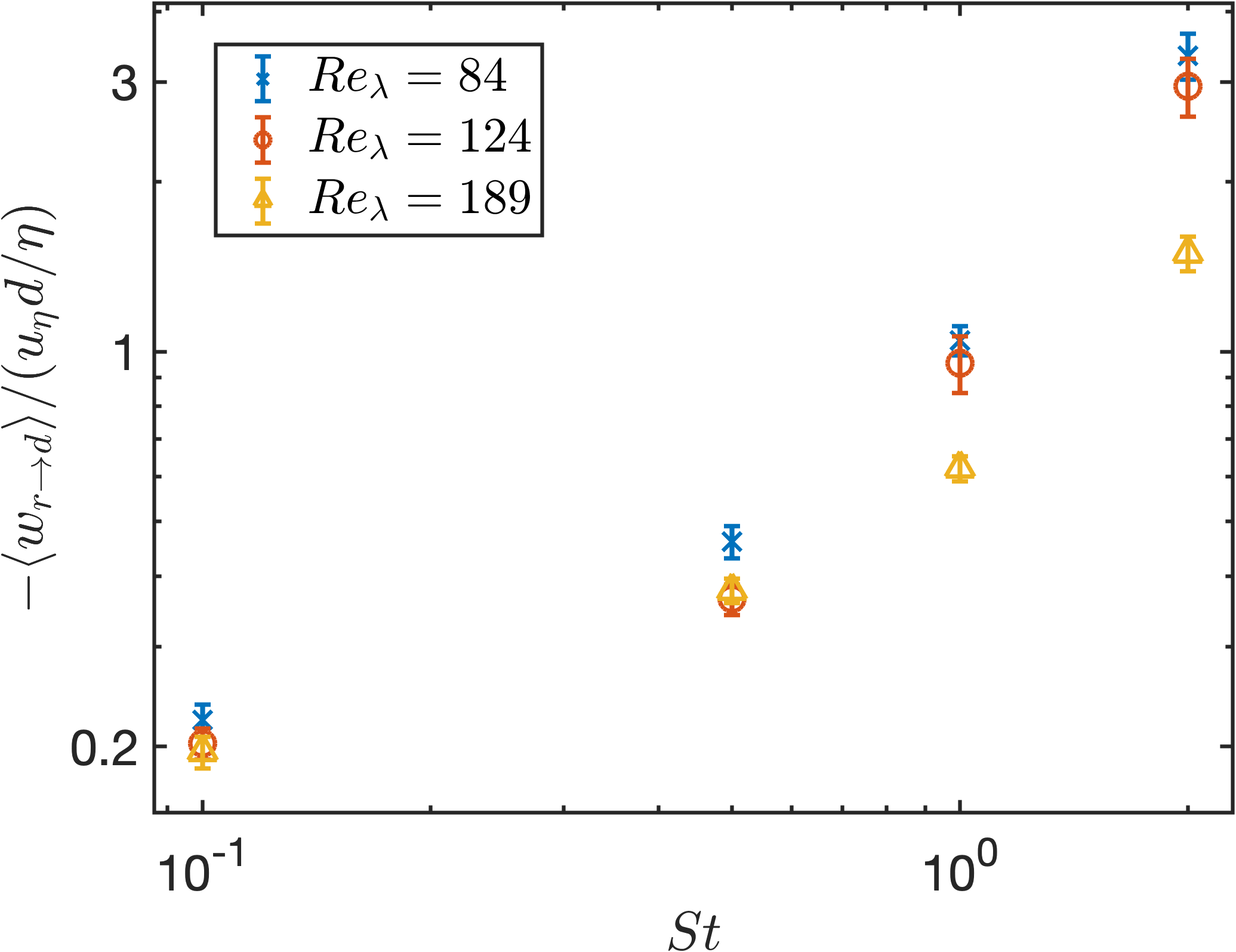
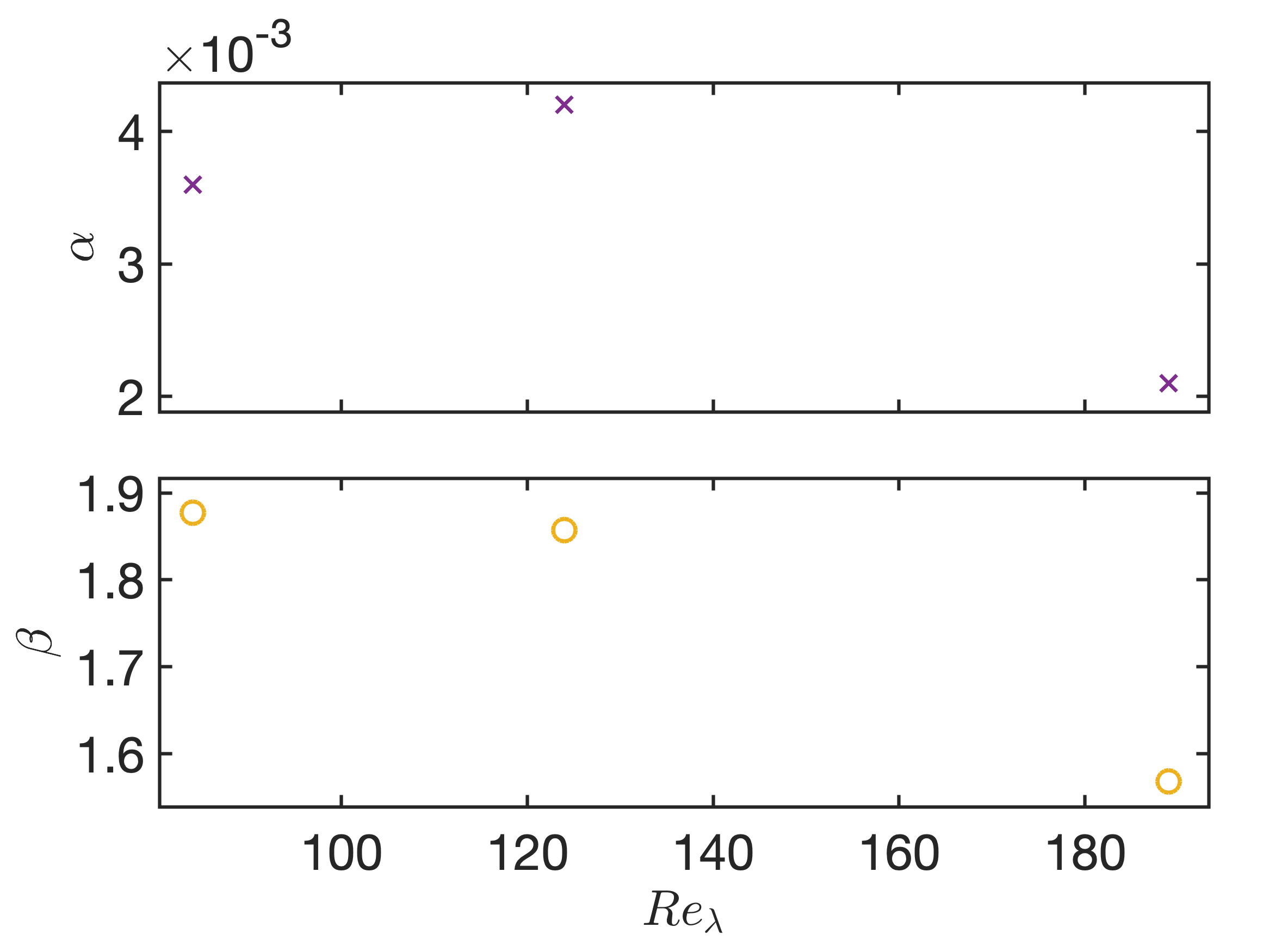
In (Ireland et al., 2016), they studied the average of negative particle relative velocities and found that its values decrease with the increase of turbulent Reynolds number, but their analysis focused on particles with large (e.g., ), ignoring the particles results of smaller . In order to be able to quantitatively analyze the influence of the turbulent Reynolds number, the value of MRV at for particles with and 1.0 in different cases are calculated and are compared with and 2.0 results, which is shown in Figure 5. We can see that the magnitude of MRV increases with increasing in different cases. However, the growth rate of MRV with gradually slows down as increases. This result shows that for particles with larger Stokes number, the distance between the spatial scale affected by non-local flow and the particle collision radius is not only related to the particle Stokes number, but also is a function of turbulent Reynolds number. The coefficients in are obtained by performing curve fitting on the DNS results in Figure 5, which is shown in Figure 5. decreases as the Reynolds number increases, while the value of first increases and then decreases.
4.3 Particle size dependence
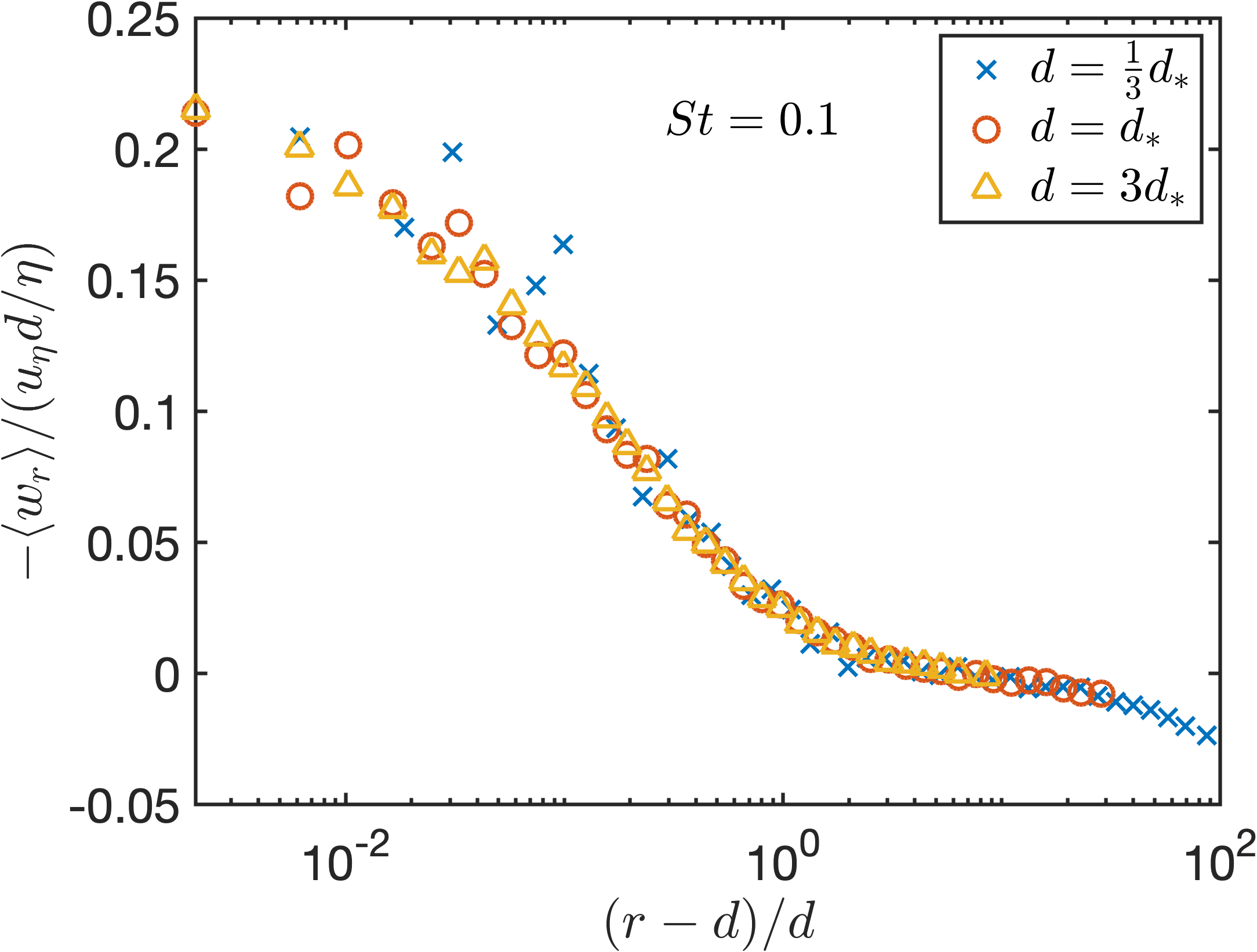
The MRV for particles with different diameter is shown in Figure 6. The particle Stokes number is 0.1 and in three cases. The magnitude of MRV is normalized by the characteristic local turbulent velocity and the MRV is plotted as a function of . From this figure, we can see that the MRV for different diameter cases collapse. This result suggests that, despite the particle diameter is different, the particles with are still mainly affected by the local turbulent velocity. The variance of the MRV with the separation distance due to particle collision-coagulation is the same for different particle diameter.
4.4 Extension of the MRV phenomenological model for finite particles
The phenomenological model described in Section 3 may be extended to predict the MRV in cases of larger (finite) Stokes numbers, if the model is multiplied by a pre-factor , which according to this Eq. 7, can be determined as:
| (8) |
Combining with the MRV model (Eq.4, 5, and 6), we make quantitative predictions for the MRV for different Stokes numbers, and compare them with the DNS results in Figure 7 (a). We see that the theoretical model is in good agreement with the DNS results.
Since a definite relationship between and is unknown, in order to evaluate the model’s ability to address possible effects, in Figure 7 (b), the DNS produced MRV for the (, ) case and (, ) case are respectively translated vertically to the position where the (, ) case lies. What is striking in this figure is that the MRV for different cases has the same shape, which is also predicted by the model in the range of . This suggests that the same ”” program is sufficient to also capture Reynolds number effects once the correct dependence of on is known.
5 Conclusion
In this paper, the mean radial relative velocity (MRV) of inertial particles is investigated when the particle collision-coagulation is considered. First, the direct numerical simulation is used to investigate the relationship between the MRV with the particle Stokes number, the turbulent Reynolds number, and the particle diameter. The results show that the magnitude of MRV increases with increasing , and the growth is pronounced when . We attribute this increase to the scale at which particles with different inertia are affected by non-local turbulent flow in their historical trajectories. Based on this analysis, the relationship function of the value of MRV at with is obtained: , where represents the distance between the scale at which particles are affected by non-local turbulent velocity and their collision radius (e.g., particle diameter ). Next, we study the relationship between the value of MRV and the turbulent Reynolds number, and also analyze it from the perspective of the scale change of the non-local turbulent flow that affects inertial particles. We find that for particles whose Stokes number is much less than 1, they are mainly affected by the local turbulent velocity, and is independent of . While for particles with larger , the coefficients and in decrease as increases. However, since this paper only selects three cases with different , it is impossible to obtain an accurate mathematical relationship between and , which needs further research in the future. In addition, this paper analyzes the MRV for particles with different diameters . The result shows that for particles with the same , although the diameters are different, the MRV under the same has the same value, and is independent of the particle diameter.
Finally, we make a correction (improvement) on the MRV phenomenological model proposed by Saw & Meng (2022) to captures the effect of collision-coagulation on MRV in the limit of . As a result, the corrected model, coupled with proper inputs from the turbulent flow’s velocity statistics, makes prediction that is in close agreement with the DNS results, an outcome that is substantially better than that in (Saw & Meng, 2022). Furthermore, based on the relationship between the value of MRV at and mentioned above, a coefficient is defined. We found that by incorporating into the MRV model, the MRV for cases with any can be accurately predicted (up to ) . Our results also suggest that the model could also accurately account for any possible Reynolds number effect through a simple generalization.
[Acknowledgements]This work was mainly supported by the National Natural Science Foundation of China (grand 11872382) and by the Thoudand Young Program of China.
References
- Bec et al. (2010) Bec, J, Biferale, L, Cencini, M, Lanotte, AS & Toschi, F 2010 Intermittency in the velocity distribution of heavy particles in turbulence. Journal of Fluid Mechanics 646, 527–536.
- Bewley et al. (2013) Bewley, Gregory P, Saw, Ewe-Wei & Bodenschatz, Eberhard 2013 Observation of the sling effect. New Journal of Physics 15 (8), 083051.
- Biferale et al. (2014) Biferale, Luca, Meneveau, Charles & Verzicco, Roberto 2014 Deformation statistics of sub-kolmogorov-scale ellipsoidal neutrally buoyant drops in isotropic turbulence. Journal of fluid mechanics 754, 184–207.
- Bragg & Collins (2014) Bragg, Andrew D & Collins, Lance R 2014 New insights from comparing statistical theories for inertial particles in turbulence: Ii. relative velocities. New Journal of Physics 16 (5), 055014.
- Eswaran & Pope (1988) Eswaran, Vinayak & Pope, Stephen B 1988 An examination of forcing in direct numerical simulations of turbulence. Computers & Fluids 16 (3), 257–278.
- Falkovich et al. (2002) Falkovich, Gregory, Fouxon, A & Stepanov, MG 2002 Acceleration of rain initiation by cloud turbulence. Nature 419 (6903), 151–154.
- Falkovich & Pumir (2007) Falkovich, Gregory & Pumir, Alain 2007 Sling effect in collisions of water droplets in turbulent clouds. Journal of the Atmospheric Sciences 64 (12), 4497–4505.
- Grabowski & Wang (2013) Grabowski, Wojciech W & Wang, Lian-Ping 2013 Growth of cloud droplets in a turbulent environment. Annual review of fluid mechanics 45, 293–324.
- Ireland et al. (2016) Ireland, Peter J, Bragg, Andrew D & Collins, Lance R 2016 The effect of reynolds number on inertial particle dynamics in isotropic turbulence. part 1. simulations without gravitational effects. Journal of Fluid Mechanics 796, 617–658.
- Johansen et al. (2009) Johansen, Anders, Youdin, Andrew & Mac Low, Mordecai-Mark 2009 Particle clumping and planetesimal formation depend strongly on metallicity. The Astrophysical Journal 704 (2), L75.
- Maxey & Riley (1983) Maxey, Martin R & Riley, James J 1983 Equation of motion for a small rigid sphere in a nonuniform flow. The Physics of Fluids 26 (4), 883–889.
- Meng & Saw (2023) Meng, Xiaohui & Saw, Ewe-Wei 2023 Sharp depletion of radial distribution function of particles due to collision and coagulation inside turbulent flow: A systematic study. Physical Review Fluids 8 (8), 084304.
- Pan et al. (2011) Pan, Liubin, Padoan, Paolo, Scalo, John, Kritsuk, Alexei G & Norman, Michael L 2011 Turbulent clustering of protoplanetary dust and planetesimal formation. The Astrophysical Journal 740 (1), 6.
- Rogallo (1981) Rogallo, Robert Sugden 1981 Numerical experiments in homogeneous turbulence, , vol. 81315. National Aeronautics and Space Administration.
- Rosa et al. (2013) Rosa, Bogdan, Parishani, Hossein, Ayala, Orlando, Grabowski, Wojciech W & Wang, Lian-Ping 2013 Kinematic and dynamic collision statistics of cloud droplets from high-resolution simulations. New Journal of Physics 15 (4), 045032.
- Saffman & Turner (1956) Saffman, PGF & Turner, JS 1956 On the collision of drops in turbulent clouds. Journal of Fluid Mechanics 1 (1), 16–30.
- Saw & Meng (2022) Saw, Ewe-Wei & Meng, Xiaohui 2022 Intricate relations among particle collision, relative motion and clustering in turbulent clouds: computational observation and theory. Atmospheric Chemistry and Physics 22 (6), 3779–3788.
- Saw et al. (2008) Saw, Ewe Wei, Shaw, Raymond A, Ayyalasomayajula, Sathyanarayana, Chuang, Patrick Y & Gylfason, Armann 2008 Inertial clustering of particles in high-reynolds-number turbulence. Physical review letters 100 (21), 214501.
- Shaw (2003) Shaw, Raymond A 2003 Particle-turbulence interactions in atmospheric clouds. Annual Review of Fluid Mechanics 35 (1), 183–227.
- Smith et al. (2002) Smith, NL, Nathan, GJ, Zhang, DK & Nobes, DS 2002 The significance of particle clustering in pulverized coal flames. Proceedings of the Combustion Institute 29 (1), 797–804.
- Squires & Eaton (1991) Squires, Kyle D & Eaton, John K 1991 Preferential concentration of particles by turbulence. Physics of Fluids A: Fluid Dynamics 3 (5), 1169–1178.
- Sundaram & Collins (1997) Sundaram, Shivshankar & Collins, Lance R 1997 Collision statistics in an isotropic particle-laden turbulent suspension. part 1. direct numerical simulations. Journal of Fluid Mechanics 335, 75–109.
- Wilkinson & Mehlig (2005) Wilkinson, M & Mehlig, Bernhard 2005 Caustics in turbulent aerosols. Europhysics Letters 71 (2), 186.
- Wilkinson et al. (2006) Wilkinson, Michael, Mehlig, Bernhard & Bezuglyy, Vlad 2006 Caustic activation of rain showers. Physical review letters 97 (4), 048501.