The effect of shear stress reduction on endothelial cells: a microfluidic study of the actin cytoskeleton

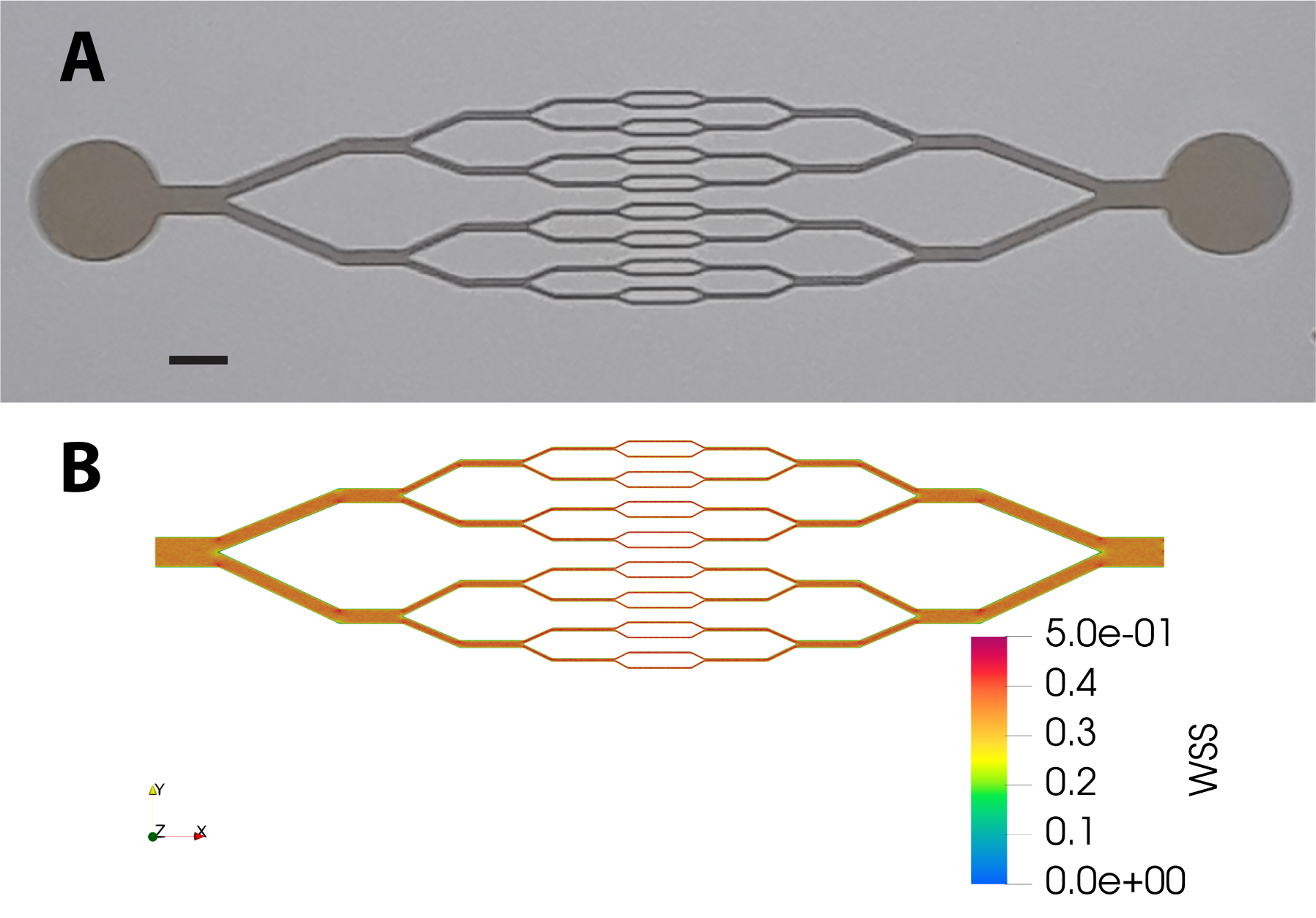
Microchannel networks displaying diverging/converging geometry (see Fig. 1A) were fabricated using a standard soft lithography technique. A master mold of the network was obtained from a positive photoresist (SU8, Gerseltec) cast onto a silicon wafer and exposed to UV light through a quartz-chromium photomask. PDMS (Sylgard 184, Dow Corning) was cast onto the mold and cured for 2 hours at 65^∘C. A glass coverslip ($\#$0, thickness $\approx$100 $\mu$m) was used as the bottom part of the microchip and was permanently sealed to the PDMS upper part after exposure of the surfaces of both elements to oxygen plasma (PDC-32G-2, Harrick). The thickness of the photoresist on the master mold was set such that the series of 16 parallel microchannels in the central part of the network had a square cross-section of 30$\times$30 $\mu$m². The circuit was connected with silicone tubing to a fluid reservoir at the inlet, and at the outlet to a 1 mL syringe installed on a high precision syringe pump (Legato 110, KD Scientific) used in withdraw mode at imposed flow rate.

The design of our circuit, in which the height of the channels is uniform ($30\,\mu$m) while their width is divided (resp. multiplied) by 2 at each branching (resp. converging) point, is such that for a given flow rate the fluid shear stress exerted at the bottom and top walls is expected to be homogeneous, irrespective of the channel size. In order to confirm this, we have performed tridimensional numerical modeling of a laminar flow within our network geometry, using Computer Fluid Dynamics (Simscale GmbH). As shown in Fig. 1B, numerical simulations indicate that wall shear stress is indeed fairly uniform across the circuit: at an imposed flow rate of $1\,\mu$L.min^-1, we compute a wall shear stress of $0.4\pm 0.05$ Pa at the bottom or top surfaces.

Single donor Human Umbilical Vein Endothelial Cells (HUVEC) were obtained from Promocell GmbH (Germany) and cultured in endothelial cells growth medium supplemented by growth factors (Supplement Mix, Promocell GmbH, Germany).

Before cell seeding, microchannels were activated by exposure to oxygen plasma and coated with human fibronectin (50 $\mu$g/mL, Corning) for 30 min at 37 ^∘C. Endothelial cells were suspended in culture medium at a concentration of 10⁷ cells/mL and filtered through a nylon cell strainer with pore diameter of 40 $\mu$m. The cell suspension was injected into the microchannel network with a pressure controller (OB-1 MK2, Elveflow, France). Consecutive steps of injection of a few seconds and sedimentation periods of several minutes were performed until about 50 % of the network surface was covered by cells.

Cells were then cultured at 37 ^∘C and 5% CO₂ under a constant flow of supplemented medium for one night at 0.6 $\mu$L/min and then maintained at 1$\mu$L/min for four days in order for cells to form a confluent layer and adapt to shear. As mentioned in the previous section, a flow rate of 1$\mu$L/min corresponds to a wall shear stress of $\sim$0.4 Pa, representative of physiological conditions in e.g. post-capillary venules Sheikh et al. (2003).

After four days of culture under 0.4 Pa, the shear-adapted cells were exposed to a reduced flow rate of 0.2 $\mu$L/min, corresponding to a reduced wall shear stress of 0.08 Pa. Reduced flow was applied for a duration of 1 or 6 hours, after which cells were fixed by perfusing the channels with a solution of 4% paraformaldehyde in PBS for 30 min at 37 ^∘C, and stained for observation.

As controls, HUVEC were also cultured under (i) static conditions into fibronectin-coated glass-bottom Petri dishes until reaching confluence, and (ii) reduced flow conditions (wall shear stress 0.08 Pa) applied from the start of the experiment, during four days of culture after seeding in the channels.

All experiments were performed in duplicates.

For confocal microscopy we used the following dyes: (i) Hoechst 33342 (Molecular Probes) for nuclei staining, (ii) Phalloidin TRITC (Sigma-Aldrich) for F-Actin staining and (iii) Wheat Germ Agglutinin (WGA) Alexa Fluor 488 Conjugate (5 $\mu$g/ml, Molecular Probes) for staining the glycocalyx. The dyes were used in accordance with manufacturer’s specification.

For glycocalyx modification, cells were exposed to Neuraminidase from Clostridium perfringens (1U/ml, Sigma-Aldrich) in a CO₂ incubator. Neuraminidase was used at 150 mUI/mL and perfused at $1\,\mu L$/min for 3 hours in non-supplemented endothelial cells culture medium. Glycocalyx was stained by WGA-Alexa 488 after enzymatic modification and fluorescence intensity was estimated with and without Neuraminidase action.

Confocal fluorescence microscopy was performed on an inverted microscope. XYZ image stacks were obtained in raster mode using a Zeiss LSM710 module and a 40$\times$/NA1.3 oil-immersion objective, with a lateral size of 1024$\times$200 pixels, a lateral resolution of 0.225 $\mu$m/pixel, and a Z-slice spacing of 0.46 $\mu$m.

The acquired image stacks were processed and analyzed using the ImageJ open-source platform and its built-in plugins. 3-dimensional XYZ image stacks were treated as follows. A point spread function (PSF) of the microscope was generated numerically with ImageJ, using the “Diffraction PSF 3D” plugin fed with the experimental characteristics of our imaging system (i.e. refraction index of immersion liquid, objective numerical aperture, lateral magnification and z slice spacing of the stack). We have further checked for the consistency of such a generated PSF by using it to deconvolve images of fluorescent latex beads of known diameter (500 nm) and ensuring that the bead size measured from the deconvolved images agreed with the expected one. PSF deconvolution was then performed on image stacks of the stained cells using the “Iterative deconvolve 3D” plugin. Z-projections of deconvolved image stacks were then made, summing the intensity of each of the slices spanning the EC monolayer adhered on the bottom surface of the channels.

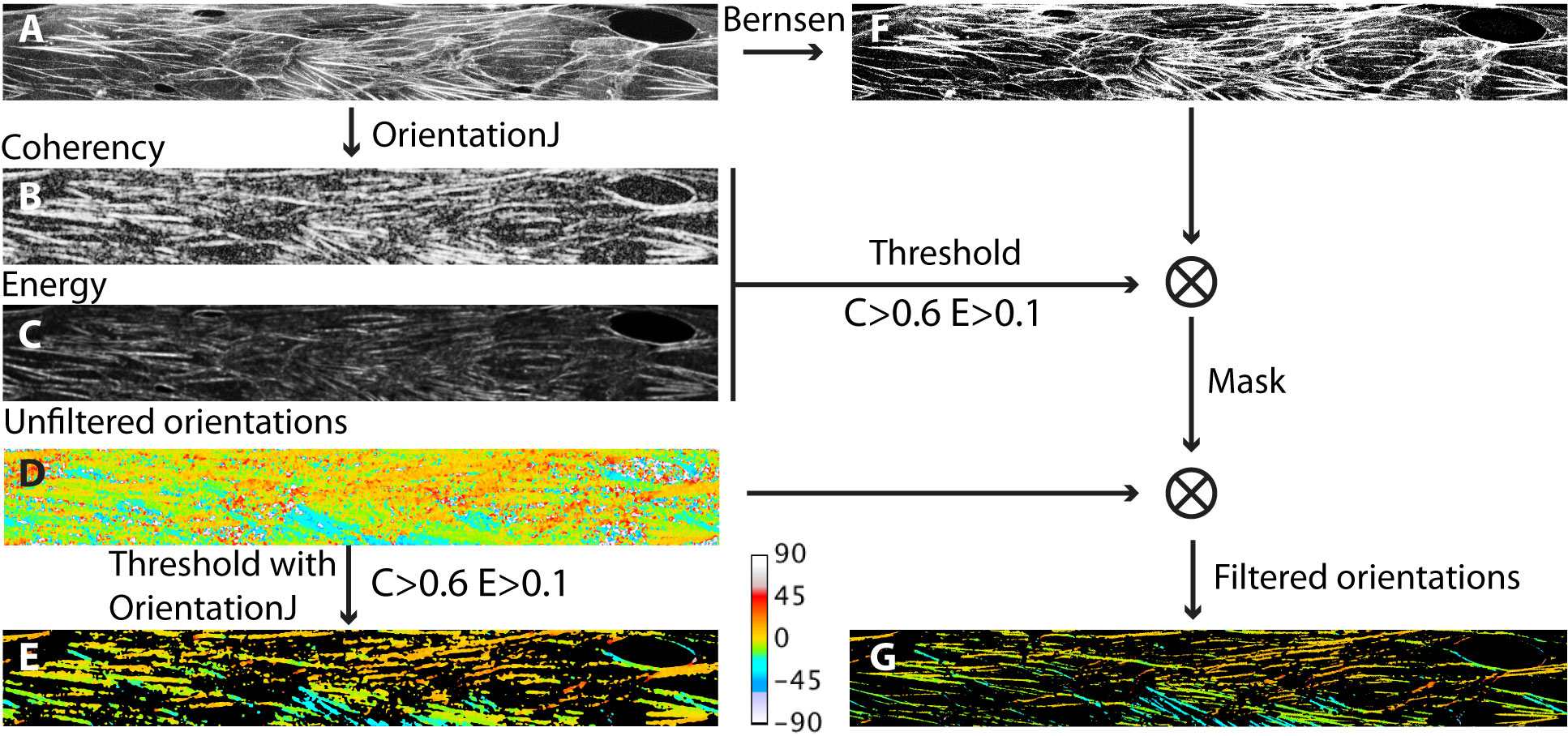
From Z-projected images obtained as described above, F-Actin structures were characterized with the ImageJ plugin “OrientationJ” Rezakhaniha et al. (2011), using the “Gaussian gradient” built-in method with a window size of 2 pixels.

The OrientationJ plugin computes the structure tensor from the intensity gradient of an image, and attributes to each pixel in the image a pair of values, between 0 and 1, corresponding to the local values of the (normalized) energy, E, and coherency, C, of the structure tensor. Low values of E correspond to regions in the image where intensity is uniform, while large values indicate regions having one or multiple orientations. C is a measure of the local degree of anisotropy, with values closer to 1 corresponding to regions of stronger anisotropy.

For each experimental conditions, we compute E and C maps of the F-actin images obtained (such as illustrated in Fig. 2A-C), and build a final map where each pixel contains the value of $\sqrt{EC}$. From such maps we determine the distribution of $\sqrt{EC}$ by building histograms over 50 bins of $\sqrt{EC}$ spanning the range $0-1$, where we compute, for each bin, a frequency corresponding to the number of pixels displaying a given value of $\sqrt{EC}$ divided by the total number of pixels in the image. Plotting the distribution of $\sqrt{EC}$ allows us assessing, for a given cell culture condition, the fraction of image pixels involved in non-uniform and strongly elongated F-actin structures.

From the computation of the structure tensor, OrientationJ also provides a map of the local orientation. The plugin associates an orientation to each pixel in the image, including in regions of low E and C where this quantity is not meaningful. Such an orientation map can then be filtered by thresholding on E and C values in order to retain only the orientation values of pixels that are actually part of anisotropic structures. Doing so using the built-in thresholding feature of OrientationJ, we observe that, with our type of images, the filtered orientation maps display a spatial resolution that is clearly lower than the initial image, with blurred features and inclusion of pixels that are actually outside of the fibers (see Fig. 2). We could not find a set of OrientationJ parameters that would allow us to increase further the resolution of the orientation map without losing part of the elongated structures that are visible in the original image. As an alternative to the built-in thresholding feature of the plugin, we find that the following procedure performs better in terms of final resolution: starting from the input image, we run orientationJ to obtain E, C and unfiltered orientation maps. We then threshold the E and C images (at the same levels used in the built-in function of the plugin, namely $C>0.6$ and $E>0.1$ in the present work) and binarize them. In parallel, we binarize the input image using the local threshold Bernsen method implemented in ImageJ. We then multiply the binarized E, C and Bernsen image in order to create a binary mask that we use to filter the orientation map. A comparison of the built-in and custom-made thresholding is provided in Fig. 2.

The orientation maps thus produced are then used to compute angular distributions. In the following, angular distributions are computed over 30 bins of width 3^∘, spanning the range between 0^∘ and +90^∘, with 0^∘ being the flow direction, and where we count in the same bin the pixels displaying an angle of $\theta$ or $-\theta$. Frequencies in each bin correspond to the ratio of the number of pixels within an angular bin to the total number of pixels involved in oriented F-actin structures.

Distributions of $\sqrt{EC}$ and angles were computed from images taken in the central part of the networks, i.e. in the channels having a cross-section of $30\times 30\,\mu$m².

The number of analyzed images was $N=53$ (389 cells) for culture under flow at 0.4 Pa, $N=32$ (311 cells) for flow reduced at 0.08 Pa for 1h, $N=26$ (235 cells) for flow reduced at 0.08 Pa for 6h, $N=16$ (151 cells) for glycocalyx degradation, $N=14$ (141 cells) for culture under 0.08 Pa for 4 days, and $N=6$ (132 cells) for static condition.

For every experimental condition, $\sqrt{EC}$ and angular distributions were computed on each of the $N$ images taken. In what follows, we present such distributions as mean frequency $\pm\,2$ s.e.m. (standard error of the mean), computed bin-by-bin over the $N$ images analyzed. When comparing the results for various experimental conditions, we take as statistically significant any difference between distributions larger than 4 s.e.m. (i.e. when the 95% confidence intervals of the distributions do not overlap).

Other quantifications (fluorescence intensity or length measurements on images) were analyzed using t-tests at the 0.05 threshold, performed using Origin software. In what follows, we indicate by (*) datasets whose means are statistically different ($p<0.05$), and by (**) those that are not ($p>0.05$).

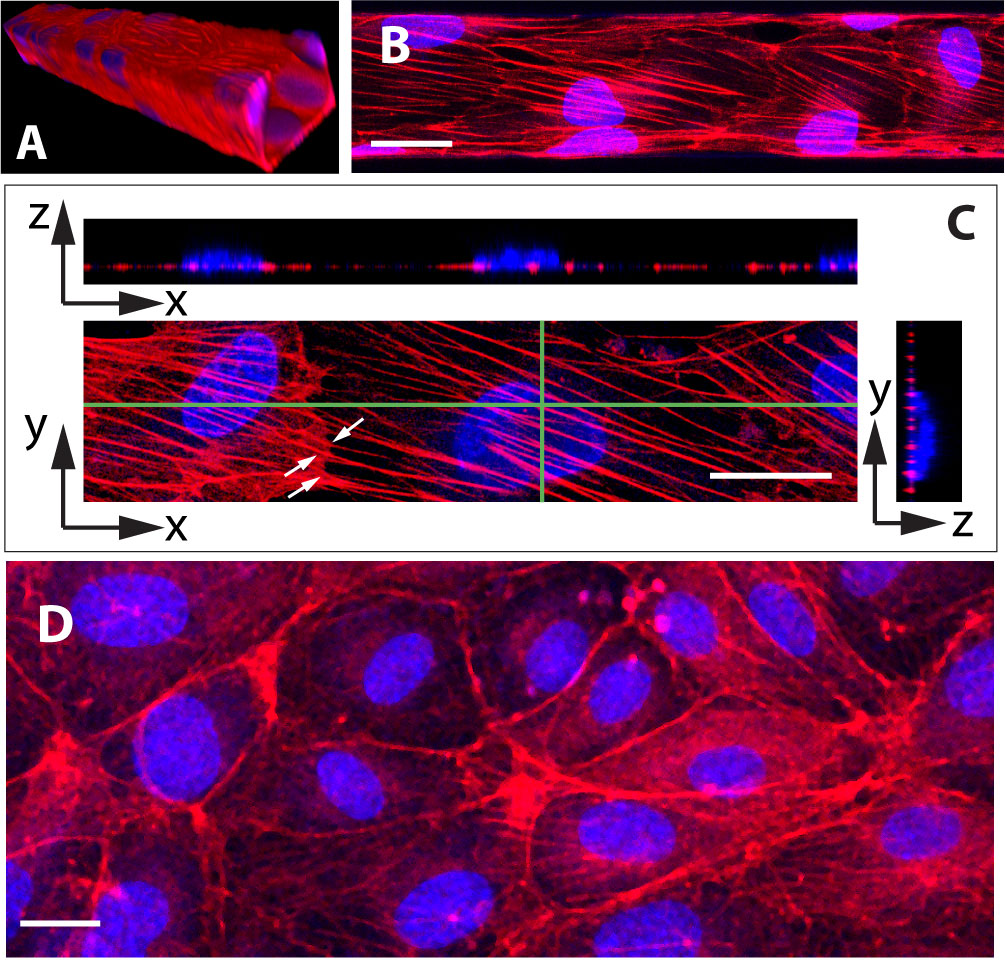
As illustrated on Fig. 3A, HUVEC cultured under 0.4 Pa of fluid shear stress for four days yield a confluent monolayer of cells covering the four walls of the microchannels. Under such conditions, we observe that cells exhibit many oriented actin stress fibers that cross the cell from side to side underneath the nucleus and seem to be attached to cell-cell junction as they continue end to end into the neighboring cell (see Fig. 3B and C). In contrast to this, HUVEC cultured under static conditions rather display a marked deep peripheral actin band, with no or few randomly oriented stress fibers (Fig. 3D).

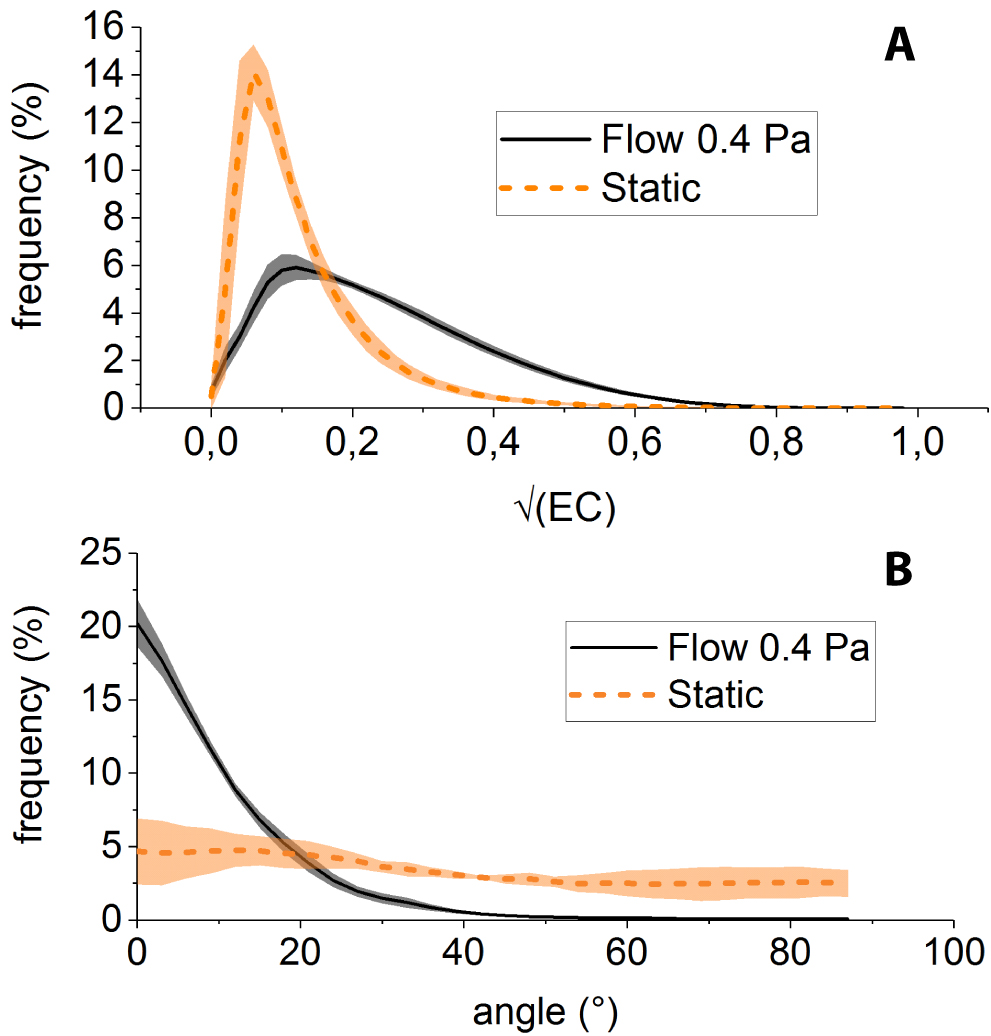
Applying the above-described procedure to F-actin images obtained under static and 0.4 Pa shear flow conditions, we observe that: (i) the distribution of $\sqrt{EC}$ is more populated towards large values ($\sqrt{EC}\geq 0.2$) for shear-adapted cells than for static condition (Fig. 4A), consistent with more anisotropic structures (i.e. stress fibers) being present in cells cultured under fllow, and (ii) the angular distribution of such structures is sharply peaked about $0^{\circ}$ (i.e. along the flow direction) for shear-adapted cells (Fig. 4B), indicating streamwise alignment of stress fibers, whereas the angular distribution of actin in static cultures is much flatter.

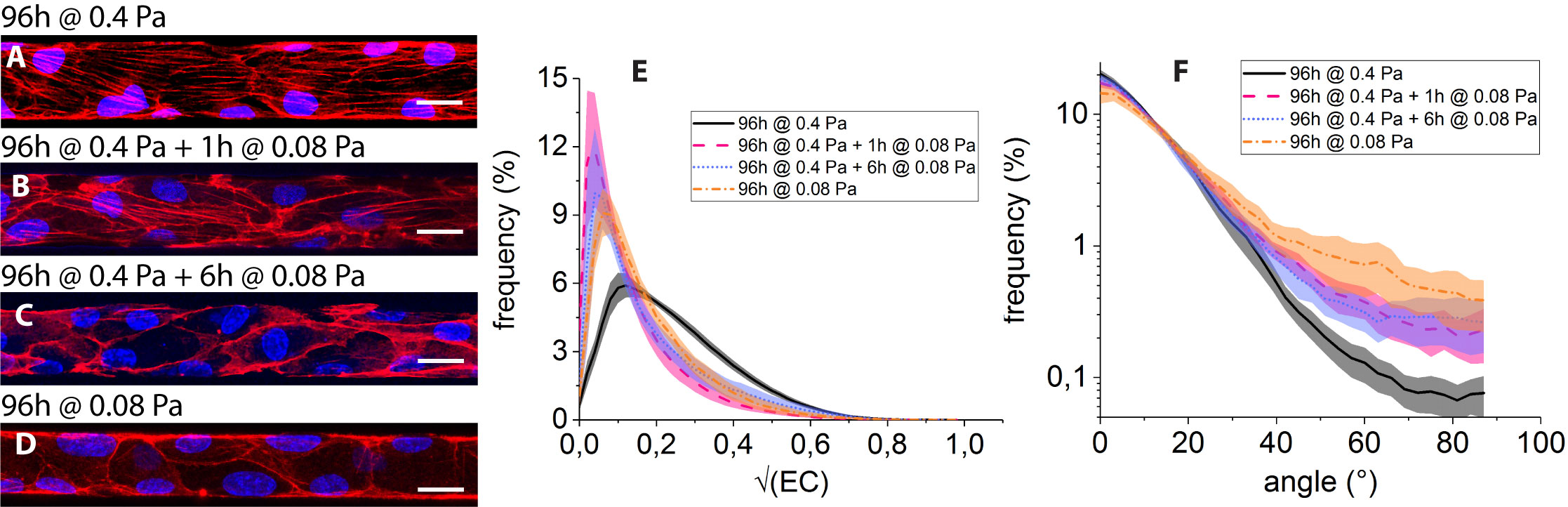
The impact on the F-actin network of culture conditions (i) to (iv) is summarized on Fig. 5.

As already mentioned, culture under 0.4 Pa for 96h (condition (i)) results in the development of flow-aligned stress fibers (Fig. 5A). In contrast to this, submitting the HUVEC, previously shear-adapted to 0.4 Pa for 96h, to 1h of shear stress lowered to 0.08 Pa (condition (ii)) leads to a marked decrease in the number of fibers and to a localization of F-actin at the periphery of the cells (Fig. 5B). Such a trend is maintained after 6h of reduced flow (condition (iii), Fig. 5C).

In addition, we observe that HUVEC constantly submitted to 0.08 Pa for 96h of culture (condition (iv), Fig. 5D) form a confluent monolayer in the microfluidic networks, and display an organization of F-actin presenting features that are qualitatively similar to those observed for conditions (ii) and (iii), with little or no stress fibers and a pronounced actin peripheral band.

The decrease in the number of filamentous structures under low shear stress can be seen on the distributions of $\sqrt{EC}$ (Fig. 5E): as observed under purely static condition, distributions computed for conditions (ii) to (iv) are not significantly different and all exhibit a peak at low values ($\sqrt{EC}\simeq 0.1$), whereas that computed for condition (i) is significantly more populated $\sqrt{EC}>0.2$.

Such a loss of actin fibers under 0.08 Pa of wall shear stress is accompanied by a broadening of the angular distributions, which exhibit tails beyond $40^{\circ}$ that are more pronounced than at 0.4 Pa (Fig. 5F). While our image analysis procedure does not allow us to discriminate between the various contributions, the observed angular broadening under reduced flow can stem from both a disorientation of stress fibers and from the buildup of peripheral actin, both contributing to large angles in the distributions.

Moreover, we see in Fig. 5F that the angular distribution computed for condition (iv) lies above those computed for conditions (ii) and (iii). This may stem from the fact that HUVEC submitted to 1 or 6h of low shear stress after 96h at 0.4 Pa do however keep a flow-elongated shape, as seen in Fig. 5B and C from the peripheral actin bands, while HUVEC submitted to permanent low shear do not exhibit flow alignment (Fig. 5D), resulting in a broader angle distribution for condition (iv).

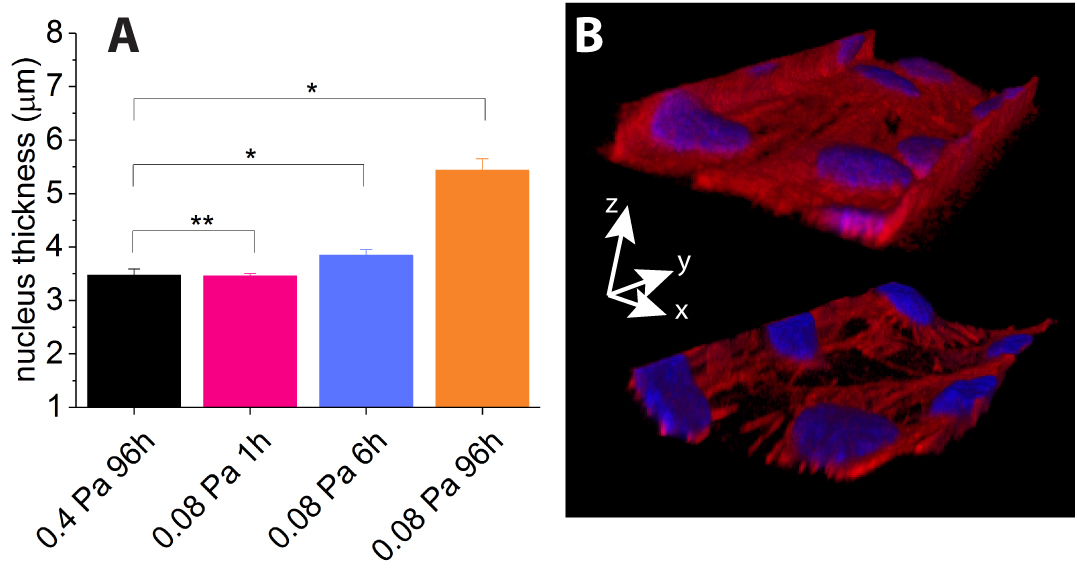
From our 3D confocal image sets, we have measured the maximum thickness of the nuclei of the cells, and notice an increase in thickness under prolonged reduced flow conditions, as shown on Fig. 6A: while nucleus thickness between conditions (i) and (ii) are not statistically different, we measure a significant increase of thickness for conditions (iii) and (iv).

In addition to this, we notice qualitatively that upon long exposure to low shear stress (>6h), 0.4Pa-shear-adapted HUVEC tend to detach from the microchannel walls, mainly from the corners, as illustrated on Fig. 6B, while maintaining cell-cell contacts.

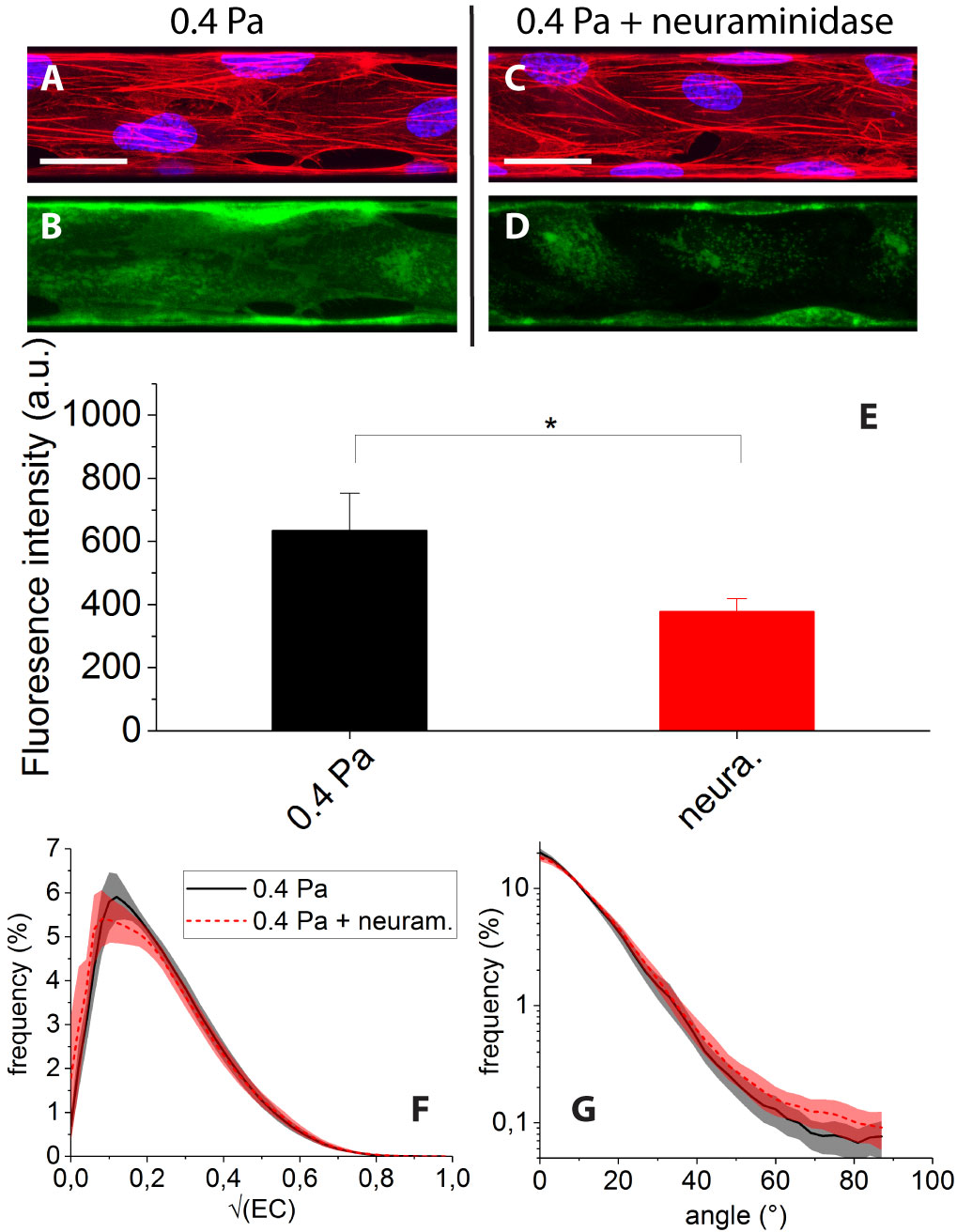
The effect of treating the cells with neuraminidase while submitting them to 0.4 Pa of shear stress is illustrated in Fig. 7. The enzymatic degradation of the glycocalyx results in a clear decrease of the WGA-Alexa fluorescence signal (see Fig. 7C and D) which indicates actual removal of part of the andothelial surface layer. This can be quantified by a statistically significant 40$\%$ decrease of image mean intensity (Fig. 7E).

However we find that neuraminidase treatment does not induce any clear change of the F-actin organization: after enzymatic degradation (condition (v)), we observe cells displaying numerous and flow oriented stress fibers (Fig. 7C), similarly to condition (i) (Fig. 7A). Accordingly, distributions of $\sqrt{EC}$ and angles for conditions (i) and (v) are found to display no significant differences (Fig. 7F and G).