The equivariant cohomology ring of a cohomogeneity-one action

Jeffrey D. Carlson, Oliver Goertsches, Chen He, and Augustin-Liviu Mare

Abstract

We compute the rational Borel equivariant cohomology ring of a cohomogeneity-one action of a compact Lie group.

1. Introduction

Cohomogeneity-one Lie group actions—that is, those whose orbit space is one-dimensional—form an intensively-studied class of examples which are a next natural object of study after homogeneous actions. In lieu of a necessarily incomplete attempt to summarize the vast geometric literature surrounding these actions, we content ourselves with a gesture toward the substantial bibliography to be found in the recent classificatory work of Galaz-García and Zarei [GGZ15].

Given the prominence of these actions, it is natural to wonder what can be said of their equivariant cohomology. Due to earlier work of two of the authors [GM14, GM17], it is known the rational Borel equivariant cohomology ring is Cohen–Macaulay, and structure theorems for this ring have been worked out in special cases [GM14, Cor. 4.2, Props. 5.1, 5.10] along with topological consequences for the manifold acted on. In this work, we describe the equivariant cohomology rings of a certain broad class of cohomogeneity-one actions (delineated precisely in the discussion after Theorem˜3.3), obtaining more explicit expressions in the case of actions on manifolds.

In the most interesting case, where the space $X$ acted on by a compact, connected Lie group $G$ is a manifold and the orbit space $X/G$ is a closed interval, Theorem˜3.2, due mostly to Mostert, implies $X$ can be written up to $G$ -equivariant homeomorphism as the double mapping cylinder $\smash{G/K^{-}\cup\big{(}[-1,1]\times G/H\big{)}\cup G/K^{+}}$ of a pair of quotient maps $G/H\rightrightarrows G/K^{\pm}$ for some closed subgroups ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}H}\leq{\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}K^{\pm}}$ of $G$ . By work of Galaz-García–Searle (Theorem˜3.3), the same holds if $X$ is an Alexandrov space. As such, the equivariant Mayer–Vietoris sequence is applicable to the cover of $X$ by the preimages of two subintervals of $X/G$ .¹¹1 The non-equivariant Mayer–Vietoris sequence of the same cover has also long been used to study such spaces [GrH87, Hoel10, EU11]. As the equivariant cohomology of the restricted actions is well-known, this approach would in general recover the additive structure up to an extension problem, but in our case, surprisingly, we are able to determine the entire ring structure. This is Section˜3.2. In Section˜5, we prove more explicit formulas depending on the numbers $\dim K^{\pm}/H\allowbreak\mkern 8.0mu({\operator@font mod}\mkern 6.0mu2)$ in the case $X$ is a manifold $M$ , so that $K^{\pm}/H$ are homology spheres. In the following result and throughout, ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}H^{*}_{\Gamma}}\coloneqq H^{*}_{\Gamma}(*\mspace{2.0mu};\mathbb Q)=H^{*}(B\Gamma;\mathbb Q)$ will denote the Borel $\Gamma$ -equivariant cohomology ring of a point with rational coefficients. In fact, all cohomology will take rational coefficients unless explicitly specified otherwise.

{restatable}

theoremHodd Let $M$ be the double mapping cylinder of the quotient maps $G/H\ext@arrow{20}{20}{20}{20}{\arrowfill@\mathrel{\mathrlap{\raisebox{2.5pt}{$\relbar$}}\raisebox{-2.5pt}{$\relbar$}}\mathrel{\mathrlap{\raisebox{2.5pt}{$\relbar$}}\raisebox{-2.5pt}{$\relbar$}}{\mathrel{\mathrlap{\raisebox{2.5pt}{$\rightarrow$}}\mathrlap{\raisebox{-2.5pt}{$\rightarrow$}}\hphantom{\vbox{\hbox{$\rightarrow$}\hbox{$\rightarrow$}}}}}}{}{}G/K^{\pm}$ for closed subgroups $H<K^{\pm}$ of a compact Lie group $G$ such that $K^{\pm}/H$ are homology spheres.

(a) Assume $K^{+}/H$ is odd-dimensional and $K^{-}/H$ even-dimensional, and the bundle $BH\longrightarrow BK^{+}$ is orientable. Then we have an ${H^{*}_{G}}$ -algebra isomorphism

{H^{*}_{G}}M\cong H^{*}_{K^{-}}\mathbin{\raisebox{0.85pt}{$\displaystyle\oplus$}}eH^{*}_{H}[e]<H^{*}_{H}[e],

where $H^{*}_{K^{+}}\cong H^{*}_{H}[e]$ for a certain class $e\in H_{K^{+}}^{1+\dim K^{+}/H}$ , the product $H^{*}_{K^{-}}\times H^{*}_{H}[e]\longrightarrow H^{*}_{H}[e]$ is determined by the injection $H^{*}_{K^{-}}\mathrel{\leavevmode\hbox to23.05pt{\vbox to9.73pt{\pgfpicture\makeatletter\hbox{\thinspace\lower-4.86601pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{}{{}}{} {{}{}}{}{}{}{{{}{}}}{{}}{}{}{{{}{}}}{{}}{}{{ {\pgfsys@beginscope \pgfsys@setdash{}{0.0pt}\pgfsys@roundcap\pgfsys@roundjoin{} {}{}{} {}{}{} \pgfsys@moveto{-2.07999pt}{2.39998pt}\pgfsys@curveto{-1.69998pt}{0.95998pt}{-0.85318pt}{0.28pt}{0.0pt}{0.0pt}\pgfsys@curveto{-0.85318pt}{-0.28pt}{-1.69998pt}{-0.95998pt}{-2.07999pt}{-2.39998pt}\pgfsys@stroke\pgfsys@endscope}} }{}{}{{}}{{ {\pgfsys@beginscope{{}} \pgfsys@setdash{}{0.0pt}\pgfsys@roundcap\pgfsys@roundjoin{} {}{}{} {}{}{} \pgfsys@moveto{2.07999pt}{2.39998pt}\pgfsys@curveto{1.69998pt}{0.95998pt}{0.85318pt}{0.28pt}{0.0pt}{0.0pt}\pgfsys@curveto{0.85318pt}{-0.28pt}{1.69998pt}{-0.95998pt}{2.07999pt}{-2.39998pt}\pgfsys@stroke\pgfsys@endscope}} }{}{}{{}}\pgfsys@moveto{2.07999pt}{0.0pt}\pgfsys@lineto{21.98894pt}{0.0pt}\pgfsys@stroke\pgfsys@invoke{ }{{}{{}}{}{}{{}}{{{}}{{{}}{\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{-1.0}{0.0}{0.0}{-1.0}{2.27998pt}{0.0pt}\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope}}{{}}}}{{}{{}}{}{}{{}}{{{}}{{{}}{\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{22.18893pt}{0.0pt}\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope}}{{}}}}\hbox{\hbox{\hbox{{\pgfsys@beginscope\pgfsys@invoke{ }{{}{}{{ {}{}}}{ {}{}} {{}{{}}}{{}{}}{}{{}{}} { }{{{{}}\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{11.19446pt}{-1.533pt}\pgfsys@invoke{ }\hbox{{\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\hbox{{\hbox{$\scriptstyle$}}} }}\pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope}}}\hbox{{\pgfsys@beginscope\pgfsys@invoke{ }{{}{}{{ {}{}}}{ {}{}} {{}{{}}}{{}{}}{}{{}{}} { }{{{{}}\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{3.0pt}{1.533pt}\pgfsys@invoke{ }\hbox{{\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\hbox{{\hbox{$\scriptstyle\ \ \ \ $}}} }}\pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}H^{*}_{H}$ , and the ${H^{*}_{G}}$ -module structure is induced by the inclusions $K^{\pm}\xhookrightarrow{\ \ \ \ }G$ . If $K^{+}/H$ is a sphere, then $e$ is the Euler class of the sphere bundle $BH\longrightarrow BK^{+}$ .

(b) Assume that both $K^{\pm}/H$ are odd-dimensional and the bundles $BH\longrightarrow BK^{\pm}$ are both orientable. Then we have an ${H^{*}_{G}}$ -algebra isomorphism

H^{*}_{G}M\,\cong\,{\raisebox{1.99997pt}{$H^{*}_{H}[e_{-},e_{+}]\,$}}\ \!\!\big{/}\!\!\ {\raisebox{-1.99997pt}{$(e_{-}e_{+})$}},

where $H^{*}_{K^{\pm}}\cong H^{*}_{H}[e_{\pm}]$ for classes $e_{\pm}\in H_{K^{\pm}}^{1+\dim K^{\pm}/H}$ and the ${H^{*}_{G}}$ -module structure is induced by the inclusions $K^{\pm}\xhookrightarrow{\ \ \ \ }G$ . If $K^{\pm}/H$ is a sphere, then $e_{\pm}$ is the Euler class of the sphere bundle $BH\longrightarrow BK^{\pm}$ .

In the event both spheres are even-dimensional, the generators of the Weyl groups $W(K^{\pm})$ with respect to a shared maximal torus generate a dihedral subgroup of the automorphisms of this torus, of order $2k$ . It is this $k$ that figures in the following result.

{restatable}

theoremHeven Let $M$ the double mapping cylinder of the quotient maps $G/H\ext@arrow{20}{20}{20}{20}{\arrowfill@\mathrel{\mathrlap{\raisebox{2.5pt}{$\relbar$}}\raisebox{-2.5pt}{$\relbar$}}\mathrel{\mathrlap{\raisebox{2.5pt}{$\relbar$}}\raisebox{-2.5pt}{$\relbar$}}{\mathrel{\mathrlap{\raisebox{2.5pt}{$\rightarrow$}}\mathrlap{\raisebox{-2.5pt}{$\rightarrow$}}\hphantom{\vbox{\hbox{$\rightarrow$}\hbox{$\rightarrow$}}}}}}{}{}G/K^{\pm}$ for closed subgroups $H<K^{\pm}$ of a compact Lie group $G$ such that $K^{\pm}/H\approx S^{2n_{\pm}}$ are even-dimensional spheres, and the bundles $BH\longrightarrow BK^{\pm}$ are both orientable. Then the number $k(n_{-}+n_{+})$ is even, and we have an ${H^{*}_{G}}$ -algebra isomorphism

{H^{*}_{G}}M\cong(\operatorname{im}\rho_{+}^{*}\cap\operatorname{im}\rho_{-}^{*})\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}S^{k(n_{-}+n_{+})+1},

where the injections $\rho_{\pm}^{*}\colon H^{*}_{K^{\pm}}\longrightarrow H^{*}_{H}$ are induced by the inclusions $H\xhookrightarrow{\ \ \ \ }K^{\pm}$ and the ${H^{*}_{G}}$ -module structure is induced by $K^{\pm}\xhookrightarrow{\ \ \ \ }G$ .

Cohomogeneity-one actions whose orbit space is $S^{1}$ arise as mapping tori of right translations $r_{n}$ of homogeneous spaces $G/K$ by elements $n\in N_{G}(K)$ , and this case admits a parallel but much more easily-proved statement we discuss in Section˜3.1.

{restatable}

theoremcircle Let $M$ be the mapping torus of the right translation by $n\in N_{G}(K)$ on the homogeneous space $G/K$ of a compact Lie group $G$ . Then one has $H^{*}S^{1}$ - and $({H^{*}_{G}}\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}S^{1})$ -algebra isomorphisms

	$\displaystyle H^{*}M$	$\displaystyle\cong H^{}(G/K)^{\langle r_{n}^{}\rangle}\operatorname{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{}S^{1},$
	$\displaystyle{H^{*}_{G}}M$	$\displaystyle\cong H^{}(BK)^{\langle r_{n}^{}\rangle}\operatorname{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{}S^{1}$

respectively, where the $H^{*}S^{1}$ -module structure is given by pullback from $M/G$ in both cases and the ${H^{*}_{G}}$ -algebra structure is induced by the inclusion $K\xhookrightarrow{\ \ \ \ }G$ .

The unexpectedly great utility of the Mayer–Vietoris sequence in our situation results from an additional structural feature of the sequence that seems not to be frequently noted, namely the fact that the connecting map preserves a module structure over the cohomology ring of the whole space. This result is proved in Section 2.

Acknowledgments. The authors would like to thank the referee for careful proofreading, for suggesting a reference, and for making an important correction to their statement of Theorem˜3.2. The first author would like to thank Omar Antolín Camarena for helpful conversations and the National Center for Theoretical Sciences (Taiwan) for its hospitality during a phase of this work.

2. The Mayer–Vietoris sequence

Let $G$ be a topological group, $X$ a $G$ -space, and $A,B\subseteq X$ two $G$ -invariant subsets whose interiors cover $X$ . The rings ${H^{*}_{G}}A\times{H^{*}_{G}}B$ and ${H^{*}_{G}}(A\cap B)$ in the Mayer–Vietoris sequence inherit an ${H^{*}_{G}}X$ -module structure by restriction. It is clear the restriction maps between these rings are ${H^{*}_{G}}X$ -module homomorphisms and we claim the connecting map is as well. It is enough to prove the analogous result for singular cohomology, as the Mayer–Vietoris sequence in equivariant cohomology is just the Mayer–Vietoris sequence of the associated cover $(A_{G},B_{G})$ of the homotopy orbit space $X_{G}$ .

Proposition 2.1.

Let $X$ be a topological space, $A$ and $B$ a pair of subspaces whose interiors cover $X$ , and $k$ any commutative ring with unity. Then the connecting map ${\delta_{\mathrm{MV}}}\colon H^{*}(A\cap B;k)\longrightarrow H^{*}(X;k)[1]$ in the Mayer–Vietoris sequence of $(X;A,B)$ is a homomorphism of $H^{*}(X;k)$ -modules.

Proof.

The covering hypothesis makes the inclusion $C_{*}(A)+C_{*}(B)\xhookrightarrow{\ \ \ \ }C_{*}(X)$ of singular chain complexes a quasi-isomorphism, whose dual $C^{*}\mspace{-2.0mu}(X;k)\mathrel{\leavevmode\hbox to23.05pt{\vbox to9.73pt{\pgfpicture\makeatletter\hbox{\thinspace\lower-4.86601pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{}{{}}{} {{}{}}{}{}{}{{{}{}}}{{}}{}{}{{{}{}}}{{}}{}{}{}{}{}{{}}\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@lineto{21.98894pt}{0.0pt}\pgfsys@stroke\pgfsys@invoke{ }{{}{{}}{}{}{{}}{{{}}{{{}}{\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{19.70895pt}{0.0pt}\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope}}{{}}{{{}}{\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{22.18893pt}{0.0pt}\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope}}{{}}}}\hbox{\hbox{\hbox{{\pgfsys@beginscope\pgfsys@invoke{ }{{}{}{{ {}{}}}{ {}{}} {{}{{}}}{{}{}}{}{{}{}} { }{{{{}}\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{11.19446pt}{-1.533pt}\pgfsys@invoke{ }\hbox{{\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\hbox{{\hbox{$\scriptstyle$}}} }}\pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope}}}\hbox{{\pgfsys@beginscope\pgfsys@invoke{ }{{}{}{{ {}{}}}{ {}{}} {{}{{}}}{{}{}}{}{{}{}} { }{{{{}}\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{3.0pt}{1.533pt}\pgfsys@invoke{ }\hbox{{\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\hbox{{\hbox{$\scriptstyle\ \ \ \ $}}} }}\pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}\operatorname{Hom}Z\!\big{(}C_{*}(A)+C_{*}(B),k\big{)}\eqqcolon{\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}L}$ is then again a quasi-isomorphism. The Mayer–Vietoris sequence in cohomology is the long exact sequence arising from the short exact sequence of cochain complexes

0\to L\overset{{\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}i}}{\longrightarrow}C^{*}(A;k)\times C^{*}(B;k)\overset{{\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}j}}{\longrightarrow}C^{*}(A\cap B;k)\to 0,

where $i(c)=(c|_{A},c|_{B})$ and $j(c_{A},c_{B})=c_{A}|_{A\cap B}-c_{B}|_{A\cap B}$ . To define the connecting map, given a homogeneous cocycle $z\in Z^{q}(A\cap B;k)$ , one selects cochains $c_{A}\in C^{q}(A;k)$ and $c_{B}\in C^{q}(B;k)$ such that $j(c_{A},c_{B})=z$ , and then $\delta_{\mathrm{MV}}[z]\in H^{q+1}(X;k)$ is the class represented by the unique element $z^{\prime}$ of $Z^{q+1}(L)$ such that $i(z^{\prime})=(\delta c_{A},\delta c_{B})$ . Now given a class in $H^{p}(X;k)$ , the restrictions of some representative $x$ to $A,B$ , and $A\cap B$ factor through the representative $x|_{L}\in Z^{p}(L)$ . Observe that $x|_{A\cap B}\mspace{-1.0mu}\smile\mspace{-1.0mu}z=j(x|_{A}\mspace{-1.0mu}\smile\mspace{-1.0mu}c_{A},x|_{B}\mspace{-1.0mu}\smile\mspace{-1.0mu}c_{B})$ . But since $\delta x=0$ , we have $\big{(}\delta(x|_{A}\mspace{-1.0mu}\smile\mspace{-1.0mu}c_{A}),\delta(x|_{B}\mspace{-1.0mu}\smile\mspace{-1.0mu}c_{B})\big{)}=({x|_{A}\mspace{-1.0mu}\smile\mspace{-1.0mu}\delta c_{A}},{x|_{B}\mspace{-1.0mu}\smile\mspace{-1.0mu}\delta c_{B}})=i(x|_{L}\mspace{-1.0mu}\smile\mspace{-1.0mu}z^{\prime})$ , so $\delta_{\rm{MV}}\big{(}[x]\mspace{-1.0mu}\smile\mspace{-1.0mu}[z]\big{)}=[x]\mspace{-1.0mu}\smile\mspace{-1.0mu}\delta_{\rm{MV}}[z]$ as claimed. ∎

Remark 2.2.

This feature turns out not to be specific to Borel equivariant cohomology, but applies to multiplicative cohomology theories in general, and the first author proves this fact and an extension of Section˜3.2 to other cohomology theories in an accompanying paper [Car18], along with analogues of the other main results in equivariant K-theory.

3. Equivariant cohomology rings

To deploy Proposition 2.1 as promised, we need the structure theorem for cohomogeneity-one actions on manifolds.

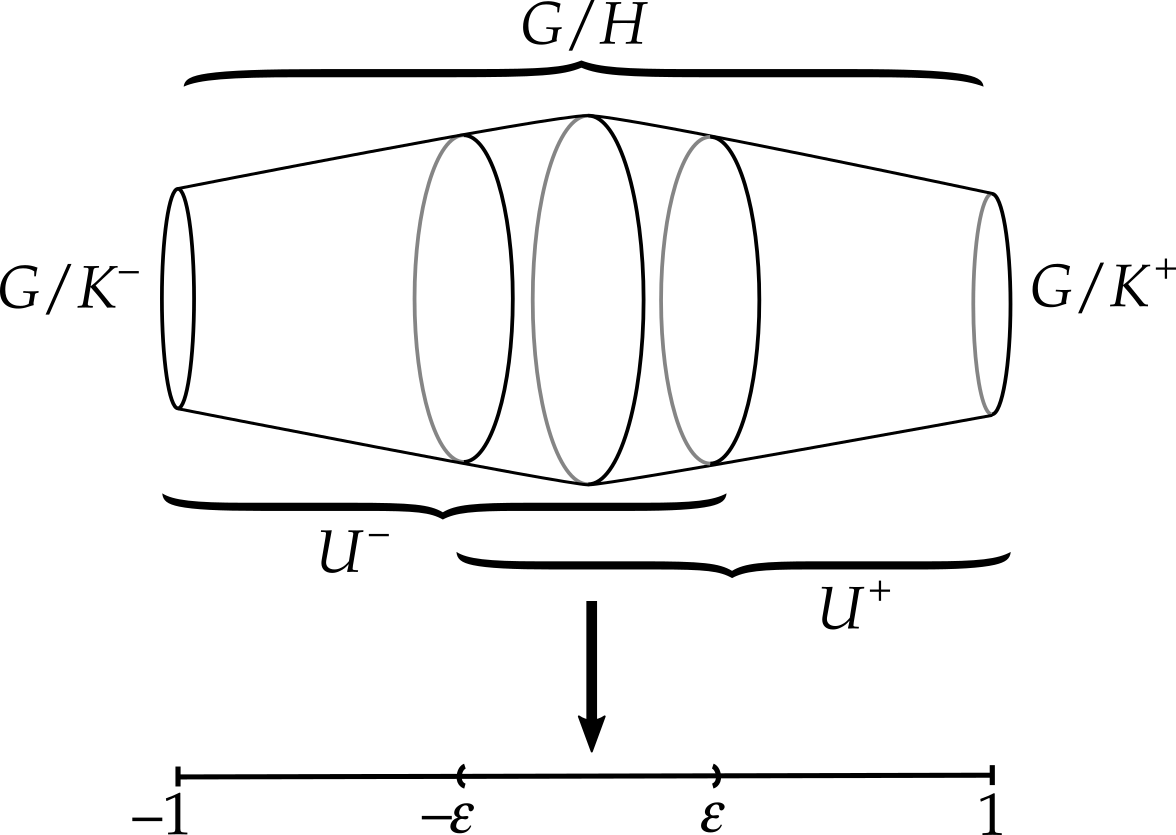
Refer to caption — Figure 3.1: Schematic of a double mapping cylinder

Theorem 3.2 ([Most57a, Thm. 4][Most57b][GGZ15, Thm. A]).

Let $G$ be a compact, connected Lie group acting continuously with cohomogeneity one on a connected topological manifold $M$ without boundary. Then $M$ is, up to $G$ -equivariant homeomorphism, as follows.

•

If $M/G\approx(-1,1)$ , there is a closed subgroup $K\leq G$ such that $M\approx(-1,1)\times G/K$ .
•

If $M/G\approx S^{1}$ , there are a closed subgroup $K\leq G$ and an element $n\in N_{G}(K)$ such that $M$ is the mapping torus of the right translation of $G/K$ by $n$ . (The equivariant homeomorphism type of the resulting space depends only on the class of $n$ in $\pi_{0}N_{G}(K)$ .)
•

If $M/G\approx[0,1)$ , there are closed subgroups $H<K\leq G$ such that $K/H$ is either a sphere $S^{n}$ or the Poincaré homology sphere $P^{3}$ and $M$ is the open mapping cylinder $\smash{G/K\underset{\pi}{\cup}\big{(}[0,1)\times G/H\big{)}}$ of the projection $\pi\colon G/H\longrightarrow G/K$ .
•

If $M/G\approx[-1,1]$ , there are closed subgroups $H<K^{\pm}\leq G$ such that each of $K^{\pm}/H$ is either a sphere $S^{n}$ or the Poincaré homology sphere $P^{3}$ and $M$ is the double mapping cylinder

${G/K^{-}\underset{\pi^{-}}{\cup}\big{(}[-1,1]\times G/H\big{)}\underset{\pi^{+}}{\cup}G/K}$

of the projections $\pi^{\pm}\colon G/H\ext@arrow{20}{20}{20}{20}{\arrowfill@\mathrel{\mathrlap{\raisebox{2.5pt}{$\relbar$}}\raisebox{-2.5pt}{$\relbar$}}\mathrel{\mathrlap{\raisebox{2.5pt}{$\relbar$}}\raisebox{-2.5pt}{$\relbar$}}{\mathrel{\mathrlap{\raisebox{2.5pt}{$\rightarrow$}}\mathrlap{\raisebox{-2.5pt}{$\rightarrow$}}\hphantom{\vbox{\hbox{$\rightarrow$}\hbox{$\rightarrow$}}}}}}{}{}G/K^{\pm}$ .

Conversely, these constructions yield only cohomogeneity-one $G$ -actions on manifolds. In the cases where $M/G$ has boundary, $M$ admits a $G$ -invariant smooth structure if and only if no isotropy quotient $K/H$ or $K^{\pm}/H$ is $P^{3}$ .

Before proceeding, we note the noncompact cases are trivial for our purposes, since in these cases $M$ equivariantly deformation retracts to the cohomogeneity-zero case $G/K$ . There is a similar classification of cohomogeneity-one actions on closed Alexandrov spaces.

Theorem 3.3 ([GGS11, Thm. A]).

Let $G$ be a compact Lie group acting effectively and isometrically with cohomogeneity one on a closed (i.e., compact and without boundary) Alexandrov space $X$ . Then $X$ is, up to $G$ -equivariant homeomorphism, as follows.

•

If $X/G\approx S^{1}$ , there are a closed subgroup $K\leq G$ and an element $n\in N_{G}(K)$ such that $X$ is the mapping torus of the right translation of $G/K$ by $n$ (and hence, by Theorem˜3.2, a smooth manifold).
•

If $X/G\approx[-1,1]$ , there are closed subgroups $H<K^{\pm}\leq G$ such that $K^{\pm}/H$ are positively-curved homogeneous spaces and $X$ is the double mapping cylinder of the projections $G/H\ext@arrow{20}{20}{20}{20}{\arrowfill@\mathrel{\mathrlap{\raisebox{2.5pt}{$\relbar$}}\raisebox{-2.5pt}{$\relbar$}}\mathrel{\mathrlap{\raisebox{2.5pt}{$\relbar$}}\raisebox{-2.5pt}{$\relbar$}}{\mathrel{\mathrlap{\raisebox{2.5pt}{$\rightarrow$}}\mathrlap{\raisebox{-2.5pt}{$\rightarrow$}}\hphantom{\vbox{\hbox{$\rightarrow$}\hbox{$\rightarrow$}}}}}}{}{}G/K^{\pm}$ .

Conversely, these constructions yield only cohomogeneity-one $G$ -actions on Alexandrov spaces.

Thus our Section˜3.2 will apply more generally than just to manifolds. Because of these two classification results, it is reasonable to focus our attention in the rest of the paper on cohomogeneity-one actions of the following types:

•

the mapping torus of a right translation on a homogeneous space $G/K$ or
•

the double mapping cylinder of a span of projections $G/K^{-}\leftarrow G/H\to G/K^{+}$ .

3.1. Mapping tori

By Theorem˜3.2, if the orbit space of a cohomogeneity-one action is a circle, the space in question can be assumed to be a manifold $M$ , the mapping torus of the right-translation ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}r_{n}}$ of some element ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}n}\in N_{G}(K)$ on $G/K$ , and hence actually a smooth manifold $M$ .

Lemma 3.4.

Let $Y$ be a topological space, $\varphi$ a self-homeomorphism of $Y$ such that some finite power $\varphi^{\ell}$ is homotopic to $\operatorname{id}_{Y}$ , and $X$ the mapping torus of $\varphi$ . Then

H^{*}X\cong{H^{*}(Y)^{\langle\varphi^{*}\rangle}}\underset{}{\mathbin{\raisebox{0.85pt}{$\displaystyle\otimes$}}}{H^{*}S^{1}}.

Proof.

Note that $X$ admits an $\ell$ -sheeted cyclic covering by the mapping torus of $\varphi^{\ell}$ , which is homeomorphic to the mapping torus $Y\times S^{1}$ of the identity. The covering action is conjugate to a $\mathbb Z/\ell$ -action on $Y\times S^{1}$ under which $1+\ell\mathbb Z$ acts, up to homotopy, as $(y,\theta)\longmapsto\big{(}\varphi(y),\theta+\frac{2\pi}{\ell}\big{)}$ , which, rotating the circle component, is in turn homotopic to $(y,\theta)\longmapsto\big{(}\varphi(y),\theta\big{)}$ . A standard lemma on the transfer map [Hat02, Prop. 3G.1] then gives

H^{*}X\cong H^{*}(Y\times S^{1})^{\mathbb Z/\ell}\cong H^{*}(Y)^{\langle\varphi^{*}\rangle}\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}S^{1}.\qed

3.2. Double mapping cylinders

Let $G$ be a compact Lie group and $H\leq K^{\pm}\leq G$ any closed subgroups. Then the double mapping cylinder $X$ of $\pi^{\pm}\colon G/H\ext@arrow{20}{20}{20}{20}{\arrowfill@\mathrel{\mathrlap{\raisebox{2.5pt}{$\relbar$}}\raisebox{-2.5pt}{$\relbar$}}\mathrel{\mathrlap{\raisebox{2.5pt}{$\relbar$}}\raisebox{-2.5pt}{$\relbar$}}{\mathrel{\mathrlap{\raisebox{2.5pt}{$\rightarrow$}}\mathrlap{\raisebox{-2.5pt}{$\rightarrow$}}\hphantom{\vbox{\hbox{$\rightarrow$}\hbox{$\rightarrow$}}}}}}{}{}G/K^{\pm}$ admits the obvious invariant open cover by the respective inverse images $U^{-}$ and $U^{+}$ of the subintervals $[-1,\varepsilon)$ and $(-\varepsilon,1]$ , for some small $\varepsilon>0$ , of $X/G\approx[-1,1]$ depicted in Figure˜3.1. Their intersection $W=U^{-}\cap U^{+}$ equivariantly deformation retracts to $G/H$ and $U^{\pm}$ to $G/K^{\pm}$ in such a way that the inclusions $W\xhookrightarrow{\ \ \ \ }U^{\pm}$ correspond to the projections $\pi^{\pm}$ . Now we can apply Proposition˜2.1.

{restatable}

theoremmainH Let $X$ be the double mapping cylinder of the projections $\pi^{\pm}\colon G/H\ext@arrow{20}{20}{20}{20}{\arrowfill@\mathrel{\mathrlap{\raisebox{2.5pt}{$\relbar$}}\raisebox{-2.5pt}{$\relbar$}}\mathrel{\mathrlap{\raisebox{2.5pt}{$\relbar$}}\raisebox{-2.5pt}{$\relbar$}}{\mathrel{\mathrlap{\raisebox{2.5pt}{$\rightarrow$}}\mathrlap{\raisebox{-2.5pt}{$\rightarrow$}}\hphantom{\vbox{\hbox{$\rightarrow$}\hbox{$\rightarrow$}}}}}}{}{}G/K^{\pm}$ . Then one has a graded ${H^{*}_{G}}$ -algebra and a graded $H^{*}_{H}$ -module isomorphism, respectively:

H_{G}^{\mathrm{even}}X\,\cong\,\smash{{H^{*}_{K^{-}}}\underset{H^{*}_{H}}{\times}{H^{*}_{K^{+}}}},\qquad H_{G}^{\mathrm{odd}}X\,\cong\mspace{1.0mu}\Big{(}\frac{H^{*}_{H}}{\operatorname{im}\rho^{*}_{-}+\operatorname{im}\rho^{*}_{+}}\Big{)}[1],

where ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}\rho^{*}_{\pm}}\colon H^{*}_{K^{\pm}}\longrightarrow H^{*}_{H}$ are induced by the inclusions $H\xhookrightarrow{\ \ \ \ }K^{\pm}$ and $H^{*}_{K^{-}}\times_{H^{*}_{H}}H^{*}_{K^{+}}$ denotes the fiber product.²²2 That is, $H^{*}_{K^{-}}\times_{H^{*}_{H}}H^{*}_{K^{+}}<H^{*}_{K^{-}}\times H^{*}_{K^{+}}$ is the subring of pairs $(x_{-},x_{+})$ such that $\rho^{*}_{-}(x_{-})=\rho^{*}_{+}(x_{+})$ . The multiplication of odd-degree elements is zero, and the product $H_{G}^{\mathrm{even}}X\times H_{G}^{\mathrm{odd}}X\longrightarrow H_{G}^{\mathrm{odd}}X$ descends from the multiplication of $H^{*}_{H}$ in that

(x_{-},x_{+})\cdot\bar{q}=\overline{\rho^{*}_{-}(x_{-})\cdot q}.

for $(x_{-},x_{+})\in\smash{{H^{*}_{K^{-}}}\underset{H^{*}_{H}}{\times}{H^{*}_{K^{+}}}}$ and $\bar{q}\in H_{G}^{\mathrm{odd}}X$ the image of $q\in H^{*}_{H}$ .

Proof.

For any $\Gamma\leq G$ we have homeomorphisms $(G/\Gamma)_{G}=EG\times_{G}G/\Gamma\approx EG/\Gamma=B\Gamma$ . As $\smash{H^{*}_{K^{\pm}}}$ and $\smash{H^{*}_{H}}$ are concentrated in even degree, the Mayer–Vietoris sequence of the cover just discussed reduces to a four-term exact sequence

0\to H_{G}^{\mathrm{even}}X\overset{{\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}i^{*}}}{\longrightarrow}H^{*}_{K^{-}}\times H^{*}_{K^{+}}\longrightarrow H^{*}_{H}\longrightarrow H_{G}^{\mathrm{odd}}X\overset{i^{*}}{\to}0,

so that $H_{G}^{\mathrm{even}}X$ is the kernel and $H_{G}^{\mathrm{odd}}X$ the cokernel of the middle map $(x_{-},x_{+})\longmapsto\rho_{+}^{*}(x_{+})-\rho_{-}^{*}(x_{-})$ . The multiplicative structure on $H_{G}^{\mathrm{even}}$ follows from the fact $i^{*}\colon{H^{*}_{G}}X\longrightarrow H^{*}_{K^{-}}\times H^{*}_{K^{+}}$ is a ring map, the description of the product $H_{G}^{\mathrm{even}}X\times H_{G}^{\mathrm{odd}}X\longrightarrow H_{G}^{\mathrm{odd}}X$ follows from Proposition˜2.1, and the fact the product $H_{G}^{\mathrm{odd}}X\times H_{G}^{\mathrm{odd}}X\longrightarrow H_{G}^{\mathrm{even}}X$ is zero follows from the observation $i^{*}$ is injective on $H_{G}^{\mathrm{even}}X$ and yet $i^{*}(xy)=i^{*}(x)i^{*}(y)=0$ for any elements $x,y\in H_{G}^{\mathrm{odd}}X$ . ∎

Example 3.5.

Let $G=\mathrm{O}(n)$ with $K=K^{\pm}=\mathrm{O}(3)$ and $H=\mathrm{O}(2)$ block-diagonal. We have ${H^{*}_{K}}\cong\mathbb Q[p_{1}]\cong H^{*}_{H}$ , where $p_{1}$ is the first Pontrjagin class of the tautological bundle over the infinite Grassmannian $\operatorname{Gr}(3,\mathbb R^{\infty})=B\mathrm{O}(3)$ , so ${H^{*}_{G}}X\cong\mathbb Q[p_{1}]$ .

Example 3.6.

In the situation where $G=K^{\pm}$ , the resulting double mapping cylinder is just the unreduced suspension $S(G/H)$ . One has

\displaystyle\phantom{\mbox{and}}\qquad H_{G}^{\mathrm{even}}S(G/H)={H^{*}_{G}},

\displaystyle\qquad H_{G}^{\mathrm{odd}}S(G/H)={\raisebox{1.99997pt}{$H^{*}_{H}\,$}}\ \!\!\big{/}\!\!\ {\raisebox{-1.99997pt}{$\operatorname{im}(\mspace{-1.0mu}{H^{*}_{G}}\to H^{*}_{H})$}}[1].

4. Maps of classifying spaces

In the event the cohomogeneity-one double mapping cylinder is a manifold $M$ , we will presently see that more precise descriptions of $H^{*}_{G}M$ can be obtained depending on the dimensions of the isotropy spheres $K^{\pm}/H$ , subject to an orientation hypothesis on the left action of $K^{\pm}$ in case these groups are disconnected, and these descriptions depend crucially on the structure of $H^{*}_{H}$ as a module over $H^{*}_{K^{\pm}}$ .

Lemma 4.1.

Let $H<K$ be compact Lie groups such that $K/H$ is a homology sphere. The $K/H$ -bundle $\smash{\rho\colon BH\longrightarrow BK}$ is orientable if and only if left multiplication on $K/H$ by any element of $K$ induces the identity in cohomology.

Proof.

Recall orientability of a fiber bundle is defined as triviality of the action of the fundamental group of the base on the cohomology of the fiber. To determine the action-up-to-homotopy of a class of $\pi_{1}(BK,e_{0}K)$ on the fiber, lift a representative loop $\eta$ to a path $\widetilde{\eta}$ in $EK$ starting at $e_{0}$ and ending at some $e_{0}k_{1}$ . Then for any $e_{0}kH$ in the fiber $\rho^{-1}(e_{0}K)$ , the path $\widetilde{\eta}kH$ lifts $\eta$ to $BH$ , starting at $e_{0}kH$ and ending at $e_{0}k_{1}kH$ , which we may define to be $\eta\cdot e_{0}kH$ . Under the identification $\rho^{-1}(e_{0}K)\approx K/H$ given by $e_{0}kH\leftrightarrow kH$ , this is just the action of $\pi_{0}K$ induced by the defining homogeneous action of $K$ on $K/H$ . The generator $1\in H^{0}(K/H)$ is invariant trivially, so the action is trivial in cohomology if and only if the fundamental class $[K/H]$ is fixed by the $\pi_{0}K$ -action. ∎

Remark 4.2.

Particularly, this rules out the case $K/H\approx S^{0}$ going forward.

Proposition 4.3 (Cf. Goertsches–Mare [GM14, Prop. 3.1][GM17, Prop. 4.2]).

Let $H<K$ be compact Lie groups such that $K/H$ is a homology sphere of odd dimension $n$ and $BH\longrightarrow BK$ is an orientable $K/H$ -bundle. Then $\rho^{*}\colon{H^{*}_{K}}\longrightarrow H^{*}_{H}$ is a surjection and can be written

H^{*}_{H}[e]\xrightarrow{e\mapsto 0}H^{*}_{H},

where ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}e}\in H^{n+1}_{H}$ is the generalized Euler class of the bundle $K/H\to BH\to BK$ .

Proof.

Let $K_{0}$ be the identity component of $K$ and write ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}H_{1}}=H\cap K_{0}$ , so that $K_{0}/H_{1}\longrightarrow K/H$ is a homeomorphism. We claim $H^{*}_{H_{1}}$ is a polynomial ring. This follows if $K/H$ is a sphere of dimension at least $2$ since then $K_{0}/H_{1}\approx K/H$ is both simply-connected and covered by $K_{0}/H_{0}$ , forcing $H_{0}=H_{1}$ . If $K/H$ is homeomorphic to $S^{1}$ or the Poincaré homology sphere $P^{3}$ , then we still know $H^{*}_{H_{1}}\cong(H^{*}_{H_{0}})^{H_{1}/H_{0}}$ , but the action of $H_{1}/H_{0}$ on $H^{*}_{H_{0}}$ is trivial because it is known [GM14, Pf., Prop. 3.1][GM17, Pf., Prop. 4.2] that $H_{0}$ is normal in $K_{0}$ in these cases, so the action of $H_{1}/H_{0}$ is the restriction of an action of $K_{0}/H_{0}$ , which is homotopically trivial since $K_{0}/H_{0}$ is path-connected.³³3 To make this account self-contained, the proof of normality is thus. The transitive action of $K_{0}$ on $K_{0}/H_{1}$ induces a map ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}\lambda}\colon K_{0}\longrightarrow\operatorname{Homeo}K_{0}/H_{1}$ whose image, which acts effectively by definition, can only be $S^{1}$ itself if $K_{0}/H_{1}\approx S^{1}$ and $\mathrm{SO}(3)$ if $K_{0}/H_{1}\approx P^{3}$ [Bre61, Thm. 1.1]. As $\ker\lambda$ stabilizes all points, it is in particular contained in $H_{1}$ . The stabilizer of the coset $1H_{1}\in K_{0}/H_{1}$ under the effective action of $\operatorname{im}\lambda$ is $\lambda(H_{1})\cong H_{1}/\ker\lambda$ , which must be finite since $\operatorname{im}\lambda$ is of rank one, so $\ker\lambda$ is of finite index in $H_{1}$ ; particularly, its identity component must be $H_{0}$ . Since $\ker\lambda$ is normal in $K_{0}$ by definition, so also must be $H_{0}$ .

We now consider the map of $K/H$ -bundles

(4.1)

The left map is equivariant with respect to the right $H$ -action, inducing an effective right action of ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}\pi}\coloneqq H/H_{1}\cong\pi_{0}K$ such that the right map is the quotient, and so we may identify [Hat02, Prop. 3G.1] the map ${H^{*}_{K}}\longrightarrow H^{*}_{H}$ with the map of invariants $(H^{*}_{K_{0}})^{\pi}\longrightarrow(H^{*}_{H_{1}})^{\pi}$ . Now let us consider a portion of the induced map of generalized Gysin sequences [MiT00, SS3.7]:

The commutativity of the diagram implies the identification ${H^{*}_{K}}\cong(H^{*}_{K_{0}})^{\pi}$ takes the one generalized Euler class to the other, or in other words that the class in the lower sequence is $\pi$ -invariant. Since $H^{*}_{K_{0}}$ is a polynomial ring, multiplication by $e$ is injective, so the horizontal maps before and after are zero, so this is actually an inclusion of short exact sequences. As the image of multiplication by $e$ is precisely the principal ideal $(e)$ , we obtain an $\pi$ -equivariant isomorphism $H^{*}_{H_{1}}\cong H^{*}_{K_{0}}/(e)$ . As $H^{*}_{K_{0}}\longrightarrow H^{*}_{H_{1}}$ is a $\pi$ -equivariant surjection between graded polynomial rings over $\mathbb Q$ on $n+1$ and $n$ generators, respectively, whose kernel is generated by the $\pi$ -invariant element $e$ , Lemma˜4.6 applies to yield a $\pi$ -equivariant isomorphism $H^{*}_{H_{1}}[e]\overset{\sim}{\longrightarrow}H^{*}_{K_{0}}$ . This restricts to an isomorphism of $\pi$ -invariants $\smash{H^{*}_{H}[e]\overset{\sim}{\longrightarrow}{H^{*}_{K}}}$ . ∎

Remark 4.4.

When $K/H$ is a sphere, the generalized Euler class featuring in Proposition˜4.3 is well known to be the standard Euler class of a sphere bundle [MiT00, Thm. 5.17, pp. 145–6]. If $K/H\approx P^{3}$ , on the other hand, from the fact that the action $K\longrightarrow\operatorname{Homeo}P^{3}$ factors through an $\mathrm{SO}(3)$ subgroup [Bre61, Thm. 1.1], one can associate to $BH\longrightarrow BK$ the principal $\mathrm{SO}(3)$ -bundle $\xi\colon EK\times_{K}\mathrm{SO}(3)\longrightarrow BK$ and show $e$ is $60$ times the first Pontrjagin class $p_{1}(\xi)$ .

Remark 4.5.

The persistent orientability hypothesis is necessary; we will see in Remark˜5.3 that Section˜5.2 fails without this hypothesis. For now, consider the case of $K=\mathrm{O}(2)$ and $H$ a subgroup of order $2$ generated by an element $h$ of determinant $-1$ . Then for $z\in\mathrm{SO}(2)$ we have $h\cdot zH=z^{-1}H$ . We have $H^{*}_{K_{0}}=H^{*}_{\mathrm{SO}(2)}=\mathbb Q[c_{1}]$ and $c_{1}=e$ in the notation of the proof since $\smash{H^{*}_{H_{0}}=H^{*}_{\{1\}}=\mathbb Q}$ . The proof would go through if we had $e=c_{1}\in{H^{*}_{K}}$ , but we do not; in fact $H^{*}_{\mathrm{O}(2)}\cong\mathbb Q[c_{1}^{2}]$ , where $c_{1}^{2}$ is represented by the first Pontrjagin class $p_{1}$ of the tautological $2$ -plane bundle over the infinite Grassmannian $G(2,\mathbb R^{\infty})=B\mathrm{O}(2)$ [Hat09, Thm. 3.16(a)]. Thus, although it is incidentally true in this case that ${H^{*}_{K}}\cong H^{*}_{H}[c_{1}^{2}]$ , the proof of Proposition˜4.3 cannot possibly go through.

Lemma 4.6.

Suppose $A$ is a graded polynomial ring in finitely many variables over $\mathbb Q$ equipped with an action of a finite group $\pi$ fixing the field of constants $\mathbb Q$ , and $x$ is a $\pi$ -invariant homogeneous element of $A$ such that $B=A/(x)$ is again a polynomial ring. Then there is a $\pi$ -invariant graded $\mathbb Q$ -subalgebra $A^{\prime}<A$ such that $A=A^{\prime}[x]$ and $\smash{A^{\prime}\hookrightarrow A\mathrel{\leavevmode\hbox to11.93pt{\vbox to14.11pt{\pgfpicture\makeatletter\hbox{\thinspace\lower-4.86601pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{}{{}}{} {{}{}}{}{}{}{{{}{}}}{{}}{}{}{{{}{}}}{{}}{}{}{}{}{}{{}}\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@lineto{10.85977pt}{0.0pt}\pgfsys@stroke\pgfsys@invoke{ }{{}{{}}{}{}{{}}{{{}}{{{}}{\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{8.57979pt}{0.0pt}\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope}}{{}}{{{}}{\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{11.05977pt}{0.0pt}\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope}}{{}}}}\hbox{\hbox{\hbox{{\pgfsys@beginscope\pgfsys@invoke{ }{{}{}{{ {}{}}}{ {}{}} {{}{{}}}{{}{}}{}{{}{}} { }{{{{}}\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{5.62988pt}{-1.533pt}\pgfsys@invoke{ }\hbox{{\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\hbox{{\hbox{$\scriptstyle$}}} }}\pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope}}}\hbox{{\pgfsys@beginscope\pgfsys@invoke{ }{{}{}{{ {}{}}}{ {}{}} {{}{{}}}{{}{}}{}{{}{}} { }{{{{}}\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{3.00002pt}{2.89409pt}\pgfsys@invoke{ }\hbox{{\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\hbox{{\hbox{$\scriptstyle{\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}\varphi}$}}} }}\pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}B}$ is a ring isomorphism.

Proof.

We consider $A$ and $B$ as modules over the group ring $\mathbb Q\pi$ . It is easy to see that any $\mathbb Q\pi$ -module $C$ complementary to $(x)$ will be taken bijectively and $\mathbb Q\pi$ -linearly to $A/(x)$ by $\varphi$ , so we just need to show such a complement can be chosen to be a ring and generators of this ring can be chosen such that together with $x$ they form a set of $\mathbb Q$ -algebra generators for $A$ . We write ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}Q}B=B^{\geq 1}/B^{\geq 1}\cdot B^{\geq 1}$ for the graded $\mathbb Q$ -module of indecomposables, in this case a free module. As $QB$ is a finite-dimensional $\pi$ -representation and the order of $\pi$ is invertible over $\mathbb Q$ , we may break $QB$ into irreducible representations of $\pi$ , which are cyclic $\mathbb Q\pi$ -modules, each generated by an element $\bar{b}_{j}$ . We may lift each of these to a homogeneous element $b_{j}\in B^{\geq 1}$ . By construction, the union of the $\pi$ -orbits of the $b_{j}$ forms a set of $\mathbb Q$ -algebra generators for $B$ . Now let $a_{j}\in C$ be a $\varphi$ -preimage of $b_{j}$ . Then the $\mathbb Q\pi$ -algebra $A^{\prime}$ generated by the $a_{j}$ is taken bijectively onto $B$ by $\varphi$ , so it is a polynomial subalgebra and in fact another $\mathbb Q\pi$ -linear complement to $(x)$ . It is clear from the isomorphism $A^{\prime}\xrightarrow{\sim}B$ that each element of $A$ can be represented uniquely as a polynomial in $x$ over $A^{\prime}$ . ∎

The case $K/H$ is even-dimensional is simpler.

Proposition 4.7 ([Bor53, Thm. 26.1(a)][Sam41, p. 1121]).

Let $H\leq K$ be compact Lie groups of equal rank. Then ${H^{*}_{K}}\longrightarrow H^{*}_{H}$ is injective. This applies particularly if $K/H$ is an even-dimensional sphere. In this case, if the bundle $\rho\colon BH\longrightarrow BK$ is orientable and $n=\dim K/H\geq 2$ , then $H^{*}_{H}$ is a free ${H^{*}_{K}}$ -module of rank two on $1$ and a lift ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}e}\in H_{H}^{n}$ of the fundamental class of $K/H$ under the surjection $H^{*}(BH)\longrightarrow H^{*}(K/H)$ .

Samelson showed the ranks are equal if $K/H$ is an even-dimensional sphere and the injectivity statement is due to Borel.

Proof.

The covering $\pi_{0}K\to BK_{0}\to BK$ coming from the action of $\pi_{0}K=K/K_{0}$ on $BK_{0}=EK/K_{0}$ , induces an isomorphism ${H^{*}_{K}}\cong(H^{*}_{K_{0}})^{\pi_{0}K}$ by a standard transfer lemma [Hat02, Prop. 3G.1]. As $H^{*}_{K_{0}}$ is a polynomial ring by Borel’s theorem, the Serre spectral sequence of $K/H\to BH\to BK$ is concentrated in even degree and so collapses. By Lemma˜4.1, the coefficients are simple, so $H^{*}_{H}\cong{H^{*}_{K}}\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}(K/H)\cong{H^{*}_{K}}\{1,e\}$ as an ${H^{*}_{K}}$ -module for some $e$ represented by $1\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}{[K/H]}$ in the associated graded algebra. ∎

Remark 4.8.

Note that the basis $\{1,e\}$ is preserved under the map

H^{*}_{H}\cong{H^{*}_{K}}\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}(K/H)\mathrel{\leavevmode\hbox to23.05pt{\vbox to9.73pt{\pgfpicture\makeatletter\hbox{\thinspace\lower-4.86601pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{}{{}}{} {{}{}}{}{}{}{{{}{}}}{{}}{}{}{{{}{}}}{{}}{}{}{}{}{{}}{}{}{}{{}}\pgfsys@moveto{2.07999pt}{0.0pt}\pgfsys@lineto{21.98894pt}{0.0pt}\pgfsys@stroke\pgfsys@invoke{ }{{}{{}}{}{}{{}}{{{}}{{{}}{\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{-1.0}{0.0}{0.0}{-1.0}{2.27998pt}{0.0pt}\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope}}{{}}}}{{}{{}}{}{}{{}}{{{}}{{{}}{\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{22.18893pt}{0.0pt}\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope}}{{}}}}\hbox{\hbox{\hbox{{\pgfsys@beginscope\pgfsys@invoke{ }{{}{}{{ {}{}}}{ {}{}} {{}{{}}}{{}{}}{}{{}{}} { }{{{{}}\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{11.19446pt}{-1.533pt}\pgfsys@invoke{ }\hbox{{\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\hbox{{\hbox{$\scriptstyle$}}} }}\pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope}}}\hbox{{\pgfsys@beginscope\pgfsys@invoke{ }{{}{}{{ {}{}}}{ {}{}} {{}{{}}}{{}{}}{}{{}{}} { }{{{{}}\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{3.0pt}{1.533pt}\pgfsys@invoke{ }\hbox{{\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\hbox{{\hbox{$\scriptstyle\ \ \ \ $}}} }}\pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}H^{*}_{K_{0}}\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}(K_{0}/H_{0})\cong H^{*}_{H_{0}}

induced by the map of $K/H$ -bundles $(BH_{0}\to BK_{0})\longrightarrow(BH\to BK)$ , so $e\in H^{*}_{H_{0}}$ may be chosen $\pi_{0}H$ -invariant.

Remark 4.9.

The lift $e$ in Proposition˜4.7 can be chosen to be the pullback under $BH\longrightarrow B\mathrm{SO}(n)$ of the universal Euler class $e_{\mathrm{SO}(n)}\in H^{n}_{\mathrm{SO}(n)}$ . To see this, note that by the classification of transitive Lie group actions on spheres [Bes87, Ex. 7.13], the action $K\longrightarrow\operatorname{Homeo}K/H$ must factor through a subgroup isomorphic to $\mathrm{SO}(n+1)$ , sending $H$ into an $\mathrm{SO}(n)$ subgroup and hence inducing a map of $S^{n}$ -bundles from $BH\to BK$ to $B\mathrm{SO}(n)\to B\mathrm{SO}(n+1)$ . Both Serre spectral sequences collapse at $E_{2}$ , and the $E_{2}$ map $H^{*}_{\mathrm{SO}(n)}\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}S^{n}\longrightarrow{H^{*}_{K}}\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}(K/H)$ sends $1\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}{[S^{n}]}\longmapsto 1\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}{[K/H]}$ . But $e$ represents $1\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}{[K/H]}$ , and since $H^{*}_{\mathrm{SO}(n)}\cong H^{*}_{\mathrm{SO}(n+1)}\{1,e_{\mathrm{SO}(n)}\}$ as an $H^{*}_{\mathrm{SO}(n+1)}$ -module, $e_{\mathrm{SO}(n)}$ represents $1\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}{[S^{n}]}$ .

5. Double mapping cylinders which are manifolds

In this section we are in the situation of Section˜3.2 and additionally the isotropy quotients $K^{\pm}/H$ are homology spheres.

5.1. The case when one of $K^{\pm}/H$ is odd-dimensional

If $K^{+}/H$ is odd-dimensional, then $H^{*}_{K^{+}}\longrightarrow H^{*}_{H}$ is surjective, so $H_{G}^{\mathrm{odd}}M$ vanishes by Section˜3.2 and ${H^{*}_{G}}M=H_{G}^{\mathrm{even}}M$ is easily described.

\Hodd

Proof.

(a) Since the map $H^{*}_{K^{+}}\xrightarrow{\sim}H^{*}_{H}[e]\to H^{*}_{H}$ is reduction modulo $(e)$ by Proposition˜4.3 and $H^{*}_{K^{-}}\longrightarrow H^{*}_{H}$ is an injection by Proposition˜4.7, the fiber product is the subring of $H^{*}_{K^{-}}\times H^{*}_{H}[e]$ consisting of the direct summands $\big{\{}(x,x)\in H^{*}_{K^{-}}\times H^{*}_{K^{-}}\big{\}}$ and $\{0\}\times e\cdot H^{*}_{H}[e]$ . We may identify the former with $H^{*}_{K^{-}}<H^{*}_{H}<H^{*}_{H}[e]$ and the latter with $eH^{*}_{H}[e]\lhd H^{*}_{H}[e]$ , and the two interact multiplicatively via the rule $x\cdot ef\leftrightarrow(x,x)\cdot(0,ef)=(0,efx)\leftrightarrow efx$ .

(b) Using Proposition˜4.3 to make identifications $H^{*}_{K^{\pm}}\cong H^{*}_{H}[e_{\pm}]$ such that $H^{*}_{K^{\pm}}\longrightarrow H^{*}_{H}$ is reduction modulo $(e_{\pm})$ , we see the fiber product is the subring of $H^{*}_{H}[e_{-}]\times H^{*}_{H}[e_{+}]$ comprising the three direct summands

\big{\{}(x,x)\in H^{*}_{H}\times H^{*}_{H}\big{\}},\qquad\qquad e_{-}H^{*}_{H}[e_{-}]\times\{0\},\qquad\qquad\{0\}\times e_{+}H^{*}_{H}[e_{+}],

on which multiplication is determined by the three rules

(x,x)\cdot(e_{-}f_{-},0)=(e_{-}f_{-}x,0),\qquad(x,x)\cdot(0,e_{+}f_{+})=(0,e_{+}f_{+}x),\qquad(e_{-}f_{-},0)\cdot(0,e_{+}f_{+})=(0,0),

so the map to $H^{*}_{H}[e_{-},e_{+}]/(e_{-}e_{+})$ sending $(x+e_{-}f_{-},x+e_{+}f_{+})\longmapsto x+e_{-}f_{-}+e_{+}f_{+}$ is a ring isomorphism. ∎

Remark 5.1.

The second and fourth author have shown [GM14, GM17] that for any cohomogeneity-one action of a compact, connected Lie group $G$ on a compact, connected topological manifold $M$ , the equivariant cohomology $H^{*}_{G}M$ is a Cohen–Macaulay module over $H^{*}_{G}$ . In the special case when all the hypotheses of Section˜1 are fulfilled, this result can be recovered easily from that theorem. Concretely, in case (a), the equivariant cohomology is a direct sum of two Cohen–Macaulay modules over $H^{*}_{G}$ and in case (b) it is an algebra over $H^{*}_{G}$ finitely generated as an ${H^{*}_{G}}$ -module and Cohen–Macaulay as a ring.

Remark 5.2.

Special cases of the actions investigated in this section are also considered by Choi and Kuroki [Kur11, CK11].

5.2. The case when both of $K^{\pm}/H$ are even-dimensional

In this subsection we assume that $K^{-}$ , $K^{+}$ , and $H$ have all three the same rank, or equivalently that $M$ is a manifold with $K^{\pm}/H$ even-dimensional. We start with the special case where $K^{-}=K^{+}$ .

{restatable}

propositionspherefiber Assume ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}K}\coloneqq K^{+}=K^{-}$ , that $K/H=S^{2n}$ is an even-dimensional sphere, and that the bundle $BH\longrightarrow BK$ is orientable. Then we have an $H^{*}(BG;\mathbb Z)$ -algebra isomorphism

{H^{*}_{G}}(M;\mathbb Z)\cong H^{*}(BK;\mathbb Z)\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}(S^{2n+1};\mathbb Z),

where the $H^{*}(BG;\mathbb Z)$ -algebra structure is induced by the inclusion $K\xhookrightarrow{\ \ \ \ }G$ .

Proof.

In this case $M_{G}$ is the homotopy pushout of $BK\leftarrow BH\to BK$ , which we may write as the quotient of $[-1,1]\times BH$ by the relation collapsing the ends $\{\pm 1\}\times BH$ to one copy of $BK$ each. There is an obvious map

	$\displaystyle{\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}\xi}\colon M_{G}$	$\displaystyle\mathrel{\leavevmode\hbox to23.05pt{\vbox to9.73pt{\pgfpicture\makeatletter\hbox{\thinspace\lower-4.86601pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{}{{}}{} {{}{}}{}{}{}{{{}{}}}{{}}{}{}{{{}{}}}{{}}{}{}{}{}{}{{}}\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@lineto{21.98894pt}{0.0pt}\pgfsys@stroke\pgfsys@invoke{ }{{}{{}}{}{}{{}}{{{}}{{{}}{\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{19.70895pt}{0.0pt}\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope}}{{}}{{{}}{\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{22.18893pt}{0.0pt}\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope}}{{}}}}\hbox{\hbox{\hbox{{\pgfsys@beginscope\pgfsys@invoke{ }{{}{}{{ {}{}}}{ {}{}} {{}{{}}}{{}{}}{}{{}{}} { }{{{{}}\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{11.19446pt}{-1.533pt}\pgfsys@invoke{ }\hbox{{\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\hbox{{\hbox{$\scriptstyle$}}} }}\pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope}}}\hbox{{\pgfsys@beginscope\pgfsys@invoke{ }{{}{}{{ {}{}}}{ {}{}} {{}{{}}}{{}{}}{}{{}{}} { }{{{{}}\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{3.0pt}{1.533pt}\pgfsys@invoke{ }\hbox{{\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\hbox{{\hbox{$\scriptstyle\ \ \ \ $}}} }}\pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}BK,$
	$\displaystyle[t,eH]$	$\displaystyle\longmapsto eK,\quad t\in(-1,1),$
	$\displaystyle[\pm 1,eK]$	$\displaystyle\longmapsto eK.$

The fiber of this map over $eK\in BK$ is the unreduced suspension $S(K/H)\approx S^{2n+1}$ , so $\xi$ is a sphere bundle. We claim the Serre spectral sequence of $\xi$ has simple coefficients and collapses at $E_{2}$ . Indeed, given $eK\in BK$ and a loop $\eta$ representing a class in $\pi_{1}(BK,eK)$ , if $\widetilde{\eta}$ is a lift to $EK$ starting at $e$ and ending at $ek$ , a lift of $\eta$ starting at $(\pm 1,eK)$ (respectively, $(t,eH)$ ) ends at $(\pm 1,ekK)=(\pm 1,eK)$ (resp., $(t,ekH)$ ). This action fixes the poles of the fiber $S(K/H)$ and acts as left multiplication by $k$ on each latitude $K/H$ , fixing the orientation of the latitude by Lemma˜4.1, so the action preserves the orientation of the fiber $S^{2n+1}$ of $\xi$ as a whole, and thus, again by Lemma˜4.1, the bundle $\xi$ is orientable. As there are only two nonzero rows, to see the spectral sequence collapses at $E_{2}\cong H^{*}\big{(}BK;H^{*}(S^{2n+1};\mathbb Z)\big{)}=H^{*}(BK;\mathbb Z)\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}(S^{2n+1};\mathbb Z)$ , it is enough to show $d_{2n+2}[S^{2n+1}]=0\in H^{2n+2}(BK)$ . But this differential must be zero because $\xi$ admits the section $eK\longmapsto[-1,eK]$ , showing $\xi^{*}\colon H^{*}(BK;\mathbb Z)\longrightarrow{H^{*}_{G}}(M;\mathbb Z)$ is injective. The collapse shows ${H^{*}_{G}}(M;\mathbb Z)\longrightarrow H^{*}(S^{2n+1};\mathbb Z)$ is surjective and ${H^{*}_{G}}(M;\mathbb Z)\cong E_{\infty}=H^{*}(BK;\mathbb Z)\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}(S^{2n+1};\mathbb Z)$ as a module over $H^{*}(BK;\mathbb Z)$ . Thus $1\in H_{G}^{0}(M;\mathbb Z)$ and any preimage $z\in H^{2n+1}_{G}(M;\mathbb Z)$ of the fundamental class $[S^{2n+1}]\in H^{2n+1}(S^{2n+1};\mathbb Z)$ generate ${H^{*}_{G}}(M;\mathbb Z)$ as an $H^{*}(BK;\mathbb Z)$ -module.

By definition, this $z$ commutes with all elements of $\operatorname{im}\xi^{*}\cong H^{*}(BK;\mathbb Z)$ , and we claim it also squares to zero. Indeed, from Section˜3.2, it is in the image of the Mayer–Vietoris connecting map from $H^{*}(BH;\mathbb Z)$ , which factors as $\smash{H^{*}(BH;\mathbb Z)\overset{\Sigma}{\to}\widetilde{H}^{*+1}(SBH;\mathbb Z)\to\widetilde{H}^{*+1}(M_{G};\mathbb Z)}$ , where $\Sigma$ is the suspension isomorphism and $M_{G}\to SBH$ is the map that collapses each end $BK$ of the double mapping cylinder to a point [May99, SS19.1–3, pp. 146–7]. Since the cup product on $\widetilde{H}^{*}(SBH)$ is identically zero and $z^{2}$ is the image of a square in $\widetilde{H}^{*}(SBH)$ , we see that indeed $z^{2}=0$ . It follows ${H^{*}_{G}}(M;\mathbb Z)\cong\Lambda_{H^{*}(BK;\mathbb Z)}[z]\cong H^{*}(BK;\mathbb Z)\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}(S^{2n+1};\mathbb Z)$ as an $H^{*}(BK;\mathbb Z)$ -algebra. ∎

Remark 5.3.

The orientability hypothesis in the proposition above is essential, as can be seen from the action of ${\rm S}{\rm O}(3)$ on $\mathbb RP^{3}\,\#\,\mathbb RP^{3}$ described by Mostert [Most57a, Thm. 7]. The isotropies are given by $K=K^{\pm}=\mathrm{S}\big{(}\mathrm{O}(2)\times\mathrm{O}(1)\mspace{-1.0mu}\big{)}\cong\mathrm{O}(2)$ and $H=\mathrm{SO}(2)\times\{1\}$ , so $K/H\approx S^{0}$ and the bundle is not orientable by Remark˜4.2. If the conclusion of Proposition 5.2 held in this instance, we would have (with $\mathbb Q$ coefficients as usual)

H^{*}_{\mathrm{SO}(3)}(\mathbb R\mathrm{P}^{3}\,\#\,\mathbb R\mathrm{P}^{3})\cong H^{*}_{\mathrm{O}(2)}\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}S^{1}.

(5.1)

But the $\mathrm{SO}(3)$ -action at hand is equivariantly formal [GM14, Cor. 1.3], so $\smash{H^{*}_{\mathrm{SO}(3)}(\mathbb R\mathrm{P}^{3}\,\#\,\mathbb R\mathrm{P}^{3})}$ is isomorphic as an $H^{*}_{\mathrm{SO}(3)}$ -module to $H^{*}(\mathbb R\mathrm{P}^{3}\,\#\,\mathbb R\mathrm{P}^{3})\otimes H^{*}_{\mathrm{SO}(3)}$ , which unlike $H^{*}_{\mathrm{O}(2)}\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}S^{1}$ is zero in dimension $1$ .

Example 5.4.

Let us now use Section˜5.2 to compute the equivariant cohomology of the action arising from the inclusion diagram $(G,K^{-},K^{+},H)=\big{(}\mathrm{Sp}(2),\mathrm{Sp}(1)^{2},\mathrm{Sp}(1)^{2},\mathrm{Sp}(1)\times\mathrm{U}(1)\big{)}$ . For a nice treatment of this manifold we refer to Püttmann [Pütt09, Sect. 4.3]. From the Mayer–Vietoris sequence, one sees the manifold $M$ has the same integral cohomology as the direct product $S^{3}\times S^{4}$ . By Proposition 5.2,

H^{*}_{\mathrm{Sp}(2)}(M;\mathbb Z)\cong H^{*}\big{(}B\mathrm{Sp}(1)^{2};\mathbb Z\big{)}\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}(S^{3};\mathbb Z).

Equivariant formality of the $\mathrm{Sp}(2)$ -action on $M$ was already known over $\mathbb Q$ [GM14, Cor. 1.3], but the inclusion $\mathrm{Sp}(1)^{2}\xhookrightarrow{\ \ \ \ }\mathrm{Sp}(2)$ induces an $H^{*}\big{(}B\mathrm{Sp}(2);\mathbb Z\big{)}$ -module isomorphism $H^{*}\big{(}B\mathrm{Sp}(1)^{2};\mathbb Z\big{)}\cong H^{*}\big{(}B\mathrm{Sp}(2);\mathbb Z\big{)}\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}(S^{4};\mathbb Z)$ , so the action is actually equivariantly formal over $\mathbb Z$ .

We will now generalize the proposition above to the case when $K^{-}$ and $K^{+}$ are not necessarily equal. Assume that $K^{\pm}/H=S^{2n_{\pm}}$ for ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}n_{\pm}}\geq 1$ . Let ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}S}\leq H$ be a maximal torus and ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}\Xi}$ the subgroup of $\operatorname{Aut}S$ generated by the Weyl groups $W(K^{\pm})$ and $W(H)$ . The Weyl groups, and hence $\Xi$ , are all contained in the image of the conjugation map $N_{G}(S)\to\operatorname{Aut}S$ sending $g\longmapsto(s\mapsto gsg^{-1})$ . Since image of this map is compact and $\operatorname{Aut}S\cong\mathbb Z^{\dim S}$ is discrete, $\Xi$ is finite. Because $K^{\pm}/H$ are even-dimensional spheres, by Proposition˜4.7, $H^{*}_{H}=({H^{*}_{S}})^{W_{H}}$ is of rank two over $H^{*}_{K^{\pm}}=({H^{*}_{S}})^{W_{K^{\pm}}}$ , so $W(H)$ is an index-two subgroup of each of $W(K^{\pm})$ and hence normal. It follows $W(H)$ is also normal in $\Xi$ , and we will be particularly interested in the quotient group $\Xi/W(H)$ . Note that the involutions ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}w_{\pm}}\in W(K^{\pm})/W(H)\cong\mathbb Z/2$ also generate $\Xi/W(H)$ , so the latter must be a dihedral group. Because we will be considering functions on the Lie algebra ${\mathfrak{s}}$ , in the rest of this section, cohomology will take real or complex coefficients.

Definition 5.5.

For a compact, disconnected Lie group $\Gamma$ with maximal torus $T$ , we continue to define its Weyl group $W(\Gamma)$ as $N_{\Gamma}(T)/Z_{\Gamma}(T)$ .⁴⁴4 We note that this is not the only definition used in the literature, and does not agree with the common definition invoking a Cartan subgroup as per Segal [Seg68, Def. 1.1][BtD85, SSIV.4].

It is easy to see every component of $\Gamma$ contains some element of $N_{\Gamma}(T)$ , and such elements in the same component differ by an element of $N_{\Gamma_{0}}(T)$ , so there is a well defined action of $\pi_{0}\Gamma$ on the fixed point set $\mathbb R[{\mathfrak{t}}]^{W(\Gamma_{0})}$ and one has

\smash{H^{*}(B\Gamma;\mathbb R)\cong H^{*}(B\Gamma_{0};\mathbb R)^{\pi_{0}\Gamma}\cong\big{(}\mathbb R[{\mathfrak{t}}]^{W(\Gamma_{0})}\big{)}\mspace{-2.0mu}{}^{\pi_{0}\Gamma}=\mathbb R[{\mathfrak{t}}]^{W(\Gamma)}}

as in the connected case.

Lemma 5.6.

The action of the dihedral group $\Xi/W(H)$ on $H^{*}(BH;\mathbb R)=\mathbb R[{\mathfrak{s}}]^{W(H)}$ is effective.

Proof.

We show any element ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}c_{g}}\mspace{-2.0mu}\colon s\mapsto gsg^{-1}$ of $\Xi$ that fixes $\mathbb R[{\mathfrak{s}}]^{W(H)}$ pointwise is already in $W(H)$ . If ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}\Ups}$ is the subgroup of $\Xi$ generated by $W(H)$ and $c_{g}$ , then clearly

\mathbb R[{\mathfrak{s}}]^{\Ups}=\mathbb R[{\mathfrak{s}}]^{W(H)}.

(5.2)

By Molien’s theorem [Kan01, SS17-3], given any action of a finite group $\Gamma$ on a real vector space $V$ , the Poincaré series in $t$ of $\mathbb R[V]^{\Gamma}$ is a polynomial in the variable $(1-t)^{-1}$ with leading coefficient $1/|\Gamma|$ . In our case, this shows $|\Ups|=|W(H)|$ , so $c_{g}$ is in $W(H)$ as claimed. ∎

Remark 5.7.

Assume that $G$ is connected and $M$ smooth and equipped with a $G$ -invariant Riemannian metric and a complete geodesic ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}\gamma}$ in $M$ meeting each orbit orthogonally. The Weyl group of $\gamma$ is defined [PT87, SS4][AA93, SS5] to be ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}W(\gamma)}\coloneqq N_{G}(\gamma)/Z_{G}(\gamma)$ , where ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}N_{G}(\gamma)}<G$ is the setwise stabilizer of $\gamma$ and ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}Z_{G}(\gamma)}$ the pointwise. The account of Alekseevsky–Alekseevsky [AA93, SS4,5] shows $G$ acts transitively on the set of such $\gamma$ , so we may assume $\gamma$ passes through $(0,1H)\in(-1,1)\times G/H\subsetneq M$ ; it can also be shown $H$ is the common stabilizer of all points of $\gamma$ in $(-1,1)\times G/H$ , so $W(\gamma)=N_{G}(\gamma)/H$ , and it follows $\gamma$ passes through $(\pm 1,1K^{\pm})\in\{\pm 1\}\times G/K^{\pm}$ as well. Further, there are unique involutions ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}\sigma_{\pm}}\in N_{K^{\pm}}(H)/H$ acting antipodally on the spheres $K^{\pm}/H$ and generating $W(\gamma)$ as a dihedral subgroup of $N_{G}(H)/H$ .

One might hope from this account that the groups $W(\gamma)$ and $\Xi/W(H)$ are isomorphic, but they are typically not, as we will see in Example˜5.15. There is at least a homomorphism from the one to the other, which is an isomorphism if $\operatorname{rk}G=\operatorname{rk}S$ . To construct it, observe first that since all maximal tori in $H$ are conjugate, for any $g\in N_{G}(H)$ there exists an ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}h_{g}}\in H$ such that $gh_{g}\in N_{G}(S)$ , and this specification uniquely determines the left coset $h_{g}N_{H}(S)$ , defining a homomorphism $g\longmapsto gh_{g}N_{H}(S)$ from $N_{G}(H)\longrightarrow\big{(}N_{G}(S)\cap N_{G}(H)\big{)}/N_{H}(S)$ ; to see multiplicativity, note that for given $gH,g^{\prime}H\in N_{G}(H)/H$ , we may make the choice $h_{gg^{\prime}}=(g^{\prime})^{-1}h_{g}g^{\prime}h_{g^{\prime}}$ . It is not hard to see the kernel is $H$ , so there is an induced monomorphism

	$\displaystyle{\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}\psi}\colon\frac{N_{G}(H)}{H}$	$\displaystyle\mathrel{\leavevmode\hbox to23.05pt{\vbox to9.73pt{\pgfpicture\makeatletter\hbox{\thinspace\lower-4.86601pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{}{{}}{} {{}{}}{}{}{}{{{}{}}}{{}}{}{}{{{}{}}}{{}}{}{}{}{}{{}}{}{}{}{{}}\pgfsys@moveto{2.07999pt}{0.0pt}\pgfsys@lineto{21.98894pt}{0.0pt}\pgfsys@stroke\pgfsys@invoke{ }{{}{{}}{}{}{{}}{{{}}{{{}}{\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{-1.0}{0.0}{0.0}{-1.0}{2.27998pt}{0.0pt}\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope}}{{}}}}{{}{{}}{}{}{{}}{{{}}{{{}}{\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{22.18893pt}{0.0pt}\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope}}{{}}}}\hbox{\hbox{\hbox{{\pgfsys@beginscope\pgfsys@invoke{ }{{}{}{{ {}{}}}{ {}{}} {{}{{}}}{{}{}}{}{{}{}} { }{{{{}}\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{11.19446pt}{-1.533pt}\pgfsys@invoke{ }\hbox{{\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\hbox{{\hbox{$\scriptstyle$}}} }}\pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope}}}\hbox{{\pgfsys@beginscope\pgfsys@invoke{ }{{}{}{{ {}{}}}{ {}{}} {{}{{}}}{{}{}}{}{{}{}} { }{{{{}}\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@transformcm{1.0}{0.0}{0.0}{1.0}{3.0pt}{1.533pt}\pgfsys@invoke{ }\hbox{{\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\hbox{{\hbox{$\scriptstyle\ \ \ \ $}}} }}\pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope}}} \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}\frac{N_{G}(S)\cap N_{G}(H)}{N_{H}(S)},$
	$\displaystyle gH$	$\displaystyle\longmapsto gh_{g}N_{H}(S).$

Following with the map ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}c}\colon\big{(}N_{G}(S)\cap N_{G}(H)\big{)}/N_{H}(S)\longrightarrow N_{\operatorname{Aut}S}\big{(}W(H)\big{)}/W(H)$ sending $g$ to conjugation of $S$ by $g$ , we obtain a map $N_{G}(H)/H\longrightarrow N_{\operatorname{Aut}S}\big{(}W(H)\big{)}/W(H)$ . When restricted to $N_{K^{\pm}}(H)/H$ , this $c\circ\psi$ takes values in $W(K^{\pm})/W(H)$ , so there is a restricted map ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}\overline{\psi}}\colon W(\gamma)\longrightarrow\Xi/W(H)$ as claimed. When $\operatorname{rk}G=\operatorname{rk}S$ , the map $c$ is injective, so $\overline{\psi}(\sigma_{\pm})=w_{\pm}$ and $\overline{\psi}$ is an isomorphism.

We henceforth write ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}D_{2k}}$ for the dihedral group $\Xi/W(H)$ , where ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}k}$ is the order of $w_{+}w_{-}$ . Our remaining goal is the following.

\Heven

This will follow from an analysis of the action of ${D_{2k}}$ on $H^{*}_{H}$ .

Lemma 5.8.

Let $E$ be a complex representation of $D_{2k}=\langle w_{-},w_{+}\mid w_{-}^{2},w_{+}^{2},(w_{+}w_{-})^{k}\rangle$ . Set ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}r}\coloneqq w_{+}w_{-}$ and ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}s}\coloneqq w_{+}$ so that $sr=w_{-}$ . Write ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}\zeta}$ for the root of unity $e^{2\pi i/k}$ and ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}E_{\ell}}$ for the $\zeta^{\ell}$ -eigenspace of $r$ .

•

The transformations $w_{-}$ and $w_{+}$ agree on $E_{0}$ and are opposite on $E_{k/2}$ if $k$ is even.
•

Both $w_{-}$ and $w_{+}$ exchange each $E_{\ell}$ with $E_{-\ell}$ .

Proof.

Multiplying the relation $\operatorname{id}=rr^{-1}$ on the left by $w_{+}$ yields the key equation

\phantom{E_{\ell}}\quad w_{+}=w_{-}r^{-1}=\zeta^{-\ell}w_{-}\quad\mbox{on}\ E_{\ell}.

(5.3)

•

The $\ell=0$ and $\ell=k/2$ cases of (5.3) show $w_{-}=w_{+}$ on $E_{0}$ and $w_{-}=-w_{+}$ on $E_{k/2}$ .
•

Since $rw_{-}=w_{+}w_{-}^{2}=w_{+}$ , (5.3) gives $rw_{-}v=w_{+}v=\zeta^{-\ell}w_{-}v$ for $v\in E_{\ell}$ . On the other hand, multiplying (5.3) on the left by $r$ yields $rw_{+}v=\zeta^{-\ell}rw_{-}v=\zeta^{-\ell}w_{+}v.$ ∎

From now on, we specialize Lemma˜5.8 to the case $E={\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}H^{*}_{H}}=H^{*}(BH;\mathbb C)$ . We write also ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}E_{\ell}^{m}}\coloneqq E_{\ell}\cap H_{H}^{m}$ .

Lemma 5.9.

There exist $\smash{{\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}p_{\pm}}\in H^{2n_{\pm}}_{H}}$ such that $w_{\pm}p_{\pm}=-p_{\pm}$ and $H^{*}_{H}=H^{*}_{K^{\pm}}\mathbin{\raisebox{0.85pt}{$\displaystyle\oplus$}}p_{\pm}H^{*}_{K^{\pm}}$ .

Proof.

Note that since $H^{*}_{K^{\pm}}=(H^{*}_{H})^{\langle w_{\pm}\rangle}$ , the $1$ -eigenspace of $w_{\pm}$ is $H^{*}_{K^{\pm}}$ . Recall that Proposition˜4.7 gives a $H^{*}_{K^{\pm}}$ -basis $\{1,e_{\pm}\}$ for $H^{*}_{H}$ ; now $p_{\pm}\coloneqq(e_{\pm}-w_{\pm}e_{\pm})/2$ is a $-1$ -eigenvector for $w_{\pm}$ and $\{1,p_{\pm}\}$ is another $H^{*}_{K^{\pm}}$ -module basis for $H^{*}_{H}$ . ∎

Let us now consider the $r$ -eigenspace decompositions $p_{\pm}=\sum{\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}q^{\pm}_{\ell}}$ where $q^{\pm}_{\ell}\in E_{\ell}$ for $\ell\in\mathbb Z/k$ . Since the $w_{\pm}$ interchange $E_{\ell}$ with $E_{-\ell}$ by Lemma˜5.8, one finds $q^{\pm}_{-\ell}=-w_{\pm}q^{\pm}_{\ell}$ , and specifically that $w_{\pm}q_{0}^{\pm}=-q_{0}^{\pm}$ , and if $k$ is even, $w_{\pm}q^{\pm}_{k/2}=-q^{\pm}_{k/2}$ . All told, the decomposition is

p_{\pm}=q^{\pm}_{0}+\sum_{0\mspace{1.0mu}<\mspace{1.0mu}\ell\mspace{1.0mu}<\mspace{1.0mu}k/2}(q^{\pm}_{\ell}-w_{\pm}q^{\pm}_{\ell})+q^{\pm}_{k/2},

(5.4)

where the last term is taken to be zero if $k$ is odd.

Lemma 5.10.

In (5.4) only one term is non-zero. Explicitly, the elements $p_{\pm}$ each lie either in $E_{0}$ , in $E_{k/2}$ , or in $E_{\ell}\mathbin{\raisebox{0.85pt}{$\displaystyle\oplus$}}E_{-\ell}$ for $0<\ell<k/2$ .

Proof.

Each of terms $q^{\pm}_{0}$ , $q^{\pm}_{k/2}$ , and $q^{\pm}_{\ell}-w_{\pm}q^{\pm}_{\ell}$ in (5.4) lies in the $-1$ -eigenspace of $w_{\pm}$ on $H_{H}^{2n_{\pm}}$ , but by Lemma˜5.9 this is the one-dimensional $\mathbb Cp_{\pm}$ , which meets at most one of $E_{0}$ , $E_{k/2}$ , and $E_{\ell}\mathbin{\raisebox{0.85pt}{$\displaystyle\oplus$}}E_{-\ell}$ nontrivially. ∎

Lemma 5.11.

Exactly one of the following cases obtains:

(i)

$k=1$ and $n_{+}=n_{-}\eqqcolon{\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}n}$ , and one can rescale $p_{\pm}$ in such a way that $p_{+}=p_{-}\in E_{0}^{2n}$ .
(ii)

$k=2$ and $p_{\pm}\in E_{1}$ .
(iii)

$k\geq 2$ and $n_{+}=n_{-}\eqqcolon{\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}n}$ , and there is one $j$ relatively prime to $k$ such that $0<j<k/2$ and up to rescaling,

$p_{\pm}=q-w_{\pm}q$

for the same single element ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}q}\in E_{j}^{2n}$ . Moreover, $\dim E_{j}^{2n}=\dim E_{-j}^{2n}=1$ .

Proof.

This is a case analysis following Lemma˜5.10.

(i) The case one of $p_{\pm}$ lies in $E_{0}$

Suppose $p_{+}\in E_{0}$ and, for a contradiction, suppose $m$ is minimal such that there exists a nonzero $x\in E_{\ell}^{m}$ for some $\ell$ indivisible by $k$ . Then $x-w_{+}x$ is a $-1$ -eigenvector of $w_{+}$ , hence divisible by $p_{+}$ by Lemma˜5.9. We must have $x=w_{+}x$ for otherwise the component of $(x-w_{+}x)/p_{+}$ in $\smash{E_{\ell}^{m-2n_{+}}}$ would contradict minimality of $m$ . Thus $x\in E_{k/2}$ by Lemma˜5.8, so $w_{-}x=-w_{+}x=-x$ by Lemma˜5.8 and $p_{-}$ divides $x$ by Lemma˜5.9. It follows, again lest we contradict minimality of $m$ , that $x/p_{-}\in E_{0}$ and so $p_{-}\in E_{k/2}$ . But then, by Lemma˜5.8 again, $w_{-}p_{+}=w_{+}p_{+}=-p_{+}$ so $p_{-}$ divides $p_{+}$ by Lemma˜5.9 and we have

w_{+}\Big{(}\frac{p_{+}}{p_{-}}\Big{)}=\frac{w_{+}p_{+}}{w_{+}p_{-}}=\frac{-p_{+}}{-w_{-}p_{-}}=-\frac{p_{+}}{p_{-}},

contradicting the fact $p_{+}$ has minimal degree in the $-1$ -eigenspace of $w_{+}$ . Thus in fact $H^{*}_{H}=E_{0}$ . Since $r$ then acts trivially but Lemma˜5.6 states the action of $D_{2k}$ is effective, it follows $k=1$ . By Lemma˜5.8 the actions of $w_{-}$ and $w_{+}$ agree on $E_{0}$ , so the $w_{\pm}$ -eigenspace decompositions of $H^{*}_{H}$ in Lemma˜5.9 coincide and by rescaling we may assume $p_{-}=p_{+}$ .

(ii) The case one of $p_{\pm}$ lies in $E_{k/2}$

If $p_{+}\in E_{k/2}$ , then in fact $H^{*}_{H}=E_{0}\mathbin{\raisebox{0.85pt}{$\displaystyle\oplus$}}E_{k/2}$ , for we could otherwise produce from any nonzero homogeneous $x\in E_{\ell}$ , where $k/2$ does not divide $\ell$ , an element $(x-w_{+}x)/p_{+}$ of smaller degree with a nonzero component in $E_{\ell-k/2}$ . It follows $r^{2}$ acts as the identity on $H^{*}_{H}$ , and since the action of $D_{2k}$ is effective by Lemma˜5.6, we have $k=2$ and $p_{+}\in E_{1}$ . As for $p_{-}$ , consulting Lemma˜5.10, it must lie in $E_{0}$ or $E_{1}$ , but if it lay in $E_{0}$ we would be in the previous case.

(iii) The case $p_{\pm}$ both lie in $E_{j^{\pm}}\mathbin{\raisebox{0.85pt}{$\displaystyle\oplus$}}E_{-j^{\pm}}$ for some $j^{\pm}$ with $0<j^{\pm}<k/2$

We first note that $n_{+}=n_{-}$ , for if we had, say, $n_{+}>n_{-}$ , then by Lemma˜5.9, $w_{+}$ would act as the identity on $\smash{H^{2n_{-}}_{H}}$ ; but this would imply $\smash{p_{-}=q_{j^{-}}-w_{-}q_{j^{-}}}$ is equal to $\smash{w_{+}p_{-}=w_{+}q_{j^{-}}-\zeta^{j^{-}}q_{j^{-}}}$ , which could only happen if $\zeta^{j^{-}}=-1$ and $j^{-}\equiv k/2\allowbreak\mkern 8.0mu({\operator@font mod}\mkern 6.0muk)$ .

Next we claim $j^{+}=j^{-}$ . As already mentioned, the $-1$ -eigenspace of $w_{+}$ in $H^{2n}_{H}$ is $\mathbb Cp_{+}$ , which lies in $E_{j^{+}}\mathbin{\raisebox{0.85pt}{$\displaystyle\oplus$}}E_{-j^{+}}$ Since the $\pm 1$ -eigenspaces of $w_{+}$ on $E_{\ell}^{2n}\mathbin{\raisebox{0.85pt}{$\displaystyle\oplus$}}E_{-\ell}^{2n}$ are $\{x\pm w_{+}x:x\in E_{\ell}^{2n}\}$ and hence both are of dimension $\dim E_{\ell}^{2n}$ , but the $-1$ -eigenspace is trivial except for $\ell=j^{-}$ , it follows all the other terms in $\bigoplus_{0<\ell<k/2}(E_{\ell}^{2n}\mathbin{\raisebox{0.85pt}{$\displaystyle\oplus$}}E_{-\ell}^{2n})$ are zero, so $j^{+}=j^{-}\eqqcolon{\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}j}$ and $\dim E_{j}^{2n}=\dim E_{-j}^{2n}=1$ . Thus we may rescale to take $q_{-}=q_{+}$ as claimed.

To see that $j$ and $k$ are coprime, first note that $H^{*}_{H}=\sum_{i}E_{i\cdot\gcd(j,k)}$ , for given a putative nonzero homogeneous element $x\in E_{\ell}$ such that $\gcd(j,k)$ does not divide $\ell$ , the component of $(x-w_{+}x)/p_{+}$ in $E_{\ell-j}$ would be nonzero of smaller degree. Thus $r^{k/\!\gcd(j,k)}\in D_{2k}$ acts trivially on $H^{*}_{H}$ , and since the $D_{2k}$ -action is effective by Lemma˜5.6, it follows $\gcd(j,k)=1$ . ∎

Lemma 5.12.

The elements $p_{\pm}$ are prime elements of $H^{*}_{H}$ .

Proof.

Recall from Remark˜4.8 that the basis element $e$ from Proposition˜4.7 may be taken $\pi_{0}H$ -invariant. Thus the same holds of the eigenvectors $p_{\pm}=(e_{\pm}-w_{\pm}e_{\pm})/2$ defined in Lemma˜5.9. It is clear in $H^{*}_{H_{0}}$ that $p_{\pm}$ are irreducible, for all elements of lesser degree lie in the $1$ -eigenspace $\smash{H\mspace{-1.0mu}\begin{subarray}{c}*\phantom{k}\\ K_{0}^{\pm}\end{subarray}}$ . Since $H^{*}_{H_{0}}$ is a polynomial ring, the principal ideals $(p_{\pm})$ are prime. In fact, the ideals $(p_{\pm})$ are prime in $H^{*}_{H}$ as well, for given $x,y\in H^{*}_{H}$ such that $xy\in(p_{\pm})$ , we know one of the two, say $x$ , is divisible by $p_{\pm}$ in $H^{*}_{H_{0}}$ . But then as $x/p_{\pm}$ is $\pi_{0}H$ -invariant as well, $x$ is also divisible by $p_{\pm}$ in $H^{*}_{H}$ . ∎

Lemma 5.13.

Write ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}V}$ for the joint $-1$ -eigenspace of $w_{\pm}$ . Then

V\longrightarrow\frac{E_{0}}{(H^{*}_{K^{-}}+H^{*}_{K^{+}})\cap E_{0}}\longrightarrow\frac{H^{*}_{H}}{H^{*}_{K^{-}}+H^{*}_{K^{+}}}

are isomorphisms.

All unelaborated claims in the proof are clauses of Lemma˜5.8.

Proof.

Write ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}E_{\neq 0}}\coloneqq\bigoplus_{\ell=1}^{k-1}E_{\ell}$ so that we have a direct sum decomposition $H^{*}_{H}=E_{0}\mathbin{\raisebox{0.85pt}{$\displaystyle\oplus$}}E_{\neq 0}$ . This decomposition is invariant under $w_{\pm}$ , so $H^{*}_{K^{\pm}}$ inherit such decompositions and

H^{*}_{K^{-}}+H^{*}_{K^{+}}=\big{(}[H^{*}_{K^{-}}\cap E_{0}]+[H^{*}_{K^{+}}\cap E_{0}]\big{)}\mathbin{\raisebox{0.85pt}{$\displaystyle\oplus$}}\big{(}[H^{*}_{K^{-}}\cap E_{\neq 0}]+[H^{*}_{K^{+}}\cap E_{\neq 0}]\big{)}.

Because $w_{+}|_{E_{0}}=w_{-}|_{E_{0}}$ , the first direct summand is the common $1$ -eigenspace of $w_{\pm}$ on $E_{0}$ , whose complement is $V$ . We will be done if we can show the second summand is all of $E_{\neq 0}$ .

•

If $k$ is even, $r=w_{+}w_{-}$ acts on $E_{k/2}$ as multiplication by $\zeta^{k/2}=-1$ , so $w_{+}|_{E_{k/2}}=-w_{-}|_{E_{k/2}}$ . Thus $E_{k/2}$ decomposes as the sum of the $1$ -eigenspace $H^{*}_{K^{+}}\cap E_{k/2}$ of $w_{+}$ on $E_{k/2}$ and its $-1$ -eigenspace, which is $H^{*}_{K^{-}}\cap E_{k/2}$ .
•

If $0<\ell<k/2$ , then since $r$ acts as $\zeta^{\ell}\neq\pm 1$ on $E_{\ell}$ , we have $w_{+}v\neq w_{-}v$ for nonzero $v\in E_{\ell}$ , so for nonzero $u,v\in E_{\ell}$ , we cannot have $u+w_{+}u=v+w_{-}v$ in $E_{\ell}\mathbin{\raisebox{0.85pt}{$\displaystyle\oplus$}}E_{-\ell}$ . Thus the $1$ -eigenspaces $(\operatorname{id}+w_{\pm})E_{\ell}$ of $w_{\pm}$ are disjoint, and since $\dim E_{\ell}^{m}=\dim E_{-\ell}^{m}$ for all $m\geq 0$ , their sum is all of $E_{\ell}\mathbin{\raisebox{0.85pt}{$\displaystyle\oplus$}}E_{-\ell}$ .∎

We are now finally in a position to prove Proposition 1.

Proof of Proposition 1.

We proceed through the trichotomy of Lemma˜5.11, in each case applying Section˜3.2.

(i) The case $p=p_{+}=p_{-}\in E_{0}^{2n}$ and $H^{*}_{H}=E_{0}$

In this case the actions of $w_{\pm}$ coincide by Lemma˜5.8, so the images ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}{H^{*}_{K}}}$ of the injections $H^{*}_{K^{\pm}}\xhookrightarrow{\ \ \ \ }H^{*}_{H}$ agree. Thus

	$\displaystyle H_{G}^{\mathrm{even}}M$	$\displaystyle=H^{}_{K^{-}}\cap H^{}_{K^{+}}={H^{*}_{K}};$
	$\displaystyle H_{G}^{\mathrm{odd}}M$	$\displaystyle=\frac{{H^{}_{K}}\mathbin{\raisebox{0.85pt}{$\displaystyle\oplus$}}p{H^{}_{K}}}{{H^{}_{K}}}[1]\cong p{H^{}_{K}}[1]\cong{H^{*}_{K}}[2n+1].$

(ii) The case $k=2$ and $H^{*}_{H}=E_{0}\mathbin{\raisebox{0.85pt}{$\displaystyle\oplus$}}E_{1}$ and $p_{\pm}\in E_{1}$ .

We show $V=p_{+}p_{-}\cdot(H^{*}_{K^{-}}\cap H^{*}_{K^{+}})$ and apply Lemma˜5.13; since $\deg p_{+}p_{-}=2n_{-}+2n_{+}$ , the result will then follow from Section˜3.2. Suppose $x$ lies in $V$ . From Lemma˜5.9 we know $x$ is divisible by both $p_{-}$ and $p_{+}$ . Note that $w_{\mp}p_{\pm}=\zeta^{-k/2}w_{\pm}p_{\pm}=p_{\pm}$ by Lemma˜5.8. As $w_{-}$ sends $x/p_{+}$ to $w_{-}x/w_{-}p_{+}=-(x/p_{+})$ , we see $p_{-}$ divides the latter as well. The quotient $w_{\pm}(x/p_{+}p_{-})=-x/{-p_{+}p}_{-}=x/p_{+}p_{-}$ is in the joint $1$ -eigenspace $H^{*}_{K^{-}}\cap H^{*}_{K^{+}}$ .

(iii) The case $p_{\pm}=q-w_{\pm}q$ for some $q\in E_{j}^{2n}$ .

We will find an element ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}P}$ of degree $2nk$ such that $V=P\cdot(H^{*}_{K^{-}}\cap H^{*}_{K^{+}})$ and apply Lemma˜5.13. Since $w_{\pm}$ generate all $w\in D_{2k}$ , we have $w\cdot x=\pm x$ for any $x\in V$ . Particularly, $x$ is also divisible by the $wp_{\pm}$ , which we explicitly enumerate. Writing ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}\eta}=\zeta^{j}$ , from Lemma˜5.8 we obtain relations $p_{-}=q-\eta w_{+}q$ and $r(q-\eta^{\ell}w_{+}q)=\eta(q-\eta^{\ell-2}w_{+}q)$ which suffice to show that if we consider elements only up to nonzero complex multiples, the sets

\{wp_{-},wp_{+}:w\in D_{2k}\}\qquad\mbox{and}\qquad\{q-\eta^{\ell}w_{+}q:\ell\in\mathbb Z\}=\{q-\eta^{\ell}w_{-}q:\ell\in\mathbb Z\}

are equal. Since $j$ and $k$ are relatively prime by Lemma˜5.11.(iii), the elements $q-\eta^{\ell}w_{+}q$ for $0\leq\ell<k$ are all distinct elements, none a scalar multiple of any other since their $E_{j}$ -components are equal, and prime by Lemma˜5.12. Since each divides $x$ , their product ${\color[rgb]{.255,.41,.884}\definecolor[named]{pgfstrokecolor}{rgb}{.255,.41,.884}P}$ also divides $x$ . Note that

P=\prod_{\ell=0}^{k-1}(q-\eta^{\ell}w_{\pm}q)=q^{k}-w_{\pm}q^{k}.

But the right-hand side is a $-1$ -eigenvector of $w_{\pm}$ , so $\displaystyle\smash{w_{\pm}\frac{x}{P}=\frac{-x}{-P}=\frac{x}{P}}$ lies in $H^{*}_{K^{-}}\cap H^{*}_{K^{+}}$ . ∎

We now illustrate Section˜1 with some examples.

Example 5.14.

There is a cohomogeneity one action of $G=\mathrm{SU}(3)$ on the sphere $S^{7}$ with isotropy groups $K^{-}={\rm S}\big{(}\mathrm{U}(2)\times\mathrm{U}(1)\big{)}$ , $K^{+}={\rm S}\big{(}\mathrm{U}(1)\times\mathrm{U}(2)\big{)}$ , and $H={\rm S}\big{(}\mathrm{U}(1)\times\mathrm{U}(1)\times\mathrm{U}(1)\big{)}$ [GWZ08, Table E]. Observe that $\operatorname{rk}G=\operatorname{rk}H$ and we have $n_{-}=n_{+}=1$ . Using Remark˜5.7 and the table in Grove et al. [GWZ08], one deduces that $k=3$ . Here $H^{*}_{H}$ is just the quotient ring $\mathbb Q[t_{1},t_{2},t_{3}]/(t_{1}+t_{2}+t_{3})$ , which admits a natural $\Sigma_{3}$ -action permuting the generators $t_{j}$ . Within $H^{*}_{H}$ we have $H^{*}_{K^{-}}=(H^{*}_{H})^{\langle(1\ 2)\rangle}$ and $H^{*}_{K^{+}}=(H^{*}_{H})^{\langle(2\ 3)\rangle}$ , whose intersection is $(H^{*}_{H})^{\Sigma_{3}}\cong H^{*}_{\mathrm{SU}(3)}$ . Section˜1 implies

H^{*}_{\mathrm{SU}(3)}S^{7}=H^{*}_{\mathrm{SU}(3)}\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}S^{7}.

This is in fact a known result, being equivalent to the equivariant formality of the action [GM14, Cor. 1.3] since there is only one possible graded $H^{*}_{\mathrm{SU}(3)}$ -algebra structure for a free graded $H^{*}_{\mathrm{SU}(3)}$ -module on generators of degrees $0$ and $7$ .

Similar calculations can be made for any of the last five examples in Grove et al. [GWZ08, Table E]. Note that they are all equivariantly formal actions. This is not the case in the next example.

Example 5.15.

The left action of $\mathrm{SU}(3)$ on itself given by $(A,B)\longmapsto ABA^{\top}$ has cohomogeneity one [Pütt09, Example 5.5]. One can see that relative to the canonical metric on $\mathrm{SU}(3)$ , there is a transversal geodesic segment joining the two singular orbits, along which the isotropies are $K^{+}=\mathrm{SO}(3)$ , $K^{-}=\mathrm{SU}(2)\times\{1\}$ , and $H=\mathrm{SO}(2)\times\{1\}$ . The Weyl group $W(\gamma)$ turns out to be $D_{4}$ , but the induced symmetry group $\Xi/W(H)$ is just $\operatorname{Aut}\mathrm{SO}(2)=D_{2}$ , so we are in the case $k=1$ . If we write $x$ for a generator of $H^{*}_{\mathrm{SO}(2)}=\mathbb Q[x]$ , then the canonical maps send $H^{*}_{\mathrm{SO}(3)}$ and $H^{*}_{\mathrm{SU}(2)}$ both isomorphically to $\mathbb Q[x^{2}]$ . Since $n_{-}=n_{+}=1$ , one concludes

H^{*}_{\mathrm{SU}(3)}\mathrm{SU}(3)\cong\mathbb Q[x^{2}]\operatorname*{\mathchoice{\raisebox{0.85pt}{$\displaystyle\otimes$}}{\raisebox{0.85pt}{$\otimes$}}{\raisebox{0.7pt}{$\scriptstyle\otimes$}}{\raisebox{0.2pt}{$\scriptscriptstyle\otimes$}}}H^{*}S^{3}.

Remark 5.16.

Again, as in Remark˜5.1, one can deduce directly that for $K^{\pm}$ and $H$ as in Section˜1, $H^{*}_{G}M$ is Cohen–Macaulay as an ${H^{*}_{G}}$ -module. This time, one notices that the equivariant cohomology is the direct sum of two copies of $H^{*}_{K^{+}}\cap H^{*}_{K^{-}}=(H^{*}_{H})^{D_{2k}}$ , the latter being a $H^{*}_{G}$ -algebra which is finitely generated as an ${H^{*}_{G}}$ -module and Cohen–Macaulay as a ring.

Remark 5.17.

When $\operatorname{rk}G$ is also equal to $\operatorname{rk}H$ , the $G$ -action is equivariantly formal. In this case $M$ is odd-dimensional and the situation is particularly nice because the restricted action of a maximal torus of $G$ is of GKM type in a sense recently defined by the third author [He16, Example 4.17].

References

[AA93] Andrey V. Alekseevsky and Dmitry V. Alekseevsky. Riemannian $G$ -manifold with one-dimensional orbit space. Ann. Global Anal. Geom., 11(3):197–211, 1993. http://link.springer.com/article/10.1007/BF00773366.
[Bes87] Arthur Besse. Einstein manifolds, volume 10 of Ergebnisse der Mathematik und ihrer Grenzgebiete, 3. Folge. Springer, 1987.
[Bor53] Armand Borel. Sur la cohomologie des espaces fibrés principaux et des espaces homogènes de groupes de Lie compacts. Ann. of Math. (2), 57(1):115–207, 1953. http://jstor.org/stable/1969728.
[Bre61] Glen E. Bredon. On homogeneous cohomology spheres. Ann. of Math., pages 556–565, 1961. http://jstor.org/stable/1970317.
[BtD85] Theodor Bröcker and Tammo tom Dieck. Representations of compact Lie groups, volume 98 of Grad. Texts in Math. Springer, 1985.
[Car18] Jeffrey D. Carlson. The equivariant K-theory of a cohomogeneity-one action. 2018. arXiv:1805.00502.
[CK11] Suyoung Choi and Shintarô Kuroki. Topological classification of torus manifolds which have codimension one extended actions. Algebr. Geom. Top., 11(5):2655–2679, 2011. http://projecteuclid.org/euclid.agt/1513715302, arXiv:0906.1335.
[EU11] Christine M. Escher and Shari K. Ultman. Topological structure of candidates for positive curvature. Topology Appl., 158(1):38–51, 2011. doi:10.1016/j.topol.2010.10.001.
[GGS11] Fernando Galaz-García and Catherine Searle. Cohomogeneity one Alexandrov spaces. Transform. Groups, 16(1):91–107, 2011. arXiv:0910.5207.
[GGZ15] Fernando Galaz-García and Masoumeh Zarei. Cohomogeneity one topological manifolds revisited. Math. Z., 2015. URL: http://link.springer.com/article/10.1007/s00209-017-1915-y, arXiv:1503.09068.
[GM14] Oliver Goertsches and Augustin-Liviu Mare. Equivariant cohomology of cohomogeneity one actions. Topology Appl., 167:36–52, 2014. arXiv:1110.6318.
[GM17] Oliver Goertsches and Augustin-Liviu Mare. Equivariant cohomology of cohomogeneity-one actions: The topological case. Topology Appl., 2017. arXiv:1609.07316.
[GrH87] Karsten Grove and Stephen Halperin. Dupin hypersurfaces, group actions and the double mapping cylinder. J. Differential Geom., 26(3):429–459, 1987. doi:10.4310/jdg/1214441486.
[GWZ08] Karsten Grove, Burkhard Wilking, and Wolfgang Ziller. Positively curved cohomogeneity one manifolds and 3-Sasakian geometry. J. Differential Geom., 78:33–111, 2008. http://projecteuclid.org/euclid.jdg/1197320603.
[Hat02] Allen Hatcher. Algebraic topology. Cambridge Univ. Press, 2002. http://math.cornell.edu/˜hatcher/AT/ATpage.html.
[Hat09] Allen Hatcher. Vector bundles and K-theory. 2009 manuscript. http://math.cornell.edu/˜hatcher/VBKT/VBpage.html.
[He16] Chen He. Localization of certain odd-dimensional manifolds with torus actions. 2016. arXiv:1608.04392.
[Hoel10] Corey A. Hoelscher. On the homology of low-dimensional cohomogeneity one manifolds. Transform. Groups, 15(1):115–133, 2010.
[Kan01] Richard Kane. Reflection groups and invariant theory, volume 5 of C. M. S. Books in Mathematics. Springer, 2001.
[Kur11] Shintarô Kuroki. Classification of torus manifolds with codimension one extended actions. Transf. Groups, 16(2):481–536, Jun 2011. doi:10.1007/s00031-011-9136-7.
[May99] J. Peter May. A concise course in algebraic topology. University of Chicago Press, 1999.
[MiT00] Mamoru Mimura and Hiroshi Toda. Topology of Lie groups, I and II, volume 91 of Transl. Math. Monogr. Amer. Math. Soc., Providence, RI, 2000.
[Most57a] Paul S. Mostert. On a compact Lie group acting on a manifold. Ann. of Math., 65(3):447–455, 1957. http://jstor.org/stable/1970056.
[Most57b] Paul S. Mostert. Errata: On a compact Lie group acting on a manifold. Ann. of Math., 66(3):589, 1957. http://jstor.org/stable/1969911.
[PT87] Richard Palais and Chuu-Lian Terng. A general theory of canonical forms. Trans. Amer. Math. Soc., 300:771–789, 1987. URL: http://ams.org/journals/tran/1987-300-02/S0002-9947-1987-0876478-4/.
[Pütt09] Thomas Püttmann. Cohomogeneity one manifolds and selfmaps of nontrivial degree. Transform. Groups, 14:225–247, 2009. URL: http://link.springer.com/article/10.1007/s00031-008-9037-6, arXiv:0710.3770.
[Sam41] Hans Samelson. Beiträge zur Topologie der Gruppen-Mannigfaltigkeiten. Ann. of Math., 42(1):1091–1137, Jan 1941. http://jstor.org/stable/1970463.
[Seg68] Graeme Segal. The representation-ring of a compact Lie group. Publ. Math. Inst. Hautes Études Sci., 34:113–128, 1968. http://numdam.org/item/PMIHES_1968__34__113_0.

Department of Mathematics, University of Toronto
jcarlson@math.toronto.edu

Fachbereich Mathematik und Informatik, Philipps-Universität Marburg
goertsch@mathematik.uni-marburg.de

Yau Mathematical Sciences Center, Tsinghua University
che@math.tsinghua.edu.cn

Department of Mathematics and Statistics, University of Regina
mareal@math.uregina.ca

The equivariant cohomology ring of a cohomogeneity-one action

Abstract

1. Introduction

2. The Mayer–Vietoris sequence

Proposition 2.1.

Proof.

Remark 2.2.

3. Equivariant cohomology rings

Theorem 3.2 ([Most57a, Thm. 4][Most57b][GGZ15, Thm. A]).

Theorem 3.3 ([GGS11, Thm. A]).

3.1. Mapping tori

Lemma 3.4.

Proof.

3.2. Double mapping cylinders

Proof.

Example 3.5.

Example 3.6.

4. Maps of classifying spaces

Lemma 4.1.

Proof.

Remark 4.2.

Proposition 4.3 (Cf. Goertsches–Mare [GM14, Prop. 3.1][GM17, Prop. 4.2]).

Proof.

Remark 4.4.

Remark 4.5.

Lemma 4.6.

Proof.

Proposition 4.7 ([Bor53, Thm. 26.1(a)][Sam41, p. 1121]).

Proof.

Remark 4.8.

Remark 4.9.

5. Double mapping cylinders which are manifolds

5.1. The case when one of K±/HK^{\pm}/H is odd-dimensional

Proof.

Remark 5.1.

Remark 5.2.

5.2. The case when both of K±/HK^{\pm}/H are even-dimensional

Proof.

Remark 5.3.

Example 5.4.

Definition 5.5.

Lemma 5.6.

Proof.

Remark 5.7.

Lemma 5.8.

Proof.

Lemma 5.9.

Proof.

Lemma 5.10.

Proof.

Lemma 5.11.

Proof.

Lemma 5.12.

Proof.

Lemma 5.13.

Proof.

Proof of Proposition 1.

Example 5.14.

Example 5.15.

Remark 5.16.

Remark 5.17.

References

5.1. The case when one of $K^{\pm}/H$ is odd-dimensional

5.2. The case when both of $K^{\pm}/H$ are even-dimensional