The extreme polygons for the self
Chebyshev radius of the boundary
Abstract.
The paper is devoted to some extremal problems for convex polygons on the Euclidean plane, related to the concept of self Chebyshev radius for the polygon boundary. We consider a general problem of minimization of the perimeter among all -gons with a fixed self Chebyshev radius of the boundary. The main result of the paper is the complete solution of the mentioned problem for : We proved that the quadrilateral of minimum perimeter is a so called magic kite, that verified the corresponding conjecture by Rolf Walter.
2020 Mathematical Subject Classification: 52A10, 52A40, 53A04.
Key words and phrases: approximation by polytopes, convex curve, convex polygon, Chebyshev radius, minimum perimeter, self Chebyshev radius.
1. Introduction and the main result
For a given metric space , we denote by the closed ball with center and radius . If is a nonempty bounded subset of a metric space , then by we denote the diameter of , and by
we denote the Chebyshev radius of . A point for which is called a Chebyshev center of . In general, a Chebyshev center of a set is not unique, and therefore we denote by the set of all Chebyshev centers of a bounded set . The mapping is known as the Chebyshev-center map.
Given a nonempty bounded subset of and a nonempty set , the relative Chebyshev radius (of the set with respect to ) is defined by the formula
In the case , we get the definition of the relative Chebyshev radius of with respect to itself i.e. the self Chebyshev radius of the set :
| (1) |
It is clear that this value depends only on the set and the restriction of the metric to this set, hence it is an intrinsic characteristic of the (bounded) metric space . It has also the following obvious geometric meaning for compact : is the smallest radius of a ball having its center in and covering .
The study of extremal problems for convex curves in the Euclidean plane with a given self Chebyshev radius started with paper [20] by Rolf Walter. In particular, he conjectured that for any closed convex curve in the Euclidean plane, where is the length of and is the Euclidean metric. In [20], this conjecture is proved for the case when is a convex curve of class and all curvature centers of lie in the interior of . It is also shown that the equality in this case holds if and only if is of constant width; for sets of constant width the reader is referred to the monograph [17].
It is also proved in [20] that all -smooth convex curves have good approximations by polygonal chains in terms of the self Chebyshev radius (1). This observation leads to natural extremal problems for convex polygons. In particular, the following result was also proved in [20]. For each triangle in the Euclidean plane, one has with equality exactly for equilateral triangles, where is the boundary of . The proof of this result was simplified by Balestro, Martini, Nikonorova, and one of the present authors in [8], where the authors determined the self Chebyshev radius for the boundary of an arbitrary triangle. Moreover, some related problems were considered in detail in [8]. In particular, the maximal possible perimeter for convex curves and boundaries of convex -gons with a given self Chebyshev radius were found.
As the authors of [8] discovered somewhat later, the original problem from [20], which was to prove the inequality for any closed convex curve in the Euclidean plane, had already been solved many years ago in paper [11] by K.J. Falconer (the results of that paper were formulated in other terms, without using the self Chebyshev radius). An exposition of the corresponding result can also be found in [17, Theorem 4.3.2]. It should be noted that the following stronger result is also proved in [11]. Instead of convexity, it requires the curve to be rectifiable and instead of the plane it is in . Let be a closed rectifiable curve in (with the Euclidean metric) such that for every point on there is a point of at distance at least from . Then has length at least , this value being attained if and only if bounds a plane convex set of constant width .
This paper is devoted to the proof of Rolf Walter’s conjecture in [20] on quadrilaterals of minimum perimeter among all quadrilaterals with a given self Chebyshev radius of their boundaries that is as follows: for any convex quadrilateral with the boundary .
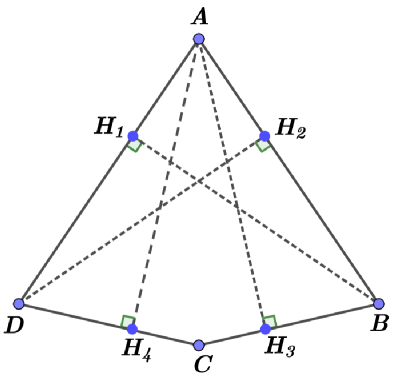
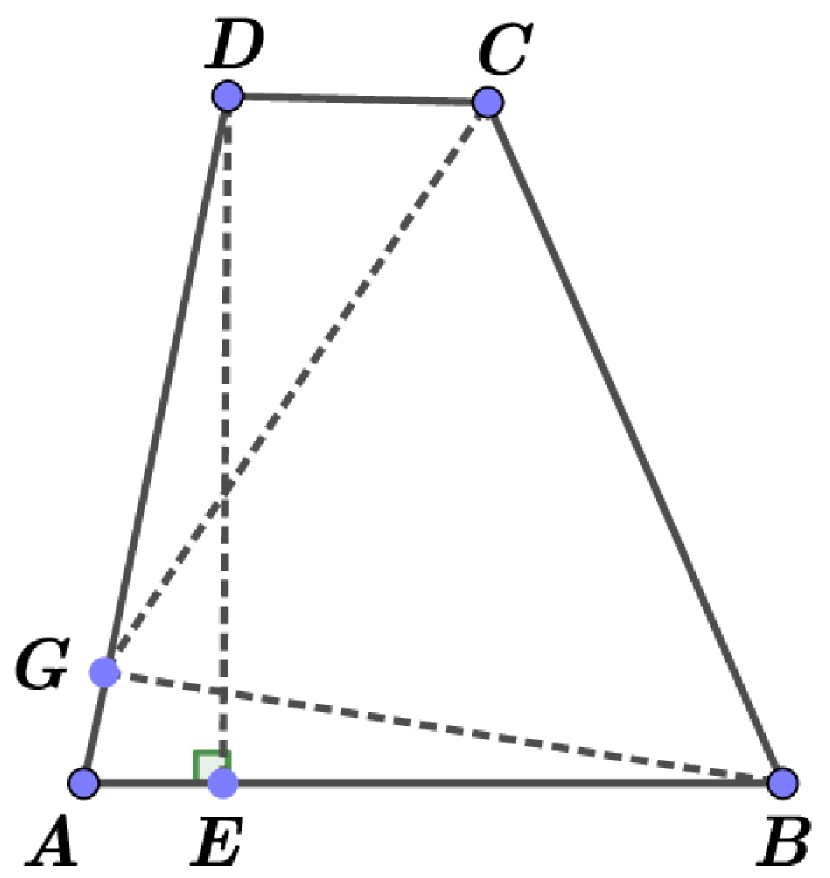
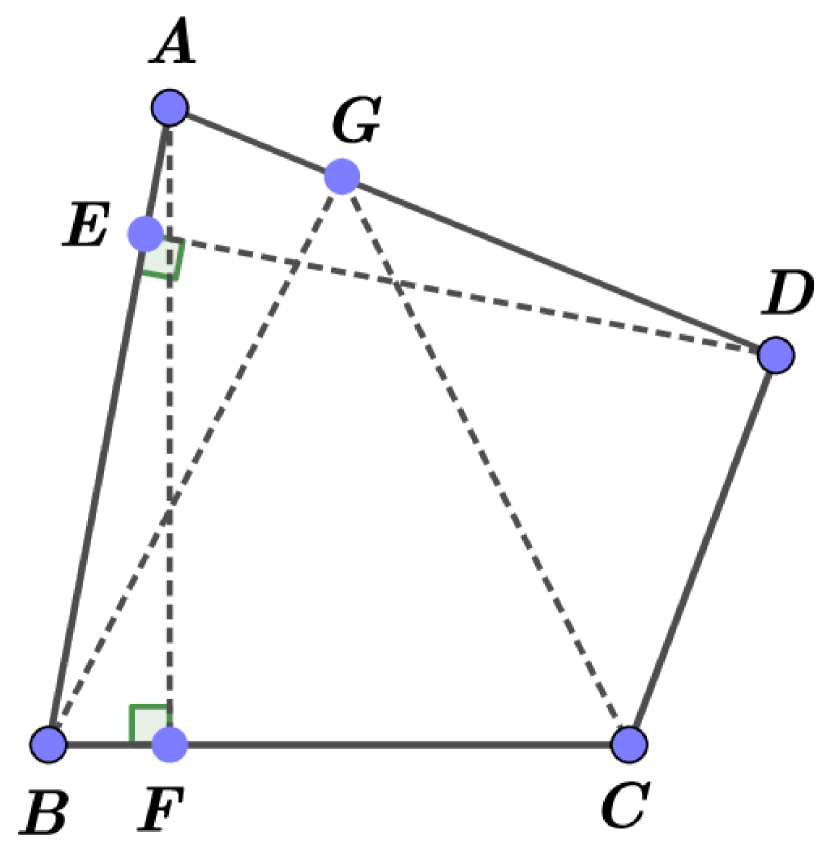
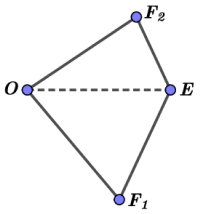
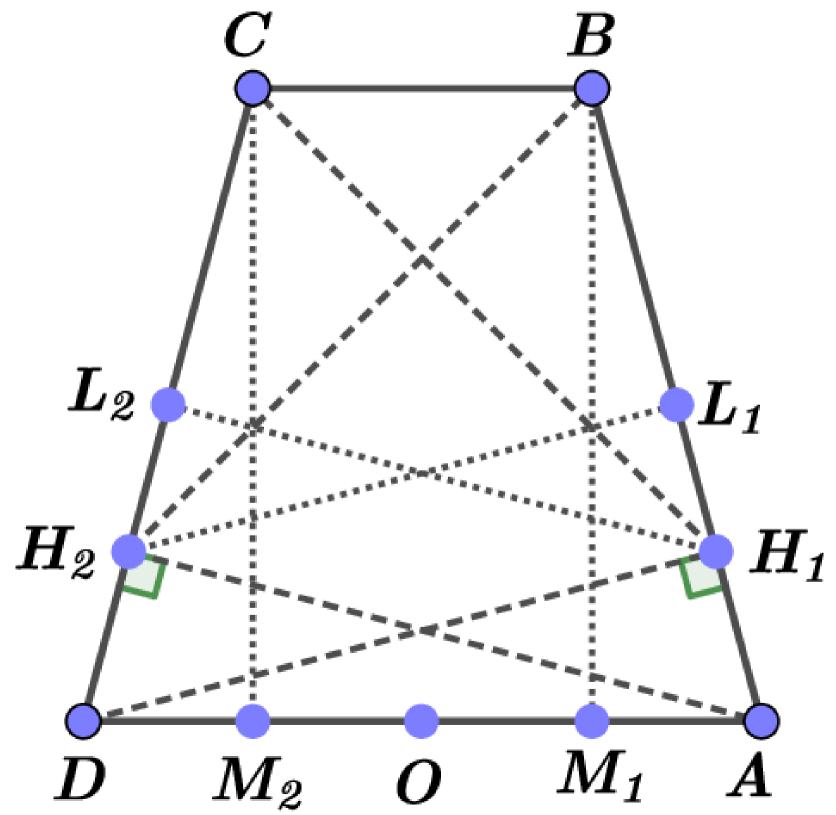
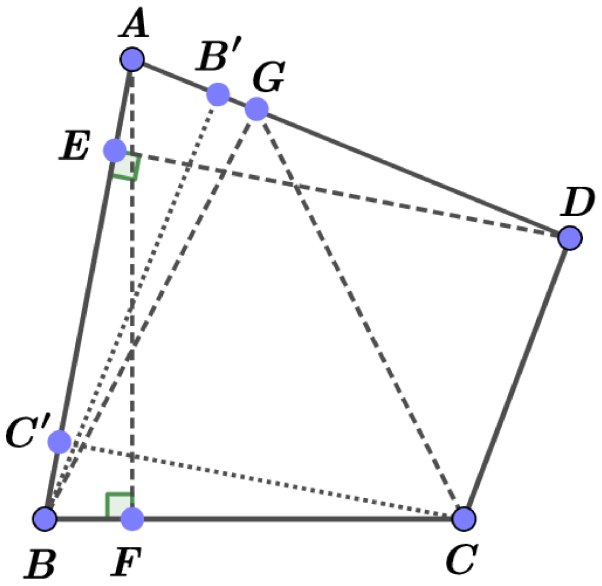
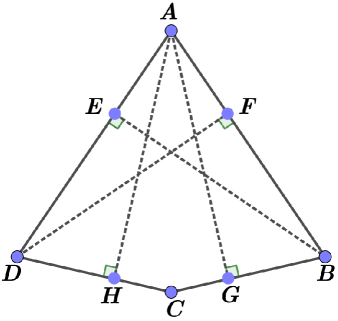
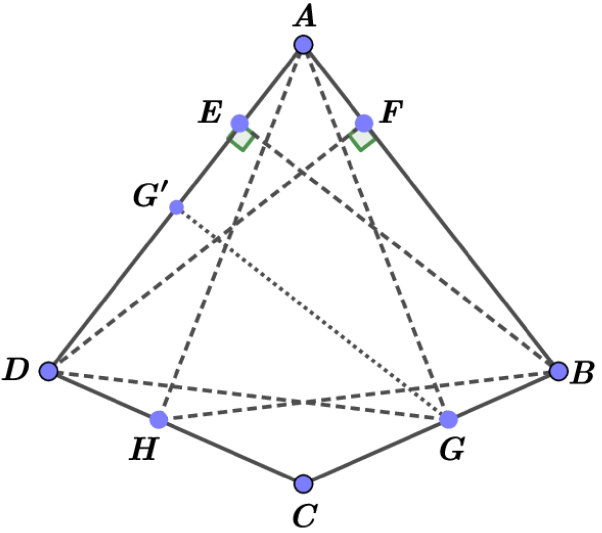
Note that this inequality becomes an equality for quadrilaterals called magic kites (squares are not extremal in this sense). This definition is taken from [20] and means convex quadrilaterals which are hypothetically extreme with respect to the self Chebyshev radius. Up to similarity, such a quadrilateral could be represented by its vertices, that are as follows (see Fig. 1):
The heights drawn from all the vertices to the sides farthest to them have the same length (, , denotes the bases of the corresponding heights on the sides of the considered quadrilateral), which coincides with the self Chebyshev radius of the boundary of this magic kite. Note that two such heights emanate from vertex , one such height emanates from vertices and , while the heights from vertex are shorter than the proper Chebyshev radius of the boundary of this polygon.
Note also that we have , where is a boundary of a square, and .
Our main result is the following theorem.
Theorem 1.
For any quadrilateral with the boundary on Euclidean plane, we have the inequality , with equality exactly for magic kites. In other words, a magic kite has the minimal perimeter among all quadrilaterals with a given self Chebyshev radius of their boundaries.
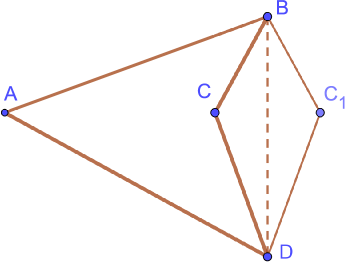
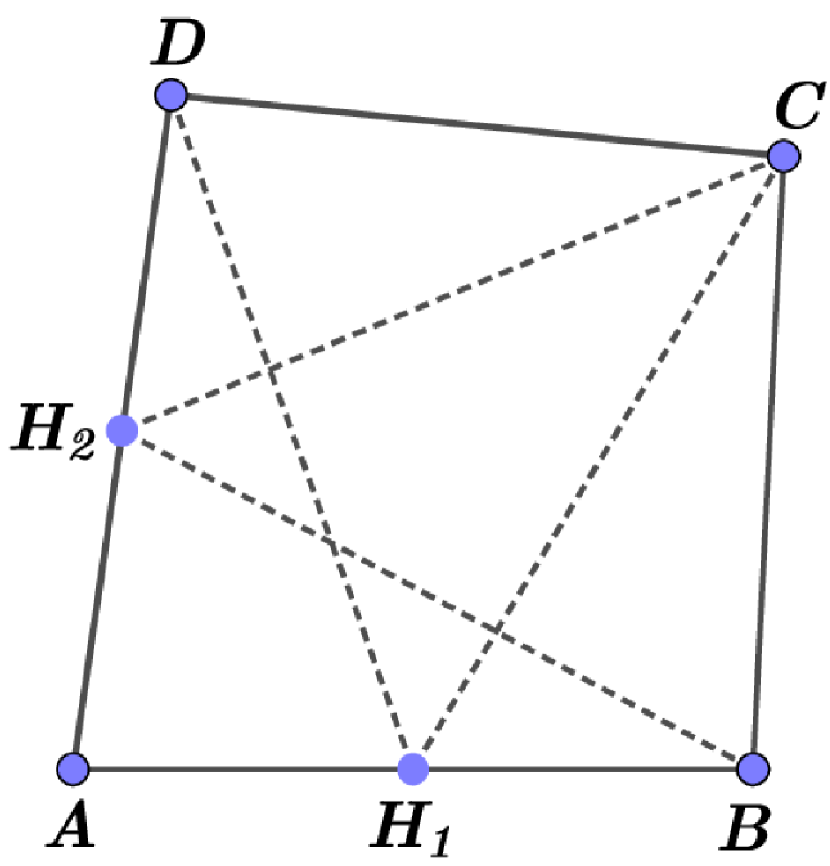
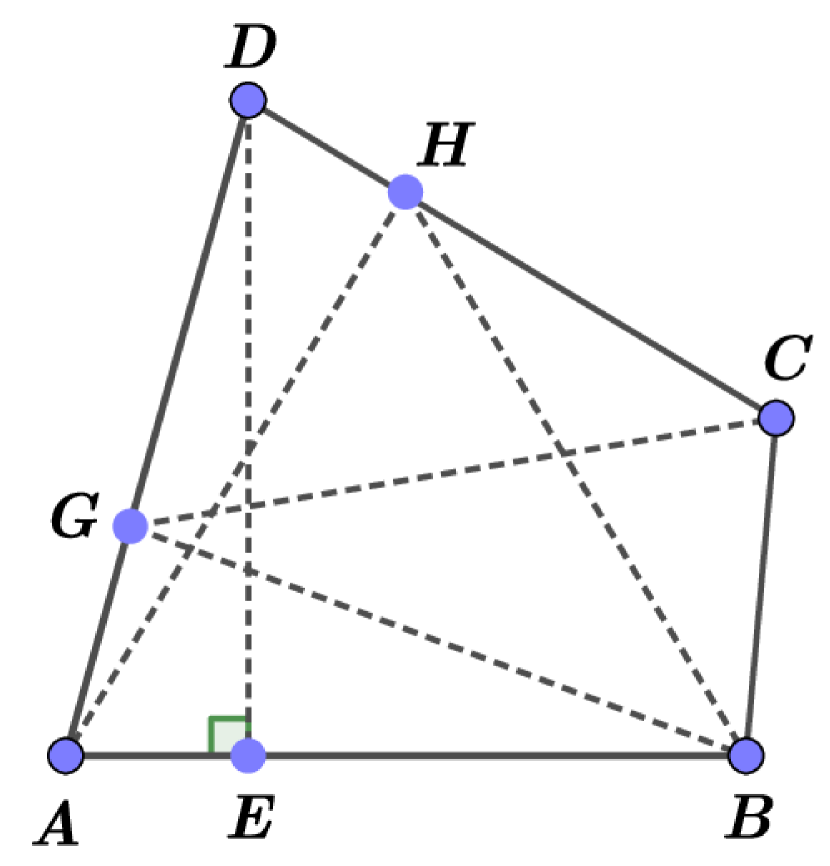
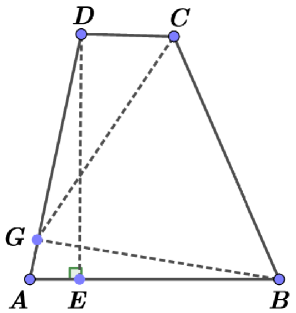
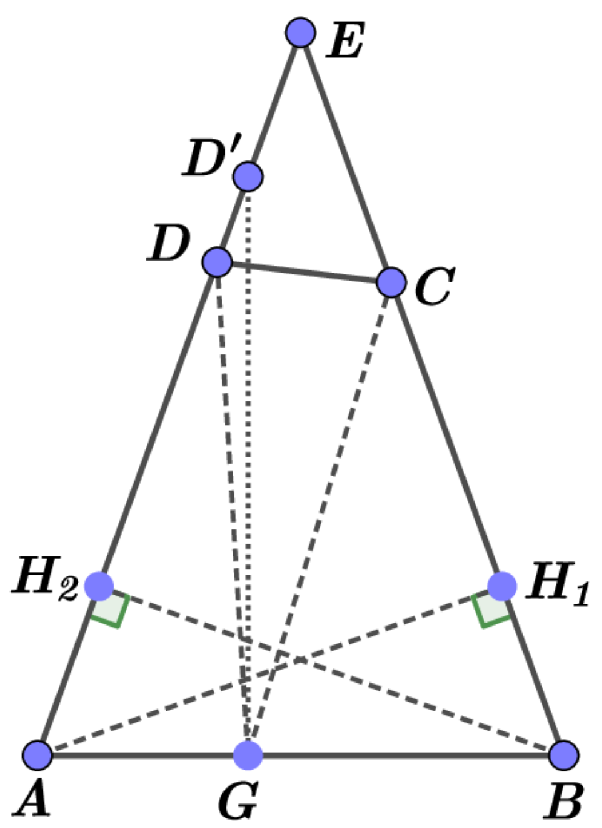
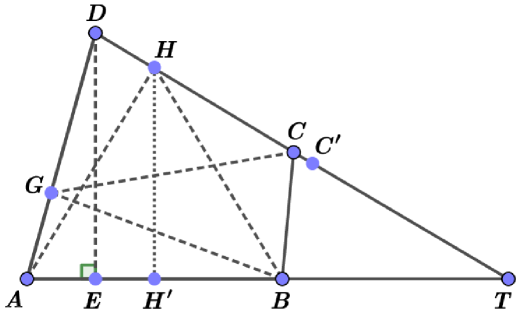
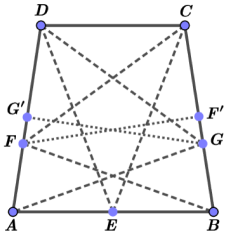
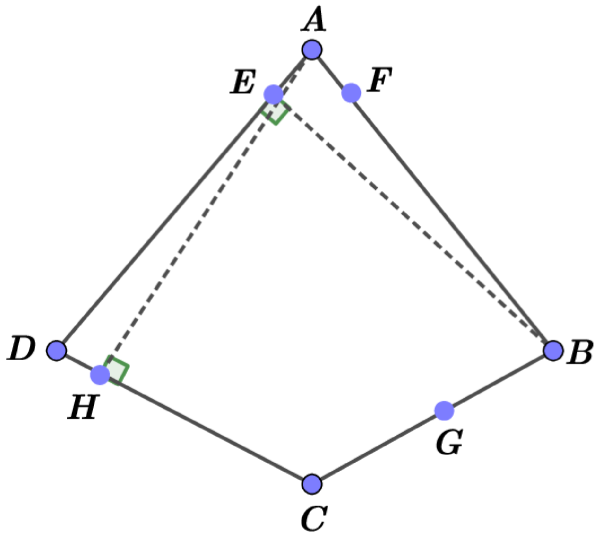
If a quadrilateral is not convex, then one can easy to find a convex quadrilateral with the same perimeter and such that the self Chebyshev radius of the boundary of is not less than the self Chebyshev radius of the boundary of . Indeed, if the convex hull of a quadrilateral is the triangle , we can consider the point that is symmetric to with respect the straight line , see Fig. 2. The quadrilateral is convex and has the same perimeter as has. For any point , denote by the point on that is symmetric to with respect the straight line . If we take any point , then the distance from to is not less that the distance from to . This observation implies that the self Chebyshev radius of the boundary of is not greater than the self Chebyshev radius of the boundary of . Therefore, the above theorem must be proved only for convex quadrilaterals.
We use mainly standard methods of Euclidean geometry and analysis to prove this theorem. Sometimes we have to resort to the help of computer algebra systems. In what follows we repeatedly use some well known properties of convex polygons. As a source on the properties of polygons, one can advise, in particular, books [12, 14, 18]. There is also a special book on the properties of quadrilaterals: [2].
The proof of the main theorem is technically quite difficult. We have to consider many special cases, and in each case we apply different methods. Despite all our attempts to simplify the proofs, we have not succeeded in doing so. We would like to believe that someone will find a shorter and more conceptual reasoning. But while this is not known, we decided to share our version of the proof.
For symbolic and numeric calculations, we used the well-established Maple, a general purpose computer algebra system (CAS). Wherever possible, we have used symbolic calculations. The Maple program provides a wide range of commands for working with symbolic expressions. Numerical calculations were used only where it was not possible to use symbolic calculations effectively and where there was no doubt about the correctness of the approximations (because there is some margin of magnitude with which to compare the result). The precision used was controlled by the Digits global variable, which has a default value of 10. However, it can be set to almost any other value. For more detailed information, see e. g. [16].
The paper is organized as follows. In Section 2 we consider some important information on Chebyshev radii and centers for bounded convex sets in an arbitrary Hilbert space. In Section 3 we prove some important results on self Chebyshev radii and centers for boundaries of convex polygons on the Euclidean plane. In Section 4 we describe a general plan of the study and obtain some auxiliary results. Sections 5, 6, 7, and 8 are devoted to the study of important partial cases of the general problem. We prove our main Theorem 1 on the basis of the results obtained in these sections. In the final section we consider some additional conjectures and outline the prospects for further research on the topic. The list of some important notations and definitions is given at the end of the paper.
The authors are grateful to Endre Makai, Jr., Horst Martini, and Yusuke Sakane for useful discussions and valuable advices. We are also grateful for the advices of both of the anonymous reviewers, whose comments and suggestions allowed us to improve the presentation of this article.
2. Some general results
All propositions in this section can be found in various sources. We give them here in the form we need and provide brief proofs for the sake of completeness.
Let us consider any Hilbert space with the inner product and the corresponding norm (in particular any with some Euclidean norm). For any set , the symbols , , and denote respectively the convex hull, the boundary, and the interior of .
For given and , we consider , , and , respectively the sphere, the open ball, and the closed ball with the center and radius . For , the symbol means the closed interval with the ends and on the line through and .
Proposition 1.
Let be a non-empty bounded set in , and a function such that . Then is a convex function and there is a real number such that for all . As a corollary, the function has a unique point of global minimum value in .
Proof. Let us consider any and any , . Then for every , we have
Therefore, , hence, the function is convex. Since is bounded, then there is a real number such that for all . Consequently,
for every and every . This means that is coercive, hence, has a point of global minimum value, see e. g. Corollary 11.30 in [9].
Now, we suppose that there are points , where attains its minimum value, say . Therefore, , , and . It is clear that . Indeed, for any , we have
Hence, , that is impossible.
Proposition 2.
Let be a non-empty convex bounded closed set in , and a function such that . Then for any , there is a point such that . Moreover, if is finite-dimensional, then .
Proof. Let be the closest point of to the point . It is clear that . Hence if for some , then . It implies that . If is finite-dimensional, then is compact, hence there is such that for all . Therefore, .
For any non-empty bounded closed set in , a point () with minimal values of the function on (respectively, on ) is the Chebyshev center (respectively, the self Chebyshev center) for . Two above propositions imply
Corollary 1.
Let be a non-empty convex bounded closed set in , then it has a unique Chebyshev center, which by necessity lies in .
Obviously has the same Chebyshev center as from the above corollary. It is not the case for self Chebyshev centers, of course.
Proposition 3.
Suppose that and are convex bounded closed set in and . If is the self Chebyshev radius of the set , , then .
Proof. For any , there is a point such that . Since , we have . If , then we put . Now, suppose that and consider the function such that . We see that . By Proposition 2, there is such that . In both cases we have . Since could be as small as we want, we get .
3. Some auxiliary results for boundaries of convex polygons
In what follows, the symbol means the cardinality of a given set . We identify the Euclidean plane with supplied with the standard Euclidean metric , where .
We call a convex curve if it is the boundary of some convex compact set in the Euclidean plane . Important examples of convex curves are convex closed polygonal chains, i.e. boundaries of convex polygons. A polygon is called an -gon if it has exactly vertices. For we get line segments. The perimeter of any -gon is defined as the double length of the line segment . Such definition is justified, since it leads to the continuity of the perimeter as a functional on the set of convex polygons with respect to the Hausdorff distance.
Let be a compact set (in particular, a convex curve). We define the function as follows:
| (2) |
For any polygon and any given point , is achieved at a vertex of (see, e.g., Lemma 4.1 in [20]), i.e., is equal to the maximal distance from to vertices of . Note also that the diameter of a polygon always connects two vertices.
The following property (monotonicity of the perimeter) of convex curves is well known (see, e.g., [10, §7]).
Proposition 4.
If a convex curve is inside another convex curve in the Euclidean plane, then the length of is less than or equal to the length of , and equality holds if and only if .
The following simple result is very useful.
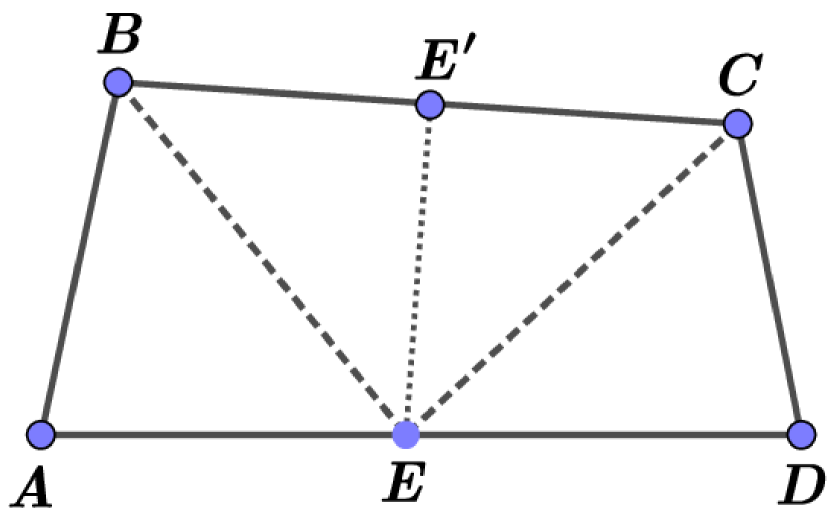
Proposition 5 ([8]).
Let be a convex curve in such that contains the line segment with the property , where is the midpoint of . Then . Moreover, is a unique self Chebyshev center for .
Let us consider and let be a boundary of a convex -gon . We will show how to estimate . Let us denote , , consecutive vertices of a polygonal line (vertices of the polygon ), assuming that indices are taken . The direction of traversing the curve in the direction is called positive, and the opposite direction to it is called negative.
a)
b)
For a given point , we denote by (respectively, ) the limit , where the points tend to via the negative (respectively, the positive) direction. These vectors have length and are called one-sided tangent vectors at the point . If is an interior point of some segment , then .
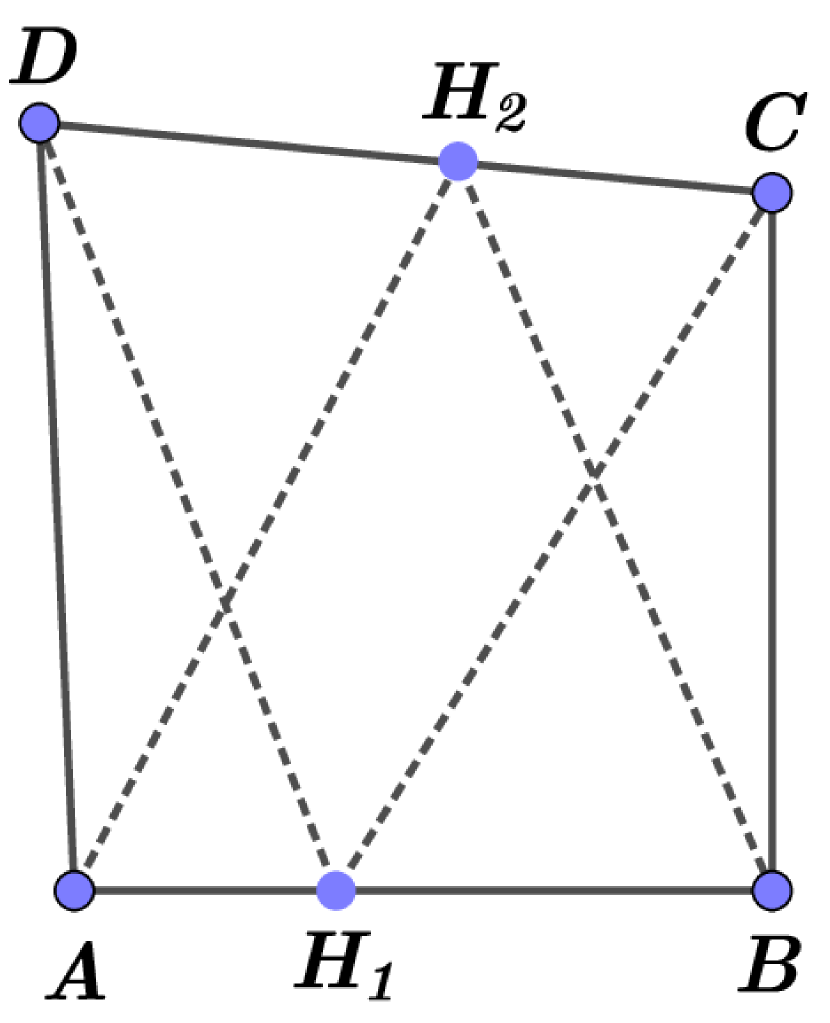
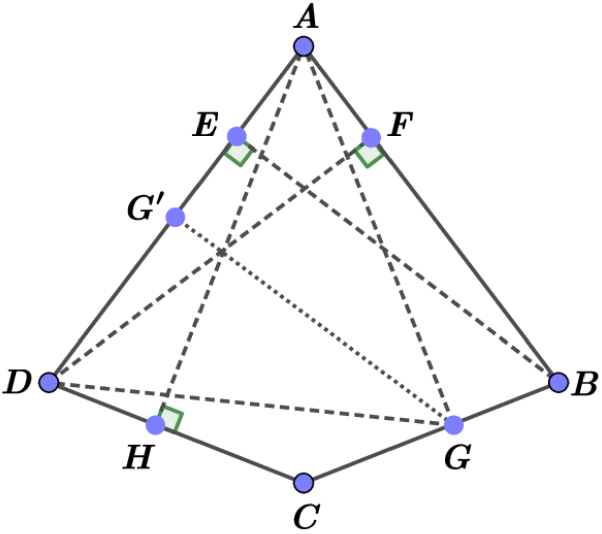
For a given point we put if is in the interior of the segment and if for some , see Fig. 3.
Proposition 6.
In the above notations, for a given point , the following conditions are equivalent:
1) The function (see (2)) attains its minimal value on the set at the point ;
2) The point is the point of local minimum of the function ;
3) For any vector , there is a point such that .
Proof. Obviously, 1) implies 2). Let us prove . Suppose that 2) holds but 3) does not hold. Choose a vector , such that for any , and consider the points . Since , then for sufficiently small . If is any vertex of that is not in , then , hence, for sufficiently small . Therefore, for any vertex of , that implies for sufficiently small . Hence, we get the contradiction with the condition 2) and, therefore, 2) implies 3).
Now, let us prove . We suppose that 3) holds. Let us choose any vector and consider the point for any . By the condition 3), there is such that . It implies . Hence, for all . Since we can take both and as , we get that is the minimal value point of on the set , hence, the condition 1) holds.
Remark 2.
This proposition also follows from Proposition 1. Indeed, the restriction of a convex function to any line segment is also a convex function. For every convex function, any point of local minimum is also a point of global minimum.
Using the equivalence of conditions 1) and 3) in the previous proposition, we obtain the following
Corollary 2.
If the angle at the vertex of the -gon is less than , then is not a minimal value point of the function on the set .
For a given point we have if and only if is on the perpendicular bisector of and . Hence, we have only finite numbers of points such that the set has more that one point. Proposition 6 implies
Corollary 3.
Suppose that the point is such that the set has only one point. If is the local minimum point of the function , then is an interior point of some segment and is orthogonal to , where .
Proposition 7.
For a given -gon with , we consider the set
If there is such that and , then .
Proof. By Corollary 3 we see that the set has at least two elements. Let us consider the set .
Now, we suppose that for every we have . Let us fix such that or (it is possible by the assumptions) and consider the points for . It is easy to see that
for all and for sufficiently small (due to the inequality ). Moreover, for all , , we have for sufficiently small (due to the inequality ). So we have for all sufficiently small , that is contradicts to .
Therefore, there are such that . It means that contains the triangle , which has the perimeter at least (we have this minimal value for ). Hence, .
In what follows, we call an -gon extremal if it has the smallest perimeter among all convex -gons whose boundaries have a given value of the self Chebyshev radius (1) (i. e. has a minimal possible value, where ).
Remark 3.
The existence of an extremal -gon for every can be proved using a limiting argument. The limit polygon cannot be an -gon with , since for any -gon we can easily construct an -gon with the same self Chebyshev radius for its boundary and with a bigger perimeter. Indeed, it suffices to replace one side of a given -gon to a suitable almost straight polygonal chain of line segments.
The self Chebyshev radius of coincides with the minimal value of the function (see (2)).
For fixed -gon with , we consider the function such that
| (4) |
We know that this function is convex with an unique point of the global minimum (Proposition 1). The point is the Chebyshev center of (and ), is the Chebyshev radius of (and ). We know also that by Corollary 1.
Since the function is convex, for any , the set is a convex set, and is a closed convex curve.
Lemma 1.
For every , the convex curve is the union of finite circular arcs of radius with the center at some vertices of . A common point of two arcs with different centers and is on the same distance from these two points.
Proof. If , then and there is a point such that . Obviously, is a vertex of (and ). Since we have only finite number of the vertices, we get the lemma.
It is clear that
| (5) |
Hence, we have and
| (6) |
If and is a smooth point of , then is necessarily in the interior of some segment . If and is a non-smooth point (an intersection point of two circular arcs with different centers) of , then could be some vertex (in this case by Corollary 2).
It is clear that the set is either empty or has exactly one point for any line segment .
Let us suppose that is extremal. Fix the vertex and consider two variations of : and , where . This polygonal lines have the same vertices as has with one exception: instead of we take respectively and . Since and , then and for all . Since is extremal, then and (by Proposition 3 we know that and ).
Now, we deal with the variation . There is a point such that for any , in particular, for all vertices , . Moreover, . If we can choose arbitrarily close to zero and such that , then we get that .
If , then , hence, (otherwise ). If we can choose arbitrarily close to zero and such that , then we get some such that . Indeed, if as , then , and as .
The variation could be considered similarly. Hence we get the following
Proposition 8.
Suppose that an -gon is extremal. If for some , then there are points such that .
4. A plan how to find extremal quadrilaterals and some preliminary considerations
The main idea is to determine all extremal -gons and to prove that this set coincides with magic kites. We use the notations from the previous sections.
Corollary 4.
If there is such that , then . Consequently, for any extremal -gon , we have for all .
Proposition 9.
Suppose that a quadrilateral is extremal. If and , then . In particular, .
Proof. By Corollary 4 we see that . Suppose that , i. e. . By Proposition 6, for the vector , there is a point such that . Hence, and . Since the triangle is a subset of the quadrilateral and has the perimeter , then . This means that is not extremal. Therefore, . Similar arguments proves .
We are going to prove that for any extremal quadrilateral . For this goal, we consider some auxiliary problems.
a)
 b)
b)
 c)
c)
 d)
d)
 e)
e)
 f)
f)
 g)
g)
Denote by the number of points in the set , or, in other words, the number of self Chebyshev centers for (see (6)). For any , the set is either empty or has exactly one point.
We denote the elements of by capital roman letter (sometimes with indices). The possible subcases depends not only of cardinality of but also on how many elements of the set satisfy the conditions and (see (3)) and the relative position of these points.
In what follows, a self Chebyshev center is called simple if and non-simple if .
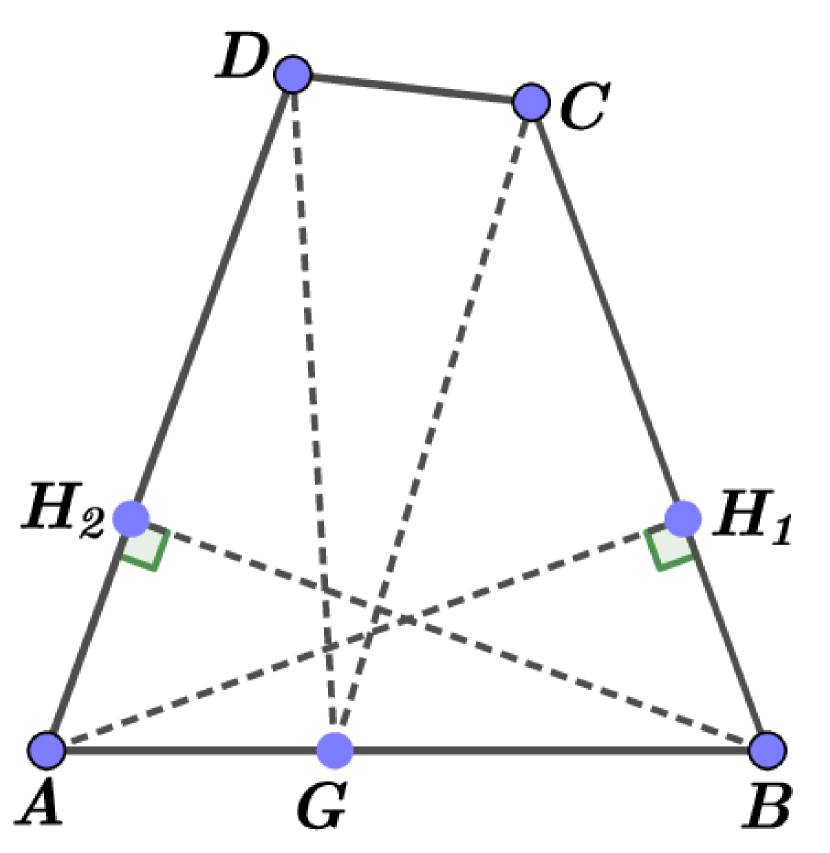
On the other hand, and, therefore, . Moreover, does not contain any vertex of by Corollary 4. We distinguish four cases according to the value of . Case is the case when , .
5. Case 1
Proposition 10.
Case 1 does not provide extremal quadrilaterals.
Proof. Suppose that and , where is an interior point of the segment (say) . Hence, and by Proposition 8. In particular, . By the triangle inequality we have also that . Therefore, . Obviously, . Therefore, Case 1 does not provide an extremal quadrilateral.
Remark 4.
Recall that we use the term ‘‘extremal’’ in this paper only for polygons with minimal perimeter among all polygons with a given self Chebyshev radius of the boundary. It should be noted that the polygon with maximal perimeter among all polygons with a given self Chebyshev radius of the boundary was determined in [8, Theorem 4]. The boundary of such a polygon has only one self Chebyshev center. For , such a polygon is a half of a regular -gon.
In the following three sections, we will consider Cases 2, 3, and 4 in turn. For all this cases, it is reasonable to consider separately some subcases. In Fig. 4, we show all the essential subcases of Cases 2 and 3.
The following auxiliary result is very useful.
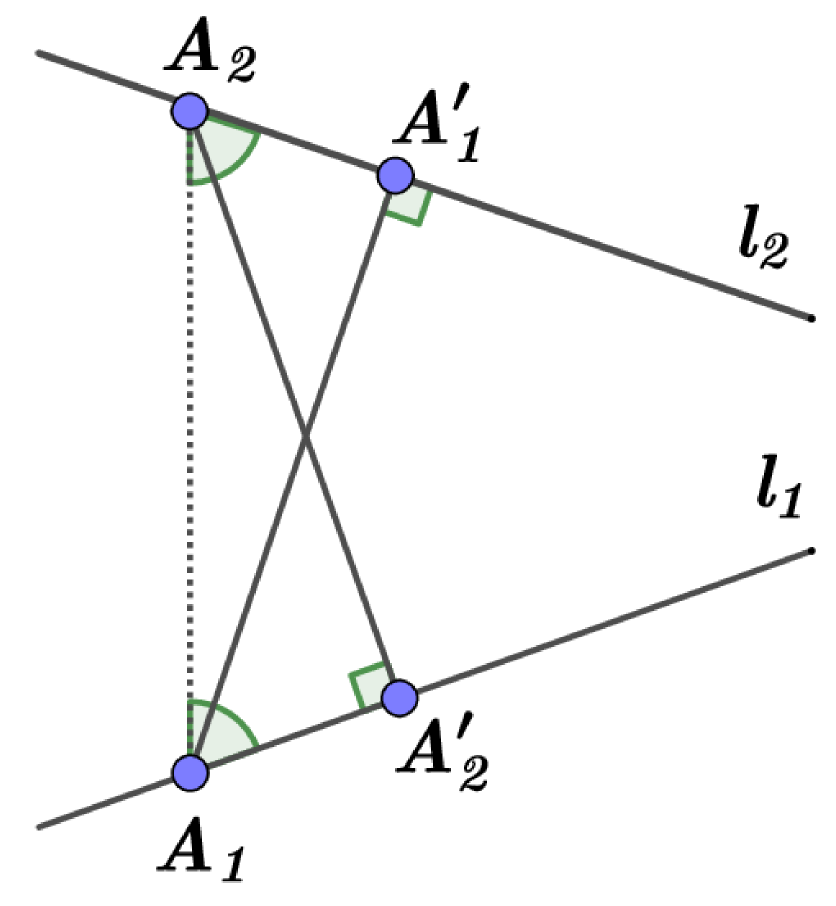
Lemma 2.
Let be a quadrilateral with for the self Chebyshev radius of its boundary. Suppose that there is a point such that and . If, moreover, (respectively, ) and for any , then either (respectively, ) or there exists a point arbitrarily close to the point , such that and .
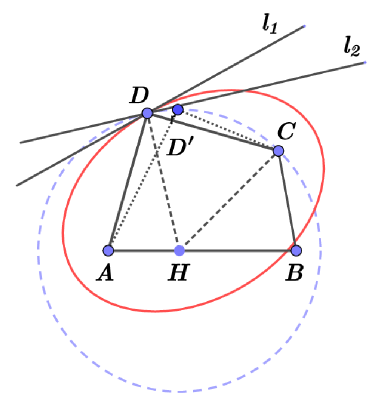
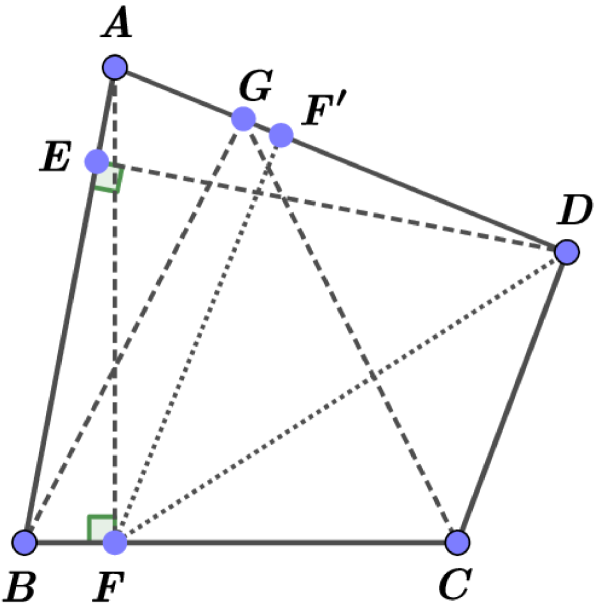
Proof. At first, we consider the case . Let us suppose that . We consider an ellipse with the foci at the points and , that contains the point (see Fig. 5). Let be a circle of radius centered at the point . Recall that .
Let be the tangent line to the ellipse at the point and the tangent line to the circle at the point . Note that . Since , then the angle between the tangent and the segment is less than the angle between the tangent and the segment .
By a well known property of the ellipse, the angle between the tangent and the line segment is equal to the angle between the tangent and the the segment . Therefore, the arc of a circle between the points and is such that any its point , that is sufficiently close to the point , lies inside the ellipse . Therefore, we have for such a point according to another one well known property of the ellipse. Hence, . It is easy to see that the self Chebyshev radius of the boundary of the quadrilateral is if is sufficiently close to .
In the case we can repeat the above arguments with one addition. In this case, we can take also the point outside the arc between and (but sufficiently close to ). Since , then such a variation of the quadrilateral does not decrease the value of the self Chebyshev radius of the boundary. On the other hand, if , such a variation decreases the perimeter. Therefore, either or there exists a point arbitrarily close to the point , such that and .
We obviously get the following important corollary.
Corollary 5.
If the quadrilateral is extremal in the assumptions of Lemma 2, then (respectively, ).
The following lemma is important for further considerations.
Lemma 3.
Let be a quadrilateral such that , , and . We consider an ellipse with the foci at the points and , that contains the point . Let be a circle of radius centered at the point . If then all points on the circle sufficiently close to the point lie inside the ellipse .
Proof. In a suitable Cartesian coordinate system, the points we need have the following coordinates:
where (see Fig. 6). Let us consider the equation of the ellipse :
By direct computations, we get
where as . Therefore, (that is equivalent to ) implies for sufficiently close to .
6. Case 2
Suppose that . Our general assumptions are as follows. Let be a quadrilateral with and with for the self Chebyshev radius of its boundary. We consider the set
where both points and are interior points of some sides of , see (6). In other words, if and only if .
We consider several subcases according to Fig. 4.
6.1. Case 2.1
Without loss of generality, we may suppose that is an interior point of , is an interior point of such that , and (see Fig. 7). Moreover, we have and by Proposition 6.
Let us suppose that the quadrilateral is extremal. Then we have by Corollary 5. Let us introduce the following notation: , , .
If , then and we obtain the following simple estimate for the perimeter: . Hence, we have , that is impossible for an extremal quadrilateral. Therefore, .
Since , then . It is easy to see that . Hence . It implies .
It is important that (otherwise the quadrilateral is not extremal by Lemma 3). Since , we get , where .
If and , then and . These inequalities imply and, consequently,
On the other hand, . Hence, or, equivalently, . We have and due to . It implies that and both satisfy the inequality , which solutions for are as follows: , where . Therefore, .
Put . It is easy to see that . The equations (the low of sines for )
imply or, equivalently,
It is easy to check that
for and . Hence . It implies . We get for . The solution of this inequality is . Therefore, , where .
Now we are going to show that the inequality does not hold for (hence, , and we get a contradiction). If we suppose that , then and, consequently, . In particular, and . On the other hand,
i.e.
Therefore, if and only if . It is easy to check that
for . Thus, the function is strictly increasing with respect to the variable for any . Further, it is easy to see that
for . Thus, the function is strictly decreasing with respect to the variable for any .
Therefore, . Now, it is easy to check that . Indeed,
Consequently, and we get a contradiction. Hence, Case 2.1 does not provide extremal quadrilaterals.
6.2. Case 2.2
Let us suppose that the quadrilateral under consideration is extremal. Assume, for definiteness, that is an interior point of , is an interior point of and (see Fig. 8).
Then and . By Corollary 5 we have and , respectively. However, and . This contradiction shows that our assumption (that is extremal) is wrong.
6.3. Case 2.3
Let us suppose that the quadrilateral under consideration is extremal. Assume for definiteness that is an interior point of , is an interior point of , and (see the left panel of Fig. 9). Without loss of generality, we may suppose that .
We know that . Suppose at first that . Then we have the inequality (for an extremal quadrilateral) by Corollary 5. Since , we get , then and we obtain the following simple estimate for the perimeter: . Hence, we have , that is impossible for an extremal quadrilateral.
Now, let us suppose that . It implies and we can repeat the above arguments changing the points to the points , respectively. Hence, if we again get by Corollary 5.
Therefore, the remaining case, called Case 2.3a, is that (together with ) implies .
Thus is an isosceles trapezoid with the bases and (see the right panel of Fig. 9). Put . It is easy to see that and
In particular, .
a)
b)
Since the straight line is orthogonal to the straight line , then . Therefore, and .
Since the straight line is orthogonal to the straight line , we get
From , we get or . Therefore, . Solving this inequality and taking into account that , we get .
Let be the midpoint of the line segment . Then
It is easy to check that the function is strictly decreasing for and takes the value for , where . It follows from the following facts: , , and for .
Consider the perimeter
It is easy to see that the function is strictly decreasing for . Indeed, , where . It is easy to check that the maximal value of for is Hence, on the segment .
Therefore, achieves its minimal value on exactly at the point . This minimal value is
Therefore, the quadrilateral is not extremal.
7. Case 3
In this section we deal with the case , i. e. has three self Chebyshev centers. We consider several subcases according to Fig. 4.
7.1. Case 3.1
Let us suppose that and . Without loss of generality, we may suppose that is an interior point of , is an interior point of , is an interior point of such that , and . It is clear that is orthogonal to and is orthogonal to . Moreover, and by Proposition 6. We put .
Lemma 4.
In the conditions as above, we get . If, in addition, , then .
Proof. Let us consider the quadrilateral as a subset of the isosceles triangle (see the left panel of Fig. 10). We put , , where .
Since , then we get and . Since and , then there is a point , such that the straight line is orthogonal to the straight line . The inequality implies . Since , then we get .
On the other hand, , hence . Therefore,
Hence, we get or, equivalently, .
Now, if , then the perimeter of the triangle is as least . Indeed, it easily follows from the relations , , and . Since quadrilateral contains the triangle , then .
a)
b)
Now we consider, the following class of quadrilaterals: a quadrilateral is in if and only if the following conditions hold: and there are , , and such that , , , , , .
Lemma 4 implies that any quadrilateral in Case 3.1 with is in the class . Now, it suffices to prove the following
Proposition 11.
For any quadrilateral in the class , we have and . In particular, there is no extremal quadrilateral in .
Proof. Since the distances from the points to is at most , then . Let us prove that . We put , , , and . We have by our assumptions. Note that , hence, . It is easy to see also that (see e.g. the proof of Lemma 4)
Let us consider , the intersection point of the straight lines and (the quadrilateral is a subset of the isosceles triangle ), see the left panel of Fig. 10.
Since , then we have and . The equalities and imply . Therefore, we get
The equalities and imply and , respectively. Since , then we get .
Now, we introduce new variables and such that and . We get
The equation
implies . Therefore, we get
We will now find useful upper and lower bounds for the value . The equation implies and , that could be rewritten as
Similarly, we get
The above equality obviously implies
It is easy to check that
Therefore, if and only if or, equivalently, .
Since we will find the value of the function at the boundary points:
Therefore, for a given . Now, we will prove that the minimal value of on the set
| (7) |
is . It will be suffices to prove the proposition.
It is easy to see that for . Therefore, the function is strictly decreasing on the interval , , . By direct computations, we get
The derivative has the same sign as the expression . Solving equation with respect to , we obtain
It is easy to show that the graph of this function does not intersect a two-dimensional connected set (see (7)). Since , then we get . Thus, the function is strictly increasing with respect to the variable for any .
Therefore, the function achieves its minimum value on at one of the points of the curve , that corresponds to the following configuration, which will be called Case 3.1a (see the right panel of Fig. 10): , . Now we are going to find the explicit expression for , .
We have , and for . Let . Since , we have . It is clear that . The equations
imply . Since , then we have
It is clear that . Since , then . The equations
imply . Therefore, and, consequently,
Since , then we get
By direct computations we get that the function achieves its maximal value on at the point , where is the root of the polynomial on the interval . This maximal value is
By direct computations we get also that the function achieves its minimal value on exactly at the point . This minimal value is . Therefore, for all . The proposition is proved.
Remark 5.
Note that minimal value of on is achieved at the point , that corresponds to a degenerate quadrilateral , where , , and . The self Chebyshev radius of the boundary of this degenerate quadrilateral (in fact, a triangle) is .
7.2. Case 3.2
Without loss of generality, we may suppose that (see Fig. 11), where is an interior point of , is an interior point of , is an interior point of such that , and . It is clear that is orthogonal to and is orthogonal to . Moreover, and by Proposition 6.
Now we are going to show that this case is impossible.
Remark 6.
It should be noted that it does not matter for the arguments below whether there is a fourth self Chebyshev center for or not. Therefore, we can use this arguments also for some quadrilaterals with four self Chebyshev centers.
a)
b)
We put , and (see the left panel of Fig. 11). Let is an interior point of such that the straight line is orthogonal to the straight line .
Since and , then we have . It is clear that . Therefore, we get
Hence, if and only if .
Since , there is a point , such that the straight line is orthogonal to the straight line (see the right panel of Fig. 11). It is easy to see that . Hence, .
The equations
imply . Therefore, and, consequently,
Let is an interior point of such that the straight line is orthogonal to the straight line (see the right panel of Fig. 11). The equations
imply .
It is easy to see that , and . Hence,
Therefore, we get
Let us now show that the inequalities and cannot hold simultaneously. For this goal, we prove the following simple result.
Lemma 5.
Let be a topological space and are closed subsets of . Let the following conditions be satisfied:
-
•
be a connected set;
-
•
;
-
•
There exists such that .
Then .
Proof. Let and . It is clear that and are open and disjoint sets. As is a connected set, we have or . By the third property, is impossible. Hence, and .
Let the connected set of solutions to the inequality (i.e. ) and the set of solutions to the inequality . If then and
Hence, and . It is easy to see that and for the point . Therefore, the inequalities and cannot hold simultaneously. Hence, the case under consideration is impossible.
7.3. Case 3.3
Suppose that and (see Fig. 12). Without loss of generality, we may suppose that is an interior point of , is an interior point of , is an interior point of , and . It is clear that is orthogonal to . Moreover, and , and by Proposition 6.
Let us consider the quadrilateral as a subset of the triangle (see Fig. 12). We put , , and . Since and , we get .
Since , we get and . It is clear that , the distance from the point to the straight line , is at most . Therefore, . It implies that and . Hence, we get and
| (8) |
Let be the midpoint of . Since triangles and are similar, then we have . Hence . Further on,
and
Moreover, we get , which implies
| (9) |
From the triangle we have
and, consequently, and
Then we get
| (10) |
Let us consider and . It is clear that . From the triangle we get equalities
imply
It is clear that . This implies
Therefore, we get the following expression for the perimeter of the quadrilateral :
We can explicitly express and in terms of and from (9) and the equality
Now we going to obtain some estimation on possible values of and . Note that
due to . Note also that (due to ), therefore we have or, dividing by ,
Hence, and , where is a unique root of the polynomial on . Therefore, we get that and , where , .
Now we will find additional important restrictions on the values of , . We are going to prove that any possible pair should lie in the following set:
| (11) |
It is easy to check that is bounded by the straight lines , , and by the curve
The above argument implies that the point lies in the intersection of and . It is easy to check also that .
Recall that we have obtained the inequalities and . Hence it suffices to prove that . In any case, all possible pairs lie in the set
| (12) |
Note that the straight line passes through the points , hence we can omit the restriction from the formal point of view.
Let us consider the point on such that (recall that and , hence, ). Note that holds if and only if or, equivalently, . We can rewrite the latter inequality using the law of cosines the triangle . It is clear that (recall that and ). Therefore,
which can be rewritten as
Now, we define the function
| (13) |
where
and the set
Now we will find the intersection point of the curve and the set . Substituting into , we easily get that and, consequently, .
Now we will find the intersection of the curve and the set . Substituting and into we get
Hence, either or
By direct computations, we get that , where is a unique root of the polynomial on the interval . Consequently, we obtain the intersection points , where , and .
If we consider for , then and for . Let us suppose that there exist such that and . Then, by the continuity, there exists such that and . Without loss of generality, we can fix such a point with the maximal possible value of . Its clear that . On the other hand, the system
| (14) |
has no solution in with . Since we have by (8), hence, we need to check only . By numerical calculations (one can use commands Maximize and Minimize for the Optimization package in Maple) we get that the maximal value of for is . On the other hand, the minimal value of for is . Since , we obtain that system (14) has no solution for .
Therefore, for all possible pair we have . Thus we have constructed the (curvilinear) triangle
| (15) |
where is the straight line (see Fig. 13).
By numerical calculations we get also that the minimum value of the value on the set is , that corresponds to (see the point at Fig. 13, this point gives a unique solution of (14) in ).
Now, we consider only pair from the curvilinear triangle , since this inclusion follows from the equality .
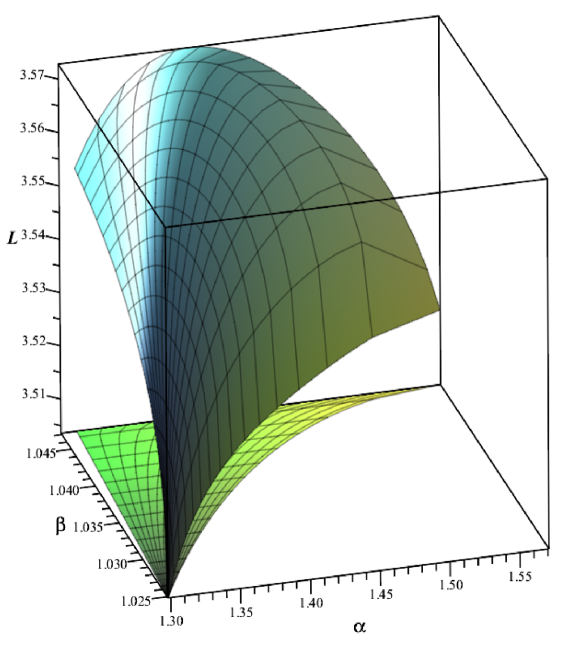
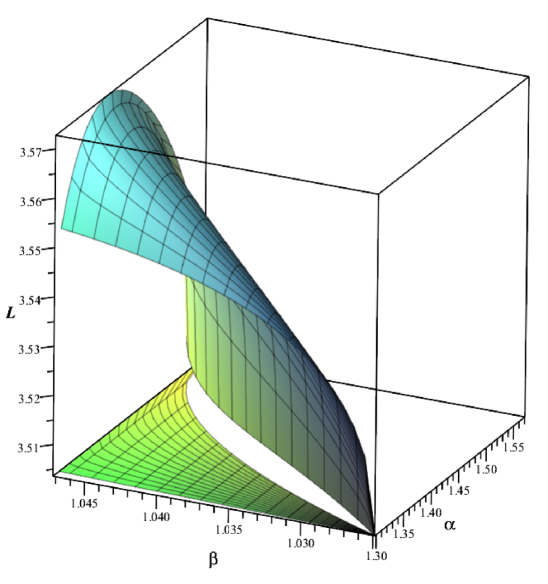
The results of numerical calculations show that the perimeter (on the curvilinear triangle ) achieves its minimal value provided that , see Fig. 14. This minimal value is . Hence, the quadrilateral is not extremal.
Remark 7.
It should be noted that in Сase 3.3, in contrast to Сase 3.2, there are real quadrilaterals with all the necessary properties, therefore, a lower estimate for the value of the perimeter is required.
Remark 8.
In Case 3.3 we ended the discussion with a reference to numerical calculations. This is sufficient, since the minimum value of the perimeter in this case is separated from the hypothetical minimum value (obtained for magic kites) by a distance greater than . It is clear that instead of referring to numerical calculations, one can carry out perimeter estimates (with some margin), using only symbolic calculations (the function being minimized is analytic and has good properties). But this will take additional space in the paper, although it is in fact some technical point. The same remark is valid for the following Case 3.4.
7.4. Case 3.4
Without loss of generality, we may suppose that , where is an interior point of , is an interior point of , is an interior point of , and (see Fig. 15). Moreover, , and by Proposition 6.
Let us consider a slightly more general case in a suitable system of Cartesian coordinates. We take the coordinates as follows: , , , where . Let be a number such that the equation of the straight line is . Without loss of generality, we may suppose that . Then , and .
If , then and we obtain the following simple estimate for the perimeter: . Hence, we have , that is impossible for an extremal quadrilateral. Thus, .
Since then . It implies or, equivalently, . Therefore, .
It is easy to see that
In particular, . Since is a point of and is a point of , there are and such that
Let be the midpoint of and be the midpoint of . Then
Since the straight line () is orthogonal to the straight line (respectively, ) then
Solving these linear equations with respect to and , we get some explicit expressions
Since and , we have the equations
with respect to . Thus, here we have four variables and two constraints, that is, roughly speaking, two degrees of freedom. Recall also that , , , moreover, , and we can assume that (otherwise the perimeter of is at least , and is not extremal).
The results of numerical calculations show that the perimeter for the quadrilaterals under consideration reaches its minimal value exactly for . This minimal value is . Hence, the quadrilateral is not extremal.
8. Case 4
Let us suppose that and . Without loss of generality we may suppose that , , and . In all subsaces of this case we have only one degree of freedom.
Recall that a self Chebyshev center for is simple if and non-simple if (see (3)).
a)
b)
Now, we are going to study a special case that we will call Case 4.0.
8.1. Case 4.0.
We consider a quadrilateral with and , such that there are two opposite sides of with non-simple self Chebyshev centers of . We will prove that such a quadrilateral can not be extremal. In other words, the following proposition holds.
Proposition 12.
Suppose that a quadrilateral with is extremal and . Then there are no two opposite sides of such that each of them has a non-simple self Chebyshev center of .
To prove this result, we need some lemmas.
Lemma 6.
Let are straight lines with points , , , that , and (see the left panel of Fig. 16). If then is rectangle, otherwise is isosceles trapezoid.
Proof. The triangle is congruent to triangle in the common hypotenuse () and legs . Hence . It implies that if then is rectangle, otherwise is isosceles trapezoid.
Lemma 7.
Let be a quadrilateral with for the self Chebyshev radius of its boundary. If and then either or and .
Proof. Suppose that . If then or . Hence and or and . But this is not possible because or . Thus, and (see the right panel Fig. 16).
Let us consider the perpendiculars from the points to the straight line . Denote by the foots of these perpendiculars, respectively. Since and then . It implies . Therefore, .
The same arguments show that also implies .
The assertion of the following lemma is well known and belongs to folklore. At one time it was proposed as an Olympiad problem in mathematics (see [12, 1997 Olympiad, Level C, Problem 2]).
Lemma 8.
Among quadrilaterals with given diagonal lengths and the angle between them, a parallelogram has the smallest perimeter.
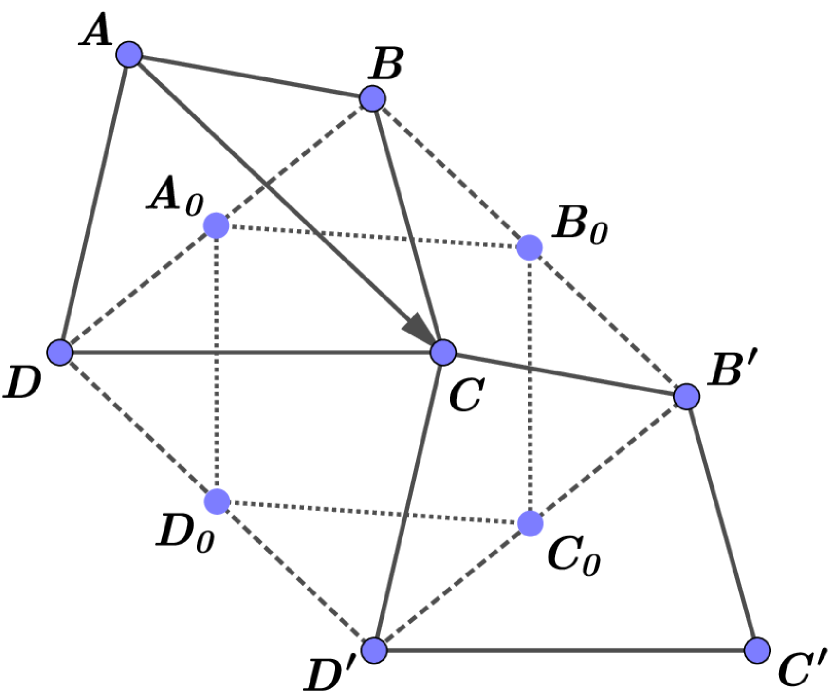
a)
b)
Proof. We present the proof for completeness. Let us translate the quadrilateral by vector (see the left panel Fig. 17). We get the quadrilateral , where and the quadrilateral is a parallelogram.
Let the points and are midpoints of and , respectively. It is easy to see that the quadrilateral is a parallelogram. Moreover, the sum of the lengths of the diagonals and the angle between them of which are equal to the sum of the lengths of the diagonals and the angle between them of the quadrilateral .
By the triangle inequality and . Adding up these inequalities we get what was required to be shown.
Lemma 8 obviously implies the following result.
Corollary 6.
We have for any quadrilateral with given diagonal lengths and the angle between them.
Proof of Proposition 12. Let us suppose the contrary. Without loss of generality, we may suppose that there are at least two non-simple self Chebyshev centers and , where is an interior point of , is an interior point of , while (see the right panel Fig. 17).
Let us consider and . It is easy to see that . Moreover, and . Thus, we have
or .
Suppose that . It implies . Consider the function on the set
| (16) |
Since for then the function is strictly increasing at a given interval. On the other hand for . Thus, the minimum of the function is possible only at three points: , and . By direct computations we get
Hence, and the quadrilateral is not extremal.
Therefore, , that implies and . By Lemma 7, we get , hence, is not extremal.
According to Proposition 12, any extremal quadrilateral with has at least simple self Chebyshev centers on some adjacent sides (otherwise there are a pair of opposite sides with non-simple centers, which is impossible due to the mentioned proposition). Fix a pair of such simple self Chebyshev centers, and .
There are three possible cases:
-
•
They have one and the same farthest vertex;
-
•
They have different farthest vertices that are adjacent;
-
•
They have different farthest vertices that are not adjacent.
We shall call this three possibilities as Cases 4.1, 4.2, and 4.3 respectively.
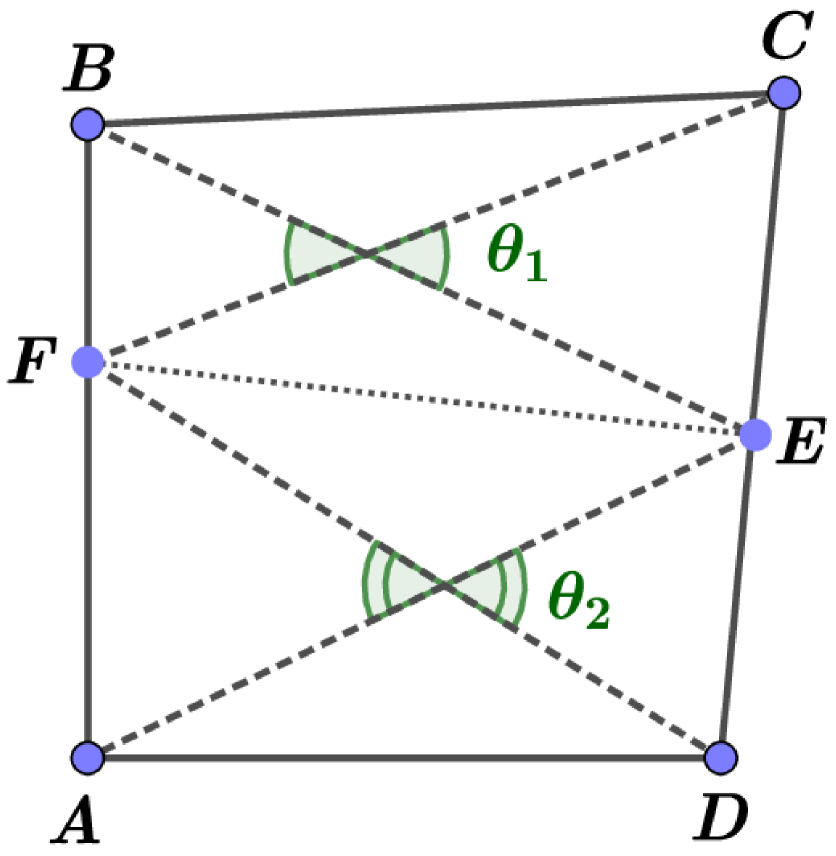
a)
b)
8.2. Case 4.1
Let us consider a quadrilateral with and , (see the left panel Fig. 18).
If , then . Hence, we have , that is impossible for an extremal quadrilateral. Thus, .
If and then is rectangle and . Therefore, and are not self Chebyshev centers. Hence is not orthogonal to as well as is not orthogonal to .
If is a simple and is not simple (or vice versa, is a simple and is not simple) self Chebyshev centers respectively, then the case is impossible (see Remark 6 for Case 3.2).
Let us consider the case when and are not simple self Chebyshev centers, i. e. (see the right panel of Fig. 18). Moreover, and by Proposition 6. We show that this case is also impossible.
We put , , and . It is clear that and . From the triangle we have . Similarly, . It implies .
From , we get , i.e. . Hence, .
Since and , then . Consequently, and we get a contradiction.
We suppose now that and are simple self Chebyshev centers. Hence and (see Fig. 19).
It is clear that the triangles and , and respectively, and are congruent. It implies and the triangles and are congruent. Hence and .
It is clear that . Hence . Since the triangles and are congruent then . It implies and .
Therefore, we get
Since then , i.e. .
By direct computations, we obtain
Solving the equation with respect to , we obtain
It is easy to check that achieves its minimal value on exactly at the point . This minimal value is
Therefore, if a quadrilateral is extremal, then it is a magic kite.
8.3. Case 4.2
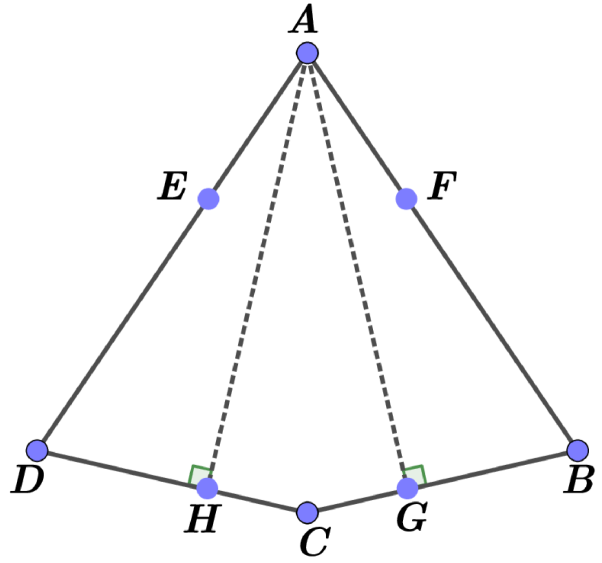
Let us consider a quadrilateral with and , (see the left panel Fig. 20).
If and then is rectangle and . Therefore, and are not self Chebyshev centers. Hence and .
If then this case is impossible (see Remark 6 for Case 3.2).
Now, we consider the case when and (see the right panel Fig. 20). We put , and denote by the midpoint of .
If , then . Hence, we have , that is impossible for an extremal quadrilateral. Thus, . It implies that .
a)
b)
It is easy to see that and . Hence and .
From we get
or, equivalently,
Since then from the triangle we have
It implies . On the other hand since we get
Thus, or, substituting the found expression for , we get
which can be rewritten as .
Solving equation with respect to , we obtain , where is the root of the polynomial on the interval . By direct computations, we get and . Hence .
It is easy to see that . The equalities
imply
Therefore, by direct computations, we get
Hence, the quadrilateral is not extremal.
a)
b)
8.4. Case 4.3
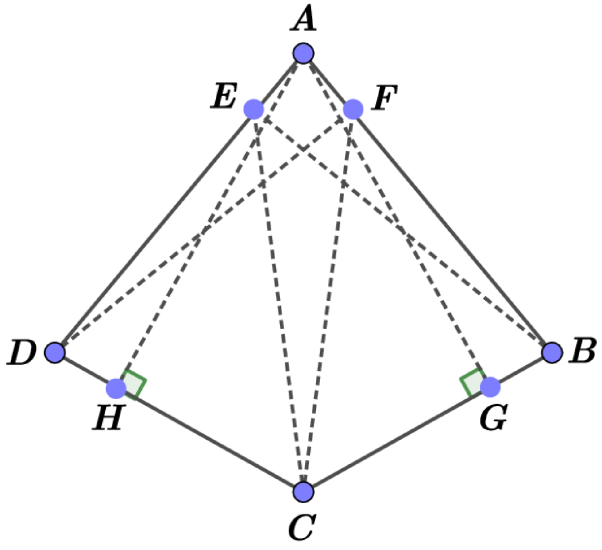
Let us consider a quadrilateral with and , (see the left panel Fig. 21).
If and then is rectangle and . Consequently, and is not self Chebyshev centers. Therefore, not and not .
Now, we suppose that and (see the right panel Fig. 21). It is easy to see that and . We put , and denote by be the midpoint of .
If , then . Hence, we have , that is impossible for an extremal quadrilateral. Thus, . It implies that .
Repeating the reasoning similar to the previous case we get . Solving this inequality for , we obtain and , where is a unique root of the polynomial on the interval .
Also similar to the previous case, we get
The results of numerical calculations show that the perimeter for the quadrilaterals under consideration reaches its minimal value exactly for or and . This minimal value is . Hence, the quadrilateral is not extremal.
It should be noted, that we found a quadralateral that can be extremal only in Case 4.1. Since at least one extremal quadrilateral does exist, we conclude that it is a magic kite from Case 4.1 and from the conjecture by Rolf Walter. This argument finished the proof of Theorem 1.
9. Computations and further conjectures
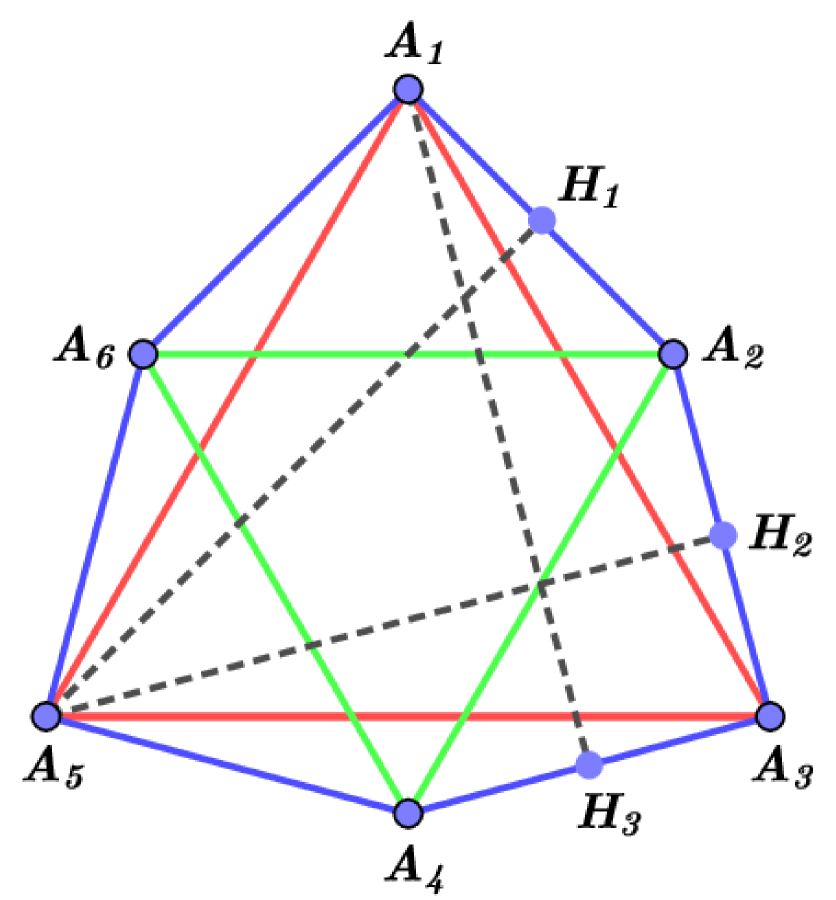
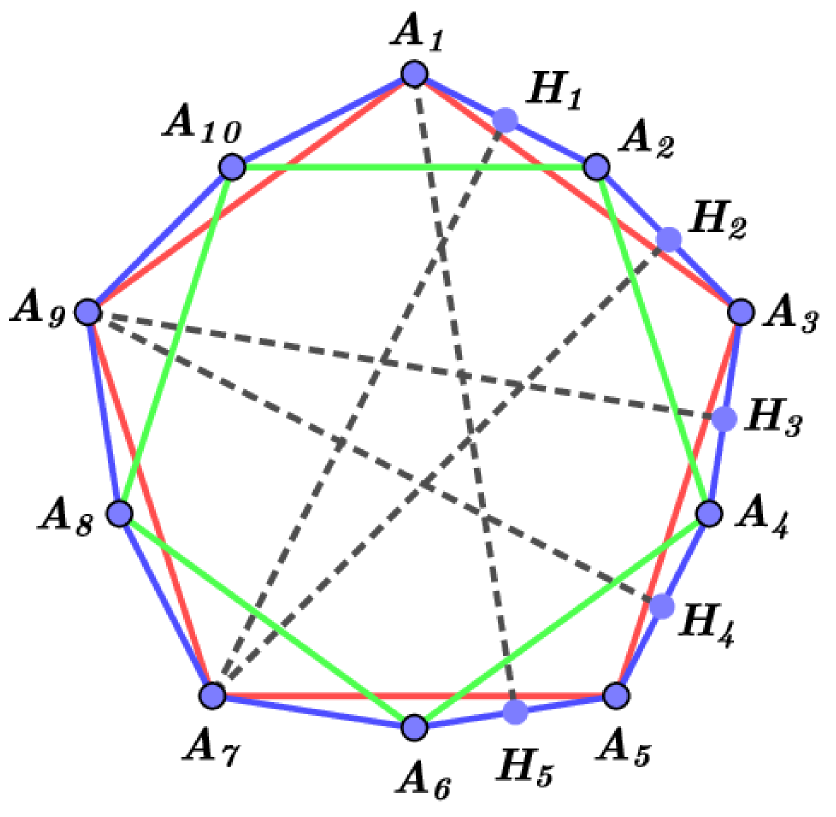
The search for possible extremal polygons for small values of was undertaken by E.V. Nikitenko. His experiments led to the conjecture that for odd , any extremal polygon is a regular -gon (this is the case for ). On the other hand, for even values of , regular -gons are not extremal in the above sense. The type of an extremal polygon (quite possibly) depends on the power of the number with which it enters to as a multiplier. See Fig. 22 for hypothetical extreme polygons for and . The calculation of the characteristics of these polygons (in particular, these polygons are equilateral), as well as numerous computer experiments, lead to the following conjectures:
a)
b)
Conjecture 1.
For any convex -gon in the Euclidean plane, one has
where is the boundary of .
Conjecture 2.
For any convex -gon in the Euclidean plane, one has
where is the boundary of .
It should be noted that there are several extremal problems for polygons, with a similar behavior of the solution with respect to the number of sides . We recall two well-known problems of such kind.
Two classical isodiametric problems for polygons are to determine the maximal area and maximal perimeter of an -gon with unit diameter. Important results in the study of these two problems were obtained by K. Reinhardt in [19].
One of the main his results is the following [19, Theorem 1, P. 252]: Let be an odd number, ; then the regular -gon has maximal area among all simple -gons of diameter .
For even this is not true. For it is true, but the square is not a unique solution: The diagonals of the square can be slightly shifted relative to each other, leaving them orthogonal.
It should be noted that a -gon of the maximum area among -gons with diameter is unique if is an odd number [19, P. 259].
The second main result by K. Reinhardt is the following [19, Theorem 2, P. 252]: Let be an integer that is not a degree of , . Then, among the convex -gons with diameter , the maximum perimeter is achieved if and only if a -gon is equilateral and inscribed in a Reulaux polygon of diameter so that the vertices of the Reulaux polygon are also the vertices of the -gon (such polygons are called Reinhardt polygons).
Moreover, this maximum perimeter coincides with the perimeter of the regular -gon of diameter , as E. Makai, J. noticed (a private conversation). Indeed, if is such a -gon, then the diameter of the polygon (this is the central symmetral of , that have the same perimeter as has) is also equal to , is inscribed into a circle of diameter , and has sides. So, this perimeter is no more than the perimeter of the regular -gon incribed into this circle (that can obtained via the above procedure from a regular -gon of diameter ).
We also note that for any simple , there is only one -gon of the maximum perimeter among -gons with diameter [19, P. 263].
The largest areas of a hexagon and an octagon, resp., of unit diameter were given by R. Graham [13], and by C. Audet, P. Hansen, F. Messine, J. Xiong [7]. The largest perimeter of an octagon of unit diameter was given in C. Audet, P. Hansen, F. Messine [5]. The cases of higher even numbers, and higher powers of seem to be open. See also [15] for more recent results on the topic.
C. Audet, P. Hansen, and F. Messine showed that the value is an upper bound for the width of any -sided polygon with unit perimeter. This bound is reached when is not a power of , and the corresponding optimal solutions are the regular polygons when is odd and clipped regular Reuleaux polygons when is even but not a power of [6].
We hope that these analogies will be useful in further research and will help to find an approach to the conjectures formulated above.
For the convenience of readers, here we provide the list of some important notations and definitions used in the paper (for each object, the page of the paper on which it is introduced is indicated).
-
•
For a given set in a given metric space , the following concepts are defined on the Page 1: the Chebyshev radius, a Chebyshev center, the relative Chebyshev radius (with respect to a given non-empty subset in ), the self Chebyshev radius.
-
•
Quadrilaterals called magic kites are defined on Page 1.
- •
- •
-
•
, the set of local minimum points of the function , is introduced on Page 7.
- •
- •
-
•
On Page 4, the notation is introduced for the number of points in the set , or, in other words, the number of self Chebyshev centers for .
-
•
Simple and non-simple self Chebyshev centers for are defined on Page 4.
-
•
A special class of quadrilaterals is introduced on Page 10.
References
- [1] A.R. Alimov, I.G. Tsar’kov, Chebyshev centres, Jung constants, and their applications, Russ. Math. Surv. 74(5) (2019), 775–849, MR4017575, Zbl.1435.41028,
- [2] C. Alsina, R.B. Nelsen, A cornucopia of quadrilaterals, The Dolciani Mathematical Expositions, 55. MAA Press, Providence, RI; American Mathematical Society, Providence, RI, 2020, MR4286138, Zbl.1443.51001
- [3] D. Amir, Characterizations of Inner Product Spaces, Operator Theory: Advances and Applications Series Profile, Vol. 20. Basel–Boston–Stuttgart: Birkhäuser–Verlag. Basel, 1986, MR0897527, Zbl.0617.46030.
- [4] D. Amir, Z. Ziegler, Relative Chebyshev centers in normed linear spaces, I, J. Approximation Theory 29 (1980), 235–252, MR0597471, Zbl.0457.41031.
- [5] C. Audet, P. Hansen, F. Messine, The small octagon with longest perimeter, J. Combin. Th. A, 114 (2007), 135–150, MR2275585, Zbl.1259.90096.
- [6] C. Audet, P. Hansen, F. Messine, Isoperimetric polygons of maximum width, Discrete Comput. Geom. 4(1) (2009), 45–60, MR2470069, Zbl.1160.52001.
- [7] C. Audet, P. Hansen, F. Messine, J. Xiong, The largest small octagon, J. Combin. Th. A, 98 (2002), 46–59, MR1897923, Zbl.1022.90013.
- [8] V. Balestro, H. Martini, Yu.G. Nikonorov, Yu.V. Nikonorova, Extremal problems for convex curves with a given self Chebyshev radius, Results in Mathematics, 76(2) (2021), Paper No. 87, 13 pp., MR4242658, Zbl.07369099.
- [9] H.H. Bauschke, P.K. Combettes, Convex analysis and monotone operator theory in Hilbert spaces, second edition, Cham: Springer, XIX+619 p. (2017), Zbl.1359.26003, MR3616647.
- [10] T. Bonnesen, W. Fenchel, Theory of Convex Bodies, BCS Associates, Moscow, ID, 1987. Translated from the German and edited by L. Boron, C. Christenson and B. Smith., MR0920366, Zbl.0628.52001.
- [11] K.J. Falconer, A characterisation of plane curves of constant width, J. Lond. Math. Soc., II. Ser. 16 (1977), 536–538, MR0461287, Zbl.0368.52003.
- [12] R. Fedorov (ed.), A. Belov (ed.), A. Kovaldzhi (ed.), I. Yashchenko (ed.), S. Levy (ed.), Moscow Mathematical Olympiads, 1993–1999. Translation of the 2006 Russian original. MSRI Mathematical Circles Library, 4. Providence, RI: American Mathematical Society (AMS); Berkeley, CA: Mathematical Sciences Research Institute (MSRI), 2011, MR2866883, Zbl.1236.00022.
- [13] R. Graham, The largest small hexagon, J. Combin. Th. A, 18 (1975), 165–170, MR360353, Zbl.0299.52006.
- [14] K.H. Hang, H. Wang, Solving problems in geometry. Insights and strategies, Mathematical Olympiad Series 10. Hackensack, NJ: World Scientific, 2017, Zbl.1372.00006.
- [15] K.G. Hare, M.J. Mossinghoff, Most Reinhardt polygons are sporadic, Geom. Dedicata 198 (2019), 1–18, MR3933447, Zbl.1412.52011.
- [16] R.H. Landau, A first course in scientific computing. Symbolic, graphic, and numeric modeling using Maple, Java, Mathematica, and Fortran90. With contributions by R. Wangberg, K. Augustson, M.J. Paez, C.C. Bordeianu and C. Barnes. Princeton University Press, Princeton, NJ, 2005, MR2136880, Zbl.1090.68120.
- [17] H. Martini, L. Montejano, D. Oliveros, Bodies of Constant Width. An Introduction to Convex Geometry with Applications. Birkhäuser/Springer, Cham, 2019, MR3930585, Zbl.06999635.
-
[18]
V.V. Prasolov
Problems in Plane Geometry, 5th ed., rev. and compl. (Russian),
Moscow, Russia: The Moscow Center for Continuous Mathematical Education, 2006.
Online access: https://mccme.ru/free-books/prasolov/planim5.pdf - [19] K. Reinhardt, Extremale Polygone gegebenen Durchmessers, Jahresbericht der Deutschen Mathematiker-Vereinigung, 31 (1922), 251–270,
- [20] R. Walter, On a minimax problem for ovals, Minimax Theory Appl. 2(2) (2017), 285–318, MR0920366, Zbl.1380.51012, see also arXiv:1606.06717.