The Finite Field Multi-Way Relay Channel with Correlated Sources: Beyond Three Users
Abstract
The multi-way relay channel (MWRC) models cooperative communication networks in which many users exchange messages via a relay. In this paper, we consider the finite field MWRC with correlated messages. The problem is to find all achievable rates, defined as the number of channel uses required per reliable exchange of message tuple. For the case of three users, we have previously established that for a special class of source distributions, the set of all achievable rates can be found [Ong et al., ISIT 2010]. The class is specified by an almost balanced conditional mutual information (ABCMI) condition. In this paper, we first generalize the ABCMI condition to the case of more than three users. We then show that if the sources satisfy the ABCMI condition, then the set of all achievable rates is found and can be attained using a separate source-channel coding architecture.
I Introduction
This paper investigates multi-way relay channels (MWRCs) where multiple users exchange correlated data via a relay. More specifically, each user is to send its data to all other users. There is no direct link among the users, and hence the users first transmit to a relay, which processes its received information and transmits back to the users (refer to Fig. 1). The purpose of this paper is to find the set of all achievable rates, which are defined as the number of channel uses required to reliably (in the usual Shannon sense) exchange each message tuple.
The joint source-channel coding problem in Fig. 1 includes, as special cases, the source coding work of Wyner et al. [1] and the channel capacity work of Ong et al. [2]. Separately, the Shannon limits of source coding [1] (through noiseless channel) and of channel coding [2] (with independent sources) are well established. However, these limits have not yet been discovered for noisy channels with correlated sources in general. For three users, Ong et al. [3] gave sufficient conditions for reliable communication using the separate source-channel coding paradigm. The key result of [3] was to show that these sufficient conditions are also necessary for a special class of source distributions, hence giving the set of all achievable rates. The class was characterized by an almost balanced conditional mutual information (ABCMI) condition. This paper extends the ABCMI concept to more than three users, and shows that if the sources have ABCMI, then the set of all achievable rates can be found. While the ABCMI condition for the three-user case is expressed in terms of the standard Shannon information measure, we will use I-Measure [4, Ch. 3] for more then three users—using Shannon’s measure is possible but the expressions would be much more complicated.
Though the ABCMI condition limits the class of sources for which the set of all achievable rates is found, this paper provides the following insights: (i) As achievability is derived based on a separate source-channel coding architecture, we show that source-channel separation is optimal for finite field MWRC with sources having ABCMI. (ii) Since ABCMI are constraints on the sources, the results in this paper are potentially useful for other channel models (not restricted to the finite field model). (iii) This paper highlights the usefulness of the I-Measure as a complement to the standard Shannon information measure.
II Main Results
II-A The Network Model
II-A1 Sources
Consider independent and identically distributed (i.i.d.) drawings of a tuple of correlated discrete finite random variables , i.e., . The message of user is given by .
II-A2 Channel
Each channel use of the finite field MWRC consists of an uplink and downlinks, characterized by
| Uplink: | (1) | |||
| Downlinks: | (2) |
where , for all , each take values in a finite field , denotes addition over , is the channel input from node , is the channel output received by node , and is the receiver noise at node . The noise is arbitrarily distributed, but is i.i.d. for each channel use. We have used the subscript to denote a user and the subscript to denote a node (which can be a user or the relay).
II-A3 Block Codes (joint source-channel codes with feedback)
Consider block codes for which the users exchange message tuples in channel uses. [Encoding:] The -th transmitted channel symbol of node is a function of its message and the symbols it previously observed on the downlink: , for all and for all . As the relay has no message, we set . [Decoding:] The messages decoded by user are a function of its message and the symbols it observed on the downlink: , for all .
II-A4 Achievable Rate
Let denote the probability that for any . The rate (or bandwidth expansion factor) of the code is the ratio of channel symbols to source symbols, . The rate is said to be achievable if the following is true: for any , there exists a block code, with and sufficiently large and , such that .
II-B Statement of Main Results
Theorem 1
Consider an -user finite field MWRC with correlated sources. If the sources have almost balanced conditional mutual information (ABCMI), then is achievable if and only if
| (3) |
The ABCMI condition used in Theorem 1 is rather technical and best defined using the -measure [4, Ch. 3]. For this reason, we specify this condition later in Section III-B after giving a brief review of the -measure in Section III-A. For now, it suffices to note that it is a non-trivial constraint placed on the joint distribution of .
The achievability (if assertion) of Theorem 1 is proved using a separate source-channel coding architecture, which involves intersecting a certain Slepian-Wolf source-coding region with the finite field MWRC capacity region [2]. The particular source-coding region of interest is the classic Slepian-Wolf region [5] with the total sum-rate constraint omitted; specifically, it is the set of all source-coding rate tuples such that
| (4) |
holds for all strict subsets . The next theorem will be a critical step in the proof of Theorem 1.
Theorem 2
Remark 1
Theorem 1 characterizes a class of sources (on any finite field MWRC) for which (i) the set of all achievable rates is known, and (ii) source-channel separation holds.
Remark 2
Remark 3
To prove Theorem 2, we need to select non-negative numbers that satisfy equations.
III Definition of ABCMI
III-A The I-Measure
Consider jointly distributed random variables . The Shannon measures of these random variables can be efficiently characterized via set operations and the I-measure. For each random variable , we define a (corresponding) set . Let be the field generated by using the usual set operations union , intersection , complement , and difference . The relationship between and is described by the I-Measure on , defined as [4, Ch. 3]
| (5) |
for any non-empty , where and .
The atoms of are sets of the form , where can either be or . There are atoms in , and we denote the atoms by
| (6) |
for all where . Note that each atom corresponds to a unique . For the atom in (6), we call the weight of the atom.
Remark 4
The I-measure of the atoms corresponds to the conditional mutual information of the variables. More specifically, is the mutual information among the variables conditioning on . For example, if , then , where is Shannon’s measure of conditional mutual information.
III-B Almost Balanced Conditional Mutual Information
For each , we define
| (7) | ||||
| (8) |
i.e., atoms of weight with the largest and the smallest measures respectively. With this, we define the ABCMI condition for random variables:
Definition 1
are said to have ABCMI if the following conditions hold:
and
for all , where
| (9) | ||||
| (10) |
where .
Remark 5
The ABCMI condition requires that all atoms of the same weight (except for those with weight equal to zero, one, or ) have about the same I-measure.
Remark 6
For any , , and , such that , it can be shown that .
Remark 7
For , we have , i.e., we recover the ABCMI condition for the three-user case [3].
IV Proof of Theorem 2
For the rest of this paper, we are interested in atoms only with weight between one and inclusive. So, we define and refer to as the set of all such atoms.
We propose to select in terms of the I-Measure:
| (11) |
where
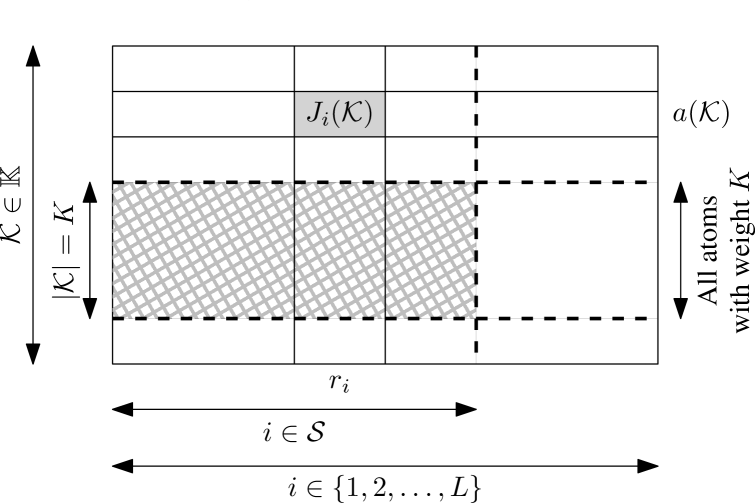
Each is chosen as the sum of the weighted (by a coefficient or ) I-measure of all atoms in . The assignments of ’s are depicted in Fig. 2. We term the contribution from the atom to . Each contribution is represented by a cell in Fig. 2, and each by a column.
IV-A For :
We first show that for any , we have
| (12) |
Since ’s are defined in terms of I-Measure, we link the measure of atoms to the entropies of the corresponding random variables:
| (13a) | ||||
| (13b) | ||||
where (13a) follows from [4, eqn. (3.43)], and (13b) is obtained by counting all the atoms in the set .
This means the RHS of (12) equals .
We now evaluate the LHS of (12) for some fixed . Consider some atom where . We evaluate the contributions from this atom to , i.e., one specific row in Fig. 2 less the cell :
-
•
of the cells each contribute .
-
•
The remaining cells each contribute .
So, summing the contributions from to , we have
| (14a) | |||
| (14b) | |||
Consider some atom where . The contributions from this atom to are as follows (again, one specific row in Fig. 2 less the cell ):
-
•
of the cells each contribute .
-
•
The remaining cells each contribute .
So, summing the contributions from to , we have
Combining the above results, we have, for a fixed ,
| (15a) | |||
| (15b) | |||
| (15c) | |||
| (15d) | |||
IV-B For :
Consider some where . We now show that if the ABCMI is satisfied, then
| (16a) | ||||
| (16b) | ||||
Define and . The LHS of (16a) is the sum of contributions from all atoms in to all . We will divide all atoms in according to their weight : (i) , (ii) , and (iii) . So, we have
| (17) |
IV-B1 Atoms with weight
For atoms with weight one,
| (18) |
Summing the contributions from all atoms with weight one to all ,
| (19) |
IV-B2 Atoms with weight
We fix . Consider the contributions from all atoms with weight to a particular , (one column in the hashed region in Fig. 2). There are
-
[]
contributions with coefficient [from atoms where ; there are ways to select the other elements in from ], and
-
[]
contributions with coefficient [from atoms where ; there are ways to select the other elements in from ].
There are atoms with weight . We can check that .
Since observations and are true for each , we have the following contributions from all atoms with weight to (the hashed region in Fig. 2): There are
-
[]
contributions with coefficient , and
-
[]
contributions with coefficient .
For an atom , we say that the atom is active if ; otherwise, i.e., , the atoms is said to be inactive,
Consider the contributions from a particular active atom to (one row in the hashed region in Fig. 2). We have the following contributions from this atom to :
-
[]
Since , cells in the hashed row each contribute .
-
[]
The remaining cells each contribute .
Summing the contributions from this active atom to ,
For any fixed , there are active atoms with weight (different ways of choosing ), and observations and are true for each active atom. Combining –, we can further categorize the contributions from all atoms with weight to :
-
[]
Out of the contributions with coefficient , of them are from active atoms.
-
[]
Out of the contributions with coefficient , of them are from active atoms.
IV-B3 Atoms with weight
Consider the contributions from all atoms with weight to , for some . From observations and , we know that there are
-
•
contributions with coefficient , and
-
•
contributions with coefficient .
Summing these contributions, we have for any that
| (22) |
Since , the ABCMI condition implies that for all . Hence, the inequality in (22) follows.
IV-B4 Combining the contributions of to
V Proof of Theorem 1
V-A Necessary Conditions
Lemma 1
Consider a finite field MWRC with correlated sources. A rate is achievable only if (3) holds for all .
Lemma 1 can be proved by generalizing the converse theorem [6, Appx. A] for to arbitrary . The details are omitted.
V-B Sufficient Conditions
Consider a separate source-channel coding architecture.
V-B1 Source Coding Region
We have the following source coding result for correlated sources:
Lemma 2
Consider correlated sources as defined in Section II-A1. Each user encodes its message to an index , for all . It reveals its index to all other users. Using these indices and its own message, each user can then decode the messages of all other users, i.e., , if (4) is satisfied for all non-empty strict subsets .
The above result is obtained by combining the results for (i) source coding for correlated sources [7, Thm. 2], and (ii) the three-user noiseless MWRC [1, Sec. II.B.1]. Note that the relay does not participate in the source code, in contrast to the setup of [1]. Instead, the relay participates in the channel code.
V-B2 Channel Coding Region
We have the following channel coding result for the finite field MWRC [2]:
V-B3 Achievable Rates
We propose the following separate source-channel coding scheme. Fix . Let , where each is i.i.d. and uniformly distributed on . We call a dither. The dithers are made known to all users. User performs source coding to compresses its message to an index and computes . The random variables are independent, with being uniformly distributed on . The nodes then perform channel coding with as inputs. If (23) is satisfied, then each user can recover , from which it can obtain . If (4) is satisfied, then each user can recover all other users’ messages , using the indices ’s and its own message . This means the rate is achievable.
Using the above coding scheme, we have the following:
V-C Proof of Theorem 1 (Necessary and Sufficient Conditions)
The “only if” part follows directly from Lemma 1 (regardless of whether the sources have ABCMI). We now prove the “if” part. Suppose that the sources have ABCMI. From Theorem 2, there exists a tuple such that conditions and are satisfied. These conditions imply that (4) is satisfied for all non-empty strict subsets . Let . Condition further implies . So, if (3) is true, then (23) is satisfied for all . From Lemma 4, is achievable. .
Remark 8
For a fixed source correlation structure and a finite field MWRC, one can check if the -dimensional polytope defined by the source coding region and that by the channel coding region (scaled by ) intersect when equals the RHS of (3). If the regions intersect, then we have the set of all achievable for this particular source-channel combination. Theorem 1 characterizes a class of such sources.
References
- [1] A. D. Wyner, J. K. Wolf, and F. M. J. Willems, “Communicating via a processing broadcast satellite,” IEEE Trans. Inf. Theory, vol. 48, no. 6, pp. 1243–1249, June 2002.
- [2] L. Ong, S. J. Johnson, and C. M. Kellett, “The capacity region of multiway relay channels over finite fields with full data exchange,” IEEE Trans. Inf. Theory, vol. 57, no. 5, pp. 3016–3031, May 2011.
- [3] L. Ong, R. Timo, G. Lechner, S. J. Johnson, and C. M. Kellett, “The finite field multi-way relay channel with correlated sources: The three-user case,” in Proc. IEEE Int. Symp. on Inf. Theory (ISIT), St Petersburg, Russia, July 31–Aug. 5 2011, pp. 2238–2242.
- [4] R. W. Yeung, Information Theory and Network Coding, Springer, 2008.
- [5] T. S. Han, “Slepian-Wolf-Cover theorem for networks of channels,” Inf. and Control, vol. 47, no. 1, pp. 67–83, Oct. 1980.
- [6] L. Ong, R. Timo, G. Lechner, S. J. Johnson, and C. M. Kellett, “The three-user finite field multi-way relay channel with correlated sources,” submitted to IEEE Trans. Inf. Theory, 2011. [Online]. Available: http://arxiv.org/abs/1201.1684v1
- [7] T. M. Cover, “A proof of the data compression theorem of Slepian and Wolf for ergodic sources,” IEEE Trans. Inf. Theory, vol. IT-21, no. 2, pp. 226–228, Mar. 1975.