The First Accurate Parallax Distance to a Black Hole
Abstract
Using astrometric VLBI observations, we have determined the parallax of the black hole X-ray binary V404 Cyg to be mas, corresponding to a distance of kpc, significantly lower than the previously accepted value. This model-independent estimate is the most accurate distance to a Galactic stellar-mass black hole measured to date. With this new distance, we confirm that the source was not super-Eddington during its 1989 outburst. The fitted distance and proper motion imply that the black hole in this system likely formed in a supernova, with the peculiar velocity being consistent with a recoil (Blaauw) kick. The size of the quiescent jets inferred to exist in this system is AU at 22 GHz. Astrometric observations of a larger sample of such systems would provide useful insights into the formation and properties of accreting stellar-mass black holes.
Subject headings:
astrometry — X-rays: binaries — stars: distances — stars: kinematics — radio continuum: stars — stars: individual (V404 Cyg)1. Introduction
Stellar-mass black holes in accreting X-ray binary systems provide unique probes of the physical properties and formation mechanism of black holes, as well as the physics of accretion and associated outflow. However, our understanding of black hole systems is hampered by the fact that distances to X-ray binaries are relatively poorly known, typically uncertain by 50% or more (Jonker & Nelemans, 2004). Standard spectroscopic estimates are handicapped by the distortions induced in the secondary by its compact partner, contamination by emission from the accretion disc (Reynolds et al., 2008), and uncertainties in estimates of interstellar absorption.
Since these distance uncertainties are systematic rather than random, they cannot be reduced by making more observations. According to Jonker & Nelemans (2004), these systematic uncertainties can artificially enlarge the difference between the quiescent X-ray luminosities of black hole and neutron star systems. If true this would undermine the claimed evidence for an event horizon (Narayan et al., 1997; Menou et al., 1999; Garcia et al., 2001). Accurate distances are also required to interpret the measured proper motions of black hole X-ray binaries, by converting a measured proper motion into a physical speed, from which we can derive the peculiar velocity of the source (e.g., Mirabel et al., 2001, 2002; Mirabel & Rodrigues, 2003; Dhawan et al., 2007; Miller-Jones et al., 2009). This can be used to place constraints on any velocity kick the black hole might have received in its natal supernova, and hence on the formation mechanism of the black hole (Brandt et al., 1995; Willems et al., 2005; Fragos et al., 2009).
The only direct, model-independent method of measuring distances is via trigonometric parallax, which has hitherto been impossible for black hole X-ray binary systems, since they lie at distances of several kpc, and hence require sub-milliarcsecond astrometry to measure their parallaxes. Very Long Baseline Interferometry (VLBI) at radio wavelengths is currently the only technique available for such high-precision astrometric measurements. However, black hole X-ray binaries spend the majority of their time in a faint quiescent state, where they are often not detected in the radio band at current sensitivities. They become bright enough to be detected during outbursts, but such outbursts are typically not sufficiently long or frequent and do not sample the Earth’s orbit well enough to make a parallax measurement feasible. During outbursts, the radio emission is often resolved at the high angular resolutions required for precision astrometry, making it difficult to determine the true location of the binary system from epoch to epoch. Lastly, many black hole X-ray binaries are located in or close to the Galactic Plane, such that the scatter-broadening along the line of sight makes high-precision astrometry impossible in the centimeter waveband where current VLBI arrays have the highest sensitivity.
Here we present High Sensitivity Array (HSA) observations of V404 Cyg, the most luminous known black hole X-ray binary in quiescence. With a mass function of (Casares & Charles, 1994), the compact object is a dynamically-confirmed black hole, accreting matter from a K0 subgiant companion star (Casares et al., 1993). The system has a quiescent radio flux density of 0.3 mJy, with a flat spectrum indicative of a self-absorbed compact jet (Gallo et al., 2005), although the jets are not resolved at the angular resolution of the HSA (Miller-Jones et al., 2008). The persistent, unresolved radio emission makes this source a good target for astrometric observations to measure its parallax.
2. Observations and results
We observed V404 Cyg every 3 months over the course of one year, using the HSA. Two of the observations were made at the times of maximum parallactic displacement in Right Ascension (R.A.), since the R.A. signal is larger, and, owing to the greater size of the array in the east-west dimension, has smaller error bars than that in Declination. We observed at a frequency of 8.4 GHz, in dual circular polarization, with an observing bandwidth of 64 MHz per polarization. To these four HSA observations we added three archival datasets, two of which have already been reported (Miller-Jones et al., 2008, 2009), and one in which the source was previously not significantly detected (Mioduszewski et al., 2008), but knowing the astrometric parameters of the source, we were able to detect it at the level. A fourth archival epoch did not detect the source to a limit of 0.36 mJy beam-1. A summary of the observations is listed in Table 1, and shows the extent of the source variability. In only one of the epochs was the source brighter than the upper limit of this archival dataset (in which none of the large dishes of the HSA were available), making the non-detection consistent with the expected source flux density.
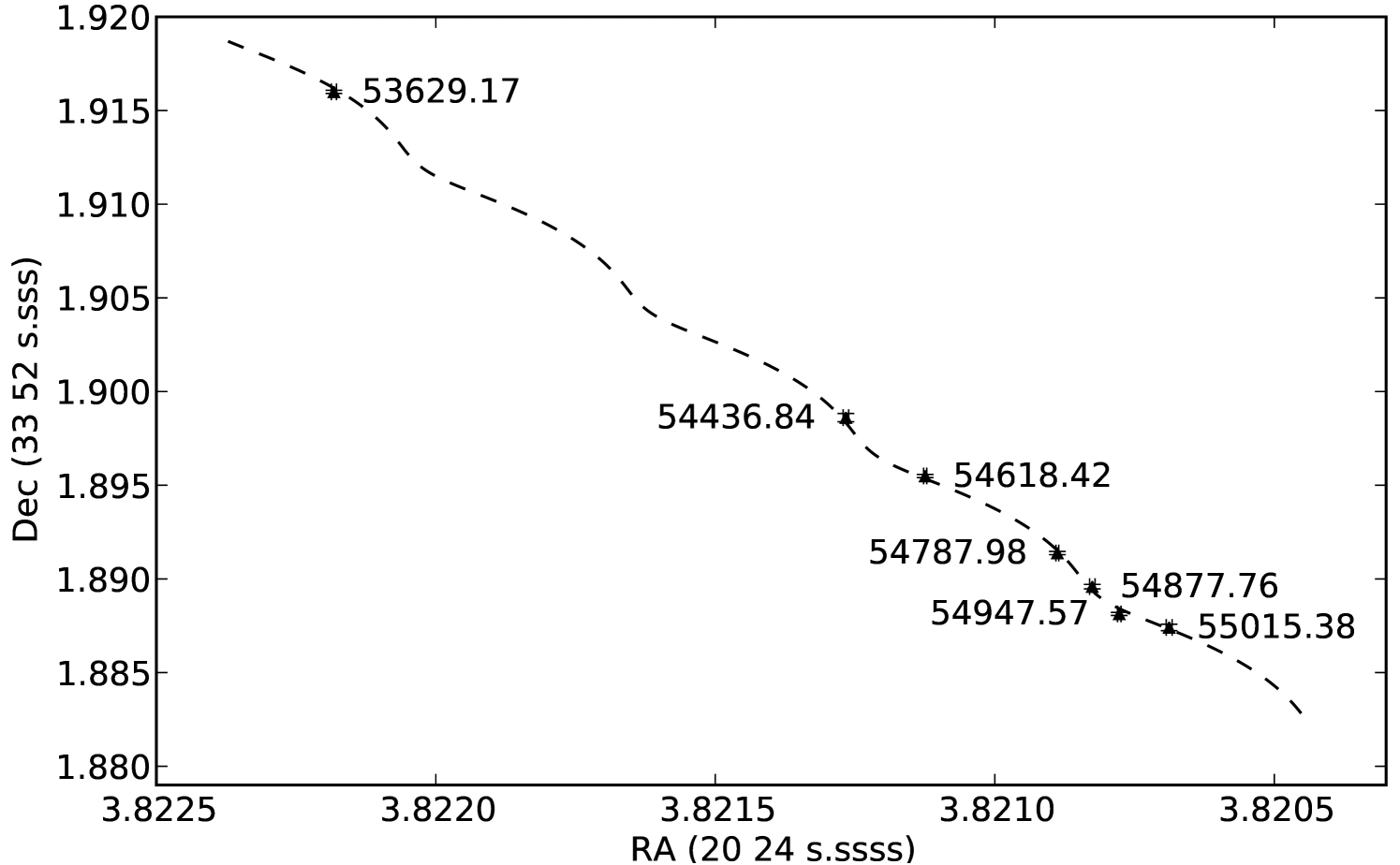
In all cases, the observations were phase-referenced to a bright, nearby calibrator from the International Celestial Reference Frame (ICRF) source list, J 2025+3343 (Ma et al., 1998), located only 16.6′ from the target source. This implies that our systematic errors, which scale with distance from the phase reference source, should be relatively small ( as; see below). We observed in 3-min cycles, spending 1 min on the phase reference source and 2 min on the target in each cycle. To maximize astrometric accuracy, all data below elevation were discarded. We also discarded data taken during the short timescale flares seen in a number of the observations (e.g., Miller-Jones et al., 2008), in case the assumed variations in the jet power responsible for the flaring events translated into positional offsets. To enable us to estimate the systematic errors affecting the astrometry, we substituted every seventh scan on the target source with an observation of a check source, the ICRF calibrator J2023+3153, located away from the phase reference source. Data were reduced according to standard procedures within AIPS (Greisen, 2003), and the source position at each epoch was determined by fitting an elliptical Gaussian to the source. In no case did the source appear to be resolved. Since the first epoch of archival data assumed a different position for the phase reference source, we corrected all epochs to a common calibrator position of , (J 2000) before fitting for the proper motion and parallax of V404 Cyg. The measured positions are shown in Figure 1, together with the best-fit parallax and proper motion.
Pradel et al. (2006) used simulations to derive an approximate formula for the systematic errors affecting various VLBI arrays. For our calibrator-target separation and source declination, the estimated systematic errors (for a mean value of the wet zenith path delay) are 26 as in R.A. and 30 as in Dec. The fitted positions of the check source show an rms scatter of 13 as in R.A. and 31 as in Dec. Since the check source is seven times further away from the phase reference source than the target, this provides a rigorous upper limit on the systematic errors in position. As seen from Table 1, our astrometric accuracy is limited by signal-to-noise rather than systematic errors. Nevertheless, the systematic errors estimated from Pradel et al. (2006) were added to the statistical errors in quadrature before using the singular value decomposition (SVD) method (as detailed in Loinard et al., 2007) to fit for a reference position and proper motion in R.A. and Dec., and for the source parallax. The best-fitting astrometric parameters, taking the mid-point of the observations, MJD 54322, as the reference date, were:
The fitted parallax signal, with the best-fitting proper motion removed, is shown in Figure 2. The reduced- value of the fit is 3.2, which, with 9 degrees of freedom, implies a %-confidence result. A bootstrap data-stripping analysis, as detailed by Chatterjee et al. (2009), confirmed the validity of these results, giving median values differing by less than from those found by the SVD fit, albeit with slightly larger error bars owing to the data stripping. Our fitted parallax corresponds to a source distance of kpc.
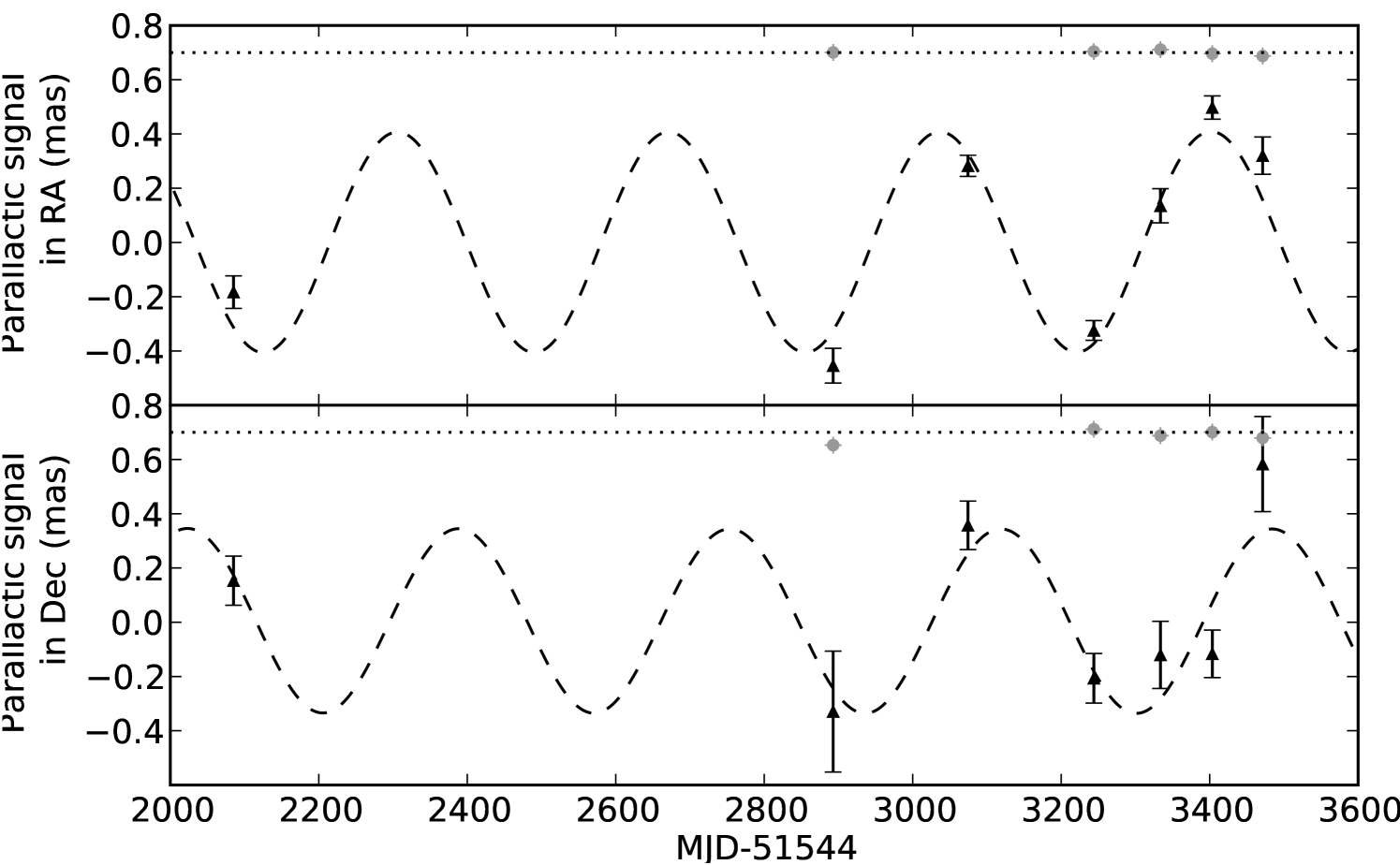
3. Discussion
3.1. Extinction-based distances
Our fitted source distance is significantly closer than the best previous distance estimate of kpc (Jonker & Nelemans, 2004). However, that estimate was derived using an assumed interstellar extinction of , and did not take into account uncertainties in the extinction. Hynes et al. (2009) fitted the full multiwavelength spectral energy distribution with a template spectrum for a K0 IV star and found a formal best fit reddening of . Indeed, we find that increasing to close to 4.0 brings the estimate of Jonker & Nelemans (2004) down into agreement with our results. This highlights the importance of using accurate extinction values when estimating source distances. Given the typical uncertainties in the extinction towards black hole soft X-ray transients (Jonker & Nelemans, 2004), we conclude that this issue is likely to affect the majority of such systems, rendering their distance estimates also uncertain.
3.2. Source luminosity
Our measured distance is significantly closer than the 3.5–4.0 kpc commonly assumed for the source (e.g., Jonker & Nelemans, 2004; Gallo et al., 2005; Bradley et al., 2007; Corbel et al., 2008), reducing its luminosity by a factor of 2.2–2.8. The quiescent 0.3–10 keV unabsorbed flux of erg cm-2 s-1, derived using a power-law model for the X-ray spectrum (Bradley et al., 2007), implies a quiescent luminosity of erg s-1. Makino (1989) measured a maximum flux of 17 Crab with Ginga during the 1989 outburst of V404 Cyg, implying a 1–70 keV luminosity of erg s-1, which is of order for the black hole mass of derived for V404 Cyg (Shahbaz et al., 1994). Thus the system was not super-Eddington during the 1989 outburst. Furthermore, in reducing the source radio and X-ray luminosities, our new distance will reduce the scatter in the radio/X-ray correlation (Gallo et al., 2003), bringing the points measured for V404 Cyg into better alignment with those of GX 339-4.
3.3. Peculiar velocity
With a more accurate distance and proper motion for the source, and the updated Galactic rotation parameters ( kpc, km s-1) given by Reid et al. (2009) (but note McMillan & Binney, 2009), we can revisit the analysis of Miller-Jones et al. (2009) to derive a more accurate peculiar velocity of km s-1. This error bar now includes the uncertainties in both the distance and in all three space velocity components. This new value is significantly lower than the best-fitting peculiar velocity of 64 km s-1 derived for a 4 kpc distance (Miller-Jones et al., 2009), and can easily be achieved via a Blaauw kick, such that no asymmetric supernova kick is required. The component of the peculiar velocity in the Galactic Plane is 39.6 km s-1, which, compared to the expected velocity dispersion in the Galactic Plane of 18.9 km s-1(Mignard, 2000) for the likely F0-F5 progenitor of the donor star, is a result, implying a probability of only 0.038 that the peculiar velocity is a result of Galactic velocity dispersion (for more details, see Miller-Jones et al., 2009). We therefore find it most probable that the peculiar velocity arises from a natal supernova kick, the magnitude of which is consistent with recoil due to mass loss (a Blaauw kick), with any additional asymmetric kick being small.
3.4. Size constraints
Miller-Jones et al. (2009) placed an upper limit of 1.3 mas on the source size, corresponding to a physical size of AU at our new distance. While we did not resolve the source, our highest-resolution data, taken with a global VLBI array at 22 GHz, constrain the source size to mas, a physical size of AU. We can therefore place a lower limit of K on the brightness temperature of the source. From the high brightness temperature, the observed flat radio spectrum (Gallo et al., 2005) characteristic of a steady, partially self-absorbed conical outflow (Blandford & Königl, 1979), and the location of the source on the radio/X-ray correlation of Gallo et al. (2003), at the high-luminosity end of which jets have been directly resolved (Stirling et al., 2001), we infer that the observed radio emission is likely to arise from compact, steady synchrotron-emitting jets.
Our upper limit on the jet size can be compared to that of the resolved jets in Cygnus X-1 (Stirling et al., 2001), with an angular size of 15 mas at 8.4 GHz. Since the jet size scales inversely with observing frequency (Blandford & Königl, 1979), this implies 5 mas at 22 GHz, for a physical scale of AU. Since Heinz (2006) found the jet length should scale as where is the jet luminosity, then the difference in radio luminosities of the two sources suggests a size scale of AU for V404 Cyg at 22 GHz. Thus we are beginning to probe the angular scales on which the jets may be resolved.
The scatter in the residuals after our parallax fit (0.10 mas in R.A. and 0.14 mas in Dec.) can also help constrain the size and stability of the jets, since any motion of unresolved emitting knots along the jet will change the brightness distribution and hence the measured centroid position. In particular, a comparison of source positions measured during flares with those from the adjacent non-flaring data from which the proper motion and parallax were derived will constrain the changes in jet morphology during flaring events. If the magnitude of the flares correlates with jet power and hence jet size, we might expect brighter flares to show the largest positional shifts. For our brightest flare, in which the flux density increased by a factor of 3, the upper limit to the shift in the centroid position is 0.3 mas. This constrains the emitting region during the flare to be at an angular separation of mas (a physical separation of AU) from the surface in the steady jet where the optical depth is unity. While such small positional shifts imply that minor flaring events should not destroy the parallax signal, if they can be better constrained during larger flares or with a higher-sensitivity array, such positional shifts could in future provide a method for determining the size scale of quiescent jets even in cases where they cannot be directly resolved.
3.5. Wider implications
These observations demonstrate that it is feasible to measure a parallax distance to a sufficiently bright quiescent black hole X-ray binary. We have shown that the radio jets inferred to exist in the quiescent state of X-ray binaries do not hinder the astrometry sufficiently to render a parallax measurement impossible. The advent of the EVLA and the ongoing VLBA sensitivity upgrade will allow us to extend this method to a number of systems with fainter quiescent jets, as well as opening up the possibility of detecting gyrosynchrotron emission from low-mass donor stars (e.g., Güdel, 2002). With accurate distances to a sample of quiescent black hole and neutron star systems, it will be possible to quantitatively assess the claim that black holes are less luminous than neutron star systems (Narayan et al., 1997; Menou et al., 1999; Garcia et al., 2001). Accurate outburst luminosities for a sample of black holes will help quantify the factor by which such systems can exceed their Eddington luminosities, with implications for the nature of Ultraluminous X-ray sources (ULXs) in external galaxies.
With a sample of black hole proper motions and parallax distances, it will be possible to derive accurate peculiar velocities to probe the formation mechanisms of black holes of different masses. The three main channels are direct collapse (giving no peculiar velocity), or via a supernova and fallback onto the proto-neutron star, with either a relatively small recoil kick for a symmetric supernova, or a potentially large kick from an asymmetric explosion. In the fallback case it is currently unclear whether and how the velocity scales with the amount of matter falling back on the neutron star. A sample of black hole peculiar velocities would provide much-needed observational constraints, and help to determine whether there is a mass cutoff between black holes forming via direct collapse and those which form via a supernova and fallback (Fryer & Kalogera, 2001). Finally, one of the methods currently employed to measure black hole spins, via fitting of the X-ray spectrum during the thermal-dominant state of the source during outburst (McClintock et al., 2006) requires accurate distances. Better distance constraints will allow for improved comparisons with spins derived via fitting the general relativistic distortions in disk reflection lines (e.g., Miller et al., 2009), providing further insights into the generation and distribution of black hole spins.
4. Conclusions
We have used HSA observations to measure the most accurate distance to a black hole to date, via the method of trigonometric parallax. The distance of V404 Cyg is kpc, significantly lower than the previous best estimate of the source distance, and demonstrating that uncertainties in the interstellar extinction can introduce significant errors into distance estimates. With the new distance, we can determine that V404 Cyg did not exceed its Eddington luminosity during the 1989 outburst, and that it is likely to have formed in a natal supernova, with the peculiar velocity being consistent with recoil from the ejected mass, and any asymmetric kick being small. We have further constrained the size of the quiescent jets in the source to AU. These observations demonstrate the feasibility of measuring parallax distances to black hole X-ray binaries using VLBI techniques, which could, with a larger sample of systems, firm up evidence for black hole event horizons, and provide new insights into black hole spins, the mechanism of black hole formation, and the nature of ULXs.
References
- Blaauw (1961) Blaauw, A. 1961, Bull. Astron. Inst. Netherlands, 15, 265
- Blandford & Königl (1979) Blandford, R. D., Königl, A. 1979, ApJ, 232, 34
- Bradley et al. (2007) Bradley, C. K., Hynes, R. I., Kong, A. K. H., Haswell, C. A., Casares, J., & Gallo, E. 2007, ApJ, 667, 427
- Brandt et al. (1995) Brandt, W. N., Podsiadlowski, P., & Sigurdsson, S., 1995, MNRAS, 277, L35
- Casares & Charles (1994) Casares, J., & Charles, P. A. 1994, MNRAS, 271, L5
- Casares et al. (1993) Casares, J., Charles, P. A., Naylor, T., & Pavlenko, E. P. 1993, MNRAS, 265, 834
- Chatterjee et al. (2009) Chatterjee, S., et al., 2009, ApJ, 698, 250
- Corbel et al. (2008) Corbel, S., Koerding, E., & Kaaret, P., 2008, MNRAS, 389, 1697
- Dhawan et al. (2007) Dhawan, V., Mirabel, I. F., Ribó, M., & Rodrigues, I. 2007, ApJ, 668, 430
- Fragos et al. (2009) Fragos, T., Willems, B., Kalogera, V., Ivanova, N., Rockefeller, G., Fryer, C. L., Young, P. A. 2009, ApJ, 697, 1057
- Fryer & Kalogera (2001) Fryer, C. L., & Kalogera, V., 2001, ApJ, 554, 548
- Gallo et al. (2003) Gallo, E., Fender, R. P., & Pooley, G. G., 2003, MNRAS, 344, 60
- Gallo et al. (2005) Gallo, E., Fender, R. P., & Hynes, R. I. 2005, MNRAS, 356, 1017
- Gallo et al. (2006) Gallo, E., Fender, R. P., Miller-Jones, J. C. A., Merloni, A., Jonker, P. G., Heinz, S., Maccarone, T. J., & van der Klis M. 2006, MNRAS, 370, 1351
- Garcia et al. (2001) Garcia, M. R., McClintock, J. E., Narayan, R., Callanan, P., Barret, D., & Murray, S. S. 2001, ApJ, 553, L47
- Greisen (2003) Greisen E. W. 2003, in Information Handling in Astronomy: Historical Vistas, ed. A. Heck (Dordrecht: Kluwer), 109
- Güdel (2002) Güdel, M., 2002, ARA&A, 40, 217
- Heinz (2006) Heinz, S., 2006, ApJ, 636, 316
- Hynes et al. (2009) Hynes, R. I., Bradley, C. K., Rupen, M., Gallo, E., Fender, R. P., Casares, J., & Zurita, C., arXiv:0907.4376
- Jonker & Nelemans (2004) Jonker, P. G., & Nelemans, G. 2004, MNRAS, 354, 355
- Loinard et al. (2007) Loinard, L., Torres, R. M., Mioduszewski, A. J., Rodríguez, L. F., González-Lópezlira, R. A., Lachaume, R., Vázquez, V., & González, E. 2007, ApJ, 671, 546
- Ma et al. (1998) Ma, C., et al. 1998, AJ, 116, 516
- Makino (1989) Makino, F., Wagner, R. M., Starrfield, S., Buie, M. W., Bond, H. E., Johnson, J., Harrison, T., & Gehrz, R. D., 1989, IAU Circ. 4786, http://www.cfa.harvard.edu/iauc/04700/04786.html#Item0
- McClintock et al. (2006) McClintock, J. E., Shafee, R., Narayan, R., Remillard, R. A., Davis, S. W., & Li, L.-X., 2006, ApJ, 652, 518
- McMillan & Binney (2009) McMillan, P. J., & Binney, J. J. 2009, arXiv:0907.4685
- Menou et al. (1999) Menou, K., Esin, A. A., Narayan, R., Garcia, M. R., Lasota, J.-P., & McClintock, J. E. 1999, ApJ, 520, 276
- Mignard (2000) Mignard, F. 2000, A&A, 354, 522
- Miller et al. (2009) Miller, J. M., Reynolds, C. S., Fabian, A. C., Miniutti, G., & Gallo, L. C., 2009, ApJ, 697, 900
- Miller-Jones et al. (2008) Miller-Jones, J. C. A., Gallo, E., Rupen, M. P., Mioduszewski, A. J., Brisken, W., Fender, R. P., Jonker, P. G., & Maccarone, T. J. 2008, MNRAS, 388, 1751
- Miller-Jones et al. (2009) Miller-Jones, J. C. A., Jonker, P. G., Nelemans, G., Portegies Zwart, S., Dhawan, V., Brisken, W., Gallo, E., & Rupen, M. P. 2009, MNRAS, 394, 1440
- Mioduszewski et al. (2008) Mioduszewski, A., Hynes, R., Rupen, M. P., & Dhawan, V. 2008, in AIP Conf. Proc., 1010, A Population Explosion: The Nature & Evolution of X-ray Binaries in Diverse Environments, ed. R. M. Bandyopadhyay, S. Wachter, D. Gelino & C. R. Gelino (Melville, NY: AIP), 74
- Mirabel et al. (2001) Mirabel, I. F., Dhawan, V., Mignani, R. P., Rodrigues, I., & Guglielmetti, F. 2001, Nature, 413, 139
- Mirabel et al. (2002) Mirabel, I. F., Mignani, R., Rodrigues, I., Combi, J. A., Rodríguez, L. F., & Guglielmetti, F. 2002, A&A, 395, 595
- Mirabel & Rodrigues (2003) Mirabel, I. F., & Rodrigues, I. 2003, Science, 300, 1119
- Narayan et al. (1997) Narayan, R., Garcia, M. R., & McClintock, J. E., 1997, ApJ, 478, L79
- Pradel et al. (2006) Pradel, N., Charlot, P., & Lestrade, J.-F. 2006, A&A, 452, 1099
- Reid et al. (2009) Reid, M. J., et al., 2009, ApJ, 700, 137
- Reynolds et al. (2008) Reynolds, M. T., Callanan, P. J., Robinson, E. L., & Froning, C. S., 2008, MNRAS, 387, 788
- Shahbaz et al. (1994) Shahbaz, T., Ringwald, F. A., Bunn, J. C., Naylor, T., Charles, P. A., & Casares, J. 1994, MNRAS, 271, L10
- Stirling et al. (2001) Stirling, A. M., Spencer, R. E., de la Force, C. J., Garrett, M. A., Fender, R. P., & Ogley, R. N. 2001, MNRAS, 327, 1273
- Willems et al. (2005) Willems, B., Henninger, M., Levin, T., Ivanova, N., Kalogera, V., McGhee, K., Timmes, F. X., & Fryer, C. L. 2005, ApJ, 625, 324
| Project | Date | MJDaaSpecified Modified Julian Dates (MJDs) are for the mid-point of the observation, with the quoted uncertainties reflecting the observation duration | Array | Frequency | Bandwidth | Flux densitybbFlux density measured after discarding short-timescale flaring events | R.A.ccAll positions are specified in J 2000 co-ordinates | Dec.ccAll positions are specified in J 2000 co-ordinates |
|---|---|---|---|---|---|---|---|---|
| (GHz) | (MHz) | (mJy beam-1) | ||||||
| BM117 | 1999 Apr 10 | 51278.60(25) | VLBA | 15.353 | 32 | ddSource not significantly detected at this epoch; upper limit given on flux density | - | - |
| BM231 | 2005 Sep 16 | 53629.17(21) | VLBA, VLA | 15.365 | 32 | |||
| BG168 | 2007 Dec 02 | 54436.84(09) | VLBA, GBT, VLA | 8.421 | 32 | |||
| GM064 | 2008 Jun 01 | 54618.42(25) | VLBA, GBT, VLA, EVNeeData taken with a global VLBI array, comprising the VLBA, GBT, phased VLA, seven dishes of the EVN (Cm, Eb, Jb2, Mc, Mh, Nt, Tr), and the Robledo antenna from the DSN | 22.220 | 64 | |||
| BM290 | 2008 Nov 17 | 54787.98(09) | VLBA, GBT | 8.408 | 64 | |||
| BM290 | 2008 Feb 15 | 54877.76(11) | VLBA, GBT, VLA | 8.408 | 64 | |||
| BM290 | 2009 Apr 26 | 54947.57(11) | VLBA, GBT, VLA | 8.408 | 64 | |||
| BM290 | 2009 Jul 03 | 55015.38(10) | VLBA, GBT, VLA | 8.408 | 64 |