The free surface of a colloidal chiral fluid: waves and instabilities from odd stress and Hall viscosity
Abstract
In simple fluids, such as water, invariance under parity and time-reversal symmetry imposes that the rotation of constituent “atoms” are determined by the flow and that viscous stresses damp motion. Activation of the rotational degrees of freedom of a fluid by spinning its atomic building blocks breaks these constraints and has thus been the subject of fundamental theoretical interest across classical and quantum fluids lenz_membranes_2003 ; yeo_rheology_2010 ; furthauer_active_2013 ; nguyen_emergent_2014 ; goto_purely_2015 ; yeo_collective_2015 ; climent_dynamic_2006 ; avron_viscosity_1995 ; wiegmann_anomalous_2014 ; ariman_microcontinuum_1973 ; rosensweig2013 ; Rinaldi2014 . However, the creation of a model liquid which isolates chiral hydrodynamic phenomena has remained experimentally elusive. Here we report the creation of a cohesive two-dimensional chiral liquid consisting of millions of spinning colloidal magnets and study its flows. We find that dissipative viscous “edge pumping” is a key and general mechanism of chiral hydrodynamics, driving uni-directional surface waves and instabilities, with no counterpart in conventional fluids. Spectral measurements of the chiral surface dynamics reveal the presence of Hall viscosity, an experimentally long sought property of chiral fluids avron_viscosity_1995 ; avron_odd_1998 ; abanov2018 ; banerjee_odd_2017 . Precise measurements and comparison with theory demonstrate excellent agreement with a minimal but complete chiral hydrodynamic model, paving the way for the exploration of chiral hydrodynamics in experiment.
Hydrodynamic theories describe the flow of systems as diverse as water, quantum electronic states bandurin_negative_2016 , and galaxies pringle_astrophysical_2007 over decades in scale secchi_massive_2016 . Since hydrodynamic equations are built on symmetry principles and conservation laws alone, systems with similar symmetries have similar descriptions and flow in the same way.
For example, symmetry under parity and time reversal – conditions met by all conventional fluids at thermal equilibrium – constrains both the stress and viscosity tensors to be symmetric. These constraints are in principle alleviated in collections of interacting units that are driven to rotate tsai_chiral_2005 ; scaffidi_hydrodynamic_2017 ; wiegmann_anomalous_2014 ; banerjee_odd_2017 ; van_zuiden_spatiotemporal_2016 ; furthauer_active_2013 ; avron_viscosity_1995 ; snezhko_complex_2016 ; kokot2017 . This seemingly innocent twist on an otherwise structureless fluid represents, however, an elemental change with rich hydrodynamic consequences common to quantum Hall fluids, vortex fluids, and chiral condensed matter. Collections of spinning particles offer a natural opportunity to engineer and study the properties of such chiral fluids; experimental examples include rotating bacteria petroff_fast-moving_2015 , colloidal and millimeter-scale magnets grzybowski_dynamic_2000 ; grzybowski_dynamic_2001 ; grzybowski_dynamics_2002 ; grzybowski_dynamic_2002 ; belovs_hydrodynamics_2016 ; yan_rotating_2014 ; yan_jing_colloidal_2015 , ferrofluids in rotating magnetic fields rosensweig2013 ; Rinaldi2014 , and shaken chiral grains tsai_chiral_2005 ; scholz_rotating_2018 . Such systems have been shown to have non-trivial dynamics. For example, ferrofluids driven by AC fields can flow against external pressure Bacri1995 and small numbers of spinning particles self-assemble into dynamic crystalline clusters grzybowski_dynamic_2000 ; grzybowski_dynamic_2001 ; grzybowski_dynamics_2002 ; grzybowski_dynamic_2002 ; climent_dynamic_2006 ; yan_rotating_2014 ; yan_jing_colloidal_2015 .

I A colloidal chiral fluid
We report the creation of a millimeter-scale cohesive chiral fluid (Fig. 1a) by spinning millions of colloidal magnets with a magnetic field (Figs. 1b, 1c), and we track its flows over hours (see Supplementary Movies 1, 2). The macroscopic flow of our chiral fluid is reminiscent of free surface flows of Newtonian fluids: nearby droplets merge (Fig. 1d and Supplementary Movie 3), fluid spreads on a surface under the influence of gravity (Fig. 1e and Supplementary Movie 4), voids collapse (Fig. 1f and Supplementary Movie 5), and thin streams go unstable, as revealed by flowing fluid past a solid object (Fig. 1g and Supplementary Movie 6). We demonstrate that these seemingly familiar features are accompanied by unique free surface flows. We then exploit the odd interfacial dynamics of this prototypical chiral liquid to infer its material constants, which remain out of reach of conventional rheology.
In contrast to Newtonian fluids, the surface of our fluid supports a spontaneous unidirectional edge flow in its rest state, as well as unusual morphological dynamics such as the rotation of asymmetric droplets illustrated in Supplementary Movie 3.
II Chiral surface waves and ‘edge pumping’
To investigate these lively surface flows, we first look at surface excitations in a simple slab geometry, as shown in Fig. 2a and Supplementary Movie 7. We measure the spectrum of surface fluctuations, , by tracing the height profile, , of the surface and Fourier-transforming it in space and time. We observe the spectrum to be peaked along a curve , revealing the existence of dispersive waves (see Fig. 2b). The curve has only one branch with odd parity, meaning that the waves are unidirectional. This behavior contrasts that of conventional surface waves that propagate in all directions.
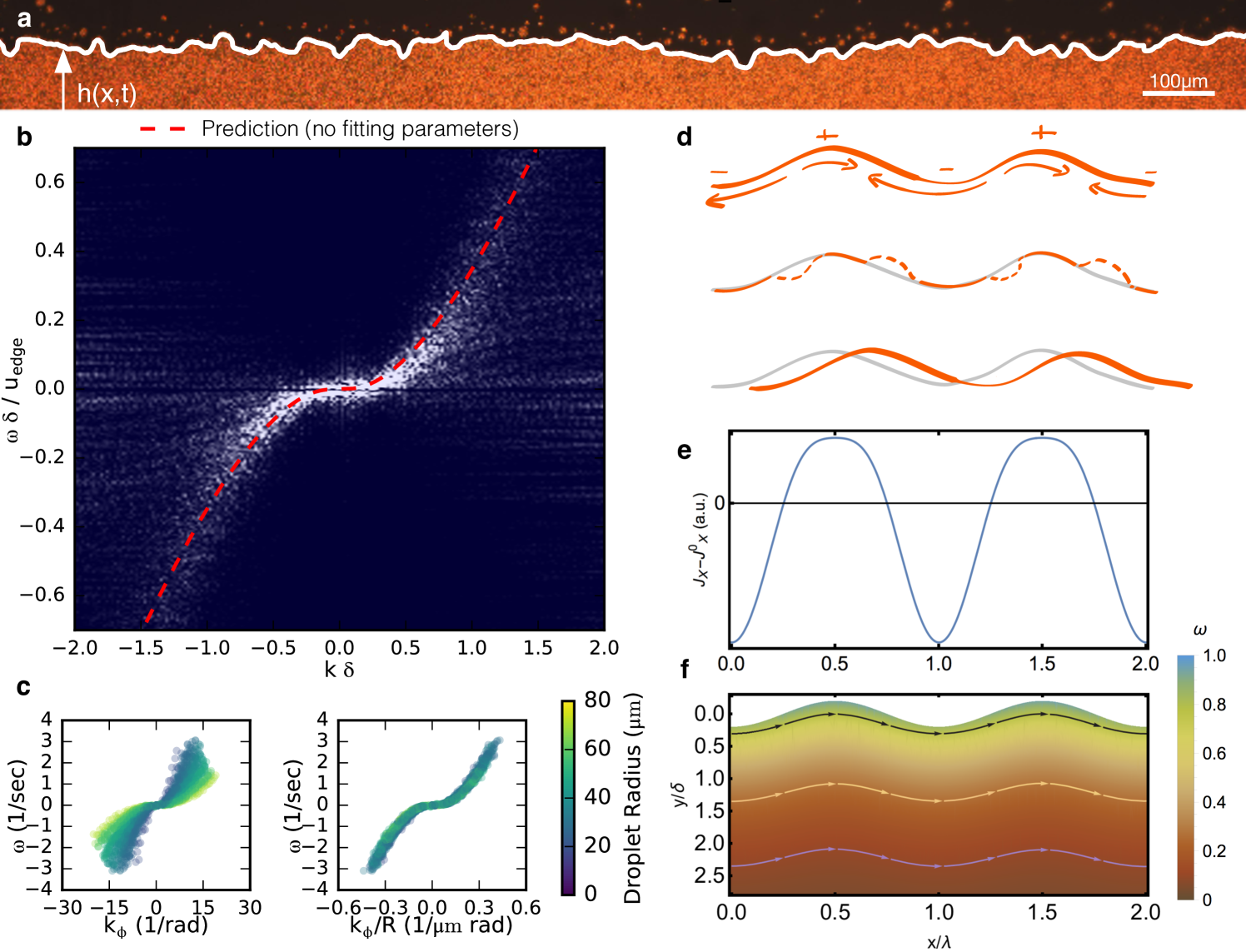
These surface waves beg a hydrodynamic description. Chiral-fluid hydrodynamics follows from conservation of momentum and angular momentum, and thus includes both the spinning rate of individual fluid particles as well as the momentum and angular momentum of their flow furthauer_active_2013 ; bonthuis_electrohydraulic_2009 ; tsai_chiral_2005 ; dahler_theory_1963 ; huang_continuum_2010 . Because our colloids are birefringent, we are able to measure their individual spinning rate by imaging through crossed polarizers. We find that all particles rotate at the same rate, , which is set by the rotating magnetic field (see Fig. 3a and Supplementary Movie 8). From this it follows that the particles’ rotational inertia is negligible; the torque exerted on each particle by the magnetic field instantly adjusts to balance the frictional torques exerted by the neighboring particles and the solid substrate. This fast response enables the decoupling of the angular momentum equation from the momentum equation. Nonetheless a strong signature of the microscopic angular momentum manifests as an ‘odd’ stress. A minimal hydrodynamic theory then balances the force generated by viscous and odd hydrodynamic stresses, , against friction with the substrate, , and surface tension at the fluid interface. In this theory, which has been used to capture the bulk flows of chiral granular fluids, the hydrodynamic stress tensor is given by:
| (1) |
includes the pressure and ordinary viscous stress also present in Newtonian fluids with a shear viscosity . The additional term containing the Levi-Civita symbol and the rotational viscosity , captures the rotational friction between neighboring particles dahler_theory_1963 ; bonthuis_electrohydraulic_2009 ; tsai_chiral_2005 ; furthauer_active_2013 . Such an odd stress builds up as the local spinning rate deviates from half the local fluid vorticity . In torque-free fluids, angular momentum conservation constrains these two quantities to be equal: odd stresses are unique to chiral fluids.
We note that there is no direct appearance of the magnetic field or its stresses in this hydrodynamic description unlike in conventional ferrofluids. In this respect, our colloidal chiral fluid can be seen as a special type of driven ferrofluid in which the only role of magnetic forces is to induce chirality.
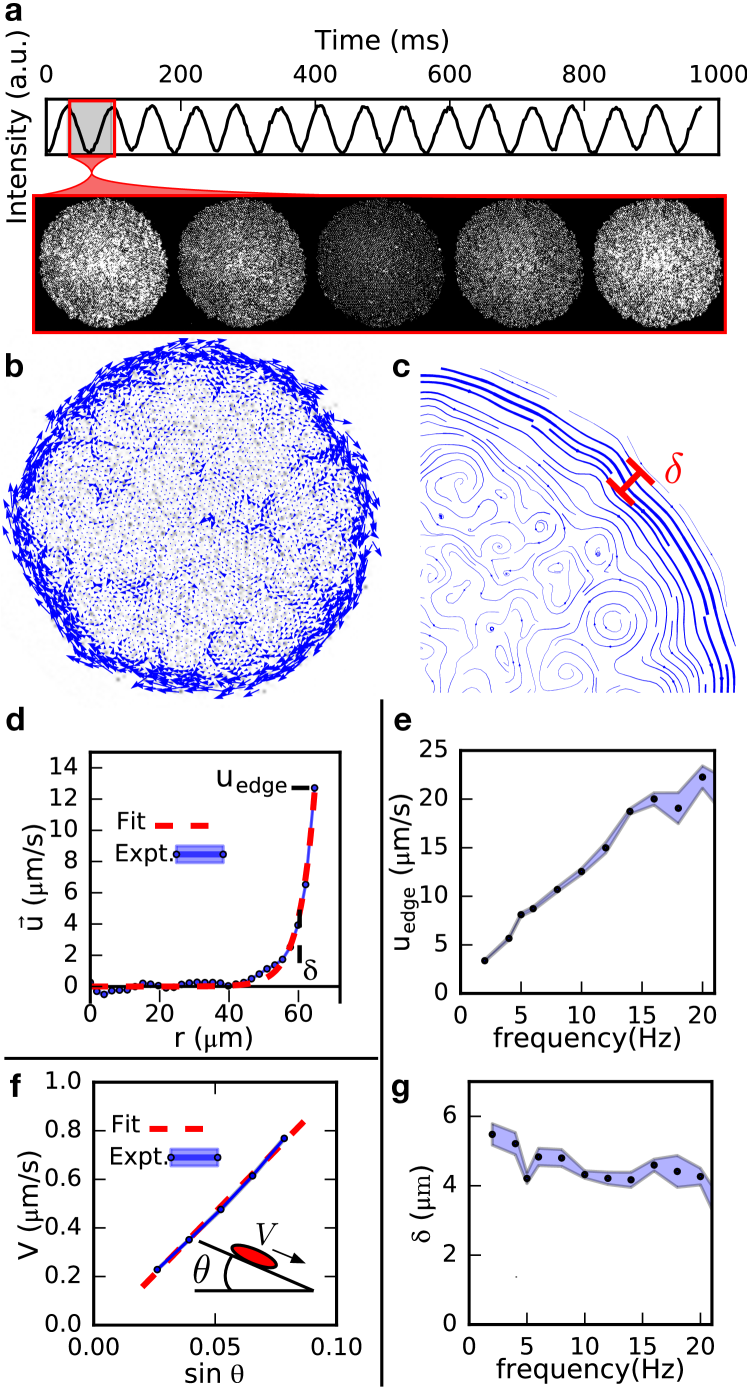
To make a quantitative comparison between our model and the flows we observe, we require a measurement of the hydrodynamic and friction coefficients , , and . Fortunately, the prominent effect of odd stress at the free surface of our chiral fluid can be effectively exploited to infer its bulk rheology. The homogeneous spinning motion of the colloidal particles gives rise to a net tangential edge flow even in the absence of pressure gradients. These tread-milling dynamics, characteristic of all chiral fluids tsai_chiral_2005 ; nguyen_emergent_2014 ; petroff_fast-moving_2015 ; yan_rotating_2014 ; van_zuiden_spatiotemporal_2016 , are illustrated in circular droplets in Figs. 3b-e and Supplementary Movie 9. The tangential flow that is localized at the free surface is readily explained by expressing the hydrodynamic equation in terms of vorticity for an incompressible chiral fluid:
| (2) |
where . This Helmholtz equation indicates that the vorticity generated at the surface decays exponentially into the fluid, with a characteristic penetration depth (see Figs. 3c, d, g). In this model, the absence of substrate friction causes the penetration depth to diverge, resulting in rigid-body rotation of the entire fluid, as observed in ferrofluid droplets Bacri1994 . The magnitude of the vorticity at the free surface, , is set by the stress-free boundary condition for a flat strip and expresses the competition between the odd and viscous stresses (see Supplementary Information). We point out that is directly proportional to , which demonstrates the importance of odd stress for the dynamics. Comparison between experiment and prediction (Fig. 3d) yields the values of and in terms of . The latter is then measured by tilting the substrate and measuring the sedimentation rate of droplets (see Fig. 3f, and Supplementary Information). Ultimately, we find , , and .
Equipped with the hydrodynamic coefficients we can now investigate the origin of the surface waves within our model. The mass flux in the tangential surface flow provides significant insight. This flow, sketched in Fig. 2d and plotted in Figs. 2e-f, is determined by the balance of the tangential odd stress at the boundary, the shear stress, and the substrate friction. In the presence of a perturbation that varies the curvature of the interface, resistance to flow due to the shear stress will be modulated. For a sinusoidal perturbation, there is enhanced flow in positively curved regions (top of the wave) and decreased flow in negatively curved regions (bottom of the wave). This ‘edge-pumping’ moves material away from curved regions towards the flat wave front, giving rise to uni-directional wave motion.
A linear stability analysis of the hydrodynamic equations (see Supplementary Information for a detailed calculation) confirms this scenario and yields a prediction for the dispersion relation, dissipation rate, and flow fields of surface waves, which we plot in Fig. 2b (red dashed curves). With no fitting parameters, our model shows excellent agreement with the experimentally measured dispersion relation. For surface waves of long wavelength , the asymptotic dispersion relation is:
| (3) |
where .
The wave dynamics are thus crucially sensitive to boundary layer flows. A natural avenue for investigation, then, is to seek to increase the thickness of the boundary in order to increase its relative role. We now show how a slight increase of the penetration depth of the boundary layer amplifies chiral effects and reveals a long sought-after source of stress, commonly referred to as Hall viscosity.
III Chiral wave damping and measurement of Hall Viscosity
We reduce the surface friction by allowing our chiral liquid to sediment upon an air-water interface (Fig. 4b), as opposed to a glass surface (Fig. 4a). Due to the difficulty in maintaining a slab geometry in this regime, we examine surface fluctuations on circular droplets.
As can be seen in Fig. 4a-b and Supplementary Movie 10, the edge flow penetrates deeper into the chiral fluid as friction is reduced. The dispersion relations for high and low friction droplets display the same trend, although the range of accessible wave vectors normalized by the penetration length () is larger in the low friction case. An extension of our theory to circular geometries (see Supplementary Information) again accurately captures the dispersion relations for high friction (Fig. 4a) and low friction (Fig. 4b).
The remarkable agreement between experiment and theory is however challenged when investigating the damping dynamics of the chiral waves. Experimentally, the damping rate of chiral waves of wave vector is given by fitting a Lorentzian to the width of the power spectrum (see Supplementary Information); the resulting damping rates are shown in Fig. 4c-d. Our hydrodynamic theory predicts this damping rate to be proportional to surface tension. This is natural since surface tension flattens interfacial deformation: in the absence of inertia, the relaxation does not overshoot and capillary waves are overdamped. In the long wavelength limit (), the damping rate stems from the competition between surface tension and substrate friction. As seen in Fig. 4c, in the high friction case we again find excellent agreement between theory and experiment, which provides a direct measurement of surface tension. The value we find, , is consistent with an estimate based on magnetic interactions between rotating dipoles (see Supplementary Information).
In the case of low surface friction, however, we observe a distinct new feature in the dissipation rate: a leveling off of the dissipation rate at short wavelengths which cannot be accounted for by the hydrodynamic theory discussed thus far, suggesting the presence of an additional mechanism for surface wave dissipation in our chiral fluid. Seeking a hydrodynamic description, we recall that isotropic chiral fluids can in principle possess an additional stress in their constitutive relation, known interchangeably as “anomalous viscosity”, “odd viscosity” or “Hall viscosity” avron_viscosity_1995 ; avron_odd_1998 ; read_non-abelian_2009 . This non-dissipative, transverse stress is linked by Onsager relations to the breaking of time-reversal symmetry.
Theoretically, odd viscosity has indeed been shown to arise in the hydrodynamics of plasmas and systems of spinning molecules, ‘gears’, as well as quantum Hall fluids and vortex fluids radin_lorentz_1972 ; robinson_variational_1962 ; pitaevskii_physical_1981 ; wiegmann_anomalous_2014 ; banerjee_odd_2017 . We therefore conjecture our chiral fluid to support an additional Hall stress . In incompressible fluids such as the one considered here, the effect of odd viscosity can solely be seen at the edge. This is because in the bulk flow Hall stress is merely absorbed into the fluid pressure. The signature of odd viscosity in our chiral fluid is thus an additional boundary stress. The component normal to the interface is given by
| (4) |
where (resp. ) is the velocity normal (resp. tangential) to the surface (see Fig. 4e), and is the local radius of curvature.
In our system, where odd stress powers a boundary-layer edge flow, we thus expect odd viscosity to flatten surface deformation in a manner akin to surface tension, . The excellent agreement between our measurements and predictions from a full hydrodynamic theory confirms this simplified picture and establishes the presence of Hall viscosity in our colloidal chiral fluid (see Fig. 4d, f-g). From the fit we obtain .
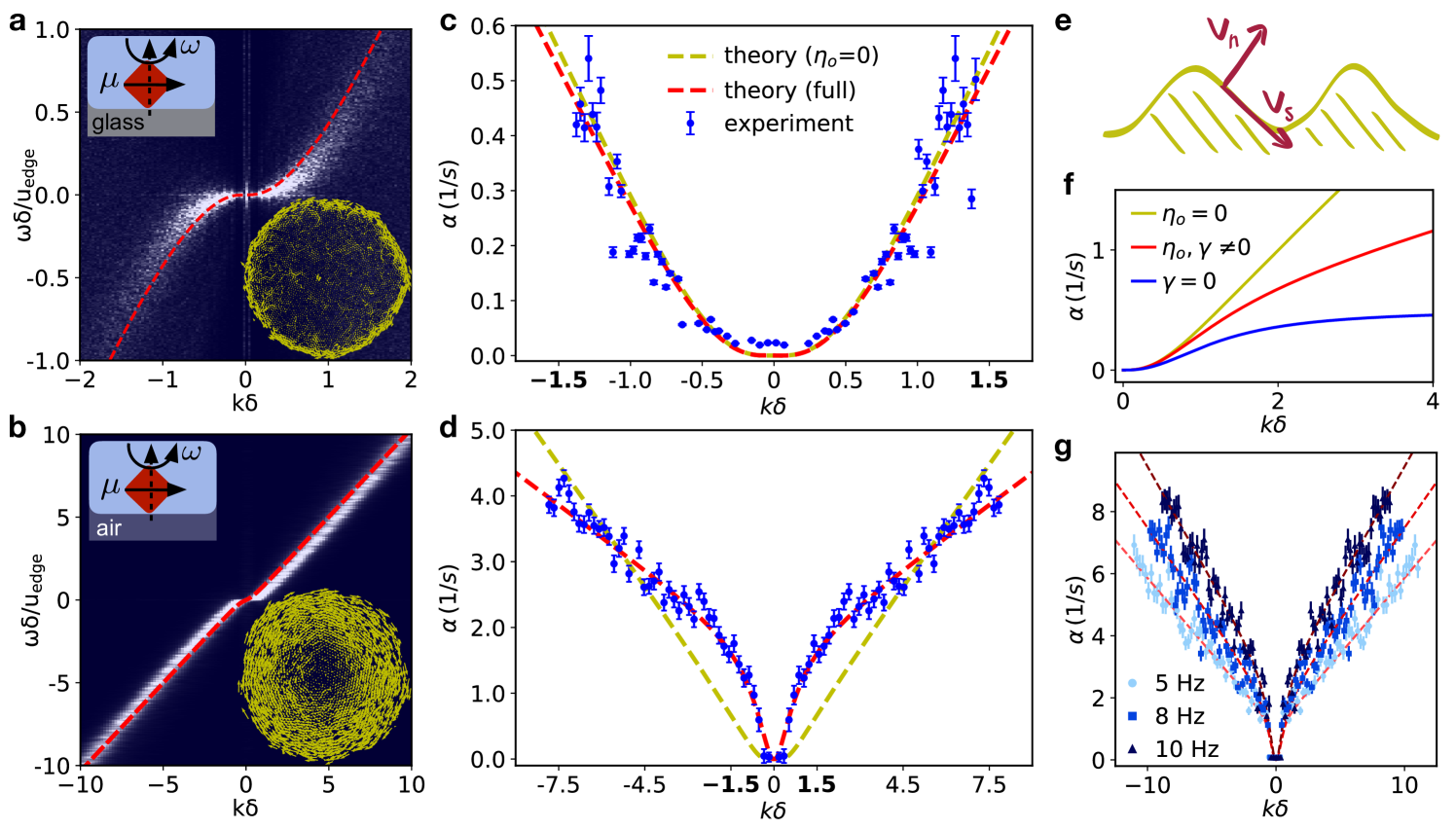
The clearly visible decrease in slope in the damping relation is the most visible signature of Hall viscosity in our data and can be understood on dimensional grounds. In the long wavelength limit, the wave relaxation time is controlled by the competition of either surface tension or Hall stress with substrate friction. Dimensionally this implies a scaling since the ratios and have dimension of volume per unit time. In contrast, in the short wavelength limit, surface friction plays no role and damping stems from the competition of surface tension or Hall stress and bulk viscosities alone. In this case dimensional analysis requires linear scaling with wavenumber in the case of surface tension, and wave-number independence in the case of Hall stress (see Supplementary Information). This change in wavenumber dependence brings about a visible rollover to a decreased slope in the wave damping rate.
We note that for small ranges of , characteristic of spectral measurements in the presence of high surface friction, the leveling off cannot be seen and the relative roles of Hall viscosity and surface tension become hard to separate. This is the case for the damping shown in Fig. 4c which can be fit well by both a non-zero and zero value of Hall viscosity (see Supplementary Information).
Having established the presence of Hall viscosity by examining wave damping, it follows to ask whether it has an effect on wave propagation. The first term in Eq. (4) suggests that Hall viscosity and surface tension could act together to support wave propagation. Surface tension acts on a sinusoidal surface deformation by pulling down peaks and pushing up troughs, generating an in-phase normal velocity component. The normal Hall stress would then act out of phase on the inflection points of the sinusoidal perturbation to propagate it in a chiral fashion. Our full theory confirms that this additional wave-pumping mechanism indeed exists and generates waves even in the absence of edge currents. However, for our hydrodynamic parameters, their effect on the dispersion is minimal.
IV An odd instability
In much of the phenomenology we have discussed, surface dynamics are essentially boundary layer dynamics. Another natural question, then, is what happens when two boundary layers meet? Draining fluid past a curved obstacle brings about the progressive thinning of a curved strip of chiral fluid, as shown in Fig. 1g and Supplementary Movie 6. The flow is smooth until the strip thickness becomes comparable to the penetration depth ; at that point the flow goes unstable, resulting in the formation of circular droplets. We study this novel pearling mechanism in experiment by creating a sequence of strips of decreasing thickness, as shown in Fig. 5a and Supplementary Movie 11. We find that over a period of 10 minutes the strips of chiral fluid are stable for thicknesses above and unstable below.
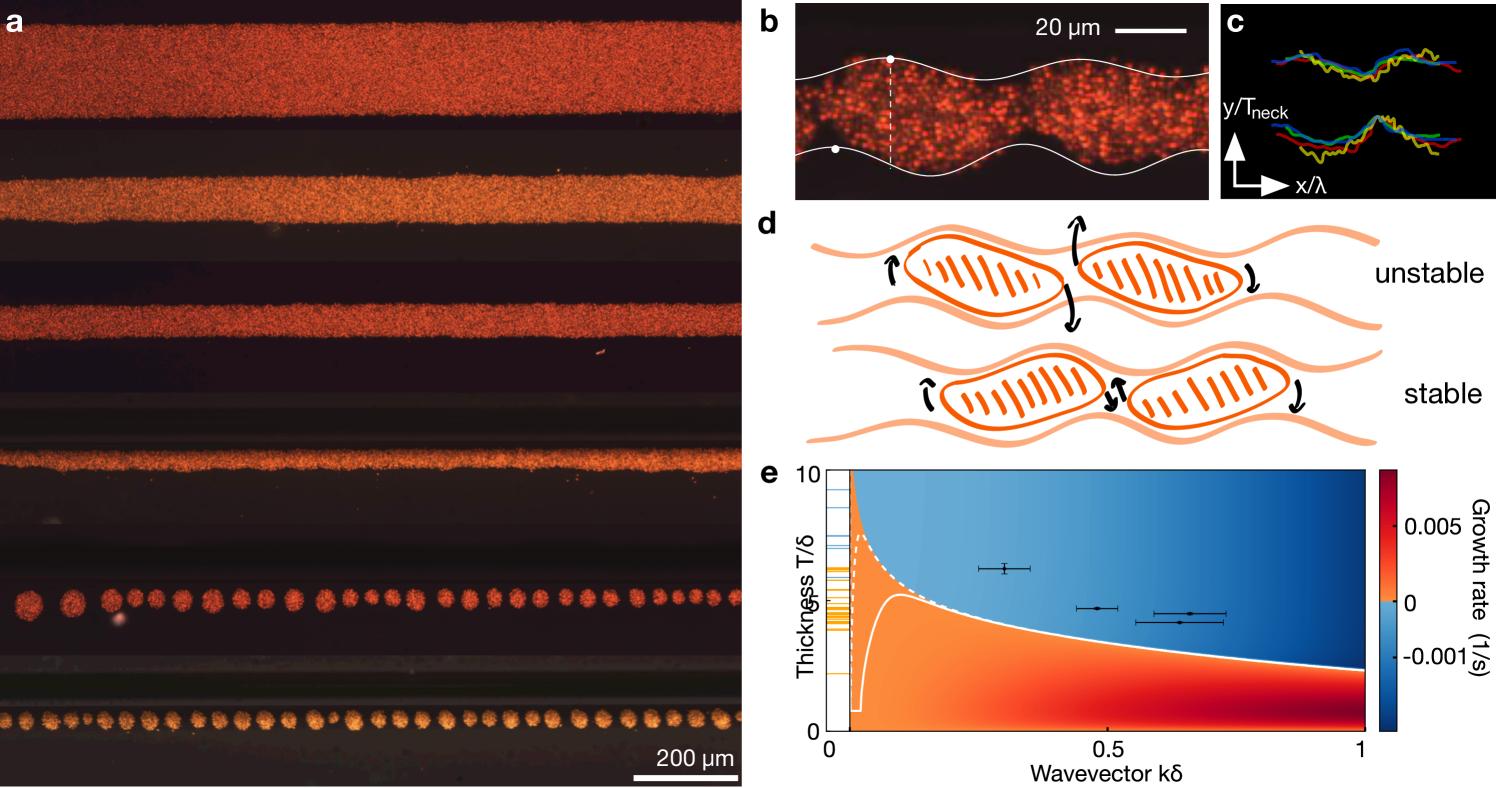
Although visually reminiscent of the Rayleigh-Plateau instability of a thin fluid cylinder jet eggers_nonlinear_1997 , this instability is fundamentally different. In our two-dimensional system, surface tension is a purely stabilizing force, as seen in the wave analysis discussed above. Instead, the instability originates from the chiral surface dynamics of our fluid. A visual signature of this origin is the consistent offset in the phase between top and bottom perturbations at the moment the instability occurs in all strips: Fig. 5b shows one such example.
A linear stability analysis of a thin strip of chiral fluid quantitatively predicts the existence of unstable modes which consist of wave-like perturbations on the top and bottom surfaces that have a relative phase offset, as sketched in Fig. 5d. These are accompanied by a stable mode with an opposite relative phase. The associated stability diagram is shown in Fig. 5e, together with our experimental observations. As the Hall stress has little effect on the stability of modes for small (see Supplementary Information), here we set .
An intuitive picture for the mechanism driving the instability is illustrated in Fig. 5d. The geometry of a thin slab with out-of-phase perturbations on the top and bottom surfaces can be approximated by a collection of elongated droplets of chiral fluid all canted in the same direction. Droplets of this kind rotate in the direction of the edge current, in this case clockwise (see Fig. 1d and Supplementary Movie 3). Depending on the phase difference between the two interfaces, the rotation of these effective droplets will either increase the amplitude of the perturbation, resulting in the breakup of the strip (top); or decrease the amplitude of the perturbation and restore the flat interface (bottom). The consistent observation of this phase relation between the top and bottom perturbations across many experiments of strips going unstable (Fig. 5c) further corroborates our theoretical picture of the instability.
We have broken parity symmetry at the microscopic level in a colloidal chiral fluid, resulting in the emergence of an odd stress that in turn generates lively surface flows. Likewise, we have broken time reversal symmetry, giving rise to Hall viscosity, a dissipationless transport property which has thus far remained experimentally elusive. The combination of these features drives rich interfacial dynamics with no analogues in conventional fluids. These dynamics include the uni-directional propagation and anomalous attenuation of surface waves and an asymmetric pearling instability. In principle, these chiral phenomena can be tuned, for instance by altering the colloidal particles’ shape and their effective interactions. Beyond enabling the study of universal aspects of a new class of hydrodynamics, colloidal chiral fluids provide a platform for engineering active materials with so far untapped, ‘odd’ behaviors avron_odd_1998 ; avron_viscosity_1995 ; banerjee_odd_2017 .
References
- (1) Lenz, P., Joanny, J.-F., Jülicher, F. & Prost, J. Membranes with Rotating Motors. Physical Review Letters 91, 108104 (2003).
- (2) Yeo, K. & Maxey, M. R. Rheology and ordering transitions of non-Brownian suspensions in a confined shear flow: Effects of external torques. Physical Review E 81, 062501 (2010).
- (3) Fürthauer, S., Strempel, M., Grill, S. W. & Jülicher, F. Active Chiral Processes in Thin Films. Physical Review Letters 110, 048103 (2013).
- (4) Nguyen, N. H., Klotsa, D., Engel, M. & Glotzer, S. C. Emergent Collective Phenomena in a Mixture of Hard Shapes through Active Rotation. Physical Review Letters 112 (2014).
- (5) Goto, Y. & Tanaka, H. Purely hydrodynamic ordering of rotating disks at a finite Reynolds number. Nature Communications 6, 5994 (2015).
- (6) Yeo, K., Lushi, E. & Vlahovska, P. M. Collective Dynamics in a Binary Mixture of Hydrodynamically Coupled Microrotors. Physical Review Letters 114 (2015).
- (7) Climent, E., Yeo, K., Maxey, M. R. & Karniadakis, G. E. Dynamic Self-Assembly of Spinning Particles. Journal of Fluids Engineering 129, 379–387 (2006).
- (8) Avron, J. E., Seiler, R. & Zograf, P. G. Viscosity of Quantum Hall Fluids. Physical Review Letters 75, 697–700 (1995).
- (9) Wiegmann, P. & Abanov, A. G. Anomalous Hydrodynamics of Two-Dimensional Vortex Fluids. Physical Review Letters 113, 034501 (2014).
- (10) Ariman, T., Turk, M. A. & Sylvester, N. D. Microcontinuum fluid mechanics–A review. International Journal of Engineering Science 11, 905–930 (1973).
- (11) Rosensweig, R. E. Ferrohydrodynamics (Courier Corporation, 2013).
- (12) Torres-Díaz, I. & Rinaldi, C. Recent progress in ferrofluids research: novel applications of magnetically controllable and tunable fluids. Soft matter 10, 8584–8602 (2014).
- (13) Avron, J. E. Odd Viscosity. Journal of Statistical Physics 92, 543–557 (1998).
- (14) Abanov, A., Can, T. & Ganeshan, S. Odd surface waves in two-dimensional incompressible fluids. SciPost Physics 5, 010 (2018).
- (15) Banerjee, D., Souslov, A., Abanov, A. G. & Vitelli, V. Odd viscosity in chiral active fluids. Nature Communications 8, 1573 (2017).
- (16) Bandurin, D. A. et al. Negative local resistance caused by viscous electron backflow in graphene. Science 351, 1055–1058 (2016).
- (17) Pringle, J. E. & King, A. Astrophysical Flows (Cambridge University Press, 2007).
- (18) Secchi, E. et al. Massive radius-dependent flow slippage in carbon nanotubes. Nature 537, nature19315 (2016).
- (19) Tsai, J.-C., Ye, F., Rodriguez, J., Gollub, J. P. & Lubensky, T. C. A Chiral Granular Gas. Physical Review Letters 94, 214301 (2005).
- (20) Scaffidi, T., Nandi, N., Schmidt, B., Mackenzie, A. P. & Moore, J. E. Hydrodynamic Electron Flow and Hall Viscosity. Physical Review Letters 118, 226601 (2017).
- (21) van Zuiden, B. C., Paulose, J., Irvine, W. T. M., Bartolo, D. & Vitelli, V. Spatiotemporal order and emergent edge currents in active spinner materials. Proceedings of the National Academy of Sciences 113, 12919–12924 (2016).
- (22) Snezhko, A. Complex collective dynamics of active torque-driven colloids at interfaces. Current Opinion in Colloid & Interface Science 21, 65–75 (2016).
- (23) Kokot, G. et al. Active turbulence in a gas of self-assembled spinners. Proceedings of the National Academy of Sciences 114, 12870–12875 (2017).
- (24) Petroff, A. P., Wu, X.-L. & Libchaber, A. Fast-Moving Bacteria Self-Organize into Active Two-Dimensional Crystals of Rotating Cells. Physical Review Letters 114, 158102 (2015).
- (25) Grzybowski, B. A., Stone, H. A. & Whitesides, G. M. Dynamic self-assembly of magnetized, millimetre-sized objects rotating at a liquid-air interface. Nature 405, 1033–1036 (2000).
- (26) Grzybowski, B. A., Jiang, X., Stone, H. A. & Whitesides, G. M. Dynamic, self-assembled aggregates of magnetized, millimeter-sized objects rotating at the liquid-air interface: Macroscopic, two-dimensional classical artificial atoms and molecules. Physical Review E 64, 011603 (2001).
- (27) Grzybowski, B. A., Stone, H. A. & Whitesides, G. M. Dynamics of self assembly of magnetized disks rotating at the liquid-air interface. Proceedings of the National Academy of Sciences 99, 4147–4151 (2002).
- (28) Grzybowski, B. A. & Whitesides, G. M. Dynamic Aggregation of Chiral Spinners. Science 296, 718–721 (2002).
- (29) Belovs, M. & Cēbers, A. Hydrodynamics with spin in bacterial suspensions. Physical Review E 93, 062404 (2016).
- (30) Yan, J., Bae, S. C. & Granick, S. Rotating crystals of magnetic Janus colloids. Soft Matter 11, 147–153 (2014).
- (31) Yan Jing, Bae Sung Chul & Granick Steve. Colloidal Superstructures Programmed into Magnetic Janus Particles. Advanced Materials 27, 874–879 (2015).
- (32) Scholz, C., Engel, M. & Pöschel, T. Rotating robots move collectively and self-organize. Nature Communications 9, 931 (2018).
- (33) Bacri, J.-C., Perzynski, R., Shliomis, M. I. & Burde, G. I. “Negative-Viscosity” effect in a magnetic fluid. Phys. Rev. Lett. 75, 2128–2131 (1995).
- (34) Bonthuis, D. J., Horinek, D., Bocquet, L. & Netz, R. R. Electrohydraulic Power Conversion in Planar Nanochannels. Physical Review Letters 103, 144503 (2009).
- (35) Dahler, J. S. & Scriven, L. E. Theory of Structured Continua. I. General Consideration of Angular Momentum and Polarization. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 275, 504–527 (1963).
- (36) Huang, H.-F., Zahn, M. & Lemaire, E. Continuum modeling of micro-particle electrorotation in couette and poiseuille flows-the zero spin viscosity limit. Journal of Electrostatics 68, 345–359 (2010).
- (37) Bacri, J.-C., Cebers, A. O. & Perzynski, R. Behavior of a magnetic fluid microdrop in a rotating magnetic field. Phys. Rev. Lett. 72, 2705–2708 (1994).
- (38) Read, N. Non-Abelian adiabatic statistics and Hall viscosity in quantum Hall states and paired superfluids. Physical Review B 79, 045308 (2009).
- (39) Radin, S. Lorentz Plasma in a Strong Magnetic Field. The Physics of Fluids 15, 91–95 (1972).
- (40) Robinson, B. B. & Bernstein, I. B. A variational description of transport phenomena in a plasma. Annals of Physics 18, 110–169 (1962).
- (41) Pitaevskii, L. P. & Lifshitz, E. M. Physical Kinetics (Butterworth-Heinemann, Oxford, UK, 1981).
- (42) Eggers, J. Nonlinear dynamics and breakup of free-surface flows. Reviews of Modern Physics 69, 865–930 (1997).