The Gonality of Chess Graphs
Abstract.
Chess graphs encode the moves that a particular chess piece can make on an chessboard. We study through these graphs through the lens of chip-firing games and graph gonality. We provide upper and lower bounds for the gonality of king’s, bishop’s, and knight’s graphs, as well as for the toroidal versions of these graphs. We also prove that among all chess graphs, there exists an upper bound on gonality solely in terms of , except for queen’s, toroidal queen’s, rook’s, and toroidal bishop’s graphs.
1. Introduction
The game of chess has a long history of inspiring problems in math. How many queens (or bishops, or knights) can be placed on a chessboard (not necessarily ) such that no pair of them can attack each other? Similarly, what is the smallest number of queens (or bishops, or knights) that can be placed so that every square on the board may be attacked in one move? Can a knight visit each square on an chessboard exactly once, returning to its starting position? These questions can be framed and studied in the language of graph theory, and relate to such topics as independence number, domination number, and Hamiltonian cycles.
Choose a chess piece, either king, queen, rook, bishop, or knight111We omit pawns from consideration, since the movement of a pawn is not symmetric between two squares, so an undirected graph does not suffice to encode their movements,. The chess graph associated to that piece has vertices, corresponding to the squares of an chessboard. Two vertices are connected by an edge if and only if the chess piece in question can move between the two corresponding squares. For example, in a king’s graph, each vertex is adjacent to at most eight other vertices, corresponding to two horizontal, two vertical, and four diagonal moves. Toroidal chess graphs are constructed similarly, with moves allowed that glue the boundaries of the chessboard to form a torus. Illustrated on the left in Figure 1 is a chessboard with a king on one of the squares. The king’s moves from that square under traditional chess rules are illustrated with solid arrows; when toroidal moves are allowed, three more moves are possible, illustrated with dashed arrows. On the right are the vertices of the king’s graph; the edges coming from one vertex are illustrated, with dashed edges for those only present in the toroidal king’s graph.
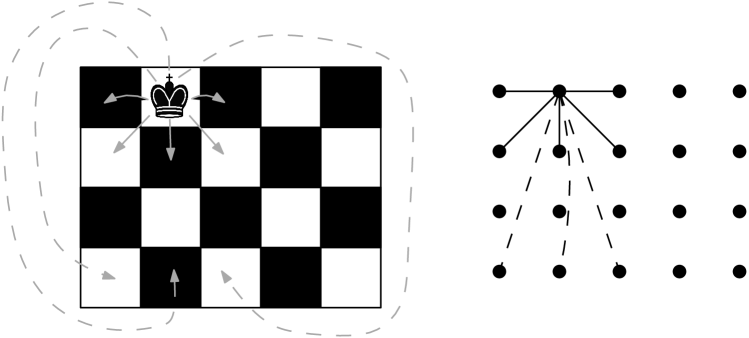
Note that on a toroidal board, a piece may be able to travel between two vertices with multiple routes; for example, on a chess board, a knight moving two squares spots up and one the right has the same effect as moving two squares down and one to the right. We follow the convention that only one edge connects the two corresponding vertices, although an interesting variant of our problems would be to encode such repeated moves with repeated edges (turning our graph into a multigraph). For some graphs, like rook’s graphs, making the board toroidal has no impact at all; for others, such as bishop’s graphs, making the board toroidal increases the number of edges and changes the graph structure drastically.
In this paper we study chess graphs through the lens of chip-firing games and graph gonality. The (divisorial) gonality of a graph, a discrete analog of the gonality of an algebraic curve, is the minimum degree of a positive rank divisor on that graph. Phrased in the language of chip-firing games, the gonality of a graph is the smallest number of chips that can be placed on so that a chip can be placed on any vertex through chip-firing moves, without any other vertex being in debt. This invariant has been of great interest due to its connection to algebraic geometry [3], and much work has been done to determine the gonality of different families of graphs.
Several families of chess graphs have already been the subject of study from this perspective. The gonality of rook’s graphs was first explored in [2], with gonality determined for graphs with . This result was generalized in [14], where gonality was determined for all rook’s graphs. More recently, the gonality of queen’s graphs and toroidal queen’s graphs was determined in [12]. In this paperwe study the remaining chess graphs, namely the traditional and toroidal versions of king’s, bishop’s, and knight’s graphs arising from chessboards. The non-toroidal versions of these graphs are illustrated in the first row Figure 2; the second row shows the edges that are gained by the upper left vertex when expanding to the toroidal version.

We compute gonality exactly for all toroidal bishop’s graphs, as well as for king’s and toroidal king’s graphs where the number of columns is sufficiently high compared to the number of rows. We also find upper and lower bounds on gonality for king’s, toroidal king’s, bishop’s, knight’s, and toroidal knight’s graphs.
We summarize our results in the following two theorems; in both we assume . The first enumerates our contribution to known bounds on gonality.
Theorem 1.1.
We have the following bounds on the gonality of chess graphs.
-
•
King’s graphs: , with equality for .
-
•
Toroidal king’s graphs: , with equality for .
-
•
Bishop’s graphs: ; and for we have , where .
-
•
Toroidal bishop’s graphs: .
-
•
Knight’s graphs: for , with smaller bounds for ; and for and we have .
-
•
Toroidal knight’s graphs: and for ; and for and we have .
The second theorem gives a qualitative summary of how different graphs behave as we fix and vary .
Theorem 1.2.
Let be an chess graph from one of the following families: rook’s, queen’s, toroidal queen’s, king’s, toroidal king’s, bishop’s, toroidal bishop’s, knight’s, and toroidal knight’s. Then, as we vary , there exists a bound on solely in terms of if and only if the graph is not rook’s, queen’s, toroidal queen’s, or toroidal bishop’s.
Proof.
The existence of bounds for king’s, toroidal king’s, bishop’s, knight’s, and toroidal knight’s follow from Theorem 1.1. The non-existence of a bound for toroidal knight’s graph follows from our result in Theorem 1.1 that , which is unbounded as increases while remains fixed. The non-existence of bounds for the remaining graphs comes from previous work: it was shown in [14] that the rook’s graph has gonality for ; and it was shown in [12] that the queen’s graph has gonality for and , and that the toroidal queen’s graph has gonality at least for . ∎
Our paper is organized as follows. In Section 2 we present background and definitions. In Section 3 we present our results on king’s graphs, followed by toroidal king’s graphs in Section 4. In Section 5 we present our results on bishop’s graphs, followed by toroidal bishop’s graphs in Section 6. In Section 7 we present our results on knight’s graphs, followed by toroidal knight’s graphs in Section 8. We present directions for future work in Section 9, and several computations referred to in earlier sections in the Appendices.
Acknowledgements. The authors were supported by Williams College and the SMALL REU, as well as by the NSF via grants DMS-2241623 and DMS-1947438. The second author was supported by Brown University.
2. Background and definitions
Let be a graph consisting of a finite set of vertices and a finite multiset of edges. If has no repeated edges, we call simple graph. If a vertex is in an edge , we say is incident to , and if , we say and are adjacent. We refer to the number of edges incident to as the valence222This is also referred to as the degree of ; however, the term degree is used with a different meaning in chip-firing games. of , denoted . For disjoint subsets , we let be the set of edges with a vertex in and a vertex in ; and we let . If for all pairs of vertices we can find vertices such that and are adjacent for all , we say is connected; otherwise it is disconnected. A subset of vertices is said to be connected if the subgraph with vertex set and edge set is connected graph.
An chess graph has vertex set
When it is more notationally convenient, we may denote the vertex as . We depict these vertices in a grid, with rows and columns, treating the upper left corner as the vertex , with denoting the row of the vertex and denoting the column. Identifying these vertices with the squares in an chess board, two vertices are adjacent if and only if the chess piece in question can move directly between the corresponding squares. In particular, we have the following adjacency rules for when distinct vertices and are adjacent in our chess graphs.
-
•
King’s graph: when
-
•
Bishop’s graph: when is an integer multiple of either or .
-
•
Knight’s graph: when .
-
•
Rook’s graph: when or .
-
•
Queen’s graph: when either is an integer multiple of either or , or or .
An toroidal chess graph has the same vertex set and the same adjacency rules, except that all equalities are considered modulo for the first coordinate and modulo for the second coordinate. When representing these graphs in figures, we either draw the graph with vertices and edges, or when such a figure would be hard to digest visually simply present a chessboard, with a caption making clear which chess piece we are considering.
We now present the theory of divisors on graphs, and refer the reader to [7] for more details. We remark that most treatments of chip-firing games assume our graph is connected; we do not assume that here, and will note when our difference in assumptions has an impact on various results.
Given a graph , a divisor is a map , i.e. an assignment of an integer to each vertex of . A divisor is thought of intuitively as a collection of poker chips placed on each vertex, where receives chips, with negative integers representing debt. If for all , we say that is effective. The total number of chips on the graph, , is referred to as the degree of the divisor, denoted . The set of all divisors forms a group under the operation defined by vertex-wise addition (i.e. ; this group is isomorphic to the free abelian group on .
Given a divisor on a graph and a vertex , we can transform into another divisor through a chip-firing move at . This removes chips from and transfers them to those vertices adjacent to , one along each edge incident to . More formally, , and for all . Two divisors and are said to be equivalent, written , if can be obtained from via some sequence of chip-firing moves. This relation is an equivalence relation on the set of all divisors.
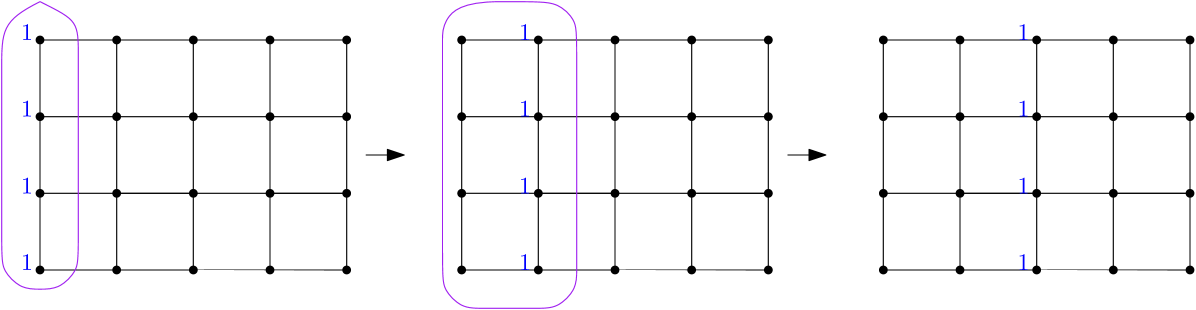
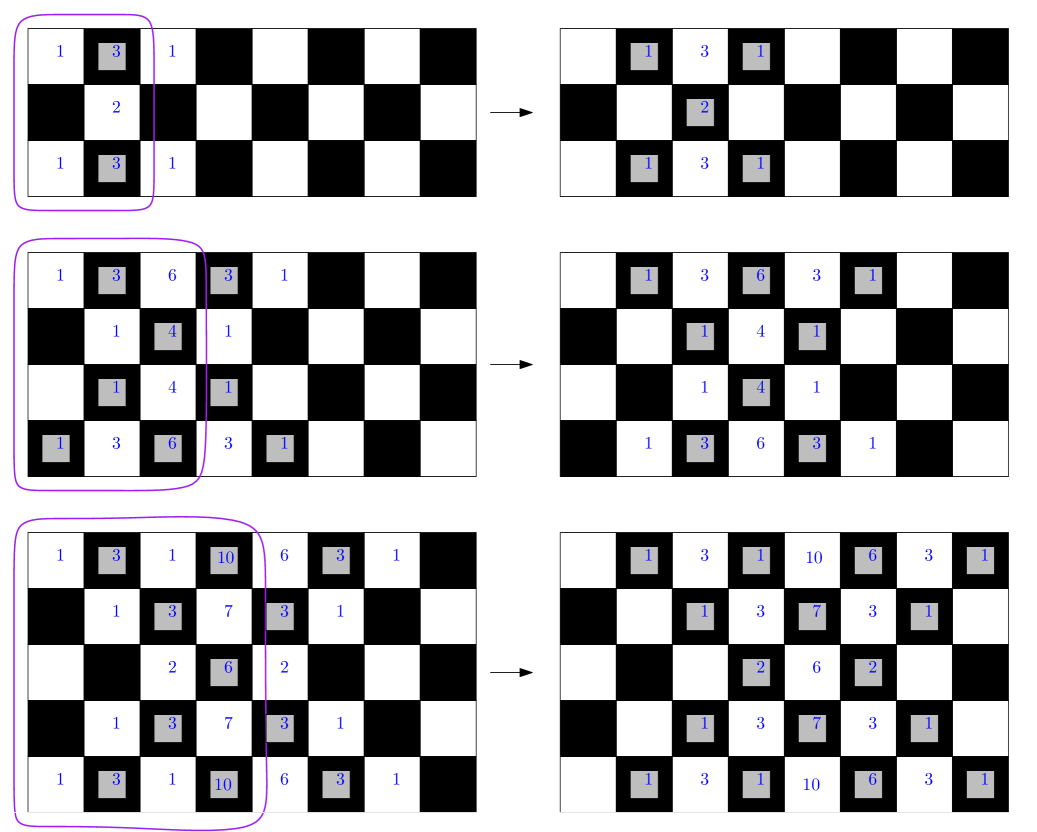
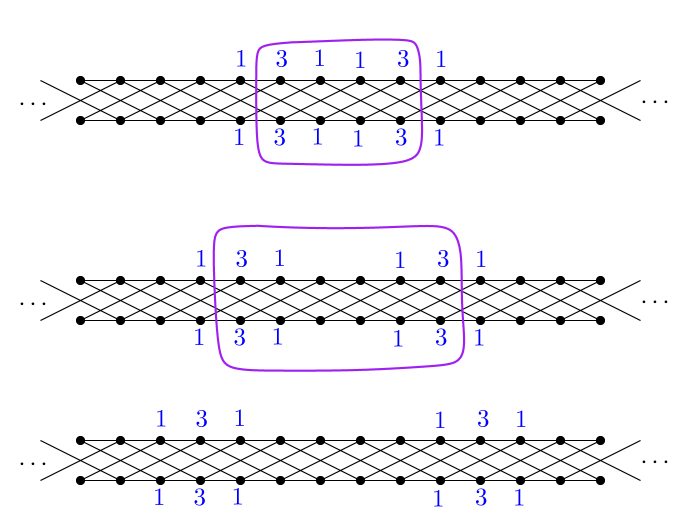
A collection of vertices can be fired in any order without changing the final outcome. This leads us to define set-firing moves: given , set-firing means to fire the vertices of in any order. This results in a net flow of chips only along the edges leaving the set, whereas for the movement of chips from to cancels with the movement of chips from to . Examples of two set-firing moves are depicted in Figure 3. Since the divisors differ by a sequence of chip-firing moves, all three are equivalent.
We now define the rank of a divisor , denoted . If is not equivalent to any effective divisor, we say . Otherwise, is the maximum integer such that, for every effective divisor with , the divisor is equivalent to some effective divisor. Intuitively, we can think of the rank of a divisor as the maximum amount of added debt that divisor can eliminate from the graph, regardless of how that debt is placed.
The (divisorial) gonality of a graph , denoted , is the minimum degree of a positive rank divisor on a graph, i.e. the minimum degree of a divisor that can eliminate debt from any vertex without introducing debt elsewhere. We can equivalently define as the minimum degree of a divisor such that for any vertex , there exists with effective and .
For example, the divisor illustrated in 3 has positive rank: firing the first column, then the first two, then the first three, and so on can move a chip to any vertex without introducing debt elsewhere. Since that divisor has degree , it follows that the gonality of that graph is at most .
Remark 2.1.
If a graph is not connected, say with connected components , then
To see this, note that we may replicate positive rank divisors on each component to obtain a positive rank divisor on the whole graph; and if a divisor places fewer than chips on any component , there must be some such that debt cannot be eliminated in , since chip-firing may be treated independently on each component.
While an explicit positive rank divisor provides an upper bound on gonality, finding a lower bound is more difficult. A priori, to show that the gonality of a graph is at least , one must consider all degree divisors, and show that for each there exists at least one vertex such that that divisor cannot eliminate debt on . While extremely brute force, this strategy can be implemented for relatively small graphs by leveraging Dhar’s burning algorithm [7], which refers to the first three steps of the following process.
-
(1)
Given a graph and an effective divisor , choose a vertex . Start a “fire” at this vertex, burning it.
-
(2)
Whenever an edge is incident to a burned vertex, that edge burns.
-
(3)
Whenever a vertex is incident to more than burning edges, the vertex burns.
-
(4)
If the whole graph burns, terminate. If some set of vertices is unburned, set-fire , and return to step (1).
An example of the start of this algorithm is illustrated Figure 4. The fire starts at the vertex , and spreads along incident edges. The adjacent vertex with chip does not immediately burn, though the one with chips does. Its edges burn, burning the left vertex with one chip, burning its edges. Here the fire stabilizes, since the two rightmost vertices have at least as many chips as burning edges. Those two vertices are fired, yielding the divisor on the right. If we ran the burning process again, the whole graph would burn (first the left vertex with chip, then the vertex with chips, and from there the rest of the graph). Since the whole graph would burn with no chips on , we know that the illustrated divisor does not have positive rank.

One can show in general that firing never introduces debt, and that this process will eventually terminate; see [7, Chapter 3] for details. Moreover, if we start with such that , then the final divisor places a chip on if and only if there exists an effective divisor such that . Thus this method can be used to check if an effective divisor has positive rank: for each , run the algorithm from , and check if ends up with at least one chip. If yes for all , then ; otherwise . From there, showing that is accomplished by performing this check for all effective divisors of degree .
Remark 2.2.
If is a connected graph, the output of the above algorithm has the property that no nonempty subset of can be set-fired without introducing debt somewhere. This property does not necessarily hold if is not connected.
To avoid such a brute-force approach, one can study graph parameters that serve as lower bounds on gonality. For instance, the well-studied parameter of treewidth, , is known to be a lower bound [16]. More recently, the scramble number of a graph, , was introduced in [11] and shown to be a lower bound on . Since for any graph [11, Theorem 1.1], scramble number is a strictly better lower bound, so we focus on it here.
A scramble on a graph is a nonempty collection of connected subsets (referred to as eggs) of . To any scramble , we associate two numbers: the hitting number , and the egg-cut number . A hitting set for is a set such that every egg in has a vertex in ; is then the minimum size of any hitting set. An egg-cut for is a subset such that deleting from disconnects the graph into multiple components, at least two of which contain an egg; is then the minimum size of any egg-cut. The order of a scramble is defined to be the minimum of the hitting number and the egg-cut number:
Finally, the scramble number of a graph is the maximum order of any scramble on the graph.
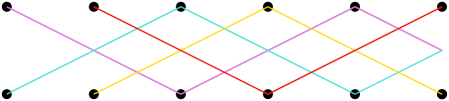
For an example of a scramble, consider the grid graph in Figure 3. Let consist of five eggs, the first consisting of the four vertices in the first column, the second consisting of the four vertices in the second column, and so on. Since these eggs do not overlap, we immediately have the the hitting number equals the number of eggs, so . The four edges connecting the first and second columns is an egg-cut, so . To see that , consider an arbitrary pair of eggs in . We can find four pairwise edge-disjoint paths between them: start at any vertex of the left egg and moving across the horizontal edges until reaching the right egg. Any egg-cut separating those two eggs must include at least one edge from each of these four paths; otherwise the eggs would be in the same component of . As our choice of eggs was arbitrary, we have that any egg-cut has at least four edges in it, so , and thus . This means that , so . In fact, since , we have , so .
For some graphs, scramble number is strictly smaller than gonality. In such instances, it is useful to have another upper bound on , so that we may rule it out as a tool for reaching a conjectured gonality. To that end we now present the screewidth of a graph, , which satisfies [6].
A tree-cut decomposition of a graph is a tree and a function , i.e. an assignment (not necessarily one-to-one, not necessarily onto) of the vertices of to the nodes of some tree . (For clarity, we refer to the vertices and edges of as its nodes and links, respectively, reserving vertices and edges for .) It is natural to represent a tree-cut decomposition as a thickened drawing of the tree with the vertices of inside its nodes, with the edges of drawn along the unique paths in between the nodes corresponding to its endpoints. Two examples of tree-cut decompositions of the grid graph are illustrated in Figure 5.
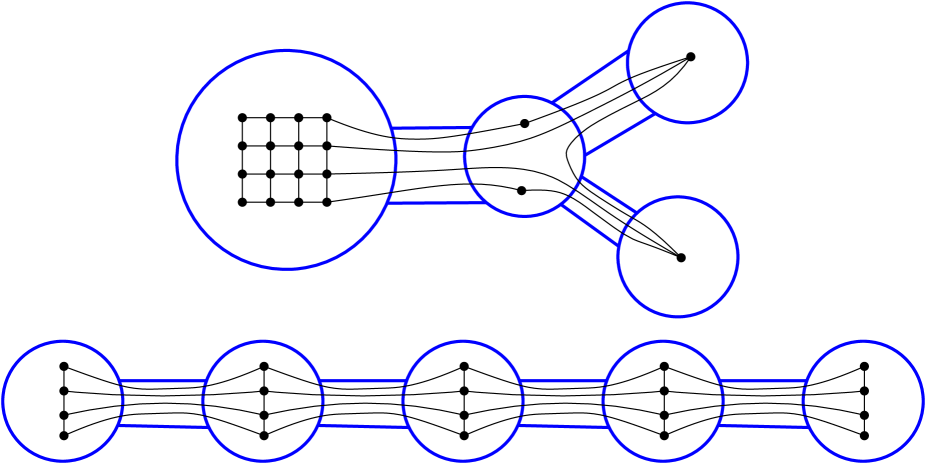
Given such a representation of a tree-cut decomposition, we compute several numbers, one for each link and one for each node. For each link of , we count the number of edges in passing through . For each node in , we count the number of vertices of drawn in , and add the number of “tunneling edges” of , which have neither endpoint in but still pass through it. The maximum of all these numbers is called the width of , denoted . In our example, the width of the first is computed as the maximum of , , (from the links), , , , and (from the nodes), so its width is ; the width of the second decomposition is .
The screewidth of , written , is the minimum width of any tree-cut decomposition of . For the grid graph, we thus have ; since , we can also deduce that . Indeed, without knowing anything about chip-firing games, this could have been used to deduce that given that .
We close this section by recalling several useful bounds on gonality from previous work.
Lemma 2.1 (§4 in [16], Theorem 1.1 in [11]).
We have the following formulas for gonality.
-
(i)
The gonality of a tree is ; moreover, trees are the only graphs of gonality .
-
(ii)
The gonality of a cycle graph is .
-
(iii)
The gonality of a complete graph on vertices is .
-
(iv)
The gonality of a complete bipartite graph is .
Moreover, in each of the above cases, scramble number equals gonality.
For the next two results, we let denote the independence number of a graph, which is the largest possible size of an independent set of vertices (i.e., a set of vertices with no two adjacent).
Lemma 2.2 (Proposition 3.1 in [9]).
If is a connected, simple graph on more than one vertex, then . The same result holds for disconnected as long as has no isolated vertices.
The original proof was for connected, but can be quickly adapted for arbitrary graphs: choose an independent set with , and place a single chip on every vertex besides those in . This divisor has positive rank: to move chips to any vertex , set-fire ; since has at least one neighbor in , and all neighbors of have a chip and exactly one edge connecting them to , this moves at least one chip to without introducing debt elsewhere.
Lemma 2.3 (Corollary 3.2 in [10]).
Let be a simple connected graph on vertices, such that the minimum valence of a vertex of is at least . Then .
3. King’s Graphs
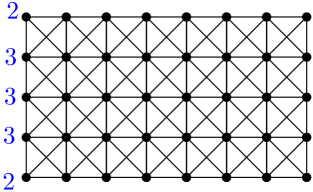
A king’s graph, denoted , consists of a grid graph with added diagonals. A king’s graph is depicted in Figure 6, with a divisor that we will see has positive rank.
Theorem 3.1.
We have , with equality for all .
Proof.
For an upper bound, consider the divisor that places chips on each vertex of the first column, except that the top and bottom vertices receive only chips; this is illustrated in Figure 6 for . Firing all vertices in the first column translates each chip one vertex to the right. Then, firing the first two columns translates each chip one vertex to the right again. Continuing in this fashion translates chips across the whole graph, so has positive rank. It follows that .
If , consider the scramble on whose eggs are the columns of the graph. Since the eggs are disjoint, . Between any two distinct eggs, we can find pairwise edge-disjoint paths: travelling horizontally (starting from any vertex in the left egg), and alternating between and moves (starting from any vertex in the left egg, except that the top vertex cannot start and the bottom vertex cannot start ). For an egg-cut to separate these eggs, it must contain at least one edge from each of these paths, so ; and in fact , for instance achieved by deleting all edges between the first two columns. The order of is , so . Combined with our upper bound, we have . ∎
It is natural to ask whether we can push these results further, to find when . We present several results to this effect for small values of .
Proposition 3.1.
We have the following formulas for the scramble number and gonality of and king’s graphs:
-
•
-
•
and , and
This provides us with as the first instance of a king’s graph whose gonality cannot be computed using scramble number.
Proof.
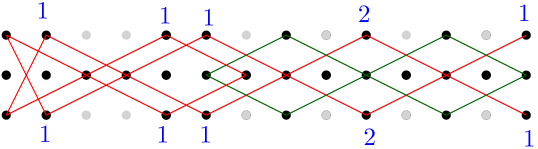
Since is the complete graph on vertices, it has gonality and scramble number by Lemma 2.1(iii). We know by Theorem 3.1. For a lower bound, we first argue that . A scramble of order on this graph is given by , illustrated on the left in Figure 7; hitting number is immediate to calculate as , and egg-cut number can be seen to be at least by finding four pairwise edge-disjoint paths between each pair of eggs. Since scramble number is subgraph monotone [11, Proposition 4.5], we have for all . This gives a lower bound on gonality, and so for

To show , we find an upper bound from the positive rank divisor illustrated in the middle of Figure 7, and a lower bound from the scramble of order illustrated on the right in the same figure (the analysis is similar to that for ). For larger , we know by Theorem 3.1. For a lower bound when , we consider the scramble on illustrated in Figure 8. Certainly the hitting number is ; to show the egg-cut number is at least , we can find pairwise edge-disjoint paths between every pair of eggs; see Lemma A.1 in Appendix A for more details. This gives for all , implying for such .
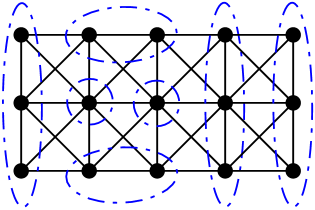
Finally, we consider . Figure 9 illustrates a scramble on the left, and a tree-cut decomposition on the right. The scramble has hitting number and egg-cut number at least (the argument is nearly identical to that from the previous paragraph for ), so the scramble has order . The tree-cut decomposition has width , giving us , and thus . To show that , we suppose for the sake of contradiction that has a positive rank divisor of degree . After carefully choosing an equivalent divisor without too many chips on any given vertex, we choose a particular vertex with no chips and argue that Dhar’s burning algorithm will burn the whole graph, a contradiction to the divisor having positive rank. This argument is long and technical, so we reserve it for Appendix A (in particular, see Lemma LABEL:lemma:appendix_k34).
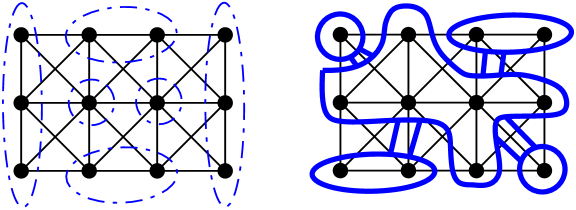
∎
We close this section with a discussion of larger knight’s graphs, some of which have unknown gonality. Using a brute-force computation (for instance, using the Chip Firing Interface website [1]), we can determine that and . However, it is not possible to prove either result using scramble number. Consider the tree-cut decompositions of in Figure 10. This decomposition has width ; since scramble number is non-increasing under taking subgraphs [11, Proposition 4.5], we have . Thus for king’s graphs, we cannot use scramble number to compute all gonalities; however, we find computationally that the eventual gonality of kicks in immediately for the graph, in contrast to having lower gonalities for , , and graphs. In light of this computational result, we pose the following conjecture.

Conjecture 3.1.
For , we have .
Example 3.1.
To see that scramble number cannot be used to prove this result for any choice of , consider the family of tree-cut decompositions on illustrated in Figure 11 for . For odd these decompositions consist of a central plus-shaped bag, with -shaped bags of decreasing size emanating towards the four corners, with two bags connected precisely when two of their vertices share an edge in . There are no tunneling edges; the largest bag has vertices; and the largest link adhesion occurs between the central bag and one of its neighboring bags. A neighboring bag has vertices, of which share edges with the central bag, shares , and the remainder share . Thus the maximum link adhesion is , which since is larger than , so the width of the tree-cut decomposition is for odd . The even case is handled similarly, except the central bag is off-centered and includes a half-column to the upper right, and some of the bags have a more oblong shape. A similar analysis shows that the largest bag size is and the largest edge adhesion is . The width is therefore . In both the even and odd cases, the width is strictly smaller than . This implies that for all , so if Conjecture 3.1 holds, it cannot be proved for any square king’s graph using scramble number.
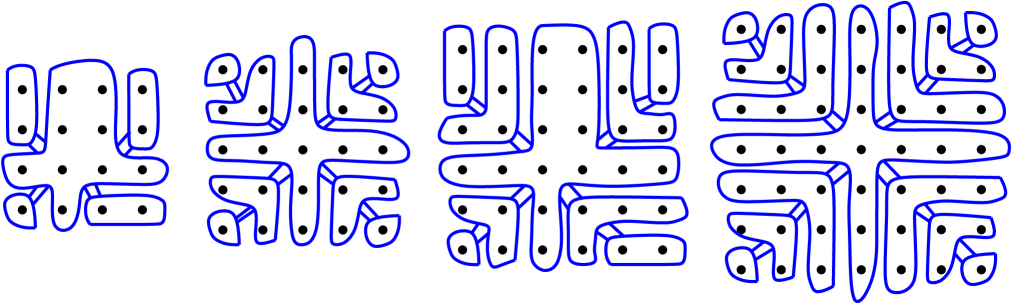
4. Toroidal king’s graphs
Toroidal king’s graphs add edges to the boundary rows and columns of a usual king’s graph. For , this yields an -regular graph, with every vertex having neighbors. When , fewer edges are added, since many of the edges that would be added are already present. We thus split our results across two theorems. First we present a lemma on the independence number of toroidal king’s graphs.
Lemma 4.1.
The toroidal king’s graph with has independence number
Proof.
We first consider . Every vertex in this graph borders both the other vertex in its column and the four vertices in neighboring columns. Thus, each column has at most one vertex in an independent set, and no two neighboring columns can both have a vertex in an independent set. Thus the largest possible size of an independent set is . Such an independent set exists: simply choose a vertex in every other column, rounded down if is odd. Thus , matching or formula.
For , we note that is the strong product333The strong product of two graphs and has vertex set , with two distinct vertices and adjacent precisely when either or is adjacent to in , and either or is adjacent to in . of the cycle graphs and . The formulas for this strong product are computed in [13, §4], and match our claim. ∎
Theorem 4.1.
The gonality of a toroidal king’s graph is given by
Proof.
For , we have that is the complete graph on vertices, and so has gonality by Lemma 2.1(iii). We note that every vertex in has valence , which is strictly more than half the number of vertices. This lets us apply Lemma 2.3 to conclude that .
For , we find an upper bound of on gonality by exhibiting a positive rank divisor of degree . Choose any column in , and place chips on each vertex. Firing both vertices in this column moves chips to each of the vertices in the adjacent columns. Then firing the original column together with the two adjacent columns moves chips to each vertex in the next columns out. Repeating this process by firing larger and larger sets of columns eventually moves chips throughout the whole graph, so this divisor has positive rank, and .
For our lower bound, we first consider the -uniform scramble on , whose eggs are all pairs of adjacent vertices. By [5, Lemma 3.2], we have . Let be an egg-cut, so that has two components and , say with and vertices, where without loss of generality . If , then since each vertex has valence we know there are at least edges in , where the comes from the double-counted edge interior to . If , then there are at most edges interior to , giving at least edges in ; and similarly if we find at least edges in . We observe that in any connected five vertex subgraph of , we can find at least two pairs of vertices (possibly overlapping) that are not in cyclically adjacent columns, meaning that such a subgraph has at most edges. Thus if , there are at most edges interior to , yielding at least edges in . In all cases, . As this was an arbitrary egg-cut, we have that , so . As scramble number is subgraph monotone, for all . This provides our desired lower bound on . ∎
We now present our most general result for toroidal king’s graphs.
Theorem 4.2.
For , we have , with equality for .
Proof.
As with king’s graphs in the previous section, we show the upper bound through positive rank divisor and the lower bound through scramble number.
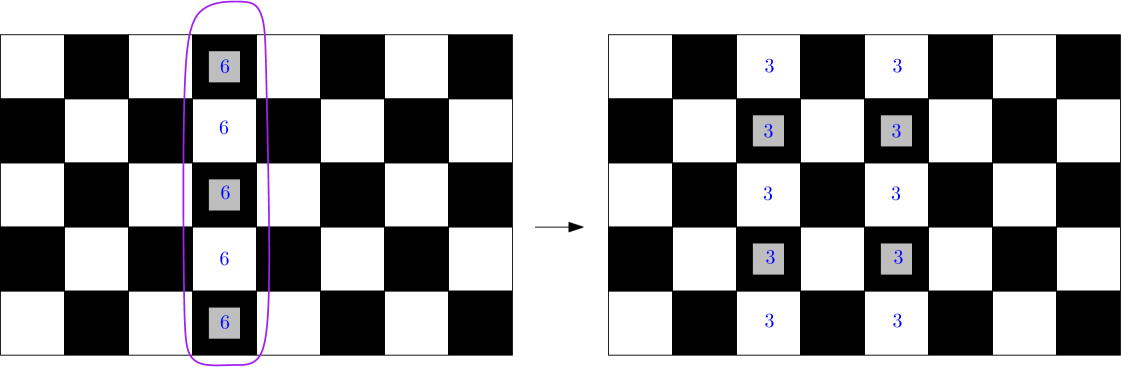
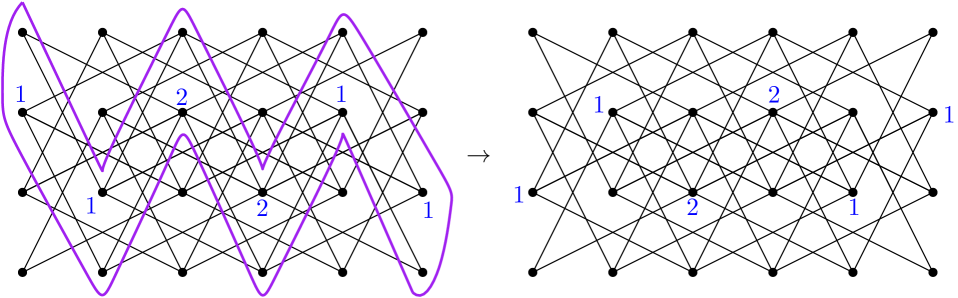
Choose a column in the graph and place chips on each vertex, for a total of chips; this divisor is illustrated on the left in Figure 12. Firing all vertices in this column moves chips to each of the vertices in the adjacent columns, as illustrated on the right. Then firing the original column together with the two adjacent columns moves chips to each vertex in the next columns out. Repeating this process by firing larger and larger sets of columns eventually moves chips throughout the whole graph, so this divisor has positive rank, and .
Now assume , and consider the scramble on whose eggs are precisely the columns. Since the eggs are disjoint, the hitting number is immediately computed as . We claim that . Since the set of edges incident to a single column forms an egg-cut, we have . To argue that , we find pairwise edge-disjoint paths between an arbitrary pair of eggs. Starting from one egg, travel to the left from any vertex horizontally, or zigzagging between and moves (starting with either) until the other egg is reached. This gives paths. Another paths can be found by travelling to the right. Any egg-cut separating those two eggs must include an edge from each of the paths. Since we chose an arbitrary pair of eggs, we have , and thus . This gives us
implying .
∎
We remark that we do not have for every choice of and with . For example, is a complete graph on vertices, and so has gonality . We can also compute and as each vertex has valence strictly larger than half the number of vertices. This implies by Lemma 2.3 that and . More generally, the upper bound of
gives a better upper bound than when .
5. Bishop’s Graphs
We now turn to bishop’s graphs. For , note that is disconnected, with exactly two components: one representing white tiles on a chess board, and the other representing black tiles. We denote these two components and , and take to contain the vertex . We remind the reader that for disconnected graphs, gonality can be computed as the sum of the gonalities of the disconnected components, so . Since consists of two path graphs, each with gonality by Lemma 2.1, we have .
Our general upper bound on with will depend solely on . Before stating this result, we consider , , and bishop’s graphs. This will allow us to build up a general strategy for the case.
Example 5.1.
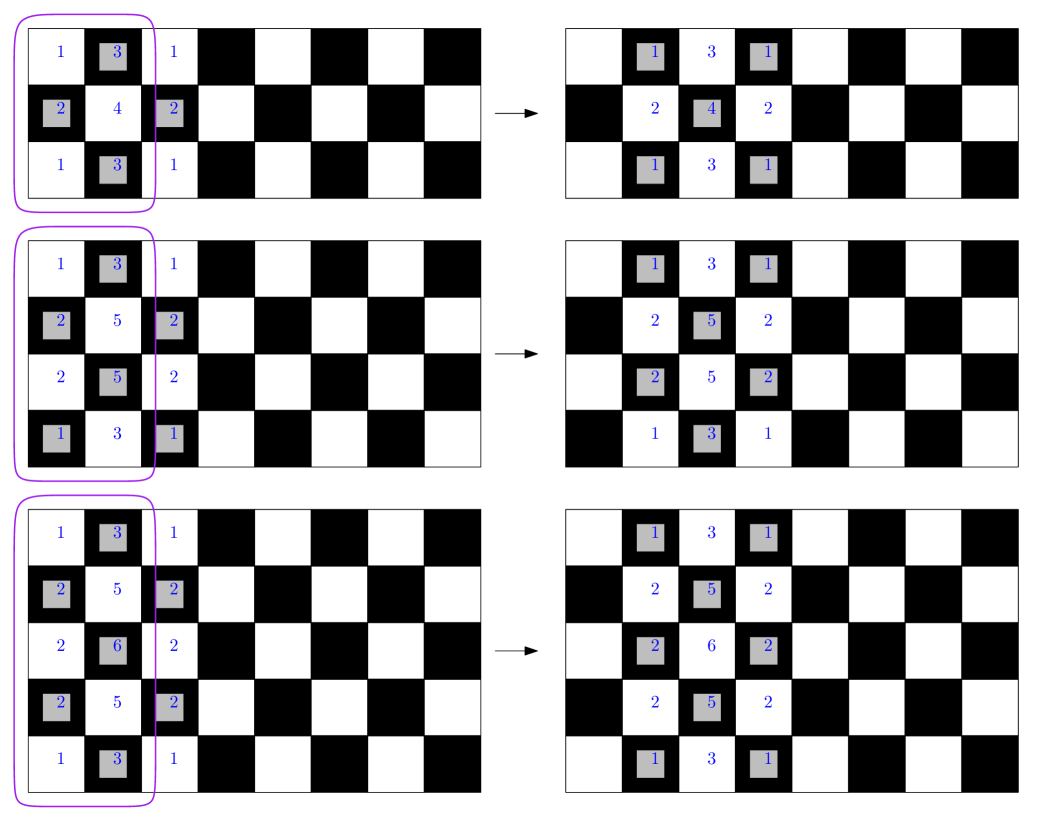
Consider the divisor on illustrated on the top left in Figure 13. Firing the first two columns transforms into , illustrated to the right. Note that appears identical to , except with each chip shifted to the right by one unit. Firing the first three columns, then the first four, and so on continues this pattern, translating the chips across the graph until there are chips in the final column. This places chips on almost every vertex, with two omitted, namely and . These can still be covered: by repeating our “fire the first ” columns strategy, and by symmetry. Thus this divisor has positive rank, regardless of the value of . It follows that for all .
Divisors are also illustrated in Figure 13 for with and . Firing the first columns translates the divisor horizontally as illustrated, and we can once again use this to argue that the divisor will have positive rank regardless of the value of . Summing up the number of chips, we find and .
Although these chip placements are clearly suboptimal for small values of , the key takeaway is that there is a universal bound for each choice of that is completely independent of . We will generalize this to all in the following theorem, but first we explain intuitively how to build these divisors. Chips are placed in the first columns, with a mirror image of the first columns in columns through . To determine how many chips a vertex in the first columns should receive, we determine how many chips it will lose as we fire the first columns, then the first columns, and so on. For instance, the vertex in will lose chip up and to the right, and chips down and to the right on the first firing move; then chips down and to the right on the second firing move; then chip down and to the right on the third firing move, for a total of chips. Due to the structure of the graph, this number will always be the sum of two triangular numbers ; in our example, we have . Choosing this many chips ensures that no vertex will go into debt through our firing process; and as we will see in the proof of the following theorem, the recursive nature of triangular numbers leads to the translation patterns we have observed thus far.
Recall that for ; by convention, we take for . Note that triangular numbers satisfy the relation for any integer .
Theorem 5.1.
For , we have .
Proof.
Without loss of generality, we may assume that ; otherwise we may use the divisor that places one chip on every vertex, which has degree smaller than . This ensures we will have enough horizontal space to build our divisor.
Define on by
We first show that has positive rank. Consider firing the first columns of the graph, transforming into . If , then the number of chips the vertex loses up and to the right is , and the number of chips it loses down and to the left is . In other words, the number of chips it loses is . This means that
for . If , the vertex starts with chips and gains chips, meaning . Finally, for , the vertex will gain a number of chips equal to . It follows that
In all cases, we have .
Thus firing the first columns has the net effect of translating the divisor one unit to the right. Firing larger and larger subsets of columns repeats this process, translating the divisor along the whole graph. This will eventually place a chip on every vertex, with the exception of two triangular wedges, one on the left and one on the right. However, continuing the process of firing larger and larger sets of columns will eventually place chips on all the vertices in the right wedge; and a symmetric argument handles the vertices in the left wedge. Thus the divisor has positive rank, as desired.
We now compute . In the row, the term yields the nonzero triangular numbers
while the term yields the nonzero triangular numbers
It follows that the total number of chips in the row is
which can be rewritten as
Summing this expression as goes from to yields for the degree of . Since has positive rank, we have that , as desired. ∎
It is natural to ask whether this bound is sharp, or at least of the right order of magnitude in terms of . Unfortunately, the tool of scramble number will not suffice to answer this question, as detailed below.
Proposition 5.1.
For and even, we have .
Proof.
To show , we consider the scramble on whose eggs are disjoint and consist of the first columns, then the next columns, and so on, with the last egg receiving between and columns. Since the eggs are disjoint, we have .
We now construct a collection of pairwise edge-disjoint paths on , which will be used to lower bound . Our strategy is as follows: choose an integer with . Choose a vertex in the first columns and the first rows of . From this vertex, alternate and moves (starting with ) until no more moves are possible. Note that there are vertices in the first columns and the first rows, of which are white. Thus we have constructed
“down-paths”, which are edge-disjoint by construction. We may similarly construct a collection of “up-paths” for each , choosing a vertex in the first columns and the last rows, alternating between and moves (starting with ) until no more moves are possible. A similar analysis gives us
“up-paths”. Taken together, we have constructed a family of
pairwise edge-disjoint paths on .
Since the eggs of are subgraphs and all moves go forward by at most , every one of our paths intersects every egg. Thus by truncating paths appropriately, for every pair of eggs we can find pairwise edge-disjoint paths connecting them. It follows that . On the other hand, ; for instance, this equals the number of edges connecting the first two eggs.
Taken together, we have . It follows that .
For the upper bound we construct a tree-cut decomposition on . Place the first columns in one bag, then the next , and so on, with the last bag receiving possibly fewer than columns; connect the bags in a path from left to right. Each bag has at most vertices, and there are no tunneling edges. The number of edges in each link is at most : indeed, every edge between a pair of adjacent bags is part of one of the down-paths or up-paths we considered previously. Every path has exactly one edge connecting two adjacent bags with columns each, so at least one link has exactly edges. Thus the width of the tree-cut decomposition is , where we use the fact that . This gives us , implying that .
An identical argument shows that . ∎
Since is a subgraph of which is a subgraph of , this immediately gives us the upper and lower bounds of
for odd; a similar bound can be found for . This means that scramble number provides us with an lower bound on , as detailed below; however, no stronger lower bound can be proved using scramble number.
Corollary 5.1.
Let , , and . We have .
Proof.
First assume is even, so . Then
by the previous result.
If is odd, then . Since has as a subgraph, we know that ; similarly, . This gives us the claimed lower bound on . ∎
The last avenue we might take to evaluate the bounds from Theorem 5.1 is from a computational perspective. This is unfeasible for , since the upper bound of will outperform our bound until is quite large, since for [4, Proposition 7.3]. For , for instance, this upper bound is at least , which outperforms the upper bound of as long as . The first graph where our result would do better is , whose components each have vertices. However, for (where we have an upper bound of on gonality), we find using the Chip-Firing Interface [1] that , so (for smaller choices of , the gonality is strictly lower than ). It is worth noting that gonality can be larger for a subgraph than a larger graph (even if both graphs are connected), so this computation does not necessarily imply that for .
6. Toroidal Bishop’s Graphs
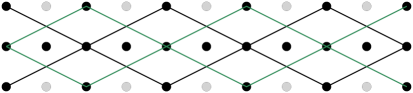
We now consider the structure of , the toroidal bishop’s graph. Following the work in [8], we classify the diagonals as -diagonals and -diagonals, where -diagonals are those that go to the right and down, whereas -diagonals go to the right and up. Several - and -diagonals are illustrated in Figure 14. There are several features that distinguish the behavior of these diagonals on a toroidal versus a non-toroidal bishop’s graph:
-
•
On a non-toroidal graph, -diagonals and -diagonals have length at most ; on a toroidal graph, they can be longer.
-
•
On a non-torodial graph, an -diagonal and a -diagonal can intersect at most once; on a toroidal graph, they can intersect more than once.
-
•
On a non-toroidal graph, diagonals are monochromatic (consisting entirely of black squares, or of white squares); on a toroidal graph, if either or is odd, -diagonals and -diagonals have multiple colors.
We present a few lemmas to better understand the structure of in terms of these diagonals.

Lemma 6.1 ([8]).
The length of each diagonal of is .
The summary of the proof from [8] is quick to give: a bishop moving along a fixed diagonal will return to its row every moves, and to its column every moves; therefore it will first return to its initial location after moves.
Since we may partition into either -diagonals or -diagonals, this immediately leads to the following corollaries.
Corollary 6.1.
There are many -diagonals, and many -diagonals.
Corollary 6.2.
The graph is isomorphic to the complete graph if and only if and are relatively prime.
We now describe the intersection properties of -diagonals with -diagonals.
Lemma 6.2.
For a toroidal bishop’s graph ,
-
(i)
if or is odd, every -diagonal intersects every -diagonal at least once; and
-
(ii)
if are both even, every -diagonal intersects every -diagonal of its color at least once.
Proof.
For claim (i) we assume at least one of and is odd. Without loss of generality, consider the -diagonal that contains all such that . Now, consider any -diagonal; for some , it contains all such that . These diagonals intersect if there is some point in common between the two; that is, if there exists such that . But this is indeed the case: is odd, so for any , either or is even. Therefore dividing or by 2 yields an integer; it follows that a diagonal starting on or will intersect the desired -diagonal.
For claim (ii) we assume and are both even. The black and white components of the graph are isomorphic, so without loss of generality, consider again the diagonal of with . The only -diagonals of the same color are of the form with for some even . So at intersections with the fixed -diagonal, . Since is even, such an exists, so the desired intersection exists. ∎
We are now ready to compute the gonality of all toroidal bishop’s graphs. Our proof is inspired by that of [14, Theorem 1.1], where the gonality of rook’s graphs was determined.
Theorem 6.1.
For , we have
Proof.
It remains to show that . First, consider the case where are not both even, so that the bishop’s graph is connected. Suppose there is an effective divisor of positive rank with degree strictly less than . Among all effective divisors equivalent to , let be one where the -diagonal with the fewest chips placed on it has the most chips. There are many diagonals, and , so if there are fewer chips than then at least one -diagonal has fewer chips than . Now,choose a vertex on the poorest -diagonal with , and run Dhar’s burning algorithm. Since the -diagonal is isomorphic to the complete graph , the fire burns the whole diagonal since there are fewer than chips [2, Proposition 14]. Since are both odd, this diagonal intersects every other diagonal at least once, and therefore starts a fire along each diagonal. Since the poorest -diagonal also has strictly less than chips, and it also burns.
Since has positive rank and has no chips, we know that the whole graph does not burn. Let be the set of vertices that do not burn, which Dhar’s algorithm dictates we now fire to obtain a new divisor . Since the burned -diagonal intersects each -diagonal, we know that each has at most vertices in . Thus when is fired, any -diagonal with vertices in moves chips to the burned vertices of that diagonal. Therefore each -diagonal that has unburned vertices has more chips than the richest poorest diagonal we started with. On the other hand every -diagonal that burned completely will gain chips, as the unburned portions of -diagonals fire along -diagonals. Thus has a richer poorest -diagonal than , a contradiction. Thus any positive rank divisor on has degree at least when at least of of and is odd.
If are both even, the gonality of the graph is simply the sum of the gonalities of its components. Thus if the gonality is less than , one of the connected components must have gonality less than . Writing , the gonality of that component must be less than . So, some -column has fewer than chips for any equivalent divisor. From there, the argument then proceeds as before. ∎
The reader may wonder whether this result could be proved by means of scramble number. For certain values of and , the answer is yes; for instance, if , then we have a complete graph, which has scramble number equal to gonality. For other values, this is not the case, even if the graph is connected.
Example 6.1.
In this example we show that the toroidal bishop’s graph has scramble number strictly smaller than gonality. By the previous theorem, we know . Suppose for the sake of contradiction that , and let be a scramble of order on . Consider the grey vertices in Figure 15. Since , these do not form a hitting set, so there must be an egg contained among the other six vertices. The only edges shared by the six black vertices are the three pictured, so the egg must consist of a single vertex or a pair of adjacent vertices. Moreover, since those six vertices also cannot form a hitting set for , there is a second egg contained among the other . Deleting the edges connecting to the rest of the graph thus forms an egg-cut. If is a single vertex, the egg-cut has size ; and if is a pair of adjacent vertices, the egg-cut has size . Either way, we have , a contradiction. Thus .
7. Knight’s Graphs
The story for knight’s graphs is similar to bishop’s graphs: we can find a bound on depending solely on , although this bound is provably suboptimal for graphs with and close to one another. We begin by presenting our most general upper bound, and then pivot to more intermediate cases.
Theorem 7.1.
For the knight’s graphs with , we have the following formulas and bounds:
-
(1)
.
-
(2)
-
(3)
for .
Proof.
We remark that has four connected components, each a path, as illustrated in Figure 16. A path has gonality , so .
For , we construct a divisor as follows. Within the first and third columns, place one chip on the top and bottom vertices, and two chips on all other vertices. Within the second column, place three chips on the top and bottom vertices. Then, if , place chips on the middle vertex of that column; and if , place chips on the vertices directly above the top vertex and directly below the bottom vertex, and chips on all remaining vertices in the column. This divisor is illustrated for and on the left in Figure 17. Note that if , we have ; and if ,
In both cases equals our claimed upper bound for , so to prove the remainder of our claim it will suffice to show that has positive rank.
Consider the effect on of firing the set of vertices in the first two columns of . This will effect the first four columns of the graph as follows:
-
•
In the first column, every vertex has as many neighbors outside as it has chips. Thus every vertex loses all its chips.
-
•
In the second column, the top and bottom vertex have two neighbors outside of , so go from chips to chip. If , the middle vertex has two neighbors outside of , and so goes from chips to chips. If , then the second topmost and second bottom-most vertices have neighbors outside of , and so go from chips to chips; and any remaining vertex has neighbors outside of , and so goes from chips to chips. In summary, the second column becomes identical to the first column in .
-
•
In the third column, the top and bottom vertex have neighbors in , and so go from chip to chips. If , the middle vertex has neighbors in , and so goes from chips to chips. If , the second top-most and second bottom-most vertices have neighbors in , and so go from chips to chips; and all other vertices have neighbors in , and so go from chips to chips. In summary, the third column becomes identical to the second column in .
-
•
Finally, in the third column, the top and bottom vertices each have neighbor in , and all other vertices have neighbors. Each vertex gains that many chips, and as each vertex in that column started with chips, it has become identical to the third column in .
Thus the net effect of firing the first two columns is to translate all chips from to the right one vertex, as illustrated in Figure 17. From here, set-firing the first three columns moves the chips to the right one vertex again. We may continue in this fashion, set-firing the first columns for increasing values of , until we have translated our chips all the way across the graph. Each of the intermediate divisors is effective, and for every vertex in the graph at least one divisor places a chip on that vertex. Thus has positive rank. ∎
The bounds from Theorem 7.1 with are certainly not optimal for all . For instance, since knight’s graphs are bipartite, they have independence number at least , giving an upper bound on gonality of . For , this outperforms the bound of for . The following theorem presents an alternate “better-than-bipartite” bound for .
Theorem 7.2.
We have the following upper bounds on the gonality of knight’s graphs.
-
(i)
For , .
-
(ii)
For , .
-
(iii)
For , .
We reserve the proof of this result for Appendix B. We remark that this theorem outperforms Theorem 7.1 for and ; for and ; and for and . We do not expect the above to be the exact formula for gonality for all these values, but rather a demonstration that there exist strategies outperforming those of Theorem 7.1 for certain values of and . Still, it is worth asking whether these formulas are optimal for any values of . When , Theorem 7.2 is optimal for :
Proposition 7.1.
We have , , and .
We prove this proposition in Appendix B. Using the Chip-Firing Interface [1], we also verify that Theorem 7.2 gives the correct gonality for and and for and , although it is unable to compute gonality for larger knight’s graphs.
We now pivot to lower bounds on gonality. In contrast to bishop’s graphs, we can use scramble number to find a lower bound on with the same order of magnitude as our upper bound from Theorem 7.1.
Proposition 7.2.
Let and let . Then .
Proof.
Construct a scramble whose first egg consists of the first three columns of , the second egg the next three columns, and so on; if is not a multiple of , then any leftover columns are included in the same egg as the last complete set of four columns. Note that is connected since , so this is a valid scramble.
As the eggs are disjoint, we have . To lower bound the egg-cut number by , we can construct pairwise edge-disjoint paths, each of which intersects every egg. First we consider paths stretching across the graph alternating between and moves. We can find pairwise edge-disjoint such paths: start at any vertex in the first two columns, and choose whether to start with a move or a move. The only restriction is that a vertex in the top row cannot perform a move, and a vertex in the bottom row cannot perform a move, accounted for by the . Then we find more paths, starting from a vertex in the first column and alternating and moves in some order. There are ways to choose a vertex and a starting move, with excluded since the top two and bottom two vertices have only one option for their first move.
This gives a total of pairwise edge-disjoint paths. Any egg-cut must include at least one edge from each of these paths, so . We conclude that .
For an upper bound, we consider the tree-cut decomposition whose bags are pairs of adjacent columns (first and second columns in one bag, third and fourth column in the next, and so on), except that the last bag has three columns if is odd. Arrange these bags in a path, from left to right. There are no tunneling edges, so the contribution of each bag is at most ; and between any two adjacent bags, every edge comes from one of the paths above, and each such path contributes exactly one edge. Since , we have , and so the width of this tree-cut decomposition is . Thus we have . This completes the proof. ∎
Thus for and much larger than , we have since scramble number is a lower bound on gonality. This means that our upper bound is, in the worst possible case, approximately a factor of larger than the actual gonality. However, scramble number cannot be used to narrow this gap any further.
8. Toroidal Knight’s Graphs
We can also find a bound on the gonality of the toroidal knight’s graph solely in terms of , where .
Theorem 8.1.
The gonality of the toroidal knight’s graph is bounded by
Proof.
For the case, if the claim is immediate as we can place a chip on every vertex. For , start at any vertex on the top row and place, from left to right, , , , , , and chip; duplicate this directly below on the bottom row. The resulting divisor is illustrated in Figure 18, along with several equivalent divisors. Firing the middle four columns has the net effect of translating the four collections of chips outward. Firing the middle six repeats this, and so on, allowing the divisor to eventually move chips to any vertex. Thus , and .
For , a similar divisor on can be built when ( is handled by the small number of vertices), except with a pattern of , , , , , replicated along the rows. Again, set-firing the middle four columns, then the middle six, and so on translates chips along the graph, giving us a positive rank divisor of degree . ∎
As for knight’s graphs, these divisors are provably suboptimal for small values of . For choices of and with , simply placing a chip on every vertex would yield a winning divisor of lower degree. Stronger bounds can be found when and are both small and even, as the graph is bipartite. It remains an open question which, if any, toroidal knight’s graphs have gonality equal to our upper bound.
As we did for traditional knight’s graphs, we test the strength of our upper bound using scramble number.
Proposition 8.1.
Let and . Then .
Proof.
For the lower bound, we construct a scramble identical to that from the proof of Proposition 7.2, with disjoint eggs consisting of columns each (with one egg receiving up to two more columns, if is not a multiple of ). The hitting number of this scramble is given by the number of eggs: .
To lower bound the egg-cut number, we consider an arbitrary pair of eggs, and . Starting in , we construct paths from to that travel to the right: starting from any vertex in the second and third column of and alternating and moves in some order; and starting from any vertex in the first column of and alternating and in some order444To ensure these paths are different, we need our assumption; if , a move is identical to a move.. We can similarly construct paths from to travelling to the left: starting from any vertex in the first and second column of and alternating and in some order; and starting from any vertex in the first column of and alternating and in some order. These paths are pairwise edge-disjoint, and any egg-cut separating and must include an edge from each. Thus we have , and so .
For the upper bound on scramble number, we construct the exact same tree-cut decomposition as in the non-toroidal case, letting our bags be groups of adjacent columns except for one final bag possibly consisting of columns. The edges between adjacent bags increases from to due to the toroidal nature of the graph. All edges from the leftmost bag to the rightmost bag are now tunneling edges; there are of these, adding a weight of to each link and each middle bag. Thus the width of this tree-cut decomposition is , giving . This completes the proof. ∎
Thus for and much larger than , we have . As with the non-toroidal knight’s graph, we have at worst a factor of overestimate of gonality with our current upper bound; and no stronger results can be gleaned from scramble number. We remark that for odd, we may modify our scramble to have eggs consisting of two adjacent columns (which form connected subgraphs), which allows us to loosen our restriction on to .
9. Future Directions
A major open question is whether our upper bounds on gonality are in fact equal to gonality for chessboards, at least for sufficiently large compared to . The answer is yes for king’s, toroidal king’s, and toroidal bishop’s, but remains open for bishop’s, knight’s, and toroidal knight’s. Such a result would not be provable using scramble number, so new lower bounds on gonality may need to be developed to prove such a result.
Another direction for future work could be modifying our chessboards, for instance by considering higher dimensional analogs of these graphs. Even in -dimensions, there is little known; for instance, the gonality the rook’s graph is only known for [14, Theorem 1.3]. Another modification could be to the “glueing” rules; for instance, instead of toroidal chessboards, one could consider half-toroidal chessboards, Möbius chessboards, or Klein-bottle chessboards.
References
- [1] The chip firing interface. https://chipfiringinterface.web.app/. Accessed: 2024-03-05.
- [2] Ivan Aidun and Ralph Morrison. On the gonality of Cartesian products of graphs. Electron. J. Combin., 27(4):Paper No. 4.52, 35, 2020.
- [3] Matthew Baker. Specialization of linear systems from curves to graphs. Algebra Number Theory, 2(6):613–653, 2008. With an appendix by Brian Conrad.
- [4] Rudolf Berghammer. Relational modelling and solution of chessboard problems. In Relational and algebraic methods in computer science, volume 6663 of Lecture Notes in Comput. Sci., pages 92–108. Springer, Heidelberg, 2011.
- [5] Lisa Cenek, Lizzie Ferguson, Eyobel Gebre, Cassandra Marcussen, Jason Meintjes, Ralph Morrison, Liz Ostermeyer, and Shefali Ramakrishna. Uniform scrambles on graphs. Australas. J. Combin., 87:129–147, 2023.
- [6] Lisa Cenek, Lizzie Ferguson, Eyobel Gebre, Cassandra Marcussen, Jason Meintjes, Ralph Morrison, Liz Ostermeyer, Shefali Ramakrishna, and Ben Weber. Scramble number and tree-cut decompositions, 2022.
- [7] Scott Corry and David Perkinson. Divisors and Sandpiles: An Introduction to Chip-firing. American Mathematical Society, 2018.
- [8] Joe DeMaio and William Faust. Domination and independence on the rectangular torus by rooks and bishops. In International Conference on Foundations of Computer Science, 2009.
- [9] Andrew Deveau, David Jensen, Jenna Kainic, and Dan Mitropolsky. Gonality of random graphs. Involve, 9(4):715–720, 2016.
- [10] Marino Echavarria, Max Everett, Robin Huang, Liza Jacoby, Ralph Morrison, and Ben Weber. On the scramble number of graphs. Discrete Appl. Math., 310:43–59, 2022.
- [11] Michael Harp, Elijah Jackson, David Jensen, and Noah Speeter. A new lower bound on graph gonality. Discrete Appl. Math., 309:172–179, 2022.
- [12] Ralph Morrison and Noah Speeter. The gonality of queen’s graphs, 2023.
- [13] Eckart Sonnemann and Olaf Krafft. Independence numbers of product graphs. J. Combinatorial Theory Ser. B, 17:133–142, 1974.
- [14] Noah Speeter. The gonality of rook graphs, 2022.
- [15] Josse van Dobben de Bruyn. Reduced divisors and gonality in finite graphs. Bachelor’s thesis, Mathematisch Instituut, Universiteit Leiden, 2012.
- [16] Josse van Dobben de Bruyn and Dion Gijswijt. Treewidth is a lower bound on graph gonality. Algebr. Comb., 3(4):941–953, 2020.
Appendix A Computations for king’s graphs
Lemma A.1.
The scramble on illustrated in Figure 9 satisfies .
Proof.
To prove this it will suffice to show that between any pair of eggs, there exist at least pairwise edge-disjoint paths between them (this is because any egg-cut separating a pair of eggs would have to include an edge from any such collection of paths).
For pairs of eggs that are each a complete column, the argument from the proof of Theorem 3.1 gives such paths. The remaining cases to handle are where the two eggs have the following numbers of vertices: and , and , and , and , and and . Representative pairings of each type are shown in Figure 19, with each row containing pairwise edge-disjoint paths between that pair of eggs. These paths can be adapted for all unpictured pairs of eggs either using the symmetry of the graph, or by extending the paths across columns using the paths from the proof of Theorem 3.1.

∎
Lemma A.2.
We have .
Proof.
We have by Theorem A. Suppose for the sake of contradiction that . Then there exists a positive rank divisor of degree on . As presented in the discussion after [2, Lemma 16], we may assume that is effective, that places at most chips on each vertex, and that does not place chips and on any pair of adjacent vertices and .
The remainder of our argument will consist of carefully choosing an unchipped vertex of and running Dhar’s burning algorithm from there. We will argue that the whole graph burns, contradicting having positive rank. We make the following observations for how fire will propagate throughout the graph.
-
(1)
If four vertices forming a subgraph have together either at most chips, or three chips placed in a - pattern, then once one vertex burns, the whole subgraph will burn.
-
(2)
There exists a vertex with no chips such that running Dhar’s from will burn the whole column of .
Certainly if some column has no chips, this is true: pick in that column. Otherwise, every column has at least one chip. The distribution of chips among the four columns is thus either , , , and or , , , and , in some order. Either way we can find two adjacent columns, and , such that has chip and has at most chips. We may view as two copies of , overlapping at the two vertices and If both copies of have chips, then ; running Dhar’s from any other vertex in burns all of . Thus we may assume one copy of has at most chips. Choose to be an unchipped vertex on that . By observation (1), that copy of burns. The remaining vertex in has at most chip and at least two burning edges, so it burns, giving us a burned column.
-
(3)
If the second column burns, then the first column will burn. (Symmetrically if the second column burns, then the first column burns.)
To see this, note that the first column has at most chips. For all three vertices to remain unburned, chips are required. For two vertices to remain unburned, either the two corner vertices need valence-many chips (a contradiction), or the middle and a corner need and chips, (also a contradiction, since no two adjacent vertices have one less than valence-many chips). And for one vertex to remain unburned, that vertex must have valence-many chips, again a contradiction.
-
(4)
If the first column burns, then the second column will burn. (Symmetrically if the fourth column burns, then the third column burns.)
There are at most chips in , and the vertices have , , and incoming burning edges from ; thus at least one vertex in must immediately burn. First we deal with the case that exactly one immediately burns. If is the only one that immediately burns, then the divisor must be . The fire spreads to , leading to the other two vertices burning. A similar argument holds if immediately burns. If is the only that immediately burns, then the divisor must be . The fire spreads to leading to the other two vertices burning. In all cases, burns.
Now we deal with the case that exactly two immediately burn. If and immediately burn, then must have at least chips, and also at most chips. It follows that contains at most chips. Consider the copy of made up of , and . If the whole burns, then for to stay unburned then so too must . This means that . However, the fire spreads to and from there burns , and from there . so all of burns. If that does not burn, then either or has three chips. This forces either or ; in both cases burns, and from there burns. A similar argument holds if and immediately burn. Finally, if and immediately burn, then must have at least chips. This means has at most one chip, and since all its vertices neighbor either or , at least two vertices in burn. This means vertices neighboring burn, and since , we have that must burn, completing the column.
-
(5)
If the second column burns, then the third column will burn. (Symmetrically if the third column burns, then the second column burns.)
The argument is nearly identical that of claim (4), with the column of each vertex shifted right by one. The one difference comes in when we find that ; here we reach a contradiction, since no two adjacent vertices can have valence-minus-one chips on them.
Taking together, we quickly have a proof: choose a vertex satisfying (2). Observations (3), (4), and (5) guarantee that once a column burns, so do all adjacent columns, meaning that running Dhar’s burning algorithm starting at burns the entire graph. Since has no chips, this is a contradiction to being a positive rank divisor. We conclude that , and thus . ∎
Appendix B Computations for knight’s graphs
Proof of Theorem 7.2(i).
First assume that is odd. Since , we know is connected. Consider the divisor that places two chips on every other column, starting with the second, on its top and bottom vertices. This divisor has degree , which since is odd is equal to . We will show that this divisor has positive rank.
In Figure 20 we illustrate the placement of chips from as gray vertices, with the connected components of illustrated as well. Some of these connected components are isolated vertices ; chips can be moved to them by set-firing . There are two other components, consisting of -cycles glued at vertices. Focus on one such component. Firing the complement of the component moves chips to each of its vertices in the top and bottom rows. At this point every vertex from that component in the middle row has a chip on each neighbor; firing the complement of that vertex moves a chip there. A symmetric argument shows we may move a chip to any vertex in the other large component. Taken together, a chip may be moved to any vertex, so our divisor has positive rank as desired.
Now consider even. The case of is handled by Proposition 7.1 (proved later in this appendix), so we consider . We use a similar chip placement to the odd case, in that we choose a set of columns and place two chips on each, one on the top vertex and one on the bottom vertex. However, the columns we choose are the , the , and the for any odd . This divisor has degree since .

We represent on the left in Figure 21 the divisor as grayed vertices, with the connected components of the remaining vertices illustrated. Moving chips to most vertices works largely as in the odd case: isolated vertex components are easily handled, as is the smaller of the two larger components. For the last component, firing its complement places chips on all its vertices except those in the middle row, and except for the top and bottom vertex in the rightmost row; this is illustrated in the right on Figure 21. Every vertex not yet chipped either has all neighbors with a chip, and so can be dealt with by firing its complement; or it is one of , , or , and firing the complement of this set places chips on all those vertices. ∎
Proof of Theorem 7.2(ii).
Consider the following divisor on the knight’s graph. Choose one vertex from each column, alternating between the second and third rows. Place chip on that vertex if it is in the two leftmost or two rightmost columns; otherwise place chips on it. Note that . We will argue that has positive rank.
Illustrated in Figure 22 is the divisor , as well as a set-firing move transforming it into another divisor . Any vertex in the second or third row has a chip placed on it by or . For every vertex in the first or fourth row, either or places a chip on all of its neighbors. Starting from that divisor and set-firing places a chip on . Having argued that we may place a chip on any vertex, we conclude that has positive rank. ∎
Proof of Theorem 7.2(iii).
Consider the following divisor on the knight’s graph. Place a chip on every vertex in the third row. Then place one more chip in each column, either in the second or fourth row, in groups of four (so the first four columns have a chip in the second row, the next four columns have a chip in the fourth row, and so on). Finally, on every fifth row, place one more chip in either the second or fourth row, whichever does not already have a chip. This divisor has degree . We will argue it has positive rank.
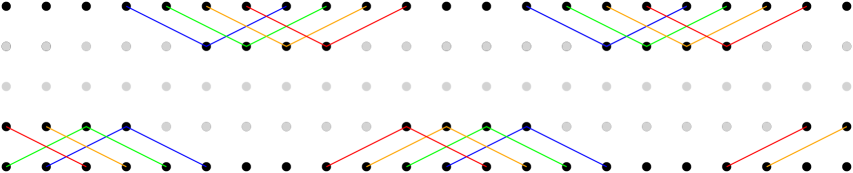
We represent the divisor in Figure 23 with gray vertices, and illustrated the connected components of . Note that these connected components are all trees, and that each vertex in has at most one neighbor in each tree. It follows from the argument in [15, Theorem 3.33] that has positive rank (indeed, firing the complement of one of the trees moves chips onto all vertices of that tree). ∎
Proof of Proposition 7.1.
The graph is disconnected, with a cycle on eight vertices and an isolated vertex as its two components. By Lemma 2.1, these components have gonality and gonality , respectively, so .
The graph is illustrated with two different pictures in Figure 24; we focus on the second rendering, which appears as a grid graph with edges missing from the middle row. A divisor of degree is illustrated on the right in Figure 24. This divisor has positive rank: by firing the first column in this grid interpretation, then the first two columns, and so on, we may move two chips to the top and bottom of any column. To place a chip on a vertex in the middle row, first move chips to its two neighbors, then set-fire the complement of . This gives . Since is not a tree, we know by Lemma 2.1, so .
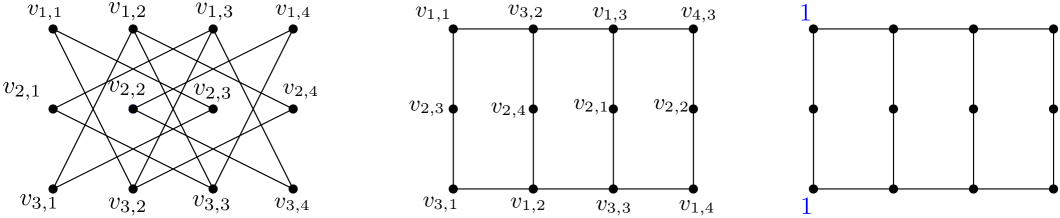
For and , an upper bound of on gonality comes from Theorem 7.2. For a lower bound we will use scramble number.
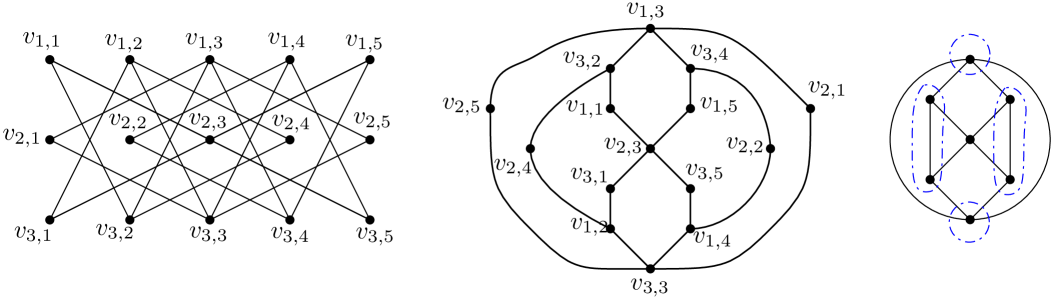
The graph is illustrated in its usual form on the left in Figure 25, with an alternate drawing in the middle. Since scramble number is invariant under “smoothing over” -valent vertices [11, Proposition 4.6], the scramble number of is equal to the scramble number of the graph illustrated on the right in Figure 25. That same figure presents a scramble on , which we claim has order . Certainly , since there are four disjoint eggs. Between any pair of eggs we can find four pairwise edge-disjoint paths, so . Thus . This gives us
allowing us to conclude that .
For the knight’s graph, we note that is a subgraph of . Since scramble number is monotone under taking subgraphs [11, Proposition 4.5], we have
so . ∎