The Grid-Minor Theorem Revisited
Abstract.
We prove that for every planar graph of treedepth , there exists a positive integer such that for every -minor-free graph , there exists a graph of treewidth at most such that is isomorphic to a subgraph of . This is a qualitative strengthening of the Grid-Minor Theorem of Robertson and Seymour (JCTB, 1986), and treedepth is the optimal parameter in such a result. As an example application, we use this result to improve the upper bound for weak coloring numbers of graphs excluding a fixed graph as a minor.
1. Introduction
The seminal Graph Minors series of Robertson and Seymour is the foundation of modern structural graph theory. In this work, treewidth is a central concept that measures how similar a given graph is to a tree. A key theorem of Robertson and Seymour [38] states that a minor-closed graph class has bounded treewidth if and only if some planar graph is not in . In particular, for every planar graph , every -minor-free graph has treewidth at most some function . This result is often called the Grid-Minor Theorem since it suffices to prove it when is a planar grid. The asymptotics of have been substantially improved since the original work. Most significantly, Chekuri and Chuzhoy [4] showed that can be chosen to be polynomial in . The current best bound is , which follows from a result of Chuzhoy and Tan [5]. Dependence on is unavoidable, since the complete graph on vertices is -minor-free, but has treewidth . Our goal is to prove a qualitative strengthening of the Grid-Minor Theorem via graph product structure theory.
Graph product structure theory describes graphs in complicated classes as subgraphs of strong products111The strong product of two graphs and is the graph with vertex set and that includes the edge with endpoints and if and only if and ; and ; or and . of simpler graphs. For example, the Planar Graph Product Structure Theorem by Dujmović, Joret, Micek, Morin, Ueckerdt, and Wood [11] says that for every planar graph there is a graph of treewidth at most and a path such that . Here, means that is isomorphic to a subgraph of .
Inspired by this viewpoint, we prove the following product structure extension of the Grid-Minor Theorem. Note that is the graph obtained from by ‘blowing-up’ each vertex of by a complete graph . Let denote the treewidth of a graph , and let denote the treedepth of (both defined in Section˜2).
Theorem 1.
For every planar graph , there exists a positive integer such that for every -minor-free graph , there exists a graph of treewidth at most such that .
The point of Theorem 1 is that the treewidth of only depends on the treedepth of , not on 222Arbitrarily large graphs can have bounded treedepth, such as edgeless graphs (treedepth 1) or stars (treedepth 2).. The described product structure of is a more refined description of compared to the output of the Grid-Minor Theorem since . This refinement is useful because various graph parameters can be bounded on by a fast-growing function of times a slow-growing (usually linear) function of ; this includes queue-number [11], nonrepetitive chromatic number [12], and others [15, 2]. As concrete applications of Theorem˜1, we use it to improve bounds for weak coloring numbers and -centered colorings of -minor-free graphs.
The Grid-Minor Theorem relates to treewidth in the same way as the Excluded-Tree-Minor Theorem by Robertson and Seymour [37] relates to pathwidth. The latter says that a minor-closed class has bounded pathwidth if and only if some tree is not in . In particular, there is a function such that for every tree , every -minor-free graph has pathwidth at most . The following product structure version of this result was proved by Dujmović, Hickingbotham, Joret, Micek, Morin, and Wood [13]: there exists a function such that for every tree , there exists a positive integer such that for every -minor-free graph , there exists a graph of pathwidth at most such that . (In fact, they prove a stronger statement in which the pathwidth of is bounded by , where is the radius of .)
We actually prove the following result for an arbitrary excluded minor, which combined with the Grid-Minor Theorem immediately implies Theorem˜1.
Theorem 2.
For every graph , there exists a positive integer such that for every positive integer and for every -minor-free graph with , there exists a graph of treewidth at most such that .
Theorem˜2 was inspired by and can be restated in terms of the parameter ‘underlying treewidth’ introduced by Campbell, Clinch, Distel, Gollin, Hendrey, Hickingbotham, Huynh, Illingworth, Tamitegama, Tan, and Wood [3]. They defined the underlying treewidth of a graph class , denoted by , to be the smallest integer such that, for some function , for every graph there is a graph of treewidth at most such that . Here, is called the treewidth binding function. Campbell et al. [3] showed that the underlying treewidth of the class of planar graphs equals 3, and the same holds for any fixed surface. More generally, let be the class of graphs excluding a given graph as a minor. Campbell et al. [3] showed that and (for . In these results, the treewidth binding function is quadratic. Illingworth, Scott and Wood [23] reproved these results with a linear treewidth binding function.
Determining the underlying treewidth of the class of -minor-free graphs, for an arbitrary graph , was one of the main problems left unsolved by Campbell et al. [3] and Illingworth, Scott and Wood [23]. Theorem˜2 together with a well-known lower bound construction given in Section˜3 shows that and are tied:
| (1) |
This shows that treedepth is the right parameter to consider in Theorems˜1 and 2. Moreover, in the upper bound the treewidth binding function is linear.
Application #1. Weak Coloring Numbers. Weak coloring numbers are a family of graph parameters studied extensively in structural and algorithmic graph theory. See the book by Nešetřil and Ossona de Mendez [31], or the recent lecture notes by Pilipczuk, Pilipczuk, and Siebertz [34] for more information on this topic. For the algorithmic side, see Dvořák [14] and also Theorem 5.2 in [34], which contains a polynomial-time approximation algorithm for -dominating set, with approximation ratio bounded by a function of a weak coloring number of the input graph. We now quickly introduce the definition. The length of a path is the number of its edges. For two vertices and in a graph , a – path is a path in with endpoints and . Let be a graph and let be an ordering of the vertices of . For an integer and two vertices and of , we say that is weakly -reachable from in , if there exists a – path of length at most such that for every vertex on the path, . The set of vertices that are weakly -reachable from a vertex in is denoted by . The -th weak coloring number of , denoted by , is defined as
where ranges over the set of all vertex orderings of . Several papers give bounds for weak coloring numbers of graphs in a given sparse class. For example, if is planar, then ; if has no -minor, then as proved by van den Heuvel, Ossona de Mendez, Quiroz, Rabinovich, and Siebertz [21]; and if , then and this bound is tight as proved by Grohe, Kreutzer, Rabinovich, Siebertz, and Stavropoulos [20].
Fix a planar graph . What is known about when is not a minor of ? Since is -minor-free, we have . However, thanks to Theorem˜1, there exists a graph with and depending only on such that . Therefore,
Indeed, the first inequality follows from the monotonicity of and the second inequality is an easy property333 Let be an ordering of such that for every . Consider an ordering of such that for every if , then . It is easy to see that , and so . of . The obtained upper bound on is polynomial in , where the exponent depends only on and not on .
As mentioned, the Grid-Minor Theorem and also Theorem˜1 hold only when the excluded minor is planar. However, Theorem˜2 does not have this restriction, hence there is no obvious obstacle for the above bound on to hold for all graphs . We prove that this is indeed the case, which is the second main contribution of this paper.
Theorem 3.
There exists a function such that for every graph , there exists a constant such that for every -minor-free graph and every positive integer ,
Again, the point of Theorem˜3 is that the degree of the polynomial in bounding depends only on and not on . In the previous best bound for weak colouring number of -minor free graphs, the degree of the polynomial in depended on the vertex-cover444The vertex-cover number of a graph is the size of a smallest set such that every edge of has at least one endpoint in . number . In particular, it follows from a result by van den Heuvel and Wood [41, Proposition 28] regarding the weak colouring number of -minor-free graphs that for every -minor-free graph and integer . Theorem˜3 is qualitatively stronger since and there are graphs with and arbitrarily large .
The proof of the theorem relies on the same decomposition lemma as the proof of Theorem˜1. The ordering of the vertices witnessing the bound on in Theorem˜3 is built via chordal partitions—a powerful proof technique originally developed in the 1980s in the context of the cops and robber game [1] that was rediscovered and used in [21] to bound weak coloring numbers, and has subsequently found several other applications in structural graph theory.
Application #2. Product Structure for Apex-Minor-Free Graphs. As already mentioned, Dujmović et al. [11] proved that every planar graph is isomorphic to a subgraph of for some graph with treewidth at most 3 and for some path . This result has been the key ingredient in the solution of several open problems on planar graphs [11, 12, 17, 8]. Building on this work, Distel, Hickingbotham, Huynh, and Wood [7] proved that every graph of Euler genus is isomorphic to a subgraph of for some graph with treewidth at most 3 and for some path . More generally, Dujmović et al. [11] characterized the graphs for which there exist integers and such that every -minor-free graph is isomorphic to a subgraph of where and is a path. The answer is precisely the apex graphs. Here a graph is apex if or is planar for some vertex of . The following natural problem arises: for a given apex graph , what is the minimum integer such that, for some integer , every -minor-free graph is isomorphic to a subgraph of where and is a path? Illingworth, Scott and Wood [23] showed that . We show, via an application of Theorem˜2, that is tied to treedepth. In particular,
| (2) |
The proof of this result is presented in Section˜8.
Application #3. -Centered Colorings. Theorem˜1 can also be used to improve bounds for -centered chromatic numbers of graphs excluding a fixed minor. For an integer , a vertex coloring of a graph is -centered if for every connected subgraph of either uses more than colors in or there is a color that appears exactly once in . The -centered chromatic number of , denoted by , is the least number of colors in a -centered coloring of . Centered colourings are important since they characterize graph classes of bounded expansion [31], and are a central tool for designing parameterized algorithms in classes of bounded expansion [35, 36]; see [15] for an overview.
If then , and this bound is again tight [35, 15]. If is a planar graph and is -minor-free, then by Theorem˜1, there exists a graph with and depending only on such that . Therefore,
where the first inequality follows from the monotonicity of and the second inequality is an easy property of -centered colorings (Lemma 8 in [15]). The obtained upper bound on is polynomial in , where the exponent depends only on . Similarly, for an apex graph , we use (2) to show that for some , every -minor-free graph satisfies .
Outline. Section˜2 gives all the necessary definitions, as well as some preliminary results about tree-decompositions. Section˜3 proves the lower bounds in (1) and (2). Section˜4 provides a decomposition lemma (Corollary˜13) for graphs avoiding an ‘attached model’ of a fixed graph, which is a key ingredient in the results that follow. This part of the argument, in particular Lemma˜12, is inspired by a result of Kawarabayashi [24] on rooted minors, which in turn is inspired by results of Robertson and Seymour [39]. Section˜5 contains the proof of Theorem˜2. Section˜6 contains the proof of Theorem˜3, which relies on chordal partitions (see Lemma 19 and Figure 5), and a variant of the Helly property for -minor-free graphs that is of independent interest (see Lemma˜21). Section 7 contains the proof of Lemma˜21. This part builds on the work of Pilipczuk and Siebertz [35] for bounded genus graphs, and on the Graph Minor Structure Theorem of Robertson and Seymour [40] for -minor-free graphs. Section˜8 presents a product structure decomposition for graphs excluding an apex graph of small treedepth as a minor. As a consequence, we obtain better bounds for the -centered chromatic number of such graphs. Section˜9 concludes with four questions that we find relevant and exciting for future work.
2. Preliminaries
For a positive integer , we use the notation , and when let . The empty graph is the graph with no vertices. All graphs considered in this paper are finite and may be empty.
Let be a graph. Recall that the length of a path , denoted by , is the number of edges of . The distance between two vertices and in , denoted by , is the minimal length of a path with endpoints in , if such a path exists, and otherwise. A path is a geodesic in if it is a shortest path between its endpoints in .
Let be a vertex of . The neighborhood of in , denoted by , is the set . For every set of vertices of , let . For every integer , we denote by . We omit in the subscripts when it is clear from the context.
A rooted forest is a disjoint union of rooted trees. The vertex-height of a rooted forest is the maximum number of vertices on a path from a root to a leaf in . For two vertices , in a rooted forest , we say that is a descendant of in if lies on the path from a root to in . The closure of is the graph with vertex set and edge set . The treedepth of a graph , denoted by , is if is empty, and otherwise is the minimum vertex-height of a rooted forest with such that is a subgraph of the closure of .
Consider the following family of graphs . For every positive integer , define to be the empty graph. For all positive integers and , define to be the closure of the disjoint union of complete -ary trees of vertex-height . Observe that has treedepth . Moreover, this family of graphs is universal for graphs of bounded treedepth: For every graph of treedepth at most , there exists such that . Thus, every -minor-free graph is -minor-free, and to prove Theorem˜2 it suffices to do so for .
A tree-decomposition of a graph is a pair , where is a tree and the sets for each are subsets of called bags satisfying:
-
(1)
for each edge there is a bag containing both and , and
-
(2)
for each vertex the set of vertices with induces a non-empty subtree of .
The width of is , and its adhesion is . The treewidth of a graph , denoted , is the minimum width of a tree-decomposition of .
A clique in a graph is a set of pairwise adjacent vertices. Given two graphs , a clique in , a clique in , a function , the clique-sum of and according to is the graph obtained from the disjoint union of and by identifying with for every . Note that does not have to be injective. It is well known that .
Given two graphs and , an -partition of is a partition of with possibly empty parts such that for all distinct , if there is an edge between and in , then . The width of such an -partition is .
Observation 4 (Observation 35 in [11]).
For all graphs and , and every positive integer , if and only if has an -partition of width at most .
A partition of a graph is a family of induced subgraphs of such that every vertex in is in the vertex set of exactly one member of . Given a partition of , define to be the graph with vertex set and edge set all the pairs such that there is an edge between and in .
A layering of a graph is a sequence of disjoint subsets of whose union is and such that for every edge of there is a non-negative integer such that . A layered partition of is a pair where is a vertex partition of and is a layering of .
Observation 5 (Observation 35 in [11]).
For all graphs and , and every positive integer , for some path if and only if there is an -partition of and a layering such that for every and .
We finish these preliminaries with three simple statements on tree-decompositions.
Lemma 6 (Statement (8.7) in [38]).
For every graph , for every tree-decomposition of , for every family of connected subgraphs of , for every positive integer , either:
-
(1)
there are pairwise vertex-disjoint subgraphs in , or
-
(2)
there is a set that is the union of at most bags of such that for every .
A tree-decomposition of a graph is said to be natural if for every edge in , for each component of , the graph The following statement appeared first in [18], see also [19].
Lemma 7 (Theorem 1 in [18]).
Let be a connected graph and let be a tree-decomposition of . There exists a natural tree-decomposition of such that for every there is with .
The following technical lemma encapsulates a step in the main proof. In this lemma, we “capture” a given set of vertices with a superset such that is not too large and each component of has a bounded number of neighbors in .
Lemma 8.
Let be a positive integer. Let be a graph and let be a tree-decomposition of . If is the union of bags of , then there is a set that is the union of at most bags of such that and for every component of , is a subset of the union of at most two bags of . Moreover, if is natural, then intersects at most two components of .
Proof.
First, we prove the following claim for rooted trees.
Claim.
Let be a rooted tree, let be the root of , and let be a non-empty subset of . Then, there exists such that , , and for each component of :
-
(1)
if , then is adjacent to at most one vertex of ;
-
(2)
otherwise, is adjacent to at most two vertices of .
Proof. We prove the claim by induction on . For a 1-vertex tree , the statement holds with . Now assume that . Let be the rooted subtrees of , where is the degree of in . If is disjoint from for some , then apply induction to and . The obtained set satisfies the claim also for . Therefore, without loss of generality, we assume that for every , intersects , and let .
First, suppose that . By induction applied to and , we obtain satisfying the assertion of the claim. Let if , and otherwise. One can immediately verify that satisfies the assertion for .
Next, suppose that . For each , by induction applied to and , we obtain satisfying the assertion. Let . Clearly, . Consider a component of . Then is a component of for some . Since , we have , and so, 1 holds. If is not adjacent to , then 2 is satisfied by induction. If is adjacent to , then the root of is in , thus, by induction, is adjacent to at most one vertex in , and so, it is adjacent to at most two vertices in . Finally, .
Now, we prove the lemma. Let . Let be a set of vertices in such that . By the claim, there exists of size at most such that and every component of has at most two neighbors in . Let . For a given component of , let be the subtree of induced by the vertices with . Observe that is connected and disjoint from , and so has size at most two. Finally, . Moreover, if is natural, then for every , is in a single component of . ∎
3. Improper Colourings and Lower Bounds
This section explores connections between our results and improper graph colorings, which lead to the lower bound on in (1) and the lower bound on in (2).
A graph is -colorable with defect if each vertex can be assigned one of colors such that each monochromatic subgraph has maximum degree at most . A graph is -colorable with clustering if each vertex can be assigned one of colors such that each monochromatic connected subgraph has at most vertices. The defective chromatic number of a graph class is the minimum integer such that for some integer , every graph in is -colorable with defect . Similarly, the clustered chromatic number of a graph class is the minimum integer such that for some integer , every graph in is -colorable with clustering . These topics have been widely studied in recent years; see [9, 41, 33, 32, 28, 27, 29, 25, 42, 16, 26] for example. Clustered coloring is closely related to the results in this paper, since a graph is -colorable with clustering if and only if for some graph with . Our results are stronger in that they replace the condition by the qualitatively stronger statement that (since ). Of course, this is only possible when itself has bounded treewidth.
The treedepth of is the right parameter to consider when studying the defective or clustered chromatic number of the class of -minor-free graphs. Fix any connected555These results hold for possibly disconnected , but with treedepth replaced by a variant parameter called connected treedepth, which differs from treedepth by at most 1. graph with treedepth . Ossona de Mendez, Oum and Wood [33, Proposition 6.6.] proved that the defective chromatic number of the class of -minor-free graphs is at least , and conjectured that equality holds. Norin, Scott, Seymour and Wood [32] proved a relaxation of this conjecture with an exponential bound, and in the stronger setting of clustered coloring. In particular, they showed that every -minor-free graph is -colorable with clustering . The proof of Norin et al. [32] went via treewidth. In particular, they showed that every -minor-free graph with treewidth is -colorable with clustering where ; that is, for some graph with . Theorem˜2 provides a qualitative strengthening of this result by showing that for some graph with where . Liu [25] recently established the original conjecture of Ossona de Mendez et al. [33], which also implies that the clustered chromatic number of -minor-free graphs is at most , by a result of Liu and Oum [26, Theorem 1.5].
For the sake of completeness, we now adapt the argument of Ossona de Mendez et al. [33] to conclude the lower bound in (1) on underlying treewidth, and the lower bound in (2) related to the product structure of apex-minor-free graphs. We start with the following well-known statement (see [3, Lemma 12] for a similar result).
Lemma 9.
Let be positive integers, and let be a graph. For every -partition of of width at most , we have .
Proof.
Let be an -partition of with width at most . Recall that is the closure of the disjoint union of complete -ary trees of vertex-height . In what follows, we refer to these underlying complete -ary trees when we consider parent/child relations, subtrees rooted at a given vertex, and leaves. For every , every vertex that is not a leaf in has a child such that the subtree rooted at in is disjoint from . This implies that there is a sequence of vertices in such that is a child of for every , and for every with pairwise distinct. Since is a clique in , is a clique in . This shows that , which implies . ∎
The next lemma proves the lower bound in (1).
Lemma 10.
For every graph , .
Proof.
Let be a graph and let . By the definition of together with Observation˜4, there exists an integer-valued function such that every -minor-free graph has an -partition of width at most for some graph of treewidth at most . Let . Note that has larger treedepth than , therefore . By Lemma˜9, every -partition of of width at most satisfies . Hence . ∎
Lemma 11.
Let be a positive integer, and let be a graph. There exists an -minor-free graph such that for every graph and every path , if , then .
Proof.
Fix and . Since , we conclude that is -minor-free. Now suppose that for some graph and path . We claim that , which would complete the proof.
By Observation˜5 there is an -partition of and a layering such that for every and . Since has radius , any layering of has at most three layers. So for every . Thus is an -partition of with width at most . Now Lemma˜9 implies , as desired. ∎
4. Attached Models
Let and be graphs. Then is a minor of if a graph isomorphic to can be obtained from by deleting edges, deleting vertices and contracting edges. If is not a minor of , then is -minor-free. A model of in is a family of pairwise disjoint subsets of such that:
-
(1)
for every , the subgraph induced by is non-empty and connected.
-
(2)
for every edge , there is an edge between and in .
The sets for are called the branch sets of the model. Note that is a minor of if and only if there is an -model in .
The join of graphs and , denoted by , is the graph obtained from the disjoint union of and by adding all edges between vertices in and vertices in . Similarly, given a set and a graph with , denote by the graph with vertex set and edge set .
Let and be graphs. Let and be integers with , and let be pairwise disjoint subsets of . A model of in is -attached in if there are distinct vertices of such that contains a neighbor of a vertex in in for each . If is a set of vertices, then we say that a model of in is -attached in if it is -attached in .
In this paper, a separation in is a pair of subgraphs of such that (where or is allowed). The order of is . Let be a graph and be two sets of vertices of . Let be a positive integer. A linkage of order between and is a family of vertex-disjoint paths from to in , with no internal vertices in . Menger’s Theorem asserts that either contains a linkage of order between and or there is a separation of of order at most such that and .
The next lemma and corollary are tools to be used in the main decomposition lemma that follows (Lemma˜14). Lemma˜12 is inspired by a result of Kawarabayashi [24].
For a graph and a subset of the vertices of , let be the graph obtained from by adding all missing edges between vertices of .
Lemma 12.
Let be a graph, and let and be positive integers with . For every graph and every set of vertices of such that there exists a model of in , at least one of the following properties hold:
-
(1)
contains an -attached model of , for some graph obtained from by removing at most vertices,
-
(2)
there is a separation in of order at most and a vertex in such that and .
Proof.
Suppose that the lemma is false and let be a graph with the minimum number of vertices for which there exist and as in the statement such that neither 1 nor 2 holds. Fix such a set and model .
We claim that for each we have or is a singleton. Suppose the opposite, that is, there exists a branch set of such that and is not a subset of . In particular, contains an edge such that and . Consider the graph obtained from by contracting . Contracting an edge inside a branch set of a model preserves the model. Let be the resulting model of in . By the minimality of , the lemma holds for , , and . If item 1 holds, that is, contains an -attached model of , where is a graph obtained from by removing at most vertices, then does as well, a contradiction. Therefore, item 2 holds and we fix a separation in of order at most and such that and . By uncontracting , we obtain a separation in of order at most such that and . This separation has to be of order exactly , in particular, and are both in , as otherwise, item˜2 would be satisfied for , , and .
Let . By Menger’s Theorem, either there exists a linkage of order between and in , or there exists a separation in of order at most such that and . In the latter case, we obtain a separation in of order at most such that and . Thus, 2 is satisfied for ,, and , which is a contradiction. Therefore, there exists a linkage of order between and in . Since , , and not all vertices of are in (since ), at least one vertex of is in . Since is adjacent to every other vertex in and , every branch set in contains a vertex of , and thus is non-empty and connected. Let be obtained from by restricting each branch set to the graph . It follows that is a model of in . Since has fewer vertices than , the triple satisfy the lemma. If item˜1 is satisfied, that is, if there is an -attached model of in , where is a graph obtained from by removing at most vertices, then we can extend the model using to obtain an -attached model of in , a contradiction. Therefore, item˜2 is satisfied for , that is, there is a separation in of order at most and with and . Observe that is a separation in of order at most such that and , a contradiction. This proves that each branch set of is either a singleton or a subset of .
Let be the union of all branch sets in that does not intersect . By Menger’s Theorem, either there is a linkage of order between and in , or there is a separation of of order at most with , . Suppose the latter is true. Observe that for every vertex in , the corresponding branch set is either contained in or intersects , since is adjacent to every other vertex of (and is not empty). Thus, since , there is a choice of such that is disjoint from . Hence, item 2 holds. Now, assume that there is a linkage of order between and in .
Let be the partition of defined by , , and
See Figure˜1 for an illustration. First, we argue that . Observe that
Combining the above with and , we obtain
It follows that there exists an injective mapping .
Let , and let . Note that is a graph obtained from by removing at most vertices. Now, define a model of as follows:
See Figure˜1 again. Now, is a linkage of order between and distinct branch sets with . We can extend the model using . Namely, for each path in we add all its internal vertices to the unique branch set that intersects the path. We obtain an -attached model of , hence, 1 holds. This contradiction concludes the proof.
∎
Corollary 13.
Let be a connected graph, let be a positive integer, and let be a set of vertices of . If is a minor of , then for some there is a separation in of order such that , and contains a -attached model of .
Proof.
We proceed by induction on . For , one can take to be a 1-vertex graph containing the vertex of , and . Note that is non empty, and since is connected, there is a vertex in adjacent to the vertex in . This vertex constitutes a -attached model of . Now, assume that and that the result holds for all positive integers less than . Let be a model of in . Apply Lemma˜12 to with being the empty graph and . If item 1 is satisfied, then take to be the graph on with no edges and to be the whole graph , and the lemma is satisfied with . Otherwise, there exists a separation in of order at most and such that and . Let be the component of containing . Since is adjacent to every other vertex in , contains a vertex of for every . Let be obtained from by replacing each branch set in by its restriction to . Let . Thus, . Observe that is a model of in . By induction applied to and , there exists a separation of order at most in such that and has a -attached model of . Finally, put and . ∎
A crucial step in the proof of Theorem˜2 relies on the following lemma, which decomposes graphs that do not have some attached models.
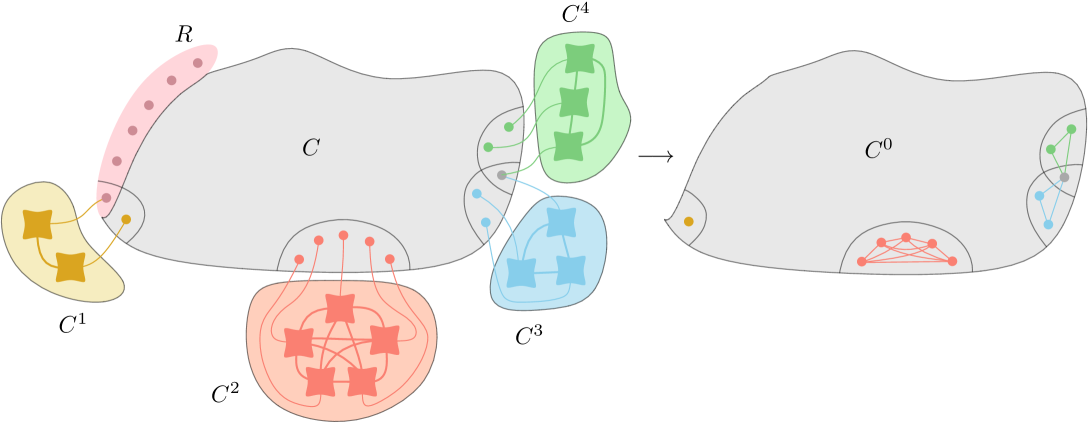
Lemma 14.
Let be a graph, let be integers with and , and let be a set of vertices of . If contains no -attached model of , then there is an induced subgraph of such that and the following items hold.
-
(1)
Let be the number of components of , let be these components, and let for every . For every , and has an -attached model of .
-
(2)
Let be the graph obtained from by adding all missing edges between vertices of for every ( is a minor of by 1). Then, is -minor-free.
Proof.
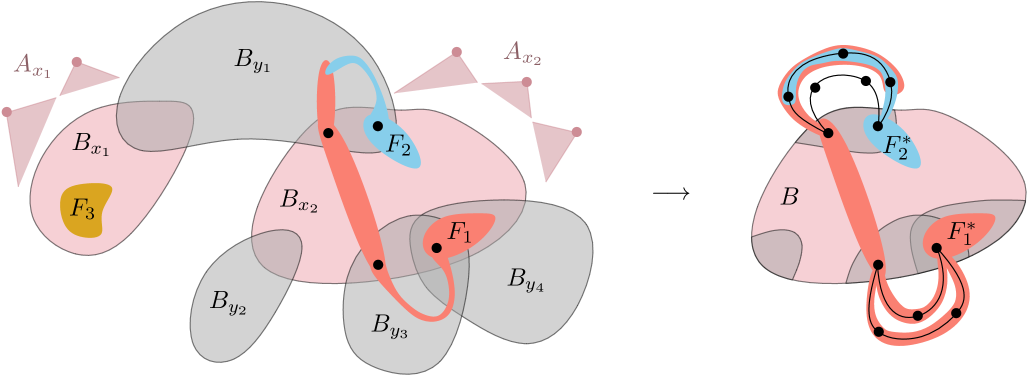
See Figure˜2 for an illustration of the assertion. We proceed by induction on . Clearly, if is -minor-free, then is the required graph. In particular, this is always the case when .
Now, assume that contains a model of and . Apply Lemma˜12 with . Observe that every graph obtained from by removing at most vertices contains as an induced subgraph. Therefore, since does not contain an -attached model of , item˜1 in Lemma˜12 does not hold. It follows that there exists a separation of order at most and such that and . We can assume that is connected. Indeed, if is disconnected, then let be a component of containing and replace with the separation .
If is a separation of order , then by induction applied to , there exists an induced subgraph of such that and items 1-2 hold. Components of are components of and . Hence, also witnesses the assertion of the lemma for . Therefore, we assume that is of order at least .
Let . Note that is non-empty and . Since is adjacent to the remaining vertices of and , for every the set contains a vertex of . Let be obtained from by replacing each branch set in by its restriction to . Observe that is a model of in . By Corollary˜13 applied to and , there is a separation in such that if , then , and contains an -attached model of . Like before, we can assume that is connected. Let be the graph obtained from by adding all missing edges between vertices in . The model of in is disjoint from . Thus, has fewer vertices than . Hence, by induction, contains an induced subgraph such that and items 1-2 hold. Let be the connected components of , and let for every . We claim that satisfies items 1-2. Note that and have the same set of vertices. Since is a complete graph, either , or for some . In the first case, , and are the components of . Observe that and items 1-2 hold. In the second case, for some and is not a subset of . In this case, is a connected component of , and so, both items of the assertion follow immediately. ∎
5. Proof of Theorem 2
Let be the function defined by
for every . One can check that for every .
Moreover, let be the function defined by
for every .
A key to our proof of Theorem˜2 is to prove the following stronger result for -minor-free graphs.
Lemma 15.
For all integers and , for every -minor-free graph with , there exists a graph with treewidth at most , and an -partition of such that for all .
This result with and Observation˜4 implies Theorem˜2. The proof of Lemma˜15 is by induction on . Considering -minor-free graphs enables the proof to trade-off a decrease in with an increase in .
We will need the following result by Illingworth, Scott, and Wood [23] for the base case of our induction.
Theorem 16 (Theorem 4 in [23]).
For all integers and , for every -minor-free graph with , there is a graph of treewidth at most and an -partition of of width at most .
Lemma 17.
For all integers , , , , with , , and , for every graph such that is not a minor of , , and for all pairwise disjoint non-empty subsets of vertices of such that for every , there exists a graph , an -partition of , and such that:
-
[label=(0), noitemsep, topsep=-7.5pt, labelindent=.2em, leftmargin=*, widest=iii]
-
(1)
,
-
(2)
for all ,
-
(3)
for all ,
-
(4)
is a clique in .
Proof.
We call a tuple satisfying the premise of the lemma an instance. We proceed by induction on in lexicographic order.
If and , then is the graph with vertices and no edges. Thus, and is a -partition of of width at most . Then, items 3 and 4 hold vacuously, and items 1 and 2 are clear since and . From now on, assume that .
If , then the -partition of satisfies 1, 3, 4. Since and , item 2 also holds and we are done. Now assume that has at least vertices. This enables us to enforce , indeed, if , then pick distinct vertices and set for every . From now on, we assume that .
If is not connected, then for every component of , Apply induction to the instance to obtain a graph with distinguished vertices , and an -partition of satisfying 1-4. In particular, for every . Let be the components of . Let be the graph obtained from the disjoint union of by identifying the vertices in into a single vertex , for each . Finally, set for every , and for every and for every . Item 1 holds since . Item 2 holds by induction. Items 3 and 4 hold by construction of . From now on, we assume that is connected.
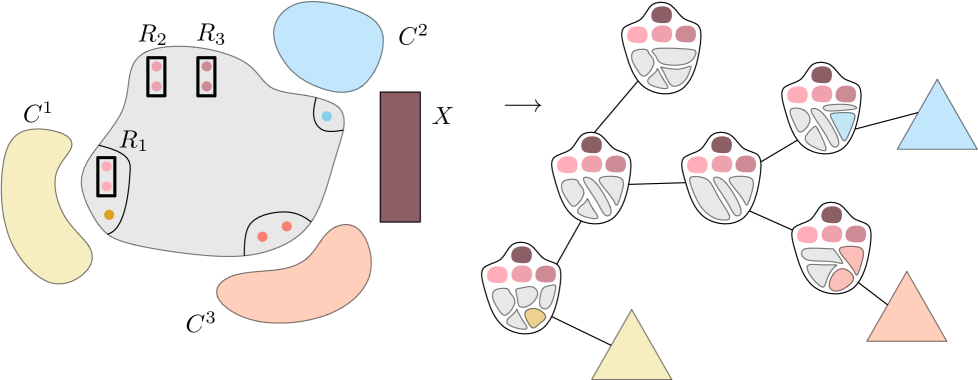
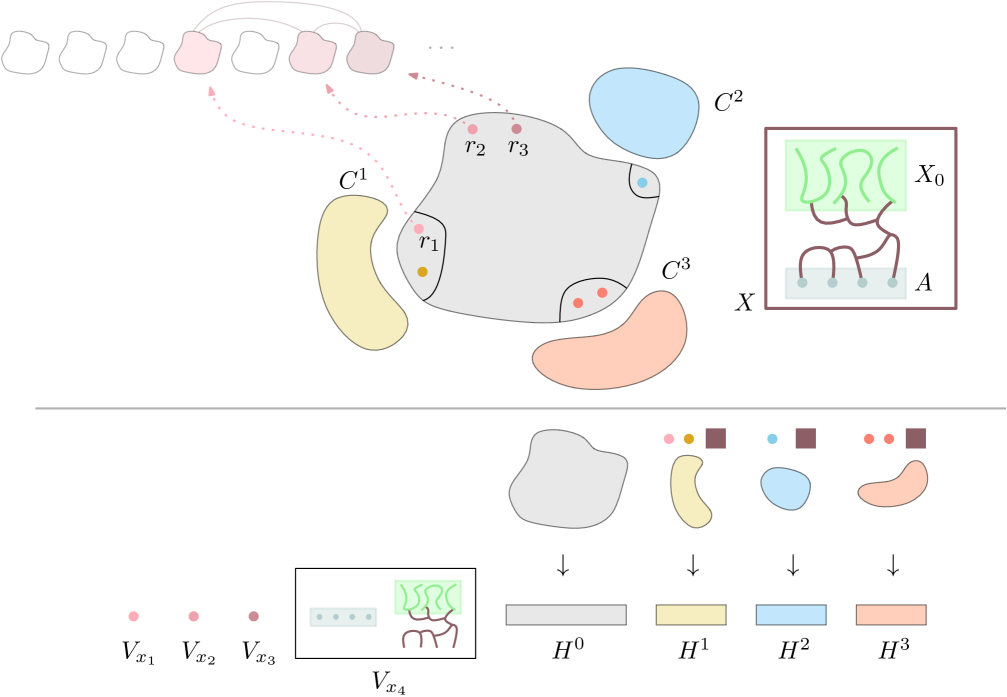
Let be the family of all connected subgraphs of containing an -attached model of . If contains pairwise disjoint subgraphs, then by the pigeonhole principle there exist with for each , and vertex-disjoint -attached models of for . We denote by the vertices of in . Since these vertices have the same closed neighborhood in , we can assume that contains a neighbor of , for all and . For each , let . Note that for every , is a model of in . Moreover, for every , , and , is adjacent to . Therefore, together with constitute a model of in , a contradiction (see Figure˜3).
Hence, there are no pairwise disjoint members in . Since and is connected, by Lemma˜7, admits a natural tree-decomposition of width at most . By Lemma 6, there exists a set of vertices of that is the union of at most bags of , such that intersects all the members of . By Lemma˜8 applied to , there exists a set of at most vertices in such that and each component of has neighbors in at most two components of .

Consider the graph obtained from by identifying the vertices in into a single vertex , for each . Let . Note that is not necessarily a minor of , however, is a subgraph of . Observe that has no -attached model of since is disjoint from and every such model in intersects . By Lemma˜14 applied with , we obtain an induced subgraph of with the following properties. Let be the connected components of , let for every , and let be the graph obtained from by adding all missing edges between vertices of for each . Observe that:
-
(1)
,
-
(2)
for each ,
-
(3)
is -minor-free,
-
(4)
is a minor of .
In particular is a minor of and .
If , then . Moreover, since , we have . So, we can apply Theorem˜16 to , which is -minor-free, to obtain a graph with and an -partition of of width at most . If , then apply induction to the instance . In both cases, we obtain a graph with and an -partition of of width at most . For every , the set is a clique in . Hence, the parts containing vertices in form a clique in .
Fix . Let be the component of containing . Let be the components of with a neighbor in . Note that by the definition of .
Let be the graph obtained from as follows:
-
(1)
identify the vertices in into a single vertex , for each ,
-
(2)
if let
and if , let -
(3)
remove all vertices outside .
Observe that is a minor of . This implies that is not a minor and . Since , is a family of at most pairwise disjoint non-empty sets, each of at most two vertices in . Since , there exists such that and therefore is disjoint from . Thus, .
Now apply induction to the instance . It follows that there is a graph with and an -partition of of width at most such that for some clique in .
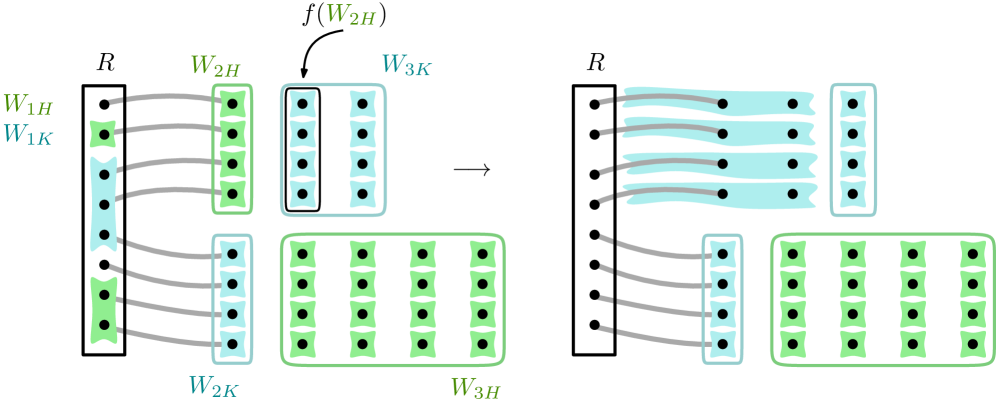
Finally, define the graph by the following process (see Figure˜4 for an informal summary of the rest of the proof). Start with the disjoint union of and . Add a clique of new vertices, each adjacent to every vertex of . For every , let be a mapping of to defined as follows:
for each . Now, identify with for every and every . This identification step can be seen as a result of the sequence of clique-sums between and the graphs according to for . This completes the definition of . Note that
Define an -partition of , where for each ,
6. Proof of Theorem 3
First, we recall the definition of weak coloring numbers. Given a graph , a linear ordering of , a vertex of , and an integer , define to be the set of vertices of such that there is a path from to of length at most whose minimum with respect to is . Then define and .
In this section, we prove the following theorem.
See 3
Theorem 3 follows immediately from the next result.
Theorem 18.
There exist functions and such that for all integers and for every -minor-free graph ,
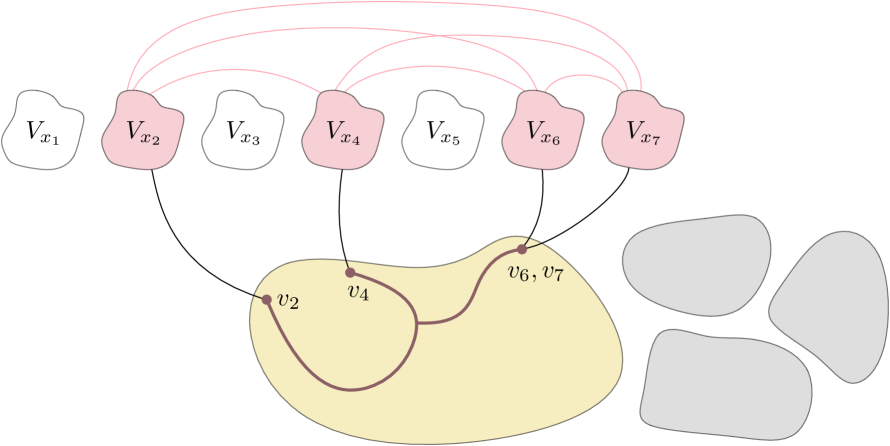
The proof of Theorem˜18 builds on a good understanding of the behavior of weak coloring numbers of graphs excluding a complete graph as a minor, and also of graphs of bounded treewidth. Van den Heuvel, Ossona de Mendez, Quiroz, Rabinovich, Siebertz [21] proved that for every integer , every -minor-free graph satisfies for every integer . Their proof technique, specifically chordal partitions of graphs, inspired a lot of follow-up research, including our work on weak coloring numbers. The base case of our main technical contribution (Lemma˜22) relies on the following structural result from [21] that underlies the upper bound on weak coloring numbers for -minor-free graphs. We include a rough sketch of the proof – see Figure˜5. Recall that a geodesic in a graph is a shortest path between its endpoints.
Lemma 19 (Lemma 4.1 in [21]).
Let and let be a -minor-free graph.666 The statement in [21] assume and item 4 bounds the number of geodesics by . However the statement also holds for with replaced by in item 4. Then there is a graph and an -partition of together with an ordering of such that
-
(1)
is connected for every , in particular, is a minor of ;
-
(2)
is a clique in , for every ;
-
(3)
;
-
(4)
is the union of the vertex sets of at most geodesics in , for every .
Let and be integers with . For every graph with , we have , as proved by Grohe, Kreutzer, Rabinovich, Siebertz, and Stavropoulos [20]. We will need the following slightly more precise statement that follows line-by-line from the proof in [20].
Lemma 20 (Theorem 4.2 in [20]).
Let and be integers with . Let be a graph and let be an ordering of such that for every , the set is a clique of size at most in . Then
Note that the above two lemmas easily imply the mentioned bound on for -minor-free graphs. To see this, order the vertices according to the index of a part of the -partition that they are in, and within each part, we order the vertices arbitrarily. Now, to verify the bound, we need a simple observation on geodesics that we will prove later, see Lemma˜23.
If a graph has bounded treewidth, say , then satisfies the Helly property articulated by Lemma˜6. Namely, when is a family of connected subgraphs of , then either there are pairwise disjoint members of , or there is subset of vertices of hitting all members of . One of the main difficulties that arises when trying to prove Theorem˜18 is to find an equally useful statement as Lemma˜6, but for -minor-free graphs. This is the motivation for Lemma˜21. We defer the proof of it to Section˜7.
Lemma 21.
There exist functions , such that for all integers , for every -minor-free graph , for every family of connected subgraphs of either:
-
(1)
there are pairwise vertex-disjoint subgraphs in , or
-
(2)
there exist such that , and a subgraph of , where is the union of at most geodesics in , and for every we have .
With Lemma˜21 in hand, we are ready to proceed with Lemma˜22, the key technical contribution standing behind Theorem˜18. The proof relies on some ideas from the proof of Lemma˜17, see Figure˜6 for a sketch of the proof. After the proof of Lemma˜22 we complete the final argument for Theorem˜18. Recall the definition of :
Let be the number of vertices in ; that is, for all and ,
Let be the function defined by
A set of vertices in a graph is a subgeodesic in if there is a supergraph of and a geodesic in such that .
Lemma 22.
For all integers with and , for every graph such that is not a minor of , for all pairwise distinct vertices in , there is a graph with an ordering of , and an -partition of such that:
-
[label=(0), noitemsep, topsep=-7.5pt, labelindent=.2em, leftmargin=*, widest=iii]
-
(1)
is a clique in for all ;
-
(2)
is a clique in ;
-
(3)
;
-
(4)
for all ;
-
(5)
for each integer with , there exists a partition of such that:
-
(a)
, and
-
(b)
is the union of at most subgeodesics in .
-
(a)
Proof.
We call a tuple satisfying the premise of the lemma an instance. We proceed by induction on in lexicographic order. Let .
If and , then is the graph with vertices and no edges. Thus , and is a -partition of of width at most . Then take where is the vertex of . Items 1, 2 are clear. Item˜3 holds as . Item˜4 holds vacuously. Finally, item˜5 holds by taking and , since . Now we assume .
If , then take with vertex set . Let for every and let . Note that is a -partition of . Let and . In particular, . It is straightforward to check that 1-5 hold. Now, if and , then set to be distinct vertices of . Therefore, from now on assume and is non-empty.
Suppose that is disconnected. Let be the components of . For every Apply induction to the instance and obtain with and an -partition of satisfying 1-5. Let be the graph obtained from the disjoint union of by identifying the vertices in into a single vertex , for each . Then order the vertices of by
Finally, set for each , and for every for each . Items 2 and 4 follow by construction of and . In order to prove item 1, consider and let be the neighbors of in that are smaller than in . If , then clearly is a clique in . If for some , let and . Observe that . Then by induction is a clique in and so is a clique in . This proves item 1. Note that which proves item 3. In order to prove item 5, consider for some and . Then by induction there exists a partition of such that and is the union of at most subgeodesics in . But since components of are components of , we deduce that is the union of at most subgeodesics in . This proves item 5.
Now assume that is connected.
Let be the family of all connected subgraphs of containing an -attached model of . If contains pairwise vertex-disjoint subgraphs, then there exist vertex-disjoint -attached models in for each . Denote by the vertices of in and since these vertices are twins in , we can assume that contains a neighbor of , for all and . For each , let . Note that for every , is a model of in . Moreover, for every , , and , is adjacent to . Therefore, together with constitute a model of in , a contradiction. Hence, there are no pairwise disjoint members in .
Let . Note that is -minor-free. By Lemma˜21, there is a set of at most vertices in , and a set which is the union of the vertex sets of at most geodesics in , such that intersects every member of . If , then take and an arbitrary singleton included in . Since is connected, we can add to at most geodesics in to obtain a set such that is connected. Let . Note that is the union of at most subgeodesics in .
By construction, is connected and does not contain an -attached model of . By Lemma˜14 applied for , we obtain an induced subgraph of with the following properties. Let be the connected components of , let for every , and let be the graph obtained from by adding all missing edges between vertices of for each . Then
-
(1)
,
-
(2)
for each ,
-
(3)
is -minor-free,
-
(4)
is a minor of .
If , then . Moreover since , and so . Thus we can apply Lemma˜19 to , which is -minor-free, and obtain a graph with and an -partition with an ordering of such that for every , is the union of at most geodesics in . Then set and for every . If , then apply induction to the instance .
In both cases, we obtain a graph with and an -partition of with an ordering of such that for every , has a partition such that and is the union of at most subgeodesics in . For every , the graph is a clique in . Hence, the parts containing vertices in form a clique in .
Fix some . Let be the graph obtained from by contracting into a single vertex . Note that is a minor of and therefore has no model of . Since , there exists such that and therefore . Thus, . Let , so . Now, apply induction to the instance . It follows that there is a graph with and an -partition of and an ordering of such that for each the set is a singleton, , the set is a clique in , and for every integer with , the set has a partition such that and is the union of at most subgeodesics in .
Finally, define the graph as follows. Start with the disjoint union of and . Add a clique of new vertices, each adjacent to every vertex of . For every , let be a mapping of to defined as follows:
for each . Now, identify with for every and every . This identification step can be seen as a result of the sequence of clique-sums between and the graphs according to for . This completes the definition of .
Note that
Now define an -partition of , where for each ,
Moreover, order the vertices of by
In order to prove item 1, consider a vertex , and let . If , then and so is a clique in . If , then is a clique in , thus is a clique in , and so in . If for some , let and . Then is a clique in , and so is a clique in . This proves item 1.
Item˜2 follows from the definition of . As mentioned before so item 3 holds. Item˜4 follows from the definition of . For item˜5, for each , define
Consider now some . First observe that . It remains to show that is the union of at most subgeodesics in . If , this follows from the definition of and . If , then there is a supergraph of such that is in the union of the vertex sets of at most geodesics in . Let be obtained from the disjoint union of and by adding every edge between and that is in , for each . Since is a clique in for every , for every two vertices , in , . Hence is the union of the vertex sets of at most geodesic in , which is a supergraph of . This shows that is the union of at most subgeodesics in , as desired. Finally, if , then is the union of at most subgeodesics in . Since components of are components of , we deduce that is the union of at most geodesics in . This proves item˜5 and concludes the proof. ∎
Lemma 23.
Let be a graph and let be a non-negative integer. For every subgeodesic in and for every vertex ,
Proof.
Let be a subgeodesic of . Let be a supergraph of and let be a geodesic with endpoints in such that . Let . Suppose for contradiction that . However, . Let and be the vertices in closest to and , respectively. Since , and , we have . However, since is a geodesic in , we have , a contradiction. ∎
Proof of Theorem˜18.
Let and let be a -minor-free graph. We will show that , which implies the theorem. By Lemma˜22 applied to with , there is a graph with an ordering of , and an -partition of such that 1-5 hold. Let be a total order on such that for all and :
-
(1)
if and , then ;
-
(2)
if , then .
Let . Consider a vertex . Let be such that . Then . In particular . By Lemma˜20
Moreover where and is the union of the vertex sets of at most subgeodesics in . Since vertices -weakly reachable from in are in , we deduce by Lemma˜23 that . Hence
It follows that
This proves the theorem. ∎
7. Proof of Lemma 21
This section proves the following lemma.
See 21
In short, Lemma˜21 follows from a result by Pilipczuk and Siebertz [35], see Theorem˜25, which we lift in order to accommodate vortical decompositions and clique-sums.
First, we recall the Graph Minor Structure Theorem of Robertson and Seymour [40], which says that every graph in a proper minor-closed class can be constructed using four ingredients: graphs on surfaces, vortices, apex vertices, and tree-decompositions.
The Euler genus of a surface with handles and cross-caps is . The Euler genus of a graph is the minimum integer such that there is an embedding of in a surface of Euler genus ; see [30] for more about graph embeddings in surfaces.
Let be a graph and let be a cyclic permutation of a subset of . An interval of is a sequence of vertices of such that is the successor of on for every . A vortical decomposition of is a pair such that:
-
[label=(0), noitemsep, topsep=-7.5pt, labelindent=.2em, leftmargin=*, widest=iii]
-
(0)
, for every ,
-
(1)
for each edge there is with , and
-
(2)
for each vertex the set of vertices with induces a non-empty interval of .
The width of a vortical decomposition is defined to be .
For any integers , a graph is -almost-embeddable if for some set with , there are graphs for some , cyclic permutations of pairwise disjoint subsets of , and a surface of Euler genus at most such that:
-
(1)
;
-
(2)
are pairwise vertex-disjoint and non-empty;
-
(3)
for each , there is a vortical decomposition of of width at most ;
-
(4)
is embedded in ;
-
(5)
there are pairwise disjoint closed discs in whose interiors are disjoint from the embedding of , and such that the boundary of meets the embedding of exactly in vertices of , and the cyclic ordering of is compatible with the ordering of the vertices around the boundary of , for each .
The vertices in are called apex vertices. They can be adjacent to any vertex in . For an integer , a graph is -almost-embeddable if it is -almost-embeddable.
Let be a graph, let be a tree-decomposition of . For , the torso of , denoted by , is the graph obtained from by adding edges so that is a clique for each neighbour of in .
We now state the Graph Minor Structure Theorem, which is the cornerstone of structural graph theory.
Theorem 24 ([40]).
There exists a function such that for every positive integer , for every -minor-free graph , there exists a tree-decomposition of such that is -almost-embeddable, for every .
Theorem 25 (Theorem 18 in [35]).
There exists a function such that for every graph of Euler genus at most , there is a partition of into geodesics in such that .
Pilipczuk and Siebertz [35] proved Theorem˜25 with , which was later improved to by Distel et al. [7].
The next lemma lifts the previous statement to -almost-embeddable graphs. This type of argument is folklore in the structural graph theory community.
We use the following convenient notation for manipulating paths in a graph. Let be a graph. A walk in is a sequence of vertices in such that for each . Let and be two walks in such that or . The concatenation of and , denoted by , is the walk if , or if . Let be a path in and let be two vertices of . Define to be the subpath of from to (which is also a walk in ). This allows us to write expressions of the form given that: are vertices in the graph; is a path containing and ; is an edge; is a path containing and ; is a path containing and .
Lemma 26.
There is a function such that for every integer , for every -almost-embeddable graph , there is a partition of into geodesics in such that .
Proof.
Let for all integers , where is the function given by Theorem˜25.
Fix and let , , be integers with . Let be a -almost-embeddable graph. If is not connected, then we can process each component independently and take the union of the resulting partitions. Now assume that is connected. Let , , , witness the fact that is -almost-embeddable, and fix a vortical decomposition of of width at most , for every . For convenience, we denote by the permutation . By definition, are pairwise disjoint, hence, for , we write for the unique such that .
Let be if , and otherwise let be a graph obtained from as follows: for every , for every pair of consecutive vertices on , if , then add the edge (note that this is compatible with the embedding of ); next pick arbitrarily a vertex and for all , if , then add the edge . Note that we may add handles to , and embed on the resulting surface, thus, has Euler genus at most .
Claim.
, for every .
Proof. Let be a geodesic in with endpoints and . If intersects in at most one vertex, then is a path between and in , and so . Now suppose that contains at least two vertices in . Let , be such vertices that are closest in to and , respectively. Then is a walk from to in of length at most , and so .
Claim.
For every geodesic in , contains at most three vertices in .
Proof. Let be a geodesic in between and . Suppose to the contrary that has at least four vertices in , and let , be such vertices that are closest in to and , respectively. Now and can be connected by a two-edge path via in . Therefore, is a walk in , and since there are at least two vertices on between and , the walk is shorter than , a contradiction.
Claim.
For every geodesic in , the vertex set of is the union of the vertex sets of at most six disjoint geodesics in , and moreover, each of these geodesics contains at most one vertex in .
Proof. Let be a geodesic in between and . Since has at most three vertices in , it can be split into the disjoint union of at most three geodesics in such that each part has at most one vertex in .
Consider now a geodesic in with at most one vertex in . The key property of is that it is also a path . We are going to prove that can be split into at most two geodesics in . Let be the endpoints of .
By a previous claim, . Since is a path in we also have . Altogether,
If then is a geodesic in and there is nothing to prove. Now suppose that . Let be the walk along with and . For each consider . Note that
These three conditions force that for all except one value, say , for which . It follows, that , and , hence,
This completes the proof that can be split into at most two geodesics in .
Altogether, is split into at most three times two geodesics in , as desired.
Since has Euler genus at most , by Theorem˜25, there is a partition of into geodesics in such that . Let be a tree-decomposition of of width at most .
For each , let be a set of at most six geodesics in whose union of vertex sets is , and such that each of them intersects in at most one vertex. Define a partition of into geodesics in by
We claim that .
The family is a partition of and the family is a partition of , thus, for each and we can define and to be such that and . For each , consider the following subsets of :
Clearly, . Moreover, we proved that every geodesic in has at most three vertices in , thus, . It follows that . Therefore, if we show that is a tree-decomposition of , then indeed, .
Claim.
is a tree-decomposition of .
Proof. Let be such that and are distinct, and suppose that . If , then there exists such that . Moreover, and . It follows that . If then there exists such that . We have for some , and this yields .
It remains to show that for every , the set induces a non-empty, connected subset of . For every , let be defined as . Since is a tree-decomposition of , we have that induces a non-empty, connected subset of . Observe that the union , where is a connected subgraph of , also induces a non-empty, connected subset of . For each , let . Since are pairwise disjoint, and is a vortical decomposition of for each , is either empty, or is an interval in some . Recall that we added cycle edges in representing each , and hence, induces a connected subgraph in .
First, suppose that for some . By definition,
Since is connected in , we conclude that induces a non-empty, connected subset of .
Now, suppose that for some . Recall that contains at most one vertex in . If , then , which induces a non-empty, connected subtree of . Otherwise, let be the unique vertex in the intersection . Then
Note that , thus , and since , we have . This shows that induces a non-empty, connected subtree of .
This completes the proof that . ∎
The next lemma is an immediate corollary of Lemma˜26 and Lemma˜6. The function is the same as in Lemma˜26.
Corollary 27.
There exists a function such that for all integers and , for every -almost-embeddable graph , for every family of connected subgraphs of either:
-
(1)
there are pairwise vertex-disjoint subgraphs in , or
-
(2)
there exist a subgraph of that is the union of at most geodesics in , and for every we have .
Consider a graph embedded in a fixed surface. It is clear that one can introduce parallel edges, subdivide edges of the graph, and the resulting graph still has an embedding into the surface. The point of the following observation is that we can do the same with -embeddable graphs and the resulting graph has the same parameters except for the width of the vortices that may go up by . This is folklore in the structural and algorithmic graph theory community.
Observation 28.
Let be non-negative integers, and let be a -almost-embeddable graph. For every graph obtained from by duplicating some edges and then subdividing some edges, is -almost-embeddable.
The following observation says that almost-embeddability is preserved under taking subgraphs but, surprisingly, this may increase the width of the vortices. A proof can be found, for example, in [10, Lemma 45].
Observation 29.
Let be non-negative integers, and let be a -almost-embeddable graph. Let be a subgraph of . Then is -almost-embeddable.
We have all the tools in hand to prove Lemma˜21.
Proof of Lemma˜21.
Let be positive integers, let be a -minor-free graph, and let be a family of connected subgraphs of . If is empty, then the result holds since . Now assume that is non-empty. Without loss of generality, we can assume that each member of is an induced subgraph. Therefore, with a slight abuse of notation, from now on we refer to as a family of subsets of such that each induces a connected graph. Suppose that item˜1 does not hold; that is, has no pairwise disjoint members. In particular, .
Let be the function from Theorem˜24. By the theorem, there exists a tree-decomposition of such that is -almost-embeddable, for every . For each , let be the apex set of (that is, is a set of at most vertices such that is -almost-embeddable). By Lemma˜6, there exists an integer and such that for every , intersects . Let . Note that , so it suffices to take . For each , let be the family of all disjoint from that intersect .
We now sketch the next steps of the proof, see also Figure˜7. First, for each we modify the graph to obtain an auxiliary graph that is -almost-embeddable. Then, we carefully project the family into . In particular, when two sets from intersect, their projections will intersect as well. Next, we will apply Corollary˜27 to the auxiliary graph to obtain a hitting set for the projected being a union of a small number of geodesics in . Finally, we will lift the hitting set to the initial graph, perhaps adding some more geodesics. Taking the union of hitting sets over all , we will finish the proof.
Fix some , let , and let . We say that two distinct vertices are interesting if and are in the same component of and there exists with such that . Let be the set of all -subsets of vertices in that are interesting.
We construct the auxiliary graph as follows. We start the construction with . For all , if and are adjacent in , then we call this length-one path or ; if and are not adjacent in , then we add to the graph a path connecting and of length where all internal vertices are new, i.e. disjoint from all the rest. Again, we call this path or . Moreover, for all , we add to the graph a path connecting and of length where all internal vertices are new. We call this path or . This completes the construction of .
Note that is obtained from by removing some vertices (from ), duplicating and perhaps subdividing some edges. Therefore, by Observation˜28, the graph is -almost-embeddable.
Now, we will define a family of connected subgraphs of that is roughly a projection of into . For a path , let denote the subpath of induced by all internal vertices of . For every , define
and . The following claim captures the critical properties of .
Claim.
Let . Then:
-
(1)
The graph is connected.
-
(2)
If intersects then intersects .
Proof. Let . We will show that there is a path from to in which will prove item˜1. If then lies on one of the added paths in the construction of . Since each such path in has at least one endpoint in , we can connect in with a vertex in . Therefore, we assume that both and are in .
Since , there is a walk connecting and in . Recall that is disjoint from , and so is . We split into segments with endpoints in vertices from , i.e., let be vertices in such that
where , and has no internal vertex in for each . Note that could be just a one-edge path for some .
We claim that we can replace each section by a path connecting and in . Fix .
If , are adjacent in , then they are also adjacent in , as desired. If and are not adjacent in , the set induces a non-empty connected subset of . Moreover, since and are both adjacent to a vertex in , there are vertices such that and . Since is acyclic in , we have , and so . This shows that . Thus, was added to and we can use this path to connect and in . This way we completed a proof that there is a path from to in .
Assume that and that intersects . To prove item˜2, we will show that is non-empty as well. Fix . If , then , and we are done. Hence, we suppose that .
Let be a path in from a vertex of to with no internal vertex in . Let be a path in from to a vertex of with no internal vertex in . If , then and we are done. Otherwise we claim that . Indeed, is a non-empty connected subgraph of , and so is a non-empty connected subset of . Then, since and both have a neighbor in , we deduce that for some . But since is a tree, we must have , and so . This shows that . Thus, and so .
By the claim, the family is a family of connected subgraphs of containing no pairwise vertex-disjoint members. Therefore, by Corollary˜27, there exists a subgraph of such that is the union of a family of at most geodesics in and for every we have .
Let . Note that if one of the endpoints of lies on for some , then one can remove from maintaining the fact that is a family of geodesics in whose union of vertex sets intersects every member of . Therefore, now assume without loss of generality that none of has an endpoint in the interior of any . We now discuss the relation of geodesics in to the paths .
Claim.
Let . No geodesic in contains as a subpath.
Proof. Let be a geodesic in . Suppose that it contains as a subpath. Then replacing the segment corresponding to in with gives a shorter walk between endpoints of in , which is a contradiction.
We need the following easy observation.
Claim.
For all , we have . Moreover, if is a geodesic in connecting and , then there exists a geodesic in connecting and such that .
Proof. Let and let be a path between and in . We will show that there exists a path between and in of length at most the length of . Let and let be (possibly empty) paths in such that
with and . Let . If is an empty path, then let be also an empty path. Otherwise, . It follows that and moreover, . Define . Let be the walk defined by
Clearly, is a walk between and in , and . This shows that .
Now, let be a path between and in . Let and let be (possibly empty) paths in such that
with and . If is an empty path, then let be also an empty path. Otherwise, by definition, it is clear that . Let be any shortest path between and in . Let be the walk defined by
Clearly, is a walk between and in , and . This shows that .
Moreover, if is a geodesic in , then is a geodesic in with .
Let be the collection of all the paths of the form in – note that all such paths are nonempty. It follows that for every , the geodesic intersects at most two distinct members of , and so, we can write that is a concatenation of , , and , where and are subpaths of paths in each, and is disjoint from . Clearly, is a geodesic in , and moreover, it connects vertices in . We aim to replace each geodesic with at most three geodesics in maintaining the property that the union of all constructed geodesics intersects every member of .
For technical reasons, we assume that the empty path is a geodesic.
Claim.
Let . There exist at most three geodesics in such that for every , if then for some .
Proof. Let be a partition of as described above. Let and be the endpoints of . By the previous claim, there exists a geodesic connecting and such that . Put . Let . If is an empty path, then set to be an empty path. Otherwise, is a segment of the path for some such that . In this case, set to be the one-vertex path containing .
Clearly, are geodesics in . We now prove that they satisfy the assertion of the claim.
Let be such that . Thus, either for some , or . If for some , then by the construction of , either or . In the first case , and in the second case .
It remains to deal with the case when . By construction of we have . However and . Therefore,
Finally, define
It follows that for each , the subgraph is the union of at most geodesics. Let . For every we have . Moreover, is a union of at most geodesics in . This proves the lemma with . ∎
8. Excluding an Apex Graph
Recall that a graph is apex if there is a vertex such that is planar. For a given apex graph , let be the minimum integer such that, for some integer , every -minor-free graph is isomorphic to a subgraph of where and is a path. In this section, we show that is tied to the treedepth of .
A tree-decomposition of a graph is rooted when is a rooted tree. For a rooted tree-decomposition of a graph , let be the supergraph of obtained by adding all edges with and is the parent of in . We use the following result of Dujmović, Esperet, Morin, and Wood [10].
Theorem 30 (Theorem 48 in [10]).
For every apex graph , there exist positive integers such that every -minor-free graph has a rooted tree-decomposition of adhesion at most , and for each , there exists a layered partition of with:
-
(1)
for each ;
-
(2)
if has a parent in , then
-
(a)
all vertices in are in the first layer of ,
-
(b)
each vertex of is in a singleton part of ; and
-
(a)
-
(3)
is a minor of and has treewidth less than .
The next result proves the upper bound in (2).
Theorem 31.
For every apex graph , there exists a positive integer such that for every -minor-free graph , there exists a graph of treewidth at most such that for some path .
Proof.
Let be an apex graph. Let be the constants depending only on given by Theorem˜30. Let be the constant depending only on given by Theorem˜2. Let .
Let be an -minor-free graph. By Theorem˜30, there is a rooted tree-decomposition of and for every there is a layered partition of such that items 1-3 hold.
Let be the root of . For each vertex in with , let be the parent of in . Let be an ordering of such that for every edge of , if , then . For every , let be the graph obtained from by adding for every with , all the missing edges with both endpoints in . Next, for each , we will construct a graph , an -partition of and a layering of such that
-
(1)
, and
-
(2)
for every and .
By Observation˜5, this yields for some path , which will complete the proof.
The construction is iterative, starting with . Observe that and . Let . By Theorem˜30.3, and is a minor of , so is -minor-free. By Theorem˜2, we obtain a graph and an -partition of such that and for every . Let for every and . Then is an -partition of such that for every and .
Next, let , and assume that , and are already defined. Let , , and . Note that is a clique in and so is a clique in . Recall that the elements of are in singleton parts of by Theorem˜30.2.2(b). Let . By Theorem˜30.3, and is a minor of , so is -minor-free. By Theorem˜2, we obtain a graph and an -partition of such that and for every . Now define to be the clique-sum of and according to the identity function on . Then . For every let
Then is an -partition of . It remains to define the layering . Let and . Since is a clique in , there is a non-negative integer such that . For every non-negative integer , let
First we show that is a layering of . Let be an edge of . Note that either is an edge of or is an edge of . If is an edge of then there is an integer such that , and so . If is an edge of , then there is an integer such that . Note that in this case . If , then . The last case to consider is when . Without loss of generality, assume that . By Theorem˜30.2.2(a), , hence, . Moreover, . It follows that . This proves that is a layering of .
Finally, for every non-negative integer , and for every , either and , or and . This concludes the proof. ∎
Dębski et al. [15] proved that if where and is a path, then .
Theorem˜31 thus implies:
Corollary 32.
9. Open Questions
We conclude the paper with a number of open problems.
Question 1.
Can the upper bound on in Equation˜1 be improved? In particular, is at most a polynomial function of ?
The next problem asks whether Theorem˜2 can be extended to the setting of excluded topological minors.
Question 2.
Is there a function such that for every graph there exists a function such that for every positive integer and for every graph with that does not contain as a topological minor, there exists a graph of treewidth at most such that ?
This question is related to various results of Campbell et al. [3] on the underlying treewidth of -topological minor-free graphs. They showed that a monotone class has bounded underlying treewidth if and only if it excludes some fixed topological minor. In particular, they proved the weakening of Question 2 with replaced by . This is tight for complete graphs. That is, the underlying treewidth of -topological minor-free graphs equals (for ), which implies Question 2 for complete graphs . Campbell et al. [3] also prove ˜2 for for , but note that it is open for . They also prove that the underlying treewidth of -free graphs equals , which gives good evidence for a positive answer to ˜2 since .
A positive answer to ˜2 would be a qualitative generalisation of both Theorem˜2 and the following result of an anonymous referee of [6] (where in ˜2): for every graph with treewidth and maximum degree , there is a tree such that .
Question 3.
Is there a function such that for every graph , there is a constant such that for every -minor-free graph , for every ?
Our results give a positive answer to ˜3 when is apex. However, we do not see a way to adjust our proof techniques and prove an analogue of Theorem˜3 for -centered colorings when is an arbitrary graph. The main obstacle is that we do not know how to use chordal partitions to construct -centered colorings. Therefore, we do not know how to set up an equivalent of Lemma˜22.
Question 4.
Let be a graph. Let be the infimum of all the real numbers such that there is a constant , such that for every -minor-free graph and every integer , . Theorem˜3 and a construction of Grohe et al. [20] imply that for some function . Is tied to some natural graph parameter of ? Is tied to some natural graph parameter?
We know that is tied to neither , nor . For treedepth or pathwidth, consider to be a complete ternary tree of vertex-height so both the pathwidth and treedepth of are . Then -minor-free graphs have bounded pathwidth, and it is easy to see that for all graphs . Thus, the exponent is which is independent of . For treewidth, consider the family from [20], which satisfy and . Note that excludes (a ladder with rungs). Since for all , when we take , the exponent becomes while treewidth remains constant. The only parameter that we are aware of that could be tied with is , as defined in [22].
References
- [1] Thomas Andreae. On a pursuit game played on graphs for which a minor is excluded. J. Combin. Theory, Series B, 41(1):37–47, 1986.
- [2] Prosenjit Bose, Vida Dujmović, Mehrnoosh Javarsineh, and Pat Morin. Asymptotically optimal vertex ranking of planar graphs, 2023. arXiv:2007.06455.
- [3] Rutger Campbell, Katie Clinch, Marc Distel, J. Pascal Gollin, Kevin Hendrey, Robert Hickingbotham, Tony Huynh, Freddie Illingworth, Youri Tamitegama, Jane Tan, and David R. Wood. Product structure of graph classes with bounded treewidth, 2022. arXiv:2206.02395.
- [4] Chandra Chekuri and Julia Chuzhoy. Polynomial bounds for the grid-minor theorem. J. ACM, 63(5), 2016. arXiv:1305.6577.
- [5] Julia Chuzhoy and Zihan Tan. Towards tight(er) bounds for the excluded grid theorem. J. Combin. Theory, Series B, 146:219–265, 2021. arXiv:1901.07944.
- [6] Guoli Ding and Bogdan Oporowski. Some results on tree decomposition of graphs. J. Graph Theory, 20(4):481–499, 1995.
- [7] Marc Distel, Robert Hickingbotham, Tony Huynh, and David R. Wood. Improved product structure for graphs on surfaces. Discrete Math. Theor. Comput. Sci., 24(2):#6, 2022. arXiv:2112.10025.
- [8] Vida Dujmović, Louis Esperet, Cyril Gavoille, Gwenaël Joret, Piotr Micek, and Pat Morin. Adjacency labelling for planar graphs (and beyond). J. ACM, 68(6):42, 2021. arXiv:2003.04280.
- [9] Vida Dujmović, Louis Esperet, Pat Morin, Bartosz Walczak, and David R. Wood. Clustered 3-colouring graphs of bounded degree. Combin. Probab. Comput., 31(1):123–135, 2022. arXiv:2002.11721.
- [10] Vida Dujmović, Louis Esperet, Pat Morin, and David R. Wood. Proof of the clustered Hadwiger conjecture, 2023. arXiv:2306.06224.
- [11] Vida Dujmović, Gwenaël Joret, Piotr Micek, Pat Morin, Torsten Ueckerdt, and David R. Wood. Planar graphs have bounded queue-number. J. ACM, 67(4), 2020. arXiv:1904.04791.
- [12] Vida Dujmović, Louis Esperet, Gwenaël Joret, Bartosz Walczak, and David R. Wood. Planar graphs have bounded nonrepetitive chromatic number. Advances in Combinatorics, #5, 2020. arXiv:1904.05269.
- [13] Vida Dujmović, Robert Hickingbotham, Gwenaël Joret, Piotr Micek, Pat Morin, and David R. Wood. The excluded tree minor theorem revisited, 2023. arXiv:2303.14970.
- [14] Zdeněk Dvořák. Constant-factor approximation of the domination number in sparse graphs. European J. Combin., 34(5):833–840, 2013. arXiv:1110.5190.
- [15] Michał Dębski, Stefan Felsner, Piotr Micek, and Felix Schröder. Improved bounds for centered colorings. Advances in Combinatorics, #8, 2021. arXiv:1907.04586.
- [16] Louis Esperet and Gwenaël Joret. Colouring planar graphs with three colours and no large monochromatic components. Combin., Probab. Comput., 23(4):551–570, 2014. arXiv:1303.2487.
- [17] Louis Esperet, Gwenaël Joret, and Pat Morin. Sparse universal graphs for planarity. J. London Math. Soc., to appear. arXiv:2010.05779.
- [18] Pierre Fraigniaud and Nicolas Nisse. Connected treewidth and connected graph searching. In José R. Correa, Alejandro Hevia, and Marcos A. Kiwi, editors, Proc. 7th Latin American Symposium on Theoretical Informatics, LATIN 2006, volume 3887 of Lecture Notes in Comput. Sci., pages 479–490. Springer, 2006.
- [19] Carla Groenland, Gwenaël Joret, Wojciech Nadara, and Bartosz Walczak. Approximating pathwidth for graphs of small treewidth. ACM Trans. Algorithms, 19(2), 2023. arXiv:2008.00779.
- [20] Martin Grohe, Stephan Kreutzer, Roman Rabinovich, Sebastian Siebertz, and Konstantinos Stavropoulos. Coloring and covering nowhere dense graphs. SIAM J. Discrete Math., 32(4):2467–2481, 2018. arXiv:1602.05926.
- [21] Jan van den Heuvel, Patrice Ossona de Mendez, Daniel Quiroz, Roman Rabinovich, and Sebastian Siebertz. On the generalised colouring numbers of graphs that exclude a fixed minor. European J. Combin., 66:129–144, 2017. arXiv:1602.09052.
- [22] Tony Huynh, Gwenaël Joret, Piotr Micek, Michal T. Seweryn, and Paul Wollan. Excluding a ladder. Combinatorica, 42(3):405–432, 2022. arXiv:2002.00496.
- [23] Freddie Illingworth, Alex Scott, and David R. Wood. Product structure of graphs with an excluded minor, 2022. arXiv:2104.06627.
- [24] Ken-ichi Kawarabayashi. Rooted minor problems in highly connected graphs. Discrete Mathematics, 287(1-3):121–123, 2004.
- [25] Chun-Hung Liu. Defective coloring is perfect for minors, 2022. arXiv:2208.10729.
- [26] Chun-Hung Liu and Sang-il Oum. Partitioning -minor free graphs into three subgraphs with no large components. J. Combin. Theory, Series B, 128:114–133, 2018. arXiv:1503.08371.
- [27] Chun-Hung Liu and David R. Wood. Clustered coloring of graphs excluding a subgraph and a minor, 2019. arXiv:1905.09495.
- [28] Chun-Hung Liu and David R. Wood. Clustered graph coloring and layered treewidth, 2019. arXiv:1905.08969.
- [29] Chun-Hung Liu and David R. Wood. Clustered variants of Hajós’ conjecture. J. Combin. Theory, Series B, 152:27–54, 2022. arXiv:1908.05597.
- [30] Bojan Mohar and Carsten Thomassen. Graphs on surfaces. Johns Hopkins University Press, 2001.
- [31] Jaroslav Nešetřil and Patrice Ossona de Mendez. Sparsity - Graphs, Structures, and Algorithms, volume 28 of Algorithms and combinatorics. Springer, 2012.
- [32] Sergey Norin, Alex Scott, Paul Seymour, and David R. Wood. Clustered colouring in minor-closed classes. Combinatorica, 39(6):1387–1412, 2019. arXiv:1708.02370.
- [33] Patrice Ossona de Mendez, Sang-il Oum, and David R. Wood. Defective colouring of graphs excluding a subgraph or minor. Combinatorica, 39(2):377–410, 2019. arXiv:1611.09060.
- [34] Marcin Pilipczuk, Michał Pilipczuk, and Sebastian Siebertz. Lecture notes for the course “Sparsity” given at Faculty of Mathematics, Informatics, and Mechanics of the University of Warsaw, Winter semesters 2017/18 and 2019/20. https://www.mimuw.edu.pl/˜mp248287/sparsity2.
- [35] Michal Pilipczuk and Sebastian Siebertz. Polynomial bounds for centered colorings on proper minor-closed graph classes. J. Combin. Theory, Series B, 151:111–147, 2021. arXiv:1807.03683.
- [36] Michał Pilipczuk and Marcin Wrochna. On space efficiency of algorithms working on structural decompositions of graphs. ACM Trans. Computation Theory, 9(4), 2018. arXiv:1509.05896.
- [37] Neil Robertson and Paul Seymour. Graph minors. I. Excluding a forest. J. Combin. Theory, Series B, 35(1):39–61, 1983.
- [38] Neil Robertson and Paul Seymour. Graph minors. V. Excluding a planar graph. J. Combin. Theory, Series B, 41(1):92–114, 1986.
- [39] Neil Robertson and Paul Seymour. Graph minors. XIII. The disjoint paths problem. J. Combin. Theory, Series B, 63(1):65–110, 1995.
- [40] Neil Robertson and Paul Seymour. Graph minors. XVI. Excluding a non-planar graph. J. Combin. Theory, Series B, 89(1):43–76, 2003.
- [41] Jan van den Heuvel and David R. Wood. Improper colourings inspired by Hadwiger’s conjecture. J. London Math. Soc., 98:129–148, 2018. arXiv:1704.06536.
- [42] David R. Wood. Defective and clustered graph colouring. Electron. J. Combin., DS23, 2018. Version 1, https://www.combinatorics.org/DS23.