The He molecular ion and the He- atomic ion in strong magnetic fields
Abstract
We study the question of existence, i.e. stability with respect to dissociation of the spin-quartet, permutation- and reflection-symmetric () state of the Coulomb system: the molecular ion, placed in a magnetic field a.u. We assume that the -particles are infinitely massive (Born-Oppenheimer approximation of zero order) and adopt the parallel configuration, when the molecular axis and the magnetic field direction coincide, as the optimal configuration. The study of the stability is performed variationally with a physically adequate trial function. To achieve this goal, we explore several Helium-contained compounds in strong magnetic fields, in particular, we study the spin-quartet ground state of the ion, and the ground (spin-triplet) state of the Helium atom, both for a magnetic field in a.u. The main result is that the molecular ion in the state is stable towards all possible decay modes for magnetic fields a.u. and with the magnetic field increase the ion becomes more tightly bound and compact with a cigar-type form of electronic cloud. At a.u., the dissociation energy of into is eV and the dissociation energy for the decay channel to is eV, latter both energies are in the energy window for one of the observed absorption features of the isolated neutron star 1E1207.4-5209.
I Introduction
It seems obvious that the chemical composition of the atmosphere of a magnetic white dwarf or a magnetized neutron star can not be established as long as we lack reliable information about the behavior of many-body Coulomb systems, especially about simple molecules and atoms in the presence of strong magnetic fields. So far, only Hydrogen-like and Helium-like atomic systems, and H-type molecular systems have been studied to a certain depth. There are indications that in addition to traditional atoms and molecules other non-standard, exotic atomic and molecular systems can also exist in strong magnetic fields (see for example, Turbiner and López Vieyra (2006); Turbiner et al. (2010)). In a recent discovery Turbiner and López Vieyra (2013) it was found that even the atomic ion becomes stable for magnetic fields a.u. with the spin doublet state as ground state at first and then, for a.u. all electron spins get aligned and antiparallel to a magnetic field direction: the corresponding state becomes the ground state of the system (see also Salas and Varga (2014)). It happens in spite of the fact that Helium belongs to the most inert (closed shell) atomic systems. Needless to say that Helium has a rich chemistry even in the absence of intense magnetic fields (see e.g. Grandinetti (2004)).
Usually, investigations of the Coulomb systems in strong magnetic fields (unreachable in the lab) are justified by the fact there exists a strong magnetic field on the surface of many neutron stars G and of some highly-magnetized white dwarfs G, see e.g. review García-Berro et al. (2016). In general, magnetic fields can reach G, or even higher, in the case of the so-called magnetars - the neutron stars with anomalously large surface magnetic field. While there is the evidence for the presence of Helium in the atmosphere of magnetic white dwarfs Jordan et al. (1998), there is no similar understanding about Helium in whatsoever form in atmospheres of neutron stars, and in general about their chemical content that can satisfactorily explain the observations.
The discovery of absorption features at 0.7 KeV and 1.4 KeV in the X-ray spectrum of the isolated neutron star 1E1207.4-5209 by Chandra X-ray observatory Sanwal et al. (2002), and its further confirmation by XMM-Newton X-ray observatory Mereghetti et al. (2002) motivated to perform studies of atoms and molecules in a strong magnetic field. At present there is a number of neutron stars whose atmospheres are characterized by absorption features: all of them are waiting to be solidly explained. These observations make clear that a detailed study of traditional atomic-molecular systems is needed, as well as for a search for new exotic chemical compounds which exist in a strong magnetic field only (see e.g. Turbiner (2007); López Vieyra et al. (2007a); Turbiner et al. (2007); López Vieyra et al. (2007b)).
As a result of such investigations, a model of helium-hydrogenic molecular atmosphere of the neutron star 1E1207.4-5209 was proposed which is based on the assumption that the most abundant components in the atmosphere are the exotic molecular ions and , with the presence of subject to a surface magnetic field G (see Turbiner (2005)). Conjectures about the absence of hydrogen envelopes in some neutron stars have also motivated the study of atmospheres composed of neutral helium. However, those simple models appear to be in conflict with observations. Models of atmosphere, composed with a large abundance of molecular systems containing helium, have been later suggested (see Turbiner (2005), van Kerkwijk and Kaplan (2007) and references therein). For reasons which are not completely clear to the present authors it has been emphasized van Kerkwijk and Kaplan (2007) that the molecule has to play a particularly important role. This molecular system exists in a field-free case in the spin-doublet, nuclei-permutation-antisymmetric , reflection-symmetric (with respect to any plane containing the internuclear axis) ground state Pauling (1933), usually denoted as . It is a rather compact system characterized by a small dissociation energy eV into . The lowest spin-doublet, nuclei-permutation-symmetric excited state Pauling (1933), usually denoted as , is repulsive. It is essentially unbound with shallow van-der-Waals minimum at large internuclear distance, see Grandinetti (2004) and references therein. It took us a number of years to perform a quantitative study of this particular system in the presence of a strong magnetic field, which is the subject of the present work. We are not aware of any similar previous study.
It is quite common in the field-free case that the ground state of simple atoms and molecules be characterized by the lowest possible total electron spin. Since the first qualitative studies of atomic and molecular systems Kadomtsev (1970); Kadomtsev and Kudryavtsev (1971a, b, 1972); Ruderman (1971, 1974) it became clear that in sufficiently strong magnetic fields the ground state is eventually realized by a state where the spins of all electrons are antiparallel to the magnetic field direction. Thus, the total electron spin takes maximal value as well as its total projection. It implies that the ground state depends on the magnetic field strength: there exists one (or several) threshold magnetic field for which one type of ground state changes to another one. This phenomenon was quantitatively observed for the first time for the molecule. It was shown that spin-singlet ground state , for small magnetic field, changes for intermediate fields a.u. to the unbound (repulsive) state as the ground state (precisely in the domain of magnetic fields typical of magnetic white dwarfs). While for stronger magnetic fields a.u., the ground state of the hydrogen molecule is realized by spin-triplet state (see Detmer et al. (1998) and references therein). Another recent example, which was mentioned above, is the case of the atomic ion where the ground state is realized first by the spin doublet state for a.u., and later by the spin-quartet state , for magnetic fields a.u., where all electron spins are aligned antiparallel to a magnetic field direction. In general, the phenomenon of change of the ground state nature with a magnetic field strength in traditional atomic systems was known since a time ago, see e.g. Ivanov and Schmelcher (2001) and reference therein.
The aim of this article is to perform a variational study of the molecular ion subject to a strong magnetic field in the state , when all electron spins get oriented anti-parallel to the magnetic field direction, the electronic total angular momentum projection is equal to 111To avoid a contradiction with the Pauli principle, thus, the appearance of the Pauli forces, it is further assumed that all three electrons have different magnetic quantum numbers, i.e. , and to show that the system is stable towards all possible decays or dissociation. Further it is naturally assumed that is the ground state. Due to extreme technical complexity we do not discuss other states of and leave the question about evolution of the type of the ground state with magnetic field changes for a future publication. Since our study is limited to the question of the existence and stability of this system in a certain state, the main attention is devoted to the exploration of all possible decay channels. A natural assumption about the optimal (equilibrium) configuration with minimal total energy is one which is achieved in the parallel configuration: where the internuclear axis connecting the two massive -particles ( nuclei) is situated along the magnetic line.
Another aim of the article is to continue to study the atomic ion in spin-quartet state for strong magnetic fields a.u., which was initiated in Turbiner and López Vieyra (2013). This study is necessary due to the possible decay mode into .
The consideration is non-relativistic, based on a variational solution of the Schrödinger equation. The magnetic field strength is restricted to magnetic fields a.u. (G) below the relativistic Schwinger limit. Also it is based on the Born-Oppenheimer approximation of zero-th order: the particles of positive charge (-particles) are assumed to be infinitely massive.
Atomic units are used throughout (). The magnetic field is given in a.u., with G. For energies given in eV, the conversion was used. All energies, which are mentioned in the article, are the total energies (with spin terms included) if it is not indicated otherwise.
II Hamiltonian
The non-relativistic Hamiltonian for a three-electron diatomic molecule with fixed nuclei in uniform constant magnetic field , directed along -axis, with vector potential in the symmetric gauge is given by
| (1) |
where is the 3-vector of the momentum of the th electron, is the charge of the nucleus , the terms correspond to the Coulomb interactions of the electrons with each charged nuclei ( is the distance between the -th electron and the -nuclei), the three terms () are the inter-electron Coulomb repulsive interactions ( are the distances between the -th electrons), and the term is the classical Coulomb repulsion energy between the nuclei, where is the internuclear distance (see Fig. (1) for notations). The Hamiltonian (1) includes, the paramagnetic terms as well as the spin Zeeman-term for the interaction of the magnetic field with the spin, and the diamagnetic term , with for each electron, . If the magnetic field is directed along the direction and parallel to the internuclear axis, the component of the total angular momentum along the -axis , the total spin , the projection of the total spin , and the total parity are conserved quantities. Sometimes, during the text the spectroscopic notation (with standard labels for etc) is used for the electronic states. Here stands for the degree of excitation for given (fixed) symmetry. In our case of a homonuclear diatomic molecule an additional subscript (gerade/ungerade) indicates a symmetric/antisymmetric state with respect to the permutation of the identical nuclei.

III Ground state in a strong magnetic field (generalities)
Before approaching to concrete calculations a description of the ground state of a Coulomb system of electrons and several heavy charged centers in a strong magnetic field should be given. In fact, a complete qualitative picture was presented in the pioneering works by Kadomtsev-Kudryavtsev Kadomtsev (1970); Kadomtsev and Kudryavtsev (1971b, a, 1972) and Ruderman Ruderman (1971, 1974):
Observation.
(i) All spins of electrons are oriented antiparallel to the magnetic field direction. Hence, the total electronic spin projection is ,
(ii) All heavy centers are situated on a magnetic line. Hence, there is no gyration,
(iii) Electronic magnetic quantum numbers are different and take values , hence, the total magnetic quantum number of the system . This configuration does not contradict to the Pauli principle and implies vanishing Pauli forces.
We are not familiar with a rigorous proof of the validity of this observation in general.
For Hydrogen atom, , validity of this observation, see item (iii), was explicitly checked by Ruder et al Ruder et al. (1994) and for other one-electron systems in Turbiner and López Vieyra (2006) - it was shown the ground state corresponds to . For Helium atom it was checked in Becken and Schmelcher (2000) - the ground state was type, thus, and for Lithium atom it was type, thus, Al-Hujaj and Schmelcher (2004) as well as for Turbiner and López Vieyra (2013). For two-electron molecules it was checked that lowest energy occurs at comparing to , see Detmer et al. (1998),Turbiner and Guevara (2007),Turbiner et al. (2010), respectively.
IV Trial Functions (general)
The variational method is used to study the state of the molecular ion (with infinitely massive centers) placed in a uniform magnetic field parallel to the molecular -axis. In general, the wavefunction of the electronic Hamiltonian (1) with two identical nuclei can be written in the form
| (2) |
where is a three-electron spin eigenfunction corresponding either to a total electronic spin or . Here are position vectors of the first, second, third electrons, respectively, see Fig.1. The function is a three particle orbital function, is the permutation operator of the two identical nuclei ( for gerade/ungerade states, respectively). The operator is the three-particle antisymmetrizer:
| (3) |
Here, represents the permutation , and stands for the permutation of into . For strong magnetic fields which are typically present in the atmosphere of neutron stars, a natural expectation is that the ground state corresponds to the case when all electron spins are aligned antiparallel to the magnetic field, i.e. and, thus, with the three-electron spin eigenfunction being totally symmetric. In this case, when , the trial function is written as
| (4) |
with a properly chosen orbital function, which then antisymmetrized by . Here is spin down function of th electron (see below).
On the other hand, for states of the total spin projection () we have two linearly independent spin eigenfunctions:
| (5) | ||||
| (6) |
where are spin up (spin down) functions of the th electron. So, the general form of a spin projection function has the form
| (7) |
where and are orbital functions. In particular we can choose these functions to be proportional and write
| (8) |
where is a variational parameter222A similar treatment was used for the study of the Li atom in a magnetic field in Guevara et al. (2009).. Thus, the trial function for states of spin can be written as (cf. (2))
| (9) |
with a properly chosen orbital function.
V Trial Functions (coordinate parts)
Variational trial functions are designed following physical relevance arguments. In particular, we construct wavefunction which allow us to reproduce both the Coulomb singularities of the potential and the correct asymptotic behavior at large distances (see, e.g. Turbiner (1984)). Following such criterion we propose the function
| (10) |
which is a type of product of Guillemin-Zener type molecular orbital functions multiplied by the product of Landau type orbitals for an electron in a magnetic field. Here and , are parameters. In the case of the fully polarized state and in order to avoid a contradiction with the Pauli principle, it is further assumed that all electrons have different magnetic quantum numbers in a certain minimal way: , hence, the total electronic quantum number is . It was already discussed in Turbiner et al. (2010) that this assumption seems obviously correct in the case of atoms and atomic ions, where the electrons are sufficiently close to each other, but not that obvious for the case of molecules for which the electrons are spread in space. All of them (or, at least, some of them) can be in the same quantum state, with the same spin projection and magnetic quantum number. This situation was observed for and , where in a domain of large magnetic fields the ground state was given by the state of maximal total spin but with the electrons having the same zero magnetic quantum number (see Turbiner et al. (2010) and references therein). However, for very strong fields the state of minimal total energy always corresponds to the situation described above with all electrons having different magnetic quantum numbers.
In (10) the variational parameters () have the meaning of screening (or anti-screening) factors (charges) for the nucleus respectively, as it is seen from the -th electron. The variational parameters are screening (or anti-screening) factors for the magnetic field seen from -th electron, and the parameters “measure” the screening (or anti-screening) of the inter-electron interaction. In total, the trial function (10) has 12 variational parameters in addition to the internuclear distance which can also be considered as a variational parameter.
The calculation of the variational energy using the trial function (4)-(10) involves two major parts: (i) 9-dimensional numerical integrations which were implemented by an adaptive multidimensional integration routine (cubature)Genz and Malik (1980), and (ii) a minimizer which was implemented with the minimization package TMinuit from CERN-lib (an old version of TMinuitMinimizer in the ROOT systemBrun and Rademakers (1997), which allows fixing/releasing parameters, was recovered and adapted to our purposes). The 9-dimensional integrations were carried out using a dynamical partitioning procedure: the domain of integration is manually divided into sub-domains following the profile of the integrand. Then each sub-domain is integrated using the routine CUBATURE. In total, we have a subdivision to subregions for the numerator and for the denominator in the variational energy. With a maximal number of sampling points for the numerical integrations (it guarantees the relative accuracy in integration) for each subregion, the time needed for one evaluation of the variational energy takes seconds with 96 processors. It was checked that this procedure stabilizes the estimated accuracy to be reliable in the first two decimal digits. However, in order to localize a domain, where minimal parameters are, the minimization procedure with much less number of sample points was used in each sub-domain and a single evaluation of the energy usually took mins. Once a domain is roughly localized the number of sample points increased by factor . Final evaluation was made with sampling points and for the strongest fields a.u. it was even with a subdivision of 7 subintervals in each -domain. Typically, a minimization procedure required several hundreds of evaluations. Computations were performed in parallel with a cluster Karen with 96 Intel Xeon processors at GHz.
VI Decay Channels, Dissociation
In this section we analyze different decay channels of the , state of the molecular ion in a magnetic field in the range a.u. Possible decay channels that we consider for the system placed in a magnetic field are
A few remarks emerge immediately: in the cases where there are free electrons 333For the total energy of a free electron (excluding the spin contribution) in the magnetic field in the symmetric gauge the -component of the angular momentum is conserved and the electron Landau levels are , where All states are degenerate. Here is the cyclotron frequency. in the decay channel (channels (c)-(f)) we can assume that the electrons are in the ground state which yields (regardless of the magnetic quantum number carried by the electron, where the spin contribution is included). In Born-Oppenheimer approximation the energy of a free -particle in a magnetic field is zero by assumption. Also, it is known that the helium atom exists for any magnetic field strength. For magnetic fields a.u. the spin-singlet state is the ground state. For a.u., the spin-triplet state (with ) becomes the ground state. For the atom in a magnetic field a.u., the corresponding total energies collected in Table (3) were taken from references Becken et al. (1999); Becken and Schmelcher (2000). Such energies were calculated for the infinite nuclear mass approximation and include the spin contributions for each electron. For magnetic fields and a.u. a simple variational Ansatz with 5 variational parameters was used to estimate the value of the energy of the spin-triplet state of Helium (see section VIII below for more details).
To obtain the energy of the ion we use the basic result of Surmelian and O’Connel for hydrogen-like atoms
| (11) |
and use the data of Kravchenko et al. (1996) for the binding energies of Hydrogen in a magnetic field (recalling that instead of the total energy , in Kravchenko et al. (1996) the authors reported the energies , which coincide with the binding energies for ). The Zeeman contribution to the total energy due to the spin of the electron is not taken into account in the results appearing in Kravchenko et al. (1996). Such contribution for the case of a spin antiparallel to the magnetic field () is a.u. and was added to the results collected in Table 3 to obtain the total energies of .
The molecular system ( molecular ion): accurate variational calculations in equilibrium configuration parallel to the magnetic field for the ground state were carried out in detail in Turbiner and López Vieyra (2006, 2007) for the range of magnetic fields where G is the non-relativistic limit. It was found that for magnetic fields a.u. the system is unstable towards decay to . Thus, in principle we can neglect in our considerations the decay channel (e) above. Nonetheless, at a.u., this compound becomes the system with the lowest total energy among the one-electron helium (helium-hydrogen) chains (for details see Turbiner and López Vieyra (2006)).
The molecular system molecular ion: this molecule was studied in detail in Turbiner and Guevara (2006) in the domain of magnetic fields . It was shown that the lowest total energy state depends on the magnetic field strength and evolves from the spin-singlet metastable state at a.u. to a repulsive spin triplet (unbound state) for a.u. and then to a strongly bound triplet state state. Hence, there exists quite a large domain of magnetic fields where the molecule is unbound and represented by two atomic helium ions in the same electron spin state but situated at an infinite distance from each other.
VII Revisited
In order to have a complete understanding about the stability of the molecular ion in magnetic fields, we need to extend the study on the atomic ion (three electron atomic system ) in magnetic fields to the regime of very strong fields a.u. In this section we review the basic notions for the study of the ion in magnetic fields. In Turbiner and López Vieyra (2013) it was found that the ground state of in a magnetic field is realized by a spin-doublet at and it becomes a fully polarized spin-quartet for larger magnetic fields. Thus, we will extend that study of the ion in strong magnetic fields, in the fully polarized, spin quartet , state only. For more details the reader is addressed to the reference Turbiner and López Vieyra (2013).
The non-relativistic Hamiltonian for an atomic system of three-electron and one infinitely massive center of charge in a magnetic field (directed along the -axis and taken in the symmetric gauge) is
| (12) |
where is the 3-vector momentum of the th electron, is the distance between the th electron and the nucleus, is the distance of the th electron to the -axis, and are the inter-electron distances. and are the -components of the total angular momentum and total spin operators, respectively. Both and are integrals of motion and can be replaced in (1) by their eigenvalues and respectively. For He- the nuclear charge is =2. The total spin and -parity are also conserved quantities. The spectroscopic notation is used to mark the states, where denotes the parity eigenvalue , and the quantum number labels the degree of excitation. For states with the same symmetry, for the lowest energy states at the notation is . We always consider states with and assuming they correspond to the lowest total energy states of a given symmetry in a magnetic field.
VII.1 Trial functions
The spin state of the system in a magnetic field is described by the trial function
| (13) |
where is the three-particle antisymmetrizer (3) and is the explicitly correlated orbital function
| (14) |
where is the magnetic quantum number and , and are non-linear variational parameters for each electron . In total, the trial function (13) contains 9 variational parameters. The function (13) is a properly anti-symmetrized product of Slater type orbitals, the lowest Landau orbitals and the exponential correlation factors .
The spin 3/2 state of the system in a magnetic field is described by the trial function (13) with . Due to the spin Zeeman contribution, the energy of this (spin ) state decreases rapidly and monotonically with the magnetic field increase and becomes the (stable) ground state for a.u.
In Turbiner and López Vieyra (2013), we made a study of the atomic system in magnetic fields a.u. Here we extend that study for magnetic fields up to a.u. In particular, we improve the value of the total energy at a.u. from a.u. (as quoted in ref. Turbiner and López Vieyra (2013)) to a.u., i.e. by a.u. (see Table 3).
The variational method used to find the energy of the system with the trial function (13) involves two major procedures of numerical minimization and integration. This was already described above for the case of the molecular ion (see section V). In particular, for strong magnetic fields, a reliable minimization depends on the accuracy of the variational energies i.e. on the accuracy of the numerical 9-dimensional integrations. Our strategy to find the minimal energy was first to make approaching minimizations with relatively low accuracy in the integrations and then followed by a manual scanning of the energy dependence on each variational parameter with high accuracy in the numerical integrations. For our final results we used a partition of the integration domain into 4800 subregions for the numerator and 4800 subregions for the denominator using 500 million points for each numerical integration. A single evaluation of the energy takes about 14 hrs of wall clock time using a cluster with 120 processors.
Our results for the spin 3/2 state of the system in magnetic fields a.u. are collected in Table 3 below. These results indicate that as the magnetic field increases, the total energy of the ion in the state decreases, but at a slower rate in comparison to the total energy of the molecular ion in the state. Also, our results confirm that as the magnetic field increases, the total energy of the ion in the state decreases more rapidly than the total energy of the atom in the spin triplet state and, therefore, becoming more stable towards decay into (see below for our extended calculations of the atom in the spin triplet state ).
VIII atom in strong magnetic fields revisited
The assertion on the stability of the molecular ion in strong magnetic fields requires a full understanding of the Helium atom and other Helium species in the presence of a strong magnetic field. It is known that the Helium atom exists for any magnetic field strength. Its ground state is realized by a singlet spin state at zero and small magnetic fields a.u. For larger magnetic fields the ground state is realized by the fully polarized spin triplet state Becken and Schmelcher (2000). Despite the fact that the Helium atom in magnetic fields is one of the most studied systems, all such studies, we are familiar with, are limited to magnetic fields up to a.u. (see, e.g. Becken and Schmelcher (2000)). For higher magnetic fields (up to the Schwinger limit G a.u.) the relativistic corrections to the energy seem to be relatively small. Thus, we extend the study of the Helium atom up to the largest magnetic field a.u. considered in the present study. In particular, a full understanding of the atom in the spin triplet (ground) state at magnetic fields a.u. is necessary.
VIII.1 Hamiltonian
The non-relativistic Hamiltonian which described the Helium atom with an infinitely massive nucleus of charge in a magnetic field oriented along the -axis is given by
| (15) |
where the symmetric gauge was used, and is the 3-vector momentum of the th electron, is the distance between the th electron and the nucleus, is the distance of the th electron to the -axis, and is the inter-electron distance. and are the -components of the total angular momentum and total spin operators, respectively. Both and are integrals of motion and can be replaced in (15) by their eigenvalues and respectively. The total spin and -parity are also conserved quantities. The spectroscopic notation is used to mark the states, where denotes the parity eigenvalue , and the quantum number labels the degree of excitation. For states with the same symmetry, for the lowest energy states at the notation is .
VIII.2 Trial functions
To study the ground state of the Hamiltonian (15) we use the variational method with trial functions chosen according to the criterion of physical relevance. The trial functions for the low lying states of (15) can be written as
| (16) |
where is the permutation operator for the electrons () and corresponds to the spin singlet () and the spin triplet () eigenstates, and are the magnetic quantum numbers of electron ( respectively). The trial function (16) depends on 5 variational parameters which account for effective screened charges: of the nucleus (as seen by electrons 1,2), of the electrons moving in the magnetic field , and the effective charge of one of the electrons as seen from the other .
The ground state of the Helium atom at strong magnetic fields is realized by the spin triplet state corresponding to and , () in (16). This simple Ansatz gives an energy a.u. at a.u., which compared to the most accurate result a.u. in Becken et al. (1999), indicates that the relative difference provided by this trial function is . The total energy of the triplet state decreases as the magnetic field increases. For a magnetic field a.u. our variational trial function gives an energy of a.u. while at a.u. it gives an energy of a.u. It is worth to notice that the total energy of Helium in the spin triplet state lies higher than the total energy of the ion in the fully polarized state , and the energy difference increases with an increase of the magnetic field.
The variational method used to find the energy of the Helium atom with the trial function (16) involves two major procedures of numerical minimization (MINUIT) and multidimensional numerical integration (Cubature). Due to the axial symmetry of the problem the dimensionality reduces to five. The integrations are performed in double cylindrical coordinates (where is the relative azimuthal angle between the electrons). The manual partitioning includes five subdomains in each coordinate, three subdomains in each coordinate and one domain for . The maximal number of point used to evaluate the numerical integrations is 50 millions. Our results for this system are presented in Tables 3 and 7 (see below).
IX Results
IX.1 Field free case: low lying states
We have carried out variational calculations for the field free ground state state as well as for the weakly bound excited state state of . The aim of this study is mainly to have an estimate of the accuracy of our variational calculations. Previous studies on one and two electron Coulomb systems in strong magnetic fields have shown that simple trial functions of the type (10) which are built following the criterion of physical adequacy, have led to very accurate results for such systems (see Turbiner and López Vieyra (2006); Turbiner et al. (2010)).
The results for the energy of the states and using the trial function (9) are collected in the Table 1. From such results, and comparing to the most accurate results to date for such states Tung et al. (2012); Xie et al. (2005), we can conclude that the energies obtained with our 10-parameter trial function have a relative accuracy . It is worth to note that the level of accuracy provided by the trial function (9) is sufficiently high to observe the shallow minimum of the state, though the equilibrium distance seems to be slightly shifted in comparison to the results of Xie et al. (2005).
In a magnetic field one can expect a relatively slow decrease in accuracy as the magnetic field increases. A similar comparison for the energies of the Helium atom in a magnetic field a.u. obtained (a) with the two-electron 5-parameter trial function (16) and (b) with the more accurate energies using a Gaussian basis set method with two-particle functions Becken et al. (1999), leads to the conclusion that even at a.u. the relative accuracy is . Thus, we can estimate that our results for the ion in magnetic fields a.u. have an accuracy of with a small decrease for higher magnetic fields. To confirm this conjecture, a separate study would be necessary.
| (a.u.) | (a.u.) | (a.u.) | (a.u.) | ||
|---|---|---|---|---|---|
| -4.955243 | 2.15 | -4.8653 | 8.61 | ||
| -4.953765 | 2.042 | -4.8651 | 8.742 | ||
| -4.994644 | 2.042 | (a) | -4.9036 | 8.742 | (b) |
First row energy and equilibrium distance for the ground state and excited state calculated with a trial function (9).
Second row the energies calculated at the equilibrium distance taken from Tung et al. (2012); Xie et al. (2005).
Third row energy (rounded) and equilibrium distance for from Tung et al. (2012) (a) and for from Xie et al. (2005) (b).
IX.2 a.u.
We begin our analysis for the total energy and equilibrium distance for the spin state with corresponding to the Hamiltonian (1) for a magnetic field a.u.
For this magnetic field the total energy of the spin-quartet, state obtained with the trial function (4-10), is a.u. with an equilibrium distance a.u. (see Table 3). The lowest energy state of corresponding to the triplet state, and , has a total energy a.u., and the total energy of the ground state of ion, is a.u. From this considerations, it is clear that for this magnetic field the state of is unstable towards decay (channel (a)) to
| (17) |
since the total energy of the sub-products a.u. is essentially lower than the total energy of the spin-quartet state of . It is also noteworthy to mention that the lowest state of with , has a total energy of a.u. (including the contribution from the spin Zeeman term) and, for this case, the state of is stable towards the (-conserved) decay into
| (18) |
since the total energy of the sub-products is a.u. Thus, in the state is a metastable state.
For this magnetic field is also unstable towards decay into two ions plus an electron infinitely separated (decay channel (d)). This separated system has a total energy a.u. On the other side, following the results summarized in Table (3) is stable towards decays into (channel (b)) or (channel (c)). Decay channels (e) and (f) are not possible since the systems and either do not exist or are unstable. For a.u., the lowest energy state of the two electron molecular ion corresponds to a purely repulsive spin-triplet (unbound) state (for a.u. this system do not exist four-body bound state, it exists in a form of two separated helium ions He+ situated at an infinitely large distance from each other), and the one electron molecular ion in its ground state is unstable towards decay into .
IX.3 a.u.
We continue our analysis for a magnetic field a.u. For this magnetic field the total energy of the quartet state with belonging to the Hamiltonian (1) is a.u. with an equilibrium distance a.u. (see Table 3).
For this magnetic field the lowest energy state of is the triplet state with magnetic quantum number , and has a total energy a.u., while the total energy of the ground state of the ion is a.u. (including the spin Zeeman contribution). From this we can conclude that the state is still unstable towards decay (17), since the total energy of the sub-products is a.u. which is slightly smaller than the total energy of the quartet state of . However, it is clear form this comparison, that for some a.u. the state of becomes stable towards decay into (see below).
Following the results summarized in Table (3) we conclude that is stable towards decays into (channel (b)) or (channel (c)) or (channel (d)) since the total energies of the corresponding separated subsystems in all these channels lie above the total energy of the quartet state. Decay channels (e) and (f) are also not possible since, for this magnetic field, the lowest energy state of the two electron molecular ion corresponds to a purely repulsive triplet state , and the system in its ground state is unstable towards decay into .
IX.4 a.u.
Our variational result for the total energy of the quartet state with belonging to the Hamiltonian (1) for a magnetic field a.u. is a.u. with an equilibrium distance a.u. (see Table 3).
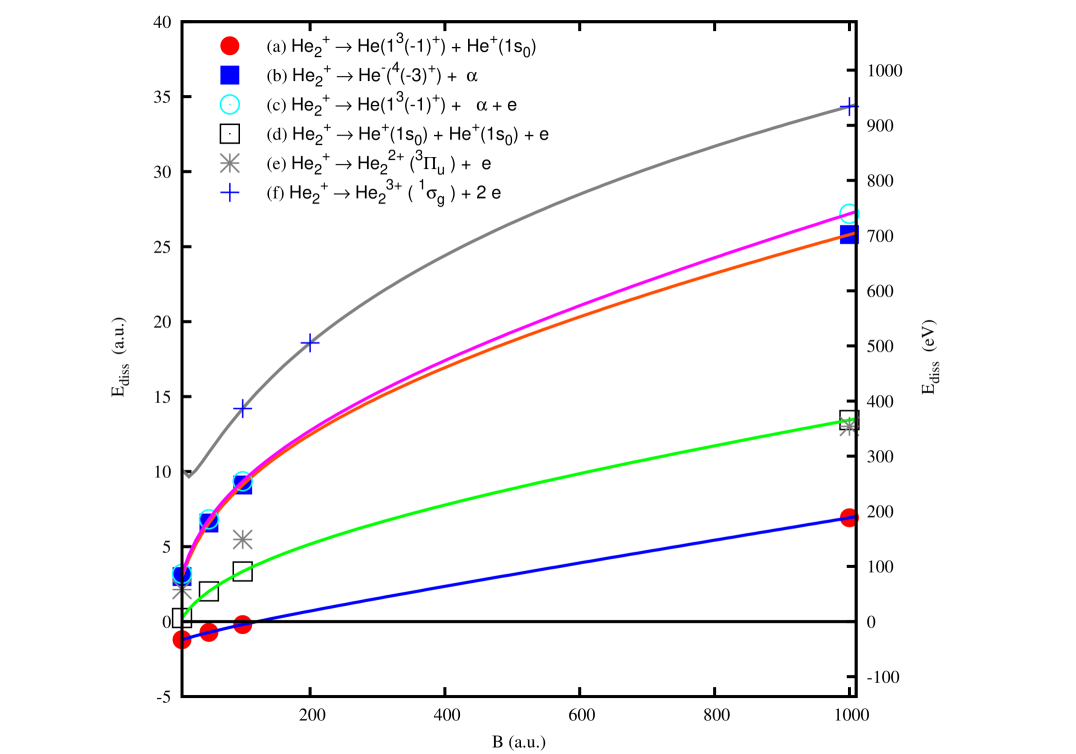
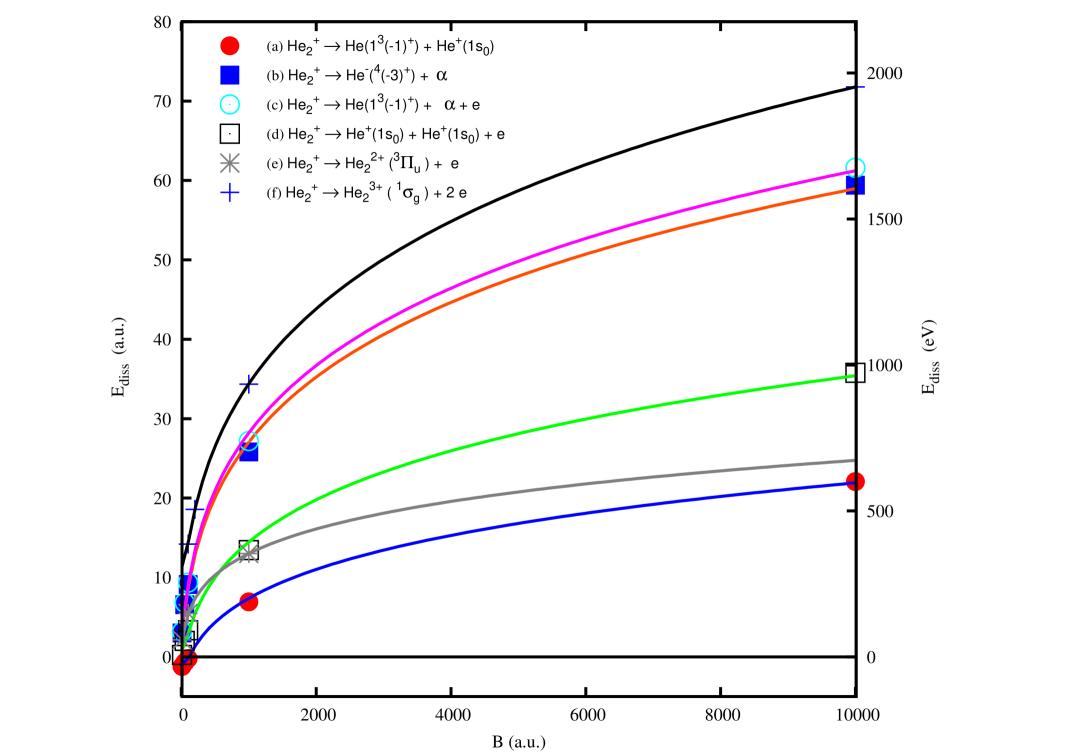
Now, for the main decay channel (a) the total energy of the sub-products is a.u. which lies higher than the total energy of the quartet state of , and thus, the molecular ion is stable towards decay to . The dissociation energy for this channel is a.u. eV at a.u.
For the case of channel (b), a direct comparison of the total energies of and at a.u. (for we made an extension of the results in Turbiner and López Vieyra (2013) at a.u.) indicates that is also stable towards decay to with a dissociation energy of eV. For the case of channel (c) , the total energy of the sub-products of this decay is larger than the total energy of the ion in the quartet state. So, the system is also stable towards this decay channel with a dissociation energy of eV. For the case of channel (d) the total energy of the sub-products of this decay is larger than the total energy of the ion in the quartet state. The dissociation energy in this case is eV. For the case of channel (e) , at a.u. the total energy of the sub-products of this decay is larger than the total energy of the ion in the quartet state. However, we should remember that for this magnetic field the ground state of the two-electron molecular ion is realized by a repulsive spin triplet state state (for a.u. this system exists in the form of two helium ions He+ situated at an infinitely large distance from each other i.e. case (d)), and the strongly bound triplet state state becomes the ground state at a.u. (see Turbiner and Guevara (2006)).
For the case of channel (f) , at a.u. the total energy of the sub-products of this decay is larger than the total energy of the ion in the quartet state, and the corresponding dissociation energy is eV. For this magnetic field the ion is stable towards and it is the most bound one-electron system made from protons and/or particles for a.u.
IX.5 a.u.
Our variational result for the total energy of the quartet state with belonging to the Hamiltonian (1) for a magnetic field a.u. is a.u. with an equilibrium distance a.u. (see Table 3). At this magnetic field the numerical integrations with different accuracies (maximal number of points) indicate that the energy has a relative accuracy of a.u. This may result in differences of a few eV in the transition energies.
For the main decay channel (a) the total energy of the sub-products is a.u. which lies higher than the total energy of the quartet state of , and thus, the molecular ion is stable towards decay to . The corresponding dissociation energy for this channel is a.u. eV at a.u.
For the case of channel (b), a direct comparison of the total energies of and at a.u. (in section VII we carried out an extension of the results in Turbiner and López Vieyra (2013) for up to a.u.) indicates that is also stable towards decay to with a dissociation energy of eV. For the case of channel (c) , the total energy of the sub-products of this decay is larger than the total energy of the ion in the quartet state. So, the system is also stable towards this decay channel with a dissociation energy of eV. For the case of channel (d) the total energy of the sub-products of this decay is larger than the total energy of the ion in the quartet state. The dissociation energy in this case is eV. For the case of channel (e) , at a.u. the total energy of the sub-products of this decay is larger than the total energy of the ion in the quartet state, and the corresponding dissociation energy is eV.
For the case (f) , at a.u. the total energy of the sub-products of this decay is larger than the total energy of the ion in the quartet state , and the corresponding dissociation energy is eV.
The total energy of the ion in the quartet state as a function of the magnetic field is presented in figure (2). This figure shows that as the magnetic field is increased, the system becomes more bound. The internuclear equilibrium distance of the ion in the quartet state as a function of the magnetic field is presented in figure (3). This figure shows that as the magnetic field is increased, the system becomes more compact. We have plotted in Figure (4) the dissociation energies, (i.e. difference of total energies between the state of and the energy of the final products) for the different decay channels described in section VI. This plot shows that the ion in the state becomes more bound with respect to all dissociation channels as the magnetic field increases and, more important, that the dissociation energies at a.u. lie in the window KeV which is the window of observed absorption features in the spectrum of the isolated neutron star 1E1207.4-5209 (see Sanwal et al. (2002) and Mereghetti et al. (2002) ).
In order to have a hint about the critical magnetic field at which the state of becomes the ground state of the Coulomb system , we have collected in Table 4 a list of atomic and molecular Coulomb systems made out of Hydrogen and/or -particles, as well as the Lithium atom, and the corresponding critical magnetic fields at which the ground state is realized by a state with all spins oriented anti-parallel to the magnetic field. A simple analysis of this table indicates that for atomic systems (with more than one-electron ()) the critical magnetic field is rather weak being a.u. For molecular type systems there seems to be two typical ranges of values for the critical magnetic field, i.e. a.u., and a.u. which is much larger than for the atomic type systems. Perhaps, this phenomenon can be explained by the fact that electrons in a molecular system are further apart than in the case of atoms. So, if this tendency is also valid for the case of the molecular ion, then it is very likely that the state becomes the ground state for magnetic fields a.u. Of course, a detailed study of other states of the molecular ion is needed in order to establish this conjecture.


IX.6 Spin states
As for the spin states of we have calculated the total energy of some states with for both gerade and ungerade parities at the magnetic field a.u. (see Table 2). It is clear from such results that, for high magnetic fields a.u., these states will lay much higher in energy than the fully polarized state that we consider in our study. For spin states the contribution to the total energy coming from the Spin-Zeeman term is a.u., while it is a.u. for the spin fully polarized state. Thus, considering only the Spin-Zeeman contribution to the total energy, the states with spin are about a.u. higher that the spin states.
| g | u | g | u | g | ||
| (a.u.) | 76.13 | 76.27 | 69.57 | 66.84 | -22.46 | |
| (a.u.) | 1.85 | 0.79 | 0.279 | 0.79 | 0.432 | |
X Conclusions
We have studied the stability of the molecular Coulomb system formed by two infinitely massive -particles and three electrons, in the range of magnetic fields a.u., in a state where all electron spins are oriented antiparallel to the magnetic field direction, hence, . It was further assumed that in the ground state, in order to suppress the appearance of the Pauli force, all electrons should have different magnetic quantum numbers, in particular, if these are equal to , the total magnetic quantum number . This choice looks natural physically. The parallel configuration, for which both the molecular axis and the magnetic field direction coincide, was adopted as the optimal configuration with minimal total energy. The stability towards possible decay channels was studied variationally, using trial functions (4), (10). We found that for all studied magnetic fields a.u., there exists a well-pronounced minimum in the potential curve of total energy vs the internuclear distance at some . The equilibrium distance decreases with the magnetic field increase, hence, the system becomes more compact at large magnetic fields. At the same time the total energy is getting more negative, while the binding energy increases making the system more bound. For a.u., the molecular ion in the state becomes stable towards all possible decay channels (see Fig. (4)). In other words, the molecular system becomes the most bound Helium specie with three electrons. It also hints to the possible relevance of other Helium chains like , , or even the hybrid molecules like the neutral , for the chemistry in a strong magnetic field.
Studying the evolution of the ground state with the magnetic field change in different Coulomb systems, with different number of electrons, we found that there is always a specific, well-defined state of maximal total spin projection, which becomes the ground state at large magnetic fields. For one-electron systems this state has and . For two-electron systems it has and with , see Table II. For two studied three-electron systems, Li and He-, it was the state and , Turbiner and López Vieyra (2013). It seems natural to assume that this state will be the ground state for for a certain critical magnetic field, see Section III. In order to find this critical magnetic field it is necessary to explore other states of , in particular, spin-quartet gerade and ungerade states with different total electron angular momentum . This will be done elsewhere.
Concluding we have to state that at a.u., the dissociation energy with respect to the main decay channel reaches a.u. (eV); while the dissociation energy for the decay channel (b) into is eV and the dissociation energy for the decay channel (c) into is eV. Thus, the two latter energies are in the energy window for one of the absorption features observed for the isolated neutron star 1E1207.4-5209.
We found that in a strong magnetic field a.u., the molecular ion is the most bound system among the atomic and molecular systems containing helium and up to three electrons. Thus, this molecule may play a particularly important role in the description of atmosphere of strongly magnetized neutron stars as it was hinted in van Kerkwijk and Kaplan (2007).
Acknowledgements.
This work was supported in part by the PAPIIT grant IN108815 and CONACyT grant 166189 (Mexico). The authors thank D. Turbiner for his valuable help in designing and optimizing the parallel programming codes in C++. Also J.C.L.V. thanks PASPA grant (UNAM, Mexico) and the Centre de Recherche Mathématiques, Université de Montréal for the kind hospitality while on sabbatical leave during which this work was ultimately completed.| (a.u.) | |||||||
|---|---|---|---|---|---|---|---|
| 1. | -4.02 | 2.18 | -3.03 | -2.4410 | - | -3.3745 | -2.9655 |
| 100. | -22.46 | 0.432 | -13.38 | -9.5605 | -8.2581 | -16.9917 | -13.1048 |
| 1000. | -53.98 | 0.196 | -28.18 | -20.2707 | -19.6338 | -40.2462 | -27.1738 |
| 10000. | -114.9 | 0.098 | -55.41 | -39.5107 | -43.1165 | -87.255 | -53.2011 |
| System | Ground State | (a.u.) | ||
|---|---|---|---|---|
| 0 | -1/2 | |||
| 0 | -1/2 | |||
| -1 | -1 | |||
| -1 | -1 | |||
| -1 | -1 | |||
| -1 | -1 | |||
| -1 | -1 | |||
| -1 | -1 | |||
| -1 | -1 | |||
| -3 | -3/2 | |||
| -3 | -3/2 |
Appendix A Variational Parameters for
| Magnetic field in a.u. | |||
| parameter | 100 | 1000 | 10000 |
| 0.93175 | 1.975 | 3.59 | |
| 3.34641 | 3.9 | 4.28 | |
| 1.41717 | 1.9 | 2.5 | |
| 2.0076 | 3.059 | 4.36 | |
| 1.53986 | 2.09 | 2.32 | |
| 1.03391 | 1.82 | 3.1 | |
| 0.58803 | 0.46 | 0.38 | |
| 0.23269 | 0.16 | 0.08 | |
| 0.17702 | 0.15 | 0.2 | |
| 0.81948 | 0.93 | 0.98 | |
| 0.87464 | 0.94 | 0.983 | |
| 0.90583 | 0.957 | 0.989 | |
| (a.u.) | 0.43177 | 0.1985 | 0.098 |
| (a.u.) | -22.460 | -53.978 | -114.908 |
Appendix B Variational Parameters for
| Magnetic field in a.u. | |||
|---|---|---|---|
| parameter | 100 | 1000 | 10000 |
| 2.86366 | 4.30183 | 5.32027 | |
| 1.91669 | 3.09290 | 3.79174 | |
| 1.20906 | 1.67689 | 2.48690 | |
| -0.13497 | 0.06847 | 0.37195 | |
| -0.12987 | 0.02558 | -0.04966 | |
| -0.11967 | 0.05634 | -0.08924 | |
| 0.84414 | 0.92115 | 0.97709 | |
| 0.91848 | 0.95373 | 0.99092 | |
| 0.96952 | 0.98367 | 0.99470 | |
| -13.3772 | -28.1756 | -55.4053 | |
Appendix C Variational Parameters for atom in spin triplet state
| Magnetic field in a.u. | |||
|---|---|---|---|
| parameter | 100 | 1000 | 10000 |
| 2.107315 | 3.085664 | 4.589369 | |
| 2.952063 | 4.151930 | 5.887318 | |
| 0.145703 | 0.117778 | 0.227942 | |
| 0.895958 | 0.958737 | 0.986090 | |
| 0.825659 | 0.930747 | 0.977742 | |
| -12.8215 | -27.1738 | -53.2011 | |
References
- Turbiner and López Vieyra (2006) A. V. Turbiner and J. C. López Vieyra, “One-electron molecular systems in a strong magnetic field,” Physics Reports 424, 309–396 (2006).
- Turbiner et al. (2010) A. V. Turbiner, J. C. López Vieyra, and N. L. Guevara, “Charged hydrogenic, helium, and helium-hydrogenic molecular chains in a strong magnetic field,” Phys. Rev. A 81, 042503 (2010), arXiv:astro-ph/0909.1910 .
- Turbiner and López Vieyra (2013) A. V. Turbiner and J. C. López Vieyra, “Stable He- can Exist in a Strong Magnetic Field,” Phys. Rev. Lett. 111, 163003 (2013), arXiv:physics.atom-ph/1307.4810 [physics.atom-ph] .
- Salas and Varga (2014) J. A. Salas and K. Varga, “He- in a magnetic field: Structure and stability,” Phys. Rev. A 89, 052501 (2014).
- Grandinetti (2004) F. Grandinetti, “Helium chemistry: a survey of the role of the ionic species,” International Journal of Mass Spectrometry 237, 243–267 (2004).
- García-Berro et al. (2016) E. García-Berro, M. Kilic, and S. O. Kepler, “Magnetic white dwarfs: Observations, theory and future prospects,” International Journal of Modern Physics D 25, 1630005 (2016).
- Jordan et al. (1998) S. Jordan, P. Schmelcher, W. Becken, and W. Schweizer, “Evidence for helium in the magnetic white dwarf GD229,” Astron. Astrophys. 336, L33–L36 (1998).
- Sanwal et al. (2002) D. Sanwal, G. G. Pavlov, V. E. Zavlin, and M. A. Teter, “Discovery of Absorption Features in the X-Ray Spectrum of an Isolated Neutron Star,” Astro Phys. Jour. Lett 574, L61–L64 (2002), astro-ph/0206195 .
- Mereghetti et al. (2002) S. Mereghetti, A. De Luca, P. A. Caraveo, W. Becker, R. Mignani, and G. F. Bignami, “Pulse Phase Variations of the X-Ray Spectral Features in the Radio-quiet Neutron Star 1E1207-5209,” Astrophys. J. 581, 1280–1285 (2002), astro-ph/0207296 .
- Turbiner (2007) A. V. Turbiner, “Molecular systems in a strong magnetic field,” Astrophysics and Space Science 308, 267–277 (2007).
- López Vieyra et al. (2007a) J. C. López Vieyra, A. V. Turbiner, and N. L. Guevara, “Exotic ion in strong magnetic fields. ground state and low-lying states,” Astrophysics and Space Science 308, 493–497 (2007a).
- Turbiner et al. (2007) A. V. Turbiner, N. L. Guevara, and J. C. López Vieyra, “ molecular ion in a magnetic field: Linear parallel configuration,” Phys. Rev. A 75, 053408 (2007).
- López Vieyra et al. (2007b) J. C. López Vieyra, A. V. Turbiner, and N. L. Guevara, “The ion in a strong magnetic field. linear configuration,” Astrophysics and Space Science 308, 499–503 (2007b).
- Turbiner (2005) A. V. Turbiner, “A helium-hydrogenic molecular atmosphere of the neutron star 1E1207.4-5209,” astro-ph/0506677 , 1–7 (2005), preprint ICN-UNAM 05-04.
- van Kerkwijk and Kaplan (2007) M. H. van Kerkwijk and D. L. Kaplan, “Isolated neutron stars: magnetic fields, distances, and spectra,” Astrophysics and Space Science 308, 191–201 (2007).
- Pauling (1933) L. Pauling, “The Normal State of the Helium Molecule-Ions He2+ and He2++,” J. Chem. Phys. 1, 56–59 (1933).
- Kadomtsev (1970) B. B. Kadomtsev, “Heavy atom in a ultrastrong magnetic field,” Zh. Eksp. Teor. Fiz. 58, 1765–1769 (1970), [Sov. Phys. - JETP Vol 31, No. 5 (1970)], (English Translation).
- Kadomtsev and Kudryavtsev (1971a) B. B. Kadomtsev and V. S. Kudryavtsev, “Atoms in an ultrastrong magnetic field,” Pis’ma Zh. Eksp. Teor. Fiz. 13, 61–64 (1971a), [Sov. Phys. - JETP Lett. Vol 13, p 42-45 (1971)], (English Translation).
- Kadomtsev and Kudryavtsev (1971b) B. B. Kadomtsev and V. S. Kudryavtsev, “Molecules in an ultrastrong magnetic field,” Pis’ma Zh. Eksp. Teor. Fiz. 13, 15–19 (1971b), [Sov. Phys. - JETP Lett. Vol 13, p 9-12 (1971)], (English Translation).
- Kadomtsev and Kudryavtsev (1972) B. B. Kadomtsev and V. S. Kudryavtsev, “Matter in a superstrong magnetic field,” Zh. Eksp. Teor. Fiz. 62, 144–152 (1972), [Sov. Phys. - JETP Vol 35, No. 1 (1972)], (English Translation).
- Ruderman (1971) M. A. Ruderman, “Matter in superstrong magnetic fields: the surface of a neutron star,” Phys. Rev. Lett. 27, 1306–1308 (1971).
- Ruderman (1974) M. A. Ruderman, “Matter in superstrong magnetic fields,” in Physics of Dense Matter, edited by Carl J. Hansen., Proceedings of IAU Symposium no. 53 (Dordrecht, Boston, Reidel, Boulder Colorado, U.S.A., 1974) pp. 117–131.
- Detmer et al. (1998) T. Detmer, P. Schmelcher, and L. S. Cederbaum, “The hydrogen molecule in a magnetic field: The lowest states of the -manifold and the global ground state of the parallel configuration,” Phys. Rev. A 57, 1767–1777 (1998).
- Ivanov and Schmelcher (2001) M V Ivanov and P Schmelcher, “The boron atom and boron positive ion in strong magnetic fields,” J. Phys. B 34, 2031 (2001).
- Ruder et al. (1994) H. Ruder, G. Wunner, H. Herold, and F. Geyer, Atoms in Strong Magnetic Fields (Springer Verlag Berlin-Heidelberg, 1994).
- Becken and Schmelcher (2000) W. Becken and P. Schmelcher, “Non-zero angular momentum states of the helium atom in a strong magnetic field,” J. Phys. B 33, 545–568 (2000), astro-ph/0006098 .
- Al-Hujaj and Schmelcher (2004) O.-A. Al-Hujaj and P. Schmelcher, “Lithium in strong magnetic fields,” Phys. Rev. A 70, 033411 (2004), physics/0407065 .
- Turbiner and Guevara (2007) A. V. Turbiner and N. L. Guevara, “The HeH+ molecular ion in a magnetic field,” J. Phys. B 40, 3249–3257 (2007), physics/0703090 .
- Guevara et al. (2009) N. L. Guevara, F. E. Harris, and A. V. Turbiner, “An accurate few-parameter ground state wave function for the lithium atom,” International Journal of Quantum Chemistry 109, 3036–3040 (2009).
- Turbiner (1984) A. V. Turbiner, “The eigenvalue spectrum in quantum mechanics and the nonlinearization procedure,” Usp. Fiz. Nauk. 144, 35–78 (1984), Soviet Phys. – Uspekhi 27, 668 (1984) (English Translation).
- Genz and Malik (1980) A Genz and A. Malik, “An adaptive algorithm for numerical integration over an N-dimensional rectangular region,” J. Comput. Appl. Math. 6, 295–302 (1980), Johnson, S. G., http://ab-initio.mit.edu/wiki/index.php/Cubature. C package for adaptive multidimensional integration (cubature) of vector-valued integrands over hypercubes.
- Brun and Rademakers (1997) R. Brun and F. Rademakers, “ROOT - an object oriented data analysis framework,” Nucl. Inst. & Meth. in Phys. Res. A, Proceedings AIHENP’96 Workshop, Lausanne 389, 81–86 (1997).
- Becken et al. (1999) W. Becken, P. Schmelcher, and F. K. Diakonos, “The helium atom in a strong magnetic field,” J. Phys. B 32, 1557–1584 (1999), physics/9902059 .
- Kravchenko et al. (1996) Y. P. Kravchenko, M. A. Liberman, and B. Johansson, “Exact solution for a hydrogen atom in a magnetic field of arbitrary strength,” Phys. Rev. A 54, 287–305 (1996).
- Turbiner and López Vieyra (2007) A. V. Turbiner and J. C. López Vieyra, “Exotic Molecular Ions (HeH)2+ and He in a Strong Magnetic Field:. Low-Lying States,” Int. Jour. Mod. Phys. A 22, 1605–1626 (2007), astro-ph/0412399v4 .
- Turbiner and Guevara (2006) A. V. Turbiner and N. L. Guevara, “He molecular ion can exist in a magnetic field,” Phys. Rev. A 74, 063419 (2006), astro-ph/0610928 .
- Tung et al. (2012) W.-C. Tung, M. Pavanello, and L. Adamowicz, “Very accurate potential energy curve of the He ion,” J. Chem. Phys. 136, 104309 (2012).
- Xie et al. (2005) J. Xie, B. Poirier, and G. I. Gellene, “Accurate, two-state ab initio study of the ground and first-excited states of He, including exact treatment of all born–oppenheimer correction terms,” J. Chem. Phys. 122, 184310 (2005).