The Integral of Secant and Stereographic Projections of Conic Sections
Abstract
We show that the four best-known substitutions used to integrate secant rely on different rational parametrizations of conic sections, coming from stereographic projections. We also investigate other possible explanations for the four substitutions, as well as connections between the buildups leading to them.
1 Introduction
The integral of secant, which competes for the unofficial title of The Most Interesting Integral in the World of Elementary Functions, can be taught in several ways [1, 8, 9, 14, 19].
We start by briefly reviewing some history [15]. The secant was integrated numerically in 1569 by Gerardus Mercator [5] to construct the famous map projection that bears his name. Mercator’s projection is especially useful for navigators because it depicts angles accurately, with zero distortion. Let longitude and latitude of a point on Earth. On Mercator’s map the -coordinate of the corresponding point on the map is the longitude, and its -coordinate depends only on the latitude
Consider an infinitesimal square on the earth with vertices at , , , and . Its sides have equal length,
where is the Earth’s radius. To avoid distorting angles the corresponding points on the map must also form an infinitesimal square. Its horizontal measure is
so its vertical measure must be the same,
Adding up these infinitesimal distances on the map as one moves away from the equator, the -coordinate of a point at latitude will be a function of , say . Then we have
Taking derivatives shows that . Note that this gives us a practical reason to integrate the secant function but it does not help us find . This is done by one of the following four available substitutions described in the next section.
2 The Four Substitutions Used to Integrate Secant
-
1.
The Gregory substitution [4, 10], . This is the method used in most modern calculus textbooks [19, 9], and is usually justified by a mysterious trick: multiplying and dividing by . Here is an explanation (found independently many times, see [8, 17, 20]) for how to come up with this: integration is about spotting derivatives. Not being able to think of a function whose derivative is secant, we go for the next best thing, i.e. finding a function which at least has a secant in its derivative. It turns out there are only two of them:
Seeing them nicely lined up like this prompts us to add the two equalities, and by doing so we get: , so
(1) This was a conjecture from 1645, based on information from logarithmic tables (and known to many people, including Newton), and it was solved by James Gregory 23 years later [15]. As explained by Turnbull in [22], Gregory actually proves (using only geometry), that
and this is how he arrives at the substitution.
- 2.
- 3.
-
4.
The modified Weierstrass substitution [14], , which leads to the integral of .
The Barrow and Weierstrass substitutions both end up by using the method of partial fractions to integrate (or , respectively). It is believed that Barrow was the first to use partial fractions in integration [15]. In the North American curriculum partial fractions are usually taught after trigonometric integrals [19], but the following well known trick helps us avoid partial fractions in this particular case, so we can teach the integral of secant using any of the four methods at any time. Moreover, the antiderivative is the same as the one obtained when using partial fractions.
A similar but sneakier trick produces the partial fraction decomposition by splitting the 1 in the numerator into , then adding and subtracting and separating the fractions.
We would to recall here that the method of partial fractions is a spectacular and surprising application of the arithmetic of the ring of polynomials in one indeterminate with real or complex coefficients to calculus [9, p. 165].
3 Connections Between the Four Substitutions and Other Ideas
We now discuss another idea for integrating secant and a different buildup to the Gregory substitution, both coming from Liouville’s Theorem on integration in finite terms, as proved in [16]. (By the way, the proof makes frequent use of partial fractions.) This is a theorem in differential algebra which explains why functions like or do not have antiderivatives which can be expressed as compositions of elementary functions (which are compositions of the functions we study in calculus). We give the full statement of the theorem, but keep in mind that an easy example of a differential field is the field of rational fractions, and for a rational fraction we can think of as the derivative of regarded as a rational function.
Liouville’s Theorem. Let be a differential field of characteristic zero and . If the equation has a solution in some elementary differential extension field of having the same subfield of constants, then there are constants and elements such that
Now, if has an elementary indefinite integral, it would be of the form in Liouville’s Theorem, and so, since we can’t think of a function whose derivative is secant, guessing in the simplest case
would be a reasonable thing to try first. We therefore try to find if . Since we are looking for , it makes sense to differentiate .
This gives
and so
which means taking works.
This also tells us that the buildup to Barrow’s substitution, combined with the avoidance of partial fractions described above, can also lead to Gregory’s substitution. Keep in mind that Barrow’s buildup involved multiplying the top and the bottom by , then adding and subtracting in the numerator. If instead we reverse the order of these two actions, i.e. we start by adding and subtracting on top, then we get:
| (2) |
(multiplying and dividing by is now hidden in the identity
this may be seen after dividing both of its sides by ), and (2) immediately gives (1).
Now we can get yet another buildup leading to Gregory’s substitution. Start with (2), and keep going instead of integrating. We get
We end this section by noting that we can also derive (2) by adding and subtracting to instead of to 1 on top of (this can be also independently motivated by the identity ).
| (3) |
4 The Substitutions Used in the Integral of Secant and Stereographic Projections
The stereographic projection of a curve from a point to a line is the function that maps any point on the curve to the intersection of that line with the secant to the curve. The usual projection parallel to a line is a particular case (the point in this case is a point at infinity).
The miraculous fact that the Weierstrass substitution always works, and turns any rational fraction in trigonometric functions into an integrable rational function in is a direct consequence of the fact that a circle is a curve of genus 0 (it has no “handles”), which also also means it has a rational parametrization. The Weierstrass substitution arises naturally from the stereographic projection of the unit circle from to the -axis. Let
be a point on the unit circle with center at the origin. The line connecting to intersects the -axis at a point . Elementary geometry (the triangle with vertices is isosceles) says the angle between this line and the -axis is . Stereographic projection of the circle from the point to the -axis is the function that maps to .
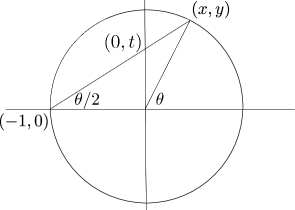
The slope of the line is . Plug into the equation , divide by , and solve for to obtain
| (4) |
a rational parametrization of the unit circle. Differentiating
and using one obtains
| hence | |||
These substitutions help convert any rational trigonometric differential , where is a quotient of polynomials (including ), to a rational differential that is sometimes easier to integrate.
We also note (see [18, p. 4]) that this rational parametrization of the circle also produces a recipe for constructing Pythagorean triples of integers such that (also see [6] for a biography of Pythagoras and [21, Theorem 6.3, p.162] for a purely algebraic description of all primitive — i.e. with no common factors — Pythagorean triples). Let where and are integers. Plug into the stereographic projection formula (4) to obtain satisfying then clear denominators to obtain where are integers. Conversely, given a Pythagorean triple one may reverse this process to find a rational that will produce or an integer multiple of it.
The modified Weierstrass substitution also uses a stereographic projection of the unit circle, but from the point to the -axis.
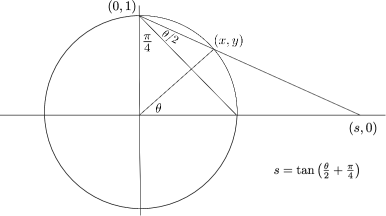
Let . The line through and intersects the -axis at , where . Its slope is so . Plug that into the equation , divide by , and solve for to obtain
another rational parametrization of the unit circle. As before, computing yields a formula for
These formulas make integrating
even simpler, without partial fractions. Finally, using ,
produces the formula that appears in the back of your textbook. This shows that the Gregory substitution is basically the same as the modified Weierstrass. Nevertheless, we give a separate geometric argument for the Gregory substitution:
The parametrization of the right branch of the hyperbola is . The line at infinity intersects the homogenized hyperbola at the two points at infinity and . The stereographic projection of the hyperbola from to the -axis (which is the projection down a line parallel to the asymptote ) sends the point on the hyperbola to the point , and we choose the parameter to be . Solving for the point where the line intersects the hyperbola, we obtain
This rational parametrization of the hyperbola does the job.
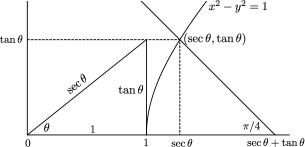
We have
so
and this provides another natural buildup to Gregory’s substitution.
Other rational parametrizations of the hyperbola also work. One possible parameter is in the point which is the stereographic projection from of the point on the hyperbola to the asymptote . Another is , which is the distance from to the origin. Both of these two parameters work just as well as the above, because , and . Other choices include the parameters we have used before: and , but these end up requiring partial fractions. The reader may wish to work out formulas for parametrizing the hyperbola with these parameters as an exercise.
We now see that all methods for integrating the secant function have something in common: they rely on certain rational parametrizations of the circle or the hyperbola. The figure below puts all these parametrizations together on the same picture. This shows how our previous three pictures are related.
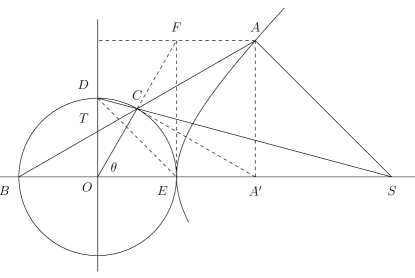
The relevant points are , , , , and the parameters are:
-
•
(Weierstrass)
- •
This picture is bursting with interesting geometry problems; see for example [11]. The most striking of these geometric facts is that the stereographic projection of the circle from the point to the -axis and the stereographic projection of the hyperbola from the point at infinity to the -axis (recall that the latter is the projection of the hyperbola to the -axis parallel to the asymptote ) turn out to be the same if we identify the circle and the hyperbola via corresponding points ( and ).
Acknowledgments
We thank Frank Miles for helpful comments.
References
-
[1]
Wikipedia, The integral of the secant function,
https://en.wikipedia.org/wiki/Integral_of_the_secant_function -
[2]
Wikipedia, Weierstrass substitution,
https://en.wikipedia.org/wiki/Weierstrass_substitution -
[3]
MacTutor, Isaac Barrow,
https://mathshistory.st-andrews.ac.uk/Biographies/Barrow/ -
[4]
MacTutor, James Gregory,
https://mathshistory.st-andrews.ac.uk/Biographies/Gregory/ -
[5]
MacTutor, Gerardus Mercator,
https://mathshistory.st-andrews.ac.uk/Biographies/Mercator_Gerardus/ -
[6]
MacTutor, Pythagoras of Samos,
https://mathshistory.st-andrews.ac.uk/Biographies/Pythagoras/ -
[7]
MacTutor, Karl Weierstrass,
https://mathshistory.st-andrews.ac.uk/Biographies/Weierstrass/ -
[8]
MIT OpenCourseWare, The integral of secant,
https://ocw.mit.edu/courses/mathematics/18-01sc-single-variable-calculus-fall-2010/unit-4-techniques-of-integration/part-a-trigonometric-powers-trigonometric-substitution-and-completing-the-square/session-71-integrals-involving-secant-cosecant-and-cotangent/MIT18_01SCF10_Ses71c.pdf - [9] Joel Feldman, Andrew Rechnitzer and Elyse Yeager, CLP-2 Integral Calculus, https://www.math.ubc.ca/~CLP/CLP2/clp_2_ic_text.pdf
- [10] Alexander Inglis, James Gregory: A survey of his work in mathematical analysis, University of St. Andrews (United Kingdom), ProQuest Dissertations Publishing, 1933. https://www-proquest-com.libproxy.csudh.edu/docview/1823909645?pq-origsite=primo
- [11] George Jennings, David Ni, Wai Yan Pong and Serban Raianu, Problem 1392, to appear in Pi Mu Epsilon J., fall 2022.
- [12] Warren P. Johnson, Down with Weierstrass, Amer. Math. Monthly, 127 (2020), 649–653.
-
[13]
Bill Kinney, Rational Function parameterization of the Unit Circle (the unit circle minus one point), YouTube channel “Bill Kinney Math”,
https://www.youtube.com/watch?v=iICpdqNny5g - [14] Michael Hardy, Efficiency in Antidifferentiation of the Secant Function, Amer. Math. Monthly, 120 (2013), page 580.
- [15] V. Frederick Rickey and Philip M. Tuchinsky, An Application of Geography to Mathematics: History of the Integral of the Secant, Mathematics Magazine, 53 (1980), 162–166. https://www.jstor.org/stable/2690106
- [16] Maxwell Rosenlicht, Integration in Finite Terms, Amer. Math. Monthly, 79 (1972), 963–972. https://www.jstor.org/stable/2318066?seq=1
- [17] Norman Schaumberger, , Amer.Math.Monthly, 68 (1961), 565.
- [18] Joseph H. Silverman, John T. Tate, Rational points on elliptic curves, Second edition, Undergraduate Texts in Mathematics, Springer, 2015.
- [19] James Stewart, Essential Calculus, Brooks-Cole, 2013.
- [20] Simon W. Strauss, The Integrals and Revisited, J. Wash. Acad. Sci., 70 (1980, 137–143.
- [21] James K. Strayer, Elementary Number Theory, Waveland Press, Inc., 1994.
- [22] Herbert W. Turnbull, The Exercitationes Geometricae, in James Gregory Tercentenary Memorial Volume, edited by H.W. Turnbull, 459–465, G. Bell and Sons LTD, London, 1939.