The Interior Volume of Kerr-AdS Black Holes
Abstract
The interior volume of black holes as defined by Christodoulou and Rovelli exhibits many surprising features. For example, it increases with time, even under Hawking evaporation. For some black holes, the interior volume is not even a monotonic increasing function of its area, which means one cannot infer how large a black hole is by just looking from the outside. Such a notion of volume, however, turns out to be useful in the context of holography, as it seems to be dual to the complexity of the boundary field theory. In this study, we investigate the properties of the interior volume of 4-dimensional Kerr-AdS black holes, fixing either the mass parameter or the physical mass , whilst varying the values of the cosmological constant. We found that the volume as a function of the radial coordinate features a “double lobe” while fixing , whereas fixing yields behaviors that are qualitatively similar to the asymptotically flat case. We briefly comment on the holographic complexity of Kerr-AdS black holes.
I Introduction: Black Hole Interior Volume
Black holes are remarkable objects that continue to surprise us even after a century of general relativity. The defining feature of a black hole is that nothing that enters its event horizon can escape from its interior. Therefore an exterior observer remains ignorant about just how the interior spacetime looks like. In particular, how big is a black hole from the inside? Take a spherical surface of area in Euclidean space , it bounds a space of volume . However, this is not the case for black holes, which, after all, has nontrivial spacetime curvature, which allows a fixed area to bound a larger than expected volume. Indeed, the first challenge is to define just what we mean by (spatial) “volume” (see 0801.1734 for some options). Unlike the event horizon, which is uniquely defined in Lorentzian geometry, there is a plethora of ways to define volume of a black hole. In this work our suject of study is the Christodoulou-Rovelli volume Christodoulou:2014yia . Hereinafter, by volume, we always mean the Christodoulou-Rovelli volume.
The idea of Christodoulou and Rovelli is to look for the volume of the largest spacelike spherically symmetric surface bounded by the event horizon of the black hole, which is a geometrical property that is coordinate independent. For a 4-dimensional asymptotically flat Schwarzschild black hole, the volume is
| (1) |
in which is the usual advanced time in the Eddington–Finkelstein coordinates. (Note that is a spacelike direction while is a timelike one inside the black hole.) The lower limit of the integral is ignored because it only gives sub-leading, negligible, contribution to the total volume at late time. The function is maximized at , which gives, when is large,
| (2) |
We see that the interior volume grows linearly in time . This result is entirely classical and is in no way controversial. If we accept that black holes are solutions to the Einstein field equations, then we should accept that the volume defined in this manner inside a black hole continues to grow linearly with time, although its area stays fixed (the volume continues to increase even if the area is decreasing under Hawking evaporation 1503.08245 ; 1604.07222 ). This is not so surprising if we recall that the interior spacetime of a static solution like Schwarzschild is nevertheless not static.
Assuming the Schwarzschild geometry, Christodoulou and Rovelli estimated that Sagittarius , the supermassive black hole at the center of our Milky Way, contains enough volume to fit a million solar systems. Its areal radius, on the other hand, is only about 10 times larger than the Earth-Moon distance Christodoulou:2014yia . Generalization of the Christodoulou-Rovelli volume to the case of asymptotically flat Kerr black hole does not change this result by much Bengtsson:2015zda , despite the rotation rate of Sagittarius is about of the extremal limit.
Generalizations to topological black holes in locally asymptotically anti-de Sitter (AdS) spacetimes further reveal surprising features of the interior volume: for some black holes, the volume is not a monotonic function of the area, which means that one cannot judge from the outside how large the volume is even if the time is known 1503.01092 . In fact, the AdS generalizations are important, for there is evidence that the interior volume is holographically dual to the (quantum) complexity of the boundary field theory in the context of gauge/gravity correspondence 1402.5674 ; 1403.5695 ; 1406.2678 ; 1411.0690 ; 1509.06614 , which also grows linearly in time (Christodoulou-Rovelli volume can be defined for maximally extended “two-sided” black holes as well) at least for a time proportional to the exponential of the black hole entropy 1507.02287 . This is now referred to as the “Complexity-Volume” (CV) Conjecture. Another proposal is that complexity is dual to the action of a certain spacetime region referred to as the “Wheeler-DeWitt patch”; this is known as the “Complexity-Action” (CA) Conjecture 1509.07876 ; 1512.04993 . Subsequently, many properties of both interior volumes and Wheeler-DeWitt action had been studied, the similarities and differences between CV and CA Conjectures investigated (see, e.g., 1606.08307 ; 1612.00433 ; 1709.10184 ; 1712.09706v2 ; Couch:2018phr ; Yang:2019alh ; 1804.01561 ; 1811.10650 ; 1902.02475 ).
In this work, we study the interior volume of 4-dimensional Kerr-AdS black holes. We shall fix the mass of the black hole (either the physical mass or the “geometric mass parameter” – see next section). In view of the recent interests in “black hole chemistry” 1608.06147 – in which the negative cosmological constant in AdS bulk is treated as thermodynamical pressure 0904.2765 ; 1106.6260 ; 1209.1272 , and holographically dual to the number of colors () of the boundary field theory via the relation 1409.3575 – we consider the effect of varying cosmological constant on the geometry of the interior volume. We find that fixing the physical mass gives rise to a “double lobe” feature in the plot of the volume as function of coordinate radius, which is absent if we fix instead the geometric mass. Our work is purely focusing on the black hole properties, though we hope that our study might be helpful for holography in the future. We will work in the Planck units so that . In the appendix, we attach two plots of the interior volume of Kerr–AdS black hole with mass and the physical mass in the unit of .
II Some Properties of Kerr–AdS Black Hole
The metric of Kerr–AdS black hole in Boyer–Lindquist coordinates in 4-dimensions is given by McInnes:2015vga
| (3) |
where
| (4) |
The cosmological constant is related to , the asymptotic curvature radius of anti–de–Sitter spacetime in 4-dimensions, via . Note that the metric has in the denominator, which puts a bound on the rotation parameter: . This bound is distinct from the cosmic censorship bound. See 1108.6234 for more discussions111The case for AdS-Kerr black hole in 5-dimensions is discussed in 1906.01169 ; 1911.08222 . Since the geometry for is quite different from the case (for example, there are closed causal curves for sufficiently small ), and furthermore starting with , one cannot cross the divide to reach branch of the solution, we shall restrict our investigation to the case..
Note that the parameter is not the physical mass of Kerr–AdS. The physical mass of Kerr–AdS is related to by 0408217
| (5) |
The physical mass, also known as the Abbott-Deser mass AD , is the conserved quantity that corresponds to the timelike Killing vector of the geometry. Naturally it plays crucial roles in physical processes. Crucially, it is this mass that enters the second law of thermodynamics of black holes; working with instead of might give misleading results that the second law could be violated under physical processes McInnes:2015vga .
On the other hand, the mass parameter is not without advantages. It is a “geometric parameter” that gives better intuiton regarding the underlying spacetime geometry of the black hole. To illustrate this, an example was given in McInnes:2015vga : Consider an AdS-Kerr black hole with a very large physical mass, say (in the units such that ), and large angular momentum such that . The black hole horizon is located at . One might expect that such a large mass concentrated at such a small value of the radial coordinate would distort the geometry by a large amount. However it turns out that the Gaussian curvature of the horizon is only of order unity (as function of , it ranges between and ). However, the mass parameter is only in this example. Thus can give a better indication of the geometry than the physical mass (although we are not being very precise here). In other words, depending on one’s purpose, and can both be useful parameters.
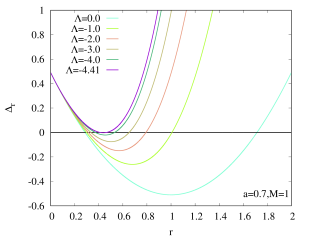
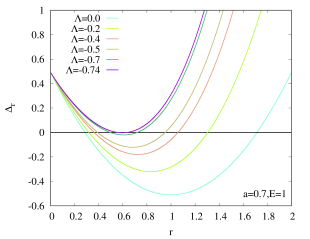
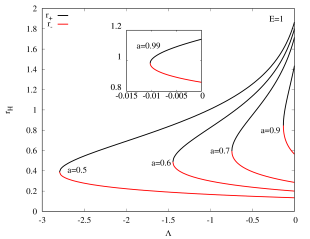
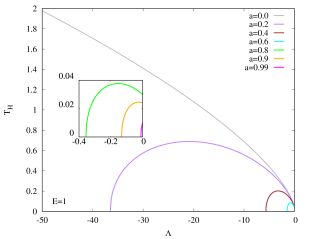
The horizons of Kerr–AdS black holes can be obtained by solving . Since the function is a fourth order polynomial, it has either 4 real roots or 2 real roots in principle. Here we exhibit the behaviour of in Fig. 1 with by fixing and , respectively. The values are chosen for simplicity only. Indeed, the qualitative features of our results remain the same if we change the values of or .
When , the function only has 2 real roots (in fact this is true for all Kerr-AdS black holes). The largest root represents the outer horizon, while the smallest root represents the inner (Cauchy) horizon, . Of course, if we fixed instead, the Kerr–AdS black hole also has outer and inner horizons, which is similar to the case with . When , the Kerr–AdS black hole reduces to Schwarzschild–AdS black hole which only has a single horizon. Furthermore, Kerr–AdS black hole also possesses a coordinate singularity on the rotation axis which is determined from the condition .
(a)
 (b)
(b)
The extremality of Kerr–AdS black hole can be determined by the condition Agnese:1999df
| (6) |
When the above condition is satisfied, the outer and inner horizons of Kerr–AdS black hole coincide, and its Hawking temperature vanishes.
II.1 The Domain of Existence
Kerr–AdS black holes are determined by 3 parameters, namely the cosmological constant , the rotation parameter and the mass parameter (either or ). For convenience, we fix the mass of black hole by setting either or 222Equation (6) and the volume (15) have the following scaling symmetry: , , and . Since , we see that can be scaled as . In our case, we fix the value of and scale the remaining parameters by , thus the parameters , and are in the unit of mass. Furthemore, if we fix the mass and scale the ramaining parameters by , then , and are in the unit of .
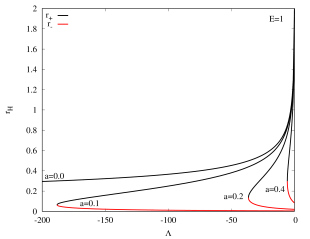
We then study the domain of existence for Kerr–AdS black holes by fixing the value of and varying to calculate the outer and inner horizon of Kerr–AdS black hole. We exhibit the domain of existence of Kerr–AdS black hole for in Figure 2 and for in Figure 3.
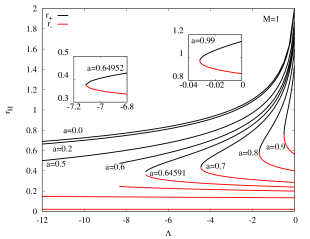
In Figure 2, the outer horizon attains its maximum value when , i.e., when the black hole is the static AdS-Schwarzschild black hole. When we decrease from zero with stays fixed, the coordinate value of the outer horizon decreases but the inner horizon increases, and at the end both horizons meet, and the black hole becomes extremal. We also observe that all else being equal, Kerr-AdS black holes become extremal at smaller value of for larger value of the rotation parameter . Note that the bound translates to . That is, with large, the allowed values of becomes smaller. This explains the gap in the plot between the outer and inner horizons. Indeed, for fixed , the curve will be gapless for any . (This value of course changes if .)
In Figure 3, analogous to the case , the Kerr–AdS black holes with also show the same qualitative behaviour, that is the outer horizon increases but the inner horizon decreases, and then both horizons meet to form extremal black hole. Again, the black holes attain extremality at smaller value of for larger value of . However, it turns out the curves are always gapless. We emphasize that the properties discussed in this subsection hold also for other values of and .
(a)
 (b)
(b)
II.2 Thermodynamical Properties
Although our result is classical, for the sake of completeness we shall give a short summary of the entropy and temperature of AdS-Kerr black holes. The Bekenstein-Hawking entropy of a Kerr–AdS black hole is given by the usual formula
| (7) |
in which is the area of the event horizon, given by McInnes:2015vga
| (8) |
The Hawking temperature is given by
| (9) |
Figures 4 (a) and (b) show that the area of horizon decreases when decreases from 0 downwards, at least initially. The area of horizon for Kerr–AdS black holes with steadily decreases to a minimum value for . However, turns around and eventually diverges for when the black holes approaches the bound . This turn-over behavior is not present in the case , the area of the black hole simply decreases to a minimal value when decreases. Eventually the black hole becomes extremal.
Figures 4 (c) and 4 (d) show that as decreases, the Hawking temperature of Kerr–AdS black holes with increases to a maximum value, and then decreases to zero, corresponding to an extremal black hole state. Note that the maximum of shifts to a larger value of (i.e. smaller ) when increases. The Kerr–AdS black holes with also exhibit the similar qualitative behaviour for the Hawking temperature, although for the extremal state is never reached.
(a) 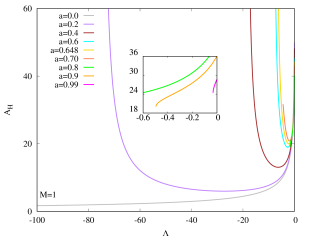 (b)
(b) 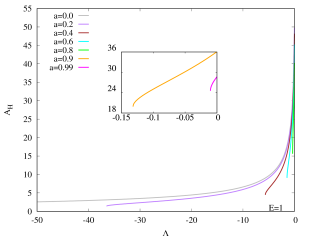 (c)
(c)
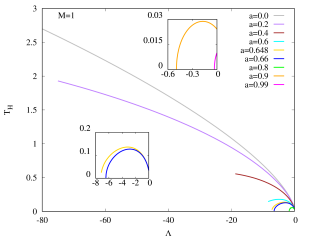 (d)
(d)
III Interior Volume of AdS-Kerr Black Holes
Here, we follow the approach of Bengtsson:2015zda to calculate the interior volume of Kerr–AdS black holes. In order to calculate the interior volume of Kerr–AdS, we first transform the Boyer–Lindquist coordinates into the Eddington–Finkelstein coordinates by introducing the following coordinate transformation:
| (10) |
where and are arbitrary real–valued functions. We can obtain the expressions of and by substituting the differential
| (11) |
into the metric of Kerr–AdS in Boyer–Lindquist form, with the condition that and being imposed. This yields the following expressions for and :
| (12) |
Therefore, the metric of Kerr–AdS spacetime in Eddington–Finkelstein coordinates is
| (13) |
The interior volume with constant hypersurface for Kerr–AdS black hole can now be calculated as follows333Although this is a direct generalization of the Christodoulou-Rovelli volume to the rotating case, as emphasized in Bengtsson:2015zda there is a difference. In fact, the hypersurface that maximizes the volume of an asymptotically flat Schwarzschild black hole has a special property: it is the solution of the polynomial obtained by setting the trace of the second fundamental form to zero bruce . For asymptotically flat Kerr black hole, the vanishing trace condition yields , which is a polynomial in of degree 7. There does not exist such that vanishes. So in this sense, what we computed here is not strictly the maximal volume, though it is arguably close to one Bengtsson:2015zda . Again, defining volume is a tricky business in general, see 1703.02396 for a recent rigorous attempt.:
| (14) | ||||
| (15) |
Henceforth we ignore , since only governs the linear growth of the volume. We are interested in the coefficient, which are nontrivial.
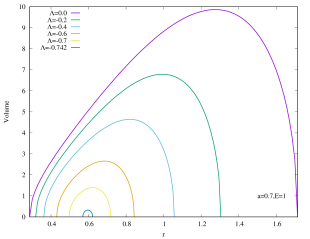
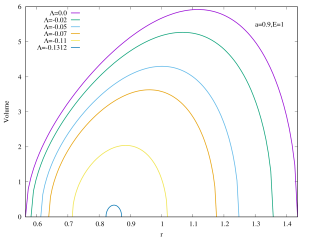
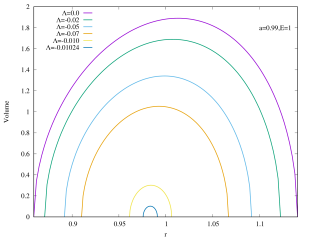
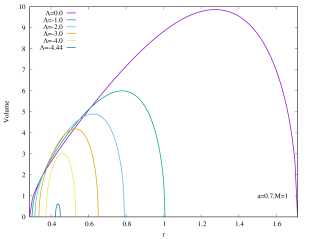
This is not yet the Christodoulou-Rovelli volume since that requires maximizing the expression. This is neither analytically realistic nor illuminating, therefore we shall follow the approach of Bengtsson:2015zda and plot Eq.(15), its peak then corresponds to the Christodoulou-Rovelli volume. The volume of Kerr–AdS black hole is shown in Figure 5 for several values of with . For all values of , we can see that asymptotically flat Kerr black hole () has the largest volume. The volume starts to shrink when decreases for fixed , and eventually becomes zero when the black holes become extremal444This does not mean that extremal black holes have zero volume. The reason for non-extremal black hole to have large growing volume is because coordinate becomes timelike direction inside the black hole. For extremal black holes this does not happen, and so the volume is the “usual” volume, much like a sphere in Euclidean space.. The peak of the volume tends to smaller values of the radial coordinate when decreases for fixed . In addition, the curves do not intersect. If , then the curve for encloses that of .
(a) 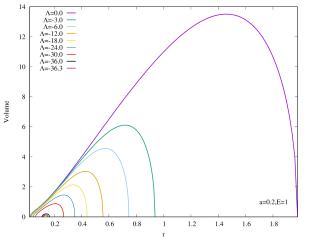 (b)
(b) 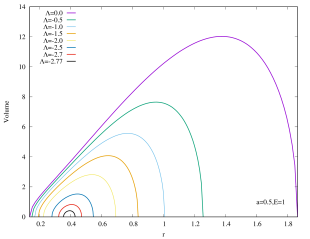 (c)
(c)
 (d)
(d)
 (e)
(e)
(a) 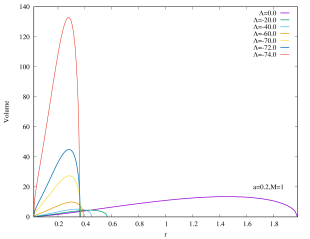 (b)
(b) 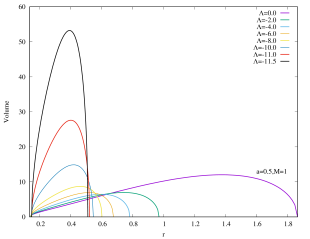 (c)
(c)
 (d)
(d)
 (e)
(e)
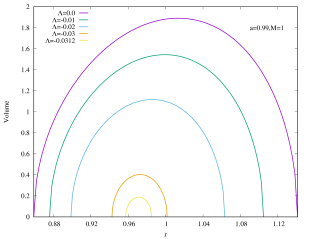
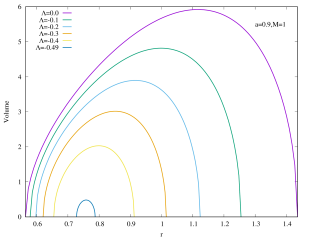
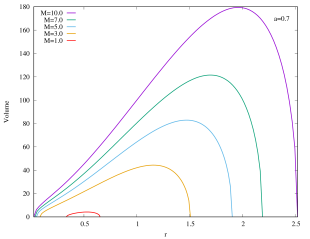
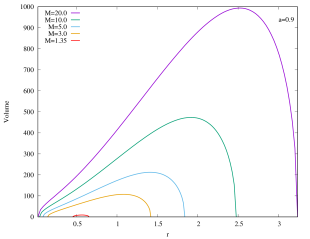
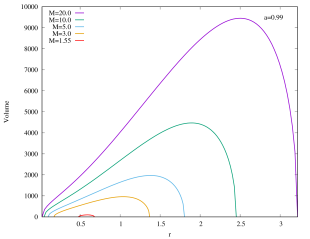
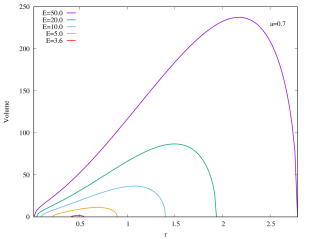
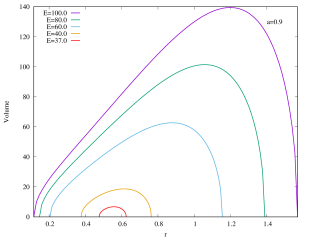
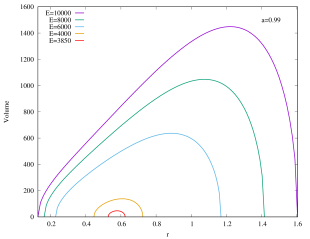
As shown in Figure 6, the rapidly rotating Kerr–AdS black holes with exhibit similar qualitative behavior for the interior volume as the case of if is large. However, for the slowly rotating () Kerr–AdS black holes, the interior volume exhibits some interesting features as is varied. The curves form a “double lobe” structure: starting with and decreasing , the curve moves towards smaller value of , shortening in length, and subsequently start to grow in height as it enters the other lobe. For example, for , the transition happens at around . This feature is due to the gap between and for sufficiently slow rotating fixed black holes. The curves in the case of also typically intersect each other except for large values of . The interior volume diverges when approaches the bound .
We can also express the interior volume of Kerr–AdS black hole in the unit of 555See footnote 2.. As shown in the Appendices, the interior volume only exhibit a single lobe structure. For a fixed , the extremal Kerr–AdS black hole possesses the lowest mass (and also the physical mass ) and has almost zero gap between outer and inner horizons, thus they have the smallest interior volume. As (as well as ) increases, the interior volume of Kerr–AdS also increases, since the gap increase. Note that the gap always closes.
Another method to approximate the peak of the volume function can be found in Couch:2018phr , in which the authors compute the maximum of the integral, , for arbitrary angle via (their case is for asymptotically flat Kerr, so )
| (16) |
The hypersurface obtained in this manner has special mathematical property: it is in some sense a maximal slice with minimal distortion. The details are described in duncan . From Figure 7, we see that the peak of the interior volume obtained by this approach is very close to the one obtained by the first method regardless of the value of : the relative error is less than percent for the case .
IV Holographic Complexity
As we have briefly mentioned in Sec.1, the notion of interior volume is not only interesting for its own sake, but also has applications in the holographic setting, specifically in the so-called “complexity-volume” conjecture: namely that interior volume is dual to the quantum complexity of the dual field system. It has been argued that there are some ambiguities regarding how this duality is supposed to be defined, since for large black holes (i.e. large compared to the AdS curvature radius ), complexity seems to behave as
| (17) |
However, for small black holes with horizon , complexity goes like
| (18) |
Such a seemingly ad hoc rule is one of the reasons why, subsequently, the “complexity-action” conjecture was proposed, in which “action” refers to the Hilbert-Einstein action restricted to a certain “Wheeler-DeWitt patch”. However, as pointed out in Couch:2018phr , the two seemingly different relations above can be understood rather naturally simply as
| (19) |
where is the maximal time to fall from the horizon to the (final) maximal slice. Indeed, the infalling time scales like for large black holes but scales like for small black holes. Specifically, the infalling time is Couch:2018phr , with , given by
| (20) |
We will assume that the maximum value is evaluated at , with the volume formula given by Eq.(16).
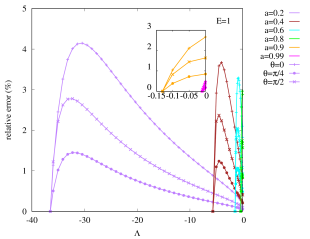
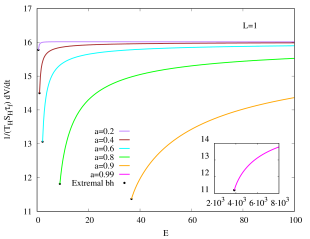
As we can see in Fig.(8), the quantity
| (21) |
for any fixed angular momentum parameter does not vary too much as the physical mass is varied. Alternatively, for a fixed , increasing would lower the value of but the value is of the same order of magnitude. This behavior is similar to the asymptotically flat case discussed in Couch:2018phr . See Fig.(11) therein. That is, the growth rate of the black hole volume scales approximately as . So this matches the complexity growth rate of the entropy 1402.5674 if one identifies complexity with .
V Conclusion
Rotating black holes in anti-de Sitter spacetimes play important roles in holography (see, e.g. 1305.3267 ; 1803.02528 ). Motivated by the complexity-volume conjecture in holography, as well as the recent interests in black hole chemistry, which treats the cosmological constant as a thermodynamic pressure that is dual to the number of colors in the boundary field theory, we take a closer look at the interior volume of Kerr-AdS black holes and the effect of varying the cosmological constant on the volume (though the actual implications for holography is beyond the scope of the current work).
While varying the cosmological constant, we have either fixed the physical mass to or the “geometric mass” to for simplicity and convenience. Our results remain qualitatively similar for other fixed values of and . The physical mass is the mass that enters the laws of thermodynamics, while the “geometric mass” gives a better measure for the underlying spacetime geometry. That is, they are good for different purposes. We found that setting fixed gives qualitatively the same features for the interior volume, compared to the asymptotically flat case. The curves become more symmetric as the rotation parameter increases. Setting fixed, however, gives rise to a “double lobe” feature in the plot of volume as function of the coordinate radius . Recall that the peak of any given curve in the plot corresponds to the Christodoulou-Rovelli volume, the physical interpretation is that the volume decreases monotonically as we decreases while holding fixed. On the other hand, holding fixed allows the volume to first decrease and then increase as is decreased, provided the rotation parameter is sufficiently small.
Using the notion of volume discussed in this work, we also evaluated the holographic complexity according to the “complexity-volume” conjecture as interpreted in Couch:2018phr . The result is that the growth rate of volume is indeed proportional to , where is the infalling time from the event horizon to the “final” maximal volume hypersurface. This agrees with the expectation that the complexity in the dual field theory should go like if volume is indeed holographically dual to quantum complexity via .
Acknowledgement
XYC would like to thank the hospitaltiy of Center for Gravitation and Cosmology of Yangzhou University during his visit to attend COSPA 2018. XYC would also like to thank Dong-han Yeom for helping him adapting to life in Busan. He thanks the National Research Foundation of Korea (grant no. 2018R1D1A1B07049126) for funding. YCO thanks the National Natural Science Foundation of China (No.11705162, No.11922508) and the Natural Science Foundation of Jiangsu Province (No.BK20170479) for funding support. He also thanks Ingemar Bengtsson for related discussions.
Appendix A Interior of Kerr–AdS with (in the unit of )
(a) 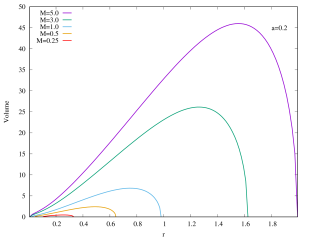 (b)
(b) 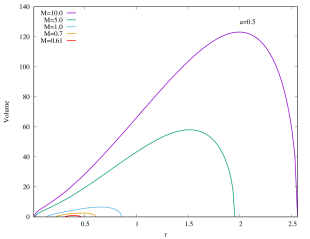 (c)
(c)
 (d)
(d)
 (e)
(e)
Appendix B Interior of Kerr–AdS with (in the unit of )
(a) 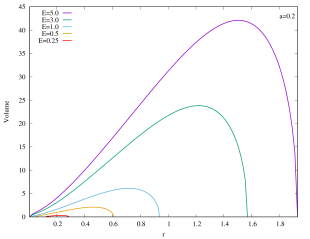 (b)
(b) 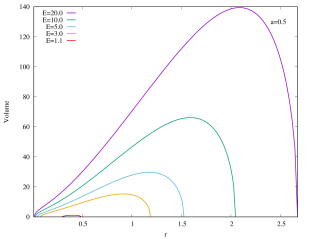 (c)
(c)
 (d)
(d)
 (e)
(e)
References
- (1) Brandon S. DiNunno, Richard A. Matzner, “The Volume Inside a Black Hole”, Gen. Rel. Grav. 42 (2010) 63, [arXiv:0801.1734 [gr-qc]].
- (2) Marios Christodoulou, Carlo Rovelli, “How Big Is a Black Hole?”, Phys. Rev. D 91 (2015) 064046, [arXiv:1411.2854 [gr-qc]].
- (3) Yen Chin Ong, “The Persistence of the Large Volumes in Black Holes”, Gen. Relativ. Gravit. 47 (2015) 88, [arXiv:1503.08245 [gr-qc]].
- (4) Marios Christodoulou, Tommaso De Lorenzo, “On the Volume Inside Old Black Holes”, Phys. Rev. D 94 (2016) 104002, [arXiv:1604.07222 [gr-qc]].
- (5) Ingemar Bengtsson, Emma Jakobsson, “Black Holes: Their Large Interiors”, Mod. Phys. Lett. A 30 (2015) 1550103, [arXiv:1502.01907 [gr-qc]].
- (6) Yen Chin Ong, “Never Judge a Black Hole by Its Area”, JCAP 04 (2015) 003, [arXiv:1503.01092 [gr-qc]].
- (7) Leonard Susskind, “Computational Complexity and Black Hole Horizons”, [arXiv:1402.5674 [hep-th]].
- (8) Leonard Susskind, “Addendum to Computational Complexity and Black Hole Horizons”, [arXiv:1403.5695 [hep-th]].
- (9) Douglas Stanford, Leonard Susskind, “Complexity and Shock Wave Geometries”, Phys. Rev. D 90 (2014) 126007, [arXiv:1406.2678 [hep-th]].
- (10) Leonard Susskind, “Entanglement Is Not Enough”, [arXiv:1411.0690 [hep-th]].
- (11) Mohsen Alishahiha, “Holographic Complexity”, Phys. Rev. D 92 (2015) 126009, [arXiv:1509.06614 [hep-th]].
- (12) Leonard Susskind, “The Typical-State Paradox: Diagnosing Horizons with Complexity”, Fortsch. Phys. 64 (2016) 84, [arXiv:1507.02287 [hep-th]].
- (13) Adam R. Brown, Daniel A. Roberts, Leonard Susskind, Brian Swingle, Ying Zhao, “Holographic Complexity Equals Bulk Action?”, Phys. Rev. Lett. 116 (2016) 191301, [arXiv:1509.07876 [hep-th]].
- (14) Adam R. Brown, Daniel A. Roberts, Leonard Susskind, Brian Swingle, Ying Zhao, “Complexity, Action, and Black Holes”, Phys. Rev. D 93 (2016) 086006, [arXiv:1512.04993 [hep-th]].
- (15) Rong-Gen Cai, Shan-Ming Ruan, Shao-Jiang Wang, Run-Qiu Yang, Rong-Hui Peng, “Complexity Growth for AdS Black Holes”, JHEP 09 (2016) 161, [arXiv:1606.08307 [gr-qc]].
- (16) Dean Carmi, Robert C. Myers, Pratik Rath, “Comments on Holographic Complexity”, JHEP 03 (2017) 118, [arXiv:1612.00433 [hep-th]].
- (17) Dean Carmi, Shira Chapman, Hugo Marrochio, Robert C. Myers, Sotaro Sugishita, “On the Time Dependence of Holographic Complexity”, JHEP 11 (2017) 188, [arXiv:1709.10184 [hep-th]].
- (18) Tamás S. Biró, Viktor G. Czinner, Hideo Iguchi, Péter Ván, “Black Hole Horizons Can Hide Positive Heat Capacity”, Phys. Lett. B 782 (2018) 228, [arXiv:1712.09706 [gr-qc]].
- (19) Josiah Couch, Stefan Eccles, Ted Jacobson, Phuc Nguyen, “Holographic Complexity and Volume”, JHEP 11 (2018) 044, [arXiv:1807.02186 [hep-th]].
- (20) Runqiu Yang, “Upper Bound About Cross-Sections Inside Black Holes and Complexity Growth Rate”, [arXiv:1911.12561 [hep-th]].
- (21) Cesar A. Aón, Matthew Headrick, Brian Swingle, “Subsystem Complexity and Holography”, JHEP 02 (2019) 145, [arXiv:1804.01561 [hep-th]].
- (22) Elena Cáceres, Josiah Couch, Stefan Eccles, Willy Fischler, “Holographic Purification Complexity”, Phys. Rev. D 99 (2019) 086016, [arXiv:1811.10650 [hep-th]].
- (23) Mahdis Ghodrati, Xiao-Mei Kuang, Bin Wang, Cheng-Yong Zhang, Yu-Ting Zhou, “The Connection Between Holographic Entanglement and Complexity of Purification”, JHEP 09 (2019) 009, [arXiv:1902.02475 [hep-th]].
- (24) David Kubiznak, Robert B. Mann, Mae Teo, “Black Hole Chemistry: Thermodynamics with Lambda”, Class. Quantum Grav. 34 (2017) 063001, [arXiv:1608.06147 [hep-th]].
- (25) David Kastor, Sourya Ray, Jennie Traschen, “Enthalpy and the Mechanics of AdS Black Holes”, Class. Quant. Grav. 26 (2009) 195011, [arXiv:0904.2765 [hep-th]].
- (26) Brian P. Dolan, “Pressure and Volume in the First Law of Black Hole Thermodynamics”, Class. Quantum Grav. 28 (2011) 235017, [arXiv:1106.6260 [gr-qc]].
- (27) Brian P. Dolan, “Where is the PdV Term in the First Law of Black Hole Thermodynamics?”, [arXiv:1209.1272 [gr-qc]].
- (28) Makoto Natsuume, “AdS/CFT Duality User Guide”, Lect. Notes Phys. 903 (2015) 1, [arXiv:1409.3575 [hep-th]].
- (29) Brett McInnes, Yen Chin Ong, “A Note on Physical Mass and the Thermodynamics of AdS-Kerr Black Holes”, JCAP 11 (2015) 004, [arXiv:1506.01248 [gr-qc]].
- (30) Brett McInnes, “Kerr Black Holes Are Not Fragile”, Nucl. Phys. B 857 (2012) 362, [arXiv:1108.6234 [hep-th]].
- (31) Brett McInnes, “Cosmic Censorship for -Kerr”, Nucl. Phys. B 950 (2020) 114845, [arXiv:1906.01169 [hep-th]].
- (32) Brett McInnes, “Cosmic Censorship and Holography”, [arXiv:1911.08222 [hep-th]].
- (33) Gary W. Gibbons, Malcolm J. Perry, Christopher N. Pope, “The First Law of Thermodynamics for Kerr-Anti-de Sitter Black Holes”, Class. Quant. Grav. 22 (2005) 1503, [arXiv:hep-th/0408217].
- (34) Larry F. Abbott, Stanley Deser, “Stability of Gravity with a Cosmological Constant”, Nucl. Phys. B 195 (1982) 76.
- (35) A. G. Agnese, Mario La Camera, “Kerr–AdS and Kerr–dS Solutions Revisited”, Phys. Rev. D 61 (2000) 087502, [arXiv:gr-qc/9907030].
- (36) Bruce L. Reinhart, “Maximal Foliations of Extended Schwarzschild Space”, Jour. Math. Phys. 14 (1973) 719.
- (37) Pawel Gusin, Andrzej Radosz, “The Volume of the Black Holes - The Constant Curvature Slicing of the Spherically Symmetric Spacetime”, Mod. Phys. Lett. A 32 (2017) 1750115, [arXiv:1703.02396 [gr-qc]].
- (38) Martin J. Duncan, “Maximally Slicing a Black Hole With Minimal Distortion”, Phys. Rev. D 31 (1985) 1267.
- (39) Irina Aref’eva, Andrey Bagrov, Alexey S. Koshelev, “Holographic Thermalization from Kerr-AdS”, JHEP 07 (2013) 170, [arXiv:1305.3267 [hep-th]].
- (40) Brett McInnes, “Applied Holography of the -Kerr Spacetime”, Int. J. Mod. Phys. A 34 (2019) 1950138, [arXiv:1803.02528 [hep-ph]].