The intrinsic core and minimal faces of convex sets in general vector spaces
Abstract
Intrinsic core generalises the finite-dimensional notion of the relative interior to arbitrary (real) vector spaces. Our main goal is to provide a self-contained overview of the key results pertaining to the intrinsic core and to elucidate the relations between intrinsic core and facial structure of convex sets in this general context.
We gather several equivalent definitions of the intrinsic core, cover much of the folklore, review relevant recent results and present examples illustrating some of the phenomena specific to the facial structure of infinite-dimensional sets.
Keywords: intrinsic core, pseudo-relative interior, inner points, convex sets, general vector spaces, minimal faces
MSC2020 Classification: 46N10, 52-02, 52A05.
1 Introduction
The relative interior of a convex set in a finite-dimensional real vector space is the interior of this convex set relative to its affine hull; a direct generalisation of this notion to real vector spaces is the intrinsic core, introduced in [kleepart1] and developed in [Holmes] (also called pseudo-relative interior [BorweinGoebel]and , the set of inner points [RelintInnerPoints] and the set of weak internal points [DYE1992983]).
In contrast to the relative interior in finite dimensions, intrinsic core may be empty for fairly regular sets, which was a key motivation for introducing the notion of quasi-relative interior [BorweinLewisPartiallyFinite] in the context of topological vector spaces. Even though the quasi-relative interior is a very interesting mathematical object (for instance, [ZalinescuThreePb, ZalinescuOnTheUse] study duality and separation in the context of quasi-relative interior and resolve a number of open questions), and has much practical importance(e.g. see [WeakEfficiency, SetValuedSystems, InfDim, RemarksInf, Lagrange, Regularity, Subconvex, EfficientCoderivatives, MR3297972, MR3735852]), we find that limiting our study to the interplay between the intrinsic core and facial structure already offers rich material and provides a valuable perspective on the structure of convex sets in general vector spaces. Such a narrowly focused overview is long overdue: the well-known results and examples discussed here are scattered in the literature, and it may be difficult to find neat references for widely known statements. Besides, we were able to prove some new results provide some new insights and discuss several examples of interesting infinite-dimensional convex sets from the perspective of facial structure (for instance, see Example 2.7, where we construct uncountable chains of faces of the Hilbert cube).
Our take on this topic is consistent with the approach of several recent papers that focus on the intrinsic core. For instance, [UnitBall, InnerStructure, MinExp] study the facial structure of convex sets in linear vector spaces with relation to the intrinsic core, [cones] is specifically focused on the intrinsic core of convex cones, and [DangEtAl] reviews the basic properties of a (less general) notion of the algebraic core, with an emphasis on separation. Notably [cones] and [DangEtAl] do not mention the facial structure that is central to our exposition.
We begin with a discussion on faces of convex sets in Section 2, obtaining a new characterisation of minimal faces in terms of the lineality subspace of the cone of feasible directions (Proposition 2.4), leading to a (known) characterisation of a face as an intersection of line segments (Corollary 2.6). We then talk about chains of faces and present an example of a convex set with uncountable chains of faces (Example 2.7).
In Section 3 we discuss several equivalent definitions of intrinsic core, and focus on characterising the intrinsic core in terms of minimal faces: specifically, in Proposition 3.11 we show that the intrinsic core of a convex set coincides with the set of points for which the minimal face of these points is the entire set , using Proposition 2.4. We also provide an extensive list of properties of the intrinsic core, with self-contained proofs and references. We end the section with the decomposition result (a convex set is a disjoint union of the intrinsic cores of its faces, Theorem 3.14)and a conjecture that every face of a convex set must be the union of a chain of minimal faces (Conjecture LABEL:conj:russian-doll).Intuitively this means that faces of convex sets are always ‘nested’, and never ‘stacked’. .
In Section 4 we discuss the notion of algebraic closure and algebraic boundary , notions of linear closure and boundary and relate these to the intrinsic core and faces of convex sets. We also talk about separation and supporting hyperplanes in general real vector spaces, outlining classic separation results pertaining to the setting of general vector spaces, and highlighting the role of intrinsic core in convex separation.We then provide a brief summary in Section 5.
2 Convex sets and their faces
Recall that a subset of a real vector space is convex if for any two points we have , where is the line segment connecting the points and ,
We will also use the notation to denote the open line segments connecting and , also and for the relevant half-open segments. Note that algebraically it makes perfect sense to consider degenerate line segments of the form , since in this case
Even though this notation may appear confusing geometrically, it allows to treat the endpoints of all line segments including the degenerate singleton ones in a unified fashion, and hence streamline much of our discussion.
Throughout the paper we assume that is a real vector space, and that all the sets we consider live in this space (unless stated otherwise). We reiterate this assumption in some of the statements for the ease of reference.
A convex subset of a convex set is called a face of if for every and every such that , we have . The set itself is its own face, and the empty set is a face of any convex set . A face of is proper if is nonempty and does not coincide with . We write for the faces that do not coincide with and for all faces of . Singleton faces Faces that consist of one point only are called extreme points. Some faces of two-dimensional convex sets are shown schematically in Figure 1.

The following two statements are well-known and follow from the definition of a face.
Lemma 2.1.
Let be a convex subset of a real vector space . If and , then if and only if .
Proof.
Suppose that is a convex set, and . By the definition of a face, is equivalent to having for any with that . However since is a face of , and , any such pair must also be in (and vice versa, as ). Hence, is equivalent to . ∎
Lemma 2.2.
Let be a collection of faces of a convex set , that is, every member of the set is a face of . Then
is also a face of .
Proof.
First notice that is a convex subset of . Now, if for some the open line segment intersects , then it intersects each , and hence , so is a face of by definition. ∎
2.1 Minimal faces
For any subset of a convex set there exists a unique minimal (in terms of the set inclusion) face that contains . We can define minimal faces of a set in a constructive way, with the help of Lemma 2.2.
Let , where is a convex subset of a real vector space . The minimal face of containing or just the minimal face of in , is
The set is a face due to Lemma 2.2, and it is the minimal smaller face (with respect to set inclusion) that contains . When is a singleton we use the notation .
By we denote the conic hull of , that is, the set of all finite nonnegative combinations of points in .
The conic hull of any set is a convex cone (it is convex and positively homogeneous, for all and ). When is convex, we have . In particular, when is convex and , then is the cone of feasible directions of at , that is, it consists of the rays along which one can move away from while staying within .
The lineality space of a nonempty convex cone is the largest linear subspace contained in (the lineality space can be defined for general convex sets, but we will only need this notion for cones). The following facts are well-known.
Proposition 2.3.
Let be a convex cone, . Then
-
(i)
for any , we have if and only if ;
-
(ii)
the lineality space is nonempty if and only if .
Proof.
The part (ii) is straightforward: since must belong to every linear subspace, if , then no linear subspace is contained in . Likewise, if , then is a trivial linear subspace contained in , and the lineality space can only be larger than that.
The necessary part of ((i)) is evident: assuming , and recalling that is a linear subspace, we must have .
To show the sufficiency, that is, if , then , first observe that it follows from convexity that , and hence by (i) . Assume that nevertheless . Let . Let
For any we have , with and for some . Now , irrespective of the sign of , since is a cone and both and are in . Now , hence (as by convexity and homogeneity), and we have demonstrated that is a linear subspace contained in that is strictly larger than , which is impossible. ∎
It follows from (i) that the lineality space of a convex cone is uniquely defined, since it is fully characterised by the set of points that belong to the cone along with their negatives.
Also recall that the Minkowski sum of two (convex) sets is
When one of the sets is a singleton, we abuse the notation and write for .
We show next that minimal faces the minimal face of any point, can be characterised in terms of the lineality linearity space of the cone of feasible directions of the point.
Proposition 2.4.
Let be a nonempty convex set and let . Then
Before moving on to the proof of Proposition 2.4, we state and prove the following elementary technical proposition that will be used as a building block in several proofs.
Proposition 2.5.
Let . If , then for any there exists such that .
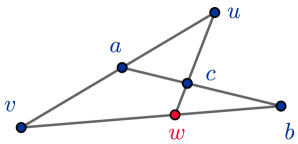
Proof.
Let , and assume that and (see Fig. 2).
Proof of Proposition 2.4.
We first show that
Let . Then for some , and by Proposition 2.3 (i) we have . This means that there exists some such that . We have
hence and for every face of containing we must have . We conclude that
It remains to show the converse, that
Since , it is then sufficient to show that
| (3) |
If we prove that
| (4) |
is a face of , then from , we must have , hence , and so (3) holds.
Let and and be such that
| (5) |
Our goal is to show that .
Let . Since , we have , and by Proposition 2.3 (i) we have . There exists such that . Applying Proposition 2.5 to the points and (cf. Figs. 2 and 3),
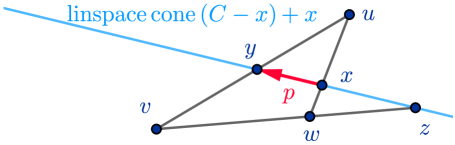
we conclude that there exists some such that , which yields , hence, , so . We conclude that . Hence, from (4) we conclude that .
∎
It follows from Proposition 2.4 that the minimal face of consists precisely of the line segments in that contain in their interiors (cf. Proposition 2.3 item 7 of [FacelessProblem]).
Corollary 2.6.
The minimal face for (where is a convex subset of a real vector space ) can be represented as
| (6) |
Proof.
It is evident that the set on the right-hand side is a subset of any face that contains , hence, it must be contained in the minimal face of in as well. It remains to show that the minimal face of in is a subset of the right-hand side. Let . Then by Proposition 2.4 we have
equivalently . This means that , and so there exists some such that , equivalently . It remains to note that
hence , and so belongs to the right-hand side of (6). ∎
2.2 Chains of faces
Recall that a chain is a totally ordered set. A chain of faces of a convex set is such a set of faces of that for every we have either or (Lemma 2.1 implies that in this case either or ).
In the finite-dimensional setting a chain of faces of a convex set is always finite, since the affine hulls generated by strictly nested faces must have strictly increasing dimensions, and there is a natural bound coming from the dimension of the ambient space (the nesting of affine hulls also works in the infinite dimensional case, see Proposition 2.9 below). The length of any chain of faces in is at most , since a chain of faces may include the empty set as well as an extreme point, which is zero-dimensional (see Fig. 4).

Polytopes have chains of faces of maximal possible length , where is the intrinsic dimension of the polytope. In the infinite dimensional setting however there are convex sets that may have not only infinite, but uncountable chains of faces. An example of a set with uncountable chains of faces is the Hilbert cube discussed next.
Example 2.7 (Hilbert cube).
Consider the subset of defined as the infinite product of diminishing line segments,
(here we assume that is the set of natural numbers does not that doesn’t contain 0, so ). It is not difficult to observe that the subsets of defined by
are faces of . We can now construct an uncountable chain of faces using a well-known trick. There exists an uncountable chain in the powerset power set of natural numbers (to see this consider any bijection between and , and then construct the that maps a real number to the set of all rational numbers that are strictly smaller than : this mapping generates the required chain).
For any we let we let
It is evident that if for some , then , hence, we have constructed an uncountable chain of faces .
Notice that in Example 2.7 we didn’t need to make the ‘edge length’ of the hypercube diminishing in , and could have considered a hypercube in the general sequence space, say with a unit edge length. However having an example in a well-behaved Hilbert space like demonstrates that the phenomenon occurs naturally in a fairly standard setting.
Another instance of a set with uncountable chains of faces is discussed in Section 4, its construction relies on an infinite Hamel basis (see Example 4.3).
Proposition 2.8.
Let be a convex set in a real vector space and suppose that is a chain of its faces. Then
is a face of .
Proof.
First observe that is a convex subset of : every point belongs to some face of , and hence belongs to ; furthermore, for any there exist such that and . Since is a chain, without loss of generality we can assume that , and hence . Therefore, , and so is convex.
Let , and let be such that . Since is a union of faces of , there must be a face such that . Since is a face of , we have
and so is a face of . ∎
Every chain of faces generates an associated set of affine subspaces, which are the affine hulls of these faces. Recall that for any (convex) subset of a real vector space we define the affine hull of as
Equivalently is the smallest affine subspace containing (a set of the form , where is a linear subspace, and ), or .
The next proposition shows that chains of faces generate chains of affine subspaces, which results in a finite bound on chains of faces in finite dimensions, as was discussed in the beginning of this section.
Proposition 2.9.
If and , then .
Proof.
It is evident from the definition of the affine hull that if , then . It is hence sufficient to show that if then there exists some . Assume the contrary, then in particular . Since , there exists , which can be represented as
By convexity
Now there must exist a such that
Let
Since for all and
we have
and since and , by the definition of a face we must have , which contradicts our assumption. ∎
3 Intrinsic core
In finite-dimensional spaces the relative interior of a convex set is usually defined as its interior with respect to the affine hull of . Intrinsic core is a generalisation of this notion to the real vector spaces (although note that for topological vector spaces the relative interior is alternatively generalised as the interior relative to the topological closure of the affine hull [BorweinGoebel]).
3.1 Definition and basic properties of the intrinsic core
There are several equivalent definitions of the intrinsic core: we discuss all of them throughout this section, however we start with the one that is perhaps the most elegant (also see the original work of Klee [kleepart1] where this approach first appears).
Definition 3.1 (Intrinsic core via line segments).
Let be a convex subset of a real vector space . Then the intrinsic core of is
In other words, if and only if one can extend the line segment connecting to any point of the set beyond the point , while staying within . This is also the definition used in [DYE1992983] (called the set of weak internal points), in [FacelessProblem] (the set of inner points) , and also in [BorweinGoebel] (called the set of relatively absorbing points or pseudo-relative interior).
Note that is a difference in the interpretation of the definition of the intrinsic core between our exposition and other literature: for instance, the discussion in [FacelessProblem, Section 1]) implies that singletons must have empty intrinsic cores, for the lack of any line segments, which we find inconsistent. It follows from Proposition 3.11 that whenever is a singleton , we have , and hence .
The definition of the intrinsic core can also be extended to general subsets of , as it is done in [InnerStructure]: in this case the instinsic core of some is defined as all points such that for any line through either there are some such that or .
Proposition 3.2.
The intrinsic core of a convex subset of a vector space is a convex set.
Proof.
Let and suppose that . Then for any there exist such that and . Then we have for some
Substituting the expressions for and into the one for , we obtain
where
by convexity (see Fig. 5).
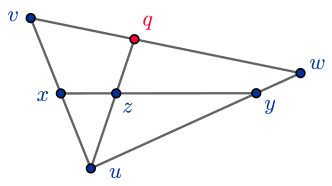
Hence, with , and by the arbitrariness of the choice of we have . ∎
In contrast to the finite-dimensional setting, where the relative interior of any nonempty convex set is also nonempty (e.g. see [RockConvAn, Theorem 6.2]), the intrinsic core of a convex set may be empty. The next example illustrates this phenomenon (cf. [InnerStructure, Theorem 5.2]).
Example 3.3.
Let be a subset of (eventually zero sequences),
| (7) |
First observe that is a convex set. We will show that for any there exists such that there isn’t any with , and hence .
Indeed, let . There is an index such that for every . Let be such that
In other words, coincides with up to and including -st entry, has 1 in the -th position and zeros beyond . If there was a such that , then for some , and in particular , hence , which is impossible by the definition of .
Convex sets that have nonempty intrinsic cores are called relatively solid in [cones]. Perhaps a better term would be to call such sets intrinsically solid. It is tempting to think about sets with empty intrinsic cores as ‘small’, however this intuition is misleading, as such sets can be very large, with their algebraic closure covering the entire space: we discuss this well-known phenomenon in more detail in Section 4.
Since an intrinsic core of some convex set may be empty, having for two convex sets and it doesn’t yield . Even though this behaviour already happens in finite-dimensional spaces, the general case is in a sense more extreme, since it may happen that the intrinsic core of is nonempty, and the intrinsic core of is empty. A trivial example is to consider some set such that and , and let for some .
We next prove a well-known technical result that effectively means that the intersection of a line passing through the intrinsic core of a convex set with this convex set lies in the intrinsic core, except possibly the endpoints of this intersection. We later prove a similar result involving the algebraic closure (Proposition 4.1 (iii)).
Proposition 3.4.
Let be a convex subset of a real vector space . If and , then there exists such that . In particular, .
Proof.
Consider some and . Fix an arbitrary . For any there exists such that by the definition of the intrinsic core. Applying Proposition 2.5 to and , we deduce that there exists such that . Since , by convexity . Then by the definition of the intrinsic core. We have hence shown that . Now since and , there must be some such that . Then by the earlier proven statement we must have . Hence . ∎
Proposition 3.5.
Let be a convex subset of a real vector space . Then .
Proof.
Observe that , so we only need to prove the converse. Now take any . Then for any we also have . Since and , by Proposition 3.4 there must be such that . This shows that . ∎
Note that the statement of Proposition 3.5 is discussed in a more general setting of not necessarily convex sets in Theorem 2.3 in [InnerStructure]; even though the notion of intrinsic core can be generalised to arbitrary (non-convex) sets, the statement of Proposition 3.5 is not true for nonconvex sets (see [RelintInnerPoints, Example 3.1]).
In the next proposition we show that when a convex subset of a convex set has empty intrinsic core, the minimal face that contains of this subset coincides with the minimal face of any point in the intrinsic core of the subset. This property is well-known in the finite dimensional case for the relative interior.
Proposition 3.6.
Let and be convex sets in a real vector space . If and , then for any we have . Moreover, .
Proof.
Under the assumptions of the proposition, suppose that . Then by Proposition 3.4 for any there exists such that . Since , Corollary 2.6 then yields . Hence the minimal face of must be a subset of , however there can be no smaller face containing (and hence ), therefore, .
Now for any we have , hence, . ∎
It doesn’t look like anything similar to Proposition 3.6 can be said about the minimal face when the subset of has empty intrinsic core. The minimal face of may or may not have empty intrinsic core in this case.
3.2 Alternative definitions of the intrinsic core
In [BorweinGoebel] the intrinsic core of a convex set (called the pseudo-relative interior, ) is defined as follows.
Definition 3.7 (Intrinsic core via the cone of feasible directions).
We next show that this definition describes the same object as the one considered previously.
Proposition 3.8 (Lemma 2.3 in [BorweinGoebel]).
Let be a convex subset of a real vector space . Then is a linear subspace if and only if for every there exists such that .
Proof.
Since is a convex set, the set is a linear subspace if and only if (additivity holds naturally), equivalently for every , where and there exists and such that . This is in turn equivalent to having, for each , the existence of and such that , which is equivalent to
∎
In a similar way to the intrinsic core we can also define the core (or algebraic interior) of a convex set (introduced by Klee [kleepart1], also see [Holmes]). For some we say that if for every there exists such that . If , then is called absorbing. Note that if and only if either or . We can equivalently define the intrinsic core of a convex set as its core with respect to its affine hull. Notice that generally speaking the affine hull of a convex set is not necessarily a linear subspace of the ambient vector space , since it may not contain zero. However as this space closed with respect to lines and segments, there is no impediment to defining the core of a convex set living in this affine subspace.
Definition 3.9 (Intrinsic core via the affine hull).
Let be a convex set of a real vector space . The intrinsic core of is the algebraic core of with respect to the affine hull of , that is,
The next proposition ensures that this new definition aligns with the original Definition 3.1.
Proposition 3.10.
Let be a convex subset of a real vector space , and let . The following statements are equivalent:
-
(i)
for every there exists such that ;
-
(ii)
for every there exists such that .
Proof.
Let and suppose (i) holds. Take any . Then
| (8) |
If , then and (ii) holds with . Otherwise for any there exists such that ; explicitly, there is some such that
| (9) |
Now let
It is easy to see using (8) and (9) that the affine representation of can be rewritten in this new notation as
| (10) |
Here , and for Now if , then , hence and for any we have . Otherwise (if ) let
Observe that and also substituting the expression for from (10) we have
It is evident that , and therefore . We have shown that (i) yields (ii). It remains to show the converse.
3.3 Intrinsic core and minimal faces
Even though the intrinsic core of a convex set may be empty (as in Example 3.3), it provides a disjoint decomposition of a convex set into the intrinsic cores of its faces. We prove this in Theorem 3.15 (cf. [FacelessProblem, Corollary 2.4]), but first we obtain a characterisation of the intrinsic core via minimal faces. Notice also that the next proposition was effectively proved in [FacelessProblem, Proposition 2.3].
Proposition 3.11.
Let be a convex set, then
Proof.
From the definition of intrinsic core we then have if and only if is a linear subspace, this is equivalent to .
Proposition 3.11 that we have just proved allows us to state yet another equivalent definition of the intrinsic core.
Definition 3.12 (Intrinsic core via minimal faces).
Let be a convex subset of a real vector space . The intrinsic core of can be defined as follows,
Example 3.13 (Revisiting Example 3.3).
Using the last definition of the intrinsic core, we can provide an alternative explanation on why the intrinsic core of the set in Example 3.3 defined by (7) is empty.
For let
It is not difficult to observe that is a face of , does not coincide with , and contains . Hence the minimal face is strictly smaller than for every . We conclude that .
Corollary 3.14.
Let be a convex subset of a real vector space , and let be a face of . Then if and only if .
Proof.
Observe that for we have
hence, under the assumptions of this corollary, and using Proposition 3.11, we obtain
which shows the equivalence. ∎
Theorem 3.15 (cf. Corollary 2.4 in [FacelessProblem]).
For a convex set and any there is a unique face such that . Consequently,
| (12) |
where by we denote a disjoint union.
Proof.
We obtain this decomposition by observing that for every there exists a unique minimal face . Evidently , hence by Proposition 3.11 we have . This shows that is the union of intrinsic cores of its faces. It remains to show that the union is disjoint.
Suppose that , where and are different faces of . Then we must have . However and hence
a contradiction. ∎
The next statement is Theorem 2.7 from [FacelessProblem], rephrased in our notation. The author calls the problem of characterising convex sets with no proper faces the ‘faceless problem’, hence the name of the theorem. It appears that this result follows from the decomposition of Theorem 3.15.
Theorem 3.16 (Faceless theorem).
A nonempty convex subset of a real vector space is free of proper faces if and only if .
Proof.
Suppose that a nonempty convex set has no proper faces. Then the only nonempty face of is the set itself, and by Theorem 3.15 we have .
Conversely, assume that is a nonempty convex set such that . Assume that on the contrary has a proper face . Since is nonempty, there is some point , and by Theorem 3.15 we can find a face such that . By Lemma 2.1 the convex set is also a face of , while by our construction . We conclude that , which contradicts the uniqueness claim of Theorem 3.15. ∎
Since only the faces that are minimal with respect to some point in the convex set feature in the decomposition (12), only minimal faces ‘contribute’ to the set. It is natural to expect that the faces that aren’t minimal can be represented in some natural way via the minimal ones. Note that in Example 3.3 the set is the union of the chainof its faces
where
however the set itself is not a member of the chain . Based on this discussion and observation, we propose the following conjecture. , for instance as the union of a chain, as is the case in Example 3.3. However this is not true, as is clear from a construction suggested by one of our referees. We come back to this construction in Section 4.1.
Every face of a convex set is the union of a chain of minimal faces.
3.4 Calculus of intrinsic cores
We next gather several key calculus rules pertaining to intrinsic cores that haven’t been covered earlier. Even though this section contains mostly well-known results, we reprove them for completeness of our exposition.
Proposition 3.17 (Lemma 3.6 (a) in [BorweinGoebel]).
If and are convex sets in a real vector space , then
| (13) |
Moreover, if and , then
| (14) |
Proof.
Note that if either one of or is nonempty, then (13) holds trivially. To show that (13) holds in general, take , , and let . Now pick any . We can represent as , where and . By the definition of intrinsic core there exist and such that and . Algebraically this means that there exist such that
Let . By convexity
Hence
It is evident that , where . Since our choice of was arbitrary, we conclude that .
Now assume that . To show (14), in view of (13) it remains to demonstrate that
Pick any point . Since , there must be and such that . Now choose any and . Then . Now , , hence there must be some such that .
Since , there must be , such that . Now by Proposition 3.5 we have and . Now for some . Since and , we conclude that
∎
Corollary 3.18.
If is a convex subset of a real vector space , then for any
Proof.
Note that in [DangEtAl, Proposition 2.5] it is shown that if , then for any convex we have
This property doesn’t generalise to intrinsic cores, even for finite dimensions. For instance, take , in the plane. Then , but
Proposition 3.19 (cf. Lemma 3.3 in [BorweinGoebel]).
Let be a convex subset of a real vector space , and let be a linear mapping from to another real vector space . Then
| (15) |
Moreover, if maps to injectively or , then
| (16) |
Proof.
Let be a subset of , and suppose is a linear mapping. If , let and take any . There must be a such that . Since , by the definition of the intrinsic core there exists such that . Hence and we conclude that . This proves (15).
We first prove that (16) holds for an injective linear mapping : we only need to show the converse of (15). So assume that maps to injectively. Consider any . There is a unique such that . Take any , and let . Since , there must be such that , and hence there is some such that . Now observe that . Indeed, we have for some , and hence . We must have , otherwise is not injective. We have therefore shown that , and by the arbitrariness of we conclude that , hence .
Now let’s deal with the case when is not injective, but . Let be the kernel of , i.e.
Since is a linear subspace of , it has a Hamel basis that can be completed to the entire space. Denote by the span of this complement, then for any we have , where and .
Let be the projection of onto the complement of , in other words,
It is evident that , and therefore
| (17) |
Furthermore, observe that is the linear image of under the projection that takes an element of to the subset by trimming off all of the -space coordinates. From (15) we have
and so is nonempty. It is evident that , hence we can apply Proposition 3.17 to and (and to and ) to obtain
we therefore have
| (18) |
In view of (17) and (18) it remains to show that
Since is an injective mapping on , the result is true by the previously proved claim. ∎
The following corollary of Proposition 3.19 was proved in [DangEtAl] for the algebraic core under the assumption of surjectivity of (see Lemma 4.1 in [DangEtAl]).
Corollary 3.20 (cf. [DangEtAl, Lemma 4.1]).
If is a surjective linear operator between two vector spaces and , and , then
| (19) |
moreover if , then (19) holds as equality.
Proof.
If , then (19) is a triviality. Assume that . Then , and by Proposition 3.19 we have
It remains to show that , and for that it is sufficiently to show that . Take any and . Since is surjective, there must be some and such that and . Since , there must be some suth that . Hence , with , so .
∎
Corollary 3.21 (Lemma 3.6 (c) in [BorweinGoebel]).
If is a convex subset of a real vector space , then
Proof.
Follows from defining an injective linear mapping and Proposition 3.19. ∎
Corollary 3.22.
Let be a convex subset of a real vector space and let be a convex subset of a real vector space , then
Proof.
First assume that and , and define two linear mappings, and as follows:
These two mappings are injective, and therefore by Proposition 3.19 we have
Now , therefore by Proposition 3.17 we have
It remains to consider the case when one of the intrinsic cores or is empty and to show that the left-hand side must also be empty in this case. Without loss of generality assume that , but there is some . Pick any . The point must be in , hence, there exists and such that
We conclude that , where and , and hence , which contradicts the assumption. ∎
4 Algebraic Linear Closure
In this section we discuss the notion of algebraic linear closure that can be defined using the natural topology of the real line. Our main goal is to relate this notion to the notion of the intrinsic core, and discuss some interesting phenomena pertaining to algebraic closures linear closure of convex sets.
4.1 Algebraic Linear closure and the intrinsic core
We say that a convex subset of a real vector space is algebraically linearly closed if for every we have . The algebraic linear closure is the smallest convex algebraically linearly closed subset of that contains . Equivalently the algebraic In a finite dimensional space the linear closure of a convex set consists of all line segments contained in together with their endpoints. It is evident that any algebraically closed set that contains must contain the closures of all line segments from , moreover, this union of closures of line segments must be a convex set. Indeed, observe that if and are such endpoints, then for some we have
where it can possibly happen that or . Then for any we have and from the convexity of
hence is an endpoint of a (possibly degenerate) line segment from , but this is not the case in the infinite-dimensional setting (see [KleeLin, nikodym] for a detailed discussion on the fascinating differences between these two notions; note also that it may happen that ). We hence distinguish between the (strong) linear closure and the (weak) linear closure .
There is a related notion of linearly accessible points discussed [Holmes, cones]: a point is linearly accessible from if and only if there is some such that . Since our notation allows in this case, this notion coincides with the algebraic closure weak linear closure (cf. [DangEtAl], where the notation is used to denote the algebraic closure). It appears that some references do not allow in the definition of linearly accessible points, and in this interpretation the set of linearly accessible points coincides with our definition whenever contains at least 2 points (see [Holmes]).
We can then define the intrinsic (weak) algebraic boundary of a convex subset of a real vector space as the set of all endpoints of the line segments that are contained in , that is,
Note that is called the set of outer points in [InnerStructure], also this reference defines such points for general (not necessarily convex) subsets of .
Proposition 4.1.
Let , and be convex subsets of a real vector space . Then we have the following relations between the algebraic weak linear closure and the intrinsic core.
-
(i)
.
-
(ii)
-
(iii)
If and , then there exists such that . In particular, .
-
(iv)
If , then , and , and .
-
(v)
We have , and if , then .
Proof.
To show (i), let and observe that if and only if there is a line segment with the endpoint that can not be continued beyond , which is equivalent to .
To show (ii), first observe that the second equality follows from (i): . For the first relation, observe that and and , hence we only need to show that . If . If , and , then must be the endpoint of some segment contained in . Since , the extension of this segment beyond , that is, must have an empty intersection with . We conclude that .
For (iii) let , . If , then we are done by Proposition 3.4. Otherwise there must exist some such that and .
Since , there exists such that . Then by Proposition 2.5 for any point there exits such that . Now fix any . Applying Proposition 2.5 again, this time to and (see Fig. 6),
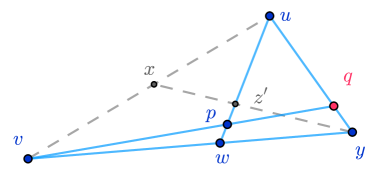
we conclude that there exists such that . Now , and . Since , with , and hence , by the arbitrariness of this proves that . Now for any point we have , hence, by Proposition 3.4 we obtain , and hence , and also by the same proposition there exists some such that .
For (iv), we begin with . Since , we only need to prove that . Take any . If , then and we are done. If , take any . By (iii) we have . Hence must be in .
Observing that , the relation that we just proved yields . It remains to prove . Since . Since we only need to prove that . Take any . Since , there exists some . Since , by (iii) there exists such that , concluding the proof of this item.
Note that in [DangEtAl] the relation (iii) is shown using separation theorems (see Theorem 3.7), however our proof is much more elementary.
In [InnerStructure, Theorem 2.1] it was shown that is an affine subspace if and only if is convex, and . Indeed we observed earlier that for a linear subspace we have , and and .
The relation Since in general , it makes sense to define -th (weak) linear closure, and we can do this for any ordinal in the following way (see [KleeLin]):
It was shown in [nikodym] that there exists a convex set for which for all ordinals (where is the first uncountable ordinal). At the same time, (see [nikodym]).
We can define the -th (weak) linear boundary as , and likewise the strong linear boundary as .
The relation fails to hold generically in infinite-dimensional spaces, this is due to the existence of proper convex sets that are ubiquitous, that is, such that their algebraic linear closure coincides with the entire space.
Theorem 4.2 (see [kleepart1]).
The linear space is inifinte dimensional if and only if contains a proper convex subset such that .
The proof of this theorem is based on an explicit construction of such set, which we study in the next example. This example was publishedin [kleepart1] and according to our Referee, can be attributed to M. M. Day.
Example 4.3.
Since any Any linear vector space has a Hamel basis that can be totally ordered, we can moreover, if the space is infinite-dimensional, we can choose the order in a way that there isn’t a greatest element. We can then represent any element as a finite linear combination of the basic points. There will be the one coordinate that is maximal with respect to the total order, and we can define the set as the set of all points with the positive last coordinate. This set is convex, and its algebraic linear closure constitutes the entire space : indeed, any point is either in , or is the endpoint of some line segment in obtained by adding a small positive coordinate with a higher index. Somewhat counterintuitively, the complement of this set is also convex and ubiquitous (following the same logic).
It is easy to see why the intrinsic core of such a set is empty: take any element in this set, and then pick with a higher positive coordinate. Evidently the line through and can not be extended beyond , so is not in the intrinsic core. Hence .
When it comes to the facial structure of this set, observe that for any there exists such that if and only if the ‘index’ of the last coordinate of is no larger than the index of the last coordinate of . Therefore, the minimal face of is the subset of that contains all elements with the last coordinate not larger than . This in particular means that the set is the union of the chain of all minimal faces, the kind of structure that we expect in all convex sets given that Conjecture LABEL:conj:russian-doll is true. .
This property of chain of minimal faces of points is not always satisfied. Take a vector space with an uncountable Hamel basis, and define the convex set as the set of all the elements from with non-negative coordinates. The faces of are the cones spanned by subsets of the Hamel basis, while minimal faces of any point in is the cone spanned by finite subsets of the Hamel basis. The only faces which are reunions of chains of minimal faces of points in are the cones spanned by finite or countable subsets of the Hamel basis. Accordingly, all the faces spanned by infinite uncountable subsets of the Hamel basis (including ) cannot be represented as the union of a chain of minimal faces of points of . We thank our referee for suggesting this example.
Recall how in finite-dimensional case faces of closed convex sets are always closed. It appears that this phenomenon is specific to the algebraic linear and not topological closure.
Proposition 4.4.
If is an algebraically a linearly closed convex subset of a vector space , then every face of is algebraically linearly closed.
Proof.
Let be an algebraically linearly closed subset of , and let be an arbitrary face of . Our goal is to show that for any we have .
Let . Since is algebraically linearly closed, . Now pick any . Since , by the definition of a face we must have . ∎
The next example shows that faces of (topologically) closed convex sets do not need to be closed. This example is used in [hitchhiker] to demonstrate that the convex hull of a compact set may not be compact (and even closed).
Example 4.5 (Example 5.34 from [hitchhiker]).
Let be defined as , where is the sequence of all ones except for in the -th position. Let and be the -closure of the convex hull of . We will show that . Note that is not closed (but is compact, see [hitchhiker]), while is closed by the definition. Also both and are convex and . It remains to show that is a face of .
Take , and suppose that are such that for some . Since is an orthonormal basis of , we can write
where , for all , and .
Since , there exists a finite index set such that
From we have
hence, and are finite convex combinations of points in , and so . Hence by the definition of a face .
In [zbMATH03075149], there is an interesting example of two convex and linearly closed sets whose convex hull is not linearly closed.
Thinking in terms of algebraic linear closure helps further refine the relations between faces and the intrinsic core.
Proposition 4.6.
Let be a convex subset of a real vector space , and let be a proper face of (that is, is nonempty and does not coincide with ). Then . Then .
Proof.
Notice that does not yield , even in the finite-dimensional case. For example, letting and , where and are distinct elements of some vector space , results in , but . We can however obtain meaningful relations between the intrinsic cores of certain structured subsets of convex sets, as shown next.
Proposition 4.7.
Let be a proper face of , where is a convex subset of a real vector space . The set is convex; moreover, .
Proof.
To show that is a convex set, let . If there is a such that , then by the definition of a face we must have , a contradiction with the original choice of and .
To show that , we first demonstrate that . Take any . From Proposition 4.6 we know that . Now pick any . Since , by Proposition 4.1 (iii) there exists such that (applying Proposition 4.6 again). Since was arbitrary, we deduce that .
It remains to show that . Take any , and let . If , then there exists a such that , so we only need to deal with the situation when . In this case . Let . If , then by the definition of a face , which is impossible. We conclude that . Then there exists such that . We conclude that . ∎
4.2 Separation and support points
Recall (see [Holmes]) that a hyperplane in a real vector space is a maximal proper affine subspace of , or equivalently a level set of some nontrivial linear functional ,
| (20) |
A hyperplane defined as in (20) is said to support a convex set if for all (alternatively for all ), where the equality is satisfied for some .
Two convex sets and are separated by a hyperplane if they lie in the two different (algebraically linearly closed) subspaces defined by the hyperplane , so that, for instance,
The sets and are properly separated by if they are separated by and do not lie in their entirety on , so . This is equivalent to the existence of a linear functional such that
Hyperplane separation in infinite-dimensional vector spaces is hinged on the following statement (see [Holmes, I.2.B]).
Lemma 4.8 (Stone).
Let and be disjoint convex subsets of . Then there exist complementary convex sets and such that and .
The proof is based on using Zorn’s lemma to build a maximal convex set that contains but not and showing that the complement must be convex.
It can be further shown that the intersection of algebraic weak linear closures of two nonempty complementary convex sets is either the entire space or a hyperplane (see [Holmes, I.4.A.]). In the former case there is no hyperplane separating these complementary convex sets. A sufficient condition for the separation of two disjoint convex sets is that at least one of them has a nonempty core (see [Holmes, I.4.B.] and [hitchhiker, 5.61]).
Theorem 4.9 (Theorem 5.61 from [hitchhiker]).
Two disjoint nonempty convex sets can be properly separated by a nonzero linear functional provided one of them has a nonempty core.
This theorem can be generalised as shown in the following corollary (both these results can be proved using the Hanh-Banach extension theorem).
Corollary 4.10 (Corollary 5.62 from [hitchhiker]).
Let and be two nonempty disjoint convex subsets of a vector space . If there exists a vector subspace including and such that either or has nonempty core in , then and can be properly separated by a nonzero linear functional on .
It is tempting to assume that it may be enough for the intrinsic core of one of the disjoint convex sets to be nonempty to achieve proper separation. However this is not true: for instance, let be the set considered in Example 4.3, and suppose is any single point in the complement of , meaning that has a nonempty intrinsic core. Notice that any hyperplane supporting some convex set should also support its algebraic linear closure. In out case the algebraic our case the linear closure of is the entire space, and hence the only linear functional supporting is the trivial one (whose kernel coincides with ) that a) doesn’t define a hyperplane and b) doesn’t properly separate and . However if both sets have nonempty intrinsic cores, this is enough to ensure proper separation (see Proposition 4.12 below).
A point is called a support point if it belongs to some supporting hyperplane. A support point is proper if it lies in a supporting hyperplane that does not contain all of (see [Holmes]). It is well-known that whenever , the proper support points of a convex set are exactly . We provide a proof for completeness.
Proposition 4.11.
If for some convex subset of a real vector space , then every is a support point of .
Proof.
Suppose that a convex set has nonempty intrinsic core, and that . Our goal is to show that there exists a linear functional such that
and moreover there is some such that , so the separation is proper.
We first prove this claim for under the assumption that . Let . Since , is a proper face of . By Proposition 4.6 the set is convex, moreover, . By Proposition 4.1 (v) we have , and together with this yields . By Definition 3.9 of the intrinsic core, coincides with the core of with respect to . Notice that since , the affine hull is actually a linear subspace of . We can now apply Corollary 4.10 to , and . There exist a linear functional such that
| (21) |
Take any . By Proposition 4.1 (iii) we have . Hence for any
and we conclude that
Now take any . Since , there exists such that . It follows from and that .
Using all this knowledge, we rewrite the earlier relations (21) as
We have found a linear functional such that this linear functional properly separates from .
We can now return to the case when . Let . Then by Corollary 3.18 we have ; moreover, since , is a linear subspace. Observe also that . By our earlier result, there exists a linear functional such that
Observe that iff for some , therefore this is equivalent to
hence we found a linear functional and a constant such that properly separates from . ∎
Proposition 4.12.
If and are convex subsets of a real vector space such that and moreover , then and can be properly separated.
We first need the following technical claim.
Proposition 4.13.
Let be a convex subset of a real vector space . If then the positive hull of ,
has nonempty intrinsic core, moreover, .
Proof.
Under the assumptions of the proposition, take any and . There exists some such that for some . Since , there must exist such that , and explicitly there is some such that
Now if , observe that
where
since the coefficient at is positive. Moreover, since , we conclude that .
It remains to consider the case when . In this case notice that , and also . Applying Proposition 2.5 to the points and , we deduce that there exists such that .
We conclude that . ∎
Proof of Proposition 4.12.
Under the assumptions of the proposition, let . By Proposition 3.17 we have . Moreover, since , we have . If , then by Corollary 4.10 can be properly separated from . Otherwise let be the positive hull of . From Proposition 4.13 we know that , moreover it is evident that , but . Therefore can be separated properly from . Since is the positive hull of , this means that the same linear functional properly separates from .
Recall that a face is exposed if there exists a supporting hyperplane to such that .
In the finite-dimensional setting whenever a face is not exposed, it is always eventually exposed: we can choose a hyperplane exposing some face of , then expose a face of that face and so on, until we reach the required face. It is unclear whether this result generalises in a sensible way to the infinite-dimensional setting (under the assumption that ).
We also note that some properties of exposed faces that naturally hold in finite dimensions are not true in infinite-dimensional spaces, for instance, the intersection of two exposed faces is not necessarily exposed [ShortNote] in a Banach space, and in [MinExp] sufficient conditions are obtained for the intersection of exposed faces to be exposed.
5 Summary
We have provided an overview of the definitions and properties of intrinsic core, intentionally focusing on the restricted setting of real vector spaces without topological structure. We note once more that the intrinsic core appears in the literature under different names, including the set of relatively absorbing points, the pseudo-relative interior and the set of inner points (see the discussion at the beginning of Section 3).
We have discussed four equivalent definitions of the intrinsic core, via line segments (Definition 3.1), the cone of feasible directions (Definition 3.7), as a core with respect to the affine hull (Defintion 3.9) and in terms of minimal faces (Definition 3.12). We have also made explicit the differences in notation and discrepancies in implicit assumptions used by different authors that should aid future work involving intrinsic cores.
We have provided an extensive collection of properties and calculus rules of intrinsic cores, and discussed in much detail the relation between the intrinsic core and algebraic boundary. We have also provided an overview and elementary proofs of separation results pertaining to this purely algebraic setting.
Acknowledgements
The authors are indebted to the two referees, who not only carefully read an earlier draft of our paper, but also generously provided many insights, including examples and references, that significantly improved both the quality of this work and our understanding of the subject matter.
We are also grateful to the Australian Research Council for financial support provided by means of the Discovery Project “An optimisation-based framework for non-classical Chebyshev approximation”, DP180100602.