The -Colorable Unit Disk Cover Problem
Abstract
In this article, we consider colorable variations of the Unit Disk Cover (UDC) problem as follows.
-Colorable Discrete Unit Disk Cover (-CDUDC): Given a set of points, and a set of unit disks (of radius=1), both lying in the plane, and a parameter , the objective is to compute a set such that every point in is covered by at least one disk in and there exists a function that assigns colors to disks in such that for any and in if , then , where denotes a set containing distinct colors.
For the -CDUDC problem, our proposed algorithms approximate the number of colors used in the coloring if there exists a -colorable cover. We first propose a 4-approximation algorithm in time for this problem and then show that the running time can be improved by a multiplicative factor of , where a positive integer denotes the cardinality of a color-set. The previous best known result for the problem when is due to the recent work of Biedl et al., (2021)[BBL19], who proposed a 2-approximation algorithm in time. For , our algorithm runs in time, faster than the previous best algorithm, but gives a 4-approximate result. We then generalize our approach to yield a family of -approximation algorithms in time, where . We further generalize this to exhibit a -approximation algorithm in time for a given , where . We also extend our algorithm to solve the -Colorable Line Segment Disk Cover (-CLSDC) and -Colorable Rectangular Region Cover (-CRRC) problems, in which instead of the set of points, we are given a set of line segments, and a rectangular region , respectively.
keywords:
Colorable Unit Disk Cover , Approximation Algorithm , Grid-Partitioning , Packing-Constraints.1 Introduction
Our motivation for studying the problem arises from practical applications in the frequency/channel assignment problem in wireless/cellular networks. In ad-hoc mobile networks, each host(station/tower) is equipped with a Radio-Frequency (RF) transceiver to provide reliable transmission inside a circular range, represented by a disk, within some distance. Each wireless client is equipped with corresponding receivers. The clients themselves are represented by a set of points in a plane. The disks representing the range (which is presumably the same for all stations) of each potential host is represented by the set . In the spirit of reducing interference in broadcast and other energy-saving measures, we aim to limit or reduce the number of different frequencies(channels) assigned to each, represented by coloring. Typically, (Wi-Fi) networks are built with 3 independent channels [BHLL10], hence the motivation for a study on the 3-CDUDC problem. In the same spirit, we generalize the 3-CDUDC to the -CDUDC problem, where is an integer. We further generalize the problem by considering line segments and a continuous rectangular region as representing potential wireless clients (resp. the -CLSDC and -CRRC problems), instead of points.
1.1 Related Work
The 3-CDUDC problem, to the best of our knowledge, was first studied by Biedl et al., [BBL19]. They gave a 2-approximation algorithm in time for the 3-CDUDC problem. Their approach first partitions the plane into horizontal strips, solves the problem for every strip optimally, then returns the union of solutions of all strips. To solve the problem for any strip they show that at most a constant number of disks of an optimal solution intersect any vertical line. Based on this, they define a directed acyclic graph such that there exists a path from source to a destination corresponding to this optimal solution. In this paper, we attempt to improve upon this impractical running time. Our approach, however, focuses on the specific geometric properties that arise from the dual conditionals of the problem statement. Although both of the approaches, initially, begin by dividing the plane, we recognize a unique bound that exists in our need to bound the colorability and provide a novel solution in the same regard.
A notion of conflict-free coloring (CF-coloring) was introduced by Even et al., [ELRS03]. and Smorodinsky [S03]. In the CF-coloring problem we are given a set of points (representing client locations) and a set of base stations, the objective is to assign colors (representing frequencies) to the base stations such that any client lying within the range of at least one base station is covered by the base station whose color is different from the colors of the other base stations covering the client, and the number of colors used should be as minimum as possible. Here, the range of base stations is modeled as regions e.g., disks or other geometric objects. Even et al., [ELRS03] proved that colors are always sufficient to CF-color a set of disks in the plane, and in the worst case, colors are required. Note that this CF-coloring of disks is different from our notion of -colorable disk cover of points. In the former overlapping disks may be given the same color if they dont share a client, whereas in the -CDUDC overlapping disks must be colored with distinct colors regardless of whether they cover a common client. A generalization of CF-coloring is called a -fault-tolerant CF-coloring. Cheilaris et al., [CGRS14] presented a polynomial-time -approximation algorithm for the -fault-tolerant CF-coloring in 1-dimensional space. Horev et al., [HKS10] proved that colors are sufficient for any set of disks in the plane. For dynamic CF-coloring and results on CF-coloring of other geometric objects, we refer to [BM19] and references therein.
A related problem of the -CDUDC problem in the literature is the Discrete Unit Disk Cover (DUDC) problem. In the DUDC problem, we are given a set of points and a set of unit disks, our goal is to select as the smallest number of disks from as possible such that the union of these selected disks covers all points in . As in the -CDUDC, here also, the sets and can be considered as representing a set of wireless clients and a set of base stations or towers, respectively. The DUDC problem is NP-hard and is a very well studied one. There is a polynomial time approximation scheme (PTAS) with impractical running time for this problem [MR10]. The current best approximation algorithm with reasonable running time is for any [BAD15]. However, a series of approximation algorithms have been proposed for this problem by various authors over the past two decades, and a complete survey on this can be found in [FL12]. When a line segment is used to represent a potential wireless client, the DUDC problem becomes a Line Segment Disk Cover (LSDC) problem. In a similar line, there is another variant of the DUDC problem, a Rectangular Region Cover (RRC) problem, in which all the continuous set of points lying in a rectangular region represent wireless clients. All the available results for the DUDC problem also extend to the LSDC and RRC problems [B18], with slightly different running time. We also extend our results for the -CDUDC problem to solve the colorable variants of the LSDC and RRC problems, namely, the -CLSDC and -CRRC problems.
2 -CDUDC Problem
In this section we consider the following problem.
-
-Colorable Discrete Unit Disk Cover (-CDUDC): Given a set of points, and a set of unit disks (of radius=1), both lying in the plane, and a parameter , the objective is to compute a set that covers all points in such that the set can be partitioned into , where for each the disks in are pairwise disjoint, i.e., the disks in can be colored with at most colors such that the overlapping disks receive distinct colors and every point in is covered by a disk in .
As it was pointed out in [BBL19] that there is a related problem, namely, Unit Disk Chromatic Number (UDCN) problem, that aims to color all nodes in a given unit disk graph with at most colors. The UDCN problem is NP-hard for any [CCJ90]. Similar to Biedl et al. [BBL19], we can center a set of unit disks in the plane such that there are at least pairwise non-disjoint disks that have a common intersection region and a unit disk graph induced by is connected. Let us then place a set of points in this intersection region. Now observe that the set has a cover which is at most -colorable, whereas the graph is at least -colorable. Hence, the -CDUDC problem is different from the UDCN problem. Biedl et al. [BBL19] showed that the 3-CDUDC problem is NP-hard by carefully incorporating a set of points in the NP-hard proof of the UDCN problem with in [CCJ90]. This directly implies that the -CDUDC is NP-hard since the -CDUDC is a generalization of 3-CDUDC. It is also easy to see that the -CDUDC problem belongs to the class NP, as follows: Here, the certificate for any Yes instance of -CDUDC is a set of distinct colors identified by non-negative integers , and a mapping , where . A polynomial time verifier checks if every point in is covered by a disk in and for every pair of disks if , whether it is the case that .
2.1 4-Approximate Algorithm
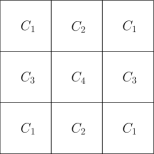
Here, our algorithm is based on partitioning the plane containing points into a grid and then determining bound on the number of unit disks that can participate in any -colorable covering of points lying within any square of the grid. We first define a grid of width units that partitions the plane into squared regions. Each of these squared regions is a grid cell with a size . For simplicity assume no point of lies on the boundary of these grid cells. Let us associate a unique ID to each grid cell as follows; let be a point in and be the grid width, then , (see Fig. 1). Note that each grid cell has a unique ID associated with it but multiple points can be associated with the same ID (if they lie within the corresponding grid cell). Let and be any two arbitrary grid cells with base points and respectively. We define the greater than operator for an ID as follows: . Note that our defintion of implies that the grid cells are indexed from bottom-left to top-right, this operator simply indicates the order of iteration that is followed by our algorithm. We move left to right row-wise starting from the bottom-left corner cell. A pre-defined order is essential to our handing-over logic at line 11 of Algorithm 1.
Given a grid cell , the following lemma provides a bound on the cardinality of the -colorable unit disks covering all points lying within the grid cell . Let be the set of -colorable unit disks covering all points of lying within the grid cell . The proof of the lemma is based on the observation that determining this bound is the same as determining a maximum number of disjoint unit disks that could potentially intersect .
Observation 1.
If is a grid cell of size , then the maximum number of pairwise disjoint unit disks that could potentially intersect is at most if is even, and is atmost if is odd.
Proof.
We will provide an upper bound to the number of pairwise disjoint unit disks that can cover a square of side length . Let us prove this by considering the two cases: being even and odd.
Since we aim at bringing an upper bound to the number of disks that have a common intersection point with , we divde the region of into two parts; the inner part of the square and the union of its outer edges on which these common intersection points can lie. To maximize the number of disks, it is intuitive to keep them as far as possible to increase the spacing between disks and thereby trying to increase the number of disks.
with even side length: When is a multiple of 2, it is quite intutive that a symmetric pattern is likely to give the best results. So we attempt two types of symmetric pattern.
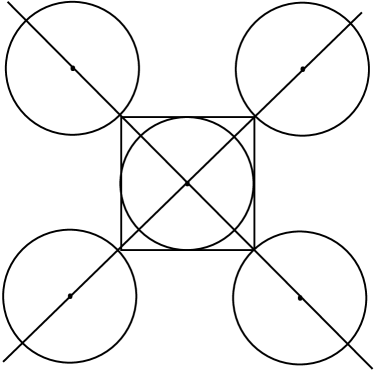
Case 1: Considering the square to be symmetric along the vertical axis, we arrange the disks in two possible cases: either a disk is arranged with edge of as tangent such that the center of lies vertically above/below the disk (see Fig. 2a), or the vertical partition is tangent to some of the disks (see Fig. 2b). In the first case the maximum number of disks along horizontal part of outer edge would be , since the diameter of disk is 2. In the second case it can be shown that the maximum number of disks along the horizontal part would be .
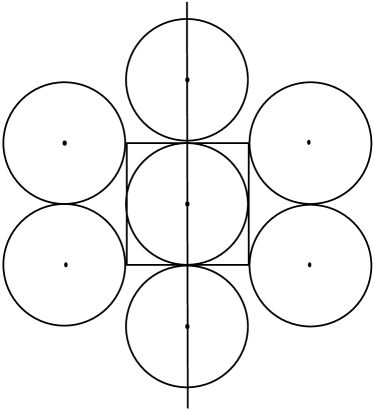
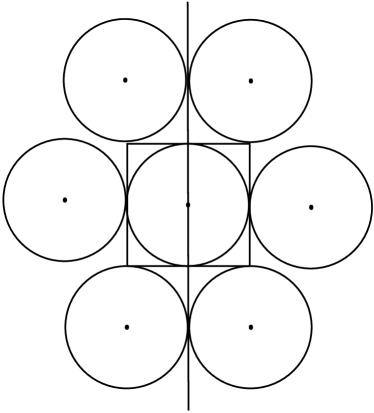
However, as we see for the case =2 (shown in Fig 2a and Fig 2b), both the cases break down to the same case since if for a given pair of parallel edges of if one of the above case is true, then for the other pair the other case stands true. By induction we can prove that this stands true for all the even values of . Through this we get an upper limit in the number of disks along the edges. For the inner area of the maximum number of disjoint disks are . So the maximum number of disjoint disks are (/2) +2 /2 +2 (/2 + 1), which is 2+2+(/2).
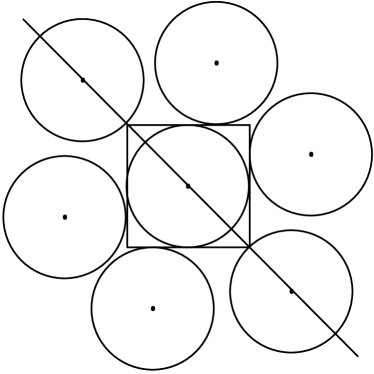
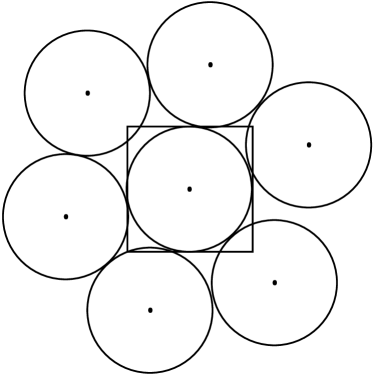
Case 2: Considering to be diagonally symmetric, here we consider one of its diagonals as the symmetry line and place the disk such that their center is on the diagonal and intersects the square at its corner. As the disk covers a part of the edge of the square, say where (i.e., radius of disk) and , apart from the case where the disks are arranged at the diagonals again (see Fig. 3a), the maximum number of disks on an edge is still equivalent to . The number of disks within the interiors of as stated above in the previous case will remain same. Therefore, the total number of maximum possible pairwise disjoint disks are , which is again equivalent to (see Fig. 3a, Fig 3b, Fig 4a, Fig 4b, and Fig 4c for illustration of the case ).
with odd side length: When is not a multiple of 2, again it is quite intutive that a symmetric pattern is likely to give the best results. So we attempt two types of symmetric pattern.
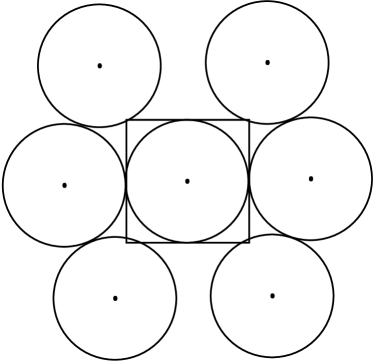
Case 1: Like the case for even values of we consider the symmetric distribution along the horizontal and vertical axes. Again we have two possibilities either the center of disk lying along the axes or symmetric about the axes for both the pairs of edges. It can be shown that for both the pair of edges we would have only one amongst the two configurations at a time for getting the miximum number of disks. In the first case, disks can completely be accomodated on one edge and one disk as a common disk between two adjacent edges. So, there will be disks in the exterior part for this case. The number of disks in the interior part as in the even case would be . So, the total becomes (see Fig. 5a and Fig. 5b).
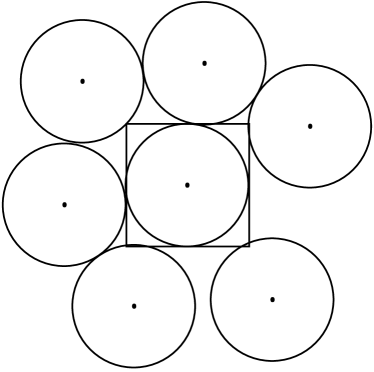
Case 2: When diagonally symmetric, the case is quite similar to the previous case with 4 disks at the corners and among the four edges of . The total again is calculating to .
∎
Lemma 1.
If is a grid cell of size and is a -colorable solution for , then .
Proof.
From Observation 1 the cardinality of any set of pairwise disjoint unit disks intersecting with a grid cell is at most 7 as . Therefore, . Now consider another sets , , , , each of which can either be a replica of the same collection of disks in or a rotation or transformation of such that disks within each set remain pairwise disjoint and intersect . Hence, any -colorable solution if the union of the disks in covers all the points in . Thus, the lemma follows. ∎
The outline of our algorithm (Algorithm 1) for computing a cover of the points is as follows. We first partition the rectangular region containing the objects in and into individual grid cells of size . By utilizing the bound obtained in Observation 1 (for e.g., for the actual bound is in Lemma 1) we compute a -colorable cover of the points lying in each grid cell, in an exhaustive manner. To ensure that there is no conflict in the overall aggregate solution, we use a handing-over logic. Only disks of any particular grid cell cover centered within the same grid cell are colored with the associated color set. If a disk is required to be a part of this grid cell cover, but is centered in another grid cell, it is handed-over to that grid cell. Based on the grid width and the diameter of the disk, we then define a coloring scheme that assigns a color to each disk in the union of all the individual grid cell covers computed. Finally, we return the pair . Since the diameter of the disks is fixed to be two units, the approximation factor of the algorithm is implied by the choice of the value . If the value of is 2, then a unit disk can participate in the -colorable covers of points lying in four adjacent grid cells. Hence, we prove that Algorithm 1 is a 4-approximate algorithm (see Theorem LABEL:theorem-2.2). Later, we show that by varying the grid width , which results in a unit disk participating in more than four individual grid cell covers, we can obtain a family of algorithms with approximation factors corresponding to the choice of the value of (see Subsection LABEL:generalize2.2).
We now define any coloring function that assigns colors to disks to be conflict-free if for any pair of non-disjoint disks (i.e., overlapping disks) the colors assigned to them are different.
Lemma 2.
The coloring defined by Algorithm 1 is conflict-free.
Proof.
For the sake of contradiction, let us assume that there are two disks such that , and , where along with is the output of Algorithm 1. Since , the distance between the centers of and is at most 2. Let the centers of and be lying in the grid cells and , respectively. Observe that and are either linearly or diagonally adjacent. If and are chosen to cover points lying only in the respective grid cells, then and are assigned colors from different color sets because the row and column numbers in their ID’s are not the same for both (see for-loop at Line 17) (contradicting that ). Therefore, the only possibility for color-conflict to arise between and is that when both and are centered in the same grid cell , where covers a point lying in the cell above and covers a point lying in the cell below and each disk is initially chosen by the respective grid cell by means of the algorithm (Note that a similar case can be studied for horizontally and diagonally opposite grid cells). As per our color scheme (Line 16-28), these grid cells are the nearest to have the same color set (say ) associated with them (see Fig. 1). Step 11 in the algorithm solves the conflict that arises in this case as follows. By means of the grid cell ID condition, disk is handed over to grid cell as its ID is greater and will receive the color set associated with that cell ( in this case, see Fig. 1). Disk however will not be handed over, but retains a color from the color set (contradicting that ). Thus, the lemma follows. ∎
Input: A set of points, a set of unit disks in the plane, and an integer such that and can provide a -colorable cover of the points in .
Output: A -colorable set that covers all the points in and a color mapping , where denotes the color set of distinct colors, and
/* the grid cells in the following loop are considered in row-wise order from bottom-left to top-right, as defined in Subsection 2.1 */
/* due to Lemma 1 */