The landscape law for tight binding Hamiltonians
Abstract.
The present paper extends the landscape theory pioneered in [FM, ADFJM2, DFM] to the tight-binding Schrödinger operator on . In particular, we establish upper and lower bounds for the integrated density of states in terms of the counting function based upon the localization landscape.
1. Introduction and main results
In this paper, we consider the discrete tight-binding Schrödinger operator on . The traditional approaches to the estimates for the integrated density of states of its continuous analogue in can roughly be split into two groups, both pertaining to the asymptotic regimes. The first one are the results akin to the Weyl law, estimating the asymptotics of the spectrum as the eigenvalue in terms of the volume in the phase space of the set , or in terms of the associated counting function according to the Fefferman-Phong uncertainty principle [Fe]. Informally speaking, letting corresponds to considering length scales which tend to zero, and hence such estimates, by design, are not relevant for a tight-binding model on . And indeed, deterministic potentials on were typically treated by more ad hoc approaches specific to their structure: periodicity, symmetries, etc, see, e.g., [DLY, HJ]. The second type of results pertains to the case when the potential is random. Then the integrated density of states exhibits the so-called Lifschitz tails, an exponential asymptotic behavior at the edge of spectrum. This regime is rather well-understood in both and , but is in essence probabilistic, restricted to disordered potentials and insensitive to their individual features exhibited, for instance, on finite sets.
The present paper introduces another approach. It takes advantage of the landscape function from [FM, DFM] to build a box-counting somewhat analogous to the Weyl law and the Fefferman-Phong uncertainty principle, but associated to a different potential, the reciprocal of the landscape . The use of the landscape in place of the original potential allows one to work in a non-asymptotic regime, contrary to aforementioned results, and in some sense to bring the ideas behind the original Weyl law to the lattice without restrictions on the potential or the pertinent eigenvalues, for both deterministic and random scenarios. In practice this approach provides a “black box”, in which the landscape, evaluated directly from the original Hamiltonian, yields an accurate approximation for the integrated density of states without any adjustable parameters, for deterministic and random potentials alike – see the numerical experiments in [FM, ADFJM1, ADFJM3]. The present paper addresses the estimates from above and below and makes the first step towards the mathematically rigorous understanding of the precision of the landscape predictions in the aforementioned works.
In order to describe our main results, we introduce some notations. Let be an integer torus, where , , and , is the congruence class, modulo . For simplicity, we will omit the bar from when it is clear. Let be a real-valued, non-constant, non-negative potential. We denote by the amplitude of the potential. The tight binding Hamiltonian is the linear operator on defined by
| (1.1) |
where is the -norm on . We may think of either as a periodic sequence indexed by or as a periodic function on . We are interested in the normalized integrated density of states of , i.e., the eigenvalue counting function per unit volume:
| (1.2) |
In 2012, a new concept called the localization landscape was introduced in [FM]. Given an operator as above, the discrete localization landscape function is the unique solution to the equation . When and vanishes on the boundary, the landscape is simply the torsion function of the Dirichlet Laplacian.
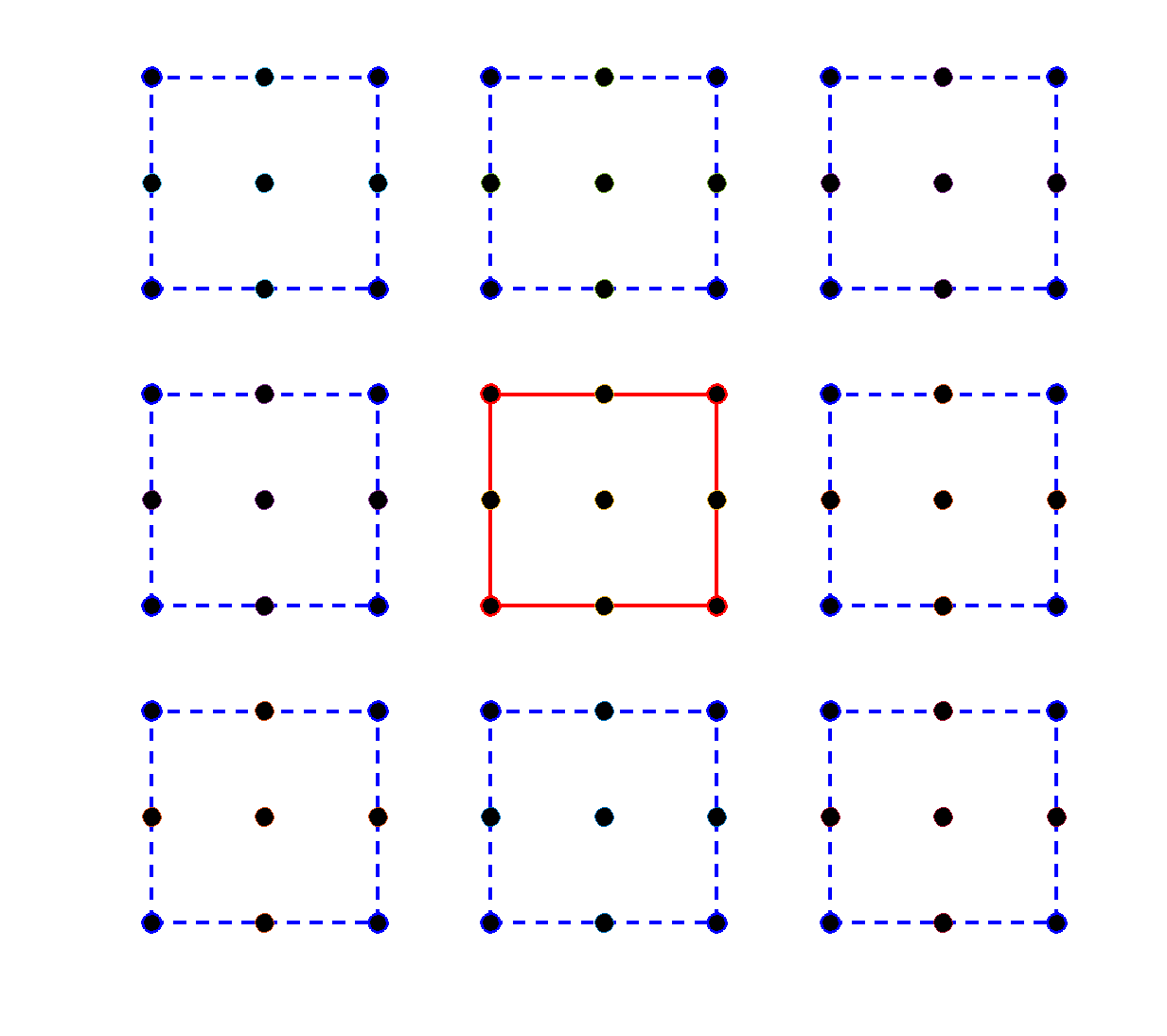
Next, let us define the landscape box counting function . We start by defining, for any positive integer , a partition of the set into subsets which are mostly boxes of side length , as follows. Writing (where the quotient and the remainder are non-negative integers and ), we define a partition of the set into subsets of consecutive elements, and, if , one additional subset of cardinality . The partition then consists of the boxes defined by the Cartesian products of subsets from , see Figure 1.

For given , we then set , and define as the number of boxes on which the minimum of does not exceed , normalized by the size of the set :
| (1.3) |
Our goal is to estimate the integrated density of states in terms of the landscape box counting function . To this end, we will establish several estimates, stated below as Theorems 1, 2, and 3, which we collectively refer to as the Landscape Law.
The first result, which will be proven in Section 3.1, shows that, after a proper scaling, provides an upper bound for over the whole range of .
Theorem 1.
Let be a non-constant, non-negative potential. Then there is a dimensional constant , such that
| (1.4) |
In saying that is a dimensional constant, we mean that it depends only on , and, in particular, is independent of and . In fact, we can take in (1.4).
The next theorem, proved in Section 3.2, contains the key estimate for obtaining a lower bound for .
Theorem 2.
Retain the hypotheses in Theorem 1. Then there are dimensional constants (in particular, independent of and ), such that
| (1.5) |
and
| (1.6) |
In order to get a positive lower bound on , we will remove the negative correction terms on the right-hand side of (1.5) and (1.6) through several complementary mechanisms. We roughly divide potentials into two regimes, corresponding to potentials satisfying a certain scaling condition and to certain disordered potentials. Note that these regimes could overlap and do not between them cover all potentials.
1.1. Deterministic potentials subject to the doubling scaling estimates
Theorem 3.
Assumption (1.7) is analogous to doubling hypotheses which are commonly used in the continuous case for elliptic PDEs. Such estimates are standard consequences of the Harnack and De Giorgi–Nash–Moser arguments which hold for homogeneous equations and for the Schrödinger equation with relatively slowly varying potentials, for instance, within the Kato class. See the discussion in [DFM, Ku, HL].
The scaling condition (1.7) also holds whenever is periodic. Indeed, suppose that is periodic in each of the coordinate directions with period vector (see, e.g., [DLY, Ea, HJ, RS]). Assume that is divisible by each . Then, as we show in Section 3.4, the scaling condition (1.7) is satisfied with depending on , and , but not on , which yields
Corollary 1.
Let be as in (1.1), with a non-trivial periodic potential as above. Then
| (1.9) |
where are dimensional constants and depends on , and only.
Perhaps the major example when (1.7) might fail is that of disordered systems. Indeed, if on a 1-dimensional lattice we could have an arbitrarily long region of followed by an arbitrarily long region of , that would correspond to a region of followed by a region of . In the first case is quadratic and in the second exponential, which clearly destroys the “doubling” required by (1.7). Fortunately, there is a complementary mechanism to obtain an improved estimate akin to (1.8) from (1.5).
To illustrate it, suppose that for belonging to some interval on the positive half-line, we have the bounds
where the power . Substituting these bounds into (1.5) and choosing sufficiently small, it is easy to deduce the lower bound (1.8) on for in the same interval. A similar argument can be used to obtain a lower bound for , or, more precisely, for the expectation of , in the case of Anderson potentials or any disordered potential near a fluctuation boundary. This is basically due to the fact that the aforementioned exponential nature of the Lifshitz tails “beats” the negative polynomial correction in (1.5).
1.2. Disordered potentials
Assume that the values are given by independent, identically distributed (i.i.d.) random variables, with common probability measure on . Denote by the common cumulative distribution function of and by
the support of the measure . We assume that and . We denote by the expectation with respect to the product measure on generated by .
Theorem 4.
Let be an Anderson-type potential as above. Let be as in Theorem 1. Then there are constants depending on , the expectation of the random variable, and , such that
| (1.10) |
Furthermore, there is a constant depending on and expectation of the random variable, such that if, in addition, , then (1.10) holds with the constants independent of .
We note that in the course of the proof of Theorem 4 we prove the following universal bound on Lifschitz tails in terms of the cumulative distribution function .
Proposition 1.
Retain the setting of Theorem 4. Then there are constants , depending only on the dimension and the expectation of the random variable (but independent of ), such that
| (1.11) |
To the best of our knowledge, this statement has never been formulated in this generality, even though perhaps it would not surprise the experts. The more traditional, weaker double log asymptotics are now considered classical (see [Li, KM2, Si, Ki]) and for certain classes of random potentials they have been improved in [BiKo, Ko, KM1] and other works. Here, Proposition 1 does not carry any a priori assumptions on the underlying probability distribution, and is a by-product of the landscape method.
1.3. The dual landscape and computational examples
Contrary to the continuous case, the spectrum of the discrete Schrödinger operator is a compact subset in . The eigenvalue counting near the top of the spectrum for close to can be converted into the counting near the bottom of the spectrum for close to . Such a conversion is obtained via a dual model , see [LMF, WZ]. One defines the dual landscape function as the solution to and the box-counting function using (1.3), leading to
Corollary 2.
If one carefully tracks the values of the constants in (1.10) and (1.12) obtained in the proofs, they are of course far from optimal. However, the formulas emphasize the correct features of the spectrum and, as we have mentioned above, the numerical experiments actually yield even more satisfactory results than the formal estimates seem to warrant. In [DM+] and accompanying numerical work still in preparation, we show that there are very stable constants such that a practical landscape law holds: , see Figure 2.
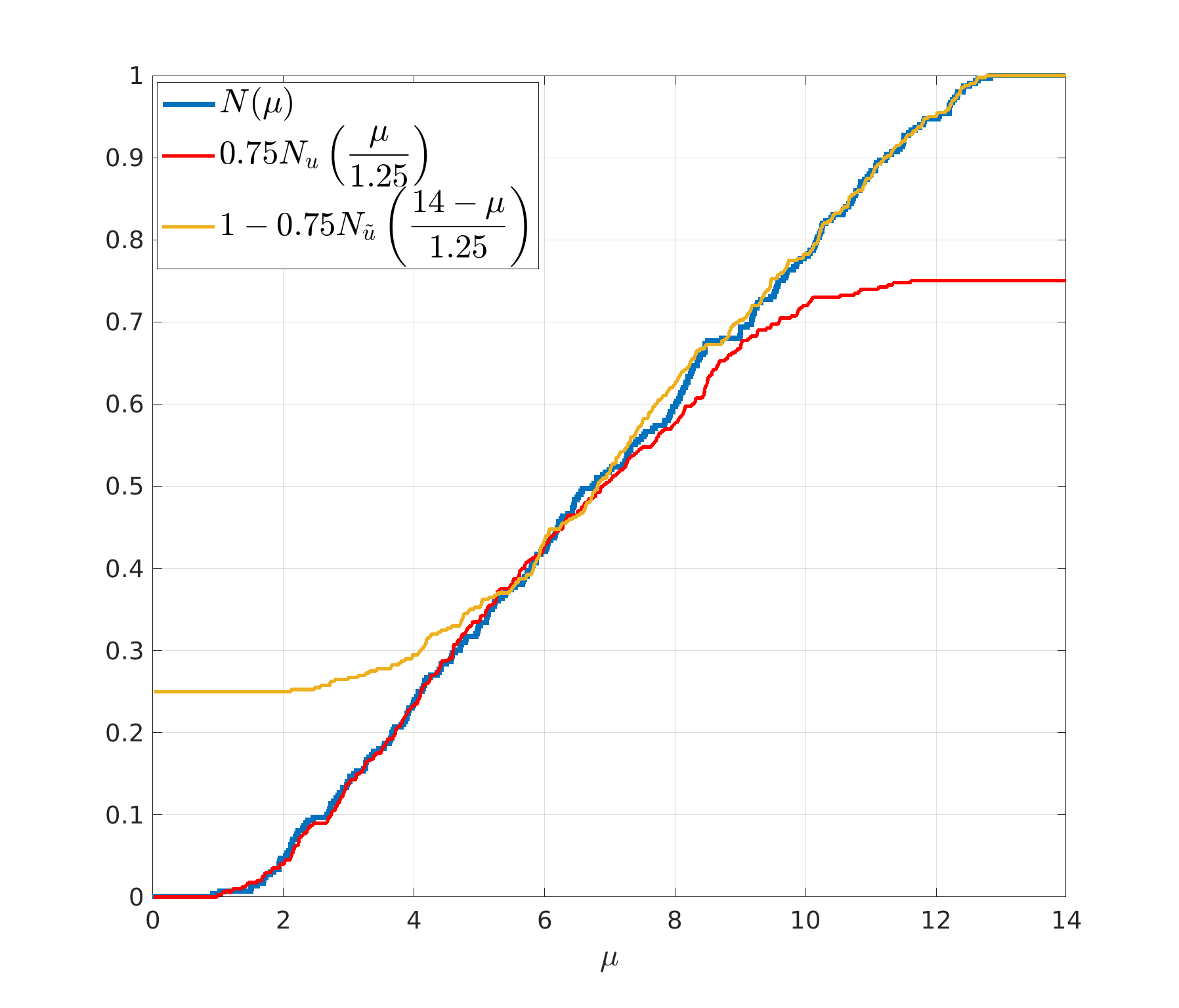
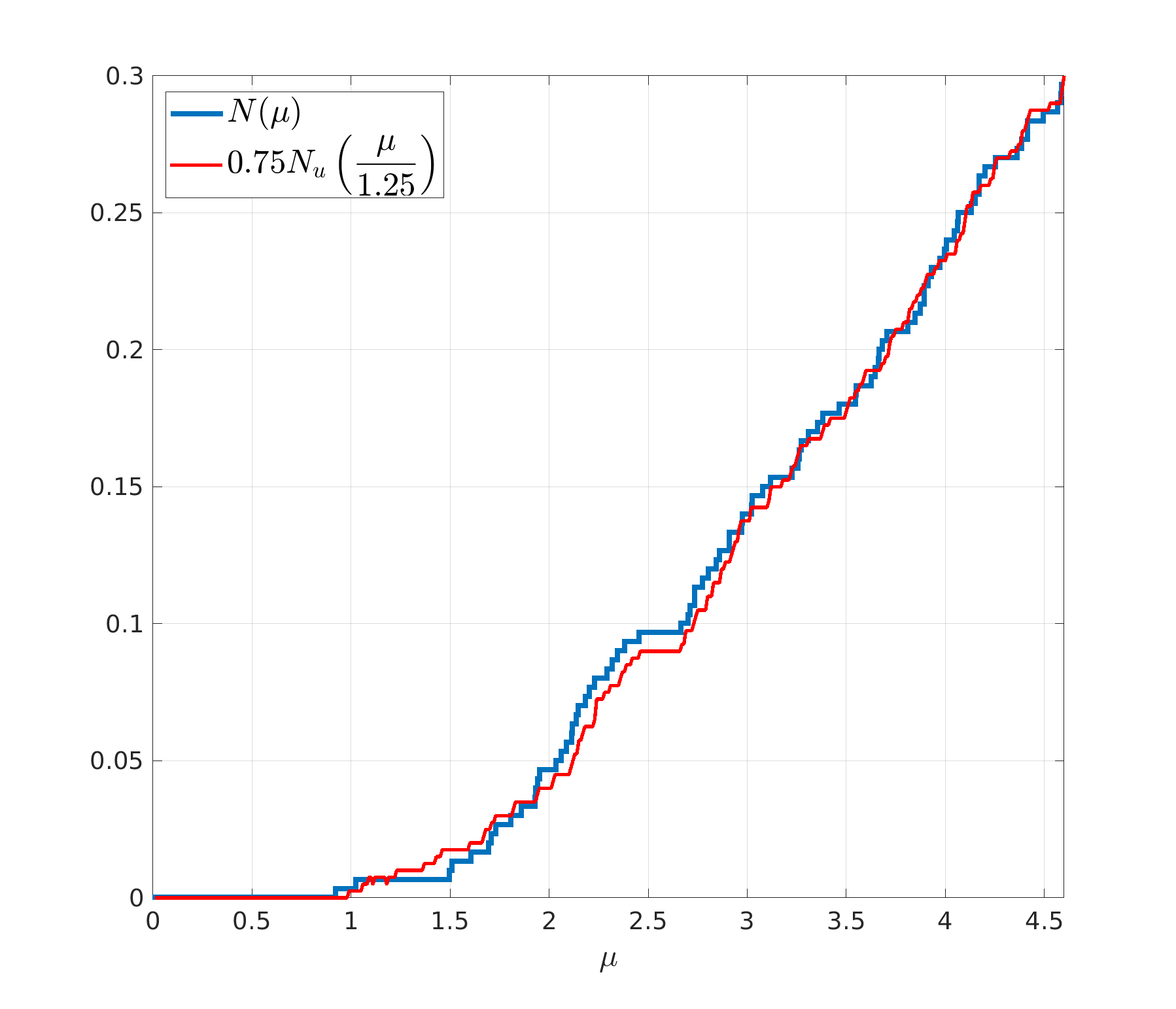
We would like to point out that the landscape counting function, being a deterministic rather than a probabilistic tool, even picks up a spectral gap around the energy – a feature which would not be feasible, for instance, via the Lifschitz tail estimates. These details would of course disappear in the limit of an infinite domain but they demonstrate a surprising precision of the Landscape Law compared to any other currently available method.
The rest of the paper is organized as follows. We state preliminaries for tight-binding Hamiltonians and the discrete landscape theory in Section 2. In Section 3, we study deterministic potentials and prove Theorem 1, 2, 3, and Corollary 1. In Section 4, we concentrate on the Anderson model. We first prove the Lifshitz tail estimates for and finally conclude Theorem 4 in Section 4.2. Section 4.3 is a discussion of the dual landscape theory. In the Appendix, we include some technical estimates for discrete harmonic functions and a well known probability result called Chernoff-Hoeffding bound. The key properties of the landscape function strongly rely on the foundations of the theory of elliptic PDEs. Many of these results require different techniques on compared to their continuous analogues. For instance, because of the lack of rotational symmetry and dilational invariance, many estimates for the Poisson kernel and the Green’s function are not known on a lattice, and are technically difficult to prove. A substantial portion of the paper is devoted to the discrete analogues of these elliptic estimates, and we hope they will be of independent interest.
Acknowledgments. Arnold is supported by the NSF grant DMS-1719694 and Simons Foundation grant 601937, DNA. Filoche is supported by Simons Foundation grant 601944, MF. Mayboroda is supported by NSF DMS 1839077 and the Simons Collaborations in MPS 563916, SM. Wang is supported by Simons Foundation grant 601937, DNA. Zhang is supported in part by the NSF grants DMS1344235, DMS-1839077, and Simons Foundation grant 563916, SM.
2. Preliminaries
In the tight-binding model, the Hilbert space is taken as the space of sequences where we may think of either as a function on or as a sequence indexed by . The lattice is equipped with the -norm:
| (2.1) |
which reflects the graph structure of . We will also frequently need the infinity (maximum) norm
| (2.2) |
Two vertices are called the nearest neighbors if . We also say that nearest neighbors are connected by an edge of the discrete graph . We denote by the elements of the canonical basis of . For , its -th directional (forward) difference is defined as
| (2.3) |
and its gradient is
We also denote the dot product and the induced norm of the resulting vectors by , and The discrete (graph) Laplacian on is defined as usual, acting on , via
| (2.4) |
For a real sequence on , the potential is a multiplication operator acting on as . The operator is called the discrete Schrödinger operator on . If one takes as independent, identically distributed random variables (in some probability space), the random operator is usually referred to as the Anderson model. We refer readers to [AW, Ki] for more details and a complete introduction to tight-binding Hamiltonians and the Anderson model.
Throughout the rest of the paper, we consider the discrete Schrödinger operator restricted to a finite domain in . Let , where and , is the congruence class, modulo . For simplicity, we often treat as a subset of . Slightly abusing the notation, we denote by the induced 1-norm of on the congruence class , where, for example, we consider two points and to be nearest neighbors and to have distance one from each other in . From now on, we will concentrate on the finite dimensional subspace of . We frequently write for simplicity. The linear space is equipped with the usual inner product on , which is denoted by . It is easy to check that for ,
| (2.5) |
which specifies the periodicity of .
We assume that is real valued and non-constant, and that . We set and let be the restriction of to :
| (2.6) |
Similar to the continuous case, the discrete Hamiltonian can be written in its Dirichlet form on the periodic lattice :
where .
It is easy to check that all eigenvalues of in (2.6) are contained in for any finite . For the Anderson model acting on the entire space , it is well known that the spectrum is (almost surely) the non-random set .
A linear operator acting a finite dimensional space may be viewed as a matrix. For example, acting on in (2.6) may be identified with the sum of the two matrices,
| (2.7) |
It is easy to verify that is invertible. Moreover, by the maximum principle (see Lemma A.2), all the matrix elements of its inverse are positive, for all . Therefore, there is a unique positive vector solving the equation . The equation will be referred to as the landscape equation and the solution , will be called the landscape function. The function thus defined is the discrete analogue of the landscape function in [FM] in the continuum setting. The discrete landscape function was first introduced in [LMF], for a one dimensional lattice with zero boundary conditions. It was studied on a higher dimensional lattice with periodic boundary conditions in [WZ]. The following result can be found in [WZ].
Theorem 5 (Theorem 2.10, Lemma 2.12 in [WZ]).
Assume that and is not identically zero. Let be the unique solution of the landscape equation . Then
| (2.8) |
As shown in [ADFJM2] for the continuous case and in [WZ] for the discrete case, serves as an effective potential via the following landscape uncertainty principle:
Theorem 6 (Lemma 2.14 in [WZ]).
For any ,
| (2.9) |
where .
Let us introduce a few more notations. For , we denote by consecutive integers from to . We will frequently work with cubes in , and their images in . For , we say that is a cube in of side length , which is the cardinality of projected in each direction. We denote by the total cardinality of and call it the volume of when it is clear. For any , is the translation of in , respectively having the same side length and volume. For a cube , we denote by the cube concentric with of side length
| (2.10) |
see Figure 3.
Let be the (inner) boundary of :
| (2.11) |
and let be the flat part of the boundary, removing all the corners:
| (2.12) |
For an integer interval of side length , we denote by the middle third interval of . For a cube , we denote by the middle third cube of , defined as:
| (2.13) |
It is easy to verify that is the “thin” middle third part of in the sense that and . The relation becomes if .
3. Landscape law: the general case and the self-improvement under the scaling condition
In this section, we study Theorems 1, 2, and 3. Let us recall some of the notations first. Let be the periodic domain of side length . Let be the (finite volume) integrated density of states (IDS) of on , as defined in (1.2).
Let be the landscape function of defined in the introduction. For , let and let be the landscape box counting function, defined with respect to the partition as in (1.3), see Figures 4, 5 for examples on .
Remark 3.1.
The landscape box counting function is defined with respect to to the partition . Consider any translation of by , i.e., . Then is also a partition of of size since is a periodic torus. Each can be covered by finitely many cubes , and vice versa. The number of cubes from one partition needed to cover a cube from another partition is at most . Therefore, if we use to define a landscape box counting function , the counting function will differ by at most a factor of , i.e., for any
Furthermore, if , then is a finer partition than . Each can be covered by at most cubes . Therefore, the number of such that will differ from the number of such that at most by a factor of . In other words, for ,
Based on the above discussion, we are allowed to estimate by either shifting the original partition or tweaking the side length of the partition slightly. The change of the partition will lead to a different box-counting function, but the new counting function will differ from only by some multiplicative dimensional constants. This will be very useful in the proofs.
3.1. Upper bound. Proof of Theorem 1
Let be as in (2.6) acting on . We denote by the inner product on induced by the usual one on .
Case I: . We will actually start with , and then consider the rescaling in the end. To get an upper bound for , it is enough to bound from below on some subspace of . For , let be the partition of side length . Let
Let be the linear subspace of the vectors in whose average on each is zero, i.e.,
The subspace has many linear independent constraints since all are disjoint. Therefore, has codimension .
By the landscape uncertainty principle (2.9),
We see that
which implies
Therefore, for ,
| (3.1) |
In the second sum, since . Therefore,
To bound the gradient term on the right-hand side of (3.1), we need the discrete version of the Poincaré inequality (Lemma A.4 in Appendix A): for any cube of side length ,
Notice that the last in each direction may not be a regular box of equal side length, the above estimate remains the same since the side length of the irregular box does not exceed , see (A.3) in Lemma A.4.
Putting these two parts together, one has for
Therefore, using the mini-max characterization of eigenvalues, the number of eigenvalues of below is bounded from above by the codimension of the subspace , which is equal to . Hence,
Equivalently,
| (3.2) |
Case II: . Similar to Case I, we will work with , and then consider the rescaling in the end. The construction is similar to the previous case. Let
From the definition of in (1.3) and the fact that , we see that .
Due to (2.9),
where we have used the fact that on for the first equality. Notice that in this case, we do not need the Poincaré inequality.
Therefore, for all , . Since is non-decreasing, it implies that for . Equivalently,
| (3.3) |
3.2. General lower bound in the non-scaling case. Proof of Theorem 2
Similarly to the upper bound, if one can bound from above on a subspace of , then the eigenvalue counting function will be bounded from below by the dimension of this subspace.
Proof.
Given , let .
Case I: , i.e., for some . We will deal with the following three sub-cases for small, mild, and large .
Case I(a): We first consider and therefore . In this case, one has . Therefore,
| (3.4) |
Consider the partition of of side length , and, for each of side length , consider the finer partition of side length . Clearly, the collection of all for all also forms a partition for of size :
| (3.5) |
Since , then due to (3.4). For each , let be a cube in such that , where is the center of in and the distance is measured in . We call such a centric cube with . We see that a centric cube satisfies , cf. (2.10), (2.13), since . The notion of centric cube means that we consider cubes in and as subsets of , and then pick to be a cube in closest to the center of in . Note that the choice of a centric cube may not be unique. That would not effect the estimates below and the translation arguments in (3.16) due to Remark 3.1.
For any , let
| (3.6) |
Given , let be the middle third of as usual. Let be a discrete cut-off function supported on and such that
| (3.7) |
and
for . Such a cut-off function is the discrete analogue of a smooth bump function in the continuous case. We include an explicit construction in Appendix A.3 for reader’s convenience.
Let be the linear subspace of which is spanned by the cut-offs of to each in . More precisely, we define
The subspace has dimension since all are disjoint and .
We aim to estimate from above for each in . First, by the landscape uncertainty principle (2.9),
| (3.8) |
On the other hand, recall that , so that
Since , applying the discrete Moser-Harnack inequality in Lemma A.11, Appendix A.6, to on the smaller cubes with , one has
| (3.9) |
By the definition of in (3.6), one has
| (3.10) |
Notice that implies , i.e.,
| (3.11) |
Therefore, putting (3.8) and (3.9) together and using ,
| (3.12) |
where . In the last line, we used (3.4) with .
Then, by orthogonality of the for , we get for
| (3.13) |
the estimate
| (3.14) |
Given an integer , , we consider a translation , by the vector , i.e., for any . For the partition , denote by the partition translated by . Recall that is the finer partition of side length , see (3.5). Denote by the translation of , which again is a refinement for . For any , it is easy to check that In other words, the collection of all will cover the entire , provided enough tanslations of (at most many).
For each translated centric cube in the corresponding , we repeat the construction of and starting from (3.6). By exactly the same argument as for (3.14),
| (3.15) |
where is the same as in (3.13) since the eigenvalue counting will be the same for all the translations, and
Recall that has side length and is located near the center of each . We repeat the above process exactly times so that , and therefore, , which is exactly the fine partition of the entire domain. One translated corresponds to exactly one small cube in the original partition . The number of the translations we need can be bounded from above by . Notice that for all , we have for some dimensional constant because of Remark 3.1. Then, summing up (3.15) over all possible translations,
| (3.16) | ||||
Therefore, the upper bound on the number of the translations implies
| (3.17) |
Notice that the partition in the counting of is of side length , which is exactly the side length needed in the definition of . On the other hand, the partition in the counting of is of side length . The side length needed in the definition of should be , which is larger than used in . But the two counting functions defined by or will only differ by a dimensional factor since , see Remark 3.1. Therefore,
Then by (3.17)
which implies that
| (3.18) |
provided that , .
We notice that the construction above also needs the entire domain to be large enough, i.e., . The restrictions on can be removed easily. If , then we can repeat the above construction by setting directly, the proof for (3.18) is exactly the same. If then there are at most boxes in the partition. Therefore, . On the other hand, the argument for (3.8) can be used to show that the ground state eigenvalue of is bounded from above by , with a dimensional constant . Therefore, . Then (3.18) holds trivially by picking small, and the smallness only depends on the dimension.
Case I(b): Next we consider . Note that the range of requires , which is fulfilled by the assumption of . In this case, the side length and . For each , we pick to be a centric cube with , then construct in the same way as (3.6). The upper bound (3.8) for remains the same. To bound from below, one has trivially since . The bounds on and the definition of imply
Hence,
| (3.19) |
where the constant only depends on and . We obtain the bound as in (3.12), and therefore the same bound (3.18) holds for all .
Case I(c): The remaining case is . Since , then . In this case, the range of implies and . We construct with cube of side length instead. Note that this will not change the counting for and . The change will only result a different counting for , which we denote by the new counting using . Since , one has , due to Remark 3.1. Similar to (3.19), one has
since . Then we repeat the arguments for (3.15)-(3.18) using translations. Notice that the number of translations needed in this case is bounded from above by a dimensional constant . We obtain instead
| (3.21) |
Finally, we require further that so that where . Therefore, the estimates (3.20) and (3.22) cover and respectively. This completes the proof of Theorem 2.
Case II: either or , where and are the same in Case I. Without loss of generality we assume that
The other two cases, where either or , are similar. Recall the construction of the partition for and . In the last row and column of each direction we need to use a rectangular box instead of a cube. We denote the regular cube of side length or still by and , and denote the remaining special rectangular boxes by and , whose side lengths are and , respectively, in at least one direction, and write
| (3.23) |
Notice in this case, the union is not the original partition , but it is a finer one. Therefore, the counting function defined through will be bounded from below by the counting function defined through .
In this case, we define only using the regular cubes and ignoring all the . Then by exact the same construction, we obtain (3.14), i.e., . Next, we need to translate the partition and by vectors of length several steps in each direction, so that the centric small cubes can cover the large cubes . In the previous case, we needed at most steps in each direction. In Case II, we want to continue the translation up to steps in each direction, where the total number of translations in all directions is at most . By doing this, the translated centric cubes will cover . In particular, they will cover all the irregular boxes near the boundary of the domain. Notice that for the regular cubes , translations up to steps will cause an overlap, which leads to an overestimate in the corresponding sum as in (3.16). But since and the are contained in for each , the over-counting will be at most times more. In conclusion, we can obtain
Note that in the last line the collection of pertinent cubes or already includes the irregular boxes or respectively. Together with the fact that is finer than , we obtain that
which implies . This is the same estimate as we obtained in (3.18). Replacing by as in the remaining arguments in Case I, we can obtain (3.20) and (3.22) in a similar manner. ∎
3.3. Lower bound in the scaling case. Proof of Theorem 3
Let
| (3.24) |
where is a dimensional constant that will be specified later.
We need to consider two cases, corresponding to and . Similar to the arguments in the previous subsection, the latter can be be reduced to the former by a translation argument. For simplicity, we will only deal with the case for some . Also, we first assume that is small and , so that the cube of side length is large enough to construct cut off functions as in (3.7). Otherwise, when is large and is small, we start with and tweak the dimensional constants in the end by Remark 3.1 as in the previous subsection.
For , i.e., , one has . We consider the partition consisting cubes of side length as usual. Let
where is the cut-off function as in (A.7) on each . The dimension of equals .
Our goal, once again, is to establish estimates similar to (3.12). The upper bound for remains the same as we obtained in (3.8):
| (3.25) |
It remains to obtain the lower bound for . First, the Moser-Harnack inequality (A.41) implies that
Then we apply the scaling condition (1.7) twice, to write
Hence,
where depends on , and . By the choice of in (3.24),
and by definition for , . Then we have
Therefore,
Putting the upper and lower bounds together, we have that
where depends only on and the dimension . Therefore,
Notice that in the definition of , the side length of the cube is smaller than the side length required in the definition of . The box counting using can be bounded from below by the box counting using , due to Remark 3.1. The above estimates also require , i.e., . The restriction on can be removed exactly in the same way as for the non-scaling case, by multiplying counting functions by a dimensional constant . Therefore, we obtain for all . Equivalently, one has that
| (3.26) |
Next, we consider and . In this case, we construct and using cubes of side length and tweak the dimensional constants in the counting in the end by Remark 3.1. The upper bound for remains the same as in (3.25)
| (3.27) |
for some dimensional constant . For the lower bound on , we apply the Harnack inequality (A.43) to on . We obtain
| (3.28) |
for some constant depending on . Therefore,
| (3.29) |
for some constant depending on , and . Then
Equivalently, one has
| (3.30) |
Clearly, in (3.26), we can make so that the estimates (3.26) and (3.30) cover all . This completes the proof of Theorem 3.
3.4. Lower bound for the periodic potential
In this part, we prove Corollary 1 for a periodic potential . It is enough to show that the landscape function associated with the periodic potential satisfies the scaling condition (1.7). Informally, this is quite obvious. Indeed, at small scales (below ) we simply use the Harnack inequality. The emerging constant is roughly of the order of then. At large scales we simply use periodicity to reduce to small scales. Here are the details.
Suppose is periodic with period . Let be the fundamental cell of . Notice that the condition , guarantees that contains finitely many copies of . Let be the restriction of on with the periodic boundary conditions, and let be the landscape function for , i.e., . By the uniqueness of the landscape function (Theorem 5), will be the periodic extension of to the entire domain .
For and , let be cube in of side length . Consider , a collection of disjoint translations (copies) of the fundamental cell by . Suppose . It is easy to verify that the maximal number of copies of in the collection which lie inside (we will call their union ) and the minimal number of copies of in the collection which cover (we will call their union ) differs by a dimensional multiplicative constant. Therefore, denoting the number of copies of in by and using the periodicity of with respect to all translations of , one has,
which shows the scaling condition (1.7) is true for relatively large cubes.
4. Landscape law for the Anderson model
There must be changes propagating from changes in the previous section, at treatment of small scales. I do not bother about it for now. In the present section we will concentrate on the Anderson model. To this end, we consider with the values given by independent, identically distributed (i.i.d.) random variables, with common probability measure on , subject to the conditions stated in the beginning of Section 1.2. In particular, denoting by the common cumulative distribution function of , we have if , if , and there is a , such that
| (4.1) |
We note that can be picked to be less than since . Hence . Some constants used in the proof of this section receive their dependence on through and .
4.1. Estimates for in the Anderson model
We will study the following tail estimates for first.
Theorem 7.
Let be an Anderson-type potential as above. Then there are dimensional constants such that
| (4.2) |
Furthermore, there are constants , and depending on only, such that
| (4.3) |
Remark 4.1.
All the constants are independent of .
After we establish these tail estimates for , we will combine them with the deterministic result Theorem 1,2 to prove Theorem 4, and (1.11).
Proof. The proof of (4.2). For , let Let be partition of size as usual. It is enough to assume that for some , otherwise the counting can always be bounded from below by ignoring the irregular boxes in the last rows/columns of . For all cubes , let if and otherwise. Direct computation shows that
| (4.4) |
For each , consider translations of by the vectors for all directions and . Here is some large integer that will be specified later. Let be the union of these translated cubes,
Similarly to (A.7), one can construct a discrete cut-off function , supported on , and satisfying
By the landscape uncertainty principle (2.9), one has
provided . Therefore, for all ,
where and . On the other hand, notice that all the translations still belong to . Then we can rewrite as which implies that for all
Summing the left-hand side of the above inequality over all , one has
Combining this together with (4.4), one has
Note that we also need to impose the condition on the size of domain so that , i.e., .
This will be the most delicate part. We need several technical lemmas concerning the growth of the landscape function. Some of these estimates may have independent interest in the landscape theory.
For any , let be cube of side length and let be the middle third cube as defined in (2.13). We are going to show that there is a suitable (large, and only depending on the expectation of the random variable), such that for any (small enough, depending on ), and any cube of side length
| (4.6) |
for some suitable constants (depending only on the dimension and , and independent of ).
We start from the following deterministic statement. The lemma states that the landscape function is forced to grow at a certain rate if is reasonably non-degenerate.
Lemma 4.1.
Let be the landscape function given by Theorem 5. Let be a cube of side length , and let be the middle third as usual. For any , there is such that for all , there are constants , and , such that the following statement holds. If satisfies conditions
- (i):
-
(4.7) - (ii):
-
there is a such that
(4.8)
then for all , there is a such that and
| (4.9) |
Remark 4.2.
This lemma holds for any , and works for any cube of side length . The choice of , and only depend on , and is independent of the choice of , neither on its size nor the position.
Remark 4.3.
Note that this Lemma is a completely deterministic result. It has nothing to do with the randomness (structure of ). It can be applied to any and as long as locally on the lattice (containing the cube and its neighborhood). In our proof, Lemma 4.1 will lead to some important probability estimates. The small parameter will be picked at the very end when we are about to prove (4.6).
We need some technical preparations for the average of . We will frequently write to make the notations of the sub-index easier to read. For , and , we denote by the box centered at of side length :
We will omit the center (fixed) and write when it is clear. We denote by the inner boundary of as defined in (2.11), and by the boundary removing the “corners” as defined in (2.12). For , we have the “degenerate cube” . Notice that . Let be the average of on with respect to the (discrete) Poisson kernel (see the definition and properties of in (A.12) in Appendix A.4):
| (4.10) |
in other words, a harmonic function with data on the boundary. Let be the corresponding weighted average of on :
| (4.11) |
where for any , and
| (4.12) |
By the properties of the discrete Poisson kernel, one has
| (4.13) |
The first two estimates are lower bounds on and .
Lemma 4.2.
There is dimensional constant , such that for any and
| (4.14) | |||
| (4.15) |
Proof.
Let be the landscape function for the free Laplacian on with zero Dirichlet boundary condition:
Let . Direct computation shows that
By the maximum principle (Lemma A.1), one has for all , . Let be the harmonic function on with the boundary data equal to , i.e.,
Then by the Poisson integral formula (A.15), . On the other hand,
Therefore, for all . In particular, proving (4.14), and a similar statement is true for , so that
Summing over , one has
which implies as desired. ∎
Lemma 4.3.
For any and there is a constant (independent of ) and a constant such that for any cube of side length , there is a subset such that and
| (4.16) |
Remark 4.4.
The lemma is true in all dimensions. However, for , we actually do not need to remove any portion of the cube (an interval in ) to obtain (4.16) since the 1-d Poisson kernel is rather trivial (constantly ), and so is .
Proof.
Write . The estimate follows from the lower bound of on each as long as is away from the edges (and the corners). Given , according to Lemma A.9, there exist and such that for all , on except for many , where only depends on the dimension. Therefore, on except for many . For , we then have except for those on the edges and corners, whose total cardinality is at most . This again implies for all except for many . Therefore, for some constant only depending on and , and the cardinality of the exceptional set of violating this, is at most . ∎
With these two technical lemmas, we are ready to the
Proof of Lemma 4.1.
Let and be given as in Lemma 4.1, where . Clearly, . Denote by the set in condition (4.7), that is, where will be be picked later. Fix , we assume that . Let be defined in (4.11). Let and let
| (4.17) |
where the last equality follows from (4.13).
Now we are ready to look for satisfying (4.9) in the following two cases:
Case I:
Let be the constant from Lemma 4.3, then pick and let be also the constant from Lemma 4.3. Then
Therefore,
Direct computation shows that
By the definition of and (4.17), this implies that
Therefore, there is one point such that By (4.15) and (4.8),
provided Therefore, (4.9) holds for .
Case II:
Take for some small , which gives . Let and be the surface average and the Green’s function on respectively, as defined in (4.10),(A.13). Applying the discrete Green’s identity (integration by parts formula) (A.15) on and , one has
Then
Notice that in . By the maximum principle, Lemma A.3, one has
where we used for and the discussion for an annular region after Lemma A.3.
Notice that Lemma 4.1 is deterministic and requires no randomness of . A direct consequence is the following estimate on the probability that grows.
Lemma 4.4.
Let be the Anderson-type potential as in Theorem 7. Fix , and retain from Lemma 4.1. For any cube of side length , define the event
| (4.18) |
Assume that , otherwise, just reset to be . For any , set
| (4.19) |
where is the largest integer such that . Let , and .
Proof.
The idea is to repeatedly use Lemma 4.1 to construct a sequence of growing cubes and stop when the final cube exceeds the size of the entire domain.
We start with of side length . Assume that . We pick some such that . Then (4.8) is satisfied. Suppose furthermore that fails. Then (4.7) holds for . All in all, Lemma 4.1 gives a point , such that where is measured in for lattice points and
Additionally, we can require which implies that . Clearly,
Therefore, can be covered by at most disjoint cubes in of side length , namely, . Recall the definition of the middle third set in (2.13). Now extend each to a cube such that has side length and contains each as a middle third part for . Note that these are not disjoint. But the overlap does not effect our estimate on the probability of the events from above.
In order for the induction driven by Lemma 4.1 to continue, we need to exclude the event that (4.7) fails for all . To this end, we define Assume that fails, which implies that (4.7) holds for all . Let be the one that contains . Now for , Lemma 4.1 gives such that
| (4.21) |
Repeat the construction for and ,
Therefore, can be covered by at most disjoint cubes of side length , . Extend to in the same way, and define We assume that fails, and find by Lemma 4.1. Inductively, at step , we assume that all the previous events, fail, and obtain satisfying (4.9) and then define . The same estimates as for hold for all , and hence,
| (4.22) |
and
| (4.23) |
Then , are defined in the same way as we did in the previous steps. Because of (4.23), for all , we need many to cover . Then we define the event Since are i.i.d., the probability of each is translation invariant, and only depends on the size of the cube . In particular, Therefore, for some dimensional constant ,
| (4.24) |
provided that .
We will continue the construction until we reach the -th step and obtain , , , and .
We need to apply Lemma 4.1 two more times for the final step. However, according to our choice of , assuming that fails will already result a cube of side length which may exceed the maximal size of the entire domain . To alleviate this issue, we need to enlarge the domain at this point for the last two steps, by making several copies of 111We can do this from the very beginning of the construction, but it will not make any difference until we reach the size of .. We need many copies where .
Let so that and denote
We extend the potential periodically to , where and Now we consider the landscape equation on for with periodic boundary conditions. The enlarged system has a unique solution by Theorem 5, which is a periodic extension of the original to . Now we can return to the construction at the -th step.
Assume that the event fails. Then (4.7) holds for all possible that may contain . We have Applying Lemma 4.1 to on , we obtain , such that
| (4.25) |
where the last inequality follows from the definition of . Now let be a point where attains its maximum. Clearly, also attains its maximum at ,
| (4.26) |
Together with (4.25), we have Now consider , which is the middle third of . Let
Since , one has
| (4.27) |
Now if fails, apply Lemma 4.1 one last time to on 222One also needs to take nine times larger, so that in (4.26) to meet the requirement in Lemma 4.1.. Then (4.9) implies that there is a such that . This is a contradiction. Recall that it happens when we start with and assume that all fail. Therefore, at least one must be true. In other words,
Together with (4.24) and (4.27), this completes the proof. ∎
The next lemma allows us to estimate the probability of each term on the right hand side of (4.20).
Lemma 4.5.
Let be the Anderson potential as in Theorem 7. Let and be as in (4.1). For any and , if is such that , then
| (4.28) |
where
| (4.29) |
is the Kullback–Leibler divergence between Bernoulli distributed random variables with parameters and respectively.
As a consequence, for any ,
| (4.30) |
where .
Furthermore, there is a , which only depends on such that for all and any , one has
| (4.31) |
Remark 4.5.
The can be taken as of order , see (4.37).
Proof.
Let be the characteristic function for the event , i.e., for and otherwise. Since are i.i.d. random variables, all are i.i.d. Bernoulli random variables, taking values in , with common expectation . Let By the Chernoff–Hoeffding Theorem, [Ho] (see Lemma B.1),
| (4.32) |
where and is as in (4.29). Then (4.28) follows directly from (4.32) since
Examining the the Kullback–Leibler divergence with parameter and , one has
where we used and . Therefore,
| (4.33) |
which yields (4.30).
Let . For ,
| (4.34) |
On the other hand, it is easy to check that
| (4.35) |
Then there is a such that for all ,
| (4.36) |
Combined with (4.33), this gives
which completes the proof of Lemma 4.5.
One can be more specific regarding the exact value of . For , . If , then , and Let
| (4.37) |
Then for ,
which gives (4.36) similarly to the argument above. ∎
Lemma 4.6.
Remark 4.6.
The exponent can be made arbitrarily close to , by taking smaller, however, it will also result a large factor in front of .
Proof.
Let and define the sequence as in Lemma 4.4 and . Let , and . By the construction of and (4.22), one has
For and , one has provided that . Notice that in the proof of Lemma 4.5, by the choice of in (4.1), one has . Therefore,
since the distribution is non-decreasing. Now apply Lemma 4.5 to all . Combining (4.31) with (4.20), one has
which is the desired bound. ∎
Now we are ready to complete:
Proof of (4.3) in Theorem 7.
For any , let so that . To apply Lemma 4.6, one also needs to ensure that , which requires to be taken in the range .
Now for any cube of side length and its middle third part , Lemma 4.6 implies that
where in given by (4.38) depending on and . Then
| (4.39) |
Notice that . Recall that the cubes used in the definition of have side length . Any can be covered by at most disjoint cubes of side length for some which only depends on . Notice also that the estimate (4.39) is independent of the position of , and can be applied to all cubes of the same size. Therefore,
for any . Together with (4.5), we obtain the desired upper bound
for all . The constants only depend on and , which eventually only depend on and . ∎
4.2. Lifschitz tails for the integrated density of states
Putting together the general upper/lower bounds in Theorem 1,2 for the deterministic case, and the Lifshitz tails in Theorem 7 for the Anderson model, we have
Theorem 8.
Let be as in Theorem 1 and be as in Theorem 7. Then there are constants depending on , and such that
| (4.40) |
If furthermore are as in Theorem 7, depending only on and , and , then the estimate (4.40) holds with constants which are independent of .
If, in addition, , then there are constants depending only on such that
| (4.41) |
Proof.
The upper bound in (4.40) is the average of the upper bound in Theorem 1. We only need to study the lower bound with the help of Theorem 2 and Theorem 7. Let and , be as in Theorem 2. If then and the left-hand side of (4.40) holds trivially. Fix , let us denote and . Assume further that . Then (1.5) in Theorem 2 implies that
| (4.42) |
Therefore,
| (4.44) |
for and . This requires , where
Let be as in (4.1). If we assume, in addition, that is smaller than both and ,
then for all , one has . Therefore, , where , , and The difference term in (4.44) is then bounded from below by
We want to pick small enough (independent of ) so that,
| (4.45) |
that is,
| (4.46) |
Notice that , hence, and provided that . Then the fact that implies that
Solving for , we observe that
would yield (4.46).
Putting everything together, set
Then, for all , (4.44), (4.45) and (4.43) imply that
which completes the proof for the first inequality in (4.40).
It is also easy to verify that if we are only interested in small , then all the can be picked independently of . Therefore, the final constants are also independent of . In particular, let be as in Theorem 7. Then for all
and
where the constants only depend on and , and are independent of . ∎
4.3. Dual landscape and the top edge of the spectrum.
Let be as in (1.1) acting on . In this part, we will briefly discuss the so-called dual landscape and see how it is applied to the eigenvalue-counting for high energy modes. We refer readers to Section 2.4 in [WZ] for more details. For , we define a dual vector
| (4.47) |
where for . We assume, in addition, that is an even number so that . Now suppose is an eigenpair of in . A direct computation shows that
| (4.48) |
where is a non-negative potential and
| (4.49) |
In other words, is an eigenpair of if and only if is an eigenpair of a dual operator . This dual operator is the same type of discrete Schrödinger operator as , only with a different potential (and also taking values in ). We can define a dual landscape function satisfying , and a dual box-counting function as in (1.3) for .
It is easy to check that the cardinality of the eigenvalues of which are smaller than or equal to is the difference of the volume of and the cardinality of the eigenvalues of which are smaller than . Therefore,
| (4.50) |
where and are the finite volume integrated density of states for and , respectively. Here, the counting is defined for eigenvalues strictly less than , which is different from the definition of in (1.2). If is the Anderson-type potential with common distribution , then is also an Anderson-type potential, with common distribution . We denote by . We now apply Theorems 1, 2, 4 and 7 to the dual operator and the dual counting function for near . All the estimates still hold if we replace by and . In particular, the first part of Theorem 4 implies that there are constants depending on , the expectation of the random variables, and such that for all ,
| (4.51) |
Therefore, by (4.49) and (4.50), one has for all ,
Appendix A Discrete Laplacian and harmonic functions
A.1. Maximum principle for sub-solutions
Lemma A.1 (The maximum principle for subharmonic functions).
Let be a box in and let the inner boundary be defined as in (2.11), and let be the flat part of the boundary as defined in (2.12). Let be a non-negative potential on . A vector is called a sub-solution, on (the interior of) if
If is a sub-solution, then the minimum of in must be attained on , i.e.,
| (A.1) |
Proof.
Let . It is enough to prove that whenever for all , we have for all . Suppose not, then Let be such that the minimum is attained, i.e., and . Then implies that . Therefore, , and . If any of belongs to the flat boundary , then it is a contradiction with the assumption that for all . If not, then we pick any of them and repeat the procedure until eventually, after a finite number of steps, we reach the boundary and arrive at the contradiction again. ∎
There will be several direct corollaries of the above maximum principle. We will simply list them as independent lemmas and omit the details for the proof.
Lemma A.2 (Positivity of solutions for periodic boundary conditions).
Let . If is a non-negative potential which is not constantly zero and for all , then for all .
See [WZ], Lemma 2.12, for the proof.
Lemma A.3 (Maximum principle for discrete harmonic functions).
Let be a box in and let be defined as in Lemma A.1. Suppose is a discrete harmonic function on (the interior of) , i.e.,
Then for all
| (A.2) |
This is a direct application of Lemma A.1, to and . We only state maximum principles as above for the boxes in for simplicity, it is not hard to check that the same conclusion would hold for more general domains in , as long as they are “connected” with respect to the discrete Laplacian operator in a suitable sense. In particular, it works for the “annular” domain given by the difference of two cubes, . To be precise, if the boundary of is defined in the same as in (2.11), i.e., and for , then
A.2. The discrete Poincaré inequality
The result essentially can be generalized to any “connected” region in . We only need the version on a rectangular domain.
Lemma A.4.
Let be a a rectangular domain in , where for some and , . For any (real-valued) sequence , let and . Then
| (A.3) |
Proof.
Without loss of generality, we assume that . It is enough to prove (A.3) for . It is easy to check that
| (A.4) |
For , let be a discrete path in connecting and , defined taking the maximal steps along every coordinate. That is, all vertices , are given by , , , and the all edges connecting the consecutive vertices are parallel to . Then
| (A.5) |
We now prove (A.6) for . Fix . Write , where . Assume that . Then . Write for . Direct computation shows that
The same estimate holds for . Therefore, fix , summing over gives
Then summing over gives
which proves (A.6) for . The cases can be proved in a similar manner. This completes the proof of (A.6) and Lemma A.3.
∎
A.3. Discrete cut-off functions
Let be a cube of side length on and let . Let and be given by (2.11) and (2.13). Let the distance be measured by the infinity norm on . Let , be a dimensional subset of which is distance away from :
By the definition of in (2.13), the side length of satisfies It is easy to check that and all are pairwise disjoint for . And .
Now we can define the cut-off function as
| (A.7) |
It is easy to see that if , and otherwise, for all .
A.4. Dirichlet problem on a cube
We study the Dirichlet problem for the discrete Laplacian on a cube in . Recall the definitions of , , , for , and , given right before Lemma 4.2.
Lemma A.5 (Green’s formula).
For any ,
| (A.8) | ||||
| (A.9) |
As a consequence,
| (A.10) |
The Green’s formula for discrete graphs is rather standard, existing in various lecture notes, e.g. Theorem 1.37 in [Ba], see also in [Ch, Gu]. We omit the proof here.
Given and , we proceed to solve the linear system on
| (A.11) |
The problem can be decomposed into the following two systems, which give us the discrete Poisson Kernel and the discrete Green’s function for the Dirichlet Laplacian.
The discrete Poisson kernel is the unique solution to the system
| (A.12) |
for a fixed . Similarly, the discrete Green’s function with pole at , is the unique solution to the system
| (A.13) |
for a fixed , Consider with zero boundary condition as an invertible matrix of the size . Clearly, for , since is self-adjoint.
Moreover, for fixed and , if we apply the Green’s formula (A.10) to and , then
which implies for any and ,
| (A.14) |
Notice that this can be considered as the (negative) normal derivative of in the direction of the outward pointing to the surface of .
Back to the system (A.11), using and , we can solve the system
In particular, we have the following integration by parts formula (Green’s identity) for any at the center of the box :
| (A.15) |
In particular, for any and ,
| (A.16) |
A.5. Estimates on the Green’s function and the Poisson kernel
Retain the definitions in the previous section, for , let be the discrete cube centered at of side length , and let be the discrete Green’s function as defined in (A.13). In this part, we study the behavior of the discrete Green’s function away both from the pole and the boundary . We will approximate the discrete Green’s function by a continuous one to obtain the desired estimates. Let us also recall some of the definitions for the continuous case. Fix , let be a cube in centered at of side length . Let be the continuous Green’s function on the cube with zero boundary conditions:
| (A.17) |
where is the standard Laplacian on , and is the Dirac delta function at in the distribution sense. For any , consider a square mesh of size on . Denote the collection of all the mesh points by
| (A.18) |
We see that is indexed (one-to-one) by , and hence . For , let
| (A.19) |
It is easy to verify that the equation for in (A.13) implies that
| (A.20) |
We see that is the finite difference approximation to the solution of the continuous problem (A.17). The approximation can be quantified as follows.
Lemma A.6.
There are positive dimensional constants such that if , then
| (A.21) |
Remark A.1.
Such an approximation is proved in a rectangular domain in in [La]. It was later generalized to the interior of a domain of any dimension with smooth boundary by Schatz and Wahlbin, see Theorem 6.1 [SW], using the finite elements approach. The method in [SW] potentially can be generalized to any convex polyhedral domains, up to the boundary. Here we present a direct proof using the series expansion of and . Similar estimate also holds for where the pole is not far away from the center . We will only deal with the case which will be enough for our use.
Proof.
Without loss of generality we assume that . In this case, the mesh points and , where . Due to the symmetry of the problem, it is also enough to prove (A.21) on the upper half cube . Below, we construct the analytic series representations of and on .
For the continuous case, the analytic expression of is well known by the method of the partial eigenfunction representation. Throughout the rest of the proof, we denote , and where . Let
| (A.22) |
By separation of variables, for ,
| (A.23) |
The partial eigenfunction representation can be used to derive a similar formula for solving (A.20) on the finite dimensional space. We may abuse the notation and write when it is clear. Notice that satisfies zero boundary condition on , it is enough to consider as a discrete function only for . Similar to the notations for the continuous case, we write , where , and . Denote by . We first construct a basis for the subspace . For and , let
| (A.24) |
We claim that form a normalized basis for . This can be verified by direct computations of the finite dimensional inner product. For , let .
If , then
| (A.25) |
If , then . Hence,
Therefore,
which implies for ,
This shows that the dimensional matrix is unitary. Hence, its column vectors form a normalized basis.
Now we fix and expand with respect to the normalized basis :
| (A.26) |
where is the coefficient function to be solved. We also expand the dimensional discrete delta function as .
Write the discrete Laplacian as , where is the second order difference with respect to the first variables and is the second order difference with respect to the last variable . Applying to gives
Combing with the expansion (A.26), we obtain
Hence, the dimensional equation can be reduced to a one dimensional difference equation of :
| (A.27) |
Define to be the positive solution solving
| (A.28) |
For , let and . Then . Hence, solves the homogeneous part of (A.27):
| (A.29) |
with boundary conditions . Define for , and for . Then satisfies (A.29) for all except . At , the definition of and implies
Finally, let . Then solves the inhomogeneous equation (A.27) for all , with zero boundary condition .
Together with (A.24) and (A.26), we obtain the analytic series expansion of , on the upper half cube :
| (A.30) |
It was proved in [La] that for , and , one has . The method can be extended to higher dimensions. We will not bother to give the full generalization of the exact singularity of order . We only need the version for with some logarithm corrections as in (A.21). To do that, it is enough to study the asymptotic behavior of in (A.28) as .
Let be given by (A.28). First, it was shown in [GuMa] (see also in [Gu]) that either or for all and . We sketch the proof for reader’s convenience. If , then
| (A.31) |
which gives . In (A.31), we used the elementary inequalities , for and for . Therefore, for any , the coefficients of decays exponentially
On the other hand, for any fixed , we want to expand in explicitly. Let be as in (A.22), one has
Therefore, for (with any constant only depending on the dimension). For any and , we compare the coefficients of and in (A.23) and (A.30) up to . Let . Then for any . Therefore, . Notice that implies
Putting all these together, we have
Then we split the series expression of into low frequency and high frequency part for ,
for sufficiently large . This completes the proof of (A.21). ∎
For any , by the positivity and smoothness (away from the pole) of the the continuous Green’s function , there are such that for all . Combining this with the approximation in (A.21), we have for and . Then by (A.19), one has for . Notice that is equivalent to
| (A.32) |
For any and , if we set , then it is easy to verify that , which implies that In other words, if , then will satisfy (A.32). In conclusion, we have obtained
Lemma A.7.
For any , and , let . There are constants depending on and such that if , then for all
We are also interested in the behavior of and near the boundary.
Lemma A.8.
Let be the center of the top surface of . For any , let be the semi cube contained in , cetered at , and away from the other surfaces of by distance :
There is a constant such that for all , one has
| (A.33) |
Proof.
Consider a larger semi-cube such that Let Clearly, and are two strictly positive harmonic functions on the interior of . By the comparison principle for harmonic functions, see, e.g. [Da, Ke], there is a constant only depends on and such that for all . Take so that . Then , and therefore, where only depends on and . ∎
Lemma A.9.
Let be a cube in centered at , with side length . Let be the discrete Poisson kernel on given by (A.12) with pole at the center . Let be the “top surface” of :
Let be the center of . Suppose . There are constants and depending only on the dimension and such that
| (A.34) |
for all and satisfying
The same estimate holds for on the other surfaces when is -away from the edges and the corners.
Proof.
It is enough to prove the result for centered at . We consider the approximation (A.21) on with the mesh size . Retain the definitions of and in Lemma A.6. By the definition of the mesh , for , the mesh points . Then Lemma A.6 implies that
for .
A.6. Harnack type inequalities
We prove the discrete sub-mean value property and the Moser-Harnack inequality first.
Lemma A.10.
Suppose is a discrete nonnegative subharmonic function on in the sense that
There is a dimensional constant such that
| (A.36) |
As a consequence, for any cube , if is non-negative and subharmonic on a domain containing the tripled cube , then
| (A.37) |
Proof.
Fix , let be the discrete harmonic function on which coincides on , i.e., , and By the integration by parts formula (A.15), where is the discrete Poisson kernel on from (A.12). It was showed in [Gu, GuMa] that there is a dimensional constant such that for all .
As a direct consequence, we have
Lemma A.11 (Moser-Harnack inequality for sub-solutions).
Let be a cube of side length , and let be the tripled cube (2.10). Suppose is a non-negative sub-solution to an inhomogeneous equation on a domain containing , so that and for Then there is a dimensional constant such that
| (A.41) |
Proof.
Suppose , , where is the side length of . Denote by its cardinality as usual. For , let
Direct computations show that
Let . Then and . We can apply Lemma A.10 to the non-negative subharmonic function . The estimate (A.37) implies that
as desired.
∎
Next, we study the discrete Harnack inequality for sup-solutions of a homogeneous Schrödinger equation with a bounded potential.
Lemma A.12.
Suppose , , is a bounded potential. Let be a non-negative super-solution for the Schrödinger equation on a cube so that
| (A.42) |
There is a constant depending on and such that for any cube of side length ,
| (A.43) |
Proof.
Assume that the finite dimensional vector attains its minimum and maximum at respectively. Connect by a discrete path in , where and for some . It is easy to check that the minimum number of steps needed to reach from is . The upper bound for and (A.42) imply for all . Then
Therefore,
which gives (A.43). ∎
Appendix B Chernoff bound
Lemma B.1 (Chernoff–Hoeffding Theorem, [Ho]).
Suppose and are i.i.d. Bernoulli random variables, taking values in with common expectation . Then for any ,
| (B.1) |
where
| (B.2) |
is the Kullback–Leibler divergence between Bernoulli distributed random variables with parameters and respectively.
We sketch the proof, following the arguments used in [DFM] (which is also close to the original proof of Hoeffding), for readers’ convenience.
References
- [AW] Aizenman, M., and Warzel, S., Random Operators: Disorder Effects on Quantum Spectra and Dynamics. Vol. 168. American Mathematical Soc., 2015.
- [ADFJM1] Arnold, D. N., David, G., Jerison, D., Mayboroda, S., and Filoche, M., Effective confining potential of quantum states in disordered media. Phys. Rev. Lett. 116.5 (2016): 056602.
- [ADFJM2] Arnold, D. N., David, G., Filoche, M., Jerison, D., and Mayboroda, S., Localization of eigenfunctions via an effective potential. Comm. Partial Differential Equations 44.11 (2019): 1186-1216.
- [ADFJM3] Arnold, D. N., David, G., Filoche, M., Jerison, D., and Mayboroda, S., Computing spectra without solving eigenvalue problems. SIAM J. Sci. Comput. 41.1 (2019): B69-B92.
- [Ba] Barlow, M.T., Random walks and heat kernels on graphs. volume 438 of London Mathematical Society Lecture Note Series. Cambridge University Press, Cambridge, 2017.
- [BiKo] Biskup, M., and König, W., Long-time tails in the parabolic Anderson model. Ann. Probab. (2001): 636-682.
- [Ch] Chung, F. R., Spectral graph theory. CBMS Lectures, Fresno 6.92 (1996): 17-21.
- [Da] Dahlberg, B., On estimates for harmonic measure. Arch . Rat. Mech . Anal. 65.3 (1977): 275-288.
- [DFM] David, G., Filoche, M., and Mayboroda, S., The landscape law for the integrated density of states. arXiv preprint arXiv:1909.10558 (2019).
- [DLY] Damanik, D., Lukic, M., and Yessen, W., Quantum dynamics of periodic and limit-periodic Jacobi and block Jacobi matrices with application to some quantum many body problems. Comm. Math. Phys. 337(3), 1535–1561 (2015).
- [DM+] Desforges, P., Mayboroda, S., Zhang, S., David, G., Arnold, D. N., Wang, W., and Filoche, M., Sharp estimates for the integrated density of states in Anderson tight-binding models. arXiv preprint arXiv:2010.09287 (2020).
- [Ea] Eastham, M. S. P., The spectral theory of periodic differential equations. Scottish Academic Press [distributed by Chatto & Windus, London, 1973.
- [Fe] Fefferman, C., The uncertainty principle. Bull. Amer. Math. Soc. 9.2 (1983): 129-206.
- [FM] Filoche, M., and Mayboroda, S., Universal mechanism for Anderson and weak localization. Proc. Natl. Acad. Sci. USA 109.37 (2012): 14761-14766.
- [Gu] Guadie, M., Harmonic functions on square lattices: uniqueness sets and growth properties. PhD thesis. Norwegian University of Science and Technology, Trondheim (2013).
- [GuMa] Guadie, M., and Malinnikova, E., On Three Balls Theorem for Discrete Harmonic Functions. Comput. Methods Funct. Theory 14.4 (2014): 721-734.
- [Ho] Hoeffding, W., Probability Inequalities for Sums of Bounded Random Variables. J. Amer. Statist. Assoc. 58.301 (1963): 13-30.
- [HJ] Han, R., and Jitomirskaya, S., Discrete Bethe–Sommerfeld conjecture. Comm. Math. Phys. 361(1) (2018): 205-216 .
- [HL] Han, Q., and Lin, F., Elliptic partial differential equations. Vol. 1. American Mathematical Soc., 2011.
- [Ke] Kenig, C. E., Harmonic analysis techniques for second order elliptic boundary value problems. Vol. 83. American Mathematical Soc., 1994.
- [Ki] Kirsch, W., An invitation to random Schrödinger operators. arXiv preprint arXiv:0709.3707 (2007).
- [KM1] Kirsch, W., and Metzger, B., The integrated density of states for random Schrödinger operators in spectral theory and mathematical physics: a Festschrift in honor of Barry Simon’s 60th birthday. Proc. Sympos. Pure Math. Vol. 76. 2007.
- [KM2] Kirsch, W., and Martinelli, F., Large deviations and Lifschitz singularity of the integrated density of states of random Hamiltonians, Comm. Math. Phys. 89.1 (1983): 27-40.
- [Ko] König, W., The parabolic Anderson model. Random walk in random potential. P Birkhäuser, 2016.
- [Ku] Kurata, K., On doubling properties for non-negative weak solutions of elliptic and parabolic PDE. Israel J. Math. 115.1 (2000): 285-302.
- [La] Laasonen, P., On the solution of Poisson’s difference equation. J. ACM 5.4 (1958): 370-382.
- [Li] Lifshitz, I. Y. M., Energy spectrum structure and quantum states of disordered condensed systems. Sov. Phy. Usp. 7.4 (1965): 549.
- [LMF] Lyra, M. L., Mayboroda, S., and Filoche, M., Dual hidden landscapes for Anderson localization in discrete lattices. Europhys. Lett. EPL 109.4 (2015): 47001.
- [RS] Reed, M., and Simon, B., Methods of modern mathematical physics. IV: Analysis of operators. New York - San Francisco - London: Academic Press (1978).
- [SW] Schatz, A. H., and Wahlbin, L. B., Interior maximum norm estimates for finite element methods. Math. Comp. 31.138 (1977): 414-442.
- [Si] Simon, B., Lifshitz Tails for the Anderson Model. J. Stat. Phys. 38.1-2 (1985): 65-76.
- [WZ] Wang, W., and Zhang, S., The exponential decay of eigenfunctions for tight binding Hamiltonians via landscape and dual landscape functions. Ann. Henri Poincaré. 22.5 (2021): 1429-1457.
————————————–
D. Arnold, School of Mathematics, University of Minnesota, 206 Church St SE, Minneapolis, MN 55455 USA
E-mail address: arnold@umn.edu
M. Filoche, Physique de la Matière Condensée, Ecole Polytechnique, CNRS, Institut Polytechnique de Paris, Palaiseau, France
E-mail address: marcel.filoche@polytechnique.edu
S. Mayboroda, School of Mathematics, University of Minnesota, 206 Church St SE, Minneapolis, MN 55455 USA
E-mail address: svitlana@math.umn.edu
W. Wang, School of Mathematics, University of Minnesota, 206 Church St SE, Minneapolis, MN 55455 USA
E-mail address: wang9585@umn.edu
S. Zhang, School of Mathematics, University of Minnesota, 206 Church St SE, Minneapolis, MN 55455 USA
E-mail address: zhan7294@umn.edu