Largo Enrico Fermi 5, I–50125 Firenze, Italy
11email: salvati@arcetri.astro.it
The local Galactic magnetic field in the direction of Geminga
Abstract
Context. The Milagro hot spot A, close to the Galactic anticenter direction, has been tentatively attributed to cosmic rays from a local reservoir (at a distance 100 pc), freely streaming along diverging and smooth magnetic field lines. This is at variance with the geometry of the kpc scale Galactic magnetic field, which is known to be aligned with the spiral arms.
Aims. We investigate the information available on the geometry of the magnetic field on the scales ( 100 pc) of relevance here.
Methods. The magnetic field immediately upstream of the heliosphere has been investigated by previous authors by modeling the interaction of this field with the solar wind. At larger distances, we use the dispersion measure and the rotation measure of nearby pulsars (especially towards the third Galactic quadrant). Additional information about the local field towards the North Polar Spur is taken from previous studies of the diffuse radio emission and the polarization of starlight.
Results. The asymmetry of the heliosphere with respect to the incoming interstellar medium implies a magnetic field almost orthogonal to the local spiral arm, in the general direction of hot spot A, but more to the south. This is in good agreement with the nearby pulsar data on the one side, and the North Polar Spur data on the other.
Conclusions. The local magnetic field on scales of 100 parsecs around the Sun seems to be oriented so as to provide a direct connection between the Solar system and a possible site of the Geminga supernova; the residual angular difference and the shape and orientation of the Milagro hot spot can be attributed to the field trailing in the wake of the heliosphere.
Key Words.:
cosmic rays – supernovae: general – supernovae: individual: Geminga – ISM: magnetic field1 Introduction
The detection by Milagro of anistropies at small angular scales in the arrival directions of multi–TeV cosmic ray protons (dubbed hot spots A and B, Abdo et al. (2008)) has stirred a lively debate. Indeed, there was no surprise in the detection of anisotropies at the measured level, but the expectation was that such anisotropies would appear on large angular scales, in agreement with the diffusion mode which accounts successfully for the propagation of cosmic rays. A positive excess in the general direction of hot spot A (”tail–in” anisotropy) had been already detected by other experiments [Tibet Air Shower Array (Amenomori et al. (2006)) and Super Kamiokande I (Guillian et al. (2007))], although the narrowness of the feature (only a few degrees) had not been noticed before.
Salvati and Sacco (ss (2008), hereafter SS) pointed out that hot spot A is in the general direction of Geminga, and suggested that a plausible source could be the Geminga supernova remnant (SNR) rather than the pulsar. The SNR would be dispersed by now, and would survive only as an expanding cloud of cosmic rays. The distance to it could be much smaller than the present distance to the pulsar, if a positive radial velocity is assumed for the latter. Such a distance could be crossed by diffusion in the time elapsed since the explosion (at least with crude assumptions about the diffusion coefficient). Also the energetics turned out right, and the energy dependence of the diffusion coefficient would account for the hard spectrum (1.45) of the excess cosmic rays. Drury and Aharonian (da (2008), hereafter DA) criticized SS on the grounds that the assumed diffusion coefficient was very implausible, and, moreover, a fully diffusive approach could not account for the narrow angular size of the hot spots. They suggested instead that some nearby ”cosmic ray reservoir” was connected to the Solar system by a ”magnetic funnel”: the cosmic rays could then stream freely along the (diverging and smooth) field lines, while at the same time their pitch angle distribution would narrow down to the observed value. A hybrid scenario was finally proposed by SS: there the ”cosmic ray reservoir” coincides with the Geminga SNR; the cosmic rays have to diffuse until they reach the ”first useful magnetic line” which drives them to the funnel and then to the Solar system. The initial diffusion accounts for the spectral filtering, the final streaming accounts for the angular distribution.
There is a major caveat, however. The available information about the geometry of the Galactic magnetic field (e.g., Han et al. (2006)) indicates that on scales kpc the ordered magnetic field is in the direction of the local spiral arm, and the chaotic component of the field is somewhat larger than the ordered one. The magnetic funnel scenario, on the contrary, requires that (on smaller scales 100 pc) the field is predominantly ordered, and directed toward the anticenter. In the following we discuss evidence that this could indeed be the case.
2 The local and very local magnetic field
Information about the magnitude and direction of the magnetic field immediately upstream of the heliosphere (i.e., in the very local interstellar medium still unperturbed by the bow shock) can be gained by modeling the anistropies observed in several heliopause tracers (see, for instance, Ratkiewicz, Ben-Jaffel, & Grygorczuk jaffel (2008), and references therein). One obtains a very local magnetic field of G, oriented within the interval , . Note that this analysis is insensitive to the sign of the field, so that an equally admissible solution is , . The latter solution is plotted in Fig. 1 as a circle labeled ”B near”.
| Name | Dist | DM | RM | ||
|---|---|---|---|---|---|
| degrees | degrees | pc | cm-3 pc | rad m-2 | |
| J2144-3933 | 2.8 | -49.5 | 180 | 3.35 | -2 |
| J2124-3358 | 10.9 | -45.4 | 250 | 4.60 | 1.2 |
| J0108-1431 | 140.9 | -76.8 | 130 | 2.4 | -0.3 |
| B0656+14 | 201.1 | 8.3 | 290 | 14.0 | 23.5 |
| B0950+08 | 228.9 | 43.7 | 260 | 2.96 | -0.66 |
| J0437-4715 | 253.4 | -42.0 | 160 | 2.64 | 1.5 |
| B0833-45 | 263.6 | -2.8 | 290 | 68.0 | 31.4 |
In order to explore the field on scales of a few hundreds of parsecs from the Solar system, we use the dispersion measure (DM) and the rotation measure (RM) of nearby radio pulsars (Han et al. (2006)). We retrieve from the ATNF Pulsar Database (Manchester at al. (2005)111http://www.atnf.csiro.au/research/pulsar/psrcat/) all the pulsars with measured DM and RM, and distances less than 300 parsecs. There are seven such objects, listed in order of increasing Galactic longitude in Table 1. Their distances are obtained either from the annual parallax, or (for J0108 and J2144) from the DM and an assumed model of the electron distribution. Given the relatively small volume, we approximate the magnetic field as a constant vector, fully described by three independent components, which we find by minimizing the between the observed and the predicted RM222Even if each pulsar gives only the B component along the line of sight , three or more pulsars widely spaced over the sky are sufficient to constrain B independent of its direction.
On the other hand, the RM is well known to vary widely even for small angular displacements, so that the ordered component of the field is found by averaging the data over large regions of the sky. We do not perform any average, given the small number of entries, however we must be prepared to find a very much higher than 1 per degree of freedom. We use this estimator only to draw some qualitative guesses. The values of DM and RM of two particular objects (B0656+14 and B0833-45) are by far larger than the other values, as one could have expected because of their location in the Monogem and Vela SNR, respectively. This adds one further caveat to our results, since a dense, young SNR could be dominated by a local magnetic field of its own.
If we retain in the fit all the seven pulsars, we obtain , , with a reduced of around 470 (!). If instead we retain only the four pulsars lying in the third Galactic quadrant, since the excess cosmic rays reach the Solar system from this general direction, we obtain , , with a reduced of only (!) 40. As a check on our findings, we have repeated the analysis for all pulsars with distances less than 500 parsecs: on the one hand, we become sensitive to the field on scales somewhat larger than the ones of interest; on the other, we improve the statistics by increasing the sample to 18 objects in total, and to 8 in the third Galactic quadrant. Finally, we fitted all pulsars with distances between 500 and 2,000 parsecs (103 objects), which should reproduce the azimuthal geometry already established by previous authors. On such large scales we include a portion of the Sagittarius – Carina arm, where the field is known to reverse direction (Han et al. (2006)); so, in order to keep the sample clean, we also fitted a subsample including only the pulsars lying outside the arm (57 objects).
| sample | no. objects | B | |||
|---|---|---|---|---|---|
| degrees | degrees | G | |||
| pc | 7 | 16 | 45 | 1.9 | 470 |
| III quad | 4 | 5 | 42 | 3.3 | 40 |
| pc | 18 | 6 | 28 | 2.7 | 1,500 |
| III quad | 8 | 9 | 43 | 2.5 | 340 |
| 0.5–2 kpc | 103 | 80 | -10 | 2.5 | 10,000 |
| arm excl. | 57 | 100 | 6 | 3.1 | 2,200 |
The results are summarized in Table 2. One sees that the pc sample gives results in broad agreement with the pc sample, while the 0.5–2 kpc sample indicates clearly a rotation of the field which becomes (more or less) aligned with the Galactic plane in the direction of the local spiral arm. Note especially that restricting the analysis to the third Galactic quadrant does not change appreciably the field, but makes the reduced substantially smaller. The reduced becomes substantially smaller also in the large scale sample, as expected, if one excludes the pulsars inside the Sagittarius–Carina arm.
We regard the substantial agreement between the first four sets of values in Table 2 as a hint that our procedure is meaningful. Furthermore, the substantial agreement between the pulsar derived magnetic field (on scales 100 pc) and the very local, heliopause derived magnetic field is a hint that in our Galactic neighborhood the magnetic field is relatively smooth. An independent hint at the field smoothness (a prerequisite for the validity of the funnel scenario) comes from the very significant decrease of the reduced in the third quadrant with respect to the all sky value. The two pc pulsar–derived solutions are plotted in Fig. 1 as two crosses labeled ”B rm”; we have not computed a confidence region from the distribution because of the caveats associated with it, and guess the uncertainty from the difference between the two solutions.
The structure of the magnetic field towards the Galactic center is loosely constrained by the pulsar data, which only suggest a geometry more complex than a uniform field. A clearer picture can be obtained by modeling the intensity and polarization of the nearby extended radio emission (Wolleben (2007)) and the polarization of the light from nearby stars (Frisch (2009)).
The interstellar medium in this general direction has been perturbed by a series of explosions likely due to stars in the Sco–Cen association. The radio intensity and radio polarization maps show the traces of several shells, the most prominent of which is the North Polar Spur. One of the shells [called ”Shell 1” by Wolleben (2007)] may have reached the Sun. In order to account for both the radio and the optical data, the magnetic field in the perturbed region is described as a uniform field outside the shells and, within the shell thickness, as a compressed field lying along the meridian circles. The radio data require two different shells, while the optical data can be fitted with Shell 1 only, and help to constrain its parameters within the large radio–derived confidence region.
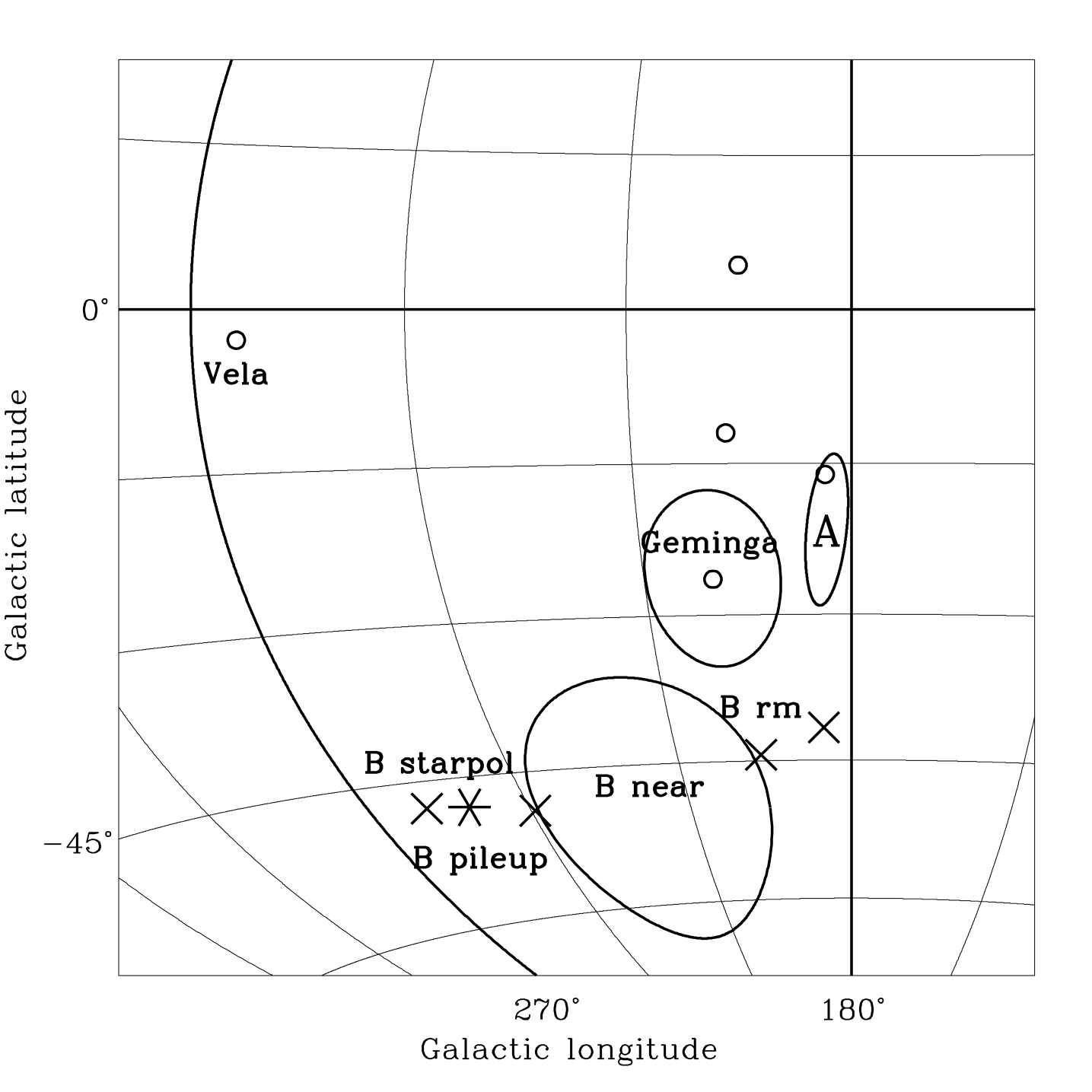
The star symbol labeled ”B starpol” in Fig. 1 is the direction of the uniform field inside which Shell 1 is expanding (Frisch (2009), no errors given). This would be the direction of the field outside the heliosphere if Shell 1 had not reached us yet. Otherwise the field would be the one compressed along the local meridian line of the shell: the two crosses labeled ”B pileup” represent two possible choices of the shell center. Note the near coincidence of ”B starpol” and ”B pileup”, which is due to the shell expansion center being at almost 90∘ with respect to ”B starpol”.
Figure 1 summarizes our findings. Here the southern half of the third Galactic quadrant is plotted in an Aitoff equal area projection. The various estimates of the B field direction have already been discussed. For the sake of comparison, all of them are represented as the respective points at , but they pertain to different physical regions: Brm should be valid at 100 pc in the third quadrant, Bnear and Bpileup should be valid only very close to the Sun, and Bstarpol should be valid at 100 pc in the first quadrant. In the latter region the field has been heavily distorted by the expansion of the radio shells, however what is plotted here is the unperturbed, pre–shell field, so that we can draw meanigful conclusions from its smooth connection with Bnear and Brm (see Section 3 and Figures 2 and 3).
The hot spot A and the heliotail direction are represented by the ellipse labeled ”A” and the small dot inside it. Finally, the three dots in descending sequence are: the present position of the Geminga pulsar; the position it would have had at explosion if its motion were parallel to the plane of the sky with the measured proper motion value; and the position it would have had if the explosion had occurred at the ”minimum” distance of 65 pc [i.e., with a positive 160 km s-1 radial velocity included, see SS; in both cases, the time elapsed since the explosion is assumed equal to the spin down age of the pulsar, yr (Bignami & Caraveo (1996))]. Around the latter dot we have drawn a circle of 10 pc radius, representing a fully developed SNR.
3 Discussion and conclusions
The first result we want to stress is the geometry displayed in Fig. 1: the direction of the local magnetic field, the direction of hot spot A, and the direction to a possible location for the Geminga SNR all lie within a few degrees from one another333Battaner, Castellano & Masip (batta (2009)) have developed a model for the dipole-like Milagro anisotropy (note: this is different from the point-like anisotropy discussed here). Their model succeeds in accounting for the dipole under the assumption of a local magnetic field basically aligned with the local spiral arm, i.e. at a large angle with the one derived here. But if one assumes a streaming motion of the cosmic rays along the magnetic field, beside the orthogonal motion derived by them based on an ad–hoc turbulent stress, the two estimates can be reconciled.. Apart from the hot spot, all the other directions in Fig. 1 are not directly measured, and are obtained by modeling the available datasets, not always plentiful. If, nonetheless, we take these results at face value, one of the main objections to a diffusion-plus-funnel scenario could be removed: the field on the relevant scales seems to be almost orthogonal to the large scale one, and to point in the right direction.
The second result concerns the smoothness of the local field, which is necessary if the cosmic rays have to stream freely along the magnetic funnel in order to be focussed within a narrow range of pitch angles. The evidence for such smoothness (admittedly meager) comes from two findings. One is the dramatic drop of the reduced if one selects for modeling only the pulsars lying in the third Galactic quadrant. The other is the near coincidence between the directions of the very local, heliopause derived magnetic field (”B near”), and the 100 pc scale one, either pulsar derived (”B rm”), or radio–optical derived (for the unperturbed configuration, ”B starpol”). Indeed, one notes that there is a regular and smooth ”rotation” of the B field vector: it comes from about the anticenter when the field is determined in the third Galactic quadrant; grows in Galactic longitude by about 30∘ at the Solar system; and grows still by another 30∘ when the (unperturbed) field is determined in the direction of the Galactic center.
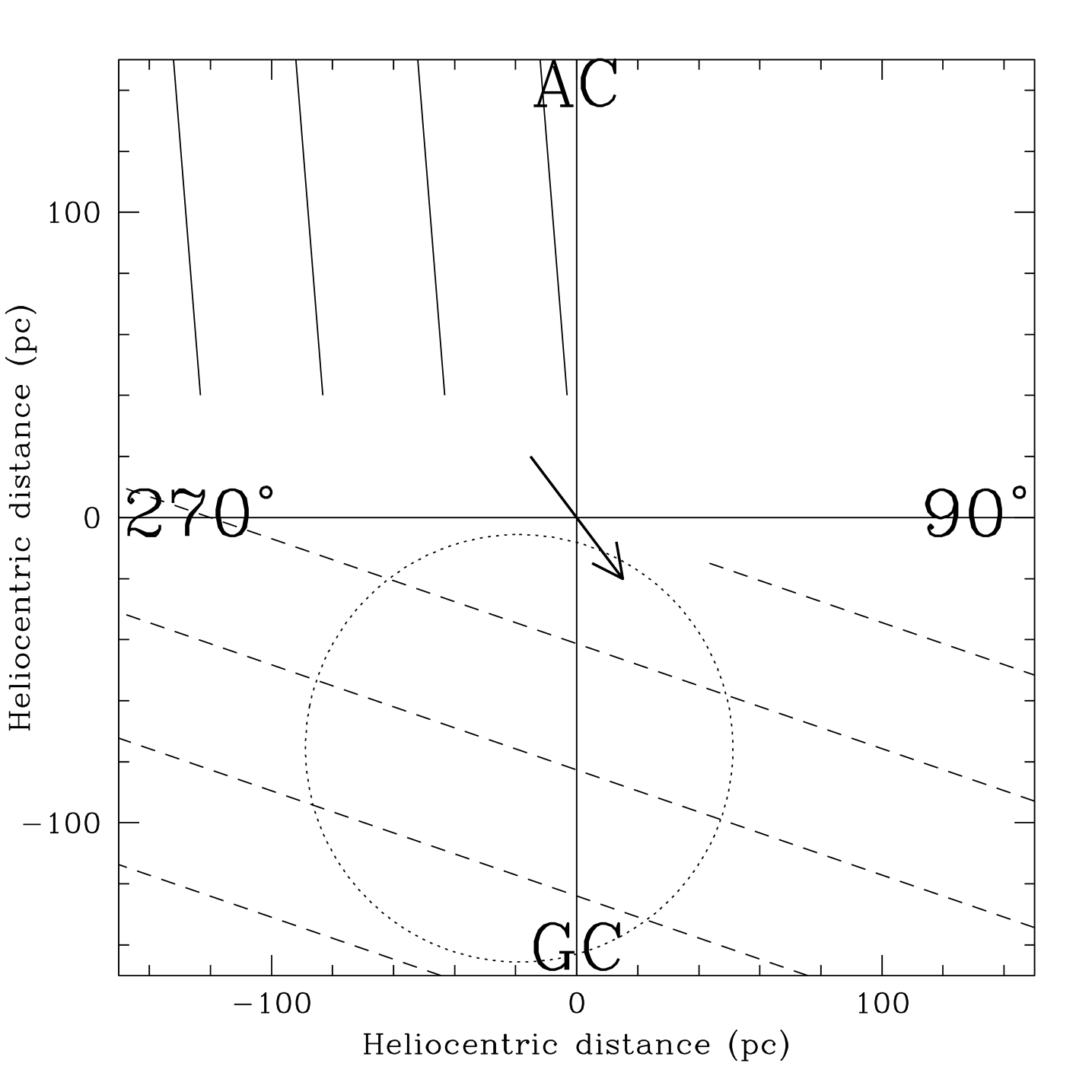
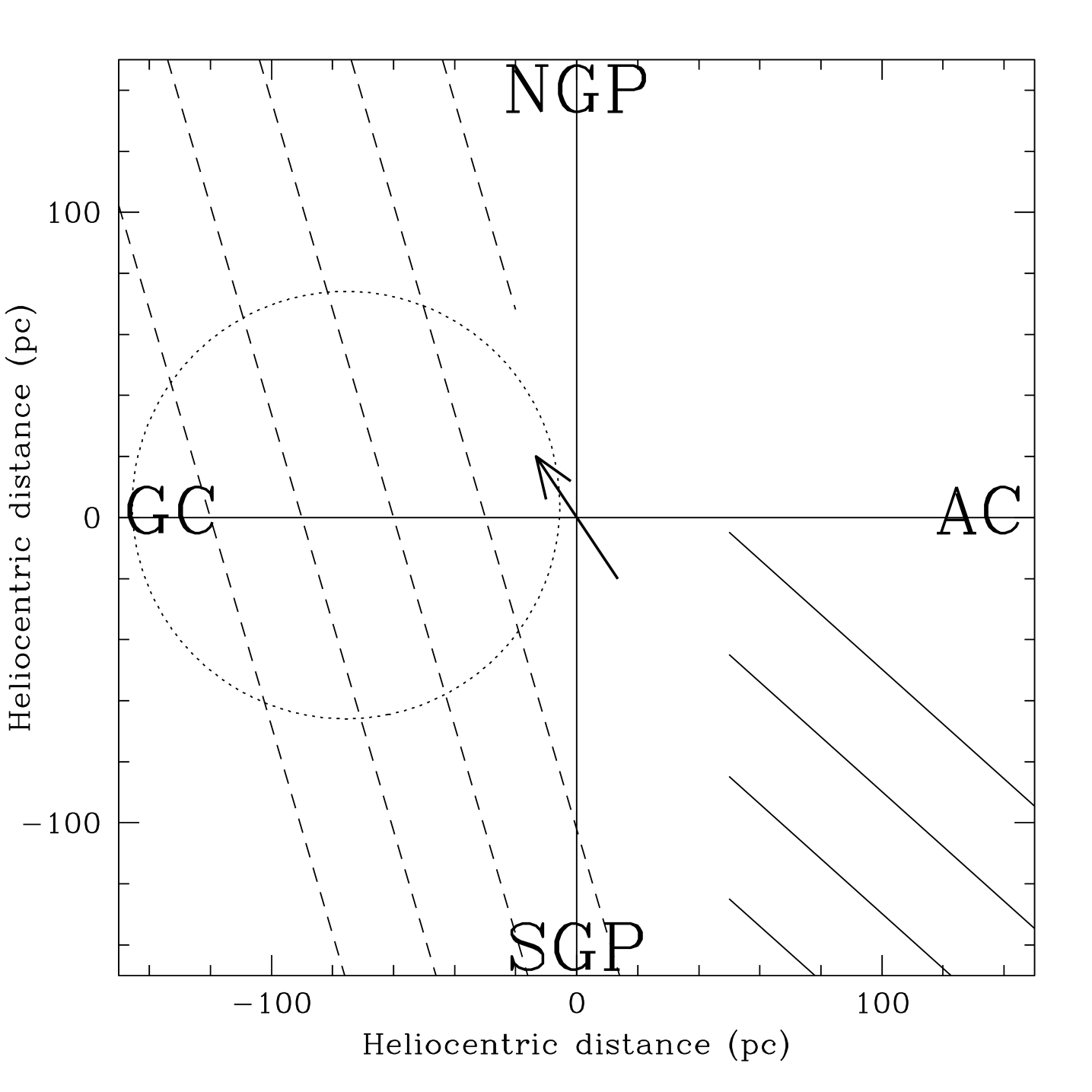
We sketch the envisaged geometry in Figures 2 and 3. They are the projection on the Galactic plane and, respectively, the meridian plane of the local and very local magnetic field, and of Shell 1 of Wolleben (2007). The crudeness of the sketch gives the impression of a sharp bend at the solar position, which would be injustified; but an equally valid (and equally arbitrary) representation could involve magnetic lines with a curvature radius as large as the Figures themselves. Also, the actual rotation in three dimensions amounts to 46 degrees only; this is strongly amplified by projection effects. Finally, the dashed lines inside the shell refer to the pre–shell situation: after the shell has overtaken them, they are draped along the shell surface.
We do not regard as a major discrepancy the residual angular separation between the assumed direction of the Geminga SNR, ”B near”, ”B rm”, and the actual position of hot spot A. However, some plausibility arguments can be given which could account for the discrepancy.
As argued in SS, the SNR responsible for the ”cosmic ray reservoir” (Geminga or other) should be close to the magnetic funnel, so that diffusion with reasonable coefficients could account for the propagation of the cosmic rays from the SNR to the funnel in the time elapsed since the explosion. At the same time, however, the SNR should not lie directly on the ”first useful field line”, otherwise one would miss the energy filtering (needed to explain the spectral hardness of the cosmic ray excess).
Second, a small meandering of the magnetic field, sufficient to account for the angular difference between ”B rm” and ”B near”, is not only plausible, but indeed very likely. The important point is that such small deflections over several tens of parsecs are by far insufficient to affect the free streaming of the cosmic rays.
Third, the actual position of hot spot A is perhaps determined by the direction of the very local magnetic field in the wake of the heliosphere. Indeed, the direction of ”B near” depicted in Fig. 1 refers to the field ahead of the heliosphere, before any interaction with it (Ratkiewicz et al. jaffel (2008)). After the wind, the field should become more aligned with the heliotail, and it is plausible than the alignment lasts for several times the distance to the heliopause, i.e. for about cm. Such a distance is comparable with the Larmor radius of a 10 TeV particle; the radius of curvature needed for a 20∘ swing over this distance is of course larger still, so that the free streaming of the cosmic rays should not be disrupted.
Note that the ambient magnetic field lines will tend to wrap around the heliosphere in the plane passing through the apex and containing the field and wind directions, while they will tend to slip apart on the two sides; the cosmic rays will then be focused in the said plane, and de-focused on the two sides. This corresponds roughly to the elliptical shape and the position angle of hot spot A. Qualitatively, the pile up of the lines toward the heliotail could also account for the gradient observed in hot spot A along the major axis, with the maximum on the heliotail side.
The geometry of the magnetic field which we have discussed thus far is perhaps too detailed in comparison with the available evidence. Still, it is by far insufficient for a quantitative estimate of the anisotropy amplitude. In order to achieve this, one should follow with high spatial and temporal resolution the expansion of the cosmic ray cloud injected by the Supernova, including the individual field irregularities throughout the cloud volume. The cloud, which we assume spherical, could well be elongated in one dimension, or have a complicated topology. The best we can do at the moment is to show that the observed anisotropy can be sustained by a minuscule gradient in the density of the cosmic rays, a gradient not implausible for a location relatively close to a relatively recent Supernova.
We write the energy flux measured from hot spot A (Abdo et al. (2008)) as follows
| (1) |
The magnetic funnel at the injection side is about 20 times narrower than at the Sun side (see DA), and the particle pitch angle squared scales inversely by the same factor, so that is constant. Hence the required density is
| (2) |
If the Supernova explosion injects erg in cosmic rays with the same spectrum as the general cosmic ray population, the 10–TeV reservoir amounts to 1.7 erg. Spreading this reservoir in a sphere of radius 100 pc (the length of the funnel suggested by DA, and a plausible distance for the Geminga explosion) one gets n , i.e. three orders of magnitude larger than Eq. (2).
Conversely, we can compute the cloud volume corresponding to the density of Eq. (2), , and deduce a diffusion coefficient. Setting the time t since the explosion of Geminga equal to yr (Bignami & Caraveo 1996), we find
| (3) |
The above value for D is not far from what is usually assumed in cosmic rays modeling (e.g. Hooper, Blasi, & Serpico (2009)), and is another plausibility argument in favor of our suggestion: hot spot A could be the first example of direct cosmic ray astronomy.
References
- Abdo et al. (2008) Abdo, A. A., et al. 2008, Phys. Rev. Lett., 101, 221101
- Amenomori et al. (2006) Amenomori, M., et al. 2006, Science, 314, 439
- (3) Battaner, E., Castellano, J., & Masip, M. 2009, ApJ, 703, L90
- Bignami & Caraveo (1996) Bignami, G. F., & Caraveo, P. A. 1996, ARA&A, 34, 331
- (5) Drury, L. O.’C., & Aharonian, F. A. 2008, Aph, 29, 420 (DA)
- Frisch (2009) Frisch, P. C. 2009, Space Sci. Rev., 143, 191
- Guillian et al. (2007) Guillian, G., et al. 2007, Phys. Rev. D, 75, 062003
- Han et al. (2006) Han, J. L., Manchester, R. N., Lyne, A. G., Quiao, G. J., & van Straten, W. 2006, ApJ, 642, 868
- Hooper, Blasi, & Serpico (2009) Hooper, D., Blasi, P., & Serpico, P. D. 2009, JCAP, 1, 25
- Manchester at al. (2005) Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993
- (11) Ratkiewicz, R., Ben-Jaffel, L., & Grygorczuk, J. 2008, What Do We Know about the Orientation of the Local Interstellar Magnetic Field? In Numerical Modeling of Space Plasma Flows, ed. N. V. Pogorelov, E. Audit, & G. P. Zank, ASP Conf. Series, vol. 385, 189
- (12) Salvati, M., & Sacco, B. 2008, A&A, 485, 527 (SS)
- Wolleben (2007) Wolleben, M. 2007, ApJ, 664, 349