The numerical range of a periodic tridiagonal operator reduces to the numerical range of a finite matrix
Abstract.
In this paper we show that the closure of the numerical range of an -periodic tridiagonal operator is equal to the numerical range of a complex matrix.
Introduction
Consider to be a finite set of complex numbers and let be a biinfinite sequence in the total shift space . In [13], the tridiagonal operator associated to is defined as
| (1) |
where the square marks the matrix entry at . In the particular case of the alphabet , the corresponding operator is related to the so called “hopping sign model” introduced in [7] and subsequently studied in many other works, such as [1, 2, 3, 4, 5, 6, 9, 10, 13], just to name a few. On the other hand, when the alphabet is some results for computing the numerical range of are presented in [13, 14]. In particular, work in [14] addresses the case when is an -periodic sequence. Relying on the fact that the closure of the numerical range of may be written as the closure of the convex hull of an uncountable union of numerical ranges of certain matrices, in [14] the closure of the numerical range of the 2-periodic case is computed by substituting such uncountable union of numerical ranges by the convex hull of the union of the numerical ranges of just two matrices. In this work, we further contribute to the study of the numerical range of when is an periodic biinfinite sequence.
Instead of working with the operators , we work with the more general tridiagonal operators defined in Section 2, since, as can be seen in [14], the computation of the closure of the numerical range of is a particular case of that of . Using a result of Plaumann and Vinzant [20], we show that the closure of the numerical range of the periodic tridiagonal operator is the numerical range of a matrix (cf. Theorem 2.6).
We divide this work in two sections. In Section 1 we briefly introduce the notation and terminologies needed in the rest of the paper. In Section 2 we develop the required machinery, first by computing the Kippenhahn polynomial of the symbol of periodc tridiagonal operatos on and then by combining our computations with results of Plaumann and Vizant. We will conclude that the closure of the numerical range of is equal to the numerical range of a matrix . Furthermore, we provide some examples where can be explicitly computed and we show that the size of is optimal.
1. Preliminaries
In this section we introduce the notation required which will be needed in the following sections. As usual, the symbols , , , and will denote the set of positive integers, the sets of nonnegative integers, the set of integers, the set of real numbers and the set of complex numbers, respectively.
For a given , let , and be -periodic infinite sequences in . We will denote by the -periodic tridiagonal operator on given by
We should observe that is a bounded operator since the sum of the moduli of the entries in each column (and in each row) is uniformly bounded (see, e.g., [16, Example 2.3]). The biinfinite matrix is also a bounded operator, as long as the biinfinite sequence arises from a finite alphabet.
If , for each , following [1, 14] we define the symbol of , as the following matrix
| (2) |
while the symbol of for is the matrix
| (3) |
Recall that given a Hilbert space and a bounded operator on it, the numerical range is defined as the set
The Toeplitz-Haussdorf Theorem establishes that is a bounded convex subset of (closed, if the Hilbert space is finite dimensional) and hence the closure of the numerical range can be seen as the intersection of the closed half-spaces containing the numerical range.
Kippenhahn [17] (see also [18]) characterized two vertical support lines of for a given matrix as and , where and are the respective largest and least eigenvalues of (recall that and ). In fact, if then (and the equalities hold for some points ). Since for each , it follows that if , then and hence . It follows that the lines are support lines of . Hence the convex set is uniquely determined by the numbers , as varies on the interval ; i.e. is determined by the largest eigenvalue of , which equals . Thus the numerical range is determined by the largest roots of the family of characteristic polynomials
The homogeneous polynomial is called the Kippenhahn polynomial of the matrix . It clearly follows that two matrices have the same numerical range if their Kippenhahn polynomials coincide. Furthermore,
for each .
2. The Kippenhahn polynomial of the symbol
In this section, after some preliminary work, we show that the closure of the numerical range of a -periodic tridiagonal operator is the numerical range of a matrix.
We will need the following lemma.
Lemma 2.1.
Consider the “almost tridiagonal” matrix
where every . Then, equals
Proof.
This follows by a long (but straightforward) application of the multilinearity of the determinant function and the Laplace Expansion Theorem. ∎
Let us set the following notation for the rest of this paper. For we define
and
We now find an expression for the Kippenhahn polynomial of the symbol matrix of an arbitrary -periodic tridiagonal matrix acting on , involving the determinants of some tridiagonal matrices. This expression will be useful in what follows.
Proposition 2.2.
Let . Consider the symbol , that is, the matrix defined as in (2) for and as in (3) for . Then the Kippenhahn polynomial of is equal to
where is the determinant of the tridiagonal matrix
and, where we set when , and, for , we set to be the determinant of tridiagonal matrix
Here we have set, for ,
and for ,
Proof.
We divide the proof in two cases. For , by computing the real and imaginary parts of the matrix in (3), we obtain that the matrix is given by
where , , and are as defined above. The determinant of this matrix can be simplified to
as desired.
Now, for the case , by computing the real and imaginary parts of the matrix in (2), we can observe that is the matrix
where we have now set
The above matrix is tridiagonal, except for the upper-right and bottom-left corners.
We can compute the determinant of the matrix polynomial by using Lemma 2.1 obtaining
Computing the real part of the last term above, we obtain the equation
which completes the proof. ∎
For every and for a fixed point , the angle is involved only in the constant term (with respect to the variable ) of the polynomial . Furthermore, for every and for every , the polynomial , seen as a polynomial in , has real roots, counting multiplicities, as it is the characteristic polynomial of the Hermitian matrix . The following lemma will be useful later when applied to the polynomial .
Lemma 2.3.
Let be a family of polynomials in given by the expression
where . Assume that the polynomial has real roots counting multiplicities for any angle . Let , be such that
Then
and
Proof.
Define as
Observe that, by assumption, the equation
has real solutions (counting multiplicities) for every . For some , we have , and hence has real roots (counting multiplicities) and the derivative of has real roots (counting multiplicities). Let be the largest root of . Hence, is increasing on the interval and the equations
have a unique solution on the interval .
Observe that for every
equality occurs on the left-hand-side inequality at while equality occurs on the right-hand-side inequality at .
For each , consider the number
Since the function is increasing on , the largest of these numbers, when varies, occurs when is the largest solution of the equation
Hence we have
Analogously, the smallest, when varies in , among the largest solutions of the equations
occurs when is the largest solution of the equation
Hence we have
In Theorem 2.7, we will show that the closure of the numerical range of is the numerical range of a single matrix. One of the key steps in the proof of said theorem will be to use the following proposition, which computes the closure of the numerical range of by using a single homogeneous polynomial, instead of the uncountable number of Kippenhahn polynomials of the symbols , which Theorem 2.8 in [14] would suggest: this is achieved by getting rid of the parameter in the expression of the Kippenhahn polynomial of the symbol in Proposition 2.2.
Proposition 2.4.
Let . Suppose that is an -periodic tridiagonal operator acting on . Let and be as in Proposition 2.2 and let be the real homogeneous polynomial of degree given by
Then and
for each .
Proof.
Notice that
The polynomial has the form outlined in Lemma 2.3 and, as was mentioned before Lemma 2.3, it has real roots, counting multiplicities. Hence, by Lemma 2.3, for and satisfying
we have that
and
Notice that
We also have, for each , that
| (4) |
The last equality follows since the roots of are those of and , so by the choice of and , the largest root of is the largest root of .
By the definition of the Kippenhahn polynomial, we have
and hence we obtain
| (5) |
The following definition will be useful.
Definition 2.5.
Suppose that is a real homogeneous polynomial in variables of degree with . If the equation in has real solutions counting multiplicities for any with , we say that is hyperbolic (with respect to ).
The above condition may also be formulated as: “the equation in has real solutions for any angle ”.
Theorem 2.6 (Plaumann and Vinzant [20]).
Suppose that is a real homogeneous hyperbolic polynomial of degree with . Then there exists an complex matrix satisfying
Remark. Helton and Vinnikov [12] (cf. [11]) proved a result stronger than the above theorem which guarantees that we can construct an complex symmetric matrix satisfying a similar property. In this paper we do not use the symmetry of the matrix .
Depending on the above Theorem 2.6, we obtain the main theorem of this paper.
Theorem 2.7.
Suppose that is an -periodic tridiagonal operator acting on . Then there exists a complex matrix such that
where the matrix is chosen so that it satisfies
where the polynomials and are as in Proposition 2.2.
Proof.
It is clear that given the operator , one can compute the polynomial which, by the Plaumann-Vinzant Theorem, is the Kippenhahn polynomial of some matrix . The question arises on whether the matrix can be explicitly computed. The paper [20] shows a method for constructing such a matrix (see also [12, 19]).
In some cases, the matrix can be found explicitly, as the next proposition shows. The reader should compare our next result to Theorem 4.1 in [1], where an alternative method for computing the numerical range of the tridiagonal operator is obtained, when , and are real -periodic sequences.
Proposition 2.8.
Let and be real -periodic sequences and let the constant sequence. If
then .
Proof.
We illustrate the above proposition with some examples.
Example 2.9.
Let be the -periodic sequence with period word , let be the constant sequence and let be the -periodic sequence with period word . Then, by Proposition 2.8, if
then . The boundary of the numerical range of is shown in Figure 1. The Kippenhahn polynomial of equals
The quartic curve in the complex projective plane has a pair of ordinary singular points of multiplicity at and there is no other singular point. So the algebraic curve theory tell us that the homogeneous polynomial is irreducible in the polynomial ring.
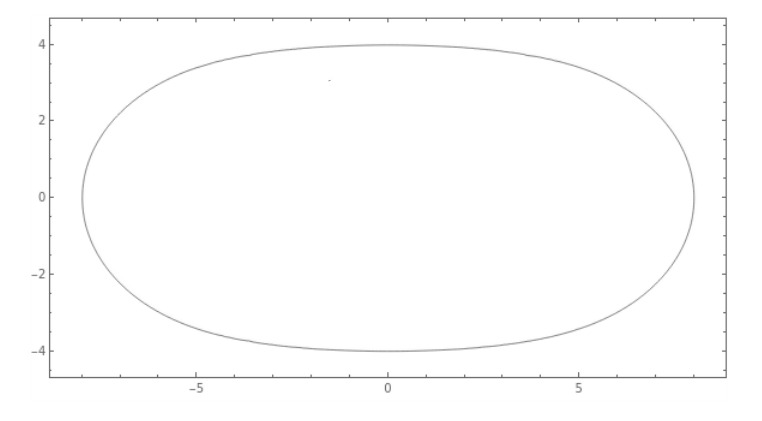
Example 2.10.
Let and be real -periodic sequences with period words and respectively, and let be the constant sequence . If , then and then, by Proposition 2.8, , where
But this implies that
where
That is, is the convex hull of two ellipses (possibly degenerate), each one a translation of a single elllipse (possibly degenarate) centered at the origin.
Example 2.11.
Let be the -periodic sequence with period word , let be the constant sequence and let be the constant sequence. Then, by Example 2.10, we have that , where
But it is easy to see that is the closed line segment joining and . Hence, equals the convex hull of the closed line segment joining and and the closed line segment joining and ; i.e., the square with vertices , , and , recovering (most of) Theorem 9 in [5].
Example 2.12.
Let and be real -periodic sequences with period words and respectively, and let be the constant sequence . If , then and then, by Proposition 2.8, , where
But if
then
But this implies that
where
That is, is the convex hull of two ellipses (possibly degenerate), each one a translation of a single elllipse (possibly degenarate) centered at the origin.
Example 2.13.
In the paper [15] we explore some sufficient conditions under which the matrix can be explicitly found, namely if and there is some symmetry in the periodic sequences and , then the polynomial can be factored as the product of the Kippenhahn polynomials of two computable matrices, which generalizes the previous four examples.
References
- [1] N. Bebiano, J. da Providência, and A. Nata. The numerical range of banded periodic Toeplitz operators. J. Math. Anal. Appl., 398:189–197, 2013.
- [2] S.N. Chandler-Wilde, R. Chonchaiya, and M. Lindner. Eigenvalue problem meets Sierpinski triangle: computing the spectrum of a non-self-adjoint random operator. Oper. Matrices, 5:633–648, 2011.
- [3] S. N. Chandler-Wilde, R. Chonchaiya, and M. Lindner. On the spectra and pseudospectra of a class of non-self-adjoint random matrices and operators. Oper. Matrices, 7:739–775, 2013.
- [4] S. N. Chandler-Wilde and E. B. Davies. Spectrum of a Feinberg-Zee random hopping matrix. J. Spectr. Theory, 2:147–179, 2012.
- [5] M. T. Chien and H. Nakazato. The numerical range of a tridiagonal operator. J. Math. Anal. Appl. 373:297-304, 2011.
- [6] R.T. Chien and I.M. Spitkovsky. On the numerical ranges of some tridiagonal matrices. Linear Algebra Appl., 470:228–240, 2015.
- [7] J. Feinberg and A. Zee. Spectral curves of non-hermitean Hamiltonians. Nuclear Phys. B, 552:599–623, 1999.
- [8] H. L. Gau and P. Y. Wu. Companion matrices: reducibility, numerical ranges and similarity to contractions. Linear Algebra Appl. 383:127–142, 2004.
- [9] R. Hagger. The eigenvalues of tridiagonal sign matrices are dense in the spectra of periodic tridiagonal sign operators. J. Funct. Anal., 269:1563–1570, 2015.
- [10] R. Hagger. On the spectrum and numerical range of tridiagonal random operators. J. Spectr. Theory, 6:215266, 2016.
- [11] J. W. Helton and I. M. Spitkovsky. The possible shapes of numerical ranges. Operators and Matrices, 6:607-611, 2012.
- [12] J. W. Helton and V. Vinnikov. Linear matrix inequality representations of sets. Communications on Pure and Applied Mathematics,60: 654-674, 2007.
- [13] C. Hernández-Becerra and B. A. Itzá-Ortiz. A class of tridiagonal operators associated to some subshifts. Open Math., 14:2391–5455, 2016.
- [14] B. A. Itzá-Ortiz and R. A. Martínez-Avendaño. The numerical range of a class of periodic tridiagonal operators. Linear Multilinear Algebra. 69:786–806, 2021.
- [15] B. A. Itzá-Ortíz, R. A. Martínez-Avendaño and H. Nakazato. The numerical range of some tridiagonal operators is the convex hull of the numerical ranges of two finite matrices. Preprint arXiv:2103.01866 [math.FA].
- [16] T. Kato. Perturbation theory for linear operators. Die Grundlehren der mathematischen Wissenschaften, Band 132. Springer-Verlag New York, Inc., New York, 1966.
- [17] R. Kippenhahn, Über den wertevorrat einer Matrix. Math. Nachr., 6:193-228, 1951.
- [18] R. Kippenhahn. On the numerical range of a matrix. Translated from the German by Paul F. Zachlin and Michiel E. Hochstenbach. Linear Multilinear Algebra 56:185-225, 2008.
- [19] D. Plaumann, B. Sturmfels and C. Vinzant, Computing linear matrix representations of Helton-Vinnikov curves, in Mathematical methods in systems, optimization, and control, Oper. Theory Adv. Appl. 222, 259–277, Birkhäuser/Springer Basel AG, Basel, 2012.
- [20] D. Plaumann and C. Vinzant. Determinantal representations of hyperbolic plane curves: An elementary approach, J. Symbolic Comput., 57:48–60, 2013.