The Rate Loss of Single-Letter Characterization:
The “Dirty” Multiple Access Channel

Consider the two-user / double-state memoryless multiple access channel (MAC) with transition and state probability distributions

respectively, where the states $S_{1}$ and $S_{2}$ are known non-causally to user $1$ and user $2$, respectively. A special case of (1) is the additive channel shown in Fig. 1. In this channel, called the doubly-dirty MAC (after Costa’s “writing on dirty paper” [1]), the total channel noise consists of three independent components: $S_{1}$ and $S_{2}$, the interference signals, that are known to user $1$ and user $2$, respectively, and $Z$, the unknown noise, which is known to neither. The channel inputs $X_{1}$ and $X_{2}$ may be subject to some average cost constraint.

Neither the capacity region of (1) nor that of the special case of Fig. 1 are known. In this paper we consider a particular binary version of the doubly-dirty MAC of Fig. 1, where all variables are in $\mathbb{Z}_{2}$, i.e., $\{0,1\}$, and the unknown noise $Z=0$. The channel output of the binary doubly-dirty MAC is given by

where $\oplus$ denotes the $\mbox{mod}\;2$ addition (xor), and $S_{1},S_{2}$ are $\mbox{Bernoulli}(1/2)$ and independent. Each of the codewords $\mathbf{x}_{i}\in\mathbb{Z}_{2}^{n}$ is a function of the message $W_{i}$ and the interference vector $\mathbf{s}_{i}\in\mathbb{Z}_{2}^{n}$, and must satisfy the input constraint, $\frac{1}{n}w_{H}(\mathbf{x}_{i})\leq q_{i}$, $\;i=1,2$, where $0\leq q_{1},q_{2}\leq 1/2$ and $w_{H}(\cdot)$ is the Hamming weight. The coding rates $R_{1}$ and $R_{2}$ of the two users are given as usual by $R_{i}=\frac{1}{n}\log|{\cal W}_{i}|$, where ${\cal W}_{i}$ is the set of messages of user $i$, and $n$ is the length of the codeword.

The double state MAC (1) generalizes the point to point channel with side information (SI) at the transmitter considered by Gel’fand and Pinsker [2]. They prove their direct coding theorem using the framework of random binning, which is widely used in the analysis of multi-terminal source and channel coding problems [3]. They obtain a general capacity expression which involves an auxiliary random variable $U$:

where the maximization is over all the joint distributions of the form $p(u,s,y,x)=p(s)p(u,x|s)p(y|x,s)$.

The channel in (1) with only one informed encoder (i.e., where $S_{2}=\{\emptyset\}$) was considered recently by Somekh-Baruch et al. [4] and Kotagiri and Laneman [5]. The common message ($W_{1}=W_{2}$) capacity of this channel is known [4], and it involves using random binning by the informed user. For the binary “one dirty user” case (i.e., (2) with $S_{2}=0$), we show that Somekh-Baruch’s common-message capacity becomes (see Appendix A)

where $H_{b}(x)\triangleq-x\log_{2}(x)-(1-x)\log_{2}(1-x)$ is the binary entropy function. Clearly, the doubly-dirty individual-message case is harder. Thus, it follows from (4) that the rate-sum in the setting of Fig. 1 is upper bounded by

In Theorem 1 we show that this upper bound is in fact tight.

One approach to find achievable rates for the doubly-dirty MAC, is to extend the Gel’fand and Pinsker solution [2] to the two-user / double-state case. As shown by Jafar [6], this extension leads to the following pentagonal inner bound for the capacity region of (1):

for some $P(U_{1},U_{2},X_{1},X_{2}|S_{1},S_{2})=P(U_{1},X_{1}|S_{1})P(U_{2},X_{2}|S_{2})$. In fact, by a standard time-sharing argument [3], the closure of the convex hull of the set of all rate pairs $(R_{1},R_{2})$ satisfying (7),

is also achievable¹¹1 As in the Gel’fand and Pinsker solution, for a finite alphabet system it is enough to optimize over auxiliary variables $U_{1}$ and $U_{2}$ whose alphabet size is bounded in terms of the size of the input and state alphabets. . To the best of our knowledge, the set $\mathcal{R}_{BSL}$ is the best currently known single-letter characterization for the rate region of the MAC with side information at the transmitters (1), and in particular, for the doubly-dirty MAC (2)²²2For the case where the users have also a common message $W_{0}$ to be transmitted jointly by both encoders, (7) can be improved by adding another auxiliary random variable $U_{0}$ which plays the role of the common auxiliary r.v. in Marton’s inner bound for the non-degraded broadcast channel [7]. In this case, the joint distribution of $(U_{0},U_{1},U_{2})$ is given by $P(U_{0},U_{1},U_{2})=P(U_{0})P(U_{1}|U_{0})P(U_{2}|U_{0})$, i.e, $U_{1}$ and $U_{2}$ are conditionally independent given $U_{0}$.. The achievability of (7) can be proved, as usual, by an i.i.d random binning scheme [6].

A different method to cancel known interference is by “linear strategies”, i.e, binning based on the cosets of a linear code [8, 9, 10]. In the sequel, we show that the outer bound (5) can indeed be achieved by a linear coding scheme. Hence, the set of rate pairs $(R_{1},R_{2})$ satisfying (5) is the capacity region of the binary doubly-dirty MAC. In contrast, we show that the single-letter region (7) is strictly contained in this capacity region. Hence, a random binning scheme based on this extension of the Gel’fand-Pinsker solution [2] is not optimal for this problem.

A similar observation has been made by Korner-Marton [11] for the “two help one” source coding problem. For a specific binary version known as the “modulo-two sum” problem, they showed that the minimum possible rate sum is achieved by a linear coding scheme, while the best known single-letter expression for this problem is strictly higher. See the discussion in [11, Section IV] and in the end of Section III.

Although the “single-letter characterization” is a fundamental concept in information theory, it has not been generally defined [12, p.35]. Csiszar and Korner [13, p.259] suggested to define it through the notion of computability, i.e., a problem has a single-letter solution if there exists an algorithm which can decide if a point belongs to an $\varepsilon$-neighborhood of the achievable rate region with polynomial complexity in $1/\varepsilon$. Since we are not aware of any other computable solution to our problem, we shall refer to (7) as the “best known single-letter characterization”.

An extension of these observations to continuous channels would be of interest. Costa [1] considered the single-user case of the dirty channel problem $Y=X+S+Z$, where the interference $S$ and the noise $Z$ are assumed to be i.i.d. Gaussian with variances $Q$ and $N$, respectively, and the input $X$ is subject to a power constraint $P$. He showed that in this case, the transmitter side-information capacity (3) coincides with the zero-interference capacity $\frac{1}{2}\log_{2}(1+SNR)$, where $SNR=P/N$. Selecting the auxiliary random variable $U$ in (3) such that

where $X$ and $S$ are independent, and taking $\alpha=\frac{P}{P+N}$, the formula (3) and its associated random binning scheme are capacity achieving. The continuous (Gaussian) version of the doubly-dirty MAC of Fig. 1 was considered in [10]. It was shown that by using a linear structure, i.e., lattice strategies [8], the full capacity region is achieved in the limit of high SNR and high lattice dimension. In contrast, it was shown that for $Q\rightarrow\infty$ no positive rate is achievable by using the natural generalization of Costa’s strategy (8) to the two user case, while a (scalar) modulo addition version of (8) looses $\thickapprox 0.254$ bit in the sum capacity. We shall further elaborate on this issue in Section IV.

Similar observations regarding the advantage of modulo-lattice modulation with respect to a separation based solution were made by Nazer and Gastpar [14], in the context of computation over linear Gaussian networks, and also by Krithivasan and Pradhan [15] for multi-terminal rate distortion problems.

The paper is organized as follows. In Section II the capacity region for the binary doubly-dirty MAC (2) is derived, and linear coding is shown to be optimal. Section III develops a closed form expression for the best known single-letter characterization (7) for this channel, and demonstrates that it is strictly contained in the the true capacity region. In Section IV we consider the Gaussian doubly-dirty MAC, and state a conjecture regarding the capacity loss of single-letter characterization in this case.

The following theorem characterizes the capacity region of the binary doubly-dirty MAC of Fig. 1.

As stated above, the achievability for the capacity region follows by time sharing the corner points $(H_{b}(q),0)$ and $(0,H_{b}(q))$ where $q=\min\{q_{1},q_{2}\}$. It is also interesting to see how to achieve the rate sum $H_{b}(q)$ for an arbitrary rate pair $(R_{1},R_{2})$ without time sharing. For that, let the message of user $1$ be $\mathbf{m}_{1}\in\mathbb{Z}_{2}^{l_{1}}$ and the message of user $2$ be $\mathbf{m}_{2}\in\mathbb{Z}_{2}^{l_{2}}$ where $l_{1}+l_{2}=n-k$. We define the following syndromes in $\mathcal{C}$

Clearly, given the syndrome $\mathbf{v}$ the syndromes $\mathbf{v}_{1}$ and $\mathbf{v}_{2}$ are fully known and the messages $\mathbf{m}_{1}$ and $\mathbf{m}_{2}$ as well. Let $\mathbf{\tilde{x}}_{i}=f(\mathbf{v}_{i})$ be the coset leader of $\mathbf{v}_{i}$ for $i=1,2$. In this case the transmission scheme is as follow:

• •

  Encoder of user $1$: transmit $\mathbf{x}_{1}=(\tilde{\mathbf{x}}_{1}\oplus\mathbf{s}_{1})\;\mbox{mod}\;\mathbb{C}=f(\mathbf{v}_{1}\oplus H\mathbf{s}_{1})$.

• •

  Encoder of user $2$: transmit $\mathbf{x}_{2}=(\tilde{\mathbf{x}}_{2}\oplus\mathbf{s}_{2})\;\mbox{mod}\;\mathbb{C}=f(\mathbf{v}_{2}\oplus H\mathbf{s}_{2})$.

• •

  Decoder: reconstruct $\hat{\mathbf{v}}=H\cdot\Big{(}\mathbf{y}\;\rm{mod}\;\mathbb{C}\Big{)}$.

Therefore, we have that

The sum capacity is achieved since $R_{1}+R_{2}=\frac{l_{1}+l_{2}}{n}=\frac{n-k}{n}\geq H_{b}(q)-\epsilon$ where $\epsilon\rightarrow 0$ as $n\rightarrow\infty$ which satisfies the input constraints.

In this section we characterize the best known single-letter region (7) for the binary doubly-dirty MAC (2), and show that it is strictly contained in the capacity region (9). For simplicity, we shall assume identical input constraints, i.e., $q_{1}=q_{2}=q$.

In the following theorem we give a closed form expression for $\mathcal{R}_{BSL}(q)$.

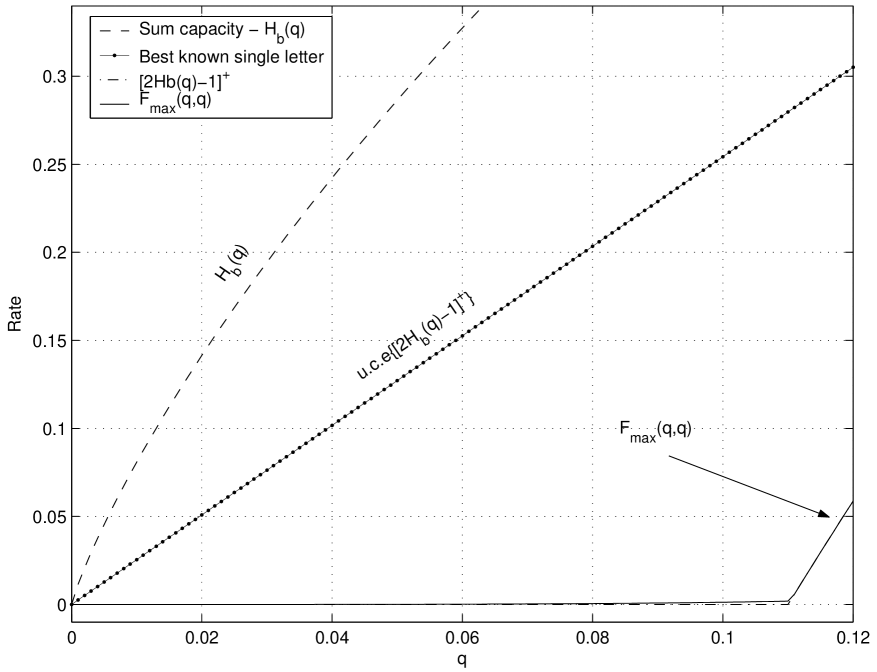
Fig. 2 shows the sum capacity of the binary doubly-dirty MAC (9) versus the best known single-letter rate sum (16) for equal input constraints. The latter is strictly contained in the capacity region which is achieved by a linear code. The quantity $[2H_{b}(q)-1]^{+}$ is not a convex - $\cap$ function with respect to $q$. The upper convex envelope of $[2H_{b}(q)-1]^{+}$ is achieved by time-sharing between the points $q=0$ and $q=q^{*}\triangleq 1-1/\sqrt{2}$, therefore it is given by

where $C^{*}\triangleq\frac{2H_{b}(q^{*})-1}{q^{*}}$.

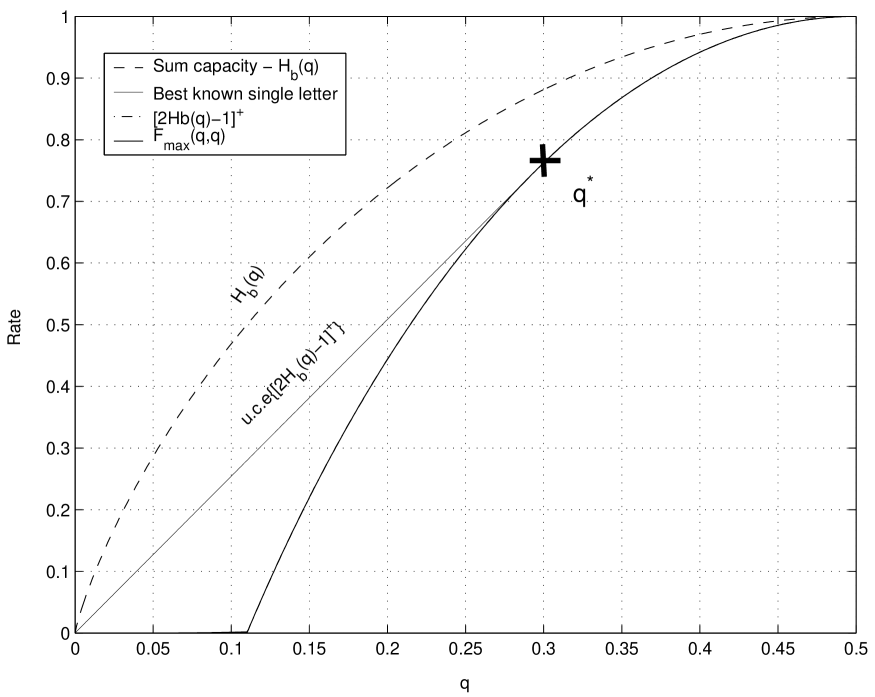
We see that the binary doubly-dirty MAC is a memoryless channel coding problem, where the capacity region is achievable by a linear code, while the best known single-letter rate region is strictly contained in the capacity region. This may be explained by the fact that each user has only partial side information, and distributed random binning is unable to capture the linear structure of the channel.

In order to understand the limitation of random binning versus a linear code, we consider these two schemes for high enough $q$, that is $2H_{b}(q)-1\geq 0$. The random binning scheme uses $U_{i}=X_{i}\oplus S_{i}$ where $X_{i}\sim\mbox{Bernoulli}(q)$ and $S_{i}\sim\mbox{Bernoulli}(1/2)$ are independent, therefore $Y=U_{1}\oplus U_{2}$ where $U_{i}\sim\mbox{Bernoulli}(1/2)$ for $i=1,2$. Each transmitter maps the message (bin) $W_{i}$ into a codeword $\mathbf{u}_{i}$ which is with high probability at a Hamming distance of $nq$ from $\mathbf{s}_{i}$. Therefore, given the vectors $(\mathbf{s}_{1}^{n},\mathbf{s}_{2}^{n})$, the available input space is approximately $2^{nH(U_{1},U_{2}|S_{1},S_{2})}=2^{nH(X_{1},X_{2})}=2^{2nH_{b}(q)}$. Given the received vector $\mathbf{y}$, the residual ambiguity is given by $2^{nH(U_{1},U_{2}|Y)}=2^{n[H(U_{1}|Y)+H(U_{2}|Y,U_{1})]}=2^{n}$, since $H(U_{1}|Y)=1$ and $H(U_{2}|Y,U_{1})=0$. As a result, the achievable rate sum is given by

The linear coding scheme shown in Theorem 1 has the same input space size as the random binning scheme, i.e., $2^{2nH_{b}(q)}$, since each user has $2^{nH_{b}(q)}$ cosets. However, given the received vector $\mathbf{y}$ there are $2^{nH_{b}(q)}$ possible pairs of cosets, i.e., the residual ambiguity is only $2^{nH_{b}(q)}$. Therefore, the linear code achieves rate sum of $R_{1}+R_{2}\approx 2H_{b}(q)-H_{b}(q)=H_{b}(q)$. The advantage of the linear coding scheme results from the “ordered structure” of the linear code, which decreases the residual ambiguity from $1$ bit in random coding to $H_{b}(q)$.

The following example illustrates the above arguments for the case that user $2$ is a “helper” for user $1$, i.e, $R_{2}=0$, and user $1$ transmits at his highest rate for each technique (random binning or linear coding). Table I summarizes the rates and codebooks sizes for each user for $q=0.3$, that is $H_{b}(q)\thickapprox 0.88$ bit.

Korner and Marton [11] observed a similar behavior for the “two help one” source coding problem shown in Fig. 3. In this problem, there are three binary sources $X,Y,Z$, where $Z=X\oplus Y$, and the joint distribution of $X$ and $Y$ is symmetric with $P(X\neq Y)=\theta$. The goal is to encode the sources $X$ and $Y$ separately such that $Z$ can be reconstructed losslessly. Korner and Marton showed that the rate sum required is at least

and furthermore, this rate sum can be achieved by a linear code: each encoder transmits the syndrome of the observed source relative to a good linear binary code for a BSC with crossover probability $\theta$.

In contrast, the “one help one” problem [19, 20] has a closed single-letter expression for the rate region, which corresponds to a random binning coding scheme. Korner and Marton [11] generalize the expression of [19, 20] to the “two help one” problem, and show that the minimal rate sum required using this expression is given by

The region (25) corresponds to Slepian-Wolf encoding of $X$ and $Y$, and it can also be derived from the Burger-Tung achievable region [21] for distributed coding for $X$ and $Y$ with one reconstruction $\hat{Z}$ under the distortion measure $d(X,Y,\hat{Z})\triangleq X\oplus Y\oplus\hat{Z}$. Clearly, the region (6) is strictly contained in the Korner-Marton region $R_{x}+R_{y}\geq 2H(Z)$ (24) (since $H(X,Y)=1+H(Z)>2H(Z)$ for $Z\sim\mbox{Bernoulli}(\theta)$, where $\theta\neq\frac{1}{2}$). For further background on related source coding problems, see [15].

In this section we introduce our conjecture regarding the rate loss of the best known single-letter characterization for the capacity region of the two-user Gaussian doubly-dirty MAC at high SNR. The Gaussian doubly-dirty MAC [10] is given by

where $Z\sim\mathcal{N}(0,N)$ is independent of $X_{1},X_{2},S_{1},S_{2}$, and where user $1$ and user $2$ must satisfy the power constraints, $\frac{1}{n}\sum_{i=1}^{n}X_{1_{i}}^{2}\leq P_{1}$ and $\frac{1}{n}\sum_{i=1}^{n}X_{2_{i}}^{2}\leq P_{2}$ see Fig. 1. The interference signals $S_{1}$ and $S_{2}$ are known non-causally to the transmitters of user $1$ and user $2$, respectively. We shall assume that $S_{1}$ and $S_{2}$ are independent Gaussian with variances going to infinity, i.e., $S_{i}\sim\mathcal{N}(0,Q_{i})$ where $Q_{i}\rightarrow\infty$ for $i=1,2$. The signal to noise ratios for the two users are $SNR_{1}=\frac{P_{1}}{N}$ and $SNR_{2}=\frac{P_{2}}{N}$.

The capacity region at high SNR, i.e., $SNR_{1},SNR_{2}\gg 1$, is given by [10],

and it is achievable by a modulo lattice coding scheme of dimension going to infinity. In contrast, it was shown in [10] that at high SNR and strong independent Gaussian interferences, the natural generalization of Costa’s strategy (8) for the two users case, i.e., with auxiliary random variables $U_{1}=X_{1}+S_{1}$ and $U_{2}=X_{2}+S_{2}$, is not able to achieve any positive rate. A better choice for $U_{1}$ and $U_{2}$ suggested in [10] is a modulo version of Costa’s strategy (8),

where $\Delta_{i}=\sqrt{12P_{i}}$, and where $X_{i}\sim\mbox{Unif}\left([-\frac{\Delta_{i}}{2},\frac{\Delta_{i}}{2})\right)$ is independent of $S_{i}$, for $i=1,2$. In this case the rate loss with respect to (27) is $\frac{1}{2}\log_{2}\Big{(}\frac{\pi e}{6}\Big{)}\thickapprox 0.254\;\rm{bit}$.

The best known single-letter capacity region for the Gaussian doubly-dirty MAC (26) is defined as the set of all rate pairs $(R_{1},R_{2})$ satisfying (7), where $X_{1}$ and $X_{2}$ are restricted to the power constraints $EX_{1}^{2}\leq P_{1}$ and $EX_{2}^{2}\leq P_{2}$. We believe that for high SNR and strong interference, the modulo-$\Delta$ strategy (28) is an optimum choice for $(X_{1},X_{2},U_{1},U_{2})$ in (7) for the Gaussian doubly-dirty MAC. This implies the following conjecture about the rate loss of the best known single-letter characterization.

Note that the right hand side of (29) is the well known “shaping loss” [22] (equivalent to a $~1.53dB$ power loss).

A heuristic approach to attack the proof of this conjecture is to follow the steps of the proof of the converse part in the binary case (Theorem 2). First, in Lemma 6 we derive a simplified single-letter formula, $\overline{G}_{max}(P_{1},P_{2})$, which is analogous to Lemma 1 in the binary case. The next step would be to optimize this expression. However, an optimal choice for the auxiliary random variables $V_{1},V_{1}^{\prime},V_{2},V_{2}^{\prime}$ (provided in the binary case by Lemma 2 and Lemma 3) is unfortunately still missing for the Gaussian case. The expression in Lemma 6 is close in spirit to the point-to-point dirty tape capacity for high SNR and strong interference [8]. In [8] it is shown that optimizing the capacity is equivalent to minimum entropy-constrained scalar quantization in high resolution, which is achieved by a lattice quantizer. Clearly, if we could show a similar lemma for the two variable pairs in the maximization of Lemma 6, i.e., that it is achieved by a pair of lattice quantizers, then the conjecture would be an immediate consequence.

It should be noted that the above discussion is valid only for strong interferences $S_{1}$ and $S_{2}$. For interference with finite power, it seems that cancelling the interference part of the time and staying silence the rest of the time (like in the time-sharing region $0\leq q\leq q^{*}$ in the binary case) may achieve better rates.

A memoryless information theoretic problem is considered open as long as we are missing a general single-letter characterization for its information performance. This goes hand in hand with the optimality of the random coding approach for those problems which are currently solved. We examined this traditional view for the memoryless doubly-dirty MAC.

In the binary case, we showed that the best known single letter characterization is strictly contained in the region achievable by linear coding, and that the latter is in fact the full capacity region of the problem. In the Gaussian case, we conjectured that the best known single-letter characterization suffers an inherent rate loss (equal to the well known “shaping loss” $0.5\log(\pi e/6)$), and we provide a partial proof. This is in contrast to the asymptotic optimality (dimension $\rightarrow\infty$) of lattice strategies, as recently shown in [10].

The underlying reason for these performance gaps is that random binning is in general not optimal when side information is distributed among more than one terminal in the network. In the specific case of the doubly-dirty MAC (like in Korner-Marton’s modulo-two sum problem [11] and similar settings [14, 15]), the linear structure of the network allows to show that linear binning is not only better, but it is capacity achieving.