The Role of Outflow Feedback on Accretion of Compact Objects in Accretion Disk of Active Galactic Nuclei
Abstract
Compact objects (COs) can exist and evolve in an active galactic nuclei (AGN) disk, triggering a series of attractive CO-related multi-messenger events around a supermassive black hole. To better understand the nature of an embedded CO and its surroundings and to investigate CO-related events more accurately, in this paper, we study the specific accretion process of a CO in an AGN disk and explore the role of outflow feedback. We show that the asymptotically isotropic outflow generated from the CO hyper-Eddington accretion would truncate the circum-CO disk and push out its surrounding gas, resulting in recurrent formation and refilling of an outflow cavity to intermittently stop the accretion. Applying this universal cyclic process to black holes (BHs) and neutron stars (NSs), we find that, even if it is above the Eddington rate, the mass rate accreted onto a BH is dramatically reduced compared with the initial gas captured rate and thus consumes few mass of the AGN disk; outflow feedback on a NS is generally similar, but possesses complexities on the existence of a stellar magnetic field and hard surface. We demonstrate that although outflow feedback itself may be unobservable, it remarkably alters the CO evolution via reducing its mass growth rate, and the AGN disk can survive from the otherwise drastic CO accretion overlooking outflow. In addition, we discuss the potential influence of underdense cavity on CO-related events, which embodies the significant role of outflow feedback as well.
1 Introduction
Accretion disks can exist around the galaxy central supermassive black holes (SMBHs), lighting up SMBHs to form the so-called active galactic nuclei (AGN). Stars and compact objects (COs), e.g. black holes (BHs) and neutron stars (NSs), are predicted to widely reside in the AGN disk via gas-capture of orbiters from the galaxy nuclei cluster to the disk, or in-situ star formation and evolution, or geometrical coincidence of a few nuclear stars and COs with the renascent disk (e.g. Ostriker, 1983; Syer et al., 1991; Cheng & Wang, 1999; Goodman, 2003; Thompson et al., 2005; McKernan et al., 2012; Fabj et al., 2020).
The AGN disk provides a venue for various CO-related astrophysical events. Especially since the BH-BH merger event GW190521 (Abbott et al., 2020) along with the plausible EM counterpart ZTF19abanrhr (Graham et al., 2020) indicates an AGN disk environment origin, the studies on CO-related events in the AGN disk are in the ascendant lately. The AGN disk channel can contribute to a large amount of unique BH-BH, BH-NS, NS-NS mergers (e.g. Tagawa et al., 2020a, 2021; McKernan et al., 2020a, b; Samsing et al., 2022) and extreme mass ratio inspirals (e.g. Pan & Yang, 2021a; Pan et al., 2022) events for gravitational wave (GW) observations. Electromagnetic (EM) events, such as gamma-ray bursts and kilonovae (Zhu et al., 2021a; Perna et al., 2021a; Yuan et al., 2022; Ren et al., 2022; Wang et al., 2022), supernovae (Zhu et al., 2021b; Grishin et al., 2021; Moranchel-Basurto et al., 2021), accretion-induced collapses of NSs (Perna et al., 2021b) and white dwarfs (Zhu et al., 2021b), micro-tidal disruption events (Yang et al., 2022), occurring in the AGN disk show characteristic transient features. All the GW and EM transients are distinguishable from the same events taking place in the classical interstellar medium on account of the COs lying within the extremely dense environment. Moreover, accretion in the AGN disk gives opportunities for BHs to be observed (Wang et al., 2021a, b; Kimura et al., 2021b). On the other hand, mass and spin of the embedded stars and COs would increase rapidly via accreting gas in the AGN disk (e.g. Jermyn et al., 2021; Dittmann et al., 2021; Tagawa et al., 2020b, 2022), markedly changing the features of stars and COs to potentially impact CO-related events and AGN disk structure. Therefore, as the prerequisite, a more comprehensive understanding of COs’ surroundings is very important to further explore the CO evolution and the CO-related events in the AGN disk.
Gas accreted onto an embedded CO from the AGN disk environment is inevitable. The CO mass capturing rate is generally hyper-Eddington, which may even exceed the mass inflow rate of the AGN disk. Previous works have artificially set upper limits for the accretion rate onto CO at the Eddington rate with various radiative efficiencies, or at the AGN disk mass inflow rate, or directly at a certain fraction of CO mass capturing rate (e.g. Tagawa et al., 2020a; McKernan et al., 2020a; Kaaz et al., 2021; Kimura et al., 2021b; Wang et al., 2021a), but none yet connected the rate to the actual accretion processes of CO. Hyper-Eddington accretion is predicted both theoretically and by numerical simulations to be accompanied with powerful outflow of mass and energy in the form of circum-CO disk wind and collimated jet (e.g. Blandford & Begelman, 1999; Begelman, 2012; Gu, 2012, 2015; Ohsuga et al., 2005; Jiang et al., 2014; Yang et al., 2014; Hashizume et al., 2015; Sa̧dowski et al., 2015; Sa̧dowski & Narayan, 2016; Kitaki et al., 2018; Hu et al., 2022), which would reduce the mass rate eventually accreted onto COs (Pan & Yang, 2021b), and would conversely interact with surroundings, acting as feedback. Several recent works have investigated the feedback of CO hyper-Eddington accretion on the AGN disk environment (Wang et al., 2021a; Kimura et al., 2021b; Tagawa et al., 2022), where Wang et al. (2021a) and Kimura et al. (2021b) did not concretely discuss the properties of the disk wind, while Tagawa et al. (2022) mainly focused on the jet-cocoon feedback from high-spin stellar-mass BHs, which may not be practicable for low-spin BHs and NSs. So, a detailed study for the formation, evolution, and feedback of outflow is needed, and then we can better understand the nature of CO accretion, evolution, and COs’ surroundings.
In this paper, we construct the circum-CO accretion disk and the induced outflow via the widely accepted description of hyper-Eddington accretion. The asymptotically isotropic outflow then interacts with the AGN disk environment, circularly opens and refills an outflow cavity, resulting in the CO undergoing periodic accretion processes. We focus on the role of outflow feedback on CO accretion and its surroundings, manifesting as the prominent reduction of time-averaged mass accretion rate, and CO mainly staying in the underdense cavity rather the AGN disk environment, which significantly impact the evolution of CO and the features of CO-related events.
This paper is organized as follows. In Section 2, we show the construction of a circum-CO accretion disk and an outflow. We describe the outflow evolution in the AGN disk, then show the features of outflow cavity, and reduction of the mass rate accreted onto a BH or NS in Section 3. Several discussions are presented in Section 4, involving the potential influence of shock radiation-cooling efficiency and CO-gravity-induced gap in Sections 4.1 and 4.2, the depletion of AGN disk inflow mass by CO accretion process in Section 4.3, the jet effect and the outflow EM radiation in Section 4.4, the role of outflow cavity on CO evolution and CO-related events in Section 4.5, and the probable accretion feedback of CO with large bulk velocity in Section 4.6. We summarize our conclusions in Section 5. We use the convention of in cgs units unless otherwise noted. The and are speed of light and gravitational constant.
2 Hyper-Eddington Accretion in the AGN Disk
The accretion disk of an AGN is typically modeled as a geometrically-thin, optically-thick disk with the -prescription representing the viscosity torque (Shakura & Sunyaev, 1973). We define the dimensionless accretion rate of SMBH by , where is the accretion rate of SMBH, is the Eddington limit accretion rate, , is the mass of SMBH in units of , is the proton mass, and is the Thompson cross section. Because the evolution of most COs should take place in the region of AGN disk during the AGN lifetime owing to the larger disk volume holding more COs and the potential existence of migration trap (Bellovary et al., 2016), where is the gravitational radius, we use the outer region solution of the standard disk model. The half-thickness, density, and mid-plane temperature of the AGN disk are (e.g. Kato et al., 2008; Wang et al., 2021a)
| (1) |
where is the constant viscosity parameter (Shakura & Sunyaev, 1973) and is the radius of disk in units of . The outer disk can be self-gravity unstable and would fragment into gas clouds and stars if the Toomre parameter (Toomre, 1964), where the local sound speed and the angular velocity for Keplerian-rotating disk.
Equation (1) would be inaccurate to describe the outer disk region because of the gas self-gravity leading to accretion processes more complicated (e.g. Goodman, 2003). Many plausible theoretical models have been proposed to describe the structure of a quasi-stationary self-gravitating accretion disk (e.g. Sirko & Goodman, 2003; Thompson et al., 2005; Mishra et al., 2020; Gilbaum & Stone, 2022, et al.); the disk structure is diverse in different models, and yet there is no general agreement. As discussed in Wang et al. (2021a), though the standard disk model may be inexact, the main characteristics of disk can be predicted qualitatively; the analytic solution can also help to better understand the dependence of CO accretion and outflow feedback properties on AGN disk parameters. So we use Equation (1) as an environment to investigate the CO accretion and outflow feedback in the AGN disk. Future works can use the CO accretion-feedback processes proposed in this work and employ specific AGN disk model to better study the evolution of CO and the astrophysical events relevant to CO.
When is extremely low, the AGN disk is likely to be advection-cooling dominated (Narayan & Yi, 1994, 1995), its properties differ from those of the radiation-cooling dominated thin disk, e.g. the much higher temperature and the much geometrically thicker inflow (see Yuan & Narayan, 2014, for a review). The evolution of CO in these low-accretion-rate AGN disks should be distinctive and thus would be studied separately in a future work.
2.1 Disk Formation around CO
As embedded in the AGN disk environment, COs (e.g. BH or NS) will capture and accrete gas within its sphere of gravity. AGN disk rotates differentially, the accreted gas hence holds shear velocity w.r.t the CO, and would form a rotating disk around the CO rather than fall directly into it. To intuitively understand this process, we take gas accretion onto a planet embedded in a proto-planetary disk as an analogy (e.g. Kimura et al., 2021b). As shown in simulations (Ayliffe & Bate, 2009; Tanigawa et al., 2012), a nearly Keplerian rotating circum-planetary disk forms around the planet; the majority of mass is concentrated in the outer region of the disk, mainly around the circularization radius of the accreted gas (see below). Back to the AGN disk case, the initially circular gas disk would then go through viscous evolution and effective accretion to the CO on viscous timescale (e.g. Kato et al., 2008)111When the initial mass inflow rate to CO is extremely large, as in the AGN disk environment we discuss, the infalling gas potentially follows an alternative structure called “zero-Bernoulli accretion” flows suggested by Coughlin & Begelman (2014); the inflow inflates nearly to the poles and forms a weakly bound, quasi-spherical structure, rather than a large-scale accretion disk. The criteria of which structure occurs under the specific environment parameters, and the distinctions of the relevant outflow feedback will be studied in another work..
The initial inflow mass rate around the disk outer boundary can be described by the Bondi-Holye-Lyttleton (BHL) formulation (see Edgar, 2004, for a review); under the corrections of the SMBH gravity effect in radial direction and the finite height of the AGN disk in vertical direction, the gas inflow rate is estimated as follows (Kocsis et al., 2011; Pan & Yang, 2021b):
| (2) |
and the outer boundary radius of the circum-CO disk can be approximate to , which can be estimated from the angular momentum conservation of the infalling gas, i.e.,
| (3) |
where is the mass of CO, is the radius of CO gravity sphere, is the Hill radius, and is the BHL radius; the canonical equation of the BHL accretion rate is
| (4) |
where is the density of AGN disk gas surrounding the CO, and is the relative velocity between the CO and the gas, which contains components of the gas relative bulk motion and shear rotation. To estimate the shear velocity , we linearize the velocity disparity at the location of CO and the boundary of the CO gravity sphere , i.e.,
| (5) |
where we consider the CO co-rotates with the Keplerian AGN disk at its midplane, , in which case the gas bulk motion can be neglected (Kocsis et al., 2011). In fact, the CO can hold large bulk velocity w.r.t. the ambient disk gas, as briefly discussed in Section 4.6. Here we primarily investigate the long-term evolution of COs in the AGN disk, which are probably on the Keplerian co-rotating orbits; the COs with large may escape from the disk, or the gas dynamical and accretion frictions reduce the relative velocity of CO, leading to the subsequent co-rotation (e.g. Ostriker, 1999; Bartos et al., 2017; Secunda et al., 2019; Fabj et al., 2020; Nasim et al., 2022).
When living in the AGN disk, the CO can interact with the surrounding disk through gravity, inducing gravitational torque to additional exchange energy and angular momentum with the AGN disk (the disk–satellite interactions would be analogous to a giant planet in a proto-planetary disk; see Armitage 2007, Baruteau et al. 2014, as the reviews). The ambient gas has the tendency to be repelled from the CO, and thus gas density is reduced in the disk annulus at . The gas density and half-width of the reduced region are estimated as and (Kanagawa et al., 2015, 2016; Tanigawa & Tanaka, 2016). We set the density used to calculate the BHL accretion rate, i.e. in Equation (4), as
| (6) |
For the circum-CO accretion disk with extremely high inflow mass rate and distant outer boundary, the outer disk region would be self-gravity unstable, accordingly the gas captured by the CO fragments, resulting in the reduction of mass inflow rate (e.g. Pan & Yang, 2021b; Tagawa et al., 2022). The Toomre parameter of the circum-CO disk can be approximatively expressed as , where is the Keplerian angular velocity, is the sound speed, is the disk surface density and is the inflow radial velocity, is the viscosity parameter, is the disk height ratio, is the vertical scale height of the disk, and ; the stabilization of circum-CO disk requires , so the modified mass inflow rate is expressed by
| (7) |
In short, when a CO accretes the AGN disk gas, a circum-CO disk would form, with the initial radius and the mass inflow rate given by Equations (3) and (7).





2.2 Hyper-Eddington Accretion Disk and Outflow
The initial mass inflow rates of COs are extremely hyper-Eddington, i.e. , as shown in Figure 1; a specific property of the accretion is photon trapping, i.e. the photons and radiation energy are trapped and advected inward with the dense gas inflow because of the photon diffusion timescale exceeding the disk accretion timescale. The radiation-effective flow converts to be radiation-ineffective nearly at the trapping radius (e.g. Kato et al., 2008; Kitaki et al., 2021):
| (8) |
where and . Inside , the disk radiation pressure efficiently drives outflow, leading to reduction of the circum-CO disk mass inflow rate; the radius-dependent rate can be written as (Blandford & Begelman, 1999):
| (9) |
where the power-law index is a free parameter and its value is taken to be ; numerical simulations show that the value lies within (Yang et al., 2014), but out to for the case of modestly circularized gas inflow (Kitaki et al., 2021). Under the uncertainty, we set three values , , to study the outflow feedback. For , the circum-CO disk is advection-dominated within , and is radiation-dominated between and ; but when , the disk is totally advective accompanied with the outflow formation222But the mass inflow rate is not large enough to become neutrino-cooling dominated, see Kohri et al. (2005) and Equation (20) in Kumar et al. (2008)., and the mass inflow rate is written as
| (10) |
The radiation-pressure-driven outflow can take away a considerable fraction of viscous heating of the circum-CO disk, as discussed in Appendix A. The local viscous heating rate per unit area is given by Equation (A7), so the total disk generated heat is
| (11) |
where is the mass inflow rate at ; for case, and for case, for which we ignore the heat generated in the outer radiation-dominated region because only tiny gravitational energy is released via accretion at large radius. We take as the inner radius outside which the self-similar solutions hold and the outflow cooling is efficient, because when , the relativistic effects of the central CO can not be neglected (Pan & Yang, 2021b), the outflow is dragged by the strong gravitational force to be weak (Jiao et al., 2015) and the cooling is dominated by advection rather than outflow (Wu et al., 2022). We roughly assume that a constant fraction of the heat is taken away by the disk wind and radiation, i.e.,
| (12) |
where contains the constant coefficients reflecting the wind property in Equation (11); we set as the fiducial value.
The accretion features of the NS are sightly different from those of the BH due to the existence of a stellar magnetic field and hard surface (Takahashi et al., 2018). A strong magnetic field may truncate the circum-NS disk at a radius where the magnetic stress of NS magnetosphere matches the disk stress (e.g. Zhang & Dai 2009; and Lai 2014, Romanova & Owocki 2015, as reviews). For a dipole field, equaling magnetic pressure to disk pressure , where the density of the circum-NS disk is given by Equation (B1), can be estimated as
| (13) |
where , which is slightly lower than the typical value (e.g. Ghosh & Lamb, 1979; Chashkina et al., 2019), the distinction may derive from the properties of hyper-Eddington accretion disk; for simplicity, we leave the specifically analysis of the disk structure and truncation for a future work, and take briefly. When magnetic field is weak, the disk can extend to the NS surface ; so in the NS accretion case, we take to determine the rate of mass eventually flowing onto the NS, where is set due to the effects of NS’s gravity as explained above (but we ignore the potential effects of the energy released near the NS surface on the accretion structure and properties, e.g. Takahashi et al. 2018). In addition, the accretion flow would release additional energy with luminosity when ultimately hitting the NS hard surface, where we crudely ignore the neutrino cooling processes around the NS surface. So the total energy injected into the wind outflow contains the disk and the accretion component (Chashkina et al., 2019), i.e.,
| (14) |
The direction of the outflow significantly affects its feedback on the environment. Many numerically simulations and analytical solutions of the super-critical accretion flow around CO predicted that the emitted winds are focused in the high latitude region, i.e. the outflow is anisotropic (e.g. Jiao et al., 2015; Sa̧dowski & Narayan, 2015), the feedback as well (e.g. Takeo et al., 2020; Tagawa et al., 2022). These works mainly investigate disk parameter regions of the mass inflow rate and the radial dimension (see Table 1 in Kitaki et al. 2021, which lists the recent simulation studies), where the outflow is automatically collimated by the geometrically thick disk and the optically thin polar funnel, but these parameters are much smaller than the case of CO accretion in the AGN disk. Also, when studying the feedback, only the kinetic energy of the outflow has been considered and the winds are set to spread over a limited solid angle, thereby, the initial setup of outflow is anisotropic.
For the hyper-Eddington accretion process of CO, winds initially take along the radiation energy when just launching. Because the outflow and the AGN disk surroundings (the optical depth from the disk midplane ) are both extremely dense, photons can not effectively diffuse away but are trapped in the outflow, coupled with and continually accelerating the optically thick gas (Hashizume et al., 2015; Sa̧dowski & Narayan, 2015). Thus, the outflow contains not only kinetic but also thermal energy. We can extrapolate the properties of winds generated by the large-scale hyper-Eddington accretion disk from the simulations and the self-similar solutions shown in Appendix A. As discussed in Begelman (2012) and can be seen by Equations (9) and (12), most of the inflow mass is turned into the outflow at large radius comparable to , conversely, most accretion energy is released closer to , carried by winds over a wide solid angle (Sa̧dowski et al., 2016; Sa̧dowski & Narayan, 2016); winds successively loaded at different radius of the circum-CO disk would go through interactions and internal collisions (Metzger, 2012; Kremer et al., 2019), causing the gas thermalization during the outward propagation and mixture. So, we predict that the outflow kinetic energy is close to the radiation-domination thermal energy within the circum-CO disk scale. Winds moving radially at bulk velocity would press and heat the circum-CO disk as well, where the thermal pressure . When the sound speed of the heated disk gas exceeds the CO local escape velocity, the gas outside is ejected and hence the disk is truncated (e.g. Tagawa et al., 2022). The truncation radius can be estimated as
| (15) |
where is the density of circum-CO disk, whose expression is shown in Appendix B; the density of the outflow is set as a simplified spherical distribution, i.e.,
| (16) |
in other words, we assume that the heavy gas would distribute roughly uniformly over a wide solid angle at large radius because of the gas thermal mixture, and we neglect the spatial existence of the circum-CO disk compressing the wind region when calculating the disk truncation, which may increase but would not significantly affect the result because of the disk thickness not too large; the velocity of the mixed disk wind can be obtained from , i.e.,
| (17) |
in the NS case we replace the energy term with . After getting , we can decide the disk outer boundary , then calculate the modified and the mass accretion rate of CO using Equations (9) and (10). As examples shown in Figure 2, we find that the mass accretion rate of CO is well hyper-Eddington when ignoring the effects of outflow feedback on the environment; and we confirm a comprehensible tendency that the mass rate increases with the decrease of index , which controls the strength of disk wind.
Even if the outflow is initially anisotropic (collimated by the geometrically thick disk) when leaving the local circum-CO disk system, because
| (18) |
where the double-greater-than symbol holds (we check numerically and find that the inequality assuredly holds for the regions we interested) as with the supersonic accretion and due to , the pressure of the environment gas is unable to prevent the outflow becoming asymptotically isotropic and spherically symmetric (though there may still have anisotropy, with lower wind mass rate and larger wind velocity at higher latitude, e.g., Kitaki et al. 2021) before sweeping a large amount of the AGN disk gas; the equatorial region’s gas captured by the CO will also be pushed away. During the adiabatic expansion, most of heat in the outflow would be converted to bulk kinetic energy and accelerate the winds with initial velocity of Equation (17) (Kremer et al., 2019; Piro & Lu, 2020), so the asymptotic velocity, kinetic energy and momentum of the outflow are
| (19) |
| (20) |
2.3 Time Evolution of Circum-CO Disk
For the moment, we ignore the detailed time-evolution of the circum-CO accretion disk, which may follow the works of Kumar et al. (2008) and Shen & Matzner (2014), determining the specific evolution of mass rate accreted onto CO and the variation of outflow generated from the accretion system. For now, the structure of the hyper-Eddington accretion disk, much less the disk evolution, has not been well studied, as discussed in Appendix B; at the same time, the qualitative properties of CO accretion can be approximatively described using the viscous timescale. So, for simplicity, we put aside the complicated time-evolution of the piecewise disk, instead we assume that the efficient accretion proceeds within , after which the efficient accretion stops.
3 Accretion and feedback of a CO in the AGN Disk
In previous sections we have discussed the asymptotically isotropic properties of wind ejected from the circum-CO disk. Taking Equations (16) and (19) as the initial injection, we study the interaction between outflow and AGN disk and its resultant effects on the CO accretion and its surroundings.



3.1 Evolution of an Outflow in the AGN Disk
In analogy with the interaction between the stellar wind and interstellar medium (Weaver et al., 1977), the wind from the circum-CO disk interacts with the surrounding AGN disk gas via a forward shock, forming a shell of shocked disk gas separated by the shocked outflow material; inside the shell, a low-density outflow cavity forms. We ignore the radial and vertical structure of the AGN disk, and roughly set the disk with uniform density and a concrete height at each . A schematic diagram of outflow evolution in the AGN disk is shown in Figure 3.
During the efficient accretion of CO sustaining timescale of , we approximately assume the properties of winds remain unchanged. The radius and velocity of the expanding shell evolve over time as (Weaver et al., 1977):
| (21) |
and
| (22) |
When , the shell will vertically break out from the AGN disk and propagate in the above lower density region (e.g. broad-line region); meanwhile, along the AGN disk, the outflow continually interacts and pushes the shocked gas shell laterally, which now shows a ringlike structure, until the efficient accretion stops. Because the vertical expansion of the shell is much more rapid (), we assume that the shocked outflow undergoes an overall rapid depressurization after the breakout (e.g. Schiano, 1985) 333Moranchel-Basurto et al. (2021) studied the supernova explosions in the AGN disk, and found that the analytic evolution (vertically and laterally) of the SNe-driven bubble under the assumption of bubble receiving rapid depressurization after the breakout matches well with the numerical simulations., and then the ring moves driven by the momentum of the long-lasting outflow ( holds within wide parameter regions, as shown in Figure 4), i.e.,
| (23) |
where we roughly assume that the ring is cylindrical and only moves laterally. Because , the ringlike shell evolves after the breakout as:
| (24) |
and
| (25) |
where we simply ignore the specific depressurization process and link the outflow-energy and outflow-momentum driven phase directly. Lastly, when the CO accretion stops, the evolution of the ringlike shell along the AGN disk translates from the outflow-momentum driven phase to its own momentum conservation snowplow phase, i.e.,
| (26) |
where and represent the radius and velocity of shell during the snowplow phase; on both sides of the equation we have eliminated , which approximatively represents the mass of the swept disk gas . With the continuous sweep, the shell will decelerate to a velocity similar to the environment sound speed, i.e., , which ends up being transonic and is unable to propagate further as a shock. So the horizontal half-width of the outflow cavity in the AGN disk can be estimated by
| (27) |
The timescale of the cavity formation can be calculated from Equation (26), i.e.,
| (28) |
which is the sum of the efficient accretion timescale and the evolution timescale of the subsequent snowplow phase.
But if , the CO would stop strong accretion before the successful shell breakout. In this case we roughly take the whole energy of the CO-accretion-generated winds, i.e., , as injection; the shell thus expands driven by , the radius and velocity are given as (e.g. Ostriker & McKee, 1988):
| (29) |
and
| (30) |
where we ignore the mass of wind for simplicity. We can also achieve the breakout time from . After the breakout accompanied with the rapid cavity depressurization, the shell propagating along the AGN disk enters the snowplow phase, i.e.,
| (31) |
the half-width and the formation timescale of the cavity can be solved similar to Equation (27) and (28).
The accretion rate of CO in the underdense cavity is too low to continuously produce powerful outflow maintaining the cavity structure (see below); conversely the relatively dense AGN disk gas will refill the cavity roughly on a timescale given by (e.g. Wang et al., 2021a):
| (32) |
Then the efficient CO accretion will be activated in the refilled cavity again; subsequently the cavity formation and refilling would take place alternately.
3.2 Reduced Mass Accretion of BH
We take and as a typical case to study the influence of outflow feedback on the BH accretion in the AGN disk environment, of which the specific processes have been discussed in Section 3.1. We can calculate the (or ) under variable AGN disk parameters, and then estimate the density of outflow cavity as
| (33) |
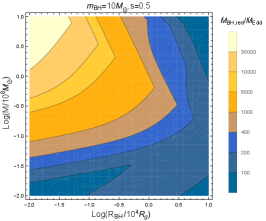
where we treat the cavity as spherical, which overestimates the density of cavity because the shell expands much faster above the AGN disk causing a much larger volume. Then we use Equation (7) to get the mass accretion rate of BH in the cavity, replacing with . Relevant properties of the cavity and BH accretion are shown in Figure 4. We find that the size of outflow-induced cavity is much larger than the BHL and Hill radius, i.e., the size of BH gravity sphere, which suppresses the BH further capturing the AGN disk gas. The density of cavity is significantly reduced compared to the initial unperturbed environment. We calculate the trapping radius of BH accretion in the cavity using Equation (8), and find that it is well smaller than the circum-BH disk outer boundary, reflecting that the BH mass accretion rate is significantly reduced, and hence the induced outflows are not powerful enough to notably affect or maintain the cavity structure. For the weak accretion in cavity, we simply neglect the specific evolution of the BH mass accretion rate and set a factitious value of , which is the approximate minimum mass inflow rate at the inner boundary of the advection-dominated disk (e.g. Pan & Yang, 2021b).



The timescale of efficient accretion is well shorter than the duration time of the cavity evolution, as shown in Figure 5. A smaller index results in a overall more powerful outflow feedback, accordingly larger size and longer duration time of the cavity. The variation trend of the contour map relies on various effects ( case as an example in Figure 5); first, a general trend of being larger for smaller BH location comes from the AGN disk gas environment being denser when closer to SMBH, which hinders the expansion of cavity; second, the varied outer boundary radius of the circum-BH disk results in different features of the major disk region, thereby different dependence of the disk accretion timescale variation on the AGN disk parameters; third, the gap-depth is larger for lighter and closer SMBH cases, or the self-gravity instability in circum-BH disk inhibits the mass inflow rate, leading to lower mass accreted onto BH and weaker outflow feedback, accordingly, the size and evolution timescale of the cavity are smaller; in addition, the relative size of BHL radius, Hill radius and AGN disk height, and the unsuccessful breakout also affect the accretion and feedback properties of the BH.
Because the accretion of BH is inefficient in the outflow cavity, though hyper-Eddington during , the averaged mass accretion rate onto the BH is well reduced in a whole circulation . We can estimate the reduced mass accretion rate as:
| (34) |
some specific cases are shown in Figure 5. Indeed, the BH accretion rate receives a markedly overall reduction, which can be directly indicated by comparing the cases ignoring circum-BH disk outflow feedback as shown in Figure 2. The general variation trend of the reduced mass rate depending on the AGN disk parameters has no significant change from the omitting-feedback cases. The reduction effect is more prominent for smaller index , which produces more powerful disk winds; but meanwhile, the initial mass accretion rate is higher, the combined effects bring about a relatively larger mass rate compared with the larger cases.
In a word, the circum-BH disk winds significantly impact the accretion processes of BH located in the AGN disk, the mass accretion rate of BH is markedly reduced, and the BH’s surroundings is observably changed in the form of a long-standing, underdense cavity, or to say, feedback of the outflow generated by the hyper-Eddington disk can not be neglected. Moreover, the mass rate accreted onto BH relies heavily on parameters and , and thus varies during the BH evolution, rather than remains as a fixed value.





3.3 Reduced Mass Accretion of NS
Compared to the BH accretion case, the NS accretion is relatively more efficient because the magnetosphere potentially truncates the circum-NS disk at a larger radius , Equation (13), to bring more mass accreted onto NS; meanwhile, feedback from the NS accretion system is more powerful because the existence of hard surface releases additional energy, Equation (14), to inject into the outflow.




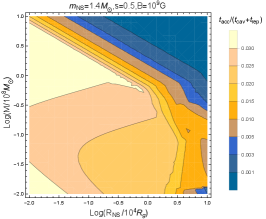




The specific properties of NS accretion are shown in Figure 6. We find that only the NS with a strong magnetic field (e.g. ) can give rise to magnetospheric disk truncation, on account of the large mass inflow rate of circum-NS disk leading to large disk pressure, which can only be resisted by large magnetic pressure; by contrast, when NS magnetic field is weak, the disk extends to the NS surface instead (comparing first and second panels in Figure 6). And we find that the NS-accretion energy is generally larger than the disk-generating energy (seeing all three panels in Figure 6), indicating that the NS surface liberation dominates the outflow energy injection, which is a remarkable feature in comparison to the BH accretion. Also, the nature of the circum-NS disk affects the accretion and the induced outflow feedback. The effects of NS mainly work in the cases of larger and smaller , where the NS mass inflow rate is relatively small, and thereby the disk is weak to confront the magnetosphere. Larger index results in more disk mass losing into wind and hence weaker disk pressure at the inner region, leading to a more outside magnetospheric truncation; but even so, fewer mass eventually flows onto NS surface, releasing less accretion energy compared with the smaller case (comparing first and third panels in Figure 6).
Similar to BH, the outflow cavity also forms in the NS accretion system. As shown in Figure 7, NS spends most of time in the underdense cavity going through inefficient accretion, and hence the averaged mass accretion rate is markedly reduced, of which the general trend is akin to the BH case. As discussed above, more energy is injected into the outflow, which results in more powerful feedback on the AGN disk environment and longer duration of the cavity evolution. Accordingly, the mass rate reduction is indeed more prominent with the existence of a NS hard surface and a strong magnetic field (comparing all three columns in Figure 7). The enhanced reduction is more effective at larger , where the AGN disk density is lower to block the cavity expansion, i.e., an additional energy injection would lead to a punchier expansion; on the contrary, when the NS is closer to SMBH, the environment is denser to block the cavity expansion, hence the cavity size would not change significantly though injecting additional energy. In addition, the more powerful for the cases of small and large causes the outflow feedback and the mass accretion rate of NS with strong magnetic fields a remarkable change. (comparing first and second columns in Figure 7).
4 Discussion







4.1 Different Treatments of Cavity Expansion
In Section 3.1, we assume that the shocked shell and outflow undergo rapid depressurization after the breakout from the AGN disk, and then the ringlike shell evolves driven by the momentum of wind and itself successively. However, the AGN disk usually holds plane-parallel stratified structure (e.g. Grishin et al., 2021), rather than a steep cutoff at the height ; even so, the shocked gas would break out and reduce pressure at (e.g. Schiano, 1985; Mac Low & McCray, 1988; Olano, 2009), hence we think our assumption can roughly describe the processes of wind-surroundings interaction. The uncertainty lies at the duration of the hot gas pushing the shell, where we simplistically link the outflow-energy and -momentum driven phase directly at . In fact, during the depressurization, the shell is still pushed laterally by the thermal pressure. On the other hand, the shocked gas perhaps experiences effective radiation cooling soon before or after the shell breakout, or even when the shell still expanding deeply in the AGN disk. Since the actual structure of the AGN disk is complex, and the shell evolution needs to contain the concrete cooling mechanisms of the shocked gas, which requires precise hydrodynamical simulations and is beyond the scope of this work, we instead consider two simplified and extreme cases, evolution following the adiabatic or momentum conservation phase in the spherically symmetric medium all the while, to study the effects of the duration of depressurization and the gas cooling. Corresponding descriptions of the evolution are shown in Appendix C.
We choose to typically reflect the features of CO accretion and outflow evolution, as shown in Figure 8. The cavity still comes into being in the two extreme cases, so we confirm that the formation of cavity and the reduction of averaged CO accretion rate are common and inevitable, regardless of the cooling efficiency. Comparing different treatments, the pure momentum conservation case leads to the largest , i.e., the weakest outflow feedback; correspondingly, cavity expansion is strongest in the entirely adiabatic case. Namely, the longer duration of the thermal energy pushing the shocked shell, the more powerful expansion of the cavity.
When estimating the strength of the disk winds, i.e. Equation (12), we set on account of the theoretical studies; but various numerical simulations show different inner radii where the outflow is observably produced, ranging (e.g. Jiang et al., 2014; Yang et al., 2014; Sa̧dowski et al., 2015; Kitaki et al., 2021). Setting the larger inner radius, the disk winds would be weaker, with . To study the selection of a larger , we decrease as a substitution, as shown in Figure 8, finding that the feedback is assuredly weaker, but still the cavity forms and the averaged CO accretion rate is significantly reduced.
We also verify the validity of our description on the outflow cavity evolution. We have assumed that the relevant environment parameters, mainly , are fixed during the outflow-AGN disk interaction; but if the size of cavity is too large, the AGN disk properties would vary with radius to affect the cavity evolution, our description are thus unfaithful. Safely, the cavity is always much smaller than the AGN disk radius, i.e. , as shown in left panel of Figure 9, so the fixed-environment assumption holds and our description is a feasible estimation. Moreover, since the half-width of the outflow cavity exceeds the CO gravity radius, as shown in Figure 4, the shear motion of the AGN disk gas would exert ram pressure to affect the shell evolution (e.g. Rozyczka et al., 1995), which limits the horizontal expansion width of the ring when its velocity decreases to the shear velocity, i.e., (Moranchel-Basurto et al., 2021). Using Equation (26), the maximum half-width of the cavity is given by
| (35) |
where the width is multiplied by 2 from the results of numerical simulation (Moranchel-Basurto et al., 2021). As shown in Figure 9, we find that , hence we think taking the shear into account can markedly deform the cavity structure, but would not significantly change the results in Section 3.
It is worth mentioning that the late evolution phase of ring driven by momentum is simplified, i.e., we ignore the ambient pressure and assume that the efficient accretion stops after in Equation (23) and (26); in practice, the accretion of CO would last for a few and launch winds to continuously push the shell. Meanwhile, there exists a stand-off radius defined by the pressure balance (e.g. Schiano, 1985), i.e.,
| (36) |
when the half-width of the cavity becomes larger than , the ambient pressure would be the dominant external force to decelerate the shell. We compare the stand-off radius with the cavity half-width, as shown in Figure 9, and find that , which implies that the wind is strong enough to push the shell, i.e., Equation (23), and the ring evolution is mainly driven by its own momentum at around , i.e., Equation (26); in other words, our simplified model can roughly describe the shell evolution. As an aside, the dropping disk wind would hinder the ambient inflow and maintain a cavity with decreasing if the CO hyper-Eddington accretion still persists during the cavity refilling phase, which can lengthen to further reduce the averaged accretion rate of CO. All in all, the long-term evolution of the circum-CO disk and the cavity are vital for the understanding of the CO accretion in the AGN disk, further researches are therefore needed.
4.2 Whether Gap Opens around CO in the AGN Disk


We have considered the effect of underdense gap when calculating the BHL inflow rate; as shown in left panel of Figure 10, the gas density is deeply reduced by the CO gravity for smaller SMBH mass and closer CO location cases. When studying the outflow feedback we briefly ignore the gap structure, instead we assume the shell expanding within the unperturbed AGN disk environment, which may underestimate the size of cavity and the reduction of averaged mass accretion rate because the shell can expand more easily in the underdense gap. Nevertheless, since the size of cavity is general larger than the gap half-width (the pink line in Figure 10), the assumption is roughly suitable except for the very light SMBH and very close CO location cases.
Note that the structure of underdense gap is commonly studied in a stable state, but the evolution of outflow cavity is dynamical and generally holds, so the properties of the gap environment around the CO may be affected by the outflow. The timescale of gap opening can be evaluated by the viscous timescale, i.e. (where we estimate the deep gap opening timescale being one-tenth of the timescale for the whole gap to attain the steady state, as shown by Figure 13 in Kanagawa et al. 2017), and the deep gap half-width can be set to (Kanagawa et al., 2018). Tagawa et al. (2022) alternatively suggests the gap opening timescale can be calculated via the angular momentum of gas within the annular gap removed by the gravitational torque of CO, i.e. , where and . Setting the cavity refilling timescale as , we find that holds within wide parameter space, i.e., or , so we boldly speculate that the deep gap around the CO has no enough time to be completely rebuilt to affect the efficient accretion of CO and would be enhanced, because after the faster refilling of gas with density from the AGN disk to the cavity within , the circum-CO disk has already being built by the denser gas before the density being completely reduced to the lower within ; conversely, the deep gap would be markedly rebuilt for the very light SMBH and very close CO location cases with , as shown by the purple line in Figure 10.
Not only the outflow would impede the build of deep gap around CO, the gap itself may not open for different AGN disk models. So we show the cases of which no gap opens in right panel of Figure 10. The most prominent feature is that the outflow feedback is more effective when is smaller, and hence more dramatically reduces the averaged CO mass accretion rate, which is in contrast to the gap-opening case as shown in Figure 5, because the gap effect is more noteworthy in these parameter regions. Overall, the outflow feedback likely impacts the gap around CO; we suggest that the CO accretion system in the AGN disk carried by lighter SMBH are useful to investigate whether the gap opens and the properties of the potential gap.
4.3 Comparison between CO-related Mass Rate and AGN Disk Inflow Rate
Since the density of environment is extremely large, the mass rate captured by the CO set in the AGN disk is hyper-Eddington, as shown in Figure 1, which even would be higher than the accretion rate of the SMBH itself; in other words, just one embedded BH (NS) can exhaust the mass supply of AGN disk if the BH (NS) accretion persists the AGN lifetime. Tagawa et al. (2022) highlighted a trouble as “ Depletion problem ”, i.e., the AGN disk gas can be depleted by COs if there is no feedback.
We argue that the AGN disk would not be starved by the accretion of embedded COs after the outflow feedback processes as described in Section 3.1 taken into account. First, due to the existence of outflow, the mass accretion rate onto CO, as shown in Figure 2, which is the actual loss of the AGN disk mass, is far below the initial mass inflow rate of circum-CO disk and the AGN accretion rate. Meanwhile, the existence of outflow cavity reduces the averaged circum-CO disk mass inflow rate akin to the reduction of averaged CO mass accretion rate, i.e.,
| (37) |
As shown in left panel of Figure 11, is generally lower than AGN accretion rate with nearly all inflow ejected into outflow , thereby even though all the circum-CO disk winds escape from the SMBH, the AGN disk is still capable to feed the SMBH. Besides, as shown in right panel of Figure 11, the wind velocity just leaving the circum-CO disk, i.e., Equation (19), is already generally lower than the escape velocity of the SMBH, . The parts of outflow moving along the AGN disk are eventually re-injected into the disk; the parts moving vertically would be dramatically decelerated by the dense environment, though breaking out, velocity of which is conceivable to be lower than , thus would eventually fallback into the AGN disk. To sum up, CO accretion with induced outflow feedback would just result in few mass loss, thus the AGN disk can live for a long time.








4.4 Jet Effect and Outflow EM Radiation
An additional process extracting the spin energy of an accreting BH via the formation of a jet would come into being when the BH is rotating, i.e. the Blandford-Znajek mechanism (Blandford & Znajek, 1977), the power of which , where is the magnetic field crossing the BH horizon and is the BH’s dimensionless spin parameter. By two valid methods, we can estimate the magnetic field strength around the BH: one is the winds produced by hyper-accreting circum-BH disk stretch the disk local magnetic fields to make large-scale poloidal components, or the AGN disk environment directly provides the ordered poloidal magnetic fields, both of which are continuously advected inwards and accumulate at the vicinity of BH, ultimately leading to a magnetically arrested disk (Kimura et al., 2021a; Kaaz et al., 2022), the maximum jet power is for (e.g. Davis & Tchekhovskoy, 2020; Curd & Narayan, 2023); another is via building pressure balance at the inner boundary of the circum-BH disk with the assumption that magnetic fields are local, the jet power is (e.g. Wang et al., 2021b). The relative strength between the wind, Equation (12), and the jet is
| (38) |
the ratio of which is nearly independent of AGN disk parameters and , and mainly dependent on index ; for instance, or for and cases. Two estimations of the jet power cause inversely relative strength to the wind, so a more physical description of the magnetic field around BH is important to determine the jet power and the relevant feedback strength, and needs to be detailedly studied.
The jet-cocoon evolution can also generate mechanical feedback to suppress the accretion of BH in the AGN disk (Kaaz et al., 2021; Tagawa et al., 2022). Assuredly, may cause jet other than wind dominants the feedback. However, the jet is highly anisotropic with narrow opening angle, and thus the size of cocoon cavity is smaller than (Figure 1 in Tagawa et al. 2022); as a contrast, we confirm that the wind outflow is nearly isotropic, and open a cavity much larger than , as shown in Figure 4. Meanwhile, for the accretors being a BH with low spin or a NS and when the magnetic field around BH is weak, the jet is feeble or even absent, leading to the feedback dominated by wind outflow. Therefore, we suggest that the jet feedback would play a secondary but non-negligible role, and for the high spin BH case, a more complete feedback mechanism containing both jet and wind needs to be built.
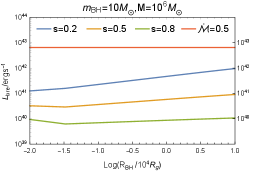
We also estimate the radiation features of the wind-outflow-driven shocked shell during breakout, which may provide an opportunity to observe the cavity evolution. Following Kimura et al. (2021b), the luminosity during shell breakout can be achieved from the photon energy released within the photon diffusion timescale, and the blackbody temperature of the breakout photon can be estimated from the shock jump condition, i.e.,
| (39) |
and
| (40) |
where is the radiation constant; the variations of and under various parameters are shown in Figure 12. As can be seen, the breakout radiation emerges as a soft X-ray/UV/optical transient depending on the CO location; meanwhile, the AGN emission is also powerful in X-ray/UV/optical bands (Shang et al., 2011). By comparing with the AGN bolometric luminosity , we loosely infer that the breakout events are general dimmer than the background emission, even though the extreme case, so the AGN disk would not be outshone. We confirm that the outflow cavity breakout events taking place in the AGN disk are generally unobservable. As in Wang et al. (2021a), the subsequent interaction between the outflow bubble and the broad-line region gas may generate flare, which can be detected in non-blazar AGNs.
4.5 Potential role of Outflow Cavity Surrounding CO
There are two noteworthy features of the outflow cavity surrounding CO: CO is commonly harbored in the cavity environment because of the always satisfied , and the gas density of cavity is much lower than the otherwise unperturbed AGN disk. These features would significantly affect the CO evolution and the CO-related events in AGN disk.
When embedded in the AGN disk, CO can not only capture the gas within its gravity sphere but also gravitational interact with the large-scale disk gas; correspondingly, the whole AGN disk gas exerts gravitational torques onto CO from the Lindblad and corotation resonances, leading to the CO migration (e.g. Ward, 1997), of which the timescale is expressed as (e.g. Kanagawa et al., 2018):
| (41) |
where . Though the cavity with large size and long duration must modify migration, the Lindblad resonance primarily originates from the whole background gas (e.g. Armitage, 2007), most of which are unaffected to provide torque, and during the cavity refilling process , AGN disk gas can enter the cavity to gravitationally interact with the CO, again producing torque; so we ignore the effect of outflow cavity on migration for simplicity. Because CO mainly stays in the underdense cavity, the averaged mass accretion rate of CO reduces significantly, and thereby the mass growth rate of CO reduces as well. We estimate the CO mass growth timescale containing outflow feedback as and the timescale omitting outflow as . By comparing relevant timescales as shown in Figure 13, we find that the outflow feedback markedly alters the nature of CO evolution. If not bringing in outflow, the extremely large mass accretion rate results in a violent mass growth, , thus the CO evolves in situ without migration. Conversely, the formation of outflow and the concomitant feedback lead to a moderate mass growth, basically , so the CO can observably migrate before significantly becoming heavier. In a word, the accretion-induced outflow strangles the mass growth of CO.
As have already been mentioned, a variety of EM events involving CO are likely to take place in the AGN disk. Since the striking difference between the cavity and AGN disk environment (e.g. density, temperature, opacity), EM events would possess distinguishable features when they separately occur in the two environments. Propagating within the unperturbed dense AGN disk, the jet, ejecta, and outflow generated by the EM events undergo rapid deceleration, which can produce characteristic radiations. On the other hand, as the cavity is much more tenuous than the AGN disk but still denser than the interstellar medium, these jet, ejecta, and outflow would not be significantly decelerated but still interact with the cavity medium (e.g. Yuan et al., 2022), the produced EM emissions would propagate within the cavity environment as well (e.g. Kimura et al., 2021b), which may thus lead to characteristic signals differing from the ones in an unperturbed AGN disk or in a classical interstellar medium. Also, as the underdense cavity has a limited size, matter penetrating along the AGN disk will firstly collide with cavity and then AGN disk gas, causing a latter effective loss of the kinetic energy and thereby latter brightening, which may apply to the events with wide-angle ejecta and outflow, as a star tidally disrupted by a stellar mass BH (e.g. Perets et al., 2016; Yang et al., 2022), or BH-NS and NS-NS mergers (e.g. Zhu et al., 2021a; Ren et al., 2022). A more precise description of the cavity structure and the properties of various EM events occurring in the cavity-AGN disk environment are left in a follow-up work.
Tagawa et al. (2020a) showed that single-single gas-capture channel dominates the binary formation in the AGN disk, where the gas dynamical friction acting on CO, which is approximately proportional to the gas density surrounding CO, i.e., (Ostriker, 1999), effectively removes the binary binding energy during the two bodies encountering in their mutual Hill radius, and thereby a CO binary forms. However, as COs are mainly harbored in the cavity environment, of which the gas density is much lower than the otherwise unperturbed AGN disk and the size is much larger than the Hill radius, as shown in Figure 4, the gas dynamical friction can be significantly weakened, , hence the efficiency of single-single gas capture channel may be markedly reduced. In brief, the outflow feedback plays an important role and should not be neglected when studying the binary formation in the AGN disk.
4.6 Accretion Feedback of CO with Large Bulk Velocity
CO can possess a large bulk velocity relative to the AGN disk gas, i.e. , e.g., the orbiting CO in the galactic nucleus holding nonzero inclination w.r.t. the disk plane will periodically cross the AGN disk with considerable perpendicular velocity (e.g. Fabj et al., 2020; Nasim et al., 2022), or the remnant of a binary CO merger will be ejected at large recoil velocity (e.g. Campanelli et al., 2007), or the CO can leave triple system with large escape velocity after the chaotic interaction (Valtonen & Karttunen, 2006), and so on. In the case of supersonic motion, CO triggers the formation of a bow shock, producing a downstream overdense shocked gas wake, which drags the CO and is accreted onto it (e.g. Antoni et al., 2019). Meanwhile, the BHL mass inflow rate is still hyper-Eddington, e.g. , so the radiation-driven outflow should emerge, the feedback of which results in the redistribution of bow shock separating the outflow and the surrounding gas, and an underdense wake region may be built, depending on the outflow geometry (Li et al., 2020). The accretion and dynamical friction on CO, which are important for the evolution of CO supersonically moving within AGN disk and the capture of CO by AGN disk (Fabj et al., 2020; Nasim et al., 2022), would be significantly affected by the potential outflow (Gruzinov et al., 2020; Li et al., 2020; Bosch-Ramon, 2022; Kaaz et al., 2022).
However, whether an outflow really forms and the concrete mechanism of its ejection from the supersonically moving CO have not been well studied, much less in the particular AGN disk environment. For BHL accretion with large , the inflow would be highly quasi-spherical (e.g. El Mellah & Casse, 2015), so no region is left to release outflow, and photons are trapped and advected inward with inflow at hyper-Eddington rate (e.g. Begelman, 1979; Blondin, 1986). Vast mass and energy ultimately flow into the horizon for the case of BH, or eventually hit the hard surface and potentially release huge energy for the case of NS (e.g. Shakura et al., 2015). On the other hand, the initial infalling gas may carry a small but unnegligible amount of angular momentum depending on the AGN disk properties, and thus an accretion disk may form around CO to launch winds via the mechanism discussed in Section 2.2; a self-consistent evolution process should come into being (probably alike Wang et al. 2021a).
Since the accretion feedback of CO with a large bulk velocity is vital but poorly understood, we would prepare another separate work to study the launch mechanisms and the properties of outflow; the interaction between the outflow and the AGN gas medium, the effects of outflow on CO accretion process and dynamical drag with the induced acceleration/deceleration of CO, the ability of AGN disk on capturing the crossing CO when considering accretion feedback, and the relevant EM radiations would be studied as well.
5 Summary
In this work, we have explored the role of outflow feedback on accretion of the CO embedded in an AGN disk. We have revealed that winds launched from the circum-CO hyper-Eddington accretion disk are asymptotically isotropic and would truncate the disk to halt CO accretion. Interaction between the outflow and the AGN disk gas gives rise to a cyclic process of formation and refilling of a long-running outflow cavity, of which the size is larger than the CO gravity sphere (BHL and Hill radius) and the density is lower than that of the unperturbed environment. Efficient CO accretion takes place in the AGN disk rather the cavity environment, and therefore the outflow feedback leads to an accretion duty-circle of . We have found that if taking the influences of outflow and its feedback into account, then the mass accretion rate onto a BH, which now ranges depending on the AGN disk parameters, the BH’s location, and the outflow strength, is extremely reduced in comparison to the initial gas captured rate. Although the outflow feedback itself is hard to be observed, it remarkably changes the CO evolution character, causing considerable CO migration before sizable mass growth via the reduction of time-averaged CO mass growth rate; and it prevents the AGN disk from being depleted by the otherwise violent CO accretion.
We have proved that both cavity formation and mass accretion reduction are the universal roles of outflow feedback, independent of the cooling efficiency of shocked gas and whether the gravity gap opens or not. Moreover, the underdense cavity environment can impact the features of CO-related EM events and the CO binary formation efficiency, which are significant roles of outflow feedback as well. We suggest that jet feedback would also play a role for the cases of BH with large spin and strong magnetic field around its horizon.
In addition, we have investigated the role of outflow feedback on NS accretion due to the existence of NS magnetic field and hard surface, of which the general properties are essentially unchanged. But for a NS case, the accretion process is relatively complex, because the more powerful outflow feedback derived from the energy released near NS surface weakens the accretion, reversely the magnetospheric disk truncation makes mass rate accreted onto NS larger. So we suggest that the NS evolution and NS-related events need to be specifically studied.
Appendix A Self-similar Solutions of Hyper-Eddington Accretion Disk
Although the hyper-Eddington accretion process around CO is complicated and should be investigated via numerical simulation methods (e.g. Ohsuga et al., 2005; Yang et al., 2014; Jiang et al., 2014; Sa̧dowski et al., 2015; Kitaki et al., 2018, et al.), analytic solutions are valuable because they can roughly match the simulation results (Jiao et al., 2015), and it is convenient to use these solutions to study the accretion systems under wide parameter space. When analytically solving the disk structure, self-similar assumption has been widely adopted (Blandford & Begelman, 1999, 2004; Begelman, 2012; Gu, 2012, 2015; Wu et al., 2022; Ghoreyshi & Shadmehri, 2020; Zahra Zeraatgari et al., 2020, et al.); though these solutions would fail near the inner and the outer boundaries, most regions of the disk can be well described. In this section, we build the self-similar disk with wind outflow taken into account, and estimate the contribution of outflow to carrying away the viscous heat of the hyper-Eddington accretion disk.
We consider a steady state axisymmetric accretion flow. For simplicity, we use the Newtonian point-mass potential , and we ignore the vertical structure of the inflow and assume that all flow variables depend only on radial distance . The vertical scale height of the disk is , where denotes the sound speed, among which and are pressure and density of the inflow, respectively. We only consider -component of the shear stress tensor and the viscosity is .
We assume that the mass inflow rate varies with radius due to the mass loss via outflow (Blandford & Begelman, 1999; Wu et al., 2022) and is described by
| (A1) |
the outflow mass rate , accordingly the wind loss rate per unit area can be calculated by:
| (A2) |
and so
| (A3) |
Including the influence of outflow (e.g. Knigge, 1999), the continuity equation, the vertically integrated radial momentum and azimuthal momentum equations are
| (A4) |
| (A5) |
| (A6) |
where Equation (A6) contains the loss of angular momentum via outflow; reflects the amount of specific angular momentum carried away by outflow, where represents the wind carrying away the local angular momentum of inflow at the radius where wind originates (Knigge, 1999). Combining Equations (A4) and (A6) with the adoption of a torque-free inner boundary condition, i.e. , and , we can get
| (A7) |
where is set to be the inner boundary of the disk. The energy equation is
| (A8) |
where , and are the viscous heating rate, the advective cooling rate and the energy rate taken away by outflow per unit area, respectively. We approximatively ignore the convection cooling term and the radiation cooling term because for hyper-Eddington accretion flow, the convection is relatively less important than the advection (Jiao et al., 2015), and the radiation is effectively trapped in the flow (Begelman, 2012), leading to a convectively and radiatively inefficient flow. The expressions of the energy terms are as follows (e.g. Abramowicz et al., 1995):
| (A9) |
| (A10) |
where is the specific entropy and is the ratio of specific heat. The energy taken away by outflow is simply assumed to be comparable with the local gas kinetic energy:
| (A11) |
where reflects the specific energy of outflow, and the square brackets part is added to ensure the self-similarity of Equation (A8).
Therefore, the specific expressions of the self-similar variables, , , , , and , can be solved using the Equations (A4), (A5), (A6), (A8) and the expression of . In this work, we primarily focus on the total heat energy and the outflow feedback energy of the hyper-Eddington accretion disk, the ratio between these two is:
| (A12) |
where the inequality holds for the criteria , and , which are satisfied in hyper-Eddington accretion disk. The outflow cooling rate needs to be less than the total viscous heating rate, yet the outflow should be fast enough to propagate far away (but see the breeze solutions in Begelman 2012), thereby restricts . We take as a reasonable ratio. The exact values of and in the large-scale hyper-Eddington accretion system should be determined by numerical simulations.
Appendix B Gas Density and Height of Hyper-Eddington Accretion Disk
Circum-CO disk with diverse values of the initial mass inflow rate would manifest piecewise structure, as discussed in Section 2.2. Inside , the disk is advection-cooling dominated, gas density of the disk region is
| (B1) |
where is the actual value of disk radius. Outside , the disk is radiation-cooling dominated, thereby the standard disk structure can probably describe the region (e.g. Kato et al., 2008). To be consistent with the expressions of AGN disk structure, i.e. Equation (1), we consider pure hydrogen medium; the pressure is the sum of radiation and gas components, ; the energy equation is , where ; and the main opacity sources include electron scattering and free-free absorption, , where and . The disk structure can be solved by combining the energy equation and Equation (A1). For the inner region where and , the disk density and height are
| (B2) |
| (B3) |
where and ; for the middle region where and , the disk density and height are
| (B4) |
| (B5) |
and for the outer region where and , the disk density and height are
| (B6) |
| (B7) |
The boundary between these three regions are radii where and , i.e.,
| (B8) |
and
| (B9) |
We tentatively use the standard disk model, in spite of the potential thermal instabilities at the radiation-cooling inner region (e.g. Shen & Matzner, 2014), because the instability is still poorly understood in the theory of accretion disks, with some simulations show the thermally stable disk (Hirose et al., 2009), and the general viscosity can relieve the instability. Also, we note that when the initial mass inflow rate is extremely large, there can be , namely the disk skips over the radiation-cooling and radiation pressure dominated state to directly become advection-dominated, which is unphysical and leads to the jump of relevant features, e.g. the discontinuity in Figure 12 and Figure 13. The inaccuracy derives from the simplified expression of the boundary and the directly connection between the outer standard disk and the inner advective disk. The accurate construction of the hyper-Eddington accretion disk should simultaneously contain advection and radiation term all the radius, and should deal with the formation of disk wind more specifically (e.g. Blandford & Begelman, 2004). In this work we build the circum-CO disk roughly, which we think is enough to reveal the disk features, to focus on the outflow feedback; we leave the specific structure of hyper-Eddington accretion disk in a future work.
Appendix C Evolution of Shell in Momentum Conservation or Adiabatic Case
For the momentum conservation case, the shocked outflow and the swept AGN disk gas are assumed to lose all thermal energy immediately, the expansion of the shell is completely driven by the outflow momentum, i.e. Equation (20). The radius and velocity of the expanding shell evolve with time as (Dyson & Williams, 1997):
| (C1) |
and
| (C2) |
After the stop of CO accretion, the evolution of shell follows:
| (C3) |
Also, if the efficient accretion stops before breakout, the swept shell expands roughly driven by the total momentum injected by the outflow, , the radius and velocity are approximately given by (Dyson & Williams, 1997)
| (C4) |
and
| (C5) |
After the breakout, the evolution of shell follows:
| (C6) |
The half-width, the formation and refilling timescales of cavity can be achieved analogously as Equations (27), (28) and (32). Or if the shell fails to punch the AGN disk, we use as a criterion to study the evolution of shell.
For the adiabatic case, we roughly assume the whole accretion-released energy drives the shell expansion all the time, thereby the radius and velocity are again approximately given as
| (C7) |
and
| (C8) |
The half-width, the formation and refilling timescales of cavity can be calculated via the criterion where
| (C9) |
References
- Abbott et al. (2020) Abbott, R., Abbott, T. D., Abraham, S., et al. 2020, Phys. Rev. Lett., 125, 101102. 10.1103/PhysRevLett.125.101102
- Abramowicz et al. (1995) Abramowicz, M. A., Chen, X., Kato, S., et al. 1995, ApJ, 438, L37. doi:10.1086/187709
- Antoni et al. (2019) Antoni, A., MacLeod, M., & Ramirez-Ruiz, E. 2019, ApJ, 884, 22. doi:10.3847/1538-4357/ab3466
- Armitage (2007) Armitage, P. J. 2007, astro-ph/0701485
- Ayliffe & Bate (2009) Ayliffe, B. A. & Bate, M. R. 2009, MNRAS, 397, 657. doi:10.1111/j.1365-2966.2009.15002.x
- Bartos et al. (2017) Bartos, I., Kocsis, B., Haiman, Z., et al. 2017, ApJ, 835, 165. doi:10.3847/1538-4357/835/2/165
- Baruteau et al. (2014) Baruteau, C., Crida, A., Paardekooper, S.-J., et al. 2014, Protostars and Planets VI, 667. doi:10.2458/azu_uapress_9780816531240-ch029
- Begelman (1979) Begelman, M. C. 1979, MNRAS, 187, 237. doi:10.1093/mnras/187.2.237
- Begelman (2012) Begelman, M. C. 2012, MNRAS, 420, 2912. doi:10.1111/j.1365-2966.2011.20071.x
- Bellovary et al. (2016) Bellovary, J. M., Mac Low, M.-M., McKernan, B., et al. 2016, ApJ, 819, L17. doi:10.3847/2041-8205/819/2/L17
- Blandford & Znajek (1977) Blandford, R. D. & Znajek, R. L. 1977, MNRAS, 179, 433. doi:10.1093/mnras/179.3.433
- Blandford & Begelman (1999) Blandford, R. D. & Begelman, M. C. 1999, MNRAS, 303, L1. doi:10.1046/j.1365-8711.1999.02358.x
- Blandford & Begelman (2004) Blandford, R. D. & Begelman, M. C. 2004, MNRAS, 349, 68. doi:10.1111/j.1365-2966.2004.07425.x
- Blondin (1986) Blondin, J. M. 1986, ApJ, 308, 755. doi:10.1086/164548
- Bosch-Ramon (2022) Bosch-Ramon, V. 2022, A&A, 660, A5. doi:10.1051/0004-6361/202142821
- Campanelli et al. (2007) Campanelli, M., Lousto, C. O., Zlochower, Y., et al. 2007, Phys. Rev. Lett., 98, 231102. doi:10.1103/PhysRevLett.98.231102
- Chashkina et al. (2019) Chashkina, A., Lipunova, G., Abolmasov, P., et al. 2019, A&A, 626, A18. doi:10.1051/0004-6361/201834414
- Cheng & Wang (1999) Cheng, K. S. & Wang, J.-M. 1999, ApJ, 521, 502. doi:10.1086/307572
- Coughlin & Begelman (2014) Coughlin, E. R. & Begelman, M. C. 2014, ApJ, 781, 82. doi:10.1088/0004-637X/781/2/82
- Curd & Narayan (2023) Curd, B. & Narayan, R. 2023, MNRAS, 518, 3441. doi:10.1093/mnras/stac3330
- Davis & Tchekhovskoy (2020) Davis, S. W. & Tchekhovskoy, A. 2020, ARA&A, 58, 407. doi:10.1146/annurev-astro-081817-051905
- Dittmann et al. (2021) Dittmann, A. J., Cantiello, M., & Jermyn, A. S. 2021, ApJ, 916, 48. doi:10.3847/1538-4357/ac042c
- Dyson & Williams (1997) Dyson, J. E. & Williams, D. A. 1997, The physics of the interstellar medium. Edition: 2nd ed. Publisher: Bristol: Institute of Physics Publishing, 1997. Edited by J. E. Dyson and D. A. Williams. Series: The graduate series in astronomy. ISBN: 0750303069. doi:10.1201/9780585368115
- Edgar (2004) Edgar, R. 2004, New A Rev., 48, 843. doi:10.1016/j.newar.2004.06.001
- El Mellah & Casse (2015) El Mellah, I. & Casse, F. 2015, MNRAS, 454, 2657. doi:10.1093/mnras/stv2184
- Fabj et al. (2020) Fabj, G., Nasim, S. S., Caban, F., et al. 2020, MNRAS, 499, 2608. doi:10.1093/mnras/staa3004
- Ghoreyshi & Shadmehri (2020) Ghoreyshi, S. M. & Shadmehri, M. 2020, MNRAS, 493, 5107. doi:10.1093/mnras/staa599
- Ghosh & Lamb (1979) Ghosh, P. & Lamb, F. K. 1979, ApJ, 234, 296. doi:10.1086/157498
- Gilbaum & Stone (2022) Gilbaum, S. & Stone, N. C. 2022, ApJ, 928, 191. doi:10.3847/1538-4357/ac4ded
- Goodman (2003) Goodman, J. 2003, MNRAS, 339, 937. doi:10.1046/j.1365-8711.2003.06241.x
- Graham et al. (2020) Graham, M. J., Ford, K. E. S., McKernan, B., et al. 2020, Phys. Rev. Lett., 124, 251102. doi:10.1103/PhysRevLett.124.251102
- Grishin et al. (2021) Grishin, E., Bobrick, A., Hirai, R., et al. 2021, MNRAS, 507, 156. doi:10.1093/mnras/stab1957
- Gruzinov et al. (2020) Gruzinov, A., Levin, Y., & Matzner, C. D. 2020, MNRAS, 492, 2755. doi:10.1093/mnras/staa013
- Gu (2012) Gu, W.-M. 2012, ApJ, 753, 118. doi:10.1088/0004-637X/753/2/118
- Gu (2015) Gu, W.-M. 2015, ApJ, 799, 71. doi:10.1088/0004-637X/799/1/71
- Hashizume et al. (2015) Hashizume, K., Ohsuga, K., Kawashima, T., et al. 2015, PASJ, 67, 58. doi:10.1093/pasj/psu132
- Hirose et al. (2009) Hirose, S., Krolik, J. H., & Blaes, O. 2009, ApJ, 691, 16. doi:10.1088/0004-637X/691/1/16
- Hu et al. (2022) Hu, H., Inayoshi, K., Haiman, Z., et al. 2022, ApJ, 934, 132. doi:10.3847/1538-4357/ac75d8
- Jermyn et al. (2021) Jermyn, A. S., Dittmann, A. J., Cantiello, M., et al. 2021, ApJ, 914, 105. doi:10.3847/1538-4357/abfb67
- Jiang et al. (2014) Jiang, Y.-F., Stone, J. M., & Davis, S. W. 2014, ApJ, 796, 106. doi:10.1088/0004-637X/796/2/106
- Jiao et al. (2015) Jiao, C.-L., Mineshige, S., Takeuchi, S., et al. 2015, ApJ, 806, 93. doi:10.1088/0004-637X/806/1/93
- Kaaz et al. (2021) Kaaz, N., Schrøder, S. L., Andrews, J. J., et al. 2021, arXiv:2103.12088
- Kaaz et al. (2022) Kaaz, N., Murguia-Berthier, A., Chatterjee, K., et al. 2022, arXiv:2201.11753
- Kanagawa et al. (2015) Kanagawa, K. D., Muto, T., Tanaka, H., et al. 2015, ApJ, 806, L15. doi:10.1088/2041-8205/806/1/L15
- Kanagawa et al. (2016) Kanagawa, K. D., Muto, T., Tanaka, H., et al. 2016, PASJ, 68, 43. doi:10.1093/pasj/psw037
- Kanagawa et al. (2017) Kanagawa, K. D., Tanaka, H., Muto, T., et al. 2017, PASJ, 69, 97. doi:10.1093/pasj/psx114
- Kanagawa et al. (2018) Kanagawa, K. D., Tanaka, H., & Szuszkiewicz, E. 2018, ApJ, 861, 140. doi:10.3847/1538-4357/aac8d9
- Kato et al. (2008) Kato, S., Fukue, J., & Mineshige, S. 2008, Black-Hole Accretion Disks — Towards a New Paradigm —, 549 pages, including 12 Chapters, 9 Appendices, ISBN 978-4-87698-740-5, Kyoto University Press (Kyoto, Japan), 2008.
- Kimura et al. (2021a) Kimura, S. S., Sudoh, T., Kashiyama, K., et al. 2021a, ApJ, 915, 31. doi:10.3847/1538-4357/abff58
- Kimura et al. (2021b) Kimura, S. S., Murase, K., & Bartos, I. 2021b, ApJ, 916, 111. doi:10.3847/1538-4357/ac0535
- Kitaki et al. (2018) Kitaki, T., Mineshige, S., Ohsuga, K., et al. 2018, PASJ, 70, 108. doi:10.1093/pasj/psy110
- Kitaki et al. (2021) Kitaki, T., Mineshige, S., Ohsuga, K., et al. 2021, PASJ, 73, 450. doi:10.1093/pasj/psab011
- Knigge (1999) Knigge, C. 1999, MNRAS, 309, 409. doi:10.1046/j.1365-8711.1999.02839.x
- Kocsis et al. (2011) Kocsis, B., Yunes, N., & Loeb, A. 2011, Phys. Rev. D, 84, 024032. doi:10.1103/PhysRevD.84.024032
- Kohri et al. (2005) Kohri, K., Narayan, R., & Piran, T. 2005, ApJ, 629, 341. doi:10.1086/431354
- Kremer et al. (2019) Kremer, K., Lu, W., Rodriguez, C. L., et al. 2019, ApJ, 881, 75. doi:10.3847/1538-4357/ab2e0c
- Kumar et al. (2008) Kumar, P., Narayan, R., & Johnson, J. L. 2008, MNRAS, 388, 1729. doi:10.1111/j.1365-2966.2008.13493.x
- Lai (2014) Lai, D. 2014, European Physical Journal Web of Conferences, 64, 01001. doi:10.1051/epjconf/20136401001
- Li et al. (2020) Li, X., Chang, P., Levin, Y., et al. 2020, MNRAS, 494, 2327. doi:10.1093/mnras/staa900
- Mac Low & McCray (1988) Mac Low, M.-M. & McCray, R. 1988, ApJ, 324, 776. doi:10.1086/165936
- McKernan et al. (2012) McKernan, B., Ford, K. E. S., Lyra, W., et al. 2012, MNRAS, 425, 460. doi:10.1111/j.1365-2966.2012.21486.x
- McKernan et al. (2020a) McKernan, B., Ford, K. E. S., O’Shaugnessy, R., et al. 2020, MNRAS, 494, 1203. doi:10.1093/mnras/staa740
- McKernan et al. (2020b) McKernan, B., Ford, K. E. S., & O’Shaughnessy, R. 2020, MNRAS, 498, 4088. doi:10.1093/mnras/staa2681
- Metzger (2012) Metzger, B. D. 2012, MNRAS, 419, 827. doi:10.1111/j.1365-2966.2011.19747.x
- Mishra et al. (2020) Mishra, B., Begelman, M. C., Armitage, P. J., et al. 2020, MNRAS, 492, 1855. doi:10.1093/mnras/stz3572
- Moranchel-Basurto et al. (2021) Moranchel-Basurto, A., Sánchez-Salcedo, F. J., Chametla, R. O., et al. 2021, ApJ, 906, 15. doi:10.3847/1538-4357/abca88
- Narayan & Yi (1994) Narayan, R. & Yi, I. 1994, ApJ, 428, L13. doi:10.1086/187381
- Narayan & Yi (1995) Narayan, R. & Yi, I. 1995, ApJ, 444, 231. doi:10.1086/175599
- Nasim et al. (2022) Nasim, S. S., Fabj, G., Caban, F., et al. 2022, arXiv:2207.09540
- Olano (2009) Olano, C. A. 2009, A&A, 506, 1215. doi:10.1051/0004-6361/200912602
- Ohsuga et al. (2005) Ohsuga, K., Mori, M., Nakamoto, T., et al. 2005, ApJ, 628, 368. doi:10.1086/430728
- Ostriker (1983) Ostriker, J. P. 1983, ApJ, 273, 99. doi:10.1086/161351
- Ostriker & McKee (1988) Ostriker, J. P. & McKee, C. F. 1988, Reviews of Modern Physics, 60, 1. doi:10.1103/RevModPhys.60.1
- Ostriker (1999) Ostriker, E. C. 1999, ApJ, 513, 252. doi:10.1086/306858
- Pan & Yang (2021a) Pan, Z. & Yang, H. 2021a, Phys. Rev. D, 103, 103018. doi:10.1103/PhysRevD.103.103018
- Pan & Yang (2021b) Pan, Z. & Yang, H. 2021b, ApJ, 923, 173. doi:10.3847/1538-4357/ac249c
- Pan et al. (2022) Pan, Z., Lyu, Z., & Yang, H. 2022, Phys. Rev. D, 105, 083005. doi:10.1103/PhysRevD.105.083005
- Perets et al. (2016) Perets, H. B., Li, Z., Lombardi, J. C., et al. 2016, ApJ, 823, 113. doi:10.3847/0004-637X/823/2/113
- Perna et al. (2021a) Perna, R., Lazzati, D., & Cantiello, M. 2021a, ApJ, 906, L7. doi:10.3847/2041-8213/abd319
- Perna et al. (2021b) Perna, R., Tagawa, H., Haiman, Z., et al. 2021b, ApJ, 915, 10. doi:10.3847/1538-4357/abfdb4
- Piro & Lu (2020) Piro, A. L. & Lu, W. 2020, ApJ, 894, 2. doi:10.3847/1538-4357/ab83f6
- Ren et al. (2022) Ren, J., Chen, K., Wang, Y., et al. 2022, ApJ, 940, L44. doi:10.3847/2041-8213/aca025
- Romanova & Owocki (2015) Romanova, M. M. & Owocki, S. P. 2015, Space Sci. Rev., 191, 339. doi:10.1007/s11214-015-0200-9
- Rozyczka et al. (1995) Rozyczka, M., Bodenheimer, P., & Lin, D. N. C. 1995, MNRAS, 276, 597. doi:10.1093/mnras/276.2.597
- Sa̧dowski et al. (2015) Sa̧dowski, A., Narayan, R., Tchekhovskoy, A., et al. 2015, MNRAS, 447, 49. doi:10.1093/mnras/stu2387
- Sa̧dowski & Narayan (2015) Sa̧dowski, A. & Narayan, R. 2015, MNRAS, 453, 3213. doi:10.1093/mnras/stv1802
- Sa̧dowski et al. (2016) Sa̧dowski, A., Lasota, J.-P., Abramowicz, M. A., et al. 2016, MNRAS, 456, 3915. doi:10.1093/mnras/stv2854
- Sa̧dowski & Narayan (2016) Sa̧dowski, A. & Narayan, R. 2016, MNRAS, 456, 3929. doi:10.1093/mnras/stv2941
- Samsing et al. (2022) Samsing, J., Bartos, I., D’Orazio, D. J., et al. 2022, Nature, 603, 237. doi:10.1038/s41586-021-04333-1
- Schiano (1985) Schiano, A. V. R. 1985, ApJ, 299, 24. doi:10.1086/163680
- Secunda et al. (2019) Secunda, A., Bellovary, J., Mac Low, M.-M., et al. 2019, ApJ, 878, 85. doi:10.3847/1538-4357/ab20ca
- Shakura & Sunyaev (1973) Shakura, N. I. & Sunyaev, R. A. 1973, A&A, 24, 337
- Shakura et al. (2015) Shakura, N. I., Postnov, K. A., Kochetkova, A. Y., et al. 2015, Astronomy Reports, 59, 645. doi:10.1134/S1063772915070112
- Shang et al. (2011) Shang, Z., Brotherton, M. S., Wills, B. J., et al. 2011, ApJS, 196, 2. doi:10.1088/0067-0049/196/1/2
- Shen & Matzner (2014) Shen, R.-F. & Matzner, C. D. 2014, ApJ, 784, 87. doi:10.1088/0004-637X/784/2/87
- Sirko & Goodman (2003) Sirko, E. & Goodman, J. 2003, MNRAS, 341, 501. doi:10.1046/j.1365-8711.2003.06431.x
- Syer et al. (1991) Syer, D., Clarke, C. J., & Rees, M. J. 1991, MNRAS, 250, 505. doi:10.1093/mnras/250.3.505
- Tagawa et al. (2020a) Tagawa, H., Haiman, Z., & Kocsis, B. 2020a, ApJ, 898, 25. doi:10.3847/1538-4357/ab9b8c
- Tagawa et al. (2020b) Tagawa, H., Haiman, Z., Bartos, I., et al. 2020b, ApJ, 899, 26. doi:10.3847/1538-4357/aba2cc
- Tagawa et al. (2021) Tagawa, H., Kocsis, B., Haiman, Z., et al. 2021, ApJ, 908, 194. doi:10.3847/1538-4357/abd555
- Tagawa et al. (2022) Tagawa, H., Kimura, S. S., Haiman, Z., et al. 2022, ApJ, 927, 41. doi:10.3847/1538-4357/ac45f8
- Takahashi et al. (2018) Takahashi, H. R., Mineshige, S., & Ohsuga, K. 2018, ApJ, 853, 45. doi:10.3847/1538-4357/aaa082
- Takeo et al. (2020) Takeo, E., Inayoshi, K., & Mineshige, S. 2020, MNRAS, 497, 302. doi:10.1093/mnras/staa1906
- Tanigawa et al. (2012) Tanigawa, T., Ohtsuki, K., & Machida, M. N. 2012, ApJ, 747, 47. doi:10.1088/0004-637X/747/1/47
- Tanigawa & Tanaka (2016) Tanigawa, T. & Tanaka, H. 2016, ApJ, 823, 48. doi:10.3847/0004-637X/823/1/48
- Thompson et al. (2005) Thompson, T. A., Quataert, E., & Murray, N. 2005, ApJ, 630, 167. doi:10.1086/431923
- Toomre (1964) Toomre, A. 1964, ApJ, 139, 1217. doi:10.1086/147861
- Valtonen & Karttunen (2006) Valtonen, M. & Karttunen, H. 2006, The Three-Body Problem, by Mauri Valtonen and Hannu Karttunen, pp. . ISBN 0521852242. Cambridge, UK: Cambridge University Press, 2006.
- Wang et al. (2021a) Wang, J.-M., Liu, J.-R., Ho, L. C., et al. 2021a, ApJ, 911, L14. doi:10.3847/2041-8213/abee81
- Wang et al. (2021b) Wang, J.-M., Liu, J.-R., Ho, L. C., et al. 2021b, ApJ, 916, L17. doi:10.3847/2041-8213/ac0b46
- Wang et al. (2022) Wang, Y.-H., Lazzati, D., & Perna, R. 2022, MNRAS. doi:10.1093/mnras/stac1968
- Ward (1997) Ward, W. R. 1997, Icarus, 126, 261. doi:10.1006/icar.1996.5647
- Weaver et al. (1977) Weaver, R., McCray, R., Castor, J., et al. 1977, ApJ, 218, 377. doi:10.1086/155692
- Wu et al. (2022) Wu, W.-B., Gu, W.-M., & Sun, M. 2022, ApJ, 930, 108. doi:10.3847/1538-4357/ac6588
- Yang et al. (2014) Yang, X.-H., Yuan, F., Ohsuga, K., et al. 2014, ApJ, 780, 79. doi:10.1088/0004-637X/780/1/79
- Yang et al. (2022) Yang, Y., Bartos, I., Fragione, G., et al. 2022, ApJ, 933, L28. doi:10.3847/2041-8213/ac7c0b
- Yuan et al. (2022) Yuan, C., Murase, K., Guetta, D., et al. 2022, ApJ, 932, 80. doi:10.3847/1538-4357/ac6ddf
- Yuan & Narayan (2014) Yuan, F. & Narayan, R. 2014, ARA&A, 52, 529. doi:10.1146/annurev-astro-082812-141003
- Zahra Zeraatgari et al. (2020) Zahra Zeraatgari, F., Mosallanezhad, A., Yuan, Y.-F., et al. 2020, ApJ, 888, 86. doi:10.3847/1538-4357/ab594f
- Zhang & Dai (2009) Zhang, D. & Dai, Z. G. 2009, ApJ, 703, 461. doi:10.1088/0004-637X/703/1/461
- Zhu et al. (2021a) Zhu, J.-P., Zhang, B., Yu, Y.-W., et al. 2021a, ApJ, 906, L11. doi:10.3847/2041-8213/abd412
- Zhu et al. (2021b) Zhu, J.-P., Yang, Y.-P., Zhang, B., et al. 2021b, ApJ, 914, L19. doi:10.3847/2041-8213/abff5a