The role of the Galactic Halo and the Single Source in the formation of the cosmic ray anisotropy
Abstract
The existence of the cosmic ray Halo in our Galaxy has been discussed for more than half a century. If it is real it could help to explain some puzzling features of the cosmic ray flux: its small radial gradient, nearly perfect isotropy and the low level of the fine structure in the energy spectra of the various particles. All these features could be understood if: (a) the Halo has a big size (b) cosmic rays in the Halo have a unform spatial or radial distribution and (c) the cosmic ray density in the Halo is comparable or even higher than that in the Galactic Disk. The main topic of the paper concerns the present status of the anisotropy and a model for its formation. In our model the extremely small amplitude of the dipole anisotropy is due to the dilution of the anisotropy in the Disk by the dominating isotropic cosmic rays from the Halo. Some minor deviations from complete isotropy in the sub-PeV and PeV energy regions point out to the possible contribution of the Single Source with the phase of its first harmonic opposite to the phase produced by the Disk.
E-mail address: erlykin@sci.lebedev.ru
Keywords: cosmic rays, anisotropy, Galactic Halo, Single Source
1 Introduction
The observed cosmic rays (CR) have several puzzling features which need to be explained and these are now listed:
(a) Firstly, there is only a small radial gradient in the Galactic Disk (GD) in contrast with expectation, the reason is as follows. The most viable theory of the CR origin is that they are generated in the supernova (SN) explosions and acclerated by the shock waves in the supernova remnants (SNR) [1]. According to recent studies [2, 3] the Galactocentric radial distribution of SNR is such that they are mostly concentrated in the Inner Galaxy with the maximum GD surface density at a Galactocentric radius of about kpc followed by a rapid decrease at larger . According to the model calculations [4] the radial CR gradient coincides with that of SNR and at the Sun, of radial distance of 8.3 kpc, it should be equal to kpc-1. Here is the CR intensity or the SNR density. However, the experimental values for the Outer Galaxy derived by us from the gamma-ray emissivity profile are kpc-1 for both the second and third quadrants [5, 6], so that the observed CR radial distribution is significantly flatter than that expected from the distribution of their proposed sources.
(b) Secondly, there is the surprising near-isotropy of the CR arrival directions. In the sub-PeV region the CR intensity is relatively high and allows the collection of good statistics with detectors of a reasonable size during an acceptable time. Theoretical calculations predict a the slow rise for the amplitude A of the first harmonic with energy E as . On the opposite side the experimental measurements indicate a decreasing amplitude above a few TeV with a minimum of about for PeV [7, 8]. The attempt to explain this decrease by an accidental spatial configuration of the sources is difficult because it shows that the probability of such a favorable configuration is definitely lower than a few percent [9].
(c) The third puzzle is connected with the observed shape of the CR energy spectrum. Due to the stochastic distribution of the SNR in space and time there should be fine structure in the spectrum at some level. All realistic simulations confirm the possible existence of such structures [4]. However, so far, only two structures are firmly established: the so called ’knee’ at 3-4 PeV and the ’ankle’ at 3-4 EeV. Below the knee, and between the knee and the ankle, measurements show quite a regular power law shape of the spectrum with only minor structure.
In the last decade due to improvements in the energy resolution and increased statistics several works find hints of fine structure both below [10, 11, 12] and above the knee [13, 14, 15, 16, 17]. In the region below the knee the experiments indicate a possible flattening of the proton and nuclei spectra above a rigidity of 200 GV. A similar flattening was also found in the primary electron plus positron spectrum [18, 19, 20]. However, the latest precise data from AMS-02 experiment do not show such features, except for positrons, in the same energy region below the knee [21]. The clarification of the situation is the duty of the experimental groups, but in any case the discussed irregularities, if they exist, are relatively small and do not disprove the basic feature of the CR energy spectrum, viz its nearly perfect regular power law shape.
The present paper is an attempt to find a reasonable explanation of this puzzle, with special attention given to the large-scale anisotropy.
2 The present status of the cosmic-ray large-scale anisotropy
The large-scale anisotropy of CR is usually described by the amplitude and phase of the first and second harmonics. The phase, expressed in terms of the right ascension (), is the direction of the maximum CR intensity. Due to the extremely small deviations from isotropy the measurement of these deviations requires large statistics. Until recently they were concentrated mostly in the TeV and sub-PeV energy regions. Only in the last decade have arrays with the necessary large aperture: Pierre Auger Observatory, Telescope Array, IceCube and IceTop, Yakutsk and KASCADE-Grande accumulated the good statistics necessary to probe PeV and even EeV energies. Also, large EAS arrays such as ARGO-YBJ and Tibet III have produced precise results in the sub-PeV region. Figure 1 shows the present situation with the measurements of the dipole anisotropy.

In general there are several features noticable in this survey:
(i) a good consistency of the results at energies up to a few PeV;
(ii) the extremely small amplitude of the anisotropy;
(iii) the visible rise of the amplitude with energy up to ;
(iv) a moderate fall of the amplitude above up to a minimum at
;
(v) the rise of the amplitude beyond this minimum up to a few PeV;
(vi) the approximately constant phase at low energies which suddenly changes its
direction at about the same energy of
where the amplitude has a minimum;
(vii) in the PeV region, where the rise of the amplitude is observed, the phase has
an apparent trend to recover up to its previous direction close to .
In what follows we shall endeavour to build a model which can reproduce these features with the minimum number of assumptions. This model contains three basic ingredients: the Galactic Disk, the Halo and the Single Source (SS). Although we separate here the role of the Single Source, we understand that, in fact, it is just part of CR in the Disk.
3 Interrelation between the Galactic Disk and the Halo
Stars in our Milky Way Galaxy are concentrated in the Disk and likewise are SNR. For simplicity we consider SNR as the only source of CR, their acceleration and the energy. As was already mentioned, the Galactocentric radial distribution of SNR is non-uniform.
It is clear that to fit the observations ( see puzzle (a) in the Introduction ) we have either to abandon the model with SNR as the dominant CR sources, because it inevitably gives a non-uniform spatial CR distribution, or to add a CR component with a uniform spatial, isotropic directional and uniform temporal distribution. The latter requirement is not strict, but the uniform temporal distribution helps to make the spatial distribution uniform, since stochastic explosions of SN in different parts of the Galaxy make the spatial distribution patchy. Another requirement is that to have a visible effect the CR energy density of this additional component should be comparable with that observed: .
Extragalactic CR cannot be such an additional component since if CR are supplied by galaxies similar to our Milky Way, with a power and the volume density of galaxies in the extragalactic space is then even the whole age of the Universe of is not enough to fill its volume with the required density. The most likely source of the additional component is the Galactic Halo with its role as a mediator between the Disk and Extragalactic Space.
3.1 The existence of the Halo
The existence and the possible role of our Milky Way Halo has been discussed for 8 decades. One of the most comprehensive reviews was made by V.L.Ginzburg in the seventies [27]. Since that time considerable progress in the studies of our Galaxy and its environment have been made. Radiohaloes have been found in several spiral galaxies seen edge-on and similar to our Milky Way (eg NGC 4631, NGC 891). Big ’fountains’ of matter emerging from our Galaxy were observed in radio - such as the North Polar Spur. X-ray observations with the ROSAT, XMM-Newton, Suzaku and Chandra satellites have found evidence for the emission of hot gas far above the Galactic Disk with features which favour its origin from the violent processes in the Disk. Also observed have been high and uniform temperature of the order , an increase of emission towards the Galactic Center, patchiness of the gas density, a Galactic latitude dependence which does not fit the disk-plane parallel model (see the bibliography in [28]). Gamma ray studies of the synchrotron emission favour a vertical scale for the gamma-ray intensity of about 10 kpc, which is already comparable with the Disk radius of 15 kpc [29]. They have also revealed the existence of big bubbles of emitting hot gas above the Disk emerging from the region close to the Galactic Center, the so called ’Fermi Bubbles’ [30].
However, all the above indications cannot be accepted as proof of the existence of a hadronic CR Halo fed by violent processes in the Disk. As an alternative explanation the hot gas could be supplied by the accretion of the extragalactic (EG) gas by the Disk. Radio and soft gamma-ray emission are definitely connected with the synchrotron radiation of relativistic electrons in the Galactic magnetic fields, but electrons comprise only a minor part % of all CR. The most convincing indication of the existence of the hadronic Halo is still measurements of radioactive isotopes in CR, which together with other arguments are nevertheless indirect. However, as E.L.Feinberg once said, ’the proof in cosmic rays is of a special kind - it is the aggregate of indications’. Thus we consider the above aggregate seriously and shortly examine a model with a hadronic Halo.
3.2 The existence of the Single Source
The existence of the Single Source has been proposed by us to explain the puzzling sharpness of the knee in the EAS size spectrum ( see [31] and later publications ). The physical basis of this proposal is the evident non-uniformity of the spatial and temporal distributions of SN explosions and subsequent SNR. As a result one SN could explode not very long ago and close to the solar system.. Its contribution to the CR intensity is rather high and it gives rise to a small peak ( knee ) above the background from other SNR - it is our Single Source.
In the last decade, the non-uniformity of the CR source distribution has been actively discussed in connection with the discovery of the peculiarities of the primary electron and positron spectra [32]. Due to the limited range and the lifetime of electrons and positrons, their emitting sources should be nearby and relatively young like the Single Source responsible for the knee. It does not mean that they are identical, but if the observed peculiarities are real they stress the importance of the non-uniformity of the CR source distribution in space and time. We shall also consider the Single Source as a real object and examine the consequences of its existence.
4 The model
4.1 The Galactic Disk and the Halo
The model is actually the generalisation of the Leaky Box scenario for the composite system of Disk+Halo. If a SNR converts a part of its kinetic energy into CR with a power law energy spectrum, then the expression for this spectrum is:
| (1) |
Here, is the total CR energy, is the slope index of the differential power law spectrum, is the speed of light, is the volume containing the CR, is the minimum energy of the spectrum. In the following calculations we adopt erg, from our model of SNR acceleration [33] and = 1GeV. We assume that the CR distribution in the volume is uniform and isotropic. The maximum energy of the spectrum is not important if .
If the system of Disk+Halo is in dynamic equilibrium the amount of CR energy supplied by SNR in the Disk, with rate , should be equal to the CR energy supplied by the Disk to the Halo and eventually transferred from the Halo to EG space. The energy spectrum of CR residing permanently in the Disk and the Halo depends on their lifetime . If this lifetime is also dependent on energy as , then the energy spectrum of CR in the Disk and the Halo is:
| (2) |
Apparently, and are different for the Disk and the Halo and should be indexed as , and .
It is known from the measurements of the secondary to primary CR ratio and of radioactive isotopes that CR spend most of their lifetime in the Halo [34]. Averaging their values for different isotopes we assume that year and [33]. We consider the Halo as an ellipsoid with radius and height , so that its volume is equal to . For the rate of SN explosions we adopt . Calculations performed with these numerical parameters give CR intensity significantly less than the experimental values. However, taking into account all the assumptions and uncertainties of the parameters used in the expression (2) we can certainly make the calculated results closer to the experimental values. The most doubtful assumption is the requirement of a uniform spatial distribution inside the Halo, the shape and the size of the Halo and .
The need for a nearly uniform intensity in the Halo suggests some form of reflecting walls. There are various possibilities, including our Galaxy being in a Giant Bubble. As is well known, there are Bubbles of a variety of sizes round stars, both singly and in clusters and an extrapolation of the idea of stellar winds can be extended to Galactic Winds. Another possibility is that there is shear-induced turbulence caused by the rotation of our galaxy with respect to the nearby Intergalactic Medium. Since all these features and possible non-uniformity of the CR distribution in the Halo are unknown we use the simplest scenario assuming the uniform spatial CR distribution in the Halo.
Finally, we normalise the absolute intensity of calculated spectrum to the results of experimental measurements of the all-particle spectrum. It is shown in Figure 2a and denoted as ’HALO’.
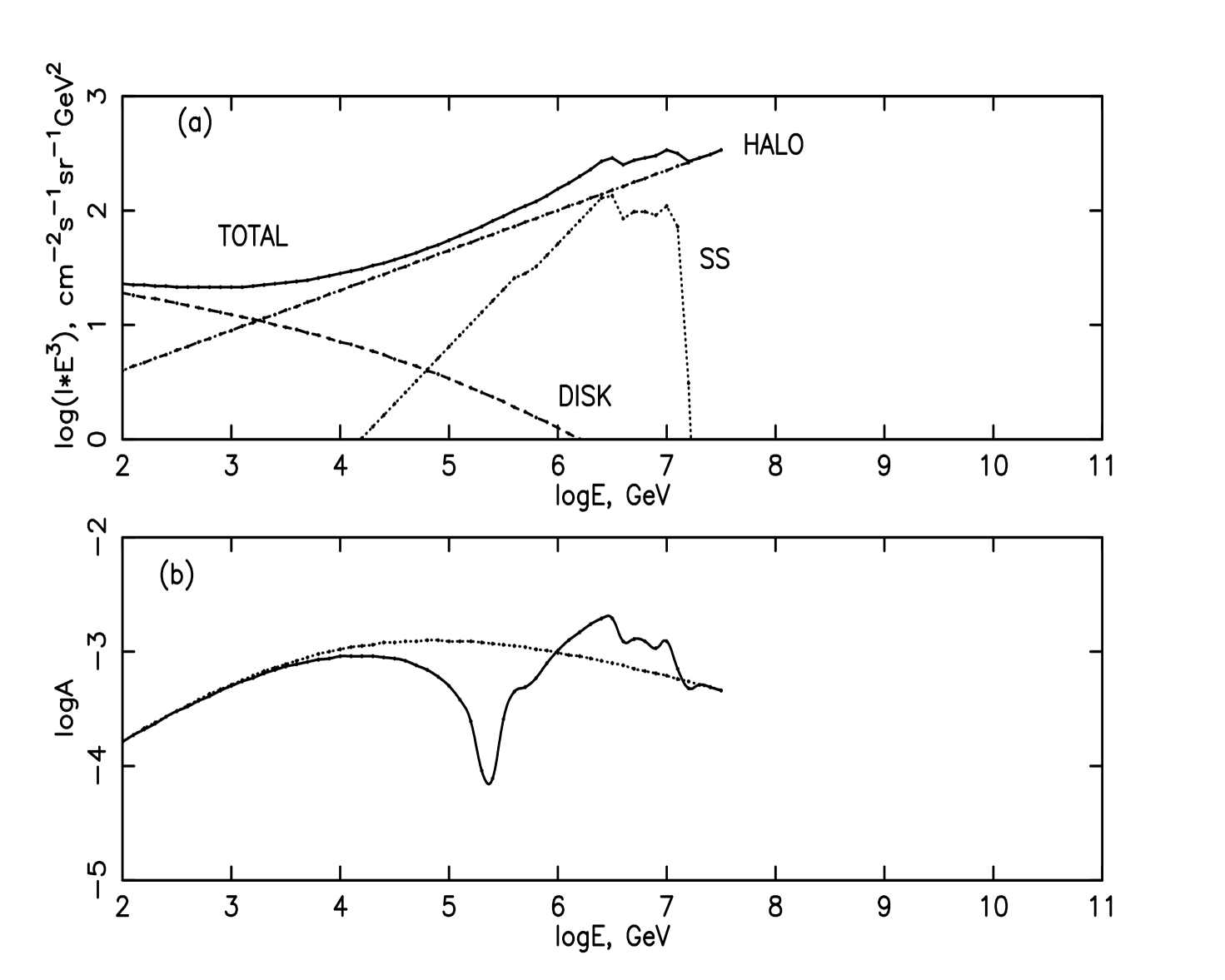
As for the Disk, we consider it as a cylinder with radius and half thickness , therefore its volume is equal to . Since we assume the dominance of the CR from the Halo we have to admit that it is difficult to extract the Disk CR from the total observed CR and our knowledge of their characteristics is poor. In order to make the contribution of the Disk to the observed CR intensity at sub-PeV energies small, we adopt . The absolute normalisation is taken such that at lower, TeV and sub-TeV, energies CR from the Disk overcome CR from the Halo. The adopted spectrum from the Disk is also shown in Figure 2a and denoted as ’DISK’. The sum of Disk and Halo CR is denoted as ’TOTAL’.
5 Anisotropy
We assume that the anisotropy appears only in the vicinity of the sources, i.e. in the Disk. The amplitude of the anisotropy is connected with the CR intensity , its gradient, , and the diffusion coefficient as . If the relative gradient and then in the Disk rises with energy as . The anisotropy of CR in the Halo is postulated as being and the isotropy of CR re-entrant from the Halo back into the Disk dilutes the anisotropy of CR produced and trapped in the Disk.
In this treatment we just consider the first harmonic. Later work will deal with higher multipoles. We calculate the amplitude of the first harmonic for the case where only Disk and Halo contribute to CR as
| (3) |
The result is shown in Figure 2b by the dotted line. The rise of the amplitude at energies above 100 GeV is due to the rise of the diffusion coefficient in the expression for mentioned above. The slow decrease of above 10 TeV is explained by the rising fraction of isotropic CR from the Halo, which overcomes the rise of . However, this scenario does not reproduce the remarkable dip in the amplitude visible in the experimental data at and the subsequent rise of the amplitude above this dip ( Figure 1a ).
We think that these features, if they are real, are connected with the existence of the Single Source, from which the CR energy spectrum is schematically shown by the dotted line in Figure 2a and denoted as ’SS’. However, this idea alone is not enough to reproduce the experimental data and here the examination of the phase of the first harmonic could help. In Figure 2b it is seen that after the moderate decrease in the energy interval 0.1 - 100 TeV the phase suddenly changes to its opposite. We consider this change seriously and propose that CR from the Single Source have a phase opposite to that of the background at lower energies. This is a necessary complementary requirement in our model. The rising part of CR coming from the opposite direction would reduce the anisotropy of the background from the Disk and Halo as
| (4) |
The result of the calculations with the contribution of the Single Source is shown in Figure 2b by the full line. A comparison with the experimental data is shown also in Figure 1a by the full line. It is seen that after minimum in the dip the amplitude of the anisotropy starts rising again and it is caused by the rising contribution of the Single Source, which has the opposite phase.
Beyond the knee, and after the end of the contribution of the Single Source at about GeV, the phase should return to its previous value. New measurements at these highest energies shown in Figure 1a [22, 24] demonstrate the rise of the anisotropy amplitude, but the comparison with the simulations led the PAO collaboration to make a conservative conclusion that ’no clear evidence for anisotropy has been found yet’ [22]. We have to wait for results of higher statistical accuracy.
6 Discussion
We think that the described model with three basic ingredients: Disk, Halo and Single Source is reasonable and is worthy of discussion. The new features advocated here are:
(a) The dominance of the Halo component in the sub-PeV region. It means that the CR which we observe and study in spite of being ourselves inside the Disk come mostly from the Halo. It is disputable but helps to understand the low anisotropy, small radial gradient of CR intensity and small level of irregularities in the regular power law energy spectrum.
(b) The idea about the Single Source, which has to be nearby and young and creates the knee, usually raises questions: ’if it is nearby why we do not see it in the anisotropy ?’. It is a very reasonable question and this work gives the answer. The Single Source causes the stronger decrease and the dip in the amplitude of the dipole anisotropy at sub-PeV energies. It is also seen in the change of the phase of the anisotropy at the same energies. It means that the Single Source should deliver CR from the direction opposite to the direction of CR from the background and it is a new assumption in the Single Source scenario. Above the dip energy the amplitude starts to rise again with the opposite phase, as expected.
The dip in this model appears as the result of subtraction of two
bigger values. Its position and shape are extremely sensitive to the choice of
parameters participating in expression (4). The relatively good agreement with the
experimental data is the result of the fitting procedure, but, nevertheless:
(i) it demonstrates the possibility of achieving agreement within the
framework of our simplistic model and
(ii) the high sensitivity of the dip to the input parameters of the expression (4)
gives the possibility of investigating these parameters when precise results in this
energy region are obtained.
(iii) The phase of the first harmonic in the PeV region, where the contribution of the Single Source is big enough, could help to locate it on the sky. The present experimental data have a too big spread to make a conclusion.
We understand that this scenario raises more questions than gives the answers. For instance, the main questions are:
(a) Do the Halo and the Single Source really exist ? Arguments for positive answers are given in the §3, but more supportive arguments are needed.
(b) Why numerical estimates for CR intensity in the Disk and the Halo, calculated with the expression (2), are smaller than in the observations ?
(c) Why the energy spectrum of CR in the Disk is steeper than the spectrum in the Halo ? According to our conception developed in [4] the spectrum in the Disk, with its higher turbulence in the interstellar medium due to SN explosions, should be flatter than in the Halo where there are no such powerful sources of turbulence as SN.
(d) To what extent are the simplified assumptions about the shapes and normalisation of the Disk, Halo and Single Source spectra as well as other parameters: and , reasonable and what the more sophisticated approach will do for the result ?
The answers to these and other questions are the subject of further work.
7 Conclusions
We develop a model which helps to give an explanation for at least one of the three puzzles mentioned in the Introduction, viz. the small radial gradient of the CR intensity, the small magnitude and peculiar energy dependence of the CR anisotropy and the small level of irregularities in the CR energy spectrum. In this paper we analyse the second puzzle - the anisotropy.
The model exploits three basic ingradients: Disk, Halo and the Single Source. We
postulate the dominant role of the Halo and its CR in our observations in spite of the
fact that we
are located inside the Disk. At PeV energies, approaching the knee, contributions from
the Single Source begins to play an important role and inspired by the experimental
evidence we assume that the phase of the CR intensity from the Single Source is
opposite to the phase of the background CR from the Disk and the Halo. Due to this
effect the amplitude of the dipole anisotropy decreases and approaches a minimum
(dip) at sub-PeV energies. After that the amplitude begins to rise again, but because
CR are mainly from the Single Source they come preferentially from the direction
opposite to that at lower sub-PeV energies. The position and the shape of the dip is
extremely sensitive to the parameters of the spectra adopted for the three ingredients:
Disk, Halo and the Single Source. This sensitivity can be used for the study of the CR
origin in the vicinity of the knee in the PeV energy region.
Acknowledgements
The authors are grateful to the Kohn Foundation for financial support. The (unknown) reviewer is thanked for very helpful comments and suggestions.
References
- [1] Ginzburg V.L. and Syrovatskii S.I., 1964, The origin of cosmic rays, Pergamon Press Ltd.
- [2] Case G. and Bhattacharya D., 1996, Astron. Astrophys. Suppl., 120, C437
- [3] Green D.A. Proc. IAU Symp., 296, ’Supernova Environmental Impacts’; arxiv:1309.3072
- [4] Erlykin A.D. et al., 2003, Astropart. Phys., 19, 351.
- [5] Abdo A.A. et al., 2010, Astrophys. J., 710, 133
- [6] Ackermann M., 2011, Astrophys. J., 726, 81
- [7] Guillian G. et al., 2007, Phys. Rev. D, 75, 062003
- [8] Erlykin A.D. and Wolfendale A.W., 2013, J. Cosmology and Astropart.Phys., JCAP04(2013)006, doi:10.1088/1475-7516/2013/04/006; arxiv:1303.2889
- [9] Erlykin A.D. and Wolfendale A.W., 2006, Astropart. Phys., 25, 183
- [10] Panov A.D. et al., 2009, Bull. Russ. Acad. Sci., 73/5, 564
- [11] Ahn H.S. et al., 2010, Astrophys. J., 714, L89
- [12] Adriani O. et al., 2011, Science, 332, 69
- [13] Haungs A. et al., 2011, Proc. 32nd Int. Cosm. Ray Conf., Beijing, 1, 263
- [14] Martirosov R.M. et al., 2011, Proc. 32nd Int. Cosm. Ray Conf., Beijing, 1, 178
- [15] Kuzmichev L.A. et al., 2011, Proc. 32nd Int. Cosm. Ray Conf., Beijing, 1, 209
- [16] Kolanoski H. et al., 2011, Proc. 32nd Int. Cosm. Ray Conf., Beijing, 1, 279
- [17] Knurenko S. et al., 2011, Proc. 32nd Int. Cosm. Ray Conf., Beijing, 1, 189
- [18] Chang J. et al., 2008, Nature, 456, 362;
- [19] Panov A.D. et al., 2011, Astrophys. Space Sci. Trans., 7, 119
- [20] Adriani O. et al., 2009, Nature, 458, 607; ibid. 2011, Phys. Rev. Lett., 106, 201101; ibid. arxiv:1308.0133
- [21] Aguilar M. et al., 2013, CERN Courier, 53/8, 23
- [22] Letssier-Selvon A. et al., 33rd Int. Cosm. Ray Conf., Rio de Janeiro, 2013, arxiv:1310.4620
- [23] Deligny O. et al., 33rd Int. Cosm. Ray Conf., Rio de Janeiro, 2013, arxiv:1306.4998
- [24] Pravdin M.I. et al., 2001, J. Exp. Theor. Phys., 92, 766
- [25] Chiavassa A. et al., 2013, Nucl. Instr. Meth. in Phys. Res. A, 2013, doi:10.1016/j.nima.2013.11.045
- [26] Kifune T. wt al., 1986, J. Phys. G: Nucl. Phys., 12, 129
- [27] Ginzburg V.L., 1977, 15th Int. Cosm. Ray Conf., Plovdiv, 10, 8
- [28] Henley D.B. and Shelton R.C., Astrophys. J, 2013; arxiv:1306.2312
- [29] Orlando E. and Strong A., 2013, MNRAS; arxiv:1309.2947
- [30] Meng Su et al., 2010, Astrophys. J., 724, 1044
- [31] Erlykin A.D. and Wolfendale A.W., 1997, J. Phys. G: Nucl. Part. Phys., 23, 979
- [32] Panov A.D., 2012, 23rd Eur.Cosm.Ray Symp. and 32nd Rus.Cosm.Ray Conf., Moscow; 2013, J. Phys: Conf. Ser., 409, 012004
- [33] Erlykin A.D. and Wolfendale A.W., 2001, J. Phys. G: Nucl. Part. Phys., 27, 941
- [34] Connell J. et al., 1997, Proc. 25th Int. Cosm. Ray Conf., Durban, 3, 397