The Tension in Light of Updated Redshift-Space Distortion Data and PAge Approximation
Abstract
One of the most prominent challenges to the standard Lambda cold dark matter (CDM) cosmology is the tension between the structure growth parameter constrained by the cosmic microwave background (CMB) data and the smaller one suggested by the cosmic shear data. Recent studies show that, for CDM cosmology, redshift-space distortion (RSD) data also prefers a smaller that is - lower than the CMB value, but the result is sensitive to the cosmological model. In the present work we update the RSD constraint on with the most up-to-date RSD data set where the correlation between data points is properly taken into account. To reduce the model dependence, we add in our Monte Carlo Markov Chain calculation the most up-to-date data sets of Type Ia supernovae (SN) and baryon acoustic oscillations (BAO), whose correlation with RSD is also taken into account, to constrain the background geometry. For CDM cosmology we find , which is larger than previous studies, and hence is consistent with the CMB constraint. By replacing CDM with the Parameterization based on cosmic Age (PAge), an almost model-independent description of the late universe, we find that the RSD + SN + BAO constraint on is insensitive to the cosmological model.
keywords: observational cosmology, large-scale structure of the Universe, dark matter
PACS: 98.80.-k, 98.80.Es, 98.65.Dx
I Introduction
The widely accepted explanation of cosmic accelerating expansion is that a dark energy component with negative pressure powers the late-time cosmic acceleration. The cold dark matter (CDM) model, where the dark energy is interpreted as the cosmological constant , has achieved great success in fitting a broad range of cosmological measurements in the last two decades (Riess et al., 1998; Perlmutter et al., 1998; Aghanim et al., 2020; Alam et al., 2021a; Heymans et al., 2021; Asgari et al., 2021). In recent few years, however, as the observational techniques continue to advance, the CDM model is challenged by a few observational tensions, of which the two most prominent ones are the Hubble tension and the tension. The Hubble constant and the structure growth parameter measured by the Planck Satellite CMB experiment Aghanim et al. (2020) are in tension with from the SH0ES distance ladder measurement Riess et al. (2021) and in tension with from the cosmic shear data of the Kilo-Degree Survey Asgari et al. (2021), respectively. While many beyond-CDM models are proposed as tentative explanations to the observed tensions, no specific model has been proven far better than CDM Di Valentino et al. (2021); Cai (2020); Guo et al. (2020); Liu et al. (2020); Aghanim et al. (2020).
The tension between CMB and cosmic shear in the inferred value of may arise from unaccounted baryonic physics Lu and Haiman (2021), other unknown systematics Chintalapati et al. (2021), or a statistical fluke. It is important to have an probe that is independent of CMB and cosmic shear. Recent studies Benisty (2021); Nunes and Vagnozzi (2021) suggest that the redshift-space distortion (RSD) data also prefer a small that is - lower than the Planck result. However, the RSD constraint on is sensitive to the cosmological model. Ref. Benisty (2021) shows that a model-independent (Gaussian process) analysis yields a much weaker constraint on that is not very useful for resolving the tension.
The present work aims at updating the RSD constraint on with the most up-to-date RSD data sets. Because is degenerate with the background geometry parameters, we use in addition the data sets of Type Ia supernovae (SN) (Scolnic et al., 2018) and baryon acoustic oscillations (BAO) (Alam et al., 2021b) to determine the background geometry. In addition to the standard analysis for CDM cosmology, we also perform our analysis for the Parameterization based on cosmic Age (PAge), which is an almost model-independent parameterization of the late universe Huang (2020); Luo et al. (2020); Huang et al. (2021a); Cai et al. (2021); Huang et al. (2021b). To compute the growth parameter in PAge, we assume that the clustering of the non-matter component is negligible in the late universe. This assumption in the present work excludes clustering dark energy models, which are typically very model-dependent and often studied in a model-by-model manner Abramo et al. (2007); Batista and Pace (2013); Batista and Marra (2017); Hassani et al. (2019); Herrera et al. (2019); Velten and Fazolo (2020); Creminelli et al. (2020); Hassani et al. (2021).
Unless otherwise specified, we work with a spatially flat Friedmann–Robertson–Walker background metric with scale factor and Hubble parameter , where is cosmological redshift and is the cosmological time. The structure growth parameter is defined as
| (1) |
where is the matter density fraction at redshift zero. The root mean square of the matter density fluctuation is defined in a spherical top-hat window with comoving radius at redshift . Eq. (1) reflects the main degeneracy direction of and parameters in cosmic shear surveys, where without redshift argument implicitly refers to .
II PAge Approximation
PAge models the late-time cosmological evolution under two assumptions: i) the high-redshift universe is dominated by matter; ii) the dimensionless combination varies slowly and can be approximated as a quadratic function of . It follows from the two assumptions and general relativity that
| (2) |
where is the dimensionless age of the universe and is a phenomenological parameter. Roughly speaking, characterizes the deviation from Einstein de-Sitter universe (flat CDM model) Huang et al. (2021b).
By integrating Eq. (2), we obtain the explicit expression of the scale factor
| (3) |
Numeric inverse function of the right hand side of Eq. (3) gives a mapping . The Hubble parameter at redshift is then obtained by substituting into Eq. (2). Integrating yields comoving angular diameter distance, which can be straightforwardly converted to the observable luminosity distance and angular diameter distance.
Further assuming that the clustering of non-matter component is negligible in the late universe, we can use the linear growth equation
| (4) |
to evolve the linear growth factor of matter density fluctuations, at the price of introducing an extra parameter . The redshift-space distortion data measure the combination , where the linear growth rate .
Refs. Huang (2020); Luo et al. (2020); Huang et al. (2021a) have shown that many physically motivated or phenomenological models can be approximately mapped to PAge, with only sub-percent errors in the distance observables. Here we demonstrate the good accuracy in the observable with PAge approximation. A given model can be approximately mapped to space by matching the cosmic age and the decelerating parameter at redshift zero. For a few typical examples, Table 1 shows the maximum relative error of and angular diameter distance in the redshift range .
| models | parameters | ||||
|---|---|---|---|---|---|
| CDM | 0 | 0 | 0 | ||
| flat CDM | 0.951 | 0.359 | 0.416 | 0.874 | |
| flat CDM | 0.976 | 0.619 | 0.579 | 1.07 | |
| flat -CDM | 0.941 | 0.373 | 0.249 | 0.504 |
In Figure 1 we show some typical data points used in this article. The data uncertainties are much larger than the modeling errors of PAge approximation. Thus, for the presently achievable data precision, PAge can accurately represent many models in a very compact parameter space.
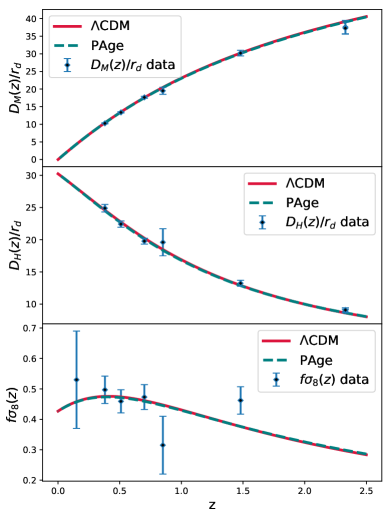
III Data and Methodology
The growth rate data in the form of from RSD measurements have been widely used to study the tension (Nesseris et al., 2017; Kazantzidis and Perivolaropoulos, 2018; Sagredo et al., 2018a, b; Anagnostopoulos et al., 2019; Skara and Perivolaropoulos, 2020; Li et al., 2021; Benisty, 2021; Nunes and Vagnozzi, 2021). We carefully select the RSD measurements from different surveys to construct the data set, as listed in Table 2. The data set contains the latest SDSS-IV and ALFALFA releases that are not included in the previous studies. We have also avoided using data points with unknown correlations that are possibly non-negligible due to redshift and sky-area overlap.
| Index | Dataset | Redshift | Fiducial Cosmology | Refs. | |
|---|---|---|---|---|---|
| 1 | 2MTF | 0.001 | (Howlett et al., 2017) | ||
| 2 | ALFALFA | 0.013 | (Avila et al., 2021) | ||
| 3 | 6dFGS+SnIa | 0.02 | (Huterer et al., 2017) | ||
| 4 | SNeIa+IRAS | 0.02 | (Turnbull et al., 2012; Hudson and Turnbull, 2013) | ||
| 5 | 2MASS | 0.02 | (Hudson and Turnbull, 2013; Davis et al., 2011) | ||
| 6 | 2dFGRS | 0.17 | (Song and Percival, 2009) | ||
| 7 | GAMA | 0.18 | (Blake et al., 2013) | ||
| 8 | GAMA | 0.38 | |||
| 9 | WiggleZ | 0.44 | (Blake et al., 2012) | ||
| 10 | WiggleZ | 0.60 | |||
| 11 | WiggleZ | 0.73 | |||
| 12 | Vipers PDR-2 | 0.60 | (Pezzotta et al., 2017) | ||
| 13 | Vipers PDR-2 | 0.86 | |||
| 14 | FastSound | 1.40 | (Okumura et al., 2016) | ||
| 15 | SDSS-MGS | 0.15 | (Howlett et al., 2015) | ||
| 16 | SDSS-BOSS-Galaxy | 0.38 | (Alam et al., 2017) | ||
| 17 | SDSS-BOSS-Galaxy | 0.51 | |||
| 18 | SDSS-eBOSS-LRG | 0.70 | (Bautista et al., 2020; Gil-Marin et al., 2020) | ||
| 19 | SDSS-eBOSS-ELG | 0.85 | (de Mattia et al., 2021; Tamone et al., 2020) | ||
| 20 | SDSS-eBOSS-Quasar | 1.48 | (Hou et al., 2020; Neveux et al., 2020) |
In SDSS-IV survey, the systematic errors and consensus estimates are incorporated directly into the covariance matrices. Therefore, for the MGS (Howlett et al., 2015), BOSS Galaxy (Alam et al., 2017), eBOSS LRG (Bautista et al., 2020; Gil-Marin et al., 2020) and eBOSS Quasar (Hou et al., 2020; Neveux et al., 2020) in BAO+RSD measurements, we take their covariance matrices into consideration to avoid missing correlation information. While for the eBOSS ELG (de Mattia et al., 2021; Tamone et al., 2020), Ly-Ly (du Mas des Bourboux et al., 2017; Bautista et al., 2017) and Ly-Quasar (du Mas des Bourboux et al., 2020) measurements, we directly introduce their publicly available likelihoods into our analyses. All of the likelihood information for the completed SDSS-IV are summarized on the public SDSS svn repository111 https://svn.sdss.org/public/data/eboss/mcmc/trunk/likelihoods. The correlations of three WiggleZ data at different redshifts are considered as well.
Converting the redshift to distance by assuming a fiducial cosmology in RSD measurements leads to additional anisotropies known as Alcock-Paczynski (AP) effect. We multiply a correction factor to reduce the bias due to AP effect (Macaulay et al., 2013). The corrected for a model is
| (5) |
the superscript ”fid” represents the fiducial flat CDM cosmology assumed in RSD measurements. Eq. (5) does not exactly eliminate the impact of AP effect. We will demonstrate that, however, AP correction has negligible impact on our results. Thus, the approximate correction in Eq. (5) would suffice.
Finally, we construct our joint likelihood by multiplying the likelihoods of each survey in SDSS-IV, the WiggleZ survey, the rest RSD surveys, and the Pantheon catalog, respectively.
We use flat priors , and for CDM model, and additionally , for PAge. To reveal the impact of the AP correction, we also perform in parallel the analysis without the AP correction for a comparison.
IV Results
| models | ||||||||
|---|---|---|---|---|---|---|---|---|
| without AP correction | CDM | - | - | 1064.9 | ||||
| PAge | 1060.3 | |||||||
| with AP correction | CDM | - | - | 1065.6 | ||||
| PAge | 1060.8 |
We present the posterior mean and 68 confidence level inferences in Table 3. Comparing the results with and without the AP correction, we conclude that the AP correction has little influence on the inferences of cosmological parameters. Thus, hereafter we only focus on the result with AP correction.
Because none of the BAO, SN, RSD data directly measures , we can only obtain a combined constraint on , where is the comoving sound horizon at the end of the baryonic-drag epoch. Only when a Planck prior Aghanim et al. (2020) is used, can we obtain constraints on ( for CDM and for PAge).
Compared to the previous works (Nesseris et al., 2017; Kazantzidis and Perivolaropoulos, 2018; Sagredo et al., 2018a, b; Anagnostopoulos et al., 2019; Skara and Perivolaropoulos, 2020; Li et al., 2021; Benisty, 2021; Nunes and Vagnozzi, 2021), the present work prefers a higher value. The constraints for CDM and for PAge are both consistent with CMB + CDM measurement. The difference between previous work and ours may originate from the new RSD data and BAO data we have included in our analysis. To test this hypothesis, we utilize another catalog that contains cosmic chronometer (CC) data Simon et al. (2005); Stern et al. (2010); Zhang et al. (2014); Moresco et al. (2012); Moresco (2015); Moresco et al. (2016); Ratsimbazafy et al. (2017); Luo et al. (2020), the Pantheon Type Ia supernova samples Scolnic et al. (2018) and the “Gold-2017” RSD compilation in Ref. Nesseris et al. (2017). The inference results are listed in Table 4. We find the previous “Gold-2017” RSD data do support a lower value that is consistent with previous works.
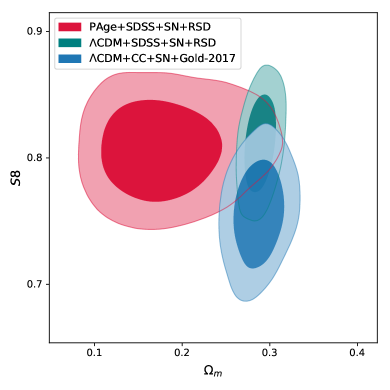
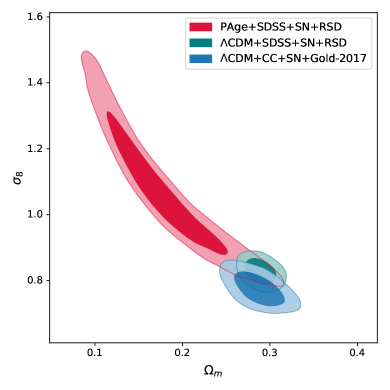
Figure 2 shows the marginalized joint constraints on the - and - planes. Note that in PAge is only used to evolve the linear growth factor . Thus, there is a strong degeneracy between and in the PAge case. In CDM, the much tighter constraint on from the measurement of background evolution breaks such degeneracy. The discrepancies of and parameters in different cosmologies, as shown in the right panel of Figure 2, are and , respectively. The seemingly large difference in minimal , per degree of freedom, originates from a non-realistic parameter range ( that is strongly disfavored by other cosmological observations Aghanim et al. (2020)), and hence should not be regarded as a significant preference of PAge against CDM. The left panel of Figure 2 shows that, however, the uncertainty in in PAge has no much impact on measurement, indicating that for RSD data the combination Eq. (1) also roughly eliminates the degeneracy between and .
V Conclusions and Discussion
RSD is an independent probe that is expected to help resolve the tension between CMB and cosmic shear measurements. However, the currently available RSD data are still very limited, and their constraint on is sensitive to the assumed background evolution model. In this work, we construct a clean and most up-to-date RSD catalog and use BAO + SN to eliminate the uncertainty of background evolution. The value inferred from our updated catalog is higher than many previous works. We have shown that it is mainly due to the inclusion of new RSD data and the usage of BAO + SN, which breaks the degeneracy between and the background evolution. Both the inference results of in CDM and PAge agree well with the most updated result of Dark Energy Survey (DES Y3) (Zürcher et al., 2021). And they are found to be more consistent with CMB + CDM measurement while the previous works (Nesseris et al., 2017; Kazantzidis and Perivolaropoulos, 2018; Sagredo et al., 2018a, b; Anagnostopoulos et al., 2019; Skara and Perivolaropoulos, 2020; Li et al., 2021; Benisty, 2021; Nunes and Vagnozzi, 2021) tend to give a smaller that is more consistent with the cosmic shear data of the Kilo-Degree Survey Asgari et al. (2021).
We have been working with a spatially flat cosmology. While including the spatial curvature parameter into the analysis, we do not find significant impact on the constraint, which becomes (almost unchanged) in the CDM case and (shifted by ) in the PAge case. This is because the background evolution is mostly data-driven (by SN+BAO) rather than theory-driven.
In the PAge framework, the geometric information and structure-growth information are well split. The parameter only affects the growth of structure via Eq. (4). For the first time, we exclude the baryon-only () and matter-only () scenarios without assuming the Friedmann equations. This adds one more consistency of results from a broad variety of ways to observe aspects of the universe, which, in the view of Ref. Peebles (2021), makes the modern CDM-like interpretation of the universe more robust.
The growth of the structure beyond General Relativity has been intensively discussed in the literature (Kazantzidis and Perivolaropoulos, 2018; Anagnostopoulos et al., 2019; Skara and Perivolaropoulos, 2020; Nunes and Vagnozzi, 2021; Di Valentino et al., 2016; Solà Peracaula et al., 2019, 2020; Yan et al., 2020), some are found to be beneficial for relieving the Hubble tension and the tension Yan et al. (2020). In the present work, General Relativity is implicitly assumed in the evolution equation of the growth factor. Thus, alternative gravity theories where the Poisson equation of gravity is modified are beyond the scope fo this paper. We leave this as our future work.
VI Acknowledgements
This work is supported by the National SKA Program of China No. 2020SKA0110402, National Natural Science Foundation of China (NSFC) under Grant No. 12073088, National key R&D Program of China (Grant No. 2020YFC2201600), the science research grants from the China Manned Space Project with No. CMS-CSST-2021-B01, and Guangdong Major Project of Basic and Applied Basic Research (Grant No. 2019B030302001).
References
- Riess et al. (1998) A. G. Riess et al. (Supernova Search Team), Astron. J. 116, 1009 (1998), arXiv:astro-ph/9805201 .
- Perlmutter et al. (1998) S. Perlmutter et al., The Astrophysical Journal 517, 565 (1998).
- Aghanim et al. (2020) N. Aghanim et al. (Planck), Astron. Astrophys. 641, A6 (2020), arXiv:1807.06209 [astro-ph.CO] .
- Alam et al. (2021a) S. Alam et al. (eBOSS), Phys. Rev. D 103, 083533 (2021a), arXiv:2007.08991 [astro-ph.CO] .
- Heymans et al. (2021) C. Heymans et al., Astron. Astrophys. 646, A140 (2021), arXiv:2007.15632 [astro-ph.CO] .
- Asgari et al. (2021) M. Asgari et al. (KiDS), Astron. Astrophys. 645, A104 (2021), arXiv:2007.15633 [astro-ph.CO] .
- Riess et al. (2021) A. G. Riess, S. Casertano, W. Yuan, J. B. Bowers, L. Macri, J. C. Zinn, and D. Scolnic, Astrophys. J. Lett. 908, L6 (2021), arXiv:2012.08534 [astro-ph.CO] .
- Di Valentino et al. (2021) E. Di Valentino, O. Mena, S. Pan, L. Visinelli, W. Yang, A. Melchiorri, D. F. Mota, A. G. Riess, and J. Silk, Class. Quant. Grav. 38, 153001 (2021), arXiv:2103.01183 [astro-ph.CO] .
- Cai (2020) R.-G. Cai, Science China Physics, Mechanics, and Astronomy 63, 290401 (2020).
- Guo et al. (2020) R.-Y. Guo, J.-F. Zhang, and X. Zhang, Science China Physics, Mechanics, and Astronomy 63, 290406 (2020), arXiv:1910.13944 [astro-ph.CO] .
- Liu et al. (2020) M. Liu, Z. Huang, X. Luo, H. Miao, N. K. Singh, and L. Huang, Sci. China Phys. Mech. Astron. 63, 290405 (2020), arXiv:1912.00190 [astro-ph.CO] .
- Lu and Haiman (2021) T. Lu and Z. Haiman, Mon. Not. Roy. Astron. Soc. 506, 3406 (2021), arXiv:2104.04165 [astro-ph.CO] .
- Chintalapati et al. (2021) P. R. V. Chintalapati, G. Gutierrez, and M. H. L. S. Wang, (2021), arXiv:2108.11518 [astro-ph.CO] .
- Benisty (2021) D. Benisty, Phys. Dark Univ. 31, 100766 (2021), arXiv:2005.03751 [astro-ph.CO] .
- Nunes and Vagnozzi (2021) R. C. Nunes and S. Vagnozzi, MNRAS 505, 5427 (2021), arXiv:2106.01208 [astro-ph.CO] .
- Scolnic et al. (2018) D. M. Scolnic et al., Astrophys. J. 859, 101 (2018), arXiv:1710.00845 [astro-ph.CO] .
- Alam et al. (2021b) S. Alam et al. (eBOSS), Phys. Rev. D 103, 083533 (2021b), arXiv:2007.08991 [astro-ph.CO] .
- Huang (2020) Z. Huang, Astrophys. J. Lett. 892, L28 (2020), arXiv:2001.06926 [astro-ph.CO] .
- Luo et al. (2020) X. Luo, Z. Huang, Q. Qian, and L. Huang, arXiv e-prints , arXiv:2008.00487 (2020), arXiv:2008.00487 [astro-ph.CO] .
- Huang et al. (2021a) L. Huang, Z. Huang, X. Luo, and Y. Fang, Phys. Rev. D 103, 123521 (2021a), arXiv:2012.02474 .
- Cai et al. (2021) R.-G. Cai, Z.-K. Guo, S.-J. Wang, W.-W. Yu, and Y. Zhou, (2021), arXiv:2107.13286 [astro-ph.CO] .
- Huang et al. (2021b) L. Huang, Z. Huang, Z. Li, and H. Zhou, RAA 21, 277 (2021b), arXiv:2108.03959 .
- Abramo et al. (2007) L. R. Abramo, R. C. Batista, L. Liberato, and R. Rosenfeld, JCAP 2007, 012 (2007), arXiv:0707.2882 [astro-ph] .
- Batista and Pace (2013) R. C. Batista and F. Pace, JCAP 2013, 044 (2013), arXiv:1303.0414 [astro-ph.CO] .
- Batista and Marra (2017) R. C. Batista and V. Marra, JCAP 2017, 048 (2017), arXiv:1709.03420 [astro-ph.CO] .
- Hassani et al. (2019) F. Hassani, J. Adamek, M. Kunz, and F. Vernizzi, JCAP 2019, 011 (2019), arXiv:1910.01104 [astro-ph.CO] .
- Herrera et al. (2019) D. Herrera, I. Waga, and S. E. Jorás, Physics of the Dark Universe 26, 100335 (2019), arXiv:1906.04326 [astro-ph.CO] .
- Velten and Fazolo (2020) H. Velten and R. E. Fazolo, Phys. Rev. D 101, 023518 (2020), arXiv:1912.00094 [astro-ph.CO] .
- Creminelli et al. (2020) P. Creminelli, G. Tambalo, F. Vernizzi, and V. Yingcharoenrat, JCAP 2020, 002 (2020), arXiv:1910.14035 [gr-qc] .
- Hassani et al. (2021) F. Hassani, J. Adamek, and M. Kunz, MNRAS 500, 4514 (2021), arXiv:2007.04968 [astro-ph.CO] .
- Nesseris et al. (2017) S. Nesseris, G. Pantazis, and L. Perivolaropoulos, Phys. Rev. D 96, 023542 (2017), arXiv:1703.10538 [astro-ph.CO] .
- Kazantzidis and Perivolaropoulos (2018) L. Kazantzidis and L. Perivolaropoulos, Phys. Rev. D 97, 103503 (2018), arXiv:1803.01337 [astro-ph.CO] .
- Sagredo et al. (2018a) B. Sagredo, J. S. Lafaurie, and D. Sapone, (2018a), arXiv:1808.05660 [astro-ph.CO] .
- Sagredo et al. (2018b) B. Sagredo, S. Nesseris, and D. Sapone, Phys. Rev. D 98, 083543 (2018b), arXiv:1806.10822 [astro-ph.CO] .
- Anagnostopoulos et al. (2019) F. K. Anagnostopoulos, S. Basilakos, and E. N. Saridakis, Phys. Rev. D 100, 083517 (2019), arXiv:1907.07533 [astro-ph.CO] .
- Skara and Perivolaropoulos (2020) F. Skara and L. Perivolaropoulos, Phys. Rev. D 101, 063521 (2020), arXiv:1911.10609 [astro-ph.CO] .
- Li et al. (2021) E.-K. Li, M. Du, Z.-H. Zhou, H. Zhang, and L. Xu, Mon. Not. Roy. Astron. Soc. 501, 4452 (2021), arXiv:1911.12076 [astro-ph.CO] .
- Howlett et al. (2017) C. Howlett, L. Staveley-Smith, P. J. Elahi, T. Hong, T. H. Jarrett, D. H. Jones, B. S. Koribalski, L. M. Macri, K. L. Masters, and C. M. Springob, Mon. Not. Roy. Astron. Soc. 471, 3135 (2017), arXiv:1706.05130 [astro-ph.CO] .
- Avila et al. (2021) F. Avila, A. Bernui, E. de Carvalho, and C. P. Novaes, MNRAS 505, 3404 (2021), arXiv:2105.10583 [astro-ph.CO] .
- Huterer et al. (2017) D. Huterer, D. Shafer, D. Scolnic, and F. Schmidt, JCAP 05, 015 (2017), arXiv:1611.09862 [astro-ph.CO] .
- Turnbull et al. (2012) S. J. Turnbull, M. J. Hudson, H. A. Feldman, M. Hicken, R. P. Kirshner, and R. Watkins, Mon. Not. Roy. Astron. Soc. 420, 447 (2012), arXiv:1111.0631 [astro-ph.CO] .
- Hudson and Turnbull (2013) M. J. Hudson and S. J. Turnbull, Astrophys. J. Lett. 751, L30 (2013), arXiv:1203.4814 [astro-ph.CO] .
- Davis et al. (2011) M. Davis, A. Nusser, K. Masters, C. Springob, J. P. Huchra, and G. Lemson, Mon. Not. Roy. Astron. Soc. 413, 2906 (2011), arXiv:1011.3114 [astro-ph.CO] .
- Song and Percival (2009) Y.-S. Song and W. J. Percival, JCAP 10, 004 (2009), arXiv:0807.0810 [astro-ph] .
- Blake et al. (2013) C. Blake et al., Mon. Not. Roy. Astron. Soc. 436, 3089 (2013), arXiv:1309.5556 [astro-ph.CO] .
- Blake et al. (2012) C. Blake et al., Mon. Not. Roy. Astron. Soc. 425, 405 (2012), arXiv:1204.3674 [astro-ph.CO] .
- Pezzotta et al. (2017) A. Pezzotta et al., Astron. Astrophys. 604, A33 (2017), arXiv:1612.05645 [astro-ph.CO] .
- Okumura et al. (2016) T. Okumura et al., Publ. Astron. Soc. Jap. 68, 38 (2016), arXiv:1511.08083 [astro-ph.CO] .
- Howlett et al. (2015) C. Howlett, A. Ross, L. Samushia, W. Percival, and M. Manera, Mon. Not. Roy. Astron. Soc. 449, 848 (2015), arXiv:1409.3238 [astro-ph.CO] .
- Alam et al. (2017) S. Alam et al. (BOSS), Mon. Not. Roy. Astron. Soc. 470, 2617 (2017), arXiv:1607.03155 [astro-ph.CO] .
- Bautista et al. (2020) J. E. Bautista et al., Mon. Not. Roy. Astron. Soc. 500, 736 (2020), arXiv:2007.08993 [astro-ph.CO] .
- Gil-Marin et al. (2020) H. Gil-Marin et al., Mon. Not. Roy. Astron. Soc. 498, 2492 (2020), arXiv:2007.08994 [astro-ph.CO] .
- de Mattia et al. (2021) A. de Mattia et al., Mon. Not. Roy. Astron. Soc. 501, 5616 (2021), arXiv:2007.09008 [astro-ph.CO] .
- Tamone et al. (2020) A. Tamone et al., Mon. Not. Roy. Astron. Soc. 499, 5527 (2020), arXiv:2007.09009 [astro-ph.CO] .
- Hou et al. (2020) J. Hou et al., Mon. Not. Roy. Astron. Soc. 500, 1201 (2020), arXiv:2007.08998 [astro-ph.CO] .
- Neveux et al. (2020) R. Neveux et al., Mon. Not. Roy. Astron. Soc. 499, 210 (2020), arXiv:2007.08999 [astro-ph.CO] .
- du Mas des Bourboux et al. (2017) H. du Mas des Bourboux et al., Astron. Astrophys. 608, A130 (2017), arXiv:1708.02225 [astro-ph.CO] .
- Bautista et al. (2017) J. E. Bautista et al., Astron. Astrophys. 603, A12 (2017), arXiv:1702.00176 [astro-ph.CO] .
- du Mas des Bourboux et al. (2020) H. du Mas des Bourboux et al., Astrophys. J. 901, 153 (2020), arXiv:2007.08995 [astro-ph.CO] .
- Macaulay et al. (2013) E. Macaulay, I. K. Wehus, and H. K. Eriksen, Phys. Rev. Lett. 111, 161301 (2013), arXiv:1303.6583 [astro-ph.CO] .
- Simon et al. (2005) J. Simon, L. Verde, and R. Jimenez, Phys. Rev. D 71, 123001 (2005), arXiv:astro-ph/0412269 .
- Stern et al. (2010) D. Stern, R. Jimenez, L. Verde, M. Kamionkowski, and S. A. Stanford, JCAP 02, 008 (2010), arXiv:0907.3149 [astro-ph.CO] .
- Zhang et al. (2014) C. Zhang, H. Zhang, S. Yuan, T.-J. Zhang, and Y.-C. Sun, Res. Astron. Astrophys. 14, 1221 (2014), arXiv:1207.4541 [astro-ph.CO] .
- Moresco et al. (2012) M. Moresco et al., JCAP 08, 006 (2012), arXiv:1201.3609 [astro-ph.CO] .
- Moresco (2015) M. Moresco, Mon. Not. Roy. Astron. Soc. 450, L16 (2015), arXiv:1503.01116 [astro-ph.CO] .
- Moresco et al. (2016) M. Moresco, L. Pozzetti, A. Cimatti, R. Jimenez, C. Maraston, L. Verde, D. Thomas, A. Citro, R. Tojeiro, and D. Wilkinson, JCAP 05, 014 (2016), arXiv:1601.01701 [astro-ph.CO] .
- Ratsimbazafy et al. (2017) A. Ratsimbazafy, S. Loubser, S. Crawford, C. Cress, B. Bassett, R. Nichol, and P. Väisänen, Mon. Not. Roy. Astron. Soc. 467, 3239 (2017), arXiv:1702.00418 [astro-ph.CO] .
- Zürcher et al. (2021) D. Zürcher et al. (DES), (2021), arXiv:2110.10135 [astro-ph.CO] .
- Peebles (2021) P. J. E. Peebles (2021) arXiv:2106.02672 [astro-ph.CO] .
- Di Valentino et al. (2016) E. Di Valentino, A. Melchiorri, and J. Silk, Phys. Rev. D 93, 023513 (2016), arXiv:1509.07501 [astro-ph.CO] .
- Solà Peracaula et al. (2019) J. Solà Peracaula, A. Gomez-Valent, J. de Cruz Pérez, and C. Moreno-Pulido, Astrophys. J. Lett. 886, L6 (2019), arXiv:1909.02554 [astro-ph.CO] .
- Solà Peracaula et al. (2020) J. Solà Peracaula, A. Gómez-Valent, J. de Cruz Pérez, and C. Moreno-Pulido, Class. Quant. Grav. 37, 245003 (2020), arXiv:2006.04273 [astro-ph.CO] .
- Yan et al. (2020) S.-F. Yan, P. Zhang, J.-W. Chen, X.-Z. Zhang, Y.-F. Cai, and E. N. Saridakis, Phys. Rev. D 101, 121301 (2020), arXiv:1909.06388 [astro-ph.CO] .