The signed Varchenko Determinant for Complexes of Oriented Matroids
Abstract.
We generalize the (signed) Varchenko matrix of a hyperplane arrangement to complexes of oriented matroids and show that its determinant has a nice factorization. This extends previous results on hyperplane arrangements and oriented matroids.
1. Introduction
Varchenko [17] considered a symmetric matrix which may be viewed as a bilinear form on the vector space of linear forms of the set of regions of a hyperplane arrangement over some ordered field . The value of the product of the characteristic vectors of regions and is given by a product , where the are weights on the hyperplanes of the arrangements and is the set of hyperplanes that have to be crossed on a shortest path from to . The corresponding Varchenko Matrix has entries of the form for any pair of regions and , also see Theorem 2.0. In order to determine when the bilinear form is degenerate, Varchenko [17] gave an elegant factorization of the determinant of that matrix, considering the weights as variables.
Theorem 1.0 (Varchenko 1993 [17]).
Let be a real hyperplane arrangement, its Varchenko matrix, and the geometric lattice formed by the intersections of hyperplanes in , then
where and are positive integers depending only on .
After the original proof of Varchenko there were several approaches to provide cleaner proofs of this result. Denham and Henlon [6] sketched an elegant alternative way to prove the result. Gente [7] provided some more details for that proof and generalized their approach to cones, which are also called topcones or in our notation supertopes, i.e. convex sets of regions. This method was generalized by Hochstättler and Welker [9] to oriented matroids, which form a combinatorial model for hyperplane arrangements reflecting their local linear structure but allowing for some global non-linearities. Aguiar and Mahajan [1] generalized the original proof of Varchenko to a signed version of the matrix and also derived the result for topcones. In the signed case one considers an oriented hyperplane arrangement and the entries of the signed Varchenko matrix depend on which side of a hyperplane a cell lies, see Definition 2.0. Randriamaro [12] generalized their proof to oriented matroids and proved the factorization formula also for topoplane arrangements [13]. In his habilitation thesis he furthermore showed very recently that topoplane arrangements form a topological representation for complexes of oriented matroids (COMs) [14], leading to our result from a different perspective. Note that Varchenko and Brylawski [5] already generalized another, simpler bilinear form from hyperplane arrangements to matroids.
Bandelt et al. generalized oriented matroids to COMs by relaxing the global symmetry while maintaining convexity and local symmetry. This framework captures a variety of classes beyond oriented matroids, e.g., distributive lattices, CAT(0)-cube complexes, lopsided sets, linear extension graphs, and affine oriented matroids, see [2]. Hochstättler and Welker proved the factorization formula not only for the full oriented matroid but also for supertopes, i.e. topal fibers in oriented matroids. Every supertope is a COM and it has even been conjectured in [2, Conjecture 1] and [10, Conjecture 1] that any COM can be realized as a supertope of an oriented matroid. Also see Problem 6.0. However, that conjecture seems out of reach at the moment. A big part of the motivation for the work in the present paper is to support that conjecture by explicitly proving the factorization formula for general COMs. The presentation as well as the proof follow the lines of Hochstättler and Welker [9]. We furthermore achieve a generalization to the signed version of the Varchenko matrix, thus generalizing Randriamaro [12].
The paper is organized as follows. In Section 2 we introduce the considered structures. In Section 3 we present some tools from algebraic topology that we need for the proof of the main theorem. The latter is presented in Section 4. We give some examples and applications in Section 5 and conclude the paper with some further remarks in Section 6.
2. The Varchenko Determinant and Complexes of Oriented Matroids
Before we introduce the Varchenko Determinant, we need to get familiar with COMs. COMs have been introduced in [2] as a common generalization of oriented matroids, affine oriented matroids, and lopsided sets. We will use the notation from [2] and [4]. Note that the symbols and act like and when it comes to negation and multiplication. We start with the following definitions and axioms.
Definition 2.0.
We consider sign vectors on a finite ground set , i.e., elements of . The composition of two sign vectors and is defined as the sign-vector
The reorientation of with respect to is defined as the sign-vector
The separator of and is defined as
The support of is defined as
The zero-set of is defined as
For a set we introduce five axioms:
- (FS):
-
Face Symmetry
- (SE):
-
Strong Elimination
- (C):
-
Composition
- (Z):
-
Zero
- (Sym):
-
Symmetry
Now we can define the term COM.
Definition 2.0 (Complex of Oriented Matroids (COM)).
Let be a finite set and . The pair is called a COM, if satisfies (FS) and (SE). The elements of are called covectors.
Let us first present OMs as special COMs.
Definition 2.0 (Oriented Matroid (OM)).
Let be a finite set and . The pair is called an OM, if it is a COM that satisfies (Z).
Remark 2.0.
Usually OMs are defined satisfying (C),(Sym),(SE). But note that (FS) implies (C). Indeed, by (FS) we first get and then for all . Further, (Z) together with (FS) clearly implies (Sym). Conversely, (Sym) and (C) imply (FS) while (Sym) and (SE) imply (Z).
Let be a COM. In the following we assume that is simple, i.e.
In this setting the sign-vectors in of full support are called topes and their collection is denoted by .
The restriction of a sign-vector to , , denoted by , is defined by for all . We also write . The deletion of a COM is defined by , where , also written as .
Let be a COM and such that there exists a tope where is a subset of the positive elements of and is part of the negative elements of . The topal fiber is defined by the covectors . We denote by the set of topes of . Since all covectors of a topal fiber have the same entries on , we usually suppress the redundant coordinates in , to obtain a simple COM on the groundset . We will make use of the fact (shown in [2]) that the class of simple COMs is closed under deletion and under taking topal fibers.
For a covector , the set is usually called the face of . We define , where the componentwise ordering with respect to is used. Note that is the set of topes of , which is well-known and easily seen to be an oriented matroid.
Let us look at a special OM which we will need in the next chapter.
Definition 2.0 (Graphic OM of a directed -cycle).
This OM has a ground set of size and its set of covectors consists of and all compositions of sign-vectors from with exactly one positive and exactly one negative entry. Those generating sign-vectors are called the cocircuits of .
It can easily be checked that is the set of covectors of an OM. We use as an example:
Example 2.0 (Graphic OM of a directed triangle).
We look at a digraph with three vertices which just consists of a directed cycle, i.e.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/88c3c702-5852-4ed9-9ffb-b7e0daccc615/x1.png)
The ground set of this OM corresponds to the three arcs. One gets the covectors of such an OM by looking at the sign vectors of directed cuts (indicated with dotted lines). These sign vectors are , , , , and . Their compositions additionally yield the covectors , , , , and . We see that consists of all full support sign vectors, except and .
We define the signed Varchenko matrix for COMs analogously to this matrix for hyperplane arrangements in [1]. For this purpose we introduce two variables , for each element . Let be a field and let the polynomial ring in the set of variables , , .
Definition 2.0 (Signed Varchenko Matrix of a COM).
Let be a COM. The signed Varchenko matrix of is defined by a -Matrix over
Its rows and columns are indexed by the topes in a fixed linear order. For
Note that the diagonal entries of the matrix are equal to 1. Let us illustrate this definition with the graphic OM of a directed triangle.
Example 2.0 (continued).
The signed Varchenko Matrix of the graphic OM of a directed triangle is
In this work we will prove the following theorem.
Theorem 2.0.
Let be the signed Varchenko matrix of the COM . Then
where and are nonnegative integers that can be explicitly computed, see Remark 4.0.
Example 2.0 (continued).
For our example the determinant of the signed Varchenko matrix factorizes to
A corollary of this result, namely the case where , which is the original version of the Varchenko matrix, has been already proven for OMs in [9]. We formulate it for COMs.
Corollary 2.0.
Let be the (unsigned) Varchenko matrix (i.e. ) of the COM . Then
where and are nonnegative integers.
Example 2.0 (continued).
For our example the determinant of the (unsigned) Varchenko matrix factorizes to
3. Preparation
We start with some basics about partially ordered sets (posets). For an introduction we recommend [18]. One can associate an abstract simplicial complex , called order complex, to every poset. The elements of are the vertices of this complex and the chains (i.e. totally ordered subsets) the faces. Two posets are homotopy equivalent if their order complexes are homotopy equivalent. A poset is called contractible if its order complex is homotopy equivalent to a point. Clearly a poset is contractible if it has a unique minimal or a unique maximal element, since this element is contained in every maximal chain and consequently in every maximal face of the order complex. For details see [18]. We introduce now the Möbius function of a poset:
The bounded extension of a poset is the poset together with a new maximal element and a new minimal element . The Möbius number of is defined by
where the right-hand-side is evaluated in .
Example 3.0.
Let us look at the poset which consists only of one element. In the following its bounded extension and the value of the Möbius function of the elements of the bounded extension are depicted.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/88c3c702-5852-4ed9-9ffb-b7e0daccc615/x2.png)
Hence, the Möbius number of the poset consisting of only one element is
It follows from the following fact that the Möbius number is a topological invariant with respect to homotopic equivalence.
Theorem 3.0.
[18, Philip Hall Theorem] The Möbius number of a poset equals the reduced Euler characteristic of its order complex, i.e.
In particular we get the following corollary, whose second part follows from the definition of contractability and Example 3.0.
Corollary 3.0.
For two homotopy equivalent posets and we have . In particular, if is contractible then .
For a poset and we denote by the subposet .
Proposition 3.0.
[11, Quillen Fiber Lemma] Let and be posets and order preserving. If for all we have that is contractible, then and are homotopy equivalent.
We will now associate posets with COMs, so let be a COM and let be a fixed sign vector. We consider as a poset with order relation
We write if we consider with this partial order and we call the base pattern of the poset.
Now we will introduce a theorem which will help us with our crucial Lemma 3.3.
Theorem 3.0.
Let be a topal fiber of a COM , a tope of and its restriction to . Then the order complex of is contractible.
Note that the restriction in the statement of Theorem 3.0 is not necessarily a tope of . In order to apply the Quillen Fiber Lemma in the proof of Theorem 3.0 we need the following lemma.
Lemma 3.1.
Let and . Let denote the set of topes of and the corresponding tope poset with base pattern . Consider the order-preserving map given by restriction. Let . Then
Proof.
Let . As is all positive, we must have and hence implying . If on the other hand , then . Hence . ∎
We need two preparatory results for the proof of Theorem 3.0. For the first one also see [8, Lemma 10]. We reprove that result here, since in the presentation in [8] the signs are chosen the opposite way. Recall from Example 2.0 that is the set of covectors of the OM of the directed cycle on vertices.
Proposition 3.0.
Let , , be a COM with tope set and let . If for all we have , then the poset is contractible.
Proof.
We will show by induction that if , then all covectors which contain exactly one plus-entry and at least one minus-entry are in . Since then in particular all covectors which contain exactly one minus-entry and one plus-entry (i.e. the cocircuits of ) exist in , we get by (SE) that the all zero vector is in . Together, we can conclude that , since we obtain all its covectors by composition of those vectors. Since is uniform and contains , every other COM containing it has to be a OM which is free. This means that every possible sign-vector vector is a covector and is a consequence of the strong elimination axiom. Therefore , since . Taking the contraposition we see that if , then , so the poset has a unique maximal element. In particular, it is contractible.
So let for all and . We will use induction over the number of zero-entries in the covectors, i.e. we want to show that for every all sign-vectors with zero entries, one plus-entry and minus-entries are in .
: By the existence of there is nothing to show. We fix and assume that all covectors with or fewer zero-entries, exactly one plus-entry and at least one minus-entry exist in .
: We will show that there exists a covector with zero-entries in the i-th position, , , a plus-entry in the j-th position, and everywhere else. We choose an and consider two covectors with in , where one has a in the -th position and the other one in the j-th position and both have a everywhere else. These do exist by inductive assumption. W.l.o.g. those two covectors look like this:
If we now perform strong elimination on with those two covectors we get the covector
If was , then . Since we have and have the covector we were looking for, so .
∎
Lemma 3.2.
Let be a topal fiber of a COM , a tope of and its restriction to . If , then , in particular .
Proof.
Let be a COM such that there is a COM , with and for some and . We saw in Definition 2.0 that . By the definition of there exists with
Since the composition of with every other covector in is in (see Remark 2.0), we see that . So in this case , so every tope restricted to has to be in . Since , .
∎
Now we are in position to prove Theorem 3.0.
Proof of Theorem 3.0.
Let be a COM such that there is a COM , with and for some , a tope of and its restriction to . First we look at the case . From Lemma 3.2 we know, is a tope of . So we have a unique minimal element and is contractible. Now let . Possibly reorienting elements we may assume that . We proceed by induction on . If then either is a singleton or a chain of length 2 and thus contractible. Hence assume . If for all there exists as in Proposition 3.0, then is contractible by Proposition 3.0. Hence we may assume that there exists such that . Let denote the tope poset in with base pattern . Since the class of COMs is closed under deletion, we know that is a COM. Since evolved from by setting for some and , evolves in the same way from , i.e. (note that cannot be in , since and ). Also is the restriction to of the tope of . We see that together with fulfills the assumptions of Theorem 3.0. Furthermore, , this follows from Lemma 3.2. Hence, is contractible by inductive assumption. We now want to show that and are homotopy equivalent by using Proposition 3.0. So consider the order-preserving map given by restriction. Let . By Lemma 3.1
is the set of topes of . If , then has fewer elements than . Furthermore, by Lemma 3.2, . Hence is contractible by inductive assumption. If then by the choice of the preimage is the all minus vector. Hence, this is the unique maximal element in and that fiber is also contractible. So by Proposition 3.0 and are homotopy equivalent and the claim follows. ∎
We now introduce , which is a truncated version of . For and we define as the poset with as its artificial least element and the remaining poset structure induced from . For we write for the interval from to in . The following result will help us later in the main proof to obtain a factorization of the Varchenko matrix.
Lemma 3.3.
Let be a COM, a tope, an element, and such that . Then
| (3) |
and
| (6) |
Proof.
In order to prove (3) we assume . We prove the assertion by induction on . If then
Note that . The poset has the maximal element , so it is contractible and has Möbius number . Therefore we have
Assume . Set
Then
| (7) |
is the set of topes of the COM , where the associated poset is contractible by Theorem 3.0 (note that we did not suppress the redundant coordinates here to keep notation simple). Since the right hand side of (7) ranges over the elements of a contractible poset, we have again
and showed
| (8) |
Now rewrite the left hand side of (8) as
| (9) |
From this we conclude
The second claim follows analogously by reorienting all the signs. ∎
We conclude this section with another result on contractability needed in the proof of our main theorem. We start with a lemma:
Lemma 3.4.
Let be a COM, and . The tope is the only tope in such that for all we have
| (10) | ||||
| (11) |
Proof.
In the case where is a tope there is nothing to show, so we assume . It is easy to see that fulfills (10) and (11). Let us assume there is another tope in which has this property. By the definition of we have
Since and can only contain elements from , has to contain at least one element from . Now considering we see that , so does not fulfill the property and we have a contradiction. ∎
For and we say that defines a proper face of if there is a covector with and with . Note that in this case there is a unique maximal such covector, namely the composition of all of them. Otherwise, we say that does not define a proper face of .
Theorem 3.0.
Let be a COM, a tope, and let define a proper face of . Let be the maximal covector such that and and choose . Then is contractible. In particular, .
Proof.
Let . Then by Lemma 3.4 the tope is the unique tope in such that for all we have
Since and it also follows that . Since , clearly and hence . This shows . We now define the map
and prove that it is a closure operator by showing that it is order preserving and idempotent (i.e. ). So let . Then . Since it follows that . Obviously . So is a closure operator and it follows that is homotopy equivalent to its image (see e.g, [3, Corollary 10.12]).
Since and , it also follows that for all . Hence the image of has a unique maximal element and hence is contractible. ∎
4. Main Proof
In this Section we assume that is a COM with topes and signed Varchenko matrix . Recall that we assume to be linearly ordered. Note however that swapping two topes leads to a row swap and a column swap at the same time, so we do not change the sign of our determinant. Hence, in this section we will rearrange the ordering on , whenever it is convenient for the proof. Moreover, for the proof we also fix a linear ordering on , i.e., .
For any sign vector let be a matrix with rows indexed by for , for and columns indexed by for , for . For a tope indexing a row and a tope indexing a column we set . After reordering this yields a block decomposition of as
| (14) |
We fix such a linear ordering on and set to
Note that this matrix has the following form
where
and the identity matrix with and .
Lemma 4.1.
Let be the maximal element of . Then factors as
| (15) |
and as
| (16) |
Proof.
Let us prove (15) first. For and the entry in row and column on the left hand side of (15) is . On the right hand side the corresponding entry is:
This follows from the fact that is the maximal element of any separator of the topes indexing . By definition we have for
We see that if . Thus the claim of the lemma is proved once we have shown that for a fixed subset and fixed we have:
| (19) |
Next we use the matrices to factorize . The following lemma yields the base case for the inductive step in the factorization.
Lemma 4.2.
Let be the maximal element of and let be the matrix after evaluating and to . Then
Proof.
Now we are in position to state and prove the crucial factorization.
Proposition 4.0.
Let be a fixed ordering. Then
Proof.
We will prove by downward induction on that
| (33) |
For the assertion follows directly from Lemma 4.2. For the inductive step assume and (33) holds for . We know from Lemma 4.2 that if we choose a linear ordering on for which is the largest element then
| (34) |
where is defined as
Since for this particular ordering. Now we go back to the ordering in the assumption and set in . We see that
But then .
Now (34) implies
With the induction hypothesis this completes the induction step by
Before we prove the following proposition, we quote [9, Corollary 3], which is a result for oriented matroids.
Lemma 4.3.
Let and let such that does not define a proper face of . Then the Möbius number is if and if .
Now let and be the maximal element of . Define as the set of topes such that is the maximal element of for which and .
Proposition 4.0.
For any pair of topes we have
Proof.
By the definition of we have , so for all . Thus, if we consider the poset in the restriction we find that the interval is isomorphic to , since the elements in only differ in . We saw in Section 2, that is an OM. Further, is a poset and is an interval in this particular OM. Furthermore, since is the maximal element satisfying and , does not define a proper face of . Since our interval is in an OM, we can use Lemma 4.3 and the claim follows. ∎
We define if is not the maximal element of and otherwise. Since together with is a perfect pairing on it follows that contains an even number of topes. In particular, is a nonnegative integer. We denote by the submatrix of obtained by selecting rows and columns indexed by .
Lemma 4.4.
Let and . If . then
where .
Proof.
If then . Using the definition of and Proposition 4.0 we find
We order rows and columns of so that the elements and are paired in consecutive rows and columns. With this ordering is a block diagonal matrix having along its diagonal two by two matrices
if is the maximal element of and identity matrices otherwise. In any case we find as desired. ∎
Lemma 4.5.
After suitably ordering the matrix is the block lower triangular matrix with the matrices for with and on the main diagonal.
Proof.
Note that for each tope there is exactly one with , and that . We fix a linear ordering of such that for each the topes from form an interval and such that the topes from precede those of if .
For this order the claim follows if we show that the entry is zero whenever , and .
If then by we have . Hence it suffices to consider the case . Since , is a proper face of .
If and then it follows from Theorem 3.0 that and therefore . Analogously if and then and therefore .
On the other hand, if , then in particular . Since by definition of we have that is the maximal covector such that and it follows that . Since we must have that , i.e. is an entry below the diagonal and we are done.
∎
Proof of Theorem 2.0.
After fixing a linear order on it follows from Proposition 4.0 that is the product of the determinants of for . By Lemma 4.5 the determinant of each is a product of determinants of for and for which . Then Lemma 4.4 completes the proof. ∎
Remark 4.0 (Description of ).
In Theorem 2.0 we describe as a nonnegative integer, but this can be made more precise: Fix any linear order on and let be the maximal element of . From Lemma 4.4 we deduce, that . Thus counts the topes such that is the maximal element of for which and . In particular, does not depend on the choice of the linear ordering on .
5. Applications
We give two applications of our formula for the Varchenko determinant on two COMs associated to a poset : its lattice of ideals and its set of linear extensions. As an example we will use the poset in Figure 1.
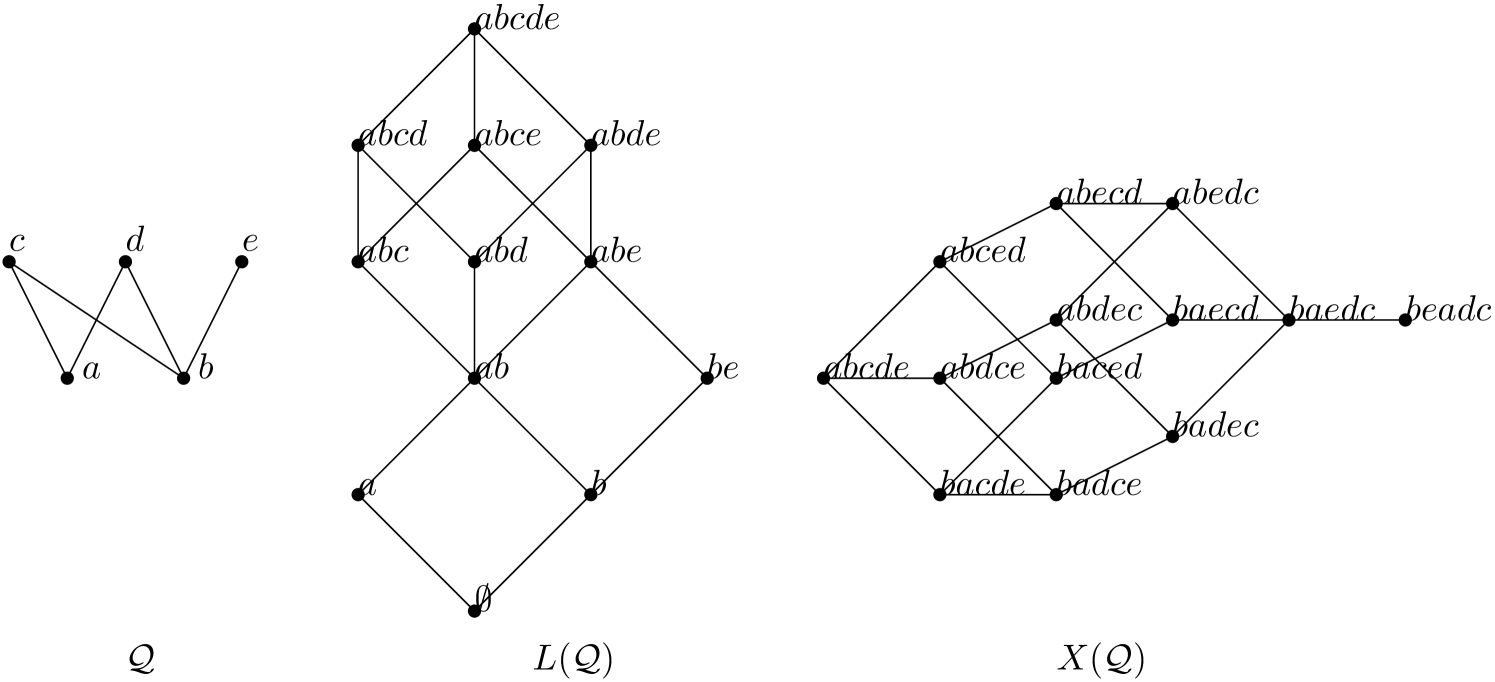
5.1. Distributive Lattices
By the Fundamental Theorem of Finite Distributive Lattices, for every distributive lattice there exists a poset , such that ordering the ideals (downward closed sets) of by inclusion yields a lattice isomorphic to . The topes of the COM associated to correspond to the ideals of , the empty set can be seen as the all-plus vector, the ground set of this COM is the ground set of , and the separator of two ideals is the symmetric difference . So this allows, to quickly write down the (unsigned) Varchenko matrix of . In our example we indicate in the following way, where we just display the elements of the symmetric difference of two ideals to make it easier to read. Note that in order to get the Varchenko matrix itself one has to exchange a string for the product . The translates therefore to the empty product, which is 1.
Let us define the covectors of that COM: Let be two ideals such that forms an antichain. Then these two ideals define a covector by setting
In particular, when , we get a tope corresponding to the ideal and the all-plus tope corresponds to the empty ideal.
Now, if we pick a linear ordering on , let be the largest element of , then counts those ideals such that we have
-
•
,
-
•
if and is the largest element of , then .
But note that this condition is only satisfied if and for some or and for some . Indeed, if otherwise and is the largest element of one can set and , a contradiction to the above condition. Hence is if and otherwise. All pairs with look like , where is a maximal element of .
Thus, Corollary 2.0 and Remark 4.0 yield that
where denotes the set of ideals of , the set of maximal elements of an ideal and denotes the number of ideals having as maximal element. In our example we get the following formula for :
5.2. Linear extensions
Another instance is the ranking COM of a poset , that was described in [2]. The topes are the linear extensions of , and the separator of two linear extensions is the set of pairs of elements of that are ordered differently in and . In particular, the ground set of this COM consists of the set of incomparable pairs of , e.g., . We can thus define the (unsigned) Varchenko matrix . We get a description of . We deem it too large to display it entirely, but for example the entry corresponding to extensions is .
The covectors of the ranking COM are the weak extensions of , i.e., those poset extensions of that are chains of antichains. The set of such an extension corresponds to its set of incomparable pairs . In order to properly define the signs of the covectors, one can pick an arbitrary linear extension of , and set non-zero coordinates of to if the corresponding incomparable pair of is ordered the same way in and and to otherwise. To define we can fix an arbitrary linear order on the set and let be the largest element of . Then counts linear extensions of such that
-
•
is a linear extension of ,
-
•
if another weak extension of has as largest incomparable pair, then either is not an extension of or is not an extension of .
In this setting one can see that no such can exist if and only if is a chain of antichains only one of which - say - has size larger than . In this case the feasible are extensions of that extend by starting and ending with an element among . Hence, there are such linear extensions. By Corollary 2.0 and Remark 4.0 we have
where denotes the set of antichains of size at least of .
6. Conclusion
One might wonder to what extent our result could be further generalized to other classes. A natural next class are partial cubes, i.e., isometric subgraphs of the hypercube . These generalize (tope graphs of) COMs and allow for an analogous definition of the Varchenko matrix, where the entry contains a product of monomials indexed by those coordinates in where and differ. The smallest partial cube that is not the tope graph of a COM is the full subdivision of , see [10]. In this case the Varchenko matrix looks like the following
and its determinant is of the following form:
Thus, in this case there is no nice factorization.
Problem 6.0.
Are there classes of partial cubes beyond COMs, that allow for a factorization theorem of the Varchenko matrix?
As mentioned in the introduction, we are not aware of an example of a COM which cannot be extended to become the supertope of an oriented matroid. The conjectures from [2, Conjecture 1] and [10, Conjecture 1] in our language are equivalent to the following:
Problem 6.0.
Are supertopes of oriented matroids a proper subclass of the class of complexes of oriented matroids?
Acknowledgements:
We sincerely thank the referees for their attentive review and valuable comments, which have significantly improved the quality of this work. KK was partially supported by the French Agence nationale de la recherche through project ANR-17-CE40-0015 and by the Spanish Ministerio de Economía, Industria y Competitividad through grant RYC-2017-22701, grant PID2019-104844GB-I00 and grant PID2022-137283NB-C22.
References
- [1] M. Aguiar, S. Mahajan, Topics in hyperplane arrangements, Mathematical Surveys and Monographs 226, American Mathematical Society, Providence, RI, 2017.
- [2] H.-J. Bandelt, V. Chepoi , K. Knauer, COMs: complexes of oriented matroids, J. Combin. Theory Ser. A, 156 (2018) 195–237.
- [3] A. Björner, Topological methods, in: Handbook of combinatorics, Volume 2, 1819–1872, Elsevier Sci. B. V., Amsterdam, 1995.
- [4] A. Björner, M. Las Vergnas, B. Sturmfels, W. White, G.M. Ziegler, Oriented matroids. Second edition. Encyclopedia of Mathematics and its Applications 46. Cambridge University Press, Cambridge, 1999.
- [5] T. Bryławski, A. Varchenko, The determinant formula for a matroid bilinear form, Adv. Math. 129 (1997) 1–24.
- [6] G. Denham, P. Hanlon, Some algebraic properties of the Schechtman-Varchenko bilinear forms, in: New perspectives in algebraic combinatorics (Berkeley, CA, 1996–97), 149–176, Math. Sci. Res. Inst. Publ., 38, Cambridge University Press, Cambridge, 1999.
- [7] R. Gente, The Varchenko Matrix for Cones, PhD-Thesis, Philipps-Universität Marburg, 2013.
- [8] W. Hochstättler, S. Keip, and K.Knauer. ”Kirchberger’s theorem for complexes of oriented matroids.” Linear Algebra and its Applications 693 (2024): 288-296.
- [9] W. Hochstättler, V. Welker. ”The Varchenko determinant for oriented matroids.” Mathematische Zeitschrift 293.3 (2019): 1415-1430.
- [10] K. Knauer, T. Marc, On tope graphs of complexes of oriented matroids, Discrete Comput. Geom. 63 (2020): 377-417.
- [11] D. Quillen, ”Homotopy properties of the poset of nontrivial p-subgroups of a group.” Advances in Mathematics 28.2 (1978): 101-128.
- [12] H. Randriamaro, The Varchenko Determinant of an Oriented Matroid, Trans. Comb. (10) 4 (2021), 7–18.
- [13] H. Randriamaro. ”The Varchenko matrix for topoplane arrangements.” Communications in Contemporary Mathematics 24.10 (2022): 2150086.
- [14] H. Randriamaro, Computer Algebra of Conditional Oriented Matroids, Habilitation, (2023) Universität Kassel.
- [15] V.V. Schechtman, A.N. Varchenko, Arrangements of hyperplanes and Lie algebra homology, Invent. Math. 106 (1991) 139–194.
- [16] R.P. Stanley, Enumerative combinatorics. Volume 1. Second edition. Cambridge Studies in Advanced Mathematics 49,
- [17] A. Varchenko, Bilinear form of real configuration of hyperplanes, Adv. Math. 97 (1993) 110–144.
- [18] M. L. Wachs, Poset topology: tools and applications. (2006).