The spectra $ko$ and $ku$ are not Thom spectra: an approach using ${\rm THH}$

This is a consequence of the calculations of [AHL], as follows. Modulo the image of the $13$-skeleton, the reduced object $\overline{{\rm THH}}(ko)$ has cells in degrees $15$, $16$, and $20$, with the generator in degree $16$ attached to $4$ times the generator in degree $15$ and the generator in degree $20$ attached to $2v_{1}^{2}$ times the generator in degree $15$.

Let $S$ be the $15$-skeleton of $Z$, and $U$ the $8$-skeleton. There exists a cofiber sequence

where $U$ is the unique connective spectrum whose homology is an “upside-down question mark” starting in degree 5, and $Q$ is the unique connective spectrum whose homology is a “question mark” starting in degree 12. (For this reason, the spectrum $S$ is informally called the “Spanish question.”) By the previous lemma, it suffices to show that any attaching map for the $16$-cell cannot be $2\nu$-torsion.

The following charts display the final results of the Adams spectral sequence for the homotopy of $U$ (Figure 2) and $Q$ (Figure 3). The nontrivial differentials for $U$ are deduced from corresponding differentials for the sphere.

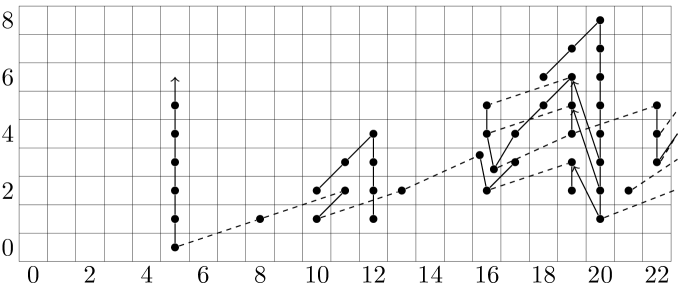
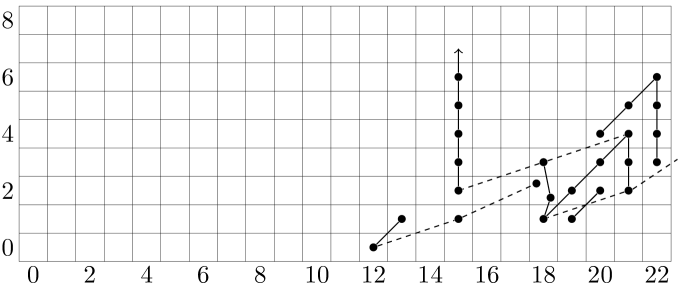
We note two things about the homotopy of $U$.

• •

  First, by comparison with the sphere, there are no hidden multiplication-by-$4$ extensions in total degree $19$. The image of $\pi_{19}\Sigma^{5}\mathbb{S}$ is an index $2$ subgroup isomorphic to $(\mathbb{Z}/2)^{2}$.

• •

  Second, let $x$ be any class in total degree $11$. As $\eta$-multiplication surjects onto degree $11$, we would have $x=\eta y$ for some $y$ in total degree $10$. However, then as $\eta$-multiplication is surjective onto total degree $17$ we would have $\sigma y=\eta z$ for some $z$, and therefore

  $$\sigma\eta x=\eta^{3}z=4\nu z.$$

  However, by the previous note there can be no hidden multiplication-by-$4$ extensions in degree $19$, so $\sigma\eta x=0$.

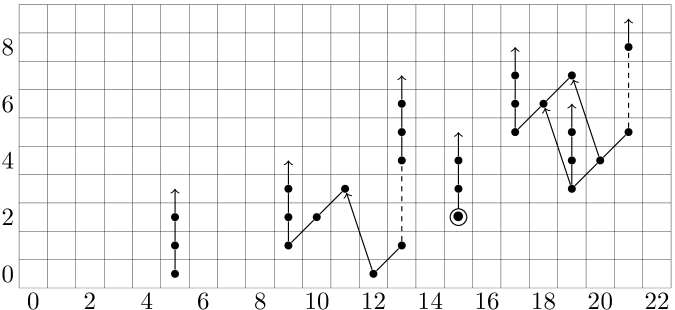
The attaching map $f\colon\thinspace\Sigma^{-1}Q\to U$ for $S$ must be a lift of the corresponding $ko$-module attaching map $ko\mathop{\wedge}f\colon\thinspace\Sigma^{-1}ko\mathop{\wedge}Q\to ko\mathop{\wedge}U$ for $ko\mathop{\wedge}S$. We display here the Adams charts computing the homotopy groups of the function spectra parametrizing the possible attaching maps.

Figure 4 displays the Adams spectral sequence chart for the homotopy of $F(\Sigma^{-1}Q,U)\simeq\Sigma DQ\mathop{\wedge}U$.

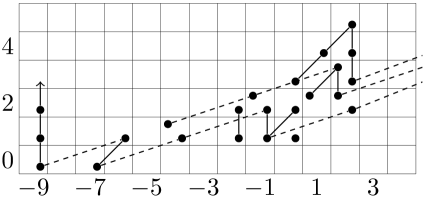
The Adams spectral sequence chart for $F_{ko}(\Sigma^{-1}ko\mathop{\wedge}Q,ko\mathop{\wedge}U)\simeq ko\mathop{\wedge}F(\Sigma^{-1}Q,U)$ is shown in Figure 5.

We note that there is a unique nontrivial attaching map over $ko$; the homotopy computations of [AHL] show that the attaching map $ko\mathop{\wedge}f$ must be the unique nontrivial element in $\pi_{0}$ of $ko\mathop{\wedge}F(\Sigma^{-1}Q,U)$. In the figure, this class is circled. The lift to the sphere must be of Adams filtration $2$ or higher, as a lift of Adams filtration $1$ would give the cohomology of $S$ visible squaring operations ${\rm Sq}^{8}$ out of dimensions below $8$.

We then note that the product $(ko\mathop{\wedge}f)\eta$ is nontrivial, and lifts to the unique map $(f\eta)$ over the sphere which is an $\eta$-multiple. It has Adams filtration $4$.

Figure 6 is an Adams spectral sequence chart for the homotopy of $S$. The indicated arrows are not necessarily differentials; they describe the unique nontrivial map $g\colon\thinspace\Sigma^{-1}Q\to U$ of Adams filtration 3 in ${\rm Ext}$. We note that $g$ and $f$ agree on multiples of $\eta$, and so these do describe $d_{3}$ differentials on multiples of $\eta$.

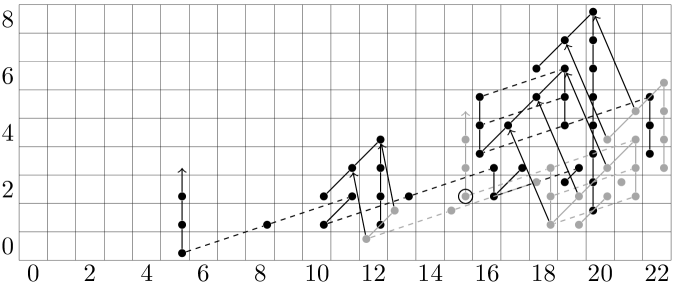
In particular, there must be a $d_{3}$ differential out of degree $(t-s,s)=(19,2)$. By comparing with the spectral sequences for $Q$ and $U$, we find that the only other possible differential supported on a class in total degree $19$ would be a $d_{5}$ on the class in degree $(19,1)$. However, this class is $\sigma y$ for the class $y$ in bidegree $(12,0)$, and as previously noted we must have $\sigma\eta f(y)=0$ where $f$ is the attaching map. Therefore, the specified $d_{5}$ differential does not exist and the class in degree $(19,1)$ survives to homotopy.

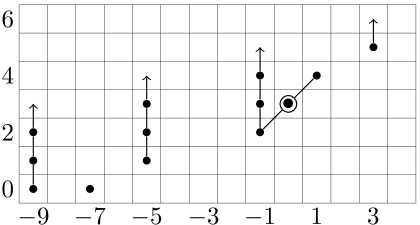
Figure 7 describes the Adams $E_{3}$ page for the homotopy of $ko\mathop{\wedge}S$. The indicated differentials are the image of $ko\mathop{\wedge}g=ko\mathop{\wedge}f$.

Comparing these, we find that the (marked) attaching map $ko\mathop{\wedge}h$ for the $16$-cell has two possible lifts to a map $h$ over the sphere up to multiplication by a $2$-adic unit: there is one map in Adams filtration $1$ and one map in Adams filtration $2$. These two lifts differ by a $2$-torsion element (as the image is torsion-free), and so the element $2\nu h$ is uniquely defined. One possible choice of $h$ is marked in Figure 6.

We claim that there is a hidden extension

As a result, by the previous lemma the attaching map for the $20$-cell cannot possibly lift.

The image of $\nu h$ is $2$-torsion in $\pi_{*}Q$, and hidden multiplication-by-2 can be detected on Ext by the Massey product $\langle f,\nu h,2\rangle$. Multiplying this by $\eta$, we find

However, the Massey product $\langle\nu h,2,\eta\rangle$ is the nontrivial element in bidegree $(20,4)$ in $\pi_{*}Q$: the element $\langle\nu h,2,\eta\rangle\eta$ has a nontrivial image under $f$, and therefore so does $\langle\nu h,2,\eta\rangle$.