The spectra of Laplace operators on covering simplicial complexes

Yi-Zheng Fan Center for Pure Mathematics, School of Mathematical Sciences, Anhui University, Hefei 230601, P. R. China fanyz@ahu.edu.cn , Yi-Min Song Center for Pure Mathematics, School of Mathematical Sciences, Anhui University, Hefei 230601, P. R. China songym@stu.ahu.edu.cn and Yi Wang Center for Pure Mathematics, School of Mathematical Sciences, Anhui University, Hefei 230601, P. R. China wangy@ahu.edu.cn

Abstract.

In this paper, by the representation theory of symmetric group, we give a decomposition of the Laplace operator (in matrix form) of a covering simplicial complex into the direct sum of some matrices, including the Laplace operator of the underlying simplicial complex. So, the spectrum of a covering simplicial complex can be expressed into a union of the spectrum of the underlying simplicial complex and the spectra of some other matrices, which implies a result of Horak and Jost. In particular, we show that the spectrum of a $2$ -fold covering simplicial complex is the union the that of the underlying simplicial complex and that of an incidence-signed simplicial complex, which is an analog of Bilu and Linial’s result on graphs. Finally we show that the dimension of the cohomology group of a covering simplicial complex is greater than or equal to that of the underlying simplicial complex.

Key words and phrases:

Simplicial complex, signed complex, covering, Laplace operator, hypergraph

2000 Mathematics Subject Classification:

55U05, 05E45, 47J10, 05C65

*The corresponding author. This work was supported by National Natural Science Foundation of China (Grant Nos. 12331012, 12171002).

1. Introduction

The study of graph Laplacians has a long and prolific history. It first appeared in a paper by Kirchhoff [18], where he analysed electrical networks and stated the celebrated matrix tree theorem. In the early 1970s Fiedler [13] established a relation between the second smallest eigenvalue and the connectivity of a graph. Since then there has been a number of papers on the Laplacian spectra of graphs; see [26]. The normalized graph Laplacian was introduced by Bottema [4] who studied a transition probability operator on graphs; also see [10] for more introduction.

The graph Laplacian was generalized to simplicial complexes (simply called complex) by Eckmann [9], who proved the discrete version of the Hodge theorem, which can be formulated as

\text{ker}(\delta_{i}^{*}\delta_{i}+\delta_{i-1}\delta_{i-1}^{*})=\tilde{H}_{i}(K,\mathbb{R}),

where $L_{i}=\delta_{i}^{*}\delta_{i}+\delta_{i-1}\delta_{i-1}^{*}$ is the higher order combinatorial Laplacian. There have already been several attempts towards the normalization of the combinatorial Laplace operator; see Chung [11], Taszus [31], Lu and Peng [24], Garland [15]. Horak and Jost developed a general framework for Laplace operators defined in terms of the combinatorial structure of a complex, including the combinatorial Laplacian and the normalized Laplacian.

The graph covering (also called lift) has been introduced and studied in many literatures [25, 28, 2] from the viewpoint of topological or complex. It was generalized to hypergraph covering in [7, 22, 29] in different versions. The complex covering was introduced by Rotman [28], which was adopted by Gustavson [17] to study the Laplacian spectrum. As remarked by Horak and Jost [20], there exist counterexamples to the Universal Lifting Theorem for discrete covering maps from [28] (Theorem 2.1), and the spectral inclusion theorem from [17] (Theorem 4.4). Horak and Jost [20] introduced the notion of strong covering to fix the problems; see Section 3.

By the representation theory of symmetric group, the characteristic polynomial of the adjacency matrix of a covering graph was formulated in a product of the characteristic polynomials of some matrices [27, 12], which implies that the spectrum of the adjacency matrix (simply called the adjacency spectrum) of a covering graph contains that of its underlying graph. In particular, if a graph $\bar{G}$ is a $2$ -fold covering (or $2$ -lift) of a graph $G$ , then the adjacency spectrum of $\bar{G}$ is a multi-set union of that of $G$ and that of a signed graph $G_{s}$ with $G$ as underlying graph, which was proved by Bilu and Linial [3] by eigenvector approach. (Note it can also be shown by the sign representation of symmetric group $\mathbb{S}_{2}$ ). Li and Hou [23] applied the above idea to formulate the characteristic polynomials of the Laplacian matrix or normalized Laplacian matrix of a covering graph.

Under the strong covering of complex, Horak and Jost [20] proved that the inclusion relation between the spectrum of a covering complex and that of its underlying complex; see Corollary 4.3. What we are interested in is the remaining eigenvalues of the covering complex except the eigenvalues of the underlying complex. In this paper, by the representation theory of symmetric group, we will give a decomposition of the Laplace operator (in matrix form) of a covering complex into the direct sum of some matrices, including the Laplace operator of the underlying complex. So, the spectrum of a covering complex can be expressed into a union of the spectrum of the underlying complex and the spectra of some other matrices, which implies a result of Horak and Jost [21]. In particular, we show that the spectrum of a $2$ -fold covering complex is the union the that of the underlying complex and that of an incidence-signed complex, which is an analog of Bilu and Linial’s result on graphs. Finally we show that the dimension of the homology group of a covering complex is greater than or equal to that of the underlying complex.

2. Preliminaries

2.1. Simplical complex and Laplace operator

Let $V$ be a finite set. An abstract simplicial complex (simply called a complex) $K$ over $V$ is a collection of the subsets of $V$ which is closed under inclusion. An $i$ -face or an $i$ -simplex of $K$ is an element of $K$ with cardinality $i+1$ . The dimension of an $i$ -face is $i$ , and the dimension of $K$ is the maximum dimension of all faces of $K$ . The faces which are maximum under inclusion are called facets. We say $K$ is pure if all facets have the same dimension. So, a complex can be considered as a hypergraph with facets as the edges of the hypergraph, and a pure complex will correspond to a uniform hypergraph, where a hypergraph is called uniform if all edges have the same size.

We assume that $\emptyset\in K$ , called the empty simplex with dimension $-1$ . Let $S_{i}(K)$ be the set of all $i$ -faces of $\mathcal{K}$ , where $S_{-1}:=\{\emptyset\}$ . The $p$ -skeleton of $K$ , written $K^{(p)}$ , is the set of all simplices of $K$ of dimension less than or equal to $p$ . So, $K^{(1)}\backslash\{\emptyset\}$ is the usual graph, where the $0$ -faces are usually called vertices denoted by $V(K)$ , and $1$ -faces are called the edges. We say $K$ is connected if the graph $K^{(1)}\backslash\{\emptyset\}$ is connected.

We say a face $F$ is oriented if we assign an ordering of its vertices and write it as $[F]$ . Two ordering of the vertices of $F$ are said to determine the same orientation if there is an even permutation transforming one ordering into the other. If the permutation is odd, then the orientation are opposite. The $i$ -chain group of $K$ over $\mathbb{R}$ , denoted by $C_{i}(K,\mathbb{R})$ , is the vector space over $\mathbb{R}$ generated by all oriented $i$ -faces of $K$ modulo the relation $[F_{1}]+[F_{2}]=0$ , where $[F_{1}]$ and $[F_{2}]$ are two different orientations of a same face. The cochain group $C^{i}(K,\mathbb{R})$ is defined to be the dual of $C_{i}(K,\mathbb{R})$ , i.e. $C^{i}(K,\mathbb{R})=\text{Hom}(C_{i}(K,\mathbb{R}),\mathbb{R})$ , which are generated by the dual basis consisting of $[F]^{*}$ for all $F\in S_{i}(K)$ , where

[F]^{*}([F])=1,[F]^{*}([F^{\prime}])=0\text{~{}for~{}}F^{\prime}\neq F.

The functions $[F]^{*}$ are called the elementary cochains. Note that $C_{-1}(K,\mathbb{R})=\mathbb{R}\emptyset$ , identified with $\mathbb{R}$ , and $C^{-1}(K,\mathbb{R})=\mathbb{R}\emptyset^{*}$ , also can be identified with $\mathbb{R}$ , where $\emptyset^{*}$ is the identify function on the empty simplex.

For each integer $i=0,1,\ldots,\text{dim}K$ , The boundary map $\partial_{i}:C_{i}(K,\mathbb{R})\to C_{i-1}(K,\mathbb{R})$ is defined to be

\partial_{i}([v_{0},\ldots,v_{i}])=\sum_{j=0}^{i}(-1)^{j}[v_{0},\ldots,\hat{v}_{j},\ldots,v_{i}],

for each oriented $i$ -face $[v_{0},\ldots,v_{i}]$ of $K$ , where $\hat{v}_{j}$ denotes the vertex $v_{j}$ has been omitted. In particular, $\partial_{0}[v]=\emptyset$ for $v\in S_{0}(K)$ . We will have the augmented chain complex of $K$ :

\cdots\longrightarrow C_{i+1}(K,\mathbb{R})\stackrel{{\scriptstyle\partial_{i+1}}}{{\longrightarrow}}C_{i}(K,\mathbb{R})\stackrel{{\scriptstyle\partial_{i}}}{{\longrightarrow}}C_{i-1}(K,\mathbb{R})\rightarrow\cdots\longrightarrow C_{-1}(K,\mathbb{R})\to 0,

satisfying $\partial_{i}\circ\partial_{i+1}=0$ .

Here, by abuse of notation, we use $\partial\bar{F}$ to denote the set of all $i$ -faces in the boundary of $\bar{F}$ when $\bar{F}\in S_{i+1}(K)$ . If $[\bar{F}]:=[v_{0},\ldots,v_{i}]$ and $[F_{j}]:=[v_{0},\ldots,\hat{v}_{j},\ldots,v_{i}]$ , then we define $\operatorname{sgn}([F_{j}],\partial[\bar{F}]]=(-1)^{j}$ , namely, the sign of $[F_{j}]$ appeared in $\partial[\bar{F}]$ , and $\operatorname{sgn}([F],\partial[\bar{F}]]=0$ if $F\notin\partial\bar{F}$ .

The coboundary map $\delta_{i-1}:C^{i-1}(K,\mathbb{R})\to C^{i}(K,\mathbb{R})$ is the conjugate of $\partial_{i}$ such that $\delta_{i-1}f=f\partial_{i}.$ So

(\delta_{i}f)([v_{0},\ldots,v_{i}])=\sum_{j=0}^{i}(-1)^{j}f([v_{0},\ldots,\hat{v}_{j},\ldots,v_{i}]).

Similarly, we have the augmented cochain complex of $K$ :

\cdots\longleftarrow C^{i+1}(K,\mathbb{R})\stackrel{{\scriptstyle\delta_{i}}}{{\longleftarrow}}C^{i}(K,\mathbb{R})\stackrel{{\scriptstyle\delta_{i-1}}}{{\longleftarrow}}C^{i-1}(K,\mathbb{R})\longleftarrow\cdots{\longleftarrow}C^{-1}(K,\mathbb{R})\longleftarrow 0,

satisfying $\delta_{i}\circ\delta_{i-1}=0$ . The $i$ -th reduced cohomology group for every $i\geq 0$ is defined to be

\tilde{H}^{i}(K,\mathbb{R})=\ker\delta_{i}/\text{im~{}}\delta_{i-1}.

By introducing inner products in $C^{i}(K,\mathbb{R})$ and $C^{i+1}(K,\mathbb{R})$ respectively, we have the adjoint $\delta^{*}_{i}:C^{i+1}(K,\mathbb{R})\to C^{i}(K,\mathbb{R})$ of $\delta_{i}$ , which is defined by

(\delta_{i}f_{1},f_{2})_{C^{i+1}}=(f_{1},\delta^{*}_{i}f_{2})_{C^{i}}

for all $f_{1}\in C^{i}(K,\mathbb{R}),f_{2}\in C^{i+1}(K,\mathbb{R})$ .

Definition 2.1.

[21] The following three operators are defined on $C^{i}(K,\mathbb{R})$ .

(1) The $i$ -dimensional combinatorial up Laplace operator or simply the $i$ -up Laplace operator:

\mathcal{L}_{i}^{up}(K):=\delta_{i}^{*}\delta_{i}.

(2) The $i$ -dimensional combinatorial down Laplace operator or the $i$ -down Laplace operator:

\mathcal{L}_{i}^{down}(K):=\delta_{i-1}\delta_{i-1}^{*}.

(3) The $i$ -dimensional combinatorial Laplace operator or the $i$ -Laplace operator:

\mathcal{L}_{i}(K)=\mathcal{L}_{i}^{up}(K)+\mathcal{L}_{i}^{down}(K)=\delta^{*}_{i}\delta_{i}+\delta_{i-1}\delta^{*}_{i-1}.

Horak and Jost [20, 21] suggested to define an inner product on $C^{i}(K,\mathbb{R})$ such that the elementary cochains are orthogonal to each other, which is equivalent to define a weight function on all faces of $K$ :

w:\bigcup_{i=-1}^{\text{dim}K}S_{i}(L)\to\mathbb{R}^{+}.

Then

(f,g)_{C^{i}}=\sum_{F\in S_{i}(K)}w(F)f([F])g([f]).

In this paper, the weight is implicit from the context for the Laplace operator. If $w\equiv 1$ on all faces, then the underlying Laplacian is the combinatorial Laplace operator, denoted by $L_{i}(K)$ , as discussed in [8, 14]. If the weights of all facets are equal to $1$ , and $w$ satisfies the normalizing condition:

w(F)=\sum_{\bar{F}\in S_{i+1}(K):F\in\partial\bar{F}}w(\bar{F}),

for every $F\in S_{i}(K)$ which is not a facet of $K$ , then $w$ determines the normalized Laplace operator, denoted by $\Delta_{i}(K)$ , as analyzed in [21].

Horak and Jost [20, 21] give explicit formulas for $\mathcal{L}_{i}^{up}$ and $\mathcal{L}_{i}^{down}$ . Here we consider the matrix forms of the above operators. Let $D_{i}$ be the matrix of $\delta_{i}:C^{i}\to C^{i+1}$ under the basis consisting of elementary cochains. We have

(D_{i})_{[\bar{F}]^{*},[F]^{*}}=\operatorname{sgn}([F],\partial[\bar{F}]).

Let $W_{i}$ be the diagonal matrix consisting of the weight on $S_{i}(K)$ . The matrix $D_{i}^{*}$ of $\delta_{i}^{*}$ satisfies

(D_{i}^{*})_{[F]^{*},[\bar{F}]^{*}}=\frac{w(\bar{F})}{w(F)}\operatorname{sgn}([F],\partial[\bar{F}]).

D_{i}^{*}=W_{i}^{-1}D_{i}^{\top}W_{i+1},

where $W_{i}$ and $W_{i+1}$ are diagonal matrices such that $(W_{i}){[F]^{*},[F]^{*}}=w(F)$ and $(W_{i+1})_{[\bar{F}]^{*},[\bar{F}]^{*}}=w(\bar{F})$ . Hence

(2.1)

\mathcal{L}_{i}^{up}(K)=W_{i}^{-1}D_{i}^{\top}W_{i+1}D_{i},~{}\mathcal{L}_{i}^{down}(K)=D_{i-1}W_{i-1}^{-1}D_{i-1}^{\top}W_{i}.

2.2. Incidence-weighted and incidence-signed complex

Let $K$ be a complex, and let $F,\bar{F}\in K$ . If $F\in\partial\bar{F}$ , then $(F,\bar{F})$ is an incidence of $K$ . We will introduce the weights of incidences of $K$ , which is different from the weights of faces for the definition of Laplace operators. We first consider a simple case: the weights of incidences are from $\{-1,1\}$ .

Definition 2.2.

The incidence-signed complex is a pair $(K,s)$ , where $K$ is a complex, and $s:K\times K\to\{-1,0,1\}$ such that $s(F,\bar{F})\in\{-1,1\}$ if $F\in\partial\bar{F}$ , and $s(F,\bar{F})=0$ otherwise.

The signed boundary map $\partial_{i}^{s}:C_{i}(K,\mathbb{R})\to C_{i-1}(K,\mathbb{R})$ is defined to be

\partial_{i}^{s}[v_{0},\ldots,v_{i}]=\sum_{j=0}^{i}(-1)^{j}[v_{0},\ldots,\hat{v}_{j},\ldots,v_{i}]s(\{v_{0},\ldots,\hat{v}_{j},\ldots,v_{i}\},\{v_{0},\ldots,v_{i}\}).

The signed co-boundary map $\delta^{s}_{i}:C^{i}(K,\mathbb{R})\to C^{i+1}(K,\mathbb{R})$ is the conjugate of $\partial_{i+1}^{s}$ , namely, for all $f\in C^{i}$ ,

\delta^{s}_{i}f=f\partial_{i+1}^{s}.

The signed adjoint $(\delta_{i}^{s})^{*}:C^{i+1}(K,\mathbb{R})\to C^{i}(K,\mathbb{R})$ is the adjoint of $\delta_{i}^{s}$ satisfying

(\delta_{i}^{s}f_{1},f_{2})_{C^{i+1}}=(f_{1},(\delta^{s}_{i})^{*}f_{2})_{C^{i}}

for all $f_{1}\in C^{i},f_{2}\in C^{i+1}$ .

Definition 2.3.

Let $(K,s)$ be a signed complex.

(1) The $i$ -up Laplace operator of $(K,s)$ is defined to be $\mathcal{L}_{i}^{up}(K,s)=(\delta_{i}^{s})^{*}\delta_{i}^{s}$ .

(2) The $i$ -down Laplace operator of $(K,s)$ is defined to be $\mathcal{L}_{i}^{down}(K,s)=\delta_{i-1}^{s}(\delta_{i-1}^{s})^{*}$ .

(3) The $i$ -Laplace operator of $(K,s)$ is defined to be $\mathcal{L}(K,s)=\mathcal{L}_{i}^{up}(K,s)+\mathcal{L}_{i}^{down}(K,s)$ .

Let $D_{i}^{s}$ be the matrix of $\delta_{i}^{s}:C^{i}\to C^{i+1}$ under the basis consisting of elementary cochains. Then

(D_{i}^{s})_{[\bar{F}]^{*},[F]^{*}}=\operatorname{sgn}([F],\partial[\bar{F}])s(F,\bar{F}).

The matrix $(D_{i}^{s})^{*}$ of $(\delta_{i}^{s})^{*}$ satisfies

((D_{i}^{s})^{*})_{[F]^{*},[\bar{F}]^{*}}=\frac{w(\bar{F})}{w(F)}\operatorname{sgn}([F],\partial[\bar{F}])s(F,\bar{F}),

where $w$ is a weight function on the faces of $K$ . So

(D_{i}^{s})^{*}=W_{i}^{-1}(D_{i}^{s})^{\top}W_{i+1}.

Hence the matrix of $\mathcal{L}_{i}^{up}(K,s)$ is

(2.2)

\mathcal{L}_{i}^{up}(K,s)=W_{i}^{-1}(D_{i}^{s})^{\top}W_{i+1}D_{i}^{s},

and the matrix of $\mathcal{L}_{i}^{down}(K,s)$ is

\mathcal{L}_{i}^{down}(K,s)=D^{s}_{i-1}W_{i-1}^{-1}(D^{s}_{i-1})^{\top}W_{i}.

If $s\equiv 1$ , then $\mathcal{L}_{i}^{up}(K,s)=\mathcal{L}_{i}^{up}(K)$ and $\mathcal{L}_{i}^{down}(K,s)=\mathcal{L}_{i}^{down}(K).$ From this point of view, the signed complex $(K,s)$ is a generalization of the usual complex. If $s(F,\bar{F})=\operatorname{sgn}([F],\partial[\bar{F}])$ for all pairs $(F,\bar{F})$ with $F\in\partial\bar{F}$ , then $D_{i}^{s}=|D_{i}^{s}|$ , which is a nonnegative matrix, where $|A|:=[|a_{ij}|]$ if $A=[a_{ij}]$ . In this case, $\mathcal{L}_{i}^{up}(K,s)=|\mathcal{L}_{i}^{up}(K,s)|=|\mathcal{L}_{i}^{up}(K)|$ , and $\mathcal{L}_{i}^{down}(K,s)=|\mathcal{L}_{i}^{down}(K,s)|=|\mathcal{L}_{i}^{down}(K)|$ .

Let $|D_{i}|$ be the $i$ -th incidence matrix of $K$ with rows indexed by $S_{i+1}(K)$ and columns indexed by $S_{i}(K)$ , which is defined to be $|D_{i}|_{\bar{F},F}=1$ if $F\in\partial\bar{F}$ , and $|D_{i}|_{\bar{F},F}=0$ otherwise. Then

|\mathcal{L}_{i}^{up}(K)|=W_{i}^{-1}|D_{i}|^{\top}W_{i+1}|D_{i}|.

We call $|\mathcal{L}_{i}^{up}(K)|$ the $i$ -up signless Laplace operator of $K$ , denoted by $\mathcal{Q}_{i}^{up}(K)$ . Similarly, we have

|\mathcal{L}_{i}^{down}(K)|=|D_{i-1}|W_{i-1}^{-1}|D_{i-1}|^{\top}W_{i},

which is called the $i$ -down signless Laplace operator of $K$ , denoted by $\mathcal{Q}_{i}^{down}(K)$ .

Note that, if taking $W_{0}$ and $W_{1}$ both be identity matrix, then $\mathcal{Q}_{0}^{up}(K)$ is called the signless Laplacian of a graph or the $1$ -skeleton of $K$ [19], which is studied in [6] for the nonbipartiteness of a graph, and surveyed in [5].

In general, let the underlying field of the chain group and the cochain group of $K$ be the complex field $\mathbb{C}$ . We take the weight of each incidence of $K$ from $\mathbb{C}^{*}:=\mathbb{C}\backslash\{0\}$

Definition 2.4.

The incidence-weighted complex is a pair $(K,\omega)$ , where $K$ is a simpicial complex, and $\omega:K\times K\to\mathbb{C}$ such that $s(F,\bar{F})\in\mathbb{C}^{*}$ if $F\in\partial\bar{F}$ , and $s(F,\bar{F})=0$ otherwise.

By a similar discussion, the weighted boundary map $\partial_{i}^{\omega}:C_{i}(K,\mathbb{C})\to C_{i-1}(K,\mathbb{C})$ is defined to be

\partial_{i}^{\omega}[v_{0},\ldots,v_{i}]=\sum_{j=0}^{i}(-1)^{j}[v_{0},\ldots,\hat{v}_{j},\ldots,v_{i}]\omega(\{v_{0},\ldots,\hat{v}_{j},\ldots,v_{i}\},\{v_{0},\ldots,v_{i}\}).

We will have the $\delta_{i}^{\omega}$ , the conjugate of $\partial_{i}^{\omega}$ , and $(\delta_{i}^{\omega})^{*}$ , the adjoint of $\delta_{i}^{\omega}$ . Note that the inner product over $\mathbb{C}$ is defined as

(f,g)_{C^{i}}=\sum_{F\in S_{i}(K)}w(F)f([F])\overline{g([f])},

where, $w$ is a weight function on the faces of $K$ , $\overline{\alpha}$ denotes the conjugate of a complex number $\alpha$ .

Definition 2.5.

Let $(K,\omega)$ be weighted simplical complex.

(1) The $i$ -up Laplace operator of $(K,\omega)$ is defined to be $\mathcal{L}_{i}^{up}(K,\omega)=(\delta_{i}^{\omega})^{*}\delta_{i}^{\omega}$ .

(2) The $i$ -down Laplace operator of $(K,\omega)$ is $\mathcal{L}_{i}^{down}(K,\omega)=\delta_{i-1}^{\omega}(\delta_{i-1}^{\omega})^{*}$ .

(3) The $i$ -Laplace operator of $(K,\omega)$ is $\mathcal{L}_{i}(K,\omega)=\mathcal{L}_{i}^{up}(K,\omega)+\mathcal{L}_{i}^{down}(K,\omega)$ .

The matrix $D_{i}^{\omega}$ of $\delta_{i}^{\omega}$ is

(D_{i}^{\omega})_{[\bar{F}]^{*},[F]^{*}}=\operatorname{sgn}([F],\partial[\bar{F}])\omega(F,\bar{F}).

The matrix $(D_{i}^{\omega})^{*}$ of $(\delta_{i}^{\omega})^{*}$ satisfies

((D_{i}^{\omega})^{*})_{[F]^{*},[\bar{F}]^{*}}=\frac{w(\bar{F})}{w(F)}\operatorname{sgn}([F],\partial[\bar{F}])\overline{\omega(F,\bar{F})}.

Hence the matrix of $\mathcal{L}_{i}^{up}(K,\omega)$ is

(2.3)

\mathcal{L}_{i}^{up}(K,\omega)=W_{i}^{-1}(D_{i}^{\omega})^{\star}W_{i+1}D_{i}^{\omega},

and the matrix of $\mathcal{L}_{i}^{down}(K,s)$ is

\mathcal{L}_{i}^{down}(K,\omega)=D^{\omega}_{i-1}W_{i-1}^{-1}(D^{\omega}_{i-1})^{\star}W_{i},

where $D^{\star}$ denotes the conjugate transpose of a complex matrix $D$ to avoid the confusion of $*$ used for the adjoint operator.

3. Covering complexes

Definition 3.1.

Let $K,L$ be two complexes. A simplical map from $K$ to $L$ is a map $\phi:V(K)\to V(L)$ if whenever $\{v_{0},\ldots,v_{k}\}\in K$ , then $\{f(v_{0}),\ldots,f(v_{k})\}\in L$ . We often use the notation $\phi:K\to L$ .

Definition 3.2.

[28] Let $K,L$ be complexes. A pair $(K,\phi)$ is called a covering complex of $L$ if the following conditions hold.

(1) $K$ is a connected complex;

(2) $\phi:K\to L$ is a simplicial map;

(3) for each $G\in L$ , $\phi^{-1}(G)$ is a union of pairwise disjoint simplices, namely, $\phi^{-1}(G)=\cup_{i}F_{i}$ such that $\phi|_{F_{i}}:F_{i}\to G$ is a bijection for each $i$ .

In Definition 3.2, the map $\phi$ is called a covering map, $K$ is called a covering complex of $L$ , and $L$ is called the underlying complex of the covering. By definition, $\phi(F)\in S_{i}(L)$ for every $F\in S_{i}(K)$ . As noted by Horak and Jost [20], the covering complexes are an inaccurate discretization of covering spaces (continuous setting), since it does not contain a discrete analogue of the homeomorphic neighborhood requirement of covering topological spaces. They provide the definition of a strong covering, which accurately discretizes the notion of covering from the continuous setting.

Definition 3.3.

[21] A covering map $\phi:K\to L$ is a strong covering if for every $G\in S_{i}(L)$ which is face of $\bar{G}\in S_{i+1}(L)$ , then for each $F\in\phi^{-1}(G)$ , there exists $\bar{F}\in S_{i+1}(K)$ such that $F\in\partial\bar{F}$ and $\phi(\bar{F})=\bar{G}$ .

Lemma 3.4.

Let $\phi:K\to L$ be a strong covering. Then for every $G\in S_{i}(L)$ and every $F\in\phi^{-1}(G)$ , there exists a bijection also denoted by $\phi$ such that

\phi:\{\bar{F}\in S_{i+1}(K):F\in\partial\bar{F}\}\to\{\bar{G}\in S_{i+1}(L):G\in\partial\bar{G}\},\bar{F}\mapsto\phi(\bar{F}).

Proof.

Surely $\phi$ is a map as $G=\phi(F)\subset\phi(\bar{F})$ or $G\in\partial\phi(\bar{F})$ . Also $\phi$ is an injective map; otherwise, if $\phi(\bar{F})=\phi(\bar{F}^{\prime}):=\bar{G}$ , then $\phi^{-1}(\bar{G})$ would contain $\bar{F}$ and $\bar{F}^{\prime}$ with $\bar{F}\cap\bar{F}^{\prime}=F$ , a contradiction to Definition 3.2 (3). Finally $\phi$ is a surjective map by Definition 3.3. ∎

Lemma 3.5.

[21] Let $\phi:K\to L$ be a strong covering. There exists a constant $k\in\mathbb{Z}^{+}$ such that for each $G\in S_{i}(L)$ and each $i=0,1,\ldots,\text{dim}K$ ,

|\{F\in S_{i}(K):F\in\phi^{-1}(G)\}|=k.

The quantity $k$ in Lemma 3.5 is called the degree of the covering, and $K$ is called a $k$ -fold covering of $L$ in this case.

Now we return to the graph coverings. Let $G$ be a simple graph. The vertex set of $G$ is denoted by $V(G)$ and edge set is denoted by $E(G)$ . The neighborhood of a vertex $v\in V(G)$ is denoted and defined by $N_{G}(v)=\{u:\{u,v\}\in E(G)\}$ .

Definition 3.6.

Let $\bar{G}$ and $G$ be simple graphs, where $G$ is connected. A surjective map $\phi:V(\bar{G})\to V(G)$ is called a covering map if

(1) $\phi$ is a homomorphism, namely $\phi(e)\in E(G)$ for each $e\in E(\bar{G})$ ,

(2) for each vertex $v\in V(G)$ and each vertex $\bar{v}\in\phi^{-1}(v)$ , $\phi|_{N_{\bar{G}}(\bar{v})}:N_{\bar{G}}(\bar{v})\to N_{G}(v)$ is a bijection.

The above definition could be found in [1, 30]. The covering of a graph was is exactly the strong covering of the $1$ -skeleton of a complex if we require $\bar{G}$ is connected. Gross and Tucker [16] established a relationship between $k$ -fold coverings and derived graphs. We need some preparation. Let $D$ be digraph possibly with multiple arcs, and let $\mathbb{S}_{k}$ be the symmetric group on the set $[k]$ . Let $\psi:E(D)\to\mathbb{S}_{k}$ which assigns a permutation to each arc of $D$ . The pair $(D,\psi)$ is called a permutation voltage digraph. A derived digraph $D^{\psi}$ associated with $(D,\psi)$ is a digraph with vertex set $V(D)\times[k]$ such that $((u,i),(v,j))$ is an arc of $D^{\psi}$ if and only if $(u,v)\in E(D)$ and $i=\psi(u,v)(j)$ . For a simple graph $G$ , let $\overleftrightarrow{G}$ denote the symmetric digraph obtained from $G$ by replacing each edge $\{u,v\}$ by two arcs with opposite directions, written as $e=(u,v)$ and $e^{-1}:=(v,u)$ respectively. Let $\psi:E(\overleftrightarrow{G})\to\mathbb{S}_{k}$ be a permutation assignment of $\overleftrightarrow{G}$ which holds that $\psi(e)^{-1}=\psi(e^{-1})$ for each arc $e$ of $\overleftrightarrow{G}$ . The derived digraph $\overleftrightarrow{G}^{\psi}$ , simply written as $G^{\psi}$ , has symmetric arcs by definition, and is considered as a simple graph.

Lemma 3.7.

[16] Let $G$ be a connected graph and let $\bar{G}$ be a $k$ -cover of $G$ . Then there exists an assignment $\psi$ of permutations in $\mathbb{S}_{k}$ on $G$ such that $G^{\psi}$ is isomorphic to $\bar{G}$ .

Remark 3.8.

In Lemma 3.7, if $\eta:V(G^{\psi})\to V(\bar{G})$ is the isomorphism, $\phi:V(\bar{G})\to V(G)$ is the covering map, and $p:V(G^{\psi})\to V(G)$ is the natural projection such that $p(v,i)=v$ for all $i\in[k]$ , then from the proof of the Lemma 3.7 (see [16, Theorem 2]),

\phi\eta=p,

or equivalently, for all $v\in V(G)$ and $i\in[k]$ ,

\phi\eta(v,i)=v.

Let $K$ be a complex. The $i$ -incidence graph $B_{i}(K)$ is a bipartite graph with vertex set $S_{i}(K)\cup S_{i+1}(K)$ such that $\{F,\bar{F}\}$ is an edge if and only if $F\in\partial\bar{F}$ .

Lemma 3.9.

Let $\phi:K\to L$ be a $k$ -fold covering. Then $\phi$ induces a $k$ -fold covering from $B_{i}(K)$ to $B_{i}(L)$ , and there exists a $\psi:E(B_{i}(L))\to\mathbb{S}_{k}$ such that $B_{i}(L)^{\psi}$ is isomorphic to $B_{i}(K)$ by a map which sends $S_{i}(L)\times[k]$ to $S_{i}(K)$ , $S_{i+1}(L)\times[k]$ to $S_{i+1}(K)$

Proof.

By the definition of strong covering, $\phi$ maps $S_{i}(K)$ to $S_{i}(L)$ , and $S_{i+1}(K)$ to $S_{i+1}(L)$ . So $\phi$ induces a surjective $k$ to $1$ map (also denoted by $\phi$ ) from the vertex set of $B_{i}(K)$ to that of $B_{i}(L)$ . If $F\in\partial\bar{F}$ , then $\phi(F)\in\partial\phi(\bar{F})$ . So $\phi$ maps edges of $B_{i}(K)$ to those of $B_{i}(L)$ . By Lemma 3.4, for each $G\in S_{i}(L)$ and $F\in\phi^{-1}(G)$ , $\phi|_{N_{B_{i}(K)}(F)}:N_{B_{i}(K)}(F)\to N_{B_{i}(L)}(G)$ is bijective. For each $\bar{G}\in S_{i+1}(L)$ and $\bar{F}\in\phi^{-1}(\bar{G})$ , noting that $N_{B_{i}(K)}(\bar{F})=\partial\bar{F}$ and $N_{B_{i}(L)}(\bar{G})=\partial\bar{G}$ , $\phi|_{N_{B_{i}(K)}(\bar{F})}:N_{B_{i}(K)}(\bar{F})\to N_{B_{i}(L)}(\bar{G})$ is also bijective, as $\phi|_{\bar{F}}:\bar{F}\to\bar{G}$ is bijective. So $\phi$ induces a $k$ -fold covering from $B_{i}(K)$ to $B_{i}(L)$ .

By Lemma 3.7, there exists a $\psi:E(B_{i}(L))\to\mathbb{S}_{k}$ such that $B_{i}(L)^{\psi}$ is isomorphic to $B_{i}(K)$ . Let $\eta:B_{i}(L)^{\psi}\to B_{i}(K)$ be the isomorphism. For any $(F,i)\in S_{i}(L)\times[k]$ , $\eta(F,i)\in S_{i}(K)$ ; otherwise, if $\eta(F,i)\in S_{i+1}(K)$ , and then $\phi\eta(F,i)\in S_{i+1}(L)$ , a contradiction to Remark 3.8 as $\phi\eta(F,i)=p(F,i)=F\in S_{i}(L)$ . So $\eta$ sends $S_{i}(L)\times[k]$ to $S_{i}(K)$ , and $S_{i+1}(L)\times[k]$ to $S_{i+1}(K)$ by a similar discussion. ∎

Example 3.10.

Let $K,L$ be the complexes in Fig. 3.1, where each triangle represents a $2$ -simplex. It is easy to see $K$ is a $2$ -fold covering of $L$ .

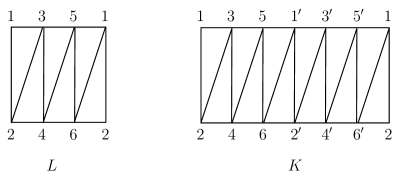
Refer to caption — Figure 3.1. A complex $L$ and its $2$ -fold covering $K$

The $1$ -incidence graph $B_{1}(L)$ and $B_{1}(K)$ are listed in Fig. 3.2 and Fig. 3.3 respectively, where an edge $\{a,b\}$ is simply written as $ab$ , and an face $\{a,b,c\}$ is written as $abc$ .

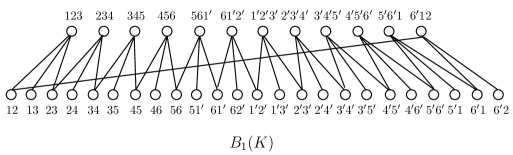
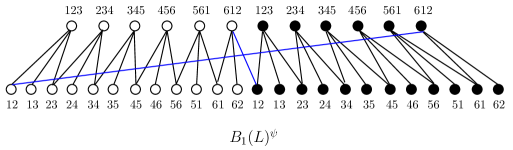
Define a permutation assignment $\psi:E(B_{1}(L))\to\mathbb{S}_{2}$ such that $\psi(12,612)=(12)$ (see the blue edge in Fig. 3.2) and $\phi(F,\bar{F})=1$ for all other incidences $(F,\bar{F})$ with $F\in\partial\bar{F}$ . Then the derived graph $B_{1}(L)^{\psi}$ is listed in Fig. 3.4, where a vertex $abc$ or $ab$ drawn with hollow circle represents the vertex $(abc,1)$ or $(ab,1)$ , and a vertex $def$ or $de$ drawn with solid circle represents the vertex $(def,2)$ or $(de,2)$ . It is easily seen there exists an isomorphism $\eta:B_{1}(L)^{\psi}\to B_{1}(K)$ which sends $S_{1}(L)\times\{1,2\}$ to $S_{1}(K)$ and $S_{2}(L)\times\{1,2\}$ to $S_{2}(K)$ .

4. The spectrum of covering complex

Let $\phi:K\to L$ be a $k$ -fold covering. Let $F,\bar{F}\in K$ with $F\in\partial\bar{F}$ and $G=\phi(F),\bar{G}=\phi(\bar{F})$ . By Formula (3.5) in [21],

(4.1)

\operatorname{sgn}([G],\partial[\bar{G}])=\operatorname{sgn}([F],\partial[\bar{F}])\operatorname{sgn}([F],[G])\operatorname{sgn}([\bar{F}],[\bar{G}]),

where, if $[F]=[v_{0},\ldots,v_{i}]$ , then $\operatorname{sgn}([F],[G])=1$ if $[\phi(v_{0}),\ldots,\phi(v_{i})]$ is positively oriented, and $\operatorname{sgn}([F],[G])=-1$ otherwise.

By Lemma 3.9, $B_{i}(K)$ is a $k$ -fold covering of $B_{i}(L)$ , and there exists a permutation assignment $\psi$ on $B_{i}(L)$ such that $B_{i}(L)^{\psi}$ is isomorphic to $B_{i}(K)$ via a map $\eta$ by sending $S_{i}(L)\times[k]$ to $S_{i}(K)$ and $S_{i+1}(L)\times[k]$ to $S_{i+1}(K)$ .

Recall that $\mathcal{L}_{i}^{up}(K)=W_{i}(K)^{-1}D_{i}(K)^{\top}W_{i+1}(K)D_{i}(K)$ , where

D_{i}(K)_{[\bar{F}]^{*},[F]^{*}}=\operatorname{sgn}([F],\partial[\bar{F}]),W_{i}(K)_{[F]^{*},[F]^{*}}=w(F),W_{i+1}(K)_{[\bar{F}]^{*},[\bar{F}]^{*}}=w(\bar{F}),

for $F\in S_{i}(K)$ and $\bar{F}\in S_{i+1}(K)$ . By the isomorphism $\eta$ , let $\eta^{-1}(\bar{F})=(\bar{G},i)$ and $\eta^{-1}(F)=(G,j)$ . We now use $(G,j)$ and $(\bar{G},i)$ to label the rows or columns of $D_{i}(K),W_{i}(K)$ and $W_{i+1}(K)$ corresponding to $[F]^{*}$ and $[\bar{F}]^{*}$ respectively, that is,

(4.2)

\begin{split}&D_{i}(K)_{(\bar{G},i),(G,j)}=\operatorname{sgn}([\eta(G,j)],\partial[\eta(\bar{G},i)]),\\ &W_{i}(K)_{(G,j),(G,j)}=w(\eta(G,j)),W_{i+1}(K)_{(\bar{G},i),(\bar{G},i)}=w(\eta(\bar{G},i)).\end{split}

Note that $\eta(G,j)\in\partial\eta(\bar{G},i)$ , or equivalently $\{\eta(G,j),\eta(\bar{G},i)\}\in E(B_{i}(K))$ if and only if $\{(G,j),(\bar{G},i)\}\in E(B_{i}(L)^{\psi})$ , or equivalently $G\in\partial\bar{G}$ and $j=\psi(G,\bar{G})i$ by the definition of derived graph.

As $\phi\eta=p$ by Remark 3.8,

\phi\eta(\bar{G},i)=p(\bar{G},i)=\bar{G},~{}\phi\eta({G},j)=p({G},j)=G.

So, by Eq. (4.1), we have

(4.3)

\begin{split}\operatorname{sgn}([\eta(G,j)],\partial[\eta(\bar{G},i)])&=\operatorname{sgn}([\phi\eta(G,j)],\partial[\phi\eta(\bar{G},i)])\operatorname{sgn}([\eta(G,j)],[\phi\eta(G,j)])\operatorname{sgn}([\eta(\bar{G},i)],[\phi\eta(\bar{G},i)])\\ &=\operatorname{sgn}([G],\partial[\bar{G}])\operatorname{sgn}([\eta(G,j)],[G])\operatorname{sgn}([\eta(\bar{G},i)],[\bar{G}]).\end{split}

Let $\Lambda_{i+1}(L)^{\eta}$ be the diagonal matrix with rows indexed by $S_{i+1}(L)\times[k]$ such that

(4.4)

\Lambda_{i+1}(L)^{\eta}_{(\bar{G},i),(\bar{G},i)}=\operatorname{sgn}([\eta(\bar{G},i)],[\bar{G}]),

and $\Lambda_{i}(L)^{\eta}$ the diagonal matrix with rows indexed by $S_{i}(L)\times[k]$ such that

(4.5)

\Lambda_{i}(L)^{\eta}_{(G,i),(G,i)}=\operatorname{sgn}([\eta(G,i)],[G]).

Let $D_{i}(L)^{\psi}$ be the matrix with rows indexed by $S_{i+1}(L)\times[k]$ and columns indexed by $S_{i}(L)\times[k]$ such that

(4.6)

D_{i}(L)^{\psi}_{(\bar{G},i),(G,j)}=\left\{\begin{array}[]{ll}\operatorname{sgn}([G],\partial[\bar{G}]),&\mbox{if~{}}G\in\partial\bar{G},i=\psi(\bar{G},G)j,\\ 0,&\mbox{else}.\end{array}\right.

So by (4.2) and (4.3), we have

(4.7)

D_{i}(K)=\Lambda_{i+1}(L)^{\eta}D_{i}(L)^{\psi}\Lambda_{i}(L)^{\eta}.

We summarize the above the discussions into the following result.

Lemma 4.1.

Let $\phi:K\to L$ be a $k$ -fold covering map, and let $\psi:E(B_{i}(L)\to\mathbb{S}_{k}$ be the permutation assignment such that $\eta:B_{i}(L)^{\psi}\to B_{i}(K)$ is an isomorphism. Then

D_{i}(K)=\Lambda_{i+1}(L)^{\eta}D_{i}(L)^{\psi}\Lambda_{i}(L)^{\eta},

where $\Lambda_{i+1}(L)^{\eta}$ , $\Lambda_{i}(L)^{\eta}$ and $D_{i}(L)^{\psi}$ are defined in (4.4), (4.5) and (4.6), respectively.

Next we will give a decomposition of $D_{i}(L)^{\psi}$ , where $\psi:E(B_{i}(L))\to\mathbb{S}_{k}$ . Let

(4.8)

\Psi_{i}=\langle\psi(G,\bar{G}):G\in S_{i}(L),\bar{G}\in S_{i+1}(L),G\in\partial\bar{G}\rangle,

the subgroup of $\mathbb{S}_{k}$ generalized by the permutations assignment by $\psi$ . For each $g\in\Psi_{i}$ , define $D^{g}_{i}(L)=(D^{g}_{\bar{G},G})$ such that

(4.9)

D^{g}_{\bar{G},G}=\left\{\begin{array}[]{ll}\operatorname{sgn}([G],\partial[\bar{G}]),&\mbox{if~{}}G\in\partial\bar{G},\psi(G,\bar{G})=g,\\ 0,&\mbox{else}.\end{array}\right.

Then

(4.10)

D_{i}(L)=\sum_{g\in\Psi}D_{i}^{g}(L).

The permutation representation $\varrho$ of $\Psi$ maps each $g\in\Psi$ to a permutation matrix, namely

\varrho:\Psi\to GL_{k}(\mathbb{C}),g\mapsto P^{g}=(p_{ij}^{g}),

where $p_{ij}^{g}=1$ if $i=g(j)$ and $p_{ij}^{g}=0$ else. So

(4.11)

D_{i}(L)^{\psi}=\sum_{g\in\Psi_{i}}D_{i}^{g}(L)\otimes P^{g}.

By the representation of symmetric group, let

\varrho=\varrho_{1}\oplus\varrho_{2}\oplus\cdots\oplus\rho_{t}

be the decomposition of $\varrho$ into the sum of irreducible sub-representation, where $\varrho_{1}=1$ is the identity representation of degree one. So, there exists an invertible matrix $T$ such that for all $g\in\Psi$ ,

(4.12)

T^{-1}P^{g}T=I_{1}\oplus\varrho_{2}(g)\oplus\cdots\oplus\rho_{t}(g),

where $I_{1}$ is the identity matrix of order $1$ corresponding to $\varrho_{1}$ , and $\varrho_{2}(g),\ldots,\varrho_{t}(g)$ are the matrices corresponding to $\varrho_{2},\ldots,\varrho_{t}$ of $\varrho$ respectively.

Theorem 4.2.

Let $\phi:K\to L$ be a $k$ -fold covering map, and let $\psi:E(B_{i}(L)\to\mathbb{S}_{k}$ be the permutation assignment such that $\eta:B_{i}(L)^{\psi}\to B_{i}(K)$ is an isomorphism. Let $\Psi_{i}$ be the group defined in (4.8) whose permutation representation $\varrho$ has a decomposition (4.12) for some invertible matrix $T$ . Suppose that $w_{K}(F)=w_{L}(\phi(F))$ for all $F\in K$ . Then

(I\otimes T)^{-1}\Lambda_{i}(L)^{\eta}\mathcal{L}_{i}^{up}(K)(\Lambda_{i}(L)^{\eta})^{-1}(I\otimes T)\\ =\mathcal{L}_{i}^{up}(L)\oplus\oplus_{j=2}^{t}\left(\sum_{g\in\Psi_{i}}(W_{i}(L)^{-1}(D_{i}^{g}(L))^{\top})\otimes\varrho_{j}(g^{-1})\right)\left(\sum_{g\in\Psi_{i}}(W_{i+1}(L)D_{i}^{g}(L))\otimes\varrho_{j}(g)\right),

where $\Lambda_{i}(L)^{\eta}$ is defined in (4.5).

Proof.

By (4.2) and Lemma 4.1,

	$\displaystyle\mathcal{L}^{u}_{i}(K)$	$\displaystyle=W_{i}(K)^{-1}D_{i}(K)^{\top}W_{i+1}(K)D_{i}(K)$
		$\displaystyle=W_{i}(K)^{-1}(\Lambda_{i}(L)^{\eta})^{\top}(D_{i}(L)^{\psi})^{\top}(\Lambda_{i+1}(L)^{\eta})^{\top}W_{i+1}(K)\Lambda_{i+1}(L)^{\eta}D_{i}(L)^{\psi}\Lambda_{i}(L)^{\eta}.$

So, $\Lambda_{i}(L)^{\eta}\mathcal{L}^{up}_{i}(K)(\Lambda_{i}(L)^{\eta})^{-1}$ has the following form:

\tilde{\mathcal{L}}^{up}_{i}(K):=\Lambda_{i}(L)^{\eta}W_{i}(K)^{-1}(\Lambda_{i}(L)^{\psi})^{\top}(D_{i}(L)^{\psi})^{\top}(\Lambda_{i+1}(L)^{\eta})^{\top}W_{i+1}(K)\Lambda_{i+1}(L)^{\eta}D_{i}(L)^{\eta}.

As $\Lambda_{i}(L)^{\eta}$ and $\Lambda_{i+1}(L)^{\eta}$ are both signature matrices,

\tilde{\mathcal{L}}_{i}^{up}(K)=W_{i}(K)^{-1}(D_{i}(L)^{\psi})^{\top}W_{i+1}(K)D_{i}(L)^{\psi}.

By (4.2), the assumption on weight and Remark 3.8,

W_{i}(K)_{(G,i),(G,i)}=w(\eta(G,i))=w(\phi\eta(G,i))=w(G),

and similarly $W_{i+1}(K)_{(\bar{G},i),(\bar{G},i)}=w(\bar{G})$ . So

(4.13)

W_{i}(K)=W_{i}(L)\otimes I_{k},~{}W_{i+1}(K)=W_{i+1}(L)\otimes I_{k}.

So, by Eq. (4.13) and Eq. (4.11),

	$\displaystyle\tilde{\mathcal{L}}_{i}^{up}(K)$	$\displaystyle=(W_{i}(L)^{-1}\otimes I_{k})\left(\sum_{g\in\Psi_{i}}D_{i}^{g}(L)^{\top}\otimes P_{g}^{\top}\right)(W_{i+1}(L)\otimes I_{k})\left(\sum_{g\in\Psi_{i}}D_{i}^{g}(L)\otimes P_{g}\right)$
		$\displaystyle=\sum_{g,g^{\prime}\in\Psi_{i}}\left(W_{i}(L)^{-1}D_{i}^{g}(L)^{\top}W_{i+1}(L)D_{i}^{g^{\prime}}(L)\right)\otimes\left((P^{g})^{\top}P^{g^{\prime}}\right).$

By (4.12), noting that $(P^{g})^{\top}=P^{g^{-1}}$ , we have

	$\displaystyle(I\otimes T)^{-1}\tilde{\mathcal{L}}^{up}(K)(I\otimes T)$	$\displaystyle=\sum_{g,g^{\prime}\in\Psi_{i}}\left(W_{i}(L)^{-1}D_{i}^{g}(L)^{\top}W_{i+1}(L)D_{i}^{g^{\prime}}(L)\right)\otimes\left(T^{-1}(P^{g})^{\top}P^{g^{\prime}}T\right)$
		$\displaystyle=\sum_{g,g^{\prime}\in\Psi_{i}}\left(W_{i}(L)^{-1}D_{i}^{g}(L)^{\top}W_{i+1}(L)D_{i}^{g^{\prime}}(L)\right)\otimes\left(I_{1}\oplus\oplus_{j=2}^{t}\varrho_{i}(g^{-1})\varrho_{i}(g^{\prime})\right)$
		$\displaystyle=\sum_{g,g^{\prime}\in\Psi_{i}}\left(W_{i}(L)^{-1}D_{i}^{g}(L)^{\top}W_{i+1}(L)D_{i}^{g^{\prime}}(L)\right)$
		$\displaystyle~{}~{}~{}\oplus\sum_{g,g^{\prime}\in\Psi_{i}}\left(W_{i}(L)^{-1}D_{i}^{g}(L)^{\top}W_{i+1}(L)D_{i}^{g^{\prime}}(L)\right)\otimes\left(\oplus_{j=2}^{t}\varrho_{j}(g^{-1})\varrho_{j}(g^{\prime})\right)$
		$\displaystyle=W_{i}(L)^{-1}\left(\sum_{g\in\Psi_{i}}D_{i}^{g}(L)\right)^{\top}W_{i+1}(L)\left(\sum_{g\in\Psi}D_{i}^{g}(L)\right)$
		$\displaystyle~{}~{}~{}\oplus\oplus_{j=2}^{t}\sum_{g,g^{\prime}\in\Psi_{i}}\left(W_{i}(L)^{-1}D_{i}^{g}(L)^{\top}W_{i+1}(L)D_{i}^{g^{\prime}}(L)\right)\otimes\varrho_{j}(g^{-1})\varrho_{j}(g^{\prime}).$

By Eq. (4.10), we have

(4.14)

\begin{split}(I\otimes T)^{-1}\tilde{\mathcal{L}}^{up}(K)(I\otimes T)&=W_{i}(L)^{-1}D_{i}(L)^{\top}W_{i+1}(L)D_{i}(L)\\ &~{}~{}~{}\oplus\oplus_{j=2}^{t}\left(\sum_{g\in\Psi_{i}}(W_{i}(L)^{-1}D_{i}^{g}(L)^{\top})\otimes\varrho_{j}(g^{-1})\right)\!\!\!\left(\sum_{g\in\Psi_{i}}(W_{i+1}(L)D_{i}^{g}(L))\otimes\varrho_{j}(g)\right)\\ &=\mathcal{L}_{i}^{up}(\mathcal{L})\oplus\oplus_{j=2}^{t}\!\left(\sum_{g\in\Psi_{i}}(W_{i}(L)^{-1}D_{i}^{g}(L)^{\top})\otimes\varrho_{j}(g^{-1})\right)\!\!\!\left(\sum_{g\in\Psi_{i}}(W_{i+1}(L)D_{i}^{g}(L))\otimes\varrho_{j}(g)\!\right).\end{split}

The result follows. ∎

Corollary 4.3.

[21] Let $\phi:K\to L$ be a $k$ -fold covering map. Then

\text{~{}Spec}L_{i}^{up}(L)\subset\text{~{}Spec}L_{i}^{up}(K),~{}\text{~{}Spec}\Delta_{i}^{up}(L)\subset\text{~{}Spec}\Delta_{i}^{up}(K).

Proof.

For the combinatorial Laplace operators $L_{i}^{up}(L)$ and $L_{i}^{up}(K)$ , $w(F)=w_{L}(\phi(F))=1$ for each $F\in K$ . For the normalized Laplace operators $\Delta_{i}^{up}(L)$ and $\Delta_{i}^{up}(K)$ , by Lemma 3.4, for each $F\in K$ , if $F$ is a facet, so is $\phi(F)$ , and $w(F)=w(\phi(F))=1$ ; otherwise, we still have $w(F)=w(\phi(F))$ by induction. So the result follows by Theorem 4.2. ∎

Theorem 4.4.

Let $\phi:K\to L$ be a $2$ -fold covering map. Suppose that $w_{K}(F)=w_{L}(\phi(F))$ for all $F\in S_{i}(K)\cup S_{i+1}(K)$ . Then

\text{~{}Spec}\mathcal{L}_{i}^{up}(K))=\text{~{}Spec}\mathcal{L}_{i}^{up}(L)\cup\text{~{}Spec}\mathcal{L}_{i}^{up}(L,s),

where $s(F,\bar{F})=\operatorname{sgn}\psi(F,\bar{F})$ for $(F,\bar{F})\in S_{i}(L)\times S_{i+1}(L)$ such that $F\in\partial\bar{F}$ , and $\psi:E(B_{i}(L))\to\mathbb{S}_{2}$ such that $B_{i}(L)^{\psi}$ is isomorphic to $B_{i}(K)$ .

Proof.

By Lemma 3.9, there exists a permutation assignment $\psi:E(B_{i}(L))\to\mathbb{S}_{2}$ such that $B_{i}(L)^{\psi}$ is isomorphic to $B_{i}(K)$ . Let $\Psi_{i}$ be defined as in (4.8). As $K$ is connected, so is $B_{i}(K)$ or $B_{i}(L)^{\psi}$ . If $\Psi_{i}=1$ , by definition $B_{i}(L)^{\psi}$ is a union of two disjoint copies of $B_{i}(L)$ , a contradiction. So, $\Psi=\mathbb{S}_{2}$ .

It is known $\mathbb{S}_{2}$ has two irreducible representations, namely there exists an invertible matrix $T$ such that for each $g\in\mathbb{S}_{2}$ ,

T^{-1}P^{g}T=I_{1}\oplus\operatorname{sgn}g,

where $\operatorname{sgn}g$ is called the sign representation. So, by Eq. (4.14), noting that $\operatorname{sgn}g^{-1}=\operatorname{sgn}g$ ,

(I\otimes T)^{-1}\tilde{\mathcal{L}}^{up}(K)(I\otimes T)=\mathcal{L}_{i}^{u}(L)\oplus W_{i}(L)^{-1}\left(\sum_{g\in\Psi_{i}}D_{i}^{g}(L)\operatorname{sgn}g\right)^{\top}W_{i+1}(L)\left(\sum_{g\in\Psi_{i}}D_{i}^{g}(L)\operatorname{sgn}g\right).

If we define a incidence-signed complex $(L,s)$ such that $s(F,\bar{F})=\operatorname{sgn}\psi(F,\bar{F})$ for $F\in\partial\bar{F}$ , then the matrix of $\delta_{i}^{s}$ on $(L,s)$ is

D_{i}^{s}(L)=\sum_{g\in\Psi_{i}}D_{i}^{g}(L)\operatorname{sgn}g.

So, by Eq. (2.2),

(I\otimes T)^{-1}\tilde{\mathcal{L}}^{up}(K)(I\otimes T)=\mathcal{L}_{i}^{up}(L)\oplus W_{i}(L)^{-1}(D_{i}^{s}(L))^{\top}W_{i+1}(L)D_{i}^{s}(L)=\mathcal{L}_{i}^{up}(L)\oplus\mathcal{L}_{i}^{up}(L,s).

The result follows. ∎

Example 4.5.

Let $K,L$ be the complexes in Fig. 3.1. The spectrum of $L_{1}^{up}(L)$ is

\text{~{}Spec}L_{1}^{up}(L)=\{5,4^{(2)},2^{(2)},1,0^{(6)}\},

and the spectrum of $L_{1}^{up}(K)$ is

\text{~{}Spec}L_{1}^{up}(K)=\{5,4^{(2)},3^{(2)},2^{(2)},1,(3+\sqrt{3})^{(2)},(3-\sqrt{3})^{(2)},0^{(12)}\},

where $\lambda^{(m)}$ means $\lambda$ as an eigenvalue with multiplicity $m$ .

By Example 3.10, letting $\psi:E(B_{1}(L))\to\mathbb{S}_{2}$ such that $\psi(12,612)=(12)$ and $\phi(F,\bar{F})=1$ for all other incidences $(F,\bar{F})$ with $F\in\partial\bar{F}$ , then $B_{1}(L)^{\psi}$ is isomorphic to $B_{1}(K)$ . Define a incidence-signed complex $(L,s)$ such that $s(F,\bar{F})=\operatorname{sgn}\psi(F,\bar{F})$ for each incidence $(F,\bar{F})$ with $F\in\partial\bar{F}$ . So we have $s(12,612)=-1$ and $s(F,\bar{F})=1$ for other incidences $(F,\bar{F})$ . The matrix $D_{1}^{s}$ of $\delta_{1}^{s}$ on $(L,s)$ is obtained from the matrix $D_{1}$ of $\delta_{1}$ on $L$ only by replacing the $([612],[12])$ -entry $1$ by $-1$ . The spectrum of $L_{1}^{up}(L,s)$ is

\text{~{}Spec}L_{1}^{up}(L,s)=\{3^{(2)},(3+\sqrt{3})^{(2)},(3-\sqrt{3})^{(2)},0^{(6)}\}.

So,

\text{~{}Spec}L_{1}^{up}(K)=\text{~{}Spec}L_{1}^{up}(L)\cup\text{~{}Spec}L_{1}^{up}(L,s).

Finally, we consider the case when $\Psi_{i}$ defined in (4.8) is an Abelian group.

Theorem 4.6.

Let $\phi:K\to L$ be a $k$ -fold covering map, and let $\psi:E(B_{i}(L)\to\mathbb{S}_{k}$ be the permutation assignment such that $B_{i}(L)^{\psi}$ is isomorphic to $B_{i}(K)$ . Suppose that $w_{K}(F)=w_{L}(\phi(F))$ for all $F\in S_{i}(K)\cup S_{i+1}(K)$ . Let $\Psi_{i}$ be the group defined in (4.8) which is an Abelian group. Then $\Psi_{i}$ has exactly $k$ elements with the decomposition of irreducible sub-representations of degree one:

(4.15)

\varrho=I_{1}\oplus\varrho_{2}\oplus\cdots\oplus\varrho_{k},

and

\text{~{}Spec}\mathcal{L}_{i}^{up}(K))=\text{~{}Spec}\mathcal{L}_{i}^{up}(L)\cup\cup_{j=2}^{k}\text{~{}Spec}\mathcal{L}_{i}^{up}(L,\varrho_{j}),

where $\varrho_{j}(F,\bar{F})=\varrho_{j}(\psi(F,\bar{F})$ for $(F,\bar{F})\in S_{i}(L)\times S_{i+1}(L)$ such that $F\in\partial\bar{F}$ .

Proof.

As $K$ is connected, so is $B_{i}(K)$ or $B_{i}(L)^{\psi}$ . By Theorem 3.4 of [29], $\Psi_{i}$ is transitive on $[k]$ by the permutation action. If there exists $g\in\Psi_{i}$ and $j\in[k]$ such that $g(j)=j$ , then for any $\ell\in[k]$ , as $\Psi_{i}$ is transitive, $\ell=h(j)$ for some $h\in\Psi_{i}$ . As $\Psi_{i}$ is Abelian,

g(\ell)=gh(j)=hg(j)=h(j)=\ell,

which implies that $g=1$ . So, $\Psi_{i}$ faithfully acts on $[k]$ . By the orbit-stabilizer lemma, $\Psi_{i}$ has the order of $k$ . As the irreducible representations of an Abelian group all have degree one, we get the decomposition (4.15) immediately. Also, there exists an invertible matrix $T$ such that

T^{-1}P_{g}T=I_{1}\oplus\varrho_{2}(g)\oplus\cdots\oplus\varrho_{t}(g).

By (4.14), noting that $\varrho_{j}$ are all of degree one, we have

	$\displaystyle(I\otimes T)^{-1}\tilde{\mathcal{L}}^{up}(K)(I\otimes T)$	$\displaystyle=\mathcal{L}_{i}^{up}(\mathcal{L})\oplus\oplus_{j=2}^{k}\left(\sum_{g\in\Psi_{i}}W_{i}(L)^{-1}D_{i}^{g}(L)^{\top}\varrho_{j}(g^{-1})\right)\left(\sum_{g\in\Psi_{i}}W_{i+1}(L)D_{i}^{g}(L)\varrho_{j}(g)\right)$
		$\displaystyle=\mathcal{L}_{i}^{up}(\mathcal{L})\oplus\oplus_{j=2}^{t}W_{i}(L)^{-1}\left(\sum_{g\in\Psi_{i}}D_{i}^{g}(L)^{\top}\overline{\varrho_{j}(g)}\right)W_{i+1}(L)\left(\sum_{g\in\Psi_{i}}D_{i}^{g}(L)\varrho_{j}(g)\right)$
		$\displaystyle=\mathcal{L}_{i}^{up}(\mathcal{L})\oplus\oplus_{j=2}^{t}W_{i}(L)^{-1}\left(\sum_{g\in\Psi_{i}}D_{i}^{g}(L)\varrho_{j}(g)\right)^{\star}W_{i+1}(L)\left(\sum_{g\in\Psi_{i}}D_{i}^{g}(L)\varrho_{j}(g)\right).$

Let $D^{\varrho_{j}}(L)=\sum_{g\in\Psi}D_{i}^{g}(L)\varrho_{j}(g)$ for $j=2,\ldots,k$ . Then $D^{\varrho_{j}}(L)$ is exactly the matrix $D_{i}^{\varrho_{j}}$ of $\delta_{i}^{\varrho_{j}}$ on the incidence-weighted complex $(L,\varrho_{j})$ . By Eq. (2.3), we have

(I\otimes T)^{-1}\tilde{\mathcal{L}}^{up}(K)(I\otimes T)=\mathcal{L}_{i}^{u}(\mathcal{L})\oplus\oplus_{j=2}^{t}\mathcal{L}_{i}^{up}(L,\varrho_{j}).

The result now follows. ∎

A special case in Theorem 4.6 is $\Psi=\langle g\rangle$ , where $g=(a_{1}a_{2}\ldots a_{k})$ is a cycle in $\mathbb{S}_{k}$ . In this case, the irreducible representations of $\Psi$ are easily obtained, namely, $\varrho_{j}(g)=e^{\textbf{i}\frac{2\pi j}{k}}$ for $j=0,1,\ldots,k-1$ , where $\textbf{i}=\sqrt{-1}$ .

By a similar discussion, we get the result on the $i$ -down Laplace operator of the covering complex. Let $\phi:K\to L$ be a $k$ -fold covering. By Lemma 3.9, $B_{i-1}(K)$ is a $k$ -fold covering of $B_{i-1}(L)$ , and there exists a permutation assignment $\psi$ on $B_{i-1}(L)$ such that $B_{i-1}(L)^{\psi}$ is isomorphic to $B_{i-1}(K)$ via a map $\eta$ by sending $S_{i-1}(L)\times[k]$ to $S_{i-1}(K)$ and $S_{i}(L)\times[k]$ to $S_{i}(K)$ . Suppose that $w_{K}(F)=w_{L}(\phi(F))$ for all $F\in S_{i-1}(K)\cup S_{i}(K)$ . Let

(4.16)

\Psi_{i-1}=\langle\psi(G,\bar{G}):G\in S_{i-1}(L),\bar{G}\in S_{i}(L),G\in\partial\bar{G}\rangle,

whose permutation representation $\varrho$ has a decomposition

\varrho=1\oplus\varrho_{2}\oplus\cdots\oplus\varrho_{t}.

For each $g\in\Psi_{i-1}$ , define $D^{g}_{i-1}(L)=(D^{g}_{\bar{G},G})$ as in (4.9). Then there exists an invertible matrix $T$ such that

(4.17)

\begin{split}&(I\otimes T)^{-1}(\Lambda_{i}(L)^{\eta})^{-1}\mathcal{L}_{i}^{down}(K)\Lambda_{i}(L)^{\eta}(I\otimes T)\\ &=\mathcal{L}_{i}^{down}(L)\oplus\oplus_{j=2}^{t}\left(\sum_{g\in\Psi}(D_{i-1}^{g}(L)W_{i-1}(L)^{-1})\otimes\varrho_{j}(g)\right)\left(\sum_{g\in\Psi}(D_{i-1}^{g}(L)^{\top}W_{i}(L))\otimes\varrho_{j}(g^{-1})\right),\end{split}

where $\Lambda_{i}(L)^{\eta}$ is defined as in (4.5).

Theorem 4.7.

Let $\phi:K\to L$ be a $k$ -fold covering map. Then

\text{~{}Spec}L_{i}^{down}(L)\subset\text{~{}Spec}L_{i}^{down}(K),~{}\text{~{}Spec}\Delta_{i}^{down}(L)\subset\text{~{}Spec}\Delta_{i}^{down}(K).

Theorem 4.8.

Let $\phi:K\to L$ be a $2$ -fold covering map. Suppose that $w_{K}(F)=w_{L}(\phi(F))$ for all $F\in S_{i-1}(K)\cup S_{i}(K)$ . Then

\text{~{}Spec}\mathcal{L}_{i}^{down}(K))=\text{~{}Spec}\mathcal{L}_{i}^{down}(L)\cup\text{~{}Spec}\mathcal{L}_{i}^{down}(L,s),

where $s(F,\bar{F})=\operatorname{sgn}\psi(F,\bar{F})$ for $(F,\bar{F})\in S_{i-1}(L)\times S_{i}(L)$ such that $F\in\partial\bar{F}$ , and $\psi:E(B_{i-1}(L))\to\mathbb{S}_{2}$ such that $B_{i-1}(L)^{\psi}$ is isomorphic to $B_{i-1}(K)$ .

Theorem 4.9.

Let $\phi:K\to L$ be a $k$ -fold covering map, let $\Psi$ be the group defined in (4.16) which is an Abelian group. Suppose that $w_{K}(F)=w_{L}(\phi(F))$ for all $F\in S_{i}(K)\cup S_{i+1}(K)$ . Then

\text{~{}Spec}\mathcal{L}_{i}^{down}(K))=\text{~{}Spec}\mathcal{L}_{i}^{down}(L)\cup\cup_{j=2}^{k}\text{~{}Spec}\mathcal{L}_{i}^{down}(L,\varrho_{j}),

where the permutation representation of $\Psi$ has a decomposition $\varrho=I_{1}\oplus\varrho_{2}\oplus\cdots\oplus\varrho_{k}$ , and $\varrho_{j}(F,\bar{F})=\varrho_{j}(\psi(F,\bar{F})$ for $(F,\bar{F})\in S_{i-1}(L)\times S_{i}(L)$ such that $F\in\partial\bar{F}$ .

5. Cohomology group of covering complex

As proved by Eckmann [9] (also see [21]), the $i$ -th reduced cohomology group of a complex $K$ is equal to the kernel of the $i$ -Laplace operator $\mathcal{L}_{i}(K)$ , namely. $\tilde{H}_{i}(K,\mathbb{R})=\text{ker}\mathcal{L}_{i}(K).$ In this section, we will investigate the relation between the homology group of a complex $L$ and that of its covering complex $K$ .

Lemma 5.1.

Let $\phi:K\to L$ be a $k$ -fold covering map. Suppose that $\frac{w(\bar{F})}{w(F)}=\frac{w(\phi(\bar{F}))}{w(\phi(F))}$ for each pair $(F,\bar{F})\in S_{i}(K)\times S_{i+1}(K)$ such that $F\in\partial\bar{F}$ . Let $f\in C^{i}(L,\mathbb{R})$ and $\bar{f}\in C^{i}(K,\mathbb{R})$ be such that for each $F\in S_{i}(K)$

(5.1)

\bar{f}([F])=f([\phi(F))])\operatorname{sgn}([F],[\phi(F)]).

Then the following results hold.

$(1)$ If $f\in\text{ker}\mathcal{L}^{up}_{i}(L)$ , then $\bar{f}\in\text{ker}\mathcal{L}^{up}_{i}(K)$ .

$(2)$ If $f\in\text{ker}\mathcal{L}^{down}_{i}(L)$ , then $\bar{f}\in\text{ker}\mathcal{L}^{down}_{i}(K)$ .

Proof.

(1) By the formula of the $i$ -up Laplace operator [21], if $f\in\text{ker}\mathcal{L}^{up}_{i}(L)$ , then for each $G\in S_{i}(L)$ ,

(5.2)

(\mathcal{L}_{i}^{up}(L)f)([G])=\!\!\!\sum_{\bar{G}\in S_{i+1}(L):\atop G\in\partial\bar{G}}\!\!\frac{w(\bar{G})}{w(G)}f([G])+\!\!\!\!\!\!\!\!\!\sum_{G^{\prime}\in S_{i}(L):\atop G^{\prime}\neq G,G,G^{\prime}\in\partial\bar{G}}\!\!\!\!\!\frac{w(\bar{G})}{w(G)}\operatorname{sgn}([G],\partial[\bar{G}])\operatorname{sgn}([G^{\prime}],\partial[\bar{G}])f[G^{\prime}]=0.

By Lemma 3.4, for every $G\in S_{i}(L)$ and each $F\in\phi^{-1}(G)\subseteq S_{i}(K)$ , there is a bijection also denoted by $\phi$ :

\phi:\{\bar{F}\in S_{i+1}(K):F\in\partial\bar{F}\}\to\{\bar{G}\in S_{i+1}(L):G\in\partial\bar{G}\},\bar{F}\mapsto\phi(\bar{F}).

Similarly, there is a bijection:

\phi:\{F^{\prime}\in S_{i}(K):F^{\prime}\neq F,F\cup F^{\prime}\in S_{i+1}(K)\}\to\{G^{\prime}\in S_{i}(L):G^{\prime}\neq G,G\cup G^{\prime}\in S_{i+1}(L)\},F^{\prime}\mapsto\phi(F^{\prime}).

So, by the assumption on weight and the notations $G=\phi(F)$ , $G^{\prime}:=\phi(F^{\prime})$ and $\bar{G}:=\phi(\bar{F})$ ,

	$\displaystyle(\mathcal{L}_{i}^{up}(K)\bar{f})([F])$	$\displaystyle=\sum_{\bar{F}\in S_{i+1}(K):\atop F\in\partial\bar{F}}\frac{w(\bar{F})}{w(F)}\bar{f}([F])+\sum_{F^{\prime}\in S_{i}(K):\atop F^{\prime}\neq F,F,F^{\prime}\in\partial\bar{F}}\frac{w(\bar{F})}{w(F)}\operatorname{sgn}([F],\partial[\bar{F}])\operatorname{sgn}([F^{\prime}],\partial[\bar{F}])\bar{f}([F^{\prime}])$
		$\displaystyle=\sum_{\bar{F}\in S_{i+1}(K):\atop F\in\partial\bar{F}}\frac{w(\phi(\bar{F}))}{w(\phi(F))}f([\phi(F)])\operatorname{sgn}([F],[\phi(F)])$
		$\displaystyle~{}~{}~{}+\sum_{F^{\prime}\in S_{i}(K):\atop F^{\prime}\neq F,F,F^{\prime}\in\partial\bar{F}}\frac{w(\phi(\bar{F}))}{w(\phi(F))}\operatorname{sgn}([F],\partial[\bar{F}])\operatorname{sgn}([F^{\prime}],\partial[\bar{F}])f([\phi(F^{\prime})])\operatorname{sgn}([F^{\prime}],[\phi(F^{\prime})])$
		$\displaystyle=\sum_{\bar{G}\in S_{i+1}(L):\atop G\in\partial\bar{G}}\frac{w(\bar{G})}{w(G)}f([G])\operatorname{sgn}([F],[G])$
		$\displaystyle~{}~{}~{}+\sum_{G^{\prime}\in S_{i}(L):G^{\prime}\neq G,\atop G,G^{\prime}\in\partial\bar{G}}\frac{w(\bar{G})}{w(G)}\operatorname{sgn}([F],\partial[\bar{F}])\operatorname{sgn}([F^{\prime}],\partial[\bar{F}])f([G^{\prime}])\operatorname{sgn}([F^{\prime}],[G^{\prime}])$
		$\displaystyle=\operatorname{sgn}([F],[G])\left(\!\!\sum_{\bar{G}\in S_{i+1}(L):\atop G\in\partial\bar{G}}\frac{w(\bar{G})}{w(G)}f([G])+\!\!\!\!\!\!\!\!\sum_{G^{\prime}\in S_{i}(L):G^{\prime}\neq G,\atop G,G^{\prime}\in\partial\bar{G}}\!\!\!\!\frac{w(\bar{G})}{w(G)}\operatorname{sgn}([G],\partial[\bar{G}])\operatorname{sgn}([G^{\prime}],\partial[\bar{G}])f([G^{\prime}])\right)$
		$\displaystyle=(\mathcal{L}_{i}^{up}(L)f)([G])=0,$

where the last equality follows from (5.2) and the second last equality follows from the signature relation (4.1). So $\bar{f}\in\text{ker}\mathcal{L}_{i}^{up}(K)$ .

(2) If $f\in\text{ker}\mathcal{L}^{down}_{i}(L)$ , then for each $G\in S_{i}(L)$ ,

(\mathcal{L}^{down}_{i}(L)f([G])=\!\!\!\!\!\sum_{H\in S_{i-1}(L):\atop H\in\partial G}\!\!\!\frac{w(G)}{w(H)}f([G])+\!\!\!\!\!\!\!\!\!\!\!\!\!\sum_{G^{\prime}\in S_{i}(L):\atop G\cap G^{\prime}=H\in S_{i-1}(L)}\!\!\!\!\!\!\!\!\!\!\!\!\!\frac{w(G^{\prime})}{w(E)}\operatorname{sgn}([H],\partial[G])\operatorname{sgn}([H],\partial[G^{\prime}])f([G^{\prime}])=0.

For every $G\in S_{i}(L)$ and each $F\in\phi^{-1}(G)\subseteq S_{i}(K)$ , As $\phi|_{F}:F\to G$ is bijection, there is a bijection

\phi:\{E\in S_{i-1}(K):E\in\partial F\}\to\{H\in S_{i-1}(L):H\in\partial G\},E\mapsto\phi(E).

By Lemma 3.4, there is a bijection

\phi:\{F^{\prime}\in S_{i}(K):F\cap F^{\prime}\in S_{i-1}(K)\}\to\{G^{\prime}\in S_{i}(L):G\cap G^{\prime}\in S_{i-1}(L)\},F^{\prime}\mapsto\phi(F^{\prime}).

So, by the assumption on weight and the notations $G=\phi(F)$ , $G^{\prime}:=\phi(F^{\prime})$ and $H:=\phi(E)$ ,

	$\displaystyle(\mathcal{L}_{i}^{down}(K)\bar{f})([F])$	$\displaystyle=\sum_{E\in S_{i-1}(K):\atop E\in\partial F}\frac{w(F)}{w(E)}\bar{f}([F])+\sum_{F^{\prime}\in S_{i}(K):\atop F\cap F^{\prime}=E\in S_{i-1}(K)}\frac{w(F^{\prime})}{w(E)}\operatorname{sgn}([E],\partial[F)\operatorname{sgn}([E],\partial[F^{\prime}])\bar{f}([F^{\prime}])$
		$\displaystyle=\sum_{E\in S_{i-1}(K):\atop E\in\partial F}\frac{w(\phi(F))}{w(\phi(E))}f([\phi(F)])\operatorname{sgn}([F],[\phi(F)])$
		$\displaystyle+\sum_{F^{\prime}\in S_{i}(K):\atop F\cap F^{\prime}=E\in S_{i-1}(K)}\frac{w(\phi(F^{\prime}))}{w(\phi(E))}\operatorname{sgn}([E],\partial[F])\operatorname{sgn}([E],\partial[F^{\prime}])f([\phi(F^{\prime})])\operatorname{sgn}([F^{\prime}],[\phi(F^{\prime})])$
		$\displaystyle=\sum_{H\in S_{i-1}(L):\atop H\in\partial G}\frac{w(G)}{w(H)}f([G])\operatorname{sgn}([F],[G])$
		$\displaystyle~{}~{}~{}+\sum_{G^{\prime}\in S_{i}(L):\atop G\cap G^{\prime}=H\in S_{i-1}(L)}\frac{w(G^{\prime})}{w(E)}\operatorname{sgn}([E],\partial[F])\operatorname{sgn}([E],\partial[F^{\prime}])f([G^{\prime}])\operatorname{sgn}([F^{\prime}],[G^{\prime}])$
		$\displaystyle=\operatorname{sgn}([F],[G])\left(\!\!\sum_{H\in S_{i-1}(L):\atop H\in\partial G}\!\!\frac{w(G)}{w(H)}f([G])+\!\!\!\!\!\!\!\!\!\!\!\!\!\!\sum_{G^{\prime}\in S_{i}(L):\atop G\cap G^{\prime}=H\in S_{i-1}(L)}\!\!\!\!\!\!\!\!\!\!\!\!\frac{w(G^{\prime})}{w(E)}\operatorname{sgn}([H],\partial[G)\operatorname{sgn}([H],\partial[G^{\prime}])f([G^{\prime}])\!\!\right)$
		$\displaystyle=(\mathcal{L}^{down}_{i}(L)f([G])=0,$

where the second last equality follows from (4.1). So $\bar{f}\in\text{ker}\mathcal{L}_{i}^{down}(K)$ . ∎

Theorem 5.2.

Let $K$ be a covering complex of a complex $L$ . Then

\text{dim}\tilde{H}_{i}(K,\mathbb{R})\geq\text{dim}\tilde{H}_{i}(L,\mathbb{R}).

Proof.

By Eckmann’s result, it suffices to prove the $\ker\mathcal{L}_{i}(L)$ can be embedded into $\text{ker}\mathcal{L}_{i}(K)$ as subspace. By Theorem 2.2 of [21], $\ker\mathcal{L}_{i}(L)=\ker\mathcal{L}_{i}^{up}(L)\cap\ker\mathcal{L}_{i}^{down}(L)$ . Suppose that $\phi:K\to L$ is a covering map. We choose weights on $K,L$ such that $\frac{w(\bar{F})}{w(F)}=\frac{w(\phi(\bar{F}))}{w(\phi(F))}$ for each pair $(F,\bar{F})$ such that $F\in\partial\bar{F}$ . This can easily be done by using combinatorial Laplace operator or normalized Laplace operator. By Lemma 5.1, for each $f\in\ker\mathcal{L}_{i}^{up}(L)\cap\ker\mathcal{L}_{i}^{down}(L)=\ker\mathcal{L}_{i}(L)$ , letting $\bar{f}$ be defined as in (5.1). then $\bar{f}\in\ker\mathcal{L}_{i}^{up}(K)\cap\ker\mathcal{L}_{i}^{down}(K)=\ker\mathcal{L}_{i}(K)$ .

Let $V=\{\bar{f}:f\in\ker\mathcal{L}_{i}(L)\}$ . We will show that $V$ is subspace of $\ker\mathcal{L}_{i}(K)$ with the same dimension as $\ker\mathcal{L}_{i}(L)$ . Let $f_{1},\ldots,f_{t}$ be a basis of $\ker\mathcal{L}_{i}(L)$ . Let $\lambda_{1},\ldots,\lambda_{t}\in\mathbb{R}$ be such that

\lambda_{1}\bar{f}_{1}+\cdots+\lambda_{t}\bar{f}_{t}=0.

For each $G\in S_{i}(L)$ , choosing an $F\in\phi^{-1}(G)$ , we have

(5.3)

\begin{split}\lambda_{1}(\bar{f}_{1})([F])+\cdots+\lambda_{t}(\bar{f}_{t})([F])&=\lambda_{1}f_{1}([G])\operatorname{sgn}([F],[G])+\cdots+\lambda_{t}f_{t}([G])\operatorname{sgn}([F],[G])\\ &=\operatorname{sgn}([F],[G])\left(\lambda_{1}f_{1}([G])+\cdots+\lambda_{t}f_{t}([G])\right)\\ &=0.\end{split}

So we have

\lambda_{1}f_{1}+\cdots+\lambda_{t}f_{t}=0

which implies that $\lambda_{1}=\cdots=\lambda_{t}=0$ as $f_{1},\ldots,f_{t}$ are linearly independent. So $\bar{f}_{1},\ldots,\bar{f}_{t}$ is a basis of $V$ . The result follows. ∎

Example 5.3.

Let $K,L$ be the complexes in Fig. 3.1. The $i$ -th betti number of $K$ is defined be the dimension of $\tilde{H}_{i}(K)$ , denoted by $\beta_{i}(K)$ . It is easy to see

\beta_{0}(K)=\beta_{0}(L)=0,\beta_{1}(K)=\beta_{1}(L)=1,\beta_{2}(K)=\beta_{2}(L)=0.

Let $G,\bar{G}$ be the graphs in Fig. 5.1. It is seen that $\bar{G}$ is a $2$ -fold covering of $G$ , and

\beta_{0}(G)=\beta_{0}(\bar{G})=0,\beta_{1}(G)=2<\beta(\bar{G})=3.

So it will be interesting to characterize the equality case of the inequality in Theorem 5.2.

References

[1] A. Amit, N. Linial, Random graph coverings I: General theory and graph connectivity, Combinatorica, 22(1): 1–18, 2002.
[2] Biggs, Algebraic Graph Theory, Cambridge Univ. Press, London, 1974.
[3] Y. Bilu, N. Linial, Lifts, discrepancy and nearly optimal spectral gap, Combinatorica, 26(5): 495–519, 2006
[4] O. Bottema, Über die Irrfahrt in einem Straßennetz, Math. Z., 39: 137–145, 1935.
[5] D. Cvetković, P Rowlinson, S. K. Simić, Signless Laplacians of finite graphs, Linear Algebra Appl., 423: 155–171, 2007.
[6] M. Desai, V. Rao, A characterization of the smallest eigenvalue of a graph, J. Graph Theory, 18: 181–194, 1994.
[7] W. Dörfler, Double covers of hypergraphs and their properties, Ars Combinatoria, 6: 293-313, 1978.
[8] A. M. Duval, V. Reiner, Shifted simplicial complexes are Laplacian integral, Trans. Amer. Math. Soc., 354(11): 4313–4344, 2002.
[9] B. Eckmann, Harmonische Funktionen und Randwertaufgaben in einem Komplex, Comment. Math. Helv., 17 (1): 240–255, 1944.
[10] F. Chung, Spectral Graph Theory, CBMS Regional Conference Series in Mathematics, No. 92, American Mathematical Society, 1997.
[11] F. Chung, The Laplacian of a hypergraph, DIMACS Ser. Discrete Math. Theoret. Comput. Sci., pp. 21–36, 1993.
[12] R. Q. Feng, J. H. Kwak, J. Lee, Characteristic polynomials of graph coverings, Bull. Aust. Math. Soc., 69: 133–136, 2004.
[13] M. Fiedler, Algebraic connectivity of graphs, Czechoslovak Math. J., 23 (2): 298–305, 1973.
[14] J. Friedman, Computing betti numbers via combinatorial Laplacians, Proceedings of the 28th Annual ACM Symposium on Theory of Computing, pp. 386–391, 1996
[15] H. Garland, $p$ -adic curvature and the cohomology of discrete subgroups of p-adic groups, Ann. of Math., 97: 375–423, 1973.
[16] J. L. Gross, T. W. Tucker, Generating all graph covering by permutation voltage assignments, Discrete Math., 18: 273-283, 1977.
[17] R. Gustavson, Laplacians of covering complexes, Rose Hulman Undegrad. Math. J., 12(1):1–18, 2011.
[18] G. Kirchhoff, Uber die Auflösung der Gleichungen, auf welche man bei der untersuchung der linearen verteilung galvanischer Ströme geführt wird, Ann. Phys. Chem., 72: 497–508, 1847.
[19] W. Haemers, E. Spence, Enumeration of cospectral graphs, Europ. J. Combin., 25: 199–211, 2004.
[20] D. Horak, J. Jost, Interlacing inequalities for eigenvalues of discrete Laplace operators, Ann. Global Anal. Geom., 43: 177–207, 2013.
[21] D. Horak, J. Jost, Spectra of combinatorial Laplace operators on simplicial complexes, Adv. in Math., 244: 303–336, 2013.
[22] D. Li, Y. Hou, Hypergraph coverings and their zeta functions, Electronic J. Combin., 25: #P4.59, 2018.
[23] D. Li, Y. Hou, Laplacian of a graph covering and its applications, Bull. Malays. Math. Sci. Soc., 42: 2569–2583, 2019.
[24] L. Lu, X. Peng, High-ordered random walks and generalized Laplacians on hypergraphs, Proc. Algorithms and Models for the Web-Graph, 2011.
[25] W. Massey, Algebraic Topology: An Introduction, Springer-Verlag, New York, 1967
[26] R. Merris, Laplacian matrices of graphs: a survey, Linear Algebra Appl., 197/198: 143-176, 1994.
[27] H. Mizuno, I. Sato, Characteristic polynomials of some graph coverings, Discrete Math., 142: 295–298, 1995.
[28] J. J. Rotman, Covering complexes with application to algebra, Rocky Mountain J. Math., 3: 641–674, 1973.
[29] Y.-M. Song, Y.-Z. Fan, Y. Wang, M.-Y. Tian, J.-C. Wan, The spectral property of hypergraph covering, Discrete Math., 347, 113830, 2024.
[30] H. M. Stark, A. A. Terras, Zeta functions of finite graphs and coverings, Adv. in Math., 121: 124-165, 1996.
[31] C. Taszus, Higher order Laplace Beltrami spectra of networks, Master’s Thesis, Friedrich Schiller Universität Jena, 2010.