The SRG/eROSITA All-Sky Survey
Recent advancements in methods utilized in wide-area surveys have demonstrated the reliability of the number density of galaxy clusters as a viable tool for precision cosmology. Beyond testing the current cosmological paradigm, cluster number counts can also be utilized to investigate the discrepancies currently affecting current cosmological measurements. In particular, cosmological studies based on cosmic shear and other large-scale structure probes routinely find a value of the amplitude of the fluctuations in the universe smaller than the one inferred from the primary cosmic microwave background. In this work, we investigate this tension by measuring structure evolution across cosmic time as probed by the number counts of the massive halos with the first SRG/eROSITA All-Sky Survey cluster catalog in the Western Galactic Hemisphere complemented with the overlapping Dark Energy Survey Year-3, KiloDegree Survey, and Hyper Suprime-Cam data for weak lensing mass calibration, by implementing two different parameterizations and a model-agnostic method. In the first model, we measure the cosmic linear growth index as , in tension with the standard value of , but in good statistical agreement with other large-scale structures probes. The second model is a phenomenological scenario in which we rescale the linear matter power spectrum at low redshift to investigate a potential reduction of structure formation, providing similar results. Finally, in a third strategy, we consider a standard cosmology, but we separate the cluster catalog into five redshift bins, measuring the cosmological parameters in each and inferring the evolution of the structure formation, finding hints of a reduction. Interestingly, the value inferred from eRASS1 cluster number counts, when we add a degree of freedom to the matter power spectrum, recover the value inferred by cosmic shear studies. The observed reduction in the growth rate or systematic uncertainties associated with various measurements may account for the discrepancy in the values suggested between cosmic shear probes and eROSITA cluster number counts, Planck CMB measurements.
Key Words.:
modified gravity – cosmological parameters – galaxies: clusters: general – large-scale structures of the universe1 Introduction
In the standard cosmological formalism, most of the energy content of the universe is formed by a non-relativistic component called Cold Dark Matter (Rubin & Ford 1970, hereafter) and an unknown Dark Energy (Riess et al. 1998, DE) responsible for the accelerated expansion of the universe, and frequently represented by the cosmological constant . The third ingredient is an early phase of exponential expansion called Inflation (Brout et al. 1978). Under the influence of these elements, quantum fluctuations evolved in the early universe to form the large-scale structure (LSS) that we observe today. This standard formalism, the CDM model, has been successful at describing a broad range of observations, from the statistical distribution of the fluctuations of the Cosmic Microwave Background (CMB) to the spatial correlations of galaxies in the late universe (Planck Collaboration et al. 2020; Amon et al. 2022; DESI Collaboration et al. 2024). Despite its success, the standard concordance model, CDM, is being challenged by several tensions, such as discrepancies reported in the measurements of the Hubble constant (). The Hubble constant measured by early time probes is in 4 to 6 statistical tension with the one directly measured by late-time distance ladders (Di Valentino et al. 2021b). Whether these differences in the expansion rate measurements originate from fundamental physics or systematic effects is still debated (Freedman et al. 2024). This tension is supplemented by numerous but less significant discordant observations, such as anomalies in the CMB anisotropies like a higher lensing amplitude than the one predicted by (Planck Collaboration et al. 2020), discrepancies in the abundance of galaxy satellites (Kanehisa et al. 2024; Bullock 2010), potential anisotropies in the large-scale distribution of galaxy clusters (Migkas et al. 2020), or the unlikely presence of high velocity colliding clusters (Asencio et al. 2021) (see Peebles (2022) and Perivolaropoulos & Skara (2022) for a review of the most common reported anomalies). Recently, DESI Collaboration et al. (2024) reported a significant preference for an evolving dark energy equation of state when measuring the cosmological parameters from the baryonic acoustic oscillations. The tension is reported as high as when BAO are combined with the CMB and supernovae data. Interestingly, this preference is consistent with earlier cluster observations like Mantz et al. (2015) for which the best-fit values suggested that , however still in excellent agreement with . The same was observed for galaxy clustering and weak lensing data from the Dark Energy Survey collaboration Abbott et al. (2023a).
Another reported tension is found in the measurement of the growth of structures. The values reported by the CMB are higher than the ones measured by a number of late-time cosmological probes (see Di Valentino et al. 2021a, and references therein). This tension is best seen in the plane, where the CMB constraints lie above the degeneracy of the LSS probes, and is usually quantified in terms of the parameter. Although statistically less significant than the tension, various probes report the tension as a motivation to investigate a potential physical origin. Among the most prominent early time probes, Planck Collaboration et al. (2020) (Planck20 hereafter), measured (TT+TE+EE+lensing). Similar ”early-time” measurements are reported in the results of the Wilkinson Microwave Anisotropy Probe (Hinshaw et al. 2013, WMAP). This value is confirmed by the results of the South Pole Telescope (SPT) data through the lensing of the CMB combined with baryon acoustic oscillation (Bianchini et al. 2020), who found , and the recent result of the sixth data release of the Atacama Cosmology Telescope (ACT) using the same method and who measured (Madhavacheril et al. 2024). Since CMB lensing probes linear scales with most of the signal coming from a redshift range of , the good agreement between the primary CMB and the CMB lensing compared to other late-time probes might suggest a change in the non-linear regime at low redshift. Conversely, cosmic shear surveys tend to find a lower amplitude of structure formation. For example, the Dark Energy Survey (Abbott et al. 2022) finds .
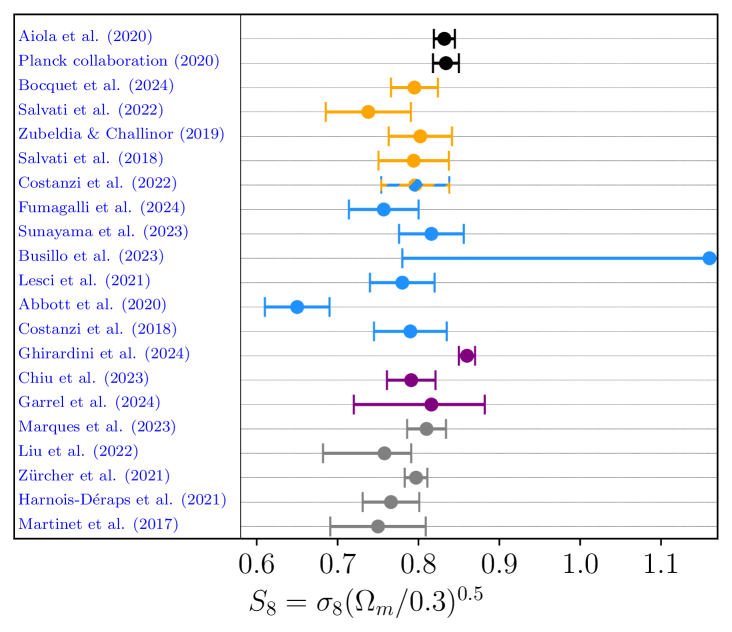
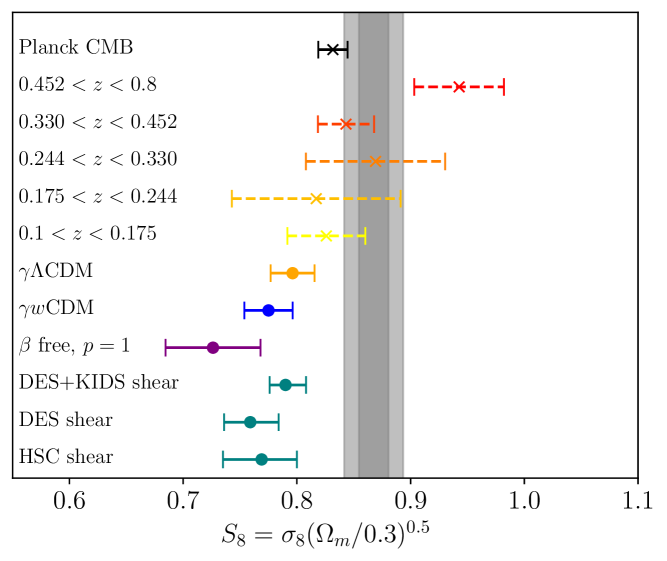
Cluster counts have also been utilized in the measurements in recent years. In the millimeter wavelength, Zubeldia & Challinor (2019) used Planck-detected galaxy clusters with CMB lensing mass calibration to find . Recently, the SPT collaboration used a sample of 1,005 galaxy clusters with weak gravitational lensing data from DES and the Hubble Space Telescope (HST) and found (Bocquet et al. 2024). Similarly, Salvati et al. (2022) combined the Planck and SPT samples and reported . Aymerich et al. (2024) reanalyzed the same Planck cluster sample with external Chandra data and obtained . In the optical wavelength, a preliminary study on the clusters detected in the Sloan Digital Sky Survey DR8 produced an value of (Costanzi et al. 2019), while the latest DES results combined with SPT find (Costanzi et al. 2021). Furthermore, Sunayama et al. (2023) analyzed a sample of 8,379 clusters detected by the redMaPPer algorithm with HSC weak lensing data and found . Additionally, an analysis of a sample of 3652 galaxy clusters detected in KIDS produced . The recent results for the first eROSITA All-Sky-Survey (eRASS1, Ghirardini et al. 2024; Artis et al. 2024) established cluster number counts as a precision cosmological probe, placing tight constraints on . Interestingly, the eROSITA, as a later-time probe analysis, has no tension with the Planck20 measurements. These measurements in the literature are compared in Figure 1.
As the cluster mass function is established as a reliable cosmological probe, and the samples have reached a sizable number of clusters to ensure statistical precision with the launch of SRG/eROSITA All-Sky Survey, we take our primary cosmology analysis one step further and constrain the structure growth over cosmic time. The overarching goal of this paper is to measure the parameterization of the growth factor using the cosmic linear growth index (), a late-time reduction of the power spectrum, and a model agnostic method where the sample is divided into five different redshift bins 6. The first approach aims at modifying the growth rate of structure formation and defines it as a power-law of the matter density parameter, i.e., . This method has been widely discussed in the literature in the context of testing general relativity (GR) at large scales. For instance, Wang & Steinhardt (1998) shows that the non-linear theory of structure formation assuming general relativity yields a growth rate well modeled by this function when . Thus, deviations from this value would indicate that structures do not evolve as predicted and, more generally, suggest a potential departure from GR-. A higher is equivalent to a reduction of structure formation. Previous galaxy cluster surveys have been utilized in GR studies. Rapetti et al. (2009) used a sample of 78 X-ray selected clusters to constrain the luminosity-mass scaling relation in combination with CMB, SNe Ia, and X-ray cluster gas-mass fractions () and found consistent results with GR. Mantz et al. (2015) used a sample of 224 X-ray clusters detected by ROSAT (Truemper 1993), with weak lensing (WL hereafter) mass measurements obtained from the Subaru telescope and the Canada-France Hawaii Telescope (von der Linden et al. 2014). This cosmological study combines cluster abundance with the cluster gas fraction, primordial nucleosynthesis, and priors to constrain the background expansion and break the degeneracy and found no evidence for physics beyond GR. Bocquet et al. (2015) used the same approach on a sample of 100 clusters detected by their millimeter-wave signature, the so-called Sunyaev Zel’dovich (SZ) effect, through the South Pole Telescope (SPT), agreeing with the previous studies when clusters are combined with the CMB measurement from the Planck Collaboration et al. (2014), as well as BAO and supernoave type Ia (SNe Ia). However, recent cosmological studies based on the LSS find a higher value of the cosmic linear growth index for the GR prediction (). Studies based on the galaxy clustering of the Sloan Digital Sky Survey (SDSS) data (Samushia et al. 2013; Beutler et al. 2014; Gil-Mar´ın et al. 2017) found a lower structure growth rate than the one inferred from the CMB. This was later confirmed by DES data (Basilakos & Anagnostopoulos 2020), once again using galaxy clustering in combination with galaxy-galaxy lensing, implying a damping of structure formation at low redshifts. This recurrent finding is intriguing and may indicate that the theory of structure formation does not describe observations accurately. If so, it might hint at physics beyond GR and , or an unknown systematic effect related, for example, to baryonic feedback.
Apart from the parametrization using the cosmic linear growth index , another method used in this work is to directly measure the evolution of the parameter across cosmic time. Surveys using galaxy clustering provide robust constraints on parameter (Zarrouk et al. 2018; de Mattia et al. 2021, among others). The measurements of the evolution of the parameter, , is probed by redshift space distortions (RSD) where is the linear growth rate defined as . Recent surveys have used weak lensing and galaxy clustering to probe this evolution (Jullo et al. 2019; Garc´ıa-Garc´ıa et al. 2021; White et al. 2022; Abbott et al. 2023b). In the context of cosmology with cluster number counts, Bocquet et al. (2024) probed the growth of structures by using a non-parametric approach on their SPT-SZ sample of 1,005 clusters combined with sound horizon priors from Planck20. They divided their sample into five redshift bins, allowing them to obtain a quasi-direct measurement of , and finding good agreement with predictions from the primary CMB probes.
The paper is organized as follows: Section 2 describes the survey data employed, while Section 3 discusses modifying the structure growth framework. Section 4 shows our result on the cosmic linear growth index. Section 5 and Section 6 present the results on the power spectrum reduction and the model agnostic method. Section 7 demonstrates the robustness of the analysis. Discussions and relation to current cosmological tensions are provided in Section 8. Throughout this paper, we use the notation , and . Reported uncertainties correspond to a 68% confidence level unless noted otherwise.
2 Survey Data
The data used in this work is identical to the catalogs presented in Bulbul et al. (2024); Kluge et al. (2024). The weak lensing follow-up for mass calibration uses the data utilized in (Grandis et al. 2024b; Kleinebreil et al. 2024). The cosmological pipeline and analysis framework is the same in (Ghirardini et al. 2024; Artis et al. 2024). We summarize the multi-wavelength data, including X-ray, optical, and weak lensing observations, utilized in this work in the following section.
2.1 eROSITA All-Sky Survey
The X-ray telescope, eROSITA, on board the Spectrum Roentgen Gamma Mission (SRG), completed its first All-Sky Survey program on June 11, 2020, 184 days after the start of the survey. In this work, we use the data of the Western Galactic half of the eROSITA All-Sky survey (359.9442 deg 179.9442 deg), where the data rights belong to the German eROSITA consortium. Two catalogs of clusters detected are compiled in this region by Bulbul et al. (2024) and Kluge et al. (2024) based on the catalog of the X-ray sources in the soft band (0.2–2.3 keV) provided in Merloni et al. (2024). The primary galaxy group and cluster catalog adopts a lower extent likelihood threshold to maximize the discovery space than the cosmological subsample, which maximizes the purity of the sample for scientific applications. In this work, we utilize the eRASS1 cosmological subsample due to its high fidelity confirmation rate, well-defined and -tested selection function, and low contamination fraction, which adopts a selection cut of extent likelihood, (see Bulbul et al. 2024; Clerc 2023, for further details). The optical identification of the clusters selected in the Legacy Survey Data Release 10 in the Southern Hemisphere (LS DR10-South) common footprint of 12791 deg2 yields a final cosmology sample of 5259 clusters of galaxies reaching purity levels of 95%, an ideal sample for the studies of growth of structure (Kluge et al. 2024). Unlike the primary cluster catalog, the redshifts in the cosmological subsample are purely photometric measurements, allowing a consistent assessment of the systematics in our analysis. The count rates are extracted with the 2D-image fitting tool MBProj2D as described in Bulbul et al. (2024) and are employed as a mass proxy in the weak lensing mass calibration likelihood (Ghirardini et al. (2024), G24 hereafter).
2.2 Weak Lensing Survey Data
To perform the mass calibration in a minimally biased way, we utilize the deep and wide-area optical surveys for lensing measurements with the overlapping footprint with eROSITA in the Western Galactic Hemisphere. The three major wide-area surveys used in this work for mass calibration include the Dark Energy Survey (DES), Kilo Degree Survey (KiDS), and the Hyper Suprime-Cam Survey (HSC). We briefly describe the weak lensing survey data here.
The three-year weak-lensing data (S19A) covered by the HSC Subaru Strategic Program (Aihara et al. 2018; Li et al. 2022) weak lensing measurements are made around the location of eRASS1 clusters using in the , , , , and bands in the optical. The total area coverage of HSC is deg2. The shear profile , the lensing covariance matrix that serves the measurement uncertainty, and the photometric redshift distribution of the selected source sample are obtained as the HSC weak-lensing data products for 96 eRASS1 clusters, with a total signal-to-noise of 40.
We utilize data from the first three years of observations of the Dark Energy Survey (DES Y3). The DES Y3 shape catalog (Gatti et al. 2021) is built from the -bands using the Metacalibration pipeline (Huff & Mandelbaum 2017; Sheldon & Huff 2017). Considering the overlap between the DES Y3 footprint and the eRASS1 footprint, we produce tangential shear data for eRASS1 galaxy clusters, with a total signal-to-noise of 65 in the tangential shear profile. The analysis and shear profile extraction details are presented in Grandis et al. (2024b).
We use the gold sample of weak lensing and photometric redshift measurements from the fourth data release of the Kilo-Degree Survey (Kuijken et al. 2019; Wright et al. 2020; Hildebrandt et al. 2021; Giblin et al. 2021), hereafter referred to as KiDS-1000. We extract individual reduced tangential shear profiles for a total of 236 eRASS1 galaxy clusters in both the KiDS-North field (101 clusters) and the KiDS-South field (136 clusters), as both have overlap with the eRASS1 footprint with a total signal-to-noise of 19.
3 Framework and parameterization with the cosmic linear growth index
Galaxy cluster number counts efficiently place constraints on the low-redshift and large-scale regime, which cannot be explored by every cosmological probe, such as the anisotropies of the CMB. In this section, we describe the first framework we explore in this paper, namely the linear growth parametrization scenario (-model hereafter). The power spectrum reduction model and the model agnostic method are described respectively in section 5 and section 6.
3.1 Cosmology with eRASS1 cluster count
The cosmology analysis presented in this paper is similar to the one introduced in G24, and we refer the reader to this work for a detailed review. For readability, this section provides the main characteristics and fundamental assumptions of this analysis. The abundance of dark matter halos per units of mass , redshift , and solid angle (sky positions are noted ) follows
| (1) |
where is the matter density at present, is the root mean square density fluctuation defined by Equation (3.2), is the differential comoving volume per redshift per steradian and for we adopt the multiplicity function introduced by Tinker et al. (2008), with its parameters assumed to be fixed and universal in the considered models. In the case of the X-ray cluster analysis developed in G24, the astrophysical quantities used in this study are the observed X-ray count-rates , the observed cluster richness computed from the DESI Legacy Survey Data Release 10 (Dey et al. 2019) and detailed in Kluge et al. (2024), and the weak lensing shear profiles of clusters that belong in the overlapping KIDS, DES, and HSC regions (see Section 2). The observed number density of galaxy clusters is obtained through
| (2) |
where is the vector of the astrophysical observable quantities. is the probability distribution function related to the observables at a given mass and redshift. Following G24, the observed cluster count (combined with a mixture model for AGN contaminants and background fluctuations) is modeled through a Poisson likelihood.
This work explores a class of effective and redshift-dependent modifications of the linear matter power spectrum. We, therefore, assume that the multiplicity function function (Equation 1) parameterization remains valid in the considered models. This is justified as the applied modification is only redshift-dependent. In practice, we are changing the redshift dynamic of the collapse while keeping the critical overdensity for collapse to the value. This method thus impacts the modeling of the non-linear scales. However, quantities entering the computation of the halo number density like are computed from the linear matter power spectrum in the case of cluster count. Thus, we cannot consider scale-dependant changes of the matter power spectrum in the non-linear regime, like the one presented in Amon et al. (2022) and Preston et al. (2023), without risking our parameterization of to be invalid. However, both methods are related, impacting the physics of non-linear structure formation.
3.2 Growth rate parameterization
A standard method of probing structure formation physics is to consider the cosmic linear growth index. Initially, it was introduced in the context of observational cosmology as a test for departures from general relativity at cosmological scales Nesseris & Perivolaropoulos (2008). Using classical gravity111Relativistic corrections on scales relevant to galaxy cluster formation and evolution are negligible. Thus, Newtonian gravity is an excellent approximation to GR (Hwang & Noh 2006)., the linear theory of the growth of the density field perturbations in a spatially flat universe predicts that the density contrast is,
| (3) |
where is the Hubble parameter at time , is the universal gravitational constant, and is the mean matter density at time . We highlight that the derivatives in this equation and its coefficients depend only on the time. Thus, the solutions are the sum of two products of a spatial function and a time dependence. The growing mode of the time dependence is noted with . We follow the formalism of Rapetti et al. (2009). The linear growth rate is defined as
| (4) |
where is the time-dependent scale factor, and is the growth factor (equation 8). This function can be parameterized as a power-law of the matter density parameter (e.g. Wang & Steinhardt 1998). is thus expressed as
| (5) |
where is the cosmic linear growth index. In general, can be expressed as a function of redshift (Linder & Cahn 2007; Batista 2014). In the literature, various methods are used to characterize the redshift evolution of the growth index, including linear analytical relation with redshift (e.g. Polarski & Gannouji 2008). Many theoretical frameworks also imply an evolving growth index over cosmic time, including dark energy models in GR (Polarski et al. 2016). However, most of these theories predict that the cosmic linear growth index is quasi-constant between and the beginning of the matter-dominated era at . As cluster counts experiments probe redshift well after this epoch, we can safely assume a constant growth index of .
In the absence of neutrinos (see Section 8), which would introduce a scale dependence, we can express the growth factor as
| (6) |
which can be expressed for a standard GR + cosmology as (up to a proportionality constant)
| (7) |
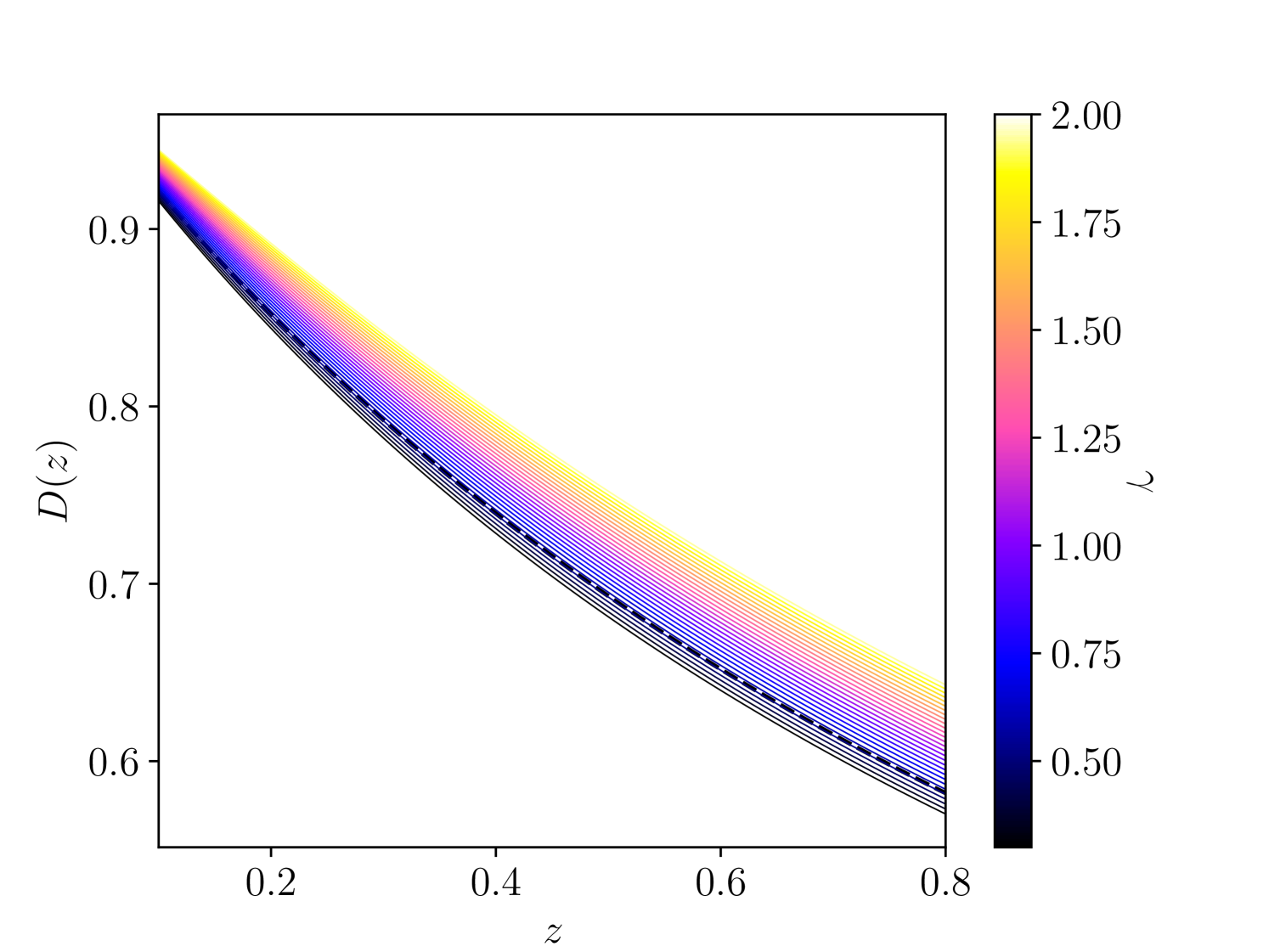
Figure 2 illustrates how this expression differs from the -parametrization. In this case, Equation (6), with the linear growth rate provided by Equation (5), should be used. We can then define the normalized growth as
| (8) |
and we thus have the usual power spectrum evolution
| (9) |
which in turn yields the standard root mean square (r.m.s.) density fluctuation definition:
| (10) |
where is the spherical Bessel function of the first kind of order one. Wang & Steinhardt (1998) reports that for the case of a slowly varying dark energy equation of state, for the standard linear perturbation theory approach within the context of GR, with a weak dependence on dark energy equation of state ,
| (11) |
Different dark energy equation-of-state parameters correspond to varying growth indices. For example, yields and yields . Consequently, departures larger than a few percent from this value of the growth index may be a hint for direct measurement of potential deviations from GR. Although Equation (3.2) suggests a degeneracy, we independently fit for and in the rest of the paper (see Section 4.2 for the constraints from the data).
4 Constraints on the structure growth through the parametrization
| Cosmological parameters | Priors | |
| Mean matter density at present time | ||
| + priors (See Appendix E) | ||
| Amplitude of the primordial power spectrum | ||
| Hubble expansion rate () at present time | ||
| Mean baryon density at present time | ||
| Spectra index of the primordial power spectrum | ||
| Dark energy equation of state. Fixed to -1 in CDM | ||
| Power spectrum suppression | Priors | |
| Cosmic linear growth index | ||
| Power spectrum reduction parameter | ||
| Power spectrum reduction index | Fixed to | |
| X-ray scaling relation | Priors | |
| Normalization of the scaling relation | ||
| Mass slope of the scaling relation | ||
| Luminosity distance evolution of the scaling relation | Fixed to -2 | |
| Scale factor evolution of the scaling relation | Fixed to 2 | |
| Redshift evolution of the mass slope of the scaling relation | ||
| Redshift evolution of the normalization of the scaling relation | ||
| Intrinsic scatter of the scaling relation | ||
| Richness mass calibration | Priors | |
| Normalization of the scaling relation | ||
| Mass slope of the scaling relation | ||
| Redshift evolution of the normalization of the scaling relation | ||
| Redshift evolution of the mass slope of the scaling relation | ||
| Intrinsic scatter of the scaling relation | ||
| Intrinsic correlation between richness and count rate | ||
In this work, we aim to constrain the growth of structure utilizing the eRASS1 cosmology sample with weak lensing mass calibration from the DES, KIDS, and HSC surveys. The results presented here are obtained by combining cluster counts with priors from the sound horizon scale at recombination () indicated by the CMB measurements presented in Planck20, as this represents one of the most robust cosmological measurements to date. Details on the sound horizon priors used can be found in Appendix E. Additionally, differently than the G24 framework, we use a conservative . A comprehensive description of the different priors can be found in Table 1.
Here, we present constraints on the cosmic linear growth index for the parametrizations described in Section 3. In particular, we focus on two different models: the canonical model with the cosmic linear growth index parameterized as in Equation (5) ( model) and the model with the dark energy equation of state parameter, , free ( model). The standard is shown in Figure 3. Neutrinos suppress the amplitude of the power spectrum, introducing a scale dependence of the growth factor (Equation 6), which leaves imprints on the halo mass function. Although Costanzi et al. (2013) presents a method to account for the effect of neutrinos on the halo mass function by replacing the total matter power spectrum with the cold dark matter power spectrum, this method is incompatible with the growth parameterization using the cosmic linear growth index employed in this work. Therefore, we do not consider the impact of neutrinos and assume that neutrinos are massless throughout this work. At our current statistical constraining power, this modeling choice does not affect our results, as shown in section 8.
We also emphasize that a higher value of the cosmic linear growth index leads to a flattening of the growth factor, which in turn yields a lower measurement of . This definition does not imply that we expect a lower for all redshifts, as found with probes that include non-linear physics (Abbott et al. 2022; White et al. 2022).
4.1 Constraints on the Model
We first fit the cluster number density to the eRASS1 cosmology sample with a free cosmic linear growth index in the model. In the case of cluster counts combined with sound horizon priors, we find
| (12) |
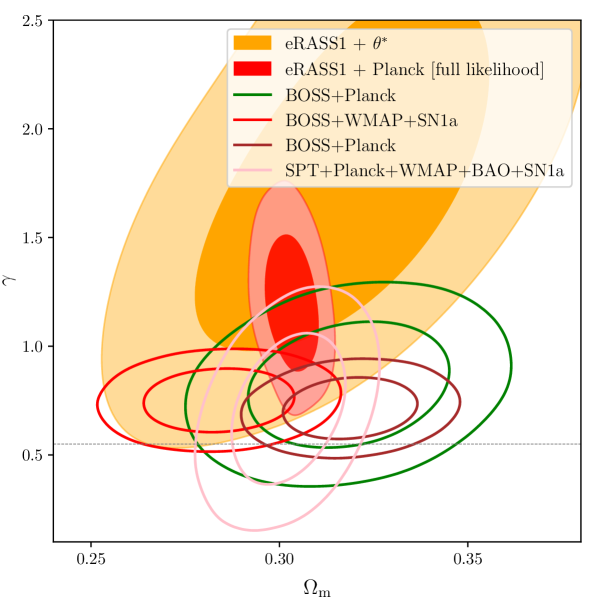
at the 68% confidence level. We compare our results in the baseline concordance cosmology with the primary eRASS1 cosmology analysis presented in G24, shown in Figure 4. Unlike the case of galaxy clustering, cluster counts exhibit a clear anti-correlation between , the amplitude of the primordial power spectrum, and , the cosmic linear growth index. This is explained in Figure 2. As such, increasing leads to a flattening of , thus increasing the number of high-redshift clusters for a fixed amplitude. Freeing the linear growth index, , decreases the value of measured by cluster number counts, based on the following equation.
| (13) |
where is the matter transfer function. This effect is significantly reflected in a decrease in the value measured by clusters to the abovementioned constraint.
Overall, although eRASS1 cluster counts tend to prefer higher values of , which could hint at a weakening of gravity at low redshifts () considered in this work, our posteriors are in broad agreement with the value expected from GR () in statistical uncertainties and consistent with the results from galaxy clustering and cluster counts in the literature when combined with other probes (see the contours in orange in Figure 3 for comparison). The corner plot of the main cosmological parameters constrained with our cluster number counts is shown in Appendix A. The primary conclusion of this analysis is that adding a degree of freedom to the growth of structure, in this case, through the cosmic linear growth index , decreases the value of , and therefore , constrained by cluster number counts.
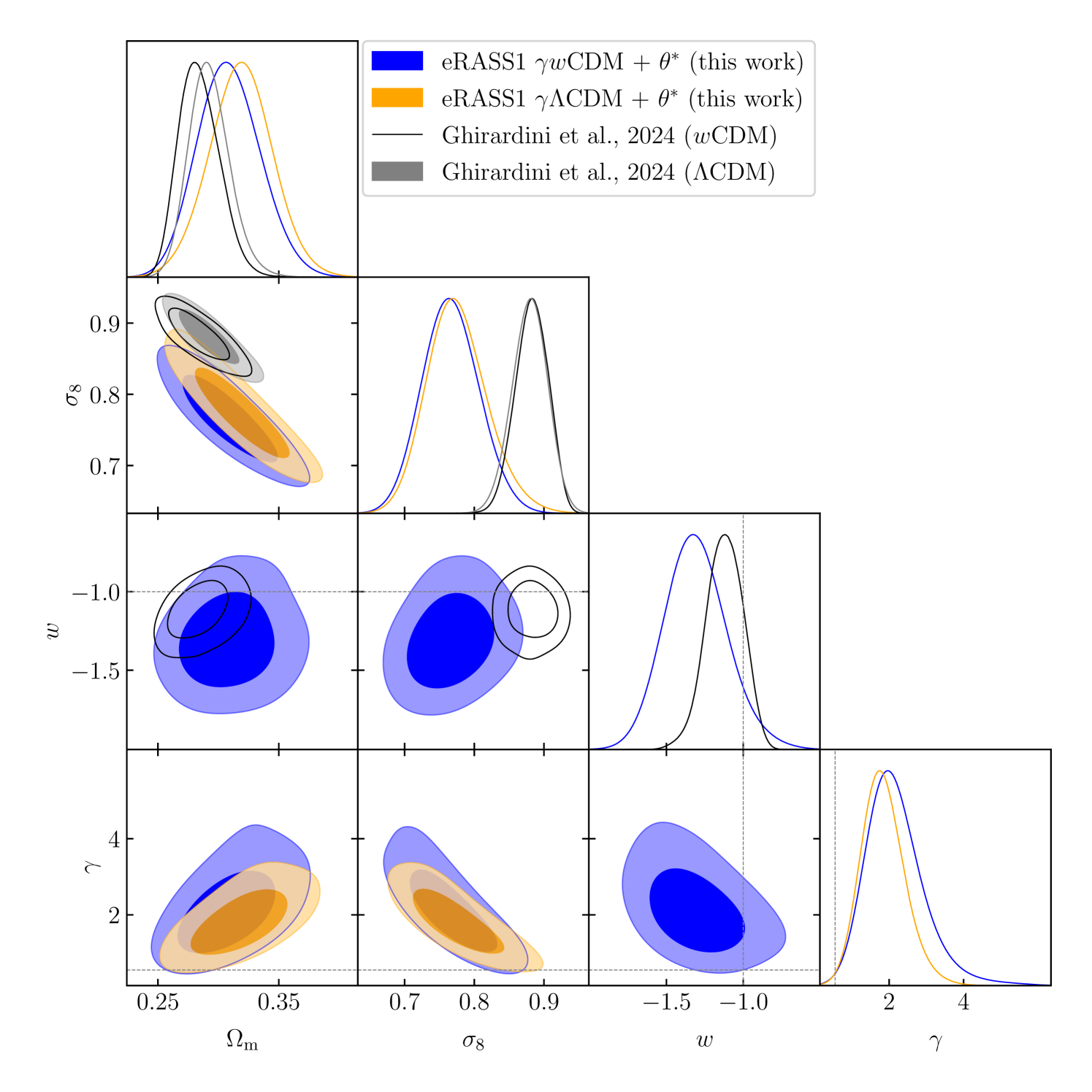
In these fits, as explicitly demonstrated in the corner plots in Appendix A, the cosmic linear growth index exhibits a strong degeneracy with and . It requires robust external priors to be constrained. To break this degeneracy, we combine our eRASS1 measurements with the Planck20’s CMB measurements, specifically TTTEEE+lowl+lowE. This time, we are considering the full likelihood and not only the sound horizon measurements. In this case, we find
| (14) |
As the combination with the CMB data increases the precision, our combined results are in tension with the standard of in the GR framework. However, it is in statistical agreement with the other probes, as shown in Figure 3. Overall, this hints again that structure growth might undergo a late-time reduction, which only reflects on the data from the late-time probes, such as clusters of galaxies. This conclusion is strengthened by other probes, including other cluster count experiments, which remains consistent with , but skew to higher values. Indeed, Bocquet et al. (2015) used SZ-detected clusters from SPT in combination with CMB, SNIa, and BAO data to find . In comparison, earlier constraints from Rapetti et al. (2013) report a value of when combining number counts from 238 clusters detected by ROSAT with CMB data, galaxy clustering, SNIa, and BAO, as well as the cluster gas fraction. Additionally, Bocquet et al. (2015) finds using a sample of 100 SPT-SZ selected clusters, where cluster abundance is combined with BAO, supernovae, and CMB data. Constraints on the cosmic linear growth index are also found to be systematically higher by galaxy clustering constraints. Combining data from the Baryon Oscillation Spectroscopic Survey (BOSS hereafter) with WMAP and SNIa data, Samushia et al. (2013) found , while combining BOSS and CMB data from Planck Collaboration et al. (2016), Beutler et al. (2014) found , consistently higher. Other probes also find similar results. With the combination of redshift space distortion and cosmic chronometers, (Moresco & Marulli 2017) obtained . Using the clustering of luminous red galaxies from DES (Basilakos & Anagnostopoulos 2020) found . Finally, combining CMB data from Planck20 and weak lensing, galaxy clustering, and cosmic velocities Wen et al. (2023) found . These data sets favor a higher cosmic linear growth index value in all these cases. Our best-fit value is also higher than the one obtained in GR, which may hint that cluster number counts tend to favor suppression of structure growth at the low- regime. A significant finding of this section is the fact that we find a significant reduction of the parameter compared to the one obtained in G24. This result is extensively discussed in Section 8.
4.2 Constraints on the Model
In addition to the parameter, we vary the dark energy equation of state parameter, , as the most straightforward extension of the model. and are fit as independent parameters. The constraints provided by the eRASS1 cluster counts with the sound horizon priors produce the following best-fit results:
| (15) |
The results of this fit are shown in Figure 4, where the uncertainties are plotted as contours at the 68% and 95% levels. The dark energy equation of state posterior distribution is consistent with the value of within the statistical uncertainties. Our value also agrees with the primary eROSITA cosmology analysis presented in the G24, which reports a best-fit value of in their model. Our results favor a higher value of , consistent with model, which once again hints at a modification of the growth of structures and potential damping at the redshift range considered in this work (although we remain compatible with the standard at the level due to the large error bars). Appendix B presents the corner plot of the main cosmological parameters constrained in this fit. We note that the dark energy equation of state parameter, , is positively correlated with the normalization of the power spectrum . This potentially increases the uncertainties on the magnitude of the power spectrum.
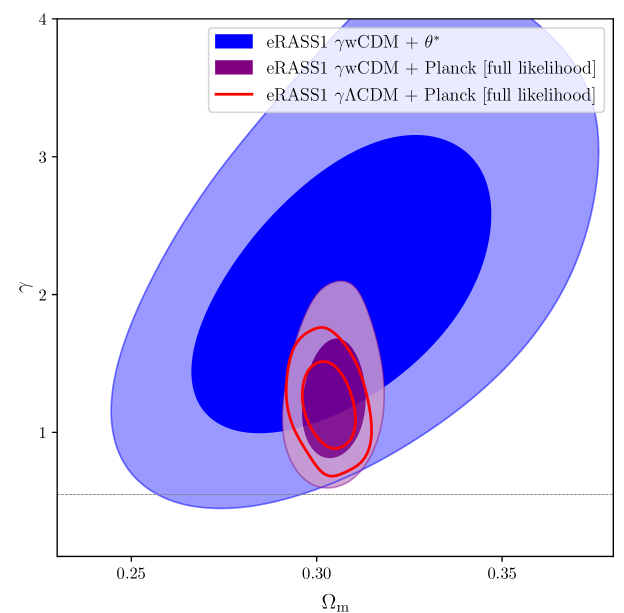
We proceed by combining our cluster number density constraints with the full likelihood from the Planck20 CMB (TT-TEEE+lowl+lowE) chains. The results are shown in Figure 5. We find
| (16) |
Including the Planck20 CMB results in our chains lowers the best-fit value of the parameter similar to the case presented in the previous section. The result is in tension with the canonical value 0.55 predicted by the GR model. However, in this case, similarly to the results presented in Section 4.1, finding a higher value of the cosmic linear growth index is consistent with earlier works presented in the literature. When combining ROSAT cluster counts with CMB data, galaxy clustering, SNIa, and BAO, as well as the cluster gas fraction, Rapetti et al. (2013) found , favoring higher values, although the measurement remains in perfect agreement with the GR value. Additionally, Bocquet et al. (2015) found, when freeing the dark energy equation of state . Similarly to Section 4.1, the parameter is reduced to a value similar to the one expected from cosmic shear surveys. The new values that appear to reconcile the linear regime measurements and the ones inferred from cosmic shear surveys are discussed in Section 8.
5 Constraints on the structure growth through the power spectrum suppression model
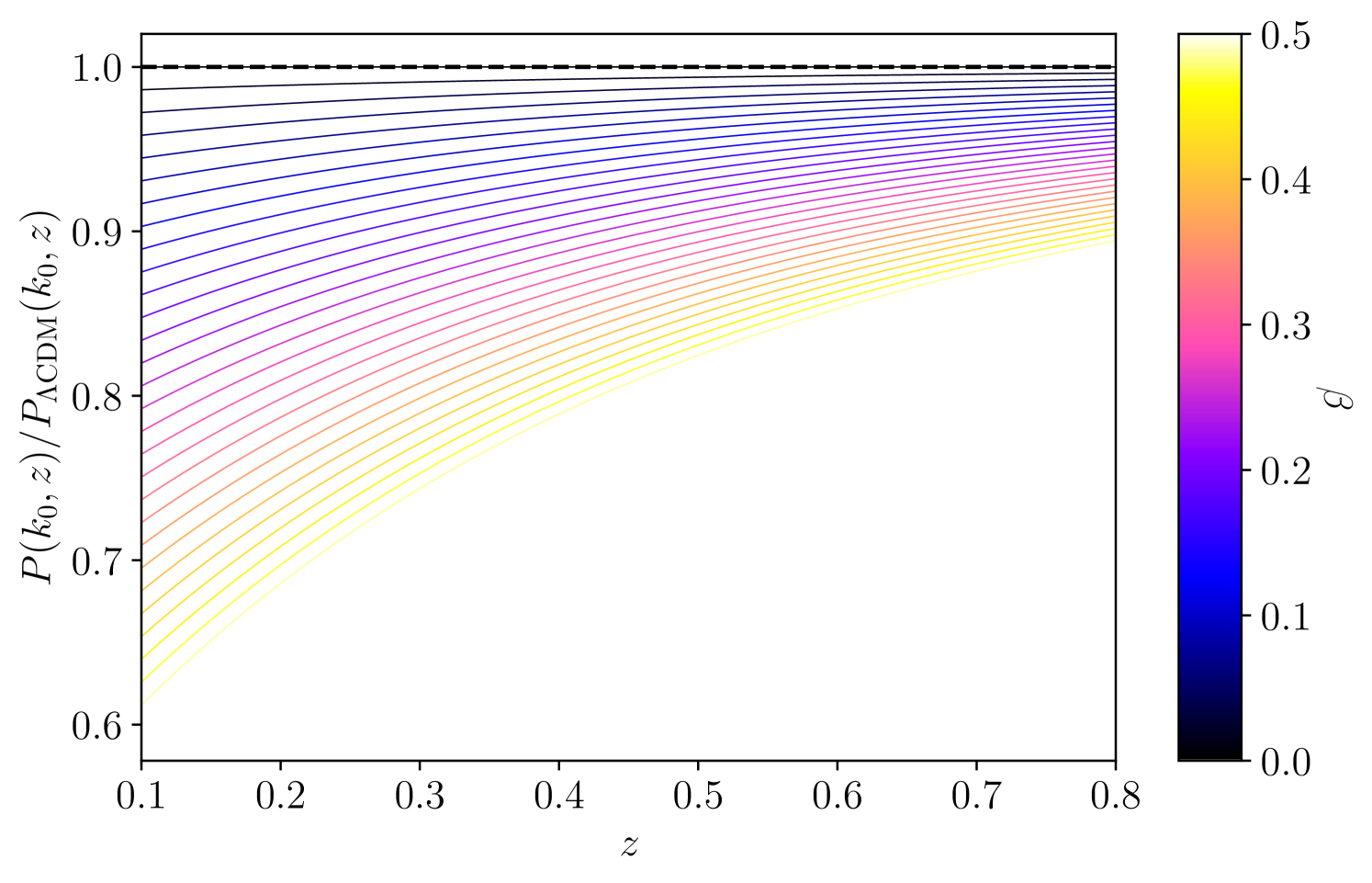
Previous sections present hints for departures from the standard structure formation scenario and potential damping in the formation of halos indicated by the eRASS1 cluster counts in the redshift range . It is thus interesting to explore if these findings are consistent with other models describing a reduction of the power spectrum at low redshift. Following the results, we implement the late-time power spectrum reduction model proposed by Lin et al. (2024) as an additional effective parameterization of the observed deviations from the standard structure formation scenario. We stress that this model is a new parameterization of the modification of the linear growth factor, and we do not use the framework described in Section 3. Here, we use the standard growth factor introduced in equation 7, and thus the cosmic linear growth index is irrelevant in this section. However, both models describe a reduction of structure formation as described in Section 8, and are thus complementary. The modified matter power spectrum is defined as
| (17) |
where is the standard linear matter power spectrum expected in , and is a correction factor following
| (18) |
where is the energy density of dark energy at a given redshift, and is the same quantity as . and are two constants quantifying the redshift dependence of the power modification. For , a suppression of the matter power spectrum occurs at later times if . In this work, we fix the index to , as the most direct power spectrum reduction. The parameterization is linked to the parameters of the late-time suppression of the power spectrum through:
| (19) |
where is presented in Equation 17 and is the scale factor. The two approaches are thus related, and we expect any potential deviation from the standard scenario appearing in one to be reflected in the other. Thus, we expect to confirm the results obtained in Section 4. Additionally, as reported in Section 1, there is good agreement between the measurements from the primary anisotropies of the CMB () and the CMB lensing, which probes a redshift range of . Consequently, a reduction of the power spectrum should be investigated in the low redshift Universe. Quantitatively, the best-fit energy density of dark energy reported in the last CMB anisotropy results of Planck20 is . This value is significantly reduced when the redshift increases. Consequently, significantly differs from 1 only at low redshift, indicating that the power spectrum is left unchanged at early times.
Fitting the eRASS1 cluster number counts with the sound horizon prior to this model, we find
| (20) |
at 68% confidence level, and where we fixed . We recall that the priors on all the parameters can be found in Table 1, and especially that the priors on are . Since we are measuring a non-zero parameter consistently with the findings of Lin et al. (2024) and Section 4, these results suggest that a significant reduction of structure formation happens at low redshift. Although significant, this finding must be interpreted in cluster count cosmology, where the density of dark matter halos hosting clusters is computed through the halo mass function. The parameters of the HMF are assumed to be universal in all the models considered (see Section 3.1). The impact of the change that we apply to the power spectrum on these parameters should be further investigated in the future. Additionally, another main result is that the best-fit value of the parameter decreases when we add the new degree of freedom to the power spectrum, consistent with the results presented in Section 4. The measurements become consistent with the cosmic shear inferred values. For example, (Li et al. 2023) reports a value of obtained from the two-point correlation functions from the HSC data.
Galaxy clusters probe the linear regime of structure formation and involve only the linear matter power spectrum. Remarkably, adding a degree of freedom to the matter power spectrum suggests a reduction of structure formation and decreases the value. This finding is discussed in Section 8. Overall, the parameter quantifies how the power spectrum could be reduced due to unknown physical processes or systematic effects at low redshift. Our results suggest that such reduction exists, although its nature remains to be identified.
6 Direct measurements of the structure growth through redshift evolution
The frameworks and results presented in Section 3, Section 4, and Section 5 assume a functional form of the growth rate presented in Equation (5), or the power spectrum in Equation (18). To independently probe the structure growth free of any functional parametrization and test the potential deviations from the standard structure formation scenario, we use a different method to measure the structure evolution using eRASS1 cluster counts.
In Section 4, we assume a value of the growth index , we then compute the associated growth factor with equations 6 and 8 and obtain the evolution of the r.m.s density fluctuations through . However, the cosmic linear growth index lacks an immediate physical interpretation. Indeed, even though a redshift evolution of the cosmic linear growth index can be expected in some theoretical models (Linder & Cahn 2007; Wen et al. 2023), the cosmic linear growth index remains an effective parameterization. The same issue exists with the power spectrum reduction model we used in Section 5, also a phenomenological parameterization. To avoid these issues, another method commonly used in the literature for probing the growth of structure is to divide the cluster sample into multiple bins and to compute the cosmological parameters directly in those subsamples employing the standard CDM parametrization in each bin (e.g., Bocquet et al. 2024).
The fluctuations of the density field probed by clusters number count over comoving spheres with a radius of () in several redshift bins traces the evolution of structure growth with redshift. This is possible since cluster abundance in each redshift bin is indeed a direct probe of the halo mass function, defined in Equation 1. Although we can express using its value at redshift zero multiplied by the normalized growth rate, the halo mass function depends only on the value of at the redshift of interest, and therefore is probed quasi-directly. In practice, the difference in growth rate modeling between the model and the canonical model with the standard GR will act just as a normalization difference in , given that the growth rate is a function of redshift. This method works independently of modeling assumptions as long as the growth rate is only a function of redshift, . Although this method is assumed to be model-independent compared to the model, it still relies on the assumptions of linear perturbation theory with a conventional growth within the corresponding redshift bins. For this reason, we consider both approaches (the model and the binning method in the redshift) jointly and test them using the eRASS1 observations. In the case of damped structure growth at lower redshifts, we expect that the normalization of the power spectrum is affected, creating discrepancies between our measurement and values inferred from the CMB measurements.
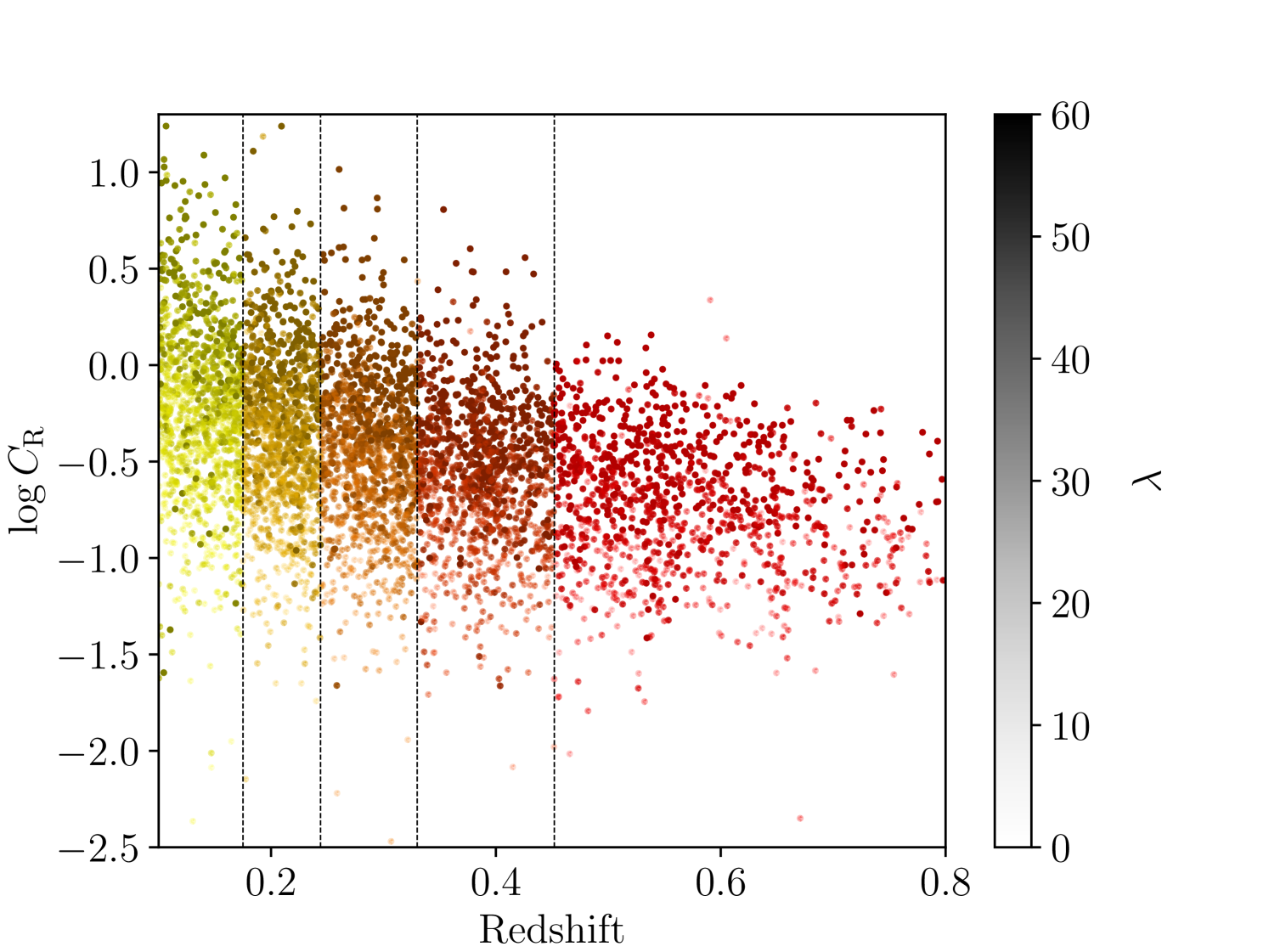
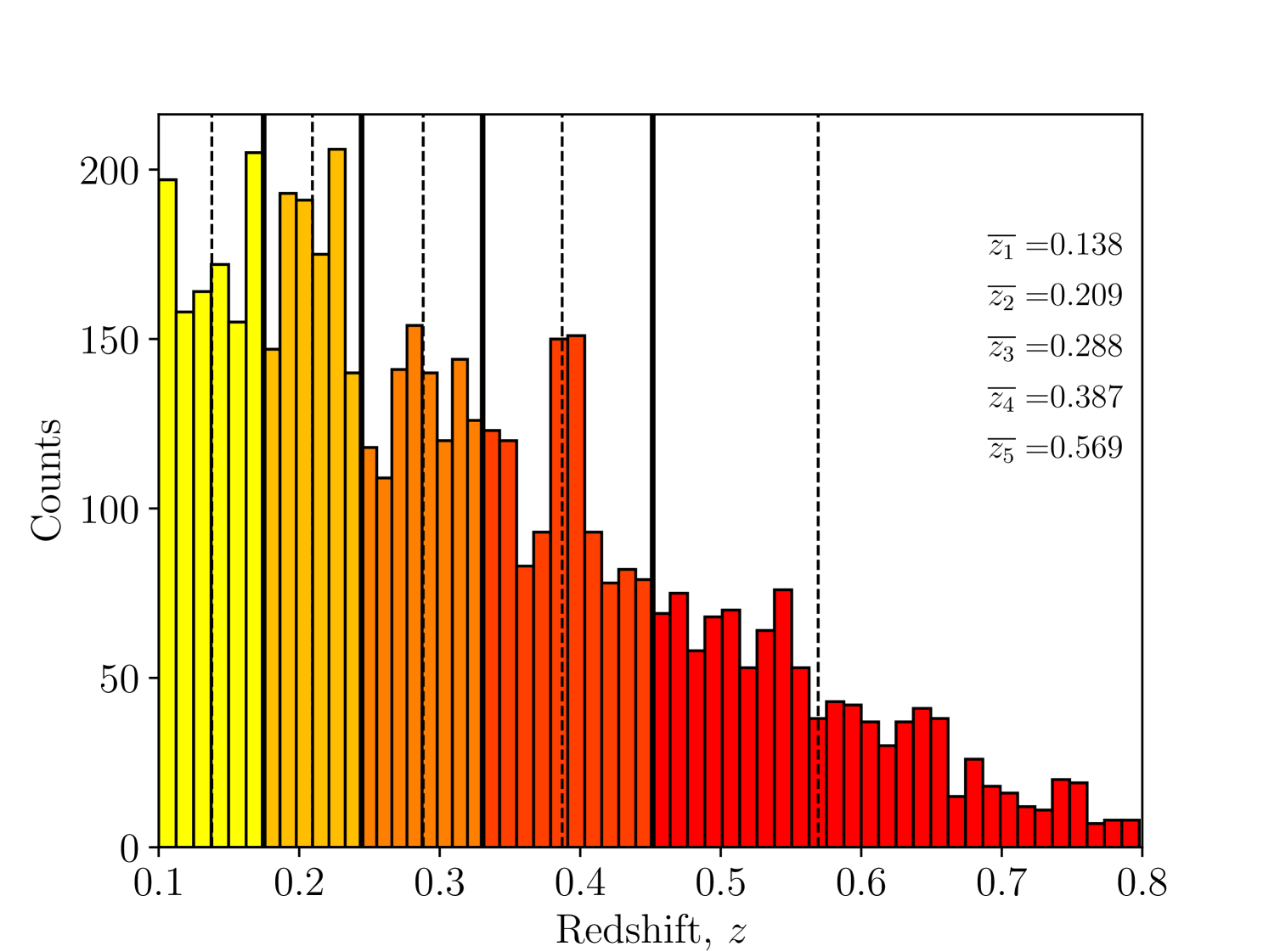
Our approach to measuring the redshift evolution in structure growth is based on binning the cluster number counts in redshift to measure the evolution of structure growth. The eRASS1 cosmology sample, comprising 5,259 ICM-selected and optically confirmed clusters of galaxies, is the largest ICM-selected sample to date. The cosmological parameter inference reaches a statistical precision similar to CMB experiments (see G24). We determine the number of clusters in each bin such that the matter density parameter is measured with at least 15% precision and has a similar number of clusters. With this requirement, the sample provides sufficient statistical power to generate five independent222Although the bins are never totally uncorrelated, they are large enough so that we can neglect the covariance. redshift bins (see Table 2). The first four bins have 1,052 clusters each with this binning scheme, leaving 1,051 clusters for the last highest redshift bin (). The corresponding redshift ranges are , and . The X-ray count-rate distribution as a function of redshift and richness of the subsamples are displayed in Figure 7.
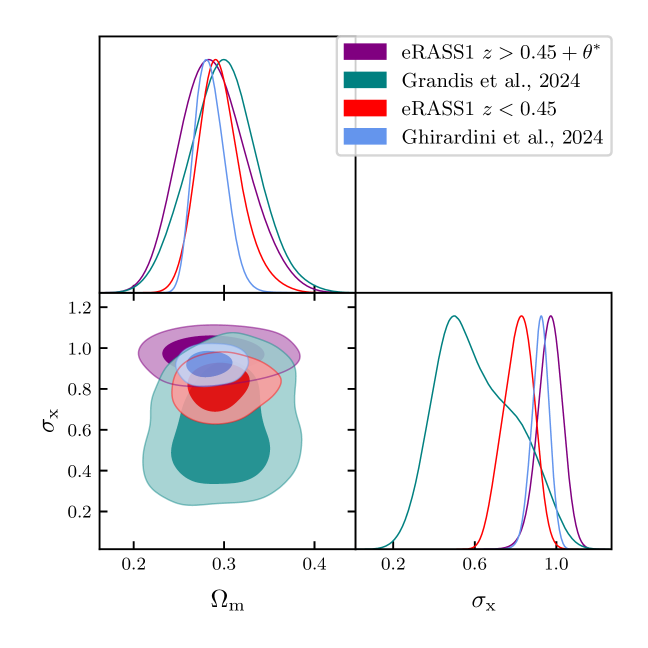
Our sample has sufficient statistical constraining power to measure the scaling relation parameters independently in each redshift bin jointly with the cosmological parameters shown in Table 1, unlike the previously published ICM-selected samples (e.g. Bocquet et al. 2024). Consequently, we fix the pivot redshift of the count-rate to mass () and richness to mass () scaling relations as described in G24 to the mean redshift in each bin . Particularly relevant measurements are the normalization of the power spectrum , and the matter density . These parameters are combined to recover the parameter in the redshift bin space specified above. We utilize the Boltzmann solver CAMB (Lewis & Challinor 2011) to compute the power spectrum for each redshift bin and infer the cosmological parameters. This process additionally provides a consistency check for our standard cosmology analysis presented in G24, also shown in Figures 8 and 11. For instance, our posteriors on the cosmological parameters, , , and , are consistent with each other within the five redshift bins, and the results in G24 at the confidence level. Our results are summarized in Table 2.
| Ghirardini et al. (2024) | ||||||
|---|---|---|---|---|---|---|
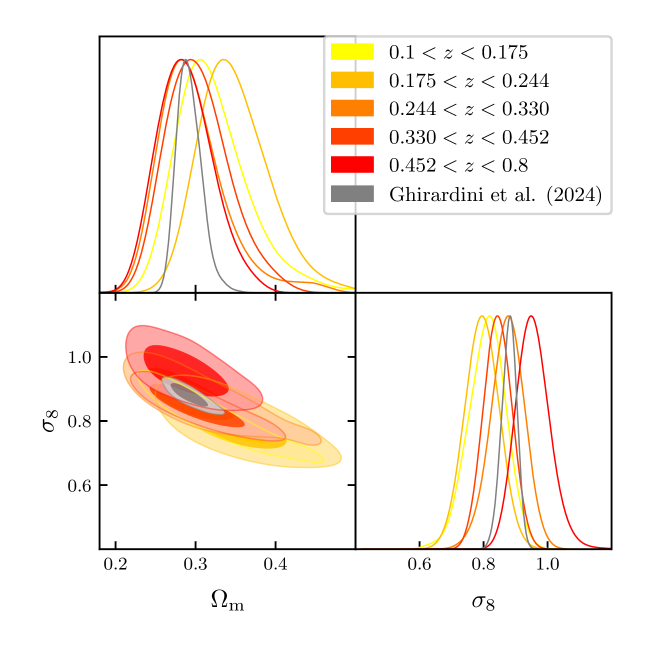
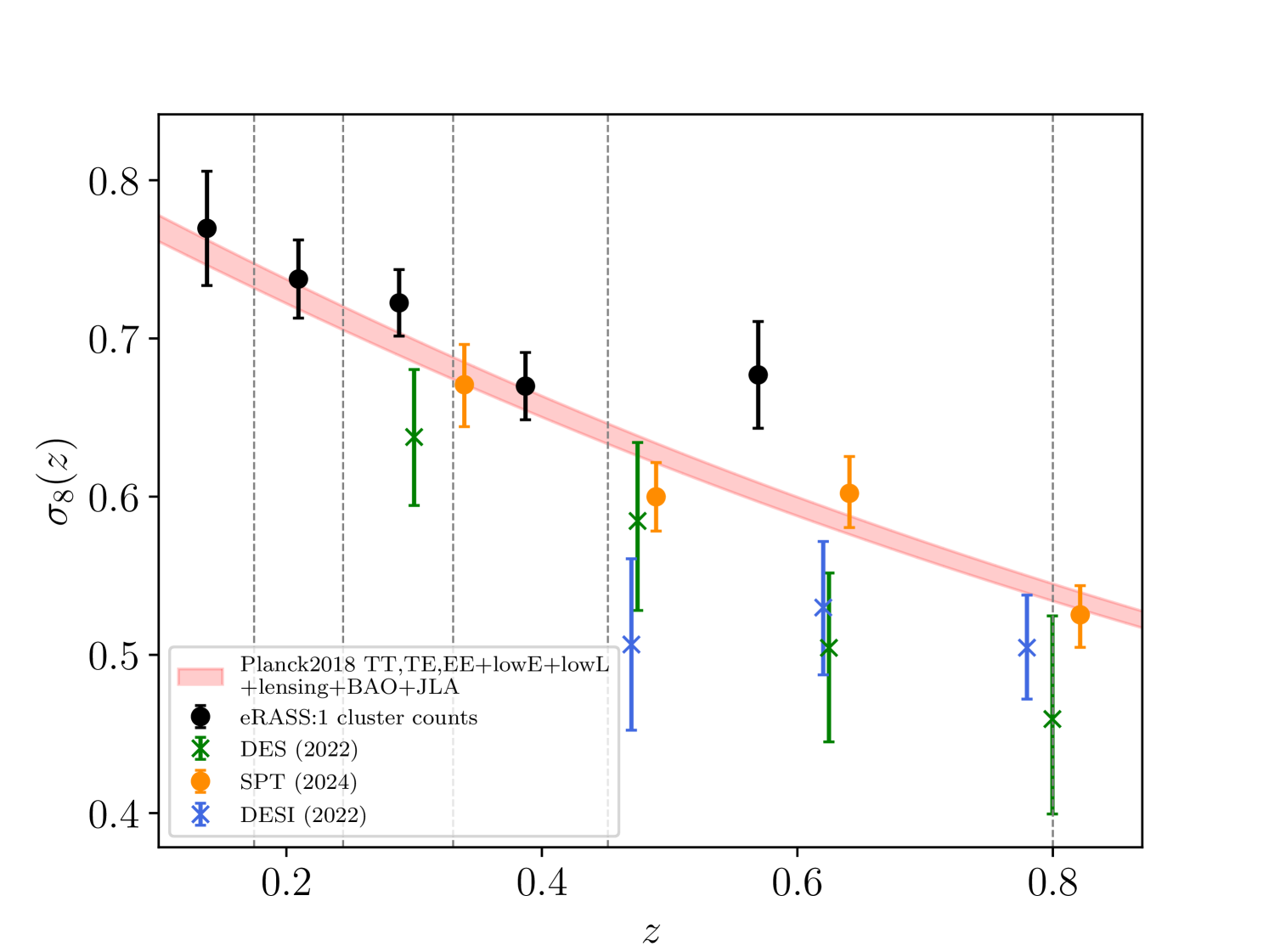
Finally, we can use these posteriors to recover the redshift evolution of the r.m.s of the density fluctuations, i.e., parameter. Similarly, we present our results that combine the sound horizon priors with eRASS1 cluster number counts in data points in black in Figure 9. The eRASS1 cosmology sample, when divided into five redshift intervals, shows hints of a reduction of structure formation at low redshifts. Although all the data points are compatible with the combined analysis of Planck, BAO, and JLA results (see Planck20) in Figure 9, they all remain above the CMB expectations. Although not significantly significant, this trend is visible in Figure 9. Consequently, we are compatible with the results provided in Section 4 and Section 5.
Our measurements broadly agree with the cluster abundance analysis from the SPT SZ experiment combined with the same sound horizon priors used in this work (Bocquet et al. 2024). However, it is worth noting that, unlike our approach, the analysis presented in Bocquet et al. (2024) uses the same scaling relation parameters for all redshift bins, as well as a unique at all redshift. Although their sample size is significantly smaller (1005 clusters of galaxies as opposed to 5259 clusters used in this work), this assumption is reflected in the uncertainties in the quoted results. This might explain why they do not recover the power suppression trend found in this work, as their sample covers a larger and broader redshift range.
We also compare our result with the DES Y3 combined cosmic shear and galaxy clustering results (Abbott et al. 2023b), who provided results with the same approach using cosmic shear and galaxy clustering. They divide their sample in redshift bins in a range of , similar to the redshift coverage of eRASS1 clusters. The observed trend of lower structure formation in DES-Y3 data reported in the low redshift regime is in tension with our and CMB measurements. The same trend is found in the DESI Legacy Imaging Survey Luminous Red Galaxies (LRG) combined with CMB lensing (White et al. 2022).
In this work, we first defined a reduction of structure formation as a higher value of the cosmic linear growth index (see Section 3). Indeed, equation 4 and equation 5 show that a higher leads to a lower , and thus, the clustering of matter with time occurs at a slower rate. Consequently, we show that the growth factor is flattened, as shown in Figure 2. All the models we consider show the same trend, including the last measurements through the sample binning method. As a consequence, the flattening of the growth factor leads to a lower measurement of . We emphasize that this definition does not imply that we expect a lower for all redshifts, as found with probes that include non-linear physics (Abbott et al. 2022; White et al. 2022).
Overall, our model agnostic method agrees well with the CMB extrapolated values while hinting at a reduction of structure growth at low-. We note that the fifth bin () has a higher inferred compared to the trend observed in the previous ones. We investigate the impact of this specific bin in our analysis and the origin of this systematic effect in Section 7.
7 Systematic effects and robustness tests of the cosmology analysis
In this section, we evaluate the effect of the possible systematic effects on the results presented in this work, scaling relations, and cosmological constraints in general, shown G24 and Artis et al. (2024). Among those is the impact of neutrinos (see Section 8) and the large scatter observed in the scaling relations between the X-ray observable, i.e., count-rate, in the high redshift bin used to infer cluster mass. We examine the redshift-dependent scatter (the count rates follow a log-normal probability distribution function with scatter ) in the count-rate mass scaling relation () to understand the effect of it in the subsequent cosmology analyses using the binned analysis presented in Section 6.
7.1 Impact of the high redshift clusters on cosmology and observed scatter
Motivated by the results obtained in Section 6, we examine the cosmology results obtained from the standard analysis presented in G24 and the results of the binned analysis presented in this work further (see the comparison shown in Figure 8). As noted earlier, the cosmological parameters primarily constrained by cluster counts, , and , are consistent at the level in each redshift bin with the full sample analysis. In this subsection, we further investigate the robustness of our results when the analysis is limited to only lower redshift clusters at and explore the dependence on the assumptions on the mass scaling relations.
As a first test, we repeat the standard cosmology analysis performed in G24 while considering the sample with . The catalog in this redshift range comprises a sample of 4196 clusters, which represent 79.8% of the cosmology sample provided in Bulbul et al. (2024). The best-fit parameters of the concordance model in the redshift interval of are;
| (21) |
In parentheses, the best-fit parameters of the model from the full sample analysis reported in G24 are provided. Although the statistical precision is diminished due to the lower number of clusters in the analysis, we do not observe any departures from the full sample analysis of G24 within the confidence level. The results are displayed in Figure 10. Consequently, despite the fifth bin () having a best-fit value higher than those of the low-redshift regime, we conclude that the cosmological parameter inference is, for the most part, insensitive to the subdivision of the full sample to high and low-redshift clusters. A similar analysis has been performed for a full sample of clusters in a redshift range of in G24; the authors reached the same conclusion that the exclusion of the highest redshift clusters in the sample has minimal effect on the best-fit parameters and of the concordance model.
We repeat the same exercise for the model to test if an impact could be detected when we free the structure growth parameters. We reach a similar conclusion that excluding the highest redshift clusters above a redshift of does not produce significant tension on the constraints on the , , and parameters in the case, they remain consistent at level. The comparisons of the results based on both samples are shown in Figure 20. However, the tension between the measurements of eROSITA combined with the CMB and the standard GR inferred value is reduced as we remove the high redshift clusters from our sample; the tension obtained with the full sample analysis is reduced to confidence level due to the increase in the uncertainties. The results of this analysis are presented in Appendix D. We conclude that while high redshift clusters might have a small impact on the analysis, our main conclusions are preserved.
One interesting outcome of this test is the potential systematics related to the high redshift cluster sample at . The posterior value of is slightly higher in the highest redshift bin (), consequently increasing the value compared to the lower redshift bins as clearly seen in Figure 9. Although excluding the highest redshift range produces consistent results with the full sample analysis as presented in the previous section and proves that our standard cosmology analysis is robust against sample selection in a wide redshift interval utilized in the consequent cosmology analyses, we further investigate the effect of the high redshift clusters on the scatter of the count-rate and mass scaling relation. The observed large scatter on the X-ray count-rate scaling relations of the full sample decreases from to when the highest redshift bin excluded in the analysis. As seen in Figure 12, this result indicates that the high redshift clusters are mostly responsible for the high observed scatter in the scaling relations utilizing the full sample in the redshift range of , presented in. This result can also be noticed in Table 2. This high scatter is likely due to a higher contamination fraction of the sample at high redshifts. Our implementation of the mixing model partially mitigates the effect of contamination in the results presented on eRASS1 data in G24. However, the increased number of AGN in clusters of galaxies may lead to skewness and high scatter in the count rate mass scaling relation (Biffi et al. 2018). Future work on the deeper eROSITA and DES data will carefully investigate and model the high redshift AGN contamination in clusters with a reduced scatter in scaling relations. It is important to note that the tests performed in this work prove that our modeling through scaling relations accurately represents the underlying cluster population regardless of the observed large scatter due to potential observational effects or cluster physics. Therefore, we conclude that the observed large scatter does not significantly affect our results presented in G24, Artis et al. (2024).
7.2 Consistency of the mass scale
Another key ingredient of cluster abundance cosmology is the scaling relation between the observable used in the detection chain and the underlying cluster/dark matter halo mass. Our cosmological framework uses the X-ray count rate measured within R500 as the primary observable. The parameters of this count rate to mass () relation are fitted jointly with the cosmological parameters. The X-ray scaling relation is described as follows:
| (22) |
As in G24, cts / s, , and . Note that the pivot value is changed accordingly in each redshift bin in the binned analysis. The other terms follow
| (23) |
and
| (24) |
Since the modifications of the power spectrum applied here do not concern mass estimation, we should find consistent scaling relations in the different models. In all this work, we fix the luminosity distance dependence to and normalized Hubble parameter dependence to 2, which are the values expected in the self-similar model (Kaiser 1986). In Appendix C, we show the corner plot obtained for the scaling relation parameters for the two models. We present the , , and the models as reference cases. Overall, there is good agreement between our different models whenever we consider modifications of the power spectrum. Thus, the shape of the scaling relation remains consistent in different cosmological models. This means that the mass calibration is robust and that changes in the cosmological model primarily affect the underlying distribution of clusters represented by the halo mass function. One exception to this general agreement is the parameters , which encapsulates the redshift dependence of the scaling relation. It is significantly lower at the 2 level in than for our standard CDM case. Indeed, in , the best-fit value of this parameter is consistent with . Since we modify the growth rate of structures in the different considered models, we expect a propagation on this parameter without it being related to a specific systematic effect. However, it seems that for the case, the preferred value tends to be lower.
We also note that when freeing the dark energy equation of state, we recover a good agreement between the different posteriors of the scaling relations. Overall, the scaling relations parameter estimates are robust against our modeling at the level.
We also directly estimate a possible redshift evolution of the scaling relation, thanks to the framework described in Section 6. We provide a corner plot of all the X-ray scaling relation parameters compared in Appendix C. We do not observe a statistically significant difference between the scaling relation parameters in our redshift bins. We defined the redshift bins to possess the same number of observed clusters. As fewer clusters are observed at high redshift (due to the halo mass function and the eRASS1 selection function), high redshift bins cover a larger redshift space. As a consequence, the parameters describing the redshift evolution of the X-ray scaling relation and (see G24) are better constrained using the last and largest redshift bins. This also confirms that our weak-lensing mass calibration performs well at all redshifts.
7.3 Goodness of fit
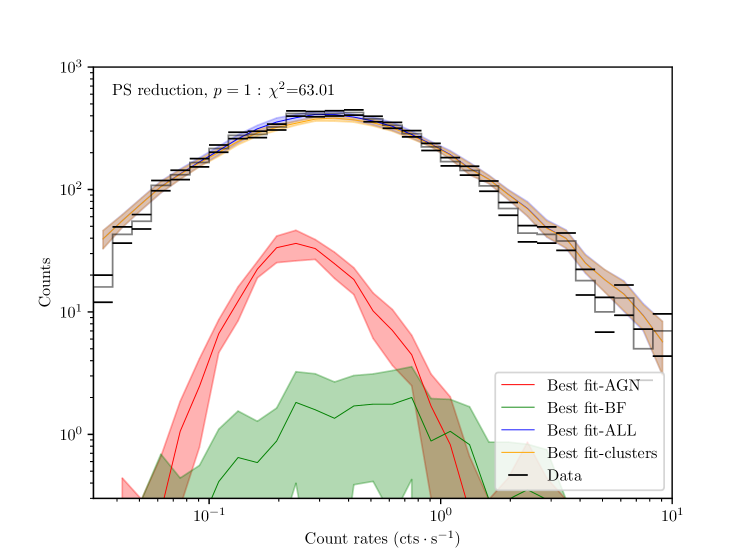
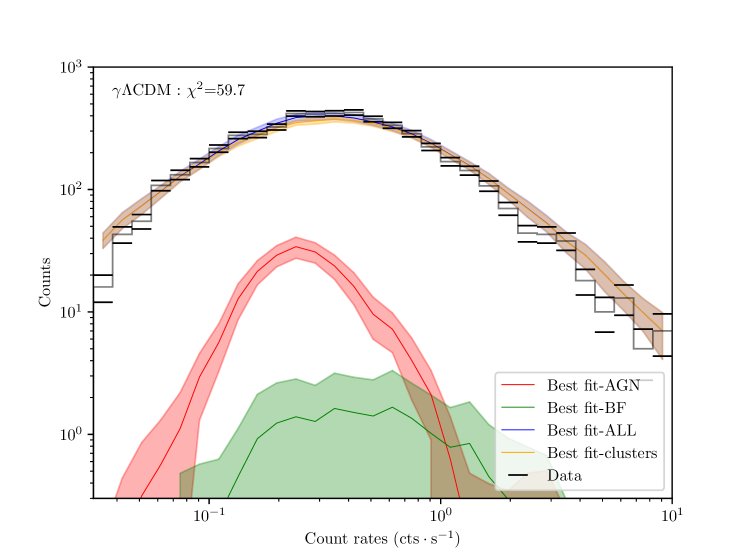
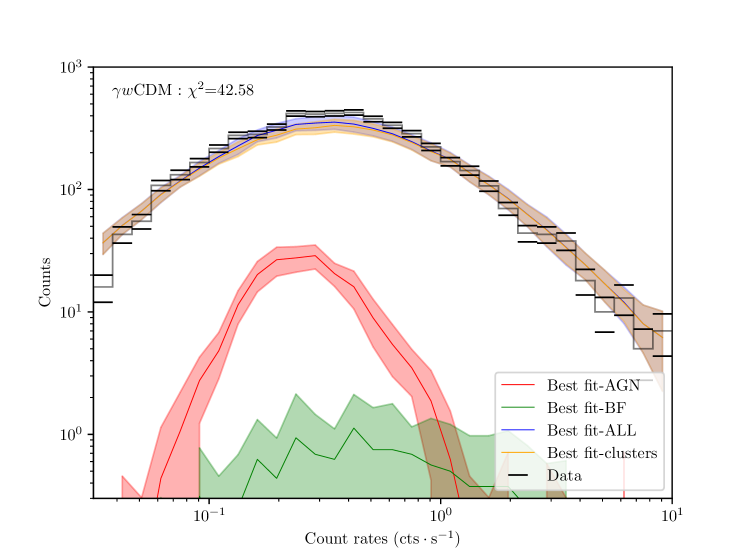
This work uses the formalism described in G24 to fit the cosmological parameters. In particular, we are using a Poison likelihood with a complex underlying model. Consequently, it is not straightforward to produce a goodness-of-fit metric for our measurements. Nevertheless, since we fit multiple models, we estimate how successfully our model reproduces the data distribution. We proceed as follows: for each of the three models, we produce 500 mock observations from the posterior distribution of the model parameters obtained in Section 4 and Section 5. We produce the mock observation for the galaxy clusters and the contaminant part, composed of active galactic nuclei (AGN) and false detection due to background fluctuations (BF). From these mocks, we produce the expected distribution of objects in the catalog, i.e., the number density of objects per unit of X-ray count rates. We then compare this distribution with the observed distribution of clusters. The results are shown in Figure 13. In all cases, the fit is visibly a good data reproduction. For the case of the power spectrum reduction model, we find , while for and for , , all of these obtained with 30 d.o.f.
We conclude that our model reliably reproduces the data distribution, with a preference for the . We emphasize that this quantitative estimation primarily verifies that our model performs well. The next data releases will provide a full goodness-of-fit analysis for our cluster abundance Poisson statistics.
8 Discussion and conclusions
In this work, we present results on the measurement of the growth of structure using X-ray detected eRASS1 clusters, in combination with optical surveys, such as LS DR10-South for optical confirmation and redshift measurements, the DES, KiDS, and HSC for weak lensing mass calibration. Specifically, the parameterization of the growth factor presented in equation 5 modifies the structure growth rate (Section 4) in connection with the power spectrum reduction model (Section 5). Secondly, a model agnostic strategy aiming at measuring the cosmological parameters at different redshifts to reconstruct the history of the evolution in density fluctuations (Section 6).
We also probe the evolution of structure formation with the late-time power suppression presented in Section 5. The two approaches are thus related, and we expect any potential deviation from the standard scenario appearing in one to be reflected in the other. In all three cases, we combine our structure growth constraints with the sound horizon priors from the cosmic microwave background as it is one of the most robust cosmological measurements available. In all three cases, we find observations that can be interpreted as a low redshift reduction of structure formation. First, the parameterization of the growth factor, while still compatible with the standard value at both in and , has a best-fit value that favors higher values of the cosmic linear growth index. Additionally, the model agnostic redshift splitting of the eRASS1 cosmological catalog shows a similar pattern. Indeed, Figure 2 shows how the cosmic linear growth index increases the growth factor at low redshift. Our binned cosmological results indicate a preference for the same trend while still being statistically consistent with CMB measurements. Finally, the power spectrum reduction model shows a best-fit value that significantly excludes an absence of power reduction.
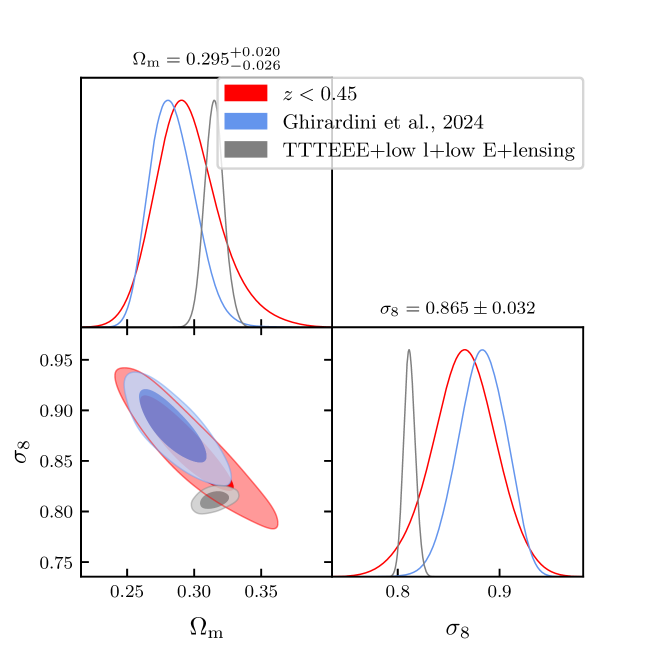
These three results indicate a deviation from the widely accepted paradigm of structure formation. Interestingly, in the case of the cosmic linear growth index and power spectrum reduction models, we find that modifying the power spectrum leads to a decrease in the value, and thus our inferred value. Consequently, these observations may offer evidence that the tension could be accounted for by a modification of the matter power spectrum at the scales investigated by cosmic shear and other lensing studies (Nguyen et al. 2023), provided that the explanation for the tension as a result of systematic uncertainties related to baryonic effects is ruled out. Indeed, Figure 11 shows that the in all of the three models used in this work (, , and the power spectrum reduction model) the value of the parameter is reduced from the value found in G24 in the case, to
| (25) |
These values are compatible with the ones routinely inferred by cosmic shear studies but in and at small scales. Using KIDS data, Li et al. (2023) found , close to the HSC results presented in Dalal et al. (2023) of . Using DES data and the same cosmological probe, Amon et al. (2022) found . Finally, combining DES and KIDS data, Dark Energy Survey and Kilo-Degree Survey Collaboration et al. (2023) found . We also note that other probes affected by non-linear physical effects also find lower values. For example Palanque-Delabrouille et al. (2020) used the Ly forest to infer . Given that cosmological probes sensitive to the non-linear regime yield a lower , our findings may imply that this discrepancy may be simply due to non-linear effects influencing those probes. Although galaxy clusters are highly non-linear structures, their number density can be described using the linear matter power spectrum. Effects related to non-linear physics are restricted to the HMF parameterization, which is assumed to be universal. Thus, when inferring cosmology using galaxy cluster number counts, we obtain values closer to the one inferred by the CMB. Introducing an additional degree of freedom in the power spectrum analysis could suggest that the reduction in structure formation is scale-dependent, potentially resolving the tension.
Neutrinos smooth structure formation at small scales, thus reducing the power spectrum at high . Therefore, their effect on the cosmological parameter estimation impacts the power spectrum reduction we are probing here. However, in this work, we have chosen to consider massless neutrinos. This modeling choice thus requires a very careful justification. We show that the impact of neutrinos is negligible and intrinsically different compared to the power spectrum reduction reported here. We leave the combined measurement of the neutrino masses and the power spectrum reduction parameterization to future works.
Three main reasons explain our consideration of massless neutrinos: the lack of theoretical background for considering neutrinos together with a power spectrum reduction at low redshift, the relative size of the shift in the cosmological parameter space, and the intrinsic nature of the power impression we are investigating.
First, since Costanzi et al. (2013), we know that the effect of neutrinos on the halo mass function is well captured when the cold dark matter only power spectrum is considered instead of the total matter power spectrum in the fitting function parameterized by Tinker et al. (2008). However, in this formalism, neutrinos also induce a scale dependence in the growth factor presented in equation 9. In other words, we have
| (26) |
as . Consequently, when using the cold dark matter spectrum, we need to compute the spectrum directly at the considered redshift. Analytical models exist for the linear growth factor in the presence of neutrinos (Kiakotou et al. 2008), but they are not compatible with the cosmic linear growth index. In general, we do not currently have a satisfying way of parameterizing the linear growth factor in the presence of neutrinos together with the cosmic linear growth index in the context of galaxy cluster number counts. This consideration highlights the difficulty of finding a model that fits both. The following two paragraphs, however, show that the effect of neutrinos can be neglected in this work.
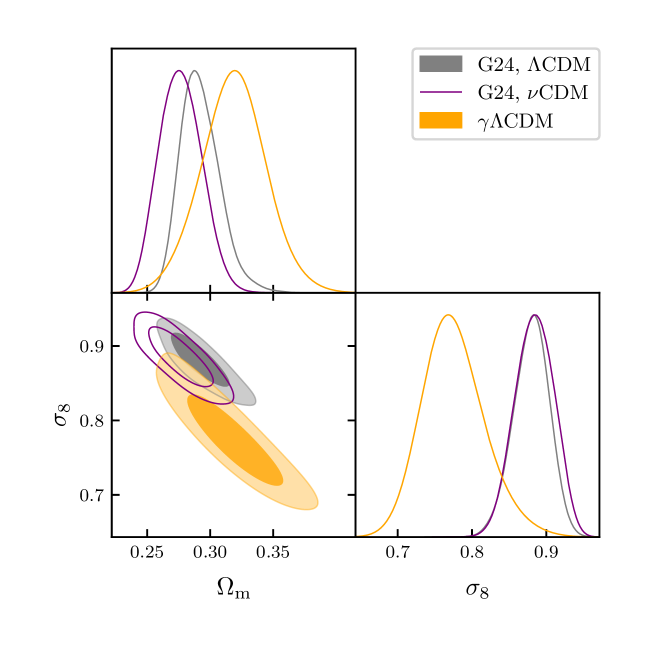
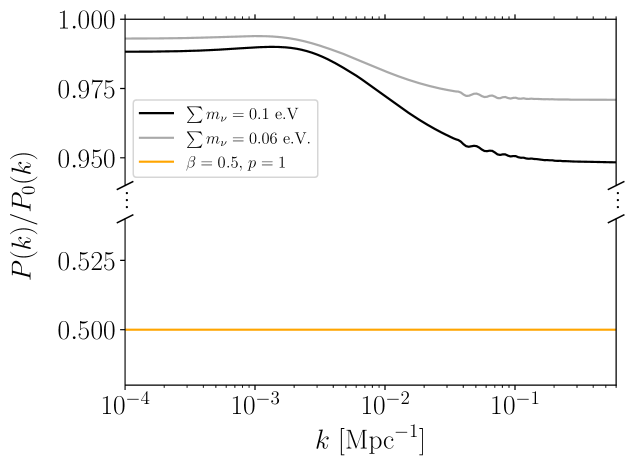
Figure 14 shows how neutrinos impact cosmological parameter estimation. Indeed, the shift in the cosmological parameter space produced by neutrinos compared to a model when they are massless is of in the plane. This number must be compared with the shift produced by the power spectrum reduction models considered in this work. In other words, neutrinos alone cannot explain the reduction observed and presented here. Although their effect is indeed degenerate with the power spectrum reduction, it is negligible compared to our results for a catalog of clusters of the size of eRASS1.
Finally, this work investigates a potential redshift reduction of the power spectrum. Neutrinos induce a scale-dependent damping of the power spectrum in the redshift range probed by eRASS1 galaxy cluster count. Indeed, at a fixed scale , the reduction induced by neutrinos on the matter power spectrum is constant in the redshift range . Figure 15. On the other hand, the models we are probing only modify structure formation at low redshift but at all scales. Consequently, both effects are different and do not affect the result in a way that can be compared.
For the aforementioned reasons, our results are primarily not affected by the absence of massive neutrinos. However, more theoretical efforts will be necessary to probe the structure reduction we detect when larger and deeper eRASS catalogs are available. At this time, it will not be possible to neglect the effect of neutrinos anymore.
Recent studies show the current implementation of baryonic feedback in numerical simulations isn’t enough to account for the reduction in observed in surveys sensitive to small scales, as demonstrated in (Grandis et al. 2024a). However, if baryonic feedback is poorly understood and its effects are greater than anticipated, it could potentially reconcile the linear and non-linear regimes and explain the observed tension (Preston et al. 2023).
Our results agree with other studies that infer a reduction of the structure formation at low redshifts (Samushia et al. 2013; Beutler et al. 2014; Kazantzidis & Perivolaropoulos 2021; Lin et al. 2024). However, a robust conclusion can only be provided if every potential systematic effect is extensively studied through numerical simulations. We also investigate redshift-dependent potential systematic effects in this work and our CDM analysis. Although statistically consistent, the fifth and highest redshift bin () has a higher value than the other four at lower redshifts. Although the scatter in this bin is significantly higher, it does not affect the results of this work. However, the reason for this scatter in the high redshift regime, e.g., increased AGN contamination or photometric redshift uncertainties, will be investigated in upcoming cosmology analyses.
Acknowledgements.
This work is based on data from eROSITA, the soft X-ray instrument aboard SRG, a joint Russian-German science mission supported by the Russian Space Agency (Roskosmos), in the interests of the Russian Academy of Sciences represented by its Space Research Institute (IKI), and the Deutsches Zentrum für Luft und Raumfahrt (DLR). The SRG spacecraft was built by the Lavochkin Association (NPOL) and its subcontractors and is operated by NPOL with support from the Max Planck Institute for Extraterrestrial Physics (MPE). The development and construction of the eROSITA X-ray instrument was led by MPE, with contributions from the Dr. Karl Remeis Observatory Bamberg & ECAP (FAU Erlangen-Nuernberg), the University of Hamburg Observatory, the Leibniz Institute for Astrophysics Potsdam (AIP), and the Institute for Astronomy and Astrophysics of the University of Tübingen, with the support of DLR and the Max Planck Society. The Argelander Institute for Astronomy of the University of Bonn and the Ludwig Maximilians Universität Munich also participated in the science preparation for eROSITA. The eROSITA data shown here were processed using the eSASS software system developed by the German eROSITA consortium.E. Bulbul, V. Ghirardini, A. Liu, S. Zelmer, and X. Zhang acknowledge financial support from the European Research Council (ERC) Consolidator Grant under the European Union’s Horizon 2020 research and innovation program (grant agreement CoG DarkQuest No 101002585). N. Clerc was financially supported by CNES. T. Schrabback and F. Kleinebreil acknowledge support from the German Federal Ministry for Economic Affairs and Energy (BMWi) provided through DLR under projects 50OR2002, 50OR2106, and 50OR2302, as well as the support provided by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under grant 415537506.
The Innsbruck authors acknowledge the support provided by the Austrian Research Promotion Agency (FFG) and the Federal Ministry of the Republic of Austria for Climate Action, Environment, Energy, Mobility, Innovation and Technology (BMK) via the Austrian Space Applications Programme with grant numbers 899537, 900565, and 911971.
The Legacy Surveys consist of three individual and complementary projects: the Dark Energy Camera Legacy Survey (DECaLS; Proposal ID #2014B-0404; PIs: David Schlegel and Arjun Dey), the Beijing-Arizona Sky Survey (BASS; NOAO Prop. ID #2015A-0801; PIs: Zhou Xu and Xiaohui Fan), and the Mayall z-band Legacy Survey (MzLS; Prop. ID #2016A-0453; PI: Arjun Dey). DECaLS, BASS, and MzLS together include data obtained, respectively, at the Blanco telescope, Cerro Tololo Inter-American Observatory, NSF’s NOIRLab; the Bok telescope, Steward Observatory, University of Arizona; and the Mayall telescope, Kitt Peak National Observatory, NOIRLab. Pipeline processing and analyses of the data were supported by NOIRLab and the Lawrence Berkeley National Laboratory (LBNL). The Legacy Surveys project is honored to be permitted to conduct astronomical research on Iolkam Du’ag (Kitt Peak), a mountain with particular significance to the Tohono O’odham Nation.
Funding for the DES Projects has been provided by the U.S. Department of Energy, the U.S. National Science Foundation, the Ministry of Science and Education of Spain, the Science and Technology FacilitiesCouncil of the United Kingdom, the Higher Education Funding Council for England, the National Center for Supercomputing Applications at the University of Illinois at Urbana-Champaign, the Kavli Institute of Cosmological Physics at the University of Chicago, the Center for Cosmology and Astro-Particle Physics at the Ohio State University, the Mitchell Institute for Fundamental Physics and Astronomy at Texas A&M University, Financiadora de Estudos e Projetos, Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro, Conselho Nacional de Desenvolvimento Científico e Tecnológico and the Ministério da Ciência, Tecnologia e Inovação, the Deutsche Forschungsgemeinschaft, and the Collaborating Institutions in the Dark Energy Survey. The Collaborating Institutions are Argonne National Laboratory, the University of California at Santa Cruz, the University of Cambridge, Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas-Madrid, the University of Chicago, University College London, the DES-Brazil Consortium, the University of Edinburgh, the Eidgenössische Technische Hochschule (ETH) Zürich, Fermi National Accelerator Laboratory, the University of Illinois at Urbana-Champaign, the Institut de Ciències de l’Espai (IEEC/CSIC), the Institut de Física d’Altes Energies, Lawrence Berkeley National Laboratory, the Ludwig-Maximilians Universität München and the associated Excellence Cluster Universe, the University of Michigan, the National Optical Astronomy Observatory, the University of Nottingham, The Ohio State University, the OzDES Membership Consortium, the University of Pennsylvania, the University of Portsmouth, SLAC National Accelerator Laboratory, Stanford University, the University of Sussex, and Texas A&M University. Based on observations made with ESO Telescopes at the La Silla Paranal Observatory under program IDs 177.A-3016, 177.A-3017, 177.A-3018, and 179.A-2004, and on data products produced by the KiDS consortium. The KiDS production team acknowledges support from: Deutsche Forschungsgemeinschaft, ERC, NOVA and NWO-M grants; Target; the University of Padova, and the University Federico II (Naples). This paper makes use of software developed for the Large Synoptic Survey Telescope. We thank the LSST Project for making their code available as free software at http://dm.lsst.org
This work made use of the following Python software packages: SciPy333https://scipy.org/ (Virtanen et al. 2020), Matplotlib444https://matplotlib.org/ (Hunter 2007), Astropy555https://www.astropy.org/ (Astropy Collaboration et al. 2022), NumPy666https://numpy.org/ (Harris et al. 2020), CAMB (Lewis & Challinor 2011), pyCCL777https://github.com/LSSTDESC/CCL (Chisari et al. 2019), GPy888https://github.com/SheffieldML/GPy (GPy since 2012), climin999https://github.com/BRML/climin (Bayer et al. 2015), ultranest101010https://github.com/JohannesBuchner/UltraNest/ (Buchner 2021)
References
- Abbott et al. (2020) Abbott, T. M. C., Aguena, M., Alarcon, A., et al. 2020, Phys. Rev. D, 102, 023509
- Abbott et al. (2022) Abbott, T. M. C., Aguena, M., Alarcon, A., et al. 2022, Phys. Rev. D, 105, 023520
- Abbott et al. (2023a) Abbott, T. M. C., Aguena, M., Alarcon, A., et al. 2023a, Phys. Rev. D, 107, 083504
- Abbott et al. (2023b) Abbott, T. M. C., Aguena, M., Alarcon, A., et al. 2023b, Phys. Rev. D, 107, 083504
- Aihara et al. (2018) Aihara, H., Armstrong, R., Bickerton, S., et al. 2018, PASJ, 70, S8
- Aiola et al. (2020) Aiola, S., Calabrese, E., Maurin, L., et al. 2020, J. Cosmology Astropart. Phys., 2020, 047
- Amon et al. (2022) Amon, A., Gruen, D., Troxel, M. A., et al. 2022, Phys. Rev. D, 105, 023514
- Artis et al. (2024) Artis, E., Ghirardini, V., Bulbul, E., et al. 2024, arXiv e-prints, arXiv:2402.08459
- Asencio et al. (2021) Asencio, E., Banik, I., & Kroupa, P. 2021, MNRAS, 500, 5249
- Astropy Collaboration et al. (2022) Astropy Collaboration, Price-Whelan, A. M., Lim, P. L., et al. 2022, ApJ, 935, 167
- Aymerich et al. (2024) Aymerich, G., Douspis, M., Pratt, G. W., et al. 2024, arXiv e-prints, arXiv:2402.04006
- Basilakos & Anagnostopoulos (2020) Basilakos, S. & Anagnostopoulos, F. K. 2020, European Physical Journal C, 80, 212
- Batista (2014) Batista, R. C. 2014, Phys. Rev. D, 89, 123508
- Bayer et al. (2015) Bayer, J., Osendorfer, C., Diot-Girard, S., Rueckstiess, T., & Urban, S. 2015, TUM, Tech. Rep.
- Beutler et al. (2014) Beutler, F., Saito, S., Seo, H.-J., et al. 2014, MNRAS, 443, 1065
- Bianchini et al. (2020) Bianchini, F., Wu, W. L. K., Ade, P. A. R., et al. 2020, ApJ, 888, 119
- Biffi et al. (2018) Biffi, V., Dolag, K., & Merloni, A. 2018, MNRAS, 481, 2213
- Bocquet et al. (2024) Bocquet, S., Grandis, S., Bleem, L. E., et al. 2024, arXiv e-prints, arXiv:2401.02075
- Bocquet et al. (2015) Bocquet, S., Saro, A., Mohr, J. J., et al. 2015, ApJ, 799, 214
- Brout et al. (1978) Brout, R., Englert, F., & Gunzig, E. 1978, Annals of Physics, 115, 78
- Buchner (2021) Buchner, J. 2021, The Journal of Open Source Software, 6, 3001
- Bulbul et al. (2024) Bulbul, E., Liu, A., Kluge, M., et al. 2024, A&A, 685, A106
- Bullock (2010) Bullock, J. S. 2010, arXiv e-prints, arXiv:1009.4505
- Busillo et al. (2023) Busillo, V., Covone, G., Sereno, M., et al. 2023, MNRAS, 524, 5050
- Chisari et al. (2019) Chisari, N. E., Alonso, D., Krause, E., et al. 2019, CCL: Core Cosmology Library, Astrophysics Source Code Library, record ascl:1901.003
- Chiu et al. (2023) Chiu, I. N., Klein, M., Mohr, J., & Bocquet, S. 2023, MNRAS, 522, 1601
- Clerc (2023) Clerc, N. e. a. 2023
- Costanzi et al. (2019) Costanzi, M., Rozo, E., Simet, M., et al. 2019, MNRAS, 488, 4779
- Costanzi et al. (2021) Costanzi, M., Saro, A., Bocquet, S., et al. 2021, Phys. Rev. D, 103, 043522
- Costanzi et al. (2013) Costanzi, M., Villaescusa-Navarro, F., Viel, M., et al. 2013, J. Cosmology Astropart. Phys., 2013, 012
- Dalal et al. (2023) Dalal, R., Li, X., Nicola, A., et al. 2023, Phys. Rev. D, 108, 123519
- Dark Energy Survey and Kilo-Degree Survey Collaboration et al. (2023) Dark Energy Survey and Kilo-Degree Survey Collaboration, Abbott, T. M. C., Aguena, M., et al. 2023, The Open Journal of Astrophysics, 6, 36
- de Mattia et al. (2021) de Mattia, A., Ruhlmann-Kleider, V., Raichoor, A., et al. 2021, MNRAS, 501, 5616
- DESI Collaboration et al. (2024) DESI Collaboration, Adame, A. G., Aguilar, J., et al. 2024, arXiv e-prints, arXiv:2404.03002
- Dey et al. (2019) Dey, A., Schlegel, D. J., Lang, D., et al. 2019, AJ, 157, 168
- Di Valentino et al. (2021a) Di Valentino, E., Anchordoqui, L. A., Akarsu, Ö., et al. 2021a, Astroparticle Physics, 131, 102604
- Di Valentino et al. (2021b) Di Valentino, E., Mena, O., Pan, S., et al. 2021b, Classical and Quantum Gravity, 38, 153001
- Freedman et al. (2024) Freedman, W. L., Madore, B. F., Jang, I. S., et al. 2024, arXiv e-prints, arXiv:2408.06153
- Fumagalli et al. (2024) Fumagalli, A., Costanzi, M., Saro, A., Castro, T., & Borgani, S. 2024, A&A, 682, A148
- Garc´ıa-Garc´ıa et al. (2021) García-García, C., Ruiz-Zapatero, J., Alonso, D., et al. 2021, J. Cosmology Astropart. Phys., 2021, 030
- Garrel et al. (2022) Garrel, C., Pierre, M., Valageas, P., et al. 2022, A&A, 663, A3
- Gatti et al. (2021) Gatti, M., Sheldon, E., Amon, A., et al. 2021, MNRAS, 504, 4312
- Ghirardini et al. (2024) Ghirardini, V., Bulbul, E., Artis, E., et al. 2024, arXiv e-prints, arXiv:2402.08458
- Giblin et al. (2021) Giblin, B., Heymans, C., Asgari, M., et al. 2021, A&A, 645, A105
- Gil-Mar´ın et al. (2017) Gil-Marín, H., Percival, W. J., Verde, L., et al. 2017, MNRAS, 465, 1757
- GPy (since 2012) GPy. since 2012, GPy: A Gaussian process framework in python, http://github.com/SheffieldML/GPy
- Grandis et al. (2024a) Grandis, S., Aricò, G., Schneider, A., & Linke, L. 2024a, MNRAS, 528, 4379
- Grandis et al. (2024b) Grandis, S., Ghirardini, V., Bocquet, S., et al. 2024b, arXiv e-prints, arXiv:2402.08455
- Harnois-Déraps et al. (2021) Harnois-Déraps, J., Martinet, N., Castro, T., et al. 2021, MNRAS, 506, 1623
- Harris et al. (2020) Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357
- Hildebrandt et al. (2021) Hildebrandt, H., van den Busch, J. L., Wright, A. H., et al. 2021, A&A, 647, A124
- Hinshaw et al. (2013) Hinshaw, G., Larson, D., Komatsu, E., et al. 2013, ApJS, 208, 19
- Huff & Mandelbaum (2017) Huff, E. & Mandelbaum, R. 2017, arXiv e-prints, arXiv:1702.02600
- Hunter (2007) Hunter, J. D. 2007, Computing in Science & Engineering, 9, 90
- Hwang & Noh (2006) Hwang, J.-c. & Noh, H. 2006, MNRAS, 367, 1515
- Jullo et al. (2019) Jullo, E., de la Torre, S., Cousinou, M. C., et al. 2019, A&A, 627, A137
- Kaiser (1986) Kaiser, N. 1986, MNRAS, 222, 323
- Kanehisa et al. (2024) Kanehisa, K. J., Pawlowski, M. S., Heesters, N., & Müller, O. 2024, A&A, 686, A280
- Kazantzidis & Perivolaropoulos (2021) Kazantzidis, L. & Perivolaropoulos, L. 2021, in Modified Gravity and Cosmology; An Update by the CANTATA Network, ed. E. N. Saridakis, R. Lazkoz, V. Salzano, P. V. Moniz, S. Capozziello, J. Beltrán Jiménez, M. De Laurentis, & G. J. Olmo, 507–537
- Kiakotou et al. (2008) Kiakotou, A., Elgarøy, Ø., & Lahav, O. 2008, Phys. Rev. D, 77, 063005
- Kleinebreil et al. (2024) Kleinebreil, F., Grandis, S., Schrabback, T., et al. 2024, arXiv e-prints, arXiv:2402.08456
- Kluge et al. (2024) Kluge, M., Comparat, J., Liu, A., et al. 2024, arXiv e-prints, arXiv:2402.08453
- Kuijken et al. (2019) Kuijken, K., Heymans, C., Dvornik, A., et al. 2019, A&A, 625, A2
- Lesci et al. (2022) Lesci, G. F., Nanni, L., Marulli, F., et al. 2022, A&A, 665, A100
- Lewis & Challinor (2011) Lewis, A. & Challinor, A. 2011, CAMB: Code for Anisotropies in the Microwave Background, Astrophysics Source Code Library, record ascl:1102.026
- Li et al. (2022) Li, X., Miyatake, H., Luo, W., et al. 2022, PASJ, 74, 421
- Li et al. (2023) Li, X., Zhang, T., Sugiyama, S., et al. 2023, arXiv e-prints, arXiv:2304.00702
- Lin et al. (2024) Lin, M.-X., Jain, B., Raveri, M., et al. 2024, Phys. Rev. D, 109, 063523
- Linder & Cahn (2007) Linder, E. V. & Cahn, R. N. 2007, Astroparticle Physics, 28, 481
- Liu et al. (2023) Liu, X., Yuan, S., Pan, C., et al. 2023, MNRAS, 519, 594
- Madhavacheril et al. (2024) Madhavacheril, M. S., Qu, F. J., Sherwin, B. D., et al. 2024, ApJ, 962, 113
- Mantz et al. (2015) Mantz, A. B., von der Linden, A., Allen, S. W., et al. 2015, MNRAS, 446, 2205
- Marques et al. (2024) Marques, G. A., Liu, J., Shirasaki, M., et al. 2024, MNRAS, 528, 4513
- Martinet et al. (2018) Martinet, N., Schneider, P., Hildebrandt, H., et al. 2018, MNRAS, 474, 712
- Merloni et al. (2024) Merloni, A., Lamer, G., Liu, T., et al. 2024, A&A, 682, A34
- Migkas et al. (2020) Migkas, K., Schellenberger, G., Reiprich, T. H., et al. 2020, A&A, 636, A15
- Moresco & Marulli (2017) Moresco, M. & Marulli, F. 2017, MNRAS, 471, L82
- Nesseris & Perivolaropoulos (2008) Nesseris, S. & Perivolaropoulos, L. 2008, Phys. Rev. D, 77, 023504
- Nguyen et al. (2023) Nguyen, N.-M., Huterer, D., & Wen, Y. 2023, Phys. Rev. Lett., 131, 111001
- Palanque-Delabrouille et al. (2020) Palanque-Delabrouille, N., Yèche, C., Schöneberg, N., et al. 2020, J. Cosmology Astropart. Phys., 2020, 038
- Peebles (2022) Peebles, P. J. E. 2022, Annals of Physics, 447, 169159
- Perivolaropoulos & Skara (2022) Perivolaropoulos, L. & Skara, F. 2022, New A Rev., 95, 101659
- Planck Collaboration et al. (2014) Planck Collaboration, Ade, P. A. R., Aghanim, N., et al. 2014, A&A, 571, A16
- Planck Collaboration et al. (2016) Planck Collaboration, Ade, P. A. R., Aghanim, N., et al. 2016, A&A, 594, A13
- Planck Collaboration et al. (2020) Planck Collaboration, Aghanim, N., Akrami, Y., et al. 2020, A&A, 641, A6
- Polarski & Gannouji (2008) Polarski, D. & Gannouji, R. 2008, Physics Letters B, 660, 439
- Polarski et al. (2016) Polarski, D., Starobinsky, A. A., & Giacomini, H. 2016, J. Cosmology Astropart. Phys., 2016, 037
- Preston et al. (2023) Preston, C., Amon, A., & Efstathiou, G. 2023, MNRAS, 525, 5554
- Rapetti et al. (2009) Rapetti, D., Allen, S. W., Mantz, A., & Ebeling, H. 2009, MNRAS, 400, 699
- Rapetti et al. (2013) Rapetti, D., Blake, C., Allen, S. W., et al. 2013, MNRAS, 432, 973
- Riess et al. (1998) Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009
- Rubin & Ford (1970) Rubin, V. C. & Ford, W. Kent, J. 1970, ApJ, 159, 379
- Salvati et al. (2018) Salvati, L., Douspis, M., & Aghanim, N. 2018, A&A, 614, A13
- Salvati et al. (2022) Salvati, L., Saro, A., Bocquet, S., et al. 2022, ApJ, 934, 129
- Samushia et al. (2013) Samushia, L., Reid, B. A., White, M., et al. 2013, MNRAS, 429, 1514
- Sheldon & Huff (2017) Sheldon, E. S. & Huff, E. M. 2017, ApJ, 841, 24
- Sunayama et al. (2023) Sunayama, T., Miyatake, H., Sugiyama, S., et al. 2023, arXiv e-prints, arXiv:2309.13025
- Tinker et al. (2008) Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709
- Truemper (1993) Truemper, J. 1993, Science, 260, 1769
- Virtanen et al. (2020) Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nature Methods, 17, 261
- von der Linden et al. (2014) von der Linden, A., Allen, M. T., Applegate, D. E., et al. 2014, MNRAS, 439, 2
- Wang & Steinhardt (1998) Wang, L. & Steinhardt, P. J. 1998, ApJ, 508, 483
- Wen et al. (2023) Wen, Y., Nguyen, N.-M., & Huterer, D. 2023, J. Cosmology Astropart. Phys., 2023, 028
- White et al. (2022) White, M., Zhou, R., DeRose, J., et al. 2022, J. Cosmology Astropart. Phys., 2022, 007
- Wright et al. (2020) Wright, A. H., Hildebrandt, H., van den Busch, J. L., & Heymans, C. 2020, A&A, 637, A100
- Zarrouk et al. (2018) Zarrouk, P., Burtin, E., Gil-Marín, H., et al. 2018, MNRAS, 477, 1639
- Zubeldia & Challinor (2019) Zubeldia, Í. & Challinor, A. 2019, MNRAS, 489, 401
- Zürcher et al. (2022) Zürcher, D., Fluri, J., Sgier, R., et al. 2022, MNRAS, 511, 2075
Appendix A posteriors
In appendix A, we show the full cosmological corner plot in the case of the CDM model and the correlation of the cosmological parameters with the scaling relation parameters. The constraints presented are obtained from cluster count only. We only show the main parameters of interest.
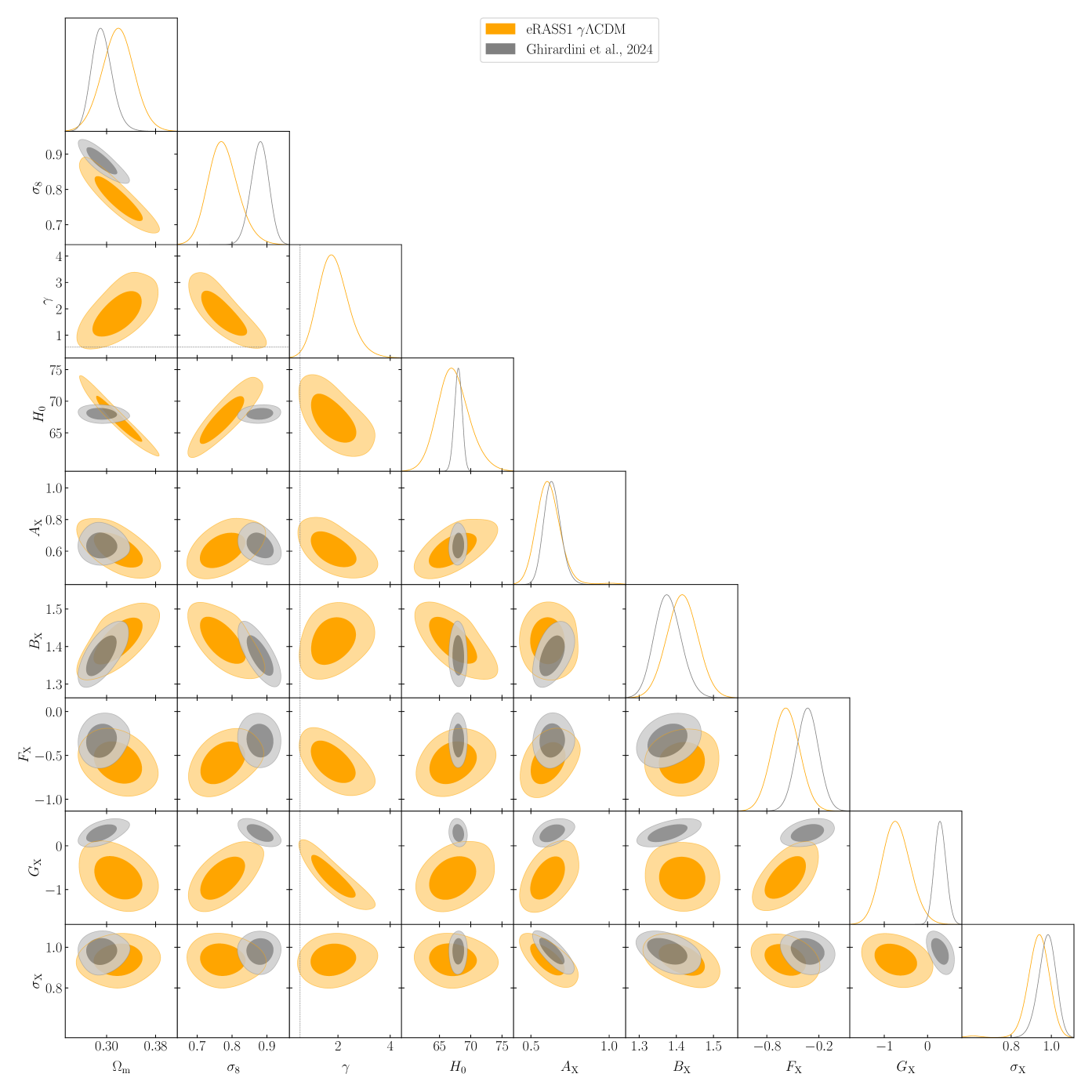
Appendix B posteriors
In appendix B, we show the full cosmological corner plot in the case of the CDM model and the correlation of the cosmological parameters with the scaling relation parameters.
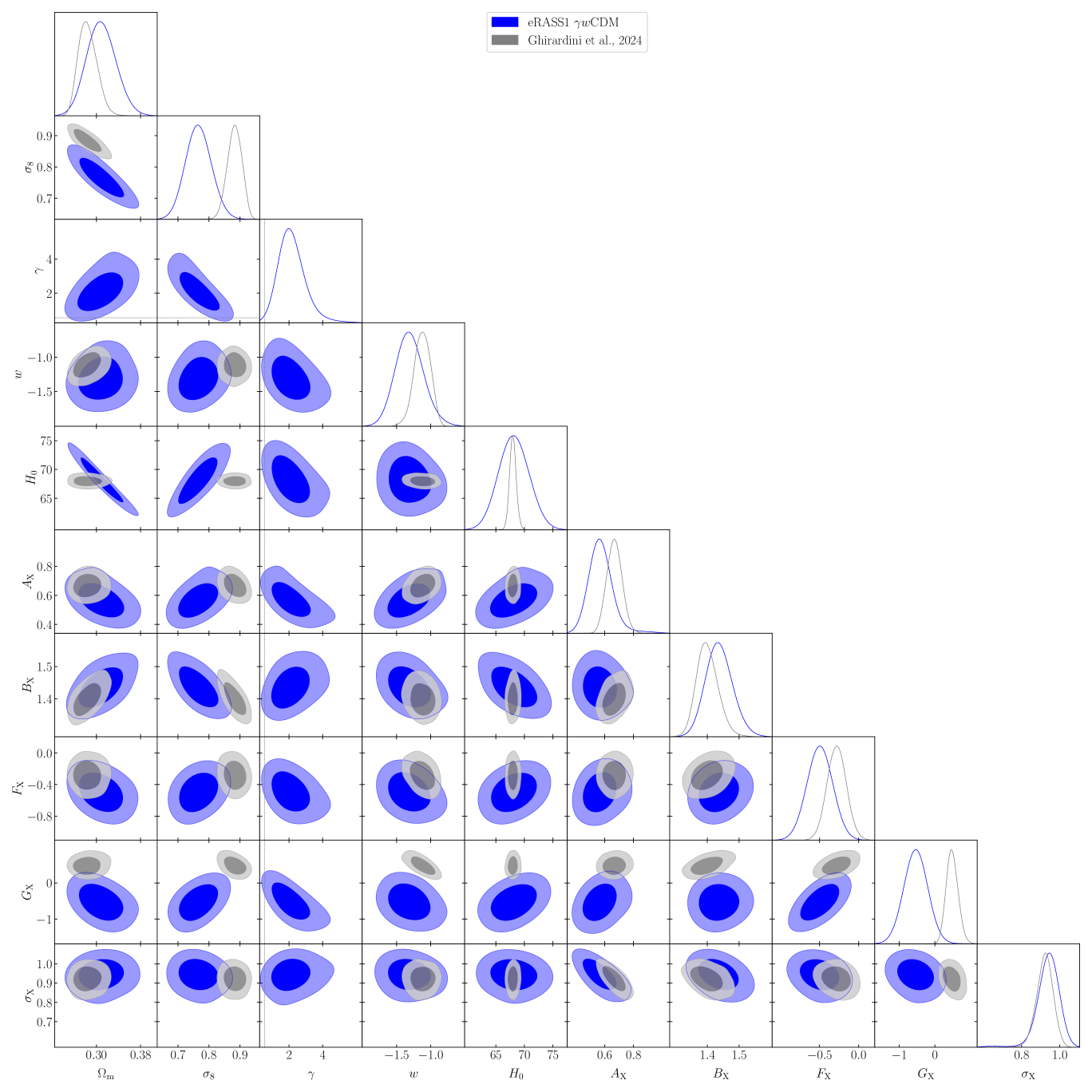
Appendix C Scaling relations
In this appendix, we show the consistency of the scaling relations parameters fitted by different models. We first show the consistency in the case of CDM and CDM compared to the results of the CDM analysis presented in Ghirardini et al. (2024), and the weak lensing constraints obtained by Grandis et al. (2024b). Then, we compare the result of the scaling relations in different redshift bins. We note that in the case of the variation of the cosmic linear growth index, the value of the parameter is lowered. This is due to the reduction of structure formation, which impacts the redshift dependence of the x-ray observable to mass scaling relation.
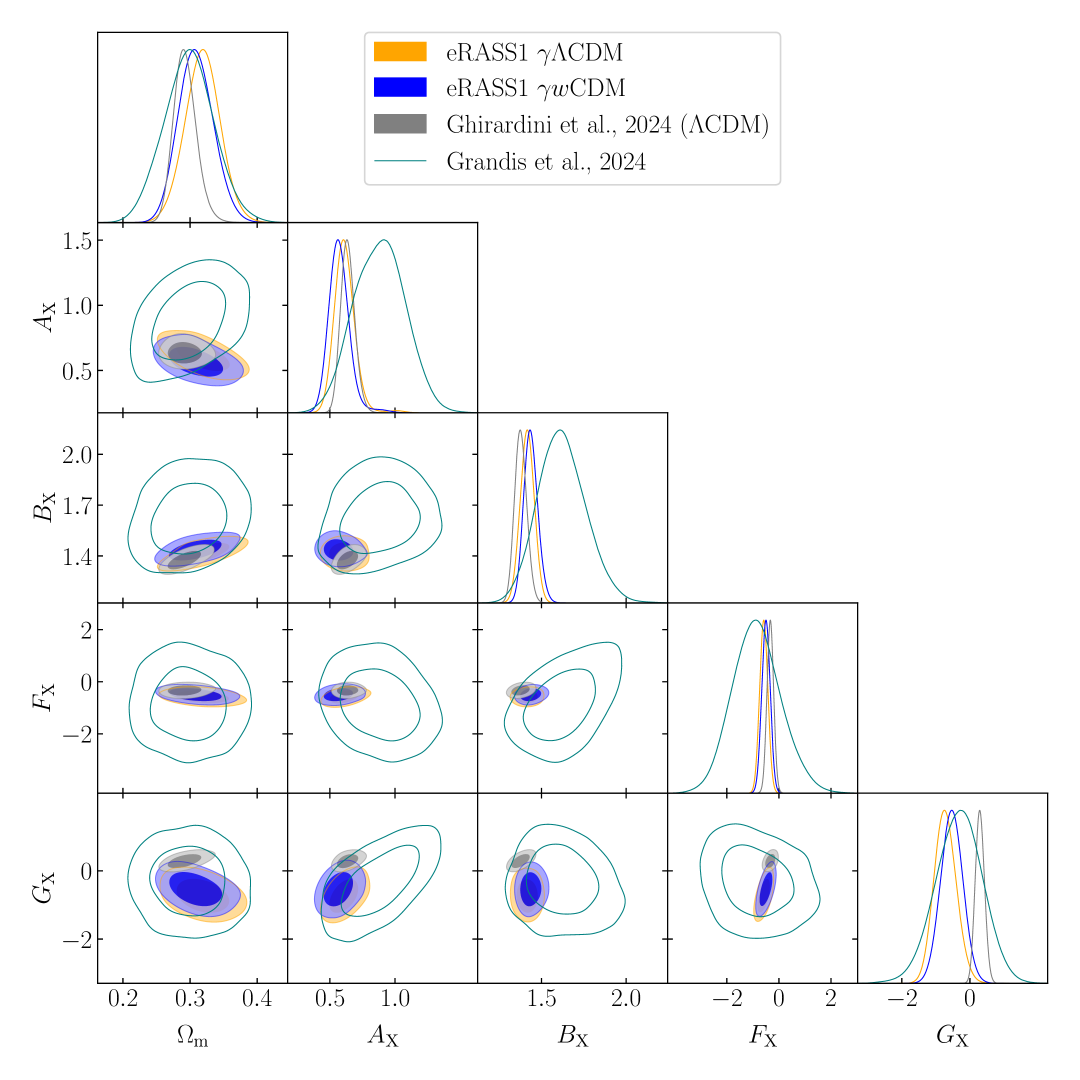
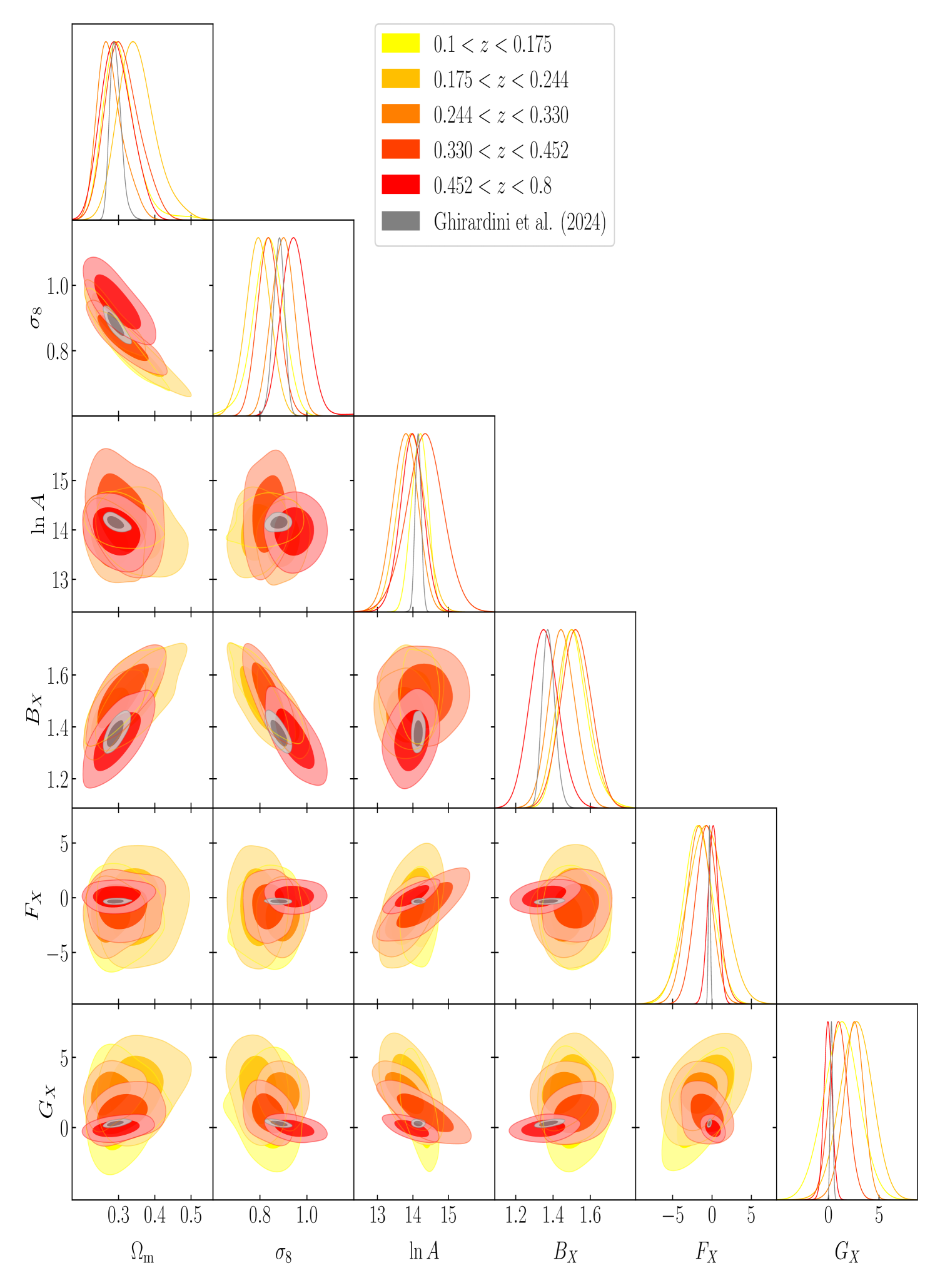
Appendix D Redshift dependant systematic effect
As shown in Figure 8, our highest redshift bin yields a best-fit values that are higher than the one obtained in the other redshift bins. Although we stay in statistical agreement, this motivates us to investigate this process in detail. This is also seen in the measurement in Figure 11. Finally, it can also be seen in the redshift dependence of the scaling relation parameters corner plot shown in appendix C. This might be the hint for an unknown systematic effect in the selection of the high redshift cluster population. By construction, this does not affect our model-agnostic binned results. To check the robustness of our results on model-based growth of structures against this putative effect, we rerun the whole pipeline, excluding the highest redshift bin. The results of the fit of the cosmic linear growth index are shown in the figure below. The obtained subcatalog contains a sample of 4196 clusters (80% of the full cosmology sample).
In the absence of the high- clusters, we find a good agreement between both cluster catalogs, as well as with other LSS surveys that tested for the cosmic linear growth index. However, the tension with the standard GR value ( in the standard CDM case) is reduced to if we ignore the high redshift clusters. The systematic effect will be investigated in the next eRASS data releases, but our main results are conserved.
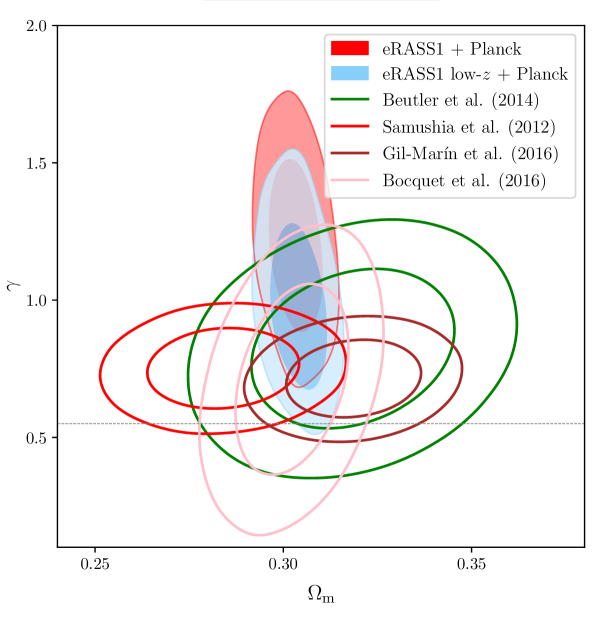
Appendix E Sound horizon priors
Through this paper, we consider as priors the sound horizon scale at recombination. as this constitutes one of the most robust cosmological measurements to date:
| (27) |
where is the maximum distance sound waves can travel, is the recombination redshift, and is the angular diameter distance. The priors on and are taken from the latest cosmic microwave background measurements (Planck20). Assuming that the recombination physics is well understood, the sound horizon is one of the most robust cosmological measurements to date. As it is an angular distance measurement, it is mostly sensitive to a degeneracy between and , illustrated in this appendix.
This prior is combined with a conservative , and mostly provides a measurement of the matter density parameter. This provides an anchor for our measurements since our constraints are significantly altered in the three cases we are exploring. The prior that we obtain is .