The streaks of wall-bounded turbulence need not be long
Abstract
The effect of damping the longest streaks in wall-bounded turbulence is explored using numerical experiments. It is found that long streaks are not required for the self-sustenance of the bursting process, which is relatively little affected by their absence. In particular, there are turbulence states in which the fluctuations of the streamwise velocity have approximately the same length as the bursts, and are thus presumably associated with the bursts themselves, while the burst structure is essentially indistinguishable from flows in which longer velocity fluctuations are present. This suggests that the long streaks found in unmodified flows may be byproducts, rather than active parts of the energy generation cycle.
1 Introduction
Elongated streaks of the streamwise velocity have long been recognised as important features of wall-bounded turbulence (Kline et al., 1967), and it was soon proposed that their instability is the cause of the intermittent ‘bursting’ that was later shown to be a dominant contributor to the cross-stream transfer of momentum and to the generation of turbulent drag (Lu & Willmarth, 1973). While this causal relation was initially hypothetical, detailed mechanisms were eventually suggested (Swearingen & Blackwelder, 1987), and more concrete evidence appeared. For example, Jiménez & Moin (1991) showed that a minimal self-sustaining unit of plane Poiseuille turbulence consists of a streak that is infinitely long when compared to the minimal computational box, and a pair of shorter quasi-streamwise vortices, whose intensity evolves in counter-phase with the streak. The kinematics of this unit was made clearer in plane Couette flow by Hamilton et al. (1995), and eventually became codified in a turbulence regeneration cycle in which the vortices generate the streaks by deforming the mean velocity profile, and the streaks create the vortices by some sort of instability (Jiménez, 1994; Hamilton et al., 1995). Flores & Jiménez (2010) extended minimal simulations to the logarithmic layer and, by analogy with the viscous-layer results, concluded that a similar regeneration cycle is active across the shear-dominated part of the channel, with the streamwise vortices substituted by more generic transient bursts mainly involving the cross-stream velocities, as in figure 1(a). Although seldom made explicit, it was usually implied that the arrows in this figure represent time. Reduced dynamical models by Waleffe (1997) and others also typically include infinitely long streaks and shorter vortices, and Jiménez & Pinelli (1999), by modifying different terms of the evolution equations in turbulent channels at low Reynolds numbers, showed that both components are required. Damping the streaks leads to the decay of the vortices, and vice versa, and the result in both cases is laminarisation of the flow. Exact travelling waves and other invariant solutions that mimic the near-wall structures also include an infinitely long streak of the streamwise velocity and quasi-streamwise vortices (Nagata, 1990; Kawahara et al., 2012).
Although no linear instability of the mean velocity profile is known for wall-bounded turbulence (Reynolds & Tiederman, 1967), each of the branches of the regeneration cycle in figure 1(a) can be modelled by transient, non-modal, linear amplification processes. The bursts generate the streaks by linear advection of the mean profile, and the bursts are amplified by the shear, through a tilting process in which eddies at different distance from the wall are reinforced when they overtake each other (Orr, 1907; Jiménez, 2013). The optimum transient growth of linearised perturbations of the mean velocity profile results in streaks and bursts compatible with those observed in experiments (Butler & Farrell, 1993; del Álamo & Jiménez, 2006; Jiménez, 2013), and Vaughan et al. (2015), among others, have presented plausible self-sustaining models of wall turbulence based on time-dependent infinitely long streaks. All these mechanisms are nonlinear in the sense of requiring initial perturbations of sufficiently high amplitude to self sustain. Bursts are essentially linear and grow by drawing energy from the mean shear (Jiménez, 2013), but infinitesimally small initial perturbations only create infinitesimally weak bursts, which then result in infinitesimally weak streaks. Only sufficiently strong streaks are unstable (Schoppa & Hussain, 2002), and no linear self-sustaining mechanism is known.
Bursts and streaks have been extensively studied in turbulence simulations, both in the viscous and in the logarithmic layer. Down- and up-drafts (the sweeps and ejections that form the bursts) are statistically found in pairs consistent with the short quasi-streamwise rollers that substitute the above-mentioned vortices outside the buffer layer. They sit at the interface between longer high- and low-velocity streaks (Lozano-Durán et al., 2012). Their lifetime is controlled by the shear of the mean velocity profile (Lozano-Durán & Jiménez, 2014b) and, when their evolution is conditionally averaged with respect to the maximum intensity of the burst, the progressive tilting of the Orr mechanism is clearly seen (Encinar & Jiménez, 2020). Jiménez (2018) reviews these observations and their relation with theory.
Considering the above evidence, it may be surprising that the rest of this paper is dedicated to showing that long streaks are not essential features of wall-bounded turbulence, which can be maintained by short fluctuations of the streamwise velocity presumably associated with the bursts themselves, and that the relation between bursts and streaks is closer to the one in figure 1(b), with a self-contained burst that only generates the observed longer streaks as by-products. Although it may be debatable whether flows without long streaks can be described as ‘wall turbulence’, as is otherwise the case for most of the artificial systems used to analyse turbulence, we will show that the structure of the transverse velocity components of the remaining short scales differs little from unmodified flows. There are three related questions in this respect. The first one, whether infinitely long streaks can become unstable at streamwise wavelengths comparable to the observed bursts, has been amply answered in the affirmative by the authors mentioned above, and by many others. The second question is whether this ‘direct cascade’, from long streaks to shorter bursts, is a necessary part of the turbulent cycle, and the third one is whether, even if this downward cascade is shown not to be a required part of the cycle, it still is an important ingredient of turbulence dynamics. We argue below that the answer to the second question is negative, and that the third question is probably only true to the extent that similarly sized fluctuations of the three velocity components must be present in self-sustained bursts, because bursts exclusively involving velocities in the cross plane are equivalent to unforced two-dimensional turbulence and must decay. A fourth question, related to the ‘inverse cascade’ by which short bursts may create long streaks, will be left unanswered.
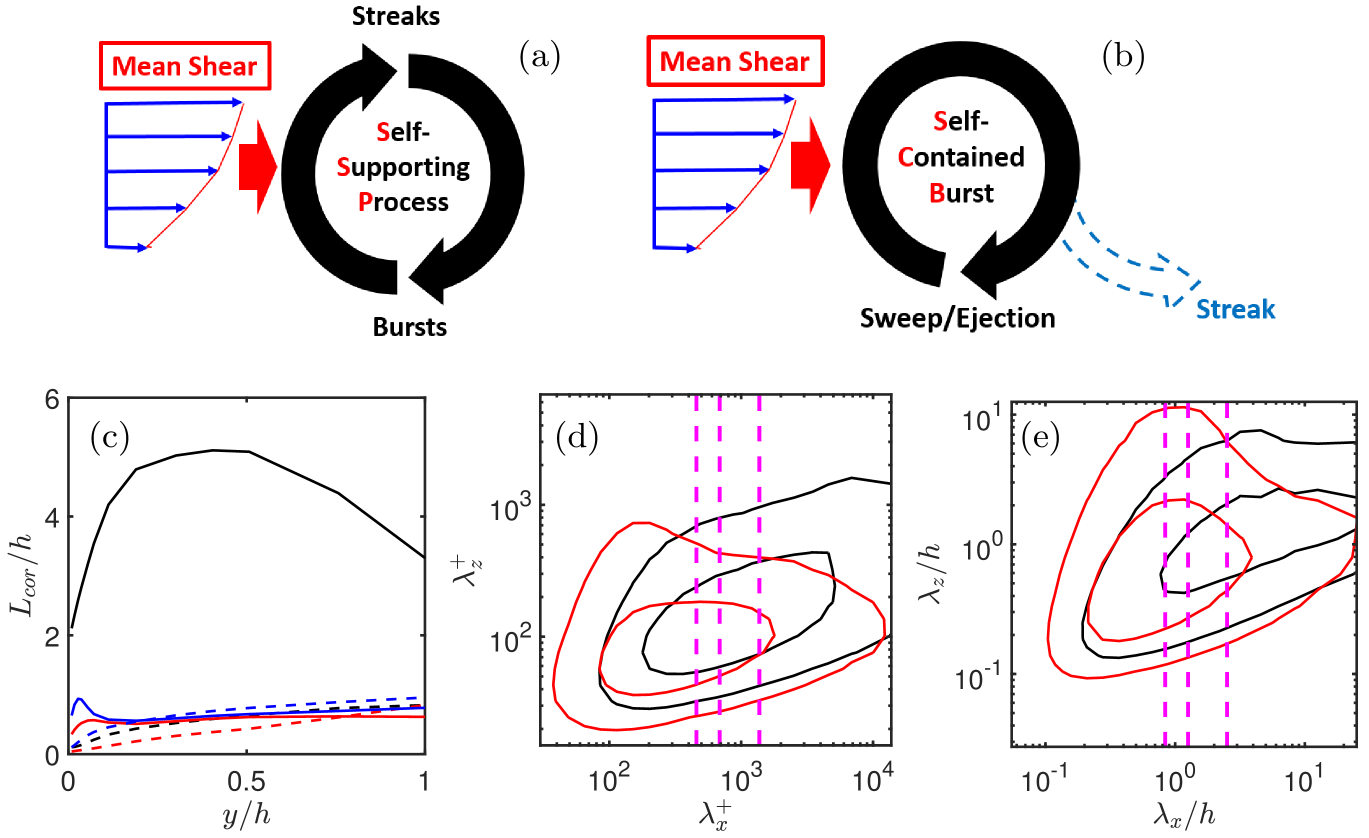
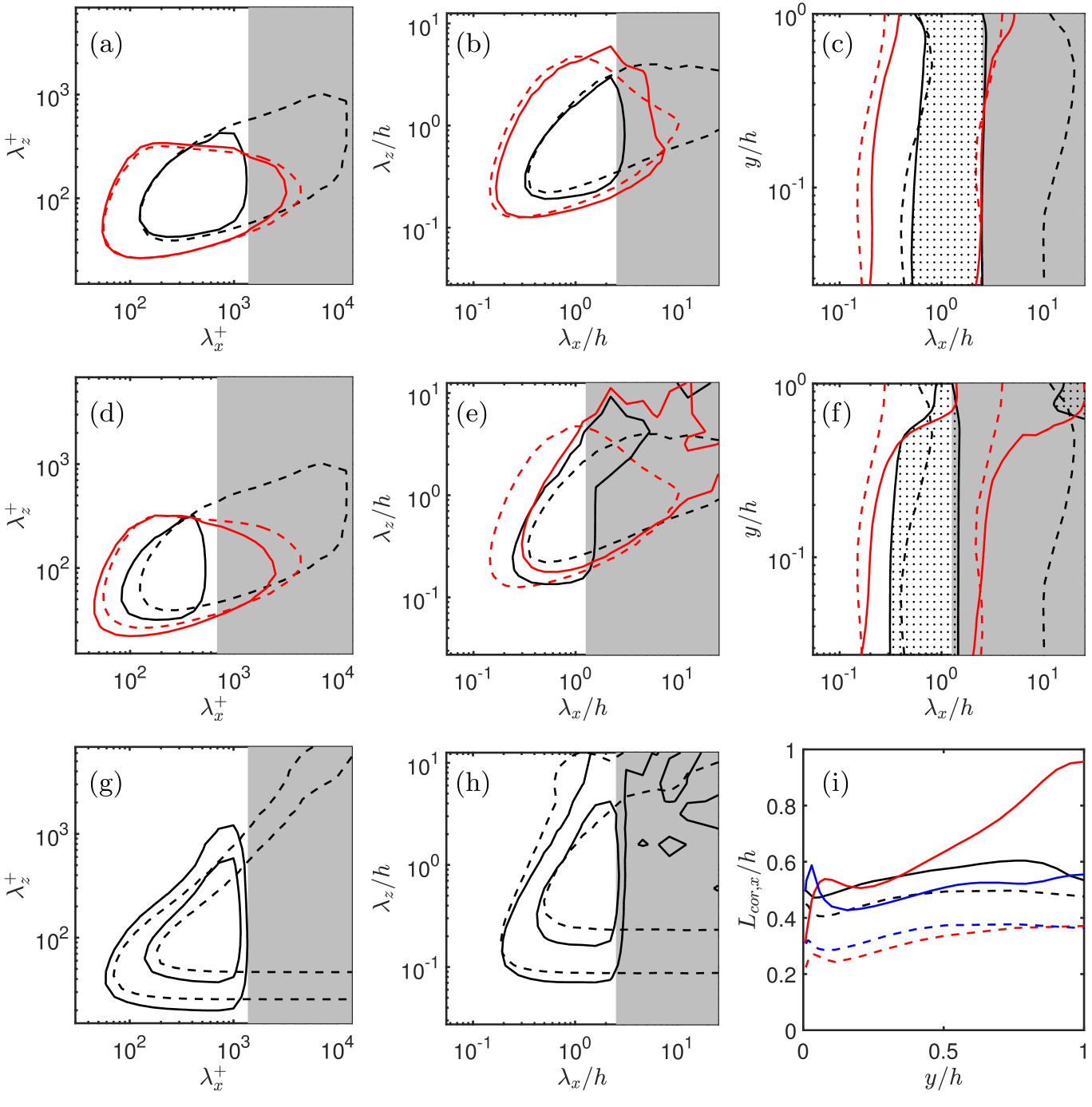
In fact, the evidence for a close connection between the bursts and the much longer streaks is not strong. Figure 1(c) shows that their dimensions are very different. The same-height correlation lengths in the figure underestimate the actual dimensions, which increase when correlations at different heights are taken into account (Sillero et al., 2014), but the ratio among structures is not modified. If we denote the streamwise, wall-normal, and spanwise directions by , and , respectively, and the corresponding velocity components by , and , the three-dimensional correlations of the transverse velocities, and , are approximately isotropic in the cross plane, , and only moderately elongated streamwise, . The correlation of the streamwise velocity is much more elongated, with spanwise dimensions similar to those of the transverse velocities, but with –30. The same difference emerges from spectra (see figure 1d,e) and from the structural analysis of the bursts by Lozano-Durán et al. (2012). On the other hand, when the thresholding method used for bursts is applied to the fluctuations of , their dimensions are only (see figure 22 in Jiménez, 2018), suggesting that the correlations of represent a higher level of organisation of shorter units, each of them presumably associated with a burst or with a group of bursts. Moreover, the -correlations of boundary layers are two or three times shorter than channels, but the two flows have very similar statistics below the outer intermittent region (Sillero et al., 2014), and, if we denote by the channel half-width or other suitable flow thickness, the longest correlations in channels have –15, while Moser et al. (1999) and Lozano-Durán & Jiménez (2014a) showed that shorter computational boxes, with lengths , give good statistics.
However, all these simulations, which are typically spectral, contain the longitudinal wavenumber that corresponds to an infinitely long streamwise wavelength, and it could be argued that these infinitely long features are responsible for maintaining the flow, as in some of the theoretical models mentioned above. This was explicitly tested by Jiménez & Pinelli (1999), who forcibly zeroed all the Fourier components with of the wall-normal vorticity, preventing the formation of infinitely long spanwise inhomogeneities of . The flow laminarised in a computational box with , where the ‘+’ superscript denotes wall units defined from the friction velocity, , and from the kinematic viscosity . Repeating the experiment in a longer box failed to laminarise the flow, which could only be done by zeroing the first two wavenumbers ( and ), thus only retaining uniform streaks with . These experiments were performed at low Reynolds numbers, , and were interpreted to mean that features of at least this length are required for the survival of the near-wall buffer region.
The present paper revisits the experiments of Jiménez & Pinelli (1999), which can now be performed at higher Reynolds numbers and in larger boxes, and analysed in the context of the structural information gained since then. The numerical details are given in §2, results are presented in §3, and are discussed and summarised in §4.
| Case | Damping height | Result | ||||||
|---|---|---|---|---|---|---|---|---|
| F00 | 550 | 8.9 | 5.5 | 6.7 | del Álamo & Jiménez (2003) | |||
| D10 | 452 | 7.4 | 3.7 | 5.5 | 2.28 | 1033 | Full channel | turbulent |
| D15 | 381 | 6.2 | 3.1 | 4,7 | 1.57 | 598 | Full channel | turbulent |
| D20 | 345 | 5.6 | 2.8 | 4.2 | 1.20 | 413 | Full channel | transitional |
| D30 | 252 | 5.6 | 2.8 | 4.2 | 0.81 | 280 | Full channel | laminar |
| D10out | 453 | 7.4 | 3.7 | 5.6 | 2.28 | 1035 | Above | turbulent |
| D10in | 472 | 7.7 | 3.8 | 5.8 | 2.28 | 1078 | Below | turbulent |
2 Numerical experiments
We analyse simulations of pressure-driven incompressible turbulent channels between flat plates separated by a distance , in doubly periodic computational boxes whose streamwise and spanwise periods are and , respectively. The code is Fourier-spectral in and Tchebychev-spectral in , and follows closely Kim et al. (1987). More details are found in del Álamo & Jiménez (2003), whose simulation at is used here as a reference. The code integrates evolution equations for and for the wall-normal vorticity, , from where other variables are obtained using continuity. The volume flux per unit span, is kept constant. To control the spanwise inhomogeneity of the streamwise velocity, the variable to be modified is , which is approximately equal to for long and narrow features. Following Jiménez & Pinelli (1999), this modification is implemented by explicitly zeroing at each time step all the long harmonics of the Fourier expansion , so that
| (1) |
This includes the infinitely long modes with . A few simulations were run in which the damping is only applied above or below a given distance from the wall, ,
| (2) |
with
| (3) |
The plus sign damps the vorticity below , and the minus sign damps it above that level. In our simulations, and . No modification is applied to the equation. Other numerical parameters are summarised in table 1, and some wavelength limits are overlaid on the spectra in figure 1(d,e). It should be noted that, because of the choice of simulation variables, arbitrarily manipulating them respects continuity.
The damping of the vorticity is equivalent to a body force (or torque) acting in planes parallel to the wall, but because of homogeneity, and because it acts on velocity derivatives rather than on the velocities themselves, its average cancels over time. The total stress profile of all the simulations discussed below is linear.
3 Results
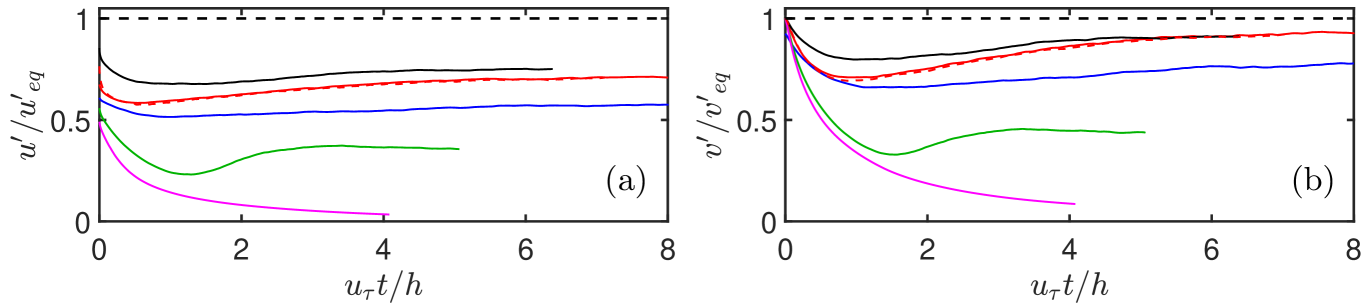
The temporal evolution of the norm of two velocity components of the damped simulations is given in figure 2, normalised with the equilibrium values of an undamped reference simulation at the same nominal Reynolds number (del Álamo & Jiménez, 2003, F00). The damped cases initially decay, but later recover and stabilise at a lower friction Reynolds number than the reference. Case D30 laminarises completely, and does not recover. Figure 3 shows wall-parallel sections of the streamwise velocity in the buffer and outer regions of the reference case and of two surviving damped cases, D10 and D20.
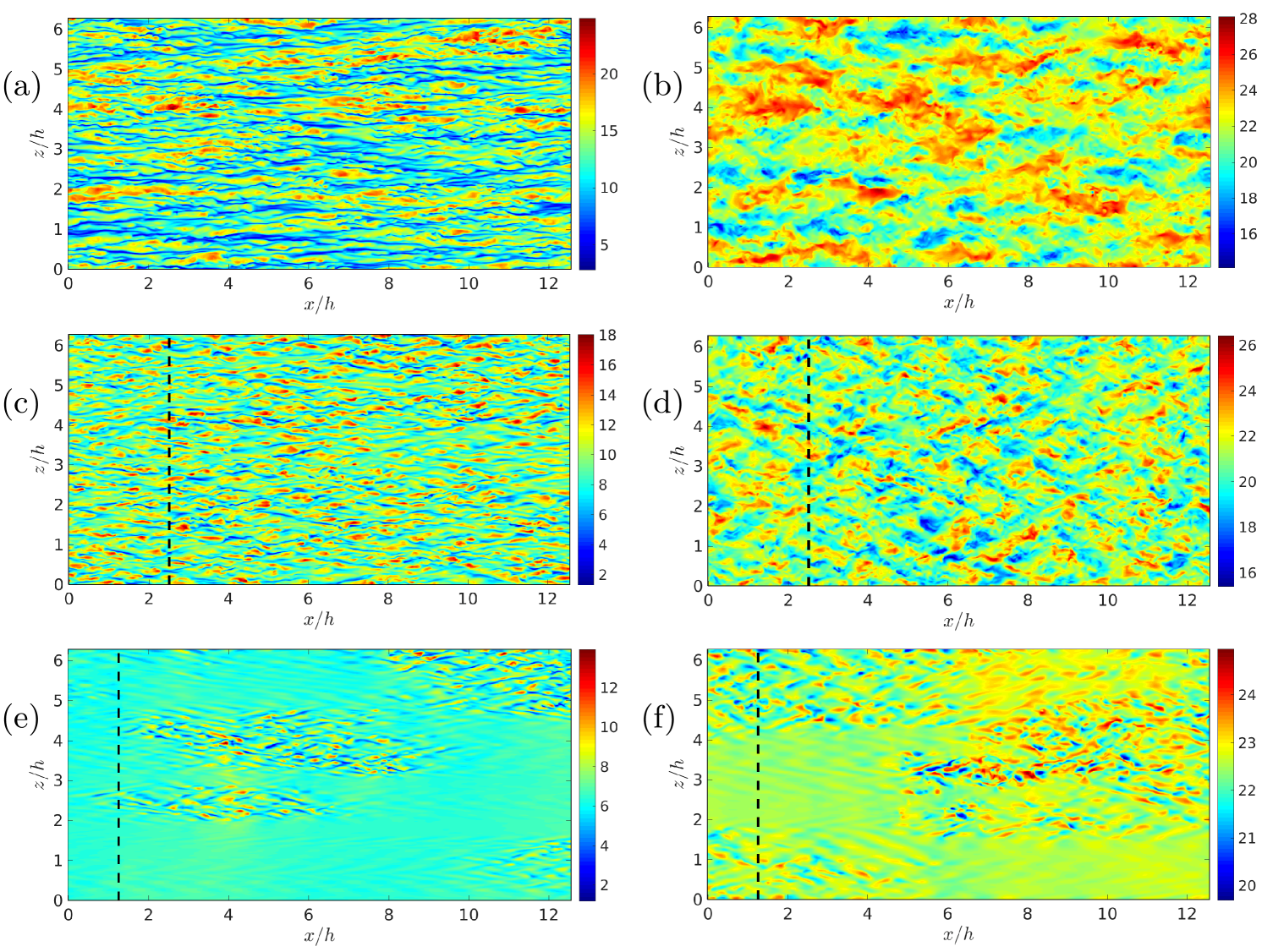
Case D20 contains a mixture of laminar and turbulent patches, reminiscent of transition, which persists for as long as the case was run. Case D10, which filters only wavelengths longer than , stays turbulent, but with a very different organisation from the nominal case, whose streaky structure is substituted by a rhomboidal pattern. This organisation is easy to rationalise, because the damping ensures that the streamwise average of the velocity fluctuations vanishes over streamwise distances longer than , so that a positive fluctuation has to be followed by a negative one. But the most interesting aspect of figure 3(c,d) is that the spanwise wavelength of the velocity is approximately the same as in the nominal case, so that the angle of the rhombuses increases as this wavelength increases with the distance from the wall. It is intriguing that a weaker, but similar, rhomboidal pattern with an angle close to 45 degrees is observed in the spanwise velocity of natural flows (Sillero et al., 2014). If the above explanation applied to it, it would imply that the mean value of tends to cancel over streamwise distances of the order of its spanwise scale. This is consistent with the lack of long tails in its spectrum (Jiménez, 2018), and may be linked to the streak meandering discussed by Hutchins & Marusic (2007). It also has the right dimensions to be related to the bursts described in the introduction.
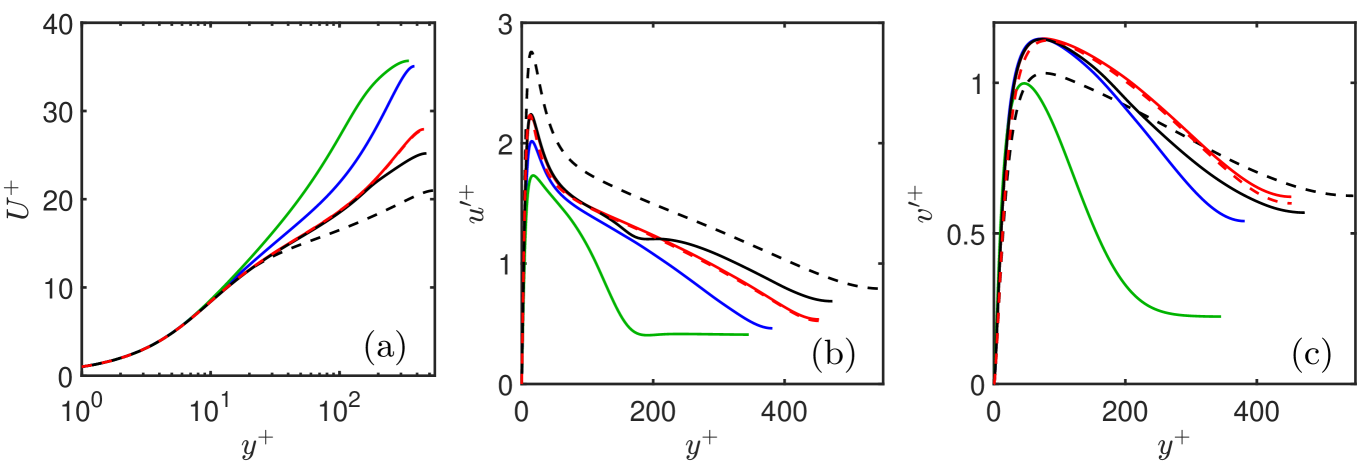
The mean and fluctuation velocity profiles of the damped simulations are shown in figure 4, compared with the reference case. In all cases except the transitional D20, the streamwise fluctuations are weaker than the reference case, while the wall-normal ones are stronger. Although not shown, the behaviour of follows the same trend as . This is characteristic of controlled flows, because the relative magnitudes of and have to adjust themselves to generate the tangential Reynolds stress used to define wall units. It is clear from the mean velocity profiles in figure 4(a) that D20 is basically laminar above , with no trace of a logarithmic layer, but the behaviour of D10 is interesting. When the whole channel is damped, as in D10, the mean velocity can be described as a logarithm with a low von Kármán constant, reflecting the missing Reynolds stresses. The same is true when only the outer layer is filtered, as in D10out, whose red dashed line is difficult to distinguish from the solid line of D10. However, when only the inner layer is filtered, as in the black solid line of D10in, the mean velocity and the fluctuation profile of tend to recover their turbulent behaviour in the undamped layer above . This supports the idea that the large scales of the outer part of the channel are not driven by the wall.
The premultiplied spectra in figure 1(b,c) suggest that the behaviour of the flow depends on how much of the spectrum is damped. Case D10 barely modifies , either in the buffer or in the outer layer, but D20 damps a large fraction of , especially in the outer layer where figure 4 shows that turbulence has died. The streamwise velocity spectrum, , is heavily damped in both cases, but it does not appear to have a strong effect on (or in ). This is confirmed by figure 5, which compares spectra of damped and undamped simulations. In figure 5(a-c), is heavily truncated in D10, but the remaining part agrees well with a truncated version of the undamped spectrum. Up to a point, the same is true of , most likely because its truncation is minor. The truncation of in the near-wall region of D20 is also moderate, but all the spectra are heavily distorted in the outer layer of D20 in figure 5(e), where half of is damped. In fact, although the contours in these figures are chosen to represent a fixed fraction of the fluctuation energy (75%), figure 4 shows that the outer spectra in figure 5(e) correspond to weak residual fluctuations, which are not turbulent. Another interpretation of these spectra, especially clear from the projections in figure 5(c,f), is that turbulence requires that the fluctuations of be longer than those of , but only by a small factor of two or three.
While these spectra suggest that filtering the long wavelengths of has relatively little effect on , it is interesting to compare the shorter surviving scales with those at similar wavelengths in a full channel. This is difficult in absolute terms, because it is unclear which to use for individual wavenumbers, but a simple dimensionless indicator of flow ‘sanity’ is the structure parameter formed by the – co-spectrum normalised with the spectra of and . This is shown in figure 5(g,h) for D10. The long wavelengths that have been damped lose all correlations, and do not contribute to the tangential Reynolds stress, but the structure parameter of the undamped wavelengths is essentially unchanged with respect to the full channel, even near the edge of the damped region. Figure 5(i) shows streamwise correlation lengths for the damped channel and for a full one in which the damped wavenumbers have been zeroed during postprocessing. It should be compared with the unfiltered results in figure 1(c). The size of the transverse velocities has changed little, but the long streamwise correlations of have disappeared. There is very little effect on the spanwise correlation lengths (not shown). The implication is that, while damping the transverse velocities (and therefore the bursts) kills turbulence at the damped wavenumbers, the large difference between the length of and (and ) in nominal turbulence is not required for its survival.
| Case | Result | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| F950 | 949 | 7.8 | 3.9 | 7.8 | 1490 | 745 | Jiménez (2013) | ||
| D950-0 | 830 | 6.8 | 3.4 | 6.8 | 1300 | 651 | 1.57 | 1300 | Turbulent |
| D950-1 | 555 | 4.5 | 2.3 | 4.5 | 870 | 435 | 0.78 | 436 | Turbulent |
| D950-2 | 241 | 4.5 | 2.3 | 4.5 | 870 | 435 | 0.52 | 291 | Laminar |
To explore the dependence on the Reynolds number, and since the previous results suggest that features longer than do not have a strong effect on the dynamics of the structures in the core of the spectrum, two sets of simulations were run in the relatively small boxes used by Jiménez (2013) to study the logarithmic layer (case F950 in table 2). According to Flores & Jiménez (2010), turbulence in these boxes should be healthy below . The first set of simulations, detailed in table 2, are damped ones in which the first few wavenumbers are zeroed. The second set are undamped versions of F950 in which the streamwise length of the box is progressively shrunk until turbulence is no longer sustained. This second set of simulations retains the mode, and are represented by solid symbols in figure 6(a).
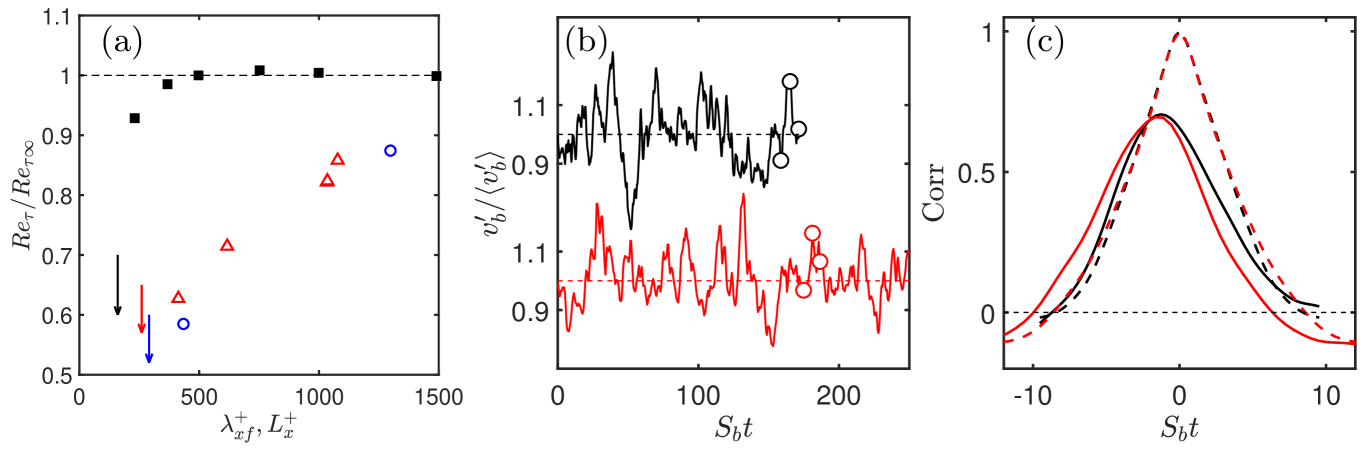
The open symbols in this figure summarise the behaviour of the damped boxes, compared with the corresponding undamped simulations. As the damping becomes more severe and the Reynolds stress from the damped scales disappears, the friction Reynolds number decreases with respect to its undamped value, and the flow laminarises for . We have already mentioned that Jiménez & Pinelli (1999) were able to sustain turbulence for , but not for shorter wavelengths. This is also the limit found by Jiménez & Moin (1991) for the of minimal channels at , suggesting that the flow only fully laminarises when the box is too short even for the smallest structures in the buffer layer. This is confirmed by the collapse of figure 6(a) in wall units, although the limit at the higher Reynolds number of the present simulations in closer to . On the other hand, the behaviour of damped and undamped boxes is different. The undamped simulations represented by the solid symbols in figure 6(a) retain their infinitely long structures and the associated Reynolds stress, and the figure shows very little degradation of until they laminarise for very short . The limit of short and wide channels has been extensively explored by Toh & Itano (2005) and coworkers, who also find little degradation for boxes longer than at . Figure 6(a) confirms that a similar limit holds at higher Reynolds number. It may be significant that the undamped limit is shorter than the damped one by a factor of about two, which would confirm the similar suggestion from the spectra in figure 5.
An advantage of small boxes is that the uppermost band of wall distances for which turbulence remains healthy is essentially minimal for the energy-containing eddies, and their temporal evolution can be studied by tracking band-averaged integral quantities. For the rest of this section we will use fluctuation intensities averaged over , denoted by a ‘’ subscript.
Figure 6(b) displays the temporal behaviour of in cases F950 and D950-0 of table 2, which only differ by the zeroing in the latter of . Both quantities burst intermittently with an approximately similar period, and with an amplitude that is only slightly larger in the undamped case. The temporal evolution can be quantified by the temporal correlation, which is defined for any two variables and as,
| (4) |
where the average is taken over time and over the two sides of the channel.
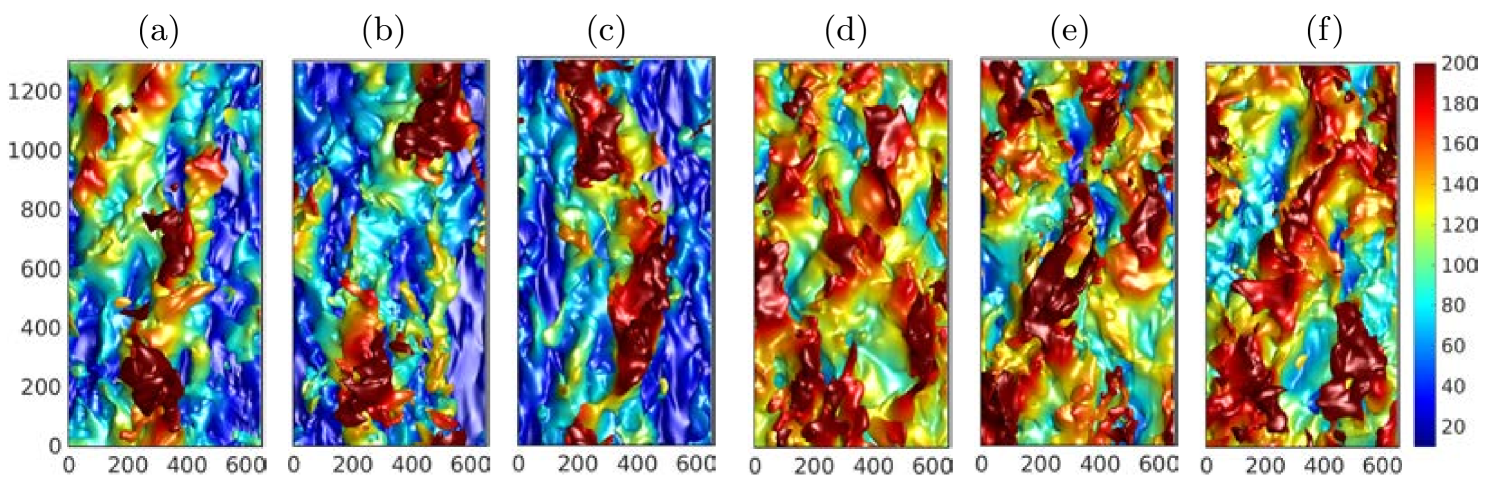
Figure 6(c) shows correlations of and , and should be compared with figure 6 in Jiménez (2013). The correlation is symmetric and agrees very well for the two flows, again suggesting that the dynamics of is unaffected by damping longer structures. Jiménez (2013) shows that this evolution represents well an Orr (1907) burst. As mentioned in the introduction, such bursts also typically involve , but the correlation is not necessarily symmetric, and depends on the location of the burst with respect to pre-existing fluctuations. In agreement with Jiménez (2013), is tilted towards negative times in F950, suggesting that the streak weakens as the burst develops (curiously, in apparent contradiction with the idea that bursts generate the streaks, but see figure 7c in Encinar & Jiménez, 2020). This is not substantially changed for the damped flow.
Snapshots of flow fields in small boxes are presented in figure 7. The three leftmost panels are the undamped case F950, and the three rightmost ones are D950-0. The figures map the distance from the wall of the isosurface, which has been chosen because its average position is in both flows. In practice, it ranges over , and the colour code is uniform among panels. The three snapshots in each flow are chosen to span a ‘burst’ of , with its peak at the central panel. Red areas are low-velocity regions, and it is interesting that the maps of D950-0 show the same rhomboidal pattern as the large-box damped flows in figure 3(c-f). The burst in figure 7(e) forms when the symmetry of the rhombuses is broken and one orientation dominates over the other. It is tempting to see a similar process in the undamped flow fields, where the breakdown takes places as the tail of the streak ‘catches up’ with itself, although it should be remembered that these snapshots cover a spatially periodic domain, and that their behaviour may partly be an artefact of periodicity.
4 Discussion and conclusions
This note can be seen as a further step in the simplification of minimal models for wall turbulence. We have shown that there are turbulence states in which bursting takes place without long structures of the streamwise velocity, while the undamped wavelengths burst in essentially the same way as in unmodified flows. This suggests that the long correlations of the streamwise velocity found in the latter are not central to the dynamics, and that models are possible in which the reference to streaks in figure 1(a) is absent. Our results can even be understood to mean that streaks are not required for the maintenance of wall-bounded turbulence, since there is little that can be interpreted as a streak in figures 3(c-f) or 7(d-f). In fact, the length limits in figure 6(a) imply that the minimal dimensions of the fluctuations of are , which is much closer to a minimal burst than to an elongated streak. The spectra in figure 5 show that the damped wavenumbers do not contribute to the tangential Reynolds stress, leading to a lower effective , but that the undamped modes of the manipulated simulations are little affected by the absence of the longer wavelengths. This is particularly clear in the agreement of the dimensionless spectral structure parameters in figure 5(g,h).
This suggests that the classical sketch of the self-sustaining process in figure 1(a) may be substituted by the (solid) one-loop process in figure 1(b), at least in the manipulated flows. The dashed arrow in this figure reflects that, in this model, the long streaks found in natural flow would be by-products of the shorter bursts. This opens the question of how bursts are restarted, because, as was the case of figure 1(a), the new figure portraits a transient process. The hope is that the new system might be easier to model than the previous one, because one of the components of the latter is missing. A second question is what the role of the long streaks in maintaining turbulence may be. It is unlikely that they have none, because they generate Reynolds stresses at their wavelengths, and the decay of in figure 6(a) shows that their contribution to the total stress is substantial (see also Liu et al., 2001). What we have shown is that they are not essential components of the bursting cycle, which continues relatively undisturbed when they are removed. But they are present in unmodified flows, and may participate in some other important process. The geometrical collocation of bursts with the interface between streaks is well documented (Lozano-Durán et al., 2012), and the asymmetry of the correlation in figure 6(c) suggests that, in unmodified flows, bursts appear within streaks that later weaken. Lastly, the related ‘reverse-cascade’ question of how short transient bursts create long and long-lasting streaks, remains open.
This work was supported by the European Research Council under the Caust grant ERC-AdG-101018287.
References
- del Álamo & Jiménez (2003) del Álamo, J. C. & Jiménez, J. 2003 Spectra of very large anisotropic scales in turbulent channels. Phys. Fluids 15, L41–L44.
- del Álamo & Jiménez (2006) del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.
- Butler & Farrell (1993) Butler, K. M. & Farrell, B. F. 1993 Optimal perturbations and streak spacing in wall-bounded shear flow. Phys. Fluids A 5, 774–777.
- Encinar & Jiménez (2020) Encinar, M. P. & Jiménez, J. 2020 Momentum transfer by linearised eddies in turbulent channel flows. J. Fluid Mech. 895, A23.
- Flores & Jiménez (2010) Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22, 071704.
- Hamilton et al. (1995) Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.
- Hutchins & Marusic (2007) Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 467–477.
- Jiménez (1994) Jiménez, J. 1994 On the structure and control of near wall turbulence. Phys. Fluids 6, 944–953.
- Jiménez (2013) Jiménez, J. 2013 How linear is wall-bounded turbulence? Phys. Fluids 25, 110814.
- Jiménez (2018) Jiménez, J. 2018 Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, P1.
- Jiménez & Moin (1991) Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.
- Jiménez & Pinelli (1999) Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.
- Kawahara et al. (2012) Kawahara, G., Uhlmann, M. & van Veen, L. 2012 The significance of simple invariant solutions in turbulent flows. Ann. Rev. Fluid Mech. 44, 203–225.
- Kim et al. (1987) Kim, J., Moin, P. & Moser, R. D. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.
- Kline et al. (1967) Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.
- Liu et al. (2001) Liu, Z., Adrian, R. J. & Hanratty, T. J. 2001 Large-scale modes of turbulent channel flow: transport and structure. J. Fluid Mech. 448, 53–80.
- Lozano-Durán et al. (2012) Lozano-Durán, A., Flores, O. & Jiménez, J. 2012 The three-dimensional structure of momentum transfer in turbulent channels. J. Fluid Mech. 694, 100–130.
- Lozano-Durán & Jiménez (2014a) Lozano-Durán, A. & Jiménez, J. 2014a Effect of the computational domain on direct simulations of turbulent channels up to . Phys. Fluids 26, 011702.
- Lozano-Durán & Jiménez (2014b) Lozano-Durán, A. & Jiménez, J. 2014b Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascade. J. Fluid Mech. 759, 432–471.
- Lu & Willmarth (1973) Lu, S. S. & Willmarth, W. W. 1973 Measurements of the structure of the Reynolds stress in a turbulent boundary layer. J. Fluid Mech. 60, 481–511.
- Moser et al. (1999) Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to . Phys Fluids 11, 943–945.
- Nagata (1990) Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.
- Orr (1907) Orr, W. M. 1907 The stability or instability of the steady motions of a perfect liquid, and of a viscous liquid. Part I: A perfect liquid. Proc. Royal Irish Acad. A 27, 9–68.
- Reynolds & Tiederman (1967) Reynolds, W. C. & Tiederman, W. G. 1967 Stability of turbulent channel flow, with application to Malkus’ theory. J. Fluid Mech. 27, 253–272.
- Schoppa & Hussain (2002) Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.
- Sillero et al. (2014) Sillero, J. A., Jiménez, J. & Moser, R. D. 2014 Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to 2000. Phys. Fluids 26, 105109.
- Swearingen & Blackwelder (1987) Swearingen, J. D. & Blackwelder, R. F. 1987 The growth and breakdown of streamwise vortices in the presence of a wall. J. Fluid Mech. 182, 255–290.
- Toh & Itano (2005) Toh, S. & Itano, T. 2005 Interaction between a large-scale structure and near-wall structures in channel flow. J. Fluid Mech. 524, 249–262.
- Vaughan et al. (2015) Vaughan, T. L., Farrell, B. F., Ioannou, P. J. & Gayme, D. F. 2015 A minimal model of self-sustaining turbulence. Phys. Fluids 27, 105104.
- Waleffe (1997) Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.