The stringent upper limit on jet power in the persistent soft state source 4U 1957+11

The Karl G. Jansky Very Large Array (VLA) observed 4U 1957+11 for a total of 21 hours in 14 observing sessions between 20 February 2014 and 23 March 2014, with 17 hours on source, and 4 hours for calibration and slewing. The data were collected between 8 and 10 GHz under project code 14A-256. Two of the observations (on 22 and 23 February) were very badly affected by radio frequency intereference in the nonlinear regime and were excluded. The phase calibrator for the observations was J1950+0807, and the flux calibrator was 3C48. The data were reduced using standard procedures in CASA (McMullin et al., 2007), and we obtain a noise level of 1.07 $\mu$Jy/beam for the full data set.

Because of the large number of dynamically scheduled radio observations, along with the high brightness of the source in X-rays, we chose to use all-sky monitor data in the X-ray band rather than to obtain new X-ray data. The Monitor of All-sky X-ray Image (MAXI – Matsuoka et al. 2009) data for the source show a weighted mean count rate of 0.103 cts s^-1 cm^-2 in the date range from MJD 56712.5 to 56739.5, over which the data were taken. This corresponds to a flux of $1.1\times 10^{-9}$ erg s^-1 cm^-2 (2-20 keV) for thermal models within the range typically seen from this source (Nowak et al., 2012).

Additionally, we look at the X-ray data from proposal 50128 (PI: Nowak), the longest campaign on the source by the Rossi X-ray Timing Explorer (Swank, 2006). This campaign had about 300 kiloseconds of data on source. We look at these data to determine whether any Type I X-ray bursts took place. The least frequent burster among the "banana state" neutron star systems is Ser X-1 (Galloway et al., 2008), which bursts about once per 8 hours. It had already been found in 26 kiloseconds of data that 4U 1957+11 shows no Type I bursts (Wijnands et al., 2002), which already provided suggestive evidence that it is not a soft-state accreting neutron star. With this additional data set of 300 kiloseconds, about 10 bursts would have been expected if the source bursted as frequently as Ser X-1, and the lack of bursts thus provides very strong, albeit non-dynamical, evidence against a neutron star accretor.

Because 4U 1957+11 has never gone into quiescence, its optical flux has consistently been dominated by its accretion disk, rather than by its donor star. An orbital period of 9.33 hours has been measured from photometric modulations (Thorstensen, 1987), likely due to illumination of the donor star by the accretion disk (Thorstensen, 1987; Bayless et al., 2011). Emission lines give a tentative mass ratio of $\approx 0.3$ (Longa-Peña, 2015) but neither reliable direct radial velocity curves of the donor star’s absorption lines nor inclination angle estimates from the orbital data have been produced.

The donor star may be slightly evolved. A halo star is possible, but would have to be toward the metal rich end of the halo star distribution and to be slightly evolved; 10 Gyr old stars filling a Roche lobe at a period of 9.3 hours with [Fe/H]$\approx-1$ can still have cool enough envelopes to allow convection (Pietrinferni et al., 2006). For donors that are significantly more metal poor, stars that fill this Roche lobe will have radiative envelopes even after 10 Gyr, suppressing magnetic braking, and hence would not have substantial mass transfer rates.

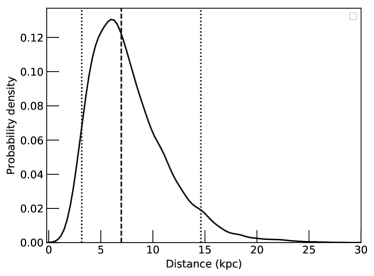
The object is detected in Gaia DR2 (Gaia Collaboration et al., 2018) with a parallax measurement of 0.025$\pm$0.239 mas, and a proper motion of $-0.19\pm 0.36$ mas yr^-1 in RA and of $-1.94\pm 0.29$ mas yr^-1 in Declination. After correcting for the global zeropoint offset of -0.029 mas in Gaia’s parallax measurement (Luri et al., 2018; Chan & Bovy, 2019) the parallax measurement can be used to constrain the distance to the source with the use of an appropriate prior. For "normal" stars, Bailer-Jones et al. (2018) provide such a prior. Because X-ray binaries typically have a larger scaling height than disk stars, we use a Milky Way-like prior (Atri et al., 2019) with scale height parameters derived in Grimm et al. (2002) for X-ray binaries. We determine the posterior distance distribution to the source with a median of 7 kpc and 5^th and 95^th percentile of 3 and 15 kpc, respectively (see Figure 1, left panel). We note that some additional considerations based on the X-ray properties, discussed in the next subsection, disfavor the lower end of this range.

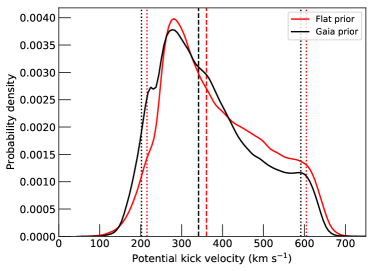
The center of mass radial velocity, $\gamma$ of the binary, is -180${}^{+30}_{-38}$ km s^-1 (Longa-Peña, 2015). This comes from Bowen fluorescence measurements. Given that this source is located at a Galactic longitude of $+51$ degrees, it is expected that its radial velocity would be positive, not negative. As a result it must have had a substantial natal kick, or it must be a halo system. We used the proper motion, the systemic radial velocity and the distance constraints derived above to constrain the current three dimensional space velocity of the system. The age of the system is unknown but most X-ray binaries are assumed to be born in the Galactic plane. We use galpy (Bovy, 2015) and Monte Carlo simulations to integrate and sample 5000 Galactocentric orbits of the system and derive the probability distribution for the peculiar velocity of the system when it crosses the Galactic plane, called the potential kick velocity (PKV, Atri et al., 2019). As can be seen in Figure 1 (right panel), the PKV distribution of the system has a median of 346 km s^-1, with a 5^th and 95^th percentile of 203 and 594 km s^-1, respectively. Due to the large uncertainty on the Gaia parallax, we also test a loosely constrained uniform distance prior of 5–25 kpc and find that the PKV distribution is not affected considerably, with a median of 360 km s^-1, and 5^th and 95^th percentiles of 215 and 602 km s^-1, respectively. Thus, regardless of the distance of the source the PKV of the system is always in excess of 100 km s^-1.

The PKV distribution of the source is too large to be accommodated in a straightforward manner with just the Blaauw (1961) mechanism of mass loss from a moving component of a binary. The maximum kick in such a scenario is given in (Nelemans et al., 1999) as:

where $\Delta{M}$ is the mass lost during the supernova (limited to half the total system mass if the system remains bound after the supernova), $m$ is the donor mass, $M_{\rm BH}$ is the black hole mass, and $P_{\rm re-circ}$ is the period of the binary after re-circularization. Allowing for substantial mass transfer in the system to have already taken place, 100 km s^-1 could be achieved, but 200 km s^-1 cannot be achieved without very unreasonable assumptions. The possible range of kicks could easily be produced if there is an asymmetric natal kick (Brandt & Podsiadlowski, 1995). This would make the system the fastest moving black hole X-ray binary known in our Galaxy.

The potential halo nature of the object is intriguing. For this object, the strengths of the Bowen fluorescence lines are typically a factor of 2 weaker than the He II emission lines at 4686 Å(Longa-Peña, 2015). In most other systems, the Bowen lines are stronger than the He II lines. Without careful photoionization modelling, this does not definitively indicate that the abundance ratio of helium to carbon and nitrogen is anomlously high for this system, but it does indicate that this is potentially the case and hence worth such an investigation. This tentative evidence for a halo origin plays against the low mass of the black hole, given that low metallicity environments lead to weaker winds and more massive remnants, while the highest kick black holes are expected to be the least massive ones (Belczynski & Bulik, 2002).

There is no direct evidence for a black hole in this system. There is some evidence that if the system contains a black hole, the black hole is toward the low mass end of the mass spectrum (Nowak & Wilms, 1999), possibly in the "mass gap" between 2 and 5 $M_{\odot}$ (Özel et al., 2010; Farr et al., 2011). Bayless et al. (2011) make a series of arguments, none of which they claim to be conclusive, that suggest that the system contains a neutron star. The two most important of these arguments are (1) the lack of superhumps seen in the system, and (2) the amplitude of the optical periodicity. It is not clear that the lack of superhumps is strongly constraining; the ratio of viscous heating to reprocessing in X-ray binaries in the optical band is much lower than in cataclysmic variables, and the strength of superhump emission is significantly weaker (Haswell et al., 2001; Russell et al., 2010). The amplitude of the orbital periodicity is also used by Bayless et al. (2011) to argue for a relatively small mass ratio, but here, the conclusions depend strongly on the inclination angle of the system and assumptions about the size of the accretion disc relative to its circularization radius and its temperature. Longa-Peña (2015) also find evidence for a mass ratio of $0.25-0.3$ from the ratios of the amplitudes of the radial velocity curves for the accretion disc and the donor star as inferred from emission lines of both. All these results are consistent with a black hole of relatively low mass ($\sim 4M_{\odot}$), as long as one understands that the optical superhumps may be quite weak in a system where the optical emission is dominated by reprocessing. Furthermore, using a similar approach to that of Bayless et al. (2011) with a larger data set, Gomez et al. (2015) conclude that a low mass black hole is the most likely accretor.

The X-rays from the source consistently exhibit low amplitude variability ($\lesssim$ 2% rms amplitude), and show a very soft spectrum, with rare instances at the faint end of the luminosity range for the source where it show some tentative increase in the characteristic radius of the accretion disc and strength of the power law component, possibly indicating an intermediate state (Nowak et al., 2012). Black hole X-ray binaries show this behavior in their "soft states", which typically occur above 2% of the Eddington luminosity (Maccarone, 2003; Vahdat Motlagh et al., 2019). Neutron stars tend to show this low amplitude variability behavior in “banana states", which also occur in the same Eddington fraction range (Maccarone, 2003). This likely gives a distance of $\approx 15$ kpc for a black hole X-ray binary, and for a neutron star X-ray binary, it gives a value of $\approx 7~{}$kpc. The most likely range of distances thus excludes most of the range with the slowest velocities, bolstering the case made above for a halo orbit, regardless of whether that orbit results from birth in the halo or a strong natal kick.

Beyond this, we can also consider the likely range of accretion rates for the source based on binary stellar evolution. Re-scaling equation (9) of King et al. (1996) (and leaving out the negligible gravitational radiation component), we can see that, for a 9.33 hour orbital period, the mass transfer rate can be expected to be:

with the mass transfer due to magnetic braking. Taking this accretion rate, we find that if the donor is a main sequence star, the X-ray luminosity will be $6\times 10^{37}$ erg s^-1 if the source is an accreting neutron star, at about 30% of the Eddington luminosity for a standard accreting neutron star, making it likely to show the strong variability characteristic of the Z-sources. For an accreting black hole, it will be at about 2–4$\times 10^{37}$ erg s^-1, perhaps a bit brighter if the black hole is rapidly rotating and hence more radiatively efficient, as has been suggested based on its hot accretion disc (Nowak et al., 2012). If the donor star is a mildly evolved halo star, the $m_{2}^{7/3}$ term may cancel out the increased efficiency due to the deeper potential well for the rotating black hole. Binary evolution thus provides another argument in favor of a black hole nature (in addition to the X-ray spectral considerations already presented in Nowak et al. 2012 and the lack of Type I bursts discussed above). The sum total of these arguments is that there is reasonably good evidence for a black hole of lower mass than is typically seen in LMXBs, but that there is also strong, albeit not dynamical, evidence against a neutron star.

An alternative to the scenario in which the jets have their power suppressed is one in which power is injected into the jets, but the power is not effectively dissipated, so that the ratio of radio power to kinetic power is substantially smaller than in hard states. In most systems, this could occur for a few reasons – Poynting flux domination (Lovelace et al., 2002) or poor dissipation of the power due to the lack of variability (Drappeau et al., 2017). The results on Cygnus X-3, where the return from the soft to hard state is where the strongest jet emission is seen (Koljonen et al., 2018), strongly argue that the jets genuinely turn down in power during the soft state. In principle, Poynting flux could pass through the stellar wind without being dissipated, and numerical calculations specific to this problem, but outside the scope of this paper should be done to test this possibility, but one of the original motivations for considering Poynting flux jets over matter-dominated jets was to increase the radiative efficiency (Giannios & Spruit 2005). The Cyg X-3 results are more clearly problematic for the weak dissipation model of Drappeau et al. (2017). Shocks will necessarily develop against the stellar wind, whose velocity is roughly perpendicular to the jets in the inner jet region, and this will be true regardless of the level of velocity variability in the ejected material.

At least according to theoretical work, jet power can be strongly suppressed in all spectral states if a black hole has a low rotation rate. Observational work on this topic indicates mixed results; relatively little evidence exists for spin affecting the production of jets in hard states (e.g. Fender et al. 2010; Russell et al. 2013; McClintock et al. 2014; Middleton et al. 2014), and may result from the correlation of both inferred spin and peak $L_{X}$ with period (Wu et al., 2010). The spin-period correlation may have a physical origin if e.g. black holes grow dramatically after birth (Fragos & McClintock, 2015), while the period-X-ray peak correlation has a very clear physical explanation in the larger accretion discs at longer period (Wu et al., 2010).

Several investigations of the spin of this black hole have been made, via disc continuum fitting (Nowak et al., 2012; Maitra et al., 2014). All favor the idea that the black hole is rapidly rotating, and furthermore find that the distance must be at least 10 kpc in the context of this model (and that would require a low black hole mass of 3$M_{\odot}$ – Nowak et al. 2012).

The alternative then, is that the jet power is fundamentally lower in the soft state than in the hard state. One possibility is that the analytic work of Meier (2001) is not a good approximation to reality, and the process of accelerating the jets, and that the magnetic forces are much less effective at extracting power from soft state black holes relative to hard state black holes. If the scalings of jet power to disk properties are correct, then this would indicate that the accretion disks in soft states are substantially thinner than the approximations used by Meier (2001), or, more likely, that the ad hoc assumptions made about the ratios of their large scale magnetic fields to their dynamo fields scale . Additionally, the low mass of the black hole may be responsible for a factor of $\sim 1.5$ reduction in the ratio of radio power to jet power(Merloni et al., 2003). We regard this combination of effects as the most likely possibility at the present time, but we also encourage more theoretical work to determine if the jet power may be genuinely suppressed by a larger factor in the soft states than previously estimated.