The system of translates and the special affine Fourier transform
Abstract.
The translation operator associated with the special affine Fourier transform (SAFT) is introduced from harmonic analysis point of view. The analogues of Wendel’s theorem, Wiener theorem, Weiner-Tauberian theorem and Bernstein type inequality in the context of the SAFT are established. The shift invariant space associated with the special affine Fourier transform is introduced and studied along with sampling problems.
Key words and phrases:
Convolution, Poisson summation formula, shift invariant space, Wendel’s theorem, Zak-transform.*Corresponding author: Radha Ramakrishnan, email:radharam@iitm.ac.in
2020 Mathematics Subject Classification:
Primary 42A38; Secondary 42A85, 42C151. Introduction and background
The special affine Fourier transform (SAFT) was first considered by S. Abe and J. T. Sheridan in [1] for the study of certain operations on optical wave functions. The SAFT is formally defined as
| (1.1) |
where stands for the set of real parameters which satisfy the relation . The integral transform (1.1) is related to the special affine linear transform of the phase space
| (1.2) |
Due to the conditions on the parameters the matrix in (1.2) belongs to the special linear group and the affine transform (1.2) is therefore given by elements from the inhomogeneous linear group
This justifies the name special affine Fourier transform for (1.1). The action of the group on the time frequency plane and the relation to quadratic Fourier transforms is well studied. We will not go into the details here but refer to the book [11].
A number of important transforms are special cases of the SAFT. For example, gives the ordinary Fourier transform and its inverse. The parameter set gives the fractional Fourier transform, and produces the Fresnel transform.
In optics, certain one parameter subgroups of the are of special interest. Among them are the fractional Fourier transform, the Fresnel transform (also called free space propagation in this context), the hyperbolic transform , the lens transform , and the magnification transform . The latter two cases need a careful analysis for the limit case which we will not consider in this paper. We will not try to expound the various connections to optics further but refer to [15] for more details.
In this paper, we consider (1.1) from the point of view of applied harmonic analysis and take it as a signal transform of a (suitable) function. We are mainly interested in studying the principal shift invariant spaces and sampling theorems related to the SAFT. In the classical case, the principal shift invariant space generated by is defined as . The classical Fourier transform ( in (1.1)) plays a crucial role for the analysis of such spaces. The crucial point is that the ordinary translation and the classical Fourier transform are intimately related. This is due to the identity which gives, as a consequence the convolution theorem, the relation between translation, modulation, Fourier transform etc. These theorems are used over and over again in Fourier analysis and in the study of shift invariant spaces in particular. It is completely obvious that the ordinary translation does not interact nicely with the SAFT (resp. its complex exponential kernel). Hence working with the SAFT a new concept of a translation is needed. This generalized translation should be linked to the SAFT in an analogous manner as the ordinary translation is linked to the classical Fourier transform. If this is the case, then it seems reasonable to expect that the central theorems (convolution theorem etc.) hold in a similar manner. An idea for the construction of such generalized translation comes from the observation that in the classical setting we have
In this paper, we define a new translation operator , which serves our purpose in the case of SAFT.
In [6] A. Bhandari and A.I. Zayed considered chirp-modulation and used this to obtain a convolution theorem. However, they did not define a generalized translation operator explicitly, and hence did not investigate the consequences of this concept with respect to harmonic analysis. We shall demonstrate that the generalized translation is the suitable concept to obtain analogues of fundamental theorems such as Wendel’s theorem for the multipliers, Wiener theorem and Weiner-Tauberian theorem in connection with the closed ideals of translation invariant spaces in the context of the SAFT. For a study of multipliers and Wendel’s theorem for the Fourier transform we refer to [18], for Wiener theorem and Wiener-Tauberian theorem we refer to [12] and [22]. The novelty of this approach is that apart from these theorems, one can look into the study of multiplier theory, including Hörmander multiplier theorem in the SAFT domain. Moreover, one can define an appropriate modulation operator in connection with the SAFT, using which one can define modulation spaces associated with the SAFT. This in turn, motivates to study multiplier results for the new modulation spaces. (See [7] in this connection.)
Using the new translation operator the -shift invariant spaces are defined as for an appropriate function . When belongs to the Wiener amalgam space the space turns out to be a reproducing kernel Hilbert space. Moreover, we give characterization theorems for the system of translates to be a frame sequence, orthogonal system or a Riesz sequence.
If the system of translates is a frame then an important question is about the nature of the dual frame elements. We show that in our setting, the elements of the dual frame of system of -translates are also -translates of a single function. For a study of shift invariant spaces, system of translates, frames and Riesz basis in the classical case, we refer to Christensen [10].
In the final part of the paper we study the sampling in -shift invariant spaces. A fundamental problem in sampling theory is to find, for a certain class of
functions, appropriate conditions on a countable sampling set under which a given function can be reconstructed
uniquely and stably from the samples . We refer to the work of Butzer and Stens [8] for a review on sampling theory and its history. When is the classical principal shift invariant space with a single generator or multi-generators , there is a huge literature available on several interesting problems connected with sampling theory starting from the fundamental Shannon sampling theorem. We cite only a few references in this connection for the reader to get familiarity with this subject matter. (See [2], [3], [4], [5], [9], [13], [14], [17], [19], [20], [24], [25], [26], [27]).
In this paper, similar to Theorem of [3] and Theorem of [23], we obtain equivalent conditions for a set to be a stable set of sampling for in terms of the operator where , the reproducing kernel and the Zak transform , which we introduce here. We also obtain a sufficient condition for the set of integers to be a stable set of sampling for
In the study of non uniform sampling and average sampling, Bernstein type inequalities play an important role. In this paper we obtain an analogue of Bernstein type inequality for . However, we do not intend to study non-uniform sampling and average sampling in this paper. We focus on uniform sampling. In particular, when turns out to be a stable set of sampling, we obtain a reconstruction formula and hence a sampling theorem in the sense of convergence for certain -shift invariant spaces . Further, under some additional hypotheses on , we obtain a sampling formula in the sense convergence and uniform convergence. As corollaries we obtain Shannon sampling theorem in the SAFT domain and sampling theorem for the -shift invariant space generated by second order -spline.
We organize our paper as follows. In section , we define -convolution of a measure and a function and chirp modulation of a measure . Using this and the function , we obtain a relation between classical translation and -translation. We prove an analogue of Wendel’s theorem for the SAFT. In section , we study closed ideals in the Banach algebra . We obtain analogues of Wiener theorem and Wiener-Tauberian theorem in the context of the SAFT. In section , we study -shift invariant spaces and their theoretical aspects. Section as well as Section are devoted to sampling theorems in -shift invariant spaces. Finally in Section , we present a local reconstruction method for sampling in -shift invariant spaces along with implementation.
Now we shall provide the necessary terminology and background for this paper.
Let be a separable Hilbert space.
Definition 1.1.
A sequence of elements in is a frame for if there exist such that
The numbers are called frame bounds. If we have the right hand side inequality for a sequence in , then that sequence is called a Bessel sequence.
Definition 1.2.
Let be a Bessel sequence in , then the synthesis operator is defined by
The adjoint of is given by , called the analysis operator. Composing and we obtain the frame operator
The operator is invertible. Further if is a frame for , then is also a frame for and it is called the canonical dual frame of the frame
Definition 1.3.
A sequence in is said to be a Riesz basis if there exist a bounded invertible operator on and an orthonormal basis of such that The sequence is called a Riesz sequence if it is a Riesz basis for its closed linear span.
Equivalently is a Riesz sequence if there exist such that
Definition 1.4.
Let be a Riesz basis for . The dual Riesz basis of is the unique sequence in satisfying
Definition 1.5.
The Gramian associated with the Bessel sequence is an operator on whose entry in the matrix representation with respect to the canonical orthonormal basis is
It is well known that a sequence is a Riesz sequence if there exist such that its Gramian satisfy the following inequality:
Definition 1.6.
A closed subspace in is said to be a shift invariant space if where
In particular, for is called the principal shift invariant space.
Definition 1.7.
A set is said to be a stable set of sampling for a closed subspace of if there exist constants such that
for every
Definition 1.8.
The Wiener amalgam space , is defined as
2. The new translation
In this section, we introduce -translation operator in connection with the SAFT. Using -translation operator, we define -convolution of a regular Borel measure and a function. Further, we obtain an analogue of Wendel’s theorem. Towards this end, first we extend the definition of SAFT to the space of all regular Borel measures.
Definition 2.1.
Let . Then the special affine Fourier transform is defined as
| (2.1) |
where stands for the set of six parameters with and .
With the help of the following auxiliary functions
| (2.2) | ||||
| (2.3) |
the SAFT can be expressed as
| (2.4) |
Since for all , we immediately see from (2.4) that with . Moreover, (2.4) also shows that can be extended to and defines a unitary operator on that space. In particular,
The inverse of on can also be easily determined using (2.4)
Finally, (2.4) also provides an extension of the SAFT to , the space of all complex valued bounded regular Borel measures on , equipped with the total variation norm. For , we have
with and .
We now introduce the generalized translation operator associated with SAFT. In order to do so, we fix the following notation
| (2.5) | ||||
| (2.6) |
Definition 2.2.
Let and be a function. Then -translation of by , denoted by , is defined as
It is easy to see that is norm preserving in all spaces or .
We can relate our new translation and the classical translation in the following way, using and the chirp modulation operator where
| (2.7) |
| (2.8) | |||
| (2.9) |
In fact,
Similarly one can show (2.9).
Now, we collect the properties of
Proposition 2.3.
We have the following
-
(i)
-
(ii)
-
(iii)
Let . Then .
-
(iv)
Let . Then
(2.10)
Proof.
The proof is straightforward. ∎
It is interesting to note that the map is a group representation, whereas from Proposition 2.3 (i) it follows that is just a projective representation in general, which shows that the new translation is fundamentally different from that of the classical translation. Proposition 2.3 (iii) is what is known in harmonic analysis as a product formula. The relation (2.10) extends to functions as well. For those functions we have in particular
| (2.11) |
where the equality holds in the sense of functions.
Definition 2.4.
Let and , then is defined by
Clearly, Similarly, we can define as .
Using the -translation, we define the -convolution of and as
| (2.12) |
The integral in (2.9) can also be viewed as a vector-valued integral as follows.
| (2.13) |
where the right hand side is a Bochner integral. The convergence of the integral follows from
Now we give a relation between classical convolution and -convolution of a measure and a function. Consider
using (2.8), which in turn implies that
| (2.14) |
Further, using (2.9), one can show that
| (2.15) |
The convolution theorem for the SAFT reads as follows.
Proposition 2.5.
Let and . Then
| (2.16) |
Proof.
The proof is straightforward using the operator . ∎
In particular, if for some then
See [6] for more details.
The concept of chirp modulation was used in [6] to define a chirp convolution and to get sampling theorems. Although the -translation is somehow included implicitly in the definition of the chirp convolution, it has not been used to its full extent in [6] and hence the harmonic analysis of the special affine Fourier transform has not been developed. However we want to make use of our new translation from harmonic analysis point of view. Towards this end we first we prove an analogue of Wendel’s theorem for the SAFT.
We are now in a position to state one of our main results. The following statement is an analogue of Wendel’s theorem in the context of the SAFT.
Theorem 2.6 (Wendel).
Let be a bounded linear operator. Then the following statements are equivalent.
-
(i)
for all .
-
(ii)
, for all
-
(iii)
There exists a unique such that .
-
(iv)
There exists a unique such that
-
(v)
There exists a unique such that
Proof.
Let and define by . Then using (2.9) we get
which shows that iff . Similarly we can show that iff , and iff . The equivalence of (i),(ii), and (iii) now follows from Wendel’s theorem in the classical case. That (iii) implies (iv) and (iv) implies (v) is obvious. To show that (i) follows from (v), let . For we have
∎
We end this section by establishing an analogue of the Poisson summation formula for the SAFT and the corresponding -translation. From now on, we use the following notation.
Theorem 2.7.
Let . Then the following formula holds.
We refer to [6] for the proof.
3. Closed ideals in
We have seen that
Thus it is easy to see that , from which it follows that is a commutative Banach algebra. In this section, we aim to study the closed ideals in . Towards this end, first we show that possesses a bounded approximate identity as in the classical case .
Theorem 3.1.
The space possesses a bounded approximate identity.
Proof.
Let be a bounded approximate identity in and define . Then using (2.15), we get
as . Hence is a bounded approximate identity for .
∎
Now, we aim to study -translation invariant closed ideals in . First we prove the following theorem in this context.
Theorem 3.2.
Let be a closed subspace of . Then is an ideal in if and only if it is invariant under -translations.
Proof.
Proposition 3.3.
The collection is dense in .
Proof.
We know that is dense in . Thus, for , there exists such that has compact support and . This implies that
Further, has compact support as has compact support and
which completes the proof. ∎
Lemma 3.4 (Lemma 4.59 in [12]).
Let and . Then for every , there exists with such that
for every in some neighbourhood of .
Now we are in a position to state and prove an analogue Weiner’s theorem in connection with the SAFT.
Theorem 3.5.
Let be a closed -translation invariant subspace of such that , where . Then .
Proof.
In view of Proposition 3.3, it is enough to show that for all such that has compact support. Let be such that has compact support. Let .
Step 1: In this step we show that for each , there exists such that in a neighbourhood of .
Since , we can choose such that . Then using Lemma 3.4, there exists with and
in a neighbourhood of . This implies that
| (3.1) |
in a neighbourhood of . Let (-times). Then using the fact that is a Banach algebra, we can show that the series converges in . Let . Then using convolution theorem, we obtain
in a neighborhood of , using (3.1). The second equality in the above equation follows from the fact that . Thus
in a neighbourhood of . As , by Theorem 3.2, our claim is established.
Step 2: In this step we show that . Appealing to Step 1, for each , choose such that on a neighborhood of . Using compactness of , we get and such that and on . Now choose open such that
Again using the compactness of , there exist such that and , where . Take such that
Then on . This implies that
This can be rewritten as , where being one of the ’s or their convolutions, and , for some . But
As , . This completes the proof. ∎
Corollary 3.6.
Let . Then the closed linear span of -translates of is if and only if never vanishes.
Proof.
Let be the closed linear span of -translates of .
Let for all . Since is a closed -translation invariant subspace, appealing to Wiener’s theorem, we get .
Conversely assume that . Suppose for some . Then for all . Since is dense in and , we can conclude that , for all , which is an impossibility. Hence the result follows.
∎
Now, we shall state the analogue of Wiener’s theorem for functions.
Theorem 3.7.
Let . Then the closed linear span of -translates of is if and only if a.e.
Proof.
Let . Then if and only if , for all . For , consider
Thus is equivalent to
which is same as This shows that if and only if a.e. ∎
We conclude this section by establishing an analogue of Wiener-Tauberian theorem. Recall that denotes the modulation operator which is defined in (2.6).
Theorem 3.8 (Wiener-Tauberian).
Let be such that , for all and
Then
for all .
Proof.
Since, , for all , , for all . Further,
Furthermore,
using . Thus
| (3.2) |
Hence
using given hypothesis. Now using the classical Wiener-Tauberian theorem, we get
This implies that
This in turn implies that
using (3.2). ∎
As a special case, we state the following analogue of the Wiener-Tauberian theorem associated with the fractional Fourier transform.
Corollary 3.9.
Let , be such that , for all and
Then
for all .
4. -shift invariant spaces
In this section, we aim to study shift invariant spaces associated with the SAFT, called -shift invariant spaces, in detail. Recall that the -shift invariant space is defined by for . First, we obtain the following result whose proof is similar to that of Theorem 2 in [2] in the classical case.
Theorem 4.1.
Let be such that forms a Riesz basis for . Then
-
(i)
.
-
(ii)
If is separated, then there is such that
Corollary 4.2.
Let . Then is a reproducing kernel Hilbert space with the reproducing kernel
where is the frame operator for .
Proof.
Let be fixed. Then, taking in the previous theorem we get such that , for every , which shows that is a RKHS. The reproducing kernel for is . Now, using the definition of our assertion follows. ∎
Theorem 4.3.
If is a frame sequence, for , then the members of its canonical dual frame also are -translates of a single function.
Proof.
Let be the frame operator for . First we prove that Let . Then for , we have
Since is invertible, and we have for every
Thus, if is a frame for then the canonical dual frame is given by Taking , we conclude that the canonical dual frame is also of the form ∎
Remark 4.4.
If we assume is a Riesz basis for , then is the dual Riesz basis of .
Now we obtain a characterization for the system of -translates to be a frame sequence in terms of the weight function .
Theorem 4.5.
Let . Then the system of -translates is a frame sequence with bounds if and only if
| (4.1) |
where and .
Proof.
Let be a frame sequence with bounds . Then
| (4.2) |
Let be a finite subset of . Let . Then , where . Thus
| (4.3) |
Similarly,
where . Hence
| (4.4) |
Now, using (4.2), we get
for every -periodic trigonometric polynomial . This implies that
a. e. , from which (4.1) follows.
Conversely, assume that (4.1) holds. Then using (4.3), (4.4), we can show that (4.2) holds for all . Since is dense in , the proof follows.
∎
In a similar way, we can obtain the characterizations for the system to be a Riesz sequence or an orthonormal system. We state the results without proof. The interested readers can see the proof form [16] and from [6].
Theorem 4.6.
Let . Then the collection is a Riesz basis for if and only if there are such that
for almost all
Theorem 4.7.
Let . Then the collection is an orthonormal system in if and only if
| (4.5) |
for almost all
5. Sampling in -shift invariant spaces
In order to get an equivalent condition for the stable set of sampling in terms of the Zak transform, we first introduce -Zak transform.
Definition 5.1.
The -Zak transform of a function is a function on , defined as
One can simplify the right hand side and get
Remark 5.2.
In particular, if we take , then -Zak transform reduces to the classical Zak transform.
Theorem 5.3.
The -Zak transform is an isometry between the spaces and .
See [6] for the proof.
Define an operator by
where . Clearly is an orthonormal basis for
Suppose is a Riesz sequence. Then there are constants such that
for all . Since is an orthonormal basis for and , the above inequality reduces to
This shows that is bounded above and bounded below. By Riesz-Fischer theorem is onto. Hence is invertible. Moreover, we have
| (5.1) |
Now, we are in a position to prove equivalent conditions for stable set of sampling for a shift invariant space
Theorem 5.4.
Assume that is a reproducing kernel Hilbert space, for , such that forms a Riesz basis for . Then the following statements are equivalent.
-
(i)
The set is a stable set of sampling for
-
(ii)
There are constants such that
where the operator is defined by
-
(iii)
The set of reproducing kernels for is a frame for .
-
(iv)
The set is a frame for .
Proof.
The proof is similar to the classical case. However for the sake of completion, we give the outline of the proof. (i) (ii): If then there is such that , and hence . Since is a Riesz basis for , the following statements are equivalent.
-
(a)
There are constants such that for every
-
(b)
There are constants such that for
In fact, if (a) holds, then
Now by using the fact that is a Riesz sequence, one can find such that . Thus (b) follows from (a). Similarly one can prove (b) implies (a).
(i) (iii): Let be the set of reproducing kernels for . Then the equivalence follows from the identity .
(iii) (iv): Using (5.1) we obtain
here . Since is invertible, we get the equivalence of (iii) and (iv). ∎
Let . Then we define the function on the interval , by
From the definition of the -Zak transform we obtain .
Theorem 5.5.
Let . Then the operator defined by satisfies the inequalities
where
Proof.
Let . Then
Since is an orthonormal basis for , we have
This implies
or equivalently , from which the result follows. ∎
As a consequence we obtain the following
Corollary 5.6.
Let be such that forms a Riesz basis for and for all . Then is a stable set of sampling for
We end this section by proving Bernstein type inequality for . Let denote the class of continuously differentiable functions such that
-
(i)
and , for sufficiently large , for some .
-
(ii)
.
Theorem 5.7.
Let be such that is a Riesz basis for . Then we have the Bernstein type inequality
where and
Proof.
Let .
Then . Since , the above equalities hold pointwise. Thus
Further, , where . Now, using (see Proposition 3.5 in [7]), we obtain
proving our assertion. ∎
6. Sampling theorems
In this section, our aim is to obtain reconstruction formulae for the functions belonging to certain from integer samples. We prove sampling formulae with convergence as well as uniform convergence. As a corollary, we obtain the result proved in [6], namely Shannon sampling theorem for the functions which are bandlimited in the SAFT domain.
Theorem 6.1.
Let be such that forms a Riesz basis for . Then there is a function such that
| (6.1) |
for all if and only if
Proof.
Assume that there is a such that (6.1) holds. Then . Taking SAFT on both sides we obtain
| (6.2) |
This implies that . Since is periodic, we have
Since , we have and hence is not a set of measure zero. We shall show that If not, then there exists a , a set of positive measure such that and This in turn implies that on . This is a contradiction to our assumption that is a Riesz sequence. So for almost every Using (6.2), we get and
where . Since forms a Riesz sequence, . Consequently
Conversely, assume that . Since forms an orthonormal basis for , there is a sequence such that
Let Then
where . Since is a Riesz sequence, . Hence . Then there is exactly one such that . From the definition of we get
which shows that and hence . Now let with representation . Taking SAFT leads to
The last equality finally gives ∎
In Theorem 6.1, we obtained a sampling formula for functions belonging to -shift invariant spaces with convergence. Now, our aim is to obtain another version of a sampling theorem where we obtain both convergence and pointwise convergence of the corresponding reconstruction formula. Towards this end, we prove the following
Lemma 6.2.
Let . Then the following statements are equivalent.
-
(i)
For any , the series of functions converges to a continuous function.
-
(ii)
and .
Proof.
Since , the proof follows as in Lemma 1 in [27]. ∎
For a sequence , we define
For two sequences and , we define
Using the fact that , is an orthonormal basis for , we get
Further, one can show that
Thus
| (6.3) |
Theorem 6.3.
Let be a frame sequence for . Then the following are equivalent.
-
(i)
The series converges to a continuous function for any and there exists a frame for such that
(6.4) where the convergence is both in and uniform on .
-
(ii)
, is bounded on and
(6.5) for some , where , .
Proof.
In order to show that (i) implies (ii), it is enough to show that (6.5) holds. Taking in (6.4), we get
Taking SAFT on both sides we obtain . This implies that , from which it follows that . Since and are frame sequences, there exist such that
using Theorem 4.5. We now show that a.e. on . To see this, take Then , for some . Since , taking inverse SAFT, we obtain , for all . In particular,
Thus using (6.3), we get
which proves our claim.
Conversely assume that (ii) holds. Let
Then is a frame sequence by appealing to Theorem 4.5. Since , it can be easily seen that . With the similar reasoning, we can say that . Thus . Now define,
We show that is the canonical dual of . Let be the frame operator associated with the frame . Since commutes with , for all , it is enough to show that . Consider
which proves our claim. Let . Then , where , for some . For , consider
Hence
We notice that . Thus, in order to show the uniform convergence of the above series, it is enough to show that
for some . Since , , where , for some . Thus . Since and are frames for , is bounded on . This implies that is bounded on . Let , for some . Since , . Thus
proving our assertion. ∎
As a consequence of Theorem 6.1, we obtain Shannon sampling theorem for the SAFT domain by taking where We also write down the sampling theorem when is taken to be the second order symmetric -spline.
Corollary 6.4.
Let and . Then for every , we have the following representation
| (6.6) |
Proof.
We have
from which it follows that for almost all , and this implies that is an orthonormal basis for the space . Moreover, we have . Consequently So by Theorem 6.1 we have which implies that Hence for we have
∎
Corollary 6.5.
Let . Let . Then , where
Proof.
It is clear from Corollary 6.4 that . Now we shall show that is a closed subspace of and the orthogonal complement of in is zero, which will prove our assertion. As we have , is an isometry from onto . Therefore is a closed subspace of . In Corollary 6.4 we have seen that is an orthonormal basis for . Consider such that . Now we shall show that . For all we have
Using the fact that is an orthonormal basis for , we get for a.e. , which in turn implies that , proving our assertion. ∎
As a consequence of Corollary 6.4, Corollary 6.5 can be restated as Shannon sampling theorem for the SAFT domain.
Corollary 6.6.
Let be such that the . Then the following sampling formula holds
Corollary 6.7.
Let Then for every , we have the following reconstruction formula
Proof.
Let be the Gramian associated with the sequence Then is a tridiagonal operator with all the diagonal elements, . The elements above the diagonal are given by
and the elements below the diagonal are given by
Notice that for is strictly diagonally dominant and hence invertible, for are dominated by Now let with , then is strictly diagonally dominant and hence invertible. In other words forms a Riesz basis for Further on , from which the required assertion follows.
∎
7. A local reconstruction method
As in the case of classical shift invariant space we can obtain a local reconstruction method for functions belonging to with continuous generators satisfying polynomial decay from their samples. We state the results without the proof as the proofs follow similar lines. We refer to the works [20], [21].
Proposition 7.1.
Let be a complex valued continuous function on satisfying Assume that is a Riesz basis for . Let and be an interval in Then for a given there exist a positive integer and a sequence such that
for all , for all and . In other words can be approximately determined by a finite number of coefficients locally.
Theorem 7.2.
Fix Let be a complex valued continuous function on satisfying Assume that is a Riesz basis for . Let be an interval in and . Let be a positive integer obtained in Proposition 7.1. Consider those points in the sample set such that . Let , where denotes the number of points in . Define . Then there exist such that
where is the pseudoinverse of .
Experimental results
Local reconstruction method in the SAFT domain is implemented using Mathematica. We take in the implementation.
We take and , a linear combination of integer -translates of Here we reconstruct in the interval from a sample set We also plot the SAFT of and tabulate error for various values of in Table 1.
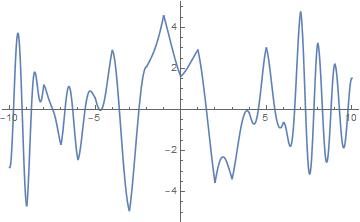
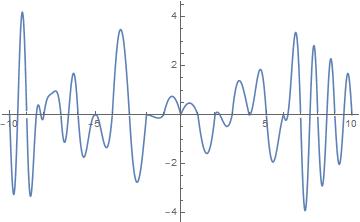
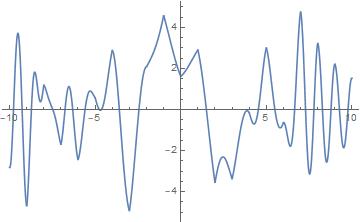
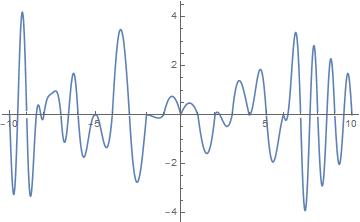
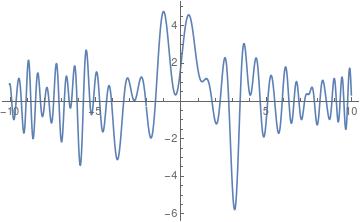
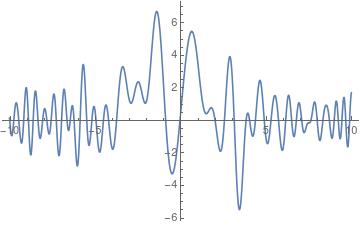
Computation of error
| Error | |
|---|---|
Acknowledgement
F.F. was partially supported by the Helmholtz Pilot Project Ptychography4.0 ZT-I-0025 and by the project ZT-I-PF-4-024 within the Helmholtz Imaging Platform.
References
- [1] S. Abe and J. T. Sheridan, Optical operations on wave functions as the Abelian subgroups of the special affine Fourier transformation, Optics Letters 19 (1994), no. 22, 1801–1803.
- [2] A. Aldroubi and K. Gröchenig, Beurling-Landau-type theorems for non-uniform sampling in shift invariant spline spaces, J. Fourier Anal. Appl. 6 (2000), no. 1, 93–103. MR 1756138
- [3] A. Aldroubi and K. Gröchenig, Nonuniform sampling and reconstruction in shift-invariant spaces, SIAM Rev. 43 (2001), no. 4, 585–620. MR 1882684
- [4] A. Aldroubi, Q. Sun, and W.-S. Tang, -frames and shift invariant subspaces of , J. Fourier Anal. Appl. 7 (2001), no. 1, 1–21. MR 1812992
- [5] A. Aldroubi, Q. Sun, and W.-S. Tang, Nonuniform average sampling and reconstruction in multiply generated shift-invariant spaces, Constr. Approx. 20 (2004), no. 2, 173–189. MR 2036639
- [6] A. Bhandari and A. I. Zayed, Shift-invariant and sampling spaces associated with the special affine Fourier transform, Appl. Comput. Harmon. Anal. 47 (2019), no. 1, 30–52. MR 3958693
- [7] M. H. A. Biswas, H. G. Feichtinger, and R. Ramakrishnan, Modulation spaces, multipliers associated with the special affine Fourier transform, Complex Anal. Oper. Theory 16 (2022), no. 6, Paper No. 86, 30. MR 4458766
- [8] P. L. Butzer and R. L. Stens, Sampling theory for not necessarily band-limited functions: a historical overview, SIAM Rev. 34 (1992), no. 1, 40–53. MR 1156288
- [9] W. Chen and S. Itoh, A sampling theorem for shift-invariant subspace, IEEE Trans. Signal Process. 46 (1998), no. 10, 2822–2824. MR 1718413
- [10] O. Christensen, An Introduction to Frames and Riesz Bases, second ed., Applied and Numerical Harmonic Analysis, Birkhäuser/Springer, [Cham], 2016. MR 3495345
- [11] M. A. de Gosson, Symplectic Methods in Harmonic Analysis and in Mathematical Physics, Pseudo-Differential Operators. Theory and Applications, vol. 7, Birkhäuser/Springer Basel AG, Basel, 2011. MR 2827662
- [12] G. B. Folland, A Course in Abstract Harmonic Analysis, Studies in Advanced Mathematics, CRC Press, Boca Raton, FL, 1995. MR 1397028
- [13] H. Führ and J. Xian, Relevant sampling in finitely generated shift-invariant spaces, J. Approx. Theory 240 (2019), 1–15. MR 3926050
- [14] A. G. García, M. A. Hernández-Medina, and G. Pérez-Villalón, Generalized sampling in shift-invariant spaces with multiple stable generators, J. Math. Anal. Appl. 337 (2008), no. 1, 69–84. MR 2356055
- [15] J. J. Healy, M. A. Kutay, H. M. Ozaktas, and J. T. Sheridan, Linear Canonical Transforms: Theory and Applications, vol. 198, Springer, 2015.
- [16] E. Hernández and G. Weiss, A First Course on Wavelets, Studies in Advanced Mathematics, CRC Press, Boca Raton, FL, 1996, With a foreword by Yves Meyer. MR 1408902
- [17] M. I. Kadets, The exact value of the Paley–Wiener constant, Dokl. Akad. Nauk SSSR 155 (1964), 1253–1254. MR 0162088
- [18] R. Larsen, An Introduction to the Theory of Multipliers, Springer-Verlag, New York-Heidelberg, 1971, Die Grundlehren der mathematischen Wissenschaften, Band 175. MR 0435738
- [19] M. Z. Nashed and Q. Sun, Sampling and reconstruction of signals in a reproducing kernel subspace of , J. Funct. Anal. 258 (2010), no. 7, 2422–2452. MR 2584749
- [20] R. Radha, K. Sarvesh, and S. Sivananthan, Sampling and reconstruction in a shift invariant space with multiple generators, Numer. Funct. Anal. Optim. 40 (2019), no. 4, 365–385. MR 3924210
- [21] R. Radha and S. Sivananthan, Local reconstruction of a function from a non-uniform sampled data, Appl. Numer. Math. 59 (2009), no. 2, 393–403. MR 2484929
- [22] W. Rudin, Functional Analysis, second ed., International Series in Pure and Applied Mathematics, McGraw-Hill, Inc., New York, 1991. MR 1157815
- [23] A. A. Selvan and R. Radha, Sampling and reconstruction in shift-invariant spaces on , Ann. Mat. Pura Appl. (4) 194 (2015), no. 6, 1683–1706. MR 3419912
- [24] Q. Sun, Local reconstruction for sampling in shift-invariant spaces, Adv. Comput. Math. 32 (2010), no. 3, 335–352. MR 2595176
- [25] J. Xian and S. Li, Sampling set conditions in weighted multiply generated shift-invariant spaces and their applications, Appl. Comput. Harmon. Anal. 23 (2007), no. 2, 171–180. MR 2344609
- [26] Q. Zhang, B. Liu, and R. Li, Dynamical sampling in multiply generated shift-invariant spaces, Appl. Anal. 96 (2017), no. 5, 760–770. MR 3613029
- [27] X. Zhou and W. Sun, On the sampling theorem for wavelet subspaces, J. Fourier Anal. Appl. 5 (1999), no. 4, 347–354. MR 1700088
Statements and Declarations
1. All authors read and approved the final manuscript. There is no conflict of interest.
2. There is no associated data in the manuscript.