The TRAPUM Small Magellanic Cloud pulsar survey with MeerKAT –
II. Nine new radio timing solutions and glitches from young pulsars
Abstract
We report new radio timing solutions from a three-year observing campaign conducted with the MeerKAT and Murriyang telescopes for nine Small Magellanic Cloud pulsars, increasing the number of characterised rotation-powered extragalactic pulsars by 40 per cent. We can infer from our determined parameters that the pulsars are seemingly all isolated, that six are ordinary pulsars, and that three of the recent MeerKAT discoveries have a young characteristic age of under 100 kyr and have undergone a spin-up glitch. Two of the sources, PSRs J00407337 and J00487317, are energetic young pulsars with spin-down luminosities of the order of 1036 erg s-1. They both experienced a large glitch, with a change in frequency of about 30 Hz, and a frequency derivative change of order Hz s-1. These glitches, the inferred glitch rate, and the properties of these pulsars (including potentially high inter-glitch braking indices) suggest these neutron stars might be Vela-like repeating glitchers and should be closely monitored in the future. The position and energetics of PSR J00487317 confirm it is powering a new Pulsar Wind Nebula (PWN) detected as a radio continuum source; and similarly the association of PSR J00407337 with the PWN of Supernova Remnant (SNR) DEM S5 (for which we present a new Chandra image) is strengthened. Finally, PSR J00407335 is also contained within the same SNR but is a chance superposition. It has also been seen to glitch with a change of frequency of Hz. This work more than doubles the characterised population of SMC radio pulsars.
keywords:
stars: neutron – pulsars: general – galaxies: individual: Small Magellanic Cloud – Magellanic Clouds – ISM: supernova remnants – pulsars: individual: PSR J00407326, PSR J00407335, PSR J00407337, PSR J00437319, PSR J00447314, PSR J00487317, PSR J00517204, PSR J00547228, PSR J010572081 Introduction
The Small and Large Magellanic Clouds (SMC and LMC) are the only galaxies outside our own in which radio pulsars have been discovered to date. They are nearby galaxies that are unobstructed by the Milky Way’s (MW) Galactic plane. Indeed, the Small Magellanic Cloud is just 60 kpc away (Karachentsev et al., 2004), and the expected Milky Way Dispersion Measure (DM) contribution in its direction is low: about pc cm-3 according to the YMW2016 electron density model (Yao et al., 2017), and pc cm-3 according to the NE2001 model (Cordes & Lazio, 2004). Of the nearly 3400 radio pulsars that have been discovered, only 38 are extragalactic. 14 are in the Small Magellanic Cloud, discovered by McConnell et al. 1991 (one pulsar), Crawford et al. 2001 (one), Manchester et al. 2006 (three), Titus et al. 2019 (two) and Carli et al. 2024 (seven). Their median DM is approximately 110 pc cm-3.
TRAPUM (TRAnsients and PUlsars with MeerKAT) is a Large Survey Project of the MeerKAT telescope (trapum.org, Stappers & Kramer 2016). The collaboration has already discovered over 200 pulsars111http://trapum.org/discoveries/ in the Milky Way (e.g. Padmanabh et al., 2023; Clark et al., 2023; Ridolfi et al., 2022). In Carli et al. 2024 (Paper I of this series), TRAPUM reported the discovery of seven new radio pulsars in the Small Magellanic Cloud. One of TRAPUM’s science goals is to characterise these extragalactic pulsars to better understand their population. The SMC has undergone recent episodes of star formation (Harris & Zaritsky, 2004), which should allow the detection of a higher proportion of short-lived and young objects than in the Milky Way’s older population, such as Pulsar Wind Nebulae (PWNe), and a high density of Supernova Remnants (SNRs) as shown in e.g. Cotton et al. (2024) and Maggi et al. (2019). Indeed, we presented the discovery of the first two radio pulsars in the SMC to be associated with PWNe in Paper I: PSR J00407337 in the SNR DEM S5 (Alsaberi et al., 2019; Haberl et al., 2000; Payne et al., 2007) and PSR J00487317 in a new PWN (Cotton et al., 2024). The associations were based on preliminary positions and, in the case of PSR J00487317, an age estimate from two survey observations. In addition, two young pulsars (not accretion-powered) have been discovered, via their X-ray pulsations only, in the SMC: the magnetar CXOU J010043.1721134 by Lamb et al. 2002 (recently associated with a new supernova remnant by Cotton et al. 2024) and the rotation-powered pulsar J00587218 by Maitra et al. 2021 (see also Carli et al. 2022). The latter is embedded in a Pulsar Wind Nebula in the supernova remnant IKT 16 (Inoue et al., 1983; Mathewson et al., 1984; Owen et al., 2011; Maitra et al., 2015). There are no other rotation-powered pulsars known in the other 19 supernova remnants of the SMC.
Pulsar timing is the process of measuring the evolution of a pulsar’s rotation rate over a period of time. It enables the position and spin period derivatives of the neutron star to be measured precisely, and, assuming a magnetic dipole model (Gold, 1968), allows a simplified characterisation of its age, magnetic field, and rotational energy loss rate (see Lorimer & Kramer, 2005). It also monitors variations in the pulsars’ properties, due for example to the effects of binary motion. The SMC hosts the only known extragalactic binary pulsar222There are no known extragalactic compact binaries with variations on shorter timescales (or millisecond pulsars, that are often found in such systems).: PSR J00457319, an ordinary pulsar with a massive main sequence B star companion. It was discovered by McConnell et al. (1991) and its binarity was revealed after several years of timing by Kaspi et al. (1994). Further, this monitoring of the spin period of pulsars enables the detection of glitches. Most glitches are detected in young, energetic pulsars (e.g. Basu et al., 2022) and consist of a sudden spin-up event. They might be caused by the unpinning of superfluid vortices in the neutron star interior, although this is still debated (Anderson & Itoh 1975, see Antonopoulou et al. 2022 for a review). Characterising and reporting these events is important for studies of superdense matter states (e.g. Lyne et al., 2000; Ho et al., 2015; Antonopoulou et al., 2022). There are only two extragalactic pulsars that have been observed to glitch, both in the Large Magellanic Cloud. These are PSR J05376910, only detected in X-ray pulsations in a PWN in the SNR N157B (Wang et al., 2001; Wang & Gotthelf, 1998); and the ‘Crab pulsar twin’ PSR J05406919 in the PWN of SNR 054069.3 (Manchester et al., 1993b; Gotthelf & Wang, 2000; Brantseg et al., 2013), the only known extragalactic multi-wavelength pulsar (Seward et al., 1984; Middleditch & Pennypacker, 1985; Manchester et al., 1993a; Marshall et al., 2016). Recently, a possible ‘anti-glitch’ – a sudden spin-down event – has been witnessed in PSR J05406919, the first for a rotation-powered pulsar (Tuo et al., 2024). PSR J05376910 is not only the fastest spinning young pulsar known, but also the most prolific glitching pulsar known, with frequent, large spin-ups and a unique, strong correlation between the glitch size and the time until the following event (Middleditch et al., 2006; Antonopoulou et al., 2018; Ferdman et al., 2018). Overall, the exotic behaviour revealed by extragalactic pulsar timing emphasises the importance of monitoring young extragalactic systems.
In this paper, we detail the results of a three-year radio timing campaign to characterise the pulsar discoveries from the Carli et al. 2024 (Paper I) and Titus et al. (2019) surveys of the SMC as part of TRAPUM’s goal to expand the known sample of the extragalactic neutron star population. We describe our observations with the MeerKAT and Murriyang telescopes in section 2. The timing methods and solutions of non-glitching pulsars are reported in section 3 and section 4 respectively. All the pulsar discoveries of Paper I which we now determine to be young333With a characteristic age under 100 ky. have glitched during our monitoring. We describe our modelling of these events and their implications in section 5. The parameters derived from the radio timing solutions enable us to interpret the pulsars’ associations which we discuss in section 6.
2 Observations
We collated a dataset of observations for nine SMC radio pulsars with no timing solutions: 7 pulsar discoveries from Carli et al. 2024 (PSRs J00407326, J00407335, J00407337, J00447314, J00487317, J00547228, and J01057208) and 2 from Titus et al. 2019 (PSRs J00437319 and J00517204 which were localised in Paper I). The observations span nearly 3 years in total. We recorded data with the MeerKAT 64-antenna radio interferometer in South Africa, described in subsection 2.1 below, and the 64-m single dish Murriyang telescope at Parkes, Australia (subsection 2.2). We included the survey data of all the new pulsars from Paper I, including the discovery data. The details of these observations are reported there. We did not use the single Murriyang discovery observation for PSR J00437319 and PSR J00517204 of Titus et al. (2019) to keep the timing datasets to a single observatory.
2.1 MeerKAT observations
We conducted three pseudo-logarithmically spaced timing campaigns with the full array of the MeerKAT telescope at L-band (central frequency of 1284 MHz, Lehmensiek & Theron, 2012). The data were recorded on the APSUSE on-site computing cluster (Accelerated Pulsar Searching User-Supplied Equipment, used by TRAPUM, Barr 2017, Padmanabh 2021) with a bandwidth of 856 MHz split into 4096 channels and a sampling time of 76 s, in sigproc filterbank format (Lorimer, 2008) with no coherent de-dispersion. The observations started with a short separation (half a day to a day) between observations to ensure phase connection. The separation between observations then increased in a pseudo-logarithmic fashion to an intended total time span of about nine months per campaign.
We used the Filterbanking Beamformer User Supplied Equipment (FBFUSE, used by TRAPUM, Barr, 2017; Padmanabh, 2021; Chen et al., 2021) to form several simultaneous MeerKAT closely packed coherent beams on and around the location of each timed pulsar within a pointing. We initially employed the seeKAT multi-beam localisation software (Bezuidenhout et al., 2023) to obtain a more precise position than had been possible from the discovery data. Then, we repeated the process by centring the next observation’s beam tiling on the new localisation. This increased the S/N of the pulsars (reducing the integration time from 30 minutes to 10-15 minutes) and provided a precise pre-timing position. When this precision was sufficient, pulsars were observed with a single beam. The accurate position obtained is crucial in reducing the timing baseline where a covariance between the spin period derivative and position error is present to about 6 to 9 months. Typically, with larger position errors, this covariance would not be eliminated for closer to a year.
The first campaign aimed to determine a timing solution for the first six Carli et al. (2024) discoveries and the two Titus et al. (2019) discoveries. A pseudo-logarithmic cadence was adopted from the third observation. The campaign started in February 2022 and ended in December 2022 with a total of 11 L-band observations of each of two pointing positions. Pointing ‘SMCTIMING1a’444These target names can be used to search the records of the SARAO web archive. comprised the pulsars J00407326, J00407335, J00407337, J00447314, J00487317, J00437319 and the bright known pulsar J00457319 (McConnell et al., 1991) for testing purposes. We used the multi-beam capability of the TRAPUM backends to time these pulsars simultaneously. Pointing ‘SMCTIMING1b’ recorded pulsars J00547228 and J00517204. As part of this campaign, a single 40-minute observation of ‘SMCTIMING1a’ and ‘SMCTIMING1b’ was completed with MeerKAT’s Ultra High Frequency receiver (UHF, 544-1088 MHz, Lehmensiek & Theron 2014) with a bandwidth of 544 MHz split into 4096 channels and a sampling time of 60 s to characterise eight pulsars in this band. The resulting pulse profiles are shown in subsection 4.2. The data were not used as part of the timing solution.
The second pseudo-logarithmically spaced MeerKAT campaign consisted of observations to obtain the timing solution for a later discovery, PSR J01057208. It is spatially separated from the other pulsars in this work, and thus was timed on its own, at the centre of the ‘SMCTIMING2a’ pointing location. The campaign started in December 2022 and ended in January 2023 with a total of 8 observations. One observation was affected by lightning but could still be used. The rest of the campaign was observed with Murriyang, which is described in the next section.
The third pseudo-logarithmically spaced MeerKAT campaign was performed to provide a phase-connected post-glitch timing solution for PSR J00407335 and PSR J00407337 as they proved difficult to time with Murriyang (described in the next section). The campaign started in June 2023 and ended in August 2023 with a total of 7 observations of one pointing position. Pointing ‘SMCGLITCHERS’ was aimed directly at PSR J00407335 to obtain maximal gain on this faint pulsar. Taking advantage of the multi-beam capacity of TRAPUM, we also timed all the nearby pulsars that were in the field of ‘SMCPOINTING1a’.
2.2 Murriyang Observations
We reported in Paper I that, upon discovery of a pulsar, we attempted to obtain detections in archival Murriyang data. None of the pulsars could be detected. This prevented the extension of our timing solutions into the pre-discovery past. We also conducted our own observations with Murriyang, using the Ultra-Wide-band Low receiver (UWL, Hobbs et al., 2020), covering a frequency range from 0.7 to 4 GHz. Most pulsar discoveries of Paper I are too faint to be detected in one hour or less at Murriyang with the UWL.
We began observing our brightest discovery, PSR J00487317, with Murriyang early in the MeerKAT SMC survey. This was initially done using Director’s Time, then registered under Project P1054 (‘Follow-up of pulsar discoveries from MeerKAT searches’) from June 2021. PSR J00487317 then became part of the P1054 project from September 2021 until today. Initially, these (usually) 1-h long observations were performed with a close cadence to obtain a first timing solution, which revealed that the pulsar was young, then monthly to monitor the pulsar for possible glitches and timing noise. Extra observations were performed using Director’s Time between September 2022 and March 2023 under project code PX092555Except for the initial September 2022 Director’s Time observation that was recorded under P1054. to obtain a new coherent timing solution after the pulsar underwent a large glitch in May 2022. Search mode (64 s sampling, 3328 frequency channels, no polarisation) was initially used while there was no timing solution, then followed by search and fold mode from December 2021 to May 2022, and in fold mode with coherent de-dispersion (1024 pulse profile bins, 30 s sub-integrations, 3328 frequency channels, all Stokes parameters recorded) only afterwards when it was deemed reliable. This amounted to a total of 37 successful observations with only one non-detection.
After the first MeerKAT timing campaign determined that PSR J00407335 and PSR J00407337 were young pulsars, we began monitoring them with Murriyang Director’s Time to reveal possible glitches or timing noise. They were observed in the same beam, under the target names ‘PWN0040-7337’ or ‘J0040-7335’, in search mode (128 s sampling, 3328 frequency channels) to be able to fold both pulsars from the same observation. The observations began in January 2022 under P1054, then were attributed the Director’s Time project code PX096 from December 2022. The flux of the pulsars was very variable, and often too faint to be detected in short observation times. From March to May 2023 a denser campaign was attempted to obtain a coherent timing solution after both pulsars glitched (PSR J00407335 glitched in December 2022, PSR J00407337 glitched in February 2023). This was taken over at MeerKAT due to insufficient sensitivity. In total, 14 observations were performed successfully until December 2023, with integration times between 20 minutes and 4 hours.
Finally, after a successful test in November 2022, two 1.5 h PX096 search mode observations were conducted in March and May 2023 to extend the MeerKAT pseudo-logarithmically spaced campaign on PSR J01057208. They yielded weak detections, particularly affected by Radio Frequency Interference (RFI). In August 2023, a test 1.5 h fold mode observation was unsuccessful in detecting the pulsar, again due to RFI.
The only pulsar discoveries of Paper I that were not observed with Murriyang are J00407326 and J00447314. The two Titus et al. (2019) discoveries PSR J00517204 and PSR J00437319 were also only observed with MeerKAT. These four pulsars were timed as part of the multi-beam targets described in the previous section. A test Murriyang observation of PSR J00547228 was performed on 7 June 2021 but the pulsar was deemed too weak to observe regularly there.
3 Data reduction
In this section, we describe the methods employed to reduce the data of all nine pulsars in this study. We also describe the fitting analysis performed to determine the spin and astrometric parameters of the 6 pulsars in this study that have not glitched, resulting in phase coherent radio timing models.
3.1 MeerKAT data reduction and timing solution fitting
For each MeerKAT observation, the RFI in the raw data were cleaned using pulsarX’s filtool (Men et al., 2023). We then created a high-resolution phase-folded archive with dspsr (Van Straten & Bailes, 2011), downsampling the raw data to 512 channels, 10-s sub-integrations, and 1024 phase bins. The initial phase folding parameters were the discovery localisation666As the MeerKAT timing observations progressed, the localisations were refined with seeKAT as detailed in subsection 2.1., DM and period of each pulsar (which are stated in Paper I). The folded data were further RFI-cleaned with clfd (Morello, 2023), and if required, additional manual cleaning was performed using psrchive (Hotan et al., 2004). Initially, before an ephemeris was obtained, we searched for the highest S/N total profile of each observation with psrchive’s pdmp tool if deemed necessary. We optimised the sum of the phase-folded data over a small range of periods and DMs. Each observation’s data were independently re-folded with these parameters if needed. Eventually, ephemerides were used to re-fold all the high-resolution archives with a single ephemeris. We thus obtained a single (frequency and time summed) pulse profile for each observation with psrchive’s pam tool.
A noiseless template profile was first fitted to the discovery pulse profile of each pulsar, and later a new template was made from a higher S/N detection. This was done using psrchive’s paas tool, manually adding von Mises function components (see subsection 4.2). The final template profile was built from adding up all777One or two were omitted for some pulsars. L-band observations in phase using the ephemerides stated in section 4 with psrchive’s psradd tool, and optimising the archive over 20 pc cm-3 with pdmp to determine the final DM value of each pulsar exclusively timed at MeerKAT.
We then fitted a topocentric Time of Arrival (ToA) and ToA error to each phase-added observation with psrchive’s pat tool. We used the Fourier domain algorithm with Markov chain Monte Carlo to cross-correlate the noiseless template to each observation’s pulse profile. For the non-glitching pulsars, we fitted a timing model containing celestial coordinates and pulsar spin parameters to the ToAs with tempo2 (Hobbs et al., 2006; Edwards et al., 2006). tempo2 transformed our topocentric ToAs to the Solar System barycentre using the Jet Propulsion Laboratory’s DE405 Solar System ephemeris (Standish, 1998). We used the tempo2 model version number 5.00 and the TT(TAI) clock correction procedure. The model parameters and residuals are presented in subsection 4.1.
The pulse width of the pulsars was obtained from the final summed pulse profile of all observations (that was used to determine ToAs). The initial paas model components were refined and debased using psrsalsa’s fitvonMises tool (Weltevrede, 2016). Then, we added noise to the refined model profile using the off-pulse noise statistics of the summed profile. We again refined the model, fitting a pulse width at 50 per cent of the peak intensity to the model with added noise, and repeated this process 1000 times. The mean and standard deviation of the resulting width distribution are quoted in subsection 4.2.
3.2 Murriyang data reduction
The reduction of the Murriyang observations was performed similarly to the steps detailed in the previous section. The differences in processing are detailed here. filtool was not applied to the observations of PSR J00487317 and dspsr’s digifil was used to merge raw data time segments (‘search mode’), unless the data were already folded on-line (‘fold mode’). A static UWL channel mask was generally employed. The fold-mode data were flux calibrated using psrchive’s pac command and flux calibrators provided by the Murriyang observatory888https://www.parkes.atnf.csiro.au/observing/Calibration_and_Data_Processing_Files.html. Where polarisation products were recorded, the fold-mode data were polarisation calibrated using short noise diode recordings performed before each observation. The high-resolution stored archives have 416 channels. Due to an oversight, polarisation calibration was performed on archives with this frequency resolution. When adding observations with psradd, the phase alignment option was used if the observations were folded with an ephemeris that contained red noise terms. The Murriyang pulse template was rotated to have its peak at the same phase as MeerKAT’s, except PSR J01057208 for which our observations did not accumulate enough total S/N to produce a UWL pulse profile template. The Dispersion Measure obtained from optimising the Murriyang phase-added observations was used as the final value for pulsars timed with both MeerKAT and Murriyang, as the wide frequency range of the UWL allowed a more precise determination999This was not done for PSR J00407335 and PSR J01057208 due to their low S/N in Murriyang observations. of this value than MeerKAT’s L-band, though they were consistent. Finally, we fitted a temporal jump between the two observatories with tempo2.
4 Results
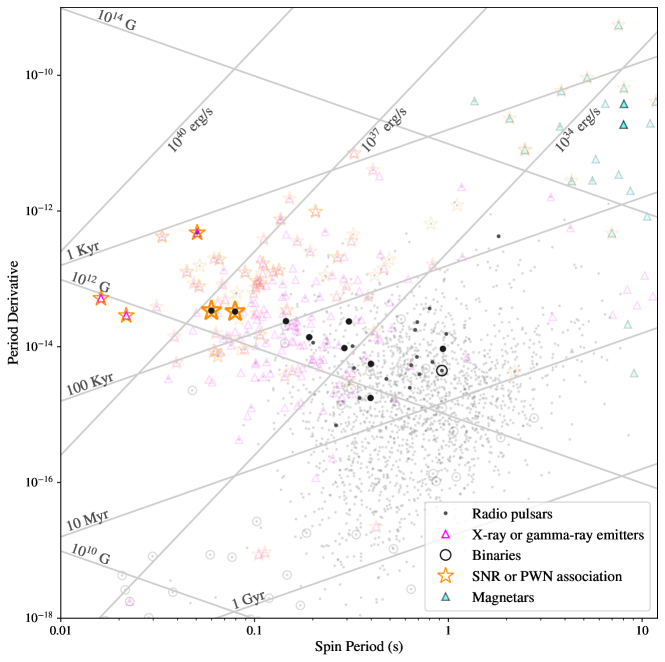
We obtained phase-coherent timing solutions for all nine pulsars. We present a new period-period derivative diagram for extragalactic pulsars in Figure 1, adding all nine pulsars in this work. Their pulse profiles are discussed in subsection 4.2. In subsection 4.1, the timing models obtained through the methods described in section 3 from the observations detailed in section 2 are used to characterise the six pulsars in this study that have not glitched. The solutions for the pulsars that have glitched are given in section 5.
4.1 Timing solutions: normal pulsars
The timing parameters from our best fit solutions for the pulsars that have not undergone a glitch are given in Table 1. The time span of the PSR J01057208 data is too short to fit a position, therefore we used our best seeKAT timing observation localisation (for which 3 errors are quoted but not used in the fit). We find that the apparent change in rotation period that would be caused by the seeKAT position error (if the period was compared at the near and far side of the Earth’s orbit) is negligible compared to the error on the first derivative of frequency for this pulsar. The DM errors quoted are obtained from a pdmp optimisation over 20 pc cm-3 of the total added L-band observations, and are not used in fitting. We note that none of the pulsars required additional parameters from e.g. binary motion. Additional derived parameters calculated by tempo2: the characteristic age, surface magnetic field strength, and rotational energy loss are also given. The residuals from these best fit models are given in Figure 2. The glitching pulsars’ timing solutions are given in subsection 5.2.
| Data and Modelling | ||||||
| Pulsar name | J00407326 | J00437319 | J00447314 | J00517204 | J00547228 | J01057208 |
| MJD range | 59514.1—60180.3 | 59328.1—60180.3 | 59328.1—60180.3 | 59328.2—59919.7 | 59328.2—60022.3 | 59900.4—60095.8 |
| Data span (yr) | 1.82 | 2.33 | 2.33 | 1.62 | 1.90 | 0.54 |
| Number of ToAs | 19 | 19 | 19 | 12 | 13 | 11 |
| Rms timing residual () | 1079.6 | 335.9 | 1404.7 | 228.7 | 431.6 | 223.9 |
| Reduced value | 0.9 | 0.8 | 1.8 | 10.5 | 40.1 | 11.0 |
| Measured quantities | ||||||
| Right ascension (hh:mm:ss) | 00:40:23.77(7) | 00:43:13.21(3) | 00:44:56.95(12) | 00:51:34.529(17) | 00:54:54.20(4) | – |
| Declination (dd:mm:ss) | 73:26:26.09(17) | 73:19:55.62(8) | 73:13:59.3(6) | 72:04:23.74(14) | 72:28:33.39(17) | – |
| Pulse frequency, (s-1) | 2.50842466468(10) | 1.066741330241(16) | 2.51944095060(7) | 5.22337600249(11) | 3.43707814666(5) | 3.2601205007(4) |
| First derivative of pulse frequency, (s-2) | 3.5271(6) | 1.06156(9) | 1.1184(6) | 3.77282(7) | 1.12930(4) | 2.5102(9) |
| Second derivative of pulse frequency, (s-3) | – | 8.3(11) | – | – | – | – |
| Set quantities | ||||||
| Dispersion measure, DM (cm-3pc) | 85.7(6) | 120.8(5) | 78.6(5) | 159.3(2) | 92.4(1) | 120.4(2) |
| Epoch (MJD) | 59692.1 | 59692.1 | 59692.1 | 59692.1 | 59692.1 | 59929.7 |
| Right ascension, (hh:mm:ss) | – | – | – | – | – | 01h05m385(3) |
| Declination, (dd:mm:ss) | – | – | – | – | – | 72°08′534(8) |
| Derived quantities | ||||||
| Characteristic age (kyr) | 1122 | 1585 | 3548 | 219 | 479 | 206 |
| (Surface magnetic field strength, G) | 12.18 | 12.48 | 11.93 | 12.22 | 12.23 | 12.44 |
| (Spin-down luminosity, , erg s-1) | 33.54 | 32.65 | 33.05 | 34.89 | 34.19 | 34.51 |
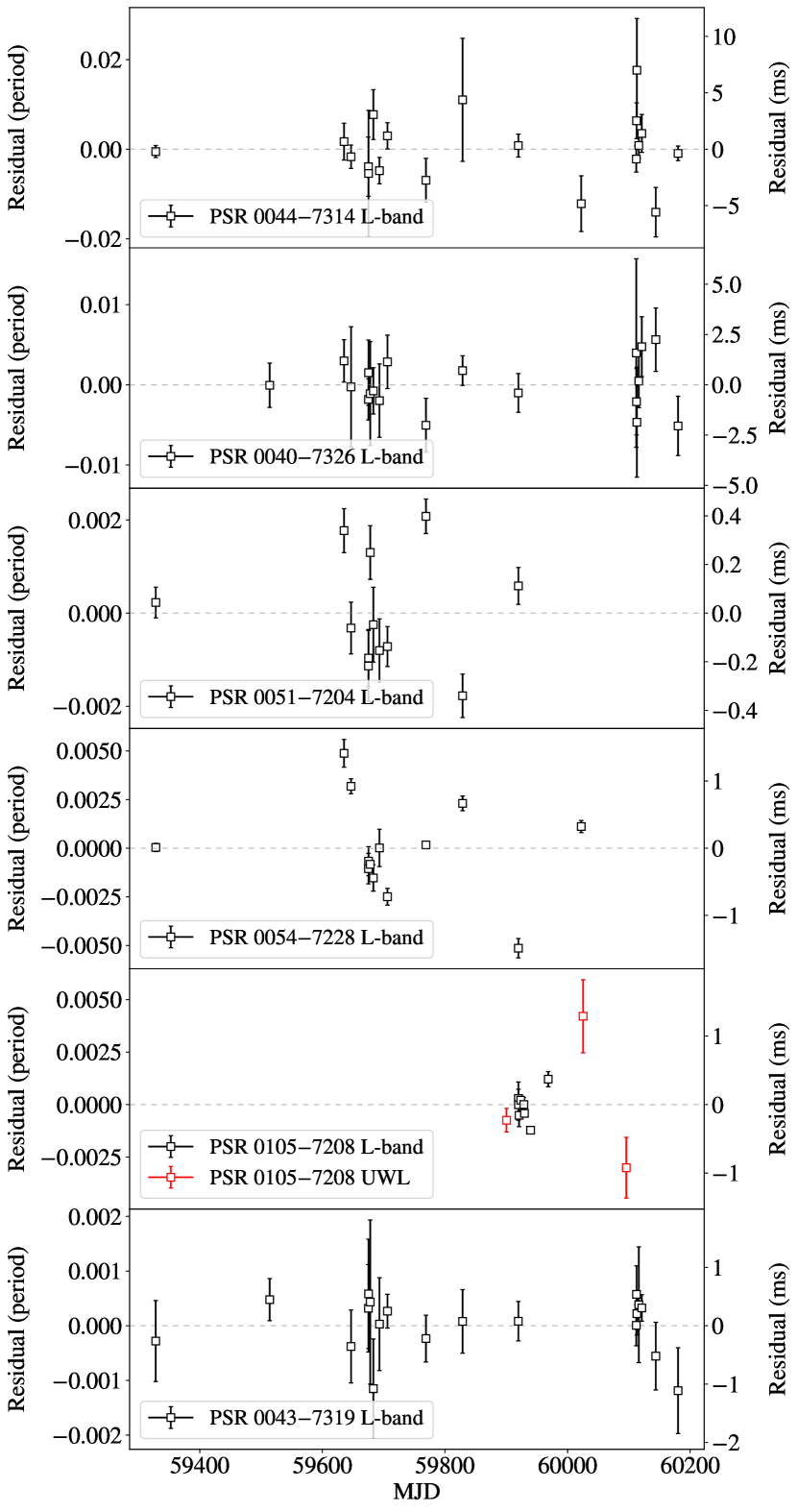
We note that two of the pulsars timed only at MeerKAT have an ‘adolescent’ age of around 200 kyr. The first of these, PSR J00517204, shows no notable timing noise. However, we could not phase-connect the discovery observation of the second adolescent pulsar PSR J01057208, which occurred five months before the beginning of the radio timing campaign presented here. We would normally expect the timing solution to successfully extrapolate back to the discovery observation, as the phase-connected time span is of similar length as the extrapolation period, thus we cannot exclude a glitch or timing noise in that observation gap. Furthermore, PSR J00437319, which has a characteristic age of 1.6 Myr, requires a component to fit the residuals, which is about two orders of magnitude larger than the expected contribution from dipole braking for a braking index of 3. The origin of this is not known, but a glitch or timing noise are again not excluded.
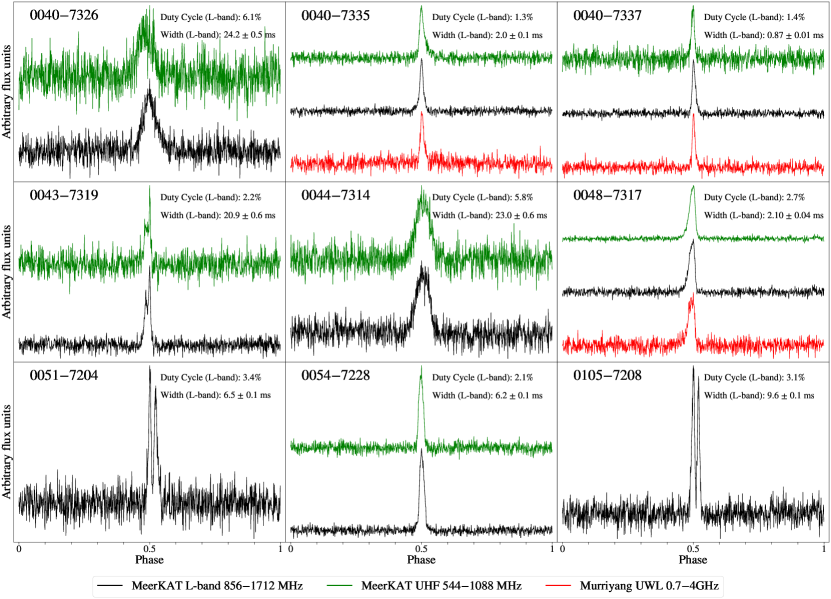
4.2 Pulse profiles
We present the total summed pulse profiles of the pulsars in Figure 3. We noted no significant pulse profile shape change between the MeerKAT L-band/UHF and Murriyang UWL band during observations, except for a longer scattering tail for PSR J00407335 in the UHF band.
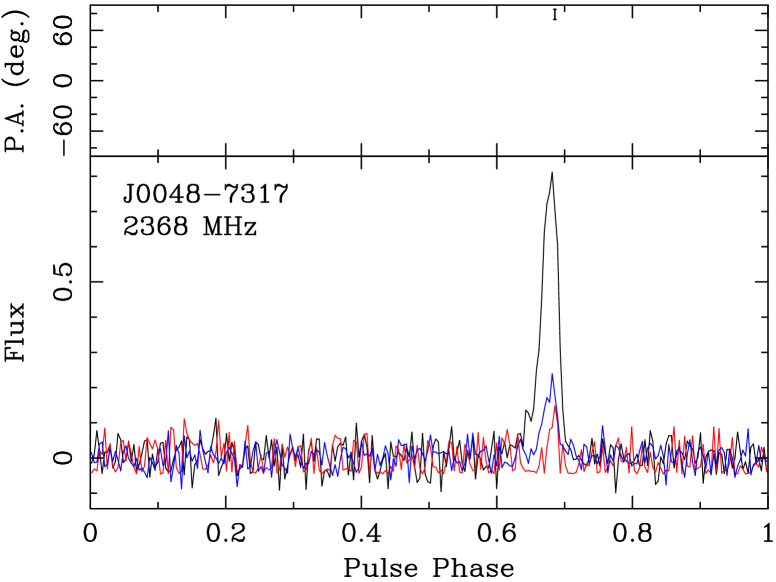
We also present the polarisation profile of PSR J00487317 over the UWL band in Figure 4. We first performed the steps described in subsection 3.2 to obtain a total flux and polarisation-calibrated phase-folded data archive with 1024 pulse profile bins and 416 frequency channels from 26 fold-mode Murriyang observations. We performed a search for Rotation Measure (RM) using psrsalsa’s rmsynth (Weltevrede, 2016) over rad m-2 (in case of a large PWN contribution, see e.g. Piro & Gaensler 2018 and the high-RM Fast Radio Bursts with persistent radio sources like FRB 20121102A Michilli et al. 2018). At the minimum, central and highest frequencies of the UWL band, a RM of rad m-2, rad m-2, and rad m-2 is required to cause a rotation of rad in a frequency channel respectively. The known range of RMs in the SMC spans to rad m-2 (Johnston et al., 2021), and this can result in 0.7–3.6 rotations across the UWL band. We were not able to constrain the RM, possibly due to the polarised S/N being too low and/or the frequency resolution too coarse. The RM can reduce the linear polarisation fraction, thus we can only provide a lower limit on the linear polarisation fraction of the total pulse profile of 6 per cent, which we estimated using psrchive’s psrstat. The circular polarisation fraction is about 20 per cent. Cotton et al. (2024) weakly detected a circular polarisation fraction of 11 per cent at the 2–3 sigma level in their image of the head of the nebula. If the circular polarisation fraction being larger than the linear fraction was an intrinsic property of the emission, this would be the first such case among extragalactic pulsars (Johnston et al., 2021), and though frequency-dependent, it is also relatively uncommon among non-recycled galactic pulsars (e.g. Serylak et al., 2021; Oswald et al., 2023). We have not yet accumulated enough polarised S/N to measure the polarisation Position Angle (PA) variation across the pulse.
5 Young pulsar glitches
5.1 Glitch and red noise parameters estimation
To model glitch and red noise parameters, we used the software run_enterprise (Keith et al., 2022; Ellis et al., 2020), a Bayesian timing parameter estimation toolkit, as expanded by Liu et al. (2024) to include glitch parameters. The fitting process is described in detail in Liu et al. (2024). We input initial solutions obtained as described in section 3 with an initial glitch size fitted with tempo2, as a starting point for the Bayesian parameter estimation. We tested two models on PSR J00487317 and PSR J00407337: a single glitch of permanent changes in frequency (Hz) and spin-down rate (Hz s-1), with or without a single exponential relaxation term (see Equation 1). We did not include in our analysis a glitch-induced change in the second order frequency derivative, , as initial modelling showed that it was consistent with zero. Likewise, we did not include a second, longer-term exponential recovery (with a timescale of up to 1000 days). Indeed, the prior on the second decay time was either too large to be well sampled, or resulted in an unconstrained decay time and amplitudes consistent with zero for the second exponential recovery.
The glitch model is thus expressed as:
| (1) |
where is the difference in predicted phase after the glitch in radians, is the time since the glitch in seconds, is the exponential relaxation timescale in seconds and its amplitude in Hertz.
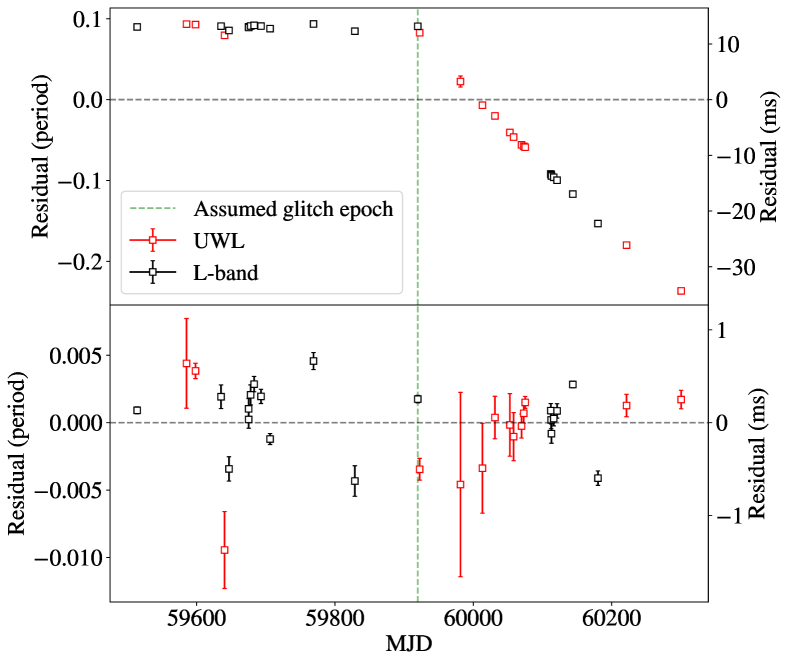
In the case of PSR J00407337, we fitted the timing model parameters to a dataset of one ToA per observation. There are about 30 days between the last pre-glitch and the first post-glitch observation101010The possibility that a glitch had occurred since the previous observation was established by inspection of the first post-glitch observation, which showed a drift in the phase of the folded pulse as a function of time.. As with most large glitches, we are unable to unambiguously track the rotation of the pulsar during this observational gap, as there is a degeneracy between the glitch epoch and the number of phase wraps occurring between these ToAs. Hence the glitch epoch cannot be precisely determined (see the Appendix of Basu et al., 2022 for a discussion of this), and we chose to set the number of rotations between the pre-glitch and post-glitch ToAs that resulted in the least difference in phase. This choice results in the latest possible glitch epoch as the initial input for the analysis (just before the first post-glitch ToA), and the glitch epoch prior was set as uniform within days of this initial value. The prior range on the exponential recovery timescale was set to be sampled uniformly in log-timescale between 0.1 to 100 days, and the remaining priors were set automatically by run_enterprise as described in Liu et al. (2024), section 3.4: the red noise amplitude prior was sampled uniformly in log-scale between to yr, the red noise power-law index was sampled uniformly in linear space between and , the exponential amplitude was sampled uniformly in linear space with a range of times the input glitch step change in frequency, and finally the priors in the glitch step change in frequency and frequency derivative spanned times the input values, sampled uniformly in linear space.
We initially fixed the DM, temporal jump between observatories, period and period derivatives using values obtained as described in section 3. The position was also fixed to the point source position (0.2–8 keV band) measured from a Chandra observation of the PWN, RA(J2000)0h40m463850, Dec(J2000)73°37′07030 (see subsection 6.1 and Figure 11). After fitting the aforementioned glitch and red noise parameters with run_enterprise, we then input the maximum likelihood solution into a new run_enterprise MCMC process (see Liu et al. 2024) to now simultaneously fit for position, period, period derivatives and refine the red noise parameters, while the glitch solution remained fixed (as well as the DM and temporal jump between observatories). This produced the final ephemeris presented in Table 2.
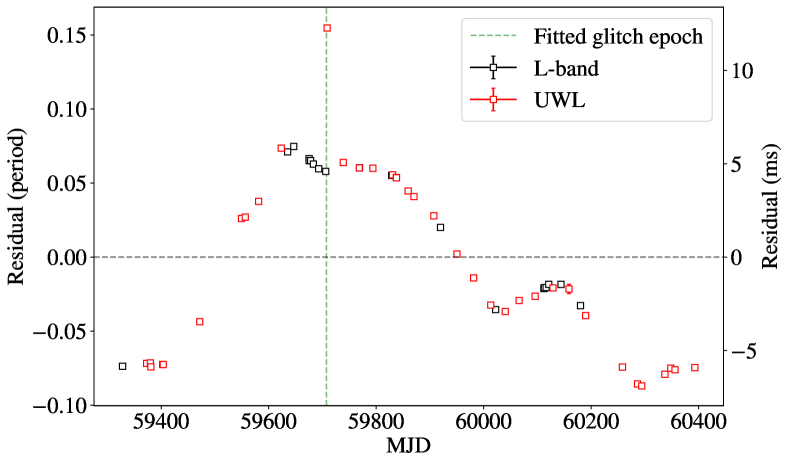
In the case of PSR J00487317, the glitch occurred between observations at MeerKAT and Murriyang separated by only three days. The pre-glitch detection with MeerKAT had a S/N of 45.3, which we divided into 10 ToAs, and the post-glitch observation with Murriyang had a S/N of 6.5, which we divided into 2 ToAs. All other observations were included as single ToAs. The next observation was performed one month after the first post-glitch observation. Initial glitch modelling indicated that the first observation after the glitch was not well modelled by a simple step change in frequency and frequency derivative (see Figure 5), and hence a short-duration transient recovery was present.
We attempted to fit the transient recovery with an exponential, however since the exponential is largely determined by two residuals from a single observation, there is a wide range of valid solutions. In order to efficiently explore the parameter space, we applied a logarithm to the prior of the amplitude of the exponential, however we re-weighted the exponential amplitude posterior, multiplying it by the amplitude values. This results in a uniform space posterior distribution (revealing larger exponential recovery sizes) between and Hz, though the amplitudes were sampled linearly in a logarithmic prior space. The exponential timescale prior was sampled uniformly in linear timescale between 0.01 and 100 days. With a short-duration exponential, there may be some correlation between the glitch epoch and the exponential parameters, and hence we want to allow solutions in the full range of glitch epochs. To achieve this, we fitted for an integer number () of phase wraps just prior to the first post-glitch ToA (MJD 59708.7).
We also ran a separate fit with the first two observations after the glitch removed, and the same priors and the two-stage fitting as described for PSR J00407337 (except that the position used was from the initial timing solution, see section 3). To visualise long-term changes in the frequency and frequency derivative using groups of ToAs, we also used the stride fitting method (see Shaw et al. 2018) on this dataset.
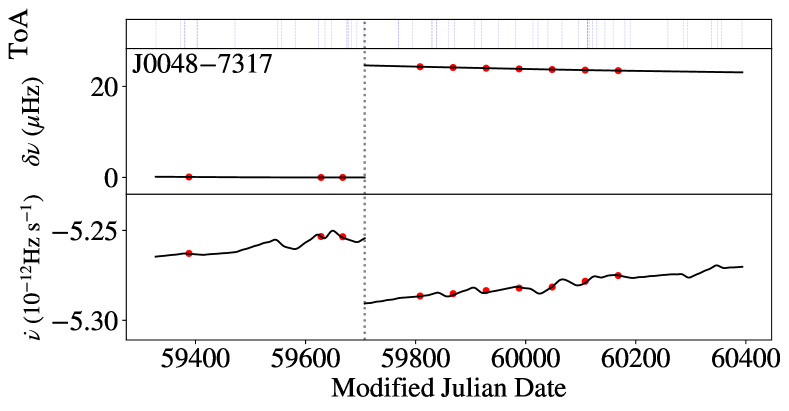
In the case of PSR J00407335, the glitch was small and phase connection appears to be preserved. As the ToAs after the glitch have quite large errors, the glitch epoch is poorly constrained. We thus set the glitch epoch to the last ToA that seemed to be consistent with the pre-glitch timing parameters and fitted only for the post-glitch change in frequency and frequency derivative with tempo2 (having first obtained a preliminary timing solution as described in section 3).
5.2 Timing solutions: glitched pulsars
For PSR J00407337, an informative exponential relaxation fit cannot be performed to the sparse post-glitch data (there are about 30 days between the last pre-glitch point and the first post-glitch point, and again 20 days before the next). A model with no recovery is preferred by run_enterprise, with an odds ratio of .
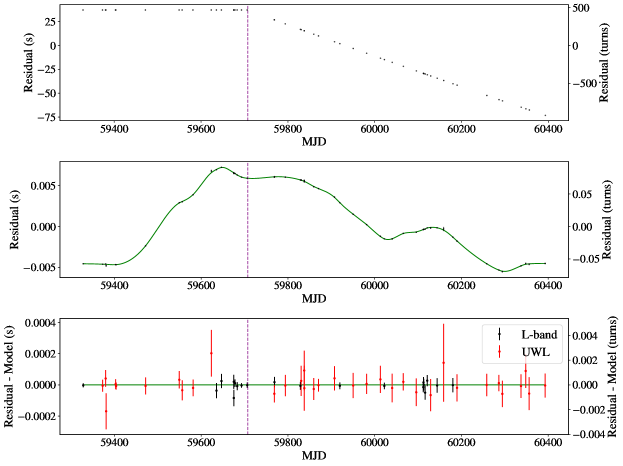
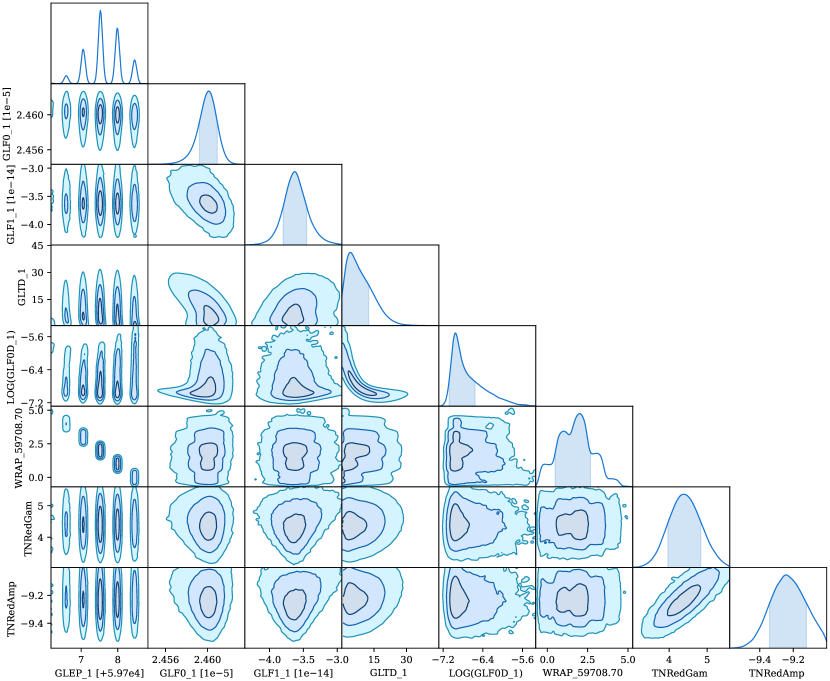
In the case of PSR J00487317, models containing an exponential recovery term are preferred by run_enterprise when using the full dataset (i.e. they have a larger likelihood); however, the constraints on the exponential timescale and amplitude are very poor due to the low number of ToAs soon after the glitch (there is also a gap of 30 days between the first and second observation after the glitch). We show the posterior distribution of the model with exponential recovery fitted on the full dataset, as described in the previous section, in Figure 10. A strong covariance between the fitted exponential recovery timescale and amplitude is present: the larger the amplitude, the shorter the timescale – to vanishingly small timescales and large amplitude. They are both poorly constrained, thus we can only provide a 95 per cent upper limit for the recovery timescale of 22 days, and for the exponential decay amplitude the 95 per cent credible interval around the median is Hz. As can be seen in the first column of Figure 10, a larger number of fitted phase wraps between the pre- and post-glitch observations results in an earlier fitted glitch epoch, with 5 likely glitch epoch solutions in this time range.
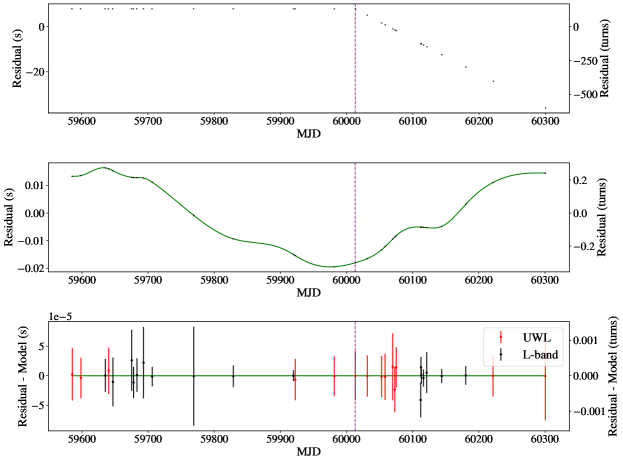
We therefore elected to remove the first two observations after the glitch from the dataset to ignore the strongest transient effect and thus get better constraints on the permanent glitch parameters. We model the data in the same way as PSR J00407337 (see subsection 5.1). A no-recovery model is preferred with an odds ratio of about 2.70.3. This is the model reported in Table 2, shown in Figure 8 and with stride fitting in Figure 6. This model’s residuals with the first two post-glitch observations included are shown in Figure 5.
We report the timing model parameters for the three glitching pulsars in Table 2. The DM errors quoted are obtained from a pdmp optimisation over 20 pc cm-3 of the total added UWL (L-band for PSR J00407335) observations and are not used in fitting. The run_enterprise model residuals for PSR J00487317 and PSR J00407337 are shown in Figures 8 and 9, while tempo2’s PSR J00407335 model residuals are given in Figure 7. For J00487317, the stride fitting results are shown in Figure 6: the datapoints in the stride windows are in accordance with our model.
| Data and Modelling | |||
| Pulsar name | J00487317 | J00407337 | J00407335 |
| MJD range | 59328.1–60393.0 | 59585.4–60300.5 | 59514.1–60300.5 |
| Data span (yr) | 2.92 | 1.96 | 2.15 |
| Number of ToAs | 54 | 31 | 33 |
| Rms timing residual (s) | 4554.4 | 14116.2 | 271.8 |
| Reduced value | 1.0 | 0.9 | 14.1 |
| Measured Quantities | |||
| Right ascension (hh:mm:ss) | 00:48:56.89(9) | 00:40:46.7(6) | 00:40:54.59(3) |
| Declination (dd:mm:ss) | 73:17:46.0(4) | 73:37:07.0(25) | 73:35:53.60(8) |
| Pulse frequency, (s-1) | 12.608085313(5) | 16.69767930(4) | 6.88618772429(7) |
| First derivative of pulse frequency, ( s-2) | 5.24925(10) | 9.4910(9) | 1.131083(20) |
| Second derivative of pulse frequency, ( s-3) | 3.33(12) | 4.9(18) | – |
| Glitch epoch (MJD) | 59707.46(2) | 60013.13(5) | – |
| Frequency change at glitch, (Hz) | 2.460(1) | 3.023(7) | 1.19(8) |
| Frequency derivative change at glitch (Hz) | 3.6(2) | 7(2) | 1.22(16) |
| Red noise power-law index | 4.0(5) | 4.3(5) | – |
| Red noise amplitude yr | 9.3(1) | 8.6(2) | – |
| Set Quantities | |||
| Epoch of frequency, position and DM determination (MJD) | 59860 | 59942 | 59692.1 |
| Dispersion measure, DM (cm-3pc) | 292.42(7) | 101.79(4) | 198.27(6) |
| Glitch epoch (MJD) | – | – | 59919.730735189097686 |
| Derived Quantities | |||
| Characteristic age (kyr) | 38 | 28 | 97 |
| (Surface magnetic field strength, G) | 12.21 | 12.16 | 12.27 |
| (Spin-down luminosity, , erg s-1) | 36.42 | 36.80 | 35.49 |
| 1.95 | 1.81 | 1.7 | |
| 7 | 7 | 1 | |
5.3 Discussion of the observed glitches
Two aspects of the aforementioned glitch activity in the SMC pulsars are worth noticing. First, the inferred glitch sizes for PSRs J00487317 and J00407337 are amongst the largest reported, falling at the high end of the known glitch size distribution (see for example Basu et al. 2022). Secondly, all three glitching pulsars displayed a glitch shortly after their discovery (just over a year later). It is therefore compelling to examine how their glitch activity compares to that of the total glitching pulsar population, which predominantly consists of Galactic neutron stars.
The two SMC sources with major glitches of Hz have relatively high spin-down rates and a similar characteristic age , around yr. On the other hand, PSR J00407335 has a lower , an age yr, and its glitch has a small inferred size. Although it is too early to draw any conclusions, the above is in general agreement with the finding that younger pulsars tend to present larger glitches (e.g. Basu et al., 2022). Glitches of small sizes like the one in PSR J00407335 are common in both young and old glitching pulsars (Basu et al. 2022; and we use theirs and Espinoza et al. 2011’s Jodrell Bank Centre for Astrophysics Glitch Catalogue in this analysis). Small glitches are harder to detect in the presence of timing noise and infrequent monitoring, thus their population is potentially underestimated.
Glitches are customarily regarded as rare events, with the vast majority of pulsars never seen to glitch at all. The situation changes, however, when we take into account the young characteristic age (and high ) of the SMC glitching sources. In the population of pulsars with , over 30 per cent of sources have at least one reported glitch111111Similarly, if we consider pulsars in the range (which also encompasses all three SMC glitching pulsars), about 50 per cent have known glitches.. This demonstrates that glitches are not an uncommon feature for pulsars similar to J00407337, J00487317, and J00407335. Their red noise parameters are also typical (Parthasarathy et al., 2019). Moreover, of the glitching pulsars in the above age range, 52 per cent have had giant glitches, which are defined by a magnitude of greater than ; in fact, over of the total detected glitches are ‘giant’ according to the Jodrell Bank Glitch Catalogue.
Earlier works on glitches noted an anti-correlation between the characteristic age of a pulsar and its glitching rate (e.g. Espinoza et al., 2011; Fuentes et al., 2017). The two most recent studies of glitch rate, which use a large sample of pulsars, confirm this relationship and explore the scaling of glitch rate with other pulsar parameters, such as and , under different assumptions. The sample of the first study (Basu et al., 2022) consists of pulsars observed at the Jodrell Bank Observatory (JBO) that have at least one detected glitch. An average glitch rate is calculated for each pulsar simply as
| (2) |
with the total number of detected glitches and the total monitoring time span (which could be accurately determined for JBO observations). A negative power-law scaling with was assumed, of the form:
| (3) |
with in kyr; and similarly, the trend for increasing rate with increasing is described as
| (4) |
with , and the proportionality constants determined by the data. To somewhat compensate for the fact that glitch rates can be underestimated, only pulsars with were considered (currently the smallest inferred rate is about ).
The second study, Millhouse et al. (2022), assumes that glitches occur stochastically and describes glitch activity as a constant-rate Poisson process with the probability of observing glitches over an observing timespan being
| (5) |
for a pulsar with a Poisson glitch rate . This assumption is to some degree supported by observations of several frequently glitching pulsars, for which the distribution of waiting times between consecutive glitches is consistent with an exponential probability density function. Not all pulsars are consistent with this description, however. For example, the Crab pulsar observations are inconsistent with a homogeneous Poisson process (e.g. Carlin & Melatos, 2019). Moreover, some neutron stars present a characteristic glitch waiting time – the Vela pulsar being a prominent example of this behaviour. Three pulsars for which the regularity in glitching patterns is well established were excluded from the study (namely, the Vela pulsar, the LMC pulsar J05376910, and PSR J13416220).
Two pulsar samples were used to calculate and infer its scaling with pulsar parameters (power-law relations with , , or a combination of the two were examined): one consisted of 174 glitching pulsars, the other additionally included 233 pulsars that have . The glitching pulsars sample significantly overlaps with the one used in Basu et al. (2022), but the used values of contained more uncertainties (see section 7 in Millhouse et al. (2022)). The preferred model (based on Bayes factor) was an anti-correlation of the Poisson glitch rate with characteristic age, modelled as
| (6) |
where yr. Note that the optimal values for the parameter in Table 3 of Millhouse et al. (2022) are in units (Millhouse, private communication).
It is noteworthy that the power-law index ( for Basu et al. 2022 and for Millhouse et al. 2022) of the rate ( and respectively) to characteristic age relationship for glitching pulsars is consistent between the two studies. Using Table 2, we calculate the observed glitch rate as in Equation 2, as well as the predicted rate based on Equations 3, 4, and 6. The results are presented in Table 3. The rate is denoted by index when the optimal parameters for the sample are used, and by index for the sample. Direct comparisons between and cannot be made: ideally, the median should be calculated for each pulsar individually from a posterior distribution of based on Equation 5. Nonetheless, the predicted rates based on the Millhouse et al. (2022) relationship are of the same order of magnitude as , and do not lead to very low probabilities of a glitch occurring during our monitoring period.
With a single glitch per pulsar, the derived rate can only be a rough approximation of the true rate, under the assumption that a stationary mean rate can indeed be defined for these sources. We used the entire time interval of observations in Equation 2 to calculate the in Table 3. Upper limits can be derived if the maximum time interval between the glitch epoch and the endpoints of the total observing span is used instead, and are close to for all three pulsars. Given the results in Table 3 for either the or relationship of Basu et al. (2022), the observed rate in the SMC pulsars is in accordance with predictions based (almost exclusively) on Galactic pulsars. Therefore, whilst lucky, it cannot – at the moment – be considered extraordinary that a glitch was detected so soon after their discovery.
| Pulsar name | J00487317 | J00407337 | J00407335 |
|---|---|---|---|
| 0.34 | 0.51 | 0.47 | |
| 0.59 | 0.66 | 0.44 | |
| 0.35 | 0.38 | 0.27 | |
| 0.14 | 0.15 | 0.11 | |
| 0.14 | 0.15 | 0.10 |
The above discussion on glitch rates does not take into account the fact that the observed glitches of PSRs J00487317 and J00407337 had amplitudes , at the higher end of the known distribution. Whilst the analysis of Basu et al. (2022) included all JBO-observed glitching pulsars, we reiterate that the Millhouse et al. (2022) analysis excludes ‘regularly’ glitching pulsars and assumes a homogeneous Poisson process, which would lead to exponential distributions of interglitch waiting times. Typically, however, pulsars for which such a waiting time distribution is an adequate fit to observational data present at the same time a power law-like distribution of their glitch sizes, with large events being far less common than small ones. On the other hand, large glitches are ordinary in regularly-glitching pulsars. The archetype of this glitch behaviour is the Vela pulsar (PSR B083345, with , and yr), characterised by predominantly giant glitches () that occur every few years. Both PSR J00407337 and PSR J00487317 present very strong similarities to Vela, not only due to their timing parameters and inferred age, but also because of their (preliminary) deduced glitch rate and their large spin-up size and spin-down rate change. For regularly-glitching neutron stars the waiting times between large glitches varies from approximately one year up to about a decade (depending on the pulsar), but typical recurrence times are in the range of 1000 to 3000 days121212The LMC PSR J05376910 also has regular large glitches, very frequently at a rate of about 3 per year (calculated with glitches of any size taken into account). It is though younger ( kyr) and has an exceptionally high .. The description of the post-glitch recovery in such pulsars often requires one or more exponentially-relaxing terms, which were not included in the models presented in subsection 5.2. Yet, for PSR J00487317, the presence of a strong transient component following the glitch, with a large decaying amplitude and a short relaxing timescale (see Figure 10 for their indicative magnitudes), further strengthens the resemblance to the Vela pulsar, for which decaying terms on similar timescales have been identified (Dodson et al., 2002). Another very distinct characteristic of post-glitch recoveries of regular glitchers is a high value of that – once any exponential terms decay – dominates the time interval between glitches and leads to ‘anomalous’ braking indices. As can be seen from Table 2, the apparent braking index for PSR J00487317 is about , whilst for PSR J00407337 . This is also suggestive of possible Vela-like glitching behaviour, though it cannot be excluded that such values of are sometimes an intrinsic property of pulsar spin-down (Parthasarathy et al., 2020). It might take a long time to confirm if that is the case as, by extrapolating from the known regularly-glitching pulsars (see for example the scaling between average waiting time and presented in Haskell et al. (2012)), we estimate an average time interval between large glitches of about 3.5 years for PSR J00407337 and around 6 years for PSR J00487317. It remains to be seen whether these pulsars are truly Vela-like, they are certainly sources of interest and should be closely monitored in the future.
6 Associations
Prior to the MeerKAT survey, all the known radio pulsars in the SMC had periods significantly larger than 100 ms, characteristic ages above 1 Myr, and spin-down luminosities spanning – erg s-1. This study extends the spin parameter space of the known SMC radio pulsars to the young pulsars associated with SNRs or PWNe (see Figure 1), like the X-ray rotation-powered SMC pulsar J00587218 (Maitra et al., 2021; Carli et al., 2022). We note that PSR J00487317 and PSR J00407337 are older and less energetic than the previously known young extragalactic pulsars with such associations, but are ordinary within the distribution of young Galactic pulsars.
6.1 PSR J0040-7337
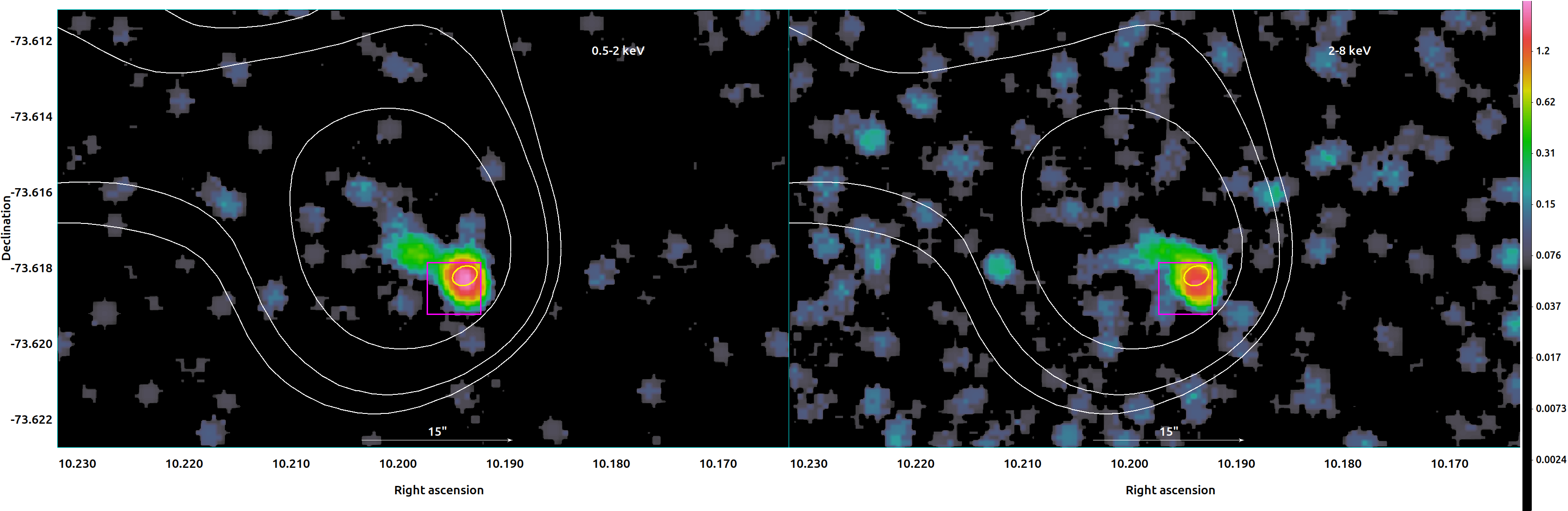
In paper I, PSR J00407337 was associated with the Pulsar Wind Nebula in the SNR DEM S5 (Haberl et al., 2000; Filipović et al., 2008; Alsaberi et al., 2019), due to a seeKAT multi-beam localisation using the discovery observation and the period of the pulsar being indicative of a young system. In Figure 11, we compare the radio timing position of PSR J00407337 with a new 97 ks Chandra ACIS-S image (OBSIDs 24633, 22704) centred on the PWN in SNR DEM S5. The point-like source with soft diffuse emission detected with XMM-Newton (Alsaberi et al., 2019) can be further resolved into a compact nebula and a point source in the Chandra image, which our radio timing position error region overlaps. A typical bow-shock morphology is detected in X-rays with harder emission at the position of the pulsar (as detected in the XMM-Newton image, Alsaberi et al., 2019), that is compatible with the radio morphology which extends further out given the longer lifetime of the radio-emitting electrons. Therefore, the position of the pulsar is consistent with the point source position and places it right behind the bow-shock.
Using the pulsar age, one can better constrain the PWN kinematics in the SNR environment, including the pulsar birth kick velocity. We note that the characteristic age from radio timing assumes a simple magnetic dipole radiation model (introduced in section 1) with a braking index, of 3 as well as a birth period much less than the current period, and thus may not reflect this pulsar’s true age. Alsaberi et al. (2019) proposed an age between 10 and 28 kyr for the pulsar-PWN system, and the characteristic age matches that upper value. For this higher age, Alsaberi et al. (2019) suggest a kick velocity of 700–800 km s-1, based on a distance range of 60–67.5 kpc estimated from the SMC depth. They also find that this velocity is plausible based on the PWN and SNR morphology in the local environment. This is within the known distribution of transverse velocities of bow-shock nebula pulsars, which spans 60–2000 km s-1 (Kargaltsev et al., 2017).
It is important to consider if the kick velocity is in fact different, due to the characteristic age being an incorrect evaluation of the true age. is related to the true age as
| (7) |
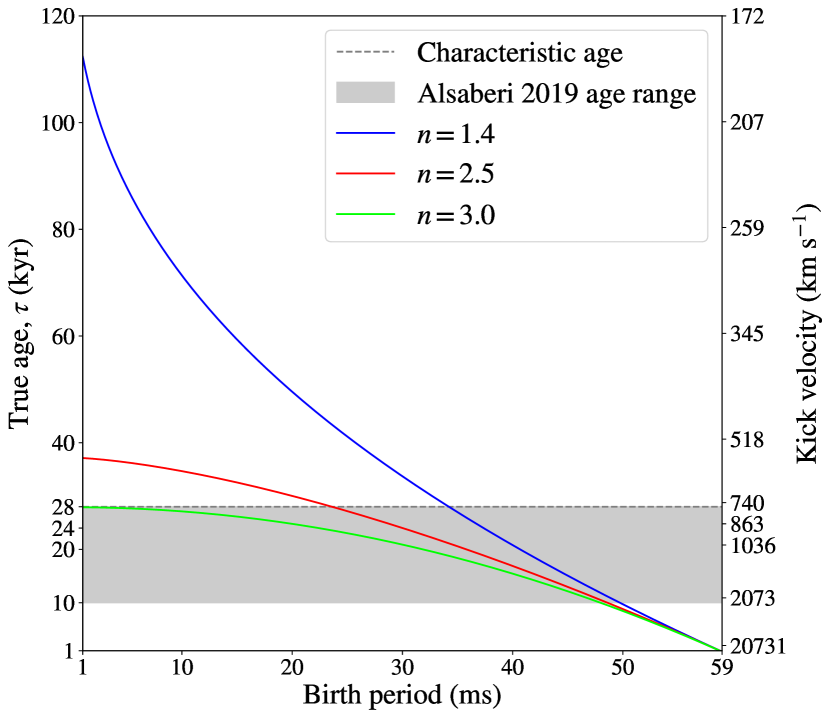
where is the birth spin period of PSR J00407337. is extremely difficult to measure (e.g. Johnston & Galloway, 1999), though a range of 1.8–3 can be assumed (Melatos, 1997). The young Galactic pulsars, Vela and the Crab (PSRs J08354510 and J05342200) have had their braking indices measured to be 1.40.2 (Lyne et al., 1996) and 2.5090.001 (Lyne et al., 1988, 1993) respectively, so we take a range of 1.4–3 for this calculation.
We plot the relationship between the true age, the birth period and the kick velocity131313We used a distance of 60 kpc, if instead we use a distance of 67.5 kpc for the Western part of the SMC (Scowcroft et al., 2016), the kick velocity for a true age of 28 kyr is 830 km s-1. in Figure 12. It shows that unless the birth period was only about 10 ms shorter than the spin period is today, the kick velocity should not exceed 2000 km s-1. For a more realistic birth period of about 15 ms, we find that the kick velocity should be lower than 800 km s-1. It is not probable that the true age is much larger than the upper limit set by Alsaberi et al. (2019), and thus the kick velocity much lower, based on the PWN and SNR morphology they present. Therefore, a Vela-like true braking index is unlikely.
The proper motion of the pulsar across the sky, extrapolated from the 700–800 km s-1 kick velocity range from Alsaberi et al. (2019), does not induce a significant change in the period derivative that has been measured from timing, in part due to the large distance to the system. This change, known as the Shklovskii effect (Shklovskii, 1970), increases the observed period derivative by ( s s-1, which is 2 orders of magnitude smaller than the error on the period derivative resulting from our timing solution.
The spin-down luminosity of this pulsar is erg s-1. Alsaberi et al. (2019) measured the X-ray luminosity of the compact, hard X-ray emission region from the PWN and the pulsar in DEM S5 to be erg s-1 at a distance of 60 kpc (Karachentsev et al., 2004). The ratio of is thus about . This so-called ‘PWN X-ray efficiency’ is similar to that of other PWNe presented in Kargaltsev et al. (2008). The PWN X-ray power-law spectral index was measured in Alsaberi et al. (2019) to be 20.3. Kargaltsev et al. (2008) also relate the ‘PWN X-ray efficiency’ to the PWN X-ray power-law spectral index, and the values for the PWN of DEM S5 fit well within the scatter of the relationship they present.
We calculate the radio luminosity of the PWN of DEM S5, using the radio flux density and spectral index measurements from Alsaberi et al. (2019)’s Table 2, with Equation 4 from Frail & Scharringhausen (1997). This gives erg s-1, and a PWN radio efficiency of . This is similar to the Vela radio pulsar-PWN system (Frail & Scharringhausen, 1997). Rescaling the MeerKAT L-band discovery flux density of PSR J00407337 to 1400 MHz assuming a power-law radio spectral index of 1.60 (Jankowski et al., 2018), we find an approximate radio flux density of Jy. We can estimate the pulsar’s radio luminosity using Szary et al. 2014’s equation (2): erg s-1 at 60 kpc. Thus the radio efficiency of the pulsar is . This fits within the large scatter of the - relationship from Szary et al. (2014), among young pulsars with pulsed high-energy radiation and SNR association.
According to the expected X-ray efficiency of pulsars, where the ratio of pulsed X-ray luminosity to spin-down luminosity should be around (Becker & Trümper, 1997), we can expect PSR J00407337 to have a pulsed X-ray luminosity of about erg s-1 if its X-ray beam crosses our line of sight. This would be the case if the pulsar makes up for a few tenths of the total X-ray luminosity (which is of the order of erg s-1). Therefore, our radio timing localisation, the low characteristic age and large spin-down luminosity of the pulsar all confirm that PSR J00407337 is the engine powering the DEM S5 PWN.
6.2 PSR J0048-7317
In paper I, PSR J00487317 was associated with a new PWN with no known parent SNR (Cotton et al., 2024). As for PSR J00407337, this was enabled by a seeKAT multi-beam localisation using the discovery observation. Furthermore, a preliminary estimate of the period derivative of the pulsar was obtained from two survey observations, which now matches the radio timing characteristic age of 38 kyr we derive here. We show the radio timing position141414This supersedes the preliminary timing position with larger errors published in Cotton et al. (2024). of PSR J00487317 on the Cotton et al. (2024) radio continuum image of the new PWN in Figure 13. Just like PSR J00407337, the pulsar is situated at the head of the radio PWN near the possible bow-shock front, with a complex and structured tail extending south of the pulsar, presumably indicating the direction of motion. The pulsar has also a characteristic age and spin-down luminosity of the same order as PSR J00407337, consolidating this association.
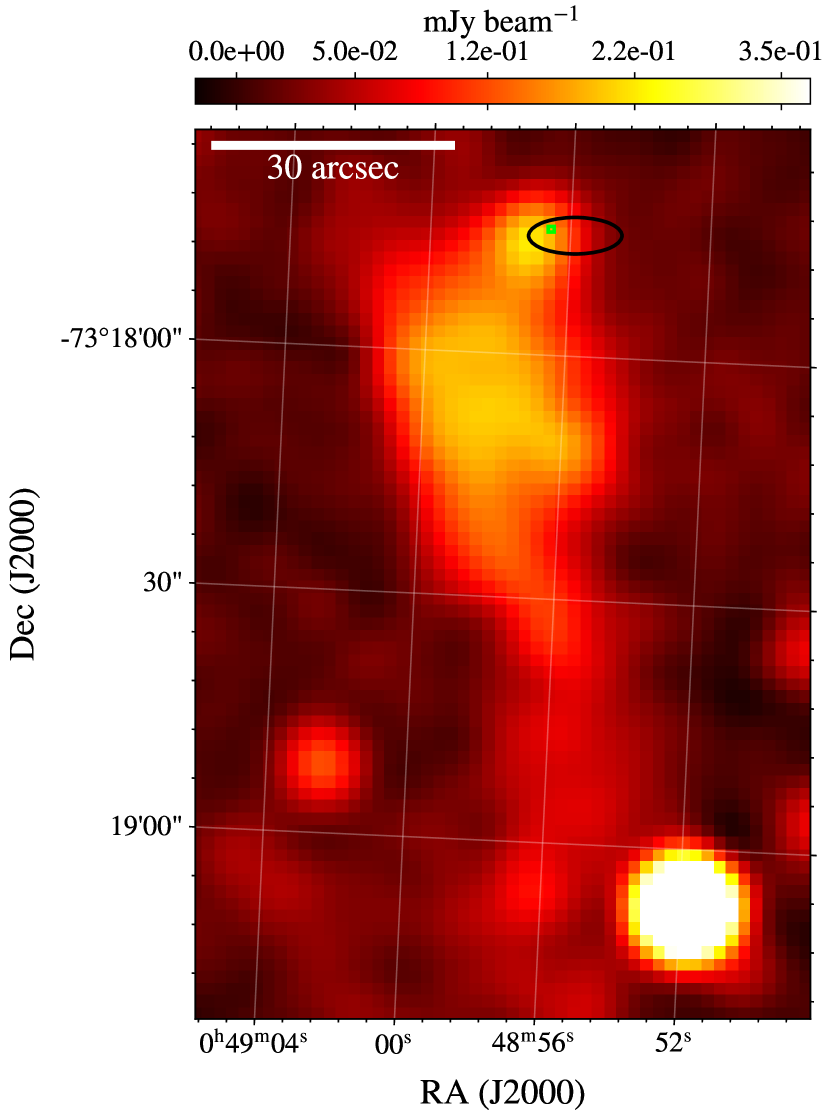
Using the same calculations as for PSR J00407337, we find an approximate radio flux density of Jy, and a luminosity erg s-1 at 60 kpc. The radio efficiency of the pulsar is . Again, this fits within the large scatter of the - relationship from Szary et al. (2014), among young pulsars with pulsed high-energy radiation and SNR association, although the pulsar is in the high end of the radio luminosity distribution.
Using the radio timing position, we can constrain the X-ray flux of the pulsar-PWN system in an XMM-Newton 23 ks EPIC-pn observation (OBSID 0110000101). Assuming a power-law index of 1.7 and a Galactic foreground absorption of N cm-2 the unabsorbed X-ray flux upper limit in the 0.2–12 keV band is erg cm-2 s-1. We also take into account the sensitivity loss due to the position being off-axis in the observation. At a distance of 60 kpc, this yields an upper limit on the PWN X-ray luminosity of erg s-1. The ratio of is thus lower than . This ‘PWN X-ray efficiency’ upper limit is on the low end of the distribution presented in Kargaltsev et al. (2008), but is still greater than e.g. the Vela PWN. If PSR J00487317 was to contribute 10 per cent of the PWN X-ray luminosity, we could expect its X-ray luminosity to be under erg s-1, which is below the XMM-Newton limiting point source luminosity in the SMC (Haberl et al., 2012). Known X-ray rotation-powered pulsars with a spin-down luminosity of erg s have X-ray luminosities that range between – erg s-1(Kargaltsev et al., 2008; Shibata et al., 2016). Therefore, this non-detection of X-rays does not rule out emission from the system. We note that our upper limit is based on a choice of absorption value and may be increased for a higher absorption level (considering PSR J00487317 has the highest DM in the SMC).
6.3 Non-associations
As stated in Paper I, the localisation of PSR J00407335 is coincident with the SNR DEM S5, just north of the PWN of PSR J00407337. However, the DM of PSR J00407335 is nearly double that of PSR J00407337, so we had deemed it to be a chance background alignment. There is no multi-wavelength emission detected in the images from Alsaberi et al. (2019) at the new, more precise position provided by our radio timing solution for this young, glitching pulsar; and its characteristic age does not match that of the SNR.
In Paper I, we also established that PSR J01057208 is unlikely to be associated with DEM S128 because of the very high implied transverse velocity given the remnant age of 12 kyr (Leahy & Filipović, 2022). Here, we determine the characteristic age for the pulsar to be 206 kyr which, even given limitations on characteristic age interpretation, does not match the age of DEM S128.
7 Conclusion
We have reported nine new SMC pulsar radio timing solutions from observing campaign conducted with the MeerKAT and Murriyang telescopes with a time span of up to three years, increasing the number of characterised rotation-powered extragalactic pulsars by 40 per cent. Though all pulsars we examined seem isolated, a longer timing baseline could reveal long-term binary motion (e.g. Kaspi et al., 1994). All fitted timing positions in this paper are within the 3 seeKAT discovery multi-beam localisation error presented in Paper I (except for PSR J00447314 for which it is within 4 ). Interestingly, two of the pulsars have an ‘adolescent’ characteristic age of 200 kyr; while three of the pulsars have a young characteristic age under 100 ky and have glitched within about a year of their discovery.
The inferred glitch sizes for PSRs J00487317 and J00407337 are large, with Hz, but we do not have data sampled densely enough to strongly constrain a potential post-glitch exponential recovery timescale and amplitude. For PSR J00487317, a transient recovery is observed, for which we can set an upper limit on the relaxation timescale of 22 days. PSRs J00487317 and J00407337’s position, low characteristic ages (under 40 kyr) and high spin-down luminosities (of order erg s-1) confirm they are powering the PWNe they were first associated with in Paper I. Overall, these two pulsars’ characteristics as well as our first, crude, estimate of their glitching rate and their high inferred braking indices are reminiscent of the Vela pulsar. Further observations are required to confirm this, and also to consolidate a high circular polarisation fraction of about 20 per cent in PSR J00487317: a MeerKAT observation could determine whether this fraction is greater than the linear one.
This work more than doubles the characterised population of SMC radio pulsars. This will enable an analysis of the impact of the low-metallicity, recent star formation environment of the SMC on its neutron star population and comparisons with predictions (e.g. Titus et al., 2020). We will present this population study in Paper III of this series.
Acknowledgements
The MeerKAT telescope is operated by the South African Radio Astronomy Observatory, (SARAO) which is a facility of the National Research Foundation, an agency of the Department of Science and Innovation. SARAO acknowledges the ongoing advice and calibration of GPS systems by the National Metrology Institute of South Africa (NMISA) and the time space reference systems department of the Paris Observatory.
TRAPUM observations used the FBFUSE and APSUSE computing clusters for data acquisition, storage and analysis. These clusters were funded and installed by the Max-Planck-Institut für Radioastronomie and the Max-Planck Gesellschaft.
Murriyang, the Parkes radio telescope, is part of the Australia Telescope National Facility which is funded by the Australian Government for operation as a National Facility managed by CSIRO (the Commonwealth Scientific and Industrial Research Organisation). We acknowledge the Wiradjuri people as the Traditional Owners of the Observatory site.
EC acknowledges funding from the United Kingdom’s Research and Innovation (UKRI) Science and Technology Facilities Council (STFC) Doctoral Training Partnership, project reference 2487536. For the purpose of open access, the author has applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising.
EB, MK, PVP and VVK acknowledge continuing support from the Max Planck Society.
RPB acknowledges support from the ERC under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 715051; Spiders).
MB and AP acknowledge the resources provided by the INAF Large Grant 2022 ‘GCjewels’ (P.I. Andrea Possenti) approved with the Presidential Decree 30/2022.
DA acknowledges support from an EPSRC/STFC fellowship (EP/T017325/1).
JDT acknowledges funding from the UKRI’s STFC Doctoral Training Partnership, project reference 2659479.
This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France (Wenger et al., 2000), NASA’s Astrophysics Data System Bibliographic Services and the ATNF pulsar catalogue.
EC thanks Patrick Weltevrede, Ben Shaw, Avishek Basu, Laila Vleeschower Calas and Iuliana Nitu for their help with pulsar software.
Data Availability
The MeerKAT data underlying this article will be shared upon reasonable request to the TRAPUM collaboration. The observations parameters can be found on the SARAO Web Archive under observer Emma Carli or the target names specified in this publication. The Murriyang data can be downloaded from the Parkes (Murriyang) Pulsar Data Archive, accessed through CSIRO’s Data Access Portal https://data.csiro.au/domain/atnf, as soon as the proprietary period ends. The project codes are specified in the article.
References
- Alsaberi et al. (2019) Alsaberi R. Z. E., et al., 2019, Monthly Notices of the Royal Astronomical Society, 486, 2507
- Anderson & Itoh (1975) Anderson P. W., Itoh N., 1975, Nature, 256, 25
- Antonopoulou et al. (2018) Antonopoulou D., Espinoza C. M., Kuiper L., Andersson N., 2018, Monthly Notices of the Royal Astronomical Society, 473, 1644
- Antonopoulou et al. (2022) Antonopoulou D., Haskell B., Espinoza C. M., 2022, Reports on Progress in Physics, 85, 126901
- Barr (2017) Barr E. D., 2017, in Weltevrede P., Perera B. P. B., Levin L., Sanidas S., eds, Pulsar Astrophysics the Next Fifty Years. No. S337 in Proceedings of the International Astronomical Union. Cambridge University Press, pp 175–178, doi:10.1017/S1743921317009036
- Basu et al. (2022) Basu A., et al., 2022, Monthly Notices of the Royal Astronomical Society, 510, 4049
- Becker & Trümper (1997) Becker W., Trümper J., 1997, Astronomy & Astrophysics, 326, 682
- Bezuidenhout et al. (2023) Bezuidenhout M. C., et al., 2023, RAS Techniques and Instruments, 2, 114
- Brantseg et al. (2013) Brantseg T., McEntaffer R. L., Bozzetto L. M., Filipovic M., Grieves N., 2013, The Astrophysical Journal, 780, 50
- Carli et al. (2022) Carli E., et al., 2022, Monthly Notices of the Royal Astronomical Society, 517, 5406
- Carli et al. (2024) Carli E., Levin L., Stappers B. W., Barr E. D., 2024, Monthly Notices of the Royal Astronomical Society, 531, 2835
- Carlin & Melatos (2019) Carlin J. B., Melatos A., 2019, Monthly Notices of the Royal Astronomical Society, 483, 4742
- Chen et al. (2021) Chen W., Barr E., Karuppusamy R., Kramer M., Stappers B., 2021, Journal of Astronomical Instrumentation, 10, 2150013
- Clark et al. (2023) Clark C. J., et al., 2023, Monthly Notices of the Royal Astronomical Society, 519, 5590
- Cordes & Lazio (2004) Cordes J. M., Lazio T. J. W., 2004, in Clemens D., Shah R. Y., Brainerd T., eds, Conference Series Vol. 317, Milky Way Surveys: The Structure and Evolution of Our Galaxy. Astronomical Society of the Pacific, p. 21, https://aspbooks.org/custom/publications/paper/317-0211.html
- Cotton et al. (2024) Cotton W. D., et al., 2024, Monthly Notices of the Royal Astronomical Society, 529, 2443
- Crawford et al. (2001) Crawford F., Kaspi V. M., Manchester R. N., Lyne A. G., Camilo F., D’Amico N., 2001, The Astrophysical Journal, 553, 367
- Dodson et al. (2002) Dodson R. G., McCulloch P. M., Lewis D. R., 2002, The Astrophysical Journal, 564, L85
- Edwards et al. (2006) Edwards R. T., Hobbs G. B., Manchester R. N., 2006, Monthly Notices of the Royal Astronomical Society, 372, 1549
- Ellis et al. (2020) Ellis J. A., Vallisneri M., Taylor S. R., Baker P. T., 2020, ENTERPRISE: Enhanced Numerical Toolbox Enabling a Robust PulsaR Inference SuitE, https://doi.org/10.5281/zenodo.4059815
- Espinoza et al. (2011) Espinoza C. M., Lyne A. G., Stappers B. W., Kramer M., 2011, Monthly Notices of the Royal Astronomical Society, 414, 1679
- Ferdman et al. (2018) Ferdman R. D., Archibald R. F., Gourgouliatos K. N., Kaspi V. M., 2018, The Astrophysical Journal, 852, 123
- Filipović et al. (2008) Filipović M. D., et al., 2008, Astronomy & Astrophysics, 485, 63
- Frail & Scharringhausen (1997) Frail D. A., Scharringhausen B. R., 1997, The Astrophysical Journal, 480, 364
- Fuentes et al. (2017) Fuentes J. R., Espinoza C. M., Reisenegger A., Shaw B., Stappers B. W., Lyne A. G., 2017, Astronomy & Astrophysics, 608, A131
- Gold (1968) Gold T., 1968, Nature, 218, 731
- Gotthelf & Wang (2000) Gotthelf E. V., Wang Q. D., 2000, The Astrophysical Journal, 532, L117
- Haberl et al. (2000) Haberl F., Filipović M. D., Pietsch W., Kahabka P., 2000, Astronomy and Astrophysics Supplement Series, 142, 41
- Haberl et al. (2012) Haberl F., et al., 2012, Astronomy & Astrophysics, 545, A128
- Harris & Zaritsky (2004) Harris J., Zaritsky D., 2004, The Astronomical Journal, 127, 1531
- Haskell et al. (2012) Haskell B., Pizzochero P. M., Sidery T., 2012, Monthly Notices of the Royal Astronomical Society, 420, 658
- Ho et al. (2015) Ho W. C. G., Espinoza C. M., Antonopoulou D., Andersson N., 2015, Science Advances, 1
- Hobbs et al. (2006) Hobbs G. B., Edwards R. T., Manchester R. N., 2006, Monthly Notices of the Royal Astronomical Society, 369, 655
- Hobbs et al. (2020) Hobbs G., et al., 2020, Publications of the Astronomical Society of Australia, 37, e012
- Hotan et al. (2004) Hotan A. W., van Straten W., Manchester R. N., 2004, Publications of the Astronomical Society of Australia, 21, 302
- Inoue et al. (1983) Inoue H., Koyama K., Tanaka Y., 1983, in Symposium - International Astronomical Union: Supernova Remnants and Their X-Ray Emission. Cambridge University Press, pp 535–540, doi:10.1017/S0074180900034409
- Jankowski et al. (2018) Jankowski F., van Straten W., Keane E. F., Bailes M., Barr E. D., Johnston S., Kerr M., 2018, Monthly Notices of the Royal Astronomical Society, 473, 4436
- Johnston & Galloway (1999) Johnston S., Galloway D., 1999, Monthly Notices of the Royal Astronomical Society, 306, L50
- Johnston et al. (2021) Johnston S., et al., 2021, Monthly Notices of the Royal Astronomical Society, 509, 5209
- Karachentsev et al. (2004) Karachentsev I. D., Karachentseva V. E., Huchtmeier W. K., Makarov D. I., 2004, The Astronomical Journal, 127, 2031
- Kargaltsev et al. (2008) Kargaltsev O., Pavlov G. G., Bassa C., Wang Z., Cumming A., Kaspi V. M., 2008, in AIP Conference Proceedings. AIP, pp 171–185, doi:10.1063/1.2900138
- Kargaltsev et al. (2017) Kargaltsev O., Pavlov G. G., Klingler N., Rangelov B., 2017, Journal of Plasma Physics, 83, 635830501
- Kaspi et al. (1994) Kaspi V. M., Johnston S., Bell J. F., Manchester R. N., Bailes M., Bessell M., Lyne A. G., D’Amico N., 1994, The Astrophysical Journal, 423, L43
- Keith et al. (2022) Keith M. J., Niţu I., Liu Y., 2022, run_enterprise, https://doi.org/10.5281/zenodo.5914351
- Lamb et al. (2002) Lamb R. C., Fox D. W., Macomb D. J., Prince T. A., 2002, The Astrophysical Journal, 574, L29
- Leahy & Filipović (2022) Leahy D. A., Filipović M. D., 2022, The Astrophysical Journal, 931, 20
- Lehmensiek & Theron (2012) Lehmensiek R., Theron I. P., 2012, in 2012 International Conference on Electromagnetics in Advanced Applications. IEEE, pp 321–324, doi:10.1109/ICEAA.2012.6328642
- Lehmensiek & Theron (2014) Lehmensiek R., Theron I. P., 2014, in The 8th European Conference on Antennas and Propagation (EuCAP 2014). IEEE, pp 880–884, doi:10.1109/EuCAP.2014.6901903
- Liu et al. (2024) Liu Y., et al., 2024, Monthly Notices of the Royal Astronomical Society, Accepted
- Lorimer (2008) Lorimer D., 2008, SIGPROC v3.7: (Pulsar) Signal Processing Programs, https://ascl.net/1107.016
- Lorimer & Kramer (2005) Lorimer D. R., Kramer M., 2005, Handbook of pulsar astronomy. Cambridge University Press, https://www.cambridge.org/us/catalogue/catalogue.asp?isbn=0521828236
- Lyne et al. (1988) Lyne A. G., Pritchard R. S., Smith F. G., 1988, Monthly Notices of the Royal Astronomical Society, 233, 667
- Lyne et al. (1993) Lyne A. G., Pritchard R. S., Graham Smith F., 1993, Monthly Notices of the Royal Astronomical Society, 265, 1003
- Lyne et al. (1996) Lyne A. G., Pritchard R. S., Graham-Smith F., Camilo F., 1996, Nature, 381, 497
- Lyne et al. (2000) Lyne A. G., Shemar S. L., Graham Smith F., 2000, Monthly Notices of the Royal Astronomical Society, 315, 534
- Maggi et al. (2019) Maggi P., et al., 2019, Astronomy & Astrophysics, 631, A127
- Maitra et al. (2015) Maitra C., Ballet J., Filipović M. D., Haberl F., Tiengo A., Grieve K., Roper Q., 2015, Astronomy & Astrophysics, 584, A41
- Maitra et al. (2021) Maitra C., Esposito P., Tiengo A., Ballet J., Haberl F., Dai S., Filipović M. D., Pilia M., 2021, Monthly Notices of the Royal Astronomical Society: Letters, 507, L1
- Manchester et al. (1993a) Manchester R. N., Mar D. P., Lyne A. G., Kaspi V. M., Johnston S., 1993a, The Astrophysical Journal, 403, L29
- Manchester et al. (1993b) Manchester R. N., Staveley-Smith L., Kesteven M. J., 1993b, The Astrophysical Journal, 411, 756
- Manchester et al. (2005) Manchester R. N., Hobbs G. B., Teoh A., Hobbs M., 2005, The Astronomical Journal, 129, 1993
- Manchester et al. (2006) Manchester R. N., Fan G., Lyne A. G., Kaspi V. M., Crawford F., 2006, The Astrophysical Journal, 649, 235
- Marshall et al. (2016) Marshall F. E., Guillemot L., Kust Harding A., Martin P., Smith D. A., 2016, in American Astronomical Society, AAS Meeting #227, id.423.04. https://ui.adsabs.harvard.edu/abs/2016AAS...22742304M/abstract
- Mathewson et al. (1984) Mathewson D. S., Ford V. L., Dopita M. A., Tuohy I. R., Mills B. Y., Turtle A. J., 1984, The Astrophysical Journal Supplement Series, 55, 189
- McConnell et al. (1991) McConnell D., McCulloch P. M., Hamilton P. A., Ables J. G., Hall P. J., Jacka C. E., Hunt A. J., 1991, Monthly Notices of the Royal Astronomical Society, 249, 654
- Melatos (1997) Melatos A., 1997, Monthly Notices of the Royal Astronomical Society, 288, 1049
- Men et al. (2023) Men Y., Barr E., Clark C. J., Carli E., Desvignes G., 2023, Astronomy & Astrophysics, 679, A20
- Michilli et al. (2018) Michilli D., et al., 2018, Nature, 553, 182
- Middleditch & Pennypacker (1985) Middleditch J., Pennypacker C., 1985, Nature, 313, 659
- Middleditch et al. (2006) Middleditch J., Marshall F. E., Wang Q. D., Gotthelf E. V., Zhang W., 2006, The Astrophysical Journal, 652, 1531
- Millhouse et al. (2022) Millhouse M., Melatos A., Howitt G., Carlin J. B., Dunn L., Ashton G., 2022, Monthly Notices of the Royal Astronomical Society, 511, 3304
- Morello (2023) Morello V., 2023, clfd: Clean Folded Data, https://ascl.net/2310.008
- Oswald et al. (2023) Oswald L. S., et al., 2023, Monthly Notices of the Royal Astronomical Society, 520, 4961
- Owen et al. (2011) Owen R. A., et al., 2011, Astronomy & Astrophysics, 530, A132
- Padmanabh (2021) Padmanabh P. V., 2021, PhD thesis, Rheinische Friedrich-Wilhelms-Universität Bonn, https://bonndoc.ulb.uni-bonn.de/xmlui/handle/20.500.11811/9336
- Padmanabh et al. (2023) Padmanabh P. V., et al., 2023, Monthly Notices of the Royal Astronomical Society, 524, 1291
- Parthasarathy et al. (2019) Parthasarathy A., et al., 2019, Monthly Notices of the Royal Astronomical Society, 489, 3810
- Parthasarathy et al. (2020) Parthasarathy A., et al., 2020, Monthly Notices of the Royal Astronomical Society, 494, 2012
- Payne et al. (2007) Payne J. L., White G. L., Filipović M. D., Pannuti T. G., 2007, Monthly Notices of the Royal Astronomical Society, 376, 1793
- Piro & Gaensler (2018) Piro A. L., Gaensler B. M., 2018, The Astrophysical Journal, 861, 150
- Ridolfi et al. (2022) Ridolfi A., et al., 2022, Astronomy & Astrophysics, 664, A27
- Scowcroft et al. (2016) Scowcroft V., Freedman W. L., Madore B. F., Monson A., Persson S. E., Rich J., Seibert M., Rigby J. R., 2016, The Astrophysical Journal, 816, 49
- Serylak et al. (2021) Serylak M., et al., 2021, Monthly Notices of the Royal Astronomical Society, 505, 4483
- Seward et al. (1984) Seward F. D., Harnden F. R. J., Helfand D. J., 1984, The Astrophysical Journal, 287, L19
- Shaw et al. (2018) Shaw B., et al., 2018, Monthly Notices of the Royal Astronomical Society, 478, 3832
- Shibata et al. (2016) Shibata S., Watanabe E., Yatsu Y., Enoto T., Bamba A., 2016, The Astrophysical Journal, 833, 59
- Shklovskii (1970) Shklovskii I. S., 1970, Soviet Astronomy, 13, 562
- Standish (1998) Standish E., 1998, Technical report, JPL Planetary and Lunar Ephemerides
- Stappers & Kramer (2016) Stappers B., Kramer M., 2016, in Proceedings of MeerKAT Science: On the Pathway to the SKA — PoS(MeerKAT2016). Sissa Medialab, p. 009, doi:10.22323/1.277.0009
- Szary et al. (2014) Szary A., Zhang B., Melikidze G. I., Gil J., Xu R. X., 2014, Astrophysical Journal, 784, 59
- Titus et al. (2019) Titus N., Stappers B. W., Morello V., Caleb M., Filipović M. D., McBride V. A., Ho W. C. G., Buckley D. A. H., 2019, Monthly Notices of the Royal Astronomical Society, 487, 4332
- Titus et al. (2020) Titus N., Toonen S., McBride V. A., Stappers B. W., Buckley D. A. H., Levin L., 2020, Monthly Notices of the Royal Astronomical Society, 494, 500
- Tuo et al. (2024) Tuo Y., Serim M. M., Antonelli M., Ducci L., Vahdat A., Ge M., Santangelo A., Xie F., 2024, The Astrophysical Journal Letters, 967, L13
- Van Straten & Bailes (2011) Van Straten W., Bailes M., 2011, Publications of the Astronomical Society of Australia, 28, 1
- Wang & Gotthelf (1998) Wang Q. D., Gotthelf E. V., 1998, The Astrophysical Journal, 494, 623
- Wang et al. (2001) Wang Q. D., Gotthelf E. V., Chu Y., Dickel J. R., 2001, The Astrophysical Journal, 559, 275
- Weltevrede (2016) Weltevrede P., 2016, Astronomy & Astrophysics, 590, A109
- Wenger et al. (2000) Wenger M., et al., 2000, Astronomy and Astrophysics Supplement Series, 143, 9
- Yao et al. (2017) Yao J. M., Manchester R. N., Wang N., 2017, The Astrophysical Journal, 835, 29