Thermal photons as a sensitive probe of -cluster in C+Au collisions at the BNL Relativistic Heavy Ion Collider
Abstract
Different orientations of -clustered carbon nuclei colliding with heavy ions can result in a large variation in the value of anisotropic flow. Thus, photon flow observables from clustered and collisions could be a potential probe to study the ‘direct photon puzzle’. We calculate the transverse momentum spectra and anisotropic flow coefficients () of thermal photons from collisions of triangular -clustered carbon and gold at GeV at RHIC using a hydrodynamic model framework and compare the results with those obtained from unclustered carbon and gold collisions. The slope of the thermal photon spectra is found to vary moderately for different orientations of collisions. However, we find that the elliptic () and triangular flow () coefficients of direct photons for specific configurations are significantly larger and predominantly formed by the QGP radiation. A strong anti-correlation between initial spatial ellipticity and triangularity is observed in an event-by-event framework of -clustered collisions. These special features provide us an opportunity to detect the exotic nature of cluster structure inside carbon nucleus using the photon probe in the future experiments.
I Introduction
The experimental study of relativistic heavy-ion collisions provides a strong evidence of the formation of hot and dense Quark-Gluon Plasma (QGP) state of matter at the center of the collision zone Gardim:2019xjs ; Adler:2003kt ; Alver:2010gr ; Aamodt:2010pa ; Chen:2018tnh . The relativistic hydrodynamic models present a satisfactory description of fireball evolution as the copious production and large harmonic flow of hadrons have been successfully explained by these frameworks Kolb:2003dz ; Huovinen:2003fa ; Kolb:2000sd ; Teaney:2001av ; Huovinen:2006jp ; Romatschke:2007mq ; Teaney:2009qa ; Holopainen:2010gz ; Schenke:2012wb ; Heinz:2013bua ; ColemanSmith:2012ka ; Sorensen:2010zq ; Takahashi:2009na ; Yan:2017ivm . The past studies have shown that nuclear deformation can be investigated from the anisotropic flow of produced hadrons at intermediate and high collision energies Heinz:2004ir ; Rybczynski:2012av ; Shou:2014eya ; Cao:2010bc . The nuclear collisions at such energies provide us a unique way to investigate the intrinsic substructure of nuclei as the time during which the participating nuclei pass through each other is too small for any slower nuclear excitation to occur and thus one can obtain a projection of overlying nuclear distributions on the fireball.
For example, the small systems, such as and have gathered much attention for producing anisotropic flow coefficients comparable to the peripheral heavy ion collisions in recent times Heinz:2019dbd . The measurements of , , and collisions at 200A GeV have clearly shown the footprints of initial geometries (initial ellipticity and triangularity) on the anisotropic flow coefficients PHENIX:2018lia . The successful hydrodynamical description of those data has strongly suggested that the initial nucleon-level geometries have been transferred into the momentum anisotropies through hydrodynamical evolution of small droplets of the QGP in these small systems.
An analogous initial geometry effect of nuclei is also found to be present in the intermediate energy heavy-ion collisions however at a cluster level Liu:2018eyg ; Ebran . A few recent articles have argued that the geometric -clustering structure of light nuclei can be realized in the realm of relativistic collisions Broniowski:2013dia ; Rybczynski:2017nrx ; Bozek:2014cva . Gamow first proposed the possibility of clustered states in light nuclei gamow . The identification of the fusion reaction mechanism for carbon production has led to the discovery of the clustered states Hoyle:1954zz ; Cook:1957zz . However, many theoretical models such as no-core shell model Roth:2011vt , fermionic molecular dynamics Chernykh:2007zz , the variational Green’s function Pieper:2002ne , Bose-Einstein Condensate (BEC) Tohsaki:2001an ; Funaki:2003af ; Funaki:2006gt , etc. have not been successful in explaining such clustered structures of nuclei. The -clustering inside a light nucleus produces nuclear deformity and spatial correlations between clusters. It has been suggested that -clustering configurations can be identified by giant dipole resonance He:2014iqa ; He:2016cwt or photonuclear reactions Huang:2017ysr ; Huang:2017ypi ; Huang:2020iil . The strategy of investigating initial nucleon-level geometry via measuring flow in a relativistic heavy-ion collision has a great potential to identify the geometric structures of clustered nuclei Broniowski:2013dia ; Bozek:2014cva ; Zhang:2017xda ; Zhang:2018zzu .
On the other hand, the direct photons are considered as one of the efficient probes to study the properties of hot and dense QGP state of matter Srivastava:2008es ; Gale:2014dfa ; Chatterjee:2013naa ; Shen:2013cca ; Monnai:2014kqa ; McLerran:2014hza ; Liu:2012ax ; Basar:2012bp ; Tuchin:2012mf ; Zakharov:2016mmc ; Vujanovic:2014xva ; Li:2010ts ; Ma:2013bia ; Adare:2008ab ; Adam:2015lda . The thermal photon spectra obtained from the hydrodynamical model evolution combined with the prompt photon contribution from initial partonic hard scatterings have satisfactorily described the measured direct photon spectra in the range GeV in heavy-ion collisions at both Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC). The theoretical calculation of spectra in the region GeV has, however, been found to underestimate the data where the contribution from the hadronic phase is significant. The anisotropic flow of direct photons is also believed to be a potential probe for illustrating the initial state of a collision. However, the hydrodynamic model calculations of photon production failed to describe the elliptic and triangular flow data at RHIC and LHC by a large margin, which has been addressed as the “direct photon puzzle” Adare:2015lcd ; Acharya:2018bdy . Several studies using a more realistic hydrodynamic framework, initial conditions, the pre-equilibrium flow, and holographic thermal-photon emission rate have shown improvements in the theoretical prediction but could not resolve the puzzle yet Dasgupta:2017fns ; Shen:2015nto ; Gale:2020xlg ; Iatrakis:2016ugz . Recent studies have shown that the spectra and anisotropic flow coefficients of photons (i.e., ) from different collision systems and their simultaneous comparison could be valuable to understand the sources of the puzzle Chatterjee:2017akg ; Dasgupta:2016qkq ; Dasgupta:2019whr . A significant improvement in the photon anisotropic flow has been reported recently by Naboka et al. using integrated hydrokinetic model Naboka:2017dnn ; Naboka:2019vko .
In the present article, we aim to study the intrinsic geometry of the -clustered nucleus using the photon probe. We calculate the spectra and anisotropic flow coefficients () of thermal photons in (2+1) dimensional inviscid hydrodynamic framework from the -clustered collisions at the center-of-mass energy =200 GeV. The same set of observables from the unclustered collisions (see Section II) is also calculated for comparison.
This paper is organized as follows. In the next section, we briefly discuss the initial parameters and the framework for the model calculation. In section III we present how initial spatial anisotropies and the momentum anisotropies of thermal photons are calculated. In section IV we discuss the results of thermal photon spectra and anisotropic flow coefficients and finally, we summarize our results in section V.
II Initial condition and hydrodynamic framework
In the present work, we adapt the same procedures followed in Bozek:2014cva to choose the initial parameters for the nuclear density distribution of -clustered carbon. We study different collision scenarios incorporating two types of carbon nucleus in the Monte Carlo Glauber (MCG) framework :
-
•
-clustered carbon: This is an equilateral triangle shaped -clustered state of carbon. It is considered as the ground state of clustered phase with binding energy MeV/nucleon. There exists another possible excited state of the clustered structure, a chain-like structure of 3 alpha particles with binding energy MeV/nucleon. However, in this article, we emphasize only on the triangle shaped carbon. We use a parametric form of nucleon distribution function for each cluster Bozek:2014cva and centers of such three clusters are placed on the vertices of an equilateral triangle. The parameters are fixed in such a manner that one-body radial density distribution of the center of nucleons obeys the results of the BEC model Funaki:2006gt . The distribution of nucleons in each cluster is expressed through a Gaussian function as follows :
(1) where, represents the center of the cluster. determines the mean radius of each cluster. We generate positions of nucleons in each alpha cluster from the above distribution function and then shift three of such clusters to the vertices of a triangle of length . The short distance repulsion of nucleons is also an essential criterion for light nuclei, where the distance between two centers of an N-N pair cannot be less than 0.9 fm Bozek:2014cva . The nucleonic positions are finally shifted to a new coordinated system where the center-of-mass resides on the origin. The parameters and in Eq.(1) are taken as fm and fm respectively to match the results from BEC model calculations Bozek:2014cva .
-
•
Unclustered carbon: This is a mean-field state of nucleus. The nuclear distribution is isotropic for this case. A two-parameter Wood-Saxon distribution of nuclear density is considered for an unclustered carbon where the parameters are adjusted in such a way that the root mean square radius of the nuclear distribution remains the same as the clustered carbon ( fm).
To distribute the nucleons inside a gold nucleus we employ the standard two-parameter Wood-Saxon nuclear density distribution profile. We assume that the beam axis is stretched along the -direction and the impact parameter lies along the -direction in each event of the collision.
The conventional two-component MCG technique is then used to distribute initial entropy density on the transverse plane. The criterion for a collision between the two incoming nucleons is made as , where is the transverse distance between the colliding nucleons and is the inelastic nucleon-nucleon cross-section which at RHIC is about 42 mb. A participant is given a weight of and a binary collision is given a weight of , where is taken as 0.145 Bozek:2014cva . The entropy density distribution, , is obtained by taking a weighted sum over all the sources as explained in Eq.(2) below.
| (2) |
where, and denote the number of participant and binary collision sources at the position respectively. K is a normalization factor which decides the total multiplicity of an event. The function is a normalized distribution of the following form centering about the collision or participant source :
| (3) |
The initial entropy density profile which serves as an input for our hydrodynamic calculation is obtained by taking an initial state average of events with random nucleonic positions at impact parameter fm. We modify the (2+1) dimensional ideal relativistic hydrodynamic model Holopainen:2010gz to obtain the space-time evolution of the above initial entropy distribution at the mid-rapidity. The initial flow velocity component, and are taken as zero. For the sake of simplicity, we take the value of initial thermalization time as 0.17 fm/ which has been used for the collisions at RHIC Eskola:2005tx ; Chatterjee:2017akg , although one may expect a larger value of initial thermalization time for small systems. A lattice-based equation of state Laine:2006cp is used and we consider a constant temperature freeze-out at 160 MeV. The same freeze-out temperature () is used in earlier studies of Au+Au collisions at RHIC using the same hydrodynamical model Chatterjee:2013naa ; Dasgupta:2017fns ; Chatterjee:2017akg ; Dasgupta:2019whr .
III ANISOTROPIC FLOW OF THERMAL PHOTONS
The production of thermal photons from the quark gluon plasma phase is estimated by using the complete next-to-leading order photon rates from Refs. Arnold:2001ms ; Ghiglieri:2013gia . We use the parameterized rates from Ref. Turbide:2003si to calculate the photon production from the hot hadronic matter phase. The emission rates () from QGP and hadronic matter phases are integrated over the space-time history to estimate the total thermal production and anisotropic flow. The flow coefficients are calculated as:
| (4) |
where is the azimuthal angle of particle’s momentum and the event plane angle is determined by,
| (5) |
where is the energy density at an initial proper time at () point on the transverse plane, and are the spatial azimuthal angle and radial distance. The corresponding initial state anisotropy is quantified as Chatterjee:2017akg ; Dasgupta:2019whr ; Ma:2010dv :
| (6) |
IV Results and discussions
IV.1 Initial configurations
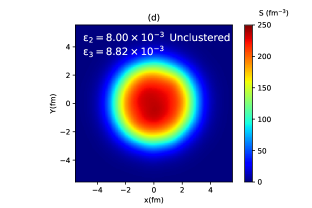
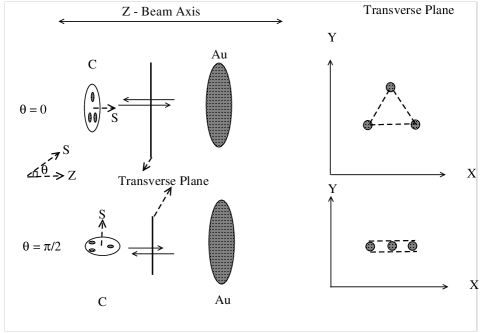
We consider three typical configurations of collisions, i.e., , , and in this study. This can be imagined as a deformed nucleus hitting a wall of a gold nucleus at different orientation angles (see Fig. 1). Thus, the angle describes situation where the symmetry axis is aligned with the beam axis producing an initial triangular geometry in the deposited entropy distribution and the highest multiplicity amongst all orientations of collision. For , the multiplicity is the lowest. While a triangular geometry vanishes for such a scenario, a large elliptic geometry appears. We consider an intermediate situation where the symmetry axis makes an angle with the beam axis producing both the intrinsic elliptic and triangular geometry in the deposited entropy distribution.
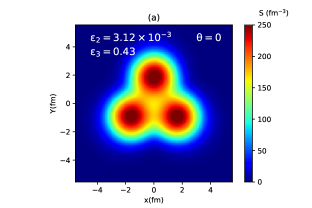
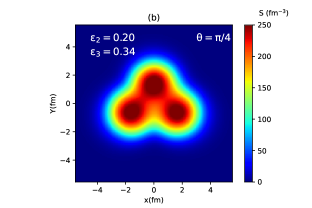
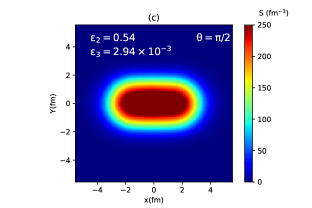
In Fig. 2 (a), (b), and (c) the event-averaged initial entropy density profile for three orientation angles 0, /4, and /2 are shown respectively, while Fig. 2(d) represents the entropy profile for the unclustered carbon. We see that the entropy density at the center of each hot spot region for the clustered case is much larger than the entropy density obtained at the center of the unclustered case. In Fig. 2(a) and (b), the entropy profiles are seen to have a triangular shape, while in Fig. 2(c) a peanut-like structure appears with no such triangular geometry. The triangular eccentricity () of the initial entropy density distribution for the cases in Fig. 2(a) and (b) is and respectively. On the other hand, the elliptic eccentricity () for the cases in Figs. 2(b) and (c) is and respectively, whereas is vanishingly small for the other two cases.
IV.2 Evolution of temperature and flow velocity
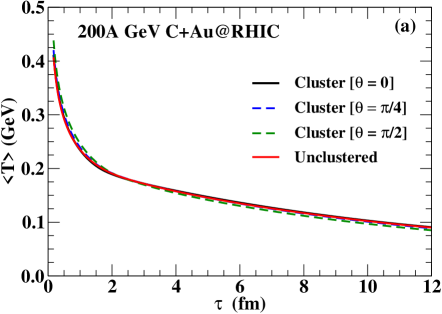
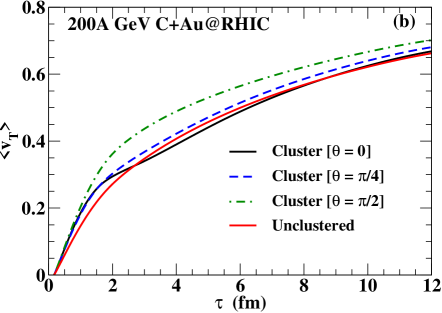
The time evolution of average temperature and average transverse flow velocity for the three configurations of collision for the clustered carbon and the unclustered carbon is shown in Fig. 3(a) and (b) respectively. The and are obtained by Eq. (7) and Eq. (8), respectively, i.e.
| (7) |
| (8) |
The initial average temperature (see Fig. 3 (a)) is found to be largest ( MeV) for the configuration and smallest for the unclustered case ( MeV). A relatively smaller area of the overlapping region leads to a larger for the configuration at the initial time. We see an almost similar time evolution of the average temperature for all the configurations. However, the evolution of the average transverse flow velocity for different configurations are distinct from each other (see Fig. 3(b)). We see that sharply rises for the clustered cases, whereas the rise is relatively slower for the unclustered case. The rise is maximum for the orientation angle . During the time interval of fm/c, we observe a sudden jerk for the configuration . However, no such effect is found for and . The radially outward ripples, originated at the boundary of each hotspot (see Fig. 2 (a) ), cause a flow cancellation when they collide, which effectively reduces the growth of the average transverse flow velocity.
IV.3 Spectra and anisotropic flow
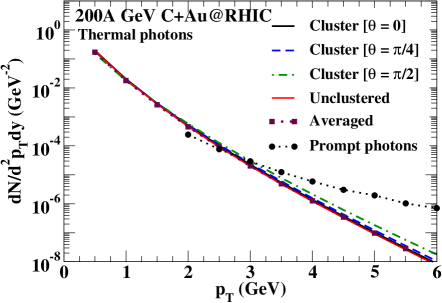
In Fig. 4, the thermal photon spectra are presented for the clustered and unclustered collisions. The thermal photon spectra for all the cases are found to be almost similar in the region GeV. However, the spectra become sensitive to the orientation angle for GeV. The thermal spectrum for the configuration is found to be slightly above the other spectra in the larger region. On the other hand, photon production from the unclustered carbon is found to be smallest. We plot a thermal photon spectrum (i.e. maroon box+dotted line) considering an orientation-averaged initial profile (averaged over 50,000 events with random orientations) for the clustered carbon and find it similar to the spectrum obtained for the unclustered carbon. We estimate the prompt photon production in the region GeV from collisions by scaling the prompt photon spectrum obtained in the p+p collisions at 200A GeV using the Monte Carlo code JETPHOX (version 1.2.2) Aurenche:2006vj . We expect similar production of prompt photons for collisions of clustered as well as unclustered carbon as the for both are close to each other. The Fig. 4 shows the prompt photons contribute significantly in the region GeV (black filled circles).
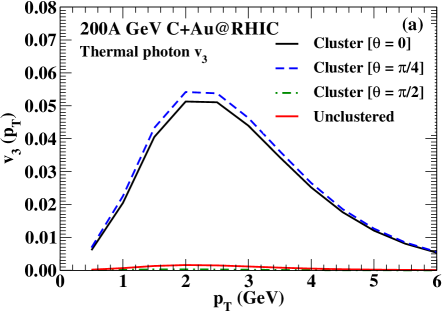
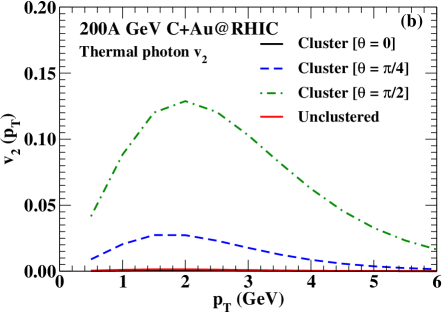
The elliptic and triangular flow of thermal photons as a function of are presented in Fig. 5(a) and (b) respectively. We see a substantially large thermal photon for the configurations and . The initial triangular geometry of the entropy density profile produced in the collision of -clustered carbon and gold nucleus gives rise to the triangular flow of thermal photons. As there exists no such triangular geometry for the configuration or the unclustered case, we obtain a vanishingly small thermal photon . The thermal photon for the configuration is seen to be slightly larger compared to the same obtained from the orientation angle even though the triangular anisotropy is smaller for the former than the latter. The reason is attributed to the larger average transverse flow velocity during the evolution for the configuration than the same obtained for the configuration . On the other hand, the elliptic flow parameter of thermal photons is found to be vanishingly small for the configuration and the unclustered case. However, the thermal photon is found to be very large for the orientation angle . The initial elliptic eccentricity and the transverse flow velocity, both play significant role in producing a large of thermal photons for the configuration . It is important to note that the obtained for the above configuration is comparable to the direct photon data obtained for the mid-central Au+Au collisions at 200A GeV at RHIC Adare:2015lcd .
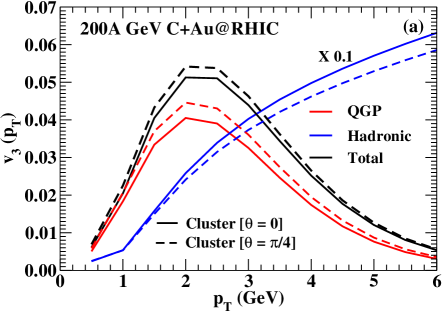
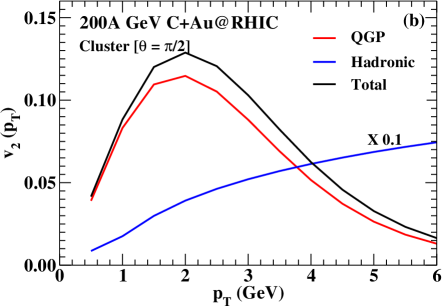
To obtain a more precise idea about the origin of the anisotropic flow coefficients of photons, we plot the individual contributions from the QGP and hadronic phases to the total value of the flow coefficients in Fig 6. We calculate the contributions of thermal photon for the clustered case with orientation angles and in Fig 6(a). We find that the maximum value of (at GeV) from the QGP phase is substantial and close to the maximum value of the total thermal photon . Hence, the response to the initial-state triangular geometry is predominantly carried by the QGP evolution. If we compare the hadronic medium contribution to the total thermal photon for these cases, we find that unlike the QGP photon , the hadronic photon for the orientation is larger compared to the same obtained at the orientation . The reason can be understood from Fig. 2, where we see that the triangular geometry associated with the hottest region is more prominent in Fig 2(b) compared to Fig. 2(a). Whereas, the boundary region, which is the source of hadronic photons, has a larger triangular geometry as shown in Fig. 2(a) compared to Fig. 2(b). The contributions of thermal photon for the clustered case with the orientation angle are plotted in Fig. 6(b), and we see a similar response. The peak value of the thermal photon from the QGP phase is found to be about of the peak value of the total thermal photon and identically, it reflects that the most of the net thermal photon has built up during the early phase of QGP evolution.
It is to be noted that the value of is fixed for Au+Au collisions by reproducing the experimental data of charged particle spectra and anisotropic flow parameters. We can not do the same for C+Au collisions due to the unavailability of experimental data. Therefore, we use the same for C+Au collisions as in Au+Au collisions. A smaller would enhance the photon yield from the hadronic phase in the region GeV and the larger part of the direct photon spectrum will remain unaltered. However, the photon anisotropic flow is expected to be larger for a smaller . To show the effect of a relatively longer hadronic phase evolution on the photon flow observables we have calculated thermal photon and considering an arbitrary small MeV, see Fig. 7) for orientation angles and respectively where, the flow coefficients are estimated to be largest. We see that and are enhanced for a smaller , however, the qualitative difference between the photon anisotropic flow parameters remains unchanged even for a significant change in the value of the freeze-out temperature.
A detailed study considering a larger formation time and dynamical freeze-out would be valuable in this regards and we postpone it for the future.
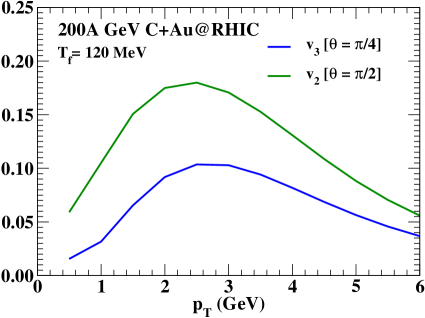
The anisotropic flow parameters of direct photons for the clustered configurations with the largest thermal photon and are shown in Fig. 8. By ‘direct photons’ we mean the combined contribution of thermal and the prompt photons (produced in initial hard scatterings). We find that the values of the anosotropic flow cofficients are substantially large even after inclusion of the prompt contribution (The prompt spectrum is generated in the region GeV (due to some constraints) using JETPHOX and as a result we could not show the anisotropic flow in the low region). The maximum value of direct photon and (at 2 GeV) are found to be about of their respective maximum thermal photon and values. It is to be noted that these values are comparable to the anisotropic flow parameter data obtained from the Au+Au and Pb+Pb collisions at RHIC and LHC energy respectively Adare:2015lcd ; Acharya:2018bdy . Thus, considering even a smooth initial condition, we can obtain a significantly large direct photon and depending upon the orientations of collision for the clustered carbon. We expect that the inclusion of initial state fluctuations would further increase the value of direct photon and . On the other hand, photon and for unclustered carbon appear only due to initial state fluctuations and are expected to be significantly smaller than the clustered carbon.
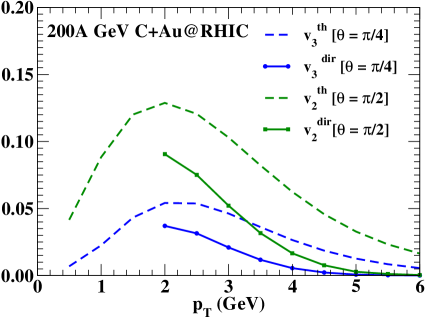
Thus, the clustered carbon and gold collisions at the RHIC have the potential to produce considerably large anisotropic flow parameters of photons even for the most central events. Furthermore, the strong sensitivity of the anisotropic flow parameters to the initial geometry and early QGP evolution also can be valuable to understand the ‘direct photon puzzle’. Our main focus in the present calculation is only to estimate the effect of initial geometry on the production and anisotropic flow parameters of photons. A more realistic calculation, using an event-by-event (3+1) dimensional hydrodynamic framework, would be valuable to precisely explore the role of fluctuations and participant asymmetry on the evolution of thermodynamic quantities and anisotropic flow parameters of photons.
IV.4 Geometry (flow) correlation
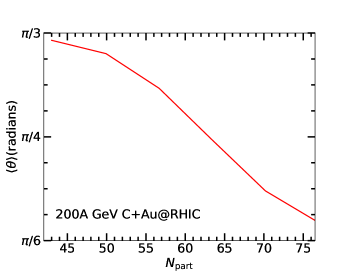
To get an idea of the experimental signature, we simulate a large number of clustered C+Au events with different configurations and compare the results obtained from the collisions of unclustered carbon. Fig. 9 shows the average orientation angle as a function of the number of participants in the collisions of clustered carbon, where and henceforth denotes an event average. We observe that with the increasing , the average angle reduces significantly. Thus, based on the multiplicity cut, it may be possible to select events with various configurations.
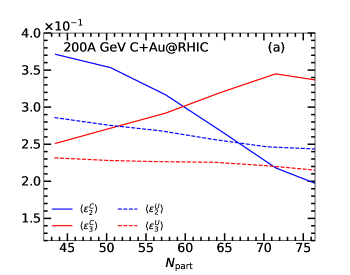
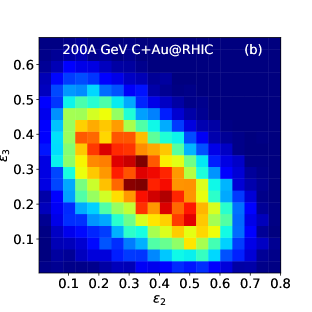
In Fig. 10(a) we present the dependence of average eccentricity and triangularity in unclustered and -clustered collisions at 200A GeV. We consider the events having . The superscripts ‘U’ and ‘C’ stand for the unclustered and clustered carbon respectively. We see that and show similar behavior with increasing . Due to vanishing geometric deformation and smaller fluctuations at a larger , the average eccentricity decreases. We observe a different trend for clustered carbon. Due to the intrinsic triangular geometry of the clustered-carbon, increases with , whereas decreases. The difference becomes substantial at larger , which indicates an obvious anti-correlation between ellipticity and triangularity exists in -clustered + collisions.
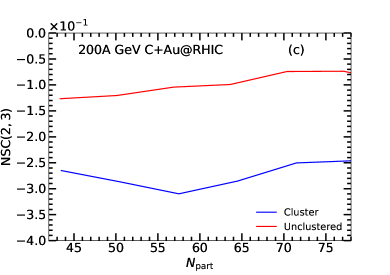
In Fig. 10(b) we plot the event density distribution in plane for the collisions of clustered carbon. To quantify the anti-correlation, we define a normalized symmetric cumulants coefficient NSC(n,m) as follows Giacalone:2016afq ,
| (9) |
The NSC(2,3) is expected to be similar to the quantity involving the anisotropic flow coefficients ( and ) under a linear response assumption Noronha-Hostler:2015dbi ; Yan:2015jma . In Fig. 10(c), we show the normalized symmetric cumulants coefficient as function of for both unclustered and -clustered cases. The negative values of coefficients signify the anti-correlation relation between the two variables. We see a larger anti-correlation for the clustered case compared to the unclustered case. The coefficients for both the cases do not show significant dependence. The NSC(2,3) for the clustered carbon is found to be three times larger than the NSC(2,3) obtained for the unclustered carbon. We find a small minimum of NSC(2,3) at , where the values of the and are close to each other. Exploring the large anti-correlation between ellipticity and triangularity (elliptic flow and triangular flow), we can detect the -cluster effects of carbon in collisions. It is to be noted that some earlier studies have explored the characteristics of the initial-state eccentricities and final hadron flow observables from the collisions of the clustered carbon and heavy-ions at various beam energies in the event-by-event framework Broniowski:2013dia ; Bozek:2014cva . In principle, we expect that the anti-correlation behavior should hold for both photons and hadrons, since their flow observables basically arise from the initial geometry.
V SUMMARY
We have calculated spectra and differential anisotropic flow coefficients of thermal photons for -clustered and collisions at RHIC using a hydrodynamic model with the event-averaged smooth initial density distribution and compared the results with those obtained from unclustered carbon and gold collisions. Three different orientations of collision for the -clustered carbon have been considered which produce notably different initial spatial ellipticities and triangularities.
The slope of the thermal photon spectrum depends on the orientation of collision. A larger initial temperature for the orientation angle results in more high photons from the early stage of system evolution compared to the other configurations. However, we see no significant difference in the direct photon spectra for various configurations due to the large contribution of prompt photons in the region GeV. We see significantly large thermal photon and from the configurations and , respectively, which are large and comparable to the experimental data of photon and from the mid-central 200A GeV Au+Au collisions at RHIC. On the other hand, photon and from the unclustered collisions are close to zero as the corresponding spatial anisotropies are vanishingly small for the system. We find that addition of the prompt photon contribution dilutes the anisotropic flow parameters but still their values are substantially larger in comparison to the theoretical estimate of anisotropic flow parameters of direct photons obtained for the mid-central Au+Au collisions. We have studied the individual contributions of the thermal photon and from QGP and hadronic phases and have found that these anisotropic flow coefficients are predominantly built during the QGP evolution. As the effect of viscosity which prolongs the evolution of the QGP is not included here, we expect that it could change the magnitude but not the qualitative nature of these photon observables. Thus, we find that anisotropic flow of photons from the clustered carbon are sensitive to the anisotropic nuclear distribution of and can potentially help us to understand the photon puzzle. A strong anti-correlation between ellipticity and triangularity is observed because of the exotic internal structure of -clustered carbon. With the aid of these special features of photon spectra and anisotropic flows, it could be a potential probe to detect the exotic internal structure of -clustered carbon in the future high energy + experiment.
Acknowledgements.
This work is supported by the National Natural Science Foundation of China under Grants No. 11835002, No. 11890710, No. 11890714, No. 11975079 and No. 11961131011, the Strategic Priority Research Program of Chinese Academy of Sciences under Grant No. XDB34030000, Shanghai Pujiang Program under Grant No. 19PJ1401400, and the Guangdong Major Project of Basic and Applied Basic Research under Grant No. 2020B0301030008.References
- (1) F. G. Gardim, G. Giacalone, M. Luzum and J. Y. Ollitrault, Nature Phys. 16, no.6, 615-619 (2020).
- (2) S. S. Adler et al. [PHENIX], Phys. Rev. Lett. 91, 182301 (2003).
- (3) B. Alver and G. Roland, Phys. Rev. C 81, 054905 (2010).
- (4) K. Aamodt et al. [ALICE], Phys. Rev. Lett. 105, 252302 (2010).
- (5) J. Chen, D. Keane, Y. G. Ma, A. Tang and Z. Xu, Phys. Rept. 760, 1 (2018).
- (6) P. F. Kolb and U. W. Heinz, [nucl-th/0305084].
- (7) P. Huovinen, [nucl-th/0305064].
- (8) P. F. Kolb, J. Sollfrank and U. W. Heinz, Phys. Rev. C 62, 054909 (2000).
- (9) D. Teaney, J. Lauret and E. V. Shuryak, nucl-th/0110037.
- (10) P. Huovinen and P. V. Ruuskanen, Ann. Rev. Nucl. Part. Sci. 56, 163 (2006).
- (11) P. Romatschke and U. Romatschke, Phys. Rev. Lett. 99, 172301 (2007).
- (12) D. A. Teaney, Quark-Gluon Plasma 4, 207 (2010).
- (13) L. Yan, Chin. Phys. C 42, 042001 (2018).
- (14) H. Holopainen, H. Niemi and K. J. Eskola, Phys. Rev. C 83, 034901 (2011).
- (15) B. Schenke, P. Tribedy and R. Venugopalan, Phys. Rev. Lett. 108, 252301 (2012).
- (16) U. Heinz, Z. Qiu and C. Shen, Phys. Rev. C 87, no.3, 034913 (2013).
- (17) C. E. Coleman-Smith, H. Petersen and R. L. Wolpert, J. Phys. G 40, 095103 (2013).
- (18) P. Sorensen, J. Phys. G 37, 094011 (2010).
- (19) J. Takahashi, B. M. Tavares, W. L. Qian, R. Andrade, F. Grassi, Y. Hama, T. Kodama and N. Xu, Phys. Rev. Lett. 103, 242301 (2009).
- (20) U. W. Heinz and A. Kuhlman, Phys. Rev. Lett. 94, 132301 (2005).
- (21) M. Rybczynski, W. Broniowski and G. Stefanek, Phys. Rev. C 87, no.4, 044908 (2013).
- (22) Q. Y. Shou, Y. G. Ma, P. Sorensen, A. H. Tang, F. Videbak and H. Wang, Phys. Lett. B 749, 215-220 (2015).
- (23) X. G. Cao, G. Q. Zhang, X. Z. Cai, Y. G. Ma, W. Guo, J. G. Chen, W. D. Tian, D. Q. Fang and H. W. Wang, Phys. Rev. C 81, 061603 (2010).
- (24) U. W. Heinz and J. S. Moreland, J. Phys. Conf. Ser. 1271, 012018 (2019).
- (25) C. Aidala et al. [PHENIX], Nature Phys. 15, no.3, 214-220 (2019).
- (26) Y. Liu and Y. L. Ye, Nucl. Sci. Tech. 29, 184 (2018).
- (27) J. -P. Ebran, E. Khan, T. Nikšić and D. Vretenar, Nature 487, 341–344 (2012).
- (28) W. Broniowski and E. Ruiz Arriola, Phys. Rev. Lett. 112, no.11, 112501 (2014).
- (29) M. Rybczyski, M. Piotrowska and W. Broniowski, Phys. Rev. C 97, no.3, 034912 (2018).
- (30) P. Bozek, W. Broniowski, E. Ruiz Arriola and M. Rybczynski, Phys. Rev. C 90, no.6, 064902 (2014).
- (31) G. Gamow, Constitution of atomic nuclei and radioactivity, p. 50 (Clarendon Press, Oxford, 1931).
- (32) F. Hoyle, Astrophys. J. Suppl. 1, 121-146 (1954).
- (33) C. W. Cook, W. A. Fowler, C. C. Lauritsen and T. Lauritsen, Phys. Rev. 107, 508-515 (1957).
- (34) R. Roth, S. Binder, K. Vobig, A. Calci, J. Langhammer and P. Navratil, Phys. Rev. Lett. 109, 052501 (2012).
- (35) M. Chernykh, H. Feldmeier, T. Neff, P. von Neumann-Cosel and A. Richter, Phys. Rev. Lett. 98, 032501 (2007).
- (36) S. C. Pieper, K. Varga and R. B. Wiringa, Phys. Rev. C 66, 044310 (2002).
- (37) A. Tohsaki, H. Horiuchi, P. Schuck and G. Ropke, Phys. Rev. Lett. 87, 192501 (2001).
- (38) Y. Funaki, A. Tohsaki, H. Horiuchi, P. Schuck and G. Ropke, Phys. Rev. C 67, 051306 (2003).
- (39) Y. Funaki, A. Tohsaki, H. Horiuchi, P. Schuck and G. Ropke, Eur. Phys. J. A 28, 259-263 (2006).
- (40) W. He, Y. G. Ma, X. Cao, X. Cai and G. Zhang, Phys. Rev. Lett. 113, 032506 (2014).
- (41) W. He, Y. G. Ma, X. Cao, X. Cai and G. Zhang, Phys. Rev. C 94, 014301 (2016).
- (42) B. Huang, Y. G. Ma and W. He, Phys. Rev. C 95, 034606 (2017).
- (43) B. S. Huang, Y. G. Ma and W. B. He, Eur. Phys. J. A 53, 119 (2017).
- (44) B. S. Huang and Y. G. Ma, Phys. Rev. C 101, no.3, 034615 (2020).
- (45) S. Zhang, Y. G. Ma, J. Chen, W. He and C. Zhong, Phys. Rev. C 95, 064904 (2017).
- (46) S. Zhang, Y. G. Ma, J. Chen, W. He and C. Zhong, Eur. Phys. J. A 54, 161 (2018).
- (47) D. K. Srivastava, J. Phys. G 35, 104026 (2008).
- (48) C. Gale, Y. Hidaka, S. Jeon, S. Lin, J. F. Paquet, R. D. Pisarski, D. Satow, V. V. Skokov and G. Vujanovic, Phys. Rev. Lett. 114, 072301 (2015).
- (49) R. Chatterjee, H. Holopainen, I. Helenius, T. Renk and K. J. Eskola, Phys. Rev. C 88, 034901 (2013).
- (50) C. Shen, U. W. Heinz, J. F. Paquet, I. Kozlov and C. Gale, Phys. Rev. C 91, no.2, 024908 (2015).
- (51) A. Monnai, Phys. Rev. C 90, no.2, 021901 (2014).
- (52) L. McLerran and B. Schenke, Nucl. Phys. A 929, 71-82 (2014).
- (53) F. M. Liu and S. X. Liu, Phys. Rev. C 89, no.3, 034906 (2014).
- (54) G. Basar, D. Kharzeev, D. Kharzeev and V. Skokov, Phys. Rev. Lett. 109, 202303 (2012).
- (55) K. Tuchin, Phys. Rev. C 87, no.2, 024912 (2013).
- (56) B. G. Zakharov, Eur. Phys. J. C 76, no.11, 609 (2016).
- (57) G. Vujanovic, J. F. Paquet, G. S. Denicol, M. Luzum, B. Schenke, S. Jeon and C. Gale, Nucl. Phys. A 932, 230-234 (2014).
- (58) H. Li, F. Liu, G. l. Ma, X. N. Wang and Y. Zhu, Phys. Rev. Lett. 106, 012301 (2011).
- (59) G. L. Ma, Phys. Lett. B 724, 278-282 (2013).
- (60) A. Adare et al. [PHENIX], Phys. Rev. Lett. 104, 132301 (2010).
- (61) J. Adam et al. [ALICE], Phys. Lett. B 754, 235-248 (2016).
- (62) A. Adare et al. [PHENIX], Phys. Rev. C 94, no.6, 064901 (2016).
- (63) S. Acharya et al. [ALICE], Phys. Lett. B 789, 308-322 (2019).
- (64) P. Dasgupta, R. Chatterjee, S. K. Singh and J. E. Alam, Phys. Rev. C 97, no.3, 034902 (2018).
- (65) C. Shen, Nucl. Part. Phys. Pro. 276?278, 72 (2016) .
- (66) C. Gale, J. F. Paquet, B. Schenke and C. Shen, Nucl. Phys. A 1005, 121863 (2021).
- (67) I. Iatrakis, E. Kiritsis, C. Shen and D. L. Yang, JHEP 04, 035 (2017).
- (68) R. Chatterjee, P. Dasgupta and D. K. Srivastava, Phys. Rev. C 96, no.1, 014911 (2017).
- (69) P. Dasgupta, R. Chatterjee and D. K. Srivastava, Phys. Rev. C 95, no.6, 064907 (2017).
- (70) P. Dasgupta, R. Chatterjee and D. K. Srivastava, J. Phys. G 47, no.8, 085101 (2020).
- (71) V. Y. Naboka, Y. M. Sinyukov and G. M. Zinovjev, Phys. Rev. C 97, no.5, 054907 (2018).
- (72) V. Y. Naboka, Y. M. Sinyukov and G. M. Zinovjev, Nucl. Phys. A 1000, 121843 (2020).
- (73) K. J. Eskola, H. Honkanen, H. Niemi, P. V. Ruuskanen and S. S. Rasanen, Nucl. Phys. A 774, 805-808 (2006).
- (74) M. Laine and Y. Schroder, Phys. Rev. D 73, 085009 (2006).
- (75) P. B. Arnold, G. D. Moore and L. G. Yaffe, JHEP 12, 009 (2001).
- (76) J. Ghiglieri, J. Hong, A. Kurkela, E. Lu, G. D. Moore and D. Teaney, JHEP 05, 010 (2013).
- (77) S. Turbide, R. Rapp and C. Gale, Phys. Rev. C 69, 014903 (2004).
- (78) G. L. Ma and X. N. Wang, Phys. Rev. Lett. 106, 162301 (2011).
- (79) P. Aurenche, M. Fontannaz, J. P. Guillet, E. Pilon and M. Werlen, Phys. Rev. D 73, 094007 (2006).
- (80) G. Giacalone, L. Yan, J. Noronha-Hostler and J. Y. Ollitrault, Phys. Rev. C 94, 014906 (2016).
- (81) J. Noronha-Hostler, L. Yan, F. G. Gardim and J. Y. Ollitrault, Phys. Rev. C 93, 014909 (2016).
- (82) L. Yan and J. Y. Ollitrault, Phys. Lett. B 744, 82-87 (2015).