Thermal Rate Coefficients for the Astrochemical Process C + CH+ C + H by Ring Polymer Molecular Dynamics
Abstract
Thermal rate coefficients for the astrochemical reaction C + CH+ C + H were computed in the temperature range 20-300 K by using novel rate theory based on ring polymer molecular dynamics (RPMD) on a recently published bond-order based potential energy surface and compared with previous Langevin capture model (LCM) and quasi-classical trajectory (QCT) calculations. Results show that there is a significant discrepancy between the RPMD rate coefficients and the previous theoretical results which can lead to overestimation of the rate coefficients for the title reaction by several orders of magnitude at very low temperatures. We argue that this can be attributed to a very challenging energy profile along the reaction coordinate for the title reaction, not taken into account in extenso by either the LCM or QCT approximation. In the absence of any rigorous quantum mechanical or experimental results, the computed RPMD rate coefficients represent state-of-the-art estimates to be included in astrochemical databases and kinetic networks.
keywords:
astrochemistry, atom diatom reaction, ring polymer molecular dynamics, thermal rate coefficientsSNS]
Scuola Normale Superiore,
Piazza dei Cavalieri 7,
56126 Pisa, Italia
CYI]Computation-based Science and Technology Research Center, Cyprus
Institute, 20
Kavafi Street, Nicosia 2121, Cyprus
\alsoaffiliation[MIT]Department of Chemical Engineering, Massachusetts Institute of Technology,
Cambridge, Massachusetts 02139, United States
{tocentry}
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/1159edab-1d26-4e24-b3c5-d7d1cf178b90/x1.png)
1 Introduction
One of the main goals of astrochemistry is to develop a complete chemical model of interstellar clouds giving an account of the nature and abundance of the molecules observed in the interstellar medium (ISM). This involves solving a large number of rate equations describing the changes in the concentration of chemical species as a result of processes—mainly gas-phase collisions or processes occurring on the surface of ice or dust particles 1—where hundreds of species act simultaneously as reactants and products. Clearly, it is crucial that the main properties of these processes, like the chemical rate coefficients, are estimated as accurately as possible.
Chemical rate coefficients for inclusion in kinetic models are made available through online kinetic databases such as the Ohio State University OSU database (available at \urlhttp://faculty.virginia.edu/ericherb/research.html), the KInetic Database for Astrochemistry KIDA 2 (available at \urlhttp://kida.obs.u-bordeaux1.fr/), and the University of Manchester Institute of Science and Technology (UMIST) Database for Astrochemistry UDfA 3, 4 (available at \urlhttp://udfa.ajmarkwick.net/). However, many of the estimates for the rates of the reactions presently available in these databases lack a sound foundation (being sometimes based on simplified models, or calculated by analogy with similar systems where the rate constant is known, or worked out by extrapolation to low temperature from high-temperature estimates) and a revision, possibly based on rigorous quantum dynamics techniques, is often in order.
The title reaction, belonging to the important class of astrochemical processes involving carbon and hydrogen atoms 5, 1, is among those reactions whose dynamics and kinetics have been little investigated. The lowest-energy reactive channel for collision of C + CH+ is
| C () + CH+ () C () + H () | (1) |
and involves two important molecular species: methylidyne cation, which is one of the firstly discovered (1941) molecules in the diffuse ISM 6 and whose abundance throughout the interstellar space still waits for an explanation (see on this Ref. 7 and references therein), and the dicarbon cation C, which was detected by the mass-spectroscopic sampling in comets Halley 8 and Giacobini–Zinner 9 and is incorporated in ion-molecule reactions for the production of hydrocarbons in interstellar clouds 10.
As shall be detailed further on, Reaction 1 is exoergic by about 1.6 eV and involves the barrierless formation of an intermediate C2H+ complex lying energetically lower than reactants by more than 6.7 eV. As is known, complex-forming reactions are difficult to characterize quantum mechanically 11. This is mainly because of the large phase space supported by the potential well(s), requiring a large basis or grid for converged quantum results. In addition, because of the attractive potential in the entrance or exit channel, a large number of partial waves is also needed. On the other side, experimental studies on ion-radical collisions such as Reaction 1 are also challenging due to the difficulties associated with making kinetic measurements on processes where both species are inherently unstable 12. As a consequence, the only available estimates for the thermal rate coefficient of this reaction have been for a long time those 13, 14 based on the simple Langevin capture model (LCM) 15, 16 and only very recently estimates obtained with quasi-classical trajectory (QCT) calculations on an ad hoc computed potential energy surface have been made available 17, 18. However, it is well-know that QCT has issues with zero-point energy (ZPE) leakage which can be expected to amplify in the case of very deep well 19, 20, 21. Therefore the reliability of the QCT results for the title reaction must be considered with caution.
Recently, an alternative approach for calculating thermal rate coefficients based on the classical isomorphism 22 between quantum system and its classical ring-polymeric replica (harmonically coupled classical copies of the original system in the form of a necklace) has been proposed 23 which is immune to many issues of QCT (as well as transition state rate theory (TST), though this aspect is more relevant to chemical reactions with an activation barrier). The method is called ring polymer molecular dynamics (RPMD) and approximates real time quantum dynamics by purely classical molecular dynamics of the ring polymer beads. While being purely classical molecular dynamics but in extended phase space, RPMD treats accurately and conserves in its real-time dynamics the quantum Boltzmann distribution and is rigorously independent of the dividing surface used to separate reactant(s) from product(s), which is particularly challenging to define when the reaction proceeds through a deep well. It also possesses numerous additional features that make this method very attractive for calculating thermal rate coefficients as observed during a comprehensive method assessment on various gas phase atom-diatom and polyatomic chemical reactions 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 19, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43 and outlined in the recent review of this method and its practical applications 44. It has been demonstrated that RPMD is accurate for prototype atom-diatom insertion chemical reactions 41, 42, 43 with deviations from the rigorous quantum dynamics results close to the convergence error (not exceeding 15 %). In particular, RPMD provided very accurate estimates of the rate coefficients for the O(1D) + H2 reaction, which, similar to the title reaction, exhibits a deep well ( 7.29 eV) and is exoergic ( 1.88 eV), 41 and for the C(1D) + H2 reaction at very low temperatures of astrochemical interest (H-transfer down to 50 K) 43. Accurate, consistent and predictable behavior of RPMD distinguishes it from all conventional methods used to calculate thermal rate coefficients 44.
Inspired by the previous success of the RPMD rate theory, in particular for barrierless reactions, we carried out the RPMD simulations of the title reaction at temperatures of astrophysical interest (20-300 K) and present them in this paper. The remaining sections of the paper are organized as follows. In Section 2 details on the potential energy surface and on ring polymer molecular dynamics are given. In Section 3 results are presented. In Section 4 some conclusions are drawn and perspectives for future work are outlined.
2 Methodology and computational details
2.1 Potential energy surface
The PES used for the RPMD calculations carried out in this work has already been described in Refs. 17 and 18. Here we briefly recall the methodology used to assemble it and describe its main features relevant to the dynamics.
The PES, in the form of a Fortran routine for use in dynamics programs and available upon request to the authors, \bibnoteThe PES is available upon request to S.R. (\urlinfo@srampino.com) was obtained by fitting the well known Aguado–Paniagua 46, 47 functional form to a set of 775 three-body and 20 two-body electronic energies obtained by second-order multi-reference perturbation theory (MRPT) in the ‘partially contracted’ PC-NEVPT2 scheme 48, 49. Configuration-space sampling (ie., the choice of the geometries at which the ab initio calculations were run) was performed according to the space-reduced bond-order (SRBO) approach recently published by one of us (S.R.) 50. In the SRBO scheme, use is made of opportunely defined diatomic bond-order (BO) variables (with being the diatom internuclear distance and its equilibrium value) where is relaxed so as to reach a desired ratio between the sampled attractive () and repulsive () regions of the diatom configuration space (see also Ref. 51). A proper tuning of and the adoption of regular grids in SRBO variables allows for a wise, process-oriented selection of geometries having built-in a force-based metric and thus providing a small, most informative set of electronic energies. \bibnoteA Fortran computer program for constructing SRBO grids is available at \urlhttp://www.srampino.com/code.html#Pestk or upon request to S.R.
The main features of the resulting PES concerning the title reaction are schematized in Fig. 1 and can be summarized as follows.
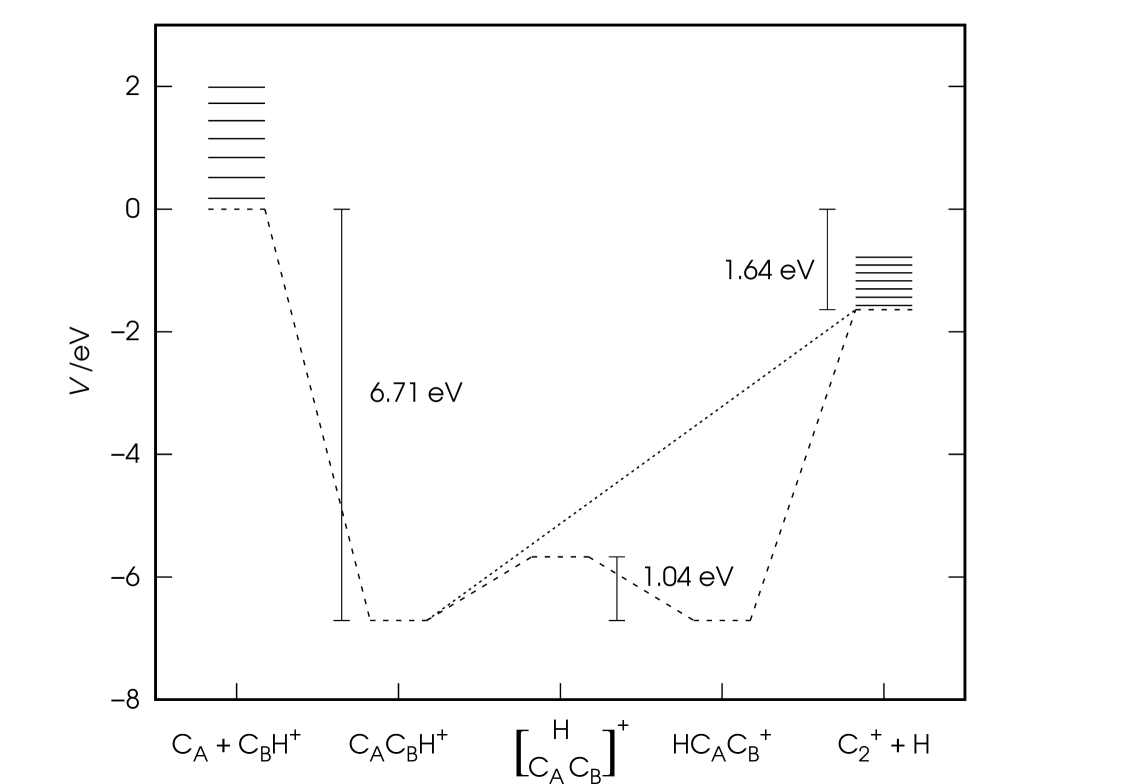
The reaction is exoergic by 1.64 eV and proceeds through the barrierless formation of a C2H+ intermediate. The energetically favoured reaction path is the collinear one with the reactant carbon CA atom approaching CBH+ from the carbon side (where labels A and B have been adopted to distinguish between the two carbon atoms) and leading to formation of a linear CACBH+ triatomic sitting at the bottom of a potential well which is as deep as 6.71 eV measured from the bottom of the reactants channel. At this point the system can either dissociate into products H and C or explore a second, identical potential well due to rotation of the hydrogen atom about the carbon-carbon bond. This last path involves overcoming a rotational barrier of 1.04 eV before forming the linear triatomic HCACB+ and further proceed to products. The reader is referred to Ref. 17 for a more detailed discussion on these alternative reaction paths and their effects on the QCT reaction dynamics. In Figure 1, the vibrational structure (first seven vibrational levels) of diatomics CH+ and C is also reported. When including zero-point energies (0.18 and 0.07 eV for the reactant and product diatom, respectively) the exoergicity of the title reaction amounts to 1.75 eV.
2.2 Ring polymer molecular dynamics
The RPMD calculations were performed using the RPMDrate code developed by one of us (Y.V.S.) 29. The computational procedure for calculating RPMD rate coefficients is well documented in the RPMDrate manual 29 and in the recent review of the RPMD rate theory and its practical applications.44 The reader is referred to the corresponding reference for more detail.
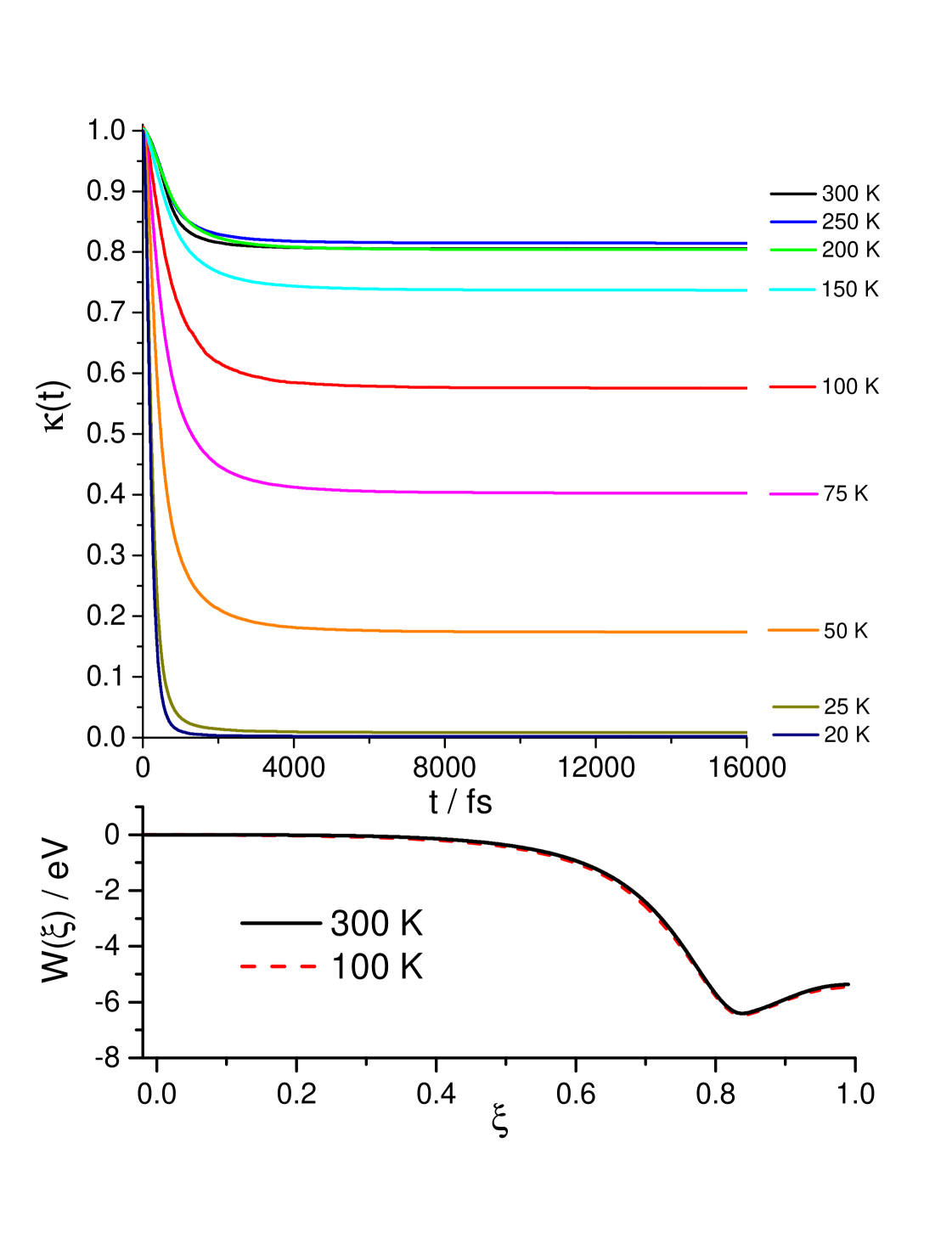
The ring polymer transmission coefficients at all temperatures of the present study (20-300 K) and potentials of mean force (free energy) at two representative temperatures (100 and 300 K) are depicted in Figure 2.
The simulation parameters are summarized in Table 1.
| Parameter | Reaction | Explanation |
| C + CH+ C + H | ||
| Command line parameters | ||
| Temp | 20; 25; 50; 75; 100; 150; 200; 250; 300 | Temperature (K) |
| Nbeads | 128 | Number of beads |
| Dividing surface parameters | ||
| 15 | Dividing surface parameter (distance) | |
| 1 | Number of forming and breaking bonds | |
| 1 | Number of equivalent product channels | |
| C(CH+) | (-1.09 Å, 0.00 Å, 0.00 Å) | Cartesian coordinates (x, y, z) |
| H(CH+) | (0.00 Å, 0.00 Å, 0.00 Å) | of the intermediate geometry |
| C | (1.27 Å, 0.00 Å, 0.00 Å) | |
| Thermostat | ’Andersen’ | Thermostat option |
| Biased sampling parameters | ||
| 7(111)a | Number of windows | |
| -0.05 | Center of the first window | |
| 0.01 | Window spacing step | |
| 0.01 (1.05) | Center of the last window | |
| 0.0001 | Time step (ps) | |
| 2.72 | Umbrella force constant ((T/K) eV) | |
| 200 | Number of trajectories | |
| 20 | Equilibration period (ps) | |
| 100 | Sampling period in each trajectory (ps) | |
| Total number of sampling points | ||
| Potential of mean force calculation | ||
| 0.00 | Start of umbrella integration | |
| 0.0031a,b | End of umbrella integration | |
| 5000 | Number of bins | |
| Recrossing factor calculation | ||
| 0.0001 | Time step (ps) | |
| 20 | Equilibration period (ps) in the constrained (parent) | |
| trajectory | ||
| 300000 | Total number of unconstrained (child) trajectories | |
| 2 | Sampling increment along the parent trajectory (ps) | |
| 50 | Number of child trajectories per one | |
| initially constrained configuration | ||
| 16 | Length of child trajectories (ps) | |
We found that 128 ring polymer beads were sufficient to converge the RPMD rate coefficients at all temperatures. The RPMD treats the atoms as distinguishable but because the title reaction is the C-to-C transfer the nuclear spin statistics is expected to play negligible role even at the lowest temperature (T = 20 K). The remaining simulation parameters are similar to those used in the previous RPMD studies of insertion chemical reactions 41, 42, 43 but with two distinctions. First, umbrella integration is terminated near reactants as the title reaction exhibits very deep well at the free energy profile (see lower panel of Fig. 2) and further propagation may only lead to enhancing the ring polymer recrossing dynamics which, in its turn, leads to poorer convergence of the final RPMD rate coefficients. (For the title reaction, we haven’t observed any tiny free-energy barrier before the entrance into the C2H+ well.) Second, the ring polymer recrossing dynamics is propagated up to 16 ps ( in Table 1) which, to our knowledge is the longest real-time dynamics ever taken into account in the RPMD studies of chemical reactions. This is again due to the presence of a very deep well along the reaction coordinate. Figure 2 shows that the free energy profile is practically temperature-independent but the transmission coefficients significantly decrease with decreasing the temperature. Note that at very low temperatures the recrossing dynamics is enhanced for the title reaction leading to very small plateau values which were challenging to converge. In future studies of such chemical reactions at low temperatures, RPMD can be coupled with the parallel replica dynamics approach 53.
3 Results
The RPMD thermal rate coefficients are compared with the previous QCT ones in Table 2 and are plotted in Figure 3, which also includes the LCM estimate.
| /K | /cm3s-1 | |
|---|---|---|
| QCT | RPMD | |
| 20 | 8.83 | 1.08 |
| 25 | 9.32 | 5.48 |
| 50 | 1.07 | 1.49 |
| 75 | 1.14 | 4.15 |
| 100 | 1.18 | 6.72 |
| 150 | 1.23 | 1.05 |
| 200 | 1.25 | 1.31 |
| 250 | 1.27 | 1.48 |
| 300 | 1.28 | 1.61 |
aQCT values taken from Ref.18. Note that QCT values of at 25 and 75 K were obtained by linear interpolation of the available neighbouring values (24 and 26 K and 70 and 80 K, respectively).
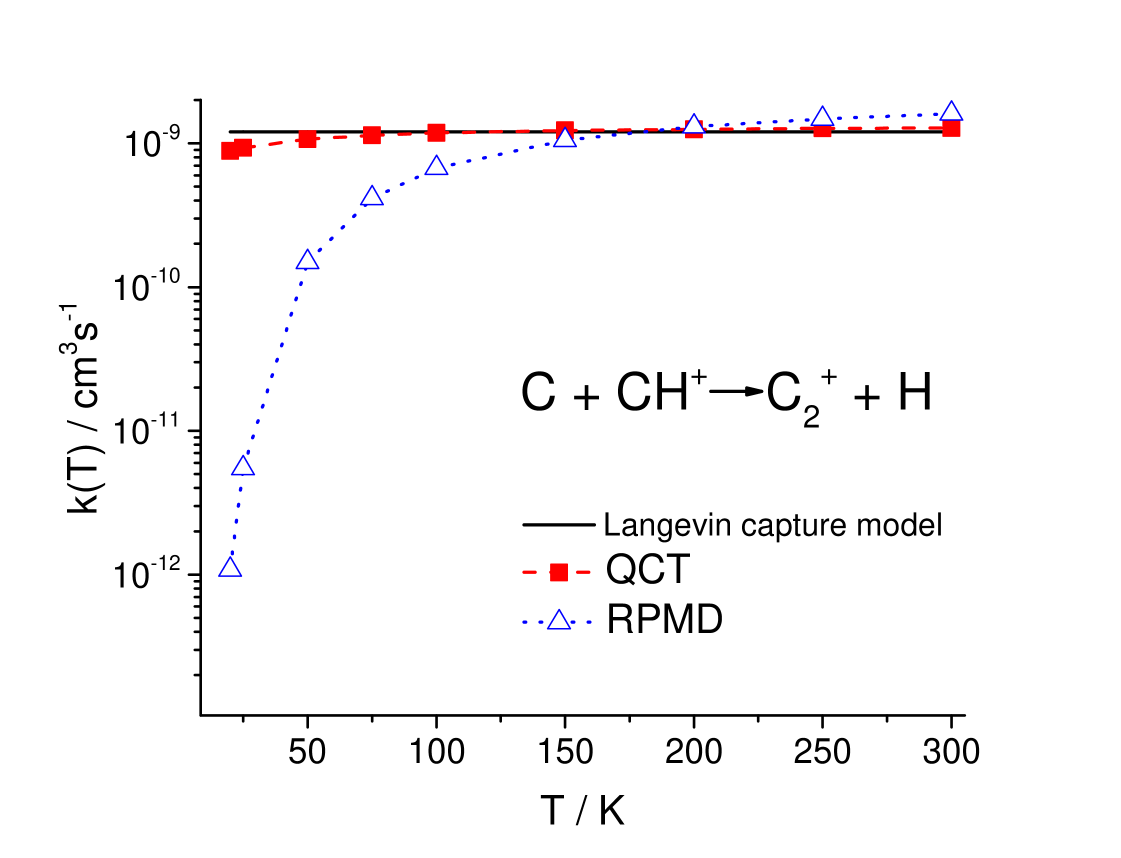
Figure 3 shows that the QCT (red squares) and RPMD (blue triangles) thermal rate coefficients are lower than the Langevin estimate (black solid line) at the lowest temperatures, and that both tend to increase with increasing getting to cross the Langevin value in the temperature interval between 100 and 200 K. However, despite this qualitative similarity in the temperature dependence, QCT and RPMD results differ substantially, especially as the temperature goes down to 20 K. In fact, whereas the QCT and RPMD curves cross each other at about 200 K and at the highest considered temperature (300 K) both the QCT and RPMD results agree with the LCM estimate within approximately 25 %, at 20 K the discrepancy between QCT and RPMD results attains several orders of magnitude. It is worth recalling here that QCT does not take into account the change in ZPE along the reaction coordinate and that the problem with ZPE can be particularly significant in the case of barrierless reactions as the title one with very deep well and complex profile of the minimum energy path as depicted in Figure 1. The QCT trajectories exiting the potential well may in fact violate the ZPE and lead to substantial erroneous increase of the rate coefficients 19, 20, 21.
As mentioned in the Introduction, thermal rate coefficients for use in astrochemical kinetic networks are made available through dedicated databases such as the already quoted OSU, KIDA and UDfA. Thermal rate coefficients are therein provided in the form of a set of parameters expressing their temperature dependence via popular parametrized formulations. Rather than the original Arrhenius equation
| (2) |
(with being the pre-exponential factor, the activation energy, and the gas constant) the Arrhenius–Kooij formula 54 (also known to chemists as modified Arrhenius equation 55 and allowing for a temperature dependence of the pre-exponential factor)
| (3) |
is adopted in astrochemical kinetic networks. In the already quoted Ref. 18, we also investigated the suitability of the so-called ‘deformed Arrhenius’ equation recently proposed by Aquilanti and Mundim56, 57
| (4) |
to account for deviations from the Arrhenius behaviour. We found therein that indeed the temperature dependence of the QCT thermal rate coefficients for the same reaction analyzed in this paper better conforms to the ‘Aquilanti–Mundim’ law.
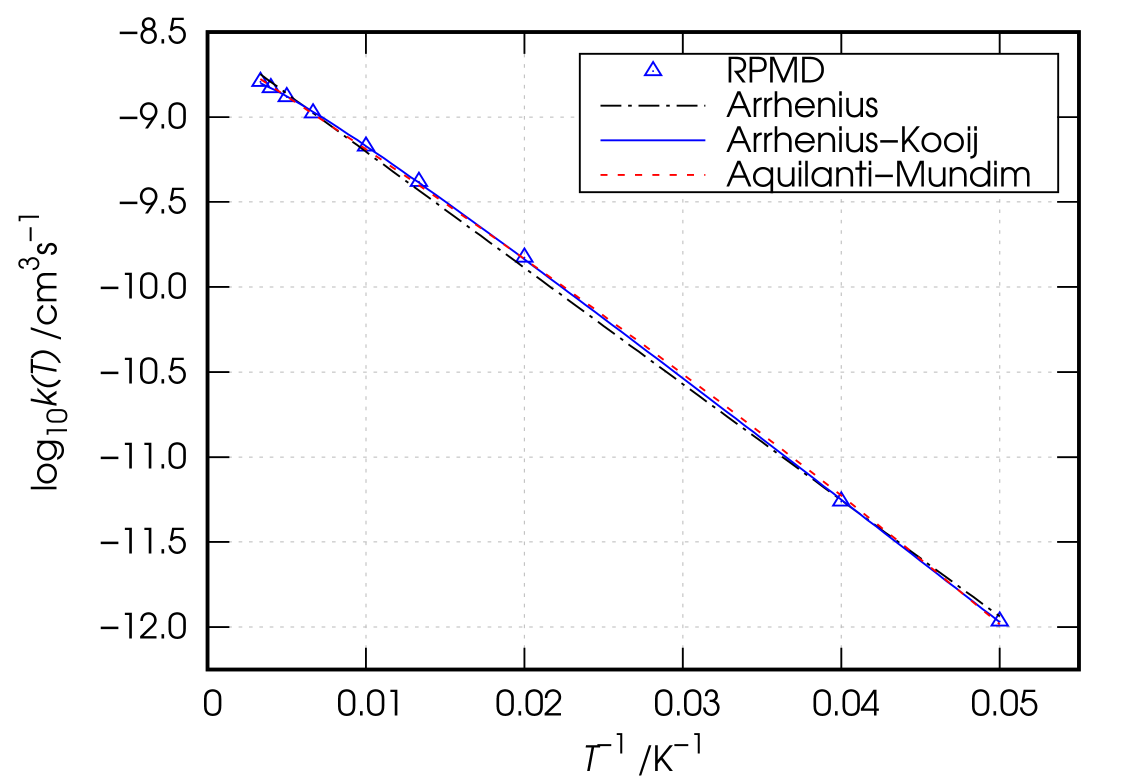
For the sake of comparison and to the purpose of providing more reliable estimates for the rates of the title process to be included in astrochemical kinetic networks, we performed the non-linear fits of Eqs. 2-4 to the computed RPMD thermal rate coefficient in the temperature range 20-300 K to determine the related best-fitting parameters. Results of the fitting procedures are summarized in Table 3, including values of and correlation coefficients. The Arrhenius, Arrhenius–Kooij and Aquilanti–Mundim best-fitting curves are also shown in Fig. 4 as dashed-dotted black line, solid blue line and dashed red line, respectively, for a comparison with the computed RPMD values (blue triangles). According the present RPMD calculations, the thermal rate coefficients for the title reaction display substantially Arrhenius behaviour with the Arrhenius–Kooij and Aquilanti–Mundim best-fitting curves excellently reproducing the computed data (correlation coefficient ).
4 Conclusions and perspectives
In this paper we use ring polymer molecular dynamics (RPMD) to compute thermal rate coefficients for reaction C + CH+ C + H in the temperature range 20-300 K on a recently published potential energy surface. Results are compared with previous estimates based on Langevin capture model (LCM) and quasi-classical trajectory (QCT) calculations. Non-linear fits of the computed RPMD data are also carried out using several parametrized formulations of and the related best-fitting parameters are given for inclusion in astrochemical databases. In the absence of rigorous quantum dynamics or experimental results, the present RPMD calculations are expected to provide the most accurate available estimates for the thermal rates of the title reaction to be used in astrochemical kinetic networks.
In a previous work of ours 18, it has been shown that QCT calculations of the rate coefficients for this reaction lead to a deviation from the LCM value as the temperature is decreased from the room one to the astrochemical diapason. The QCT thermal rate coefficient at 10 K resulted, in fact, lower than the LCM estimate by a factor of two. However, the present results suggest that even the QCT calculations substantially overestimate the rate of C formation (and, consequently, CH+ consumption) at low temperatures leading to an error of several orders of magnitude at 20 K. Accordingly, the present results also partially address the already mentioned issue of the unexplained observed abundance of methylidyne cation throughout the interstellar medium. Though in this respect reactions of CH+ with atomic and molecular hydrogen are undoubtedly more decisive than the reaction with atomic carbon, the present results show that the destruction route of CH+ is erroneously enhanced in kinetic models using either LCM or QCT estimates for the process considered in this paper.
The title reaction exhibits a very complex energy profile along the reaction coordinate as shown in Figure 1. As is known, proper treatment of the zero-point energy along the reaction coordinate is the Achilles’ heel of many approximations including QCT. RPMD is immune to this issue as well as it possesses several other advantages over conventional approaches for calculating rate coefficients 44, especially for astrochemical elementary reactions (with either deep well 43 or barrier 32 along the reaction coordinate), where quantum mechanical effects of nuclear motions play a crucial role. We hope therefore that RPMD will find wide application in improving astrochemical kinetic databases in the future.
S.R. thanks the European Research Council for funding through the European Union’s Seventh Framework Programme (FP/2007-2013) / ERC Grant Agreement n. [320951] and Prof. V. Barone for useful discussion. Y.V.S. thanks the European Regional Development Fund and the Republic of Cyprus for support through the Research Promotion Foundation (Project Cy-Tera NEA / /0308/31).
References
- Herbst 2001 Herbst, E. The chemistry of interstellar space. Chemical Society Reviews 2001, 30, 168–176
- Wakelam et al. 2012 Wakelam, V.; Herbst, E.; Loison, J.-C.; Smith, I. W. M.; Chandrasekaran, V.; Pavone, B.; Adams, N. G.; Bacchus-Montabonel, M.-C.; Bergeat, A.; Béroff, K. et al. A KInetic Database for Astrochemistry (KIDA). The Astrophysical Journal, Supplement Series 2012, 199, 21 (19), see http://kida.obs.u-bordeaux1.fr, Accessed October 9, 2015
- Woodall et al. 2007 Woodall, J.; Agundez, M.; Markwick-Kemper, A. J.; Millar, T. J. The UMIST database for astrochemistry 2006. Astronomy & Astrophysics 2007, 466, 1197–1204
- McElroy et al. 2013 McElroy, D.; Walsh, C.; Markwick, A. J.; Cordiner, M. A.; Smith, K.; Millar, T. J. The UMIST database for astrochemistry 2012. Astronomy & Astrophysics 2013, 550, A36
- Solomon and Klemperer 1972 Solomon, P. M.; Klemperer, W. The Formation of Diatomic Molecules in Interstellar Clouds. The Astrophysical Journal 1972, 178, 389–422
- Douglas and Herzberg 1941 Douglas, A. E.; Herzberg, G. Note on CH+ in Interstellar Space and in the Laboratory. The Astrophysical Journal 1941, 94, 381
- Myers et al. 2015 Myers, A. T.; McKee, C. F.; Li, P. S. The CH+ abundance in turbulent, diffuse molecular clouds. Monthly Notices of the Royal Astronomical Society 2015, 453, 2747–2758
- Krankowsky et al. 1986 Krankowsky, D.; Lämmerzahl, P.; Herrwerth, I.; Woweries, J.; Eberhardt, P.; Dolder, U.; Herrmann, U.; Schulte, W.; Berthelier, J. J.; Illiano, J. M. et al. In situ gas and ion measurements at comet Halley. Nature 1986, 321, 326–329
- Coplan et al. 1987 Coplan, M. A.; Ogilvie, K. W.; A’Hearn, M. F.; Bochsler, P.; Geiss, J. Ion composition and upstream solar wind observations at comet Giacobini-Zinner. Journal of Geophysical Research: Space Physics 1987, 92, 39–46
- Winnewisser 1981 Winnewisser, G. Cosmo- and Geochemistry; Topics in Current Chemistry; Springer Berlin Heidelberg, 1981; Vol. 99; pp 39–71
- Guo 2012 Guo, H. Quantum dynamics of complex-forming bimolecular reactions. International Reviews in Physical Chemistry 2012, 31, 1–68
- Smith 2011 Smith, I. W. Laboratory Astrochemistry: Gas-Phase Processes. Annual Review of Astronomy and Astrophysics 2011, 49, 29–66
- Woon and Herbst 2009 Woon, D. E.; Herbst, E. Quantum Chemical Predictions of the Properties of Known and Postulated Neutral Interstellar Molecules. The Astrophysical Journal Supplement Series 2009, 185, 273–288
- Wakelam et al. 2010 Wakelam, V.; Smith, I.; Herbst, E.; Troe, J.; Geppert, W.; Linnartz, H.; Öberg, K.; Roueff, E.; Agúndez, M.; Pernot, P. et al. Reaction Networks for Interstellar Chemical Modelling: Improvements and Challenges. Space Science Reviews 2010, 156, 13–72
- Langevin 1905 Langevin, P. Annales de chimie et de physique 1905, 5, 245
- Gioumousis and Stevenson 1958 Gioumousis, G.; Stevenson, D. P. Reactions of Gaseous Molecule Ions with Gaseous Molecules. V. Theory. The Journal of Chemical Physics 1958, 29, 294–299
- Pacifici et al. 2016 Pacifici, L.; Pastore, M.; Garcia, E.; Laganà, A.; Rampino, S. A dynamics investigation of the C + CH+ C + H reaction on an ab initio bond-order like potential. The Journal of Physical Chemistry A 2016, 120, 5125–5135
- Rampino et al. 2016 Rampino, S.; Pastore, M.; Garcia, E.; Pacifici, L.; Laganà, A. On the temperature dependence of the rate coefficient of formation of C from C + CH+. Monthly Notices of the Royal Astronomical Society 2016, 460, 2368–2375
- de Tudela et al. 2014 de Tudela, R. P.; Suleimanov, Y. V.; Menendez, M.; Castillo, J. F.; Aoiz, F. J. A Ring Polymer Molecular Dynamics Study of the Cl + O3 Reaction. Phys. Chem. Chem. Phys. 2014, 16, 2920–2927
- Varandas 1994 Varandas, A. J. C. A Novel Non-Active Model to Account for the Leak of Zero-Point Energy in Trajectory Calculations. Application to H + O2 Reaction near Threshold. Chem. Phys. Lett. 1994, 225, 18–27
- Guo 2012 Guo, H. Quantum Dynamics of Complex-Forming Bimolecular Reactions. Int. Rev. Phys. Chem. 2012, 31, 1–68
- Chandler and Wolynes 1981 Chandler, D.; Wolynes, P. G. Exploiting the isomorphism between quantum theory and classical statistical mechanics of polyatomic fluids. The Journal of Chemical Physics 1981, 74, 4078–4095
- Craig and Manolopoulos 2005 Craig, I. R.; Manolopoulos, D. E. Chemical reaction rates from ring polymer molecular dynamics. The Journal of Chemical Physics 2005, 122, 084106
- Collepardo-Guevara et al. 2009 Collepardo-Guevara, R.; Suleimanov, Y. V.; Manolopoulos, D. E. Bimolecular Reaction Rates from Ring Polymer Molecular Dynamics. J. Chem. Phys. 2009, 130, 174713
- Collepardo-Guevara et al. 2010 Collepardo-Guevara, R.; Suleimanov, Y. V.; Manolopoulos, D. E. Erratum: "Bimolecular Reaction Rates from Ring Polymer Molecular Dynamics" [J. Chem. Phys.130, 174713 (2009)]. J. Chem. Phys. 2010, 133, 049902
- Suleimanov et al. 2011 Suleimanov, Y. V.; Collepardo-Guevara, R.; Manolopoulos, D. E. Bimolecular Reaction Rates from Ring Polymer Molecular Dynamics: Application to H + CH4 H2 + CH3. J. Chem. Phys. 2011, 134, 044131
- Pérez de Tudela et al. 2012 Pérez de Tudela, R.; Aoiz, F. J.; Suleimanov, Y. V.; Manolopoulos, D. E. Chemical Reaction Rates from Ring Polymer Molecular Dynamics: Zero Point Energy Conservation in Mu + H2 MuH + H. J. Phys. Chem. Lett. 2012, 3, 493–497
- Suleimanov et al. 2013 Suleimanov, Y. V.; de Tudela, R. P.; Jambrina, P. G.; Castillo, J. F.; Saez-Rabanos, V.; Manolopoulos, D. E.; Aoiz, F. J. A Ring Polymer Molecular Dynamics Study of the Isotopologues of the H + H2 Reaction. Phys. Chem. Chem. Phys. 2013, 15, 3655–3665
- Suleimanov et al. 2013 Suleimanov, Y. V.; Allen, J. W.; Green, W. H. RPMDrate: Bimolecular Chemical Reaction Rates from Ring Polymer Molecular Dynamics. Comp. Phys. Comm. 2013, 184, 833–840
- Allen et al. 2013 Allen, J. W.; Green, W. H.; Li, Y.; Guo, H.; Suleimanov, Y. V. Communication: Full Dimensional Quantum Rate Coefficients and Kinetic Isotope Effects from Ring Polymer Molecular Dynamics for a Seven-Atom Reaction OH + CH4 CH3 + H2O. J. Chem. Phys. 2013, 138, 221103
- Li et al. 2013 Li, Y.; Suleimanov, Y. V.; Li, J.; Green, W. H.; Guo, H. Rate Coefficients and Kinetic Isotope Effects of the X + CH4 CH3 + HX (X = H, D, Mu) Reactions from Ring Polymer Molecular Dynamics. J. Chem. Phys. 2013, 138, 094307
- Pérez de Tudela et al. 2014 Pérez de Tudela, R.; Suleimanov, Y. V.; Richardson, J. O.; Sé1ez Ré1banos, V.; Green, W. H.; Aoiz, F. J. Stress Test for Quantum Dynamics Approximations: Deep Tunneling in the Muonium Exchange Reaction D + HMu DMu + H. J. Phys. Chem. Lett. 2014, 5, 4219–4224
- Gonzalez-Lavado et al. 2014 Gonzalez-Lavado, E.; Corchado, J. C.; Suleimanov, Y. V.; Green, W. H.; Espinosa-Garcia, J. Theoretical Kinetics Study of the O() + CH4/CD4 Hydrogen Abstraction Reaction: The Role of Anharmonicity, Recrossing Effects, and Quantum Mechanical Tunneling. J. Phys. Chem. A 2014, 118, 3243–3252
- Espinosa-Garcia et al. 2014 Espinosa-Garcia, J.; Fernandez-Ramos, A.; Suleimanov, Y. V.; Corchado, J. C. Theoretical Kinetics Study of the F() + NH3 Hydrogen Abstraction Reaction. J. Phys. Chem. A 2014, 118, 554–560
- Li et al. 2014 Li, Y.; Suleimanov, Y. V.; Green, W. H.; Guo, H. Quantum Rate Coefficients and Kinetic Isotope Effect for the Reaction Cl + CH4 HCl + CH3 from Ring Polymer Molecular Dynamics. J. Phys. Chem. A 2014, 118, 1989–1996
- Meng et al. 2015 Meng, Q.; Chen, J.; Zhang, D. H. Communication: Rate Coefficients of the H + CH4 H2 + CH3 Reaction from Ring Polymer Molecular Dynamics on a Highly Accurate Potential Energy Surface. J. Chem. Phys. 2015, 143, 101102
- Suleimanov and Espinosa-Garcia 2016 Suleimanov, Y. V.; Espinosa-Garcia, J. Recrossing and Tunneling in the Kinetics Study of the OH + CH4 H2O + CH3 Reaction. The Journal of Physical Chemistry B 2016, 120, 1418–1428
- Arseneau et al. 2016 Arseneau, D. J.; Fleming, D. G.; Li, Y.; Li, J.; Suleimanov, Y. V.; Guo, H. Rate Coefficient for the 4He + CH4 Reaction at 500 K: Comparison between Theory and Experiment. The Journal of Physical Chemistry B 2016, 120, 1641–1648
- Meng et al. 2016 Meng, Q.; Chen, J.; Zhang, D. H. Ring polymer molecular dynamics fast computation of rate coefficients on accurate potential energy surfaces in local configuration space: Application to the abstraction of hydrogen from methane. The Journal of Chemical Physics 2016, 144
- Zuo et al. 2016 Zuo, J.; Li, Y.; Guo, H.; Xie, D. Rate Coefficients of the HCl + OH Cl + H2O Reaction from Ring Polymer Molecular Dynamics. The Journal of Physical Chemistry A 2016, 120, 3433–3440, PMID: 27149243
- Li et al. 2014 Li, Y.; Suleimanov, Y. V.; Guo, H. Ring-Polymer Molecular Dynamics Rate Coefficient Calculations for Insertion Reactions: X + H2 HX + H (X = N, O). J. Phys. Chem. Lett. 2014, 5, 700–705
- Suleimanov et al. 2014 Suleimanov, Y. V.; Kong, W. J.; Guo, H.; Green, W. H. Ring-Polymer Molecular Dynamics: Rate Coefficient Calculations for Energetically Symmetric (Near Thermoneutral) Insertion Reactions (X + H2) HX + H(X = C(), S()). J. Chem. Phys. 2014, 141, 244103
- Hickson et al. 2015 Hickson, K. M.; Loison, J.-C.; Guo, H.; Suleimanov, Y. V. Ring-Polymer Molecular Dynamics for the Prediction of Low-Temperature Rates: An Investigation of the C(1D) + H2 Reaction. The Journal of Physical Chemistry Letters 2015, 6, 4194–4199, PMID: 26538033
- Suleimanov et al. 2016 Suleimanov, Y. V.; Aoiz, F. J.; Guo, H. Chemical Reaction Rate Coefficients from Ring Polymer Molecular Dynamics: Theory and Practical Applications. The Journal of Physical Chemistry A 2016, 120, http://dx.doi.org/10.1021/acs.jpca.6b07140
- 45 The PES is available upon request to S.R. (\urlinfo@srampino.com)
- Aguado and Paniagua 1992 Aguado, A.; Paniagua, M. A new functional form to obtain analytical potentials of triatomic molecules. The Journal of Chemical Physics 1992, 96, 1265–1275
- Aguado et al. 1998 Aguado, A.; Tablero, C.; Paniagua, M. Global fit of ab initio potential energy surfaces I. Triatomic systems. Computer Physics Communications 1998, 108, 259–266
- Angeli et al. 2002 Angeli, C.; Cimiraglia, R.; Malrieu, J.-P. -electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants. The Journal of Chemical Physics 2002, 117, 9138–9153
- Angeli et al. 2007 Angeli, C.; Pastore, M.; Cimiraglia, R. New perspectives in multireference perturbation theory: the -electron valence state approach. Theoretical Chemistry Accounts 2007, 117, 743–754
- Rampino 2016 Rampino, S. Configuration-Space Sampling in Potential Energy Surface Fitting: A Space-Reduced Bond-Order Grid Approach. The Journal of Physical Chemistry A 2016, 120, 4683–4692
- Rampino and Laganà 2012 Rampino, S.; Laganà, A. Bond order uniform grids for quantum reactive scattering. International Journal of Quantum Chemistry 2012, 112, 1818–1828
- 52 A Fortran computer program for constructing SRBO grids is available at \urlhttp://www.srampino.com/code.html#Pestk or upon request to S.R.
- Lu et al. 2016 Lu, C.-Y.; Perez, D.; Voter, A. F. Accelerating ring-polymer molecular dynamics with parallel-replica dynamics. The Journal of Chemical Physics 2016, 144
- Kooij 1893 Kooij, D. M. Über die Zersetzung des Gasförmigen Phosphorwasserstoffs. Zeitschrift für Physikalische Chemie, Abteilung B 1893, 12, 155–161
- 55 Laidler, K. A glossary of terms used in chemical kinetics, including reaction dynamics (IUPAC Recommendations 1996). Pure and Applied Chemistry 68, 149–192
- Aquilanti et al. 2010 Aquilanti, V.; Mundim, K. C.; Elango, M.; Kleijn, S.; Kasai, T. Temperature dependence of chemical and biophysical rate processes: Phenomenological approach to deviations from Arrhenius law. Chemical Physics Letters 2010, 498, 209 – 213
- Aquilanti et al. 2012 Aquilanti, V.; Mundim, K. C.; Cavalli, S.; De Fazio, D.; Aguilar, A.; Lucas, J. M. Exact activation energies and phenomenological description of quantum tunneling for model potential energy surfaces. The F + H2 reaction at low temperature. Chemical Physics 2012, 398, 186 – 191, Chemical Physics of Low-Temperature Plasmas (in honour of Prof Mario Capitelli)