Threshold phenomena for random discrete structures
1 Erdős-Rényi model
To begin, we briefly introduce a model of random graphs. Recall that a graph is a mathematical structure that consists of vertices (nodes) and edges.
Roughly speaking, a random graph in this article means that, given a vertex set, the existence of each potential edge is decided at random. We will specifically focus on the Erdős-Rényi random graph (denoted by ), which is defined as follows.
Consider vertices that are labelled from 1 to .
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/ef29875c-0efd-4734-baa1-f856c53cffc7/n_verts.png)
Observe that on those vertices, there are potentially edges, that is, the edges labelled . Given a probability , include each of the potential edges with probability , where the choice of each edge is made independently from the choices of the other edges.
Example 1.1.
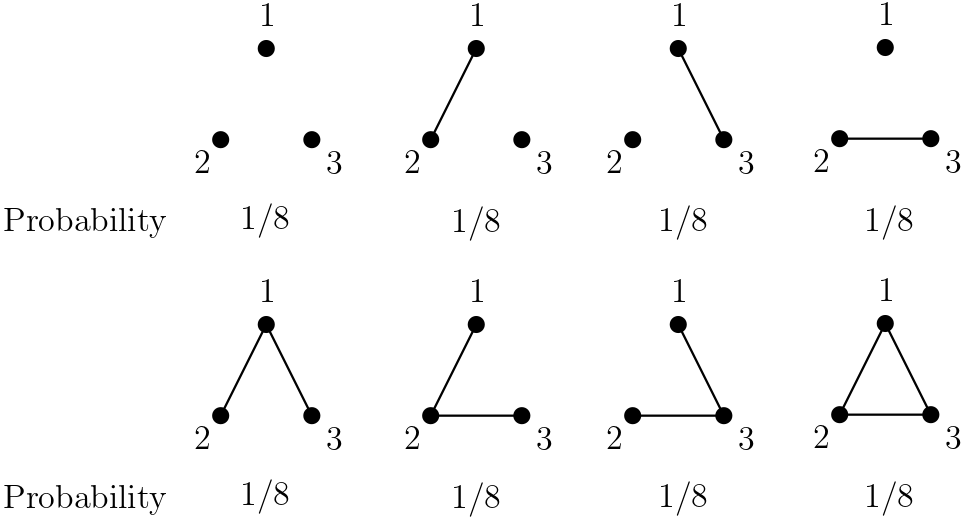
As a toy example of the Erdős-Rényi random graph, let’s think about what looks like when and the value of varies. First, if , then has the probability distribution as in Figure 2 defined on the collection of eight graphs. Observe that each graph is equally likely (since each potential edge is present with probability independently).
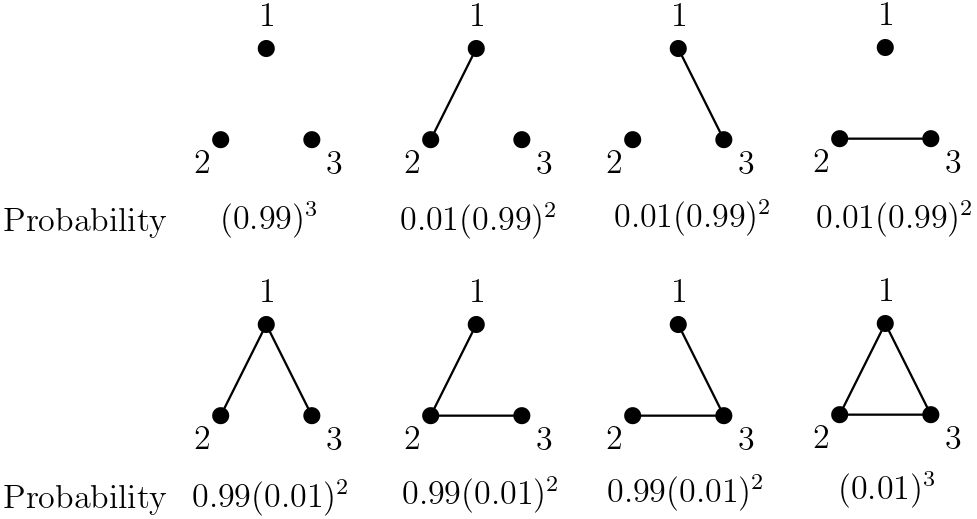
Of course, we will have a different probability distribution if we change the value of . For example, if is closer to 0, say 0.01, then has the distribution as in Figure 3, where sparser graphs are more likely (as expected). On the other hand, if is closer to 1, then denser graphs will be more likely.
In reality, when we consider , is a large (yet finite) number that tends to infinity, and is usually a function of that tends to zero as . For example, , , etc.
As we saw in Example 1.1, a random graph is a random variable with a certain probability distribution (as opposed to a fixed graph) that depends on the values of and . Assuming is given, the structure of changes as the value of changes, and in order to understand , we ask questions about the structure of such as
| What’s the probability that is connected? |
or
| What’s the probability that is planar? |
Basically, for any property of interest, we can ask
| What’s the probability that satisfies property ? |
In those questions, usually we are interested in understanding the typical structure/behavior of . Observe that, unless or , there is always a positive probability that all of the edges in are absent, or all of them are present (see Examples 1.2, 1.3). But in this article, we would rather ignore such extreme events that happen with a tiny probability, and focus on properties that possesses with a probability close to 1.
We often use languages and tools from probability theory to describe/understand behaviors of . Below we discuss some very basic examples.
We will write if as .
Example 1.2.
One important object in graph theory is the complete graph, a graph with all the potential edges present. The complete graph on vertices is denoted by .
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/ef29875c-0efd-4734-baa1-f856c53cffc7/K_n.png)
We can easily imagine that, unless is very close to , it is extremely unlikely that is complete. Indeed,
(since we want all the edges present), which tends to 0 unless is of order at most .
Example 1.3.
Similarly, we can compute the probability that is ”empty” (let’s denote this by ) meaning that no edges are present.111By the definition, has vertices as a default. The probability for this event is
When is small, is approximately , so the above computation tells us that
Example 1.4.
How many edges does typically have? The natural first step to answer this question is computing the expected number of edges in . Using linearity of expectation,
Remark 1.5.
For example, if , then the expected number of edges in is . But does this really imply that typically has about edges? The answer to this question is related to the fascinating topic of ”concentration of a probability measure.” We will very briefly discuss this topic in Example 2.5.
Example 1.6.
Similarly, we can compute the expected number of triangles (the complete graph ) in .
The above computation tells us that
from which we can conclude that is typically triangle-free if . (If the expectation tends to 0, then there is little chance that contains a triangle.)
Remark 1.7.
On the contrary, we cannot conclude that typically contains many triangles for from the above expectation computation. Just think about a lottery of the prize money dollars with the chance of winning , to see that a large expectation does not necessarily imply a high chance of the occurence of an event. In general, showing that a desired structure typically exists in is a very challenging task, and this became a motivation for the Kahn–Kalai Conjecture that we will discuss in the latter sections.
2 Threshold phenomena
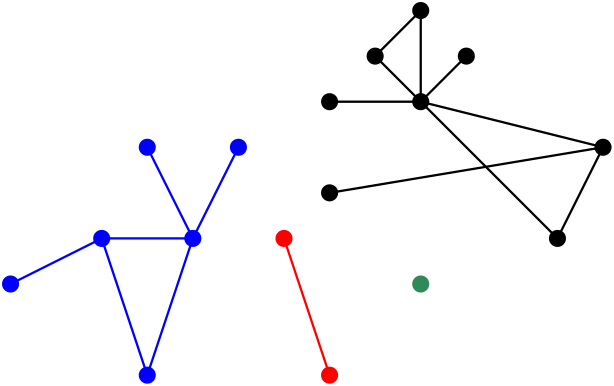
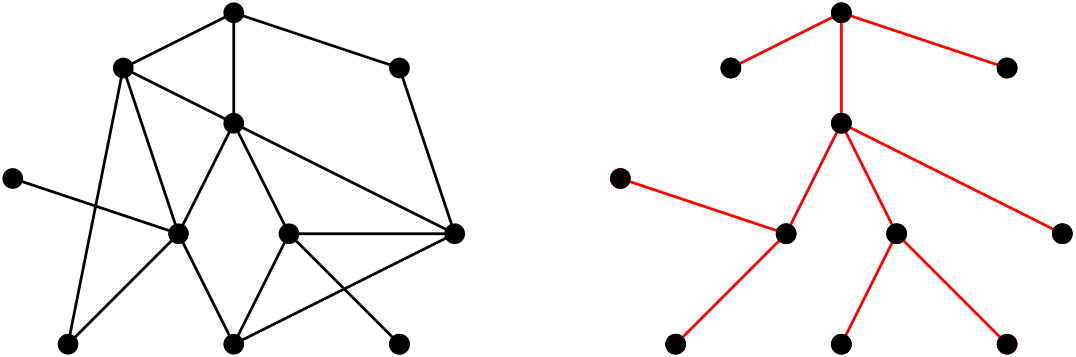
One striking thing about is that appearance and disappearance of certain properties are abrupt. Probably one of the most well-known examples that exhibit threshold phenomena of is appearance of the giant component. A component of a graph is a maximal connected subgraph. For example, the graph in Figure 4 consists of four components, and the size (the number of vertices) of each component is and .
For , observe that, when , the size of a largest component of is 1; in this case all of the edges are absent with probability 1, so each of the components is an isolated vertex. On the other hand, when , is the complete graph with probability 1, so the size of its largest component is .

Then what if is strictly between and ?
Question 2.1.
What’s the (typical) size of a largest component in ?
Of course, one would naturally guess that as increases from to , the typical size of a largest component in would also increase from 1 to . But what is really interesting here is that there is a ”sudden jump” in this increment.
In the following statement and everywhere else, with high probability means that the probability that the event under consideration occurs tends to 1 as .
Theorem 2.2 (Erdős-Rényi [6]).
For any , the size of a largest component of is
with high probability, where depend only on .
The above theorem says that if is ”slightly smaller” than , then typically all of the components of are very small (note that is much smaller than the number of vertices, ).
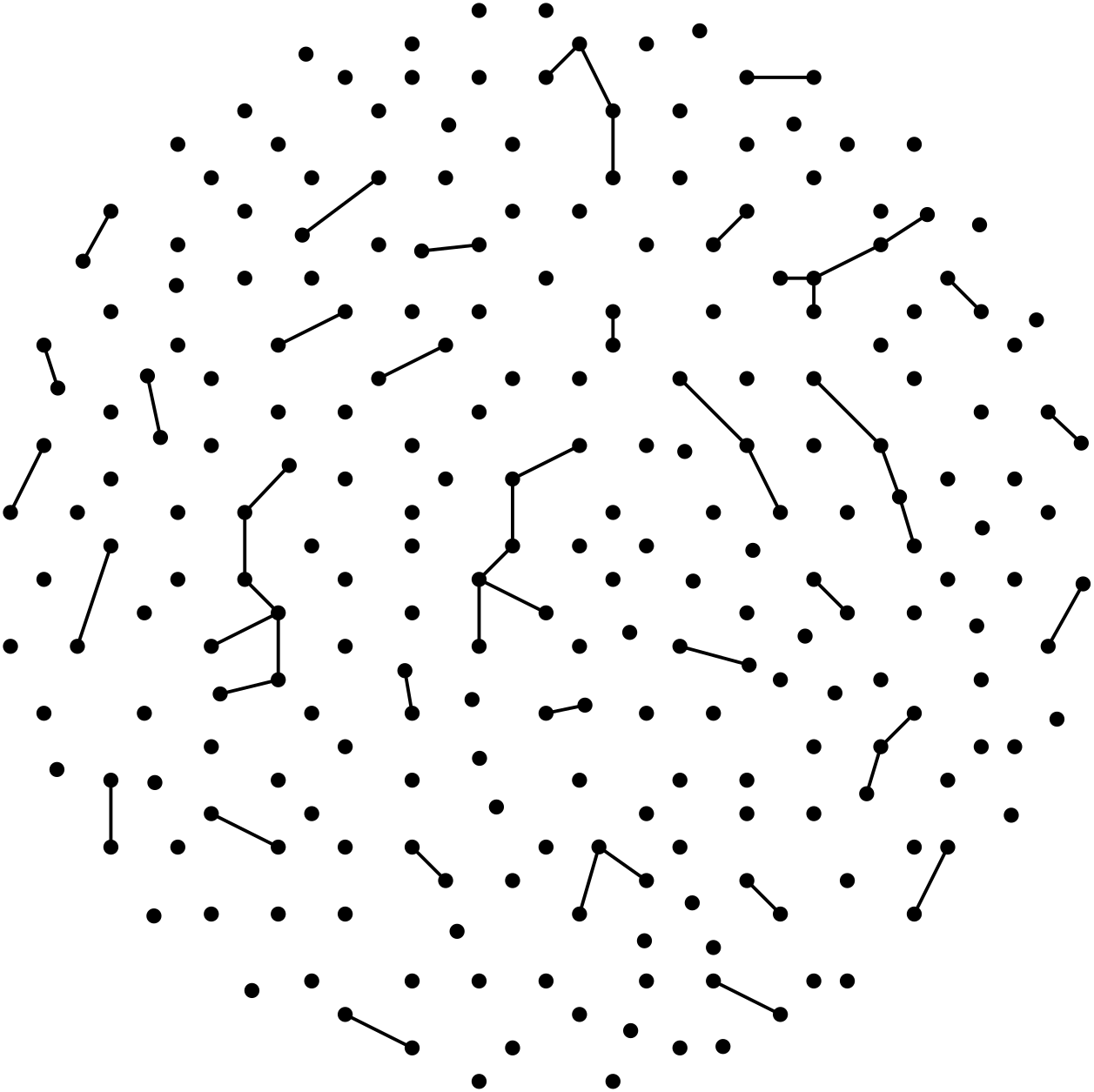
On the other hand, if is ”slightly larger” than , then the size of a largest component of is as large as linear in . It is also well-known that all other components are very small (at most of order ), and this unique largest component is called the giant component.

So around the value , the giant component ”suddenly” appears, and therefore the structure of also drasitically changes. This is one example of the threshold phenomena that exhibits, and the value is a threshold function for of having the giant component. (The formal definition of a threshold function is given in Definition 2.3. See also the definition of the threshold in Section 5.)
The abrupt appearance of the giant component of is just one instance of vast threshold phenomena for random discrete structures. In this article, we will mostly deal with for the sake of concreteness, but there will be a brief discussion about a more general setting in Section 5.
Now we introduce the formal definition of a threshold function due to Erdős and Rényi. Recall that, in , all the vertices are labelled . A graph property is a property that is invariant under graph isomorphisms (i.e. relabelling the vertices), such as , , , etc. We use for a graph property, and denotes that has property .
Definition 2.3.
Given a graph property , we say that is a threshold function222By the definition, a threshold function is determined up to a constant factor thus not unique, but conventionally people also call this the threshold function. In this article, we will separately define the threshold in Section 5, which is distinguished from a threshold function. (or simply a threshold) for if
For example, is a threshold function for the existence of the giant component.
Note that it is not obvious at all whether a given graph property would admit a threshold function. Erdős and Rényi proved that many graph properties have a threshold function, and about 20 years later, Bollobás and Thomason proved that, in fact, there is a wide class of properties that admit a threshold function. In what follows, an increasing (graph) property is a property that is preserved under addition of edges. For example, connectivity is an increasing property, because if a graph is connected then it remains connected no matter what edges are additionally added.
Theorem 2.4 (Bollobas-Thomason [5]).
Every increasing property has a threshold function.
Now it immediately follows from the above theorem that all the properties that we have mentioned so far – connectivity, planarity333We can apply the theorem for non-planarity, which is an increasing property., having the giant component, etc. – have a threshold function (thus exhibit a threshold phenomenon). How fascinating it is!
On the other hand, knowing that a property has a threshold function does not tell us anything about the value of . So it naturally became a central interest in the study of random graphs to find a threshold function for various increasing properties. One of the most studied classes of increasing properties is subgraph containment, i.e., the question of for what , is likely/unlikely to contain a copy of the given graph. Figure 8 shows some of the well-known threshold functions for various subgraph containments (and that for connectivity).
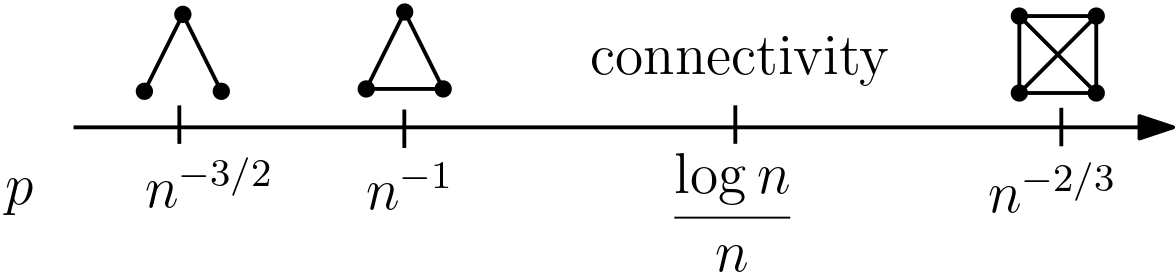
Example 2.5.
Figure 8 says that is a threshold function for the property . Recall from the definition of a threshold that this means
-
(i)
if then ; and
-
(ii)
if then
We have already justified (i) in Example 1.2 by showing that
However, showing (ii) is an entirely different story. As discussed in Remark 1.7, the fact that
does not necessarily imply that typically contains many triangles. Here we briefly describe one technique, which is called the second moment method, that we can use to show (ii): let be the number of triangles in , noting that then is a random variable. By showing that the variance of is very small, which implies that is ”concentrated around” , we can derive (from the fact that is huge) that typically the number of triangles in is huge. We remark that the second moment method is only a tiny part of the much broader topic of concentration of a probability measure.
We stress that, in general, finding a threshold function for a given increasing property is a very hard task. To illustrate this point, let’s consider one of the most basic objects in graph theory, a spanning tree – a tree that contains all of the vertices.
The question of finding a threshold function for of containing a spanning tree444This is equivalent to is connected. was one of the first questions studied by Erdős and Rényi. Already in their seminal paper [6], Erdős and Rényi showed that a threshold function for containing a spanning tree is . However, the difficulty of this problem immensely changes if we require to contain a specific (up to isomorphisms) spanning tree (or more broadly, a spanning graph555A spanning graph means a graph that contains all of the vertices). For example, one of the biggest open questions in this area back in 1960s was finding a threshold function for a Hamiltonian cycle (a cycle that contains all of the vertices).
This problem was famously solved by Pósa in 1976.
Theorem 2.6 (Pósa [16]).
A threshold function for to contain a Hamiltonian cycle is
Note that both threshold functions for contain any spanning tree and are of order , even though the latter is a stronger requirement. Later we will see (in the discussion that follows Example 4.6) that is actually an easy lower bound on both threshold functions. It has long been conjectured that for any spanning tree666More precisely, for any sequence of spanning trees with a constant maximum degree, its threshold function is of order . This conjecture was only very recently proved by Montgomery [14].
3 The Kahn–Kalai Conjecture: a preview
Henceforth, always denotes an increasing property.
In 2006, Jeff Kahn and Gil Kalai [12] posed an extremely bold conjecture that captures the location of threshold functions for any increasing properties. Its formal statement will be given in Conjecture 4.11 (graph version) and Theorem 5.7 (abstract version), and in this section we will give an informal description of this conjecture first. All of the terms not defined here will be discussed in the forthcoming sections.
Given an , we are interested in locating its threshold function, .777We switch the notation from to to emphasize its dependence on . But again, this is in general a very hard task.
Kahn and Kalai introduced another quantity which they named the expectation threshold and denoted by , which is associated with some sort of expectation calculations as its name indicates. By its definition (Definition 4.5),
| for any , |
and, in particular, is easy to compute for many interesting increasing properties . So provides an ”easy” lower bound on the hard parameter . A really fascinating part is that then Kahn and Kalai conjectured that is, in fact, bounded above by multiplied by some tiny quantity!
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/ef29875c-0efd-4734-baa1-f856c53cffc7/KKC.png)
So this conjecture asserts that, for any , is actually well-predicted by (much) easier !
4 Motivating examples
The conjecture of Kahn and Kalai is very strong, and even the authors of the conjecture wrote in their paper [12] that ”it would probably be more sensible to conjecture that it is not true.” The fundamental question that motivated this conjecture was:
Question 4.1.
What drives thresholds?
All of the examples in this section are carefully chosen to show the motivation behind the conjecture.
Recall that the definition of a threshold (Definition 2.3) doesn’t distinguish constant factors. So in this section, we will use the convenient notation , and to mean (respectively) , and up to constant factors. Finally, write for a threshold function for of containing a copy of , for notational simplicity.
Example 4.2.
Let be the graph in Figure 11. Let’s find .
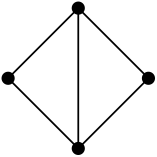
In Example 2.5, we observed that there is a connection between a threshold function and computing expectations. As we did in Examples 1.4 and 1.6,
where is because the number of ’s in is of order (since has four vertices), and is precisely (since has five edges). So we have
| (1) |
and let’s (informally) call the value
| ”the threshold for the expectation of .” |
This name makes sense since is where the expected number of ’s drastically changes. Note that (1) tells us that
so, by the definition of a threshold, we have
This way, we can always easily find a lower bound on for any graph .
What is interesting here is that, for in Figure 11, we can actually show that
using the second moment method (discussed in Example 2.5). This tells us a rather surprising fact that is actually equal to the threshold for the expectation of .
Dream. Maybe is always equal to the threshold for the expectation of for any graph ?
The next example shows that the above dream is too dreamy to be true.
Example 4.3.
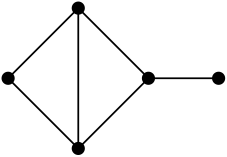
By repeating a similar computation as before, we have
so the threshold for the expectation of is . Again, this gives that
so we have . However, the actual threshold is , which is much larger than the lower bound.
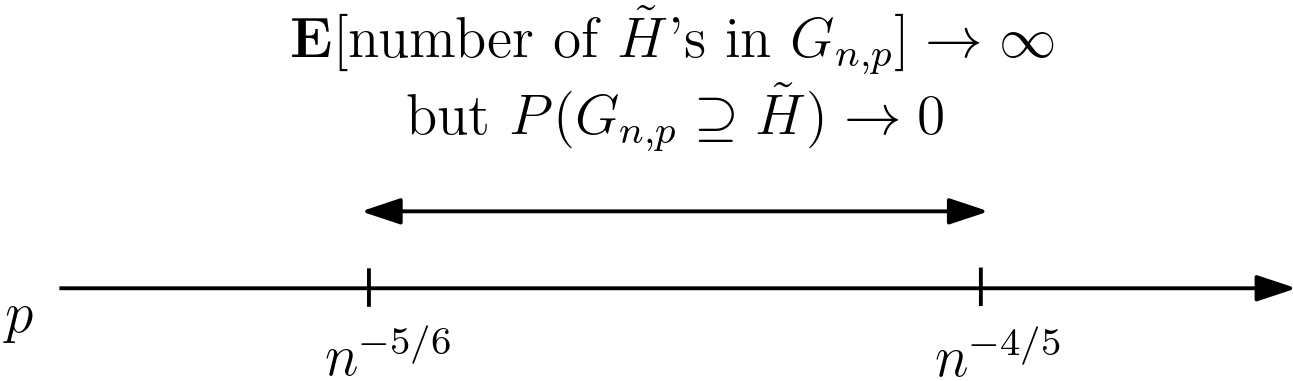
This is interesting, because Figure 13 tells us that when , contains a huge number of ”on average,” but still it is very unlikely that actually contains . What happens in this inverval?
Here is an explanation. Recall from Example 4.2 that if , then is unlikely to contain . But
| the absence of implies the absence of , |
because is a subgraph of !
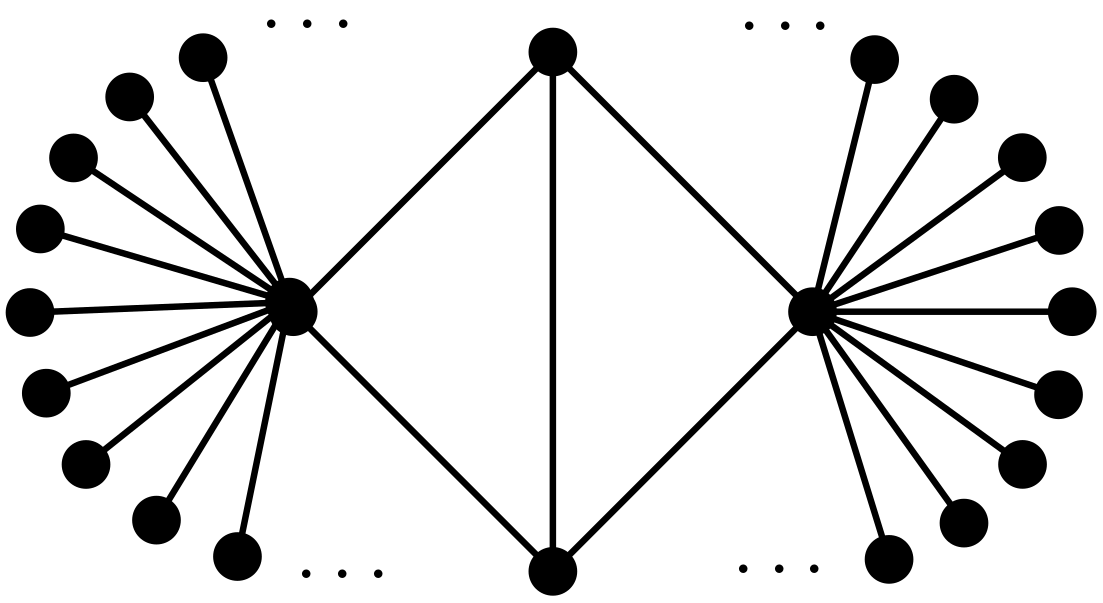
So when , it is highly unlikely that contains because it is already unlikely that contains . However, if happens to contain , then that copy of typically has lots of ”tails” as in Figure 14. This produces a huge number of copies of ’s in .
Maybe you have noticed the similarity between this example and the example of a lottery in Remark 1.7.
In Example 4.3, is not predicted by the expected number of , thus the Dream is broken. However, it still shows that is predicted by the expected number of some subgraph of , and, intriguingly, this holds true in general. To provide its formal statement, define the density of a graph by
The next theorem tells us the exciting fact that we can find by just looking at its densest subgraph, as long as is fixed.888For example, a Hamiltonian cycle is not a fixed graph, since it grows as grows.
Theorem 4.4 (Bollobás [4]).
For any fixed graph , is equal to the threshold for the expectation of the densest subgraph of .
For example, in Example 4.2, the densest subgraph of is itself, so is determined by the expectation of . This also determines in Example 4.3, since the densest subgraph of is again .
Motivated by the preceding examples and Theorem 4.4, we give a formal definition of the expectation threshold.
Definition 4.5 (Expectation threshold).
For any graph , the expectation threshold for is
Note that this gives a beautiful answer to Question 4.1 whenever is a property of containing a fixed graph.
Example 4.6.
Theorem 4.4 characterizes threshold functions for any fixed graphs. To extend our exploration, in this example we consider a graph that grows as grows. We say a graph is a matching if is a disjoint union of edges. is a perfect matching if is a matching that contains all the vertices. Write PM for perfect matching.
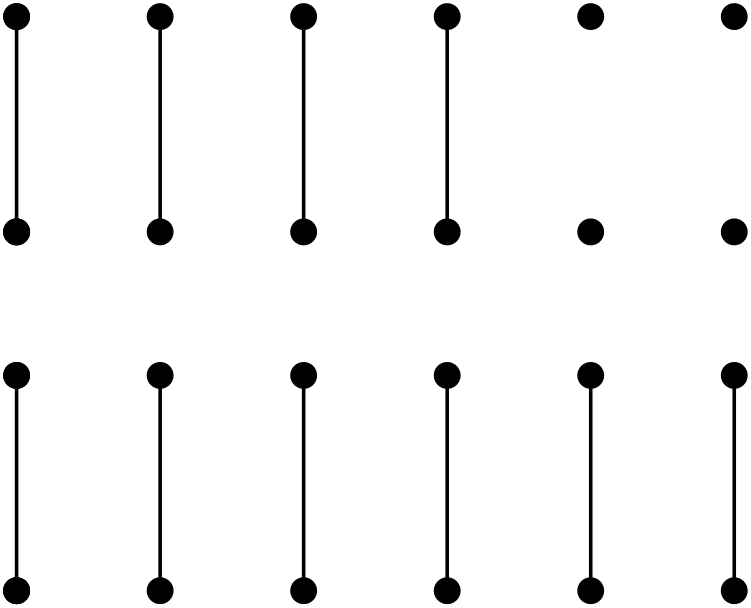
Keeping Question 4.1 in mind, let’s first check the validity of Theorem 4.4 to a perfect matching999We assume to avoid a trivial obstruction from having a perfect matching., which is not a fixed graph. By repeating a similar computation as before, we obtain that
which tends to if In fact, it is easy to compute (by considering all subgraphs of a perfect matching) that , so by (2),
However, unlike threshold functions for fixed graphs, is not equal to ; it was proved by Erdős and Rényi that
| (3) |

Notice that, in Figure 16, what happens in the gap is fundamentally different from that in Figure 13. When , contains huge numbers of PMs and all its subgraphs ”on average.” This means the absence of a subgraph of a PM is not the obstruction for from having a PM when . Then what happens here, and what’s the real obstruction?
It turned out, we have
for a very simple reason: the existence of an isolated vertex101010a vertex not contained in any edges in . It is well-known that if , then contains an isolated vertex with high probability (this phenomenon is elaborated in Example 4.7). Of course, if there is an isolated vertex in a graph, then this graph cannot contain a perfect matching.
So (3) says the very compelling fact that once is large enough that avoids isolated vertices, contains a perfect matching!
The existence of an isolated vertex in is essentially equivalent to the Coupon-collector’s Problem:
Example 4.7 (Coupon-collector).
Each box of cereal contains a random coupon, and there are different types of coupons. If all coupons are equally likely, then how many boxes of cereal do we (typically) need to buy to collect all coupons?
The well-known answer to this question is that we need to buy boxes of cereal. This phenomenon can be translated to in the following way: in , the vertices are regarded as coupons. If a vertex is contained in a (random) edge in , then that is regarded as being ”collected.” Note that if , then typically the number of edges in is , and then the Coupon-collector’s Problem says that there is typically an ”uncollected coupon,” which is an isolated vertex.
Observe that, in Example 4.6, the ”coupon-collector behavior” of provides another lower bound on , pushing up the first lower bound, , by . And it turned out that this second (better) lower bound is equal to the threshold.
| Lower bounds | Threshold | |
|---|---|---|
| Expectation threshold | ||
| Coupon collector | ||
Hitting time. Again, the existence of an isolated vertex in a graph trivially blocks this graph from containing any spanning subgraphs. In Example 4.6, we observed the compelling phenomenon that if is large enough that typically avoids isolated vertices, then for those , contains a perfect matching with high probability. Would this mean that, for , isolated vertices are the only barriers to the existence of spanning subgraphs?
To investigate this question, we consider a random process defined as below. Consider a sequence of graphs on vertices
where is obtained from by adding a random edge.

Then , the -th graph in this sequence, is the random variable that is uniformly distributed among all the graphs on vertices with edges. The next theorem tells us that, indeed, isolated vertices are the obstructions for a random graph to having a perfect matching.
Theorem 4.8 (Erdős-Rényi [7]).
Let denote the first time that contains no isolated vertices. Then, with high probability, contains a perfect matching.
We remark that Theorem 4.8 gives much more precise information about (back in setting). For example, Theorem 4.8 implies:
Theorem 4.9.
Let . Then
We observe a similar phenomenon for Hamiltonian cycles. Notice that in order for a graph to contain a Hamiltonian cycle, a minimum requirement is that every vertex is contained in at least two edges. The next theorem tells us that, again, this naive requirement is essentially the only barrier.
Theorem 4.10 (Ajtai-Komlós-Szemerédi [1], Bollobás [3]).
Let denote the first time that every vertex in is contained in at least two edges. Then, with high probability, contains a Hamiltonian cycle.
Returning to Question 4.1, so far we have established that there are two factors that affect threshold functions. We first observed that always gives a lower bound on . We then observed that, when it applies, the coupon-collector behavior of pushes up this expectational lower bound by . Conjecture 4.11 below dauntingly proposes that there are no other factors that affect thresholds.
Conjecture 4.11 (Kahn-Kalai [12]).
For any graph ,
Conjecture 4.11 is still wide open even after the ”abstract version” of this conjecture is proved. We close this section with a very interesting example in which lies strictly in between and . A triangle factor is a (vertex-) disjoint union of triangles that contains all the vertices.

The question of a threshold function for a triangle-factor111111or, more generally, a -factor for any fixed was famously solved by Johansson, Kahn, and Vu [10]. Observe that an obvious obstruction for a graph from having a triangle factor is the existence of a vertex that is not contained in any triangles. The result below is the hitting time version of [10], which is obtained by combining [11] and [9].
Theorem 4.12.
Let denote the first time that every vertex in is contained in at least one triangle. Then, with high probability, contains a triangle factor.
The above theorem implies that
5 The Expectation Threshold Theorem
The abstract version of the Kahn–Kalai Conjecture, which is the main content of this section, is recently proved in [15]. We remark that the discussion in this section is not restricted by the languages in graph theory anymore.
We introduce some more definitions for this general setting. Given a finite set , the -biased product probability measure, , on is defined by
We use for the random variable whose law is
In other words, is a ”-random subset” of , which means contains each element of with probability independently.
Example 5.1.
If , then
So is a special case of the random model .
We redefine increasing property in our new set-up. A property is a subset of , and is an increasing property if
Informally, a property is increasing if we cannot ”destroy” this property by adding elements. Note that in this new definition, is not required to possess the strong symmetry as in increasing graph properties; for example, there is no longer a requirement like ”invariant under graph isomorphisms.”
Observe that is a polynomial in , thus continuous. Furthermore, it is a well-known fact that is strictly increasing in unless (see Figure 20). For the rest of this section, we always assume .
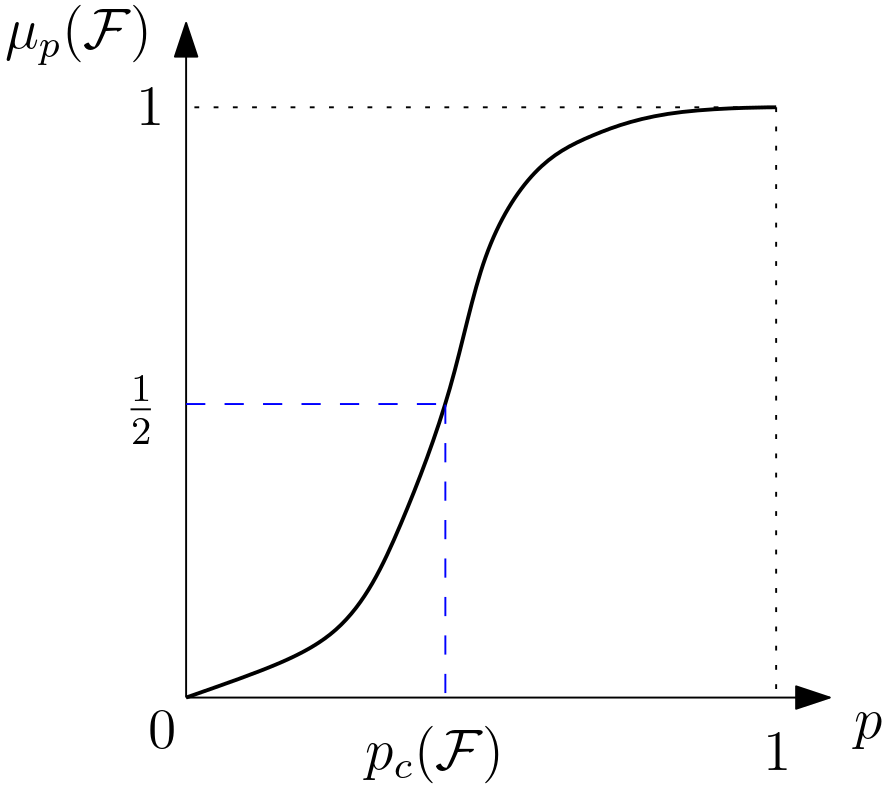
Because is continuous and strictly increasing in , there exists a unique for which . This is called the threshold for .
Remark 5.2.
The definition of does not require sequences. Incidentally, by Theorem 2.4, for any increasing graph property , is an (Erdős-Rényi) threshold function for .
For a general increasing property , the definition of is not applicable anymore. Kahn and Kalai introduced the following generalized notion of the expectation threshold, which is also introduced by Talagrand [17].
Definition 5.3.
Given a finite set and an increasing property , is the maximum of for which there exists satisfying the following two properties.
-
(a)
Each contains some member of .
-
(b)
.
A family that satisfies (a) is called a cover of .
Remark 5.4.
The next proposition says that still provides a lower bound on the threshold.
Proposition 5.5.
For any finite set and increasing property ,
Justification..
Write . By the definition of , it suffices to show that . We have
where the first inequality uses the fact that covers . ∎
For a graph , write for the increasing graph property of containing a copy of . The example below illustrates the relationship between and .
Example 5.6 (Example 4.3 revisited).
The above discussion shows that, for any (not necessarily fixed) graph ,
(whether is unknown). The abstract version of the Kahn–Kalai Conjecture is similar to its graph version, with replaced by . This is what’s proved in [15].
Theorem 5.7 (Park-Pham [15], conjectured in [12, 17]).
There exists a constant such that for any finite set and increasing property ,
where is the size of a largest minimal element of .
Theorem 5.7 is extremely powerful; for instance, its immediate consequences include historically difficult results such as the resolutions of Shamir’s Problem [10] and the ”Tree Conjecture” [14]. Here we just mention one smaller consequence:
Example 5.8.
Sunflower Conjecture, and ”fractional” Kahn-Kalai. The proof of Theorem 5.7 is strikingly easy given its powerful consequences. The approach is inspired by remarkable work of Alweiss, Lovett, Wu, and Zhang [2] on the Erdős-Rado Sunflower Conjecture, which seemingly has no connection to threshold phenomena. This totally unexpected connection was first exploited by Frankston, Kahn, Nayaranan, and the author in [8], where a ”fractional” version of the Kahn-Kalai conjecture (conjectured by Talagrand [17]) was proved, illustrating how two seemingly unrelated fields of mathematics can be nicely connected!
Note that is in theory hard to compute. For instance, in Example 4.3, we can estimate by finding with the maximum . On the other hand, to compute , we should in principle consider all possible covers of , which is typically not feasible. The good news is that there is a convenient way to find an upper bound on , which is often of the correct order. Namely, Talagrand [17] introduced a notion of fractional expectation threshold, , satisfying
for any increasing property He conjectured (and it was proved in [8]) that the (abstract) Kahn-Kalai Conjecture (now Theorem 5.7) holds with in place of . This puts us in linear programming territory: by LP duality, a bound () is essentially equivalent to existence of an ”-spread” probability measure on . In all applications of Theorem 5.7 to date, what is actually used to upper bound is an appropriately spread measure.121212The problem of constructing well-spread measure is getting growing attention now: see e.g. [13] for a start. So all these applications actually follow from the weaker Talagrand version.
We close this article with a very interesting conjecture of Talagrand [17] that would imply the equivalence of Theorem 5.7 and its fractional version:
Conjecture 5.9.
There exists a constant such that for any finite set and increasing property
Acknowledgement. The author is grateful to Jeff Kahn for his helpful comments.
References
- [1] M. Ajtai, J. Komlós and Szemerédi, The first occurrence of Hamilton cycles in random graphs, Annals of Discrete Mathematics, 27 (1985) 173-178. MR0821516
- [2] R. Alweiss, S. Lovett, K. Wu, and J. Zhang, Improved bounds for the sunflower lemma, Ann. of Math. (2) 194 (2021), no. 3, 795–815. MR4334977
- [3] B. Bollobás, The evolution of sparse graphs, Graph theory and combinatorics, Cambridge (1983), 35–57. MR0777163
- [4] B. Bollobás, Random Graphs, second ed., Cambridge Studies in Advanced Mathematics, vol. 73, Cambridge University Press, Cambridge (2001). MR1864966
- [5] B. Bollobás and A. Thomason, Threshold functions, Combinatorica 7 (1987), 35-38. MR0905149
- [6] P. Erdős and A. Rényi, On the evolution of random graphs, Publ Math Inst Hungar Acad Sci 5 (1960), 17-61. MR0125031
- [7] P. Erdős and A. Rényi, On the existence of a factor of degree one of a connected random graph, Acta. Math. Acad. Sci. Hungar. 17 (1966) 359-368. MR0200186
- [8] K. Frankston, J. Kahn, B. Narayanan, and J. Park, Thresholds versus fractional expectation-thresholds, Ann. of Math. (2) 194 (2021), no. 2, 475-495. MR4298747
- [9] A. Heckel, M. Kaufmann, N. Müller, and M. Pasch, The hitting time of clique factors, Preprint, arXiv 2302.08340
- [10] A. Johansson, J. Kahn, and V. Vu, Factors in random graphs, Random Structures Algorithms 33 (2008), 1–28. MR2428975
- [11] J. Kahn, Hitting times for Shamir’s problem, Transactions of the American Mathematical Society 375, no. 01 (2022), 627-668. MR4358678
- [12] J. Kahn and G. Kalai, Thresholds and expectation thresholds, Combin. Probab. Comput. 16 (2007), 495-502. MR2312440
- [13] D. Kang, T. Kelly, D. Kühn, A. Methuku, and D. Osthus Thresholds for Latin squares and Steiner triple systems: Bounds within a logarithmic factor, Transactions of the American Mathematical Society, to appear.
- [14] R. Montgomery, Spanning trees in random graphs, Adv. Math. 356 (2019), 106793, 92. MR3998769
- [15] J. Park and H. T. Pham, A proof of the Kahn–Kalai Conjecture, Journal of the American Mathematical Society, to appear.
- [16] L. Pósa, Hamiltonian circuits in random graphs, Discrete Math. 14 (1976), 359-364. MR0389666
- [17] M. Talagrand, Are many small sets explicitly small?, STOC’10 – Proceedings of the 2010 ACM International Symposium on Theory of Computing, 13-35, ACM, New York, 2010. MR2743011