Time-Aware Knowledge Representations of
Dynamic Objects with Multidimensional Persistence

Recurrent Neural Networks (RNNs) are the most successful deep learning techniques to model datasets with time-dependent variables (Lipton, Berkowitz, and Elkan 2015). Long-Short-Term Memory networks (LSTMs) addressed the prior RNN limitations in learning long-term dependencies by solving known issues with exploding and vanishing gradients (Yu et al. 2019), serving as basis for other improved RNN, such as Gate Recurrent Units (GRUs) (Dey and Salem 2017), Bidirectional LSTMs (BI_LSTM) (Wang, Yang, and Meinel 2018), and seq2seq LSTMs (Sutskever, Vinyals, and Le 2014). Despite the widespread adoption of RNNs in multiple applications (Xiang, Yan, and Demir 2020; Schmidhuber 2017; Shin and Kim 2020; Shewalkar, Nyavanandi, and Ludwig 2019; Segovia-Dominguez et al. 2021; Bin et al. 2018), RNNs are limited by the structure of the input data and can not naturally handle data-structures from manifolds and graphs, i.e. non-Euclidean spaces.

New methods on graph convolution-based methods overcome prior limitations of traditional GCN approaches, e.g. learning underlying local and global connectivity patterns (Veličković et al. 2018; Defferrard, Bresson, and Vandergheynst 2016; Kipf and Welling 2017). GCN handles graph-structure data via aggregation of node information from the neighborhoods using graph filters. Lately, there is an increasing interest in expanding GCN capabilities to the time series forecasting domain. In this context, modern approaches have reached outstanding results in COVID-19 forecasting, money laundering, transportation forecasting, and scene recognition (Pareja et al. 2020; Segovia Dominguez et al. 2021; Yu, Yin, and Zhu 2018; Yan, Xiong, and Lin 2018; Guo et al. 2019; Weber et al. 2019; Yao et al. 2018). However, a major drawback of these approaches is the lack of versatility as they assume a fixed graph-structure and rely on the existing correlation among spatial and temporal features.

Multipersistence (MP) is a highly promising approach to significantly improve the success of single parameter persistence (SP) in applied TDA, but the theory is not complete yet (Botnan and Lesnick 2022). Except for some special cases, the MP theory tends to suffer from the problem of the nonexistence of barcode decomposition because of the partially ordered structure of the index set $\{(\alpha_{i},\beta_{j})\}$. The existing approaches remedy this issue via the slicing technique by studying one-dimensional fibers of the multiparameter domain. However, this approach tends to lose most of the information the MP approach produces. Another idea along these lines is to use several such directions (vineyards), and produce a vectorization summarizing these SP vectorizations (Carrière and Blumberg 2020). However, again choosing these directions suitably and computing restricted SP vectorizations are computationally costly which restricts these approaches in many real-life applications. There are several promising recent studies in this direction (Botnan, Oppermann, and Oudot 2022; Vipond 2020), but these techniques often do not provide a topological summary that can readily serve as input to ML models. In this paper, we develop a highly efficient way to use the MP approach for time-dependent data and provide a multidimensional topological summary with TMP Vectorizations. We discuss the current fundamental challenges in the MP theory and the contributions of our TMP vectorizations in Section D.2.

Persistent homology (PH) is a mathematical machinery to capture the hidden shape patterns in the data by using algebraic topology tools. PH extracts this information by keeping track of the evolution of the topological features (components, loops, cavities) created in the data while looking at it using different resolutions. Here, we give basic background for PH in the graph setting. For further details, see (Dey and Wang 2022; Edelsbrunner and Harer 2010).

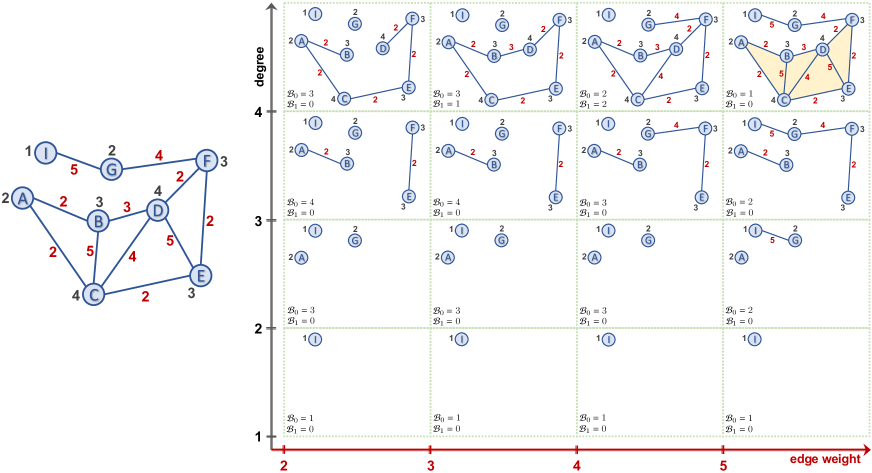
For a given graph $\mathcal{G}$, consider a nested sequence of subgraphs $\mathcal{G}^{1}\subseteq\ldots\subseteq\mathcal{G}^{N}=\mathcal{G}$. For each $\mathcal{G}^{i}$, define an abstract simplicial complex $\widehat{\mathcal{G}}^{i}$, $1\leq i\leq N$, yielding a filtration of complexes $\widehat{\mathcal{G}}^{1}\subseteq\ldots\subseteq\widehat{\mathcal{G}}^{N}$. Here, clique complexes are among the most common ones, i.e., clique complex $\widehat{\mathcal{G}}$ is obtained by assigning (filling with) a $k$-simplex to each complete $(k+1)$-complete subgraph in $\mathcal{G}$, e.g., a $3$-clique, a complete $3$-subgraph, in $\mathcal{G}$ will be filled with a $2$-simplex (triangle). Then, in this sequence of simplicial complexes, one can systematically keep track of the evolution of the topological patterns mentioned above. A $k$-dimensional topological feature (or $k$-hole) may represent connected components ($0$-hole), loops ($1$-hole) and cavities ($2$-hole). For each $k$-hole $\sigma$, PH records its first appearance in the filtration sequence, say $\widehat{\mathcal{G}}^{b_{\sigma}}$, and first disappearance in later complexes, $\widehat{\mathcal{G}}^{d_{\sigma}}$ with a unique pair $(b_{\sigma},d_{\sigma})$, where $1\leq b_{\sigma}<d_{\sigma}\leq N$ We call $b_{\sigma}$ the birth time of $\sigma$ and $d_{\sigma}$ the death time of $\sigma$. We call $d_{\sigma}-b_{\sigma}$ the life span of $\sigma$. PH records all these birth and death times of the topological features in persistence diagrams. Let $0\leq k\leq D$ where $D$ is the highest dimension in the simplicial complex $\widehat{\mathcal{G}}^{N}$. Then $k^{th}$ persistence diagram ${\rm{PD}_{k}}(\mathcal{G})=\{(b_{\sigma},d_{\sigma})\mid\sigma\in H_{k}(\widehat{\mathcal{G}}^{i})\mbox{ for }b_{\sigma}\leq i<d_{\sigma}\}$. Here, $H_{k}(\widehat{\mathcal{G}}^{i})$ represents the $k^{th}$ homology group of $\widehat{\mathcal{G}}^{i}$ which keeps the information of the $k$-holes in the simplicial complex $\widehat{\mathcal{G}}^{i}$. With the intuition that the topological features with a long life span (persistent features) describe the hidden shape patterns in the data, these persistence diagrams provide a unique topological fingerprint of $\mathcal{G}$.

As one can easily notice, the most important step in the PH machinery is the construction of the nested sequence of subgraphs $\mathcal{G}^{1}\subseteq\ldots\subseteq\mathcal{G}^{N}=\mathcal{G}$. For a given unweighted graph $\mathcal{G}=(\mathcal{V},E)$, the most common technique is to use a filtering function $f:\mathcal{V}\to\mathbb{R}$ with a choice of thresholds $\mathcal{I}=\{\alpha_{i}\}_{1}^{N}$ where $\alpha_{1}=\min_{v\in\mathcal{V}}f(v)<\alpha_{2}<\ldots<\alpha_{N}=\max_{v\in\mathcal{V}}f(v)$. For $\alpha_{i}\in\mathcal{I}$, let $\mathcal{V}_{i}=\{v_{r}\in\mathcal{V}\mid f(v_{r})\leq\alpha_{i}\}$. Let $\mathcal{G}^{i}$ be the induced subgraph of $\mathcal{G}$ by $\mathcal{V}_{i}$, i.e. $\mathcal{G}^{i}=(\mathcal{V}_{i},\mathcal{E}_{i})$ where $\mathcal{E}_{i}=\{e_{rs}\in\mathcal{E}\mid v_{r},v_{s}\in\mathcal{V}_{i}\}$. This process yields a nested sequence of subgraphs $\mathcal{G}^{1}\subset\mathcal{G}^{2}\subset\ldots\subset\mathcal{G}^{N}=\mathcal{G}$, called the sublevel filtration induced by the filtering function $f$. Choice of $f$ is crucial here, and in most cases, $f$ is either an important function from the domain of the data, e.g. amount of transactions or volume transfer, or a function defined from intrinsic properties of the graph, e.g. degree, betweenness. Similarly, for a weighted graph, one can use sublevel filtration on the weights of the edges and obtain a suitable filtration reflecting the domain information stored in the edge weights. For further details on different filtration types of networks, see (Aktas, Akbas, and El Fatmaoui 2019; Hofer et al. 2020).

In the previous section, we discussed the single-parameter persistence theory. The reason for the term ”single” is that we filter the data in only one direction $\mathcal{G}^{1}\subset\dots\subset\mathcal{G}^{N}=\mathcal{G}$. Here, the choice of direction is the key to extracting the hidden patterns from the observed data. For some tasks and data types, it is sufficient to consider only one dimension (or filtering function $f:\mathcal{V}\to\mathbb{R}$) (e.g., atomic numbers for protein networks) in order to extract the intrinsic data properties. However, often the observed data may have more than one direction to be analyzed (for example, in the case of money laundering detection on bitcoin, we may need to use both transaction amounts and numbers of transactions between any two traders). With this intuition, multiparameter persistence (MP) theory is suggested as a natural generalization of single persistence (SP).

In simpler terms, if one uses only one filtering function, sublevel sets induce a single parameter filtration $\widehat{\mathcal{G}}^{1}\subset\dots\subset\widehat{\mathcal{G}}^{N}=\widehat{\mathcal{G}}$. Instead, if one uses two or more functions, then it would enable us to study finer substructures and patterns in the data. In particular, let $f:\mathcal{V}\to\mathbb{R}$ and $g:\mathcal{V}\to\mathbb{R}$ be two filtering functions with very valuable complementary information of the network. Then, MP idea is presumed to produce a unique topological fingerprint combining the information from both functions. These pair of functions $f,g$ induces a multivariate filtering function $F:\mathcal{V}\mapsto\mathbb{R}^{2}$ with $F(v)=(f(v),g(v))$. Again, we can define a set of nondecreasing thresholds $\{\alpha_{i}\}_{1}^{m}$ and $\{\beta_{j}\}_{1}^{n}$ for $f$ and $g$ respectively. Then, $\mathcal{V}^{ij}=\{v_{r}\in V\mid f(v_{r})\leq\alpha_{i},g(v_{r})\leq\beta_{j}\}$, i.e. $\mathcal{V}^{ij}=F^{-1}((-\infty,\alpha_{i}]\times(-\infty,\beta_{j}])$. Then, let $\mathcal{G}^{ij}$ be the induced subgraph of $\mathcal{G}$ by $\mathcal{V}^{ij}$, i.e. the smallest subgraph of $\mathcal{G}$ containing $\mathcal{V}^{ij}$. Then, instead of a single filtration of complexes, we get a bifiltration of complexes $\{\widehat{\mathcal{G}}^{ij}\mid 1\leq i\leq m,1\leq j\leq n\}$. See Figure 2 (Appendix) for an explicit example.

As illustrated in Figure 2, we can imagine $\{\widehat{\mathcal{G}}^{ij}\}$ as a rectangular grid of size $m\times n$ such that for each $1\leq i_{0}\leq m$, $\{\widehat{G}^{i_{0}j}\}_{j=1}^{n}$ gives a nested (horizontal) sequence of simplicial complexes. Similarly, for each $1\leq j_{0}\leq n$, $\{\widehat{G}^{ij_{0}}\}_{i=1}^{m}$ gives a nested (vertical) sequence of simplicial complexes. By computing the homology groups of these complexes, $\{H_{k}(\mathcal{G}^{ij})\}$, we obtain the induced bigraded persistence module (a rectangular grid of size $m\times n$). Again, the idea is to keep track of the $k$-dimensional topological features via the homology groups $\{H_{k}(\widehat{\mathcal{G}}^{ij})\}$ in this grid. As detailed in Section D.2, because of the technical issues related to commutative algebra coming from the partially ordered structure of the multipersistence module, this MP approach has not been completed like SP theory yet, and there is a need to facilitate this promising idea effectively in real-life applications.

In this paper, for time-dependent data, we overcome this problem by using the naturally inherited special direction in the data: Time. By using this canonical direction in the multipersistence module, we bypass the partial ordering problem and generalize the ideas from single parameter persistence to produce a unique topological fingerprint of the data via MP. Our approach provides a general framework to utilize various vectorization forms defined for single PH and gives a multidimensional topological summary of the data.

While PH extracts hidden shape patterns from data as persistence diagrams (PD), PDs being a collection of points $\{(b_{\sigma},d_{\sigma})\}$ in $\mathbb{R}^{2}$ by itself are not very practical for statistical and machine learning purposes. Instead, the common techniques are by accurately representing PDs as kernels (Kriege, Johansson, and Morris 2020) or vectorizations (Ali et al. 2023). Single Persistence Vectorizations transform obtained PH information (PDs) into a function or a feature vector form which are much more suitable for ML tools. Common single persistence (SP) vectorization methods are Persistence Images (Adams et al. 2017), Persistence Landscapes (Bubenik 2015), Silhouettes (Chazal et al. 2014), and various Persistence Curves (Chung and Lawson 2022). These vectorizations define a single variable or multivariable functions out of PDs, which can be used as fixed size $1D$ or $2D$ vectors in applications, i.e $1\times m$ vectors or $m\times n$ vectors. For example, a Betti curve for a PD with $m$ thresholds can be written as $1\times m$ size vectors. Similarly, persistence images is an example of $2D$ vectors with the chosen resolution (grid) size. See the examples below and in Section D.1 for further details.

Finally, we define our Temporal MultiPersistence (TMP) framework for time-dependent data. In particular, by using the existing single-parameter persistence vectorizations, we produce multidimensional vectorization by effectively using the time direction in the multipersistence module. The idea is to use zigzag homology in the time direction and consider $d$-dimensional filtering for the other directions. This process produces $(d+1)$-dimensional vectorizations of the dataset. While the most common choice would be $d=1$ for computational purposes, we restrict ourselves to $d=2$ to give a general idea. The construction can easily be generalized to higher dimensions. Below and in Section D.1, we provide explicit examples of TMP Vectorizations. While we mainly focus on network data in this part, we give how to generalize TMP vectorizations to other types of data (e.g., point clouds, images) in Section D.3.

Again, let $\widetilde{\mathcal{G}}=\{\mathcal{G}_{1},\mathcal{G}_{2},\dots,\mathcal{G}_{T}\}$ be a sequence of weighted (or unweighted) graphs for time steps $t=1,\ldots,T$ with $\mathcal{G}_{t}=\{\mathcal{V}_{t},\mathcal{E}_{t},W_{t}$} as defined in Section 3. By using a filtering function $F_{t}:\mathcal{V}_{t}\to\mathbb{R}^{d}$ or weights, define a bifiltration for each $t_{0}$, i.e. $\{\mathcal{G}_{t_{0}}^{ij}\}$ for $1\leq i\leq m$ and $1\leq j\leq n$. For each fixed $i_{0},j_{0}$, consider the sequence $\{\mathcal{G}^{i_{0}j_{0}}_{1},\mathcal{G}_{2}^{i_{0}j_{0}},\dots,\mathcal{G}_{T}^{i_{0}j_{0}}\}$. This sequence of subgraphs induces a zigzag sequence of clique complexes as described in Section C.1:

$\displaystyle\widehat{\mathcal{G}}_{1}^{i_{0}j_{0}}\hookrightarrow\widehat{\mathcal{G}}^{i_{0}j_{0}}_{1.5}\hookleftarrow\widehat{\mathcal{G}}^{i_{0}j_{0}}_{2}\hookrightarrow\widehat{\mathcal{G}}^{i_{0}j_{0}}_{2.5}\hookleftarrow\widehat{\mathcal{G}}_{3}\hookrightarrow\dots\hookleftarrow\widehat{\mathcal{G}}^{i_{0}j_{0}}_{T}.$

Now, let $ZPD_{k}(\widetilde{\mathcal{G}}^{i_{0}j_{0}})$ be the induced zigzag persistence diagram. Let $\varphi$ represent an SP vectorization as described above, e.g. Persistence Landscape, Silhouette, Persistence Image, Persistence Curves. This means if $PD(\mathcal{G})$ is the persistence diagram for some filtration induced by $\mathcal{G}$, then we call $\varphi(\mathcal{G})$ is the corresponding vectorization for $PD(\mathcal{G})$ (see Figure 1 in Appendix F7). In most cases, $\varphi(\mathcal{G})$ is represented as functions on the threshold domain (Persistence curves, Landscapes, Silhouettes, Persistence Surfaces). However, the discrete structure of the threshold domain enables us to interpret the function $\varphi(\mathcal{G})$ as a $1D$-vector $\vec{\varphi}(\mathcal{G})$ (Persistence curves, Landscapes, Silhouettes) or $2D$-vector $\vec{\varphi}(\mathcal{G})$ (Persistence Images). See examples given below and in the Section D.1 for more details.

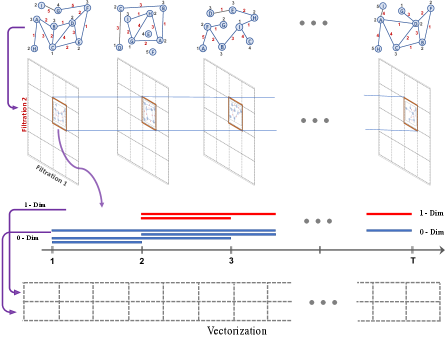
Now, let $\vec{\varphi}(\widetilde{\mathcal{G}}^{ij})$ be the corresponding vector for the zigzag persistence diagram $ZPD_{k}(\widetilde{\mathcal{G}}^{ij})$. Then, for any $1\leq i\leq m$ and $1\leq j\leq n$, we have a ($1D$ or $2D$) vector $\vec{\varphi}(\widetilde{\mathcal{G}}^{ij})$. Now, define the induced TMP Vectorization $\mathbf{M}_{\varphi}$ as the corresponding tensor $\mathbf{M}_{\varphi}^{ij}=\vec{\varphi}(\widetilde{\mathcal{G}}^{ij})$ for $1\leq i\leq m$ and $1\leq j\leq n.$

In particular, if $\vec{\varphi}$ is a $1D$-vector of size $1\times k$, then $\mathbf{M}_{\varphi}$ would be a $3D$-vector (rank-$3$ tensor) with size $m\times n\times k$. if $\vec{\varphi}$ is a $2D$-vector of size $k\times r$, then $\mathbf{M}_{\varphi}$ would be a rank-$4$ tensor with size $m\times n\times k\times r$. In the examples below, we provide explicit constructions for $\mathbf{M}_{\varphi}$ for the most common SP vectorizations $\varphi$.

While we describe TMP Vectorizations for $d=2$, in most applications, $d=1$ would be preferable for computational purposes. Then if the preferred single persistence (SP) vectorization $\varphi$ produces $1D$-vector (say size $1\times r$), then induced TMP Vectorization would be a $2D$-vector $M_{\varphi}$ (a matrix) of size $m\times r$ where $m$ is the number of thresholds for the filtering function used, e.g. $f:\mathcal{V}_{t}\to\mathbb{R}$. These $m\times r$ matrices provide unique topological fingerprints for each time-dependent dataset $\{\mathcal{G}_{t}\}_{t=1}^{T}$. These multidimensional fingerprints are produced by using persistent homology with two-dimensional filtering where the first dimension is the natural direction time $t$, and the second dimension comes from the filtering function $f$.

Here, we discuss explicit constructions of two examples of TMP vectorizations. As we mentioned above, the framework is very general, and it can be applied to various vectorization methods. In Section D.1, we provide details of further examples of TMP Vectorizations for time-dependent data, i.e., TMP Silhouettes, and TMP Betti Summaries.

We now prove that when the source single parameter vectorization $\varphi$ is stable, then so is its induced TMP vectorization $\mathbf{M}_{\varphi}$. We discuss the details of the stability notion in persistence theory and examples of stable SP vectorizations in Section C.2.

Let $\widetilde{\mathcal{G}}=\{\mathcal{G}_{t}\}_{t=1}^{T}$ and $\widetilde{\mathcal{H}}=\{\mathcal{H}_{t}\}_{t=1}^{T}$ be two time sequences of networks. Let $\varphi$ be a stable SP vectorization with the stability equation

$$\mathrm{d}(\varphi(\widetilde{\mathcal{G}}),\varphi(\widetilde{\mathcal{H}}))\leq C_{\varphi}\cdot\mathcal{W}_{p_{\varphi}}(PD(\widetilde{\mathcal{G}}),PD(\widetilde{\mathcal{H}}))$$

for some $1\leq p_{\varphi}\leq\infty$. Here, $\mathcal{W}_{p}$ represents Wasserstein-$p$ distance as defined in Section C.2.

Now, consider the bifiltrations $\{\widehat{\mathcal{G}}_{t}^{ij}\}$ and $\{\widehat{\mathcal{H}}_{t}^{ij}\}$ for each $1\leq t\leq T$. We define the induced matching distance between the multiple persistence diagrams (See Remark 2) as $\mathbf{D}(\{ZPD(\widetilde{\mathcal{G}})\},\{ZPD(\widetilde{\mathcal{H}})\})=\max_{i,j}\mathcal{W}_{p_{\varphi}}(ZPD(\widetilde{\mathcal{G}}^{ij}),ZPD(\widetilde{\mathcal{H}}^{ij}))$

Now, define the distance between TMP Vectorizations as $\mathbf{D}(\mathbf{M}_{\varphi}(\widetilde{\mathcal{G}}),\mathbf{M}_{\varphi}(\widetilde{\mathcal{H}}))=\max_{i,j}\mathrm{d}(\varphi(\widetilde{\mathcal{G}}^{ij}),\varphi(\widetilde{\mathcal{H}}^{ij}))$.

The proof of the theorem is given in Appendix E.

To model the hidden dependencies among nodes in the spatio-temporal graph, we define the spatial graph convolution operation based on the adaptive adjacency matrix and given node feature matrix. Inspired by (Wu et al. 2019), to investigate the beyond pairwise relations among nodes, we use the adaptive adjacency matrix based on trainable node embedding dictionaries, i.e., $Z^{(\ell)}_{t,\text{Spatial}}=LZ_{t,\text{Spatial}}^{(\ell-1)}W^{(\ell-1)}$, where $L=\text{Softmax}(\text{ReLU}(E_{\theta}E^{\top}_{\theta}))$ (here $E_{\theta}\in\mathbb{R}^{N\times d_{c}}$ and $d_{c}\geq 1$), $Z_{\text{Spatial}}^{(\ell-1)}$ and $Z_{\text{Spatial}}^{(\ell)}$ are the input and output of $(\ell-1)$-th layer, and $Z_{\text{Spatial}}^{(0)}=X\in\mathbb{R}^{N\times F}$ (here $F$ represents the number of features for each node), and $W^{(\ell-1)}$ is the trainable weights.

In our experiments, we use CNN based model to learn the TMP topological features. Given the TMP topological features of resolution $p$, i.e., $\text{TMP}_{t}\in\mathbb{R}^{p\times p}$, we employ CNN-based model and global max pooling to obtain the image-level local topological feature $Z_{t,\text{TMP}}$ as

$$Z_{t,\text{TMP}}=f_{\text{GMP}}(f_{\theta}(\text{TMP}_{t})),$$

where $f_{\text{GMP}}$ is the global max pooling, $f_{\theta}$ is a CNN based neural network with parameter set $\theta_{i}$, and $Z_{t,\text{TMP}}\in\mathbb{R}^{d_{c}}$ is the output for TMP representation.

Lastly, we combine the two embeddings to obtain the final embedding $Z_{t}$:

$$Z_{t}=Concat(Z_{t,\text{Spatial}},Z_{t,\text{TMP}}).$$

To capture both spatial and temporal correlations in time-series, we feed the final embedding $Z_{t}$ into Gated Recurrent Units (GRU) for future time points forecasting.

We compare our TMP-Nets with 6 state-of-the-art baselines. We use three standard performance metrics Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Mean absolute percentage error (MAPE). We provide additional experimental results in Appendix A. In Appendix B, we provide further details on the experimental setup and empirical evaluation. Our source code is available at the link ¹¹1https://www.dropbox.com/sh/h28f1cf98t9xmzj/AACBavvHc˙ctCB1FVQNyf-XRa?dl=0.

An interesting question is why TMP-Nets performs differently on Golem vs. Bytom and Decentraland. Success on each network token depends on the diversity of connections among nodes. In cryptocurrency networks, we expect nodes/addresses to be connected with other nodes with similar transaction connectivity (e.g. interaction among whales) as well as with nodes with low connectivity (e.g. terminal nodes). However, the assortativity measure of Golem (-0.47) is considerably lower than Bytom (-0.42) and Decentraland (-0.35), leading to disassortativity patterns (i.e., repetitive isolated clusters) in the Golem network, which, in turn, downgrade the success rate of forecasting.

Finally, we applied our approach in a different domain with a benchmark electrocardiogram dataset, ECG5000. Again, our model gives highly competitive results with the SOTA methods (Section A.4).