TimeMIL: Advancing Multivariate Time Series Classification via a Time-aware Multiple Instance Learning

Xiwen Chen Peijie Qiu Wenhui Zhu Huayu Li Hao Wang Aristeidis Sotiras Yalin Wang Abolfazl Razi

Abstract

Deep neural networks, including transformers and convolutional neural networks, have significantly improved multivariate time series classification (MTSC). However, these methods often rely on supervised learning, which does not fully account for the sparsity and locality of patterns in time series data (e.g., diseases-related anomalous points in ECG). To address this challenge, we formally reformulate MTSC as a weakly supervised problem, introducing a novel multiple-instance learning (MIL) framework for better localization of patterns of interest and modeling time dependencies within time series. Our novel approach, TimeMIL, formulates the temporal correlation and ordering within a time-aware MIL pooling, leveraging a tokenized transformer with a specialized learnable wavelet positional token. The proposed method surpassed 26 recent state-of-the-art methods, underscoring the effectiveness of the weakly supervised TimeMIL in MTSC. The code will be available at https://github.com/xiwenc1/TimeMIL.

Multivariate Time Series Classification, Weakly-supervised Learning

1 Introduction

Time series data mining has witnessed considerable growth in the last decade with numerous applications in classification (Ismail Fawaz et al., 2019), forecasting (Lim & Zohren, 2021), and anomaly detection (Malhotra et al., 2015). Particularly, multivariate time series classification (MTSC), which aims to assign labels to time sequences, is challenging but crucial in most real scenarios, such as healthcare (Vrba & Robinson, 2001; Tang et al., 2023), human action recognition (Shokoohi-Yekta et al., 2017; Amaral et al., 2022), audio signal processing (Ruiz et al., 2021), Internet of Things (Bakirtzis et al., 2022), and semantic communication (Zhao et al., 2023).

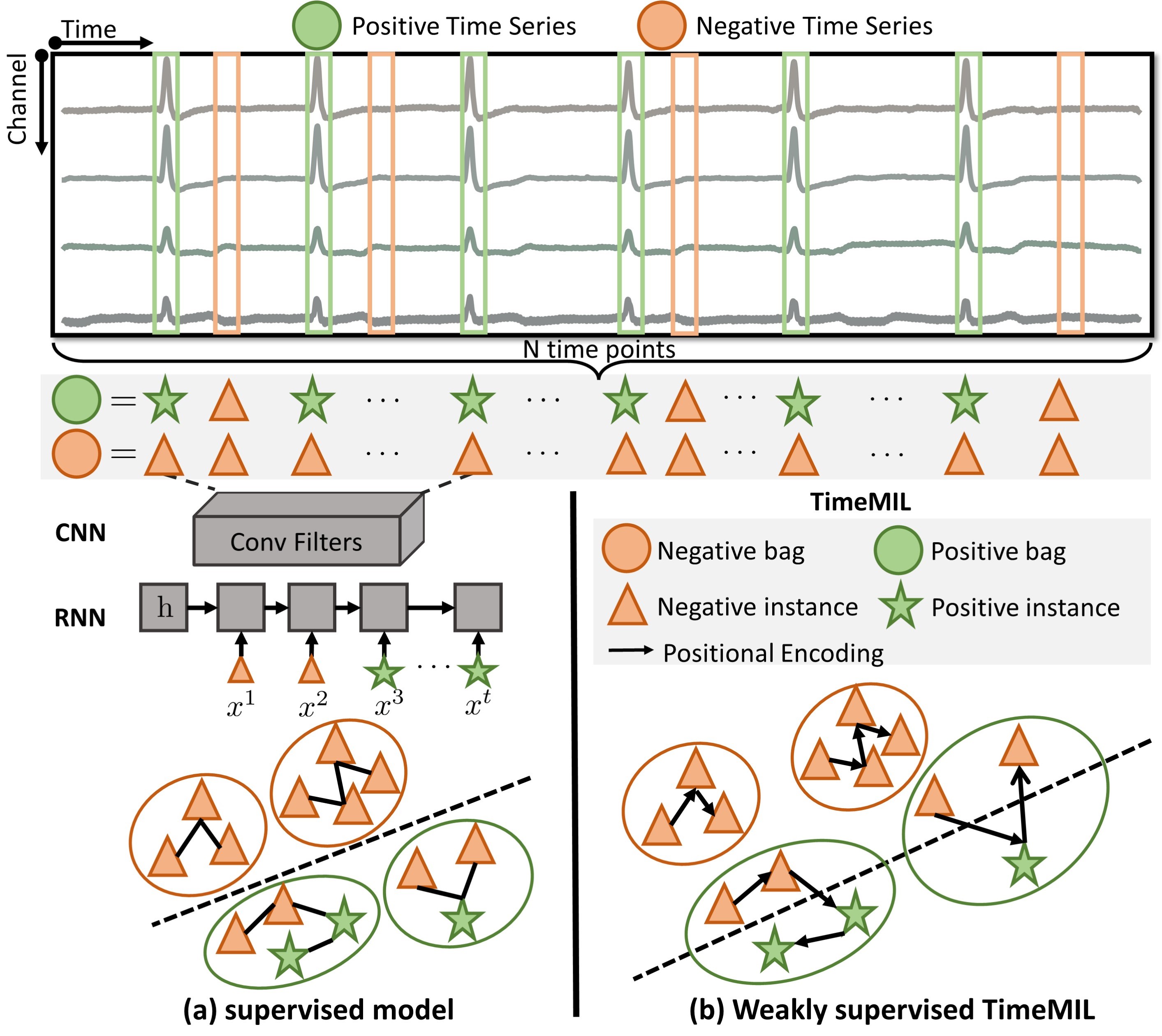
Refer to caption — Figure 1: (a): The decision boundary of fully supervised methods is determined by assigning a label to each time series. (b): TimeMIL makes decisions by discriminating positive and negative instances in time series, where each time point is an instance, and its label is typically not available in reality.

Recently, deep neural networks have achieved state-of-the-art performance in various time series tasks compared to traditional methods (Seto et al., 2015; Schäfer & Leser, 2017; Li et al., 2023a; Tang et al., 2022; donghao & wang xue, 2024; Li et al., 2024a). Their popularity and success in time series modeling can be attributed to their automatic feature extraction in conjunction with inductive biases. To this end, the time series task is typically formulated as a fully supervised learning task by employing a wide variety of architectures, such as recurrent neural networks (RNN) (Franceschi et al., 2019; Lai et al., 2018b), long short-term memory (LSTM), (Karim et al., 2019; Tang et al., 2022; Karim et al., 2019), convolution neural networks (CNN) (Zhang et al., 2020; Ismail Fawaz et al., 2020; Wu et al., 2023; Tang et al., 2022; donghao & wang xue, 2024), and transformers (Zhou et al., 2022; Zhang & Yan, 2023; Nie et al., 2023; Li et al., 2024b, c). Although these methods vary in their architectural biases for modeling time series, they share a common underlying strategy: dividing a time series into a set of time points and then modeling the local and global dependencies among them, such as changes over time and the presence of multiple periodic patterns. Importantly, patterns of interest in time series are typically sparse and localized (Lin et al., 2012; Jiang et al., 2011; Fulcher, 2018; Cheng et al., 2009), while the most discriminative time points within a time series are typically unknown due to their laborious annotation. This poses a significant challenge for fully supervised learning in accurately determining the decision boundary (see Fig. 1(a)). Instead, given the inherent properties of time series, we formulate the MTSC tasks as a weakly supervised learning paradigm (see Fig. 1(b)).

Multiple instance learning (MIL) is a weakly supervised learning method that assigns a label to a collection of instances, known as a bag. This makes MIL a natural choice for the MTSC task by collectively treating each time point as an instance and an entire time series as a bag. Early attempts of MIL in time series relied on hand-crafted features and classic MIL models (Stikic et al., 2011; Guan et al., 2016). In contrast, modern MILs which use deep neural networks to extract the feature automatically and consistently exhibit superior performance compared to the classic MILs with handcrafted features (Wang et al., 2018; Ilse et al., 2018; Early et al., 2024). However, standard MILs may fail to capture correlations between instances, since standard MILs assume the independence and identical distribution of instances with a permutation-invariant property (Ilse et al., 2018). In contrast, MTSC data typically exhibits temporal correlations and ordering dependencies, posing significant challenges for directly translating MIL into MTSC.

This paper introduces a generic MIL framework for time series, termed TimeMIL. We address several limitations when using standard MIL methods, such as their failure to model the permutation information and temporal correlation among instances. We explore their necessity from an information-theoretic perspective, which suggests that modeling the permutation information and temporal correlation can lower the uncertainty of classification systems. To this end, we propose a time-aware MIL pooling, leveraging the self-attention mechanism and a novel learnable wavelet positional encoding, where the former is used to capture the temporal correlation between instances, and the latter is used to characterize time ordering information.

Contributions: (i) To the best of our knowledge, we are the first to formally formulate a generic MIL framework for multivariate and multi-class time series classification from an information-theoretic perspective. (ii) We propose a Time-aware MIL pooling based on a tokenized transformer and a novel learnable wavelet positional encoding (WPE) to model complex patterns within time series. The proposed method outperforms 26 recent state-of-the-art methods in 28 datasets and offers inherent interpretability.

2 Related Works

Multivariate Time Series Classification. The recent DL methods specifically designed for MTSC can roughly be divided into two categories: (i) CNN/LSTM Hybrid architecture (Karim et al., 2019; Zhang et al., 2020), where LSTM is often used to capture sequential dependencies and CNN is used to capture the local features. (ii) Purely CNN architecture (Ismail Fawaz et al., 2020; Li et al., 2021b; Tang et al., 2022), where long-term dependencies, short-term dependencies, and cross-channel dependencies are claimed to be captured by multiple kernels with varying kernel sizes.

Recently, General Time Series Analysis Framework (Wu et al., 2023; donghao & wang xue, 2024) has been also proposed for multiple mainstream tasks, including classification, imputation, short-term forecasting, long-term forecasting, and anomaly detection, with simple modifications. Transformer-based models (Zhou et al., 2022; Zhang & Yan, 2023; Nie et al., 2023) and MLP-based models (Zeng et al., 2023; Zhang et al., 2022b; Li et al., 2023c, b) have also been developed and improved over the last few years for this purpose due to their excellent scaling behaviors. Nonetheless, they did not yet fully replace CNN-based models, which continue to exhibit impressive performance (Liu et al., 2022; Wang et al., 2023; donghao & wang xue, 2024).

Although the aforementioned methods have witnessed extensive use in time series analysis applications, as discussed in the introduction, these methods are rooted in supervised learning and often focus on optimizing their architectural designs (e.g., CNN and transformer), which still cannot solve the essential issue that they are challenging to determine the accurate decision boundary. In contrast, our work introduces TimeMIL, which provides a novel perspective to describe the decision boundary of time series in a weakly supervised view. In addition, the proposed TimeMIL is inherently interpretable.

Multiple Instance Learning. MIL, a weakly supervised method, is widely used for histological image classification due to its advantage in localizing tumors within gigapixel images (Ilse et al., 2018; Li et al., 2021a; Zhang et al., 2022a). However, the application of MIL to time series data has rarely been explored. An early exploration by (Stikic et al., 2011) applied classic multi-instance SVM (Andrews et al., 2002) to wearable sensor data. However, this method fails to model sequential dependencies among time points (instances). To address this limitation, (Guan et al., 2016) proposes incorporating an autoregressive hidden Markov model into the MIL framework to model the dependencies between instances. However, both methods rely on FFT and hand-crafted statistical features. Alternatively, modern MILs typically employ deep neural networks for automatic feature extraction and aggregation (Wang et al., 2018), achieving superior performance over conventional instance-based MIL, like the one used in (Zhu et al., 2021) for MTSC. Most notably, the attention-based MIL (ABMIL) is proposed by (Ilse et al., 2018), which makes MIL inherently interpretable by weighting each instance according to its importance. Since its invention, ABMIL has emerged as the standard paradigm for modern MIL applications (Li et al., 2021a; Zhu et al., 2023; Shao et al., 2021; Zhang et al., 2022a; Qiu et al., 2023; Xiang & Zhang, 2023). Following this line of work, a related but concurrent work (Early et al., 2024) attempted to apply ABMIL and its variants to time series. However, ABMIL operates under the assumption that instances are independent and identically distributed, which inherently limits the modeling of the temporal dependencies among instances in time series data.

While being related to methods presented in (Guan et al., 2016; Early et al., 2024), our method differs from them in the following ways. (i) Unlike the autoregressive hidden Markov used in (Guan et al., 2016), which struggles with long-range and complex dependencies, the proposed method employs self-attention to model the instance dependencies regardless of their distance, offering inherent interpretability. (ii) Authors of (Early et al., 2024) directly applied MIL to the time series classification problem to obtain interpretability without providing a theoretical justification of how time series classification can be framed as a MIL problem. Especially for the multi-class cases, they violated the MIL assumption that a bag is positive as long as a positive instance is present. Additionally, their proposed method also falls into the category of ABMIL, which does not naturally model the temporal correlation and ordering of time points within a time series. In contrast, we re-frame the MIL for more complex multi-class MTSC tasks. Specifically, we show how to effectively tackle multi-class problems in the context of the binary MIL paradigm (Section 3.2), clarifying and addressing the limitations of standard (AB)MIL techniques used for time series analyses (Section 3.3).

3 Method

In this section, we introduce three key components for applying the proposed TimeMIL to MTSC. First, we formulate the MTSC as a MIL problem in Sec. 3.1 and 3.2. Second, we introduce a time-aware MIL pooling to capture the temporal ordering in time series through a wavelet-augmented transformer (Sec. 3.3). Third, we introduce how to quantify the importance of instances in Sec. 3.4. The entire framework of the proposed TimeMIL is depicted in Fig. 2. A summary of the proposed framework is presented in Algorithm 1.

3.1 Problem Formulation

Multivariate time series data is typically presented as $\{\boldsymbol{X}_{1},\cdots,\boldsymbol{X}_{n}\}$ , where $\boldsymbol{X}_{i}=\left\{\boldsymbol{x}_{i}^{1},\cdots,\boldsymbol{x}_{i}^{T}\right\}$ is a time series contains $T$ time points, with each time point $\boldsymbol{x}_{i}^{t}\in\mathbb{R}^{d}$ being a $d$ -dimensional vector. It is noteworthy that the time points are shift-variant and ordered. The goal of MTSC is to learn a direct mapping from feature space $\mathcal{X}$ to label space $\mathcal{Y}$ using the training data $\{(\boldsymbol{X}_{1},y_{1}),\cdots,(\boldsymbol{X}_{n},y_{n})\}$ , where $y_{i}$ is the label for each time series.

3.2 MTSC as A MIL Problem

Binary MTSC. Without violating the MIL assumption, we take binary MTSC as a starting point in the following derivations, then extend it to the multi-class scheme. The goal of a binary MIL is to assign a label to a bag of instances. The MTSC can naturally be formulated as a MIL problem by treating each time series as a bag, with each time slot being an instance. Formally, the binary MTSC under the MIL formulation is defined as

y_{i}=\left\{\begin{array}[]{l}0,\text{ iff }\sum_{t=1}^{T}y_{i}^{t}=0,\ y_{i}^{t}\in\{0,1\}\\ 1,\text{ otherwise, }\end{array}\right.

(1)

where $y_{i}^{t}$ denotes the label for each time point indicating if an event of interest has happened at time point $\boldsymbol{x}_{i}^{t}$ . The $\{y_{i}^{1},\cdots,y_{i}^{t}\}$ are also known as the instance-level labels in the context of MIL, which are unknown in most scenarios. Eq. 1 implies that a time series (bag) $\boldsymbol{X}_{i}$ is labeled as positive if and only if any of its instance labels is positive, negative otherwise.

The bag-level prediction $\hat{y}_{i}$ of a MIL is given as a score function $S:\mathcal{X}\rightarrow\mathbb{R}$ (Ilse et al., 2018):

\hat{y}_{i}=S(\boldsymbol{X}_{i}),

(2)

where the outcome of a score function is a probability.

Theorem 1.

(Ilse et al., 2018; Shao et al., 2021) Suppose the score function $S$ is a $(\delta_{\varepsilon},\varepsilon)$ -continuous symmetric function w.r.t Hausdorff distance $d_{H}(\cdot,\cdot)$ , i.e. $\forall d_{H}(\boldsymbol{X}_{i},\boldsymbol{X}_{j})<\delta_{\varepsilon}$ , we have $|S(\boldsymbol{X}_{i})-S(\boldsymbol{X}_{j})|<\varepsilon$ , for $\forall\varepsilon>0$ . For any invertible map $\sigma:\mathcal{X}\rightarrow\mathbb{R}^{d}$ , $S$ can be approximated by certain continuous functions $g$ and $f$ :

\displaystyle|S(\boldsymbol{X}_{i})-g(\sigma\{f(\boldsymbol{x}_{i}^{t}):\boldsymbol{x}_{i}^{t}\in\boldsymbol{X}_{i}\})|<\varepsilon.

(3)

Theorem 1 defines the generic pipeline of a MIL, which consists of three main parts: (i) The function $f$ is a feature extractor that projects the input instances into $L$ -dimensional vector embeddings $\tilde{\boldsymbol{X}}_{i}$ . (ii) $\sigma$ is known as the MIL pooling function that aggregates instance vector embeddings into a single vector. It should be noted that the original MIL pooling function $\sigma$ should be permutation-invariant (Ilse et al., 2018). (iii) $g$ denotes the bag-level classifier (e.g., a linear classifier) that maps the vector embedding after applying MIL pooling to a bag-level probability prediction $\hat{y}_{i}\in[0,1]$ .

Mutli-Class MTSC. A multi-class time series classification with a total of $C$ classes can be performed as several one-vs-rest binary MIL without violating its assumption:

\displaystyle y_{i,c}=\left\{\begin{array}[]{l}0,\text{ iff }\sum_{t=1}^{T}y_{i,c}^{t}=0,\ y^{t}_{i,c}\in\{0,1\}\\ 1,\text{ otherwise,}\end{array}\right.

(6)

where $y_{i,c}^{t}=1$ denotes a time point with significant contribution to class $c\in\{1,\cdots,C\}$ . The final bag-level prediction $y_{i}$ for a bag is computed as the class with the highest probability:

\hat{y}_{i}=\operatorname{argmax}\limits_{c}\ \hat{y}_{i,c},

(7)

which is consistent with the one-vs-rest scheme.

Remark 1.

The MIL in Theorem 1 fails to model the temporal ordering among time points within a time series.

Remark 1 arises from the symmetric (permutation-invariant) property of the MIL pooling function $\sigma$ . The function $\sigma$ remains the same for every permutation of the instances within a bag, thereby neglecting the temporal ordering between time points (instances) in time series modeling. This hinders the direct translation of classic MIL into MTSC tasks. To address this limitation, we propose a time-aware MIL pooling in Sec. 3.3.

Algorithm 1 Time-aware MIL (Forward Propagation)

0: Input sequence

\boldsymbol{X}_{i}=\left\{\boldsymbol{x}_{i}^{1},\cdots,\boldsymbol{x}_{i}^{T}\right\}

. A neural network contains:

f

: feature extractor,

g

: bag-level classifier,

\operatorname{WPE}

bases, and class token

\boldsymbol{x}^{\operatorname{cls}}

0: Predicted label

\hat{y}_{i}

1: Get embedding:

\left\{\boldsymbol{x}_{i}^{1},\cdots,\boldsymbol{x}_{i}^{T}\right\}\leftarrow f(\left\{\boldsymbol{x}_{i}^{1},\cdots,\boldsymbol{x}_{i}^{T}\right\})

#MIL pooling from here (Section 3.3)

2: Init class token for the bag:

\boldsymbol{x}_{i}^{\operatorname{cls}}\leftarrow\boldsymbol{x}^{\operatorname{cls}}

3: Add class token:

\boldsymbol{X}_{i}^{\operatorname{cls}}=\boldsymbol{x}_{i}^{\operatorname{cls}}\cup\boldsymbol{X}_{i}

4: for j=1:2 do

5: PE:

\boldsymbol{X}_{i}\leftarrow\boldsymbol{X}_{i}+WPE_{j}(\boldsymbol{X}_{i})

. #

WPE_{j}(\boldsymbol{X}_{i})

is from Eq. 10. Here,

\boldsymbol{X}_{i}

is the part of

\boldsymbol{X}_{i}^{\operatorname{cls}}

\boldsymbol{X}_{i}^{\operatorname{cls}}\leftarrow Transformer_{j}(\boldsymbol{X}_{i}^{\operatorname{cls}})

7: end for#Bag-level classification from here

\hat{y}_{i}\leftarrow g(\boldsymbol{x}_{i}^{\operatorname{cls}})

. #

\boldsymbol{x}_{i}^{\operatorname{cls}}

is obtained from

\boldsymbol{X}_{i}^{\operatorname{cls}}

3.3 Time-Aware MIL Pooling for MTSC

From an entropy perspective, understanding permutation-variant properties in time series can be quite insightful. As discussed in Sec. 3.2, we assume that each time point (instance) $\boldsymbol{x}_{i}^{j}$ in a time series (bag) is a realization of a random variable $\Theta^{j}$ conditioned by a time index $t^{j}$ . The resulting bag can be represented as a random variable $\boldsymbol{X}=\{(\Theta^{1}|t^{1}),\cdots,(\Theta^{T}|t^{T})\}$ , where $t^{j}\neq t^{k},\forall j\neq k$ . Likewise, $\boldsymbol{Y}$ denotes a random variable for bag label. Here, we use notation $\Theta^{j}$ for an instance to distinguish a random variable (often as uppercase) and its realization (often as lowercase). It is fair to construct a general assumption: $p(\Theta^{j}|t^{j})\neq p(\Theta^{j}|t^{k})$ , which indicates an instance varies when it is presented in different locations.

Proposition 2.

Shuffling the time points within a time series potentially disrupts its predictability. This means, under the general assumption, the entropy before and after shuffling typically differs, i.e., the equality:

\displaystyle H(\cdots,(\Theta^{j}|t^{j}),\cdots)=H(\cdots,(\Theta^{j}|t^{\bar{j}}),\cdots),

does not always hold. Here, $t^{\bar{1}},\cdots,t^{\bar{T}}$ are sampled from the set $\{t^{1},\cdots,t^{T}\}$ without replacement. The right term denotes the time series after randomly shuffling.

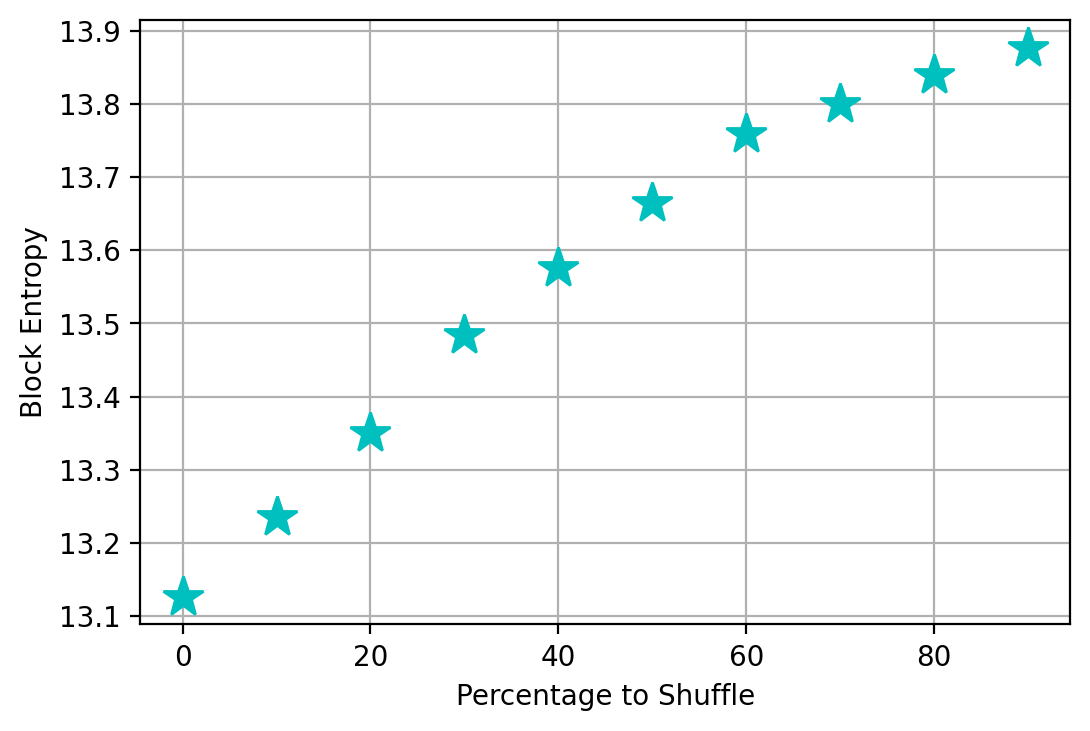
Please refer to Appendix C for its proof. Proposition 2 implies that random permutation of time points within a regular time series potentially increases its uncertainty in terms of entropy. Since it is challenging to directly compute the entropy for high-dimensional continuous-valued variables from the observation, we illustrate this fact by using a supportive example in text sequence (Shakespeare’s Sonnets¹¹1 https://shakespeares-sonnets.com/Archive/allsonn.htm.). The feasible domain of the text sequence is a discrete 1D domain, and its uncertainty can be measured directly by the Shannon block entropy (Shannon, 1951). Please refer to Appendix D for more detail about Shannon block entropy. As shown in Fig. 3, the block entropy increases as the shuffling rate increases. We will demonstrate the importance of not just modeling the random permutation but also accounting for the temporal correlation between instances.

Theorem 3.

Modeling the temporal correlation between instances lowers the complexity of developing a good classifier, which is presented by class-conditioned entropy:

\displaystyle H(\boldsymbol{X}_{c}|\boldsymbol{Y})\leq H(\boldsymbol{X}_{nc}|\boldsymbol{Y}),

(8)

where $H(\boldsymbol{X}_{c}|\boldsymbol{Y})=H((\Theta^{1}|t^{1}),\cdots,(\Theta^{T}|t^{T})|\boldsymbol{Y})$ is derived under modeling the correlation among instances within a bag while $H(\boldsymbol{X}_{nc}|\boldsymbol{Y})=\sum_{i}H((\Theta^{i}|t^{i})|\boldsymbol{Y})$ is derived under the assumption that instances are independent and identically distributed.

Proof.

For convenience, we denote $(\Theta^{j}|t^{j})$ by $\Lambda^{j}$ .

\begin{split}H(\Lambda^{1},\cdots,\Lambda^{T}|\boldsymbol{Y})&=H(\Lambda^{T}|\Lambda^{T-1},\cdots,\Lambda^{1},\boldsymbol{Y})\\ &+H(\Lambda^{T-1}|\Lambda^{T-2},\cdots,\Lambda^{1},\boldsymbol{Y})\\ &+\cdots\\ &+H(\Lambda^{1}|\boldsymbol{Y})\end{split}

(9)

Since $H(\Lambda^{i}|\Lambda^{i-1},\cdots,\Lambda^{1},\boldsymbol{Y})\leq H(\Lambda^{i}|\boldsymbol{Y})$ , which indicates knowing more information lowers the uncertainty:

\displaystyle H(\Lambda^{1},\cdots,\Lambda^{T}|\boldsymbol{Y})\leq\sum_{i}H(\Lambda^{i}|\boldsymbol{Y})

(10)

∎

Remark 2.

The conditional entropy $H(\boldsymbol{X}|\boldsymbol{Y})$ measures the uncertainty of the bag feature $\boldsymbol{X}$ given that the bag-level class label $\boldsymbol{Y}$ is known. In the context of classification, it quantifies the spread of features within each class. A high value of $H(\boldsymbol{X}|\boldsymbol{Y})$ indicates that the features belonging to the same class can vary significantly. This suggests that the features are not clustered tightly but are spread out. In contrast, a lower $H(\boldsymbol{X}|\boldsymbol{Y})$ suggests that the features from the same class are more homogeneous, exhibiting less variability. This homogeneity can make it easier to classify instances since the features within each class are more consistent, potentially resulting in a simpler decision boundary.

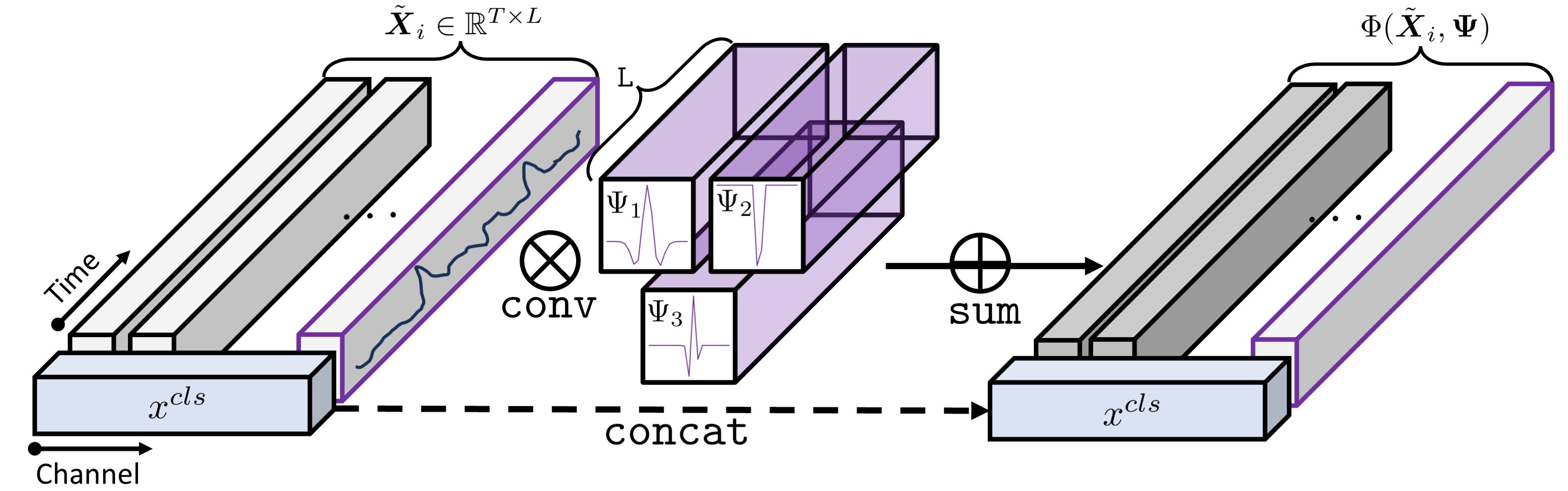
Theorem 3 immediately implies the benefit of modeling temporal permutation and correlation between instances and provides a generic formulation of time-aware MIL pooling. The realization of Theorem 3 can be achieved by a transformer with the unique token mechanism. First, transformers help tackle the conditional entropy $H(\Lambda^{t}|\Lambda^{t-1},\cdots,\Lambda^{1},\boldsymbol{Y})$ in Theorem 3 by employing a class token $\boldsymbol{x}_{i}^{\operatorname{cls}}$ . The yielded tokenized bag of instances is $\boldsymbol{X}_{i}^{\operatorname{cls}}=\{\boldsymbol{x}_{i}^{\operatorname{cls}},\boldsymbol{x}_{i}^{1},\cdots,\boldsymbol{x}_{i}^{T}\}$ . Second, we propose a novel positional encoding in our transformer-based pooling through the lens of wavelet theory to further capture the multi-scale time-frequency ordering relationship among instances.

Temporal correlation as self-Attention. The self-attention mechanism (Vaswani et al., 2017b) is proposed to capture mutual information between time points. In the context of MIL, we use multi-head self-attention (MHSA) to model the sequential correlation between instances:

\displaystyle\operatorname{MHSA}(\boldsymbol{X}_{i}^{\operatorname{cls}})=[\operatorname{head}_{1},\cdots,\operatorname{head}_{H}]\boldsymbol{W}_{0}\vspace{-0.6cm}

(11)

where:

		$\displaystyle\operatorname{head}_{h}=\operatorname{Attention}(\boldsymbol{X}_{i}^{\operatorname{cls}}\boldsymbol{W}_{h}^{Q},\boldsymbol{X}_{i}^{\operatorname{cls}}\boldsymbol{W}_{h}^{K},\boldsymbol{X}_{i}^{\operatorname{cls}}\boldsymbol{W}_{h}^{V})$
		$\displaystyle\operatorname{Attention}(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})=\operatorname{softmax}(\boldsymbol{Q}\boldsymbol{K}^{\mathbf{T}}/\sqrt{d_{k}})\boldsymbol{V},$		(12)

where $\boldsymbol{W}_{0}$ , $\boldsymbol{W}_{h}^{Q}$ , $\boldsymbol{W}_{h}^{K}$ , $\boldsymbol{W}_{h}^{V}$ are trainable parameters. It is noteworthy that after the transformer blocks, we only pass the class token to the bag-level classifier $g$ to make a prediction. However, standard self-attention has quadratic time and memory complexity $\mathcal{O}(T^{2})$ w.r.t. the number of instances in a bag ( $T$ ). Recent advances (Xiong et al., 2021; Wang et al., 2020; Shen et al., 2021) in self-attention studies have reduced the quadratic complexity to approximately linear. Specifically, we use the approximation of self-attention proposed by (Xiong et al., 2021) in our implementation to reduce the complexity of the proposed TimeMIL.

Wavelet positional encoding. The classic transformers use Sinusoidal positional encoding to capture the relative ordering in a time series, as self-attention does not take the temporal ordering of time points into account. The disadvantage of Sinusoidal positional encoding is that it is pre-defined and non-learnable. Importantly, the Sinusoidal positional encoding is independently generated away from the input context; hence, it cannot capture both the time and frequency information of time series. To address this limitation, we propose a learnable wavelet positional encoding in a conditional positional encoding fashion (Chen et al., 2023; Chu et al., 2023):

\vspace{-0.2cm}\operatorname{WPE}(\boldsymbol{X}_{i})=\sum_{j=1}^{n_{\operatorname{W}}}\Phi(\boldsymbol{X}_{i},\boldsymbol{\Psi}_{j}),\vspace{-0.1cm}

(13)

where $n_{\operatorname{W}}$ denotes the number of wavelet basis, which is empirically set to 3 in this paper. $\{\boldsymbol{\Psi}_{1},\cdots,\boldsymbol{\Psi}_{n_{\operatorname{W}}}\}$ are learnable wavelet kernels with $\boldsymbol{\Psi}_{j}=\{\psi_{a_{j1},b_{j1}}(t),\cdots,\psi_{a_{jL},b_{jL}}(t)\}$ where $\psi$ is mother wavelet, which is chosen to be the Mexican hat in our experiments.

The Gabor-Heisenberg limit (Gabor, 1946), which is the uncertainty principle in the time-frequency version, states that it is impossible to precisely determine both the time and frequency of a signal, simultaneously. In the context of the wavelet transform, this principle implies a trade-off: the higher the resolution needed in time, the lower the resolution becomes in frequency. This implies that the careful selection of time-frequency resolution is crucial for effectively characterizing different signals. Hence, we learn the scaling and translation parameters $\{(a_{j1},b_{j1}),\cdots,(a_{jL},b_{jL})\}$ to form the wavelet basis from mother wavelet. $\Phi(\cdot)$ is the channel-wise wavelet transform, which can be formulated as convolving the input signal with the wavelet kernels:

\displaystyle\Phi(\tilde{\boldsymbol{X}}_{i},\boldsymbol{\Psi}_{j})=\left[\begin{array}[]{c}\tilde{\boldsymbol{X}}_{i1}\circledast\psi_{a_{j1},b_{j1}}\\ \vdots\\ \tilde{\boldsymbol{X}}_{iL}\circledast\psi_{a_{jL},b_{jL}}\end{array}\right]^{\top}\in\mathbb{R}^{n\times L}.

(17)

The resulting WPE is depicted in Fig. 4.

3.4 Interpretability

The proposed time-aware MIL is naturally interpretable due to its ability to localize time points of interest within a time series. One way to achieve this is to hack into the attention map of the transformer layers in the proposed time-aware MIL pooling. The attention map (refer to Eq. 3.3) measures the importance of each instance $\boldsymbol{x}_{i}^{t}$ in the series $\boldsymbol{X}_{i}$ in the MIL pooling:

\boldsymbol{A}_{i}=\operatorname{softmax}\left(\frac{\boldsymbol{x}_{i}^{\operatorname{cls}}\boldsymbol{W}_{h}^{Q}\ \boldsymbol{X}_{i}\boldsymbol{W}_{h}^{K}}{\sqrt{d_{k}}}\right),

(18)

where $\operatorname{softmax}$ is performed over the time dimension. $\boldsymbol{A}_{i}\in\mathbb{R}^{T}$ is the importance weights of all instances, with its $t$ -th element corresponding to the importance of the time point $\boldsymbol{x}_{i}^{t}$ . We only use the class token to calculate the importance weight, as it determines the most relevant time points that characterize a certain class label in MTSC tasks.

Table 1: Results of Group 1 Experiments. Comparison with the recent state-of-the-art MTSC methods on 26 datasets. The best results are highlighted by bold and the second best are highlighted by underline. ’N/A’ in the table denotes the corresponding method was unable to obtain results due to memory or computational limitations (Liu et al., 2023).

Datasets/Methods

ED-1NN

DTW-1NN-I

DTW-1NN-D

MLSTM-FCN

Neur. Net.’19

ShapeNet

AAAI’21

WEASEL+MUSE

arxiv’2017

TapNet

AAAI’20

OS-CNN

ICLR’22

MOS-CNN

ICLR’22

TodyNet

arxiv’23

Ours

ArticularyWordRecognition

0.970

0.980

0.987

0.973

0.987

0.990

0.987

0.988

0.991

0.987

0.990

AtrialFibrillation

0.267

0.200

0.267

0.400

0.333

0.233

0.183

0.467

0.733

BasicMotions

0.675

1.000

0.975

0.950

1.000

Cricket

0.944

0.986

1.000

0.917

0.986

1.000

0.958

0.993

0.990

1.000

DuckDuckGeese

0.275

0.550

0.600

0.675

0.725

0.575

0.540

0.615

0.580

0.780

EigenWorms

0.550

0.603

0.618

0.504

0.878

0.890

0.489

0.414

0.508

0.840

0.823

Epilepsy

0.667

0.978

0.964

0.761

0.987

1.000

0.971

0.980

0.996

0.971

1.000

EthanolConcentration

0.293

0.304

0.323

0.373

0.312

0.133

0.323

0.240

0.415

0.350

0.407

ERing

0.133

0.430

0.133

0.881

0.915

0.956

FaceDetection

0.519

0.513

0.529

0.545

0.602

0.545

0.556

0.575

0.597

0.627

0.698

FingerMovements

0.550

0.520

0.530

0.580

0.589

0.490

0.530

0.568

0.570

0.670

HandMovementDirection

0.279

0.306

0.231

0.365

0.338

0.365

0.378

0.443

0.361

0.649

0.487

Handwriting

0.371

0.509

0.607

0.286

0.451

0.605

0.357

0.668

0.677

0.436

0.482

Heartbeat

0.620

0.659

0.717

0.663

0.756

0.727

0.751

0.489

0.604

0.756

0.815

Libras

0.833

0.894

0.872

0.856

0.878

0.850

0.950

0.965

0.850

0.972

LSST

0.456

0.575

0.551

0.373

0.590

0.568

0.413

0.521

0.615

0.690

MotorImagery

0.510

0.390

0.500

0.510

0.610

0.500

0.590

0.535

0.515

0.640

0.720

NATOPS

0.860

0.850

0.883

0.889

0.883

0.870

0.939

0.968

0.951

0.972

0.994

PenDigits

0.973

0.939

0.977

0.978

0.977

0.948

0.980

0.985

0.983

0.987

0.600

PEMS-SF

0.705

0.734

0.711

0.699

0.751

N/A

0.751

0.760

0.764

0.780

0.931

PhonemeSpectra

0.104

0.151

0.110

0.298

0.190

0.175

0.299

0.295

0.309

0.311

RacketSports

0.868

0.842

0.803

0.882

0.934

0.868

0.877

0.929

0.803

0.908

SelfRegulationSCP1

0.771

0.765

0.775

0.874

0.782

0.710

0.652

0.835

0.829

0.898

SelfRegulationSCP2

0.483

0.533

0.539

0.472

0.578

0.460

0.550

0.532

0.510

0.550

0.639

StandWalkJump

0.200

0.333

0.200

0.067

0.533

0.333

0.400

0.383

0.467

0.733

UWaveGestureLibrary

0.881

0.869

0.903

0.891

0.906

0.916

0.894

0.927

0.926

0.850

0.900

Ours 1-to-1-Wins

Ours 1-to-1-Draws

Ours 1-to-1-Losses

Average accuracy (

\uparrow

)

0.568

0.622

0.626

0.597

0.684

0.656

0.637

0.672

0.692

0.726

0.774

Total best accuracy (

\uparrow

)

Average Rank (

\downarrow

)

9.154

7.904

7.231

7.865

4.731

5.900

6.500

5.442

4.692

4.058

2.327

Table 2: Results of Group 2 Experiments. Comparison with the recent state-of-the-art general time analysis frameworks on 10 datasets.

Datasets/Methods

LSTNet

SIGIR’18

LSSL

ICLR’22

Rocket

DMKD’18

SCINet

NeurIPS’22

MICN

ICLR’23

TimesNet

ICLR’23

Dlinear

AAAI’23

LightTS

arxiv’22

MTS-Mixer

arxiv’23

Rlinear

arxiv’23

RMLP

arxiv’23

FEDformer

ICML’22

Flowformer

ICML’22

Crossformer

ICLR’23

PatchTST

ICLR’23

ModernTCN

ICLR’24

Ours

EthanolConcentration

0.399

0.311

0.452

0.344

0.353

0.357

0.362

0.297

0.338

0.289

0.313

0.312

0.338

0.380

0.328

0.363

0.407

FaceDetection

0.657

0.667

0.647

0.689

0.652

0.686

0.680

0.675

0.702

0.656

0.673

0.660

0.676

0.687

0.683

0.708

0.698

Handwriting

0.258

0.246

0.588

0.236

0.255

0.321

0.270

0.261

0.260

0.281

0.300

0.280

0.338

0.288

0.296

0.306

0.487

Heartbeat

0.771

0.727

0.756

0.775

0.747

0.780

0.751

0.771

0.726

0.727

0.737

0.776

0.749

0.772

0.815

JapaneseVowels

0.981

0.984

0.962

0.960

0.946

0.984

0.962

0.943

0.959

0.984

0.989

0.991

0.975

0.988

0.995

PEMS-SF

0.867

0.861

0.751

0.838

0.855

0.896

0.751

0.884

0.809

0.827

0.839

0.809

0.860

0.859

0.893

0.891

0.931

SelfRegulationSCP1

0.840

0.908

0.925

0.860

0.918

0.873

0.898

0.917

0.911

0.921

0.887

0.925

0.921

0.907

0.934

0.898

SelfRegulationSCP2

0.528

0.522

0.533

0.572

0.536

0.572

0.505

0.511

0.550

0.561

0.510

0.544

0.561

0.583

0.578

0.603

0.639

SpokenArabicDigits

1.000

0.712

0.981

0.971

0.990

0.814

1.000

0.974

0.965

0.976

1.000

0.988

0.979

0.983

0.987

1.000

UWaveGestureLibrary

0.878

0.859

0.944

0.851

0.828

0.853

0.821

0.803

0.823

0.825

0.838

0.853

0.866

0.853

0.858

0.867

0.900

Ours 1-to-1-Wins

Ours 1-to-1-Draws

Ours 1-to-1-Losses

Average accuracy (

\uparrow

)

0.718

0.709

0.725

0.717

0.700

0.736

0.679

0.704

0.709

0.700

0.706

0.707

0.732

0.725

0.742

0.777

Total best accuracy (

\uparrow

)

Average Rank (

\downarrow

)

8.85

10.4

9.5

8.9

13.2

5.35

12.7

11.2

10.85

11.55

10.75

5.9

8.1

2.85

4 Experiments

4.1 Experimental setup and Baselines

We use the UEA benchmark datasets to validate the superiority of the proposed TimeMIL. These datasets have various lengths, dimensions, and training/test splits. Please refer to Appendix A for the details of these datasets. We conduct two groups of experiments as follows.

Group 1 experiments. Following (Liu et al., 2023; Li et al., 2021b), this group of experiments is conducted on selected 26 equal-length datasets from UEA to compare with the recent strong baseline methods of multivariate time series classification, including: TodyNet (Liu et al., 2023), OS-CNN and MOS-CNN (Tang et al., 2022), ShapeNet (Li et al., 2021b), TapNet (Zhang et al., 2020), WEASEL+MUSE (Schäfer & Leser, 2017), WLSTM-FCN (Karim et al., 2019). We also include several well-known traditional methods based on distance and the nearest neighbor classifier, including ED-1NN, DTW-1NN-I, and DTW-1NN-D. Please refer to (Liu et al., 2023) or Appendix F for the details of these three baselines.

Group 2 experiments. Following (donghao & wang xue, 2024; Wu et al., 2023), this group of experiments is conducted on selected 10 UEA datasets to compare with the recent strong methods in the general time series analysis, including: ModernTCN (donghao & wang xue, 2024), PatchTST (Nie et al., 2023), Crossformer (Zhang & Yan, 2023), Flowformer (Wu et al., 2022), FEDformer (Zhou et al., 2022), Rlinear and RMLP (Li et al., 2023b), MTS-Mixer (Li et al., 2023c), LightTS (Zhang et al., 2022b), Dlinear (Zeng et al., 2023), TimesNet (Wu et al., 2023), MICN (Wang et al., 2023), SCINet (Liu et al., 2022), Rocket (Dempster et al., 2020), LSSL (Gu et al., 2022), and LSTNET (Lai et al., 2018a).

Implementation details. The previous benchmark results of all baseline methods are taken from their papers, and the same training setting is used. In the implementation of our proposed model, we adopt the model in (Ismail Fawaz et al., 2020) as our backbone, where the output dimension $L$ is fixed to 128. Refer to Appendix F for details.

Evaluation metrics. Following (Liu et al., 2023; Li et al., 2021b), we evaluate the performance of our proposed method and other methods by computing the accuracy, average accuracy, average rank, and the number of pair-wise Wins/Draws/Losses.

4.2 Main Experimental Results

The proposed method demonstrates superiority over other recently proposed competing methods in both Group 1 and Group 2 experiments (refer to Table 1 and 2). Please refer to Appendix G for additional results.

Group 1 results. We obtain a 77.4% average accuracy on all 26 MTSC datasets, surpassing other methods on 18 datasets and achieving an average rank of 2.327 out of a total of 11 methods. Specifically, the proposed method outperforms the second-best methods on each dataset by an average of 4.8% in accuracy and reduces the performance rank by 1.73. This performance gain is even more substantial in those challenging datasets. Specifically, compared to the second-best performing methods, our method improves the average accuracy by 26%, 20%, 15%, 8%, 8%, 7%, and 7% on AtrialFibrillation, StandWalkJump, PEMS-SF, FingerMovements, MotorImagery, FaceDetection, and LSST datasets, respectively.
Group 2 results. The proposed method also achieved superior performance on the Group 2 datasets compared to other methods. Specifically, our method achieved a 77.7% average accuracy, surpassing the other methods in 5 out of 10 datasets and achieving an average rank of 2.85 out of a total of 17 methods. Remarkably, the proposed method outperforms the recent state-of-the-art ModernTCN (donghao & wang xue, 2024) by 3.5% in average accuracy and 1.15 in average rank.

Table 3: Comparison of different MIL pooling (Left) and positional encoding (Right) with Group 1 experiments.

MIL Pooling	Accuracy
Mean	0.715
Max	0.719
Attention	0.739
Conjunctive	0.746
Time-aware (Ours)	0.774

Positional Encoding	Accuracy
Positional Encoding	ABMIL	TimeMIL
None	0.739	0.761
Sinusoidal	0.741	0.763
WPE (Ours)	0.745	0.774

4.3 Ablation on Model Design Variants

Effectiveness of TimeMIL pooling. We compare the performance of the proposed TimeMIL with other commonly used MIL pooling methods, including MeanMIL, MaxMIL, ABMIL (Ilse et al., 2018) and the most recent ConjunctiveMIL (Early et al., 2024). We observe that learnable pooling methods (i.e., TimeMIL, ABMIL, and ConjunctiveMIL) show superior performance over non-parametric MIL pooling methods (i.e., MeanMIL and MaxMIL) (Table 3 Left). Notably, the proposed TimeMIL outperforms ABMIL and ConjunctiveMIL by 3% and 2.8% in terms of average accuracy, respectively. This supports our initial claim that modeling dependencies between time points is beneficial for MTSC.

Effectiveness of wavelet positional encoding. We compare the proposed WPE with commonly used Sinusoidal PE (Vaswani et al., 2017a). We observe that adding PE generally improves the performance of both ABMIL and TimeMIL (see Table 3 Right), which aligns with our hypothesis that incorporating PE into MIL can better model the ordering within time points and hence lower the classification error. However, we do not observe a significant performance gain ( $\sim$ 0.27%) by adding a sinusoidal PE for both ABMIL and TimeMIL. On the contrary, the addition of the proposed WPE improves ABMIL and TimeMIL by 0.6% and 1%, respectively. This may be attributed to the fact that it is challenging for predefined sinusoidal PE to capture the changing of frequencies over time within a time series. While the proposed WPE better models these time-frequency changes.

4.4 The Effectiveness of Weakly Supervised Learning

To validate the effectiveness of the proposed weakly supervised learning scheme, we provide an in-depth comparison between the proposed TimeMIL and traditional fully supervised methods. The results are shown in Fig. 5 and 6.

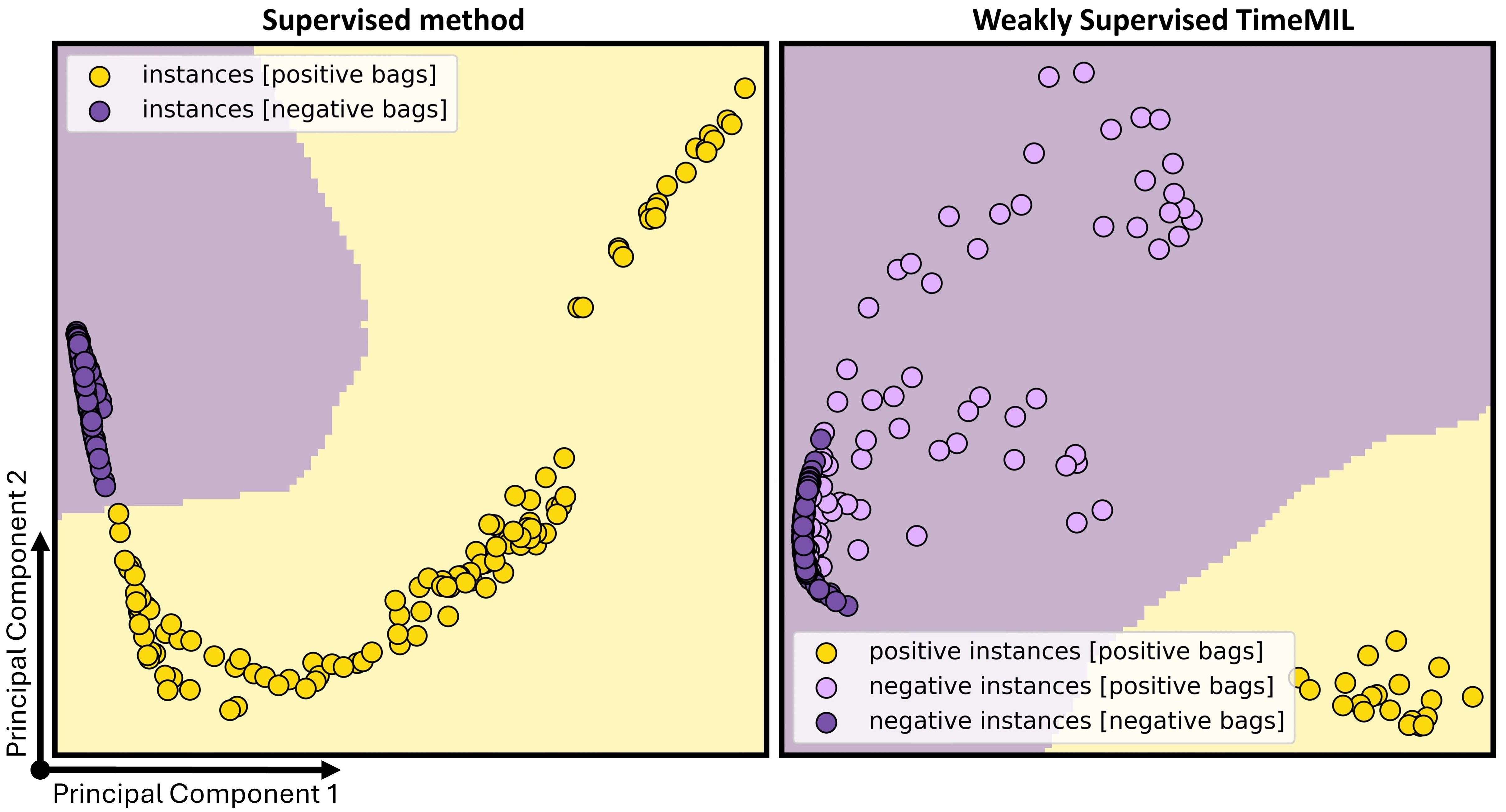
Decision boundary. We visualize the decision boundary learned in weakly supervised TimeMIL and those learned in the fully supervised method using the synthetic dataset. For the implementation of the supervised method, we maintain the same feature extractor but replace the TimeMIL pooling with a supervised classifier (Ismail Fawaz et al., 2020). For visualization of the decision boundary, we projected the time series data onto 2D space by performing PCA on the latent space (i.e., the feature embeddings after applying the feature extractor). More details of the synthetic dataset and visualizing the decision boundary can be found in Appendix H.

We observe that although the fully supervised method could differentiate positive and negative time series, there is not an apparent margin in the decision boundary between the positive and negative time series (see Fig. 6 (Left)). This is because the negative instances in positive bags (time series) resemble those negative instances in negative bags. Meanwhile, the positive instances in positive bags are typically less than negative instances. In contrast, the decision boundary of the weakly supervised TimeMIL shows a distinct decision boundary with large margins between the positive and negative instances (Fig. 6 (Right)). This unique feature of the proposed TimeMIL provides an instance differentiation between positive and negative time series, offering a precise localization of positive instances.

Inherent interpretability. The instance-level decision-making mechanism makes the proposed TimeMIL inherently interpretable. Leveraging this, we can obtain the importance score. TimeMIL accurately localized patterns of interest (i.e., positive instances) in the UEA dataset (Fig. 5; $2^{nd}$ and $3^{rd}$ row) and synthetic dataset (Fig. 5; $1^{st}$ row). This supports our initial hypothesis that time points of interest in positive time series are typically sparse and localized, making the weakly supervised TimeMIL a natural choice for MTSC.

5 Conclusion

In this work, we introduce TimeMIL, a weakly supervised MIL framework designed for multivariate time series classification. The proposed method, from the perspective of weakly supervised learning, offers a better capability to characterize the decision boundary for MTSC than commonly used fully supervised methods. As a result, TimeMIL demonstrates superiority over 26 methods in 28 datasets and illustrates impressive interpretability by accurately localizing patterns of interest.

Impact Statements

This paper presents a novel TimeMIL framework to model the temporal correlation and ordering, leveraging a tokenized transformer with a specialized learnable wavelet positional token. The potential societal consequences of TimeMIL can be summarized three-fold:

(i) Theoretical View. Commencing with a viewpoint in weakly supervised learning, we are the first to formally introduce MIL into time series-related tasks. We rigorously examine feasibility from an information-theoretic perspective. To address a variety of limitations in applying MIL in MTSC, we propose a time-aware MIL pooling to preserve the intrinsic temporal correlation and ordering properties within time series. In summary, we draw theoretical connections between the MIL and MTSC.

(ii) Applicability. Our framework potentially expands the applications of MTSC to financial forecasting, predictive maintenance, anomaly detection, healthcare monitoring, financial forecasting, environmental monitoring, and speech and signal processing.

(iii) Interpretability. Compared with the previously existing methods, TimeMIL could provide the interpretable interest of the pattern of the network. By visualizing the points of time series that strongly influence predictions, TimeMIL can assist in ensuring model robustness. This can help identify vulnerabilities and reduce the risk of adversarial attacks. Meanwhile, interpretability contributes to the explainability of MTSC, making it easier for researchers, practitioners, and stakeholders to comprehend/validate how and why a model makes specific predictions.

Limitation. We have not yet extended the MIL to consider the cross-channel information. We envision a major difference in expanding the current framework to the multi-channel version of TimeMIL, which could involve designing cross-channel temporal attention and positional encoding. This will be a topic of exploration in future work.

Acknowledgement

This material is based upon the work supported by the National Science Foundation under Grant Number CNS-2204721. It is also supported by our collaborative project with MIT Lincoln Lab under Grant Numbers 2015887 and 7000612889.

References

Amaral et al. (2022) Amaral, K., Li, Z., Ding, W., Crouter, S., and Chen, P. Summertime: Variable-length time series summarization with application to physical activity analysis. ACM Transactions on Computing for Healthcare, 3(4):1–15, 2022.
Andrews et al. (2002) Andrews, S., Tsochantaridis, I., and Hofmann, T. Support vector machines for multiple-instance learning. Advances in neural information processing systems, 15, 2002.
Bakirtzis et al. (2022) Bakirtzis, S., Qiu, K., Wassell, I., Fiore, M., and Zhang, J. Deep-learning-based multivariate time-series classification for indoor/outdoor detection. IEEE Internet of Things Journal, 9(23):24529–24540, 2022.
Chen et al. (2023) Chen, M., Zhang, L., Feng, R., Xue, X., and Feng, J. Rethinking local and global feature representation for dense prediction. Pattern Recognition, 135:109168, 2023.
Cheng et al. (2009) Cheng, H., Tan, P.-N., Potter, C., and Klooster, S. Detection and characterization of anomalies in multivariate time series. In Proceedings of the 2009 SIAM international conference on data mining, pp. 413–424. SIAM, 2009.
Chu et al. (2023) Chu, X., Tian, Z., Zhang, B., Wang, X., and Shen, C. Conditional positional encodings for vision transformers. In The Eleventh International Conference on Learning Representations, 2023. URL https://openreview.net/forum?id=3KWnuT-R1bh.
Dempster et al. (2020) Dempster, A., Petitjean, F., and Webb, G. I. Rocket: exceptionally fast and accurate time series classification using random convolutional kernels. Data Mining and Knowledge Discovery, 34(5):1454–1495, 2020.
donghao & wang xue (2024) donghao, L. and wang xue. ModernTCN: A modern pure convolution structure for general time series analysis. In The Twelfth International Conference on Learning Representations, 2024. URL https://openreview.net/forum?id=vpJMJerXHU.
Early et al. (2024) Early, J., Cheung, G. K., Cutajar, K., Xie, H., Kandola, J., and Twomey, N. Inherently interpretable time series classification via multiple instance learning. In The Twelfth International Conference on Learning Representations, 2024. URL https://openreview.net/forum?id=xriGRsoAza.
Franceschi et al. (2019) Franceschi, J.-Y., Dieuleveut, A., and Jaggi, M. Unsupervised scalable representation learning for multivariate time series. Advances in neural information processing systems, 32, 2019.
Fulcher (2018) Fulcher, B. D. Feature-based time-series analysis. In Feature engineering for machine learning and data analytics, pp. 87–116. CRC press, 2018.
Gabor (1946) Gabor, D. Theory of communication. part 1: The analysis of information. Journal of the Institution of Electrical Engineers-part III: radio and communication engineering, 93(26):429–441, 1946.
Gu & Dao (2023) Gu, A. and Dao, T. Mamba: Linear-time sequence modeling with selective state spaces. arXiv preprint arXiv:2312.00752, 2023.
Gu et al. (2022) Gu, A., Goel, K., and Re, C. Efficiently modeling long sequences with structured state spaces. In International Conference on Learning Representations, 2022. URL https://openreview.net/forum?id=uYLFoz1vlAC.
Guan et al. (2016) Guan, X., Raich, R., and Wong, W.-K. Efficient multi-instance learning for activity recognition from time series data using an auto-regressive hidden markov model. In International Conference on Machine Learning, pp. 2330–2339. PMLR, 2016.
Ilse et al. (2018) Ilse, M., Tomczak, J., and Welling, M. Attention-based deep multiple instance learning. In International conference on machine learning, pp. 2127–2136. PMLR, 2018.
Ismail Fawaz et al. (2019) Ismail Fawaz, H., Forestier, G., Weber, J., Idoumghar, L., and Muller, P.-A. Deep learning for time series classification: a review. Data mining and knowledge discovery, 33(4):917–963, 2019.
Ismail Fawaz et al. (2020) Ismail Fawaz, H., Lucas, B., Forestier, G., Pelletier, C., Schmidt, D. F., Weber, J., Webb, G. I., Idoumghar, L., Muller, P.-A., and Petitjean, F. Inceptiontime: Finding alexnet for time series classification. Data Mining and Knowledge Discovery, 34(6):1936–1962, 2020.
Jiang et al. (2011) Jiang, R., Fei, H., and Huan, J. Anomaly localization for network data streams with graph joint sparse pca. In Proceedings of the 17th ACM SIGKDD international conference on Knowledge discovery and data mining, pp. 886–894, 2011.
Karim et al. (2019) Karim, F., Majumdar, S., Darabi, H., and Harford, S. Multivariate lstm-fcns for time series classification. Neural networks, 116:237–245, 2019.
Lai et al. (2018a) Lai, G., Chang, W.-C., Yang, Y., and Liu, H. Modeling long-and short-term temporal patterns with deep neural networks. In The 41st international ACM SIGIR conference on research & development in information retrieval, pp. 95–104, 2018a.
Lai et al. (2018b) Lai, G., Chang, W.-C., Yang, Y., and Liu, H. Modeling long-and short-term temporal patterns with deep neural networks. In The 41st international ACM SIGIR conference on research & development in information retrieval, pp. 95–104, 2018b.
Li et al. (2024a) Li, A., Li, H., and Yuan, G. Continual learning with deep neural networks in physiological signal data: A survey. In Healthcare, volume 12, pp. 155. MDPI, 2024a.
Li et al. (2021a) Li, B., Li, Y., and Eliceiri, K. W. Dual-stream multiple instance learning network for whole slide image classification with self-supervised contrastive learning. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pp. 14318–14328, 2021a.
Li et al. (2021b) Li, G., Choi, B., Xu, J., Bhowmick, S. S., Chun, K.-P., and Wong, G. L.-H. Shapenet: A shapelet-neural network approach for multivariate time series classification. In Proceedings of the AAAI conference on artificial intelligence, volume 35, pp. 8375–8383, 2021b.
Li et al. (2023a) Li, H., Chen, X., Ditzler, G., Killgore, W. D., Quan, S. F., Roveda, J., and Li, A. Sleep stage classification with learning from evolving datasets. Authorea Preprints, 2023a.
Li et al. (2024b) Li, H., Carreon-Rascon, A. S., Chen, X., Yuan, G., and Li, A. Mts-lof: medical time-series representation learning via occlusion-invariant features. IEEE Journal of Biomedical and Health Informatics, 2024b.
Li et al. (2023b) Li, Z., Qi, S., Li, Y., and Xu, Z. Revisiting long-term time series forecasting: An investigation on linear mapping. arXiv preprint arXiv:2305.10721, 2023b.
Li et al. (2023c) Li, Z., Rao, Z., Pan, L., and Xu, Z. Mts-mixers: Multivariate time series forecasting via factorized temporal and channel mixing. arXiv preprint arXiv:2302.04501, 2023c.
Li et al. (2024c) Li, Z., Ding, W., Mashukov, I., Crouter, S., and Chen, P. A multi-view feature construction and multi-encoder-decoder transformer architecture for time series classification. In Pacific-Asia Conference on Knowledge Discovery and Data Mining, pp. 239–250. Springer, 2024c.
Lim & Zohren (2021) Lim, B. and Zohren, S. Time-series forecasting with deep learning: a survey. Philosophical Transactions of the Royal Society A, 379(2194):20200209, 2021.
Lin et al. (2012) Lin, J., Williamson, S., Borne, K., and DeBarr, D. Pattern recognition in time series. Advances in Machine Learning and Data Mining for Astronomy, 1(617-645):3, 2012.
Liu et al. (2023) Liu, H., Liu, X., Yang, D., Liang, Z., Wang, H., Cui, Y., and Gu, J. Todynet: Temporal dynamic graph neural network for multivariate time series classification. arXiv preprint arXiv:2304.05078, 2023.
Liu et al. (2022) Liu, M., Zeng, A., Chen, M., Xu, Z., Lai, Q., Ma, L., and Xu, Q. Scinet: Time series modeling and forecasting with sample convolution and interaction. Advances in Neural Information Processing Systems, 35:5816–5828, 2022.
Loshchilov & Hutter (2017) Loshchilov, I. and Hutter, F. Decoupled weight decay regularization. arXiv preprint arXiv:1711.05101, 2017.
Malhotra et al. (2015) Malhotra, P., Vig, L., Shroff, G., Agarwal, P., et al. Long short term memory networks for anomaly detection in time series. In Esann, volume 2015, pp. 89, 2015.
Nie et al. (2023) Nie, Y., Nguyen, N. H., Sinthong, P., and Kalagnanam, J. A time series is worth 64 words: Long-term forecasting with transformers. In The Eleventh International Conference on Learning Representations, 2023. URL https://openreview.net/forum?id=Jbdc0vTOcol.
Qiu et al. (2023) Qiu, P., Xiao, P., Zhu, W., Wang, Y., and Sotiras, A. Sc-mil: Sparsely coded multiple instance learning for whole slide image classification. arXiv preprint arXiv:2311.00048, 2023.
Ruiz et al. (2021) Ruiz, A. P., Flynn, M., Large, J., Middlehurst, M., and Bagnall, A. The great multivariate time series classification bake off: a review and experimental evaluation of recent algorithmic advances. Data Mining and Knowledge Discovery, 35(2):401–449, 2021.
Schäfer & Leser (2017) Schäfer, P. and Leser, U. Multivariate time series classification with weasel+ muse. arXiv preprint arXiv:1711.11343, 2017.
Seto et al. (2015) Seto, S., Zhang, W., and Zhou, Y. Multivariate time series classification using dynamic time warping template selection for human activity recognition. In 2015 IEEE symposium series on computational intelligence, pp. 1399–1406. IEEE, 2015.
Shannon (1951) Shannon, C. E. Prediction and entropy of printed english. Bell system technical journal, 30(1):50–64, 1951.
Shao et al. (2021) Shao, Z., Bian, H., Chen, Y., Wang, Y., Zhang, J., Ji, X., et al. Transmil: Transformer based correlated multiple instance learning for whole slide image classification. Advances in neural information processing systems, 34:2136–2147, 2021.
Shen et al. (2021) Shen, Z., Zhang, M., Zhao, H., Yi, S., and Li, H. Efficient attention: Attention with linear complexities. In Proceedings of the IEEE/CVF winter conference on applications of computer vision, pp. 3531–3539, 2021.
Shokoohi-Yekta et al. (2017) Shokoohi-Yekta, M., Hu, B., Jin, H., Wang, J., and Keogh, E. Generalizing dtw to the multi-dimensional case requires an adaptive approach. Data mining and knowledge discovery, 31:1–31, 2017.
Stikic et al. (2011) Stikic, M., Larlus, D., Ebert, S., and Schiele, B. Weakly supervised recognition of daily life activities with wearable sensors. IEEE transactions on pattern analysis and machine intelligence, 33(12):2521–2537, 2011.
Tang et al. (2022) Tang, W., Long, G., Liu, L., Zhou, T., Blumenstein, M., and Jiang, J. Omni-scale CNNs: a simple and effective kernel size configuration for time series classification. In International Conference on Learning Representations, 2022. URL https://openreview.net/forum?id=PDYs7Z2XFGv.
Tang et al. (2023) Tang, Z., Patyk, A., Jolly, J., Goldstein, S. P., Thomas, J. G., and Hoover, A. Detecting eating episodes from wrist motion using daily pattern analysis. IEEE Journal of Biomedical and Health Informatics, 2023.
Vaswani et al. (2017a) Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I. Attention is all you need. Advances in neural information processing systems, 30, 2017a.
Vaswani et al. (2017b) Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I. Attention is all you need. Advances in neural information processing systems, 30, 2017b.
Vrba & Robinson (2001) Vrba, J. and Robinson, S. E. Signal processing in magnetoencephalography. Methods, 25(2):249–271, 2001.
Wang et al. (2023) Wang, H., Peng, J., Huang, F., Wang, J., Chen, J., and Xiao, Y. MICN: Multi-scale local and global context modeling for long-term series forecasting. In The Eleventh International Conference on Learning Representations, 2023. URL https://openreview.net/forum?id=zt53IDUR1U.
Wang et al. (2020) Wang, S., Li, B. Z., Khabsa, M., Fang, H., and Ma, H. Linformer: Self-attention with linear complexity. arXiv preprint arXiv:2006.04768, 2020.
Wang et al. (2018) Wang, X., Yan, Y., Tang, P., Bai, X., and Liu, W. Revisiting multiple instance neural networks. Pattern Recognition, 74:15–24, 2018.
Wu et al. (2022) Wu, H., Wu, J., Xu, J., Wang, J., and Long, M. Flowformer: Linearizing transformers with conservation flows. In Chaudhuri, K., Jegelka, S., Song, L., Szepesvari, C., Niu, G., and Sabato, S. (eds.), Proceedings of the 39th International Conference on Machine Learning, volume 162 of Proceedings of Machine Learning Research, pp. 24226–24242. PMLR, 17–23 Jul 2022. URL https://proceedings.mlr.press/v162/wu22m.html.
Wu et al. (2023) Wu, H., Hu, T., Liu, Y., Zhou, H., Wang, J., and Long, M. Timesnet: Temporal 2d-variation modeling for general time series analysis. In The Eleventh International Conference on Learning Representations, 2023. URL https://openreview.net/forum?id=ju_Uqw384Oq.
Xiang & Zhang (2023) Xiang, J. and Zhang, J. Exploring low-rank property in multiple instance learning for whole slide image classification. In The Eleventh International Conference on Learning Representations, 2023.
Xiong et al. (2021) Xiong, Y., Zeng, Z., Chakraborty, R., Tan, M., Fung, G., Li, Y., and Singh, V. Nyströmformer: A nyström-based algorithm for approximating self-attention. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 35, pp. 14138–14148, 2021.
Zeng et al. (2023) Zeng, A., Chen, M., Zhang, L., and Xu, Q. Are transformers effective for time series forecasting? In Proceedings of the AAAI conference on artificial intelligence, volume 37, pp. 11121–11128, 2023.
Zhang et al. (2022a) Zhang, H., Meng, Y., Zhao, Y., Qiao, Y., Yang, X., Coupland, S. E., and Zheng, Y. Dtfd-mil: Double-tier feature distillation multiple instance learning for histopathology whole slide image classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 18802–18812, 2022a.
Zhang et al. (2019) Zhang, M., Lucas, J., Ba, J., and Hinton, G. E. Lookahead optimizer: k steps forward, 1 step back. Advances in neural information processing systems, 32, 2019.
Zhang et al. (2022b) Zhang, T., Zhang, Y., Cao, W., Bian, J., Yi, X., Zheng, S., and Li, J. Less is more: Fast multivariate time series forecasting with light sampling-oriented mlp structures. arXiv preprint arXiv:2207.01186, 2022b.
Zhang et al. (2020) Zhang, X., Gao, Y., Lin, J., and Lu, C.-T. Tapnet: Multivariate time series classification with attentional prototypical network. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 34, pp. 6845–6852, 2020.
Zhang & Yan (2023) Zhang, Y. and Yan, J. Crossformer: Transformer utilizing cross-dimension dependency for multivariate time series forecasting. In The Eleventh International Conference on Learning Representations, 2023. URL https://openreview.net/forum?id=vSVLM2j9eie.
Zhao et al. (2023) Zhao, B., Xing, H., Wang, X., Xiao, Z., and Xu, L. Classification-oriented distributed semantic communication for multivariate time series. IEEE Signal Processing Letters, 2023.
Zhou et al. (2022) Zhou, T., Ma, Z., Wen, Q., Wang, X., Sun, L., and Jin, R. Fedformer: Frequency enhanced decomposed transformer for long-term series forecasting. In International Conference on Machine Learning, pp. 27268–27286. PMLR, 2022.
Zhu et al. (2023) Zhu, W., Qiu, P., Dumitrascu, O. M., and Wang, Y. Pdl: Regularizing multiple instance learning with progressive dropout layers. arXiv preprint arXiv:2308.10112, 2023.
Zhu et al. (2021) Zhu, Y., Shi, W., Pandey, D. S., Liu, Y., Que, X., Krutz, D. E., and Yu, Q. Uncertainty-aware multiple instance learning from large-scale long time series data. In 2021 IEEE International Conference on Big Data (Big Data), pp. 1772–1778. IEEE, 2021.

Appendix A UEA Datasets Detail

The detail of all 30 datasets is provided in Table 4. It should be noteworthy that the datasets JapaneseVowels and SpokenArabicDigits used in the Group 2 Experiment originally have varied lengths of sequences. We pre-process it following (Wu et al., 2023), where we pad them to 29 and 93, respectively.

Table 4: Dataset Summary

Dataset	Train Size	Test Size	Dimensions	Length	Classes
ArticularyWordRecognition	275	300	9	144	25
AtrialFibrillation	15	15	2	640	3
BasicMotions	40	40	6	100	4
CharacterTrajectories	1422	1436	3	182	20
Cricket	108	72	6	1197	12
DuckDuckGeese	60	40	1345	270	5
EigenWorms	128	131	6	17984	5
Epilepsy	137	138	3	206	4
EthanolConcentration	261	263	3	1751	4
ERing	30	30	4	65	6
FaceDetection	5890	3524	144	62	2
FingerMovements	316	100	28	50	2
HandMovementDirection	320	147	10	400	4
Handwriting	150	850	3	152	26
Heartbeat	204	205	61	405	2
JapaneseVowels	270	370	12	29 (max)	9
Libras	180	180	2	45	15
LSST	2459	2466	6	36	14
InsectWingbeat	30000	20000	200	78	10
MotorImagery	278	100	64	3000	2
NATOPS	180	180	24	51	6
PenDigits	7494	3498	2	8	10
PEMS-SF	267	173	963	144	7
Phoneme	3315	3353	11	217	39
RacketSports	151	152	6	30	4
SelfRegulationSCP1	268	293	6	896	2
SelfRegulationSCP2	200	180	7	1152	2
SpokenArabicDigits	6599	2199	13	93 (max)	10
StandWalkJump	12	15	4	2500	3
UWaveGestureLibrary	120	320	3	315	8

Appendix B More detail of Theorem 1

We provide an intuition behind this from the perspective of Hausdorff distance, which is defined to measure the difference between two sets from the same feasible domain. Let $(\mathcal{X},d)$ be a metric space, for each pair of non-empty sets ( $\boldsymbol{X},\boldsymbol{X}^{\prime})\subset\mathcal{X}$ , their Hausdorff distance $d_{\mathrm{H}}$ is computed as

	$\displaystyle d_{\mathrm{H}}(\boldsymbol{X}_{i},\boldsymbol{X}_{j}):=\max\{$	$\displaystyle\sup_{\boldsymbol{x}_{i}^{t}\in\boldsymbol{X}_{i}}\inf_{\boldsymbol{x}_{j}^{t^{\prime}}\in\boldsymbol{X}_{j}}d(\boldsymbol{x}_{i}^{t},\boldsymbol{x}_{j}^{t^{\prime}}),$
		$\displaystyle\sup_{\boldsymbol{x}_{j}^{t}\in\boldsymbol{X}_{j}}\inf_{\boldsymbol{x}_{i}^{t^{\prime}}\in\boldsymbol{X}_{i}}d(\boldsymbol{x}_{j}^{t},\boldsymbol{x}_{i}^{t^{\prime}})\},$		(19)

where $\sup$ and $\inf$ denote the supremum operator and the infimum operator, respectively. Eq. B implies that Hausdorff distance measures the furthest distance of traveling from a certain point in a set to its nearest point in the other set under the worst-case scenario. Hence, Hausdorff distance can only measure the distance of time points across different sets and fails to model the time ordering information.

Appendix C Proof of Proposition 2

Proof.

The existence of equality can be easily proved by assuming the time series is always a constant value, which, regardless of permutation, the entropy is 0. The existence of inequality can be proved by contradiction. Suppose a sequence with a length of 2, presenting two tests $\{(\Theta^{1}|t^{1}),(\Theta^{2}|t^{2})\}$ for a product. Suppose the probability of passing each test obeys $(\Theta^{i})\sim Bernoulli(p=e^{-3+i})$ . Suppose the ordering information says the test with index $t^{2}$ occurs if the product passes the test with index $t^{1}$ . we have $p(0,0)=1-e^{-2},p(0,1)=0,p(1,0)=e^{-2}(1-e^{-1}),p(1,1)=e^{-1}e^{-2}$ .

	$\displaystyle H(\{(\Theta^{1}\|t^{1}),(\Theta^{2}\|t^{2})\})$	(20)
$\displaystyle=$	$\displaystyle-(1-e^{-2})\log(1-e^{-2})-0\log 0-e^{-2}(1-e^{-1})\log(e^{-2}(1-e^{-1}))-e^{-1}e^{-2}\log(e^{-1}e^{-2})$
$\displaystyle=$	$\displaystyle 0.70~{}\text{bit},$

After permuting sequence, $p(0,0)=1-e^{-1},p(0,1)=0,p(1,0)=e^{-1}(1-e^{-2}),p(1,1)=e^{-1}e^{-2}$ . The entropy of the permuted sequence is presented as,

	$\displaystyle H(\{(\Theta^{1}\|t^{2}),(\Theta^{2}\|t^{1})\})$	(21)
$\displaystyle=$	$\displaystyle-(1-e^{-1})\log(1-e^{-1})-0\log 0-e^{-1}(1-e^{-2})\log(e^{-1}(1-e^{-2}))-e^{-1}e^{-2}\log(e^{-1}e^{-2})$
$\displaystyle=$	$\displaystyle 1.16~{}\text{bit},$

which are apparently different, and the existence of inequality is proved.

∎

Appendix D Block Entropy

Block entropy, also known as N-gram entropy, is used to measure the uncertainty of a sequence by (Shannon, 1951). Suppose a list of overlapping blocks is generated via a sliding window with a size of $n$ , where the $j$ -th block is $B_{j}^{(n)}=\left(X_{j},\ldots,X_{j+n-1}\right)$ . Suppose the set of all appearance of blocks denotes $\left\{b_{1}^{(n)},\cdots,b_{i}^{(n),\cdots}\right\}$ . For example, in a sequence $AAABBCD$ , the set of all possible blocks is $\{AA,AB,BB,BC,CD\}$ . Then, the block entropy is defined by

\displaystyle H_{n}=-\sum_{i=1}^{L^{n}}p\left(b_{i}^{(n)}\right)\log\left(p\left(b_{i}^{(n)}\right)\right),

(22)

where $p\left(b_{i}^{(n)}\right)$ denotes the probability of appearance of the block sequence $b_{i}^{(n)}$ . We set $n=2$ in our experiment.

Appendix E Background of Wavelet Transform

Mathematically, a wavelet basis $\psi_{a,b}$ is a generated by scaling $a$ and translations $b$ of a single function named mother wavelet $\psi\in L^{2}(\mathbb{R})$ , where $L^{2}(\mathbb{R})$ denotes the Hilbert space of square integrable functions,

\displaystyle\psi_{a,b}(t)=\frac{1}{\sqrt{|a|}}\psi\left(\frac{x-b}{a}\right).

(23)

It is noteworthy that the basis $\psi_{a,b}$ is a Hilbert basis, which implies every basis is orthogonal with each other,

\displaystyle\left\langle\psi_{a,b},\psi_{a^{\prime},b^{\prime}}\right\rangle\equiv\int_{-\infty}^{\infty}\psi_{a,b}(t)\psi_{a^{\prime},b^{\prime}}(t)dt=0.

(24)

This also ensures that different wavelet basis are exploring diverse context of the signal. The Continuous Wavelet Transform (CWT) of a 1D signal $f(t)$ is defined by

\displaystyle f(a,b)

\displaystyle=\int_{-\infty}^{\infty}f(t)\psi_{a,b}(t)dt=f(t)\circledast\psi_{a,b}(t),

(25)

where $\circledast$ denotes the convolutional operation. We then present the uncertainty principles.

Theorem 4.

(Gabor, 1946) Uncertainty principles in the time-frequency version (also known as the Gabor-Heisenberg limit ):

\displaystyle\sigma_{t}\cdot\sigma_{f}\geq\frac{1}{4\pi},

(26)

where $\sigma_{t}$ and $\sigma_{f}$ denote the measured time and frequency standard deviations, respectively.

We show more diverse learned Wavelet kernel in Fig. 7.

Appendix F Implementation Detail

F.1 Baselines

ED-1NN, DTW-1NN-I, and DTW-1NN-D are most popular baselines for MTSC: (i) ED-1NN: It applies the nearest neighbor classifier based on Euclidean distance. (ii) DTW-1NN-I: It applies the nearest neighbor classifier based on dynamic time warping (DTW) that processes each dimension independently. and (iii) DTW-1NN-D: It applies the nearest neighbor classifier based on DTW that processes all dimensions simultaneously.

F.2 More detail about the Architecture

We use AdamW optimizer (Loshchilov & Hutter, 2017) with a fixed learning rate 1e-3 and a 1e-4 weight decay. We also use Lookahead scheduler (Zhang et al., 2019). Batch sizes are tuned based on the datasets since there are large differences in the dimension and length of each dataset.

As discussed in Section 3.3, we use Nyström Self-attention (Xiong et al., 2021) for accelerating the computation. Specifically, we set the embedding dimension $d_{model}=512$ , the number of MHSA heads to $8$ . For the Nystrom-based matrix approximation, we set the number of landmark points to 256 and the number of moore-penrose iterations for approximating pseudo-inverse to 6, which is recommended by its original paper. The final classifier consists of two fully connected layers: $\mathbb{R}^{L}\rightarrow\mathbb{R}^{L}\rightarrow\mathbb{R}^{C}$ , where $C$ denotes the number of classes. We only feed the class token to the classifier. To facilitate the assumption of TimeMIL that treats MTSC as several one-vs-rest (OvR) binary classifications in the context of MIL, we use the binary cross entropy with one-hot encoding for the sequence label. We also adopt window-based random masking augmentation and a warm-up technique, as discussed below. The importance score can be conveniently approximated by using Average-Pooling Based Attention (APBA) proposed by (Zhu et al., 2023).

F.3 Window-based Random Masking Augmentation

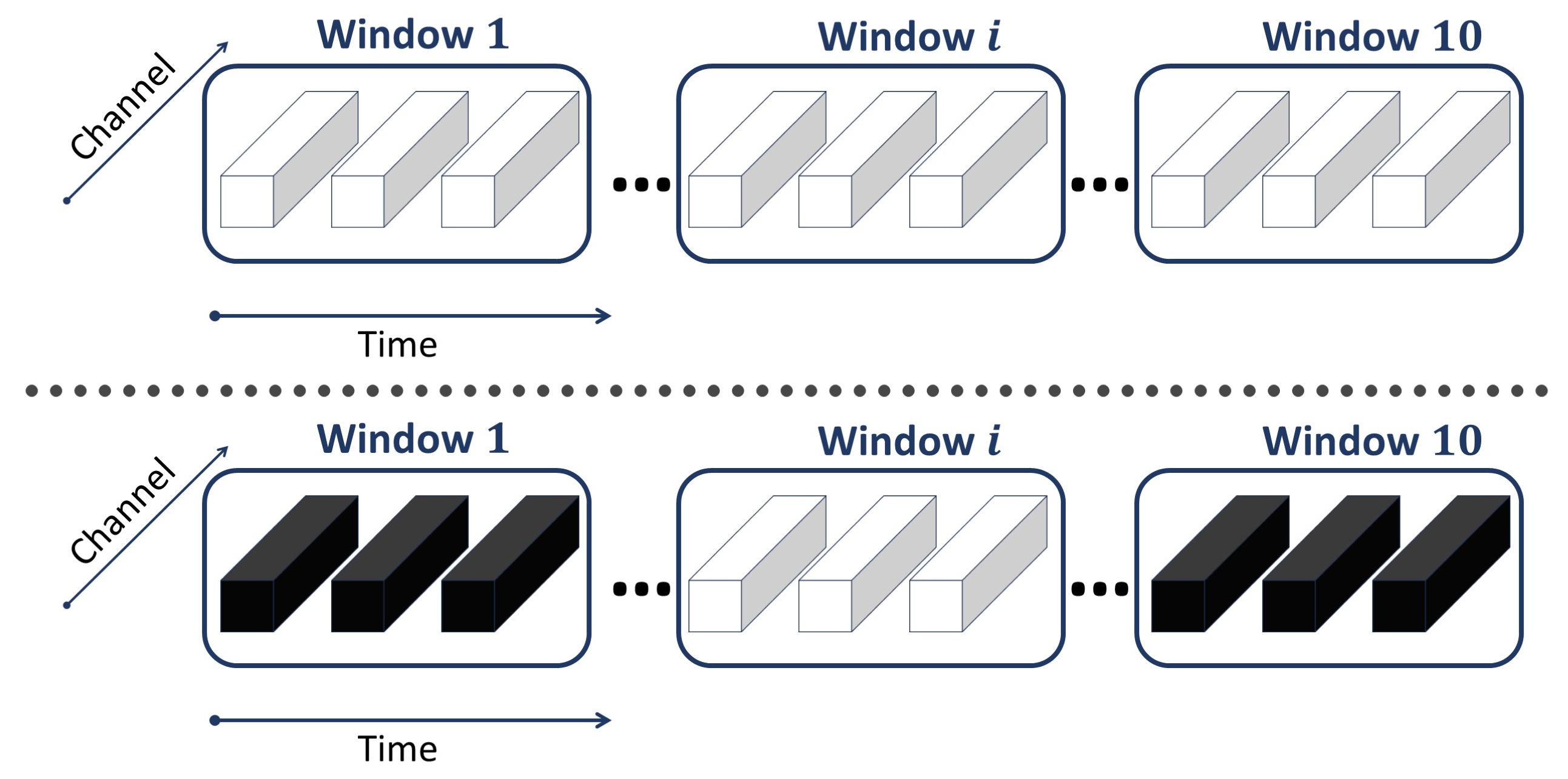
This augmentation is only applied to the raw data in the training phase and aims to lead the model to learn the occlusion-invariant features. Recall the length of the input sequence is $T$ . We first generate 10 non-overlapping windows with a size of $T/10$ that can fully cover the entire sequence. Suppose their indices are $[10]=\{1,2,\cdots,10\}$ . For each iteration, we sample a set of windows $\mathcal{S}$ with a cardinality $|\mathcal{S}|=10p,p\in(0,1)$ from $[10]$ without replacement. Then, we set the time points covered by the windows in $\mathcal{S}$ to a random noise $\mathcal{N}(0,1)$ . The example is shown in Fig. 8. We set $p\in\{0,0.5\}$ in our experiment.

F.4 warm-up Training Strategy

Considering the Transformer-like architecture learns slowly at the beginning, to facilitate the easy gradient flow to the backbone, we apply the following warm-up strategy. Recall the embedding of features is denoted as $\hat{\boldsymbol{x}}_{i}$ , and the class token $\boldsymbol{x}_{i}^{\operatorname{cls}}$ after applying two transformer blocks. At the first few epochs (empirically set 10), we use $\alpha\mathbb{E}_{t}(\hat{\boldsymbol{x}}_{i}^{t})+(1-\alpha)\boldsymbol{x}_{i}^{\operatorname{cls}}$ to feed the final classifier, where $\alpha=0.99$ . Afterwards, we still use $\boldsymbol{x}_{i}^{\operatorname{cls}}$ for the final classification.

Appendix G Additional Experiments

The additional results on all 30 UEA datasets are presented in Table 5. It is observed that classification-specific methods (TapNet, MOS-CNN, TodyNet, and Ours) often perform better. We also include Mamba (Gu & Dao, 2023), the recent state-of-the-art Selective State Spaces model. We implement the vanilla version of mamba with different numbers of blocks {1,2,4,8,10,14,22}, and the results are presented in Table 6.

Table 5: Comparison of different methods on 30 UEA datasets. (-) indicates the method is not able to obtain results due to memory limitations (we use an A100 40Gb GPU) on the EigenWorms dataset (dimension of 6 and length of 17894) and MotorImagery dataset (dimension of 64 and length of 3000).

Method	Accuracy	F1	Precision	Recall	AUC-ROC
Crossformer(-)	0.69	0.619	0.633	0.667	0.834
PatchTST	0.702	0.664	0.694	0.686	0.854
TimesNet	0.744	0.7	0.727	0.728	0.864
Dlinear	0.695	0.671	0.678	0.685	0.859
FEDformer	0.701	0.664	0.697	0.682	0.867
TapNet	0.759	0.745	0.764	0.751	0.832
MOS-CNN	0.78	0.764	0.788	0.765	0.863
TodyNet	0.762	0.744	0.759	0.751	0.869
Mamba-8	0.733	0.715	0.743	0.723	0.835
Ours	0.791	0.782	0.790	0.782	0.883

Table 6: Classification performance by Mamba with different number of blocks.

Method	Accuracy	F1	Precision	Recall	AUC-ROC
Mamba-1	0.725	0.704	0.729	0.713	0.827
Mamba-2	0.726	0.705	0.729	0.715	0.83
Mamba-4	0.729	0.711	0.73	0.718	0.832
Mamba-8	0.733	0.715	0.743	0.723	0.835
Mamba-10	0.727	0.705	0.727	0.714	0.833
Mamba-14	0.727	0.706	0.733	0.715	0.829
Mamba-22	0.726	0.708	0.727	0.716	0.829
Ours	0.791	0.782	0.790	0.782	0.883

Appendix H Synthetic Dataset

H.1 Dataset Generation

We simulate a binary dataset similar to noisy pulse signals. Consider the length of a sequence is 120. Again, $\boldsymbol{x}_{i}^{t}$ and ${y}_{i}^{t}$ denote the $t$ th time point of the sequence $\boldsymbol{X}_{i}$ and its instance-level label. A negative sequence is generated as,

\displaystyle\boldsymbol{x}_{i}^{t}\sim\mathcal{N}(0,0.5)\text{ and }{y}_{i}^{t}=0.

(27)

A positive sequence, which consists of a noisy pulse, is generated as,

\displaystyle\boldsymbol{x}_{i}^{t}\sim\left\{\begin{array}[]{l}\mathcal{N}(5,0.5)\text{ and }{y}_{i}^{t}=1\text{, for }t\in[a,a+20]\\ \mathcal{N}(0,0.5)\text{ and }{y}_{i}^{t}=0,\text{ otherwise}\end{array}\right.,

(30)

where, $a\sim\mathcal{U}(55,65)$ , is a random starting point for the pulse signal.

H.2 Decision Boundary

We randomly choose a positive sequence (i.e., a bag) and a negative one from the synthetic dataset. After applying feature extractor, both the positive sequence and negative sequence are projected onto a fixed-length (i.e., $L=128$ ) feature vectors (a positive bag $\boldsymbol{X}_{p}\in\mathbb{R}^{T\times 128}$ and a negative one $\boldsymbol{X}_{n}\in\mathbb{R}^{T\times 128}$ ). In this case, we have a total of 240 time points/instances ( $T=240$ ). Subsequently, we apply PCA for these 240 instances, which reduces their dimensions from 128 to 2 for visualization, meaning we only use the first two principle components.