Topological parafermion corner states
in clock-symmetric non-Hermitian second-order topological insulator

It follows from Eq.(6) that only the zero-energy states form a set of degenerate states respecting $\mathbb{Z}_{3}$ clock symmetry. They are $\mathbb{Z}_{3}$ parafermion states. We denote them as $\left|\psi_{0}\right\rangle$, $\left|\psi_{1}\right\rangle$ and $\left|\psi_{2}\right\rangle$. They are characterized by the properties

	$\displaystyle\tau\left|\psi_{0}\right\rangle$	$\displaystyle=\left|\psi_{1}\right\rangle,\quad\tau\left|\psi_{1}\right\rangle=\left|\psi_{2}\right\rangle,\quad\tau\left|\psi_{2}\right\rangle=\left|\psi_{0}\right\rangle,$		(7)
	$\displaystyle\sigma\left|\psi_{0}\right\rangle$	$\displaystyle=\left|\psi_{0}\right\rangle,\quad\sigma\left|\psi_{1}\right\rangle=\omega\left|\psi_{1}\right\rangle,\quad\sigma\left|\psi_{2}\right\rangle=\omega^{2}\left|\psi_{2}\right\rangle,$		(8)

from which the matrix representations (3) and (4) follow. Then, the $\mathbb{Z}_{3}$ parafermion relations (5) are verifed. Namely, it is necessary and sufficient to examine Eqs.(7) and (8) for a triplet set of zero-energy states in order to show that they are $\mathbb{Z}_{3}$ parafermions.

We propose a model possessing parafermions on the breathing Kagome lattice. The bulk Hamiltonian is given by

$$H=\left(\begin{array}[]{ccc}0&h_{12}&\omega h_{13}\\ h_{12}^{\ast}&0&\omega^{2}h_{23}\\ \omega h_{13}^{\ast}&\omega^{2}h_{23}^{\ast}&0\end{array}\right),$$

(9)

with

	$\displaystyle h_{12}$	$\displaystyle=t_{a}+t_{b}e^{ik_{x}},$		(10)
	$\displaystyle h_{23}$	$\displaystyle=t_{a}+t_{b}e^{-i\left(k_{x}/2+\sqrt{3}k_{y}/2\right)},$		(11)
	$\displaystyle h_{13}$	$\displaystyle=t_{a}+t_{b}e^{-i\left(k_{x}/2-\sqrt{3}k_{y}/2\right)},$		(12)

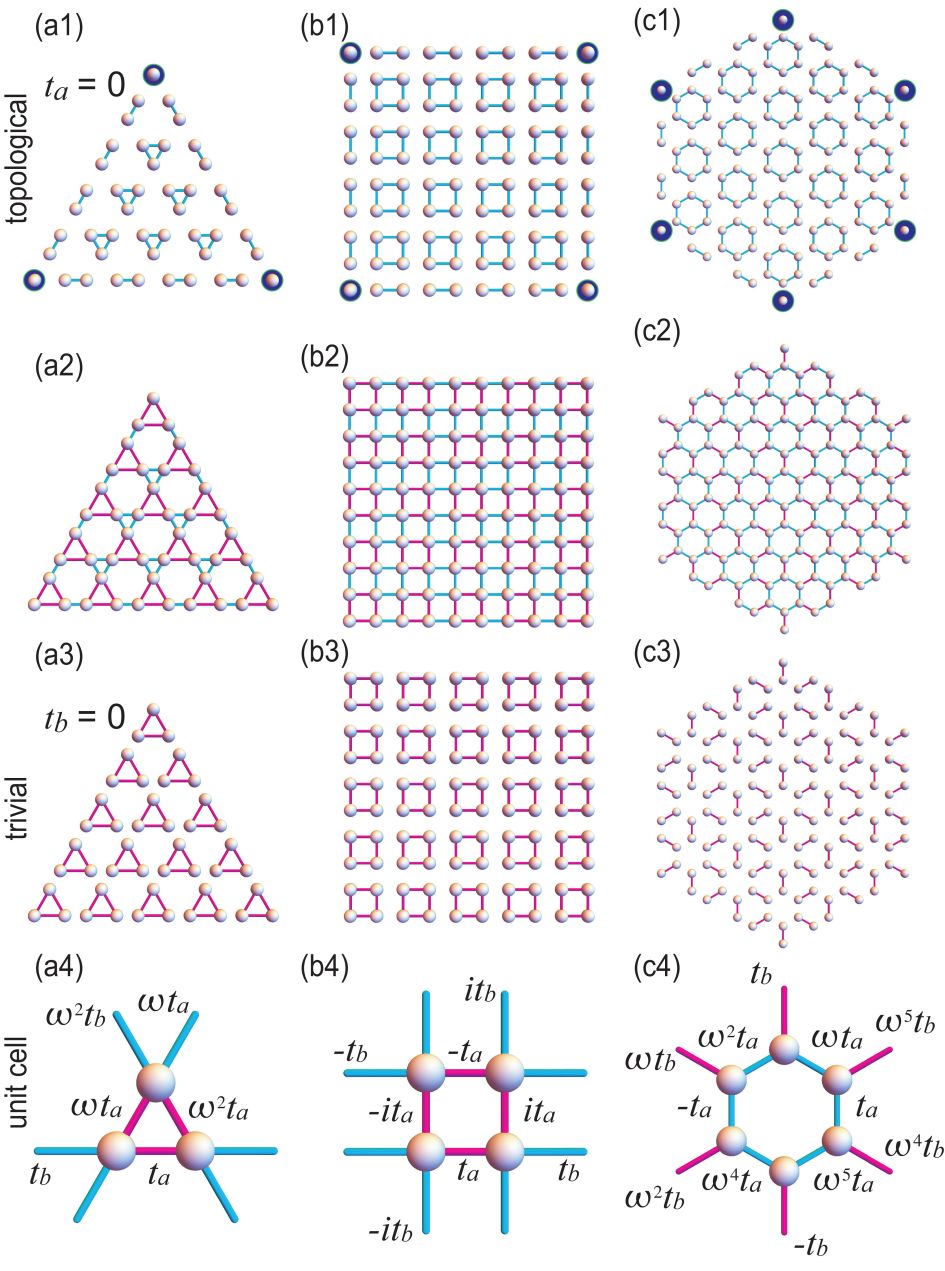
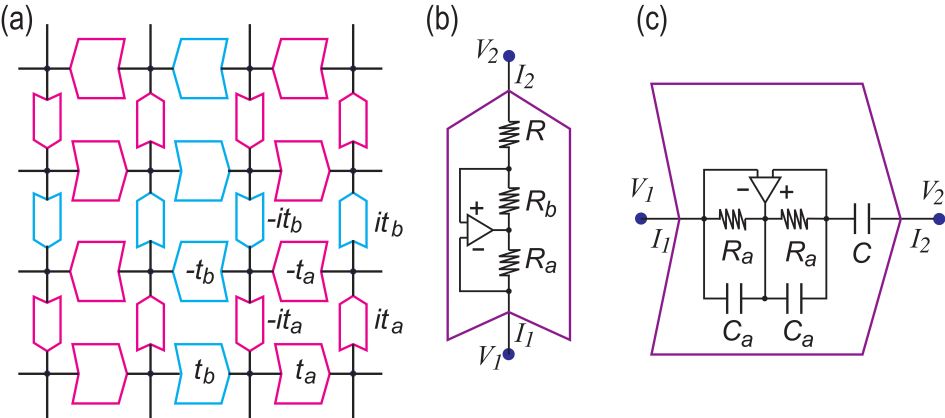
where we have introduced two hopping parameters $t_{a}$ and $t_{b}$, corresponding to the magenta link and the cyan link along the horizontal axis in Fig.1(a4). The hopping parameters along the other two triangle sides are given by $\omega t_{a}$ and $\omega^{2}t_{a}$ for a magenta triangle, and $\omega t_{b}$ and $\omega^{2}t_{b}$ for a cyan triangle. This model is non-Hermitian due to the presence of $\omega$.

A comment is in order with respect to the breathing Kagome model. It is a typical model for the conventional second-order topological insulatorKagome , where the factor $\omega$ is absent and it is Hermitian. The present generalization of the breathing Kagome lattice model provides us with a new type of non-Hermitian second-order topological insulators.

The Hamiltonian (9) has $\mathbb{Z}_{3}$ clock symmetryFend ,

$$\tau H\left(\mathbf{k}\right)\tau^{\dagger}=\omega H\left(R\mathbf{k}\right),$$

(13)

where $R$ rotates the momentum by 120 degrees as

	$\displaystyle R\left(k_{x},0\right)$	$\displaystyle=\left(-\frac{k_{x}}{2},\frac{\sqrt{3}k_{y}}{2}\right),$		(14)
	$\displaystyle R\left(-\frac{k_{x}}{2},\frac{\sqrt{3}k_{y}}{2}\right)$	$\displaystyle=\left(-\frac{k_{x}}{2},-\frac{\sqrt{3}k_{y}}{2}\right),$		(15)
	$\displaystyle R\left(-\frac{k_{x}}{2},-\frac{\sqrt{3}k_{y}}{2}\right)$	$\displaystyle=\left(k_{x},0\right),$		(16)

making the energy spectrum have $\mathbb{Z}_{3}$ symmetry in the complex plane as in Eq.(6). In addition, there is an anti-unitary symmetry

$$KH\left(\mathbf{k}\right)K=H^{\ast}\left(\mathbf{k}\right),$$

(17)

where $K$ implies complex conjugate. It leads to reflection symmetry between $E$ and $E^{\ast}$. As a result, the energy spectrum has $C_{3v}$ symmetry in the complex plane, which consists of the three-fold rotational symmetry and three reflection symmetries.

The system also has a generalized chiral symmetry for a three-band modelNi ,

	$\displaystyle\sigma H\sigma^{-1}$	$\displaystyle=$	$\displaystyle H_{1},\qquad\sigma H_{1}\sigma^{-1}=H_{2},$
	$\displaystyle H+H_{1}+H_{2}$	$\displaystyle=$	$\displaystyle 0.$		(18)

We show the bulk energy spectrum in Fig.3(a) and Fig.4(a), where $C_{3v}$ symmetry is manifest for all parameters.

The notion of insulator and metal is generalized to the non-Hermitian Hamiltonian in two ways. On is a point-gap insulatorGong ; Kawabata , where $|E|$ has a gap. The other is a line-gap insulatorGong ; Kawabata , where Re$\left[E\right]$ or Im$\left[E\right]$ has a gap. In our model, we adopt the definition of the point-gap insulator due to $\mathbb{Z}_{3}$ symmetry. We are able to determine the energy spectrum analytically at the $\Gamma=(0,0)$ point as

$$E\left(0,0\right)=(t_{a}+t_{b}),\quad\omega(t_{a}+t_{b}),\quad\omega^{2}(t_{a}+t_{b}),$$

(19)

and at the $K=(4\pi/3,0)$ and $K^{\prime}=(-4\pi/3,0)$ points as

$$E^{3}(\pm 4\pi/3,0)=\left(t_{a}+t_{b}\right)\left(t_{a}-2t_{b}\right)\left(2t_{a}-t_{b}\right).$$

(20)

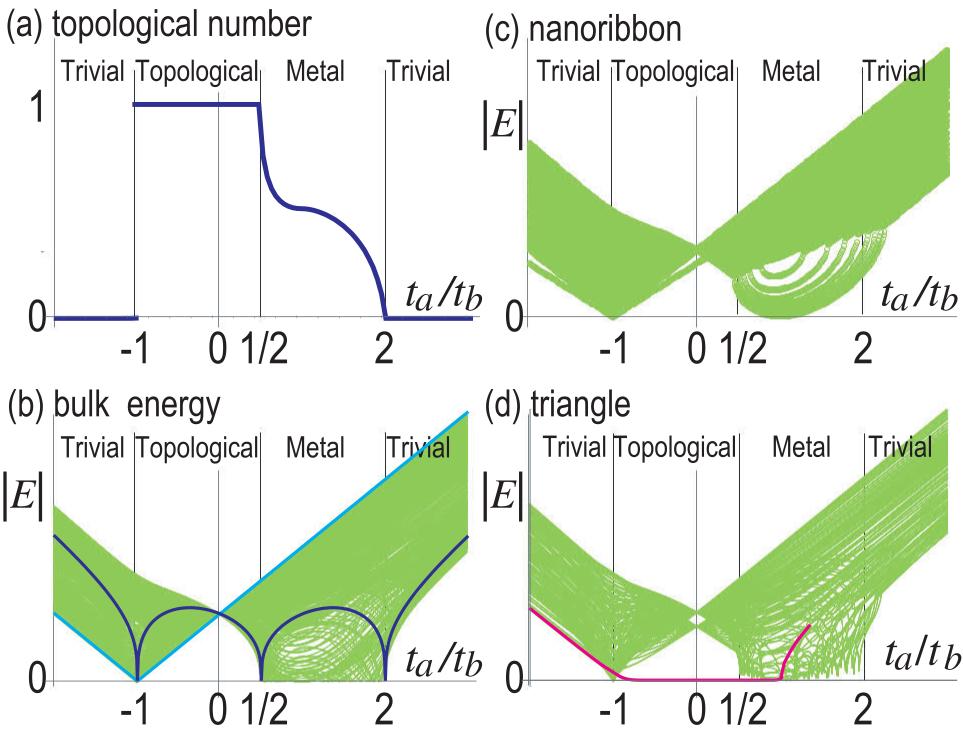
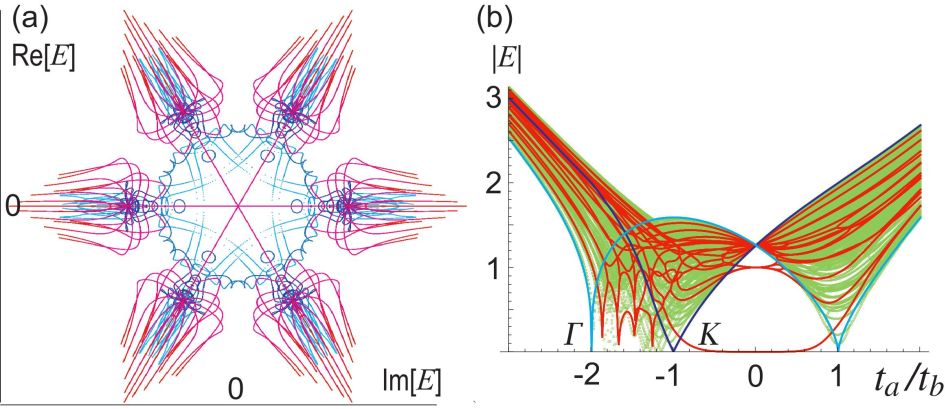
The point gap closes at the $K$ and $K^{\prime}$ points for $t_{a}/t_{b}=1/2$, $t_{a}/t_{b}=2$, and at the $K$, $K^{\prime}$ and $\Gamma$ points for $t_{a}/t_{b}=-1$, as in Fig.2(b). This is also confirmed numerically by calculating the band spectrum as in Fig.2(b).

The topological number is given by the Berry phase defined by

$$Q\equiv\frac{1}{2\pi i}\int_{0}^{2\pi}\left\langle\psi_{0}\left(k_{x},0\right)\right|\partial_{k_{x}}\left|\psi_{0}\left(k_{x},0\right)\right\rangle dk_{x},$$

(21)

where $\psi_{0}$ is the eigen function of the Hamiltonian (9) for the bulk, whose eigen energy is real along the $k_{x}$ axis (i.e., $k_{y}=0$). We calculate it numerically, whose results are shown in Fig.2(a). We find $Q=1$ for $-1<t_{a}/t_{b}<1/2$, and $Q=0$ for $t_{a}/t_{b}<-1$ and $t_{a}/t_{b}>2$, while it continuously changes from $1$ to $0$ for $1/2<t_{a}/t_{b}<2$. In fact, $Q$ is quantized in the insulator phases.

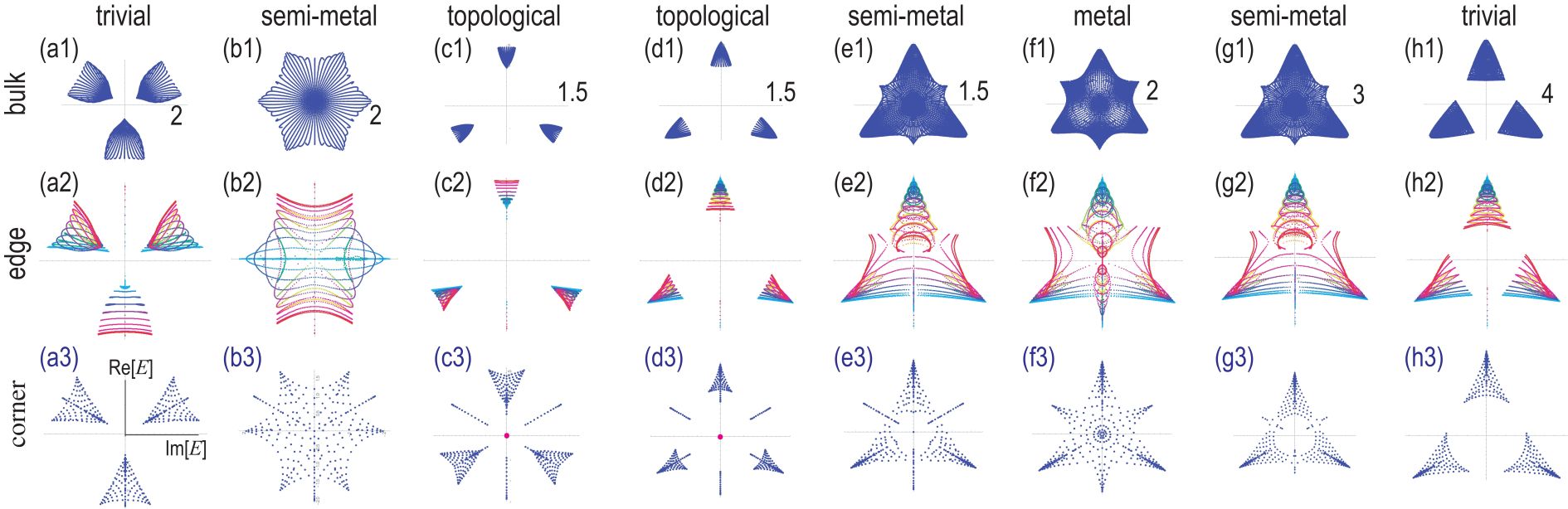
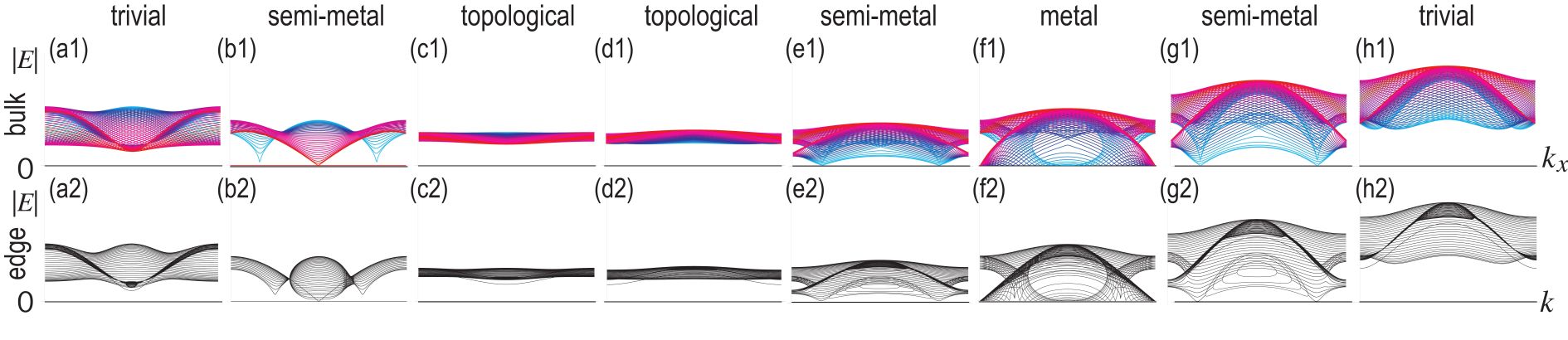
We calculate the energy spectrum in a nanoribbon numerically. Edge states are observed in Fig.4(a2)$\sim$(h2), where the complex energy spectrum is shown for various momentum $k$ specified by color. Three-fold symmetry is slightly broken in nanoribbon geometry. It is due to the finite size effect of a nanoribbon.

We present the band structure of a nanoribbon in Fig.5(a2)$\sim$(h2), where we observe the absence of gapless edge states in the topological phase.

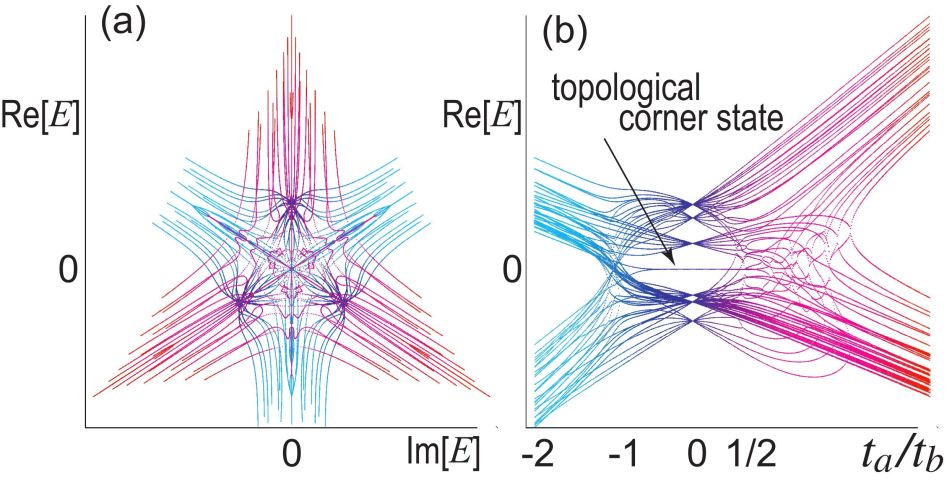
We calculate the energy spectrum in triangle geometry numerically. $C_{3v}$ symmetry is manifest as shown in Fig.3(a) and in Fig.4(a3)$\sim$(h3). It is because the triangle respects $\mathbb{Z}_{3}$ clock symmetry. We find zero-energy states in the region $-1<t_{a}/t_{b}<1/2$, as indicated by a magenta line in Fig.2(d). We also show the energy spectrum as a function of $t_{a}/t_{b}$ in Fig.3(b), where the emergence of the zero-energy states is manifest in the topological phase.

Consequently, the present model is a second-order topological insulator in the region $-1<t_{a}/t_{b}<1/2$, being characterized by the emergence of topological corner states.

It is possible to obtain explicitly the wave functions of the three corner states by numerical calculation. We have numerically confirmed that they satisfy the relations (7) and (8). Therefore, they are $\mathbb{Z}_{3}$ parafermions.

Electric circuits are governed by the Kirchhoff current law. By making the Fourier transformation with respect to time, the Kirchhoff current law is expressed as

$$I_{a}\left(\omega\right)=\sum_{b}J_{ab}\left(\omega\right)V_{b}\left(\omega\right),$$

(22)

where $I_{a}$ is the current between node $a$ and the ground, while $V_{b}$ is the voltage at node $b$. The matrix $J_{ab}\left(\omega\right)$ is called the circuit Laplacian. Once the circuit Laplacian is given, we can uniquely setup the corresponding electric circuit. By equating it with the Hamiltonian $H$ asTECNature ; ComPhys

$$J_{ab}\left(\omega\right)=i\omega H_{ab}\left(\omega\right),$$

(23)

it is possible to simulate various topological phases of the Hamiltonian by electric circuitsTECNature ; ComPhys ; Hel ; Lu ; YLi ; EzawaTEC ; EzawaLCR ; EzawaSkin ; Garcia ; Hofmann ; EzawaMajo ; Tjunc . The relations between the parameters in the Hamiltonian and in the electric circuit are determined by this formula.

The circuit Laplacian is constructed as follows. To simulate the positive and negative hoppings in the Hamiltonian, we replace them with the capacitance $i\omega C$ and the inductance $1/i\omega L$, respectively. We note that $\sin k=(e^{ik}-e^{-ik})/2i$ represents an imaginary hopping in the tight-bind model. The imaginary hopping is realized by an operational amplifierHofmann .

We thus make the following replacements with respect to hoppings in the Hamiltonian to derive the circuit Laplacian: (i) $+X\rightarrow i\omega C_{X}$ for $X=t_{a}$ and $t_{b}$, where $C_{X}$ represents the capacitance whose value is $X$ [pF]. (ii) $-X\rightarrow 1/i\omega L_{X}$ for $X=t_{a}/2$ and $t_{b}/2$, where $L_{X}$ represents the inductance whose value is $X$ [$\mu$H].

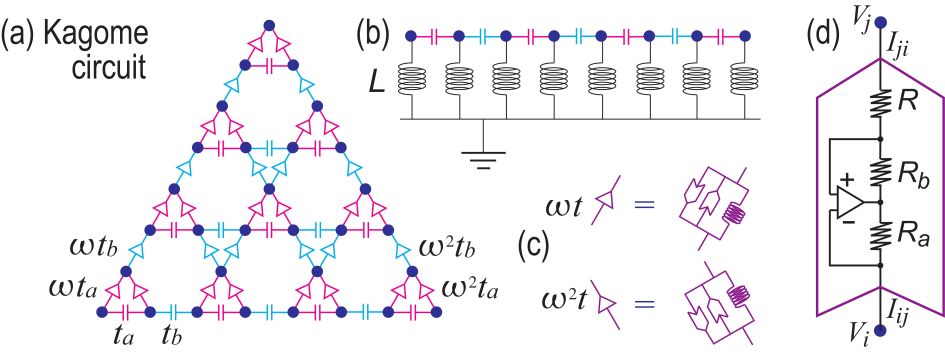
We explicitly study the breathing Kagome lattice described by (9), where the electric circuit is given by Fig.6(a). The Hamiltonian (9) is decomposed into

$$H=H_{1}+H_{2},$$

(24)

with

$$H_{1}=\left(\begin{array}[]{ccc}0&h_{12}&-\frac{1}{2}h_{13}\\ h_{12}^{\ast}&0&\omega^{2}h_{23}\\ -\frac{1}{2}h_{13}^{\ast}&\omega^{2}h_{23}^{\ast}&0\end{array}\right)$$

(25)

and

$$H_{2}=\frac{\sqrt{3}}{2}\left(\begin{array}[]{ccc}0&0&ih_{13}\\ 0&0&-ih_{23}\\ ih_{13}^{\ast}&-ih_{23}^{\ast}&0\end{array}\right),$$

(26)

where $H_{1}$ is Hermitian ($H_{1}^{\dagger}=H_{1}$), and $H_{2}$ is anti-Hermitian ($H_{2}^{\dagger}=-H_{2}$). It is necessary to construct imaginary hopping Hamiltonians

$$\frac{\sqrt{3}}{2}t_{a}\left(\begin{array}[]{ccc}0&0&i\\ 0&0&0\\ i&0&0\end{array}\right),$$

(27)

and

$$\frac{\sqrt{3}}{2}t_{a}\left(\begin{array}[]{ccc}0&0&0\\ 0&0&-i\\ 0&-i&0\end{array}\right)$$

(28)

for the magenta lines in Fig.6(a). They are constructed by using operational amplifiers and resistors.

We review a negative impedance converter with current inversion based on an operational amplifier with resistorsHofmann . The voltage-current relation for the operational amplifier circuit is given byHofmann

$$\left(\begin{array}[]{c}I_{1}\\ I_{2}\end{array}\right)=\frac{1}{R}\left(\begin{array}[]{cc}-\nu&\nu\\ -1&1\end{array}\right)\left(\begin{array}[]{c}V_{1}\\ V_{2}\end{array}\right),$$

(29)

with $\nu=R_{b}/R_{a}$, where $R$, $R_{a}$ and $R_{b}$ are the resistances in an operational amplifier: See Fig.6(d). We note that the resistors in the operational amplifier circuit are tuned to be $\nu=1$ in the literatureHofmann so that the system becomes Hermitian, where the corresponding Hamiltonian represents a spin-orbit interaction.

In this paper, we use two negative impedance converters parallelly connected with the opposite direction as in Fig.6(c). The circuit Laplacian due to these two converters is given by

$$\frac{1}{R}\left[\left(\begin{array}[]{cc}-\nu&\nu\\ -1&1\end{array}\right)+\left(\begin{array}[]{cc}1&-1\\ \nu&-\nu\end{array}\right)\right]=\frac{1}{R}\left(\begin{array}[]{cc}1-\nu&\nu-1\\ \nu-1&1-\nu\end{array}\right).$$

(30)

It corresponds to the Hamiltonian

$$H=\frac{1}{i\omega R}\left(\begin{array}[]{cc}1-\nu&\nu-1\\ \nu-1&1-\nu\end{array}\right).$$

(31)

It is embedded in the 3$\times$3 matrix as

$$H=\frac{1}{i\omega R}\left(\begin{array}[]{ccc}1-\nu&0&\nu-1\\ 0&0&0\\ \nu-1&0&1-\nu\end{array}\right),$$

(32)

where we have set

$$\frac{\sqrt{3}}{2}t_{a}=\frac{1-\nu}{\omega R}$$

(33)

with $\nu<1$, and

$$H=\frac{1}{i\omega R}\left(\begin{array}[]{ccc}0&0&0\\ 0&1-\nu&\nu-1\\ 0&\nu-1&1-\nu\end{array}\right),$$

(34)

where we have set

$$\frac{\sqrt{3}}{2}t_{a}=\frac{\nu-1}{\omega R}$$

(35)

with $\nu>1$. These matrices are different from Eqs.(27) and (28) by the diagonal terms. They are cancelled by adding a resistor (for $\nu>1$) or an operational amplifier (for $\nu<1$) with the amount of

$$\frac{1-\nu}{i\omega R}$$

(36)

between a lattice site and the ground.

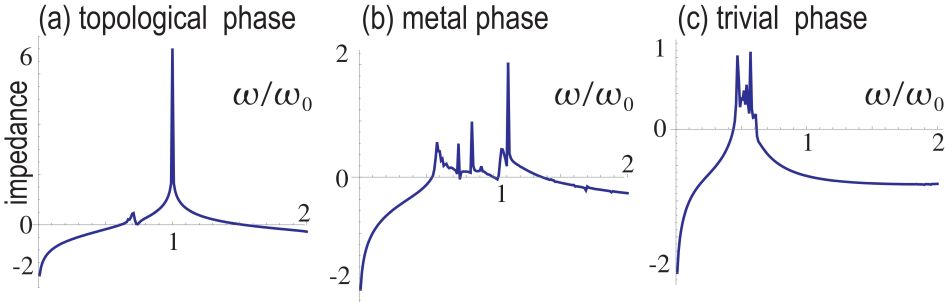
The zero-energy parafermion corner states are well observed by impedance resonance, which is definedHel by

$$Z_{ab}=V_{a}/I_{b}=G_{ab}$$

(37)

where $G=J^{-1}$ is the Green function. It diverges at the frequency where the admittance is zero ($J=0$). Taking the nodes $a$ and $b$ at two corners, we show the impedance in topological, metallic and trivial phases in Figs.7(a)$\sim$(c), respectively. A strong impedance peak is observed at the critical frequency $\omega_{0}\equiv 1/\sqrt{LC}$ only in the topological phase. It signals the emergence of zero-energy parafermion corner states.

It follows from Eq.(41) that only the zero-energy states form a set of degenerate states respecting $\mathbb{Z}_{4}$ clock symmetry. They are $\mathbb{Z}_{4}$ parafermion states. We denote them as $\left|\psi_{0}\right\rangle$, $\left|\psi_{1}\right\rangle$, $\left|\psi_{2}\right\rangle$ and $\left|\psi_{3}\right\rangle$. They are characterized by the properties

	$\displaystyle\tau\left|\psi_{0}\right\rangle$	$\displaystyle=\left|\psi_{1}\right\rangle,\quad\tau\left|\psi_{1}\right\rangle=\left|\psi_{2}\right\rangle,$		(42)
	$\displaystyle\tau\left|\psi_{2}\right\rangle$	$\displaystyle=\left|\psi_{3}\right\rangle,\quad\tau\left|\psi_{3}\right\rangle=\left|\psi_{0}\right\rangle,$		(43)
	$\displaystyle\sigma\left|\psi_{0}\right\rangle$	$\displaystyle=\left|\psi_{0}\right\rangle,\quad\sigma\left|\psi_{1}\right\rangle=i\left|\psi_{1}\right\rangle,$		(44)
	$\displaystyle\sigma\left|\psi_{2}\right\rangle$	$\displaystyle=-\left|\psi_{2}\right\rangle,\quad\sigma\left|\psi_{3}\right\rangle=-i\left|\psi_{3}\right\rangle,$		(45)

from which the matrix representations (3) and (4) follow. Then, the $\mathbb{Z}_{4}$ parafermion relations (5) are verified. Namely, it is necessary and sufficient to examine Eqs.(7) and (8) for a triplet set of zero-energy states in order to show that they are $\mathbb{Z}_{4}$ parafermions.

The quadrupole insulator has been proposed on the breathing square latticeScience . We propose a model possessing $\mathbb{Z}_{4}$ parafermions on the breathing square lattice. The bulk Hamiltonian is given by

$$H=\left(\begin{array}[]{cccc}0&f_{x}^{\ast}&0&if_{y}^{\ast}\\ -f_{x}&0&if_{y}^{\ast}&0\\ 0&-if_{y}&0&-f_{x}\\ -if_{y}&0&f_{x}^{\ast}&0\end{array}\right),$$

(46)

with

$$f_{x}=t_{a}+t_{b}e^{ik_{x}},\qquad f_{y}=t_{a}+t_{b}e^{ik_{y}},$$

(47)

where we have introduced two hopping parameters $t_{a}$ and $t_{b}$, which are shown in Fig.1(b4).

The Hamiltonian (46) has $\mathbb{Z}_{4}$ clock symmetryFend ,

$$\tau H\left(\mathbf{k}\right)\tau^{\dagger}=-iH\left(R\mathbf{k}\right),$$

(48)

where $R$ rotates the momentum by $90$ degrees as

	$\displaystyle R\left(k_{x},0\right)$	$\displaystyle=\left(0,-k_{y}\right),$		(49)
	$\displaystyle R\left(0,k_{y}\right)$	$\displaystyle=\left(k_{x},0\right),$		(50)

making the energy spectrum have $\mathbb{Z}_{4}$ symmetry in the complex plane as in Eq.(41).

The topological number is defined by (21), where $\psi_{0}$ is the eigen function of the Hamiltonian (46) for the bulk. We find the topological insulator phase for $\left|t_{a}/t_{b}\right|<1$, where $Q=1$ and the trivial insulator phase for $\left|t_{a}/t_{b}\right|>1$, where $Q=0$.

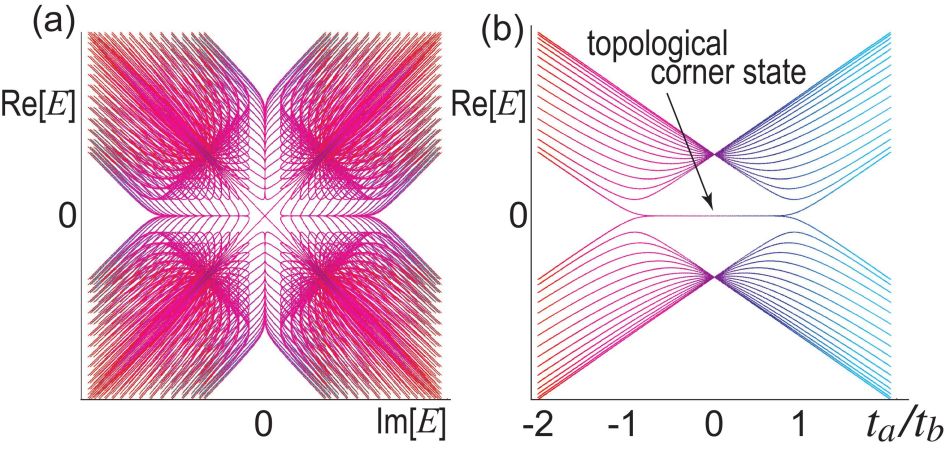
We calculate the energy spectrum in square geometry numerically. $C_{4v}$ symmetry is manifest as shown in Fig.8(a). It is because the square lattice respects $\mathbb{Z}_{4}$ clock symmetry. We also show the energy spectrum as a function of $t_{a}/t_{b}$ in Fig.8(b), where the emergence of the zero-energy states is manifest in the topological phase.

Consequently, the present model is a second-order topological insulator in the region $|t_{a}/t_{b}|<1$, being characterized by the emergence of topological corner states.

It is possible to obtain numerically the wave functions of the four corner states. We have confirmed that they satisfy the relations (7) and (8). Therefore, they are $\mathbb{Z}_{4}$ parafermions.

In the Hamiltonian (46), there are nonreciprocal hopping terms along the $x$ axis. Nonreciprocal hopping is constructed by a combination of operational amplifier and capacitorsNonR ,

$$\left(\begin{array}[]{c}I_{ij}\\ I_{ji}\end{array}\right)=i\omega C\left(\begin{array}[]{cc}-1&1\\ -1&1\end{array}\right)\left(\begin{array}[]{c}V_{i}\\ V_{j}\end{array}\right),$$

(51)

It corresponds to the Hamiltonian

$$H=C\left(\begin{array}[]{cc}-1&1\\ -1&1\end{array}\right).$$

(52)

We add an inductor or a capacitor in order to cancel the diagonal term.

We construct an electric circuit as shown in Fig.9(a), where the $x$ axis is constructed by Fig.9(c) and the $y$ axis is constructed by Fig.9(b).