Towards a reliable effective field theory of inflation
Abstract
We present the first quantum field theory model of inflation that is renormalizable in the matter sector, with a super-Hubble inflaton mass and sub-Planckian field excursions, which is thus technically natural and consistent with a high-energy completion within a theory of quantum gravity. This is done in the framework of warm inflation, where we show, for the first time, that strong dissipation can fully sustain a slow-roll trajectory with slow-roll parameters larger than unity in a way that is both theoretically and observationally consistent. The inflaton field corresponds to the relative phase between two complex scalar fields that collectively break a gauge symmetry, and dissipates its energy into scalar degrees of freedom in the warm cosmic heat bath. A discrete interchange symmetry protects the inflaton mass from large thermal corrections. We further show that the dissipation coefficient decreases with temperature in certain parametric regimes, which prevents a large growth of thermal inflaton fluctuations. We find, in particular, a very good agreement with the Planck legacy data for a simple quadratic inflaton potential, predicting a low tensor-to-scalar ratio .
keywords:
warm inflation , strong dissipation regime , model buildingBuilding a consistent quantum field theory (QFT) model for inflation [1] remains one of the great challenges of modern cosmology. On the one hand, the lack of empirical evidence for beyond the Standard Model particle physics motivates using a “bottom-up” approach, with as few novel ingredients as possible. On the other hand, the slow-roll inflationary dynamics is extremely sensitive to unknown physics at or even below the Planck scale, at least within the more conventional cold inflation paradigm. Given also that in cold inflation the simplest renormalizable scalar potentials and have been ruled out by observation [2], in the last few years inflation model building has become almost entirely “top-down”, based on some putative high-energy theory such as string theory. But this means that most models involve at least one and usually more major new features that have not been empirically confirmed, like supersymmetry/supergravity, special geometries, modified gravitational couplings, non-renormalizable operators, etc. We argue that this need not be the case, and that a reliable inflationary model may remain close to what has been empirically confirmed, while making predictions that are insensitive to the high-energy completion of the model.
One of the main problems in developing an inflation model is incorporating the light scalar inflaton field. Light scalars are extremely unnatural in any effective quantum field theory, since quantum corrections to their mass are quadratically divergent — a symptom of their sensitivity to new physics above the cut-off energy scale below which the theory can describe physical phenomena. The Higgs boson is the paramount example of this technical naturalness problem, better known as electroweak hierarchy problem, as its mass should naturally lie close to the Planck scale if no new particle states exist below the latter (see, e.g., Refs. [3, 4]). According to ’t Hooft [5], this is related to no new symmetries emerging for vanishing scalar masses, as opposed to, e.g., fermions, for which a chiral symmetry is gained in this limit.
An effective field theory of inflation based on general relativity or any classical gravity theory necessarily fails above the Planck scale, making the scalar potential sensitive to Planck-suppressed non-renormalizable operators that generically drive the inflaton mass towards values above the Hubble scale . This is the well-known ”eta-problem” in e.g. F-term supergravity and string theory (see, e.g., Ref. [6]), which are but examples of a more general inflationary naturalness problem, given that the cut-off scale for the effective field theory of inflation must necessarily lie above the Hubble scale, thus driving the inflaton mass to super-Hubble values, in tension with the slow-roll conditions.
Many have tried to overcome this issue by employing symmetries that could enforce cancellations between different quantum corrections to the inflaton’s mass. The best-known example is supersymmetry, where bosonic and fermionic quantum corrections cancel out, but supersymmetry is broken by the finite energy density during inflation, leaving corrections to the inflaton mass except, e.g., for some fine-tuned Kähler potentials. Global symmetries should be broken in quantum gravity, such that shift symmetries also cannot guarantee the flatness of the potential. This is inherently assumed in models with axion-like fields [7], as well as models with plateaux in the scalar potential, like Higgs inflation [8] and attractor models [9, 10], hence necessarily involving some degree of fine-tuning. Fine-tuning is, of course, undesirable in a theory that is supposed to dynamically generate the otherwise extremely fine-tuned initial conditions of standard cosmology.
There has also been an increased interest in the “swampland conjectures”, which pose stringent conditions on effective QFTs admitting a consistent quantum gravity completion, motivated by explicit string theory constructions [11, 12, 13]. In particular, these require that , , and more recently the transplankian censorship conjecture (TCC) on the lifetime of the de Sitter state [14, 15, 16]. While some inflationary scenarios can satisfy the first criteria, the last two are in tension with inflation slow-roll and expansion conditions.
In addition, inflationary predictions for CMB observables rely on the consistency of QFT in curved space-time, which is also not free from ambiguities, and for which we have no empirical guidance (see, e.g., Ref. [17, 18, 19, 20, 21, 22]). In particular, the form of the primordial spectrum of density perturbations on super-horizon scales depends on the particular choice of the Bunch-Davies vacuum, which is not unique and is, moreover, sensitive to transplanckian physics.
It had been understood early on in the development of warm inflation that, in the strong dissipative regime, all these crucial issues can be overcome [23, 24] (see also [26, 25, 27, 28, 29, 16]), but realizing this in a QFT model has proven very challenging. This letter develops the first such model, which within the matter sector, thus apart from the coupling to gravity, has only renormalizable matter field interactions and it is both theoretically and observationally consistent.
Dissipation is an inherent process to any system interacting with its environment. This has long been embodied in the warm inflation paradigm [30, 31, 32], where it is shown that interactions between the inflaton and particles in the cosmic bath necessarily lead to dissipative effects and associated particle production. Part of the inflaton’s energy is thus continuously transferred to the radiation bath, acting as a heat source that keeps it warm despite the supercooling effect of accelerated expansion.
Dissipative effects are encoded in the effective equation for the inflaton field,
| (1) |
alongside the sourced equation for the radiation energy density, ,
| (2) |
which can be derived from energy-momentum conservation or from an explicit computation of particle production rates. The dissipation coefficient can be computed from first principles using standard thermal field theory techniques, at least close to thermal equilibrium and in the regime where space-time curvature effects can be neglected (see Ref. [33] for a review).
In the slow-roll regime we then have , where is the dissipative ratio, and , provided that the slow-roll conditions, are satisfied, where and are the standard slow-roll parameters. Hence, if strong dissipation can be achieved throughout inflation, , the eta-problem is avoided and inflation can occur for inflaton masses above the Hubble scale [23, 24, 34]. It is also manifest that radiation is a sub-dominant component in the slow-roll regime, while it may come to dominate if becomes large at the end of inflation. In warm inflation there can thus be a smooth transition between inflation and the radiation era with no need for a separate reheating period [32] where the inflaton decays away, allowing e.g. for cosmic magnetic field generation [35], baryogenesis [36, 37] and inflaton dark matter [38] or dark energy [39, 40, 41].
Dissipative effects also lead to thermal inflaton fluctuations, according to the fluctuation-dissipation theorem [42, 23], which are sourced by a thermal noise term with variance , for . Thus, thermal fluctuations are generically larger than their quantum counterparts, such that primordial density fluctuations are generated by classical field perturbations. Moreover, in the strong dissipation regime, when , their amplitude freezes out before they become superhorizon [23], nevertheless producing a nearly scale-invariant spectrum of classical curvature perturbations [43, 44, 45]. Finally, such an enhancement of the primordial scalar perturbations typically leads to a lower inflationary energy scale and, therefore, to a lower tensor-to-scalar ratio, since gravitational wave production is unaffected by thermal effects below the Planck scale, as observed e.g. in [34, 46, 47].
Despite all these appealing features, consistently realizing warm inflation in QFT models has proved to be an enormous challenge [48, 49]. The inflaton typically gives a large mass to the particles it interacts with, similarly to the Higgs mechanism, and it is extremely hard to sustain sufficiently strong dissipative effects due to Boltzmann suppression. Even if this can be avoided, thermal backreaction generically reintroduces the eta-problem through thermal inflaton mass corrections up to dimensionless couplings 111Dissipative effects mediated by heavy virtual particles may be sufficient to sustain a thermal bath during inflation, but only at the expense of very large field multiplicities in supersymmetric models [50, 51, 52, 53], which may only be found in specific constructions in string theory [54] or possibly other scenarios with extra-dimensions [55]..
These problems were recently overcome by employing symmetry arguments, in a model akin to “Little Higgs” models for electroweak symmetry breaking and dubbed the “Warm Little Inflaton” (WLI) model [56]. In this model, the inflaton corresponds to the relative phase between two complex scalar fields, and , equally charged under a gauge symmetry, and which spontaneously break the latter. In the unitary gauge, the resulting vacuum manifold can be parametrized as
| (3) |
where is the symmetry breaking scale and is the gauge-invariant inflaton field222 We emphasize that the relative phase between two equally charged complex scalars does not change under gauge transformations, making our inflaton field distinct from other (pseudo-)Goldstone bosons such as axions used in natural inflaton [7] and string monodromy scenarios [57]. Note, in particular, that the symmetry does not, therefore, constrain the inflaton potential.. In the original model, these complex scalar fields were coupled to fermion fields through Yukawa interactions satisfying a discrete interchange symmetry , . This symmetry then ensures that if e.g. the fermion couples to the linear combination , then couples to . As a result, the fermions acquire masses which are trigonometric functions of the inflaton field,
| (4) |
where denotes the Yukawa coupling. These masses are thus bounded even if , and can be below the temperature during inflation. Moreover, the leading terms in the finite-temperature effective potential for ,
| (5) |
are independent of the inflaton field, thus eliminating the troublesome thermal corrections to the inflaton’s mass.
This model thus yields a consistent realization of warm inflation, and we have moreover shown that its observational predictions are in agreement with the Planck data for a quartic inflaton potential, [56, 58, 59, 60]. However, this agreement requires weak dissipation, , at the time the relevant CMB scales become super-horizon, about 60 e-folds before the end of inflation. Even though becomes large towards the end of the slow-roll regime, the eta-problem remains in this case.
This is an inherent consequence of the form of the dissipation coefficient in this scenario, . As originally shown in [44] and further analyzed numerically in [61], the temperature dependence of the dissipation coefficient necessarily leads to a coupling between inflaton fluctuations and perturbations in the radiation fluid that modifies the evolution of the former. In particular, for , this results in a substantial enhancement of inflaton fluctuations if . Physically, this is a consequence of dissipation increasing the temperature more in regions where it is already higher than average. If grows during inflation, as for the quartic potential, the primordial perturbation spectrum then becomes blue-tilted, which is ruled out by Planck [2].
If, however, , inflaton perturbations are damped. More concretely, the dimensionless curvature power spectrum in the strong dissipation regime, , is generically well approximated by:
| (6) |
where the last factor results from the interplay between the inflaton and radiation fluctuations, with and depending on at horizon-crossing. For instance, numerically solving the coupled system of perturbations as detailed in e.g. [61], we find for , while for yields . Thus, it is tantamount to find a model with a dissipation coefficient decreasing with temperature, such as too allow for strong dissipation in an observationally consistent way.
Here, the complex scalar fields and are coupled to two other complex scalars and in the thermal bath. The interactions have a renormalizable bi-quadratic form and, as in the original WLI model, satisfy the discrete interchange symmetry , . Without loss of generality, we may write the relevant interaction Lagrangian density in the form333Note that other possible interaction terms involving the gauge-invariant inflaton field may be neglected in a technically natural way.:
| (7) |
which is a straightforward generalization of the fermionic WLI model. With the vacuum parametrization in Eq. (3), the zero-temperature masses of the and fields are also given by Eq. (4), being bounded functions of the inflaton field . Most importantly, their leading contributions to the inflaton thermal mass also cancel out as in the fermionic case.
The main difference between coupling fermions or scalars to the inflaton field lies in the form of the dissipation coefficient, due to their different statistics at non-zero temperature, which will be fundamental to set the present model apart from previous model building realizations of warm inflation. For on-shell particle production, which is the dominant process for , the dissipation coefficient is given by
| (8) |
where is the Bose-Einstein distribution, , is the thermally corrected mass of the fields and their thermal decay width. These depend on interactions within the thermal bath, which we model as Yukawa interactions with light fermions (with appropriate charges) and scalar self-interactions,
| (9) |
Scalar self-interactions contribute only at two-loop order to the thermal decay width, and we focus on parametric regimes where the decay into light fermions is dominant. Both types of interactions contribute nevertheless to the thermal mass at the same order, yielding . The resulting dissipation coefficient is then given by:
| (10) |
where we have taken the average of the oscillatory terms for field excursions , yielding an average mass for both scalar fields.
Although the dissipation coefficient has, in general, a non-trivial temperature dependence, when is dominated by thermal effects we have and . This will then yield the required damping of inflaton fluctuations as discussed above.
Furthermore, the generalization of the result for the finite temperature effective potential (5), when now accounting for the interactions (7) and (9) and that can be easily obtained through the standard means [62, 63], gives
| (11) |
where is a renormalization scale, and accounts for the degrees of freedom of the thermal radiation bath, which, when considering the and fields, gives (for a non-thermalized inflaton), which is the value we have used in our numerical examples below. Adding the contribution of both scalars , from the form for their masses , which are still given by Eq. (4), we immediately see that the terms that would otherwise contribute as a quadratic thermal mass correction to the inflaton, , become actually independent of the inflaton field, as we have already anticipated above, and it is just a constant term contributing to the radiation energy density. Note also that this cancellation holds beyond the one-loop approximation for the effective potential, e.g., when resumming self-energy corrections, as the so-called ring diagrams [63], which corresponds to including the leading thermal corrections to the masses from the Yukawa and inter- and self-interactions given in Eq. (9), which gives the additional contribution to the effective potential,
| (12) |
where is the finite temperature corrected mass for the fields. Putting together the results from Eqs. (11) and (12), we are then left with only sub-leading Coleman-Weinberg and radiation terms, with an overall contribution to the inflaton potential given by
| (13) |
We also note that the renormalization scale dependence of the effective potential is, of course, an artifact of working at finite order in perturbation theory and, as standard in the literature, we can choose (besides of also absorbing the constant into the definition of inside the log term) in order to minimize this dependence at horizon-crossing when the relevant observables are measured. Since and with an explicit potential for the inflaton, one always has during inflation as long as the slow-roll conditions are satisfied. The dependence on Eq. (13) are only through highly oscillatory (and bounded terms), since , for the relevant parameters of the model (see below). We have nevertheless explicitly checked and confirmed numerically that these oscillatory terms do not significantly affect the dynamics of inflation. This result is also very much analogous to the one found in the earlier model introduced in Ref. [56].
Let us consider the simplest scenario with a quadratic inflaton potential444Strictly speaking the interchange symmetry implies , but for we may take for simplicity., , since as we discussed above there are no symmetries protecting the inflaton from acquiring at least a Hubble-scale mass. The slow-roll equations can be integrated analytically for this potential when , and from the form of the primordial perturbation spectrum at strong dissipation in Eq. (6) we obtain for the scalar spectral index . While this actually gives a too red-tilted spectrum for e-folds of inflation, the zero-temperature mass of the fields generically leads to non-negligible deviations from that make the spectrum more blue-tilted.
We have then solved numerically the background and perturbation equations for both the inflaton field and radiation fluid with the full form of the dissipation coefficient in Eq. (10), following the procedure described in detail in e.g. [61]. In Fig. 1, we show the observational predictions in the interesting parametric regime where the mass of the fields is dominated by thermal effects. To obtain the results shown in Fig. 1, the product appearing in the dissipation coefficient (10) was kept fixed in the value and we also considered for definiteness. Variations in these parameters tend only to shift the values of with respect to the ones seen in Fig. 1. We have controlled the magnitude of the dissipation ratio through the ratio of the coupling constants in the prefactor of (10). We have also fixed the amplitude of the curvature power spectrum as , consistent with the Planck legacy data [2]. This allows one to obtain the mass parameter of the inflaton potential in a consistent way for each value of , using, e.g., Eq. (6).
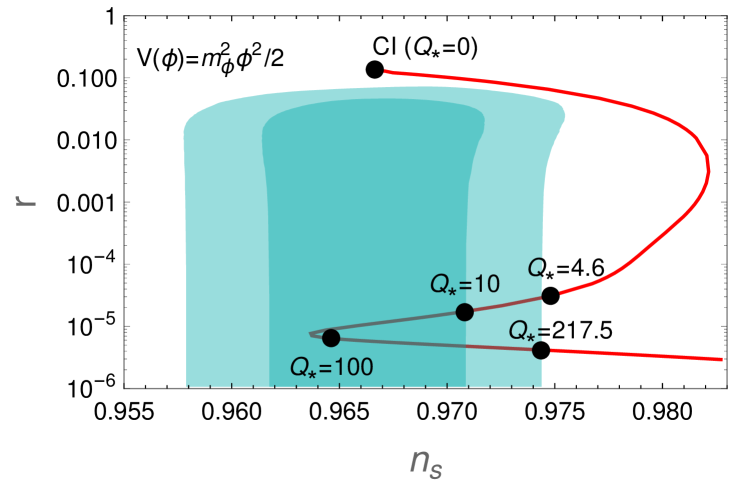
As one can see in Fig. 1, for dissipation ratio values at horizon-crossing , the spectral tilt is too large, exceeding the corresponding cold inflation prediction. This is due to the thermal nature of inflaton fluctuations and the increase of the dissipative ratio during inflation. As we increase , however, the spectrum becomes more red-tilted as a consequence of the damping induced by the stronger coupling with radiation fluctuations near horizon-crossing. For , we in fact find a spectral tilt in very good agreement with the Planck C.L. results and a low tensor-to-scalar ratio , as typical of warm inflation models. In particular, for the case of and parameters shown in Fig. 1, we have that and .
In this strong dissipative regime, primordial non-Gaussianity should generically be at the level [64], and the dedicated searches by the Planck collaboration for the warm shape of the bispectrum [65, 66] allow for (95% C.L.). Our scenario thus lies comfortably within these limits. We have, moreover, made a preliminary analysis of non-Gaussianity for the particular form of the dissipation coefficient in the present scenario, using the numerical codes developed in [67], obtaining for .
Scenarios with within this model typically require larger values of the coupling and hence larger zero-temperature masses. This results in larger deviations from and thus to a less efficient damping of inflaton fluctuations and a more blue-tilted spectrum.
The agreement with observational data for is, however, our most significant result, since in this regime the slow-roll parameters throughout inflation. The slow-roll trajectory is thus fully sustained by the dissipative friction, yielding a consistent effective field theory for inflation with , 555The swampland distance conjecture states that a tower of massive states become exponentially light as , where , for (see e.g. [68]). In our model, we obtain at horizon-crossing for in the observationally viable window, which does not constitute a significant mass suppression, such that these states may consistently be integrated out in the effective field theory. and . We illustrate the dynamical evolution of the inflaton-radiation system in a representative case with in Fig. 2, where it is manifest that inflation can consistently occur with a super-Hubble inflaton mass and a sub-Planckian field excursion. As explained above, for the choice of parameters for Fig. 1, given the value of , we have the full set of explicit model parameters that reproduces Fig. 2 as given by , , , and the couplings in (9) given by , and we have also chosen .
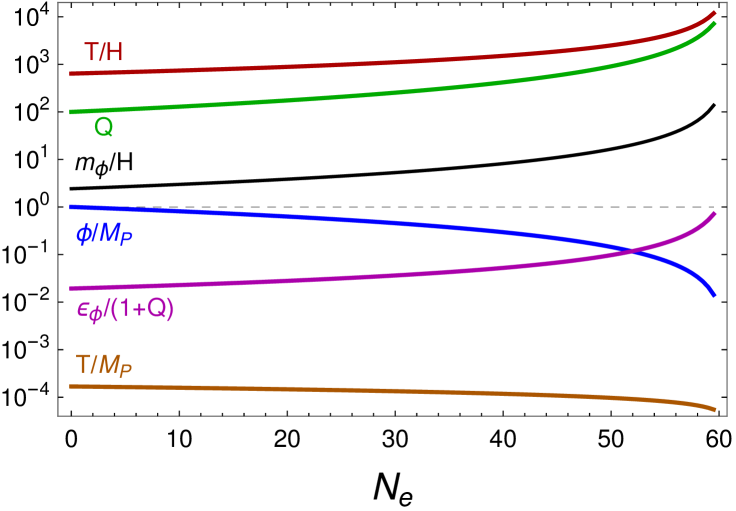
In the example shown in Fig. 2, it is also manifest that strong dissipation can be sustained for a whole of 60 e-folds of inflation, maintaining a slowly decreasing temperature666Although not explicitly shown, we have checked that the average thermal decay width of the fields exceeds the Hubble rate, keeping the fields and their decay products close to equilibrium, and that sub-leading corrections to the finite-temperature effective potential, which give oscillatory contributions to the slow-roll parameters, have no significant effect at both the background and perturbation levels. . The temperature always satisfies , ensuring that the fields are relativistic, yet keeping the gauge symmetry broken throughout inflation777The exact critical temperature of the phase transition depends on the self-couplings of the and scalar fields which we have not specified, but we can assume within order unity factors.. The radiation abundance is in the slow-roll regime for , leading to a smooth transition to the radiation-dominated era. We note that this model also allows for a much shorter inflation period, successfully setting all the large-scale observables, along the lines of the recently proposed multi-stage warm inflation solution to the TCC [28, 16].
Hence, this letter shows, for the first time, that slow-roll inflation does not require an unnaturally light inflaton scalar field, within a simple renormalizable QFT with a quadratic scalar potential, that is robust against corrections from unknown new physics, particularly Planck-suppressed non-renormalizable operators. Because this model is renormalizable in the conventional sense, it is fully decoupled from the unknown high energy physics. Moreover, the spectrum of primordial density fluctuations is fully described by classical thermal fluctuations of the inflaton field that freeze out before becoming super-horizon, being free of ambiguities in the choice of the quantum vacuum state, which could moreover be sensitive to unknown transplanckian effects.
This model is very simple, involving only a few scalar and fermion fields, interacting via renormalizable couplings in the perturbative regime. Moreover, the fundamental scale , in line with the weak gravity conjecture and with minimal reliance on unknown gravitational physics at the Planck scale. The model involves only a symmetry alongside a discrete symmetry, which are ubiquitous in Nature. Like the Standard Model, this is truly a low energy model that can make reliable predictions without any knowledge of the high-energy completion. In particular, this model does not need supersymmetry to control quantum corrections, although a supersymmetric extension could easily be implemented should this be a feature of quantum gravity.
It had been pointed out early in the development of warm inflation [23, 24] that in the strong dissipation regime it is possible for to solve the eta-problem, with sub-Planckian field excursions, thus solving the swampland criteria well before they were stated. It had also been understood that increasing dissipation lowers the energy scale of inflation and hence the tensor-to-scalar ratio [23, 34] in line with subsequent CMB observations. However, the challenge has been to find a theoretically and observationally consistent model displaying all these appealing features. This work has achieved this by obtaining a QFT model of inflation that is reliable in this respect, involving only a few fields, being free of the fine-tuning and ambiguities that generically plague the more conventional cold scenario.
Acknowledgments
A. B. is partially supported by STFC. M.B.-G. is partially supported by MINECO grant FIS2016-78198-P and Junta de Andalucía grant SOMM/17/6104/UGR and FQM101. R.O.R. is partially supported by research grants from Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Grant No. 302545/2017-4, and Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ), Grant No. E-26/202.892/2017. J. G. R. is supported by the FCT Grant No. IF/01597/2015, the CFisUC strategic project No. UID/FIS/04564/2019 and partially by the FCT project PTDC/FIS-OUT/28407/2017 and ENGAGE SKA (POCI-01-0145-FEDER-022217).
References
- [1] A. A. Starobinsky, A New Type of Isotropic Cosmological Models Without Singularity, Phys. Lett. B 91, 99 (1980); L. Z. Fang, Entropy Generation in the Early Universe by Dissipative Processes Near the Higgs’ Phase Transitions, Phys. Lett. 95B, 154 (1980); K. Sato, First Order Phase Transition of a Vacuum and Expansion of the Universe, Mon. Not. Roy. Astron. Soc. 195, 467 (1981); A. H. Guth, The Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems, Phys. Rev. D23, 347 (1981); A. Albrecht, P. J. Steinhardt, Cosmology for Grand Unified Theories with Radiatively Induced Symmetry Breaking, Phys. Rev. Lett. 48, 1220 (1982); A. D. Linde, A New Inflationary Universe Scenario: A Possible Solution of the Horizon, Flatness, Homogeneity, Isotropy and Primordial Monopole Problems, Phys. Lett. B108, 389 (1982).
- [2] Y. Akrami et al. [Planck Collaboration], Planck 2018 results. X. Constraints on inflation, arXiv:1807.06211 [astro-ph.CO].
- [3] J. D. Wells, Higgs naturalness and the scalar boson proliferation instability problem, Synthese 194, no. 2, 477 (2017) [arXiv:1603.06131 [hep-ph]].
- [4] N. Craig, Lecture notes for Progress in Theoretical Physics Summer School (IAS, Princeton, 2017), https://pitp.ias.edu/sites/pitp/files/craig.pdf
- [5] ’t Hooft, G. (1980), in Recent Developments in Gauge Theory (New York: Plenum Press, 1980).
- [6] D. Baumann and L. McAllister, Inflation and String Theory, arXiv:1404.2601 [hep-th].
- [7] K. Freese, J. A. Frieman and A. V. Olinto, Natural inflation with pseudo - Nambu-Goldstone bosons, Phys. Rev. Lett. 65, 3233 (1990).
- [8] F. L. Bezrukov and M. Shaposhnikov, The Standard Model Higgs boson as the inflaton, Phys. Lett. B 659, 703 (2008) [arXiv:0710.3755 [hep-th]].
- [9] E. D. Stewart, Inflation, supergravity and superstrings, Phys. Rev. D 51, 6847 (1995) [hep-ph/9405389].
- [10] R. Kallosh, A. Linde and D. Roest, Superconformal Inflationary -Attractors, JHEP 1311, 198 (2013) [arXiv:1311.0472 [hep-th]].
- [11] H. Ooguri and C. Vafa, On the Geometry of the String Landscape and the Swampland, Nucl. Phys. B 766, 21 (2007) [hep-th/0605264].
- [12] G. Obied, H. Ooguri, L. Spodyneiko and C. Vafa, De Sitter Space and the Swampland, arXiv:1806.08362 [hep-th].
- [13] H. Ooguri, E. Palti, G. Shiu, and C. Vafa, Distance and de Sitter conjectures on the Swampland, Phys. Lett. B 788, 180 (2019), arXiv:1810.05506.
- [14] A. Bedroya and C. Vafa, Trans-Planckian Censorship and the Swampland, arXiv:1909.11063 [hep-th].
- [15] A. Bedroya, R. Brandenberger, M. Loverde and C. Vafa, Trans-Planckian Censorship and Inflationary Cosmology, arXiv:1909.11106 [hep-th].
- [16] A. Berera, S. Brahma and J. R. Calderón, Role of trans-Planckian modes in cosmology, [arXiv:2003.07184 [hep-th]].
- [17] C. Armendariz-Picon and E. A. Lim, Vacuum choices and the predictions of inflation, JCAP 0312, 006 (2003) [hep-th/0303103].
- [18] I. Agullo, J. Navarro-Salas, G. J. Olmo and L. Parker, Reexamination of the Power Spectrum in De Sitter Inflation, Phys. Rev. Lett. 101, 171301 (2008) [arXiv:0806.0034 [gr-qc]].
- [19] R. Durrer, G. Marozzi and M. Rinaldi, On Adiabatic Renormalization of Inflationary Perturbations, Phys. Rev. D 80, 065024 (2009) [arXiv:0906.4772 [astro-ph.CO]].
- [20] G. Marozzi, M. Rinaldi and R. Durrer, On infrared and ultraviolet divergences of cosmological perturbations, Phys. Rev. D 83, 105017 (2011) [arXiv:1102.2206 [astro-ph.CO]].
- [21] M. Beneke and P. Moch, On ”dynamical mass” generation in Euclidean de Sitter space, Phys. Rev. D 87, 064018 (2013) [arXiv:1212.3058 [hep-th]].
- [22] M. Bastero-Gil, A. Berera, N. Mahajan and R. Rangarajan, Power spectrum generated during inflation, Phys. Rev. D 87, no. 8, 087302 (2013) [arXiv:1302.2995 [astro-ph.CO]].
- [23] A. Berera, Warm inflation at arbitrary adiabaticity: A Model, an existence proof for inflationary dynamics in quantum field theory, Nucl. Phys. B 585, 666 (2000) [hep-ph/9904409].
- [24] A. Berera, Warm inflation solution to the eta problem, PoS AHEP 2003, 069 (2003) [hep-ph/0401139].
- [25] M. Motaharfar, V. Kamali and R. O. Ramos, Warm inflation as a way out of the swampland, Phys. Rev. D 99, no. 6, 063513 (2019) [arXiv:1810.02816 [astro-ph.CO]].
- [26] S. Das, Warm Inflation in the light of Swampland Criteria, Phys. Rev. D 99, no. 6, 063514 (2019) [arXiv:1810.05038 [hep-th]].
- [27] V. Kamali, M. Motaharfar and R. O. Ramos, Warm brane inflation with an exponential potential: a consistent realization away from the swampland, Phys. Rev. D 101, no.2, 023535 (2020) [arXiv:1910.06796 [gr-qc]].
- [28] A. Berera and J. R. Calderón, Trans-Planckian censorship and other swampland bothers addressed in warm inflation, Phys. Rev. D 100, no.12, 123530 (2019) [arXiv:1910.10516 [hep-ph]].
- [29] R. Brandenberger, V. Kamali and R. O. Ramos, Strengthening the de Sitter swampland conjecture in warm inflation, [arXiv:2002.04925 [hep-th]].
- [30] A. Berera, Warm inflation, Phys. Rev. Lett. 75, 3218 (1995) [astro-ph/9509049].
- [31] A. Berera, Thermal properties of an inflationary universe, Phys. Rev. D 54, 2519 (1996) [hep-th/9601134].
- [32] A. Berera, Interpolating the stage of exponential expansion in the early universe: A Possible alternative with no reheating, Phys. Rev. D 55, 3346 (1997) [hep-ph/9612239].
- [33] A. Berera, I. G. Moss and R. O. Ramos, Warm Inflation and its Microphysical Basis, Rept. Prog. Phys. 72, 026901 (2009) [arXiv:0808.1855 [hep-ph]].
- [34] M. Bastero-Gil and A. Berera, Warm inflation model building, Int. J. Mod. Phys. A 24, 2207 (2009) [arXiv:0902.0521 [hep-ph]].
- [35] A. Berera, T. W. Kephart and S. D. Wick, GUT cosmic magnetic fields in a warm inflationary universe, Phys. Rev. D 59, 043510 (1999) [hep-ph/9809404].
- [36] R. H. Brandenberger and M. Yamaguchi, Spontaneous baryogenesis in warm inflation, Phys. Rev. D 68, 023505 (2003) [hep-ph/0301270].
- [37] M. Bastero-Gil, A. Berera, R. O. Ramos and J. G. Rosa, Warm baryogenesis, Phys. Lett. B 712, 425 (2012) [arXiv:1110.3971 [hep-ph]].
- [38] J. G. Rosa and L. B. Ventura, Warm Little Inflaton becomes Cold Dark Matter, Phys. Rev. Lett. 122, no. 16, 161301 (2019) [arXiv:1811.05493 [hep-ph]].
- [39] K. Dimopoulos and L. Donaldson-Wood, Warm quintessential inflation, Phys. Lett. B 796, 26-31 (2019) [arXiv:1906.09648 [gr-qc]].
- [40] J. G. Rosa and L. B. Ventura, Warm Little Inflaton becomes Dark Energy, Phys. Lett. B 798, 134984 (2019) [arXiv:1906.11835 [hep-ph]].
- [41] G. B. Lima and R. O. Ramos, Unified early and late Universe cosmology through dissipative effects in steep quintessential inflation potential models, Phys. Rev. D 100, no.12, 123529 (2019) [arXiv:1910.05185 [astro-ph.CO]].
- [42] A. Berera and L. -Z. Fang, Thermally induced density perturbations in the inflation era, Phys. Rev. Lett. 74, 1912 (1995) [astro-ph/9501024].
- [43] L. M. Hall, I. G. Moss and A. Berera, Scalar perturbation spectra from warm inflation, Phys. Rev. D 69, 083525 (2004) [astro-ph/0305015].
- [44] C. Graham and I. G. Moss, Density fluctuations from warm inflation, JCAP 0907, 013 (2009) [arXiv:0905.3500 [astro-ph.CO]].
- [45] R. O. Ramos and L. A. da Silva, Power spectrum for inflation models with quantum and thermal noises, JCAP 1303, 032 (2013) [arXiv:1302.3544 [astro-ph.CO]].
- [46] Y. F. Cai, J. B. Dent and D. A. Easson, Warm DBI Inflation, Phys. Rev. D 83, 101301 (2011) [arXiv:1011.4074 [hep-th]].
- [47] S. Bartrum, M. Bastero-Gil, A. Berera, R. Cerezo, R. O. Ramos and J. G. Rosa, The importance of being warm (during inflation), Phys. Lett. B 732, 116 (2014) [arXiv:1307.5868 [hep-ph]].
- [48] A. Berera, M. Gleiser and R. O. Ramos, Strong dissipative behavior in quantum field theory, Phys. Rev. D 58, 123508 (1998) [arXiv:hep-ph/9803394 [hep-ph]].
- [49] J. Yokoyama and A. D. Linde, Is warm inflation possible?, Phys. Rev. D 60, 083509 (1999) [arXiv:hep-ph/9809409 [hep-ph]].
- [50] A. Berera and R. O. Ramos, Construction of a robust warm inflation mechanism, Phys. Lett. B 567, 294 (2003) [hep-ph/0210301].
- [51] I. G. Moss and C. Xiong, Dissipation coefficients for supersymmetric inflationary models, hep-ph/0603266.
- [52] M. Bastero-Gil, A. Berera and R. O. Ramos, Dissipation coefficients from scalar and fermion quantum field interactions, JCAP 1109, 033 (2011) [arXiv:1008.1929 [hep-ph]].
- [53] M. Bastero-Gil, A. Berera, R. O. Ramos and J. G. Rosa, General dissipation coefficient in low-temperature warm inflation, JCAP 1301, 016 (2013) [arXiv:1207.0445 [hep-ph]].
- [54] M. Bastero-Gil, A. Berera and J. G. Rosa, Warming up brane-antibrane inflation, Phys. Rev. D 84, 103503 (2011) [arXiv:1103.5623 [hep-th]].
- [55] T. Matsuda, Particle production and dissipation caused by the Kaluza-Klein tower, Phys. Rev. D 87, no. 2, 026001 (2013) [arXiv:1212.3030 [hep-th]].
- [56] M. Bastero-Gil, A. Berera, R. O. Ramos and J. G. Rosa, Warm Little Inflaton, Phys. Rev. Lett. 117, no. 15, 151301 (2016) [arXiv:1604.08838 [hep-ph]].
- [57] L. McAllister, E. Silverstein and A. Westphal, Gravity Waves and Linear Inflation from Axion Monodromy, Phys. Rev. D 82, 046003 (2010) [arXiv:0808.0706 [hep-th]].
- [58] M. Benetti and R. O. Ramos, Warm inflation dissipative effects: predictions and constraints from the Planck data, Phys. Rev. D 95, no. 2, 023517 (2017) [arXiv:1610.08758 [astro-ph.CO]].
- [59] M. Bastero-Gil, S. Bhattacharya, K. Dutta and M. R. Gangopadhyay, Constraining Warm Inflation with CMB data, JCAP 1802, no. 02, 054 (2018) [arXiv:1710.10008 [astro-ph.CO]].
- [60] M. Bastero-Gil, A. Berera, R. Hernández-Jiménez and J. G. Rosa, Dynamical and observational constraints on the Warm Little Inflaton scenario, Phys. Rev. D 98, no. 8, 083502 (2018) [arXiv:1805.07186 [astro-ph.CO]].
- [61] M. Bastero-Gil, A. Berera and R. O. Ramos, Shear viscous effects on the primordial power spectrum from warm inflation, JCAP 1107, 030 (2011) [arXiv:1106.0701 [astro-ph.CO]].
- [62] L. Dolan and R. Jackiw, Symmetry Behavior at Finite Temperature, Phys. Rev. D 9, 3320 (1974).
- [63] J. I. Kapusta and C. Gale, Finite-Temperature Field Theory: Principles and Applications, (Cambridge University Press, Cambridge, England, 2006).
- [64] I. G. Moss and C. Xiong, Non-Gaussianity in fluctuations from warm inflation, JCAP 0704, 007 (2007) [astro-ph/0701302].
- [65] P. A. R. Ade et al. [Planck Collaboration], Planck 2015 results. XVII. Constraints on primordial non-Gaussianity, Astron. Astrophys. 594, A17 (2016) [arXiv:1502.01592 [astro-ph.CO]].
- [66] Y. Akrami et al. [Planck Collaboration], Planck 2018 results. IX. Constraints on primordial non-Gaussianity, arXiv:1905.05697 [astro-ph.CO].
- [67] M. Bastero-Gil, A. Berera, I. G. Moss and R. O. Ramos, Theory of non-Gaussianity in warm inflation, JCAP 1412, no. 12, 008 (2014) [arXiv:1408.4391 [astro-ph.CO]].
- [68] E. Palti, The Swampland: Introduction and Review, Fortsch. Phys. 67, no. 6, 1900037 (2019) [arXiv:1903.06239 [hep-th]].